The Applications of Soft Computing Methods for Seepage Modeling: A Review
Abstract
:1. Introduction
- i.
- Estimation of quantity of seepage
- ii.
- Definition of the flow domain
- iii.
- Stability analysis
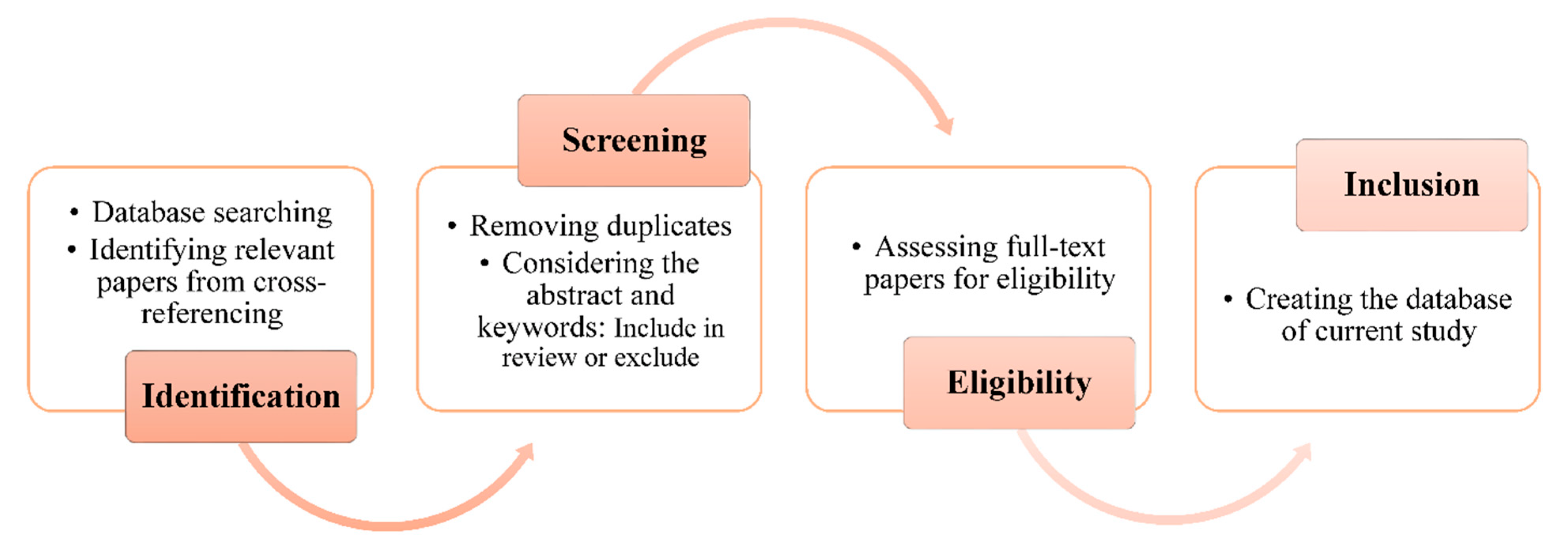
2. Methodology of Survey
3. Governing Equation
4. Soft Computing Methods for Seepage Modeling
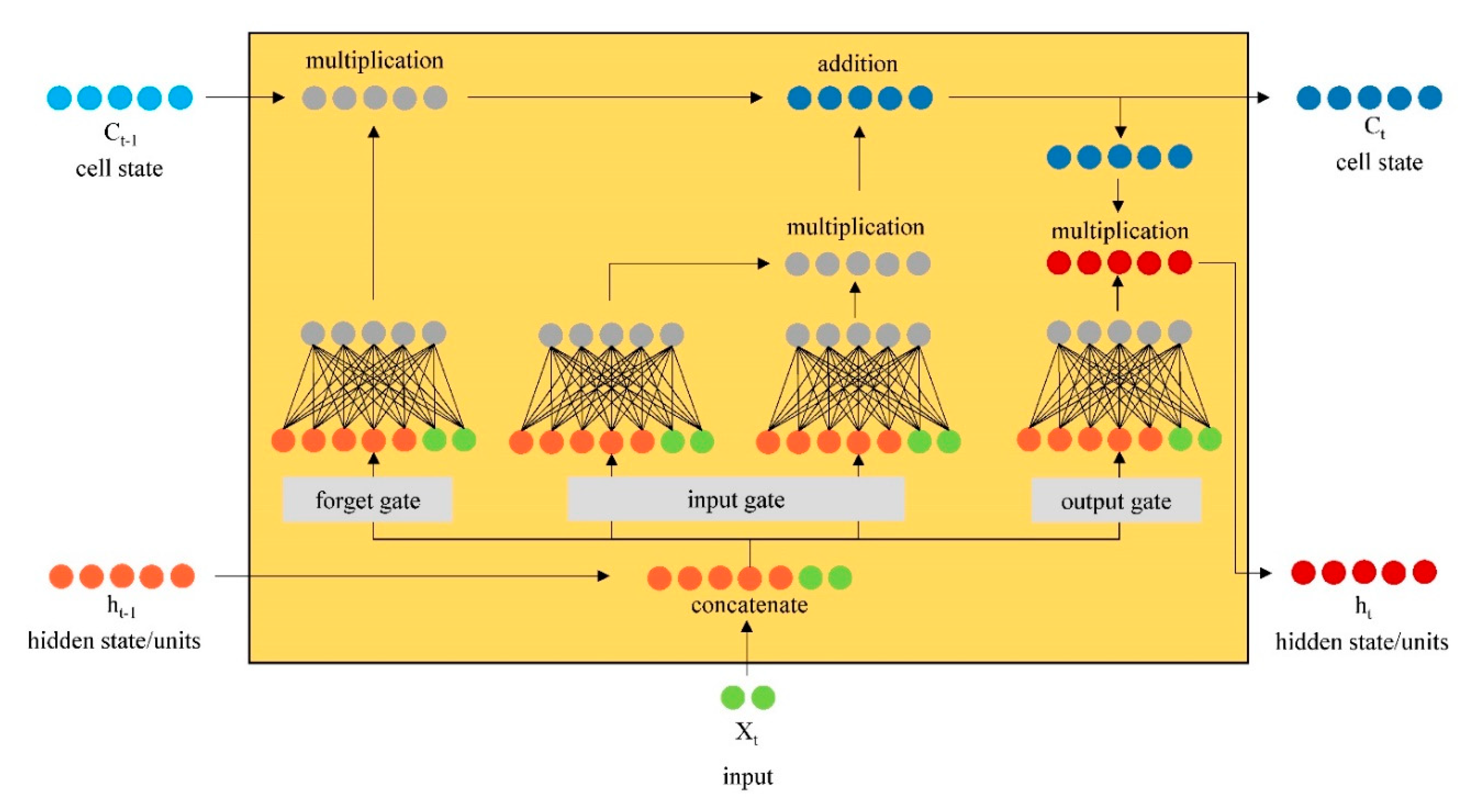
4.1. Artificial Neural Networks (ANN) for Seepage Modeling
4.2. Adaptive Neuro-Fuzzy Inference System (ANFIS) and Fuzzy-Based Models for Seepage Modeling
4.3. Support Vector Machine (SVM) for Seepage Modeling
4.4. Genetic Programming (GP) for Seepage Modeling
4.5. Deep Learning Methods for Seepage Modeling
4.6. Other Soft Computing Methods for Seepage Modeling
4.7. Hybrid Soft Computing Techniques for Seepage Modeling
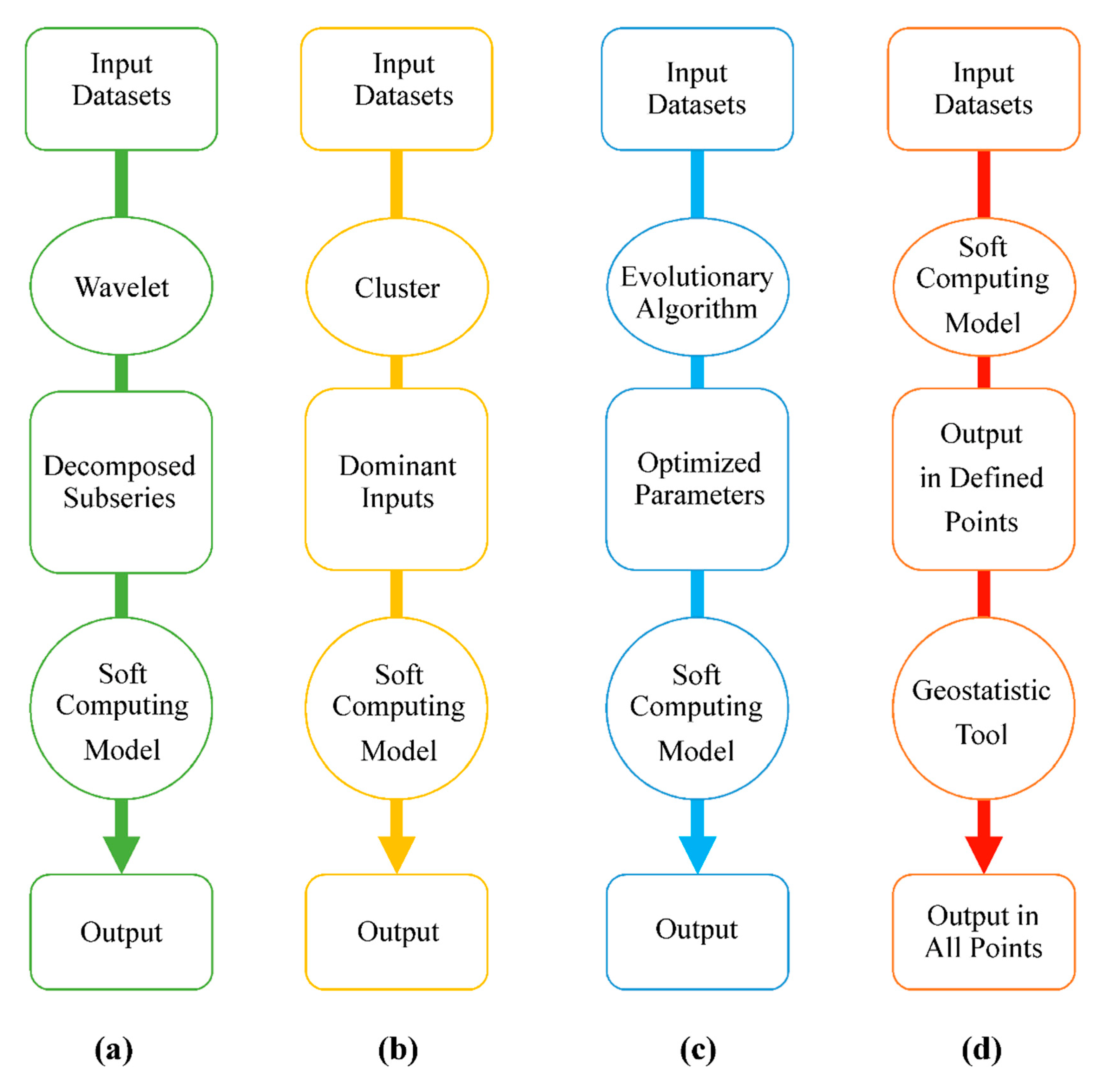
4.7.1. Wavelet-Soft Computing Methods
4.7.2. Cluster-Based Soft Computing Methods
4.7.3. Evolutionary-Based Methods
4.7.4. Soft Computing Geostatistic-Based Methods
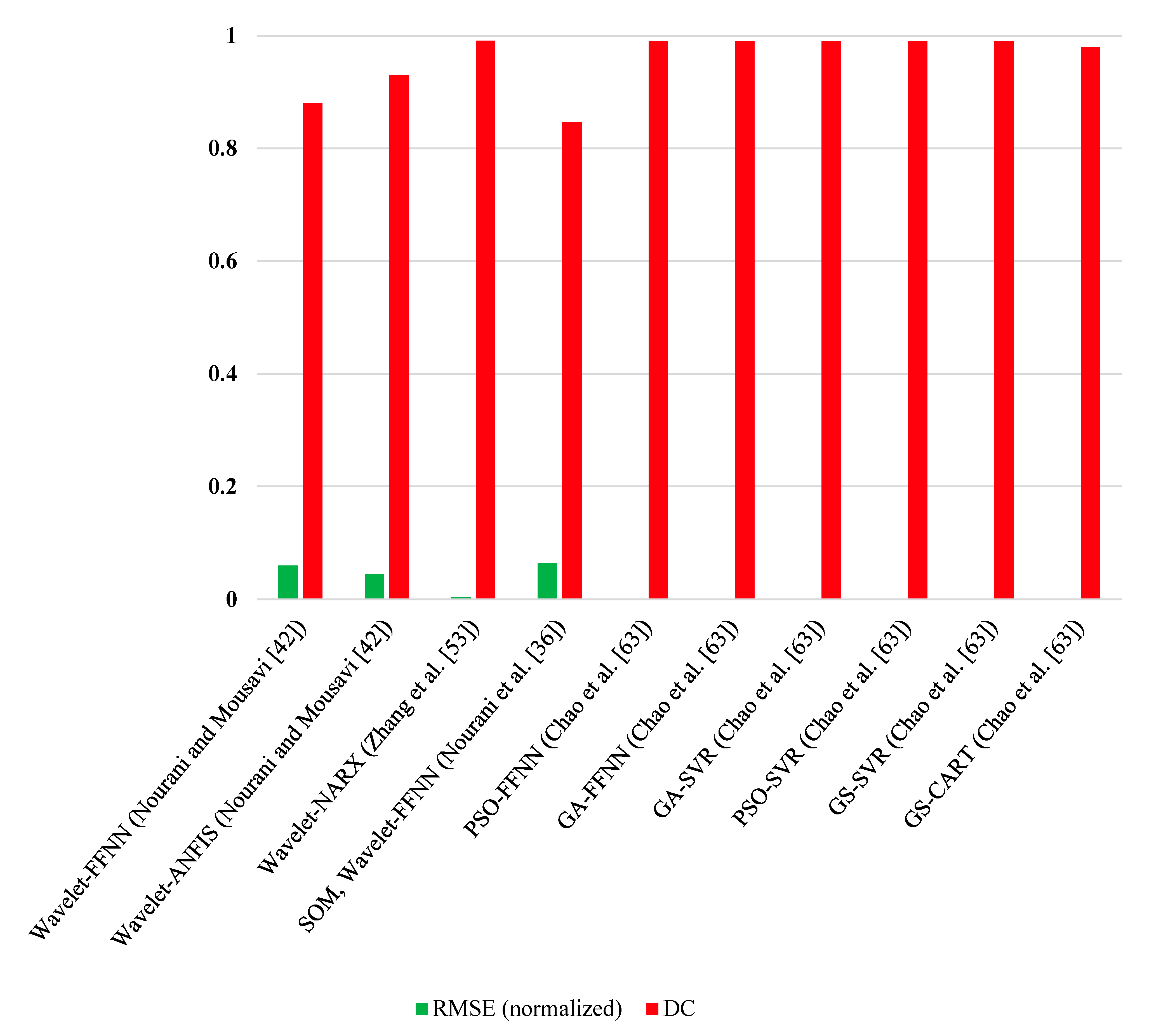
5. Comparative Performance Analysis and Discussion
6. Challenges and Future Direction
7. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kemper, K.E. Groundwater—from development to management. Hydrogeol. J. 2004, 12, 3–5. [Google Scholar] [CrossRef]
- Chen, W.; Li, Y.; Tsangaratos, P.; Shahabi, H.; Ilia, I.; Xue, W.; Bian, H. Groundwater spring potential mapping using artificial intelligence approach based on kernel logistic regression, random forest, and alternating decision tree models. Appl. Sci. 2020, 10, 425. [Google Scholar] [CrossRef] [Green Version]
- Curran, S.R.; de Sherbinin, A. Completing the picture: The challenges of bringing “consumption” into the population–environment equation. Popul. Environ. 2004, 26, 107–131. [Google Scholar] [CrossRef]
- Al-Janabi, A.M.S.; Ghazali, A.H.; Ghazaw, Y.M.; Afan, H.A.; Al-Ansari, N.; Yaseen, Z.M. Experimental and numerical analysis for earth-fill dam seepage. Sustainability 2020, 12, 2490. [Google Scholar] [CrossRef] [Green Version]
- Cedergren, H.R. Seepage, Drainage, and Flow Nets, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Harr, M.E. Groundwater and Seepage; Dover Publications: New York, NY, USA, 1991. [Google Scholar]
- Nourani, V.; Sharghi, E.; Aminfar, M.H. Integrated ANN model for earthfill dams seepage analysis: Sattarkhan Dam in Iran. Artif. Intell. Res. 2012, 1, 22–37. [Google Scholar] [CrossRef] [Green Version]
- Solomatine, D.P. Data-driven modeling and computational intelligence methods in hydrology. In Encyclopedia of Hydrological Sciences; Anderson, M.G., McDonnell, J.J., Eds.; Wiley: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Nourani, V. A review on applications of artificial intelligence-based models to estimate suspended sediment load. Int. J. Soft Comput. Eng. 2014, 3, 121–127. [Google Scholar]
- Shen, C. A transdisciplinary review of deep learning research and its relevance for water resources scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Maier, H.R.; Jain, A.; Dandy, G.C.; Sudheer, K.P. Methods used for the development of neural networks for the prediction of water resource variables in river systems: Current status and future directions. Environ. Modell. Software 2010, 25, 891–909. [Google Scholar] [CrossRef]
- Wu, W.; Dandy, G.C.; Maier, H.R. Protocol for developing ANN models and its application to the assessment of the quality of the ANN model development process in drinking water quality modelling. Environ. Modell. Softw. 2014, 54, 108–127. [Google Scholar] [CrossRef]
- Mehr, A.D.; Nourani, V.; Kahya, E.; Hrnjica, B.; Sattar, A.M.; Yaseen, Z.M. Genetic programming in water resources engineering: A state-of-the-art review. J. Hydrol. 2018, 566, 643–667. [Google Scholar] [CrossRef]
- Nourani, V.; Baghanam, A.H.; Adamowski, J.; Kisi, O. Applications of hybrid wavelet–artificial intelligence models in hydrology: A review. J. Hydrol. 2014, 514, 358–377. [Google Scholar] [CrossRef]
- Rajaee, T.; Ebrahimi, H.; Nourani, V. A review of the artificial intelligence methods in groundwater level modeling. J. Hydrol. 2019, 572, 336–351. [Google Scholar] [CrossRef]
- Haghbin, M.; Sharafati, A.; Dixon, B.; Kumar, V. Application of soft computing models for simulating nitrate contamination in groundwater: Comprehensive review, assessment and future opportunities. Arch. Comput. Methods Eng. 2020, 28, 3569–3591. [Google Scholar] [CrossRef]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef]
- Shaffril, H.A.M.; Samsuddin, S.F.; Samah, A.A. The ABC of systematic literature review: The basic methodological guidance for beginners. Qual. Quant. 2020, 55, 1319–1346. [Google Scholar] [CrossRef]
- Mengist, W.; Soromessa, T.; Legese, G. Method for conducting systematic literature review and meta-analysis for environmental science research. MethodsX 2020, 7, 100777. [Google Scholar] [CrossRef]
- Snyder, H. Literature review as a research methodology: An overview and guidelines. J. Bus. Res. 2019, 104, 333–339. [Google Scholar] [CrossRef]
- Balkhair, K.S. Aquifer parameters determination for large diameter wells using neural network approach. J. Hydrol. 2002, 265, 118–128. [Google Scholar] [CrossRef]
- Lallahem, S.; Mania, J.; Hani, A.; Najjar, Y. On the use of neural networks to evaluate groundwater levels in fractured media. J. Hydrol. 2005, 307, 92–111. [Google Scholar] [CrossRef]
- Lin, G.F.; Chen, G.R. An improved neural network approach to the determination of aquifer parameters. J. Hydrol. 2006, 316, 281–289. [Google Scholar] [CrossRef]
- Parkin, G.; Birkinshaw, S.J.; Younger, P.L.; Rao, Z.; Kirk, S. A numerical modelling and neural network approach to estimate the impact of groundwater abstractions on river flows. J. Hydrol. 2007, 339, 15–28. [Google Scholar] [CrossRef]
- Samani, N.; Gohari-Moghadam, M.; Safavi, A.A. A simple neural network model for the determination of aquifer parameters. J. Hydrol. 2007, 340. [Google Scholar] [CrossRef]
- Hwang, S.; Guevarra, I.F.; Yu, B. Slope failure prediction using a decision tree: A case of engineered slopes in South Korea. Eng. Geol. 2009, 104, 126–134. [Google Scholar] [CrossRef]
- Bashi-Azghadi, S.N.; Kerachian, R.; Bazargan-Lari, M.R.; Solouki, K. Characterizing an unknown pollution source in groundwater resources systems using PSVM and PNN. Expert Syst. Appl. 2010, 37, 7154–7161. [Google Scholar] [CrossRef]
- Kurtulus, B.; Razack, M. Modeling daily discharge responses of a large karstic aquifer using soft computing methods: Artificial neural network and neuro-fuzzy. J. Hydrol. 2010, 381, 101–111. [Google Scholar] [CrossRef]
- Sun, J.; Zhao, Z.; Zhang, Y. Determination of three dimensional hydraulic conductivities using a combined analytical/neural network model. Tunn. Undergr. Space Technol. 2011, 26, 310–319. [Google Scholar] [CrossRef]
- He, J.; Chen, S.H.; Shahrour, I. A revised solution of equivalent permeability tensor for discontinuous fractures. J. Hydrodyn. Ser. B 2012, 24, 711–717. [Google Scholar] [CrossRef]
- Kurtulus, B.; Flipo, N. Hydraulic head interpolation using anfis—model selection and sensitivity analysis. Comput. Geosci. 2012, 38, 43–51. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.W.; Sethi, R. Artificial neural network simulation of hourly groundwater levels in a coastal aquifer system of the Venice lagoon. Eng. Appl. Artif. Intell. 2012, 25, 1670–1676. [Google Scholar] [CrossRef] [Green Version]
- Fallah-Mehdipour, E.; Haddad, O.B.; Mariño, M.A. Prediction and simulation of monthly groundwater levels by genetic programming. J. Hydro-Environ. Res. 2013, 7, 253–260. [Google Scholar] [CrossRef]
- Mohanty, S.; Jha, M.K.; Kumar, A.; Panda, D.K. Comparative evaluation of numerical model and artificial neural network for simulating groundwater flow in Kathajodi–Surua Inter-basin of Odisha, India. J. Hydrol. 2013, 495, 38–51. [Google Scholar] [CrossRef]
- Tapoglou, E.; Karatzas, G.P.; Trichakis, I.C.; Varouchakis, E.A. A spatio-temporal hybrid neural network-Kriging model for groundwater level simulation. J. Hydrol. 2014, 519, 3193–3203. [Google Scholar] [CrossRef]
- Chang, J.; Wang, G.; Mao, T. Simulation and prediction of suprapermafrost groundwater level variation in response to climate change using a neural network model. J. Hydrol. 2015, 529, 1211–1220. [Google Scholar] [CrossRef]
- Kaunda, R.B. A neural network assessment tool for estimating the potential for backward erosion in internal erosion studies. Comput. Geotech. 2015, 69. [Google Scholar] [CrossRef]
- Liu, Q.Q.; Li, J.C. Effects of water seepage on the stability of soil-slopes. Procedia IUTAM 2015, 17, 29–39. [Google Scholar] [CrossRef] [Green Version]
- Nourani, V.; Alami, M.T.; Vousoughi, F.D. Wavelet-entropy data pre-processing approach for ANN-based groundwater level modeling. J. Hydrol. 2015, 524, 255–269. [Google Scholar] [CrossRef]
- Zhou, C.B.; Liu, W.; Chen, Y.F.; Hu, R.; Wei, K. Inverse modeling of leakage through a rockfill dam foundation during its construction stage using transient flow model, neural network and genetic algorithm. Eng. Geol. 2015, 187, 183–195. [Google Scholar] [CrossRef]
- Chang, F.J.; Chang, L.C.; Huang, C.W.; Kao, I.F. Prediction of monthly regional groundwater levels through hybrid soft-computing techniques. J. Hydrol. 2016, 541, 965–976. [Google Scholar] [CrossRef]
- Nourani, V.; Mousavi, S. Spatiotemporal groundwater level modeling using hybrid artificial intelligence-meshless method. J. Hydrol. 2016, 536, 10–25. [Google Scholar] [CrossRef]
- Shahrokhabadi, S.; Vahedifard, F.; Yarahmadian, S. Integration of Thiele Continued Fractions and the method of fundamental solutions for solving unconfined seepage problems. Comput. Math. Appl. 2016, 71, 1479–1490. [Google Scholar] [CrossRef]
- Hong, J.M.; Chen, Y.F.; Liu, M.M.; Zhou, C.B. Inverse modelling of groundwater flow around a large-scale underground cavern system considering the excavation-induced hydraulic conductivity variation. Comput. Geotech. 2017, 81, 346–359. [Google Scholar] [CrossRef]
- Xiang, Y.; Fu, S.Y.; Zhu, K.; Yuan, H.; Fang, Z.Y. Seepage safety monitoring model for an earth rock dam under influence of high-impact typhoons based on particle swarm optimization algorithm. Water Sci. Eng. 2017, 10, 70–77. [Google Scholar] [CrossRef]
- Ghose, D.; Das, U.; Roy, P. Modeling response of runoff and evapotranspiration for predicting water table depth in arid region using dynamic recurrent neural network. Groundw. Sustain. Dev. 2018, 6, 263–269. [Google Scholar] [CrossRef]
- Wang, S.W.; Xu, Y.L.; Gu, C.S.; Bao, T.F. Monitoring models for base flow effect and daily variation of dam seepage elements considering time lag effect. Water Sci. Eng. 2018, 11, 344–354. [Google Scholar] [CrossRef]
- Belmokre, A.; Mihoubi, M.K.; Santillan, D. Seepage and dam deformation analyses with statistical models: Support vector regression machine and random forest. Procedia Struct. Integr. 2019, 17, 698–703. [Google Scholar] [CrossRef]
- De Granrut, M.; Simon, A.; Dias, D. Artificial neural networks for the interpretation of piezometric levels at the rock-concrete interface of arch dams. Eng. Struct. 2019, 178, 616–634. [Google Scholar] [CrossRef]
- Moghaddam, H.K.; Moghaddam, H.K.; Kivi, Z.R.; Bahreinimotlagh, M.; Alizadeh, M.J. Developing comparative mathematic models, BN and ANN for forecasting of groundwater levels. Groundw. Sustain. Dev. 2019, 9, 100237. [Google Scholar] [CrossRef]
- Rohmat, F.I.; Labadie, J.W.; Gates, T.K. Deep learning for compute-efficient modeling of BMP impacts on stream-aquifer exchange and water law compliance in an irrigated river basin. Environ. Modell. Softw. 2019, 122, 104529. [Google Scholar] [CrossRef]
- Sharghi, E.; Nourani, V.; Behfar, N.; Tayfur, G. Data pre-post processing methods in AI-based modeling of seepage through earthen dams. Measurement 2019, 147, 106820. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X.; Niu, J.; Hu, B.X.; Soltanian, M.R.; Qiu, H.; Yang, L. Prediction of groundwater level in seashore reclaimed land using wavelet and artificial neural network-based hybrid model. J. Hydrol. 2019, 577, 123948. [Google Scholar] [CrossRef]
- Bao, J.; Li, L.; Redoloza, F. Coupling ensemble smoother and deep learning with generative adversarial networks to deal with non-Gaussianity in flow and transport data assimilation. J. Hydrol. 2020, 590, 125443. [Google Scholar] [CrossRef]
- Chen, J.; Tang, P.; Rakstad, T.; Patrick, M.; Zhou, X. Augmenting a deep-learning algorithm with canal inspection knowledge for reliable water leak detection from multispectral satellite images. Adv. Eng. Inf. 2020, 46, 101161. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F. Groundwater level prediction in Apulia region (Southern Italy) using NARX neural network. Environ. Res. 2020, 190, 110062. [Google Scholar] [CrossRef]
- Liu, J.; Gu, J.; Li, H.; Carlson, K.H. Machine learning and transport simulations for groundwater anomaly detection. J. Comput. Appl. Math. 2020, 380, 112982. [Google Scholar] [CrossRef]
- Panahi, M.; Sadhasivam, N.; Pourghasemi, H.R.; Rezaie, F.; Lee, S. Spatial prediction of groundwater potential mapping based on convolutional neural network (CNN) and support vector regression (SVR). J. Hydrol. 2020, 588, 125033. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, L.; Zhou, J.Q.; Wang, C. A new method for determining the hydraulic aperture of rough rock fractures using the support vector regression. Eng. Geol. 2020, 271, 105618. [Google Scholar] [CrossRef]
- Tao, K.; Zheng, W. An anthropomorphic fuzzy model for the time-spatial assessment of sandstone seepage damage. Autom. Constr. 2020, 109, 102989. [Google Scholar] [CrossRef]
- Yu, Q.; Xiong, Z.; Du, C.; Dai, Z.; Soltanian, M.R.; Soltanian, M.; Yin, S.; Liu, W.; Liu, C.; Wang, C.; et al. Identification of rock pore structures and permeabilities using electron microscopy experiments and deep learning interpretations. Fuel 2020, 268, 117416. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, G.; Huang, X.; Chen, K.; Hou, J.; Zhou, J. Development of a surrogate method of groundwater modeling using gated recurrent unit to improve the efficiency of parameter auto-calibration and global sensitivity analysis. J. Hydrol. 2021, 598, 125726. [Google Scholar] [CrossRef]
- Chao, Z.; Ma, G.; He, K.; Wang, M. Investigating low-permeability sandstone based on physical experiments and predictive modeling. Undergr. Space 2021, 6, 364–378. [Google Scholar] [CrossRef]
- Chen, Y.F.; Zeng, J.; Shi, H.; Wang, Y.; Hu, R.; Yang, Z.; Zhou, C.B. Variation in hydraulic conductivity of fractured rocks at a dam foundation during operation. J. Rock Mech. Geotech. Eng. 2021, 13, 351–367. [Google Scholar] [CrossRef]
- Daolun, L.; Luhang, S.; Wenshu, Z.; Xuliang, L.; Jieqing, T. Physics-constrained deep learning for solving seepage equation. J. Pet. Sci. Eng. 2021, 206, 109046. [Google Scholar] [CrossRef]
- Rehamnia, I.; Benlaoukli, B.; Jamei, M.; Karbasi, M.; Malik, A. Simulation of seepage flow through embankment dam by using a novel extended Kalman filter based neural network paradigm: Case study of Fontaine Gazelles Dam, Algeria. Measurement 2021, 176, 109219. [Google Scholar] [CrossRef]
- Zhang, H.; Song, Z.; Peng, P.; Sun, Y.; Ding, Z.; Zhang, X. Research on seepage field of concrete dam foundation based on artificial neural network. Alexandria Eng. J. 2021, 60. [Google Scholar] [CrossRef]
- Wei, X.; Zhang, L.; Yang, H.Q.; Zhang, L.; Yao, Y.P. Machine learning for pore-water pressure time-series prediction: Application of recurrent neural networks. Geosci. Front. 2021, 12, 453–467. [Google Scholar] [CrossRef]
- Celia, M.A.; Bouloutas, E.T.; Zarba, R.L. A general mass-conservative numerical solution for the unsaturated flow equation. Water Resour. Res. 1990, 26, 1483–1496. [Google Scholar] [CrossRef]
- Fu, J.F.; Sheng, J.I.N. A study on unsteady seepage flow through dam. J. Hydrodyn. Ser. B 2009, 21, 499–504. [Google Scholar] [CrossRef]
- Abbot, J.; Marohasy, J. Application of artificial neural networks to rainfall forecasting in Queensland, Australia. Adv. Atmos. Sci. 2012, 29, 717–730. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Richards, K.S.; Reddy, K.R. Kinetic energy method for predicting initiation of backward erosion in earthen dams and levees. Environ. Eng. Geosci. 2014, 20, 85–97. [Google Scholar] [CrossRef]
- Dernoncourt, F. Introduction to Fuzzy Logic; Massachusetts Institute of Technology: Cambridge, MA, USA, 2013. [Google Scholar]
- Jang, J.S. ANFIS: Adaptive-network-based fuzzy inference system. IEEE Trans. Syst. Man Cybern. 1993, 23, 665–685. [Google Scholar] [CrossRef]
- Vapnik, V.N. Statistical Learning Theory; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Vapnik, V.N. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Radhika, Y.; Shashi, M. Atmospheric temperature prediction using support vector machines. Int. J. Comput. Theory Eng. 2009, 1, 55–58. [Google Scholar] [CrossRef] [Green Version]
- Sivapragasam, C.; Maheswaran, R.; Venkatesh, V. Genetic programming approach for flood routing in natural channels. Hydrol. Processes 2008, 22, 623–628. [Google Scholar] [CrossRef]
- Hinton, G.E.; Salakhutdinov, R.R. Reducing the dimensionality of data with neural networks. Science 2006, 313, 504–507. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bengio, Y.; Courville, A.; Vincent, P. Representation learning: A review and new perspectives. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1798–1828. [Google Scholar] [CrossRef] [PubMed]
- Raghu, M.; Poole, B.; Kleinberg, J.; Ganguli, S.; Sohl-Dickstein, J. On the Expressive Power of Deep Neural Networks. In Proceedings of the 34th International Conference on Machine Learning, Sydney, NSW, Australia, 6–11 August 2017; Volume 70, pp. 2847–2854. [Google Scholar]
- Eldan, R.; Shamir, O. The Power of Depth for Feedforward Neural Networks. In Proceedings of the 29th Annual Conference on Learning Theory, New York, NY, USA, 23–26 June 2016; Volume 49, pp. 907–940. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Nourani, V.; Behfar, N. Multi-Station Runoff-Sediment Modeling Using Seasonal LSTM Models. J. Hydrol. 2021, 601, 126672. [Google Scholar] [CrossRef]
- Wunsch, A.; Liesch, T.; Broda, S. Groundwater level forecasting with artificial neural networks: A comparison of long short-term memory (LSTM), convolutional neural networks (CNNs), and non-linear autoregressive networks with exogenous input (NARX). Hydrol. Earth Syst. Sci. 2021, 25, 1671–1687. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. Mech. Syst. Sig. Process. 2021, 151, 107398. [Google Scholar] [CrossRef]
- Alsumaiei, A.A. A nonlinear autoregressive modeling approach for forecasting groundwater level fluctuation in urban aquifers. Water 2020, 12, 820. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Breiman, L.; Friedman, J.H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees; Routledge: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Daubechies, I. The wavelet transform, time–frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961. [Google Scholar] [CrossRef] [Green Version]
- Vantas, K.; Sidiropoulos, E.; Loukas, A. Robustness spatiotemporal clustering and trend detection of rainfall erosivity density in Greece. Water 2019, 11, 1050. [Google Scholar] [CrossRef] [Green Version]
- Hartigan, J.A. Clustering Algorithms; John Wiley & Sons: New York, NY, USA, 1975. [Google Scholar]
- Bowden, G.J.; Dandy, G.C.; Maier, H.R. Input determination for neural network models in water resources applications. Part 1—background and methodology. J. Hydrol. 2005, 301, 75–92. [Google Scholar] [CrossRef]
- Michalewicz, Z. Heuristic methods for evolutionary computation techniques. J. Heuristics 1996, 1, 177–206. [Google Scholar] [CrossRef] [Green Version]
- Hadipour, A.; Khoshand, A.; Rahimi, K.; Kamalan, H.R. Groundwater Level Forecasting by Application of Artificial Neural Network Approach: A Case Study in Qom Plain, Iran. J. Hydrosci. Environ. 2019, 3, 30–34. [Google Scholar] [CrossRef]
- Al-Fugara, A.K.; Ahmadlou, M.; Al-Shabeeb, A.R.; AlAyyash, S.; Al-Amoush, H.; Al-Adamat, R. Spatial mapping of groundwater springs potentiality using grid search-based and genetic algorithm-based support vector regression. Geocarto Int. 2020. [Google Scholar] [CrossRef]
- Farzin, S.; Singh, V.P.; Karami, H.; Farahani, N.; Ehteram, M.; Kisi, O.; Allawi, M.F.; Mohd, N.S.; El-Shafie, A. Flood routing in river reaches using a three-parameter Muskingum model coupled with an improved bat algorithm. Water 2018, 10, 1130. [Google Scholar] [CrossRef] [Green Version]
- Seifi, A.; Ehteram, M.; Soroush, F. Uncertainties of instantaneous influent flow predictions by intelligence models hybridized with multi-objective shark smell optimization algorithm. J. Hydrol. 2020, 587, 124977. [Google Scholar] [CrossRef]
- Ibrahim, I.A.; Khatib, T. A novel hybrid model for hourly global solar radiation prediction using random forests technique and firefly algorithm. Energy Convers. Manag. 2017, 138, 413–425. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J., Jr. Evaluating the use of goodness-of-fit measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Mateo-Lázaro, J.; Sánchez-Navarro, J.A.; García-Gil, A.; Edo-Romero, V.; Castillo-Mateo, J. Modelling and layout of drainage-levee devices in river sections. Eng. Geol. 2016, 214, 11–19. [Google Scholar] [CrossRef]






| No. | Authors Name | Publication Year | Employed Methods | Objectives | Journal Name | No. Citations |
|---|---|---|---|---|---|---|
| 1 | Balkhair [21] | 2002 | Feed forward neural network (FFNN) | Transmissivity and storage coefficient estimation | Journal of Hydrology | 57 |
| 2 | Lallahem et al. [22] | 2005 | Multilayer perception (MLP) | Groundwater levels estimation | Journal of Hydrology | 95 |
| 3 | Lin and Chen [23] | 2006 | FFNN | Transmissivity and storage coefficient estimation | Journal of Hydrology | 33 |
| 4 | Parkin et al. [24] | 2007 | FFNN | River–aquifer system modeling | Journal of Hydrology | 45 |
| 5 | Samani et al. [25] | 2007 | FFNN | Transmissivity and storage coefficient estimation | Journal of Hydrology | 82 |
| 6 | Hwang et al. [26] | 2009 | decision tree | Extract the rules of slope failure | Engineering Geology | 21 |
| 7 | Bashi-Azghadi et al. [27] | 2010 | Non-dominated sorting genetic algorithm-II (NSGA-II), Probabilistic support vector machine (PSVM), Probabilistic neural network (PNN) | Seepage detection from an unknown pollution source | Expert Systems with Applications | 49 |
| 8 | Kurtulus and Razack [28] | 2010 | FFNN, Adaptive neuro-fuzzy inference system (ANFIS) | Flow path estimation | Journal of Hydrology | 60 |
| 9 | Sun et al. [29] | 2011 | Backpropagation neural network (BPNN) | 3D hydraulic conductivity estimation | Tunnelling and Underground Space Technology | 31 |
| 10 | He et al. [30] | 2012 | FFNN | Dam foundation seepage simulation | Journal of Hydrodynamics, Ser. B | 5 |
| 11 | Kurtulus and Flipo [31] | 2012 | ANFIS | Hydraulic head estimation | Computers & Geosciences | 21 |
| 12 | Taormina et al. [32] | 2012 | FFNN | Groundwater levels estimation | Engineering Applications of Artificial Intelligence | 277 |
| 13 | Fallah-Mehdipour et al. [33] | 2013 | ANFIS, genetic programming (GP) | Obtaining the governing groundwater flow equations | Journal of Hydro-Environment Research | 95 |
| 14 | Mohanty et al. [34] | 2013 | FFNN | Groundwater flow estimation | Journal of Hydrology | 61 |
| 15 | Tapoglou et al. [35] | 2014 | FFNN, Fuzzy logic (FL), Kriging | Groundwater levels estimation | Journal of Hydrology | 48 |
| 16 | Chang et al. [36] | 2015 | FFNN | Groundwater levels estimation | Journal of Hydrology | 47 |
| 17 | Kaunda [37] | 2015 | FFNN | Internal erosion estimation | Computers and Geotechnics | 6 |
| 18 | Liu and Li [38] | 2015 | Genetic algorithm (GA) | Stability analysis and water-seepage modeling | Procedia IUTAM | 19 |
| 19 | Nourani et al. [39] | 2015 | Self-organizing map (SOM), Wavelet-FFNN, FFNN | Multi-scale patterns discovering of groundwater level | Journal of Hydrology | 72 |
| 20 | Zhou et al. [40] | 2015 | FFNN-GA | Transient groundwater flow estimation in dam foundation | Engineering Geology | 39 |
| 21 | Chang et al. [41] | 2016 | SOM, Nonlinear autoregressive model with exogenous inputs (NARX), Kriging | Groundwater levels estimation | Journal of Hydrology | 56 |
| 22 | Nourani and Mousavi [42] | 2016 | Wavelet-FFNN, Wavelet-ANFIS | Groundwater flow estimation | Journal of Hydrology | 36 |
| 23 | Shahrokhabadi et al. [43] | 2016 | Particle swarm optimization (PSO) | Solve the unconfined seepage problem | Computers & Mathematics with Applications | 3 |
| 24 | Hong et al. [44] | 2017 | FFNN, GA | Anisotropic hydraulic conductivity estimation | Computers and Geotechnics | 14 |
| 25 | Xiang et al. [45] | 2017 | PSO | Earth rock dam seepage modeling | Water Science and Engineering | 10 |
| 26 | Ghose et al. [46] | 2018 | Recurrent neural network (RNN) | Groundwater levels estimation | Groundwater for Sustainable Development | 15 |
| 27 | Wang et al. [47] | 2018 | Support vector regression (SVR) | Concrete gravity dam seepage modeling | Water Science and Engineering | 10 |
| 28 | Belmokre et al. [48] | 2019 | SVR | Dam seepage modeling | Procedia Structural Integrity | 1 |
| 29 | De Granrut et al. [49] | 2019 | FFNN | Uplift force analysis of an arch dam | Engineering Structures | 13 |
| 30 | Moghaddam et al. [50] | 2019 | FFNN, Bayesian network (BN) | Groundwater levels estimation | Groundwater for Sustainable Development | 17 |
| 31 | Rohmat et al. [51] | 2019 | Deep neural network (DNN), FFNN | Stream–aquifer exchange and water rights modeling | Environmental Modelling & Software | 3 |
| 32 | Sharghi et al. [52] | 2019 | FFNN, ANFIS, SVR | Earthfill dam seepage modeling | Measurement | 6 |
| 33 | Zhang et al. [53] | 2019 | Nonlinear input–output network (NIO), NARX, Wavelet-NARX | Groundwater levels estimation | Journal of Hydrology | 12 |
| 34 | Bao et al. [54] | 2020 | Generative adversarial network (GAN), Ensemble smoother with multiple data assimilation (ES-MDA) | Hydraulic head estimation | Journal of Hydrology | 1 |
| 35 | Chen et al. [55] | 2020 | Physics-guided neural network (PGNN), Convolutional neural network (CNN) | Water leak detection in canal sections | Advanced Engineering Informatics | 4 |
| 36 | Di Nunno and Granata [56] | 2020 | NARX | Groundwater levels estimation | Environmental Research | 13 |
| 37 | Liu et al. [57] | 2020 | SVR | Groundwater anomaly identification | Journal of Computational and Applied Mathematics | 4 |
| 38 | Panahi et al. [58] | 2020 | SVR, CNN | Developing the groundwater potential maps | Journal of Hydrology | 26 |
| 39 | Sun et al. [59] | 2020 | PSO-SVR | Determining the hydraulic aperture of rough rock fractures | Engineering Geology | 4 |
| 40 | Tao and Zheng [60] | 2020 | adaptive fuzzy identification | Seepage damage identification | Automation in Construction | 0 |
| 41 | Yu et al. [61] | 2020 | CNN | Pore characteristics analysis | Fuel | 8 |
| 42 | Chen et al. [62] | 2021 | Gated recurrent unit (GRU)-PSO | Groundwater flow estimation | Journal of Hydrology | 1 |
| 43 | Chao et al. [63] | 2021 | FFNN, SVR, Classification and regression tree (CART), Extreme learning machine (ELM), Grid search (GS)-CART, PSO-SVR, GA-SVR, GS-SVR, GA-FFNN, PSO-FFNN | Sandstone permeability estimation | Underground Space | 0 |
| 44 | Chen et al. [64] | 2021 | FFNN, GA | Permeability modeling of the foundation of a high arch dam | Journal of Rock Mechanics and Geotechnical Engineering | 0 |
| 45 | Daolun et al. [65] | 2021 | Signpost neural network (SNN) | Solving the seepage physics-constrained PDE | Journal of Petroleum Science and Engineering | 0 |
| 46 | Rehamnia et al. [66] | 2021 | FFNN | Embankment dam seepage modeling | Measurement | 4 |
| 47 | Zhang et al. [67] | 2021 | FFNN | Seepage modeling through the base of a dam | Alexandria Engineering Journal | 0 |
| 48 | Wei et al. [68] | 2021 | RNN, Long short-term memory (LSTM), GRU, MLP | Pore–water pressure estimation | Geoscience Frontiers | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nourani, V.; Behfar, N.; Dabrowska, D.; Zhang, Y. The Applications of Soft Computing Methods for Seepage Modeling: A Review. Water 2021, 13, 3384. https://doi.org/10.3390/w13233384
Nourani V, Behfar N, Dabrowska D, Zhang Y. The Applications of Soft Computing Methods for Seepage Modeling: A Review. Water. 2021; 13(23):3384. https://doi.org/10.3390/w13233384
Chicago/Turabian StyleNourani, Vahid, Nazanin Behfar, Dominika Dabrowska, and Yongqiang Zhang. 2021. "The Applications of Soft Computing Methods for Seepage Modeling: A Review" Water 13, no. 23: 3384. https://doi.org/10.3390/w13233384
APA StyleNourani, V., Behfar, N., Dabrowska, D., & Zhang, Y. (2021). The Applications of Soft Computing Methods for Seepage Modeling: A Review. Water, 13(23), 3384. https://doi.org/10.3390/w13233384









