The Impact of Precipitation Characteristics on the Washout of Pollutants Based on the Example of an Urban Catchment in Kielce
Abstract
1. Introduction
2. Materials and Methods
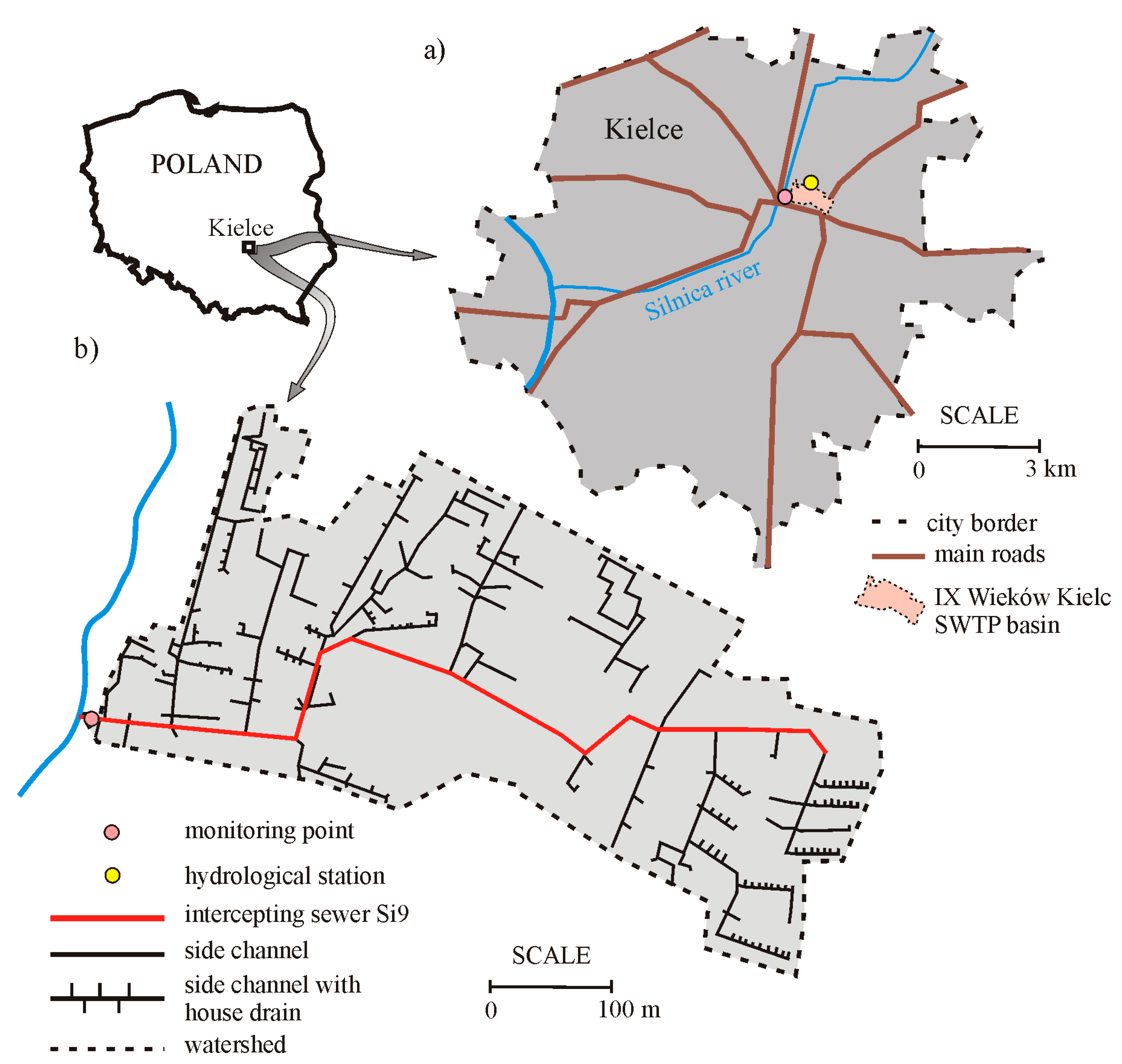
2.1. Study Area
2.2. Measurements of Precipitation and Flow Intensity
2.3. Collection of Stormwater Samples
2.4. Determination of the Physicochemical Properties of Samples
2.5. Analysis of Data
3. Results and Discussion
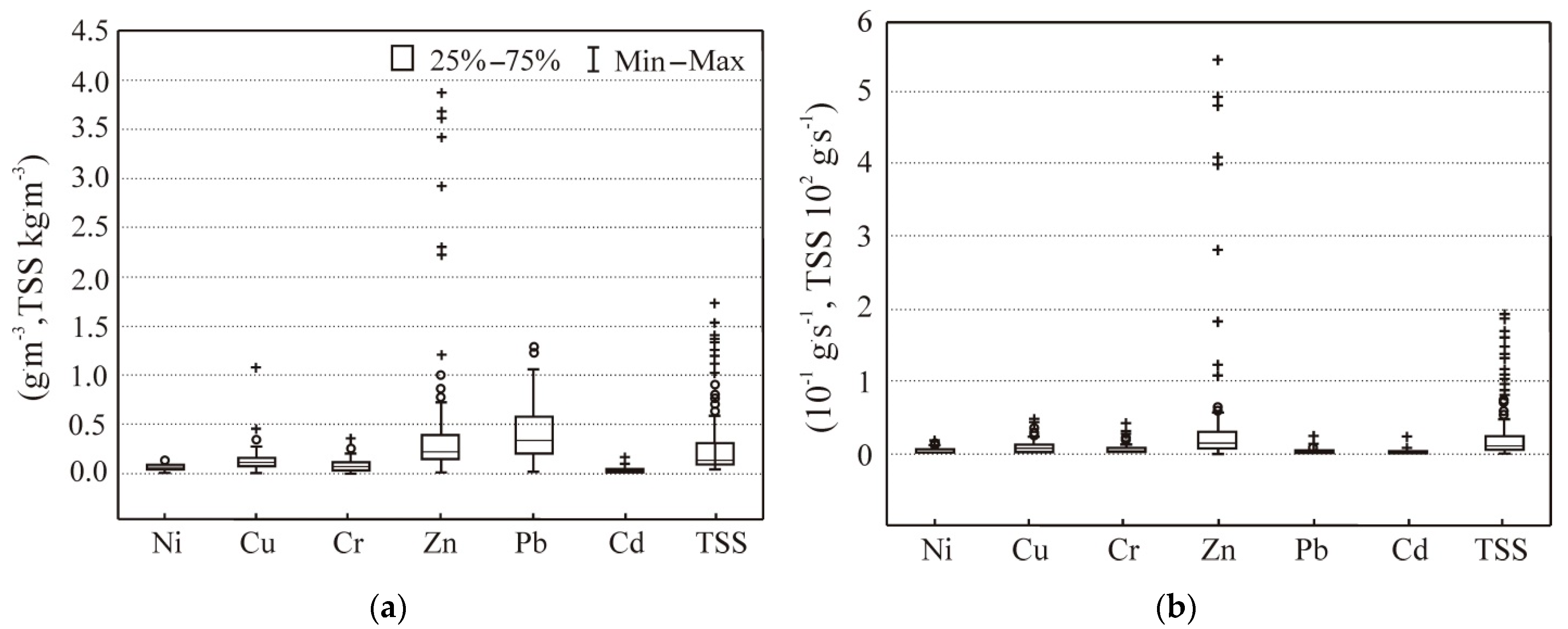
3.1. Results of Physicochemical Analyses
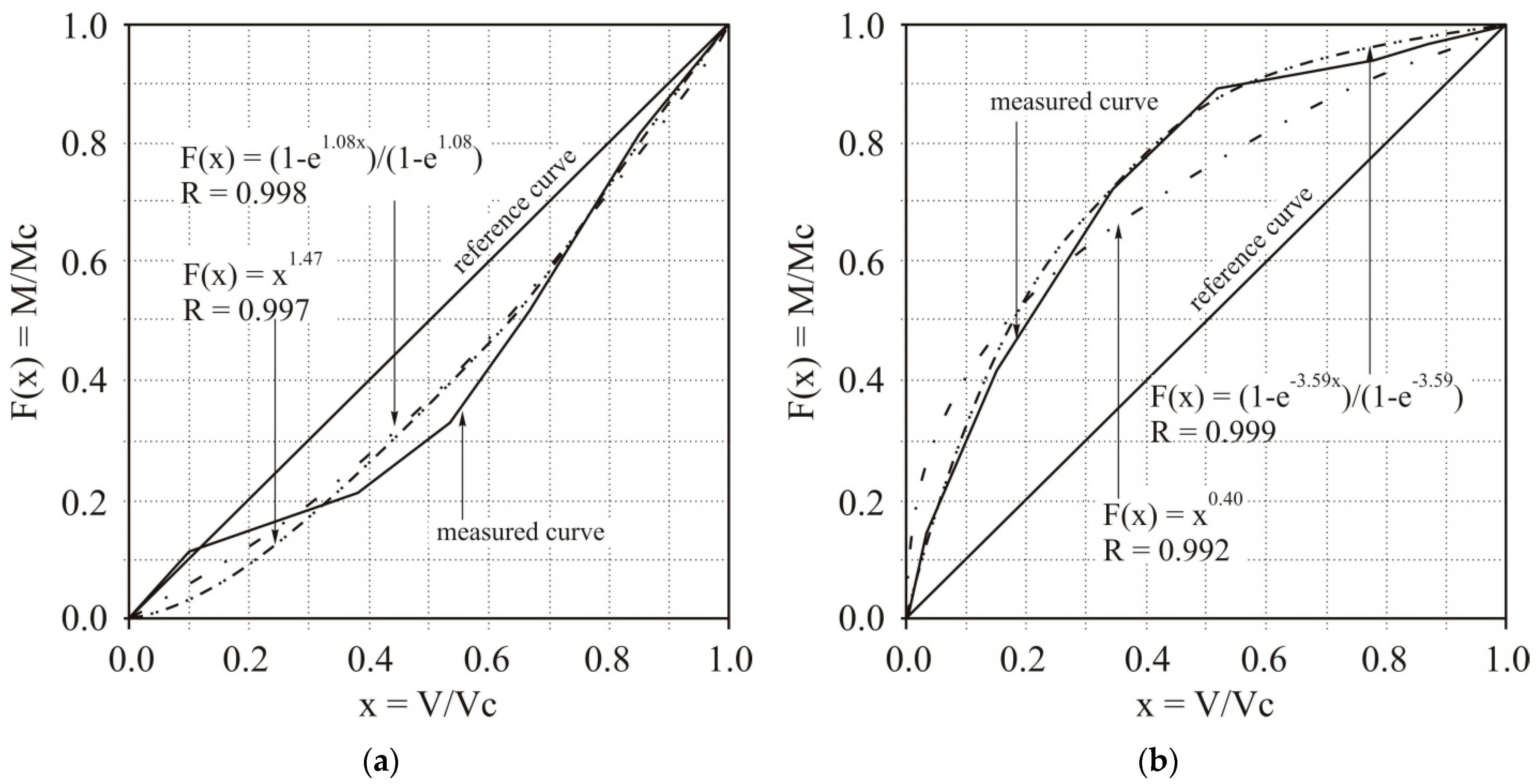
3.2. The Impact of Precipitation Characteristics and Parameters of the Runoff Hydrograph on the Value of the Washout Coefficient
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hossain, I.; Imteaz, M.; Gato-Trinidad, S.; Shanableh, A. Development of a Catchment Water Quality Model for Continuous Simulations of Pollutants Build-up and Wash-off. Int. J. Civ. Environ. Eng. 2010, 2, 210–217. [Google Scholar]
- Sartor, J.D.; Boyd, G.B.; Agardy, F.J. Water pollution aspects of street surface contaminants. Contract 1972, 14, 921. [Google Scholar]
- Bertrand-Krajewski, J.L.; Chebbo, G.; Saget, A. Distribution of pollutant mass vs volume in stormwater discharges and the first flash phenomenon. Water Resour. 1998, 32, 2341–2356. [Google Scholar]
- Osuch-Pajdzińska, E.; Zawilski, M. Model of Storm Sewer Discharge. I: Description. J. Environ. Eng. 1998, 124, 593–599. [Google Scholar] [CrossRef]
- Osuch-Pajdzińska, E.; Zawilski, M. Model for Storm Sewer Discharge. II: Calibration and Verification. J. Environ. Eng. 1998, 124, 600–611. [Google Scholar] [CrossRef]
- Berretta, C.; Gnecco, J.; Lanza, L.G.; Berbera, P. An Investigation of Wash-Off Controlling Parameters at Two Urban Sites in the Town of Genova. 2007. Available online: http://documents.irevues.inist.fr/bitstream/handle/2042/25296/1425_254berretta.pdf?sequence=1 (accessed on 15 April 2021).
- Egodawatta, P. Translation of Small-Plot Scale Pollutant Build-Up and Wash-Off Measurements to Urban Catchment Scale. 2007. Available online: https://eprints.qut.edu.au/16502/1/Prasanna_Egodawatta_Thesis.pdf (accessed on 15 April 2021).
- Alley, W.M.; Smith, P.E. Estimation of accumulation parameters for urban runoff quality modeling. Water Resour. Res. 1981, 17, 1657–1664. [Google Scholar] [CrossRef]
- Lee, J.Y.; Kim, H.; Kim, Y.; Han, M.Y. Characteristics of the event mean concentration (EMC) from rainfall runoff on an urban highway. Environ. Pollut. 2011, 159, 884–888. [Google Scholar] [CrossRef]
- Yuan, Q.; Guerra, H.B.; Kim, Y. An Investigation of the Relationships between Rainfall Conditions and Pollutant Wash-Off from the Paved Road. Water 2017, 9, 232. [Google Scholar] [CrossRef]
- Vezzaro, L.; Sharma, A.K.; Mikkelsen, P.S. Model-Based Comparison of Strategies for Reduction of Stormwater Micropollutants Emission. 2013. Available online: https://hal.archives-ouvertes.fr/hal-03303544/document (accessed on 15 April 2021).
- Zhao, H.; Li, X. Understanding the relationship between heavy metals in road-deposited sediments and washoff particles in urban stormwater using simulated rainfall. J. Hazard. Mater. 2013, 246, 267–276. [Google Scholar] [CrossRef] [PubMed]
- Deletic, A.; Maksimovic, C.; Loughreit, F.; Butler, D. Modelling the Management of Street Surface Sediments in Urban Runoff. 1998. Available online: https://www.academia.edu/2860576/Modelling_the_management_of_street_surface_sediments_in_urban_runoff (accessed on 15 April 2021).
- Avellaneda, P.; Ballestero, T.; Roseen, R.; Houle, J.; Linder, E. Bayesian Storm-Water Quality Model and Its Application to Water Quality Monitoring. J. Environ. Eng. 2011, 137, 541–550. [Google Scholar] [CrossRef][Green Version]
- Chen, J.; Adams, B.J. Analytical Urban Storm Water Quality Models Based on Pollutant Buildup and Washoff Processes. J. Environ. Eng. 2006, 132, 1314–1330. [Google Scholar] [CrossRef]
- Dotto, C.B.; Mannina, G.; Kleidorfer, M.; Vezzaro, L.; Henrichs, M.; McCarthy, D.; Freni, G.; Rauch, W.; Deletic, A. Comparison of different uncertainty techniques in urban stormwater quantity and quality modelling. Water Res. 2012, 46, 2545–2558. [Google Scholar] [CrossRef]
- Fraga, I.; Cea, L.; Puertas, J.; Suárez, J.; Jiménez, V.; Jácome, A. Global Sensitivity and GLUE-Based Uncertainty Analysis of a 2D-1D Dual Urban Drainage Model. J. Hydrol. Eng. 2016, 21, 04016004. [Google Scholar] [CrossRef]
- Perera, T.; McGree, J.; Egodawatta, P.; Jinadasa, K.; Goonetilleke, A. Catchment based estimation of pollutant event mean concentration (EMC) and implications for first flush assessment. J. Environ. Manag. 2021, 279, 111737. [Google Scholar] [CrossRef]
- Rossmann, L.A. Storm Water Management Model, User’s Manual, Version 5.1. National Risk Management Research Laboratory Office of Research and Development; U.S. Environmental Protection Agency: Cincinnati, OH, USA, 2004.
- Tuomela, C.; Sillanpää, N.; Koivusalo, H. Assessment of stormwater pollutant loads and source area contributions with storm water management model (SWMM). J. Environ. Manag. 2019, 233, 719–727. [Google Scholar] [CrossRef]
- Egemose, S.; Petersen, A.B.; Sønderup, M.J.; Flindt, M.R. First Flush Characteristics in Separate Sewer Stormwater and Implications for Treatment. Sustainability 2020, 12, 5063. [Google Scholar] [CrossRef]
- Verdaguer, M.; Clara, N.; Gutierrez, O.; Poch, M. Application of Ant-Colony-Optimization algorithm for improved management of first flush effects in urban wastewater systems. Sci. Total. Environ. 2014, 485, 143–152. [Google Scholar] [CrossRef] [PubMed]
- Mrowiec, M.; Kamizela, T.; Kowalczyk, M. Occurrence of first flush phenomenon in drainage system of Częstochowa. Environ. Prot. Eng. 2009, 35, 73–80. [Google Scholar]
- Deletic, A. The first flush load of urban surface runoff. Water Res. 1998, 32, 2462–2470. [Google Scholar] [CrossRef]
- Sansalone, J.J.; Buchberger, S.G. Partitioning and First Flush of Metals in Urban Roadway Storm Water. J. Environ. Eng. 1997, 123, 134–143. [Google Scholar] [CrossRef]
- Stahre, P.; Urbonas, B. Stormwater Detention: For Drainage, Water Quality and CSO Management, 1st ed.; Prentice Hall PTR: Hoboken, NJ, USA, 1990. [Google Scholar]
- Kim, I.; Ko, S.-O.; Jeong, S.; Yoon, J. Characteristics of washed-off pollutants and dynamic EMCs in parking lots and bridges during a storm. Sci. Total. Environ. 2007, 376, 178–184. [Google Scholar] [CrossRef]
- McCarthy, D.T. A traditional first flush assessment of E. coli in urban stormwater runoff. Water Sci. Technol. 2009, 60, 2749–2757. [Google Scholar] [CrossRef]
- Kang, J.-H.; Kayhanian, M.; Stenstrom, M.K. Predicting the existence of stormwater first flush from the time of concentration. Water Res. 2008, 42, 220–228. [Google Scholar] [CrossRef]
- Lee, J.; Bang, K.; Ketchum, L.; Choe, J.; Yu, M. First flush analysis of urban storm runoff. Sci. Total. Environ. 2002, 293, 163–175. [Google Scholar] [CrossRef]
- Qin, H.-P.; He, K.-M.; Fu, G. Modeling middle and final flush effects of urban runoff pollution in an urbanizing catchment. J. Hydrol. 2016, 534, 638–647. [Google Scholar] [CrossRef]
- Ma, Z.-B.; Ni, H.-G.; Zeng, H.; Wei, J.-B. Function formula for first flush analysis in mixed watersheds: A comparison of power and polynomial methods. J. Hydrol. 2011, 402, 333–339. [Google Scholar] [CrossRef]
- Jeung, M.; Baek, S.; Beom, J.; Cho, K.H.; Her, Y.; Yoon, K. Evaluation of random forest and regression tree methods for estimation of mass first flush ratio in urban catchments. J. Hydrol. 2019, 575, 1099–1110. [Google Scholar] [CrossRef]
- Szeląg, B.; Bąk, Ł.; Suligowski, R.; Górski, J. Statistical models to predict discharge overflow. Water Sci. Technol. 2018, 78, 1208–1218. [Google Scholar] [CrossRef]
- Bąk, Ł.; Szeląg, B.; Górski, J.; Górska, K. The Impact of Catchment Characteristics and Weather Conditions on Heavy Metal Concentrations in Stormwater—Data Mining Approach. Appl. Sci. 2019, 9, 2210. [Google Scholar] [CrossRef]
- Guide to Instruments and Methods of Observation. Volume I—Measurement of Meteorological Variables. WMO-No. 8. 2018. Available online: https://library.wmo.int/doc_num.php?explnum_id=10616 (accessed on 20 October 2021).
- Licznar, P. Preliminary results of comparative field studies on the performance of OTT Pluvio2 electronic weight-based rain gauge and Parsivel laser disdrometer. INSTAL 2009, 7, 43–50. (In Polish) [Google Scholar]
- PN-EN ISO 8288:2002. Water Quality—Determination of Cobalt, Nickel, Copper, Zinc, Cadmium and Lead—Atomic Adsorption Spectroscopy with Flame Atomization. Available online: https://infostore.saiglobal.com/en-us/Standards/PN-ISO-8288-2002-940605_SAIG_PKN_PKN_2214207/ (accessed on 20 October 2021). (In Polish).
- PN-EN ISO 15587-1:2005. Water Quality—Digestion for the Determination of Selected Elements in Water—Part 1: Aqua Regia Digestion. Available online: https://infostore.saiglobal.com/en-au/standards/pn-en-iso-15587-1-2005-937215_saig_pkn_pkn_2207427/ (accessed on 20 October 2021). (In Polish).
- PN-EN 872:2007. Water Quality–Determination of Suspended Solids—Method by Filtration through GLASS Fiber Filters. Available online: https://sklep.pkn.pl/pn-en-872-2007p.html (accessed on 20 October 2021). (In Polish).
- Rutkowski, L. Artificial Intelligence Methods and Techniques; PWN: Warszawa, Poland, 2006. [Google Scholar]
- Nocoń, W.; Barbusiński, K.; Nocoń, K.; Kernert, J. Changes in Trace Metal Load in Suspended Solids Carried Along the River. Ochr. Sr. 2013, 35, 33–38. [Google Scholar]
- Brekhovskikh, V.F.; Volkova, Z.V.; Kocharyan, A.G. Heavy Metals in the Ivan’kovo Reservoir Bottom Sediments. Water Resour. 2001, 28, 278–287. [Google Scholar] [CrossRef]
- Bibby, R.L.; Webster-Brown, J. Characterisation of urban catchment suspended particulate matter (Auckland region, New Zealand); a comparison with non-urban SPM. Sci. Total. Environ. 2005, 343, 177–197. [Google Scholar] [CrossRef]
- Brombach, H.; Fuchs, S. Datenpool gemessener Verschmutzungskonzentrationen in Misch-und Trennkanalisationen; ATV-DVWK—Forschungsfonds, Projekt 1-01; GFA: Hennef, Germany, 2001. [Google Scholar]
- Santa Monica In-Line Storm Drain Runoff Infiltration System Project: Final Report. Public Works, Civil Engineering Division, City of Santa Monica. 2014. Available online: https://www.smbrc.ca.gov/docs/sm_inline_rpt.pdf (accessed on 15 April 2021).
- Lundy, L.; Ellis, J.; Revitt, D. Risk prioritisation of stormwater pollutant sources. Water Res. 2012, 46, 6589–6600. [Google Scholar] [CrossRef] [PubMed]
- Królikowska, J.; Królikowski, A. Precipitation Water. Drainage, Management, Pre-Treatment and Use; Seidel-Przywecki: Piaseczno, Poland, 2012. [Google Scholar]
- Gnecco, I.; Berretta, C.; Lanza, L.; La Barbera, P. Storm water pollution in the urban environment of Genoa, Italy. Atmos. Res. 2005, 77, 60–73. [Google Scholar] [CrossRef]
- Gasperi, J.; Kafi–Benyahia, M.; Lorgeoux, C.; Moilleron, R.; Gromaire, M.-C.; Chebbo, G. Wastewater quality and pollutant loads in combined sewers during dry weather periods. Urban Water J. 2008, 5, 305–314. [Google Scholar] [CrossRef]
- Taebi, A.; Droste, R.L. Pollution loads in urban runoff and sanitary wastewater. Sci. Total. Environ. 2004, 327, 175–184. [Google Scholar] [CrossRef] [PubMed]
- Kabata-Pendias, A.; Pendias, H. Biogeochemistry of Trace Elements; PWN: Warszawa, Poland, 1999. [Google Scholar]
- Królikowski, A.; Garbarczyk, K.; Gwoździej-Mazur, J.; Butarewicz, A. Sediments Formed in Stormwater Sewer Facilities, Monograph 35; PAN: Lublin, Poland, 2005. [Google Scholar]
- Djukic, A.; Lekić, B.; Rajaković-Ognjanović, V.; Veljovic, D.; Vulić, T.; Đolić, M.; Naunovic, Z.; Despotović, J.; Prodanovic, D. Further insight into the mechanism of heavy metals partitioning in stormwater runoff. J. Environ. Manag. 2016, 168, 104–110. [Google Scholar] [CrossRef]
- Gan, H.; Zhuo, M.; Li, D.; Zhou, Y. Quality characterization and impact assessment of highway runoff in urban and rural area of Guangzhou, China. Environ. Monit. Assess. 2007, 140, 147–159. [Google Scholar] [CrossRef]
- Zgheib, S.; Moilleron, R.; Chebbo, G. Priority pollutants in urban stormwater: Part 1—Case of separate storm sewers. Water Res. 2012, 46, 6683–6692. [Google Scholar] [CrossRef]
- Valtanen, M.; Sillanpää, N.; Setälä, H. The Effects of Urbanization on Runoff Pollutant Concentrations, Loadings and Their Seasonal Patterns under Cold Climate. Water Air Soil Pollut. 2014, 225, 1–16. [Google Scholar] [CrossRef]
- Rogula-Kozłowska, W.; Majewski, G.; Czechowski, P.O. The size distribution and origin of elements bound to ambient particles: A case study of a Polish urban area. Environ. Monit. Assess. 2015, 187, 240. [Google Scholar] [CrossRef] [PubMed]
- Sakson, G.; Łódzka, P.; Zawiliński, M.; Badowska, E.; Brzezińska, A. Stormwater pollution as the basis of choice the method of their management. J. Civ. Eng. Environ. Arch. 2014, XXXI, 253–264. [Google Scholar] [CrossRef]
- Saget, A.; Chebbo, G.; Bertrand-Krajewski, J.-L. The first flush in sewer systems. Water Sci. Technol. 1996, 33, 101–108. [Google Scholar] [CrossRef]
- Barone, L.; Pilotti, M.; Valerio, G.; Balistrocchi, M.; Milanesi, L.; Chapra, S.C.; Nizzoli, D. Analysis of the residual nutrient load from a combined sewer system in a watershed of a deep Italian lake. J. Hydrol. 2019, 571, 202–213. [Google Scholar] [CrossRef]
- Chow, M.F.; Yusop, Z. Sizing first flush pollutant loading of stormwater runoff in tropical urban catchments. Environ. Earth Sci. 2014, 72, 4047–4058. [Google Scholar] [CrossRef]



| No. | Ptd=10 | P | td | q | Pa | Qmax | Vc | tp | tbd | Number of Samples |
|---|---|---|---|---|---|---|---|---|---|---|
| mm | mm | min | L·s−1·ha | mm | m3·s−1 | m3 | min | h | ||
| 1 | - | 2.6 | 360 | 1.20 | 1.3 | 0.313 | 632 | 50.0 | 54.0 | 8 |
| 2 | 1.8 | 2.1 | 54 | 6.48 | 3.6 | 0.360 | 510 | 23.5 | 25.0 | 8 |
| 3 | - | 6.6 | 480 | 2.29 | 2.6 | 0.076 | 200 | 32.0 | 0.6 | 8 |
| 4 | 0.5 | 1.1 | 48 | 3.82 | 1.4 | 0.094 | 263 | 33.5 | 3.1 | 12 |
| 5 | 0.5 | 5.2 | 424 | 2.04 | 2.8 | 0.274 | 1232 | 82.0 | 28.4 | 12 |
| 6 | 0.4 | 1.3 | 78 | 2.78 | 3.8 | 0.046 | 212 | 45.0 | 127.0 | 8 |
| 7 | 1.3 | 3.6 | 92 | 6.52 | 1.3 | 0.111 | 327 | 16.0 | 132.0 | 9 |
| 8 | 0.9 | 6.6 | 298 | 3.69 | 8.1 | 0.148 | 1173 | 162.5 | 137.0 | 24 |
| 9 | 0.5 | 3.1 | 170 | 3.04 | 6.6 | 0.101 | 687 | 122.0 | 6.0 | 24 |
| 10 | 4.6 | 8.3 | 24 | 57.65 | 3.6 | 0.173 | 425 | 29.5 | 43.3 | 9 |
| 11 | 2.9 | 5.4 | 56 | 16.07 | 2.8 | 0.277 | 684 | 19.0 | 71.2 | 9 |
| 12 | 0.7 | 4.0 | 168 | 3.97 | 5.4 | 0.140 | 580 | 26.0 | 8.2 | 14 |
| 13 | 0.7 | 6.3 | 106 | 9.91 | 4.8 | 0.312 | 755 | 78.0 | 10.2 | 14 |
| Pollution | Load | |||
|---|---|---|---|---|
| Range | Mean | Standard Deviation | Coefficient of Variation (%) | |
| (10−3·kg), * (kg) | ||||
| Ni | 0.54–50.15 | 15.52 | 13.17 | 84.85 |
| Cu | 19.50–94.44 | 50.83 | 25.00 | 49.18 |
| Cr | 13.25–68.54 | 28.74 | 18.72 | 65.13 |
| Zn | 52.84–1452.00 | 251.95 | 424.62 | 168.53 |
| Pb | 16.86–412.71 | 211.81 | 132.51 | 62.56 |
| Cd | 0.60–19.73 | 10.72 | 6.68 | 62.31 |
| TSS * | 22.90–796.00 | 160.23 | 220.57 | 137.65 |
| Variable | MTSS | MNi | MCu | MCr | MZn | MPb | MCd |
|---|---|---|---|---|---|---|---|
| P | 0.127 | 0.428 | 0.048 | −0.238 | 0.048 | −0.048 | 0.238 |
| td | 0.127 | 0.428 | 0.428 | 0.333 | 0.048 | 0.333 | 0.238 |
| Ptd=10 | 0.098 | 0.100 | 0.100 | 0.100 | 0.500 | 0.200 | 0.100 |
| q | −0.091 | 0.048 | −0.143 | −0.428 | 0.048 | −0.048 | 0.048 |
| Qmax | 0.454 | −0.048 | 0.333 | 0.238 | 0.524 | 0.428 | 0.333 |
| Vc | 0.454 | 0.524 | 0.524 | 0.238 | 0.333 | 0.428 | 0.524 |
| tp | 0.296 | 0.048 | 0.428 | 0.143 | 0.048 | 0.333 | 0.428 |
| tbd | −0.054 | −0.048 | −0.048 | −0.143 | −0.048 | 0.143 | −0.048 |
| Variable | kTSS | kNi | kCu | kCr | kZn | kPb | kCd |
|---|---|---|---|---|---|---|---|
| P | −0.509 | −0.289 | −0.289 | −0.333 | −0.067 | −0.067 | 0.022 |
| td | 0.409 | −0.200 | −0.067 | −0.111 | −0.200 | −0.022 | 0.067 |
| Ptd=10 | −0.658 | −0.257 | 0.029 | 0.086 | 0.371 | −0.086 | −0.143 |
| q | −0.773 | −0.155 | −0.067 | 0.067 | 0.244 | 0.156 | −0.022 |
| Qmax | −0.309 | 0.155 | 0.155 | 0.200 | 0.111 | 0.022 | −0.067 |
| Vc | 0.136 | −0.066 | −0.111 | −0.067 | 0.022 | 0.111 | 0.378 |
| tp | 0.111 | −0.363 | −0.409 | −0.272 | −0.272 | −0.182 | 0.182 |
| tbd | 0.382 | −0.111 | −0.155 | −0.289 | −0.022 | −0.556 | −0.289 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szeląg, B.; Górski, J.; Bąk, Ł.; Górska, K. The Impact of Precipitation Characteristics on the Washout of Pollutants Based on the Example of an Urban Catchment in Kielce. Water 2021, 13, 3187. https://doi.org/10.3390/w13223187
Szeląg B, Górski J, Bąk Ł, Górska K. The Impact of Precipitation Characteristics on the Washout of Pollutants Based on the Example of an Urban Catchment in Kielce. Water. 2021; 13(22):3187. https://doi.org/10.3390/w13223187
Chicago/Turabian StyleSzeląg, Bartosz, Jarosław Górski, Łukasz Bąk, and Katarzyna Górska. 2021. "The Impact of Precipitation Characteristics on the Washout of Pollutants Based on the Example of an Urban Catchment in Kielce" Water 13, no. 22: 3187. https://doi.org/10.3390/w13223187
APA StyleSzeląg, B., Górski, J., Bąk, Ł., & Górska, K. (2021). The Impact of Precipitation Characteristics on the Washout of Pollutants Based on the Example of an Urban Catchment in Kielce. Water, 13(22), 3187. https://doi.org/10.3390/w13223187







