Efficient Reservoir Modelling for Flood Regulation in the Ebro River (Spain)
Abstract
1. Introduction
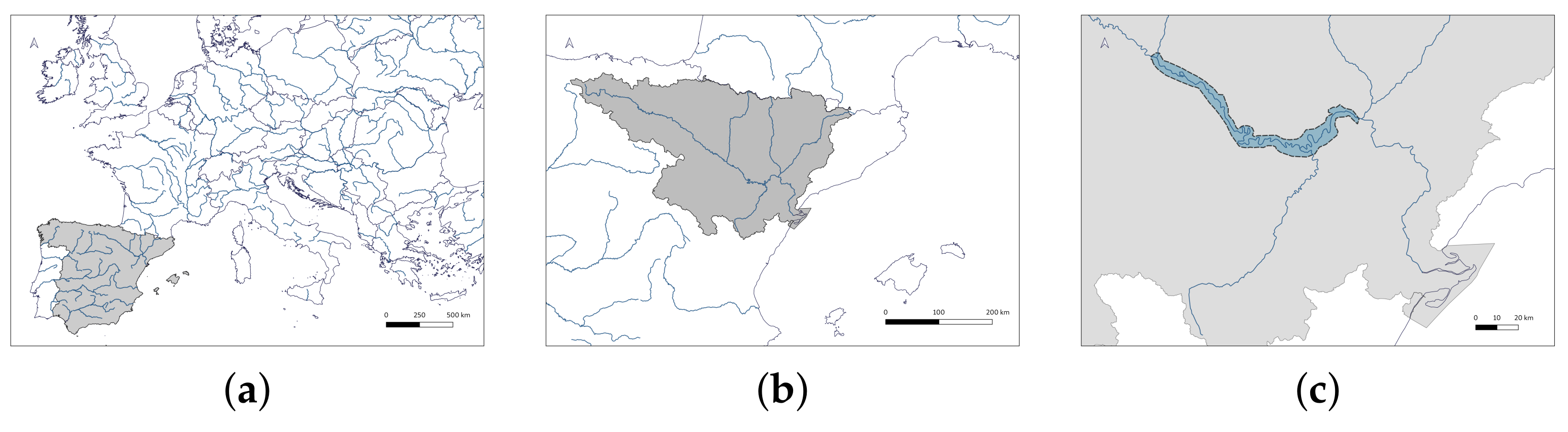
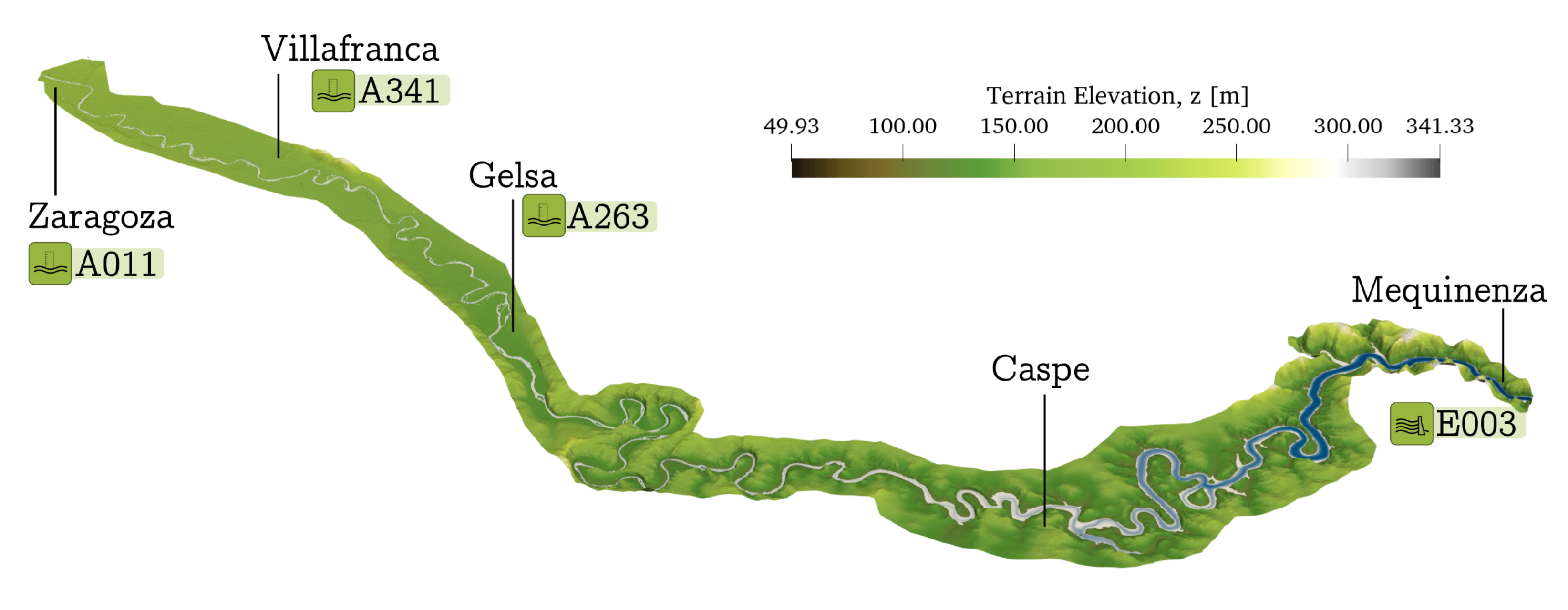
2. Study Area
3. Methodology
3.1. Two Dimensional (2D) Model
3.2. One Dimensional (1D) Model
3.3. Finite Volume Model for the 1D Flow Equations
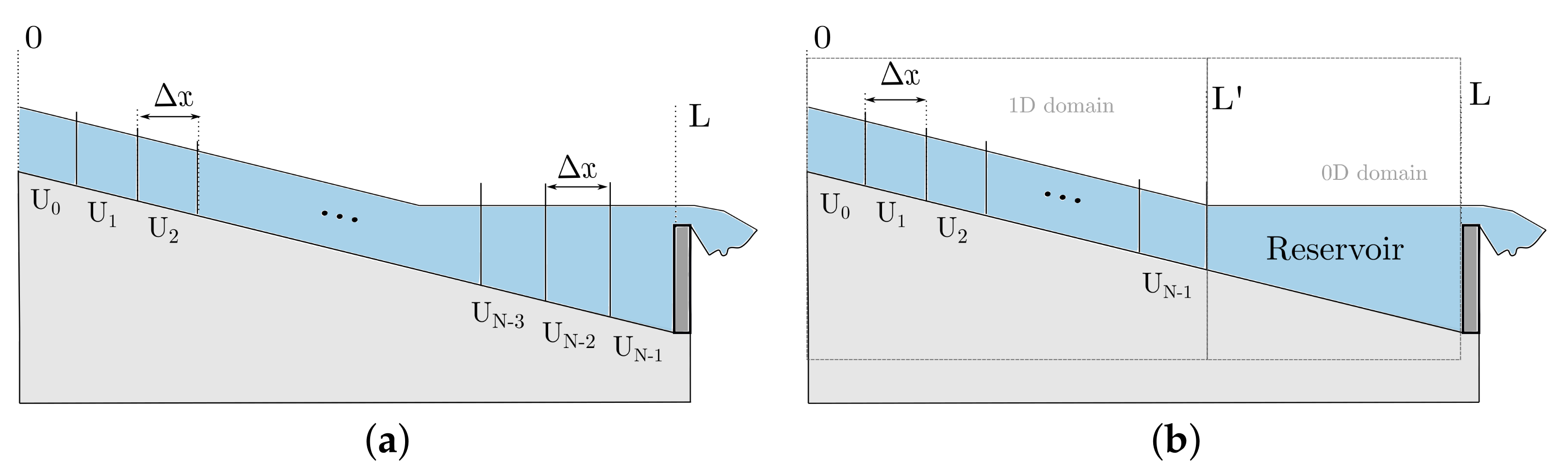
3.4. Reservoir Model
3.5. PID Regulation
- Proportional term: Expresses a proportionality between the required action and the error.
- Integral term: The required action takes into account the time integral of the error over a given period.
- Derivative term: The controller actuation is formulated from the time derivative of the error.
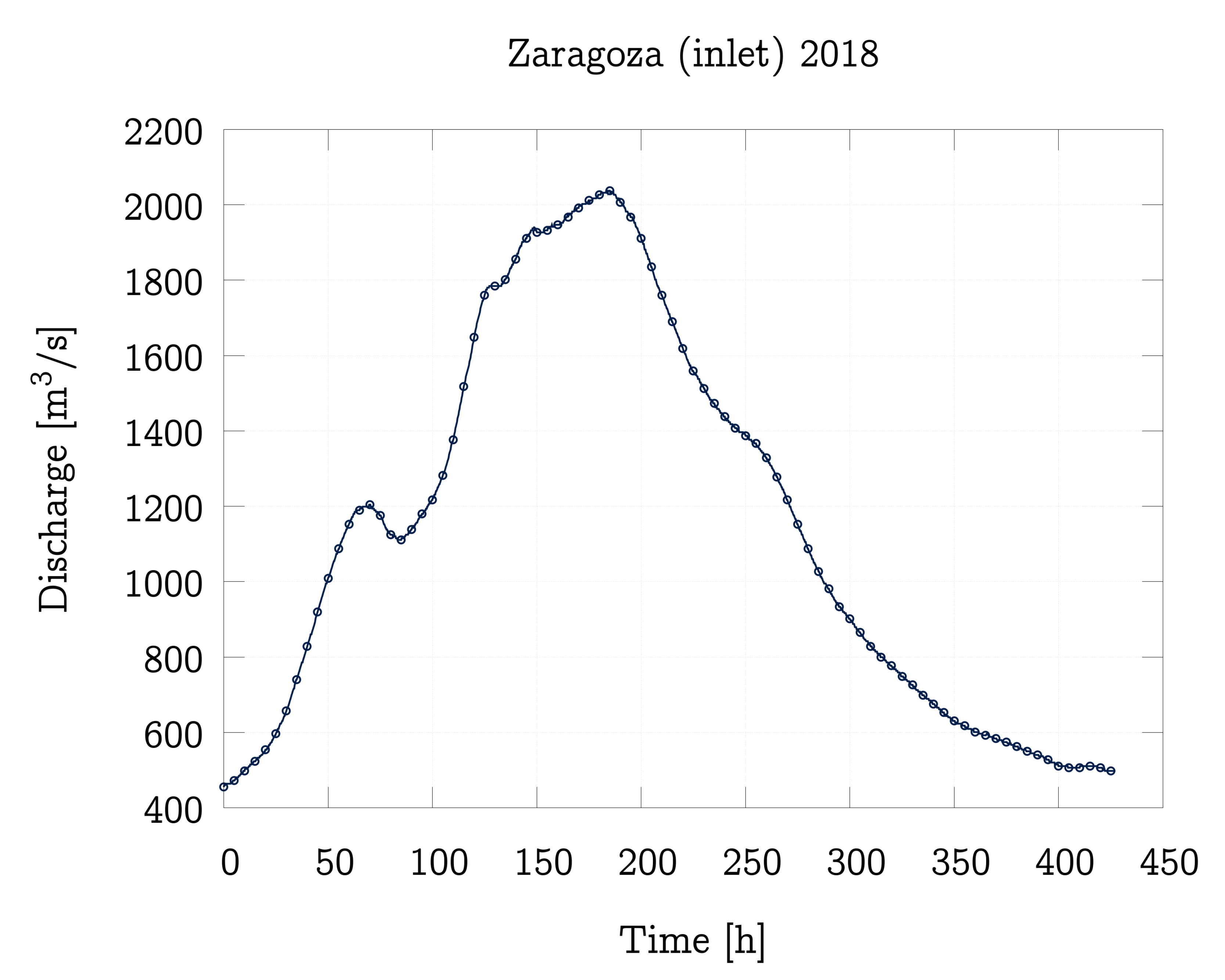
4. Model Application
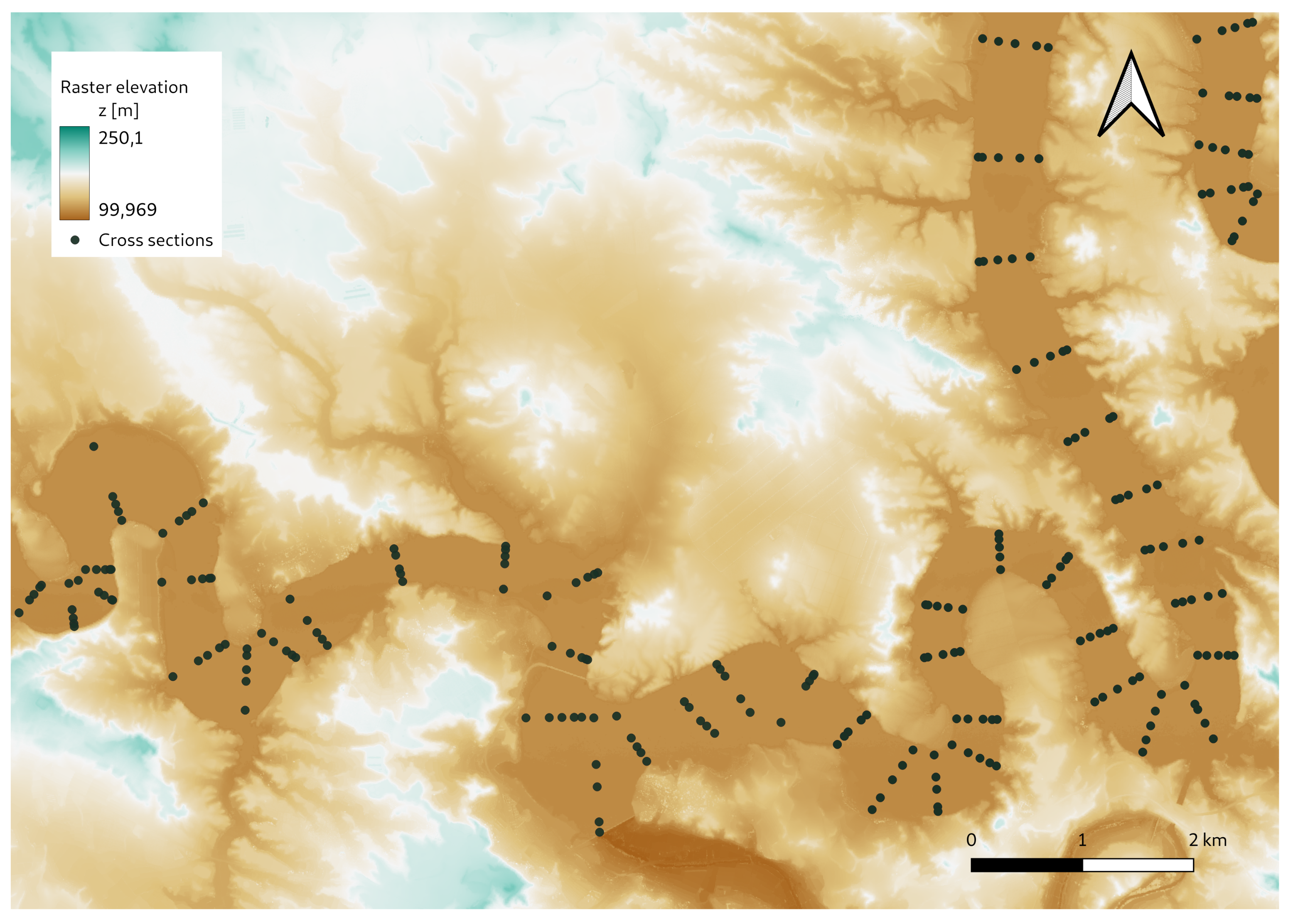
4.1. Discretisation of the Domain
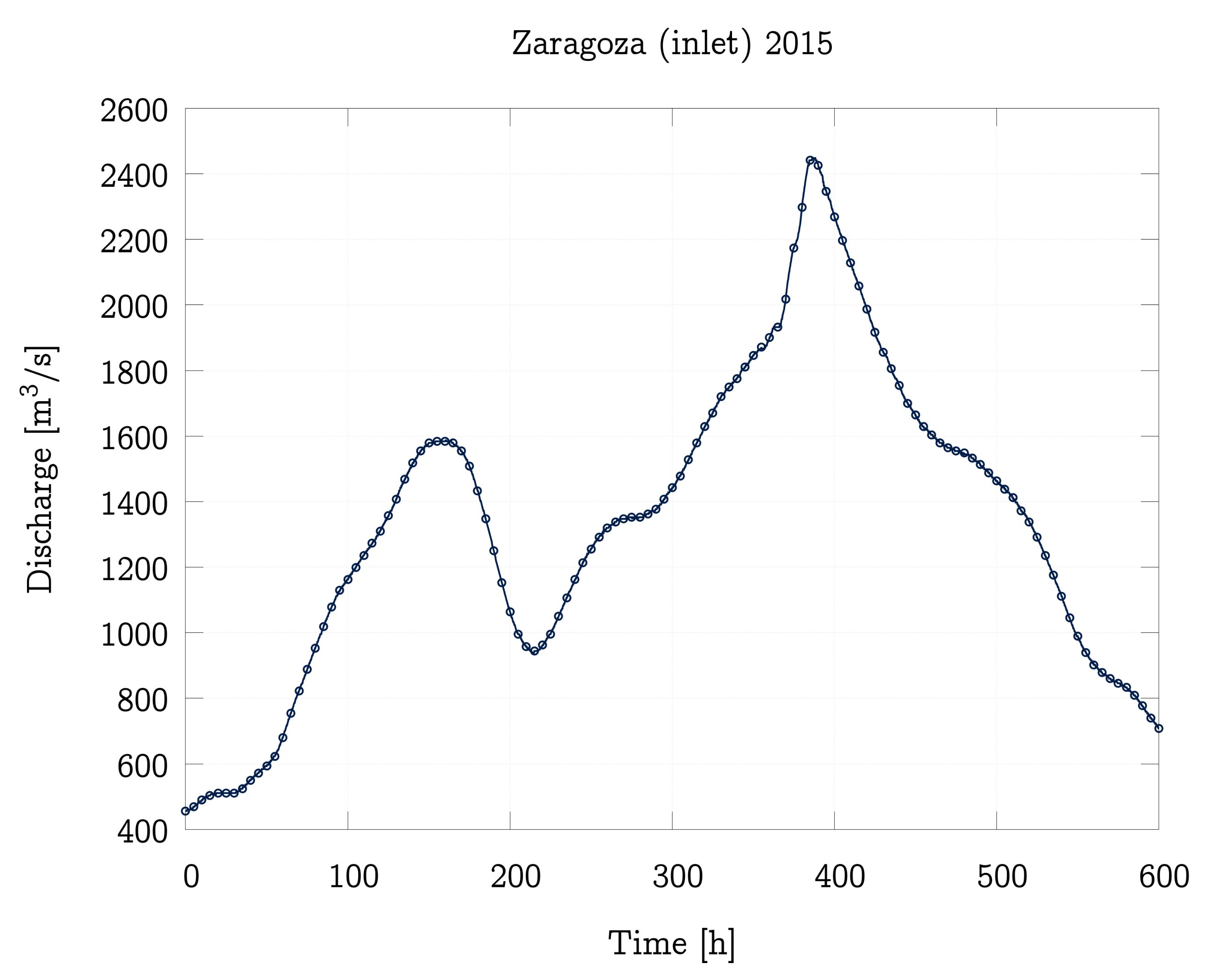
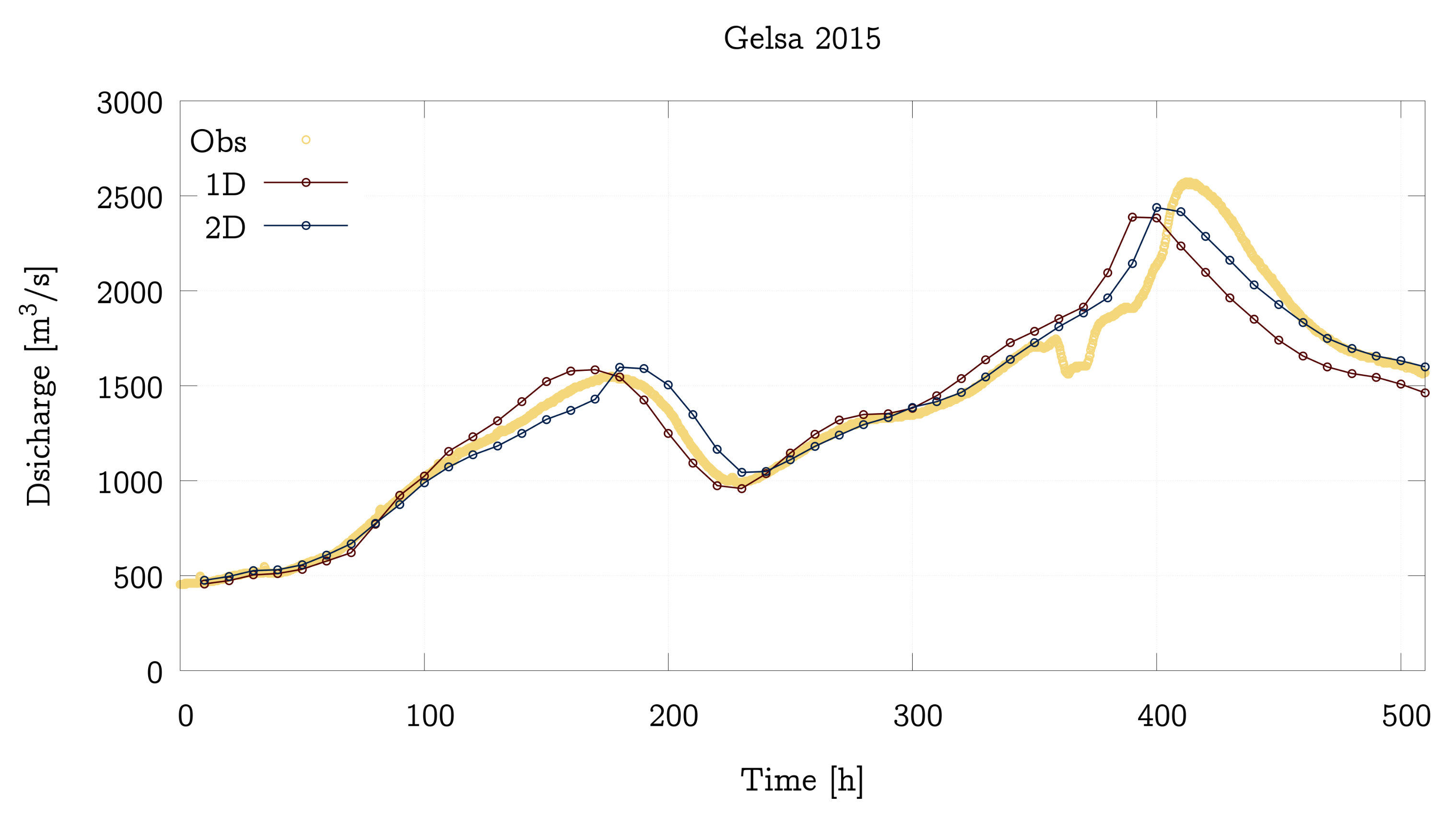
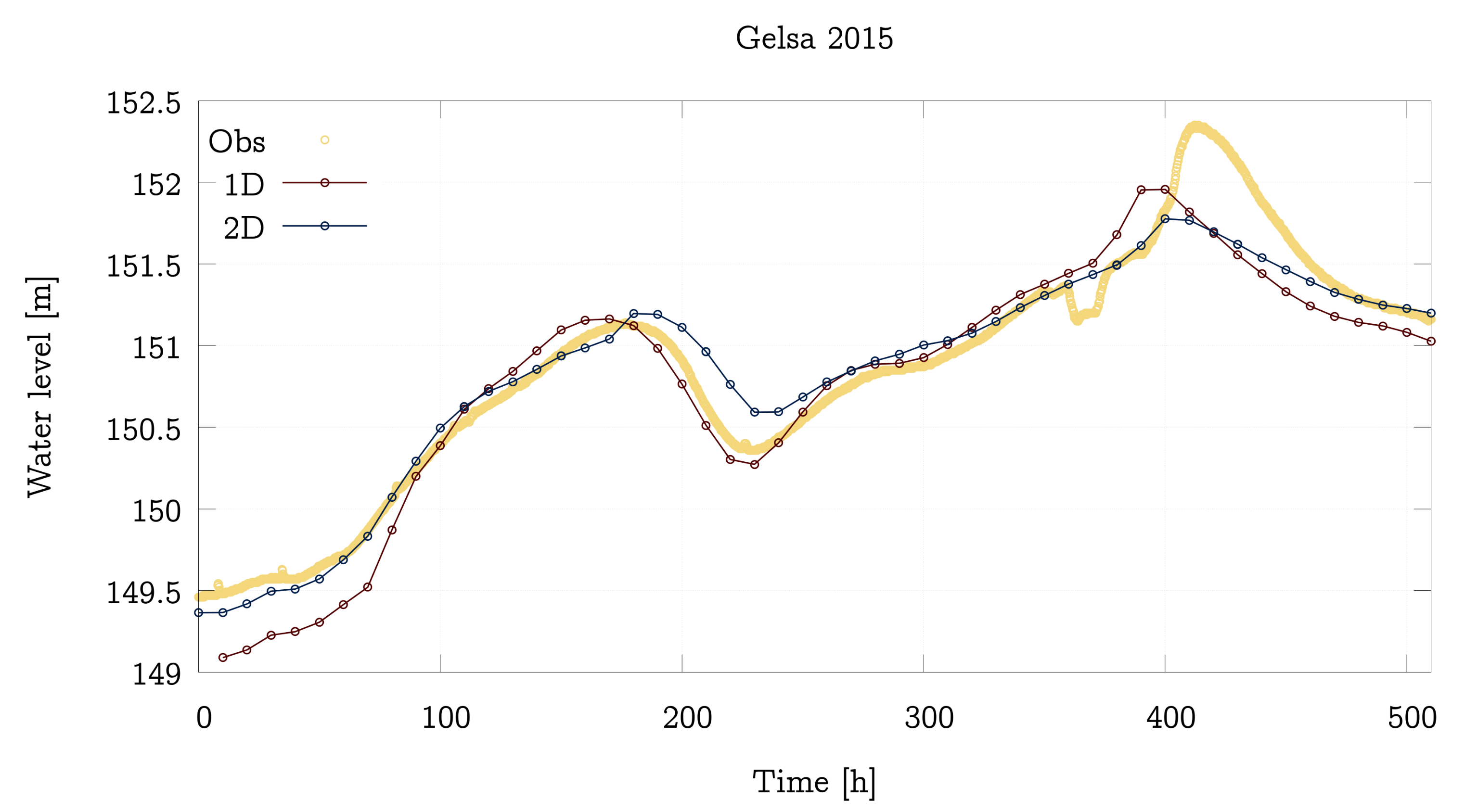
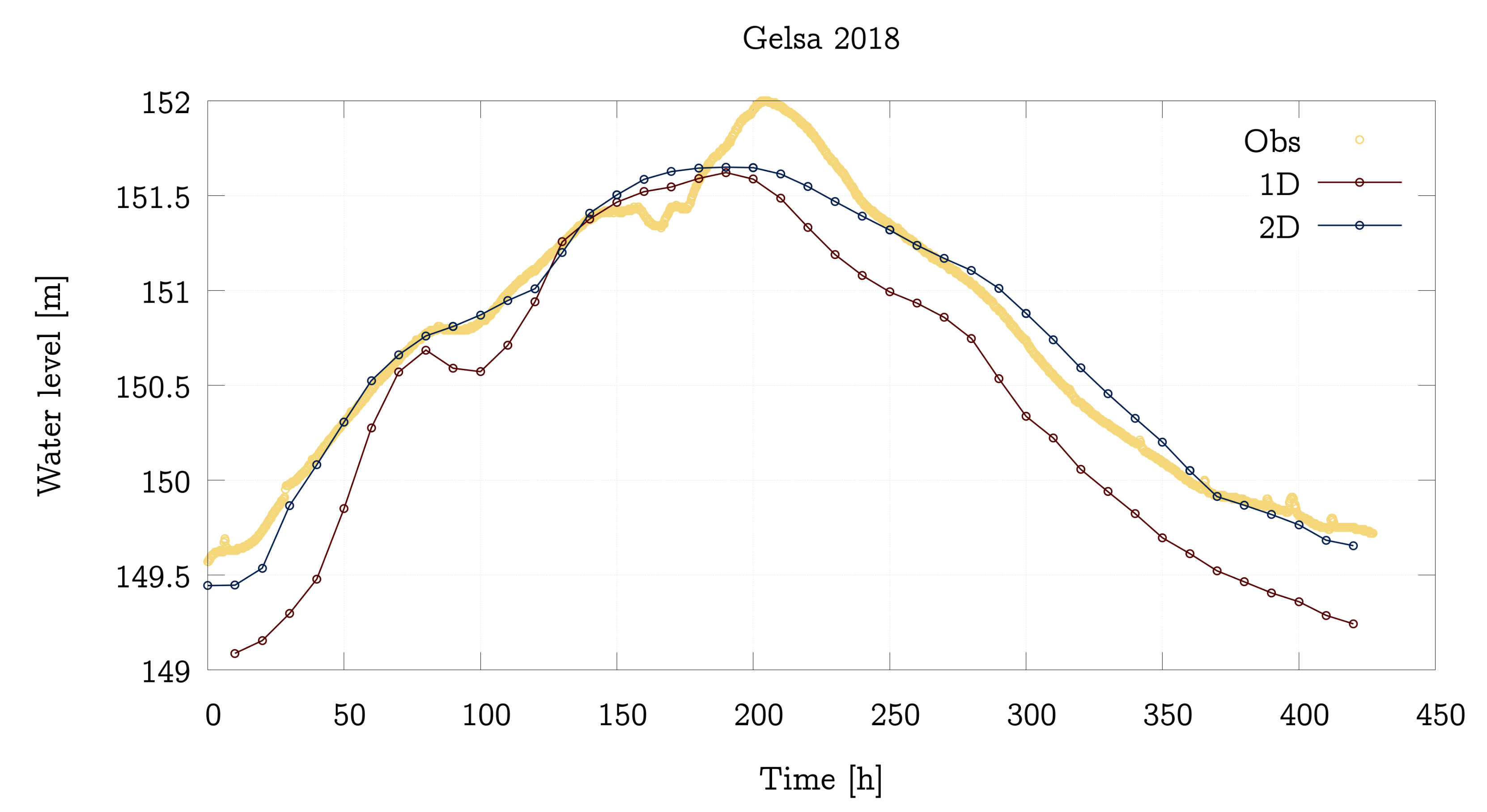
4.2. Performance Analysis of the 1D and 2D Models
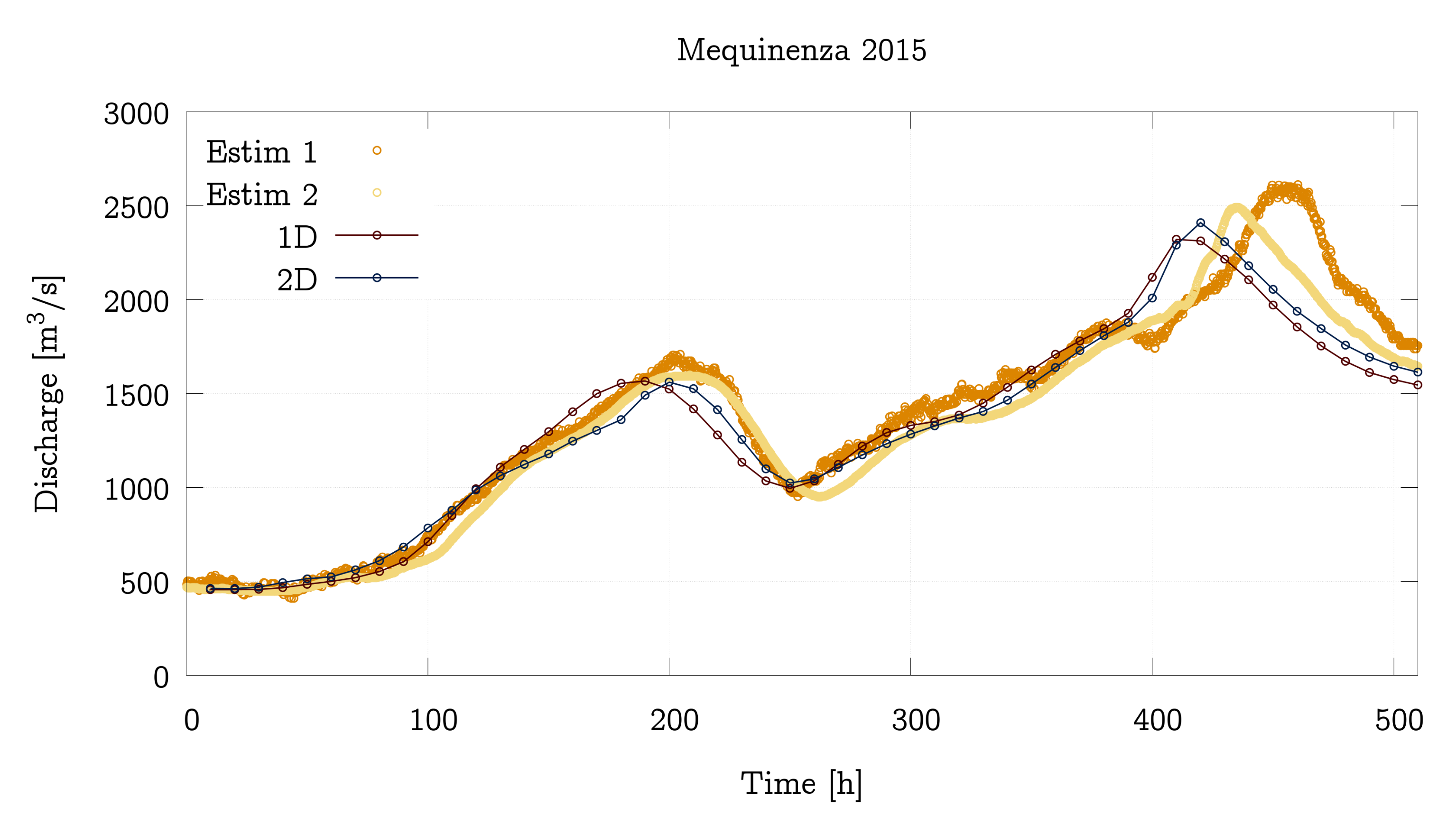
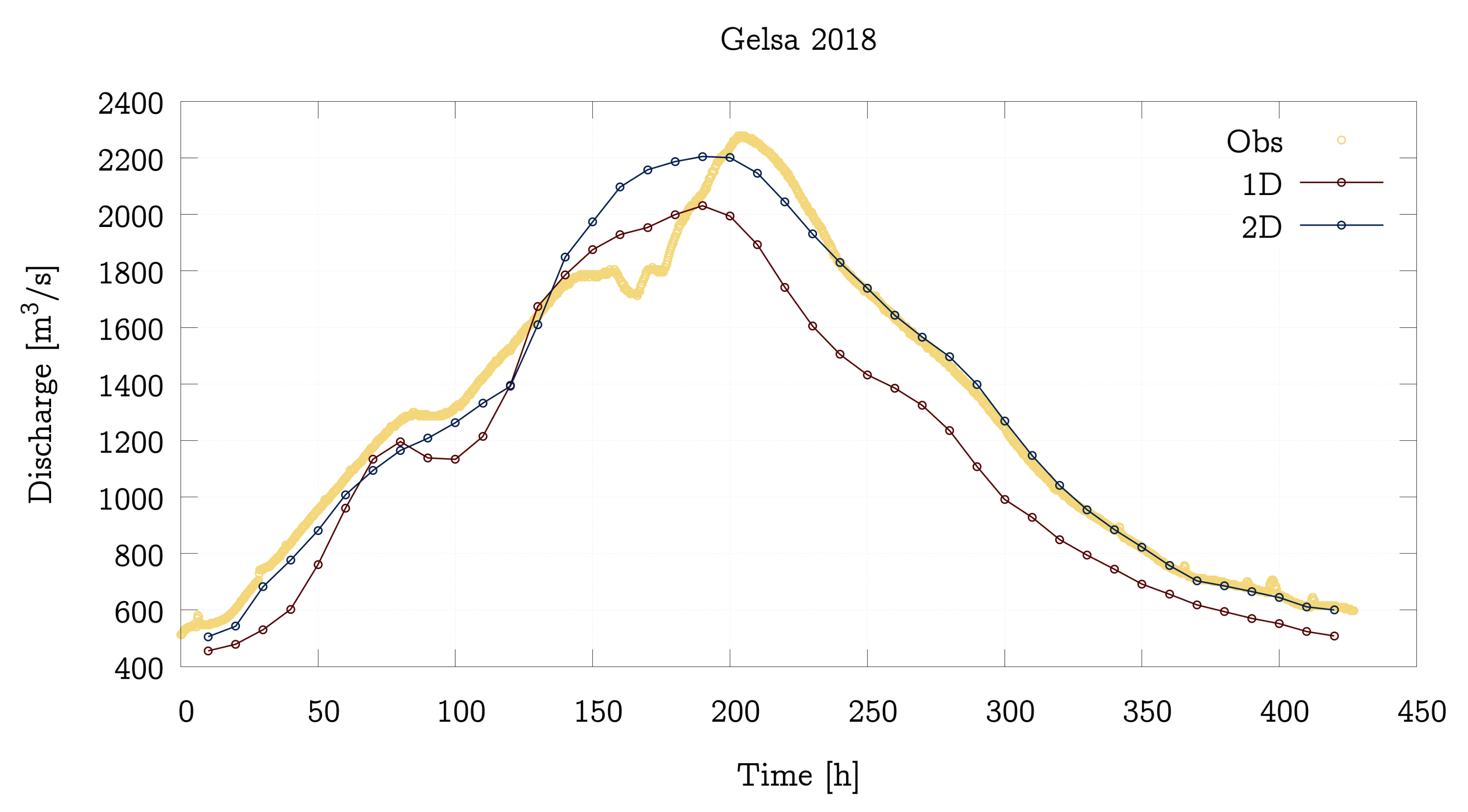
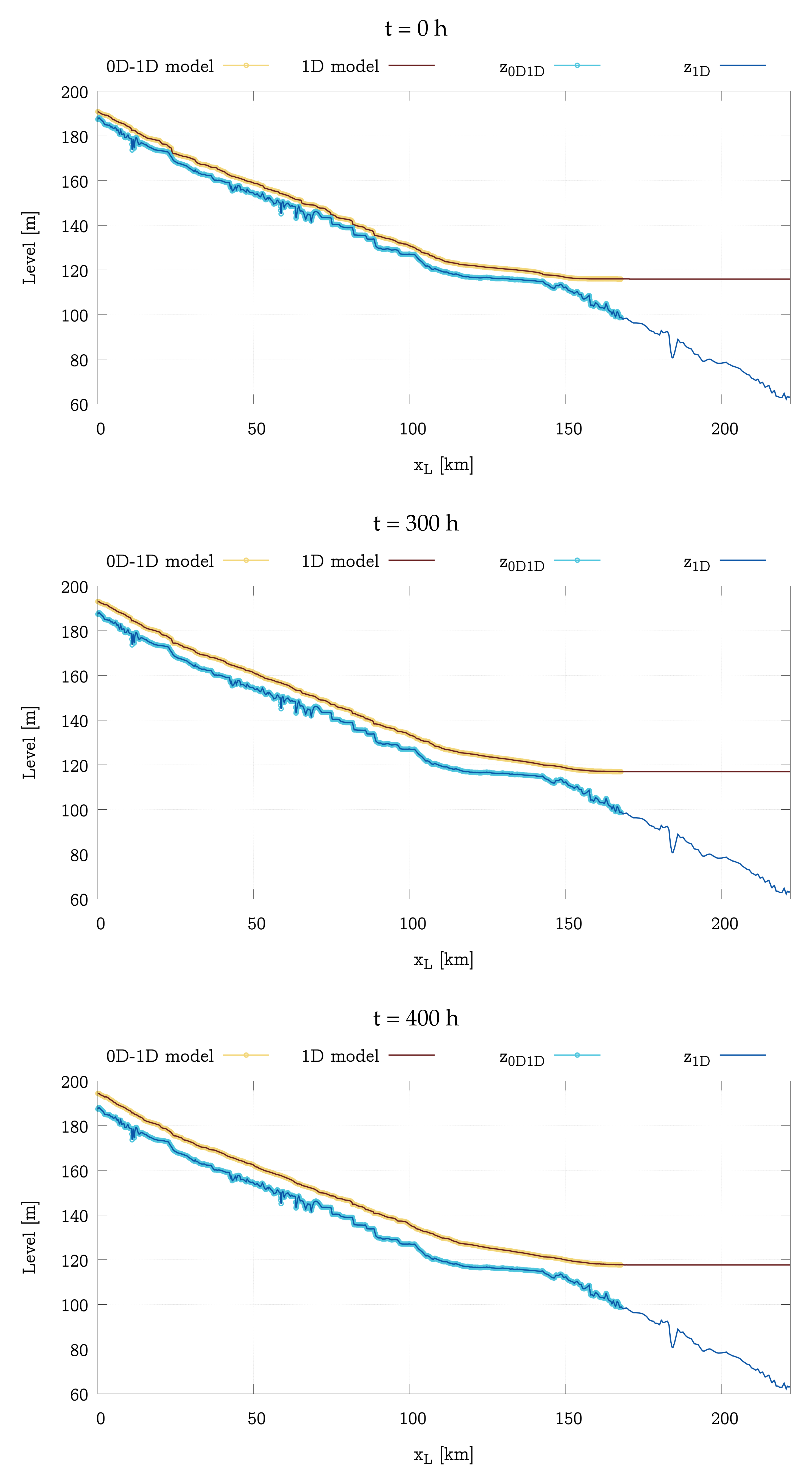
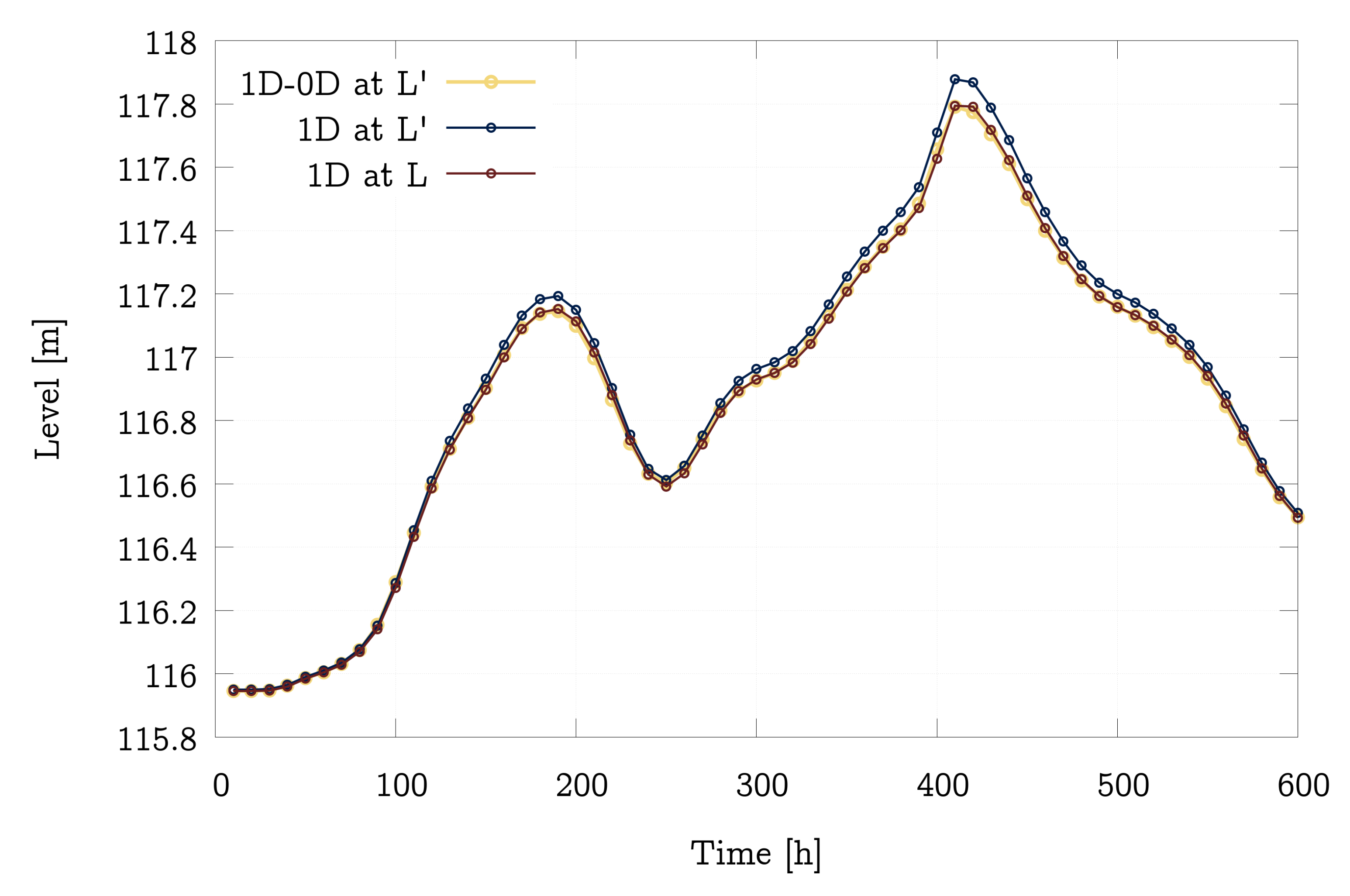
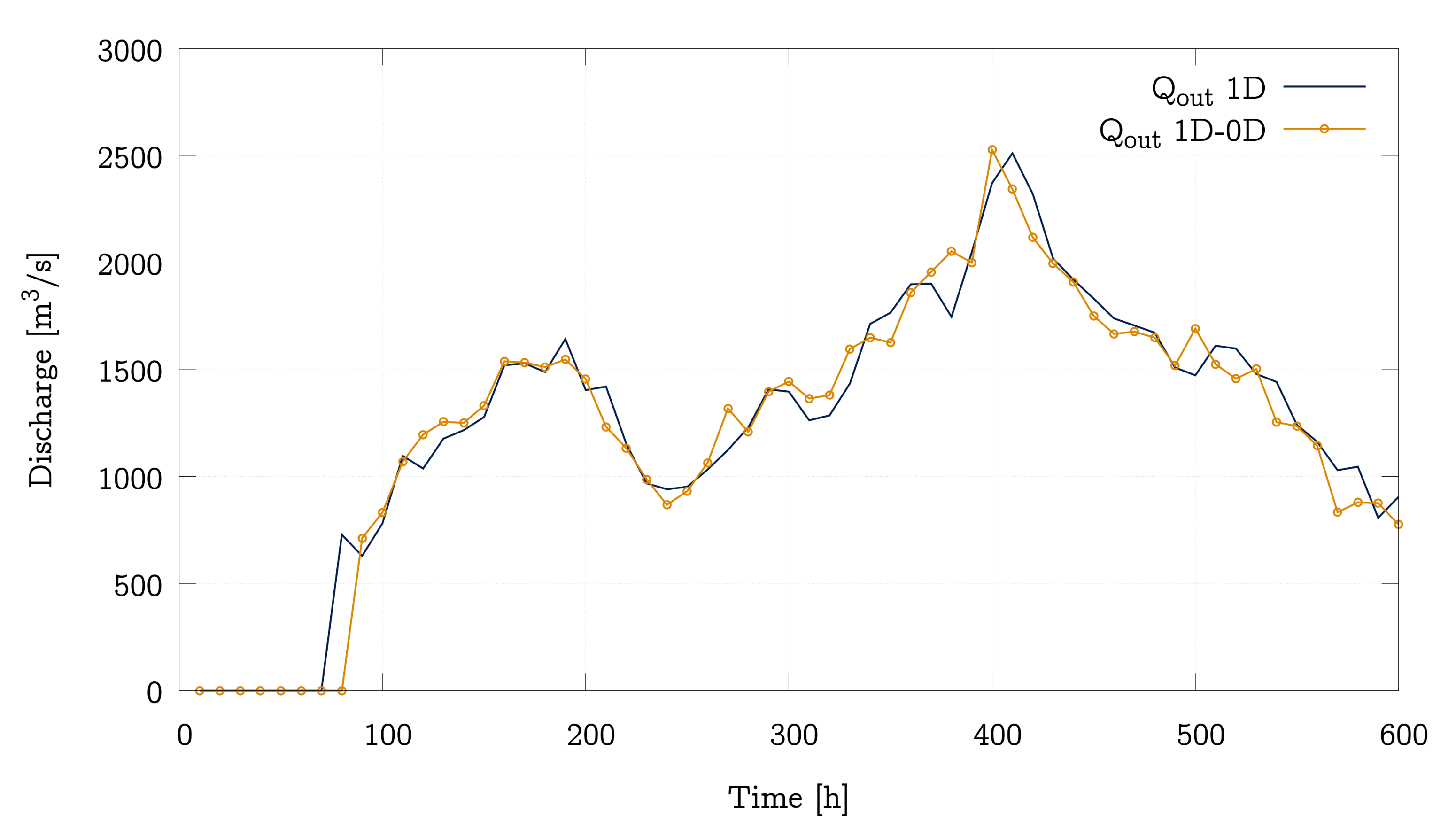
4.3. Performance Analysis of the 1D and 1D-0D Models
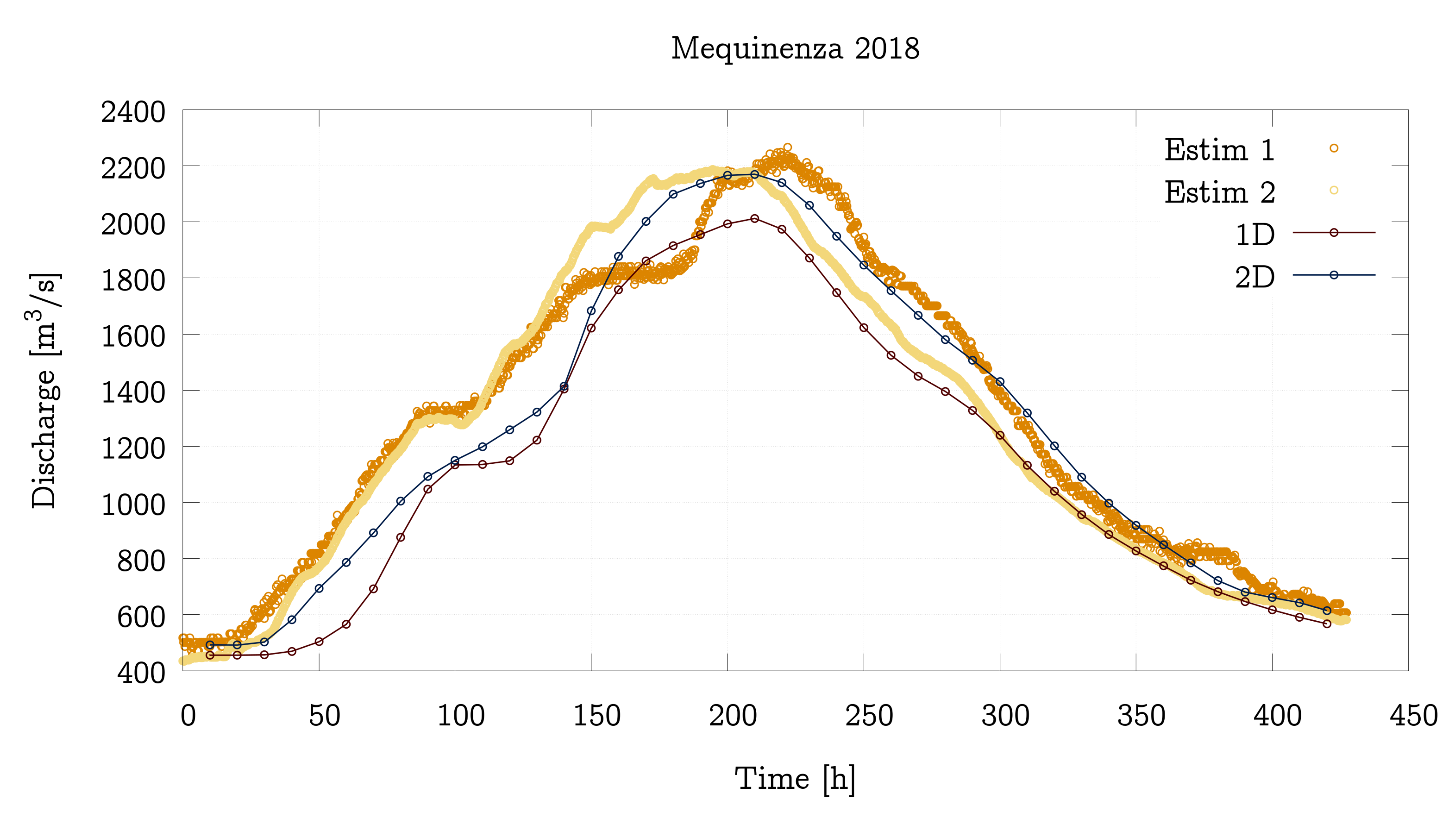
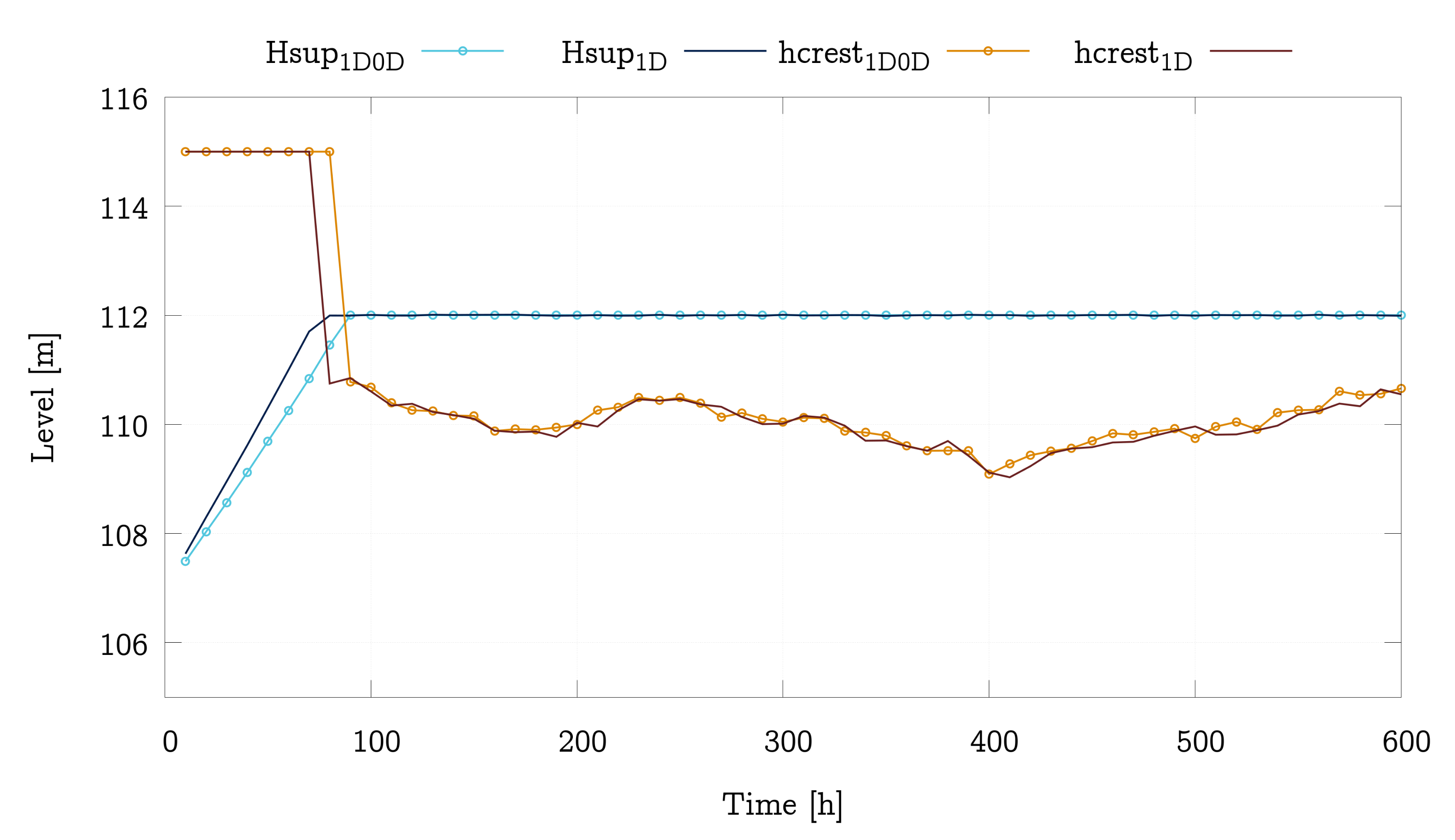
4.4. Performance Analysis of the 1D and 1D-0D Models Including DAM Regulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- C.o.t.E.U. European Parliament 2007 Directive 2007/60/EC of the European Parliament and of the Council of 23 October 2007 on the Assessment and Management of Flood Risks. EU Directive. 2007. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=celex:32007L0060 (accessed on 10 October 2021).
- Centre for Research on the Epidemiology of Disasters (CRED). The human cost of weather related disasters (1995–2015); CRED: Brussels, Belgium, 2015; pp. 1–30. [Google Scholar]
- Tanoue, M.; Taguchi, R.; Alifu, H.; Hirabayashi, Y. Residual flood damage under intensive adaptation. Nat. Clim. Chang. 2021, 11, 823–826. [Google Scholar] [CrossRef]
- Leandro, J.; Schumann, A.; Pfister, A. A step towards considering the spatial heterogeneity of urban key features in urban hydrology flood modelling. J. Hydrol. 2016, 535, 356–365. [Google Scholar] [CrossRef]
- GebreEgziabher, M.; Demissie, Y. Modeling Urban Flood Inundation and Recession Impacted by Manholes. Water 2020, 12, 1160. [Google Scholar] [CrossRef]
- Vacondio, R.; Aureli, F.; Ferrari, A.; Mignosa, P.; Palù, A. Simulation of the January 2014 flood on the Secchia River using a fast and high-resolution 2D parallel shallow-water numerical scheme. Nat. Hazards 2016, 80, 1–23. [Google Scholar] [CrossRef]
- Echeverribar, I.; Morales-Hernández, M.; Brufau, P.; García-Navarro, P. 2D numerical simulation of unsteady flows for large scale floods prediction in real time. Adv. Water Resour. 2019, 134, 103444. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Murillo, J.; García-Navarro, P. The formulation of internal boundary conditions in unsteady 2-D shallow water flows: Application to flood regulation. Water Resour. Res. 2013, 49, 471–487. [Google Scholar] [CrossRef]
- Echeverribar, I.; Morales-Hernández, M.; Brufau, P.; García-Navarro, P. Use of internal boundary conditions for levees representation: Application to river flood management. Environ. Fluid Mech. 2019, 19, 1253–1271. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Sharif, M.B.; Kalyanapu, A.; Ghafoor, S.K.; Dullo, T.T.; Gangrade, S.; Kao, S.-C.; Norman, M.R.; Evans, K.J. TRITON: A Multi-GPU open source 2D hydrodynamic flood model. Environ. Model. Softw. 2021, 141, 105034. [Google Scholar] [CrossRef]
- Chen, J.; Hill, A.A.; Urbano, L.D. A GIS-based model for urban flood inundation. J. Hydrol. 2009, 373, 184–192. [Google Scholar] [CrossRef]
- Ghansah, B.; Nyamekye, C.; Owusu, S.; Agyapong, E. Mapping flood prone and Hazards Areas in rural landscape using landsat images and random forest classification: Case study of Nasia watershed in Ghana. Civil Environ. Eng. 2021, 8, 1923384. [Google Scholar]
- Horritt, M.S.; Bates, P.D. Evaluation of 1D and 2D numerical models for predicting river flood inundation. J. Hydrol. 2002, 268, 89–99. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P.; Burguete, J.; Brufau, P. The influence of source terms on stability, accuracy and conservation in two-dimensional shallow flow simulation using triangular finite volumes. Int. J. Numer. Methods Fluids 2007, 54, 543–590. [Google Scholar] [CrossRef]
- Kalyanapu, A.J.; Shankar, S.; Pardyjak, E.R.; Judi, D.R.; Burian, S.J. Assessment of GPU computational enhancement to a 2D flood model. Environ. Model. Softw. 2011, 26, 1009–1016. [Google Scholar] [CrossRef]
- Murillo, J.; García-Navarro, P. Energy balance numerical schemes for shallow water equations with discontinuous topography. J. Comput. Phys. 2013, 236, 119–142. [Google Scholar] [CrossRef]
- Sampson, C.C.; Smith, A.M.; Bates, P.D.; Neal1, J.C.; Alfieri, L.; Freer, J.E. A high-resolution global flood hazard model. Water Resour. Res. 2015, 51, 7358–7381. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; García-Navarro, P.; Murillo, J. Influence of mesh structure on 2D full shallow water equations and SCS curve number simulation of rainfall/runoff events. J. Hydrol. 2012, 448, 39–59. [Google Scholar] [CrossRef]
- Bomers, A.; Schielen, R.M.J.; Hulscher, S.J.M.H. The influence of grid shape and grid size on hydraulic river modelling performance. Environ. Fluid Mech. 2019, 19, 1273–1294. [Google Scholar] [CrossRef]
- Fread, D.; Hsu, K. Applicability of Two Simplified Flood Routing Methods: Level-Pool and Muskingum-Cunge. In Proceedings of the ASCE National Hydraulic Engineering Conference, San Francisco, CA, USA, 25–30 July 1993; pp. 1564–1568. [Google Scholar]
- Nanía, L.S.; Gómez, M. Ingeniería Hidrológica; Grupo Editorial Universitario: Granada, Spain, 2004. [Google Scholar]
- Haun, S.; Olsen, N.R.B. Three-dimensional numerical modelling of reservoir flushing in a prototype scale. Int. J. River Basin Manag. 2012, 10, 341–349. [Google Scholar] [CrossRef]
- Mohammad, M.E.; Al-Ansari, N.; Issa, I.E.; Knutsson, S. Sediment in Mosul Dam reservoir using the HEC-RAS model. Lakes Reserv. Res. Manag. 2016, 21, 235–244. [Google Scholar] [CrossRef]
- Kawara, O.; Yura, E.; Fujii, S.; Matsumoto, T. A study on the role of hydraulic retention time in eutrophication of the Asahi River Dam reservoir. Water Sci. Technol. 1998, 37, 245–252. [Google Scholar] [CrossRef]
- Bellos, C.; Hrissanthou, V. Numerical simulation of morphological changes in rivers and reservoirs. Comput. Math. Appl. 2003, 45, 453–467. [Google Scholar] [CrossRef][Green Version]
- Henderson, F.M. Open channel flow. In Macmillan Series in Civil Engineering; McGraw-Hill: New York, NY, USA, 1966. [Google Scholar]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Fiorentini, M.; Orlandini, S. Robust numerical solution of the reservoir routing equation. Adv.Water Resour. 2013, 59, 123–132. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, W.; Wang, X. Development of a SWAT extension module to simulate riparian wetland hydrologic processes at a watershed scale. Hydrol. Process. 2008, 22, 2901–2915. [Google Scholar] [CrossRef]
- Dorchies, D.; Thirel, G.; Jay-Allemand, M.; Chauveau, M.; Dehay, F.; Bourgin, P.-Y.; Perrinb, C.; Joste, C.; Rizzolie, J.L.; Demerliac, S.; et al. Climate change impacts on multi-objective reservoir management: Case study on the Seine River basin, France. Int. J. River Basin Manag. 2014, 12, 265–283. [Google Scholar] [CrossRef][Green Version]
- Cohen Liechti, T.; Matos, J.P.; Ferràs Segura, D.; Boillat, J.-L.; Schleiss, A.J. Hydrological modelling of the Zambezi River Basin taking into account floodplain behaviour by a modified reservoir approach. Int. J. River Basin Manag. 2014, 12, 29–41. [Google Scholar] [CrossRef]
- Ginting, B.M.; Harlan, D.; Taufik, A.; Ginting, H. Optimization of reservoir operation using linear program, case study of Riam Jerawi Reservoir, Indonesia. Int. J. River Basin Manag. 2017, 15, 187–198. [Google Scholar] [CrossRef]
- Arcement, G.; Schneider, V. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; No. 2339. U.S. Geological Survey. Water-Supply Paper. USGS Publications Warehouse; 1984. Available online: https://pubs.er.usgs.gov/publication/wsp2339 (accessed on 10 October 2021).
- Toro, E.F. The Riemann Solver of Roe. In Riemann Solvers and Numerical Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Murillo, J.; García-Navarro, P. Weak solutions for partial differential equations with source terms: Application to the shallow water equations. J. Comput. Phys. 2010, 229, 4327–4368. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; Petaccia, G.; Brufau, P.; García-Navarro, P. Conservative 1D–2D coupled numerical strategies applied to river flooding: The Tiber (Rome). Appl. Math. Model. 2016, 40, 2087–2105. [Google Scholar] [CrossRef]
- Lacasta, A.; Juez, C.; Murillo, J.; García-Navarro, P. An efficient solution for hazardous geophysical flows simulation using GPUs. Comput. Geosci. 2015, 78, 63–72. [Google Scholar] [CrossRef]
- Morales-Hernández, M.; García-Navarro, P.; Burguete, J.; Brufau, P. A conservative strategy to couple 1D and 2D models for shallow water flow simulation. Comput. Fluids 2013, 81, 26–44. [Google Scholar] [CrossRef]
- Leveque, R. Numerical Methods for Conservation Laws Lectures in Mathematics; ETH Zürich; Birkhuser: Zürich, Switzerland; Basel, Switzerland, 1992. [Google Scholar]
- Sotelo, G. Hidráulica General; Limusa: Johannesburg, South Africa, 2002; Volume 1. [Google Scholar]
- Panda, R.C. Introduction to PID Controllers; IntechOpen: London, UK, 2012. [Google Scholar]
| Event | Duration | 2D GPU Time | 1D CPU Time |
|---|---|---|---|
| 2015 | 600 h | 47 h | 511 s |
| 2018 | 430 h | 23.8 h | 364 s |
| Event | Duration | Pure 1D | 1D-0D |
|---|---|---|---|
| 2015 | 600 h | 511 s | 196 s |
| Event | Duration | Pure 1D | 1D-0D |
|---|---|---|---|
| 2015 | 600 h | 484 s | 176 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Echeverribar, I.; Vallés, P.; Mairal, J.; García-Navarro, P. Efficient Reservoir Modelling for Flood Regulation in the Ebro River (Spain). Water 2021, 13, 3160. https://doi.org/10.3390/w13223160
Echeverribar I, Vallés P, Mairal J, García-Navarro P. Efficient Reservoir Modelling for Flood Regulation in the Ebro River (Spain). Water. 2021; 13(22):3160. https://doi.org/10.3390/w13223160
Chicago/Turabian StyleEcheverribar, Isabel, Pablo Vallés, Juan Mairal, and Pilar García-Navarro. 2021. "Efficient Reservoir Modelling for Flood Regulation in the Ebro River (Spain)" Water 13, no. 22: 3160. https://doi.org/10.3390/w13223160
APA StyleEcheverribar, I., Vallés, P., Mairal, J., & García-Navarro, P. (2021). Efficient Reservoir Modelling for Flood Regulation in the Ebro River (Spain). Water, 13(22), 3160. https://doi.org/10.3390/w13223160






