Possibility of Capsizing of a Dredger during Towing
Abstract
:1. Introduction
2. Freeboard and Stability Requirements for Dredgers
3. Accidents of the Dredgers
3.1. Accident of the Dredger “Kuokka Pekka 5”
3.2. Accident of the Dredger ”Rozgwiazda”
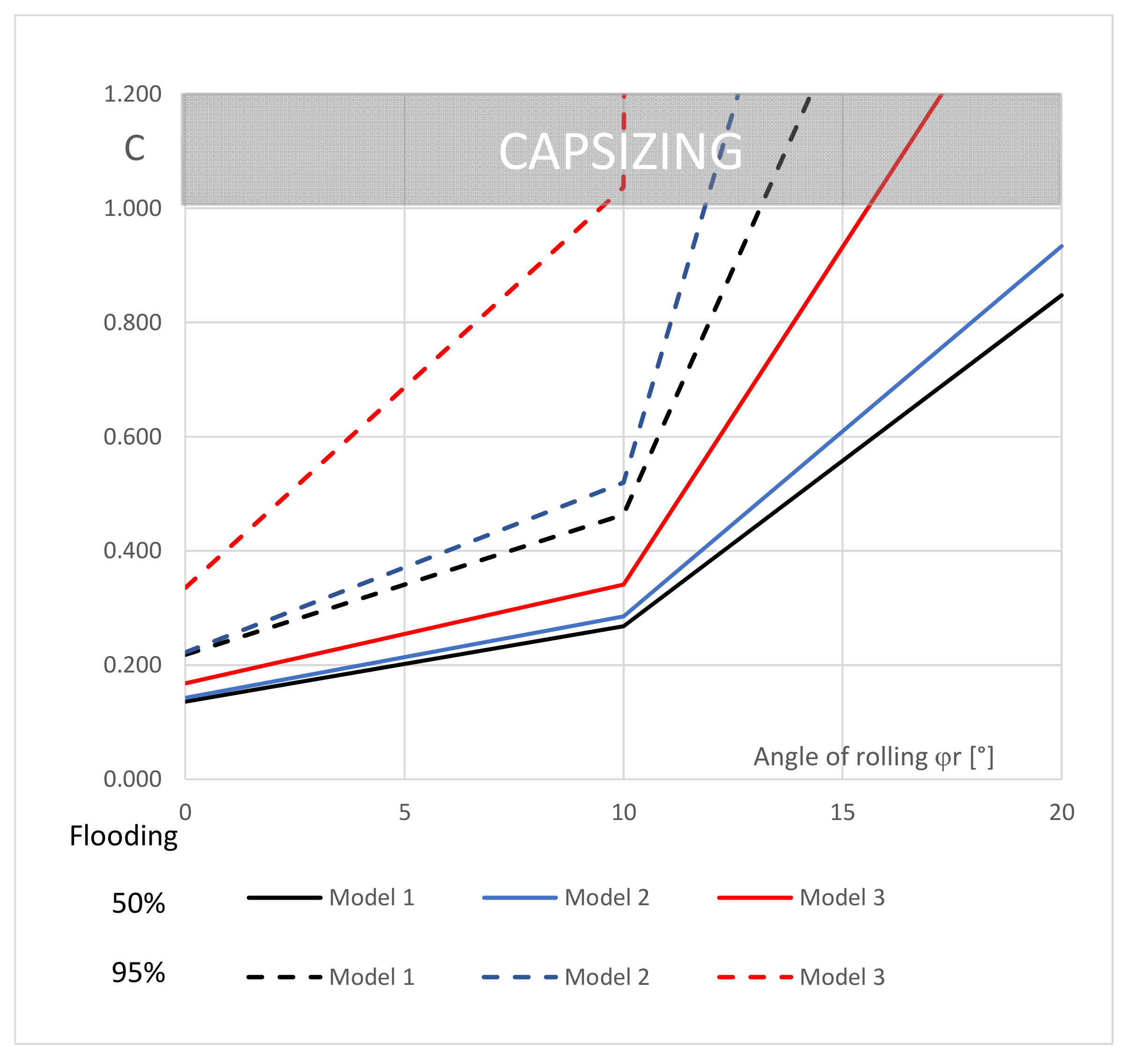
4. Simulation Test
4.1. Simulation Assumptions
- Initial draft and freeboard have been assumed to be identical for all models;
- The location of the center of mass in all models has been assumed for the seaworthy condition of the dredger and its characteristic instrumentation;
- The displacement of the dredgers has been determined on the basis of their initial draft;
- The initial trim has been assumed to be 0.00 m;
- The position of the dredger during longitudinal surging has been determined by the trim measured as the difference of drafts to the water surface;
- The watertight compartments of the models have had identical dimensions, but their number has depended on the adopted model;
- In the event of flooding of the watertight compartments, the amount of water has been assumed as a slowly changing value, and in the final stage as a constant;
- Static and dynamic heeling moments have been calculated for different model trims. They illustrate the physical trim of the dredger as well as its temporary longitudinal surging;
- Longitudinal and transverse windage areas have been assumed to be identical for each model.
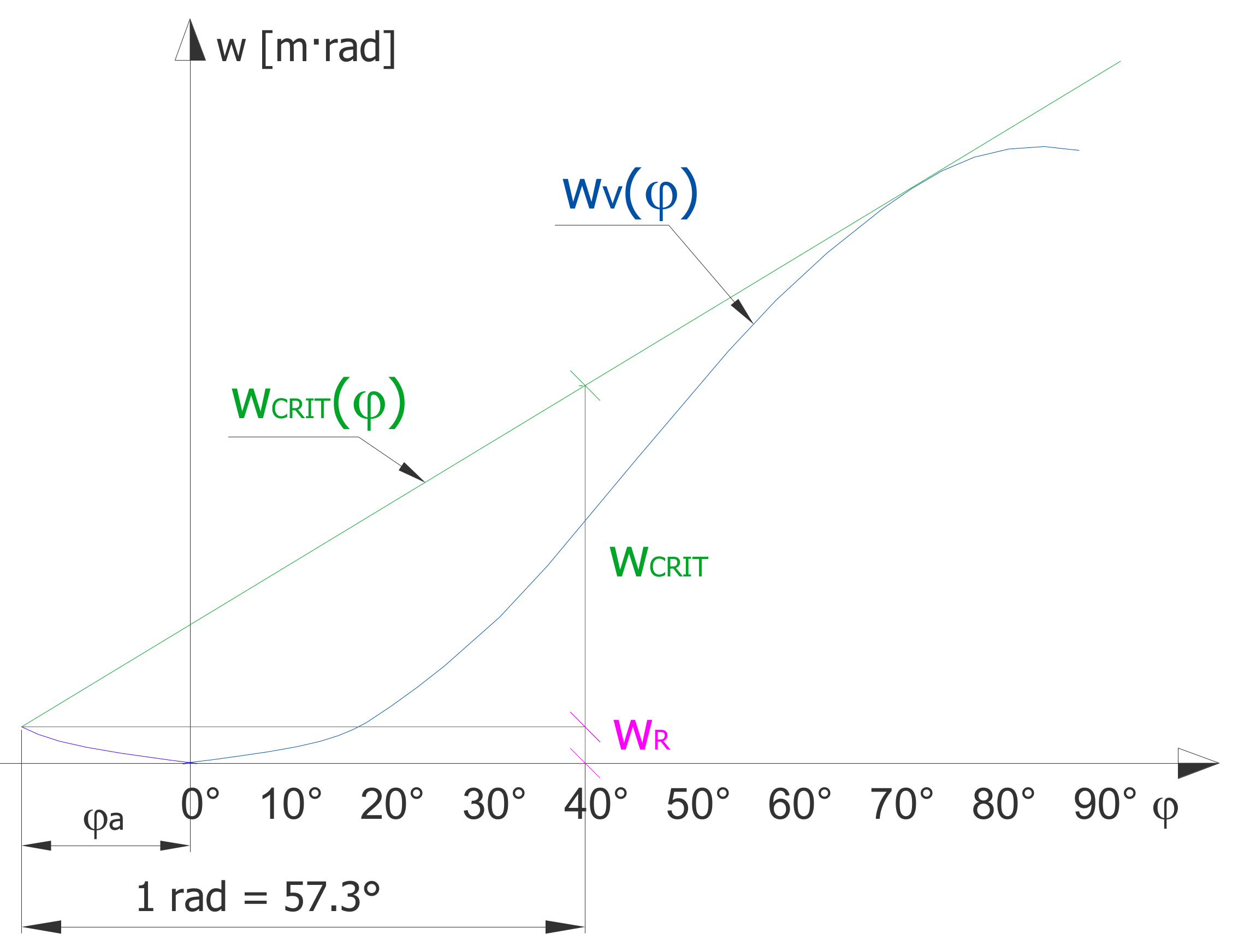
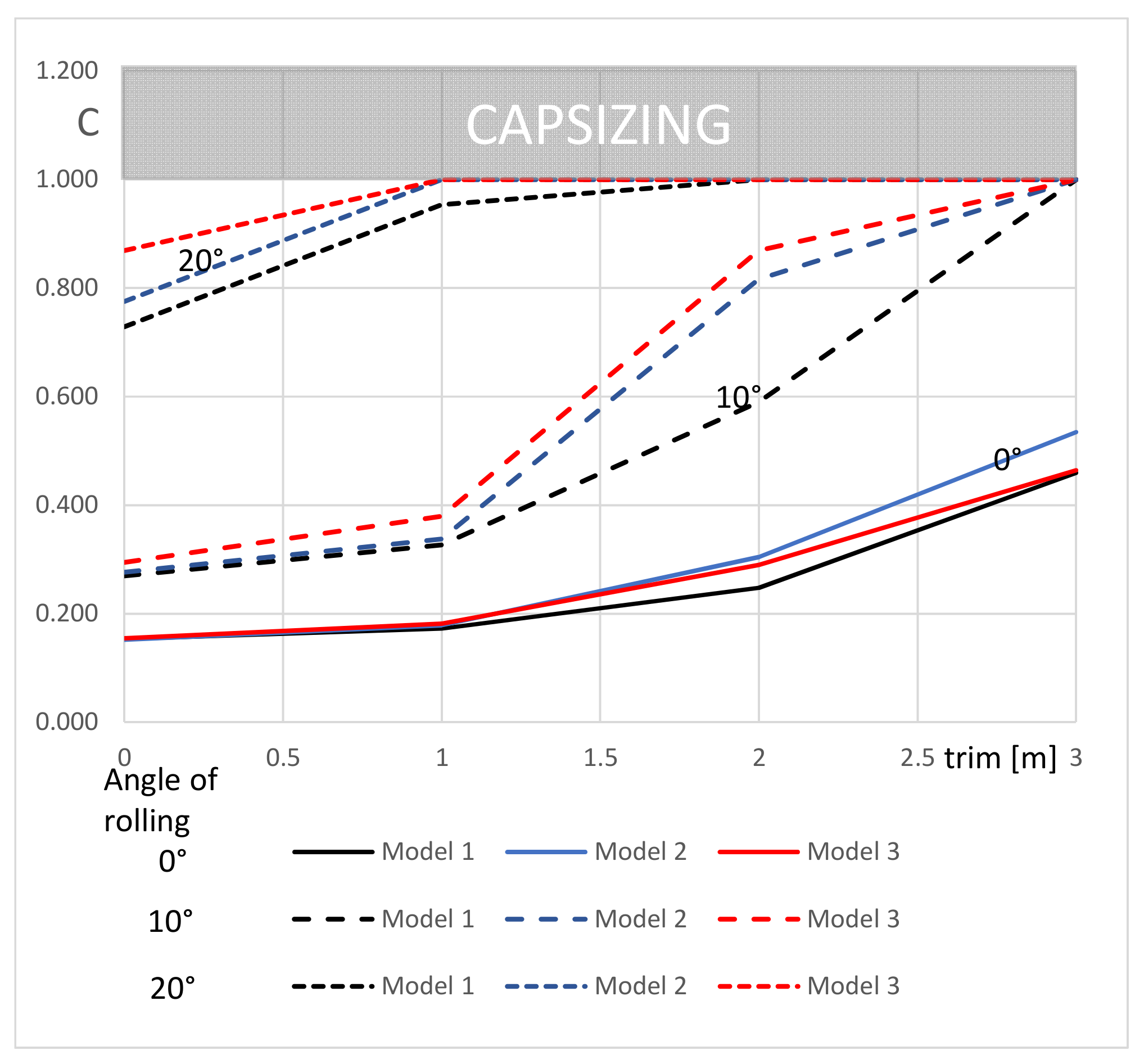
4.2. Simulation of Watercraft Capsizing
- static heeling moments caused by the action of the tow and the wind;
- dynamic heeling moments caused by the action of the tow and the wind, together with vessel pitching;
- asymmetric flooding of watertight compartments of the vessel.
- heeling moment due to tow jerk—MT;
- heeling moment due to gust of wind—MW.
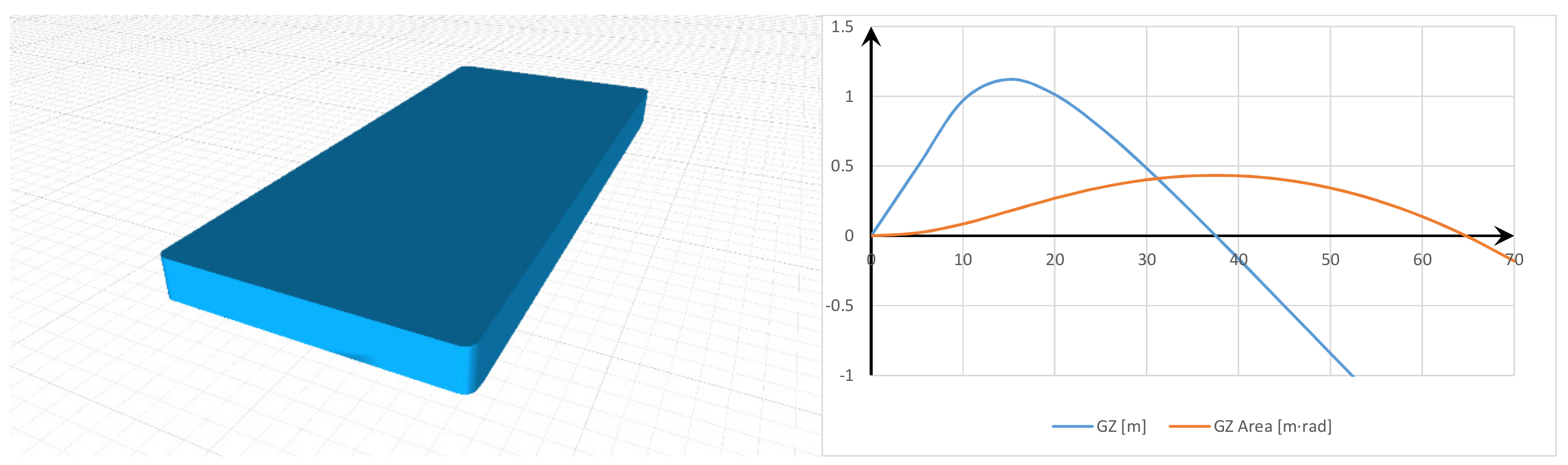
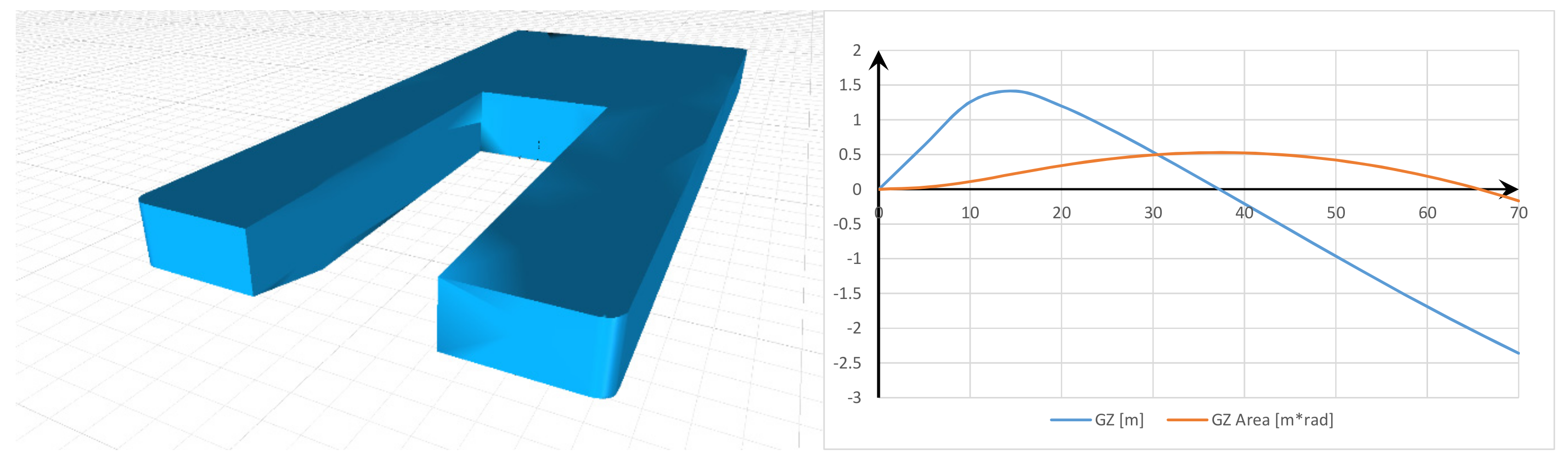
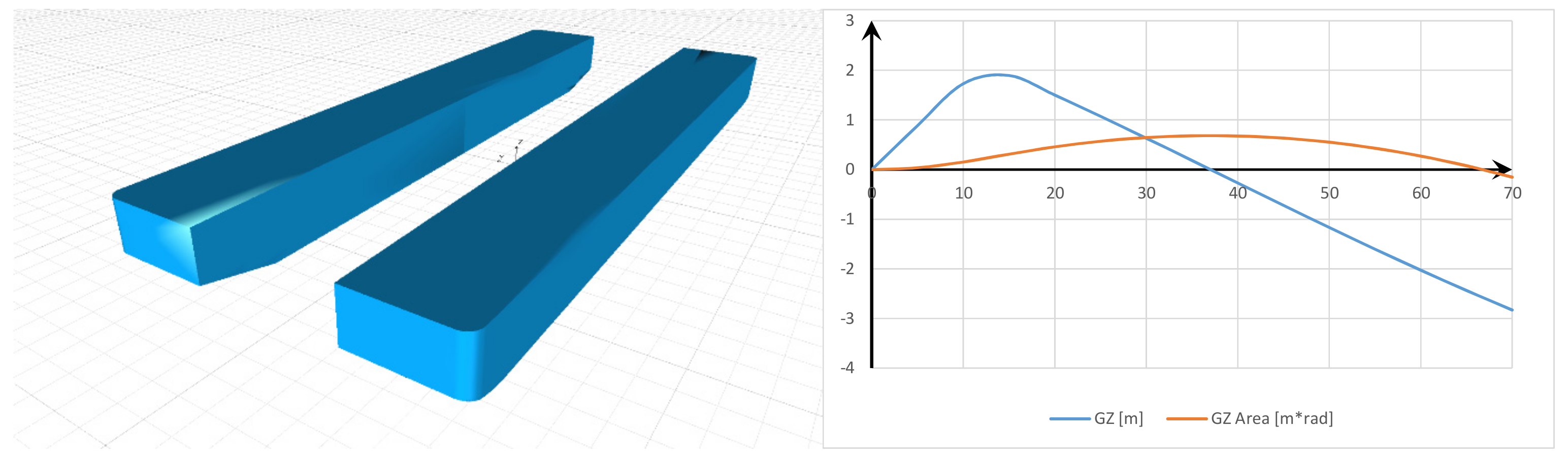
4.3. Watercraft in Undamaged Condition
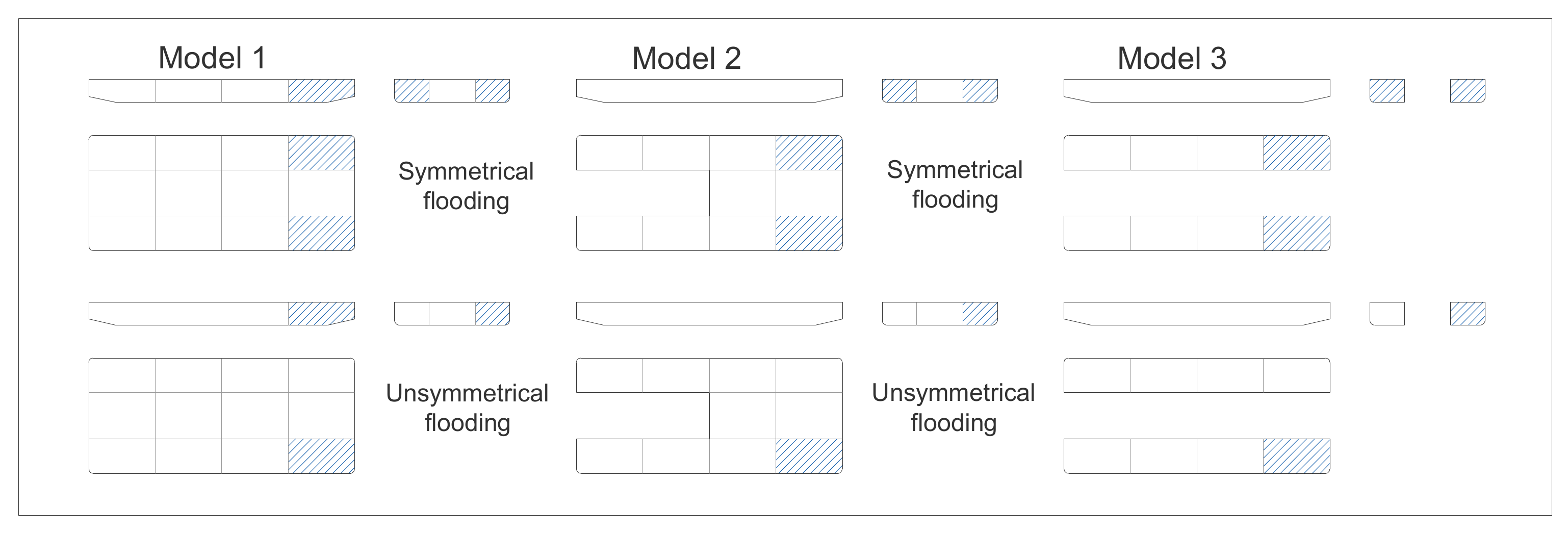
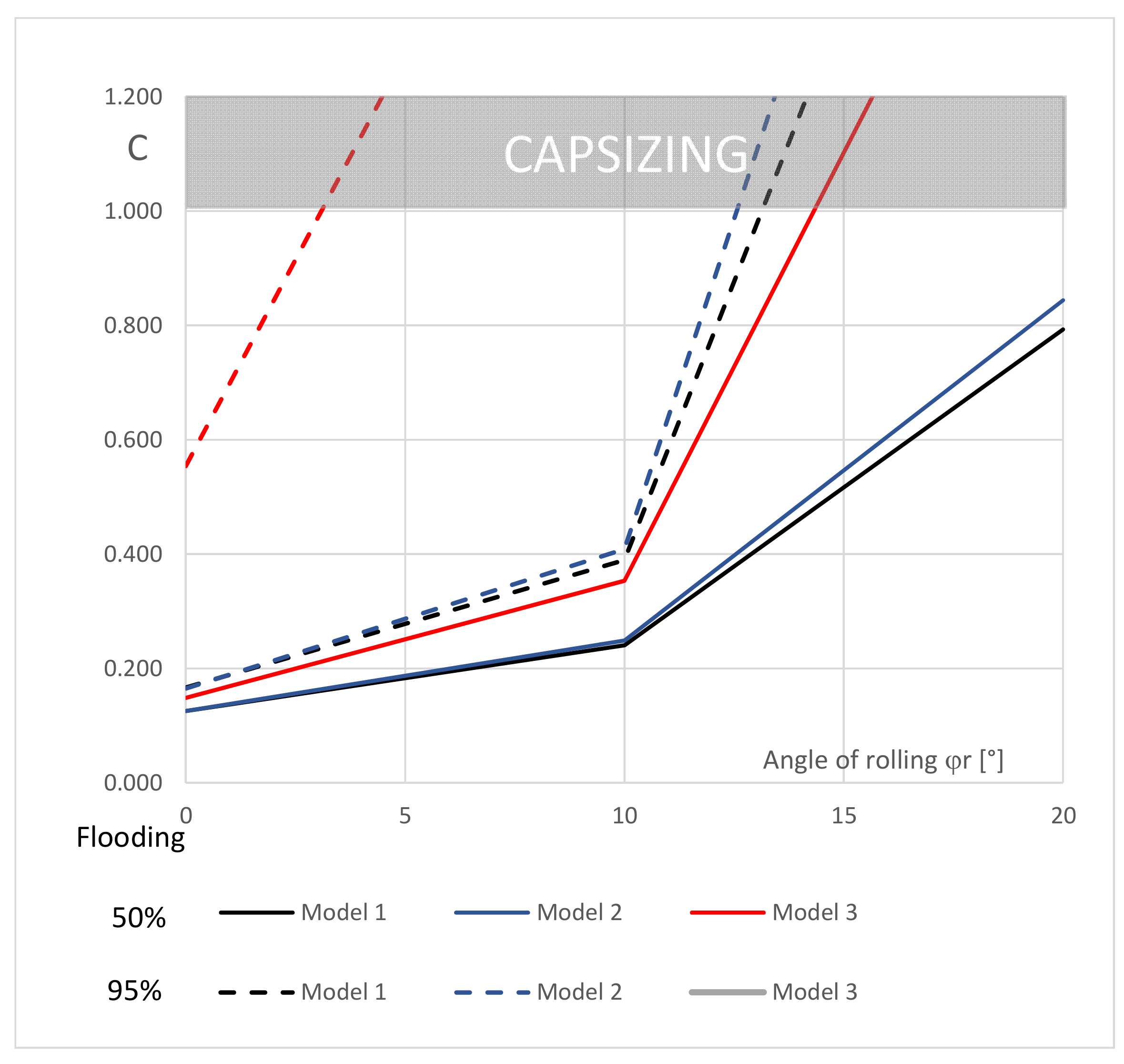
4.4. Simulation of Flooding of Watertight Compartments
- symmetrical flooding up to 50% and 95% of the compartment capacity;
- unsymmetrical flooding up to 50% and 95% of the right compartment capacity;
- The same dimensions of watertight compartments have been assumed for all models.
5. Discussion
6. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Kaizer, A. Expert Survey Method as a Technique to Support the Decision-Making Process During Dredging Activity at the Harbour. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2020, 14, 187–190. [Google Scholar] [CrossRef]
- Blokus, A.; Dziula, P. Safety Analysis of Interdependent Critical Infrastructure Networks. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2019, 13, 781–787. [Google Scholar] [CrossRef]
- Berg, T.E.; Selvik, Ø. Changes in and Recent Experiences from Norwegian Emergency Towing Service (NETS). TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2021, 15, 203–208. [Google Scholar] [CrossRef]
- Watanabe, K.; Mizuno, S. Development of a Small Tsunami Shelter and Its Sea Experiment of Towing and Drifting. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2020, 14, 75–81. [Google Scholar] [CrossRef]
- Berg, T.E.; Selvik, Ø.; Jordheim, O.K. Norwegian Emergency Towing Service–Past–Present and Future. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2020, 14, 83–88. [Google Scholar] [CrossRef]
- Dang, A.T.N.; Kumar, L.; Reid, M.; Nguyen, H. Remote Sensing Approach for Monitoring Coastal Wetland in the Mekong Delta, Vietnam: Change Trends and Their Driving Forces. Remote Sens. 2021, 13, 3359. [Google Scholar] [CrossRef]
- Kim, H.-D.; Kim, K.-H.; Shim, K.-T.; Oh, H. Applicability Study of a Sunken Vessel as an Artificial Reef in a High Wave Energy Zone. Energies 2021, 14, 4374. [Google Scholar] [CrossRef]
- Ouyang, Y.; Yang, Q.; Chen, X.; Xu, Y. An Analytical Model for Rock Cutting with a Chisel Pick of the Cutter Suction Dredger. J. Mar. Sci. Eng. 2020, 8, 806. [Google Scholar] [CrossRef]
- Pion, L.M.; Bernardino, J.C. Dredging Volumes Prediction for the Access Channel of Santos Port Considering Different Design Depths. TransNav Int. J. Mar. Navig. Saf. Sea Transp. 2018, 12, 505–514. [Google Scholar] [CrossRef]
- Woo, D.; Choe, H.; Im, N.-K. Analysis of the Relationship between GM and IMO Intact Stability Parameters to Propose Simple Evaluation Methodology. J. Mar. Sci. Eng. 2021, 9, 735. [Google Scholar] [CrossRef]
- Ruoppaaja KUOKKA PEKKA 5. In Kaatuminen Olkiluodon Edustalla; 1997; Available online: https://www.finna.fi/Record/utu.999430205405971 (accessed on 27 October 2021).
- Judgment of the Court of Appeal in Szczecin; I ACa 230/19; 2020. Available online: http://orzeczenia.szczecin.sa.gov.pl/details/$N/155500000000503_I_ACa_000230_2019_Uz_2020-01-22_001 (accessed on 27 October 2021).
- IMO. Guidelines for the Assignment of Reduced Freeboards for Dredgers, DR-68; London, UK, 2011; Available online: https://puc.overheid.nl/nsi/doc/PUC_2057_14/1/ (accessed on 27 October 2021).
- IMO. International Convention on Load Lines; London, UK, 1966; ISBN 978-92-801-4194-8. Available online: https://treaties.un.org/doc/Publication/UNTS/Volume%20640/volume-640-I-9159-English.pdf (accessed on 27 October 2021).
- IMO. Code for Special Purpose Ships (SPS); IMO: London, UK, 2008; ISBN 978-92-801-1495-9. [Google Scholar]
- IMO. IMO IC874E Intl. Code on Intact Stability (IS); IMO: London, UK, 2008; ISBN 978-92-801-1720-2. [Google Scholar]
- Sutulo, S.; Guedes Soares, C. Review on Ship Manoeuvrability Criteria and Standards. J. Mar. Sci. Eng. 2021, 9, 904. [Google Scholar] [CrossRef]
- Kaizer, A.; Neumann, T. The Model of Support for the Decision-Making Process, While Organizing Dredging Works in the Ports. Energies 2021, 14, 2706. [Google Scholar] [CrossRef]


| ISC’2008 A 2.2 | ISC’2008 B 2.5 | |
|---|---|---|
| The area under the righting lever curve from 0° to 15° if the maximum righting lever occurs at an angle of 15°. | - | 0.07 m·rad |
| The area under the righting lever curve from 0° to 30° if the maximum righting lever occurs at an angle of 30° or more. | 0.055 m·rad | 0.055 m·rad |
| The area under the righting lever curve from 0° to the maximum righting lever angle if the maximum righting lever occurs between 15° and 30°. | - | |
| The area under the righting lever curve counted from 30° to 40° or to the angle of flooding. | 0.030 m·rad | 0.030 m·rad |
| Righting lever value for an angle of heel of 30° or more than 30°. | 0.20 m | 0.20 m |
| The angle of the maximum righting arm. | 25° | 15° |
| Initial metacentric height with free liquid surface corrections. | 0.15 m | 0.15 m |
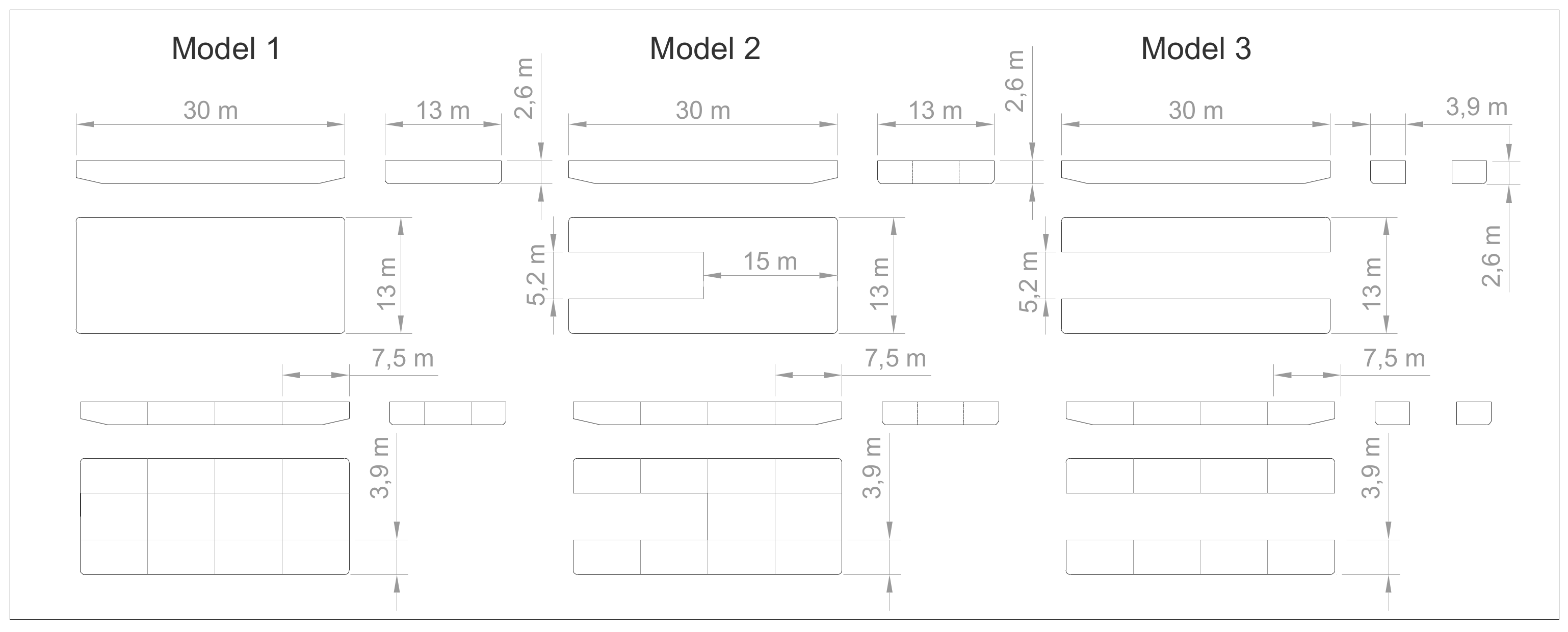
| Parameter | Symbol | Model 1 | Model 2 | Model 3 |
|---|---|---|---|---|
| Length | L | 30.00 m | 30.00 m | 30.00 m |
| Breadth | B | 13.00 m | 13.00 m | 13.00 m |
| Lateral Height | H | 2.60 m | 2.60 m | 2.60 m |
| Draft | T | 1.60 m | 1.60 m | 1.60 m |
| Freeboard | FB | 1.00 m | 1.00 m | 1.00 m |
| Displacement | D | 608 t | 486 t | 361 t |
| Vertical center of gravity | VCG | 4.50 m | 4.80 m | 5.50 m |
| Longitudinal center of gravity | LCG | 0.00 m | 1.82 m | 0.00 m |
| The transverse coordinate of the center of gravity | TCG | 0.00 m | 0.00 m | 0.00 m |
| Longitudinal metacentric height | GML | 46.62 m | 43.17 m | 44.02 m |
| Transverse metacentric height | GMT | 5.56 m | 7.21 m | 9.72 m |
| Transverse windage area | AWT | 220 m2 | 220 m2 | 220 m2 |
| Criteria | Value of gr. | Model 1 | Model 2 | Model 3 | |||
|---|---|---|---|---|---|---|---|
| A(0° → 15°) | 0.070 m·rad | 0.176 m·rad | OK | 0.227 m·rad | OK | 0.361 m·rad | OK |
| A(30° → 40°) | 0.030 m·rad | 0.030 m·rad | OK | 0.037 m·rad | OK | 0.182 m·rad | OK |
| GZMAX(φ ≥ 30°) | 0.20 | 0.40 m | OK | 0.54 m | OK | 0.63 m | OK |
| φGZMAX | 15° | 15° | OK | 15° | OK | 15° | OK |
| GM’ | 0.15 m | 5.56 m | OK | 7.21 m | OK | 9.72 m | OK |
| Weather K | 1.0 | 1.11 | OK | 1.06 | OK | 1.02 | OK |
| lw1 | 0.088 m | 0.110 m | 0.148 m | ||||
| lw2 | 0.131 m | 0.164 m | 0.221 m | ||||
| φ1 | 20.2° | 20.2° | 20.2° | ||||
| Parameters | Symmetrical Flooding | Unsymmetrical Flooding |
|---|---|---|
| Mass of water 50% | 60 t | 30 t |
| VCG 50% | 0.68 m | 0.68 m |
| Mass of water 95% | 120 t | 60 t |
| VCG 95% | 1.36 m | 1.36 m |
| LCG | 11.20 m | 11.20 m |
| TCG | 0.00 m | 4.50 m |
| Parameters | Symbol | Model 1 | Model 2 | Model 3 | |||
|---|---|---|---|---|---|---|---|
| 50% | 95% | 50% | 95% | 50% | 95% | ||
| Displacement | D | 668 | 728 | 546 | 606 | 421 | 481 |
| Longitudinal center of gravity | LCG | 0.66 | 1.22 | 2.43 | 2.92 | 1.06 | 1.85 |
| Vertical center of gravity | VCG | 4.27 | 4.13 | 4.49 | 4.29 | 4.99 | 4.69 |
| The transverse coordinate of the center of gravity | TCG | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| Draft | T | 1.75 | 1.90 | 1.76 | 1.92 | 1.85 | 2.12 |
| Trim | t | 0.48 | 0.96 | 0.48 | 0.95 | 0.77 | 1.60 |
| Draft forward | TF | 1.99 | 2.38 | 2.00 | 2.39 | 2.23 | 2.92 |
| Draft aft | TA | 1.51 | 1.42 | 1.52 | 1.44 | 1.46 | 1.32 |
| Heel | φ | 0 | 0 | 0 | 0 | 0 | 0 |
| Parameters | Symbol | Model 1 | Model 2 | Model 3 | |||
|---|---|---|---|---|---|---|---|
| 50% | 95% | 50% | 95% | 50% | 95% | ||
| Displacement | D | 638 | 668 | 516 | 546 | 391 | 421 |
| Longitudinal center of gravity | LCG | 0.35 | 0.66 | 2.14 | 2.43 | 0.57 | 1.06 |
| Vertical center of gravity | VCG | 4.32 | 4.24 | 4.56 | 4.45 | 5.13 | 4.94 |
| The transverse coordinate of the center of gravity | TCG | 0.21 | 0.40 | 0.26 | 0.50 | 0.35 | 0.64 |
| Draft | T | 1.67 | 1.74 | 1.68 | 1.75 | 1.72 | 1.84 |
| Trim | t | 0.24 | 0.48 | 0.24 | 0.48 | 0.37 | 0.78 |
| Draft forward | TF | 1.79 | 1.98 | 1.80 | 1.99 | 1.91 | 2.33 |
| Draft aft | TA | 1.55 | 1.50 | 1.56 | 1.51 | 1.54 | 1.45 |
| Heel | φ | 2.3 | 4.5 | 2.2 | 4.4 | 2.0 | 4.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Soliwoda, J.; Kaizer, A.; Neumann, T. Possibility of Capsizing of a Dredger during Towing. Water 2021, 13, 3027. https://doi.org/10.3390/w13213027
Soliwoda J, Kaizer A, Neumann T. Possibility of Capsizing of a Dredger during Towing. Water. 2021; 13(21):3027. https://doi.org/10.3390/w13213027
Chicago/Turabian StyleSoliwoda, Jarosław, Adam Kaizer, and Tomasz Neumann. 2021. "Possibility of Capsizing of a Dredger during Towing" Water 13, no. 21: 3027. https://doi.org/10.3390/w13213027
APA StyleSoliwoda, J., Kaizer, A., & Neumann, T. (2021). Possibility of Capsizing of a Dredger during Towing. Water, 13(21), 3027. https://doi.org/10.3390/w13213027






