Resilience Assessment and Critical Point Identification for Urban Water Supply Systems under Uncertain Scenarios
Abstract
1. Introduction
2. Research Methods and Data Sources
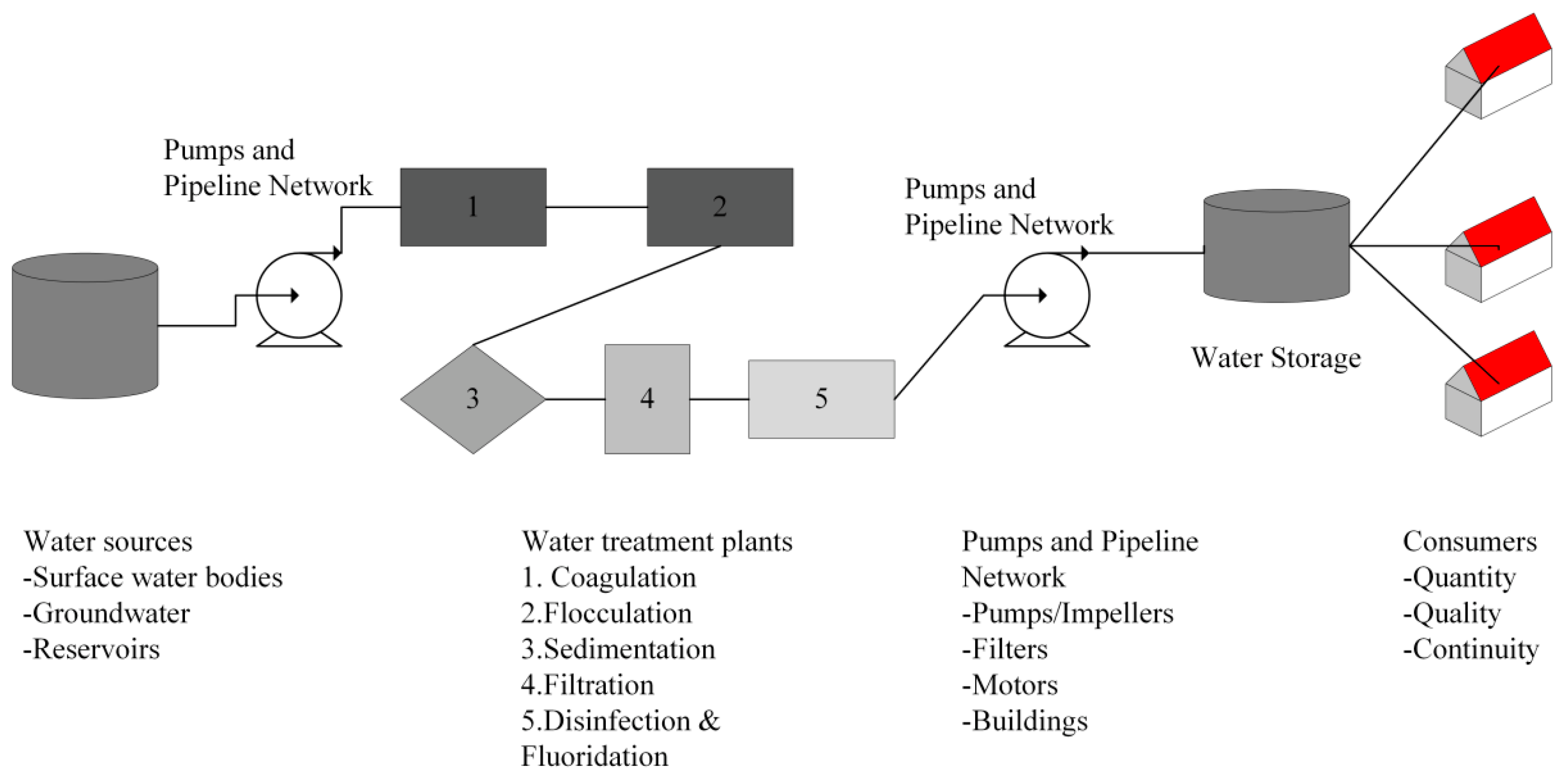
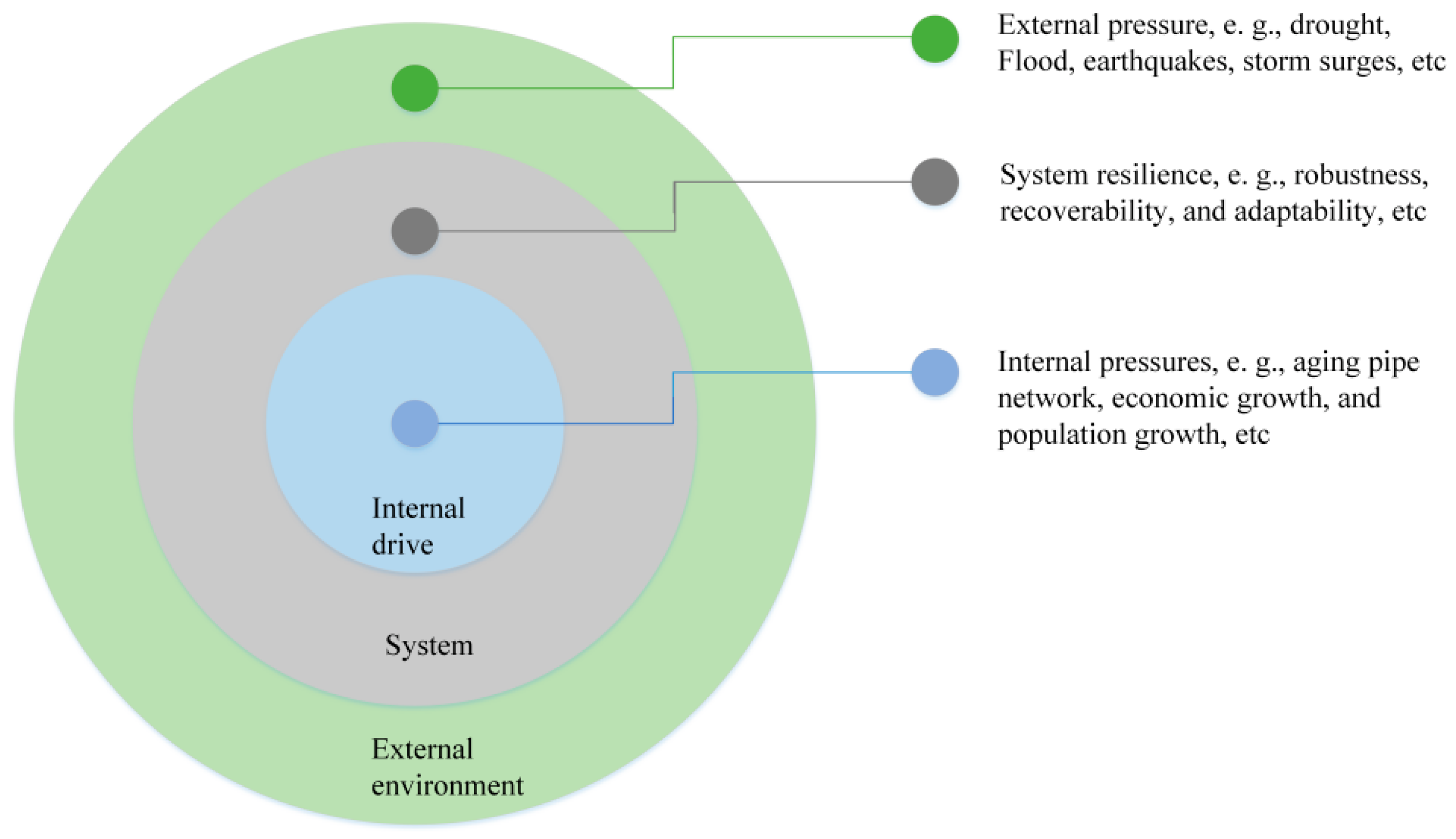
2.1. The Concept of a Water Supply System and the Definition of Resilience
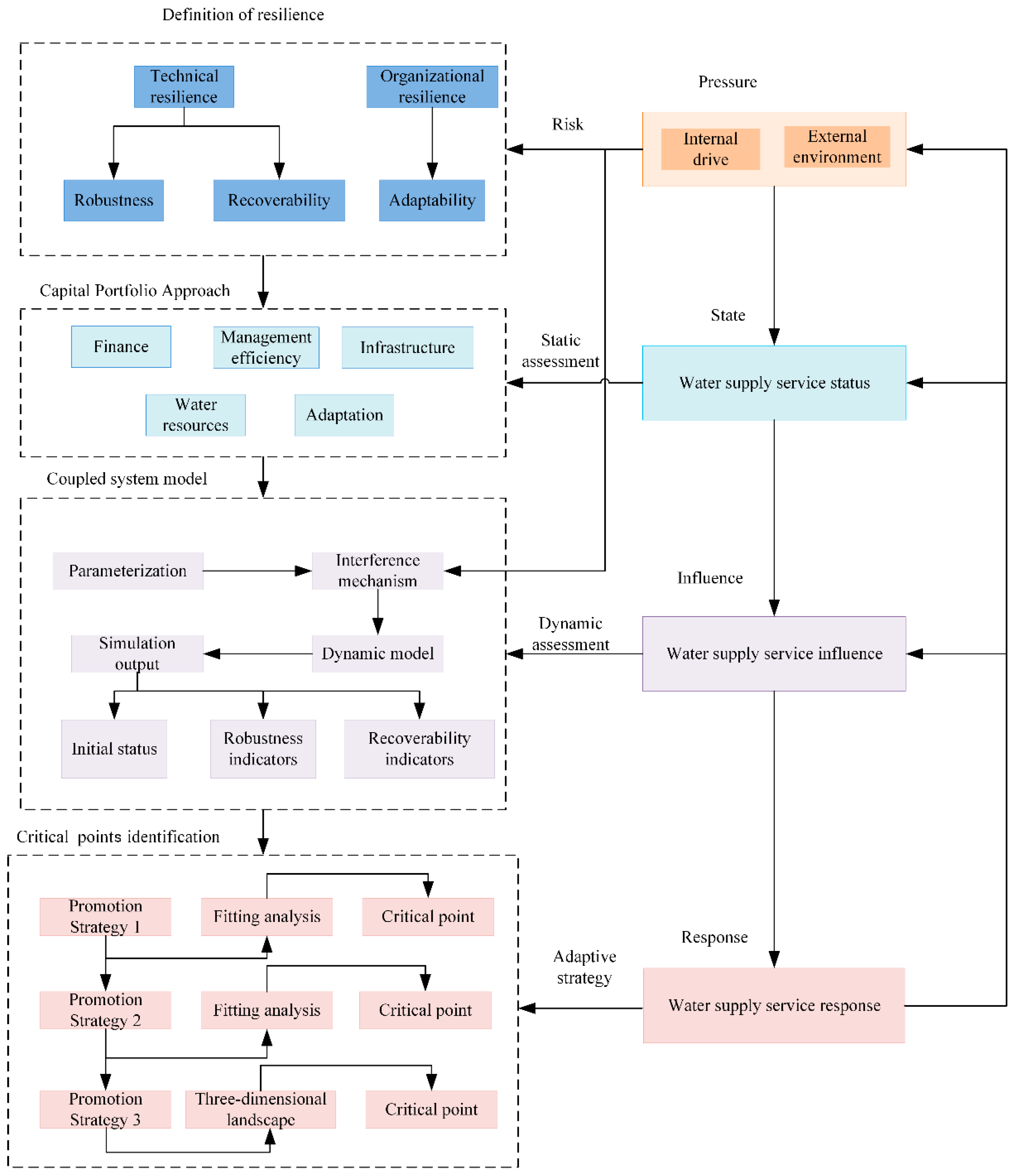
2.2. Research Theory and Framework
2.3. Static Assessment Model: Capital Portfolio Approach (CPA)
- Financial resources (financial capital (F)), including the costs of adaptation measures in the water sector, such as the construction, operation, and maintenance of water supply systems, and the financial costs of expanding infrastructure;
- Managerial efficiency (political capital (P)), which is used to support the stable operation of the water supply system and maintain the system’s water service capacity;
- Infrastructure (physical capital (I)) for the storage, treatment, and distribution of potable water to the target;
- Available water resources (natural capital (W)), including the total amount of water that is naturally available: collected rainwater, recycled water, and desalinated water;
- Organizational adaptation (social capital (A)), measures taken by managers in response to disruptive events resulting in inadequate water services.
2.4. Dynamic Assessment Model: Dynamic Model of Coupled System
2.5. Calculation of Model Parameters
2.6. Setting Disturbance Variables
2.7. Disturbance Mechanism
2.8. Data Sources
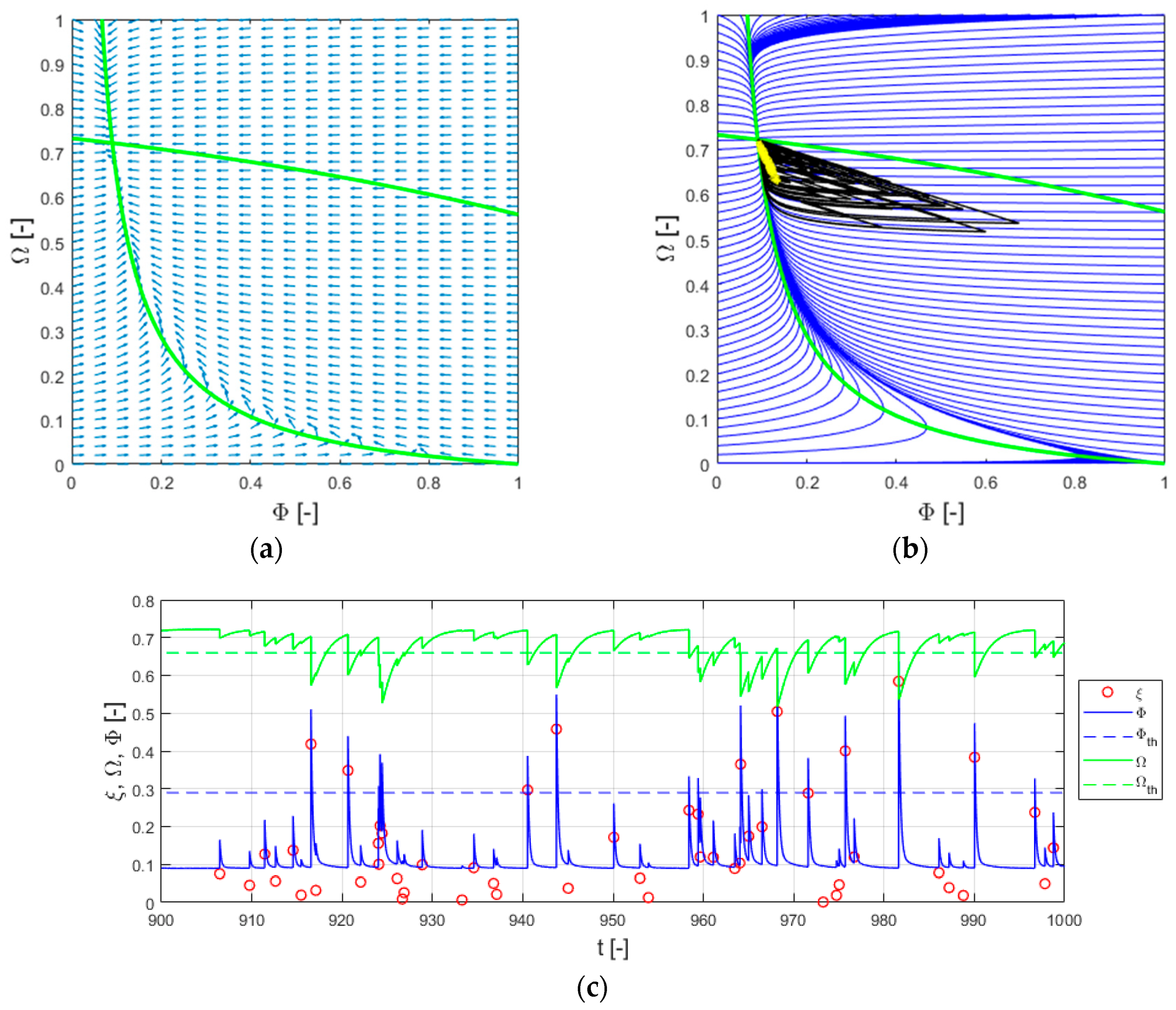
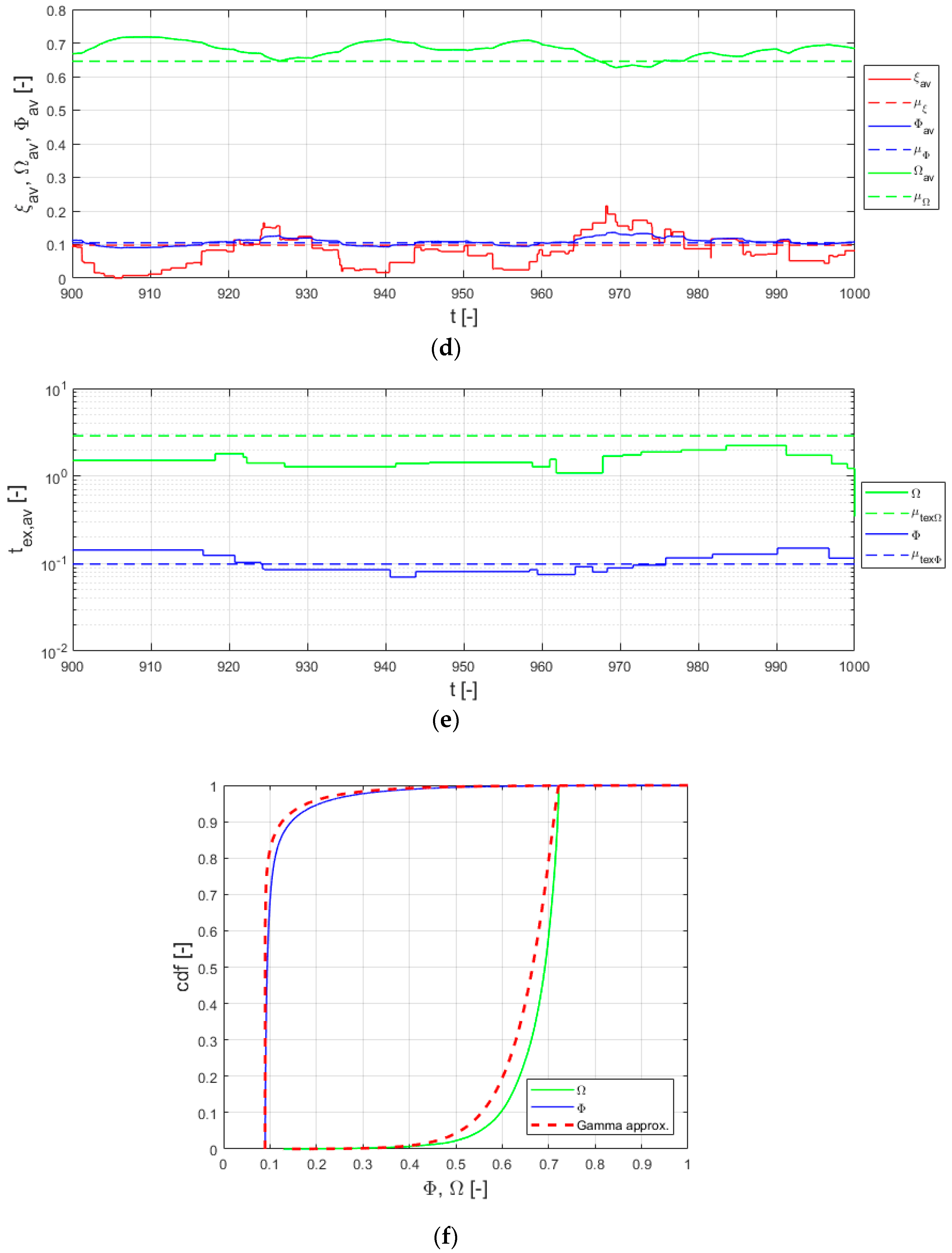
3. Results of Resilience Assessment
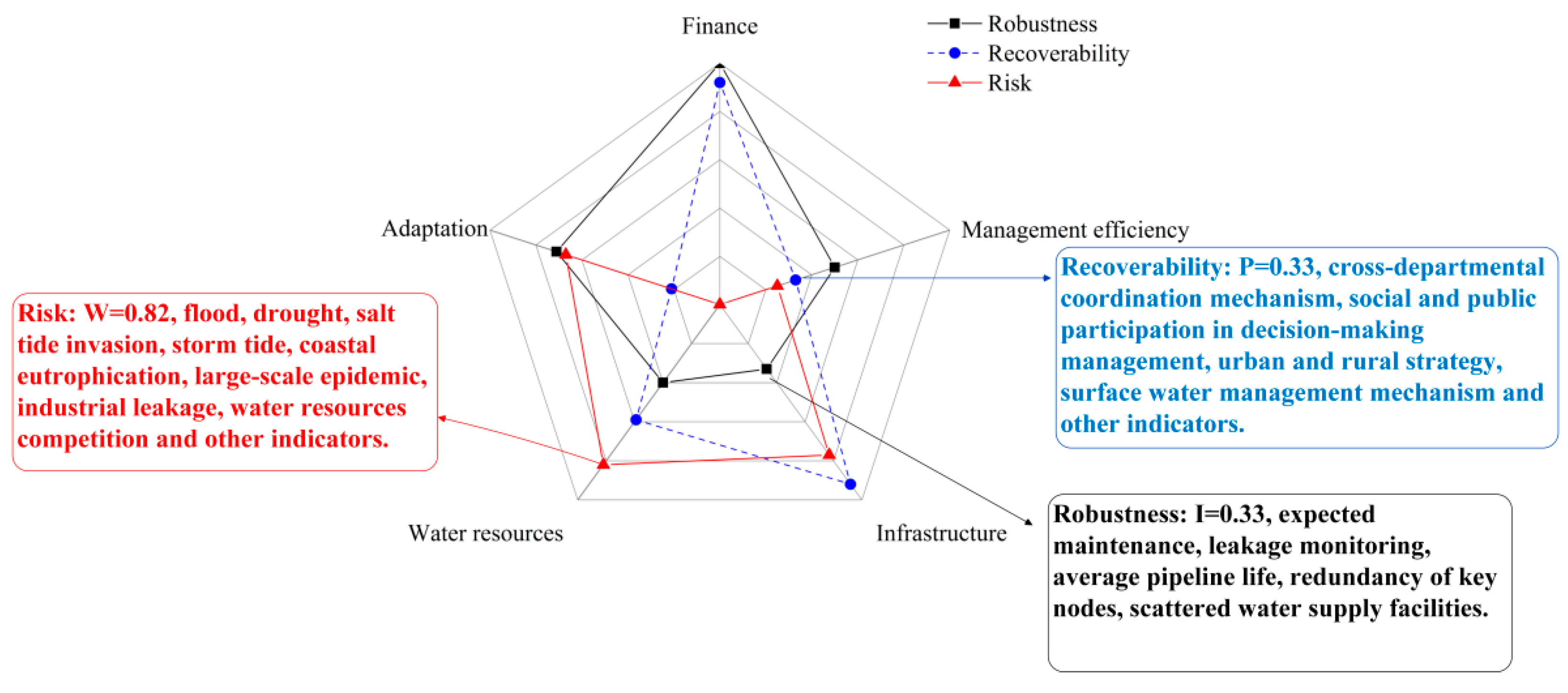
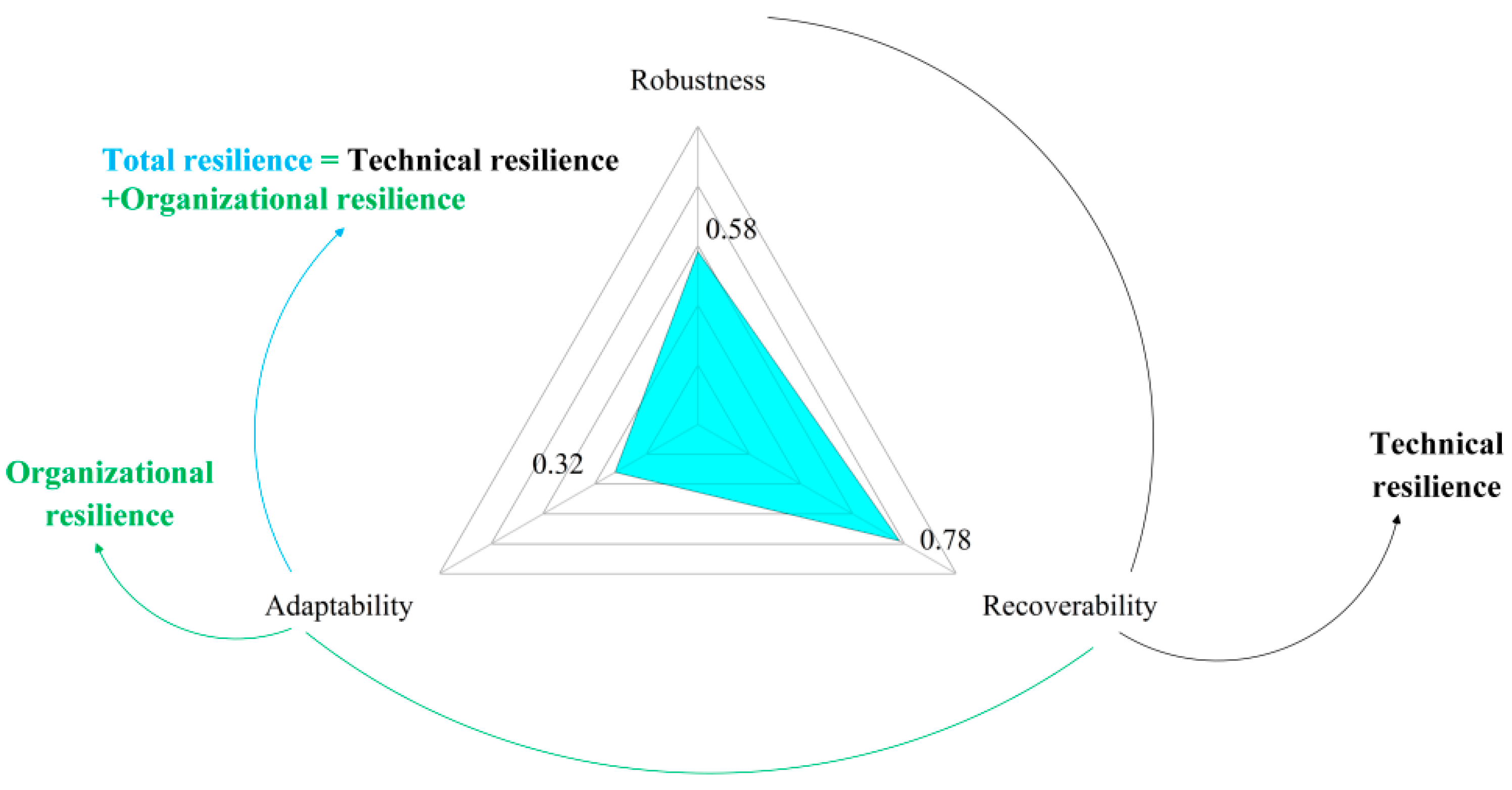
3.1. Results of Resilience Static Assessment
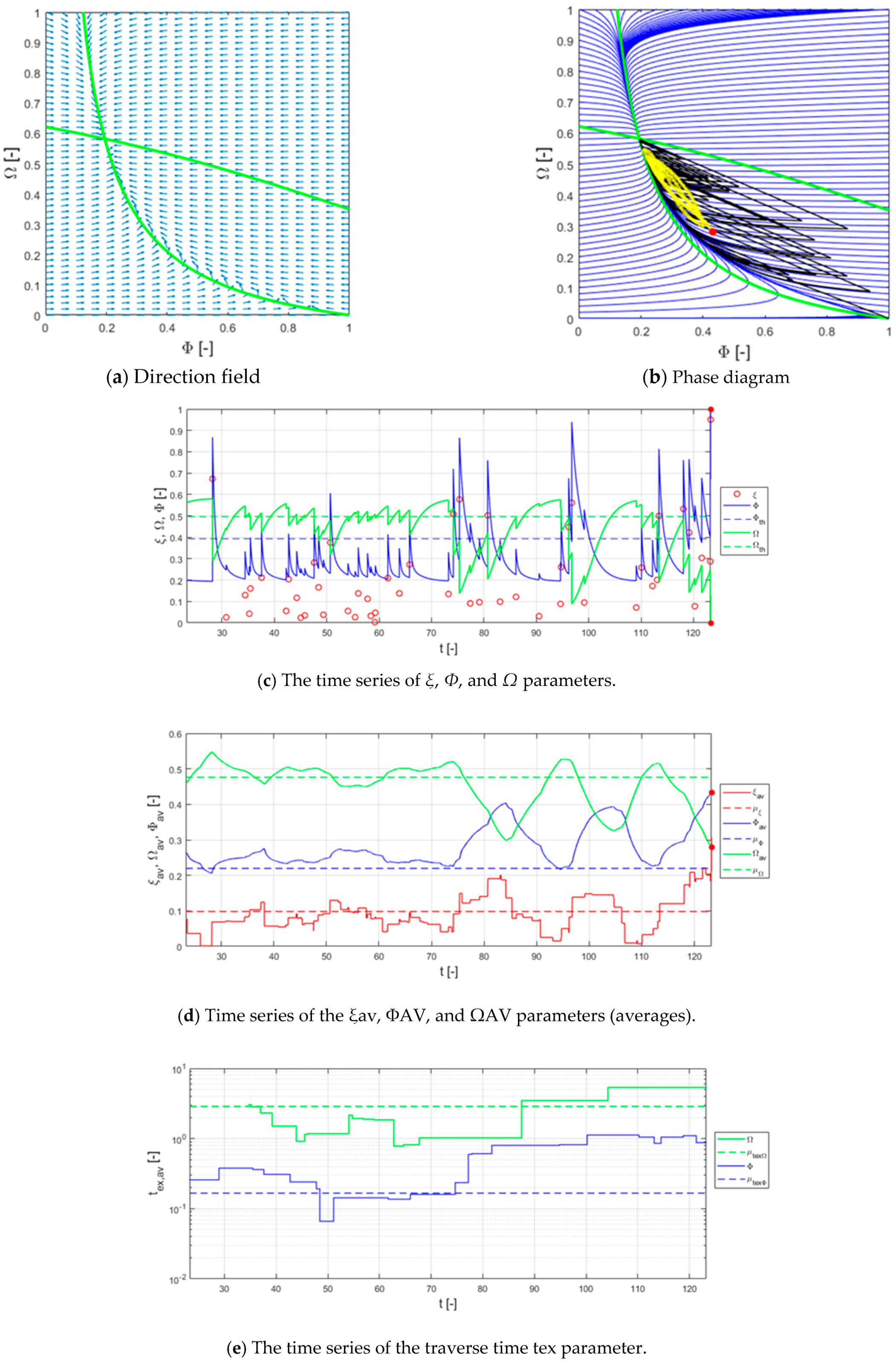
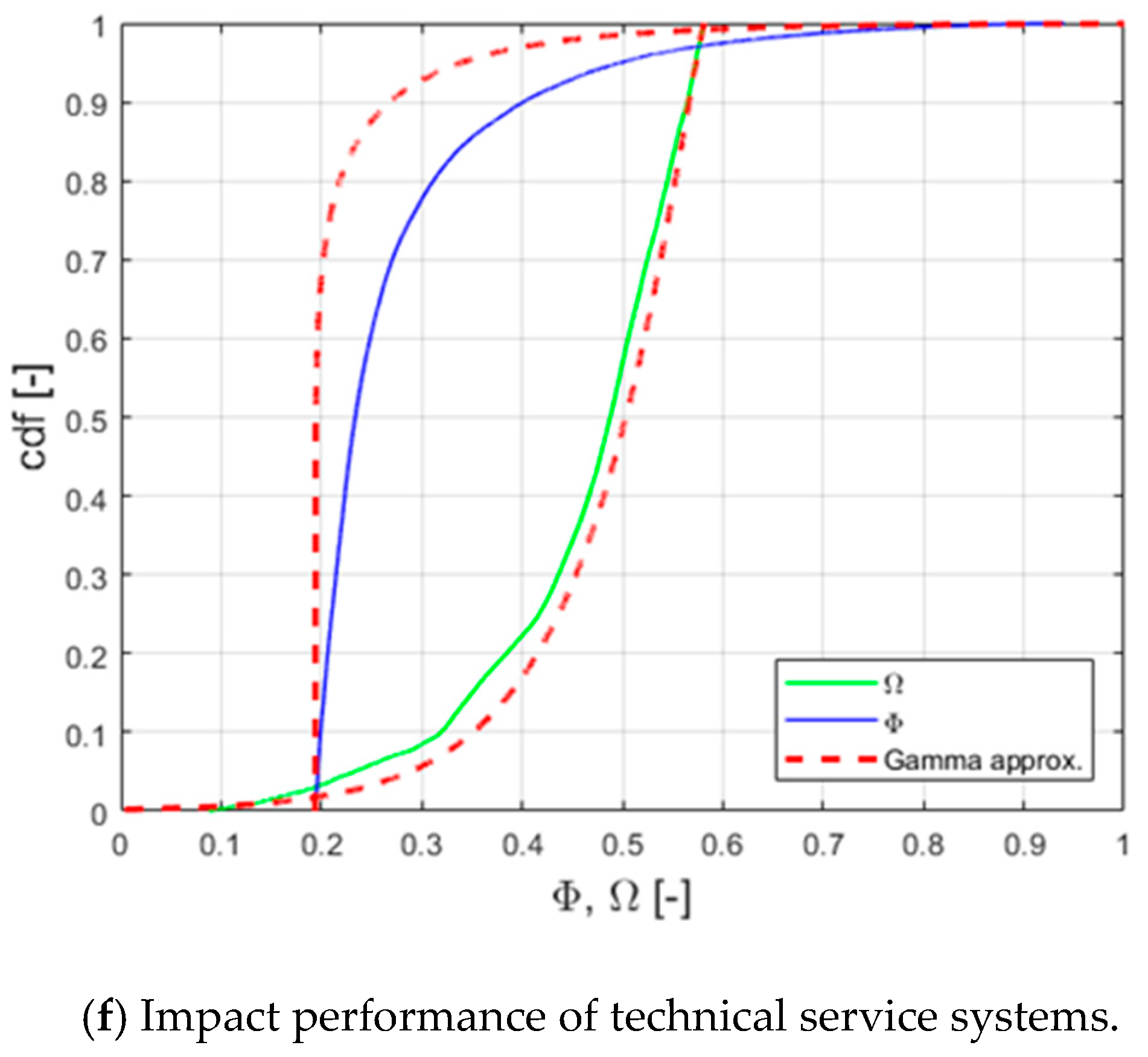
3.2. Results of Resilience Dynamic Assessment
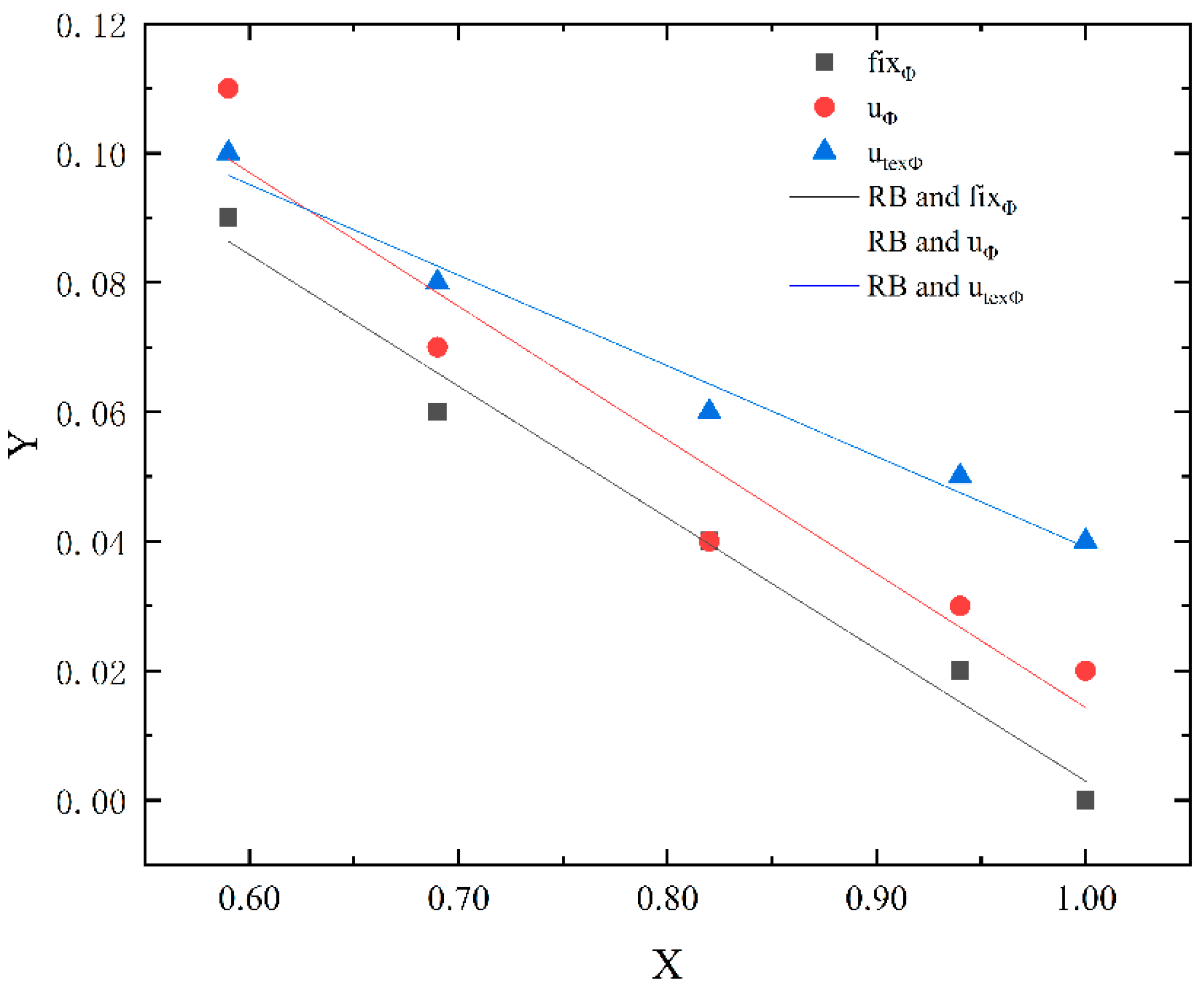
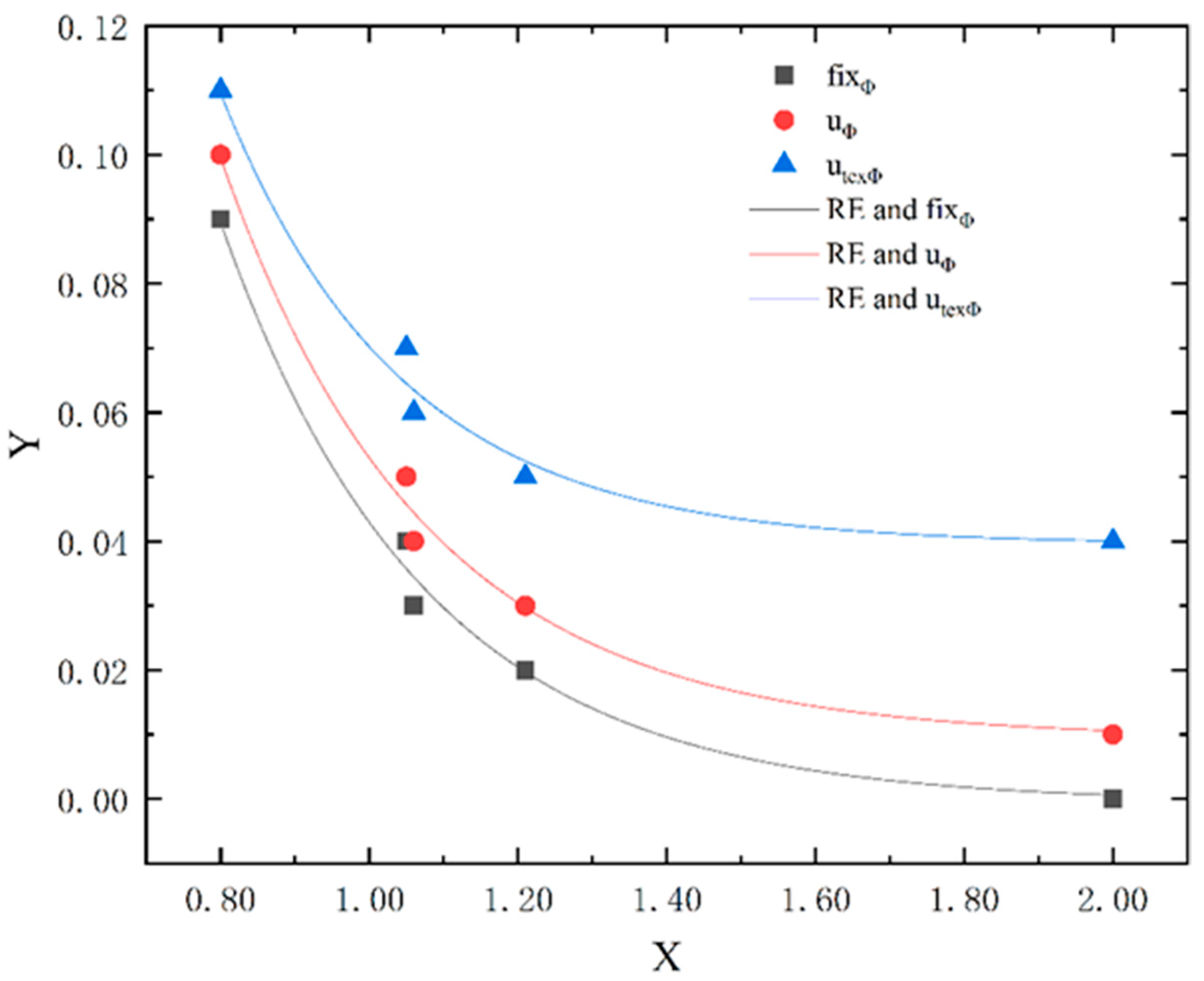
4. Results of Resilience Critical Points Identification
4.1. Critical Point Identification of Robustness
4.2. Critical Point Identification of Recoverability
- Communication protocol for sharing structured information;
- Feedback loop;
- Feedback loop mechanism for cross-department coordination;
- Training and training flexibility and sustainability innovation;
- Public participatory decision-making and management mechanism;
- Customer complaint tracking mechanism;
- Openness of government affairs;
- Flexible employing mechanism and perfect assessment and supervision mechanism;
- Urban and rural strategy;
- Transboundary agreements;
- Groundwater management mechanism;
- Surface water management mechanism.
4.3. Critical Point Identification of Resilience
5. Discussion
5.1. Discussion of Resilience Static Assessment Results
5.2. Discussion of Resilience Dynamic Assessment Results
5.3. Discussion of the Critical Point Identification Result
6. Conclusions
- The static assessment results showed that the five capital levels (financial resources, management efficiency, infrastructure, available water resources, and organizational adaptation) and three attributes (robustness, recoverability, and adaptability) of Qingdao’s water supply system resilience are unbalanced.
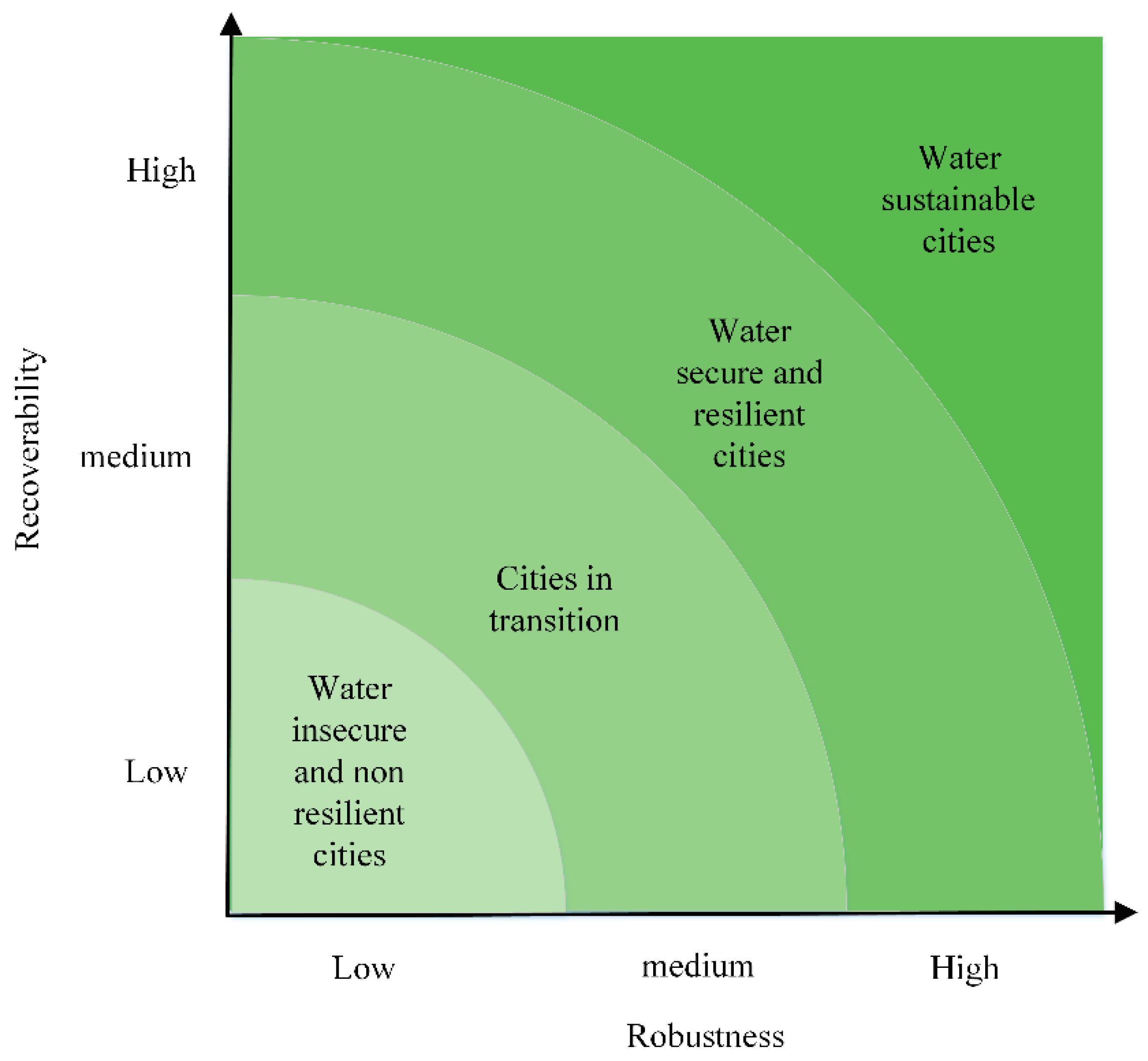
- The dynamic assessment results showed that the current trajectory of Qingdao’s water supply system resilience is as a city in transition. Among them, in an uncertain scenario, the technical service system will collapse due to the limitation of its ability to adapt, and the system state is unstable. However, the total service system with organizational adaptation can always recover through its dynamic adaptability, avoiding collapse, which indicates that organizational adaptation can significantly improve system resilience.
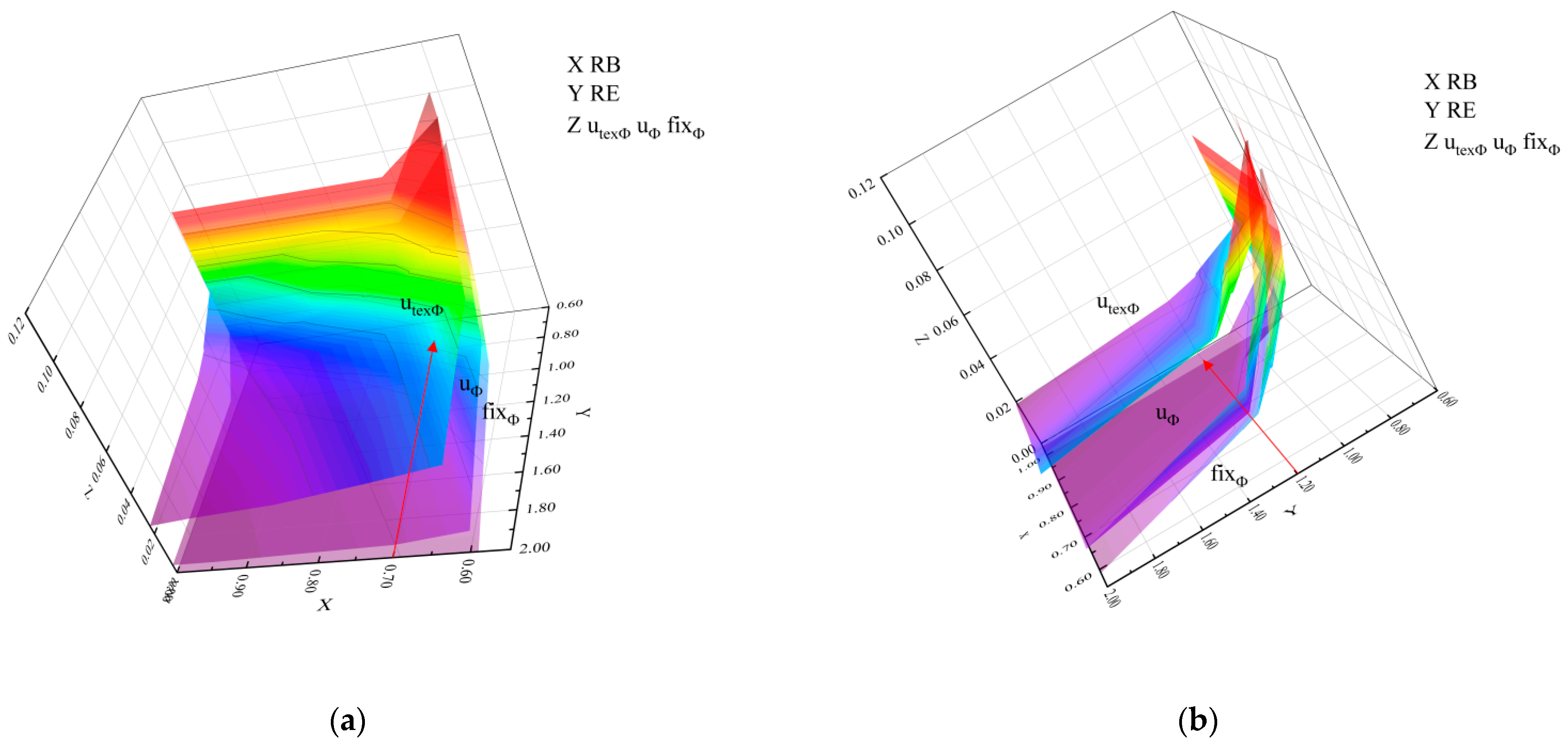
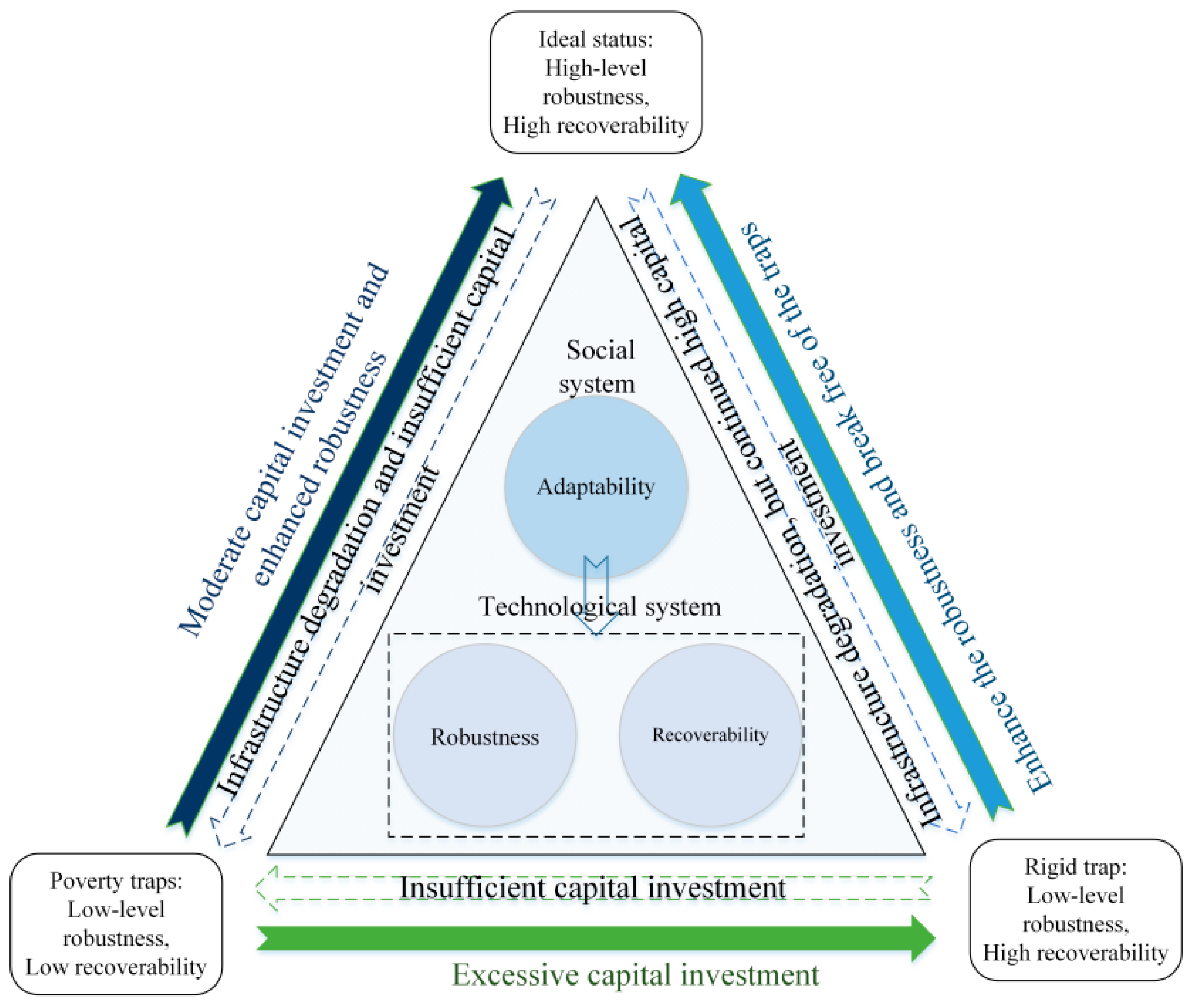
- The fitting analysis showed that a linear relationship exists between robustness and resilience, and the resilience increases linearly with the increase in capital robustness. The relationship between recoverability and resilience is nonlinear. Before the critical point, the resilience increases exponentially with the increase in recoverability, and the marginal effect is obvious. After the critical point, the increase in resilience tends to flatten. The critical points of robustness and recoverability are 0.70 and 1.20, respectively. Combined with the resilience improvement path 3D landscape, to transform the current state of the water sector to ensure water security and high resilience, adaptive ability can be used to improve the system robustness and recoverability, but there should not be only one focus in the process of improvement. To achieve the critical point capital robustness and recoverability (RB = 0.70, RE = 1.20), the city should be aware of the trap of rigidity (RE > 1.00, RB < 0.30).
- We constructed a comprehensive assessment framework combining static and dynamic assessments, which can be used as a reference for the resilience assessment of similar coupled social-technological systems in cities. For example, the power system, the communication system, the drainage system, and the road system in the urban environment can be regarded as a coupled social-technological system. The coastal city selected as a typical case in this study, although it has certain limitations, helps provide information, but the long-term dynamic resilience of different urban water supply systems differs, and water managers actively adapt their behavior in close relation to the local complex environment that is uncertain. As such, a different regional comparative study on urban water supply systems should be conducted, and water management departments should be actively contacted to obtain more timely and effective information.
- We developed a comprehensive assessment framework that evaluates both the current resilience levels and the resilience dynamics under interference. In this study, we performed a correlation analysis of the relationships between resilience properties and presented the specific value of the key critical point.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Minucci, G. Assessing adaptive capacity of water management organizations. The case study of the municipality of Tomave (Bolivia). J. Risk Res. 2016, 19, 847–872. [Google Scholar] [CrossRef]
- Ulibarri, N.; Scott, T.A. Environmental hazards, rigid institutions, and transformative change: How drought affects the consideration of water and climate impacts in infrastructure management. Glob. Environ. Chang. 2019, 59, 102005. [Google Scholar] [CrossRef] [PubMed]
- Simonovic, S.P. Systems Approach to Management of Water Resources—Toward Performance Based Water Resources Engineering. Water 2020, 12, 1208. [Google Scholar] [CrossRef]
- Sweya, L.N.; Wilkinson, S.; Mayunga, J.; Joseph, A.; Lugomela, G.; Victor, J. Development of a Tool to Measure Resilience against Floods for Water Supply Systems in Tanzania. J. Manag. Eng. 2020, 36, 0502007. [Google Scholar] [CrossRef]
- Short, M.D.; Peirson, W.L.; Peters, G.M.; Cox, R.J. Managing Adaptation of Urban Water Systems in a Changing Climate. Water Resour. Manag. 2012, 26, 1953–1981. [Google Scholar] [CrossRef]
- Hoover, D.J.; Odigie, K.O.; Swarzenski, P.W.; Barnard, P. Sea-level rise and coastal groundwater inundation and shoaling at select sites in California, USA. J. Hydrol. Reg. Stud. 2017, 11, 234–249. [Google Scholar] [CrossRef]
- Abidin, H.Z.; Andreas, H.; Gumilar, I.; Fukuda, Y.; Pohan, Y.E.; Deguchi, T. Land subsidence of Jakarta (Indonesia) and its relation with urban development. Nat. Hazards 2011, 59, 1753–1771. [Google Scholar] [CrossRef]
- Cubillo, F.; Martínez-Codina, Á. A metric approach to measure resilience in water supply systems. J. Appl. Water Eng. Res. 2019, 7, 67–78. [Google Scholar] [CrossRef]
- Balaei, B.; Wilkinson, S.; Potangaroa, R.; Hassani, N.; Alavi-Shoshtari, M. Developing a Framework for Measuring Water Supply Resilience. Nat. Hazards Rev. 2018, 19, 04018013. [Google Scholar] [CrossRef]
- Joannou, D.; Kalawsky, R.; Saravi, S.; Rivas Casado, M.; Fu, G.; Meng, F. A Model-Based Engineering Methodology and Architecture for Resilience in Systems-of-Systems: A Case of Water Supply Resilience to Flooding. Water 2019, 11, 496. [Google Scholar] [CrossRef]
- David, R.; Pavel, S.; Simona, S. Resilience of Critical Infrastructure Elements and Its Main Factors. Systems 2018, 6, 21. [Google Scholar]
- Rehak, D.; Senovsky, P.; Hromada, M.; Lovecek, T. Complex approach to assessing resilience of critical infrastructure elements. Int. J. Crit. Infrastruct. Prot. 2019, 25, 125–138. [Google Scholar] [CrossRef]
- Krueger, E.H.; Borchardt, D.; Jawitz, J.W.; Klammler, H.; Yang, S.; Zischg, J.; Rao, P.S.C. Resilience Dynamics of Urban Water Supply Security and Potential of Tipping Points. Earth’s Future 2019, 7, 1167–1191. [Google Scholar] [CrossRef]
- Zhao, S.; Liu, X.; Zhuo, Y.; Fan, B. Stuay on Recovery Strategies of Water Supply System under Emergent Water Pollution Events. Ind. Eng. Manag. 2015, 20, 135–141. [Google Scholar]
- Li, Q.; Chen, Z.; Zhao, X. Comprehensive Seismic resilience of Urban Lifeline System: Double-dimensional approach. China Civ. Eng. J. 2017, 50, 65–72. [Google Scholar]
- Liu, J.; Huang, W. Research on Resilience Capacity Assessment of Urban Water Supply System in Cities under Salt Tide Situation. Mod. City Res. 2017, 9, 32–40. [Google Scholar]
- Liu, J.; Wang, W.; Shao, Z. Research on resilience capacity assessment and promotion strategy of water supply system in Qingdao under flood and drought disaster. J. Inst. Disaster Prev. 2020, 22, 9–19. [Google Scholar]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; Von Winterfeldt, D. A Framework to Quantitatively Assess and Enhance the Seismic Resilience of Communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef]
- Lawson, E.; Farmani, R.; Woodley, E.; Butler, D. A Resilient and Sustainable Water Sector: Barriers to the Operationalisation of Resilience. Sustainability 2020, 12, 1797. [Google Scholar] [CrossRef]
- Walker, G. Come back socio technical systems theory, all is forgiven. Civ. Eng. Environ. Syst. 2015, 32, 170–179. [Google Scholar] [CrossRef]
- Quitana, G.; Molinos-Senante, M.; Chamorro, A. Resilience of critical infrastructure to natural hazards: A review focused on drinking water systems. Int. J. Disaster Risk Reduct. 2020, 48, 101575. [Google Scholar] [CrossRef]
- Xu, W.; Zhong, Z.; Proverbs, D.; Xiong, S.; Zhang, Y. Enhancing the Resilience of the Management of Water Resources in the Agricultural Supply Chain. Water 2021, 13, 1619. [Google Scholar] [CrossRef]
- Behboudian, M.; Kerachian, R.; Pourmoghim, P. Evaluating the long-term resilience of water resources systems: Application of a generalized grade-based combination approach. Sci. Total. Environ. 2021, 786, 147447. [Google Scholar] [CrossRef]
- Tantri, F.; Amir, S. Modeling a Simulation for Sociotechnical Resilience. Complexity 2019, 2019, 7950629. [Google Scholar] [CrossRef]
- Vazquez, K.; Muneepeerakul, R. Modeling Resilience and Sustainability of Water-Subsidized Systems: An Example from Northwest Costa Rica. Sustainability 2021, 13, 2013. [Google Scholar] [CrossRef]
- Brown, R.R.; Keath, N.; Wong, T.H.F. Urban water management in cities: Historical, current and future regimes. Water Sci. Technol. 2009, 59, 847–855. [Google Scholar] [CrossRef] [PubMed]
- Daniell, K.A.; Rinaudo, J.D.; Chan, N.W.W.; Nauges, C.; Grafton, Q. Understanding and managing urban water in transition. In Understanding and Managing Urban Water in Transition; Springer: Dordrecht, The Netherlands, 2015; pp. 1–30. [Google Scholar]
- Hoekstra, A.Y.; Buurman, J.; Van Ginkel, K.C. Urban water security: A review. Environ. Res. Lett. 2018, 13, 053002. [Google Scholar] [CrossRef]
- Krueger, E.; Rao, P.S.C.; Borchardt, D. Quantifying urban water supply security under global change. Glob. Environ. Chang. 2019, 56, 66–74. [Google Scholar] [CrossRef]
- Appelbaum, S.H. Socio-technical systems theory: An intervention strategy for organizational development. Manag. Decis. 1997, 35, 452–463. [Google Scholar] [CrossRef]
- Langhans, S.D.; Reichert, P.; Schuwirth, N. The method matters: A guide for indicator aggregation in ecological assessments. Ecol. Indic. 2014, 45, 494–507. [Google Scholar] [CrossRef]
- Kong, J.; Simonovic, S.P.; Zhang, C. Resilience Assessment of Interdependent Infrastructure Systems: A Case Study Based on Different Response Strategies. Sustainability 2019, 11, 6552. [Google Scholar] [CrossRef]
- Klammler, H.; Rao, P.S.; Hatfield, K. Modeling dynamic resilience in coupled technological-social systems subjected to stochastic disturbance regimes. Environ. Syst. Decis. 2018, 38, 140–159. [Google Scholar] [CrossRef]
- Lindskog, F.; McNeil, A.J. Common Poisson shock models: Applications to insurance and credit risk modelling. ASTIN Bull. J. IAA 2003, 33, 209–238. [Google Scholar] [CrossRef][Green Version]
- Angel, S.; Sheppard, S.; Civco, D.L.; Buckley, R.; Chabaeva, A.; Gitlin, L.; Kraley, A.; Parent, J.; Perlin, M. The Dynamics of Global Urban. Expansion; World Bank, Transport and Urban Development Department: Washington, DC, USA, 2005. [Google Scholar]
- Bettencourt, L.M.; Lobo, J.; Helbing, D.; Kühnert, C.; West, G.B. Growth, innovation, scaling, and the pace of life in cities. Proc. Natl. Acad. Sci. USA 2007, 104, 7301–7306. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar] [CrossRef]
- Shin, S.; Lee, S.; Judi, D.R.; Parvania, M.; Goharian, E.; McPherson, T.; Burian, S.J. A Systematic Review of Quantitative Resilience Measures for Water Infrastructure Systems. Water 2018, 10, 164. [Google Scholar] [CrossRef]
- Garrick, D.; Hall, J.W. Water Security and Society: Risks, Metrics, and Pathways. Annu. Rev. Environ. Resour. 2014, 39, 611–639. [Google Scholar] [CrossRef]
- Rasoulkhani, K.; Mostafavi, A. Resilience as an emergent property of human-infrastructure dynamics: A multi-agent simulation model for characterizing regime shifts and tipping point behaviors in infrastructure systems. PLoS ONE 2018, 13, e0207674. [Google Scholar] [CrossRef] [PubMed]
- Qiu, W.; Chen, Y.; Wan, C. Emergency safeguard measures and thinking of water Group Company Limited during COVID-19 epidemic (Water supply). Water Wastewater Eng. 2020, 56, 44–47. [Google Scholar]
- Wen, L.J.; Jiang, C.B.; Ma, Z.J.; Di, Y.; Cao, Y.Z.; Liu, G.Y. The General Situation of Marine Disaster in Shandong Province during 2010–2014 and Defense Strategies. Ocean. Dev. Manag. 2016, 33, 98–104. [Google Scholar]
- Xu, Y. Development Strategy of China’s coastal cities for addressing Climate Change. Clim. Chang. Res. 2020, 16, 88–98. [Google Scholar]
- Cai, R.; Tan, H.; Guo, H. Response and Compound Risk of the Coastal China areas to Global Change. J. Appl. Oceanogr. 2019, 38, 514–527. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Student Solutions Manual: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Laio, F.; Porporato, A.; Ridolfi, L.I.R.I.; Rodriguez-Iturbe, I. Mean first passage times of processes driven by white shot noise. Phys. Rev. E 2001, 63, 036105. [Google Scholar] [CrossRef]
- Tamea, S.; Laio, F.; Ridolfi, L.; Rodriguez-Iturbe, I. Crossing properties for geophysical systems forced by Poisson noise. Geophys. Res. Lett. 2011, 38, L18404. [Google Scholar] [CrossRef]
- Savenije, H.H.G. Water scarcity indicators; the deception of the numbers. Phys. Chem. Earth Part. B Hydrol. Ocean. Atmos. 2000, 25, 199–204. [Google Scholar] [CrossRef]
- Akhmouch, A.; Correia, F.N. The 12 OECD principles on water governance—When science meets policy. Util. Policy 2016, 43, 14–20. [Google Scholar] [CrossRef]
- Marlow, D.R.; Moglia, M.; Cook, S.; Beale, D.J. Towards sustainable urban water management: A critical reassessment. Water Res. 2013, 47, 7150–7161. [Google Scholar] [CrossRef] [PubMed]
- Padowski, J.C.; Carrera, L.; Jawitz, J.W. Overcoming urban water insecurity with infrastructure and institutions. Water Resour. Manag. 2016, 30, 4913–4926. [Google Scholar] [CrossRef]
- Mair, M.; Zischg, J.; Rauch, W.; Sitzenfrei, R. Where to find water pipes and sewers?—On the correlation of infrastructure networks in the urban environment. Water 2017, 9, 146. [Google Scholar] [CrossRef]
- Flörke, M.; Schneider, C.; McDonald, R.I. Water competition between cities and agriculture driven by climate change and urban growth. Nat. Sustain. 2018, 1, 51–58. [Google Scholar] [CrossRef]
- Christodoulou, S.E.; Fragiadakis, M. Vulnerability assessment of water distribution networks considering performance data. J. Infrastruct. Syst. 2015, 21, 04014040. [Google Scholar] [CrossRef]
- Chen, P.; Scown, C.; Matthews, H.S.; Garrett, J.H., Jr.; Hendrickson, C. Managing critical infrastructure interdependence through economic input-output methods. J. Infrastruct. Syst. 2009, 15, 200–210. [Google Scholar] [CrossRef][Green Version]
- O’Rourke, T.D. Critical Infrastructure, Interdependencies, and Resilience. 2007. Available online: https://www.nae.edu/19582/Bridge/EngineeringfortheThreatofNaturalDisasters/CriticalInfrastructureInterdependenciesandResilience.aspx (accessed on 15 August 2021).
- Rasoulkhani, K.; Mostafavi, A.; Reyes, M.P.; Batouli, M. Resilience planning in hazards-humans-infrastructure nexus: A multi-agent simulation for exploratory assessment of coastal water supply infrastructure adaptation to sea-level rise. Environ. Model. Softw. 2020, 125, 104636. [Google Scholar] [CrossRef]
- Raskin, P.; Gleick, P.; Kirshen, P.; Pontius, G.; Strzepek, K. Comprehensive Assessment of the Freshwater Resources of the World. 1997. Available online: https://www.mendeley.com/catalogue/a135e25a-c98e-358f-a3bf-bbe90fcf8fbd/ (accessed on 20 August 2021).
- Liu, J.; Yang, H.; Gosling, S.N.; Kummu, M.; Flörke, M.; Pfister, S.; Hanasaki, N.; Wada, Y.; Zhang, X.; Zheng, C.; et al. Water scarcity assessments in the past, present and future. Earth’s Future 2017, 5, 545–549. [Google Scholar] [CrossRef]
- Borchardt, D.; Ibisch, R. Integrated Water Resources Management in a Changing World; IWA Publishing: London, UK, 2013. [Google Scholar]
- Leigh, N.G.; Lee, H. Sustainable and Resilient Urban Water Systems: The Role of Decentralization and Planning. Sustainability 2019, 11, 918. [Google Scholar] [CrossRef]
- Diao, K.; Sweetapple, C.; Farmani, R.; Fu, G.; Ward, S.; Butler, D. Global resilience analysis of water distribution systems. Water Res. 2016, 106, 383–393. [Google Scholar] [CrossRef] [PubMed]
- Carpenter, S.R.; Brock, W.A. Adaptive Capacity and Traps. Ecol. Soc. 2008, 13, 40. [Google Scholar] [CrossRef]
- Brown, T.C.; Mahat, V.; Ramirez, J.A. Adaptation to future water shortages in the United States caused by population growth and climate change. Earth’s Future 2019, 7, 219–234. [Google Scholar] [CrossRef]
- Mortula, M.M.; Ahmed, M.A.; Sadri, A.M.; Ali, T.; Ahmad, I.; Idris, A. Improving Resiliency of Water Supply System in Arid Regions: Integrating Centrality and Hydraulic Vulnerability. J. Manag. Eng. 2020, 36, 0502001. [Google Scholar] [CrossRef]
| Risk Category | Risk Type Description | Influence of Capital | Risk Attributes | Urban Risk Score (with, 1/without, 0) |
|---|---|---|---|---|
| Geology and geography | Earthquake, tsunami, landslide, etc. | I A | Acute | 1 |
| Land subsidence | I | Chronic | 1 | |
| Socio-economic and geopolitical threats | Socioeconomic and political changes, unpredictably high rates of immigration | W I F P A | Chronic | 0 |
| Direct threat of terrorism or war | W I F P A | Acute | 0 | |
| Competition for water resources | W P | Chronic | 1 | |
| Trespass into water pipes | I | Chronic | 0 | |
| Immediate threat of economic crisis | F P A | Acute | 0 | |
| Pollution hazard | Industrial leakage | W I A | Acute | 1 |
| Pandemic | W I A | Acute | 1 | |
| Impact of ageing infrastructure on water pollution, waterborne diseases after floods, intensive agriculture, lack of sanitation infrastructure on ground water quality | W I A | Chronic | 1 | |
| Climate and weather-related hazards | Storms | I | Acute | 1 |
| Flood, drought | W | Acute | 1 | |
| Extreme temperature (low temperatures, heat waves) | I | Chronic | 1 | |
| Saltwater intrusion | W I A | Chronic | 1 | |
| Storm surge | W I | Acute | 1 | |
| Seawater intrusion | W I A | Chronic | 1 | |
| Eutrophication in coastal waters | W | Chronic | 1 |
| Capital | Resilience Properties | ||
|---|---|---|---|
| Robustness (RB): average of the binary fractions is calculated | Recoverability (RE) | Risk (R) | |
| Financial capital (F) | Medium to high income (income that can be used for unexpected expenses); foreign investment dependence on infrastructure investment <50%; whether the investment in water conservancy facilities is at a medium or high level | Ratio of annual water sector income (FI) to annual water sector expenditure (FS) multiplied by I (F = FI/FS Page: 11 × I) | 3 4 7 |
| Management effectiveness (P) | Emergency action plan; ability to improvise, innovate, expand action; national support plan for disaster recovery; city management efficiency ranking; | p: calculate the average of the nine binary fractions: communication protocol for sharing structured information; feedback loop; feedback loop mechanism of cross-department coordination; training and training flexibility and sustainability innovation;public participatory decision-making/management mechanism; tracking customer complaint mechanism; openness of government affairs; flexible employing mechanism and perfect assessment and supervision mechanism;urban and rural strategy; transboundary agreements; groundwater management mechanism; surface water management mechanism | 3 4 5 7 |
| Infrastructure (I) | Expected maintenance; emergency solution for power failure; cross-sectoral coordination (sanitation, drainage, energy, transport); continuous water supply; monitoring leaks;the average material life is less than 50 years;redundancy of key nodes; distributed resources;possibility of emergency quarantine | Infrastructure (I): SW = (UWA − Wleakage)/DW UWA refers to annual urban water supply, Wleakage refers to annual leakage, DW refers to annual water WDrink= Daily domestic water consumption per resident × 365 × population N/DW Annual water I = h × SW −q × WDrink h: penetration rate, q: proportion of drinking water contaminated (q = 1-water quality compliance rate) | 1 2 3 4 6 8 9 10 11 13 |
| Water resources (W) | Storage flow ratio; external water dependence; water source connectivity; water quality management levels (1: monitoring, 2: discharge regulations, 3: water source control and polluter pays for treatment, 4: precautionary principle); water source diversity (1: one source, 2: one type of source, 3: two sources and types, 4: multiple types) | Water source W = UWA city annual per capita water supply/water threshold QS | 3 4 5 8 9 10 12 |
| Organizational adaptation (A) | ARB: access to alternative water sources (e.g., desalination); ≥middle and high income cities (wages and benefits for practitioners); more than 7 days of continuous emergency water supply; access to emergency response information; an active organization; water treatment prior to water supply; direct access to backup water sources (e.g., wells, rivers, etc.) | ARE: Organizational adaptation (A): A = (passenger water + other unconventional water such as seawater desalination)/DW annual water consumption + q × WDrink + reserve water/DW annual water | 1 3 4 7 8 9 10 |
| Aggregation of summary | RBtotal = (FRB + PRB + IRB + WRB + ARB)/5; RBpublic = (FRB + PRB + IRB + WRB)/4 | REtotal = REpublic + A; REpublic = 4/(1/FRE + 1/PRE + 1/IRE + 1/WRE) | Rtotal = (RF + RP + RI + RW + RA)/5 |
| Atotal = 2/(ARB + ARE) | Total resilience = 3/(1/RBtotal + 1/REtotal + 1/Atotal) | ||
| Parameter | Technical Service | Total Service |
|---|---|---|
| b | 0.55 | 0.29 |
| ɑ | 9.92 | 14.09 |
| c1 | 0.26 | 0.21 |
| c2 | 0.29 | 0.08 |
| r | 0.29 | 0.08 |
| β | 0.74 | 0.79 |
| n | 3.34 | 3.55 |
| λchronic | 0.45 | 0.45 |
| λacute | 0.04 | 0.04 |
| Parameter | Technical Service | Total Service |
|---|---|---|
| fixΩ | 0.58 | 0.72 |
| fixΦ | 0.19 | 0.09 |
| uΩ | 0.48 | 0.65 |
| uΦ | 0.22 | 0.11 |
| Φth-above (%) | 0.10 | 0.03 |
| Ωth-below (%) | 0.58 | 0.30 |
| utexΦ-above | 0.17 | 0.10 |
| utexΩ-below | 2.87 | 2.87 |
| Number | RB | RE |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | F |
| 2 | 0 | F + P |
| 3 | 0 | F + P + I |
| 4 | 0 | F + P + I + W |
| 5 | 0 | F + P + I + W + A |
| 6 | P | 0 |
| 7 | P | F |
| 8 | P | F + P |
| 9 | P | F + P + I |
| 10 | P | F + P + I + W |
| 11 | P | F + P + I + W + A |
| 12 | P + I | 0 |
| 13 | P + I | F |
| 14 | P + I | F + P |
| 15 | P + I | F + P + I |
| 16 | P + I | F + P + I + W |
| 17 | P + I | F + P + I + W + A |
| 18 | P + I + W | 0 |
| 19 | P + I + W | F |
| 20 | P + I + W | F + P |
| 21 | P + I + W | F + P + I |
| 22 | P + I + W | F + P + I + W |
| 23 | P + I + W | F + P + I + W + A |
| 24 | P + I + W + A | 0 |
| 25 | P + I + W + A | F |
| 26 | P + I + W + A | F + P |
| 27 | P + I + W + A | F + P + I |
| 28 | P + I + W + A | F + P + I + W |
| 29 | P + I + W + A | F + P + I + W + A |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Shao, Z.; Wang, W. Resilience Assessment and Critical Point Identification for Urban Water Supply Systems under Uncertain Scenarios. Water 2021, 13, 2939. https://doi.org/10.3390/w13202939
Liu J, Shao Z, Wang W. Resilience Assessment and Critical Point Identification for Urban Water Supply Systems under Uncertain Scenarios. Water. 2021; 13(20):2939. https://doi.org/10.3390/w13202939
Chicago/Turabian StyleLiu, Jinning, Zhiguo Shao, and Wei Wang. 2021. "Resilience Assessment and Critical Point Identification for Urban Water Supply Systems under Uncertain Scenarios" Water 13, no. 20: 2939. https://doi.org/10.3390/w13202939
APA StyleLiu, J., Shao, Z., & Wang, W. (2021). Resilience Assessment and Critical Point Identification for Urban Water Supply Systems under Uncertain Scenarios. Water, 13(20), 2939. https://doi.org/10.3390/w13202939







