1. Introduction
Hydrological time series forecasting is essential for a variety of real-world managements or operation of water resources systems [
1,
2]. Precipitation is affected by many factors such as atmospheric circulation, topography, climate change, and human activities. The improvement of precipitation prediction has received a lot of attention across the world and many models have been constructed to improve the hydrological process simulation and prediction accuracy [
3,
4,
5].
These models can fall into two categories: knowledge-based models and data-based models [
6]. Knowledge-based model is a numerical simulation technology that describes natural phenomena on the basis of an internal physical mechanism of the system [
7]. However, the lack of multisource information and optimization complexity of computation parameters limit the generalization of physical-based models [
8]. In contrast, data-based models can obtain satisfying results by using historical data without involving the physical load within hydrological time series [
9,
10]. Hence data-based models have received a lot of attention in the hydrological forecasting field. In this paper, we are devoted to verifying several data-based models for monthly rainfall time series forecasting. There are many data-based models, e.g., artificial neural networks (ANN) [
11], genetic programming (GP) [
12], support vector machines (SVM) [
13], and adaptive neuro-fuzzy inference system (ANFIS) [
14].
Box–Jenkins models [
15], which are considered as the most comprehensive tool in all statistical methods of time series forecasting, include auto-regressive (AR), moving average (MA), autoregressive moving average (ARMA), ARIMA, and other models. ARIMA is a linear statistical model and normally used to simulate and forecast time series with temporal correlation [
16,
17]. With the advance of technology such as computers, communication, remote sensing, and geography information systems, the prediction ability of the ARIMA model has been greatly improved [
18]. Rahman et al. [
19] used Mann–Kendall, Spearman’s rho test, and the ARIMA model to analyze and predict rainfall trends in Bangladesh. Mishra et al. [
20] compared seasonal ARIMA and ARIMA models for runoff forecasting accuracy in the River Brahmaputra Basin, and the results indicated that ARIMA could provide higher accuracy. Rizeei et al. [
21] combined a soil conservation service–curve number (SCS-CN) model with an ARIMA and land transformation model to monitor the changes of surface runoff. Wang et al. [
22] proposed a hybrid Empirical Mode Decomposition (EMD)/Ensemble Empirical Mode Decomposition (EEMD)-ARIMA model for long-term runoff forecasting.
ANN, a nonlinear data-based model, is extensively used for hydrological applications [
23,
24]. The major application of ANN can be summarized as streamflow forecasting [
25,
26], rainfall forecasting [
27,
28], groundwater problems [
29,
30], suspended sediment estimation [
31], regional drought analysis and forecasting [
32,
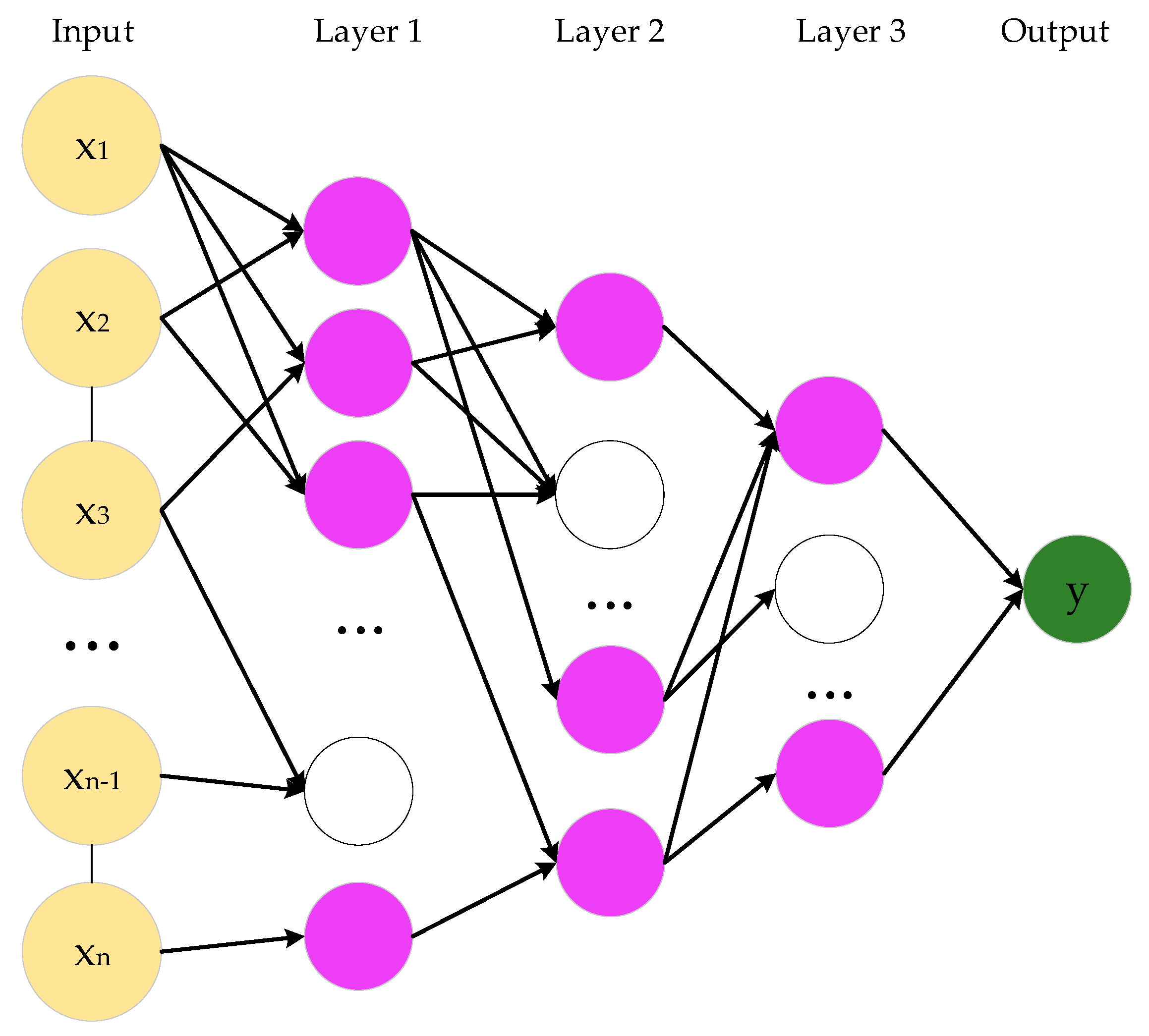
33], etc. Among different kinds of ANN, BPNN is a multilayer feed forward ANN with unidirectional transmission, which has advantages of learning and extracting the features, memory association, parallel architecture, and independent learning and adaptive capabilities [
34]. The BPNN model has been widely applied to precipitation prediction, study of rainfall prediction with meteorological parameters [
35], estimation of regional surface soil moisture [
36,
37], etc. Consequently, we attempt to use BPNN for monthly rainfall forecasting as a nonlinear data-based model.
GMDH is a sub-model of ANN for complex system modeling [
38]. The main principle is to construct an analytic function of the system by quadratic node transfer function. The coefficients of binomial transfer function are obtained by polynomial regression. GMDH has been successfully used in broad fields such as economics, engineering, science, medical diagnostics, control systems, signal processing, and water resources [
39,
40].
Although the performance of ANN is remarkable in dealing with linear problems, it cannot handle non-stationary and nonlinear problems that arise in rainfall data. Studies have shown that forecasting accuracy of models could be improved by appropriate data preprocessing techniques to eliminate noises in hydrological time series. In recent years, many scholars have performed a lot of work based on this idea to improve the prediction performance of models. Partal and Kişi [
41] proposed a wavelet-neuro-fuzzy model, especially suitable for forecasting daily rainfall time series, which have zero rainfall in summer months. Wang, et al. [
42] proposed the EEMD-ANN model to forecast medium- and long-term runoff time series. Yu, et al. [
43] explored Fourier transform (FT) and support vector regression (SVR) for forecasting monthly reservoir inflow and compared them with EEMD-SVR and SSA-SVR models, and found that FT-SVR consumed more computational resources in parameter calibration. The least-squares wavelet analysis (LSWA) [
2] has shown promising results in successful analysis of streamflow and climate time series. Feng, et al. [
44] combined variational mode decomposition (VMD), SVM, and quantum-behaved particle swarm optimization (QPSO) to forecast monthly streamflow and achieved excellent prediction results.
Most common decomposition approaches perform well only when the input variables meet certain conditions. For example, EMD may suffer from mode mixing due to intermittent signal [
45], and this effect is important to hydrological applications. The stationarity of time series has a great influence on the accuracy of position in the domain identified by FT method [
46]. Nevertheless, hydrological time series are non-stationary, which means that statistical properties will fluctuate over time [
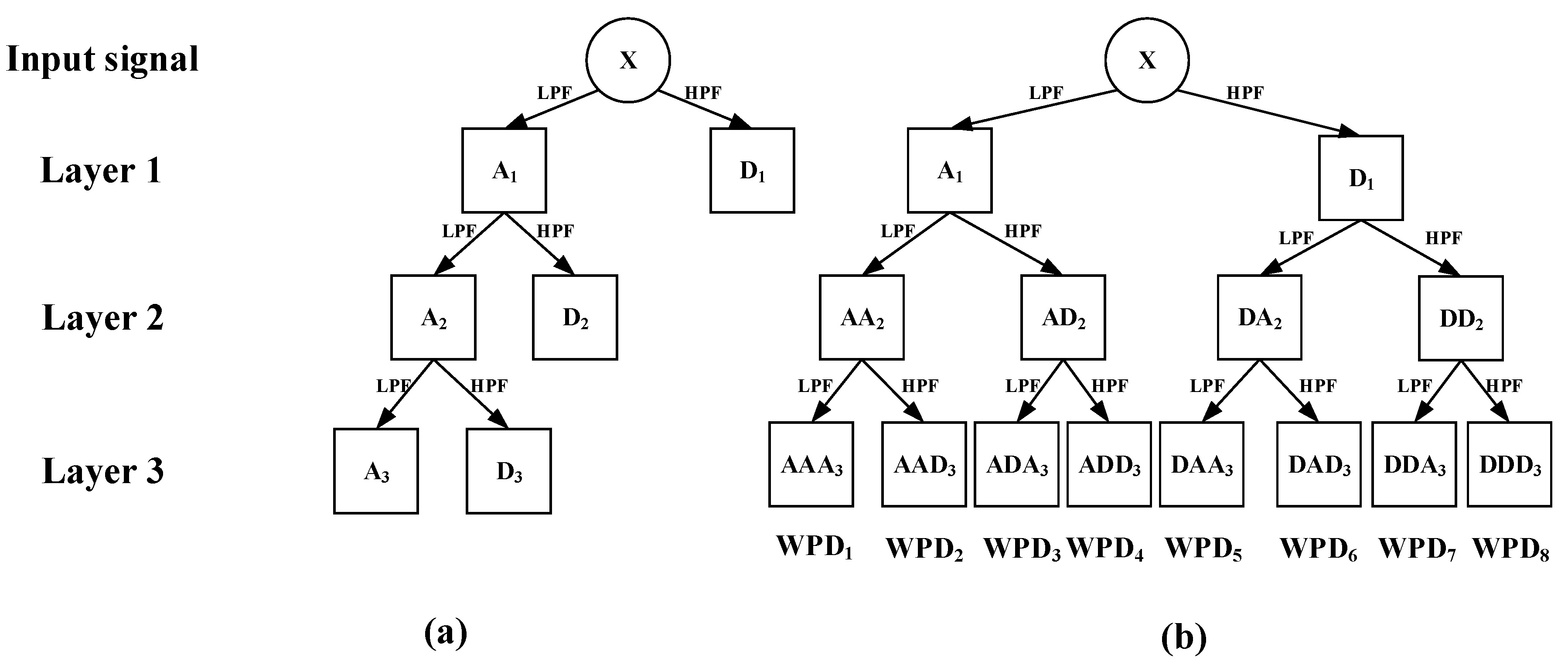
47]. In recent years, researchers have paid great attention in WPD. The main idea of WPD method is using multiple filters to decompose the original signal into more linear sub-signals with different frequency characteristics, which can be regarded as an improved version of the wavelet decomposition (WD). In discrete wavelet transform (DWT), when performing next layer decomposition, only approximate coefficients obtained from the upper layer can pass through the filter [
48]. However, when the WPD method performs the next level of decomposition, both the low-frequency sequence and high-frequency sequence can pass the filter [
49], and the total number of coefficients is still the same without redundancy. Therefore, WPD can extract the features of the original signal more comprehensively, which not only provides a wide range of possibilities for signal analysis but also allows the best matching analysis of the signal. Meanwhile, compared with DWT, the decomposition structure of WPD provides more opportunities to improve computational efficiency [
50]. Therefore, WPD is preferred in this paper in consideration of the complex nonlinearity and non-stationary characteristics of hydrologic time series.
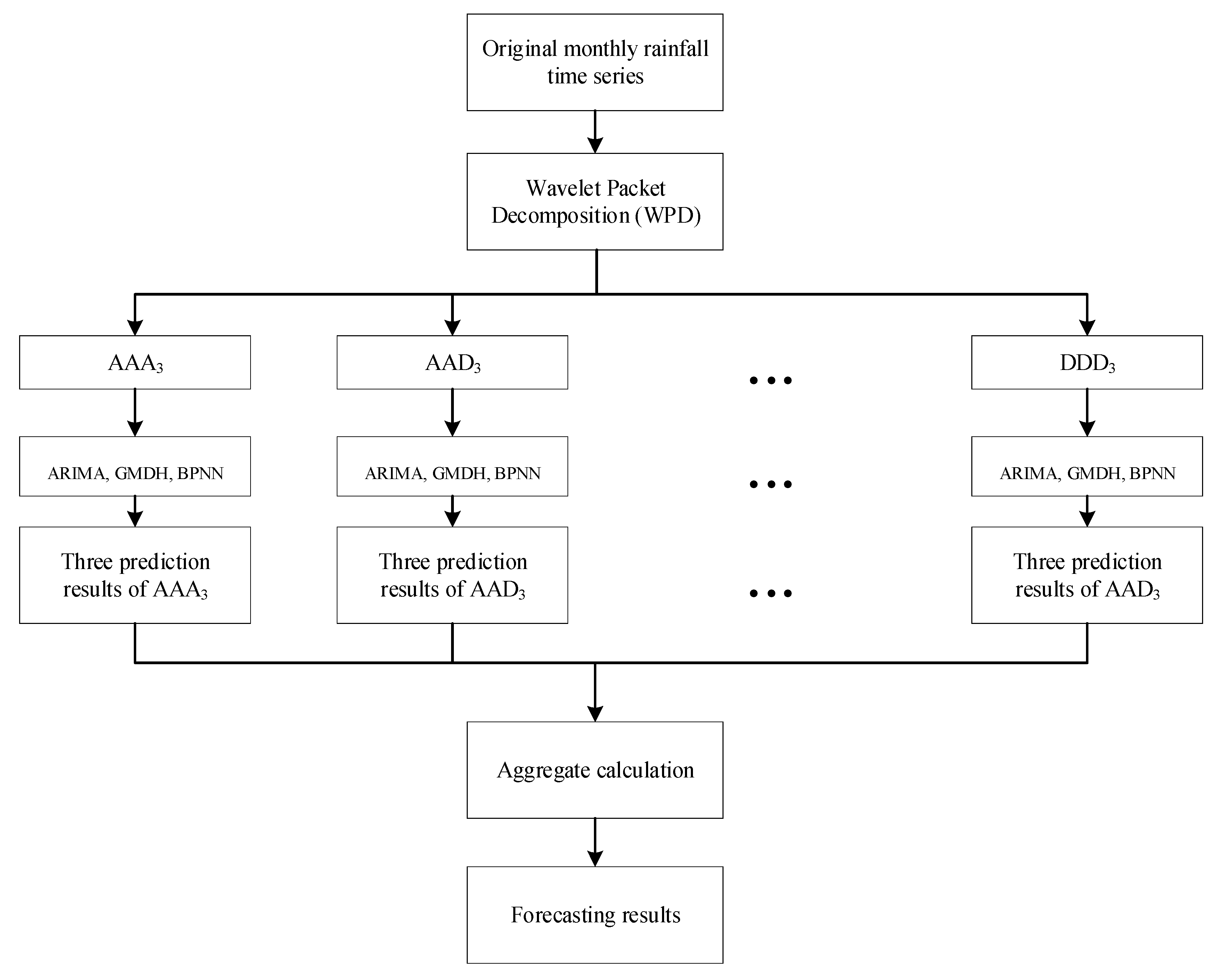
The purpose of this paper is to investigate the accuracy of ARIMA, GMDH, and BPNN models based on WPD in monthly rainfall forecasting. Most former research often improve the accuracy of prediction models by optimizing model parameters using optimization algorithms, and the improvement effect of this method is often not obvious. In this paper, the data preprocessing method is adopted to improve the accuracy of forecasting models, which can attain more linear sub-series and significantly reduce the difficulty of prediction. Firstly, we use WPD to decompose original monthly rainfall series into a series of sub-series with different frequencies and spatiotemporal resolutions. Then, the subseries decomposed by WPD are used as input data of ARIMA, GMDH, and BPNN to train for prediction. Finally, the prediction results of each hybrid model are obtained by linearly accumulating the outputs of each submodule.
The paper is arranged as follows:
Section 2 introduces the basic theory principles of methods and evaluations indices. The forecasting experiments and discussion are presented in
Section 3. Finally,
Section 4 concludes the paper.
3. Results
3.1. Decomposition Results Using WPD and Input Variables Determination
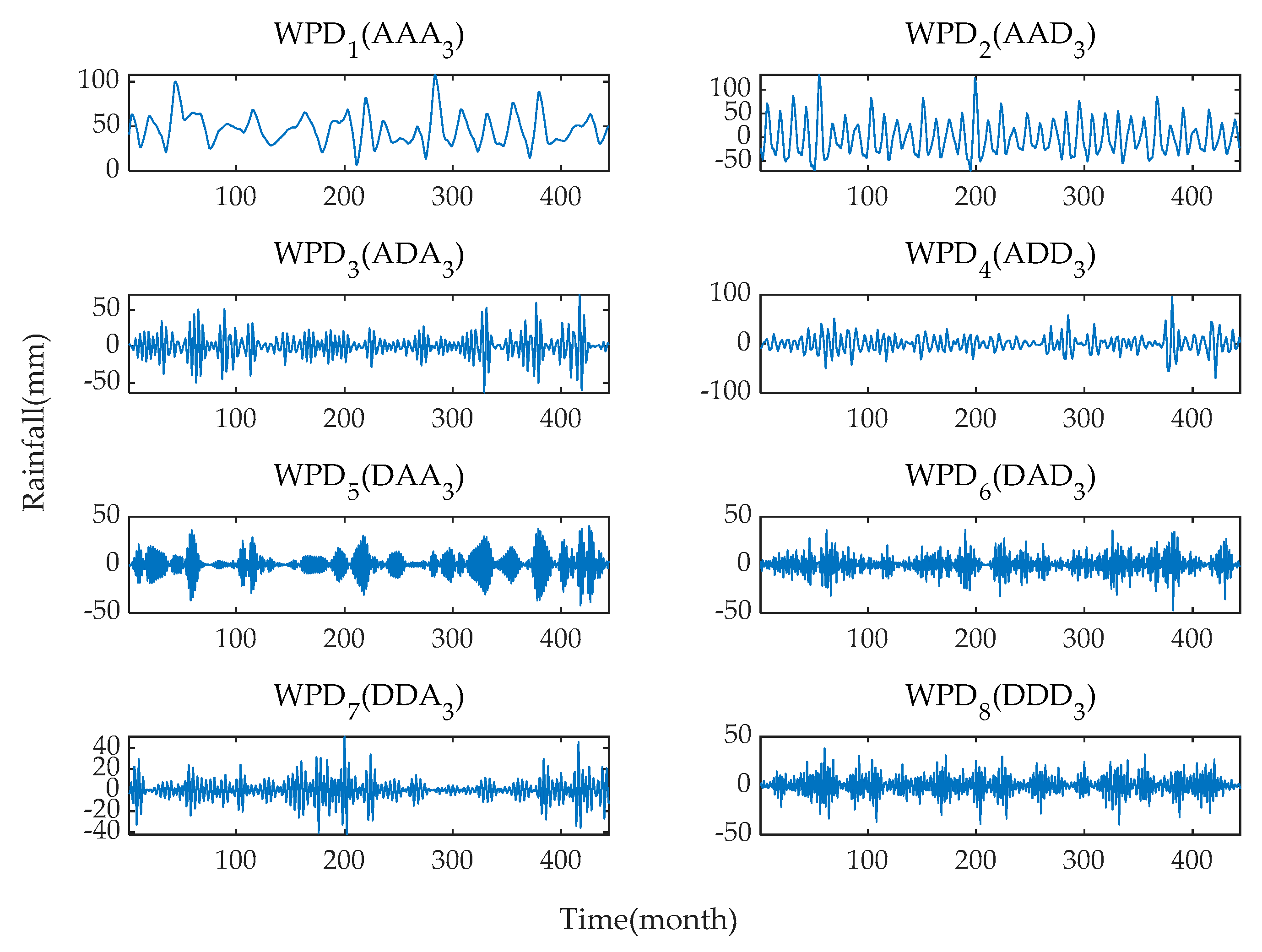
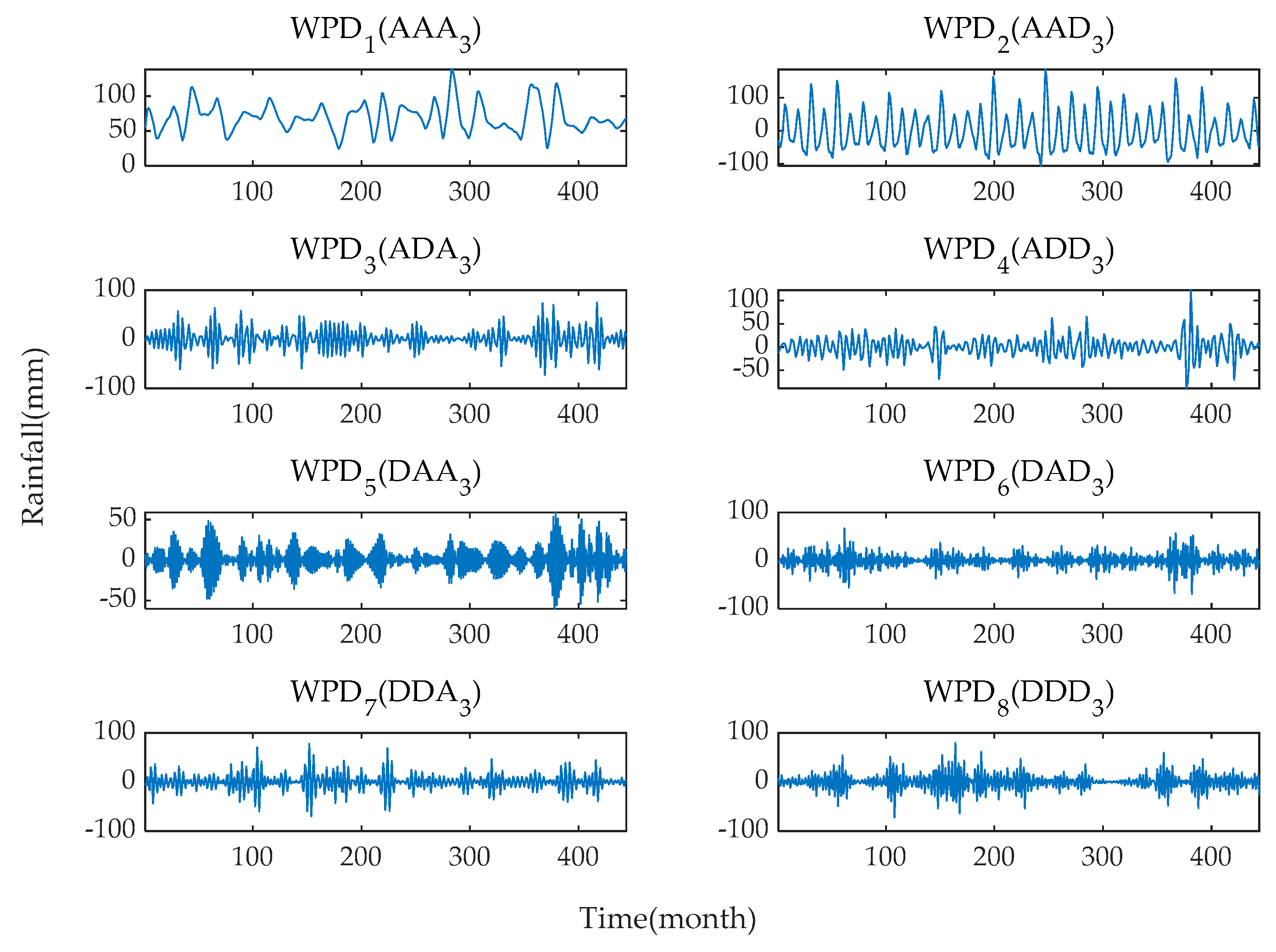
The original monthly rainfall time series are decomposed into eight subsequences with different frequencies and amplitudes using the WPD method. The frequency characteristics of each subsequence are different, and each sub-series plays a different role in the original dataset. The results of WPD of the original monthly rainfall time series data at level 3 are shown in
Figure 8 and
Figure 9.
Generally, it is very important to set an appropriate number of input variables for data-based prediction models because it is closely related to the characteristics of system to be modeled [
62]. In this paper, ACF and PACF are selected as the potential indicators for determining the appropriate input variable. ACF and PACF are normally utilized to pre-determine the sequence of the autoregressive process and modeling of time series [
63].
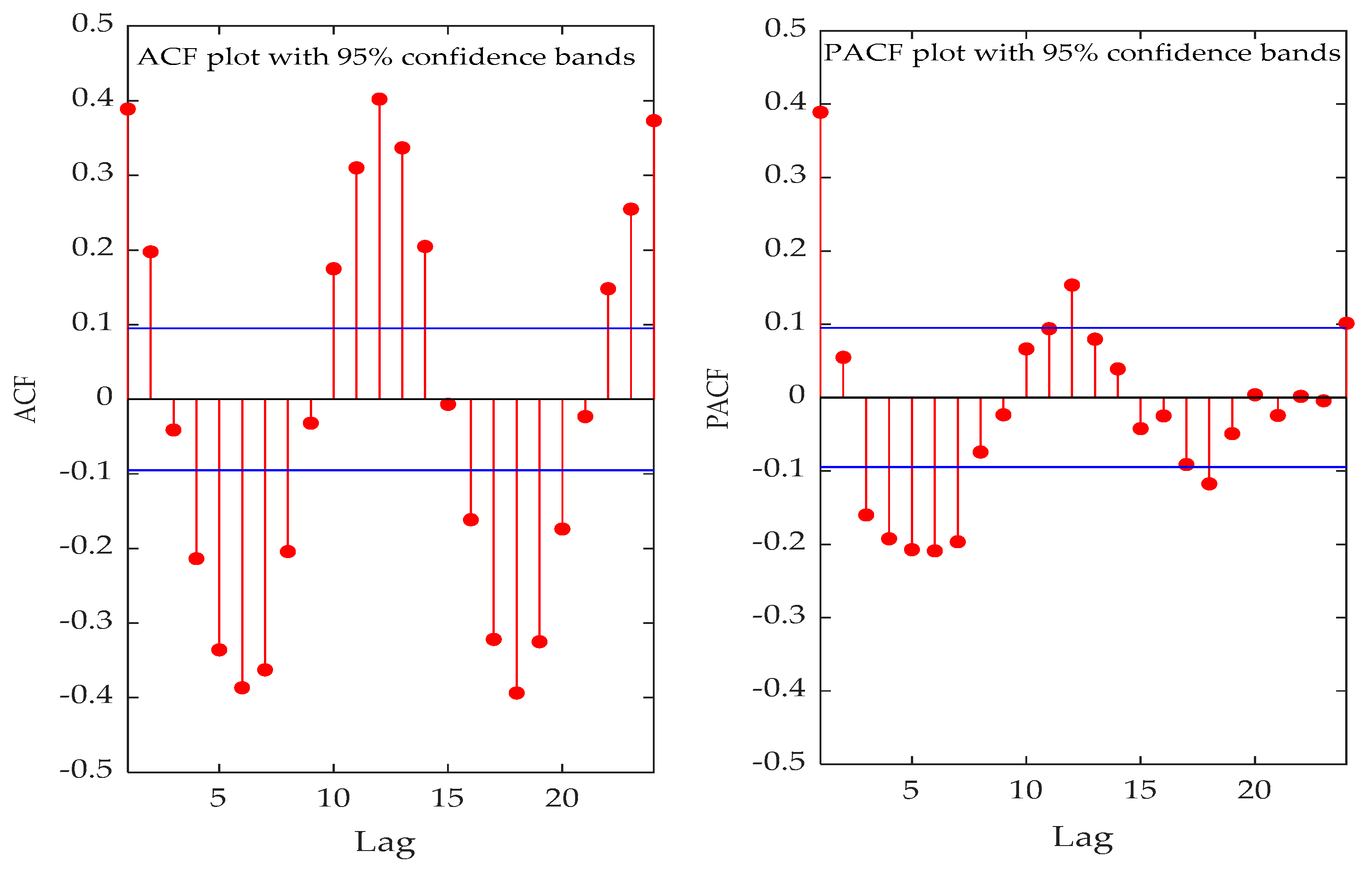
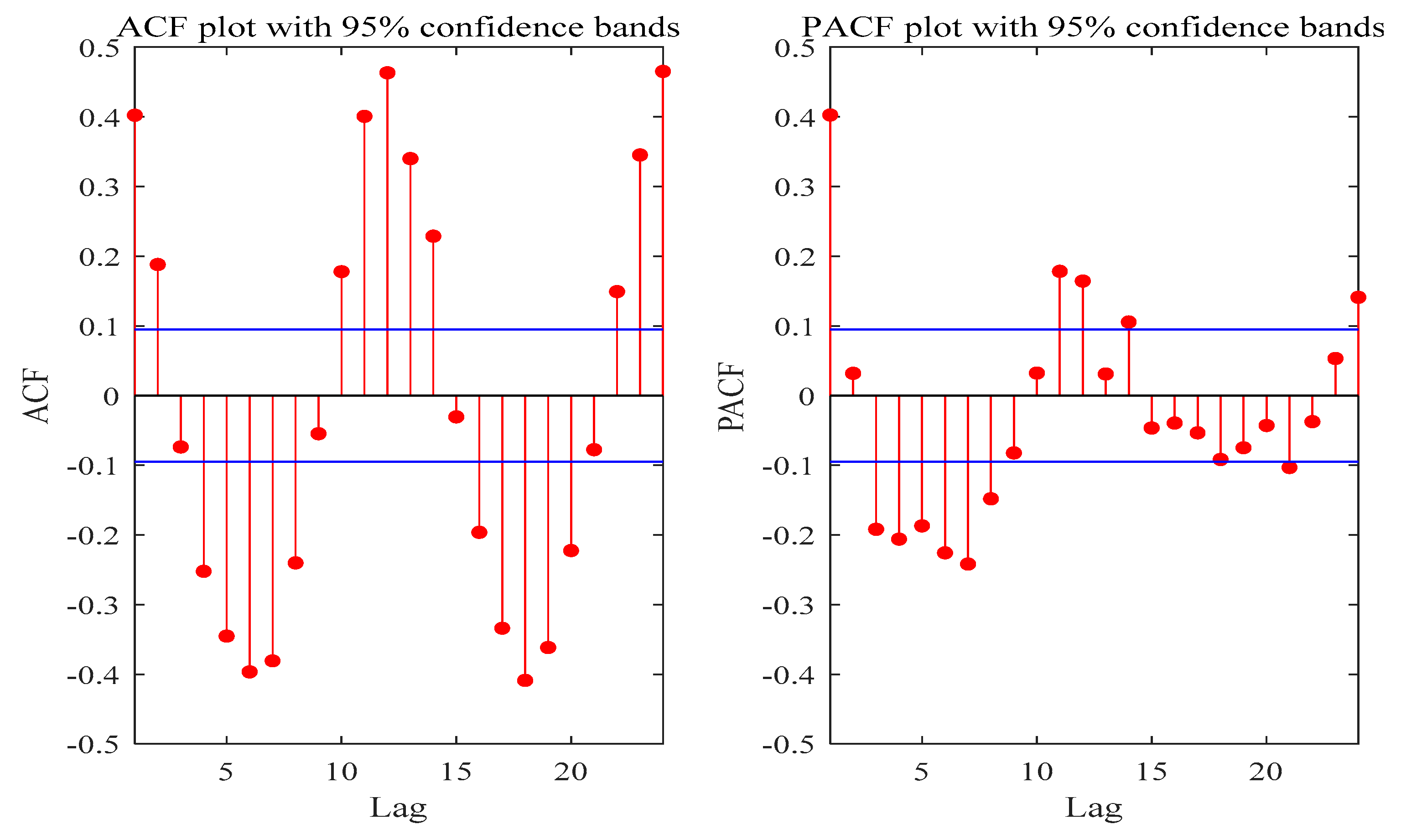
Figure 10 and
Figure 11 show ACF and PACF values of the original precipitation series for Luoning and Zuoyu stations, whilst the values of ACF and PACF for all decomposed subseries are not presented here. Referring to ACF and PACF values of the series and influencing factors of precipitation,
Table 2 lists input variables of the original series and their subsequences at Luoning and Zuoyu stations. Among them,
represents the
th variable before the target output variable.
3.2. Model Development
Six models, namely BPNN, WPD-BPNN, GMDH, WPD-GMDH, ARIMA, and WPD-ARIMA models, are employed for benchmark comparison to study the prediction performance of these conjunction methods.
(1) ARIMA
Generally, the ARIMA model based on the difference process is applied to the modeling of non-stationary series. In this paper, the stationarity of the original monthly rainfall series and subsequences are tested by the Augmented Dickey–Fuller (ADF) test. The results of ADF unit root tests are shown in
Table 3. The
value of the original and all subsequences of the two stations are zero. The
p-value of the original sequence and all sub sequences of the two stations is zero, except that the
p-value of the original sequence of Zuoyu station is 0.0004. When
,
p-value < 0.05, and the value of
t-statistic is less than the preset upper limit, the null hypothesis is rejected, and the sequence can be considered as stationary; otherwise, the series needs to be differential. It can be seen from
Table 3 that the sample set data is stationary series without a single root effect.
The next step is to choose the optimal ARIMA (
p,
d,
q) model, and the best fitted values of
p and
q are selected according to the BIC method. ACF and PACF are used to predetermine the structure of data sets. Furthermore, referring to the BIC minimum criterion, the best fitting model is determined for the original sequence and the decomposed subsequence of the two stations. The values of
p and
q are determined based on ACF and PACF, and the significance test has to be passed, that is, when
p-value is less than 0.05, select the parameter with minimum BIC statistics. ARIMA models for various sequences are shown in
Table 4. The decomposed sub-sequences of Luoning and Zuoyu stations are modeled by the ARIMA model. The original time series are modeled by seasonal ARIMA model (SARIMA), where
p,
d, and
q represent the autoregressive term, the order of difference, and the moving average term of SARIMA model, respectively.
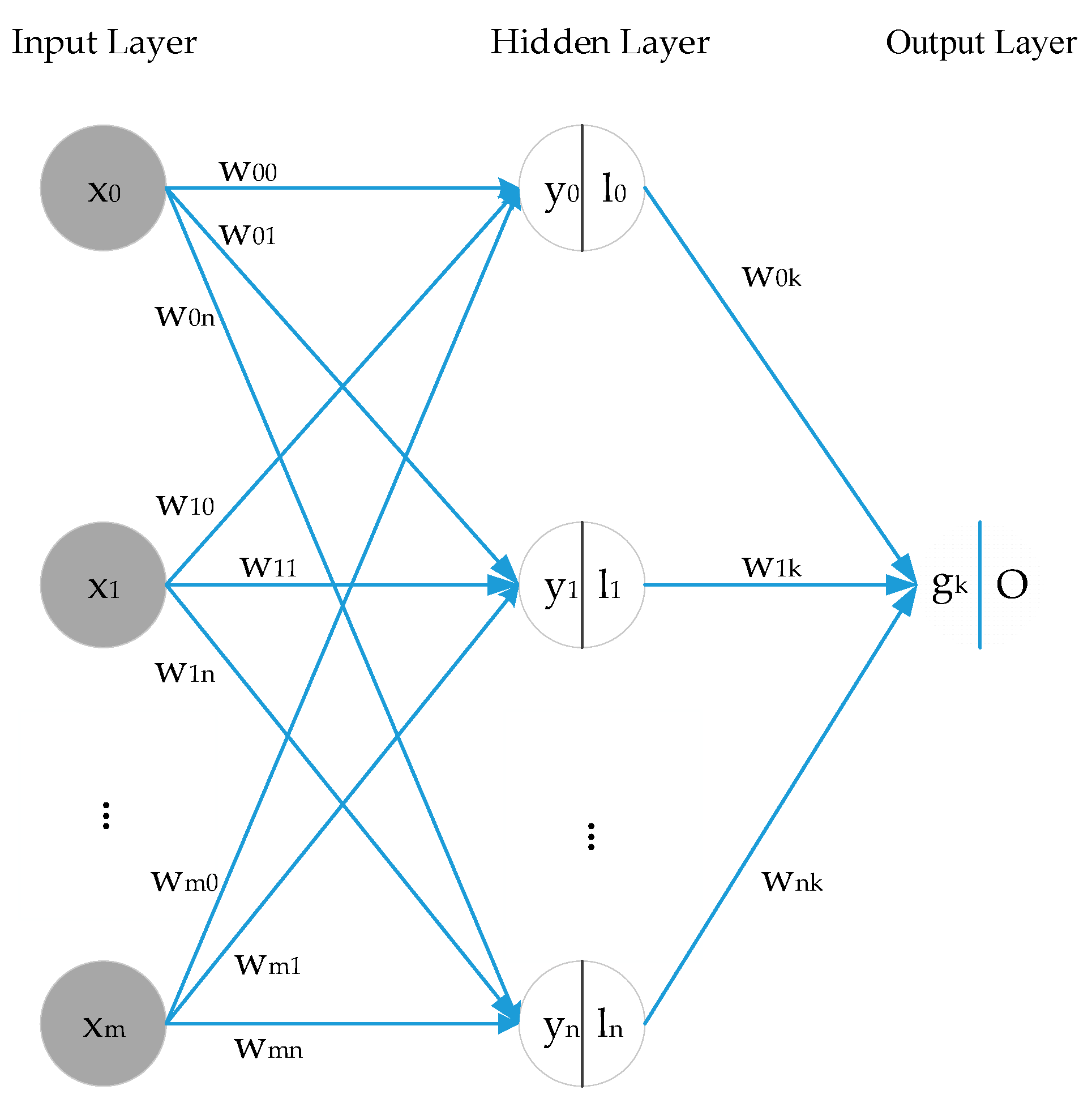
(2) BPNN
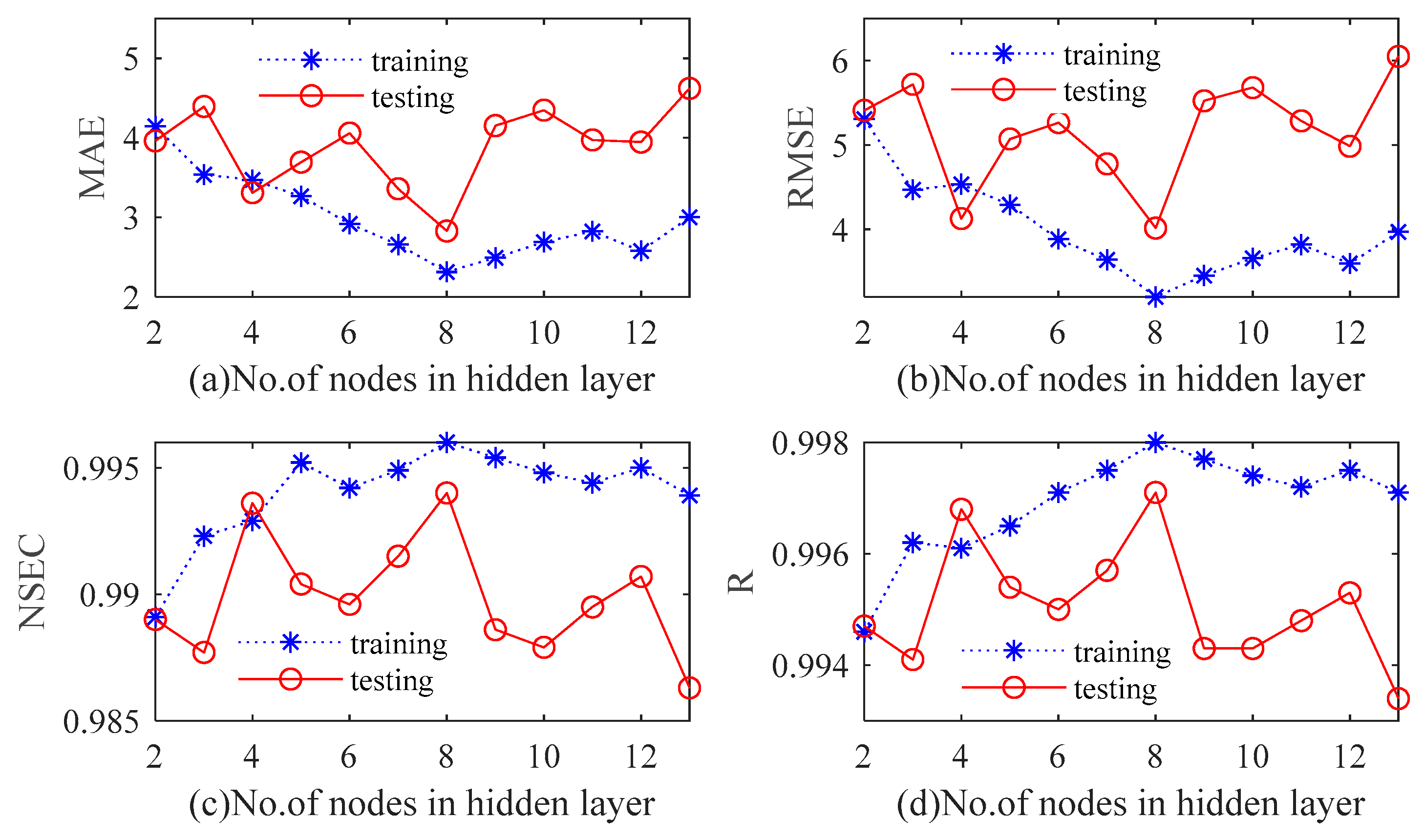
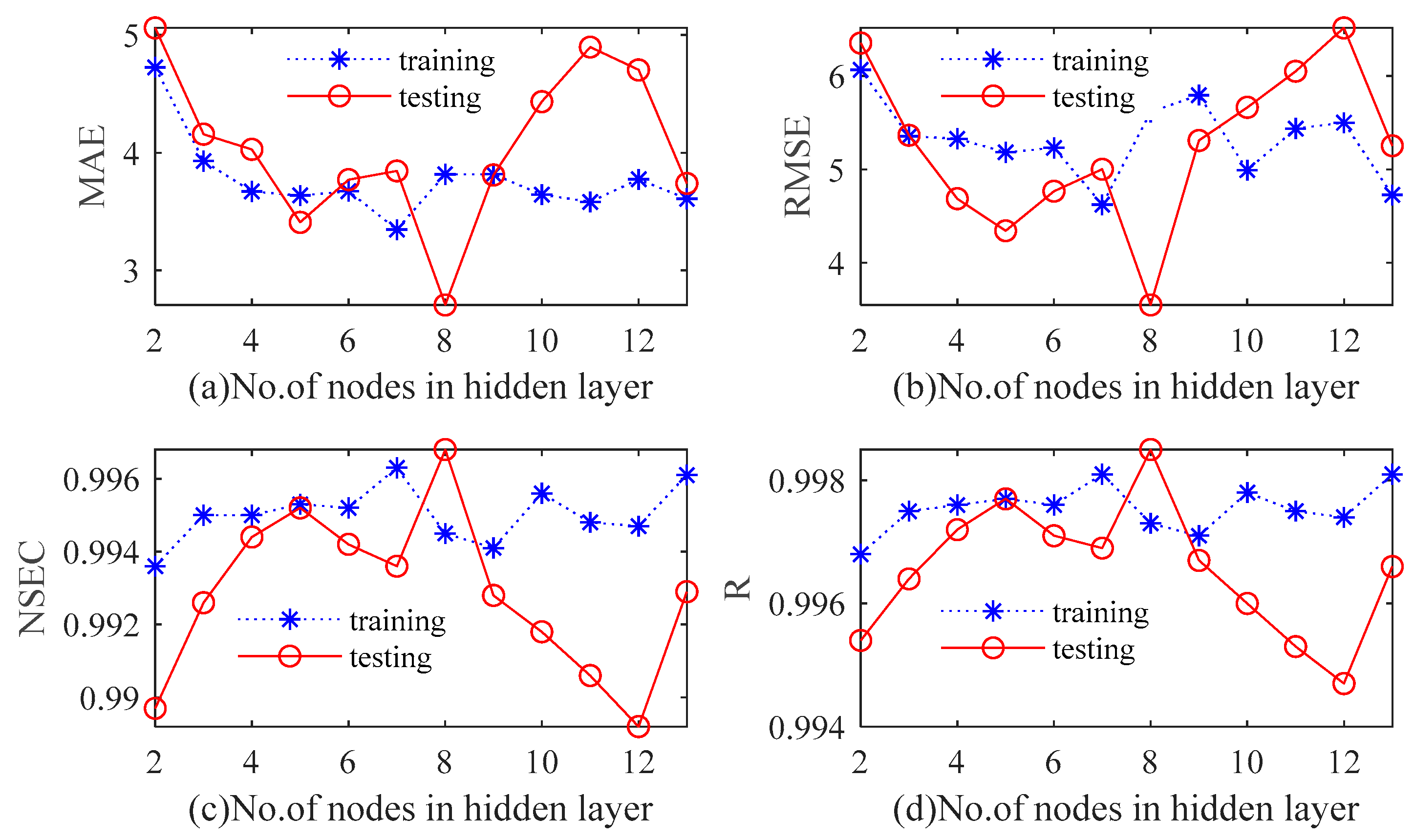
A conventional three-layer BPNN is used to establish the prediction model of monthly precipitation series in this paper. Tan-sigmoid is the transfer function between output and hidden layers, and the nonlinear Levenberg–Marquardt (LM) algorithm is the training function of BPNN. The maximum number of iterations is 100. The number of input layer nodes is the same as the number of input variables. The optimal value is determined by continuously adjusting the number of hidden layer neurons in the range of 2 to 13. The original dataset falls into training samples and test samples. According to the four quantitative indexes, a cross-validation approach is utilized to determine the number of hidden neurons. With the increase of the number of hidden neurons, variations in the statistical indicators of Luoning/Zuoyu station corresponding to different hidden layer nodes are shown in
Figure 12 and
Figure 13. In this paper, we use
to refer to the number of hidden layers. It can be observed from
Figure 12 and
Figure 13 that
is not highly correlated with the performance of BPNN model. For Luoning station, when
, RMSE and MSE of training and testing periods are both at a minimum, while R and NSEC reach a maximum. For Zuoyu station, when
, MSE and RMSE of the testing set reach the minimum value; meanwhile, NSEC and R attain the maximum value. However, when
p is seven, MSE and RMSE of the training set reach the minimum value, NSEC and R of the training set reach the maximum value. Therefore,
p is chosen to be eight for both Luoning and Zuoyu stations.
(3) GMDH
The number of input layer nodes is the same as the number of input variables, and then the regression of output value of upper layer is computed to create the second layer network. GMDH uses the best new variables in each layer to build the next layer network. The GMDH model includes three parameters, namely a denoting the maximum number of layers, b denoting the maximum number of nodes in each layer, and p denoting the selection pressure. In this paper, a and b are determined as 3 and 15, respectively, whilst p is set equal to 0.75 via a trial-and-error method, and the convergence criteria is RMSE. This paper determines an appropriate maximum number of hidden layers and nodes of GMDH model by a trial-and-error method. We set equal to 2, 3, and 5, and b equal to 5, 10, and 15. The results (not supplied) show that the numbers of and b have a significant effect on the performance of the GMDH model.
(4) WPD
WPD is adopted for data preprocessing, which can eliminate noises in hydrological time series. The selection of an appropriate mother wavelet is very significant to WPD. The Symlet wavelet function is an improved version of the classical Daubechies wavelet function, which evades the change of waveform in the process of signal decomposition [
64]. Therefore, the fourth order Symlet wavelet function is considered as the mother wavelet function. In this paper, three-scale wavelet WPD is selected because large-scale wavelet packet decomposition may lead to information loss.
3.3. Results and Discussion
Based on the above description, different methods are utilized to model the observed rainfall and extracted sub-sequences.
Table 5 and
Table 6 list the statistical indexes of different algorithms for Luoning and Zuoyu stations during training and testing periods.
For Luoning station, the WPD-BPNN model attains the best RMSE, MAE, R, and NSEC values during the training period, which are 3.292, 2.384, 0.998, and 0.956, respectively. In the testing phase, the WPD-BPNN model also attains the best R, RMSE, MAE, and NSEC statistics of 0.997, 4.054, 2.912, and 0.994, respectively. Meanwhile, for Zuoyu station, the WPD-BPNN model attains the best RMSE, MAE, R, and NSEC values during the training period, which are 5.935, 4.102, 0.997, and 0.994, respectively. In analyzing the results during the testing phase, the WPD-BPNN model attains the best R, RMSE, MAE, and NSEC statistics of 0.998, 3.705, 2.889, and 0.996, respectively. Referring to the four evaluation indicators in this paper, WPD-BPNN can attain the best performance in monthly precipitation prediction.
Table 7 and
Table 8 list the comparison of results on model prediction performance by different indicators. When forecasting monthly rainfall at Luoning station, WPD-BPNN is able to attain the best improving capability of RMSE and MAE in the training phase, while WPD-GMDH is able to attain the best improving capability of R and NSEC in the training phase. In analyzing the figures during the testing phase, WPD-BPNN attains the best improving capability of RMSE and MAE, while WPD-ARIMA attains the best improving capability of R and NSEC. In addition, it can be seen from
Table 8 that the prediction performance of the models is similar for Zuoyu and Luoning stations. Therefore, the monthly rainfall series decomposed by WPD method as the input of BPNN model can drastically improve the forecasting accuracy. This reaffirms the superior performance of WPD. Furthermore, the enhancement capabilities of different evaluation methods are different in terms of different phases and different forecasting measures.
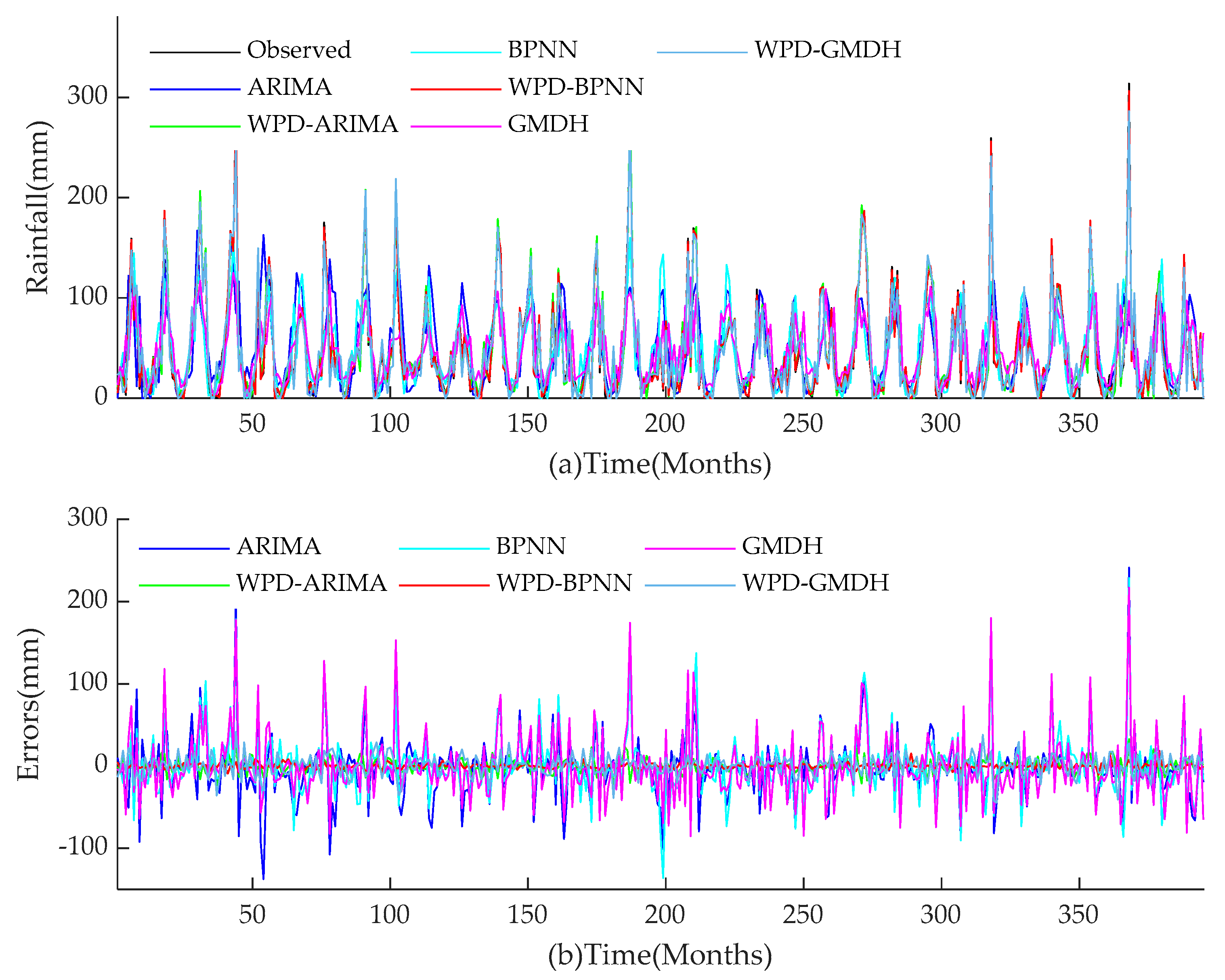
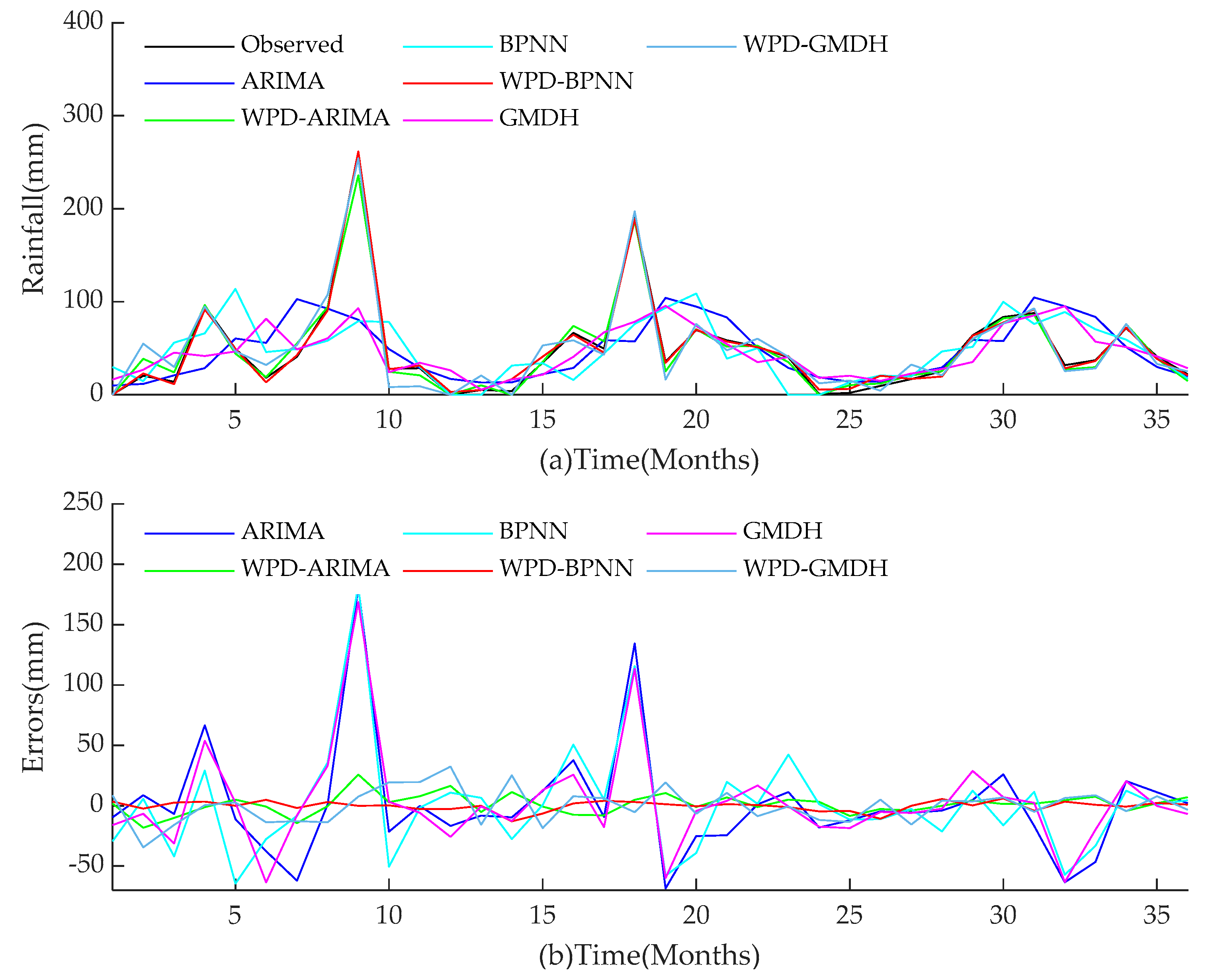
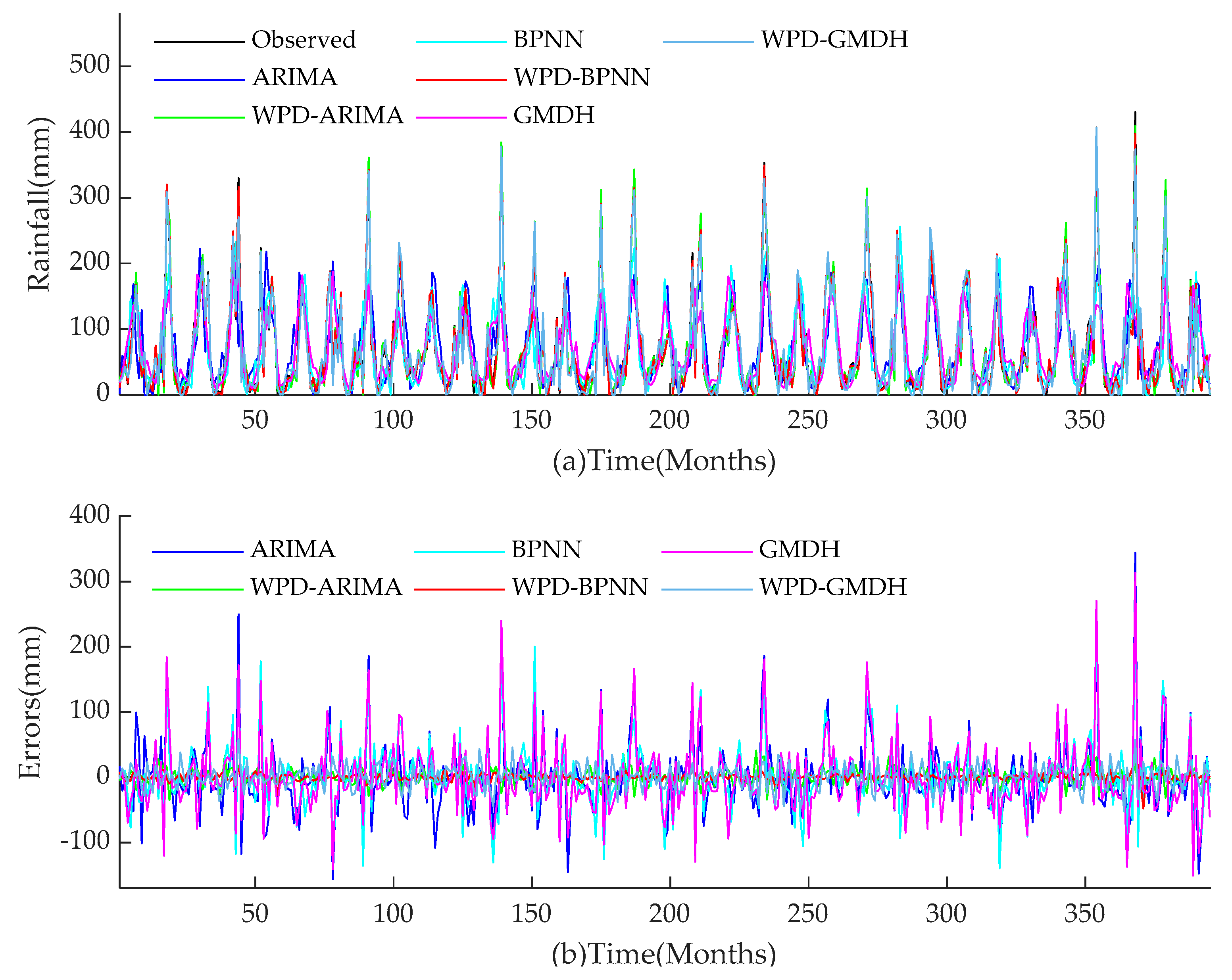
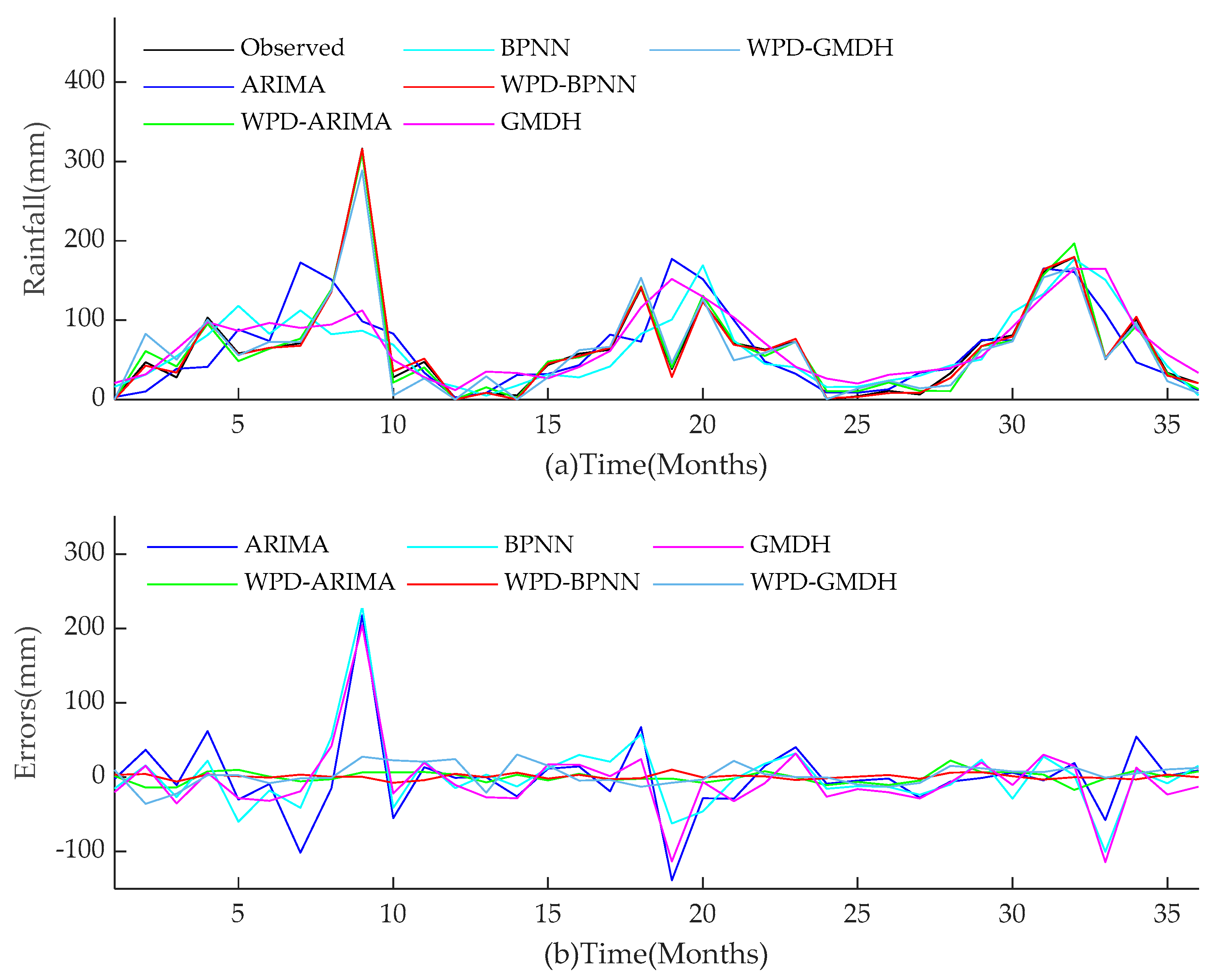
For the two research objects in this paper, the performance of all models during training and test periods are shown in
Figure 14,
Figure 15,
Figure 16,
Figure 17. The performances of hybrid models for monthly rainfall simulation are able to attain better performance than those of conventional ARIMA, BPNN, and GMDH methods. WPD-BPNN presents the best performance, and its trend line is almost perfectly close to the smooth line of the observed data. In contrast, there are huge deviations between the prediction results obtained by ARIMA, BPNN, and GMDH methods and observed data. In addition, the prediction values of the extreme points of the three single models are far less than the observed value, and the peak prediction also has an obvious lag effect. However, compared with ARIMA, GMDH, and BPNN, the three WPD-based models have greatly improved the peak value accuracy and time positioning. Meanwhile, the models prior to improvement cannot capture abrupt changes of precipitation in rainy season. Therefore, compared with several existing methods in this paper, WPD-BPNN is the most efficient tool for monthly rainfall forecasting, since it can achieve excellent prediction results.
4. Conclusions
In recent years, the improvement of hydrological forecasting accuracy has attracted widespread attention around the world. In order to broaden the scope of hydrological forecasting theory, this study explores the performance of several data-driven methods based on WPD in monthly precipitation forecasting. Firstly, the observed monthly rainfall time series are decomposed into eight subsequences with different frequencies and spatiotemporal resolutions by WPD. Then, three data-based models, namely BPNN, GMDH, and ARIMA models, are utilized to complete the prediction for the decomposed monthly rainfall series, respectively. Finally, the ensembled prediction result of the model is formulated by summing the outputs of all submodules. Monthly rainfall data from two stations in China are utilized to test the performance of these methods. To evaluate the forecast capacity of different models, four standard statistical metrics are adopted to estimate the global and local errors of the models.
The results reveal that the WPD model is suitable for the decomposition of monthly rainfall series, and WPD-BPNN can provide the best performance during both training and testing periods in terms of the four evaluation indicators in this paper. The following briefly introduces the advantages of the WPD-BPNN method. Firstly, the principle of WPD is simple and inclusive, and it can comprehensively and deeply analyze the characteristics of monthly precipitation series. Secondly, the prediction performance of BPNN only depends on the characteristics of input variables. Finally, the proposed model does not require complex decision-making for the explicit form of the model in different cases. Therefore, the hybrid forecast model based on WPD technology is an efficient tool to improve the accuracy of mid- and long-term rainfall forecasting.
It should be pointed out that, although this paper has fully verified the feasibility of WPD-BPNN in monthly precipitation forecasting, there are still several limitations to be explored in the future research. Firstly, the study is carried out based on two time series, so we will test the generalization of the proposed model. The second is to test the performance of other algorithms combined with WPD. The last major issue is to develop an appropriate optimization algorithm to improve the performance of WPD-BPNN. In future research, it is necessary to conduct in-depth research on the three aspects above to explore more efficient and accurate forecasting techniques and make contributions to the field of hydrological forecasting.