Abstract
Two-dimensional (2D) hydrodynamic models are one of the most widely used tools for flood modeling practices and risk estimation. The 2D models provide accurate results; however, they are computationally costly and therefore unsuitable for many real time applications and uncertainty analysis that requires a large number of model realizations. Therefore, the present study aims to (i) develop emulators based on SVR and ANN as an alternative for predicting the 100-year flood water level, (ii) improve the performance of the emulators through dimensionality reduction techniques, and (iii) assess the required training sample size to develop an accurate emulator. Our results indicate that SVR based emulator is a fast and reliable alternative that can predict the water level accurately. Moreover, the performance of the models can improve by identifying the most influencing input variables and eliminating redundant inputs from the training process. The findings in this study suggest that the training data size equal to 70% (or more) of data results in reliable and accurate predictions.
1. Introduction
Floods are one of the most frequent and costly natural disasters that happen throughout the world and are likely to increase in number and severity as a result of climate change [1,2]. As a result, flood related topics including flood modeling, risk analysis, flood management, etc., have always been the subject of research from the past to the present. There are a variety of tools and approaches for flood modeling purposes, such as empirical methods (e.g., measurements, surveys, remote sensing, and statistical models) and hydrodynamic models (1D, 2D, and 3D models) [3].
Two-dimensional (2D) models, as a class of hydrodynamic models, are one of the popular tools that are based on the numerical solution of the 2D Shallow Water Equations (SWE) and use different types of input parameters with complex domain spaces (e.g., hydrological data, floodplain and channel geometry, initial and boundary conditions, roughness) and provide outputs such as flow velocity, water level, and inundation extent. Two-dimensional hydrodynamic models provide accurate results. However, they are usually computationally intensive and require long run time. Therefore, these tools might not be a proper choice (i) when a large number of model realizations is needed (such as required in uncertainty analysis with GLUE, Monte Carlo, or Bayesian approaches, or in optimization studies), or (ii) for applications that require rapid model response [4] (e.g., rapid flood risk analysis or real time flood modeling). There are alternative solutions to overcome these constraints, such as simplification of the model (e.g., [5,6]) or using data-driven surrogate models or emulators.
In literature, emulators, metamodels, response surface modeling, and surrogate modeling are often considered as interchangeable concepts and generally are referred to as metamodels [7]. The principal idea of these models is to find relationships between the system state variables (input and output) without explicit knowledge of the physical behavior of the system [8]. In recent years, the application of emulators in hydraulic/hydrological modeling practices has received considerable attention and a variety of methods have been developed and used as emulators such as: polynomial regression [9,10], radial basis functions [11], kriging methods [12], and smoothing splines [13]. A comprehensive review of different emulation methods can be found in [7], in which different approaches for optimization purposes were critically reviewed. Amongst the proposed methods for development of the surrogates or emulators, artificial intelligent (AI) techniques are popular methods that have been widely applied in flood related studies. Ghalkhani et al. [14] applied Artificial Neural Network (ANN) and Adaptive Neuro-Fuzzy Inference System (ANFIS) to develop a surrogate model to emulate HEC-RAS model outputs for flood routing in rivers. Chu et al. [4] developed an ANN-based emulation modelling framework to simulate flood inundation based on information obtained from a 2D hydrodynamic model. Xie et al. [15] applied ANN-based hybrid modeling approach to improve the model performance in data-sparse regions by training an emulator using data-rich regions.
In addition to ANN, successful application of other AI techniques has also been reported in literature. The authors of [16] compared ANN and Support Vector Regression (SVR) performance for approximating the Soil and Water Assessment Tool (SWAT) model in two watersheds and reported the better performance of SVR model. Xu et al. [17] implemented SVR to investigate the effect of model structural error on calibration and prediction of real-world groundwater flows. Numerous types of emulators have been developed for different classes of 2D models such as: HecRAS2D, TELEMAC2D, TUFLOW, and MIKE FLOOD (e.g., [4,9,18,19]). According to the literature, most of the 2D models simulate flood flow for a given discharge or inflow hydrograph and accordingly the simulation scale is constrained to a limited river reach. For these 2D models, the emulators are trained based on inputs such as discharge, roughness values along river, topographic features of river channel and floodplain, and the outputs such as flood discharge or volume and flood level. Only a small number of 2D models use direct rainfall at catchment scale (global scale) to model flood, thus, the application of emulators for hydrology-hydraulic coupled models is rare. A few studies have used emulators for catchment scale flood modeling such as Bass and Bedient [20] that used a supervised machine learning approach based on coupled hydrodynamic and hydrologic modeling results to provide rapid, probabilistic estimates of joint flooding from Tropical Cyclones at the catchment scale.
Catchment or so-called global scale flood modeling is particularly important in catchments with complex topography and rivers with multiple tributaries originating from different parts of the catchment where the land cover and topography features effect can play important roles. Thus, their effect should be considered in the emulation process. In recent years, due to the advances in computational power and accessibility of graphics processing units (GPU), flood simulation at global scale has become feasible but is still time consuming. Therefore, it is important to develop accurate emulators and to do it in an efficient way.
Typically, the performance and accuracy of the trained emulators are assessed through aggregated error metrics such as root mean squared error (RMSE) and correlation coefficient (R). Al Kajbaf and Bensi [21] showed that aggregated error metrics give incomplete measures of the performance, and the accuracy of the models must be assessed beyond these metrics.
Thus, this study aims to: (i) develop an emulator by using ANN and SVR, considering inputs such as rainfall intensity, land features and outputs simulated by a coupled hydrology-hydraulic 2D model, (ii) simplify the models’ structures and improve the performance of the emulators by applying correlation tests and ANOVA analyses, (iii) investigate the predictive error structure of the emulators and select the most accurate emulator, and (iv) assess the required training sample size to develop an accurate emulator.
2. Materials and Methods
2.1. Case Study
Birkeland, located in Agder province (Norway), was selected as the case study, as floods have become a major concern there in recent years. Birkeland is located beside a river named Tovdal, where the river debouches into a small natural lake called Flakksvann (Figure 1). The length of the main river is approximately 130 km, and the catchment has an area of about 1767 km2 dominated by forests (about 74%). The elevation ranges from 10.00 to 872.34 m.a.s.l., and the average slope of the catchment along the river is about 0.65%. The mean annual precipitation is approximately 1261 mm, with most of the rainfall occurring between October and March (about 60%). On 2 October 2017, an extreme flood event occurred in the downstream parts of the river and inundated Birkeland. This event was the highest ever recorded flooding of this river. The recorded data of the event can be found in the study by [22].
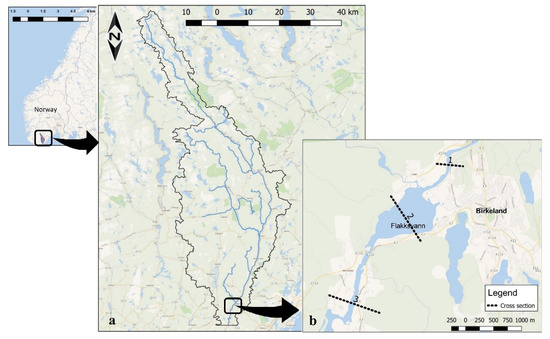
Figure 1.
(a) Map of Tovdal river’s catchment area. (b) The case study area with specified cross sections.
2.2. Hydrodynamic Simulations and Input Ranges
In the current study, a GPU based 2DH (two dimensional horizontal) hydrodynamic model named HiSTAV was used to simulate floods. The model was originally proposed by in [23] and optimized in [24]. The core of the model is a hyperbolic system of partial differential equations expressing mass and momentum conservation principles for shallow-water flows. The equations are solved using a finite volume scheme, which is applied on a spatial discretization using unstructured meshes. The initial conditions for the equations are zero water depth and zero discharge everywhere (dry surface conditions). Water enters the domain only through rainfall; hence there are no inlet boundaries. The only open boundary is at the outlet (downstream), where free outflow is assumed. For detailed information about HiSTAV and the model structure we refer the readers to the study presented by [23].
The model employs adaptable triangular meshes over the study domain to discretize the catchment and terrain parameters (i.e., elevation, bathymetry, land use, etc.). The computational domain for the simulations is the part of the catchment upstream of the small lake named Flakksvann, just beside Birkeland (Figure 1a). In order to avoid outlet boundary interference, the domain was extended 11 km further to the downstream of the lake. In this study, by employing Godunov’s finite-volume approach ([25]) a total of 401,769 mixed mesh of triangular cells are constructed in three sizes over the computational domain (Figure 1a) by Gmsh ([26]), which is a free finite element grid generator with a build-in CAD engine and post-processor. The small cells or so-called finer resolutions are assigned to the cells where the flow gradients are expected to be large, such as the river channel; medium sized cells, or average resolution over the flood plain; and coarser resolution over other parts of the catchment, where flow gradients are expected to be mild.
Prior to undertaking the simulations, warm-up simulations were performed until reaching the normal water level in the river network. A 9-day precipitation with an intensity of 2 mm/h was found to be long enough to fill the river basin and the lakes with the steady flow. Using the filled catchment (in water courses parts) as the base time step, the model was calibrated and validated using the recorded data of the 2017 flood event (including water level, discharge, hydrograph at Flakksvann cross section, and flood maps). Further details of the calibration process are presented in [22].
Once the calibration and validation were done, reasonable ranges were established for the inputs, taking into consideration the calibrated values and based on the land type, vegetation, and average antecedent soil moisture. In the present study, each simulation started from the warm-up simulation results and ran for a computational time of 34 h. The calibration simulation’s result in terms of flow depth is displayed in Figure 2.
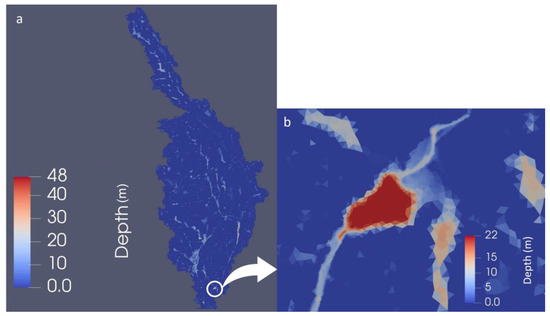
Figure 2.
Water depth ranges in the calibrated model: (a) computational domain, (b) case study region.
HiSTAV requires different data sets as input to simulate the flow, namely: the topo-bathymetric dataset, Strickler roughness coefficient values, runoff coefficient values (in form of raster files), and precipitation intensity.
A Digital Terrain Model (DTM) including the river bathymetry information is used to represent topographic features and derive hydrologic characteristics (i.e., slope, flow direction, flow accumulation, stream network, computational cascade for flow routing, etc.).
Hydraulic roughness is inserted in the model in the form of a grid structure raster file ( resolution), in which each cell represents Strickler roughness values. The spatial distribution of roughness values is determined based on land cover maps (obtained from https://land.copernicus.eu/-“Corine Land Cover (CLC) 2018, Version 20” (accessed on 10 April 2021)). Subsequently, using typical Strickler roughness coefficient tables, the roughness values were assigned for each cell [27,28].
The runoff coefficient is a dimensionless factor that is used by HiSTAV to convert the rainfall amounts to runoff (i.e., effective precipitation , being the precipitation intensity). Similar to the hydraulic roughness values, the runoff coefficient is used in the form of raster data and represents the integrated effect of catchment losses (like infiltration and surface retention). Therefore, the coefficient depends on different parameters such as land cover and use, slope, soil moisture, and rainfall intensity [29].
In this study, a combination of two different approaches to calculate the runoff coefficient was used. First, by using land cover maps and recommended values of runoff coefficients for different types of areas [30], a range was determined for each cell. Second, since the HiSTAV model assumes a uniform spatial distribution of precipitation as input, the runoff coefficient was used as an artifact to introduce spatial variability of the precipitation. For this purpose, daily precipitation data were obtained from 37 stations (Figure 3) for one of the recorded extreme floods (flood of 2 October 2017). The rainfall observations at the stations were interpolated to delineate the spatial distribution of precipitation using the inverse distance weighting interpolation method (IDW), which gave similar precipitation patterns like the ones presented by the Norwegian Meteorological Institute (http://www.senorge.no/ (accessed on 20 March 2021)). Thereafter, precipitation zones were delineated as in Figure 3. The combination of the two described approaches was used to calculate the final runoff coefficient in each cell, , as follows:
where is the maximum amount of precipitation intensity among the recorded values, is the recorded precipitation intensity in each cell, and is the runoff coefficient.
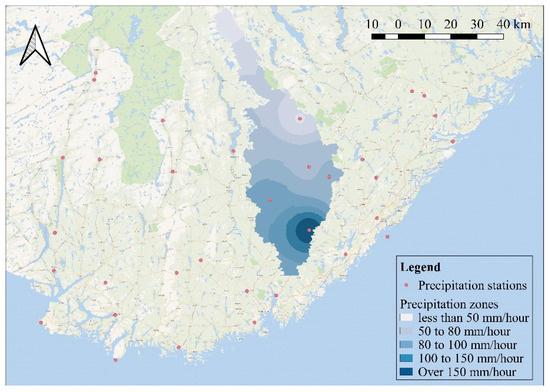
Figure 3.
Spatial distribution of the precipitation stations and the interpolated precipitation over the catchment.
The input parameters, namely hydraulic roughness parameter (), runoff coefficient (), and precipitation intensity (), were selected as the uncertain input variables that HiSTAV uses to simulate the flow. The hydraulic roughness and runoff coefficient parameter spaces are constructed for each of them based on a range that reflects the possible variation range.
The choice of ranges was based on the land type, vegetation, and average antecedent soil moisture.
Estimation of precipitation intensity is a crucial step in rainfall-runoff modelling practices, but it is incorporated with uncertainty due to the limited historical data, climate variability/change, and the complex and chaotic nature of climate. In this study, we used a Bayesian MCMC approach to define a range for precipitation intensity. For this purpose, annual maximum precipitation data were collected from different stations in the catchment and the generalized extreme value distribution (GEV) was fitted to each data series using a Bayesian MCMC approach. This approach uses a Markov chain Monte Carlo (MCMC) algorithm to estimate the GEV distribution for each data set. We used the algorithm implemented in the R-package nsRFA [31], where a Metropolis Hastings algorithm is implemented, and carried out 50,000 iterations to fit the GEV distribution.
In this study we aimed to emulate the 100-year return period flood water level. Therefore, using the fitted GEV distribution for the 100-year return period, the design rainfall and the corresponding 5% and 95% confidence intervals are selected as the precipitation range for each station. The estimated ranges for different stations were compared and finally a sufficiently wide range was selected as the catchment precipitation range. In order to consider future climate change effects, the defined precipitation interval was multiplied by a climate factor equal to 1.2. The factor was selected based on the values reported by Hanssen-Bauer et al. [32] for the case study region (Agder) under high emissions scenario (RCP8.5). For details of the Bayesian MCMC method, we refer the reader to the studies by Reis Jr and Stedinger [33], Gaume et al. [34], and Lutz et al. [35].
Table 1 presents the considered input variables with their descriptions and specified ranges used in this study. Runoff coefficient values and Strickler roughness values were assigned to each cell based on the land type.

Table 1.
Selected input descriptions and assigned ranges.
In total, there were 14 potential input variables (seven different values assigned for each land type, six types of runoff coefficient values assigned for each land type, and precipitation intensity) used to simulate the flow. The values for each of the inputs were randomly sampled assuming uniform probability distribution within the specified range (Table 1). Uniform distribution was selected ensuring equal probability for each value and avoiding any prior assumptions about the parameter distribution. The reasoning behind the use of a uniform distribution for roughness and runoff coefficients was that there was insufficient information to assume that any value in the range was more likely than any other value [36]. As displayed in Table 1, the selected range for precipitation was wide compared to the other ranges. Thus, the precipitation intensity probability distribution was divided into three equal uniformly distributed intervals with equal probabilities (1/3) and the values were sampled from these intervals. The choice of the uniform distribution for precipitation intensity was made to ensure that all possible precipitation intensities from low to extreme rainfalls were presented for training the emulator.
A total of 1100 input data sets were randomly generated, and simulations were performed using HiSTAV. Because it is crucial to predict associated extreme rainfall events (i.e., real time flood prediction purposes as in early warning systems), in addition to the 1100 samples, another 100 samples that resulted in extreme events (higher C and ip values and lower Ks values in river section) were simulated and were added to the total data set. In this study we intended to emulate the numerical flood inundation modeling. Therefore, water level was considered as the output of interest in the simulations and the values were observed in three cross sections (CS), specified along the study area (Figure 1b).
2.3. Emulation Methods
2.3.1. Support Vector Regression (SVR)
Support Vector Regression (SVR) is a supervised learning algorithm that estimates the connection between the input and output of a system from the existing samples [37]. This method attempts to identify correlations by transferring data to a higher dimension according to Equation (2) and solving the equation with the help of structural risk minimization based on Equation (3) [38]. If the relationship between the dependent and predictor variables is captured correctly, it can be used to predict the system outputs from the inputs [39].
Given a training data set (), i = 1, 2, 3, …, n , is the input vector, shows the corresponding output, and denotes the ith training sample. The variable denotes the weight factor, indicates the deviation and is constant, n is the size of data, and is the estimated target that is applied to calculate the output based on the actual input data, which has tolerance error and negligible complexity (Agustina et al., 2018). The expression is a nonlinear transfer function that maps input data to the higher dimensional feature space; and are slack variables that specify the upper and the lower training errors subject to an error tolerance ε, and C is a positive constant that determines the degree of penalized loss when a training error occurs. Using the Lagrange relations, the nonlinear regression function will be as follows:
where, , are Lagrange coefficients and is called the kernel function [38]. There are different kernel functions such as: polynomial, Gaussian radial basis, exponential radial basis, and wavelet kernel. To have an accurate model, the models’ parameters including C, ε, and the parameters of the kernel function should be determined appropriately. As a result, in the current study a grid search algorithm combined with the cross-validation method was used to optimize (tune) the different hyperparameters and models’ architecture.
2.3.2. Artificial Neural Networks (ANN)
Artificial neural networks (ANN) are nonlinear, multi-dimensional interpolating functions capable of capturing complex nonlinear relationships in the underlying data that can be missed by conventional regression methods. The topology structure of ANN is displayed in Figure 4. The network displayed in Figure 4 consists of a number of interconnected nodes (called neurons) arranged into three layers: input layer (receives input), hidden layer (represents the relationship between the input layer and the output layer), and output layer (releases the output). The implementation of the ANN model is based on three phases: a training phase to determine the model parameters from a set of training data, a validation phase to estimate the generalization ability of the model, and a test phase to calculate the output using the optimized model [40].
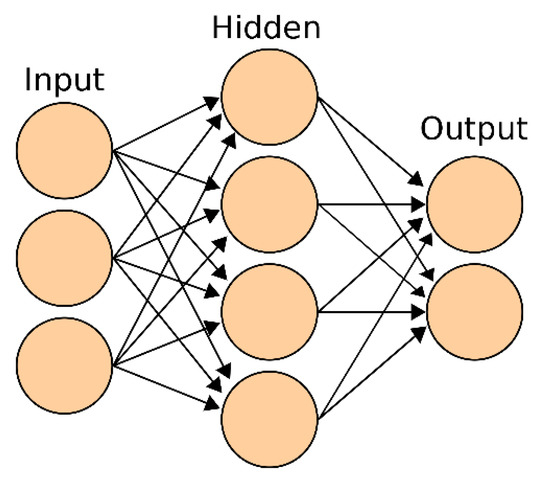
Figure 4.
ANN topology.
2.3.3. Performance Criteria
The performance of the proposed emulators is assessed by computing several metrics: root mean square error (RMSE), mean relative absolute error (MRAE), and coefficient of determination (). In addition to these metrics, maximum absolute error (MaxAE) is also selected to assess the performance of the emulator in prediction of individual extreme values (Equations (5)–(9)). The RMSE, MRAE, and MaxAE metrics have ideal values equal to zero, and the ideal value for is one.
where represents the number of observations, , and are observed, mean of observed, and predicted values, respectively.
2.4. Development of the Emulator
As was noted previously, 2D hydrodynamic models are usually computationally intensive and require long run time. In the current catchment considering the resolution of DTM and the number of mesh elements, each simulation takes about 1.5 h using 8 NVIDIA Tesla P100 (16GB) GPU (Model: 2 Intel(R) Xeon(R) CPU E5-2698 v4 @ 2.20GHz). Therefore, the main objective of this study is to produce an emulator to predict water level as close as possible to the 2D model outputs. In this section, we develop an emulator focusing on two questions: (i) how to increase the accuracy of the emulator and (ii) how much training data are required for developing an accurate emulator. We follow three steps: (1) develop the initial emulator using all the inputs, (2) improve the accuracy of the emulator by reducing the dimensionality, and (3) address the minimum data set size required for training an accurate emulator. A general overview of the workflow in this study is presented in Figure 5.
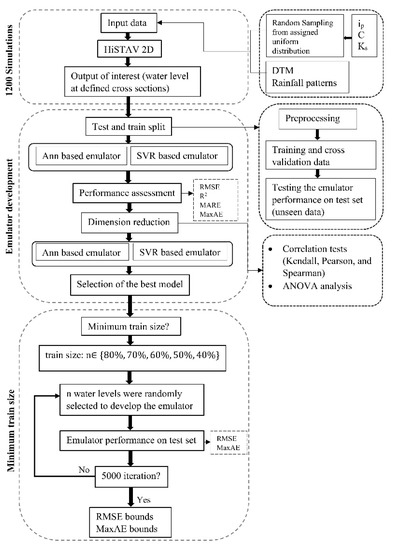
Figure 5.
General overview of the methods.
To develop the emulator, the data set is split into test and training sets. Eighty percent of the data are randomly selected as the training set and 20% as the test set for model validation. Two emulators were developed, one using SVR and another using ANN.
To configure the artificial neural networks, a trial-and-error procedure was used to identify the number of hidden layers and nodes and fix the final architecture of the neural network model. Several different model structures were tested using 1 to 4 hidden layers and 4 to 30 hidden nodes, and the number of epochs was set as four epochs’ of 1000 iterations each. Finally, a model with two hidden layers with 10 and 12 hidden neurons in each was selected as the optimal structure. To determine the optimal structure for SVR a grid search algorithm was used, combined with the cross-validation method to optimize (tune) the different hyperparameters and models’ architecture, and a model with parameters C = 10, γ = 0.1, ε = 0.01 and Radial basis function (RBF) kernel was selected as the optimal model.
The performance and accuracy of data driven approaches highly depend on the input selection and their functional relationship with outputs. Identifying suitable input variables reduces the model complexity and prevents redundant information being added into the model (i.e., input dependence), which avoids the negative impact of these inputs on model performance [41]. There are several approaches for dimensionality reduction purposes such as screening methods, correlation-based methods, variance-based techniques, principal component analysis, etc.
In this study three correlation tests—Pearson, Kendall, and Spearman—were used to identify the most correlated inputs and reduce the dimensionality. Pearson’s correlation test is the most widely used correlation statistic to measure the degree of linear association between two variables, whereas Kendall’s and Spearman’s correlation coefficients are based on ranks and measure the ranked order correlation. Further details of different correlation tests can be found in the study conducted by [42].
In addition to the correlation tests, analysis of variance (ANOVA) was performed to identify the most significant factors. This method focuses on the analysis of the variance explained by each input and is accomplished by estimating the Fischer’s test value (F-value). The impact of any factor is explained by its F-value and the corresponding sum of squares that represent variance. A higher F-value and sum of squares of any factor indicates its relative importance in the process of the response [43]. To represent the impacts of each individual parameter, the percentage contribution (PC) of each input is calculated using the following equation [44,45]:
where SST is the total sum of squares, and SSj is the sum of squared deviations for each parameter j. Both can be calculated using Equations (11) and (12), respectively:
where n is the number of observations, represents the ith observed result in the result set, is the average of the results, is the mean of results for the factor j at level i, and is the number of experiments that have factor j at level l [46].
To successfully train an emulator, the dataset on which the emulator is trained needs to be sufficiently large (i.e., consist of a sufficient number of observations) [47]. This can be challenging when the generation or collection of training data is subject to certain limitations. A number of studies have highlighted the importance of sampling and the effect of sample size on the accuracy of the models.
Hjort and Marmion [48] investigated the sample size effect on the accuracy of a geomorphological model using an ANN approach. Heckmann et al. [49] analyzed the sample size effects on logistic regression (LR) model accuracy for predicting debris flow spatial distribution and showed the negative effect of both inadequate sample size and too large sample size on results. Kalantar et al. [50] investigated the effect of different training samples on parameter estimation in SVR, LR, and ANN models and reported that the ANN model was performing better in terms of sensitivity to training samples. In this study training datasets with different sizes were created using random sampling. The procedure was repeated for +5000 times for each size and the variability in performance of the trained emulator was assessed through its predictive ability on the test set (unseen data).
3. Results and Discussion
Following the 1200 simulations obtained from random input data sets, two emulators were developed using ANN and SVR to predict water level at three different cross sections. The required time to predict 1200 water levels using ANN and SVR was about 1 min, which is 100,000 times faster compared to the simulation time using HiSTAV.
Figure 6 displays the water level predicted by ANN and SVR against the corresponding results of the 2D simulator. Moreover, to evaluate the performance of the initial emulators using a full set of inputs (14 input parameters), four statistical metrics, , , , and (Equations (6)–(9)) were calculated at each of three cross sections and the results are presented in Table 2.
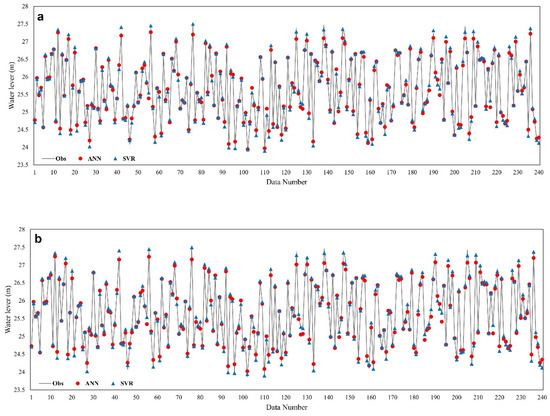
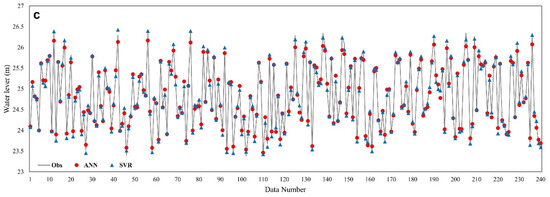
Figure 6.
Comparison of observed and predicted water level for test set by ANN and SVR at cross section 1 (a), cross section 2 (b), and cross section 3 (c).

Table 2.
Initial emulator performance (developed using 14 inputs) on test set.
According to the performance statistics presented in Table 2 and the plots displayed in Figure 6, it can be seen that the SVR with optimized model parameters , , , and Radial basis function (RBF) kernel, outperformed the ANN emulator and led to more accurate results. Looking at the MaxAE values in Table 2 and also the peak and minimum points in Figure 6, it can be observed that the performance of the emulators was not accurate enough and, in some cases, they made errors as large as 16 cm (by SVR) and 50 cm (by ANN). Therefore, in next section we try to enhance the accuracy of the models.
3.1. Dimensionality Reduction
In this section three correlation tests—namely Kendall, Pearson, and Spearman—and ANOVA were used to identify the most important inputs and reduce the dimensionality. Using 1200 simulations obtained with 14 parameters with different spaces as inputs, the correlation tests and ANOVA analysis were applied in the specified cross sections, and the results are displayed in Figure 7.
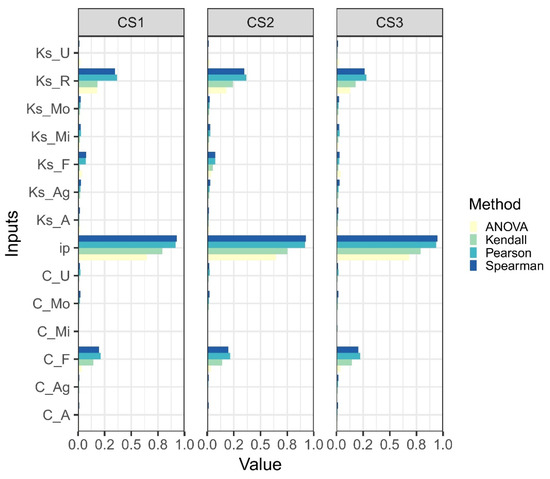
Figure 7.
Absolute correlation values resulting from Kendall, Pearson, and Spearman tests and percentage of contribution (PC) values resulting from ANOVA test (Equation (10)).
The results of the different implemented techniques presented in Figure 7 indicate a significant correlation between rainfall (ip) and water level followed by river friction (Ks_R) and forest runoff coefficient (C_F). The findings of the correlation tests and ANOVA test are consistent; however, the ANOVA results are more stable at different locations compared to the correlation tests. According to the correlation values displayed in Figure 7, forest friction (Ks_F) shows a weak correlation with water level at cross sections CS1 and CS2 and a negligible correlation at cross section CS3. Unlike correlation values, the calculated contribution value resulted from the ANOVA test shows an almost constant contribution of forest friction (Ks_F with about 4%) at different cross sections. Accordingly, two alternative approaches were adopted to train the emulators: first, the four highest correlated parameters (rainfall (ip), forest runoff coefficient (C_F), river friction (Ks_R), and forest friction (Ks_F)) were used to develop the emulators. In the second approach forest friction (Ks_F) was removed from the input set and emulators were trained using only three inputs. The results of the first approach (four inputs) are presented in Table 3. Comparing Table 2 and Table 3 (i.e., fourteen inputs and four inputs, respectively), shows that the performance of both emulators considerably improves (about 50% reduction in error values) when the number of the inputs decreases to four inputs. The results of the second approach (three inputs) showed that the predictive ability of the models considerably deteriorates when the number of inputs is decreased to three parameters. Therefore, the results are only presented for the emulators with four inputs (Table 3).

Table 3.
Emulator (with four inputs) performance on test set.
The results presented in Table 3 indicate the efficiency of the methods used for detecting the main influencing parameters. However, caution must be taken in selection of inputs. As an example, the correlation tests detected the forest friction as a weakly correlated parameter, but the performance of the models improved considerably when this parameter was added into input set.
3.2. Error Structure Analysis
In order to gain insight into the predictive ability of the selected emulators (ANN and SVR with four inputs), the error values (Equation (5)) were plotted versus observed water level for the test set in the specified locations (CS1 to CS3). Moreover, to assess the error trend and change point, linear regression and polynomial regression were used. The slope of the linear regression line indicates if there is a trend in the plotted error values. Positive values of the slope show increasing error trends, whereas negative values indicate decreasing trends. A polynomial (quadratic) line that deviates strongly from the linear regression line provides further insights regarding how ‘‘severe’’ the potential over- or under-prediction may be for large target response values [21]. As it is displayed in Figure 8, the linear and polynomial regression lines for SVR model are close to each other and are approximately horizontal in all three cross sections. This result indicates that the performance of the SVR model for different magnitudes of floods were similar and relatively constant. In contrast, the ANN model showed an increasing trend of error. The error values were negative for the smaller water levels and positive for the higher water levels. This result indicates that the ANN model tends to overpredict the smaller floods and underpredict the extreme floods. The steep slope of the polynomial regression line for ANN indicates that the potential of underprediction of extreme events is even higher than overprediction of small floods by ANN. As can be seen in the plots, the best performance of ANN was achieved for the medium size floods. Moreover, from the plots it is apparent that the error ranges for SVR were much smaller than those for ANN.
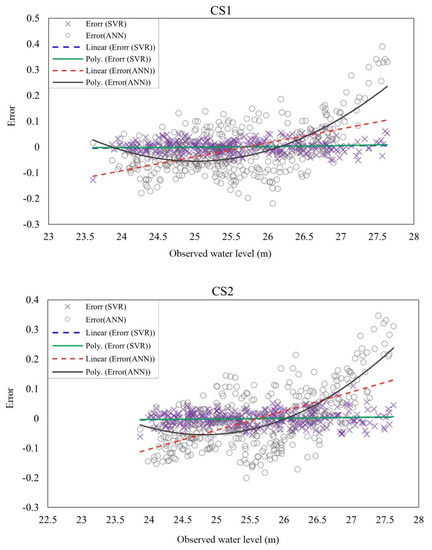
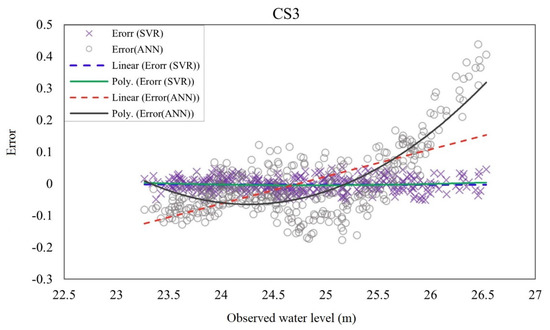
Figure 8.
Error trend and linear and polynomial regression of error values resulted from SVR and ANN predicted water level at the specified cross sections (CS1 to CS3).
In flood modeling/prediction processes the normality assumption for error values is quite common, whereas potentially error values can follow any distribution. Therefore, in this section the distribution of error is investigated using the histograms displayed in Figure 9. The histograms show that the ANN error distributions were non-symmetric and were skewed to the left (positively skewed). This result indicates that ANN generally overpredicts the water level. Unlike the ANN, the SVR error distributions were approximately symmetric, and the error ranges were much smaller compared to the ANN ones. The fitted SVR distributions in CS2 and CS3 were close to normal distribution. However, in CS1, the distribution was more peaked than the normal distribution. Thus, blindly assuming normality for errors, whereas data come from non-normal data (which is even more common), can eventuate to critical statistical inference problems.
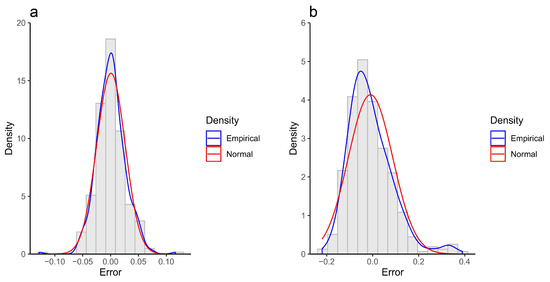
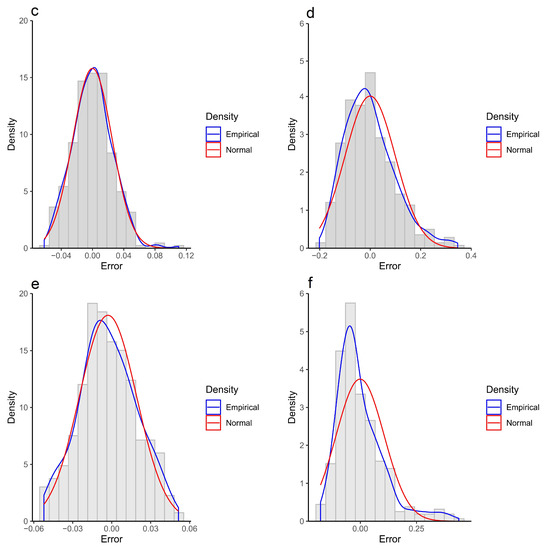
Figure 9.
Empirical distribution of error values versus the normal distribution for the SVR and ANN based emulators. (a) SVR error distribution-CS1, (b) ANN error distribution-CS1, (c) SVR error distribution-CS2, (d) ANN error distribution-CS2, (e) SVR error distribution-CS3, (f) ANN error distribution-CS3.
3.3. Sample Size
In the previous section the SVR emulator with four inputs was selected as a reliable emulator. Therefore, in this section, we aim to extend our analysis by addressing the effect of sample size on the model accuracy. For this purpose, different training sample sizes equal to 80%, 70%, 60%, 50%, and 40% of the entire data set (1200 simulations) were generated by randomly selecting the required number of observations, and the performance of the emulator is assessed through RMSE and MaxAE. As an example, the training sample size equal to 70% was obtained with 840 observations randomly selected as the training set and the remaining (30%) used as the test set. The process was repeated for +5000 times for each training sample size to ensure that different possible events were sampled for training the emulator. The effect of selecting different training samples is displayed in Figure 10.
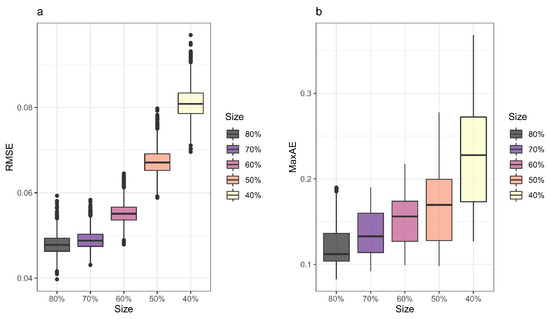
Figure 10.
The calculated (a) RMSE and (b) MaxAE box plots for test sets resulting from the models trained by different sample sizes for 5000 times.
According to the RMSE values variation (Figure 10a), the larger training sets (80% and 70%) resulted in the smaller error values. Assuming 7 cm as an acceptable performance threshold, Figure 10a indicates that the RMSE values less than 7 cm can be achieved for training sizes equal to 60% or more. As shown in Figure 10a, decreasing the training size to 50%, led to a sudden increase in RMSE values (ranges between 6 cm to 8 cm). The box plot for the 50% size shows that 75% of the provided RMSE values were less than 7 cm. This result indicates that it is possible to train an acceptable emulator using 50% of data, but this requires a proper selection of the data.
Since extreme values are the major area of interest in flood studies and play an important role in defining confidence intervals or creating flood probability distributions, maximum absolute error (MaxAE) was also considered as a performance evaluation criterion in this section. Figure 10b displays the maximum error variation for each size resulting from 5000 iterations for each sample. Based on the Figure 10b, as it was expected the larger training sets (70% and 80%) were performing well. Looking at the median line for 80% and 70% sizes in the plots, it can be seen that the maximum difference between the observed and predicted water level mostly (75% of the time) varied between 8 cm to 13 cm. Although the size of 70% may produce error values as big as 16 cm to 19 cm (the MaxAE values above third quartile) (Figure 10b), it should be noted that the probability of getting such values is low, and in 75% of the time the MaxAE values never exceed 16 cm.
As much as the training size decreased, the MaxAE range increased. For training size equal to 60%, a comparison between the RMSE values (Figure 10a) and MaxAE values (Figure 10b), indicated that the overall performance of the emulator was acceptable (small RMSE values), but according to the MaxAE values, it may be prone to low probable values such as extremes floods. Furthermore, assuming 15 cm as the error threshold for MaxAE, it can be seen that about 50% of the MaxAE values (for training sample size of 60%) were above this limit. Accordingly, it was not reliable to train an emulator with less than 50% of the data (corresponding to 600 simulations), because the errors were typically beyond the acceptable limit. As it is displayed for the size equal to 40%, there is a big difference between the minimum and maximum calculated MaxAE values (about 25 cm), which means there is a large uncertainty associated with predicted extreme water levels that can bias the performance of the emulator.
4. Conclusions
In the present study, two emulators were developed to predict cross sectional water level based on information obtained from coupled hydrology-hydraulic 2D simulations at the catchment scale. The following conclusions can be drawn from the present study:
- The statistical metrics for the developed emulators confirm the applicability of surrogates for predicting the cross-sectional water level. However, evaluating the results from different aspects (performance metrics, error trends, ranges, and distributions) showed that SVR has a better performance compared to ANN.
- Inclusion of too many variables as inputs can deteriorate the performance of the emulators; thus, simplification of the model structure through dimension reduction techniques can be used to obtain the most accurate model. The implemented correlation tests and ANOVA used in this study provided consistent results and showed that they can be a good choice to reduce the dimension of input data, improving the accuracy of the models.
- The error trend and regression plots for the SVR model and ANN model indicate that the performance of the SVR model for different magnitudes of floods are similar and relatively constant, whereas the ANN model tends to overpredict the smaller floods and underpredict the extreme floods. The best and worst performance of the ANN-based emulator is achieved for the medium size and extreme floods, respectively. Therefore, the application of the ANN model may not be safe for prediction of extreme flood events.
- The normality assumption for errors, which is typically undertaken in hazard assessment and decision making, is not always true and can eventuate to incorrect statistical inferences.
- The findings in this study suggest that the training data set size equal to 70% (or more) of data results in reliable and accurate predictions. The results also showed that it is not reliable to train an emulator with less than 50% of the data (corresponding to 600 simulations).
The use of data-driven models to emulate 2D hydrodynamic simulations at the catchment scale is feasible and will help to overcome the unaffordable computational resources of physical-based models. Finally, it is important to bear in mind the limitations of the current study. First, the time-consuming simulations prevented us from adopting a more complex approach such as synthetic hyetographs, which would increase the number of inputs and consequently would increase the total number of simulations. Therefore, we have used a time invariant precipitation intensity in this study. Second, the study is limited to 100-year design rainfall range; for the values outside of this range, the training process should be updated. Finally, this study has only focused on the water level as the output of interest. Further analyses should be done to develop an emulator to predict other important outputs such as the velocity. Nevertheless, the noted limitations do not invalidate the main conclusions presented above.
Author Contributions
Conceptualization, S.M.A. and J.L.; methodology, S.M.A.; software, S.M.A.; validation, J.L.; formal analysis, S.M.A.; investigation, J.L.; data curation, S.M.A.; writing—original draft preparation, S.M.A.; writing—review and editing, J.L.; visualization, S.M.A.; supervision, J.L. All authors have read and agreed to the published version of the manuscript.
Funding
The work presented in this paper is funded by the University of Agder, Norway (project number: 63859).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this work including precipitation data and measured flow data are available at http://www.senorge.no/ (accessed on 20 March 2021). The land cover maps are acquired from https://land.copernicus.eu/pan-european/corine-land-cover (accessed on 10 April 2021).
Acknowledgments
We would like to acknowledge the help of Ghali Yakoub in the Python coding of ANN and SVR algorithms.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Panagoulia, D.; Dimou, G. Sensitivity of flood events to global climate change. J. Hydrol. 1997, 191, 208–222. [Google Scholar] [CrossRef]
- Panagoulia, D. From low-flows to floods under global warming. In EGU General Assembly 2009; EGU General Assembly Conference Abstracts: Vienna, Austria, 2009; p. 4511. [Google Scholar]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.; Dutta, D.; Kim, S.J.E.M. Software Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Chu, H.; Wu, W.; Wang, Q.; Nathan, R.; Wei, J. An ANN-based emulation modelling framework for flood inundation modelling: Application, challenges and future directions. Environ. Model. Softw. 2020, 124, 104587. [Google Scholar] [CrossRef]
- Jamieson, R.S.; Lhomme, J.; Wright, G.; Gouldby, B. A highly efficient 2D flood model with sub-element topography. Proc. Inst. Civ. Eng. Water Manag. 2012, 165, 581–595. [Google Scholar] [CrossRef]
- Davidsen, S.; Löwe, R.; Thrysøe, C.; Arnbjerg-Nielsen, K. Simplification of one-dimensional hydraulic networks by automated processes evaluated on 1D/2D deterministic flood models. J. Hydroinform. 2017, 19, 686–700. [Google Scholar] [CrossRef] [Green Version]
- Razavi, S.; Tolson, B.A.; Burn, D.H. Numerical assessment of metamodelling strategies in computationally intensive optimization. Environ. Model. Softw. 2012, 34, 67–86. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Ostfeld, A. Data-driven modelling: Some past experiences and new approaches. J. Hydroinform. 2008, 10, 3–22. [Google Scholar] [CrossRef] [Green Version]
- Yu, J.; Qin, X.; Larsen, O. Uncertainty analysis of flood inundation modelling using GLUE with surrogate models in stochastic sampling. Hydrol. Process. 2015, 29, 1267–1279. [Google Scholar] [CrossRef]
- Castro-Gama, M.E.; Popescu, I.; Li, S.; Mynett, A.; van Dam, A. Flood inference simulation using surrogate modelling for the Yellow River multiple reservoir system. Environ. Model. Softw. 2014, 55, 250–265. [Google Scholar] [CrossRef]
- Luo, J.; Lu, W. Comparison of surrogate models with different methods in groundwater remediation process. J. Earth Syst. Sci. 2014, 123, 1579–1589. [Google Scholar] [CrossRef]
- Bacchi, V.; Hamdi, Y.; Foch, M.; Pheulpin, L. Development of a new approach for the assessment of Flood Hazard through a kriging surrogate: Application to the bi-dimensional model of the Loire River. In Advances in Extreme Value Analysis and Application to Natural Hazards, EVAN; CHATOU: Paris, France, 2019. [Google Scholar]
- Villa-Vialaneix, N.; Follador, M.; Ratto, M.; Leip, A. A comparison of eight metamodeling techniques for the simulation of N2O fluxes and N leaching from corn crops. Environ. Model. Softw. 2012, 34, 51–66. [Google Scholar] [CrossRef] [Green Version]
- Ghalkhani, H.; Golian, S.; Saghafian, B.; Farokhnia, A.; Shamseldin, A. Application of surrogate artificial intelligent models for real-time flood routing. Water Environ. J. 2013, 27, 535–548. [Google Scholar] [CrossRef]
- Xie, S.; Wu, W.; Mooser, S.; Wang, Q.; Nathan, R.; Huang, Y. Artificial neural network based hybrid modeling approach for flood inundation modeling. J. Hydrol. 2021, 592, 125605. [Google Scholar] [CrossRef]
- Zhang, X.; Srinivasan, R.; Van Liew, M. Approximating SWAT model using artificial neural network and support vector machine 1. JAWRA J. Am. Water Resour. Assoc. 2009, 45, 460–474. [Google Scholar] [CrossRef]
- Xu, T.; Valocchi, A.J.; Ye, M.; Liang, F. Quantifying model structural error: Efficient Bayesian calibration of a regional groundwater flow model using surrogates and a data-driven error model. Water Resour. Res. 2017, 53, 4084–4105. [Google Scholar] [CrossRef]
- Liu, Y.; Pender, G. A flood inundation modelling using v-support vector machine regression model. Eng. Appl. Artif. Intell. 2015, 46, 223–231. [Google Scholar] [CrossRef]
- Bermúdez, M.; Ntegeka, V.; Wolfs, V.; Willems, P. Development and comparison of two fast surrogate models for urban pluvial flood simulations. Water Resour. Manag. 2018, 32, 2801–2815. [Google Scholar] [CrossRef]
- Bass, B.; Bedient, P. Surrogate modeling of joint flood risk across coastal watersheds. J. Hydrol. 2018, 558, 159–173. [Google Scholar] [CrossRef]
- Al Kajbaf, A.; Bensi, M. Application of surrogate models in estimation of storm surge: A comparative assessment. Appl. Soft Comput. 2020, 91, 106184. [Google Scholar] [CrossRef]
- Alipour, S.M.; Engeland, K.; Leal, J. A practical methodology to perform global sensitivity analysis for 2D hydrodynamic computationally intensive simulations. Hydrol. Res. 2021, in press. [Google Scholar] [CrossRef]
- Ferreira, R.M.; Franca, M.J.; Leal, J.G.; Cardoso, A.H. Mathematical modelling of shallow flows: Closure models drawn from grain-scale mechanics of sediment transport and flow hydrodynamics. Can. J. Civ. Eng. 2009, 36, 1605–1621. [Google Scholar] [CrossRef]
- Conde, D.A.; Canelas, R.B.; Ferreira, R.M. A unified object-oriented framework for CPU+ GPU explicit hyperbolic solvers. Adv. Eng. Softw. 2020, 148, 102802. [Google Scholar] [CrossRef]
- LeVeque, R.J. Finite Volume METHODS for Hyperbolic Problems; Cambridge University Press: Cambridge, UK, 2002; Volume 31. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Arcement, G.J.; Schneider, V.R. Guide for Selecting Manning’s Roughness Coefficients for Natural Channels and Flood Plains; US Government Printing Office: Washington, DC, USA, 1989.
- Dorn, H.; Vetter, M.; Höfle, B. GIS-based roughness derivation for flood simulations: A comparison of orthophotos, LiDAR and crowdsourced geodata. Remote Sens. 2014, 6, 1739–1759. [Google Scholar] [CrossRef] [Green Version]
- Goel, M.K. Runoff Coefficient, in Encyclopedia of Snow, Ice and Glaciers; Singh, V.P., Singh, P., Haritashya, U.K., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 952–953. [Google Scholar] [CrossRef]
- Subramanya, K. Engineering Hydrology, 4th ed.; Tata McGraw-Hill Education: New Delhi, India, 2013. [Google Scholar]
- Viglione, A.; Hosking, J.R.; Laio, F.; Miller, A.; Gaume, E.; Payrastre, O.; Salinas, J.L.; N’guyen, C.C.; Halbert, K.; Viglione, M.A. Package ‘nsRFA’. Non-supervised Regional Frequency Analysis. CRAN Repository, 2020. Version 0.7-15. Available online: http://cran.r-project.org/web/packages/nsRFA/ (accessed on 20 March 2021).
- Hanssen-Bauer, I.; Drange, H.; Førland, E.; Roald, L.; Børsheim, K.; Hisdal, H.; Lawrence, D.; Nesje, A.; Sandven, S.; Sorteberg, A. Climate in Norway 2100. In Background Information to NOU Climate Adaptation (In Norwegian: Klima i Norge 2100. Bakgrunnsmateriale til NOU Klimatilplassing); Norsk Klimasenter: Oslo, Norway, 2009. [Google Scholar]
- Reis, D.S., Jr.; Stedinger, J.R. Bayesian MCMC flood frequency analysis with historical information. J. Hydrol. 2005, 313, 97–116. [Google Scholar] [CrossRef]
- Gaume, E.; Gaál, L.; Viglione, A.; Szolgay, J.; Kohnová, S.; Blöschl, G. Bayesian MCMC approach to regional flood frequency analyses involving extraordinary flood events at ungauged sites. J. Hydrol. 2010, 394, 101–117. [Google Scholar] [CrossRef]
- Lutz, J.; Grinde, L.; Dyrrdal, A.V. Estimating Rainfall Design Values for the City of Oslo, Norway—Comparison of Methods and Quantification of Uncertainty. Water 2020, 12, 1735. [Google Scholar] [CrossRef]
- Dalbey, K.; Patra, A.; Pitman, E.; Bursik, M.; Sheridan, M. Input uncertainty propagation methods and hazard mapping of geophysical mass flows. J. Geophys. Res. Solid Earth 2008, 113, B05203. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Dodangeh, E.; Panahi, M.; Rezaie, F.; Lee, S.; Bui, D.T.; Lee, C.-W.; Pradhan, B. Novel hybrid intelligence models for flood-susceptibility prediction: Meta optimization of the GMDH and SVR models with the genetic algorithm and harmony search. J. Hydrol. 2020, 590, 125423. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Shu, C.; Burn, D.H. Artificial neural network ensembles and their application in pooled flood frequency analysis. Water Resour. Res. 2004, 40, W09301. [Google Scholar] [CrossRef] [Green Version]
- Fernando, T.; Maier, H.; Dandy, G. Selection of input variables for data driven models: An average shifted histogram partial mutual information estimator approach. J. Hydrol. 2009, 367, 165–176. [Google Scholar] [CrossRef]
- Lee Rodgers, J.; Nicewander, W.A. Thirteen ways to look at the correlation coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Karmakar, B.; Dhawane, S.H.; Halder, G. Optimization of biodiesel production from castor oil by Taguchi design. J. Environ. Chem. Eng. 2018, 6, 2684–2695. [Google Scholar] [CrossRef]
- Yang, W.p.; Tarng, Y. Design optimization of cutting parameters for turning operations based on the Taguchi method. J. Mater. Process. Technol. 1998, 84, 122–129. [Google Scholar] [CrossRef]
- Sadrzadeh, M.; Mohammadi, T. Sea water desalination using electrodialysis. Desalination 2008, 221, 440–447. [Google Scholar] [CrossRef]
- Stahle, L.; Wold, S. Analysis of variance (ANOVA). Chemom. Intell. Lab. Syst. 1989, 6, 259–272. [Google Scholar] [CrossRef]
- Alwosheel, A.; van Cranenburgh, S.; Chorus, C.G. Is your dataset big enough? Sample size requirements when using artificial neural networks for discrete choice analysis. J. Choice Model. 2018, 28, 167–182. [Google Scholar] [CrossRef]
- Hjort, J.; Marmion, M. Effects of sample size on the accuracy of geomorphological models. Geomorphology 2008, 102, 341–350. [Google Scholar] [CrossRef]
- Heckmann, T.; Gegg, K.; Gegg, A.; Becht, M. Sample size matters: Investigating the effect of sample size on a logistic regression susceptibility model for debris flows. Nat. Hazards Earth Syst. Sci. 2014, 14, 259–278. [Google Scholar] [CrossRef] [Green Version]
- Kalantar, B.; Pradhan, B.; Naghibi, S.A.; Motevalli, A.; Mansor, S. Assessment of the effects of training data selection on the landslide susceptibility mapping: A comparison between support vector machine (SVM), logistic regression (LR) and artificial neural networks (ANN). Geomat. Nat. Hazards Risk 2018, 9, 49–69. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).