Inland Reservoir Water Quality Inversion and Eutrophication Evaluation Using BP Neural Network and Remote Sensing Imagery: A Case Study of Dashahe Reservoir
Abstract
:1. Introduction
2. Materials and Methods
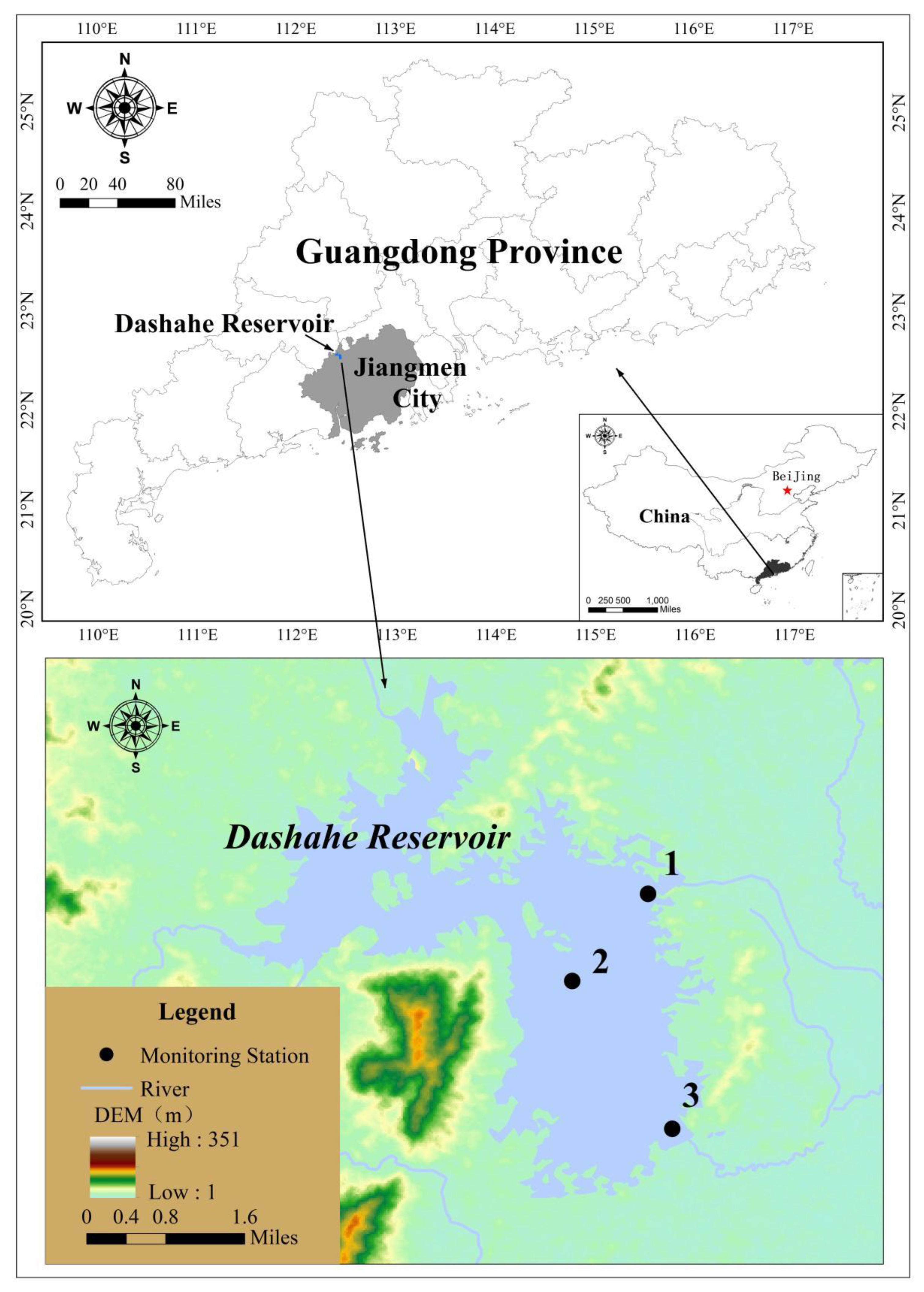
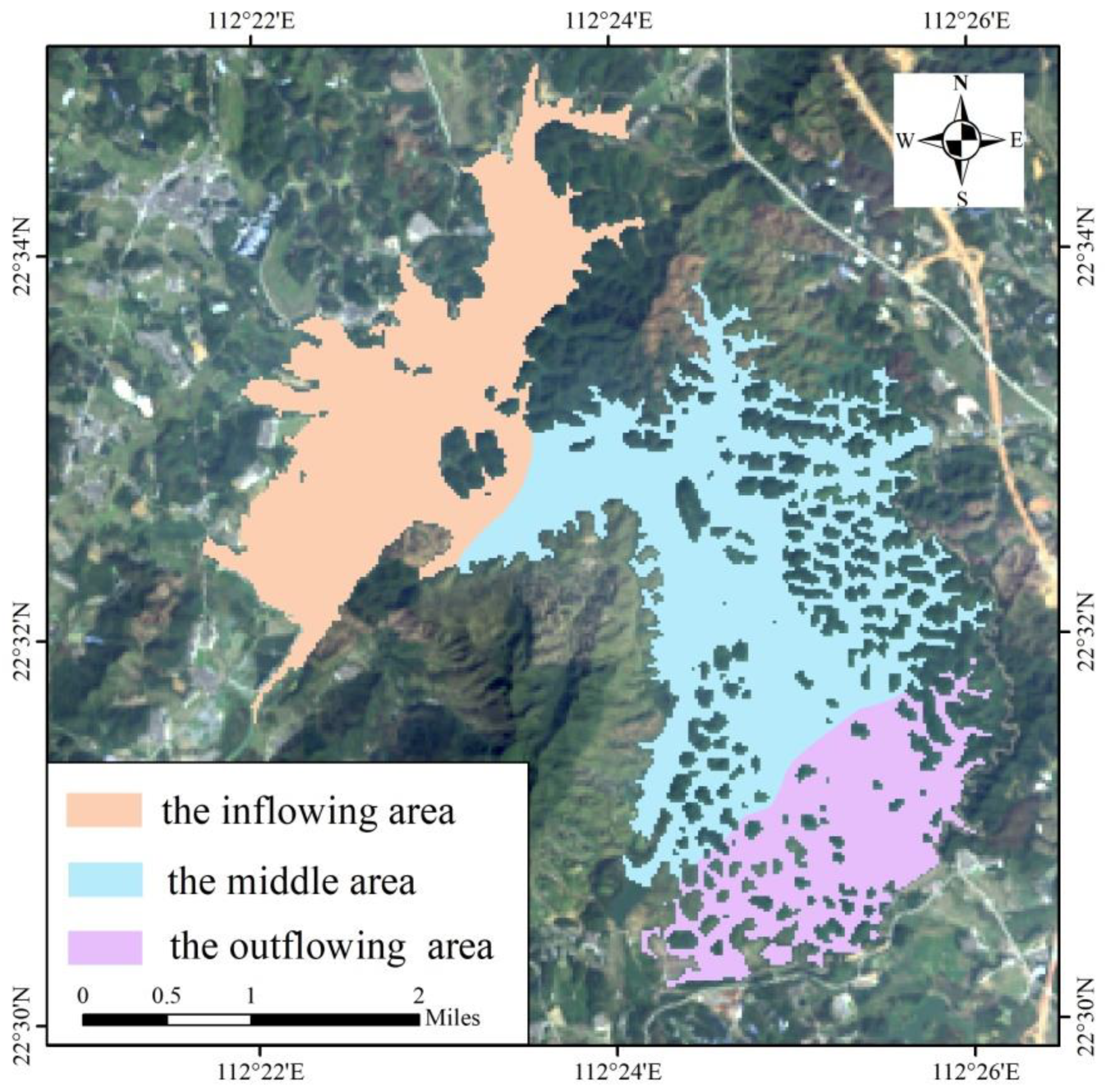
2.1. Study Area
2.2. Materials
2.2.1. Field Observations of Water Quality Parameters
2.2.2. Satellite Image Data
2.3. Methods
2.3.1. Radiation Calibration
2.3.2. FLAASH Atmospheric Correction
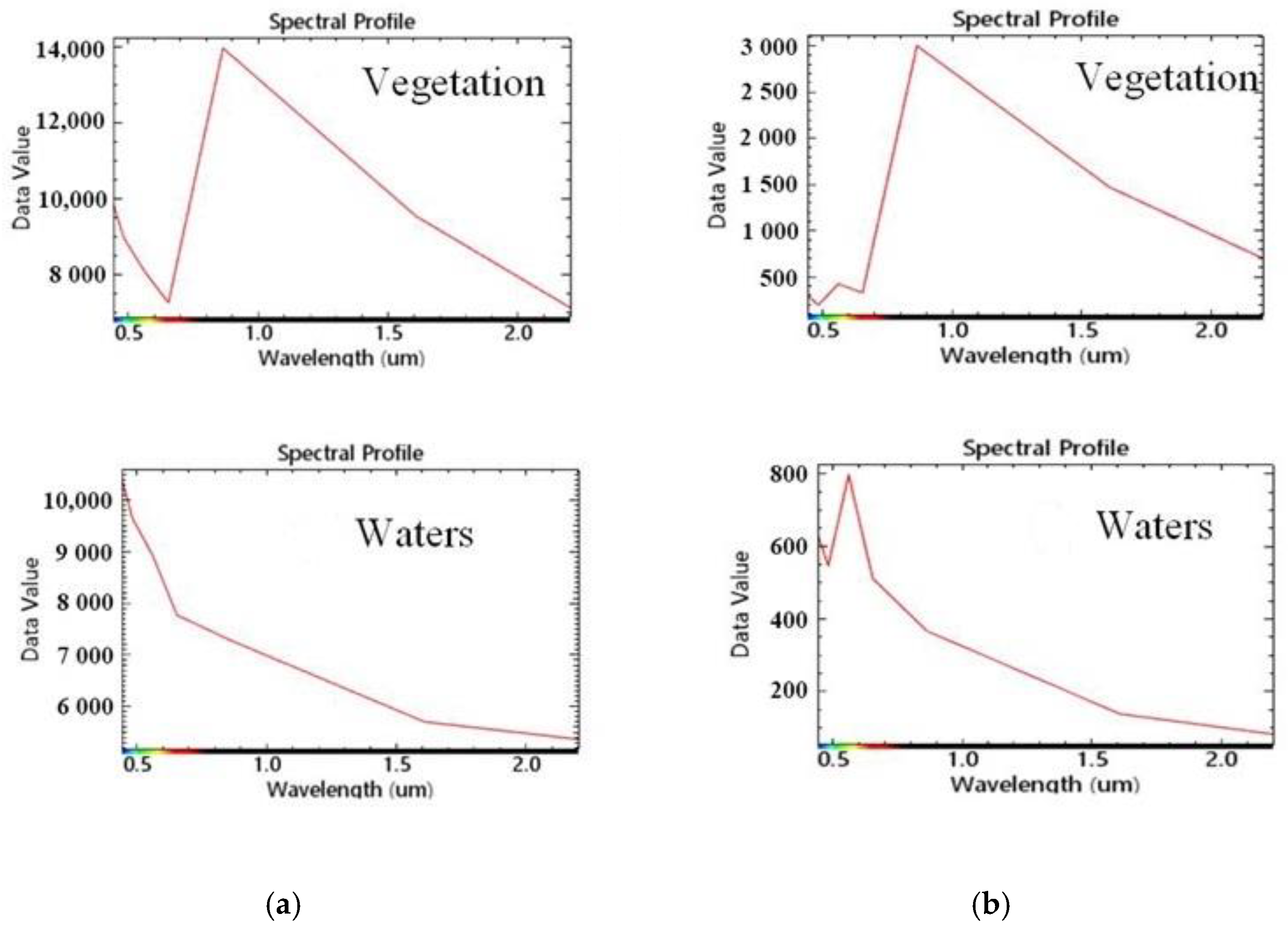
2.3.3. Water Body Extraction
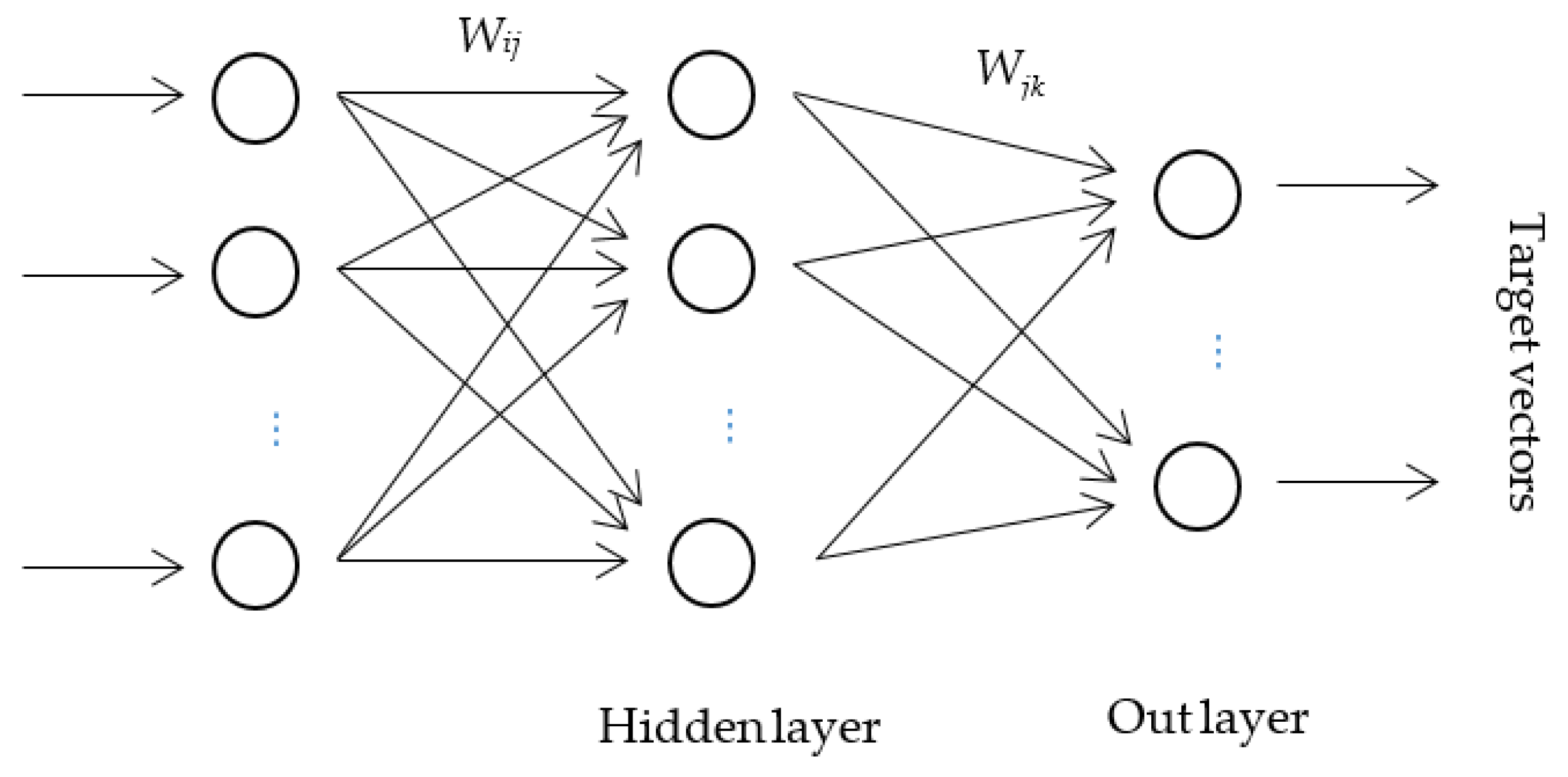
2.3.4. BP Neural Network
2.3.5. Index Method for Reservoir Eutrophication Evaluation
3. Results and Discussion
3.1. Model Construction and Verification
3.2. Comparison between the BP Inversion Model and the Multiple Linear Inversion Model
3.3. Change in Water Quality Parameters and Reservoir Eutrophication Evaluation
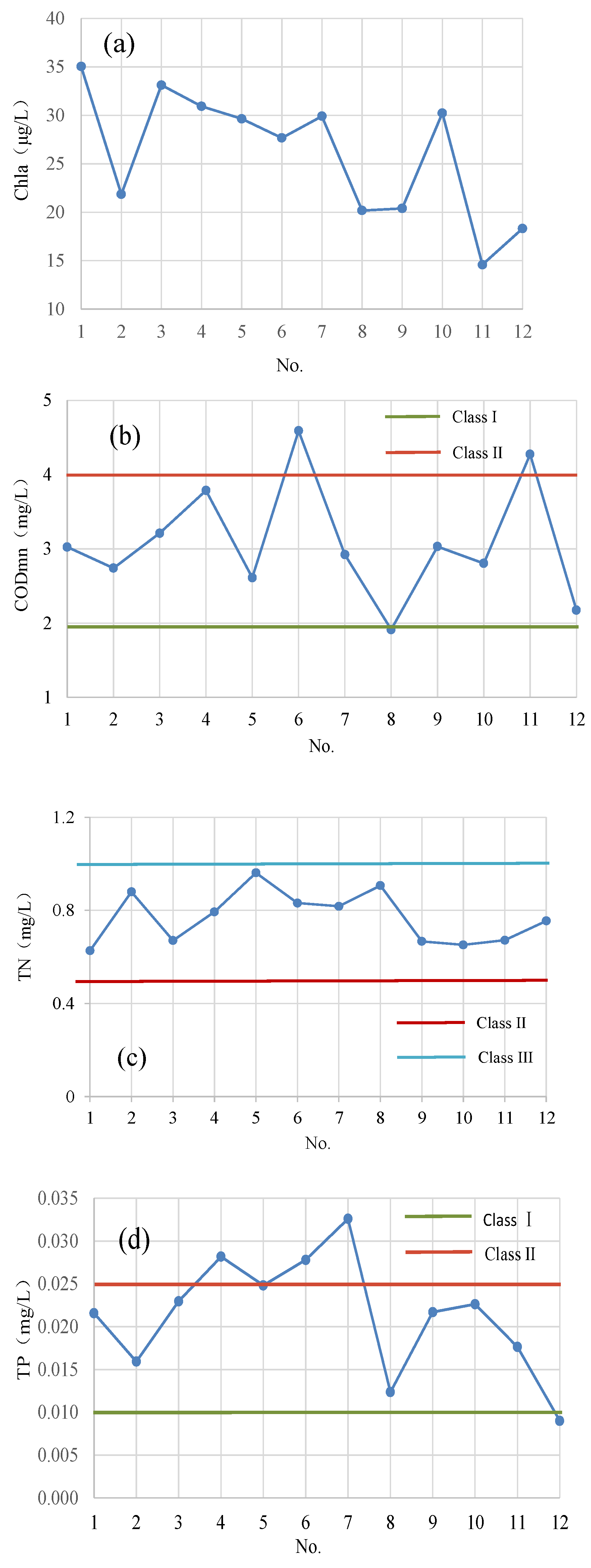
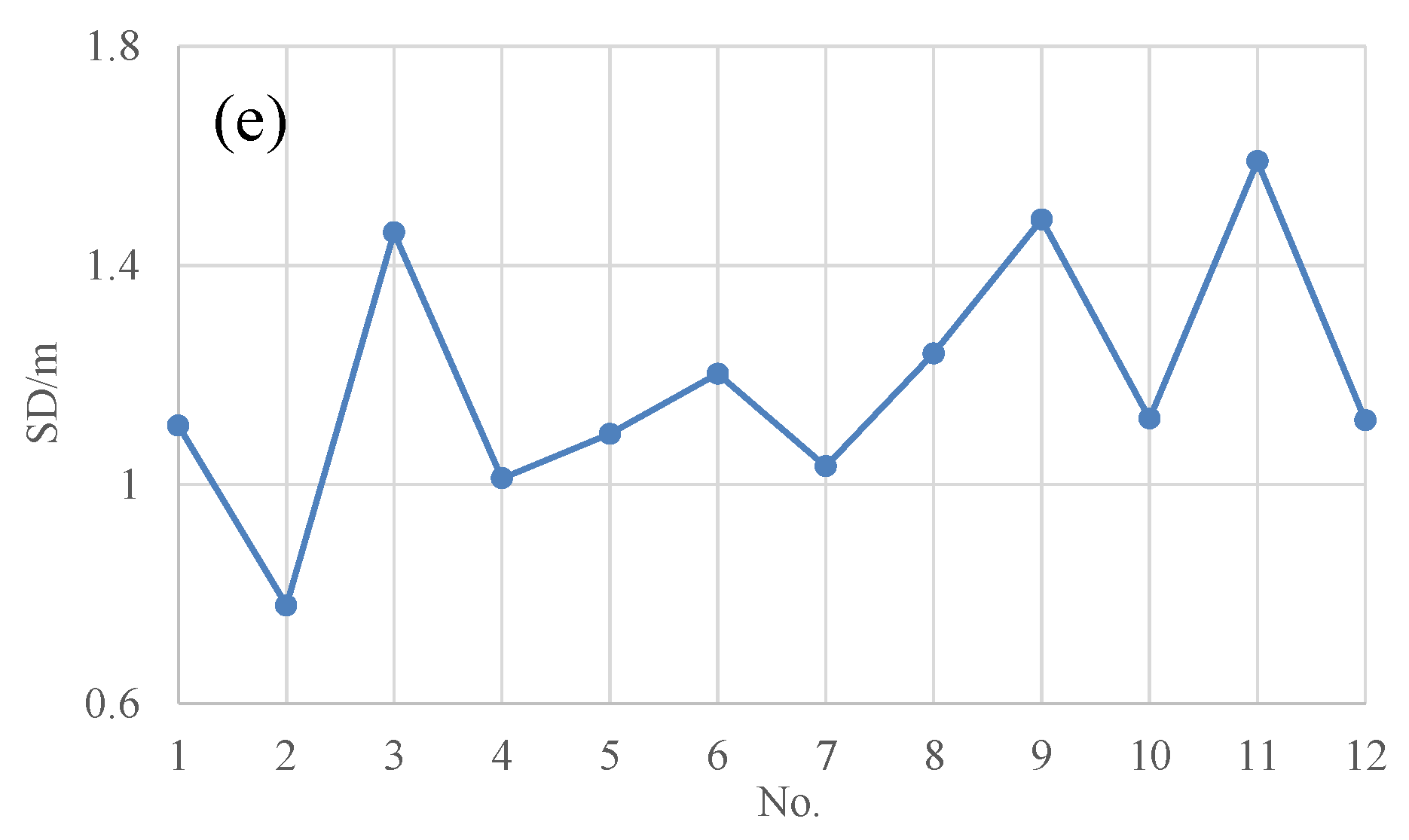
3.3.1. Change in Water Quality Parameters in Dashahe Reservoir
3.3.2. Evaluation of Trophic Condition at Dashahe Reservoir
4. Conclusions
- (1)
- The preprocessing of remote sensing images helps to highlight spectral information by eliminating the influence of reflectance on objects caused by atmospheric aerosols and removing noise. This effectively restores the real reflectance after radiation calibration and atmospheric correction.
- (2)
- The BP inversion model was built for each of the five water quality parameters of Dashahe Reservoir and the optimal node number of each inversion model was identified through multiple trainings. The accuracy of the BP inversion models of Chl-a and CODMn was superior to that of the multiple linear inversion models, due to the improved generalization of the BP neural network. The performance of the BP inversion model was better than that of the multiple linear inversion model when the water quality parameters had a larger fluctuation range.
- (3)
- Overall, Dashahe Reservoir was in the state of mesotrophication and light eutrophication. The area of light eutrophication accounted for larger proportions in spring and autumn due to algae blooms driven by appropriate temperatures and polluted reservoir inflows around the reservoir. The reservoir inflow was the main source of nutrient salts in Dashahe Reservoir.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shourian, M.; Moridi, A.; Kaveh, M. Modeling of eutrophication and strategies for improvement of water quality in reservoirs. Water Sci. Technol. 2016, 74, 1376–1385. [Google Scholar] [CrossRef]
- Li, Z.; Ma, J.R.; Guo, J.S.; Paerl, H.W.; Brookes, J.D.; Xiao, Y.; Fang, F.; Ouyang, W.J.; Lu, L.H. Water quality trends in the Three Gorges Reservoir region before and after impoundment (1992–2016). Ecohydrol. Hydrobiol. 2019, 19, 317–327. [Google Scholar] [CrossRef]
- Yang, W.; Yao, J.M.; He, Y.Z.; Huang, Y.Y.; Liu, H.Z.; Zhi, Y.; Qian, S.H.; Yan, X.M.; Jian, S.; Li, W. Nitrogen removal enhanced by benthic bioturbation coupled with biofilm formation: A new strategy to alleviate freshwater eutrophication. J. Environ. Manag. 2021, 292, 112814. [Google Scholar] [CrossRef]
- Smith, V.H.; Tilman, G.D.; Nekola, J.C. Eutrophication: Impacts of excess nutrient inputs on freshwater, marine, and terrestrial ecosystems. Environ. Pollut. 1999, 100, 179–196. [Google Scholar] [CrossRef]
- Vieira, J.M.P.; Pinho, J.L.S.; Dias, N.; Schwanenberg, D.; Van den Boogaard, H.F.P. Parameter estimation for eutrophication models in reservoirs. Water Sci. Technol. 2013, 68, 319–327. [Google Scholar] [CrossRef] [PubMed]
- Smith, V.H.; Schindler, D.W. Eutrophication science: Where do we go from here? Trends Ecol. Evol. 2009, 24, 201–207. [Google Scholar] [CrossRef] [PubMed]
- Sayers, M.J.; Bosse, K.R.; Shuchman, R.A.; Ruberg, S.A.; Fahnenstiel, G.L.; Leshkevich, G.A.; Stuart, D.G.; Johengen, T.H.; Burtner, A.M.; Palladino, D. Spatial and temporal variability of inherent and apparent optical properties in western Lake Erie: Implications for water quality remote sensing. J. Great Lakes Res. 2019, 45, 490–507. [Google Scholar] [CrossRef]
- Schaeffer, B.; Schaeffer, K.G.; Keith, D.; Lunetta, R.S.; Conmy, R.; Gould, R.W. Barriers to adopting satellite remote sensing for water quality management. Int. J. Remote Sens. 2013, 34, 7534–7544. [Google Scholar] [CrossRef]
- Kim, H.C.; Son, S.; Kim, Y.H.; Khim, J.S.; Nam, J.; Chang, W.K.; Lee, J.H.; Lee, C.H.; Ryu, J. Remote sensing and water quality indicators in the Korean West coast: Spatio-temporal structures of MODIS-derived chlorophyll-a and total suspended solids. Mar. Pollut. Bull. 2017, 121, 425–434. [Google Scholar] [CrossRef]
- Anding, D.; Kauth, R. Estimation of sea surface temperature from space. Remote Sens. Environ. 1970, 1, 217–220. [Google Scholar] [CrossRef] [Green Version]
- Morel, A.; Prieur, L. Analysis of variations in ocean color1. Limnol. Oceanogr. 1977, 22, 709–722. [Google Scholar] [CrossRef]
- Dlamini, S.; Nhapi, I.; Gumindoga, W.; Nhiwatiwa, T.; Dube, T. Assessing the feasibility of integrating remote sensing and in-situ measurements in monitoring water quality status of Lake Chivero, Zimbabwe. Phys. Chem. Earth Parts A/B/C 2016, 93, 2–11. [Google Scholar] [CrossRef]
- Alikas, K.; Kratzer, S. Improved retrieval of Secchi depth for optically-complex waters using remote sensing data. Ecol. Indic. 2017, 77, 218–227. [Google Scholar] [CrossRef]
- Seyhan, E.; Dekker, A. Application of remote sensing techniques for water quality monitoring. Hydrobiol. Bull. 1986, 20, 41–50. [Google Scholar] [CrossRef]
- Kondratyev, K.Y.; Pozdnyakov, D.V.; Pettersson, L.H. Water quality remote sensing in the visible spectrum. Int. J. Remote Sens. 1998, 19, 957–979. [Google Scholar] [CrossRef]
- Wang, X.J.; Ma, T. Application of remote sensing techniques in monitoring and assessing the water quality of Taihu Lake. Bull. Environ. Contam. Toxicol. 2001, 67, 863–870. [Google Scholar] [CrossRef]
- Koponen, S.; Pulliainen, J.; Kallio, K.; Hallikainen, M. Lake water quality classification with airborne hyperspectral spectrometer and simulated MERIS data. Remote Sens. Environ. 2002, 79, 51–59. [Google Scholar] [CrossRef]
- Gower, J.; King, S.; Borstad, G.; Brown, L. Detection of intense plankton blooms using the 709 nm band of the MERIS imaging spectrometer. Int. J. Remote Sens. 2005, 26, 2005–2012. [Google Scholar] [CrossRef]
- Matthews, M.W. A current review of empirical procedures of remote sensing in inland and near-coastal transitional waters. Int. J. Remote Sens. 2011, 32, 6855–6899. [Google Scholar] [CrossRef]
- Imen, S.; Chang, N.-B.; Yang, Y.J. Developing the remote sensing-based early warning system for monitoring TSS concentrations in Lake Mead. J. Environ. Manag. 2015, 160, 73–89. [Google Scholar] [CrossRef]
- Isenstein, E.M.; Park, M.H. Assessment of nutrient distributions in Lake Champlain using satellite remote sensing. J. Environ. Sci. 2014, 26, 1831–1836. [Google Scholar] [CrossRef]
- Politi, E.; Cutler, M.E.J.; Rowan, J.S. Evaluating the spatial transferability and temporal repeatability of remote-sensing-based lake water quality retrieval algorithms at the European scale: A meta-analysis approach. Int. J. Remote Sens. 2015, 36, 2995–3023. [Google Scholar] [CrossRef] [Green Version]
- Wu, J.; Li, Z.B.; Zhu, L.; Li, G.Y.; Niu, B.S.; Peng, F. Optimized BP neural network for dissolved oxygen prediction. IFAC-PapersOnLine 2018, 51, 596–601. [Google Scholar] [CrossRef]
- Heege, T.; Kiselev, V.; Wettle, M.; Hung, N.N. Operational multi-sensor monitoring of turbidity for the entire Mekong delta. Int. J. Remote Sens. 2014, 35, 2910–2926. [Google Scholar] [CrossRef]
- Lymburner, L.; Botha, E.; Hestir, E.; Anstee, J.; Sagar, S.; Dekker, A.; Malthus, T. Landsat 8: Providing continuity and increased precision for measuring multi-decadal time series of total suspended matter. Remote Sens. Environ. 2016, 185, 108–118. [Google Scholar] [CrossRef]
- Malthus, T.J.; Hestir, E.L.; Dekker, A.G.; Brando, V.E. The case for a global inland water quality product. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 5234–5237. [Google Scholar]
- Gholizadeh, M.H.; Melesse, A.M.; Reddi, L. A comprehensive review on water quality parameters estimation using remote sensing techniques. Sensors 2016, 16, 1298. [Google Scholar] [CrossRef] [Green Version]
- Tanaka, A.; Kishino, M.; Oishi, T.; Doerffer, R.; Schiller, H. Application of neural network method to case II water. In Proceedings of the Remote Sensing of the Ocean and Sea Ice, Barcelona, Spain, 28–29 September 2000; Volume 4172, pp. 144–153. [Google Scholar] [CrossRef]
- Moore, G.F.; Aiken, J.; Lavender, S.J. The atmospheric correction of water colour and the quantitative retrieval of suspended particulate matter in Case II waters: Application to MERIS. Int. J. Remote Sens. 1999, 20, 1713–1733. [Google Scholar] [CrossRef]
- Qin, B. Lake eutrophication: Control countermeasures and recycling exploitation. Ecol. Eng. 2009, 35, 1569–1573. [Google Scholar] [CrossRef]
- Mamun, M.; Kim, J.J.; Alam, M.A.; An, K.G. Prediction of algal chlorophyll-a and water clarity in monsoon-region reservoir using machine learning approaches. Water 2019, 12, 30. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.P.; Xu, Z.X.; Yin, H.L. Study on improved BP artificial neural networks in eutrophication assessment of China eastern lakes. J. Hydrodyn. 2006, 18, 528–532. [Google Scholar] [CrossRef]
- Lu, F.; Chen, Z.; Liu, W.Q.; Shao, H.B. Modeling chlorophyll-a concentrations using an artificial neural network for precisely eco-restoring lake basin. Ecol. Eng. 2016, 95, 422–429. [Google Scholar] [CrossRef]
- Kuo, J.T.; Hsieh, M.H.; Lung, W.S.; She, N. Using artificial neural network for reservoir eutrophication prediction. Ecol. Model. 2007, 200, 171–177. [Google Scholar] [CrossRef]
- Chang, N.B.; Xuan, Z.M.; Yang, Y.J. Exploring spatiotemporal patterns of phosphorus concentrations in a coastal bay with MODIS images and machine learning models. Remote Sens. Environ. 2013, 134, 100–110. [Google Scholar] [CrossRef]
- Zheng, Z.B.; Li, Y.M.; Guo, Y.L.; Xu, Y.F.; Liu, G.; Du, C.G. Landsat-based long-term monitoring of total suspended matter concentration pattern change in the wet season for Dongting Lake, China. Remote Sens. 2015, 7, 13975–13999. [Google Scholar] [CrossRef] [Green Version]
- Song, K.S.; Wang, Z.M.; Blackwell, J.; Zhang, B.; Li, F.; Zhang, Y.Z.; Jiang, G.J. Water quality monitoring using Landsat Themate Mapper data with empirical algorithms in Chagan Lake, China. J. Appl. Remote Sens. 2011, 5, 53506. [Google Scholar] [CrossRef]
- Chang, N.-B.; Vannah, B.W.; Yang, Y.J.; Elovitz, M. Integrated data fusion and mining techniques for monitoring total organic carbon concentrations in a lake. Int. J. Remote Sens. 2014, 35, 1064–1093. [Google Scholar] [CrossRef]
- Sun, D.; Qiu, Z.; Li, Y.; Shi, K.; Gong, S. Detection of total phosphorus concentrations of turbid inland waters using a remote sensing method. Water Air Soil Pollut. 2014, 225, 1953. [Google Scholar] [CrossRef]
- Lin, S.; Novitski, L.N.; Qi, J.; Stevenson, R.J. Landsat TM/ETM+ and machine-learning algorithms for limnological studies and algal bloom management of inland lakes. J. Appl. Remote Sens. 2018, 12, 026003. [Google Scholar] [CrossRef]
- Topp, S.N.; Pavelsky, T.M.; Jensen, D.; Simard, M.; Ross, M.R.V. Research trends in the use of remote sensing for inland water quality science: Moving towards multidisciplinary applications. Water 2020, 12, 169. [Google Scholar] [CrossRef] [Green Version]
- Arias-Rodriguez, L.F.; Duan, Z.; Sepúlveda, R.; Martinez-Martinez, S.I.; Disse, M. Monitoring water quality of valle de bravo reservoir, Mexico, using entire lifespan of MERIS data and machine learning approaches. Remote Sens. 2020, 12, 1586. [Google Scholar] [CrossRef]
- Holyoak, K.J. A Connectionist view of cognition: Parallel distributed processing. Science 1987, 236, 992–996. [Google Scholar] [CrossRef]
- Keiner, L.E.; Yan, X.-H. A Neural network model for estimating sea surface chlorophyll and sediments from thematic mapper imagery. Remote Sens. Environ. 1998, 66, 153–165. [Google Scholar] [CrossRef]
- Schiller, H.; Doerffer, R. Neural network for emulation of an inverse model operational derivation of Case II water properties from MERIS data. Int. J. Remote Sens. 1999, 20, 1735–1746. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, Y.; Yuan, D.; Song, X. Empirical estimation of total nitrogen and total phosphorus concentration of urban water bodies in China using high resolution IKONOS multispectral imagery. Water 2015, 7, 6551–6573. [Google Scholar] [CrossRef] [Green Version]
- Ioannou, I.; Gilerson, A.; Gross, B.; Moshary, F.; Ahmed, S. Deriving ocean color products using neural networks. Remote Sens. Environ. 2013, 134, 78–91. [Google Scholar] [CrossRef]
- Du, C.; Wang, Q.; Li, Y.; Lyu, H.; Zhu, L.; Zheng, Z.; Wen, S.; Liu, G.; Guo, Y. Estimation of total phosphorus concentration using a water classification method in inland water. Int. J. Appl. Earth Obs. Geoinf. 2018, 71, 29–42. [Google Scholar] [CrossRef]
- Bai, Y.; Gao, J.; Zhang, Y. Research on wind-induced nutrient release in Yangshapao Reservoir, China. Water Supply 2020, 20, 469–477. [Google Scholar] [CrossRef]
- Khan, M.S.; Suhail, M.; Alharbi, T. Evaluation of urban growth and land use transformation in Riyadh using Landsat satellite data. Arab. J. Geosci. 2018, 11, 1–13. [Google Scholar] [CrossRef]
- Wang, D.; Ma, R.; Xue, K.; Loiselle, S.A. The assessment of landsat-8 OLI atmospheric correction algorithms for inland waters. Remote Sens. 2019, 11, 169. [Google Scholar] [CrossRef] [Green Version]
- Sahana, M.; Dutta, S.; Sajjad, H. Assessing land transformation and its relation with land surface temperature in Mumbai city, India using geospatial techniques. Int. J. Urban Sci. 2019, 23, 205–225. [Google Scholar] [CrossRef]
- Nielsen, A.; Trolle, D.; Me, W.; Luo, L.; Han, B.-P.; Liu, Z.; Olesen, J.E.; Jeppesen, E. Assessing ways to combat eutrophication in a Chinese drinking water reservoir using SWAT. Mar. Freshw. Res. 2013, 64, 475–492. [Google Scholar] [CrossRef] [Green Version]
- Woo, M.-K.; Huang, L.; Zhang, S.; Li, Y. Rainfall in Guangdong province, South China. Catena 1997, 29, 115–129. [Google Scholar] [CrossRef]
- Tiwari, A.; Oliver, D.; Bivins, A.; Sherchan, S.; Pitkänen, T. Bathing water quality monitoring practices in Europe and the United States. Int. J. Environ. Res. Public Health 2021, 18, 5513. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Jiang, Q.-G.; Yu, D.-H.; Yang, Q.-L.; Wang, L.; Han, T.-C.; Xu, X.-Y. Detecting daytime and nighttime land surface temperature anomalies using thermal infrared remote sensing in Dandong geothermal prospect. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 196–205. [Google Scholar] [CrossRef]
- Rani, N.; Mandla, V.R.; Singh, T. Evaluation of atmospheric corrections on hyperspectral data with special reference to mineral mapping. Geosci. Front. 2017, 8, 797–808. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Q.; Zhao, Y.; Tian, L.Q.; Chen, X.L. Evaluation on the atmospheric correction methods for water color remote sensing by using HJ-1A/1B CCD image-taking Poyang Lake in China as a case. Spectrosc. Spectr. Anal. 2013, 33, 1320–1326. [Google Scholar]
- Bernardo, N.; Watanabe, F.; Rodrigues, T.; Alcântara, E. Atmospheric correction issues for retrieving total suspended matter concentrations in inland waters using OLI/Landsat-8 image. Adv. Space Res. 2017, 59, 2335–2348. [Google Scholar] [CrossRef] [Green Version]
- Cao, Y.; Ye, Y.; Zhao, H.; Jiang, Y.; Wang, H.; Shang, Y.; Wang, J. Remote sensing of water quality based on HJ-1A HSI imagery with modified discrete binary particle swarm optimization-partial least squares (MDBPSO-PLS) in inland waters: A case in Weishan Lake. Ecol. Inform. 2018, 44, 21–32. [Google Scholar] [CrossRef]
- Moses, W.; Gitelson, A.A.; Perk, R.L.; Gurlin, D.; Rundquist, D.C.; Leavitt, B.C.; Barrow, T.M.; Brakhage, P. Estimation of chlorophyll-a concentration in turbid productive waters using airborne hyperspectral data. Water Res. 2012, 46, 993–1004. [Google Scholar] [CrossRef] [Green Version]
- Eugenio, F.; Marcello, J.; Martin, J.; Rodríguez-Esparragón, D. Benthic habitat mapping using multispectral high-resolution imagery: Evaluation of shallow water atmospheric correction techniques. Sensors 2017, 17, 2639. [Google Scholar] [CrossRef] [Green Version]
- Lu, S.; Wu, B.; Yan, N.; Wang, H. Water body mapping method with HJ-1A/B satellite imagery. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 428–434. [Google Scholar] [CrossRef]
- McFeeters, S.K. The use of the normalized difference water index (NDWI) in the delineation of open water features. Int. J. Remote Sens. 1996, 17, 1425–1432. [Google Scholar] [CrossRef]
- He, Y.; Chen, S.; Huang, R.; Chen, X.; Cong, P. Impact of upstream runoff and tidal level on the chlorinity of an estuary in a river network: A case study of Modaomen estuary in the Pearl River Delta, China. J. Hydroinform. 2019, 21, 359–370. [Google Scholar] [CrossRef]
- Carlson, R.E. A trophic state index for lakes1 Limnology and oceanography. Limnol. Oceanogr. 1977, 22, 361–369. [Google Scholar] [CrossRef] [Green Version]
- Nazeer, M.; Nichol, J.E. Development and application of a remote sensing-based Chlorophyll-a concentration prediction model for complex coastal waters of Hong Kong. J. Hydrol. 2016, 532, 80–89. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Chen, Y.; Cai, Y.; Deng, J. Assessing river water quality using water quality index in Lake Taihu Basin, China. Sci. Total Environ. 2018, 612, 914–922. [Google Scholar] [CrossRef] [PubMed]
- Deng, Q. A BP neural network optimisation method based on dynamical regularization. J. Control. Decis. 2017, 6, 111–121. [Google Scholar] [CrossRef]
- Zhang, H.Q. BP neural network and its improved algorithm in the power system transformer fault diagnosis. Appl. Mech. Mater. 2013, 418, 200–204. [Google Scholar] [CrossRef]
- Wu, C.; Wu, J.; Qi, J.; Zhang, L.; Huang, H.; Lou, L.; Chen, Y. Empirical estimation of total phosphorus concentration in the mainstream of the Qiantang River in China using Landsat TM data. Int. J. Remote Sens. 2010, 31, 2309–2324. [Google Scholar] [CrossRef]
- Hao, C.; Wei, P.; Pei, L.; Du, Z.; Zhang, Y.; Lu, Y.; Dong, H. Significant seasonal variations of microbial community in an acid mine drainage lake in Anhui Province, China. Environ. Pollut. 2017, 223, 507–516. [Google Scholar] [CrossRef]

| No. | Date of Water Measurements | Date of the Landsat 8 Images |
|---|---|---|
| 1 | 9 October 2013 | 3 October 2013 |
| 2 | 9 December 2013 | 6 December 2013 |
| 3 | 5 August 2014 | 3 August 2014 |
| 4 | 5 August 2014 | 3 August 2014 |
| 5 | 2 December 2014 | 9 December 2014 |
| 6 | 8 April 2015 | 16 April 2015 |
| 7 | 1 March 2016 | 1 March 2016 |
| 8 | 6 December 2016 | 28 November 2016 |
| 9 | 6 September 2017 | 12 September 2017 |
| 10 | 7 November 2017 | 30 October 2017 |
| 11 | 6 December 2017 | 1 December 2017 |
| 12 | 2 February 2018 | 3 February 2018 |
| EI | En | TP (mg/L) | TN (mg/L) | Chl-a (μg/L) | CODMn (mg/L) | SD (m) |
|---|---|---|---|---|---|---|
| Oligotrophic 0 ≤ EI ≤ 20 | 10 | 0.001 | 0.020 | 0.0005 | 0.15 | 10 |
| 20 | 0.004 | 0.050 | 0.0010 | 0.4 | 5.0 | |
| Mesotrophic 20 < EI ≤ 50 | 30 | 0.010 | 0.10 | 0.0020 | 1.0 | 3.0 |
| 40 | 0.025 | 0.30 | 0.0040 | 2.0 | 1.5 | |
| 50 | 0.050 | 0.50 | 0.010 | 4.0 | 1.0 | |
| Meso-eutrophic 50 < EI ≤ 60 | 60 | 0.10 | 1.0 | 0.026 | 8.0 | 0.5 |
| Eutrophic 70 ≤ EI ≤ 80 | 70 | 0.20 | 2.0 | 0.064 | 10 | 0.4 |
| 80 | 0.60 | 6.0 | 0.16 | 25 | 0.3 | |
| Hype- eutrophic 80 < EI ≤ 100 | 90 | 0.90 | 9.0 | 0.40 | 40 | 0.2 |
| 100 | 1.3 | 16.0 | 1.0 | 60 | 0.12 |
| Model | Chl-a | CODMn | TN | TP | SD |
|---|---|---|---|---|---|
| 8 | 4 | 10 | 6 | 12 |
| Model | ||||
|---|---|---|---|---|
| Chl-a | 0.94 | 20.90 | 0.88 | 4.81 |
| CODMn | 0.81 | 11.40 | 0.65 | 0.42 |
| TN | 0.94 | 17.90 | 0.87 | 0.17 |
| TP | 0.98 | 39.80 | 0.96 | 0.01 |
| SD | 0.93 | 24.00 | 0.87 | 0.41 |
| Band/Parameters | lnChl-a | lnCODMn | lnTN | lnTP | lnSD |
|---|---|---|---|---|---|
| lnB1 | 0.35 | 0.19 | −0.11 | 0.28 | −0.02 |
| lnB2 | 0.17 | 0.22 | 0.07 | 0.30 | −0.00 |
| lnB3 | −0.17 | 0.43 | 0.29 | 0.38 | −0.02 |
| lnB4 | −0.11 | 0.22 | 0.37 | 0.46 | −0.31 |
| lnB5 | 0.60 | 0.11 | −0.37 | 0.34 | −0.37 |
| lnB6 | 0.28 | 0.08 | −0.31 | 0.50 | −0.31 |
| lnB7 | 0.11 | 0.02 | −0.26 | 0.46 | −0.22 |
| Model | (%) | |||
|---|---|---|---|---|
| BP Inversion Model | Linear Inversion Model | BP Inversion Model | Linear Inversion Model | |
| Chl-a | 20.6 | 32.6 | 4.81 | 10.38 |
| CODMn | 11.4 | 14.0 | 0.42 | 0.47 |
| TN | 17.9 | 16.1 | 0.17 | 0.14 |
| TP | 39.8 | 48.0 | 0.01 | 0.01 |
| SD | 24.0 | 22.7 | 0.41 | 0.40 |
| Date | Proportion | ||
|---|---|---|---|
| Mesotrophy | Meso-Eutrophy | Eutrophy | |
| 3 October 2013 | 79.84% | 20.11% | 0.05% |
| 6 December 2013 | 53.01% | 46.95% | 0.04% |
| 3 August 2014 | 74.10% | 25.86% | 0.05% |
| 6 October 2014 | 45.68% | 52.94% | 1.38% |
| 9 December 2014 | 39.69% | 60.15% | 0.15% |
| 16 April 2015 | 48.39% | 50.68% | 0.93% |
| 1 March 2016 | 28.78% | 71.18% | 0.04% |
| 28 November 2016 | 93.70% | 6.25% | 0.06% |
| 12 September 2017 | 90.89% | 9.11% | 0.00% |
| 30 October 2017 | 63.86% | 35.83% | 0.31% |
| 1 December 2017 | 89.30% | 10.69% | 0.01% |
| 3 February 2018 | 95.66% | 4.33% | 0.00% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, Y.; Gong, Z.; Zheng, Y.; Zhang, Y. Inland Reservoir Water Quality Inversion and Eutrophication Evaluation Using BP Neural Network and Remote Sensing Imagery: A Case Study of Dashahe Reservoir. Water 2021, 13, 2844. https://doi.org/10.3390/w13202844
He Y, Gong Z, Zheng Y, Zhang Y. Inland Reservoir Water Quality Inversion and Eutrophication Evaluation Using BP Neural Network and Remote Sensing Imagery: A Case Study of Dashahe Reservoir. Water. 2021; 13(20):2844. https://doi.org/10.3390/w13202844
Chicago/Turabian StyleHe, Yanhu, Zhenjie Gong, Yanhui Zheng, and Yuanbo Zhang. 2021. "Inland Reservoir Water Quality Inversion and Eutrophication Evaluation Using BP Neural Network and Remote Sensing Imagery: A Case Study of Dashahe Reservoir" Water 13, no. 20: 2844. https://doi.org/10.3390/w13202844
APA StyleHe, Y., Gong, Z., Zheng, Y., & Zhang, Y. (2021). Inland Reservoir Water Quality Inversion and Eutrophication Evaluation Using BP Neural Network and Remote Sensing Imagery: A Case Study of Dashahe Reservoir. Water, 13(20), 2844. https://doi.org/10.3390/w13202844







