Assessment of the Disaster Resilience of Complex Systems: The Case of the Flood Resilience of a Densely Populated City
Abstract
:1. Introduction
“the ability of a system, community or society exposed to hazards to resist, absorb, accommodate, adapt to, transform and recover from the effects of a hazard in a timely and efficient manner, including through the preservation and restoration of its essential basic structures and functions through risk management”.[31]
- (1)
- Resilience is a property of a system and not of single entities, which implies the adoption of a systemic approach;
- (2)
- Resilience is a property of the system’s dynamic response, which implies the definition of rules on how the system can adapt to, transform, and recover from the aftermath of a hazardous event.
- There is not yet a consolidated approach to quantitatively measure the resilience that takes into account its fundamental properties as appointed in the UNGA’s definition;
- The assessments of disaster risk and resilience are independent and incoherent, although they both refer to the same catastrophic events and have the same scope;
- Even the well-developed branch of research on infrastructure resilience does not adopt a systemic approach: the analysis is mostly focused on the efficiency of a single infrastructure typology rather than on the impact that its failure may have on society or, in general, on the whole system.
- To quantify disaster resilience of a complex system by means of the graph;
- To be compliant with the resilience definition by the UNGA;
- To adapt the traditional risk assessment methodology to the concept of resilience;
- To demonstrate the feasibility of the proposed methodology with a case study;
- To discuss the limits of the methodology and to propose future developments.
2. Methodology
2.1. Theoretical Framework
- Built the graph [36,37]: one without and one with resilience characteristics (as described in Section 2.2.1);
- Perturb the graphs by an external hazard (as presented in Section 2.2.2);
- Use the graph to propagate the indirect impacts (as described in Section 2.2.2);
- Built the risk curves for the two different graphs (theoretically introduced in Section 2.1 and results presented in Section 3.2);
- Estimate resilience as the area between the two curves (as described in Section 3.2).
2.1.1. System Perspective: Building the Graph
2.1.2. Dynamic Response: Defining the Adaptation Rules
2.2. Case Study: The City of Monza
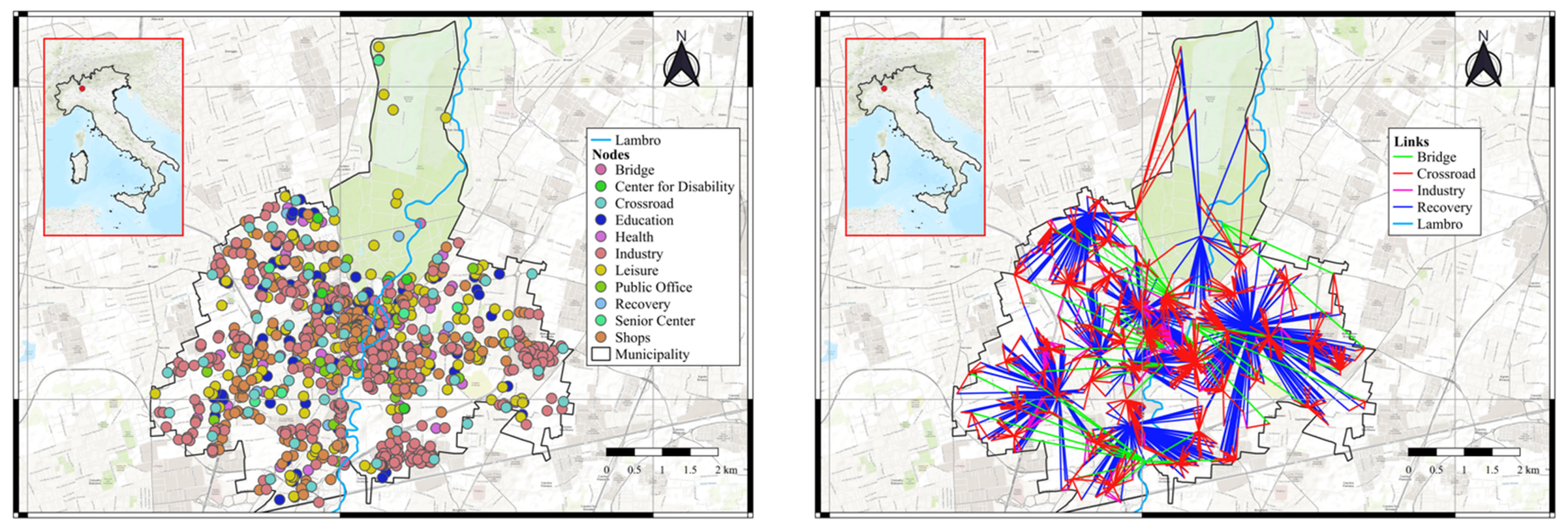
2.2.1. Construction of the Graph
2.2.2. Impact of Hazard on the Complex System
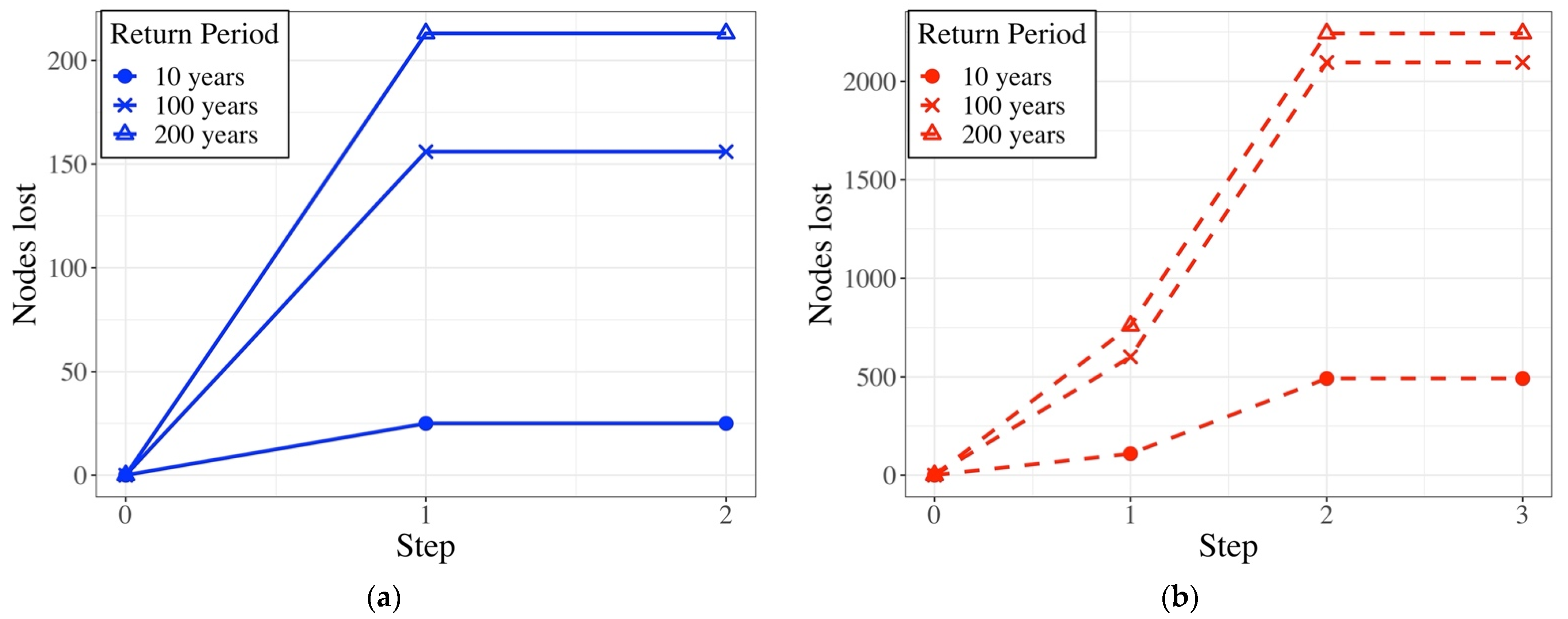
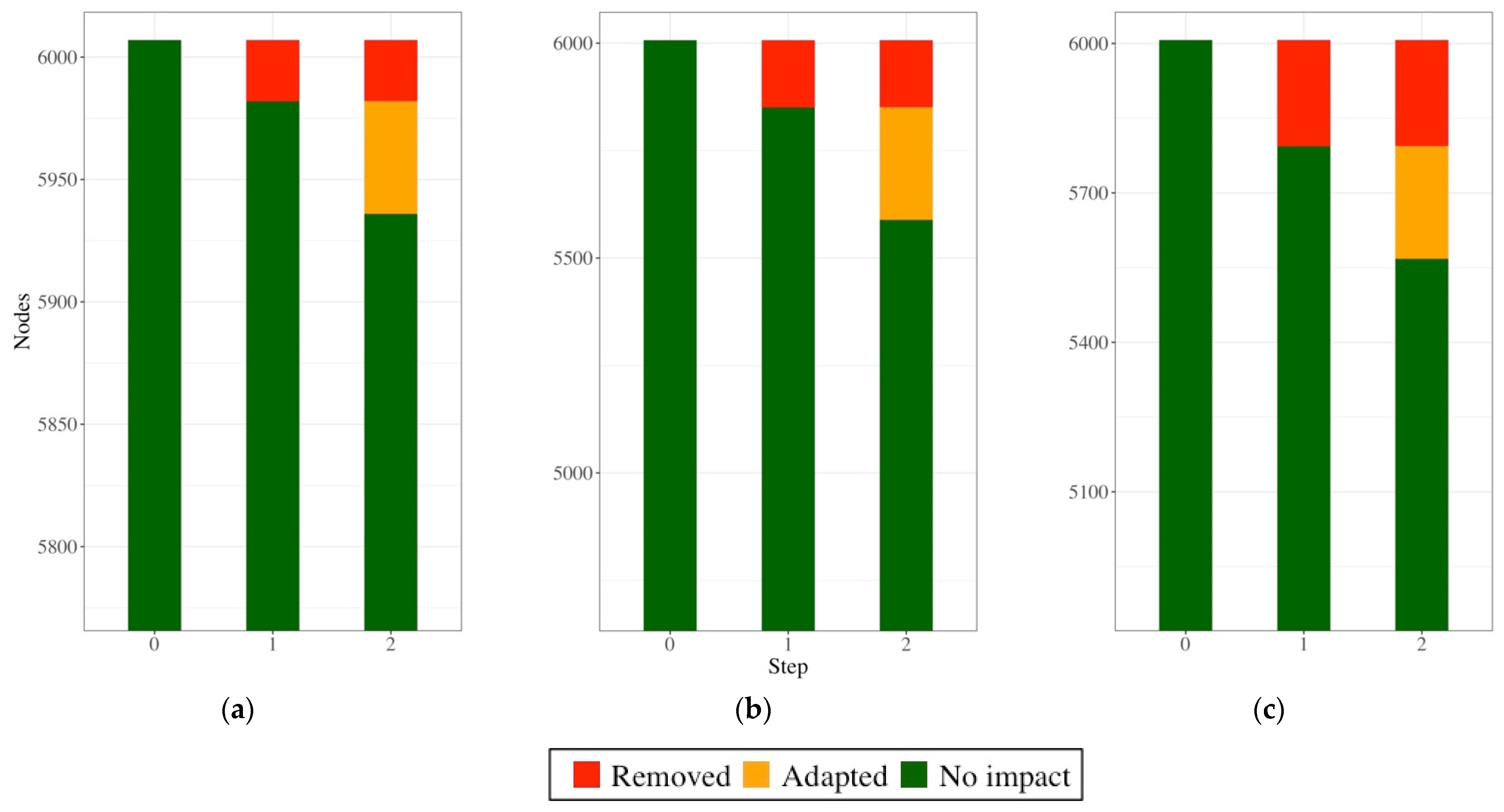
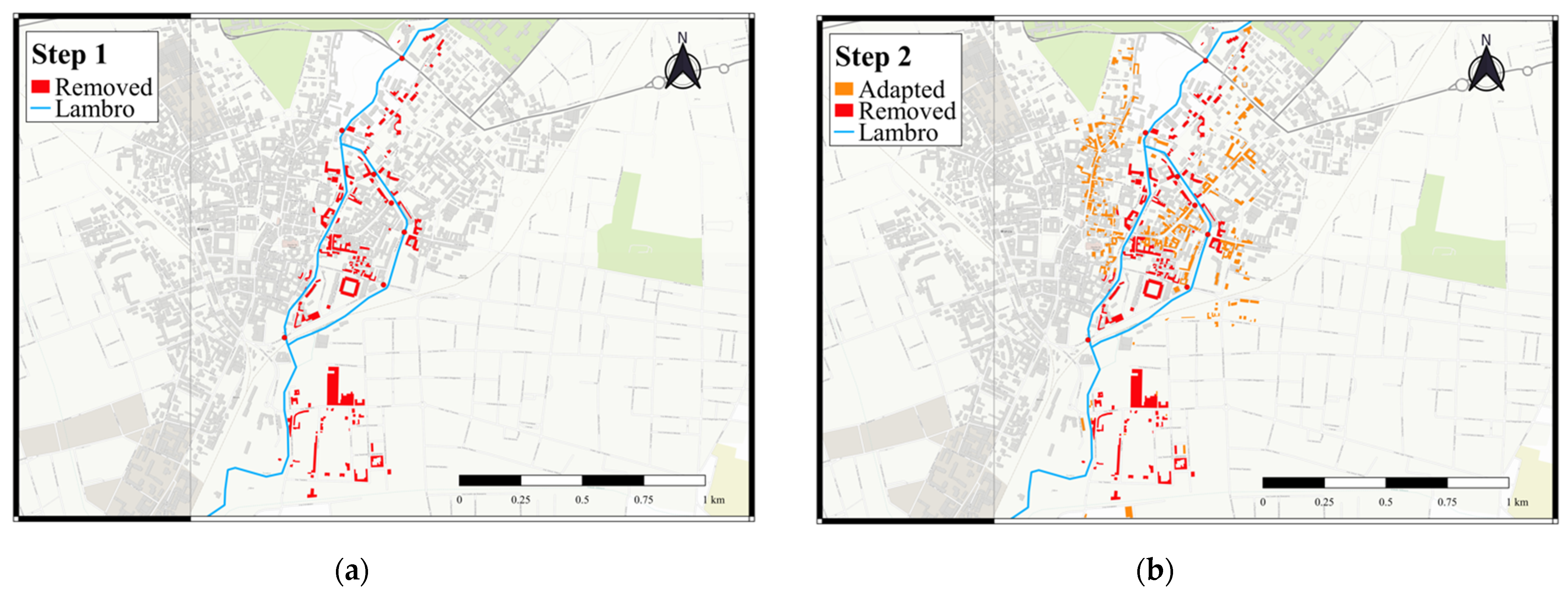
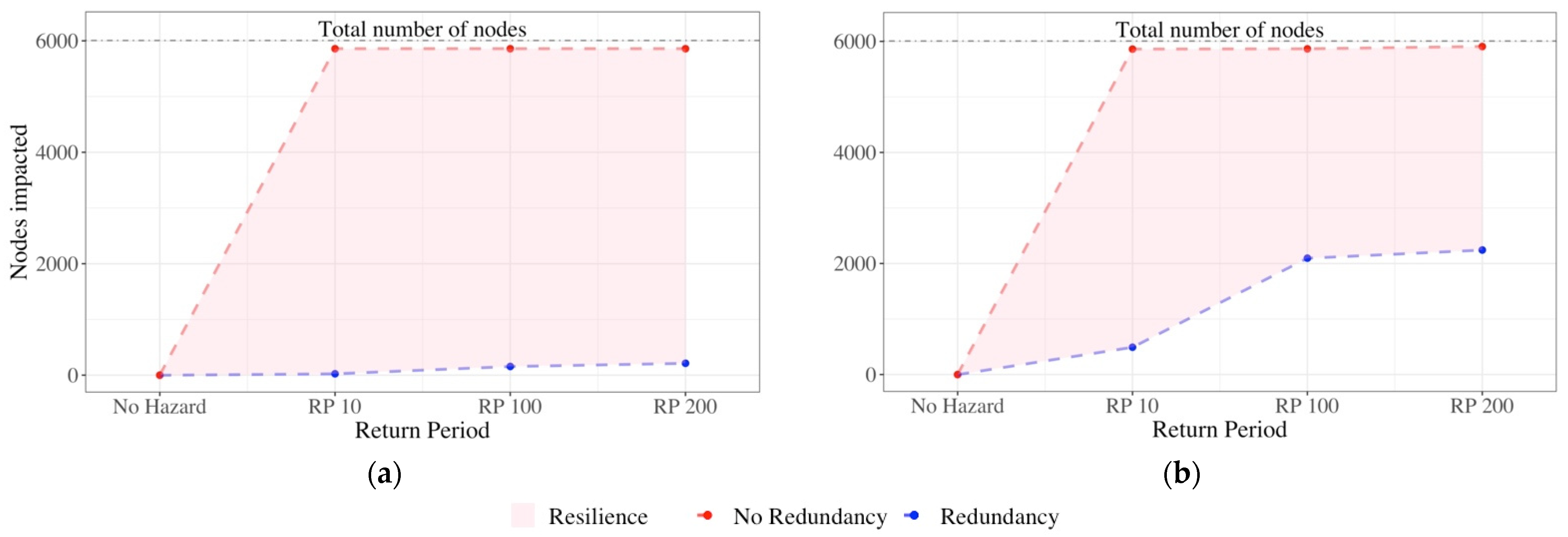
3. Results
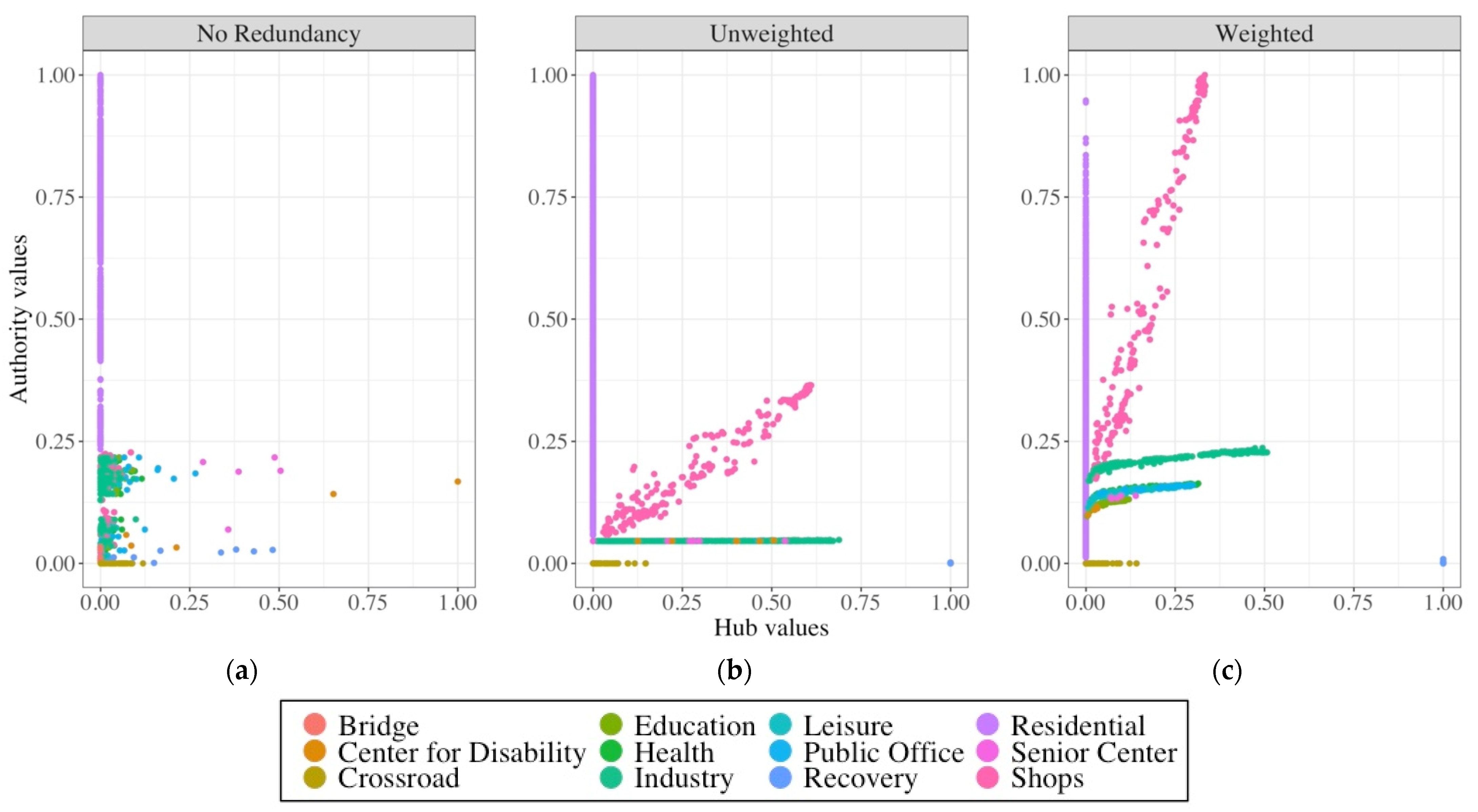
3.1. Effect of Redundancy and Weight on Graph Properties
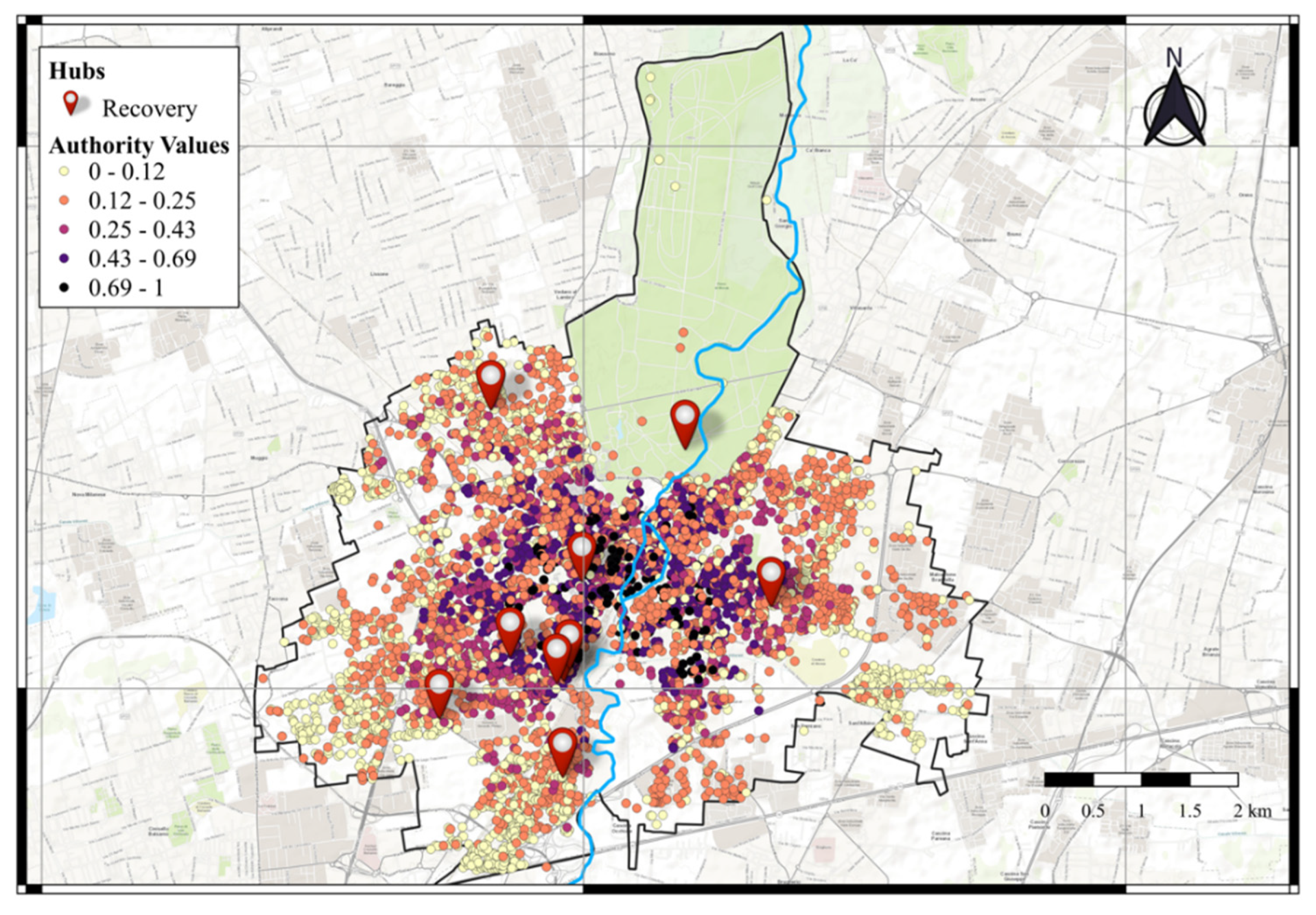
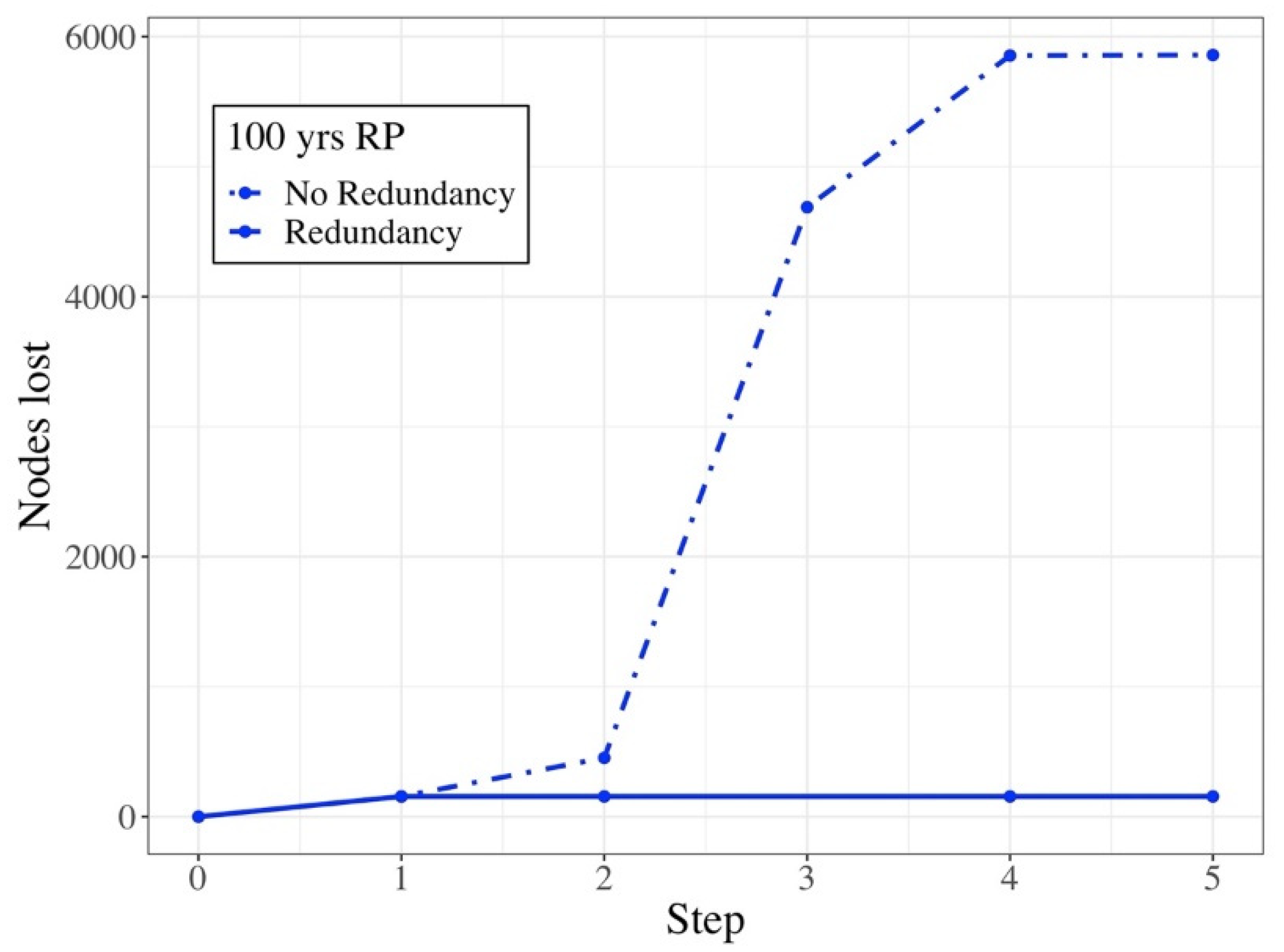
3.2. Assessment of the Resilience
4. Discussion
4.1. Model Assumptions
4.2. Significant Results Achieved
- Representation improvements of the urban system complexity through a weighted and redundant graph;
- A more accurate assessment of the central elements of the system thanks to the construction of a weighted graph based on the population distribution;
- The construction of a redundant and an adaptable graph that allowed us to reproduce most of the UNGA definition’s resilience characteristics;
- Demonstration that the methodology can assess the resilience to different hazards.
4.3. Future Developments
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Characteristics of the City Building
| Feature | Description |
|---|---|
| ID | A univocal alpha-numeric code that identifies the building |
| Height | Minimum height above sea level of the building [m] |
| Max_height | Maximum height above sea level of the building [m] |
| Rel_height | Relative height of the building obtained as Max_height—height [m] |
| Area | Area of the shapefile representing the building |
| Volume | Volume of the building obtained as the product between Area and Rel_height |
| Address | Address at which the building is registered in the municipality archive |
| Year_of_construction | The time interval during which the building was constructed. |
| State_of_conservation | Indicates the current state of conservation of the building. Three categories were given: Excellent, Good, Bad. |
| Type_building | Indicates the type of construction among masonry, reinforced concrete, and others. The latter comprises wood, steel, and other types of construction that are less frequent in the historical center of an Italian city |
| Destination_use | Indicates the activity and the destination of use of the building. The categories are reported in Table 2. |
| Number_families | Reports the number of families living in the building |
| Number_residents | Reports the number of residents living in the building |
| Number_disabled | Reports the number of disabled people living in the building |
References
- Cutter, S.L.; Ash, K.D.; Emrich, C.T. The geographies of community disaster resilience. Glob. Environ. Chang. 2014, 29, 65–77. [Google Scholar] [CrossRef]
- Klein, R.J.T.; Nicholls, R.J.; Thomalla, F. Resilience to Natural Hazards: How Useful Is This Concept? Glob. Environ. Chang. Part B Environ. Hazards 2004, 5, 35–45. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, J.; Wan, J.; Jia, H. Resilience to natural hazards: A geographic perspective. Nat. Hazards 2010, 53, 21–41. [Google Scholar] [CrossRef]
- Alexander, D.E. Resilience and disaster risk reduction: An etymological journey. Nat. Hazards Earth Syst. Sci. 2013, 13, 2707–2716. [Google Scholar] [CrossRef] [Green Version]
- Burton, C.G. A Validation of Metrics for Community Resilience to Natural Hazards and Disasters Using the Recovery from Hurricane Katrina as a Case Study. Ann. Assoc. Am. Geogr. 2015, 105, 67–86. [Google Scholar] [CrossRef]
- Timmerman, P. Vulnerability, resilience and the collapse ofsociety. In A Review of Models and Possible Climatic Applications; Institute for Environmental Studies, University of Toronto: Toronto, ON, Canada, 1981. [Google Scholar]
- Adger, W.N. Social and ecological resilience: Are they related? Prog. Hum. Geogr. 2000, 24, 347–364. [Google Scholar] [CrossRef]
- Torres, J. Crossing Borders: A Comparative Assessment of Community Resilience to Natural Hazards in Arica and Parinacota (Chile) and Tacna (Peru) Regions; Istituto Universitario di Studi Superiori di Pavia Crossing: Pavia, Italy, 2020. [Google Scholar]
- Nation, U. Sendai Framework for Disaster Risk Reduction 2015–2030; UNDRR: Geneva, Switzerland, 2015. [Google Scholar]
- Bruneau, M.; Chang, S.E.; Eguchi, R.T.; Lee, G.C.; O’Rourke, T.D.; Reinhorn, A.M.; Shinozuka, M.; Tierney, K.; Wallace, W.A.; Von Winterfeldt, D. A Framework to Quantitatively Assess and Enhance the Seismic Resilience of Communities. Earthq. Spectra 2003, 19, 733–752. [Google Scholar] [CrossRef] [Green Version]
- Burton, C.G. The Development of Metrics for Community Resilience to Natural Disasters. Ph.D. Thesis, University of South Carolina, Columbia, SC, USA, 2012; p. 198. [Google Scholar] [CrossRef]
- Cumming, G.S.; Barnes, G.; Perz, S.; Schmink, M.; Sieving, K.E.; Southworth, J.; Binford, M.; Holt, R.D.; Stickler, C.; Van Holt, T. An exploratory framework for the empirical measurement of resilience. Ecosystems 2005, 8, 975–987. [Google Scholar] [CrossRef]
- Cutter, S.L.; Barnes, L.; Berry, M.; Burton, C.; Evans, E.; Tate, E.; Webb, J. A place-based model for understanding community resilience to natural disasters. Glob. Environ. Chang. 2008, 18, 598–606. [Google Scholar] [CrossRef]
- Cutter, S.L.; Burton, C.G.; Emrich, C.T. Journal of Homeland Security and Disaster Resilience Indicators for Benchmarking Baseline Conditions Disaster Resilience Indicators for Benchmarking Baseline Conditions. J. Homel. Secur. Emerg. Manag. 2010, 7. [Google Scholar] [CrossRef]
- Francis, R.; Bekera, B. A Metric and Frameworks for Resilience Analysis of Engineered and Infrastructure Systems; Elsevier: Amsterdam, The Netherlands, 2014; Volume 121, ISBN 1202994024. [Google Scholar]
- Peacock, W. Advancing the Resilience of Coastal Localities: Developing, Implementing and Sustaining the Use of Coastal Resilience Indicators: A Final Report. Hazard Reduct. Recovery Cent. 2010. [Google Scholar] [CrossRef]
- Sherrieb, K.; Norris, F.H.; Galea, S. Measuring Capacities for Community Resilience. Soc. Indic. Res. 2010, 99, 227–247. [Google Scholar] [CrossRef]
- Lam, N.N.S.; Reams, M.; Li, K.; Li, C.; Mata, L.P. Measuring Community Resilience to Coastal Hazards along the Northern Gulf of Mexico. Nat. Hazards Rev. 2016, 17, 04015013. [Google Scholar] [CrossRef] [Green Version]
- Zimmerman, R. Social Implications of Infrastructure Network Interactions. J. Urban Technol. 2001, 8, 97–119. [Google Scholar] [CrossRef]
- Tierney, K.J. Conceptualizing and Measuring Organizational and Community Resilience: Lessons from the Emergency Response Following the 11 September 2001 Attack on the World Trade Center; Disaster Research Center: Columbus, OH, USA, 2003. [Google Scholar]
- David, R. Godschalk Urban Hazard Mitigation: Creating Resilient Cities. Nat. Hazards Rev. 2003, 4, 136–143. [Google Scholar] [CrossRef]
- Arup, T.R.F. City Resilience Framework; The Rockefeller Foundation: London, UK, 2015. [Google Scholar]
- UNDRR. Disaster Resilience Scorecard for Cities—Preliminary Level Assessment; UNDRR: Geneva, Switzerland, 2017. [Google Scholar]
- WCCD. ISO 37120 Sustainable Development of Communities: Indicators for City Services and Quality of Life; WCCD: Detroit, MI, USA, 2014. [Google Scholar]
- Zampieri, M. Reconciling the ecological and engineering definitions of resilience. Ecosphere 2021, 12, e03375. [Google Scholar] [CrossRef]
- Morecroft, M.D.; Crick, H.Q.P.; Duffield, S.J.; Macgregor, N.A. Resilience to climate change: Translating principles into practice. J. Appl. Ecol. 2012, 49, 547–551. [Google Scholar] [CrossRef]
- Quinlan, A.E.; Berbés-Blázquez, M.; Haider, L.J.; Peterson, G.D. Measuring and assessing resilience: Broadening understanding through multiple disciplinary perspectives. J. Appl. Ecol. 2016, 53, 677–687. [Google Scholar] [CrossRef]
- Scheffer, M.; Carpenter, S.R.; Dakos, V.; van Nes, E.H. Generic Indicators of Ecological Resilience: Inferring the Chance of a Critical Transition. Annu. Rev. Ecol. Evol. Syst. 2015, 46, 145–167. [Google Scholar] [CrossRef]
- Jones, L. Resilience isn’t the same for all: Comparing subjective and objective approaches to resilience measurement. Wiley Interdiscip. Rev. Clim. Chang. 2019, 10, 1–19. [Google Scholar] [CrossRef] [Green Version]
- UN Secretary-General (A/71/276). Report of the Open-Ended Intergovernmental Expert Working Group on Indicators and Terminology Relating to Disaster Risk Reduction; United Nations General Assembly: New York, NY, USA, 2017; Volume 8, pp. 49–116. [Google Scholar]
- UN Secretary-General A/71/644. Report of the Open-Ended Intergovernmental Expert Working Group on Indicators and Terminology Relating to Disaster Risk Reduction; United Nations General Assembly: New York, NY, USA, 2016; Volume 21184, pp. 1–41. [Google Scholar]
- Metzger, P.; Robert, J.; Área, P.F. Elementos de reflexión sobre la resiliencia urbana: Usos criticables y aportes potenciales. Territories 2013, 28, 21–40. [Google Scholar]
- Clark-Ginsberg, A.; Abolhassani, L.; Rahmati, E.A. Comparing networked and linear risk assessments: From theory to evidence. Int. J. Disaster Risk Reduct. 2018, 30, 216–224. [Google Scholar] [CrossRef]
- Lee, K. Appraising Adaptive Management. Biol. Divers 2001, 3, 3–26. [Google Scholar] [CrossRef] [Green Version]
- von Bertalanffy, L. An outline of general system theory. Br. J. Philos. Sci. 1950, 1, 134–165. [Google Scholar] [CrossRef]
- Arosio, M.; Martina, M.L.V.; Figueiredo, R. The whole is greater than the sum of its parts: A holistic graph-based assessment approach for natural hazard risk of complex systems. Nat. Hazards Earth Syst. Sci. 2020, 20, 521–547. [Google Scholar] [CrossRef] [Green Version]
- Arosio, M.; Martina, M.L.V.; Creaco, E.; Figueiredo, R. Indirect Impact Assessment of Pluvial Flooding in Urban Areas Using a Graph-Based Approach: The Mexico City Case Study. Water 2020, 12, 1753. [Google Scholar] [CrossRef]
- Fekete, A. Critical infrastructure and flood resilience: Cascading effects beyond water. Wiley Interdiscip. Rev. Water 2019, 6, e1370. [Google Scholar] [CrossRef] [Green Version]
- Fekete, A. Common criteria for the assessment of critical infrastructures. Int. J. Disaster Risk Sci. 2011, 2, 15–24. [Google Scholar] [CrossRef] [Green Version]
- Buldyrev, S.V.; Parshani, R.; Paul, G.; Stanley, H.E.; Havlin, S. Catastrophic cascade of failures in interdependent networks. Nature 2010, 464, 1025–1028. [Google Scholar] [CrossRef] [Green Version]
- Rinaldi, S.M.; Peerenboom, J.P.; Kelly, T.K. Identifying, understanding, and analyzing critical infrastructure interdependencies. IEEE Control Syst. Mag. 2001, 21, 11–25. [Google Scholar] [CrossRef]
- Zorn, C.; Pant, R.; Thacker, S.; Shamseldin, A.Y. Evaluating the magnitude and spatial extent of disruptions across interdependent national infrastructure networks. ASCE-ASME J. Risk Uncertain. Eng. Syst. Part. B Mech. Eng. 2020, 6. [Google Scholar] [CrossRef]
- Roy, K.C.; Hasan, S.; Mozumder, P. A multilabel classification approach to identify hurricane-induced infrastructure disruptions using social media data. Comput.-Aided Civil Infrastruct. Eng. 2020, 35, 1387–1402. [Google Scholar] [CrossRef]
- Papilloud, T.; Röthlisberger, V.; Loreti, S.; Keiler, M. Flood exposure analysis of road infrastructure—Comparison of different methods at national level. Int. J. Disaster Risk Reduct. 2020, 47, 101548. [Google Scholar] [CrossRef]
- Arrighi, C.; Pregnolato, M.; Castelli, F. Indirect flood impacts and cascade risk across interdependent linear infrastructures. Nat. Hazards Earth Syst. Sci. 2020, 21, 1955–1969. [Google Scholar] [CrossRef]
- Pant, R.; Thacker, S.; Hall, J.W.; Alderson, D.; Barr, S. Critical infrastructure impact assessment due to flood exposure. J. Flood Risk Manag. 2018, 11, 22–33. [Google Scholar] [CrossRef]
- Koks, E.; Pant, R.; Thacker, S.; Hall, J.W. Understanding Business Disruption and Economic Losses Due to Electricity Failures and Flooding. Int. J. Disaster Risk Sci. 2019, 10, 421–438. [Google Scholar] [CrossRef] [Green Version]
- Boccaletti, S.; Latora, V.; Moreno, Y.; Chavez, M.; Hwang, D.U. Complex networks: Structure and dynamics. Phys. Rep. 2006, 424, 175–308. [Google Scholar] [CrossRef]
- Börner, K.; Soma, S.; Vespignani, A. Network Science. Annu. Rev. Inf. Technol. 2007, 41, 537–607. [Google Scholar] [CrossRef]
- Nepusz, T.; Csard, G. Package “igraph”—Network Analysis and Visualization. Available online: https://cran.r-project.org/web/packages/igraph/igraph.pdf (accessed on 11 September 2021).
- Biggs, N.L.; Lloyd, E.K.; Wilson, R.J. Graph. Theory 1736–1936; Clarendon Press: Oxford, UK, 1976. [Google Scholar]
- Barabasi, A.L. Network Science. Available online: http://barabasi.com/networksciencebook/ (accessed on 11 September 2021).
- Newman, M.E.J. Networks An. Introduction; Springer Science & Business Media: Oxford, UK; New York, NY, USA, 2010; ISBN 9780199206650. [Google Scholar]
- Koenig, M.D.; Battiston, S. From Graph Theory to Models of Economic Networks. A Tutorial. In Networks, Topology and Dynamics; Springer: Berlin, Germany, 2009; pp. 23–63. ISBN 978-3-540-68407-7. [Google Scholar]
- Galuppini, G.; Quintilliani, C.; Arosio, M.; Barbero, G.; Ghilardi, P.; Manenti, S.; Petaccia, G.; Todeschini, S.; Ciaponi, C.; Martina, M.L.V.; et al. A unified framework for the assessment of multiple source urban flash flood hazard: The case study of Monza, Italy. Urban. Water J. 2020, 17, 65–77. [Google Scholar] [CrossRef]
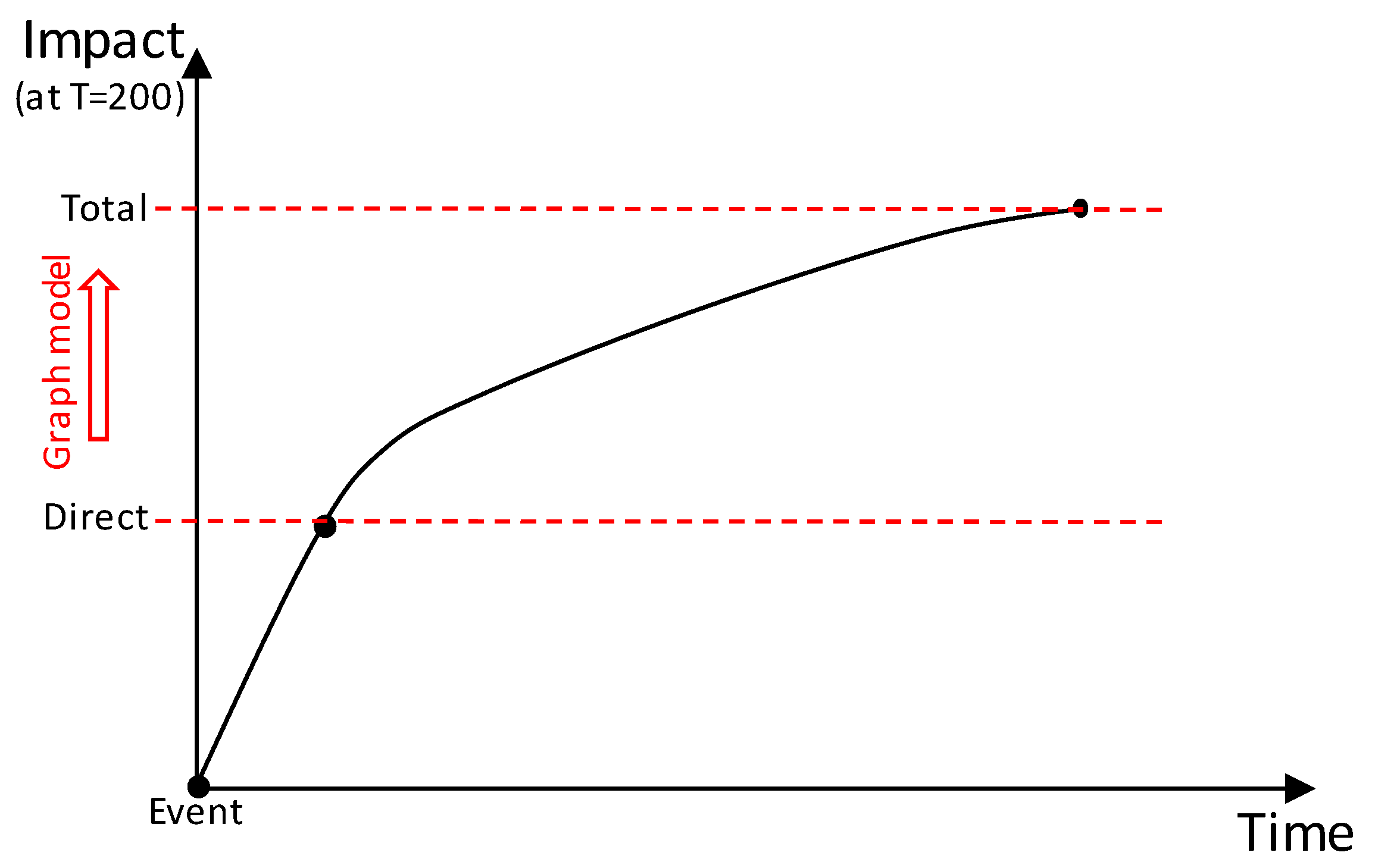
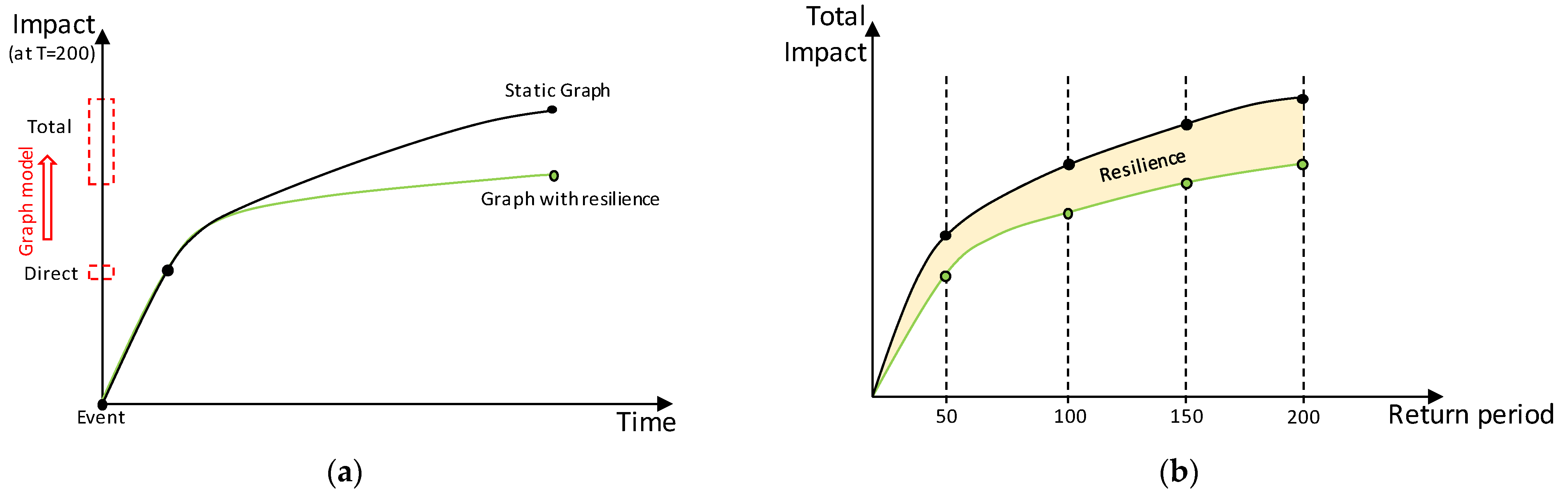
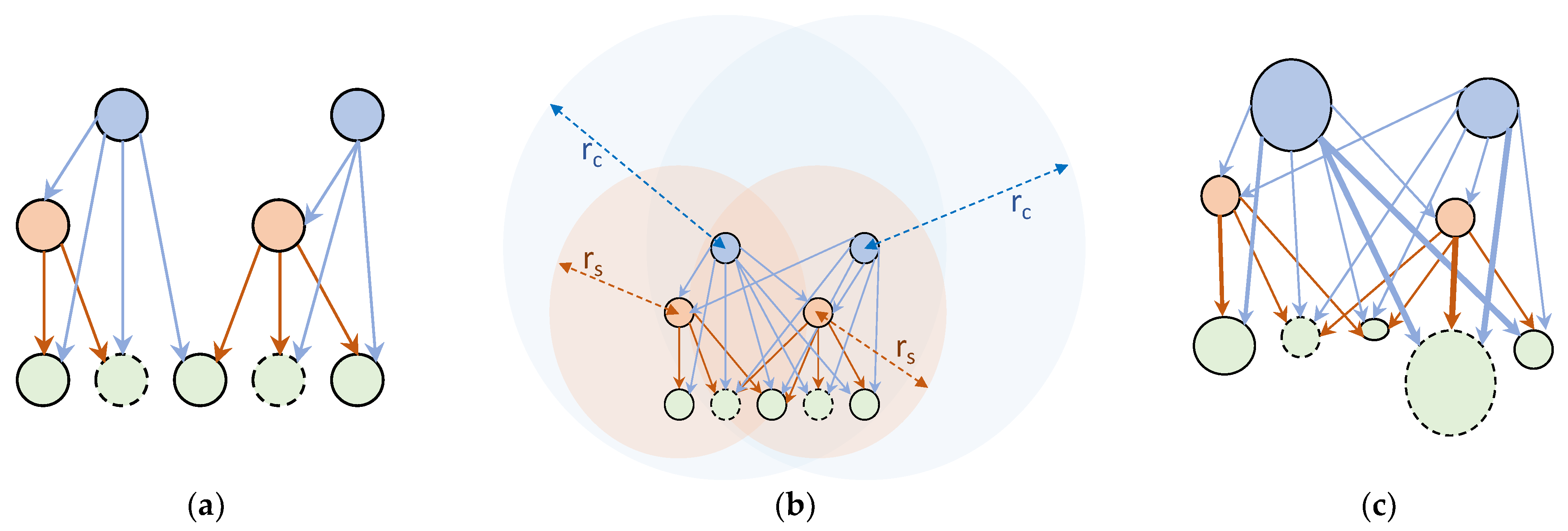
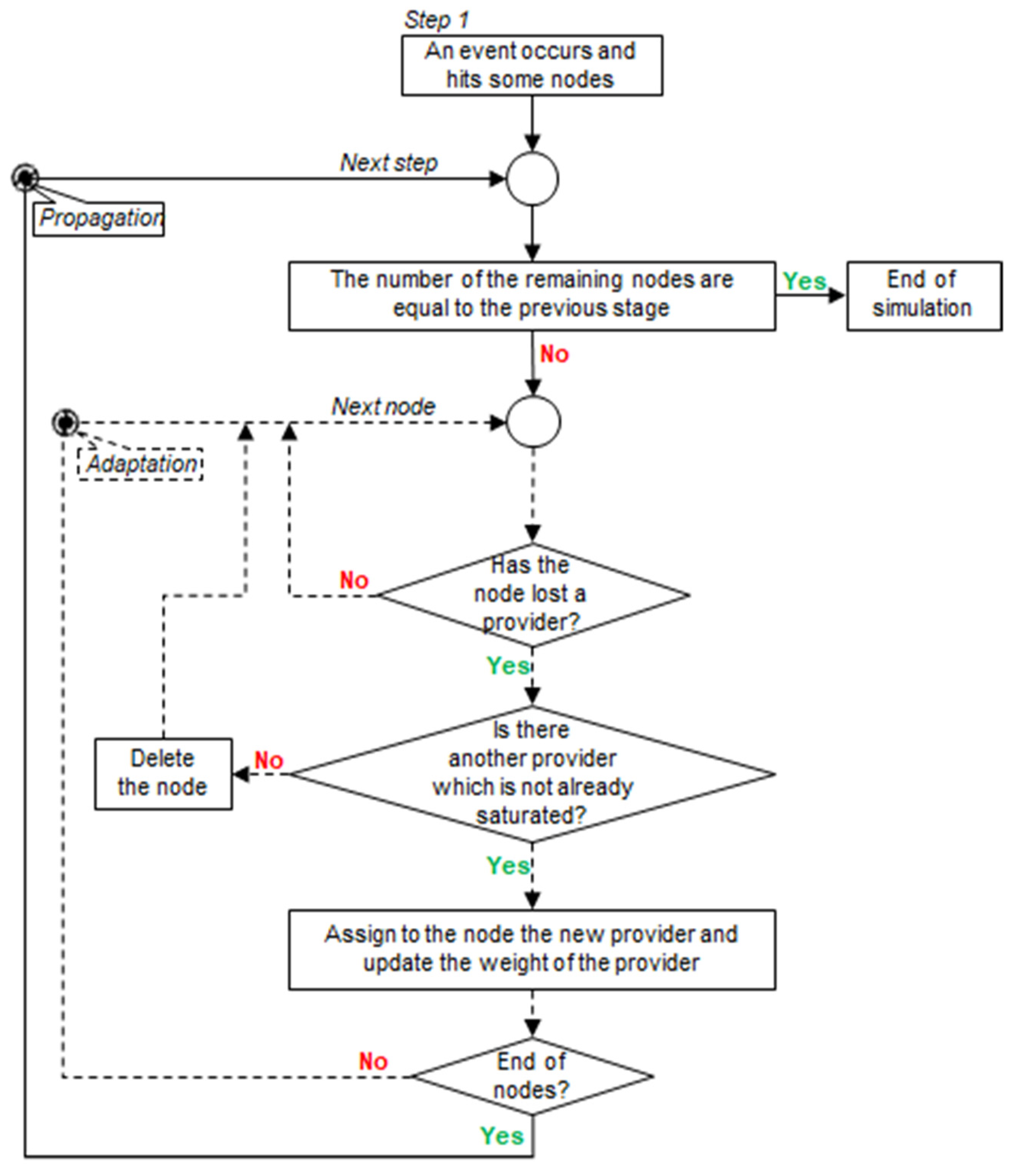
| Physical Damages | Non-Physical Damages | |
|---|---|---|
| Elements directly impacted | (a) Physical damages directly due to the event (Vulnerability of the first order) | (b) Non-physical damages due to the physical damages (Vulnerability of the second order) |
| Elements indirectly impacted | (c) Non-physical damages due to the interruption of the service provided by an impacted node (Vulnerability of the third order) |
| Category of Node | Number | The Receiver of the Service |
|---|---|---|
| Bridge | 10 | Crossroad |
| Center for Disability | 6 | Residential |
| Crossroad | 50 | All Typology |
| Education | 136 | Residential |
| Health | 80 | Residential |
| Industry | 331 | Residential, Shops |
| Leisure | 143 | Residential |
| Public Office | 28 | Residential |
| Recovery | 10 | All typology except for Bridge and Crossroad |
| Senior Center | 6 | Residential |
| Shops | 214 | Residential |
| Residential | 4990 | None |
| Provider | Receiver | Spatial Range |
|---|---|---|
| Bridge | Crossroad | Parallel Bands |
| Center for Disability | Residential | Radial Area |
| Crossroad | All Typology | Radial Area |
| Education | Residential | Radial Area |
| Health | Residential | Radial Area |
| Industry | Residential, Shops | Radial Area |
| Leisure | Residential | Radial Area |
| Public Office | Residential | Radial Area |
| Recovery | All typology except for Bridge and Crossroad | Entire City |
| Senior Center | Residential | Radial Area |
| Shops | Residential | Radial Area |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arosio, M.; Cesarini, L.; Martina, M.L.V. Assessment of the Disaster Resilience of Complex Systems: The Case of the Flood Resilience of a Densely Populated City. Water 2021, 13, 2830. https://doi.org/10.3390/w13202830
Arosio M, Cesarini L, Martina MLV. Assessment of the Disaster Resilience of Complex Systems: The Case of the Flood Resilience of a Densely Populated City. Water. 2021; 13(20):2830. https://doi.org/10.3390/w13202830
Chicago/Turabian StyleArosio, Marcello, Luigi Cesarini, and Mario L. V. Martina. 2021. "Assessment of the Disaster Resilience of Complex Systems: The Case of the Flood Resilience of a Densely Populated City" Water 13, no. 20: 2830. https://doi.org/10.3390/w13202830
APA StyleArosio, M., Cesarini, L., & Martina, M. L. V. (2021). Assessment of the Disaster Resilience of Complex Systems: The Case of the Flood Resilience of a Densely Populated City. Water, 13(20), 2830. https://doi.org/10.3390/w13202830






