Addressing Climate Internal Variability on Future Intensity-Duration-Frequency Curves at Fine Scales across South Korea
Abstract
:1. Introduction
2. Methodology
- The first task was to estimate the AWE-GEN parameters for the observed period, 1981 to 2010 (hereinafter referred to as OBS) using hourly rainfall in South Korea. The hourly time series data were collected from 40 gauge stations with an hourly record of climate variables for at least 30 years, and potential errors were examined carefully [34]. Those data are available from the Automated Surface Observing System operated by the Korea Meteorological Administration (https://data.kma.go.kr/data/grnd/selectAsosList.do?pgmNo=36, accessed on 12 December 2020). The hourly data were then used to estimate the 76 parameters of the Neyman-Scott Rectangular Pulse model in AWE-GEN. More detailed information about the Neyman-Scott Rectangular Pulse structure and parameters can be found in Fatichi, Ivanov, and Caporali [43] and Kim, Ivanov, and Fatichi [33].
- The next step was to estimate the AWE-GEN parameters for the future periods using two RCP scenarios for each of the stations used in step 1. Using daily rainfall data simulated by eighteen global climate models (see Table S1) from the fifth phase of the Coupled Model Inter-comparison Project for the future periods, the rainfall statistics of mean, variance, skewness, and frequency of non-precipitation (for a total of 158 statistics, refer to Kim, Ivanov, and Fatichi [33]) were computed and compared. The eighteen global climate models were specifically selected because they consistently provide daily rainfall data for all periods and maintain mutual independence from one another. We then attained 158 probability density functions for the resulting factors of change (FOCs) by using a Bayesian weighted averaging analysis [44]. We used that approach to account for the uncertainties among the global climate models caused by differences in their spatial resolutions and understandings of the physics of climate change. The output statistics, identified at 24-, 48-, 72-, and 96-h aggregation intervals, were then downscaled using a theoretical derivation and linearity assumption to the finer scales of 1-, 6-, 24-, and 72-h [43], respectively, required for the Neyman-Scott Rectangular Pulse process. Thus, a new set of precipitation parameters was generated across the three future periods for the two RCP scenarios.
- The new parameter set obtained in that way was applied to AWE-GEN, generating 100-member ensembles of 30-year hourly time series (hereinafter called control period (CTL) for 1981–2010; early future period (ERY) for 2011–2040; middle future period (MID) for 2041–2070; and end future period (END) for 2071–2100). Each AWE-GEN ensemble member is one of the repetitions that represent the stochasticity of precipitation and exhibits CIV [17,33,34], under the assumption of stationary climate conditions for its given period of interest. Using 100 stochastic simulations is appropriate because a larger number of model runs does not significantly increase the degree of uncertainty [33,45]. Note that each set of 100 simulations was derived from a population with the same climate information (i.e., the same AWE-GEN parameters), indicating that external forcing conditions were controlled equally [17,33,34].
- Given the 30-year hourly time series for precipitation, the next step was to reconstruct those hourly time series into series with durations of 2, 3, 6, 12, 24, 48, and 72 h by computing rainfall depths that accumulate during those durations and moving the interval window by 1 h over time [46,47]. In that way, another collection of 30-year time series was built for each duration interval chosen.
- Two common approaches are used to obtain extreme value series by sampling the maximum precipitation values required for a frequency analysis. The first is the annual maximum precipitation method, which extracts the maximum value for each year, and the second is the peak over threshold method, which selects only the largest portion of the maximum values after their ascent. Because annual maximum precipitation method is preferred over peak over threshold method for constructing IDF curves [3], we used annual maximum precipitation method in this study. For each of the 8 given durations, 100 ensemble members, and 40 locations, we extracted 30 annual extreme values.
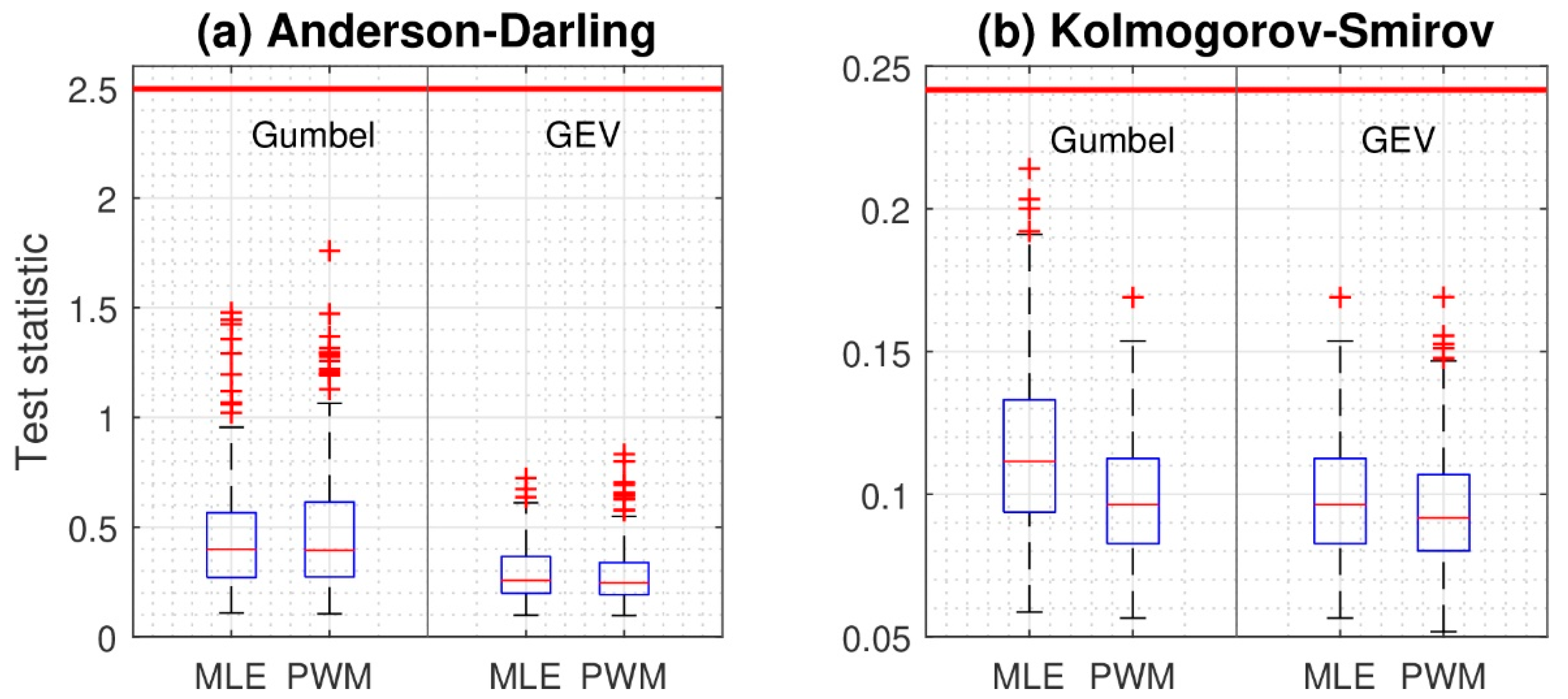
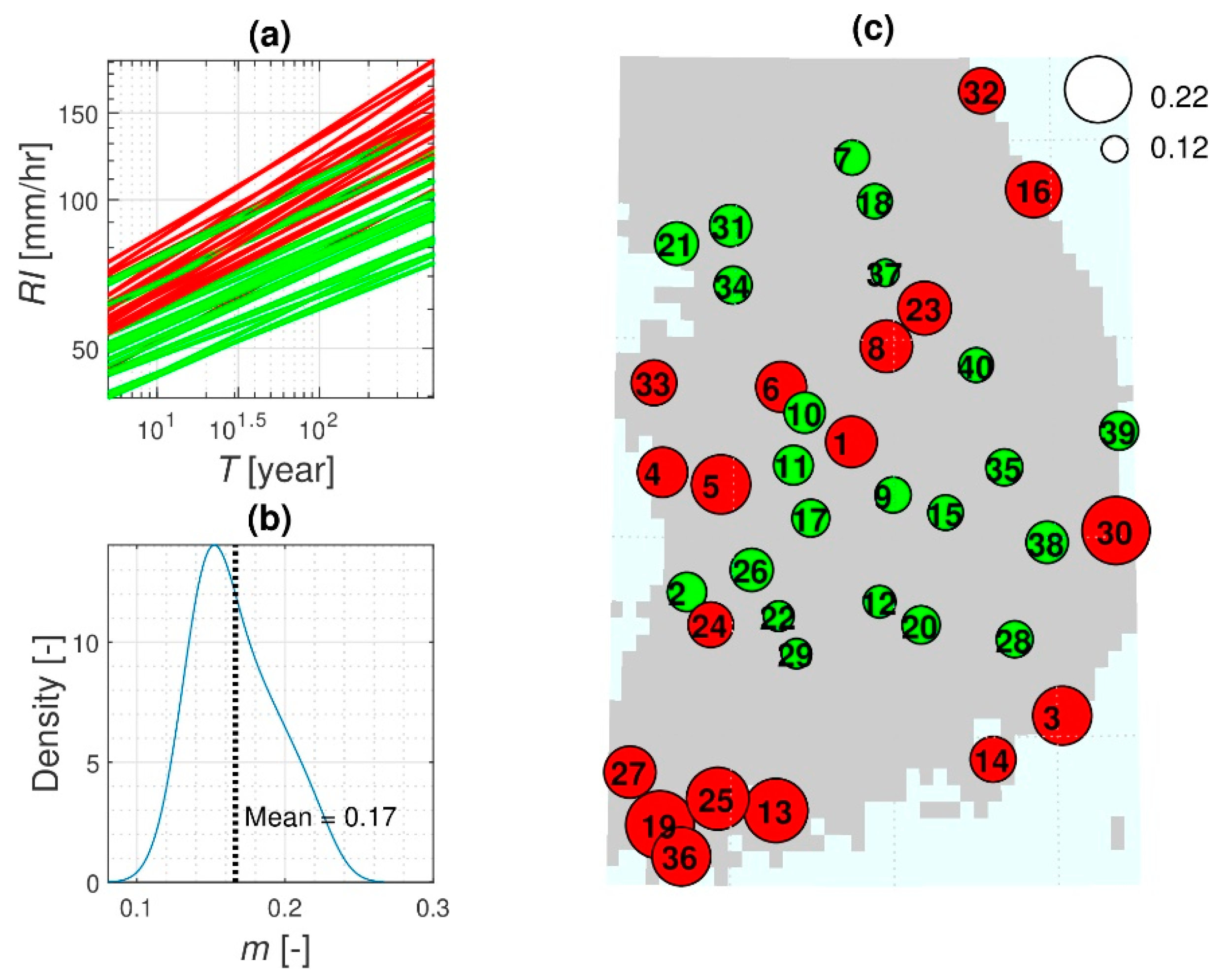
- After obtaining the annual maximum precipitation time series, we selected a probability distribution appropriate for the data and estimated its parameters. Among the common probability distributions applied to frequency analyses of extreme precipitation, such as the lognormal, log-Pearson III, generalized extreme value (GEV), and Gumbel distributions, the GEV distribution is the most popular [6,7,48,49,50]. For South Korea, both the Gumbel [51] and GEV [7] distributions have been recommended. Therefore, we chose the Gumbel and GEV distributions as appropriate to our purposes and then used maximum likelihood estimation and probabilistic weighted moment for parameter estimation. Two goodness-of-fit tests, the Anderson-Darling test [52] and Kolmogorov-Smirnov test [53], were applied to the 2 by 2 combinations to determine whether a given sample came from the hypothesized distribution. Those tests were performed for 1280 cases (2 distributions × 2 parameter estimation methods × 8 durations × 40 locations).
- The precipitation frequency estimates for various durations and return periods were computed from the cumulative distribution function using the estimated parameters of GEV and Gumbel distributions. In this study, 10 return periods (or recurrence intervals) of 5, 10, 20, 30, 50, 70, 80, 100, 200, and 500 years were considered. In total, the precipitation estimates were calculated for 10 return periods × 8 durations × 100 ensemble members × 40 locations.
- We then repeated Steps 3 to 7 for the control (CTL) and 3 future periods (ERY, MID, and END) and 2 RCP scenarios (RCP 4.5 and RCP 8.5) to assess our changing precipitation frequency estimates for the future. The total number of precipitation frequency estimates calculated was 10 return periods × 8 durations × 700 ensemble members × 40 locations.
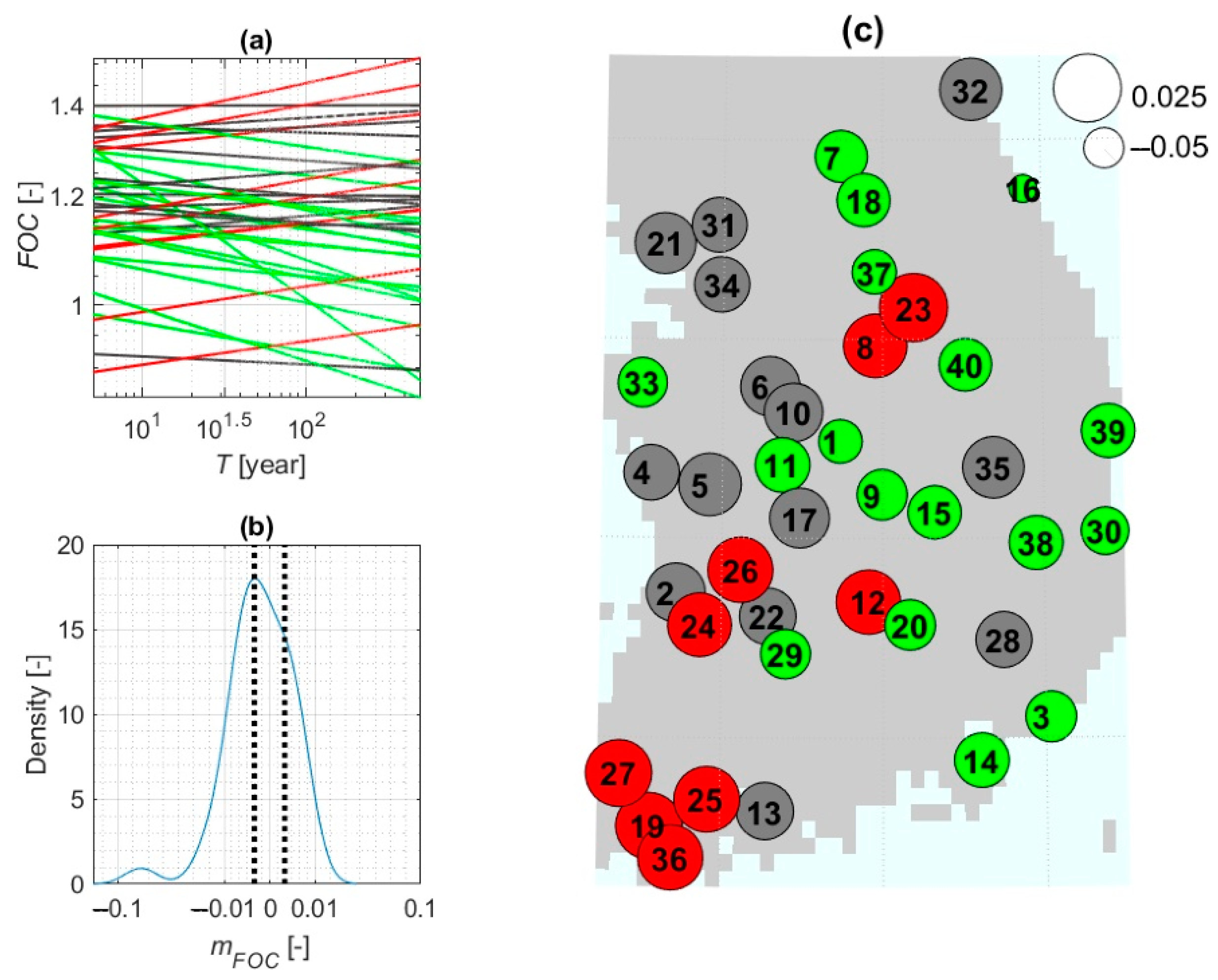
- To assess changes in the rainfall frequency estimates between the control and future periods for a given duration and return period, the FOC was introduced as the ratio of future rainfall intensity to the control intensity using the average value of 100 ensembles. Thus, the FOC represents how much the rainfall frequency estimate for a specific duration and return period increases or decreases in future periods. The total number of FOCs is 6 comparing pairs × 10 return periods × 8 durations × 40 locations.
- We were able to perform tests of significance for the mean differences between pairs of distributions because the rainfall estimates for each specific duration and return period consisted of 100 values that formed a distribution. That is, we were able to examine the distributions corresponding to the control and each future period to see how they differed from each other. A t-test can be used to test the mean difference between two independent samples with a significance level of 0.05 [54]. The null hypothesis was that the mean of the distributions would not change, and the alternative hypothesis was that they would differ significantly.
3. Results
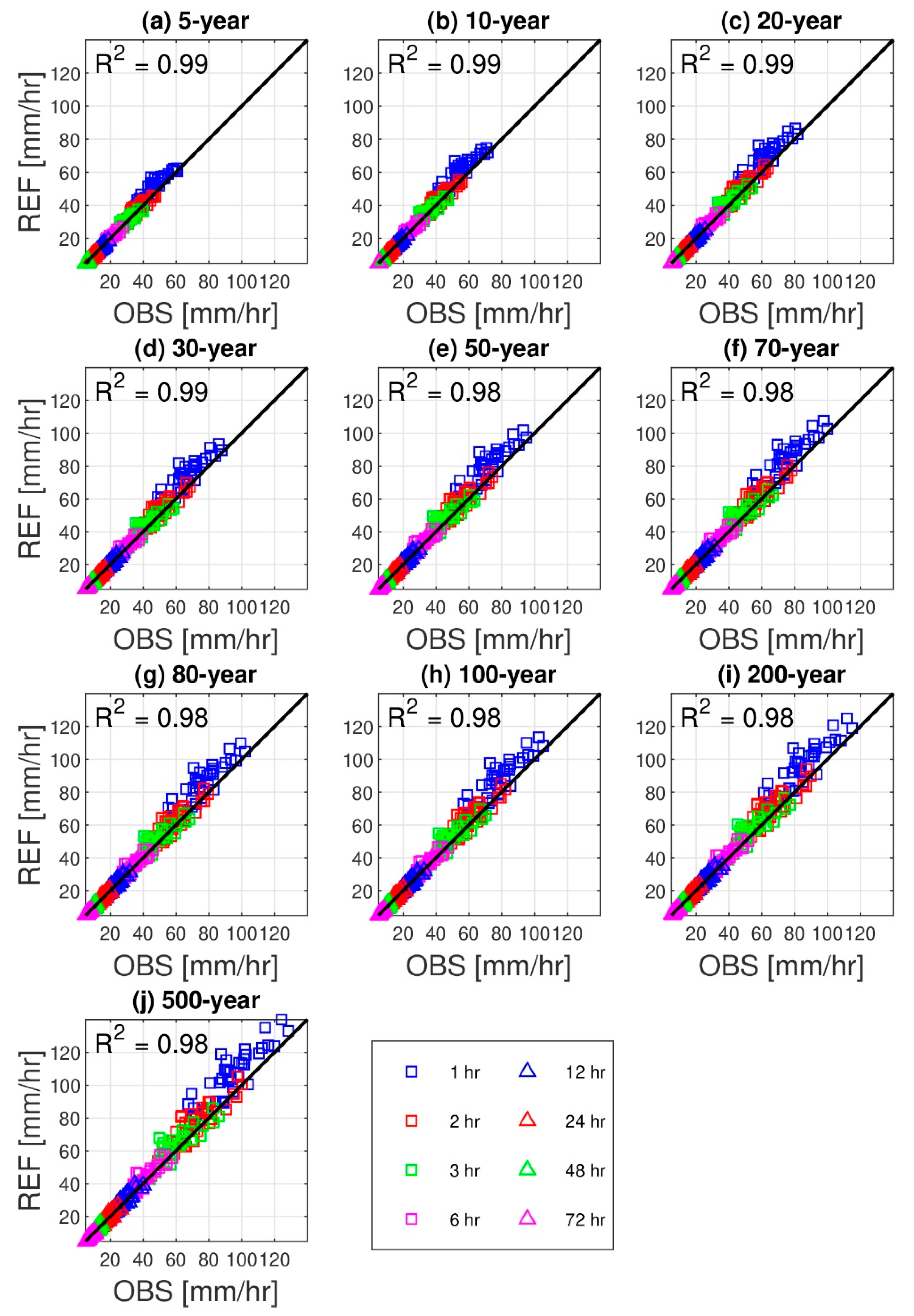
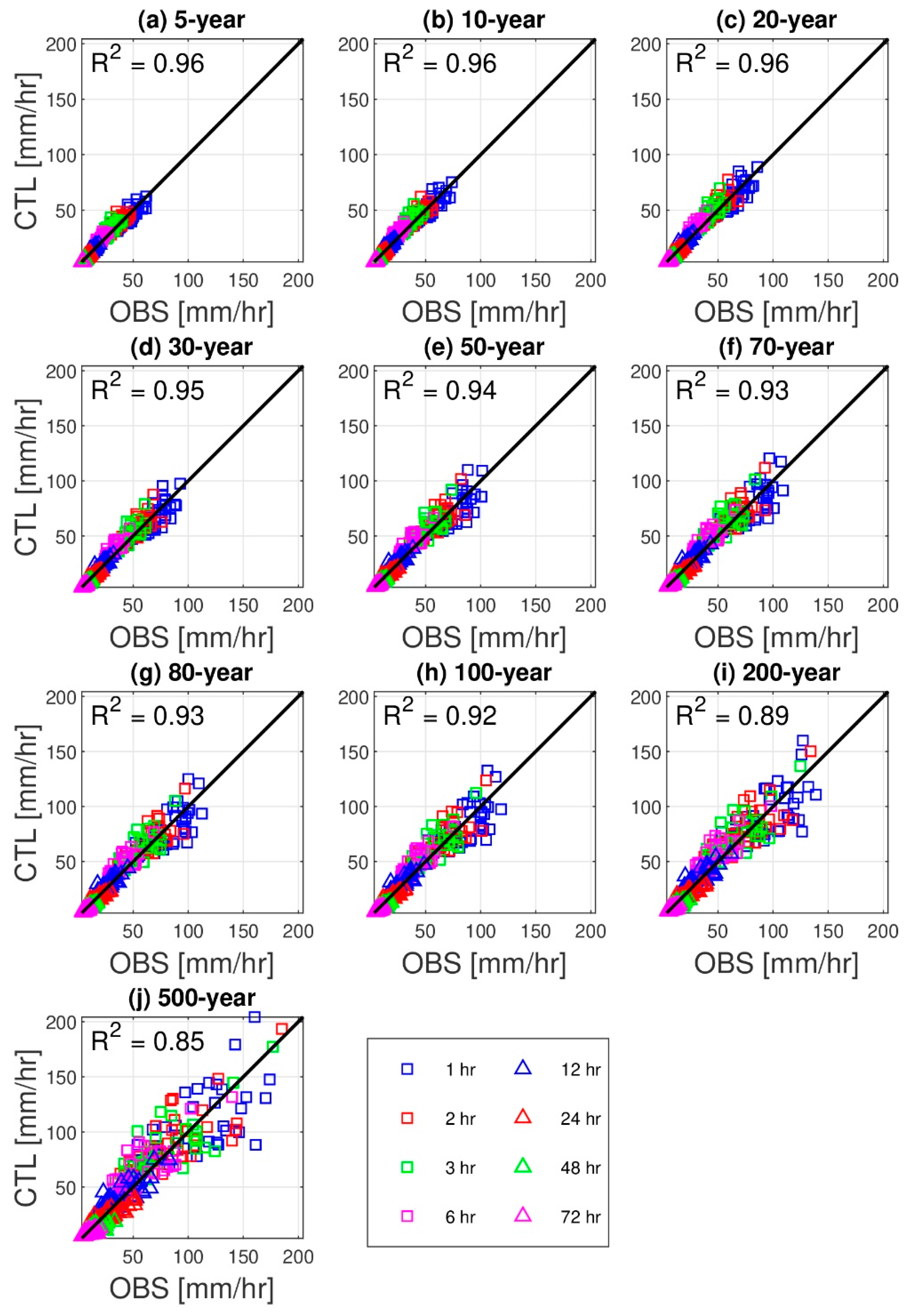
3.1. Precipitation Frequency Estimates and Their Validation
3.2. Ensemble Precipitation Frequency Estimates for Control and Future Periods
3.3. Factors of Change for Precipitation Frequency Estimates
4. Discussion
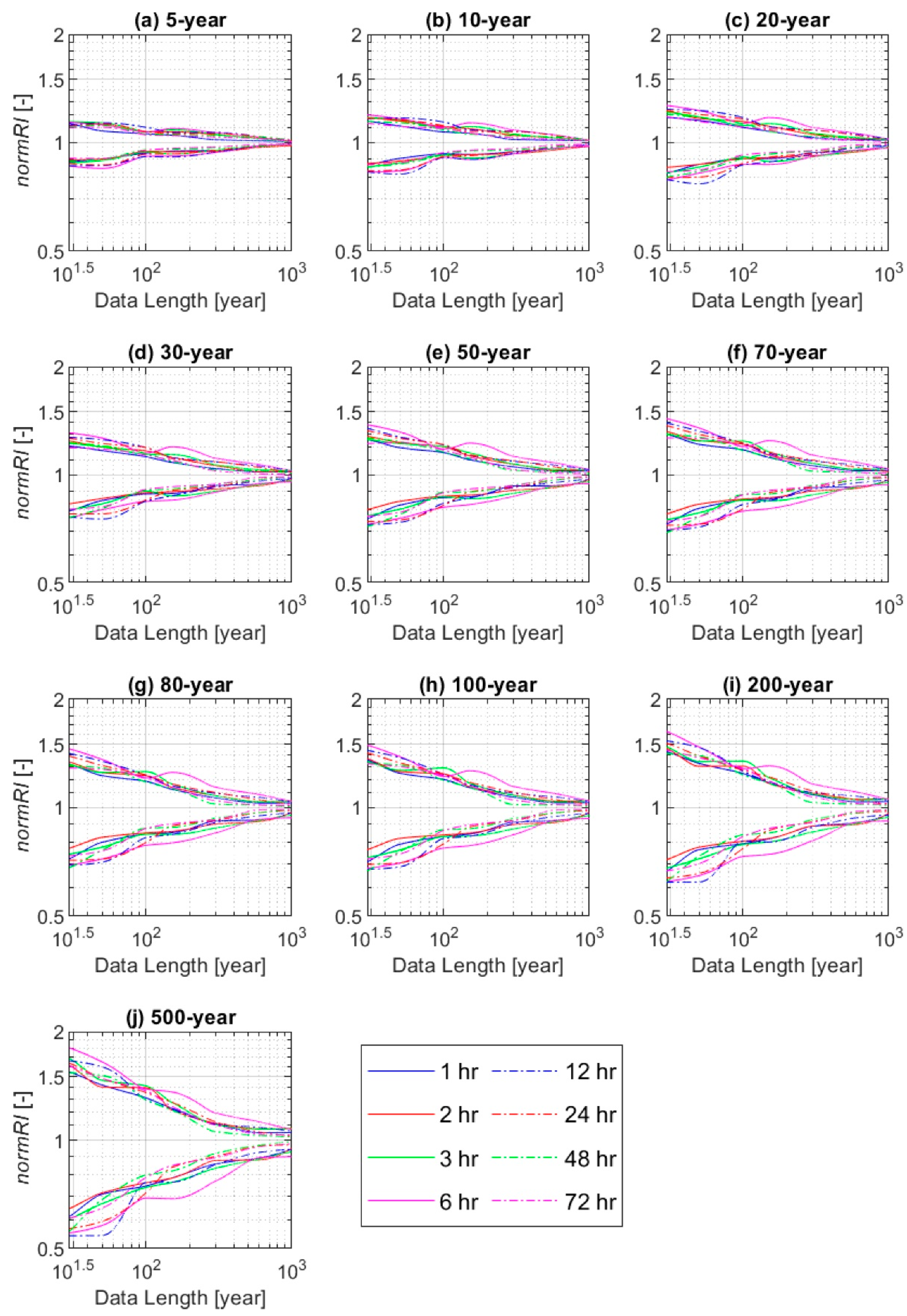
4.1. Do the Tail Characteristics of Future Extreme Rainfall Distribution Change?
4.2. Do Short-Range Data Provide Reliable Precipitation Frequency Estimates?
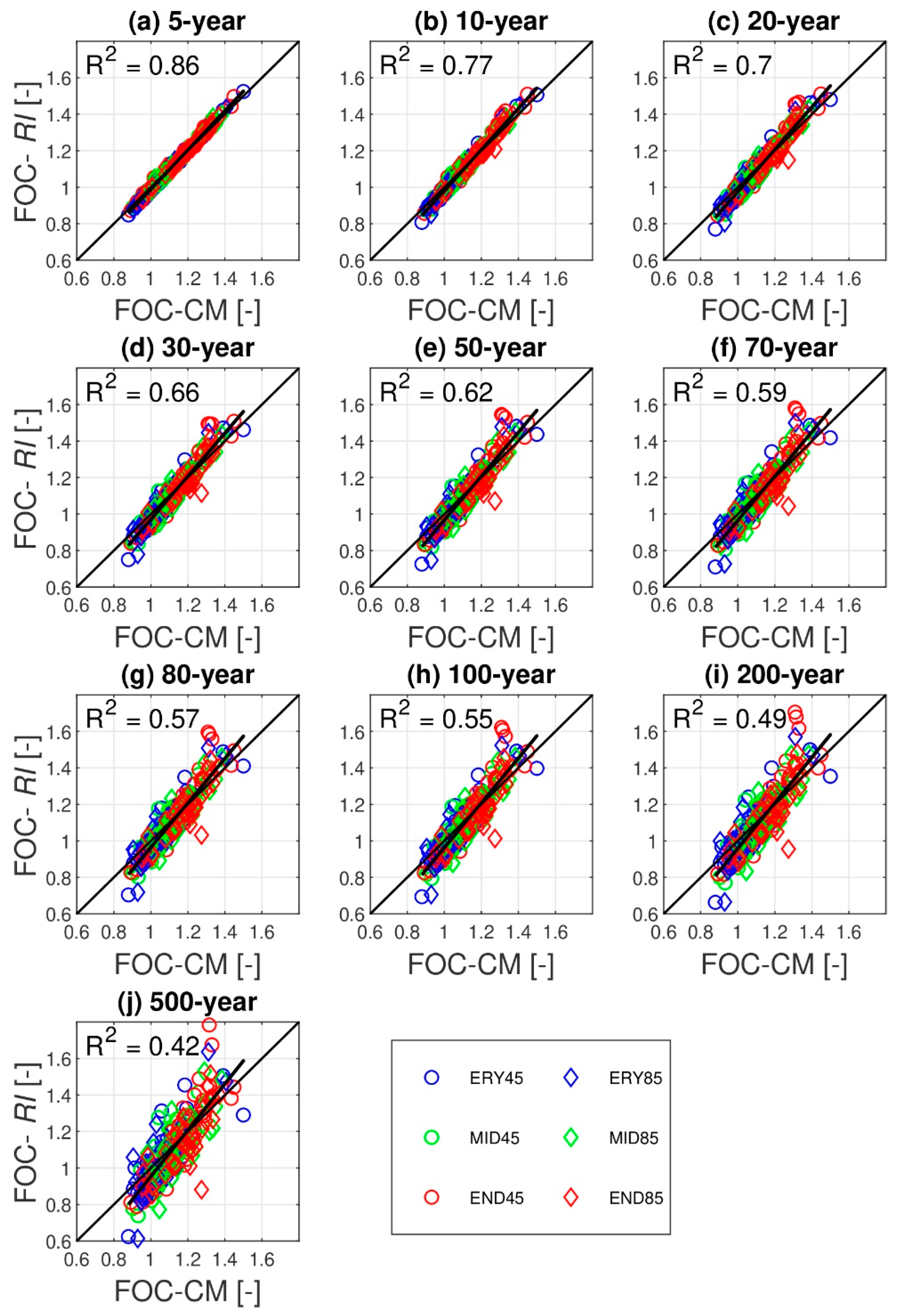
4.3. Is It Feasible to Infer Future Changes in RI from Those of Climatological Mean?
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Milly, P.C.D.; Betancourt, J.; Falkenmark, M.; Hirsch, R.M.; Kundzewicz, Z.W.; Lettenmaier, D.P.; Stouffer, R.J. Climate change. Stationarity is dead: Whither water management? Science 2008, 319, 573–574. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A.; Gilleland, E.; Katz, R. Non-stationary extreme value analysis in a changing climate. Clim. Chang. 2014, 127, 353–369. [Google Scholar] [CrossRef]
- Yilmaz, A.G.; Perera, B.J.C. Extreme Rainfall Nonstationarity Investigation and Intensity–Frequency–Duration Relationship. J. Hydrol. Eng. 2014, 19, 1160–1172. [Google Scholar] [CrossRef] [Green Version]
- DeGaetano, A.T.; Castellano, C.M. Future projections of extreme precipitation intensity-duration-frequency curves for climate adaptation planning in New York State. Clim. Serv. 2017, 5, 23–35. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A. Nonstationary Precipitation Intensity-Duration-Frequency Curves for Infrastructure Design in a Changing Climate. Sci. Rep. 2014, 4, 7093. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarhadi, A.; Soulis, E.D. Time-varying extreme rainfall intensity-duration-frequency curves in a changing climate. Geophys. Res. Lett. 2017, 44, 2454–2463. [Google Scholar] [CrossRef]
- Lima, C.H.; Kwon, H.-H.; Kim, Y.-T. A local-regional scaling-invariant Bayesian GEV model for estimating rainfall IDF curves in a future climate. J. Hydrol. 2018, 566, 73–88. [Google Scholar] [CrossRef]
- Güçlü, Y.S. Multiple Şen-innovative trend analyses and partial Mann-Kendall test. J. Hydrol. 2018, 566, 685–704. [Google Scholar] [CrossRef]
- Vu, M.T.; Raghavan, V.S.; Liong, S.-Y. Deriving short-duration rainfall IDF curves from a regional climate model. Nat. Hazards 2016, 85, 1877–1891. [Google Scholar] [CrossRef]
- Müller, H.; Haberlandt, U. Temporal rainfall disaggregation using a multiplicative cascade model for spatial application in urban hydrology. J. Hydrol. 2018, 556, 847–864. [Google Scholar] [CrossRef]
- Fadhel, S.; Rico-Ramirez, M.A.; Han, D. Uncertainty of Intensity–Duration–Frequency (IDF) curves due to varied climate baseline periods. J. Hydrol. 2017, 547, 600–612. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Johnson, F.; Evans, J.; Sharma, A. A comparison of methods to estimate future sub-daily design rainfall. Adv. Water Resour. 2017, 110, 215–227. [Google Scholar] [CrossRef]
- Shahabul Alam, M.; Elshorbagy, A. Quantification of the climate change-induced variations in Intensity–Duration–Frequency curves in the Canadian Prairies. J. Hydrol. 2015, 527, 990–1005. [Google Scholar] [CrossRef]
- Westra, S.; Evans, J.; Mehrotra, R.; Sharma, A. A conditional disaggregation algorithm for generating fine time-scale rainfall data in a warmer climate. J. Hydrol. 2013, 479, 86–99. [Google Scholar] [CrossRef] [Green Version]
- Pendergrass, A.G.; Knutti, R.; Lehner, F.; Deser, C.; Sanderson, B. Precipitation variability increases in a warmer climate. Sci. Rep. 2017, 7, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Prein, A.F.; Rasmussen, R.M.; Ikeda, K.; Liu, C.; Clark, M.P.; Holland, G.J. The future intensification of hourly precipitation extremes. Nat. Clim. Chang. 2016, 7, 48–52. [Google Scholar] [CrossRef]
- Van Doi, M.; Kim, J. Projections on climate internal variability and climatological mean at fine scales over South Korea. Stoch. Environ. Res. Risk Assess. 2020, 34, 1037–1058. [Google Scholar] [CrossRef]
- Westra, S.J.; Fowler, H.; Evans, J.; Alexander, L.; Berg, P.; Johnson, F.; Kendon, E.J.; Lenderink, G.; Roberts, N.M. Future changes to the intensity and frequency of short-duration extreme rainfall. Rev. Geophys. 2014, 52, 522–555. [Google Scholar] [CrossRef]
- Tran, V.N.; Dwelle, M.C.; Sargsyan, K.; Ivanov, V.Y.; Kim, J. A Novel Modeling Framework for Computationally Efficient and Accurate Real-Time Ensemble Flood Forecasting With Uncertainty Quantification. Water Resour. Res. 2020, 56, 1–31. [Google Scholar] [CrossRef]
- Kim, J.; Ivanov, V.Y.; Fatichi, S. Environmental stochasticity controls soil erosion variability. Sci. Rep. 2016, 6, 22065. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Ivanov, V.Y.; Fatichi, S. Soil erosion assessment-Mind the gap. Geophys. Res. Lett. 2016, 43, 12446–12456. [Google Scholar] [CrossRef]
- Cannon, A.J.; Innocenti, S. Projected intensification of sub-daily and daily rainfall extremes in convection-permitting climate model simulations over North America: Implications for future intensity–duration–frequency curves. Nat. Hazards Earth Syst. Sci. 2019, 19, 421–440. [Google Scholar] [CrossRef] [Green Version]
- Moustakis, Y.; Papalexiou, S.M.; Onof, C.J.; Paschalis, A. Seasonality, Intensity, and Duration of Rainfall Extremes Change in a Warmer Climate. Earth’s Futur. 2021, 9, 1–15. [Google Scholar] [CrossRef]
- Nerantzaki, S.D.; Papalexiou, S.M. Tails of extremes: Advancing a graphical method and harnessing big data to assess precipitation extremes. Adv. Water Resour. 2019, 134, 103448. [Google Scholar] [CrossRef]
- Papalexiou, S.M.; AghaKouchak, A.; Foufoula-Georgiou, E. A Diagnostic Framework for Understanding Climatology of Tails of Hourly Precipitation Extremes in the United States. Water Resour. Res. 2018, 54, 6725–6738. [Google Scholar] [CrossRef]
- Hawkins, E.; Sutton, R. The potential to narrow uncertainty in projections of regional precipitation change. Clim. Dyn. 2010, 37, 407–418. [Google Scholar] [CrossRef]
- Deser, C.; Phillips, A.; Bourdette, V.; Teng, H. Uncertainty in climate change projections: The role of internal variability. Clim. Dyn. 2010, 38, 527–546. [Google Scholar] [CrossRef] [Green Version]
- Deser, C.; Phillips, A.S.; Alexander, M.; Smoliak, B. Projecting North American Climate over the Next 50 Years: Uncertainty due to Internal Variability. J. Clim. 2014, 27, 2271–2296. [Google Scholar] [CrossRef] [Green Version]
- Fischer, E.M.; Sedlacek, J.; Hawkins, E.; Knutti, R. Models agree on forced response pattern of precipiation and temperature extremes. Geophys. Res. Lett. 2014, 41, 8554–8562. [Google Scholar] [CrossRef] [Green Version]
- Hingray, B.; Saïd, M. Partitioning Internal Variability and Model Uncertainty Components in a Multimember Multimodel Ensemble of Climate Projections. J. Clim. 2014, 27, 6779–6798. [Google Scholar] [CrossRef]
- Martel, J.-L.; Mailhot, A.; Brissette, F.; Caya, D. Role of Natural Climate Variability in the Detection of Anthropogenic Climate Change Signal for Mean and Extreme Precipitation at Local and Regional Scales. J. Clim. 2018, 31, 4241–4263. [Google Scholar] [CrossRef]
- Kim, J.; Ivanov, V.Y. A holistic, multi-scale dynamic downscaling framework for climate impact assessments and challenges of addressing finer-scale watershed dynamics. J. Hydrol. 2015, 522, 645–660. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Ivanov, V.Y.; Fatichi, S. Climate change and uncertainty assessment over a hydroclimatic transect of Michigan. Stoch. Environ. Res. Risk Assess. 2015, 30, 923–944. [Google Scholar] [CrossRef]
- Kim, J.; Tanveer, M.E.; Bae, D.-H. Quantifying climate internal variability using an hourly ensemble generator over South Korea. Stoch. Environ. Res. Risk Assess. 2018, 32, 3037–3051. [Google Scholar] [CrossRef]
- Deser, C.; Hurrell, J.W.; Phillips, A.S. The role of the North Atlantic Oscillation in European climate projections. Clim. Dyn. 2016, 49, 3141–3157. [Google Scholar] [CrossRef]
- Wang, J.; Bessac, J.; Kotamarthi, R.; Constantinescu, E.; Drewniak, B. Internal variability of a dynamically downscaled climate over North America. Clim. Dyn. 2017, 50, 4539–4559. [Google Scholar] [CrossRef]
- Kang, I.-S.; Shukla, J. Dynamic seasonal prediction and predictability of the monsoon. In The Asian Monsoon; Wang, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 585–612. [Google Scholar] [CrossRef]
- Peleg, N.; Molnar, P.; Burlando, P.; Fatichi, S. Exploring stochastic climate uncertainty in space and time using a gridded hourly weather generator. J. Hydrol. 2019, 571, 627–641. [Google Scholar] [CrossRef]
- Fatichi, S.; Ivanov, V.Y.; Paschalis, A.; Peleg, N.; Molnar, P.; Rimkus, S.; Kim, J.; Burlando, P.; Caporali, E. Uncertainty partition challenges the predictability of vital details of climate change. Earth’s Futur. 2016, 4, 240–251. [Google Scholar] [CrossRef]
- Fischer, E.; Beyerle, U.; Knutti, R. Robust spatially aggregated projections of climate extremes. Nat. Clim. Chang. 2013, 3, 1033–1038. [Google Scholar] [CrossRef]
- Giorgi, F.; Mearns, L.O. Calculation of average, uncertainty range, and reliability of regional climate changes from AOGCM simulations via the “reliability ensemble averaging” (REA) method. J. Clim. 2002, 15, 1141–1158. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Bras, R.L.; Curtis, D.C. A weather generator for hydrological, ecological, and agricultural applications. Water Resour. Res. 2007, 43, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Fatichi, S.; Ivanov, V.Y.; Caporali, E. Simulation of future climate scenarios with a weather generator. Adv. Water Resour. 2011, 34, 448–467. [Google Scholar] [CrossRef]
- Tebaldi, C.; Smith, R.L.; Nychka, D.; Mearns, L.O. Quantifying Uncertainty in Projections of Regional Climate Change: A Bayesian Approach to the Analysis of Multimodel Ensembles. J. Clim. 2005, 18, 1524–1540. [Google Scholar] [CrossRef] [Green Version]
- Tran, V.; Kim, J. Quantification of predictive uncertainty with a metamodel: Toward more efficient hydrologic simulations. Stoch. Environ. Res. Risk Assess. 2019, 33, 1453–1476. [Google Scholar] [CrossRef]
- Zhu, J.; Stone, M.C.; Forsee, W. Analysis of potential impacts of climate change on intensity–duration–frequency (IDF) relationships for six regions in the United States. J. Water Clim. Chang. 2012, 3, 185–196. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.; Kim, D.; Kang, B. The role of rainfall spatial variability in estimating areal reduction factors. J. Hydrol. 2018, 568, 416–426. [Google Scholar] [CrossRef]
- Ombadi, M.; Nguyen, P.; Sorooshian, S.; Hsu, K. Developing Intensity-Duration-Frequency (IDF) Curves From Satellite-Based Precipitation: Methodology and Evaluation. Water Resour. Res. 2018, 54, 7752–7766. [Google Scholar] [CrossRef]
- Ragno, E.; AghaKouchak, A.; Love, C.A.; Cheng, L.; Vahedifard, F.; Lima, C.H.R. Quantifying Changes in Future Intensity-Duration-Frequency Curves Using Multimodel Ensemble Simulations. Water Resour. Res. 2018, 54, 1751–1764. [Google Scholar] [CrossRef]
- Bairwa, A.K.; Khosa, R.; Maheswaran, R. Developing intensity duration frequency curves based on scaling theory using linear probability weighted moments: A case study from India. J. Hydrol. 2016, 542, 850–859. [Google Scholar] [CrossRef]
- So, B.-J.; Kim, J.-Y.; Kwon, H.-H.; Lima, C.H. Stochastic extreme downscaling model for an assessment of changes in rainfall intensity-duration-frequency curves over South Korea using multiple regional climate models. J. Hydrol. 2017, 553, 321–337. [Google Scholar] [CrossRef]
- Anderson, T.W. Anderson–Darling Tests of Goodness-of-Fit. In International Encyclopedia of Statistical Science; Lovric, M., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 52–54. [Google Scholar]
- Massey, F.J. The Kolmogorov-Smirnov Test for Goodness of Fit. J. Am. Stat. Assoc. 1951, 46, 68. [Google Scholar] [CrossRef]
- Lund, R.B.; Von Storch, H.; Zwiers, F.W. Statistical Analysis in Climate Research. J. Am. Stat. Assoc. 2000, 95, 1375. [Google Scholar] [CrossRef] [Green Version]
- Stephens, M.A. Goodness of Fit for the Extreme Value Distribution. Biometrika 1997, 64, 583–588. [Google Scholar] [CrossRef]
- Mielke, P.W.; Benjamin, J.R.; Cornell, C.A. Probability, Statistics and Decision for Civil Engineers. J. Am. Stat. Assoc. 1971, 66, 923. [Google Scholar] [CrossRef]
- MLIT. A Study on the Improvement and Supplement of the Rainfall Probability; Ministry of Land, Infrastructure and Transport: Seoul, Korea, 2011.
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill Series in Water Resources and Environmental Engineering; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Doi, M.V.; Kim, J. Addressing Climate Internal Variability on Future Intensity-Duration-Frequency Curves at Fine Scales across South Korea. Water 2021, 13, 2828. https://doi.org/10.3390/w13202828
Doi MV, Kim J. Addressing Climate Internal Variability on Future Intensity-Duration-Frequency Curves at Fine Scales across South Korea. Water. 2021; 13(20):2828. https://doi.org/10.3390/w13202828
Chicago/Turabian StyleDoi, Manh Van, and Jongho Kim. 2021. "Addressing Climate Internal Variability on Future Intensity-Duration-Frequency Curves at Fine Scales across South Korea" Water 13, no. 20: 2828. https://doi.org/10.3390/w13202828
APA StyleDoi, M. V., & Kim, J. (2021). Addressing Climate Internal Variability on Future Intensity-Duration-Frequency Curves at Fine Scales across South Korea. Water, 13(20), 2828. https://doi.org/10.3390/w13202828





