Upper Limit and Power Generation Loss of Water Supplement from Cascade Hydropower Stations to Downstream under Lancang-Mekong Cooperation
Abstract
:1. Introduction
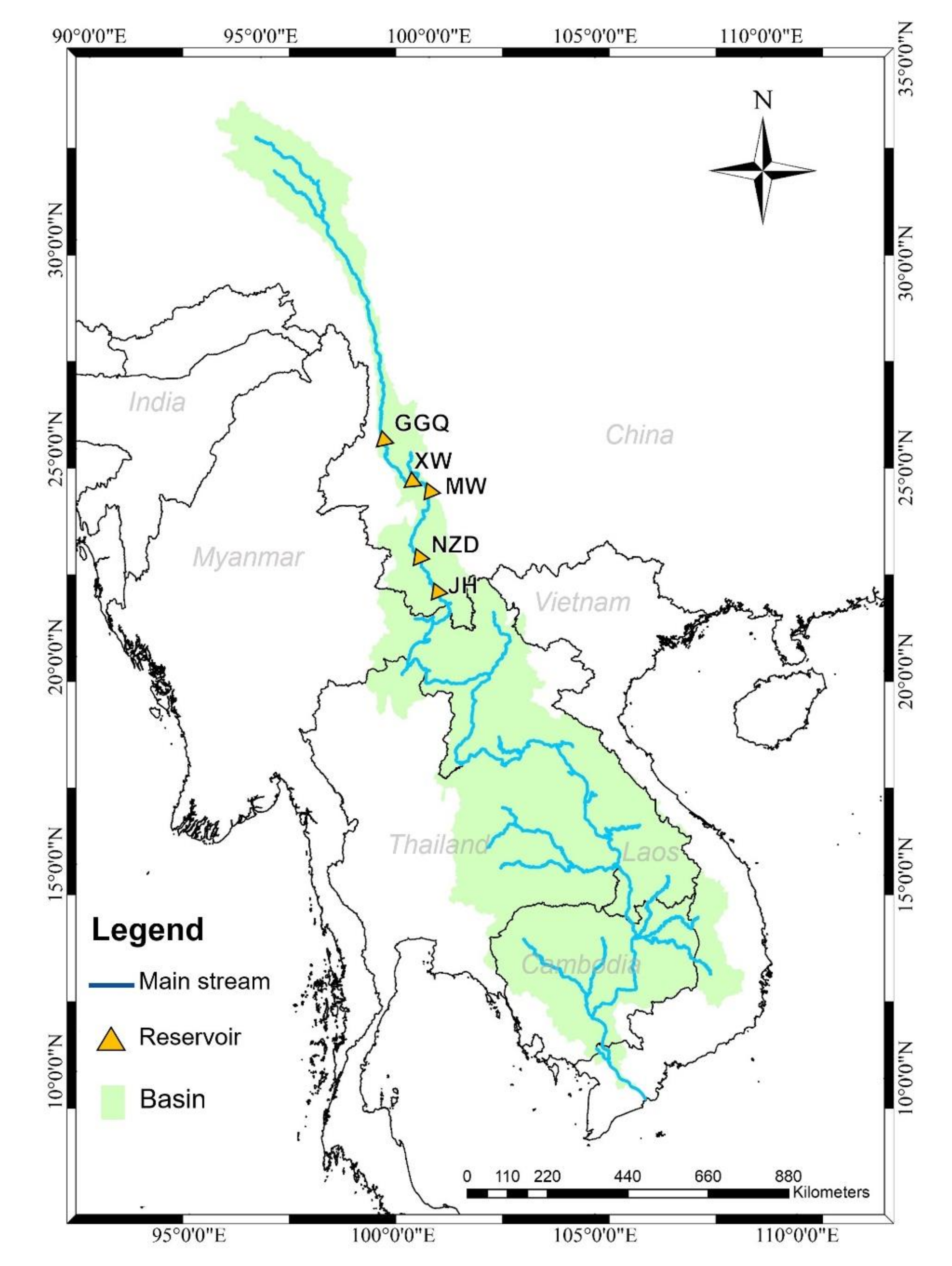
2. Study Area and Data
3. Methodology
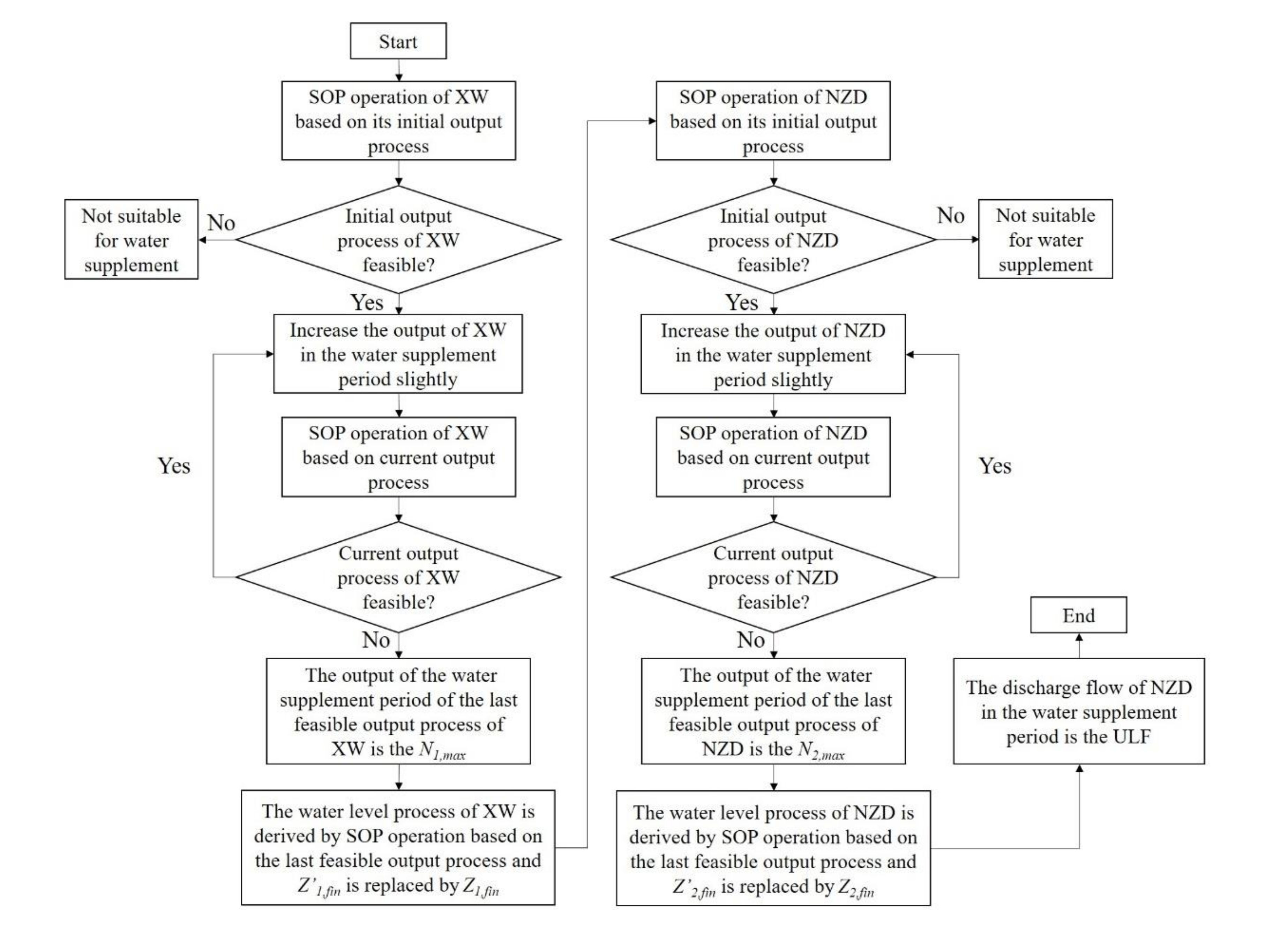
3.1. Calculation of ULF
- (1)
- Set and as the initial and final water level constraints of XW, respectively. Set and as the initial and final water level constrains of NZD, respectively.
- (2)
- The operation process of XW within the year is carried out by using SOP according to the initial output process of XW. If the initial output process is feasible, enter step (3); otherwise, it indicates that the inflow condition of the year is not suitable for water supplement, which means, even there is no water supplement requirements from the downstream countries, that part of the periods still lacks water, and water supplement may cause greater burden on the upstream power generation task.
- (3)
- Based on the initial output process of XW, increase the output in the water supplement period gradually (the output of other periods remains unchanged), until continuous increase will cause the output process to be not feasible. Save the water level process derived by SOP and the output of XW in the water supplement period at the time. Record the output of XW as , and the final water level derived by SOP operation now is . Due to the fact that must be higher than or equal to , replace with , and the water level process after the replacement is the final water level process of XW under the limit state of water supplement;
- (4)
- Keep the final water level process of XW under the limit state of water supplement obtained in step (3) unchanged, and then the operation process of NZD within the year is carried out by using SOP according to the initial output process of NZD. If the initial output process is feasible, enter step (5); otherwise, it indicates that the inflow condition of the year is not suitable for water supplement. Water supplement may cause greater burden on the upstream power generation task.
- (5)
- Based on the initial output process of NZD, increase the output in the water supplement period gradually (the output of other periods remains unchanged), until continuous increase will cause the output process to be not feasible. Save the water level process derived by SOP and the output of NZD in the water supplement period at the time. Record the output of NZD as , and the final water level derived by SOP operation now is . Due to the fact that must be higher than or equal to , replace with , and the water level process after the replacement is the final water level process of NZD under the limit state of water supplement;
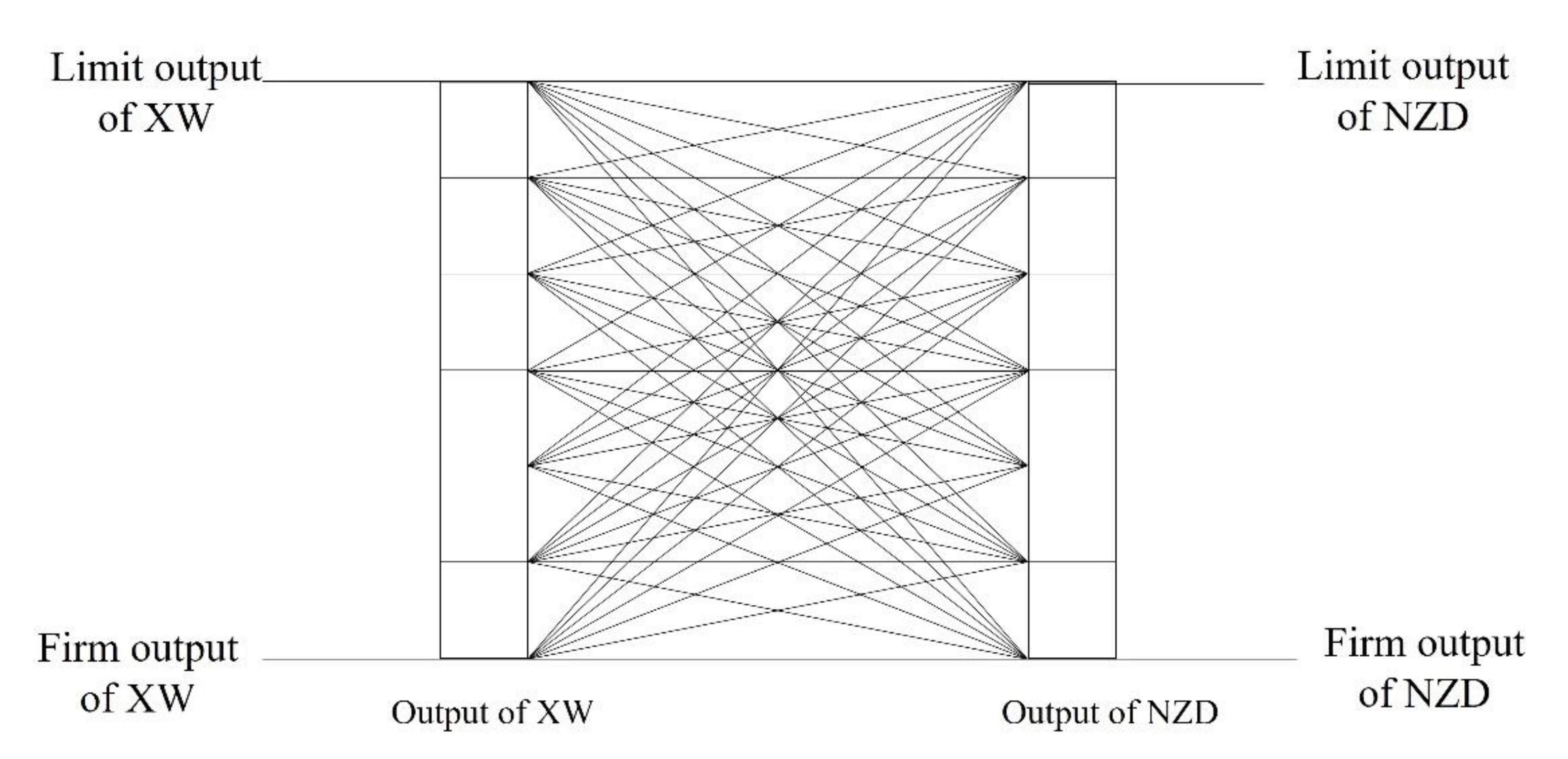
3.2. Optimization of Maximum Power Generation under Water Supplement Constraints
- (1)
- Objective function
- (2)
- Decision variables
- (3)
- Constraints
- ①
- Water balance constraints
- ②
- Water storage constraints
- ③
- Hydropower station output constraints
- ④
- Flow constraints
- (4)
- Optimization method details
4. Application Results and Analysis
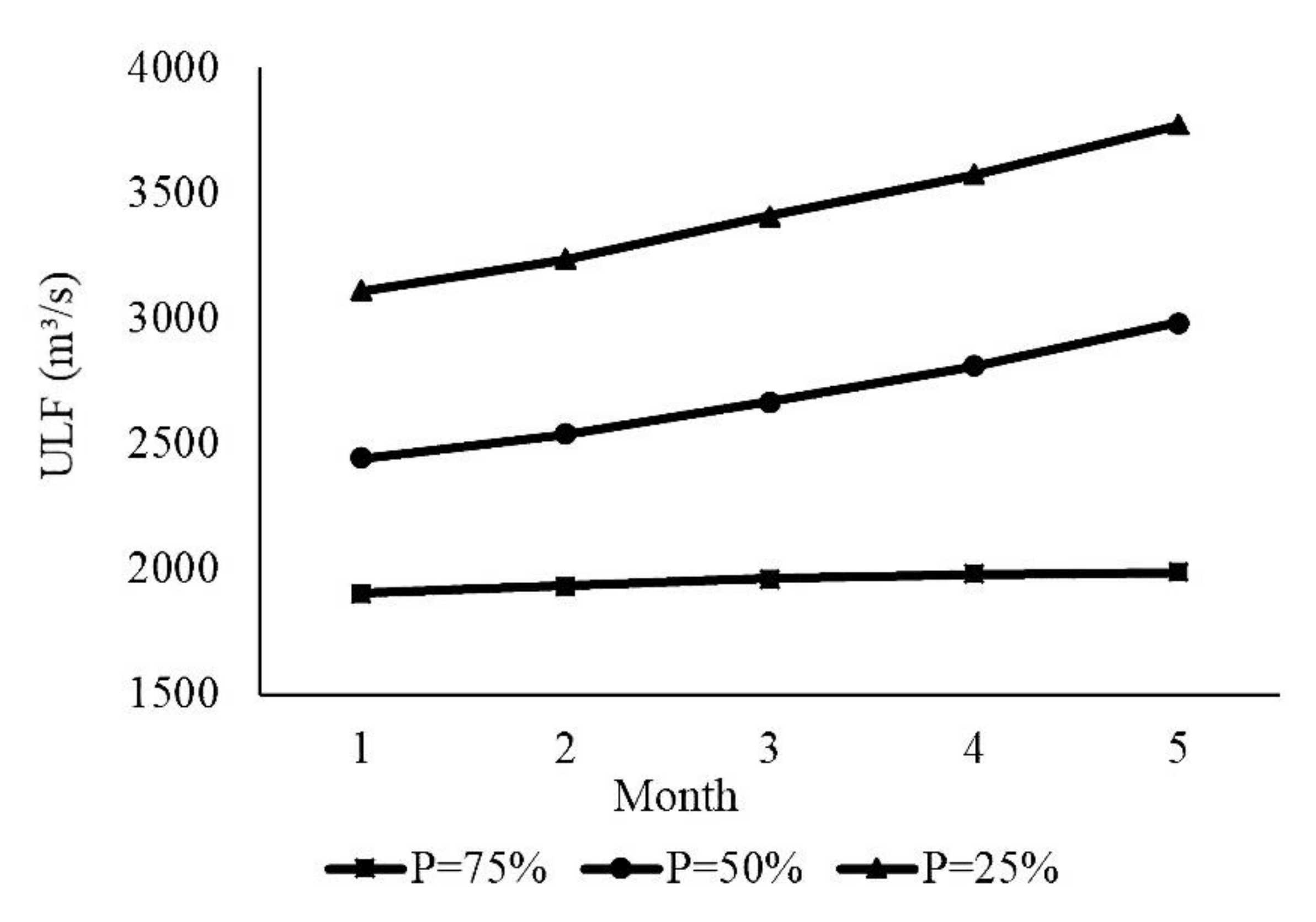
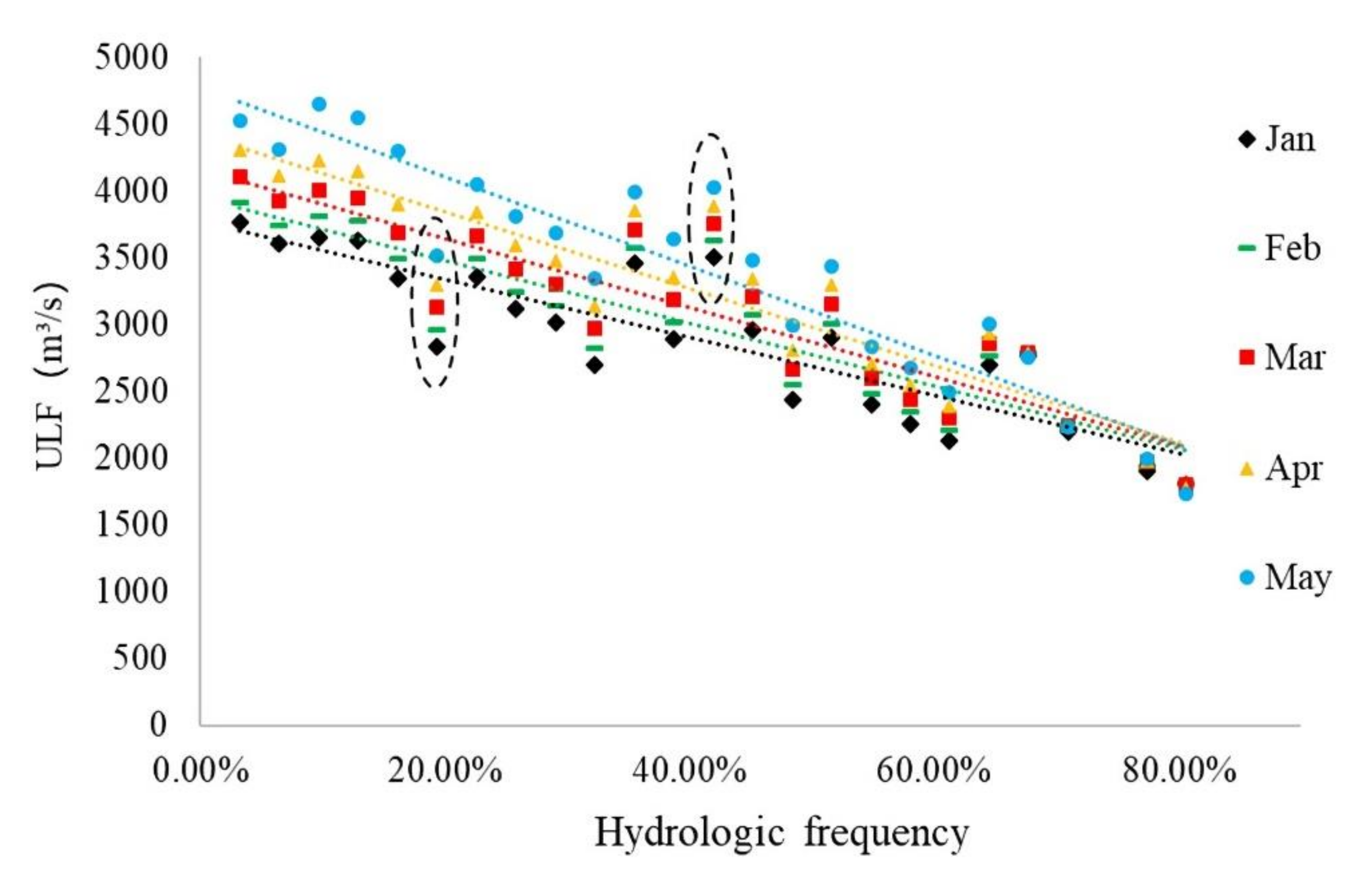
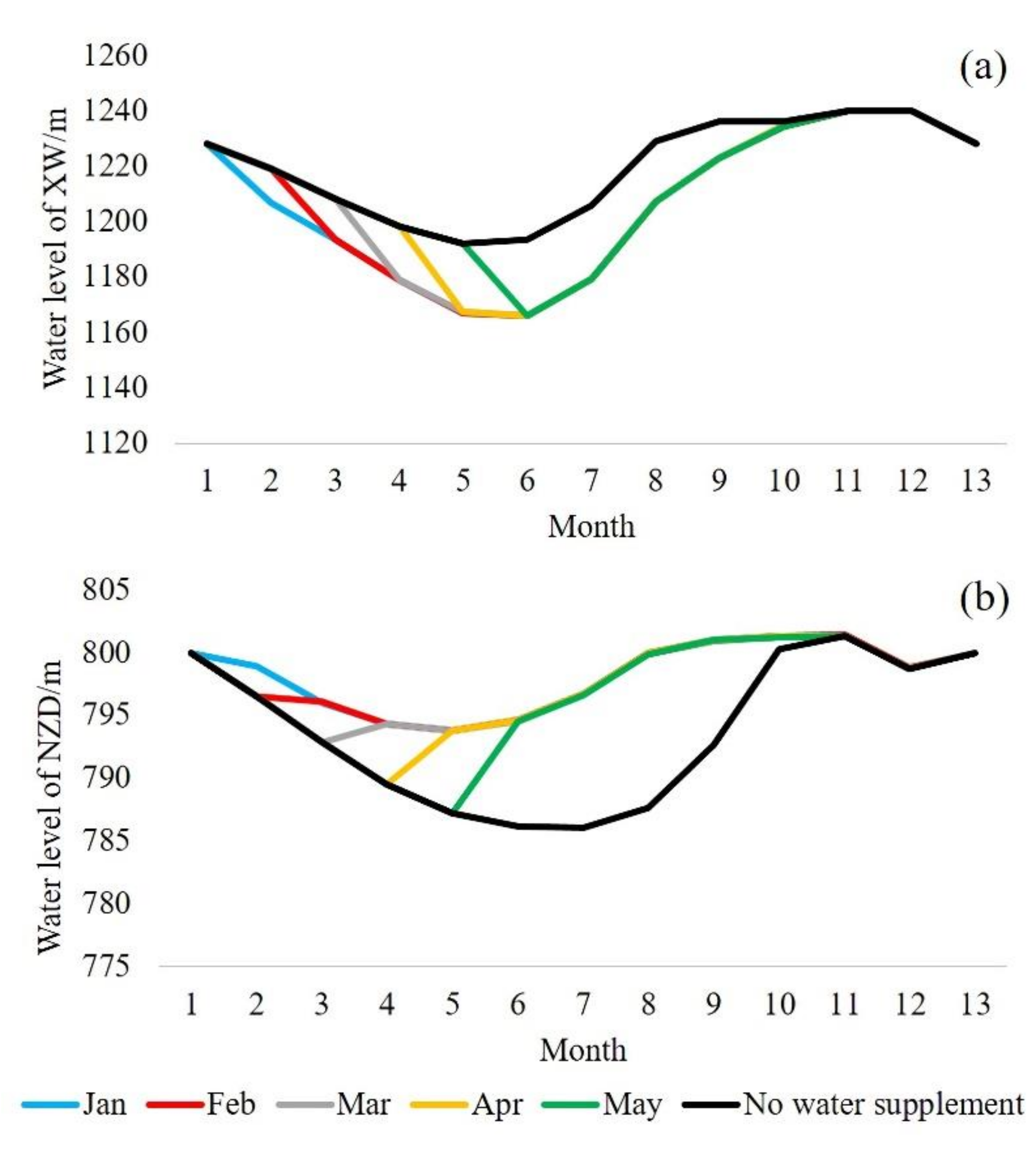
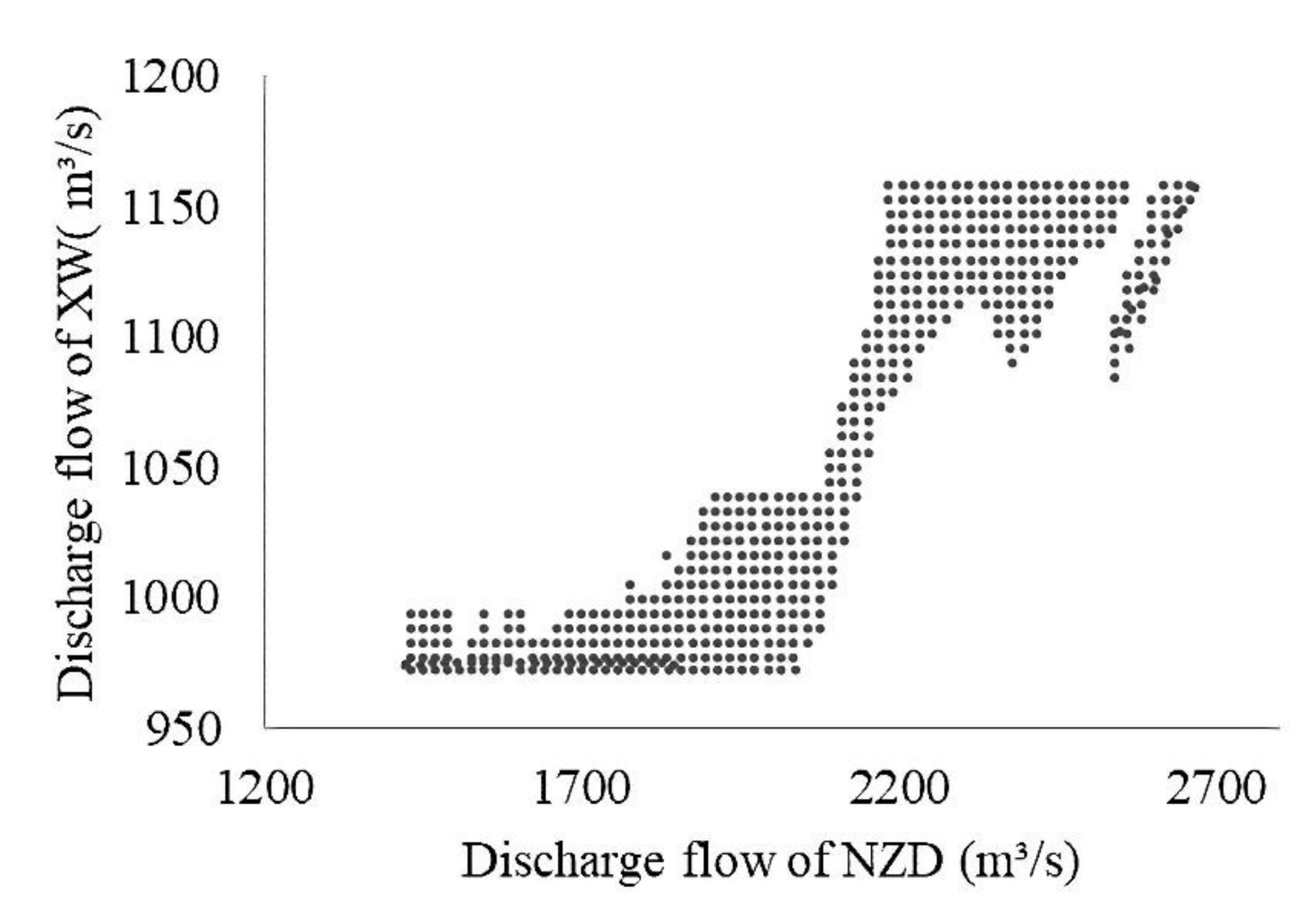
4.1. Limit State of Water Supplement
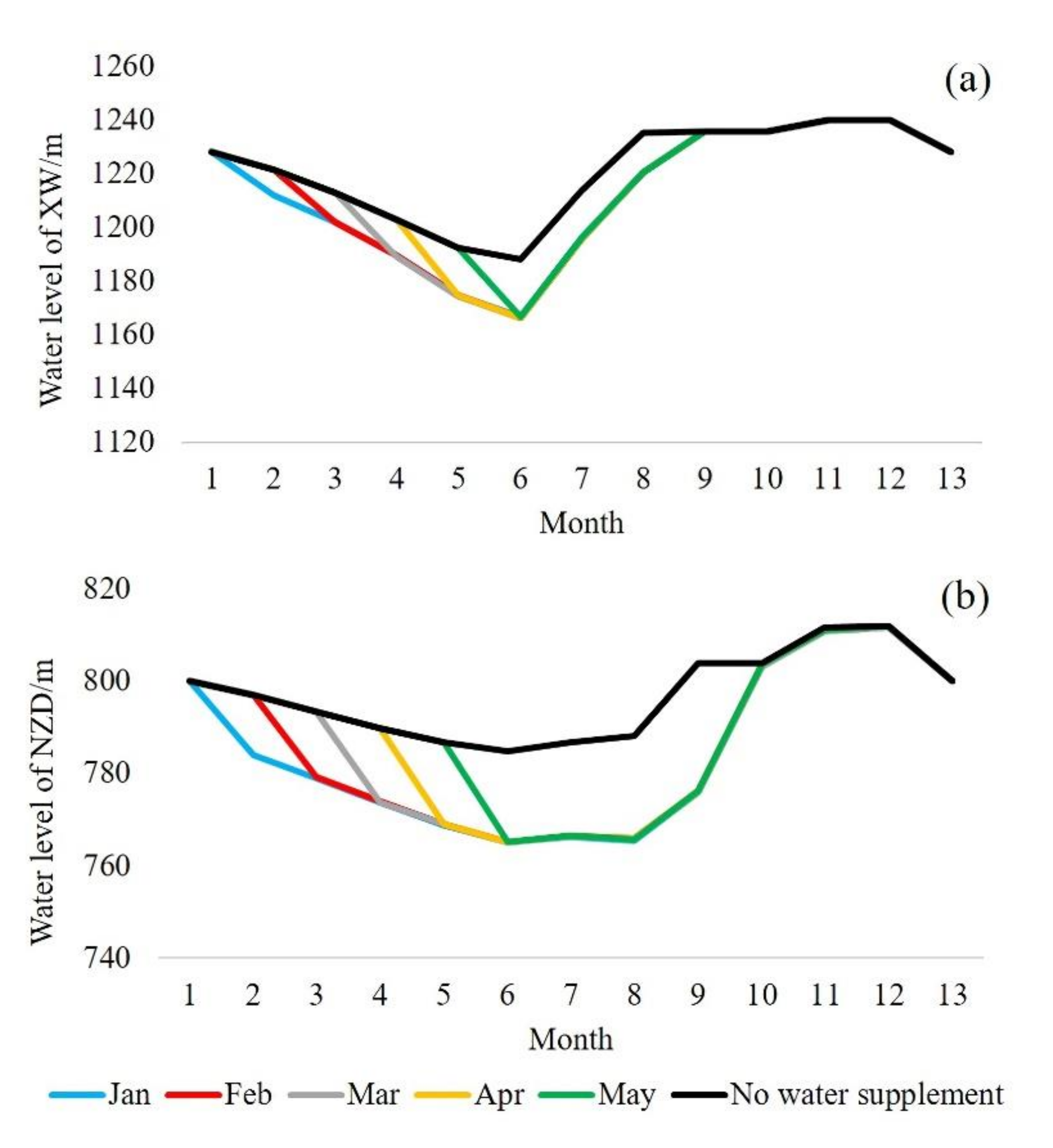
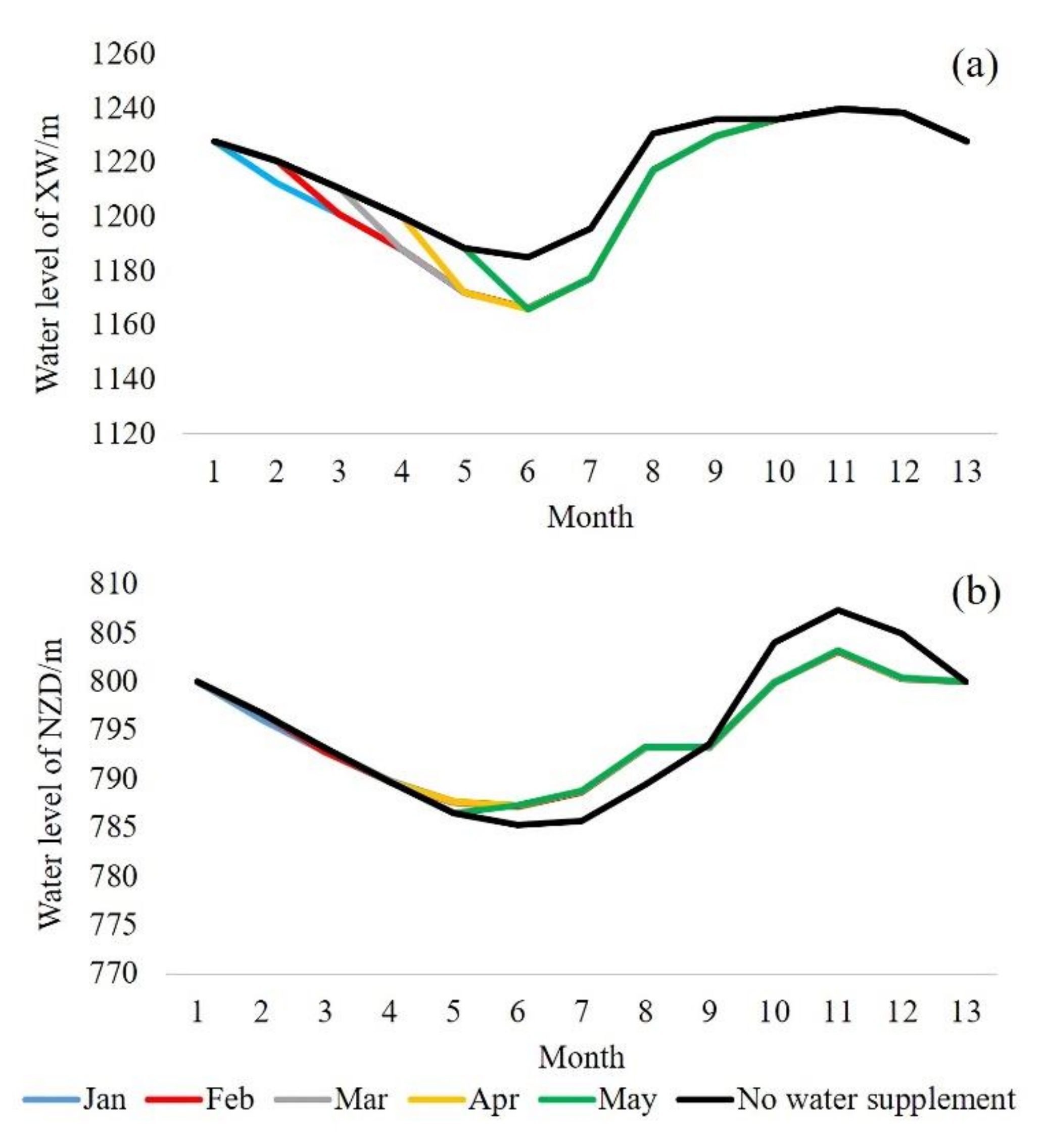
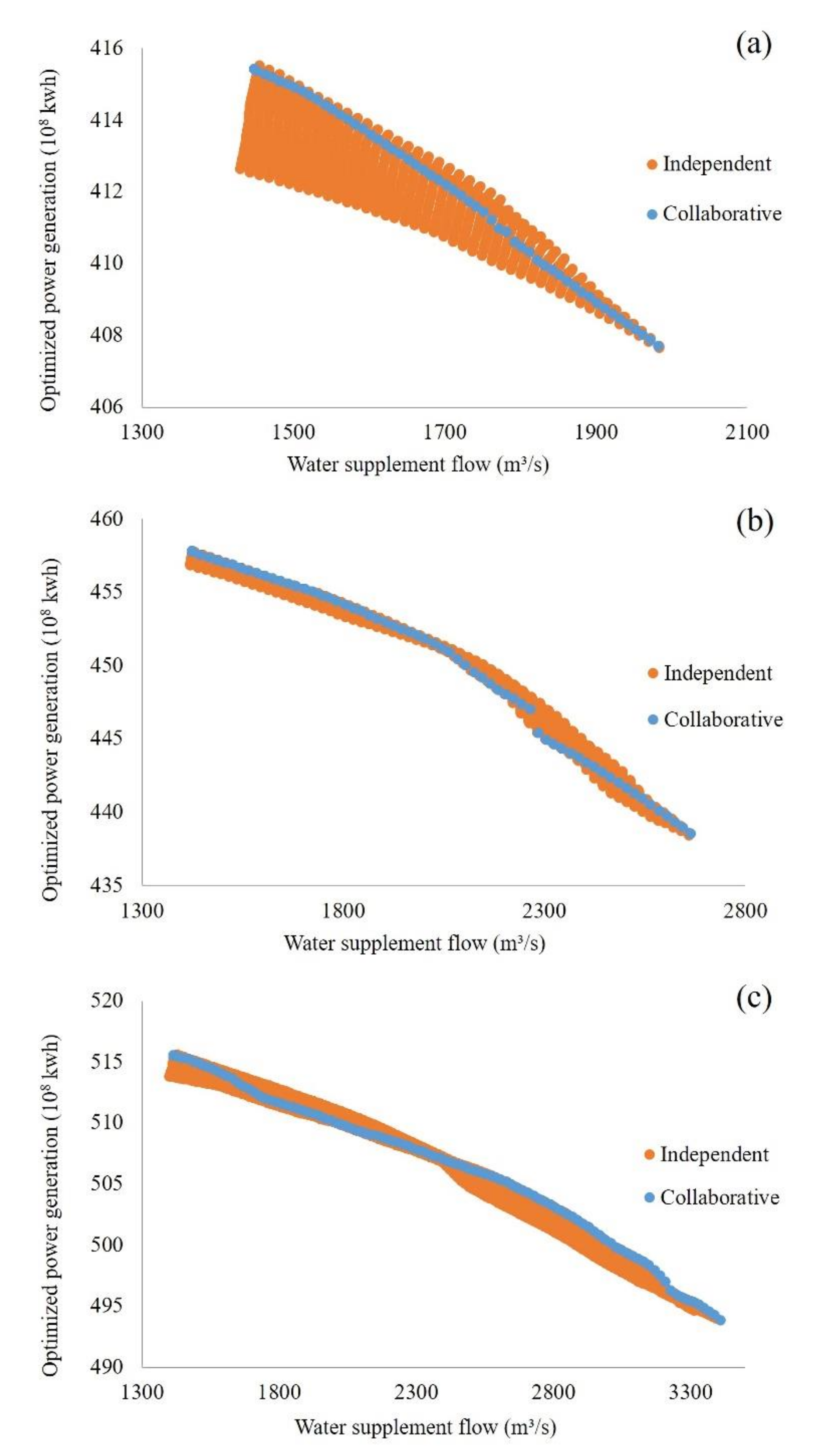
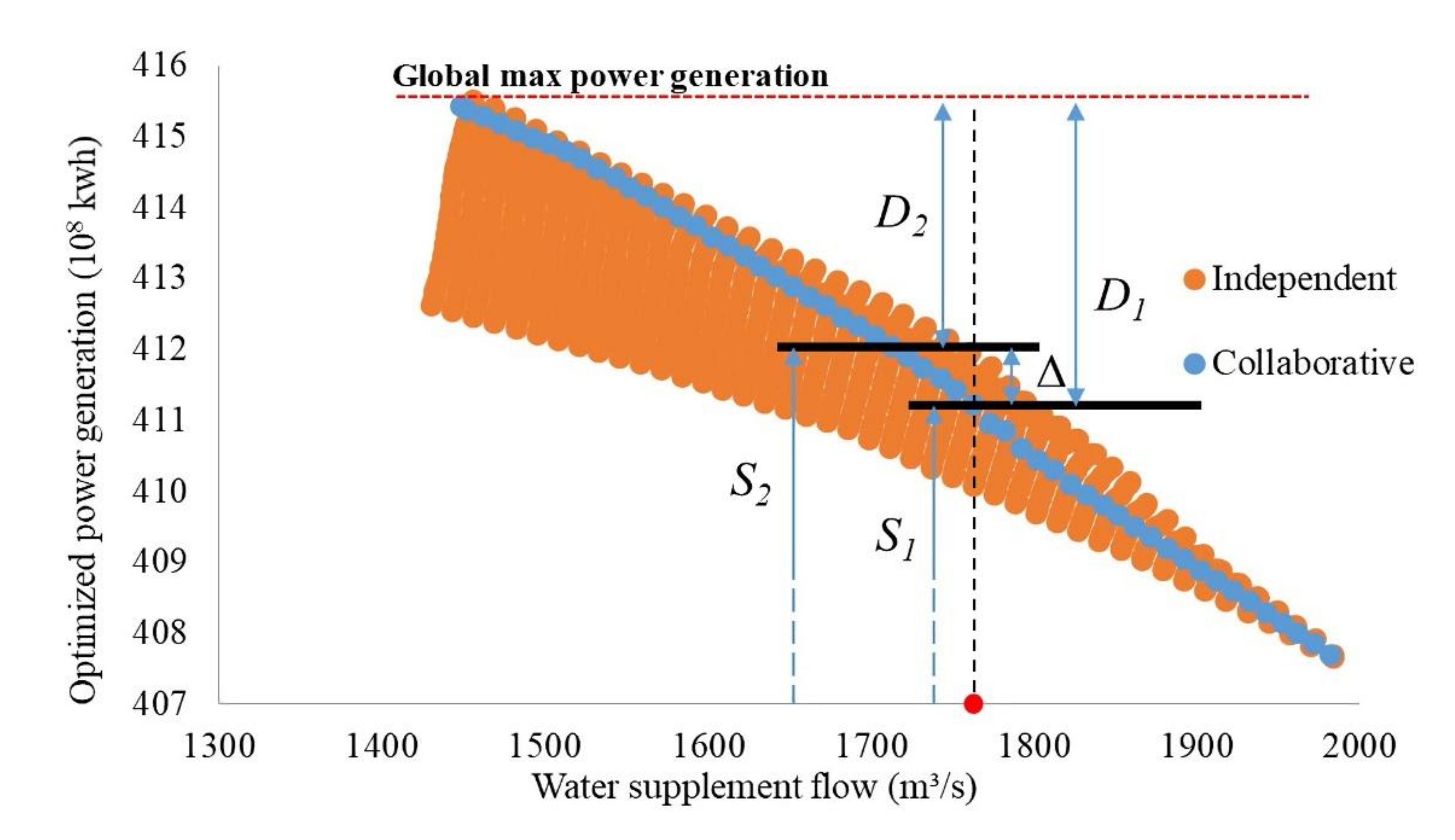
4.2. Effect Evaluation of “Collaborative Independent” Joint Optimization Method
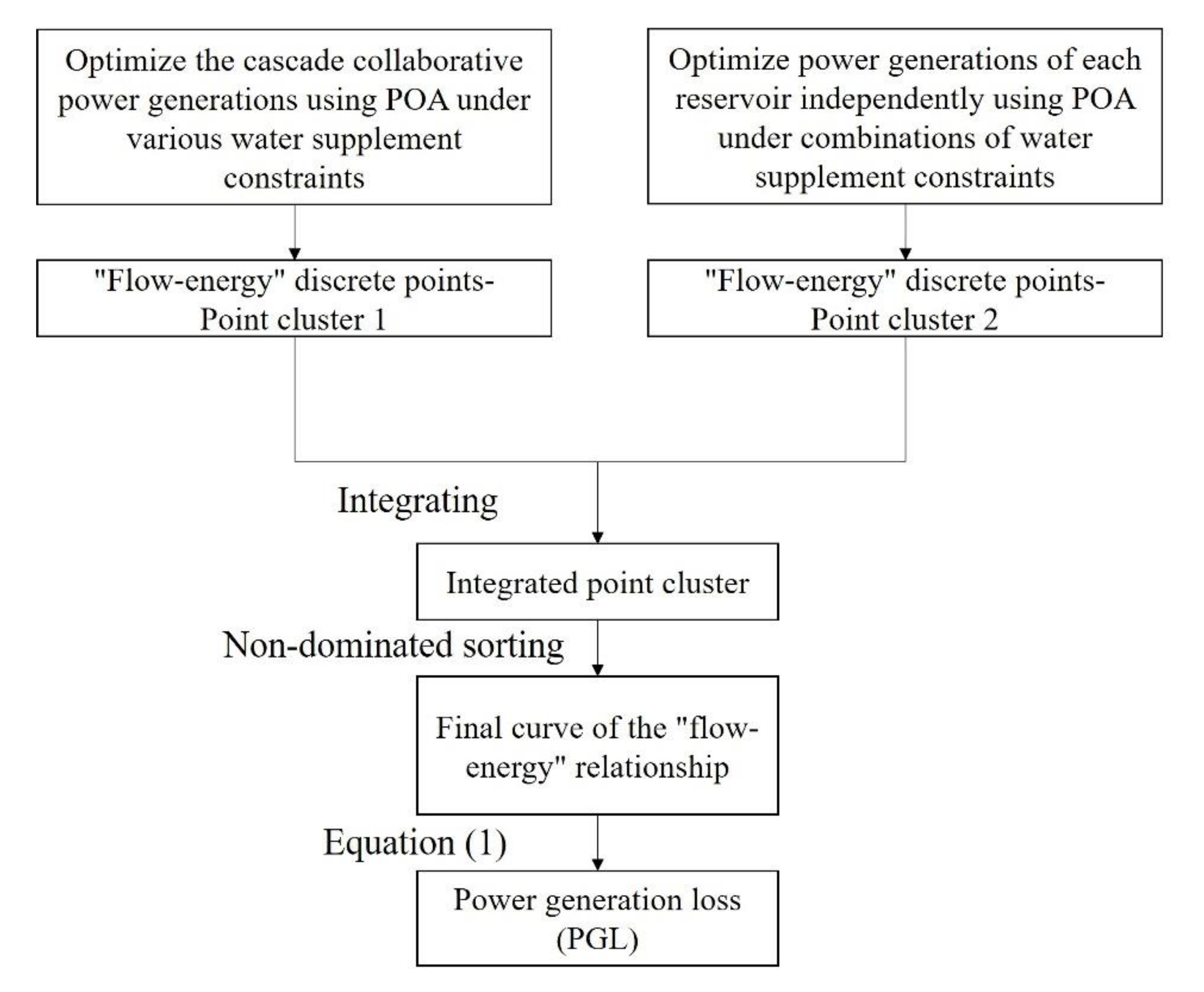
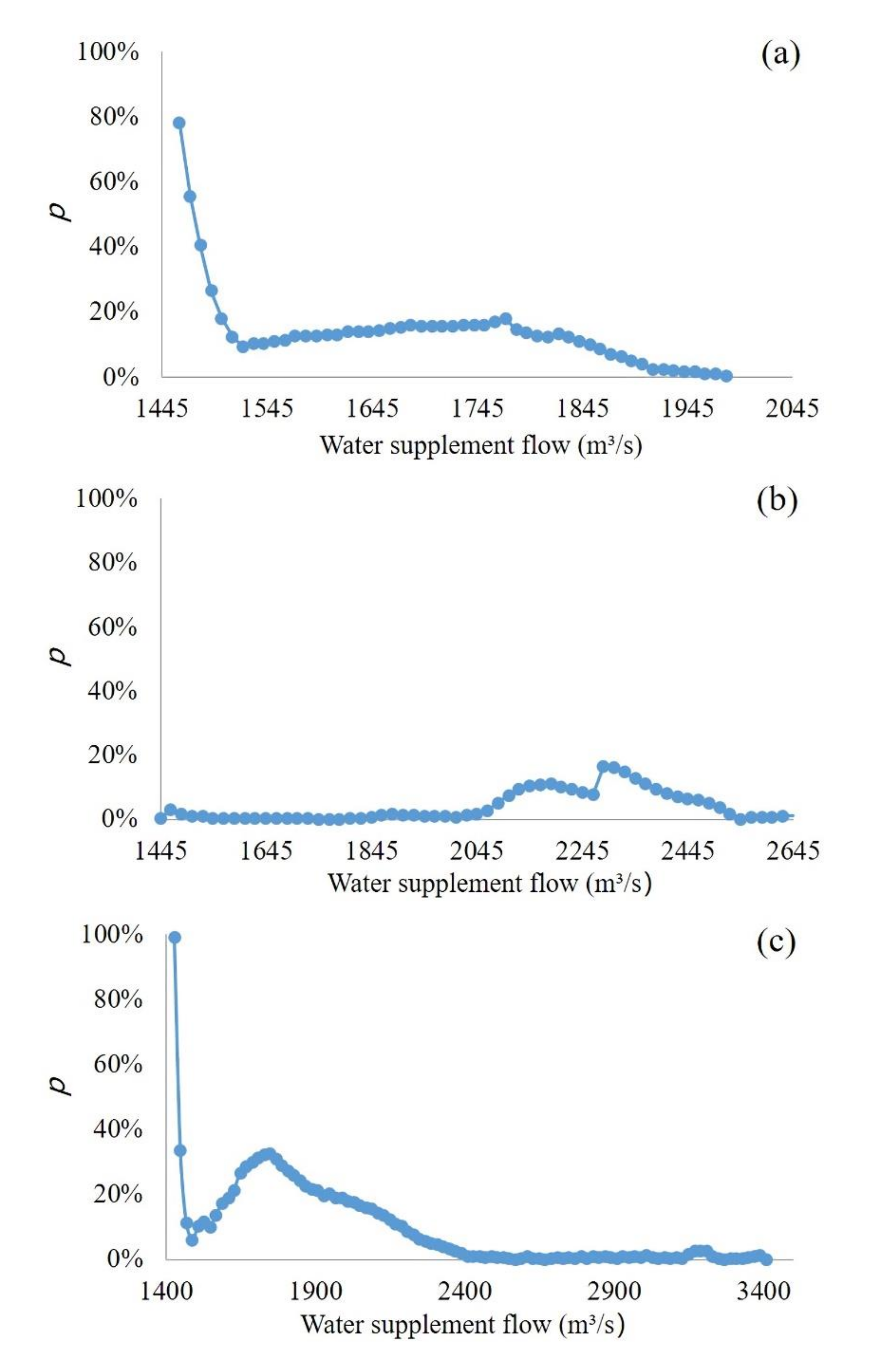
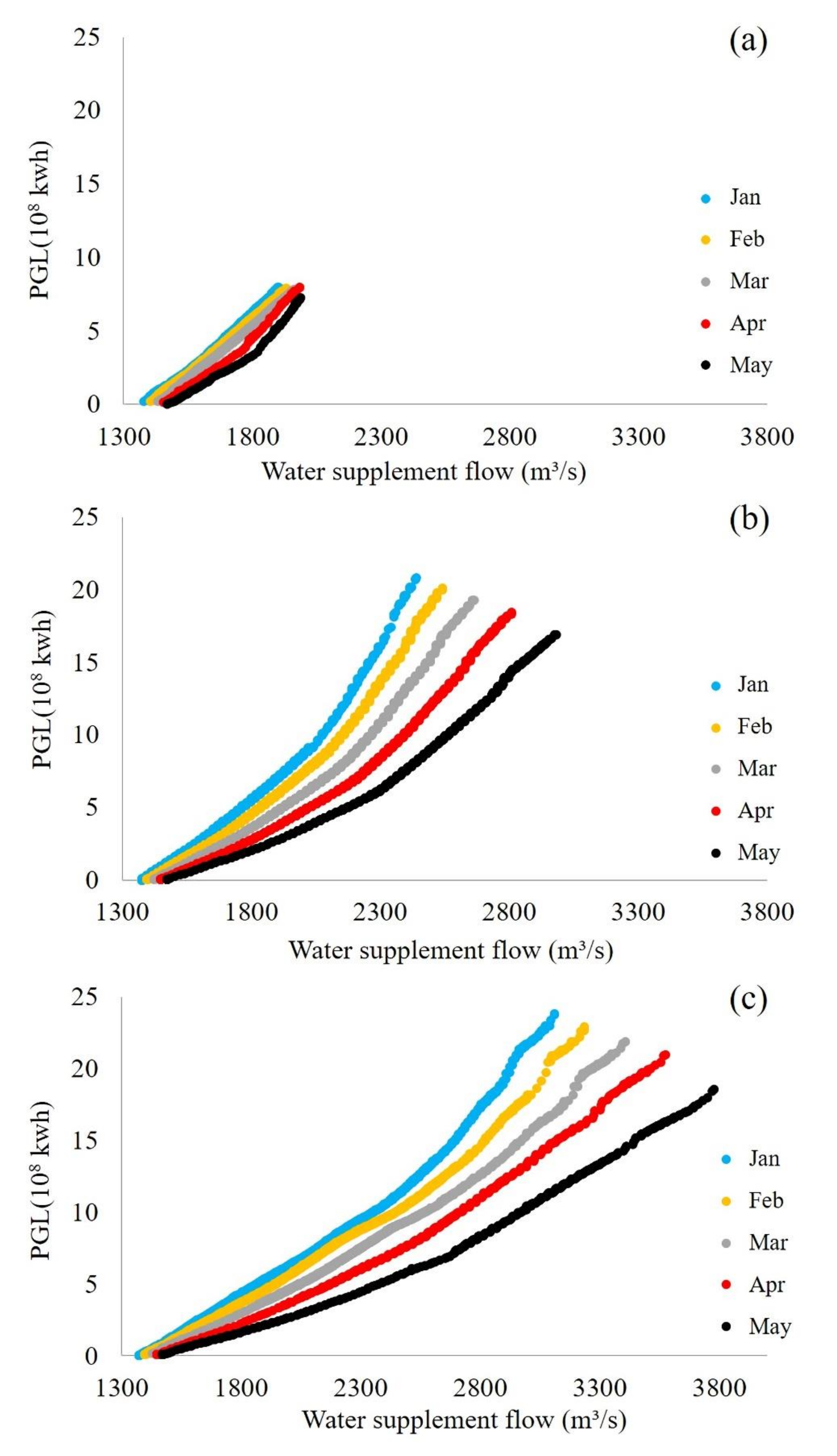
4.3. Power Generation Loss (PGL) of Water Supplement
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ohlsson, L. Water conflicts and social resource scarcity. Phys. Chem. Earth Part B 2000, 25, 213–220. [Google Scholar] [CrossRef]
- Dinar, S. Scarcity and Cooperation along International Rivers. Glob. Environ. Politi. 2009, 9, 109–135. [Google Scholar] [CrossRef]
- Dinar, S.; Katz, D.; De Stefano, L.; Blankespoor, B. Do treaties matter? Climate change, water variability, and cooperation along transboundary river basins. Political Geogr. 2019, 69, 162–172. [Google Scholar] [CrossRef]
- Dinar, S. Water, Security, Conflict, and Cooperation. SAIS Rev. 2002, 22, 229–253. [Google Scholar] [CrossRef]
- Grey, D.; Sadoff, C. Beyond the river: The benefits of cooperation on international rivers. Water Sci. Technol. 2003, 47, 91–96. [Google Scholar] [CrossRef]
- Huang, Z.; Liu, X.; Sun, S.; Tang, Y.; Yuan, X.; Tang, Q. Global assessment of future sectoral water scarcity under adaptive inner-basin water allocation measures. Sci. Total Environ. 2021, 783, 146973. [Google Scholar] [CrossRef]
- Veilleux, J.; Dinar, S. A geospatial analysis of water-related risk to international security: An assessment of five countries. Geojournal 2021, 86, 185–238. [Google Scholar] [CrossRef]
- Delbourg, E.; Dinar, S. The globalization of virtual water flows: Explaining trade patterns of a scarce resource. World Dev. 2020, 131, 104917. [Google Scholar] [CrossRef]
- Xia, Q.; Qian, C.; Du, D.; Zhang, Y. Conflict or cooperation? How does precipitation change affect transboundary hydropolitics? J. Water Clim. Chang. 2021, 12, 1930–1943. [Google Scholar] [CrossRef]
- Dinar, A.; Dinar, S.; McCaffrey, S.; McKinney, D. Bridges over Water: Understanding Transboundary Water Conflict, Negotiation and Cooperation. World Scientific Series on Energy and Resource Economics; World Scientific Publishing: Singapore, 2007; Volume 3. [Google Scholar]
- Dinar, S.; Dinar, A.; Kurukulasuriya, P. Scarcity and Cooperation along International Rivers: An Empirical Assessment of Bilateral Treaties1. Int. Stud. Q. 2011, 55, 809–833. [Google Scholar] [CrossRef]
- Wolf, A.T. Shared Waters: Conflict and Cooperation. Annu. Rev. Environ. Resour. 2007, 32, 241–269. [Google Scholar] [CrossRef] [Green Version]
- MRC (Mekong River Commission). Mekong River Commission, China Discuss Joint Study. 2016. Available online: http://www.mrcmekong.org/news-and-events/events/mekong-river-commission-china-discuss-joint-study/ (accessed on 12 August 2021).
- Yu, Y.; Zhao, J.; Li, D.; Wang, Z. Effects of hydrologic conditions and reservoir operation on transboundary coop-eration in the Lancang–Mekong River Basin. J. Water Resour. Plan. Manag. 2019, 145, 04019020. [Google Scholar] [CrossRef]
- Li, D.; Zhao, J.; Govindaraju, R.S. Water benefits sharing under transboundary cooperation in the Lancang-Mekong River Basin. J. Hydrol. 2019, 577, 123989. [Google Scholar] [CrossRef]
- Wheeler, K.G.; Hall, J.W.; Abdo, G.M.; Dadson, S.J.; Kasprzyk, J.R.; Smith, R.; Zagona, E.A. Exploring Cooperative Transboundary River Management Strategies for the Eastern Nile Basin. Water Resour. Res. 2018, 54, 9224–9254. [Google Scholar] [CrossRef]
- Alemu. Dinar The Process of Negotiation Over International Water Disputes:The Case of the Nile Basin. Int. Negot. 2000, 5, 331–356. [Google Scholar] [CrossRef]
- Li, D.; Long, D.; Zhao, J.; Lu, H.; Hong, Y. Observed changes in flow regimes in the Mekong River basin. J. Hydrol. 2017, 551, 217–232. [Google Scholar] [CrossRef]
- Lund, J.R.; Guzman, J. Derived Operating Rules for Reservoirs in Series or in Parallel. J. Water Resour. Plan. Manag. 1999, 125, 143–153. [Google Scholar] [CrossRef] [Green Version]
- Tao, F.; Jing, G.; Kong, K.; Yue, X.; Xiao, Z. Primary analysis of the loss of Longyangxia power station in abnormal water dispatch. J. Northwest Hydroelectr. Power 2019, 20, 5–8. (In Chinese) [Google Scholar]
- Bellman, R.E.; Dreyfus, S.E. Applied Dynamic Programming; Princeton University Press: Princeton, NJ, USA, 1962. [Google Scholar]
- Heidari, M.; Chow, V.T.; Kokotović, P.V.; Meredith, D.D. Discrete Differential Dynamic Programing Approach to Water Resources Systems Optimization. Water Resour. Res. 1971, 7, 273–282. [Google Scholar] [CrossRef]
- Howson, H.R.; Sancho, N.G.F. A new algorithm for the solution of multi-state dynamic programming problems. Math. Program. 1975, 8, 104–116. [Google Scholar] [CrossRef]
- Turgeon, A. Optimal short-term hydro scheduling from the principle of progressive optimality. Water Resour. Res. 1981, 17, 481–486. [Google Scholar] [CrossRef]
- Larson, R.E.; Korsak, A.J. A new algorithm for the solution of multi-state dynamic programming problems. Auto-Matica 1970, 6, 245–260. [Google Scholar]
- Yang, K.; Feng, J.; Lu, G. Study on convergence of the progressive optimality algorithm in reservoir operation. J. Hohai Univ. 1996, 24, 104–107. (In Chinese) [Google Scholar]
- MRC (Mekong River Commission). State of the Basin Report; MRC: Vientiane, Laos, 2010. [Google Scholar]
- Johnston, R.; Kummu, M. Water resource models in the Mekong Basin: A review. Water Resour. Manag. 2012, 26, 429–455. [Google Scholar] [CrossRef]
- Li, S.; Bush, R.T. Rising flux of nutrients (C, N, P and Si) in the lower Mekong River. J. Hydrol. 2015, 530, 447–461. [Google Scholar] [CrossRef]
- Zeng, Y.; Wu, X.; Cheng, C.; Wang, Y. Chance-Constrained Optimal Hedging Rules for Cascaded Hydropower Reservoirs. J. Water Resour. Plan. Manag. 2014, 140, 04014010. [Google Scholar] [CrossRef]
- Tilt, B.; Gerkey, D. Dams and population displacement on China’s Upper Mekong River: Implications for social capital and social–ecological resilience. Glob. Environ. Chang. 2016, 36, 153–162. [Google Scholar] [CrossRef] [Green Version]
- Chen, X.; Xu, B.; Zheng, Y.; Zhang, C. Nexus of water, energy and ecosystems in the upper Mekong River: A system analysis of phosphorus transport through cascade reservoirs. Sci. Total Environ. 2019, 671, 1179–1191. [Google Scholar] [CrossRef]
- Deng, J.; Li, Y.; Xu, B.; Ding, W.; Zhou, H.; Schmidt, A. Ecological optimal operation of hydropower stations to max-imize total phosphorus export. J. Water Resour. Plan. Manag. 2020, 146, 04020075. [Google Scholar] [CrossRef]
- Srinivas, N.; Deb, K. Multiobjective optimization using nondominated sorting in genetic algorithms. Evol. Comput. 1994, 2, 221–248. [Google Scholar] [CrossRef]
| Term | Explanation |
|---|---|
| Firm power | Firm power refers to the value that the output of hydropower station, under normal operation, shall not be lower than. If the output in a certain period is lower than the firm power, it indicates that the power generation task is damaged. |
| Initial output process | Initial output process is the output process in which the ouput in each time period equals to the firm power of the corresponding hydropower station. |
| Standard operating policy (SOP) | SOP means releasing water just to the meet the output of the hydropower stations in every time period. |
| Initial water level and final water level constraints | Initial water level means the water level at the beginning of the operation period in each reservoir; and final water level means the water level at the end of the operation period in each reservoir. |
| Feasible output process | If the SOP operations of the hydropower stations can be completed under the premise of meeting all constraints, and the water level at the end of the operation period is higher than or equal to the final water level constraint, then the output process is feasible, otherwise it is not feasible. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deng, J.; Li, Y.; Ding, W.; Zhang, B.; Xu, B.; Zhou, H. Upper Limit and Power Generation Loss of Water Supplement from Cascade Hydropower Stations to Downstream under Lancang-Mekong Cooperation. Water 2021, 13, 2826. https://doi.org/10.3390/w13202826
Deng J, Li Y, Ding W, Zhang B, Xu B, Zhou H. Upper Limit and Power Generation Loss of Water Supplement from Cascade Hydropower Stations to Downstream under Lancang-Mekong Cooperation. Water. 2021; 13(20):2826. https://doi.org/10.3390/w13202826
Chicago/Turabian StyleDeng, Jiahui, Yu Li, Wei Ding, Bingyao Zhang, Bo Xu, and Huicheng Zhou. 2021. "Upper Limit and Power Generation Loss of Water Supplement from Cascade Hydropower Stations to Downstream under Lancang-Mekong Cooperation" Water 13, no. 20: 2826. https://doi.org/10.3390/w13202826
APA StyleDeng, J., Li, Y., Ding, W., Zhang, B., Xu, B., & Zhou, H. (2021). Upper Limit and Power Generation Loss of Water Supplement from Cascade Hydropower Stations to Downstream under Lancang-Mekong Cooperation. Water, 13(20), 2826. https://doi.org/10.3390/w13202826






