Predicting Dam Flood Discharge Induced Ground Vibration with Modified Frequency Response Function
Abstract
:1. Introduction
2. Background
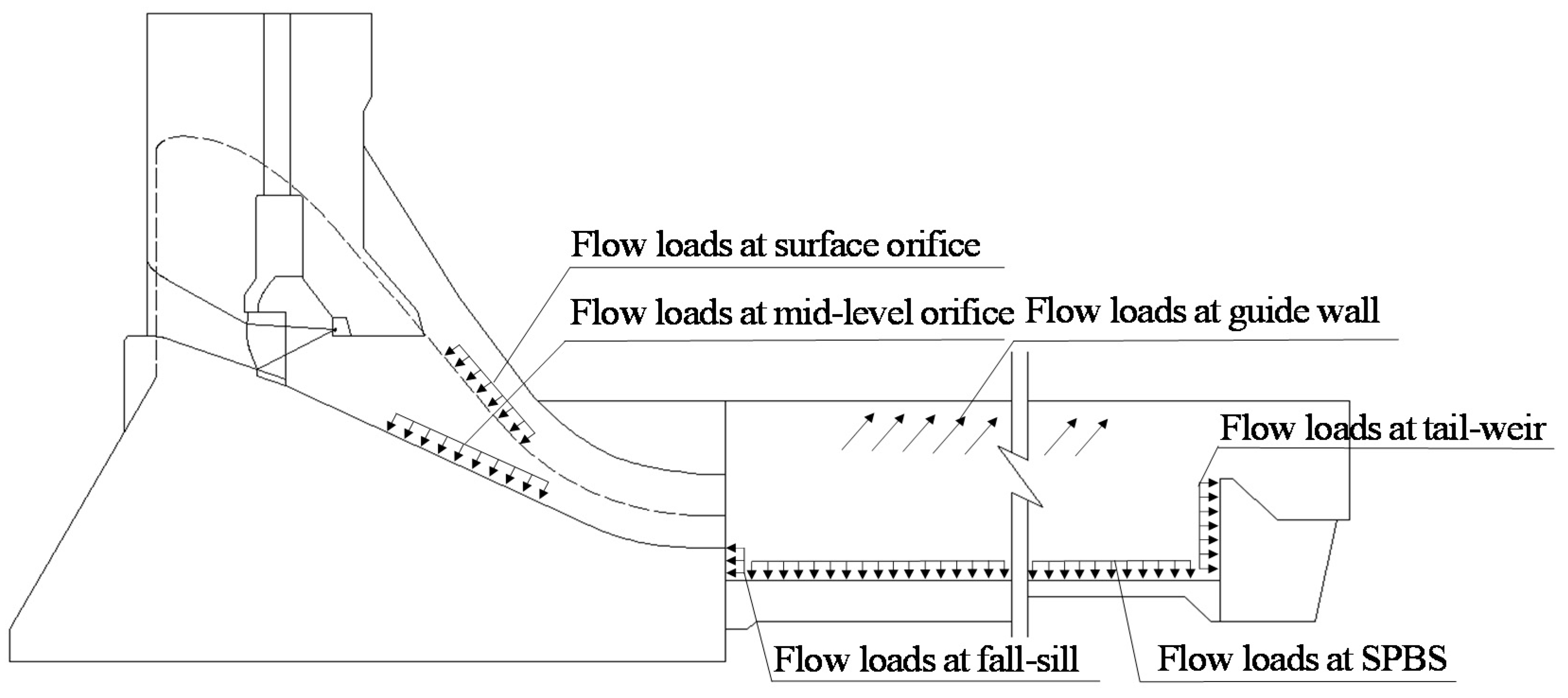
2.1. Xiangjiaba Dam and Ground Vibrations Induced by Flood Discharge
2.2. Sensors and the Signal Collection System
3. Prediction Methods with Modified FRF
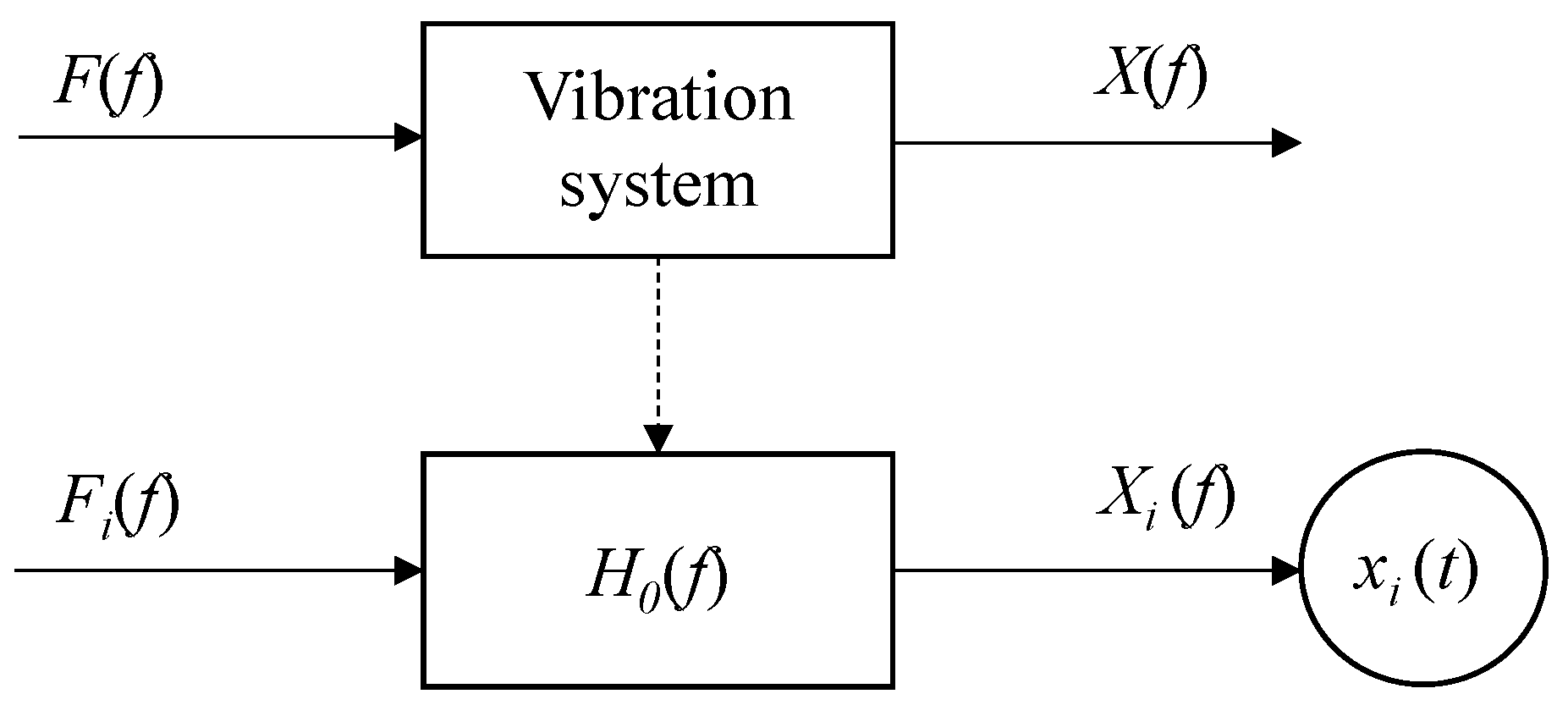
3.1. Principles of FRF
3.2. The Influencing Factors and the Multiple Averaged Power Spectrum FRF
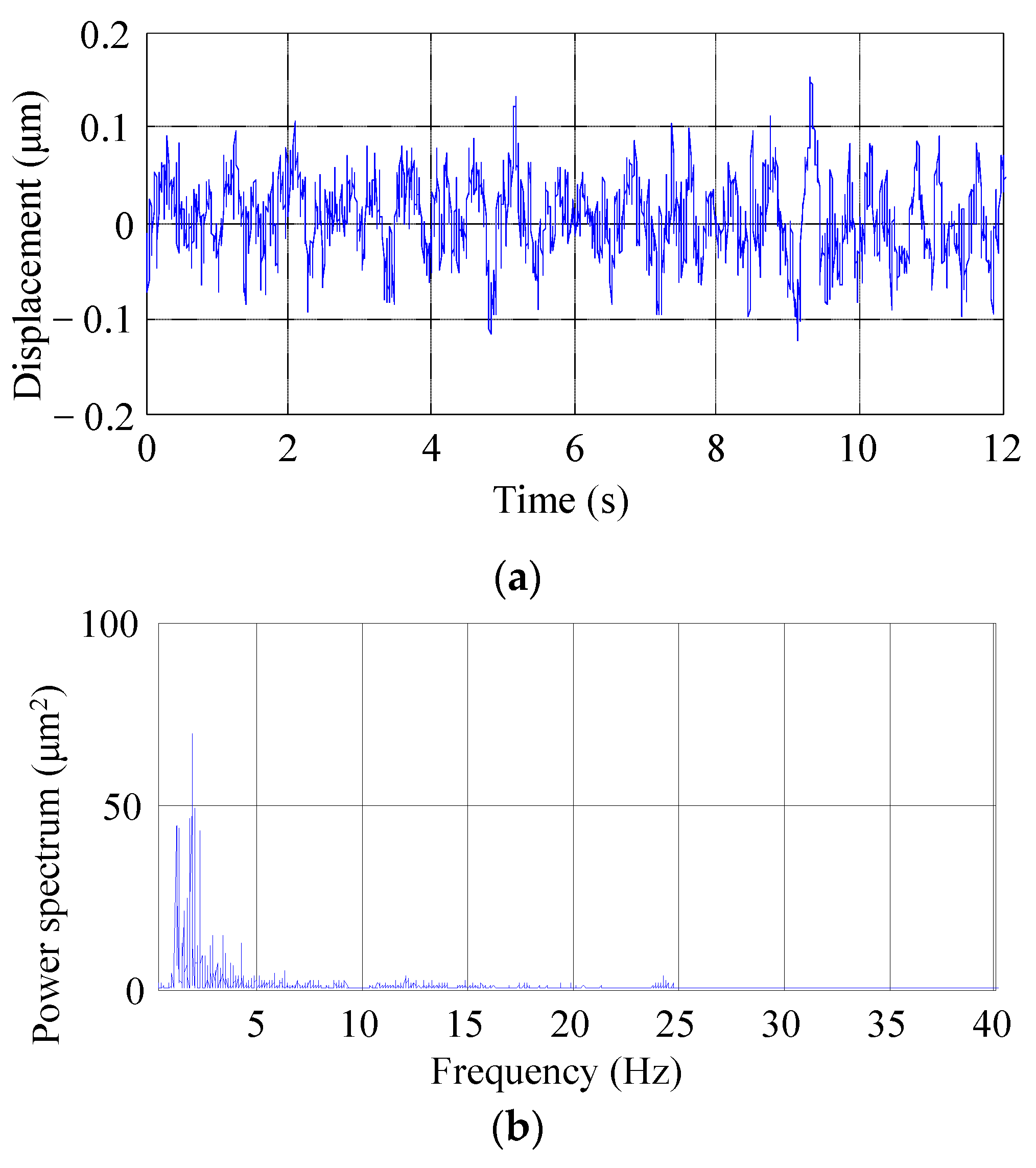
3.2.1. Influencing Factors
3.2.2. The Multiple Averaged Power Spectrum FRF
3.3. Input Comparison
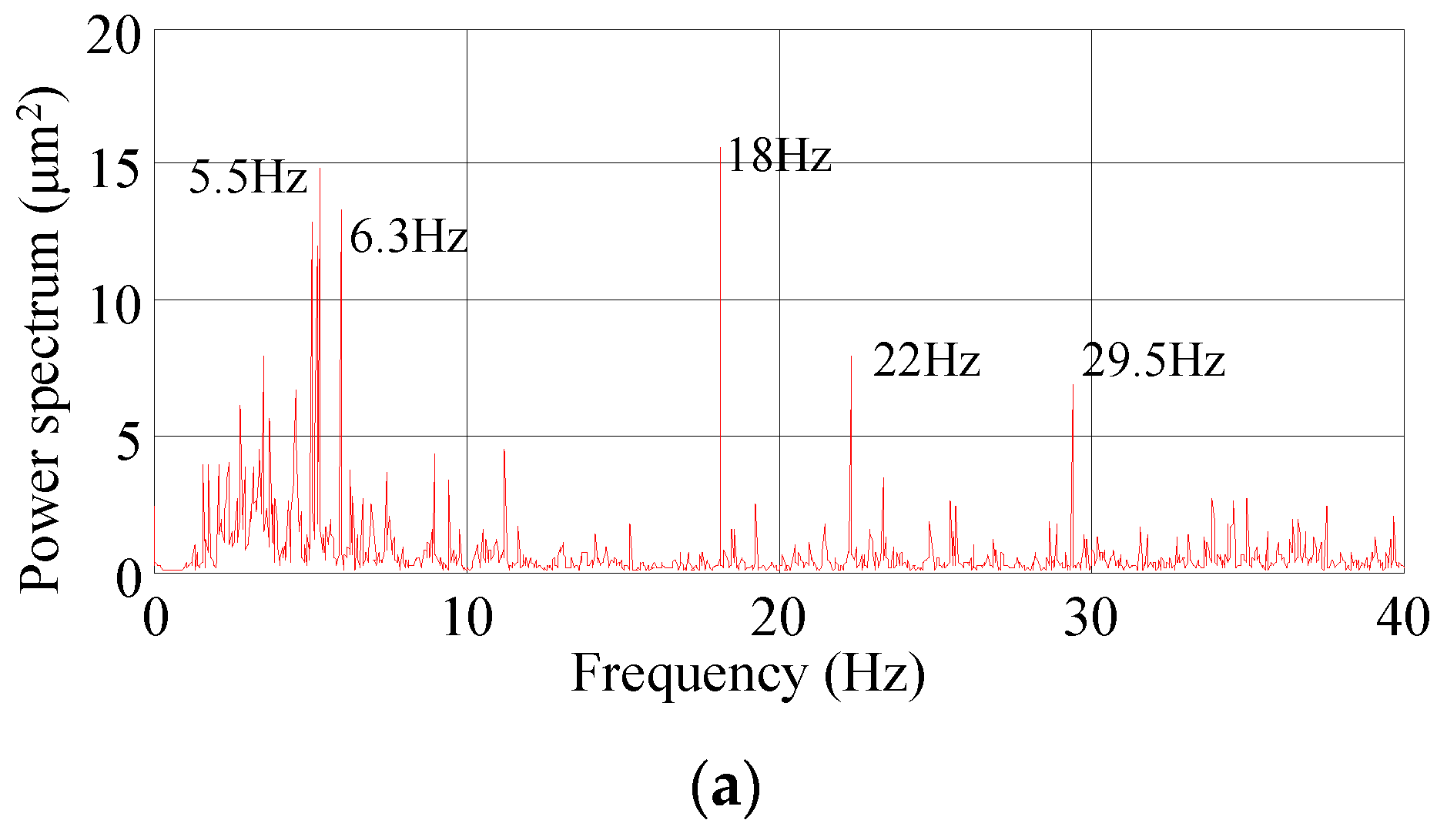
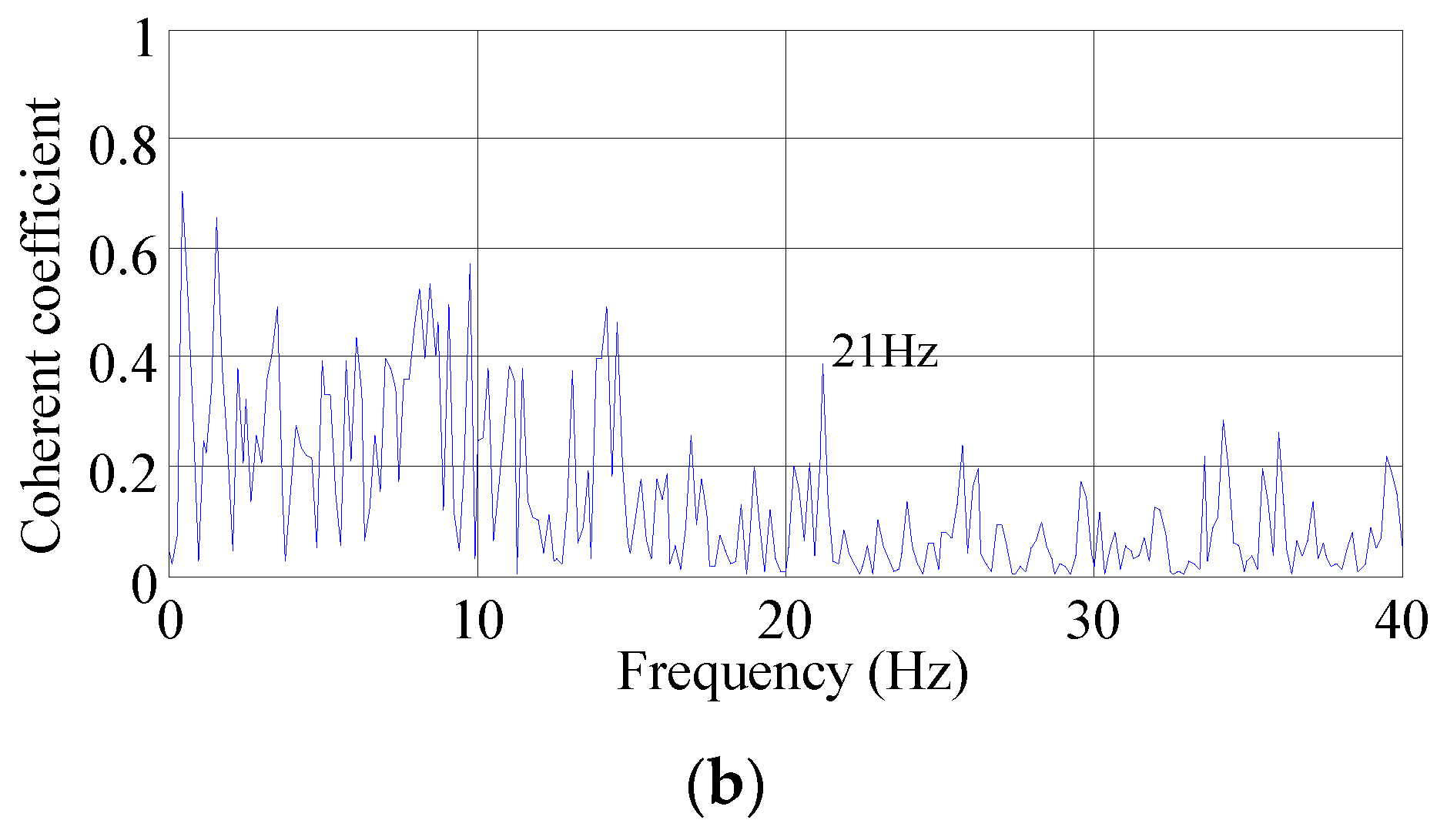
3.3.1. Multiple Vibration Sources as an Input
3.3.2. Main Vibration Source as an Input
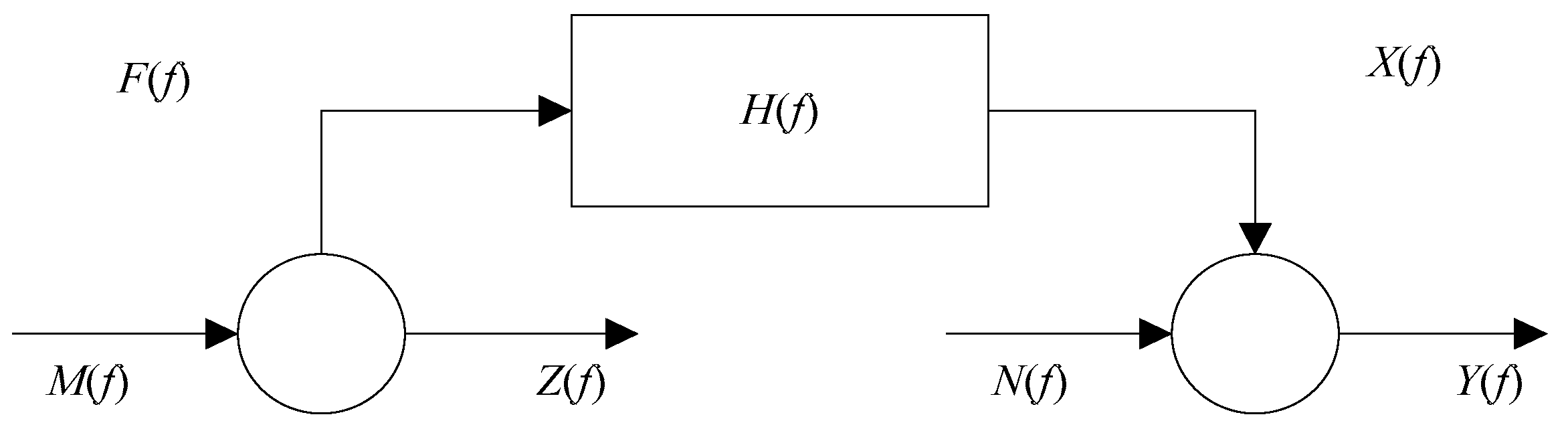
3.4. Noise Correction
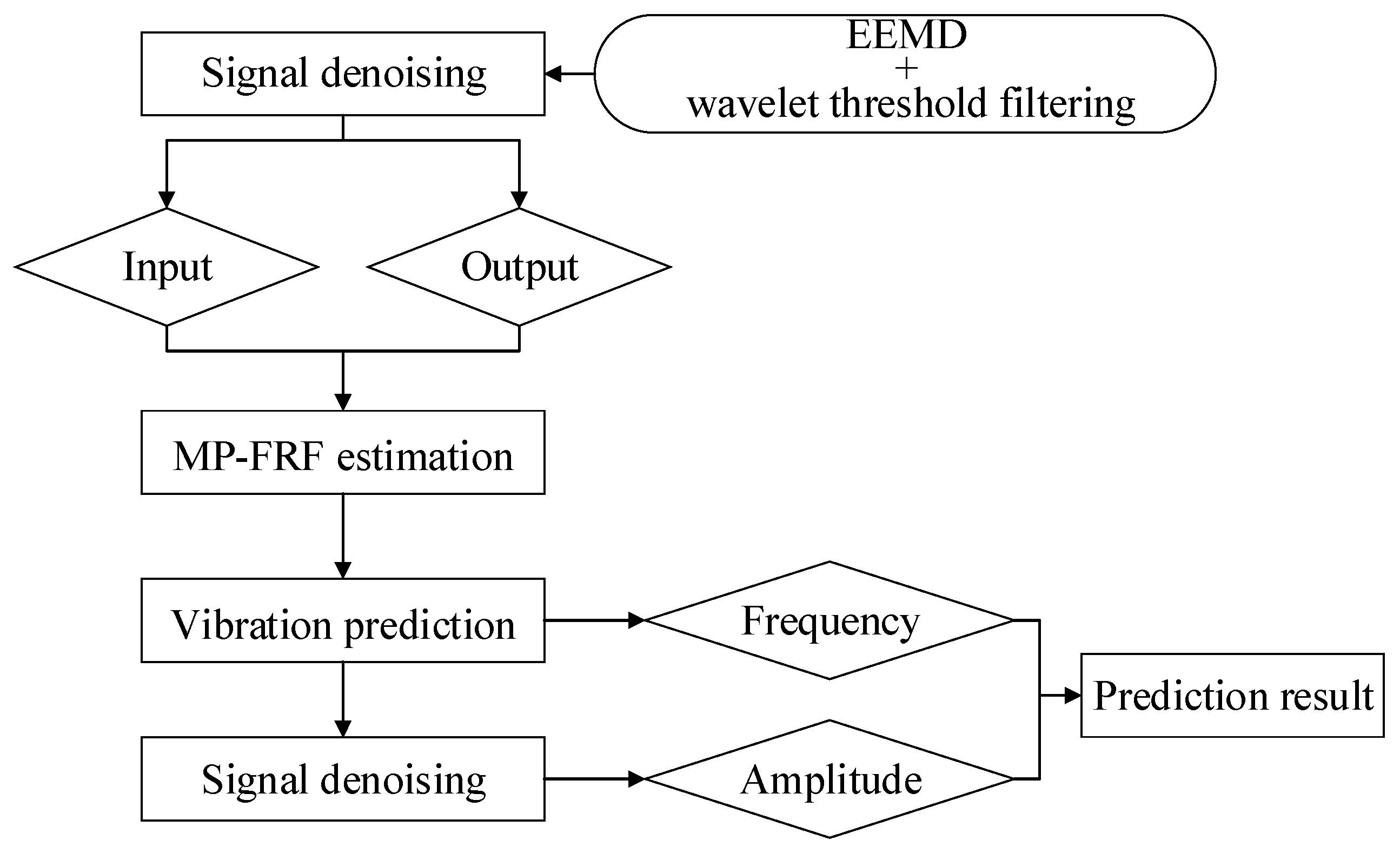
3.5. Prediction Method with Modified FRF
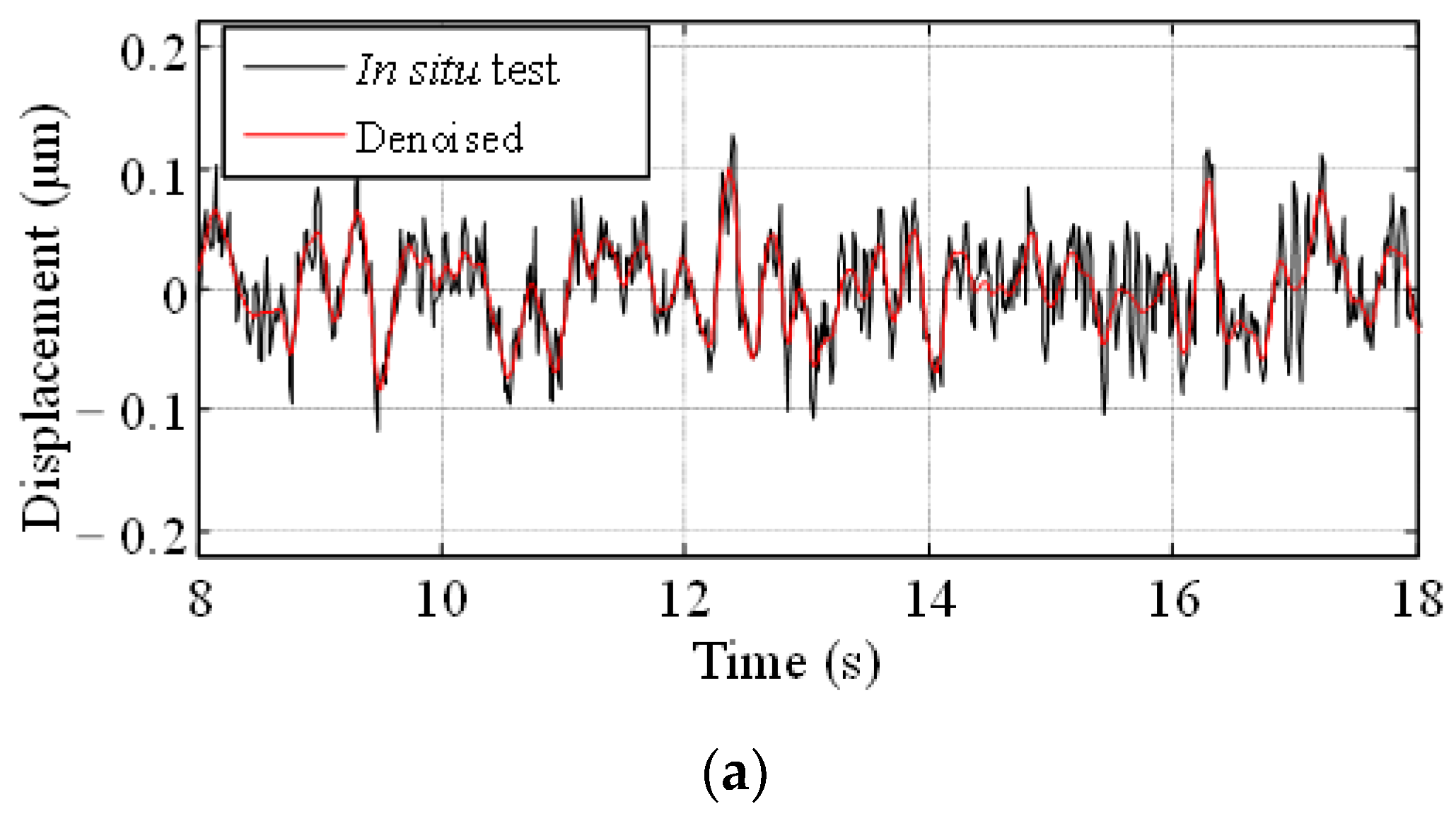
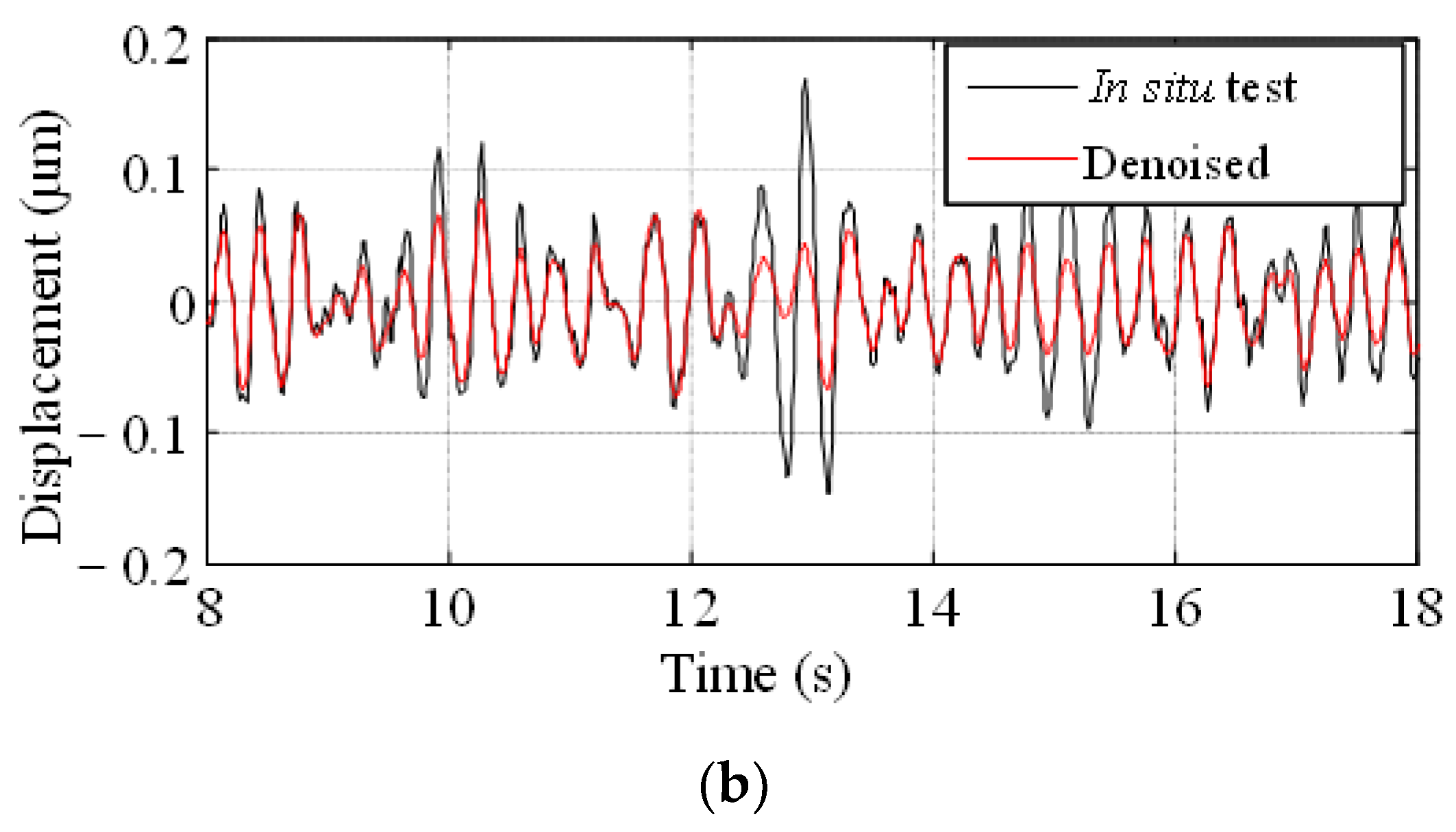
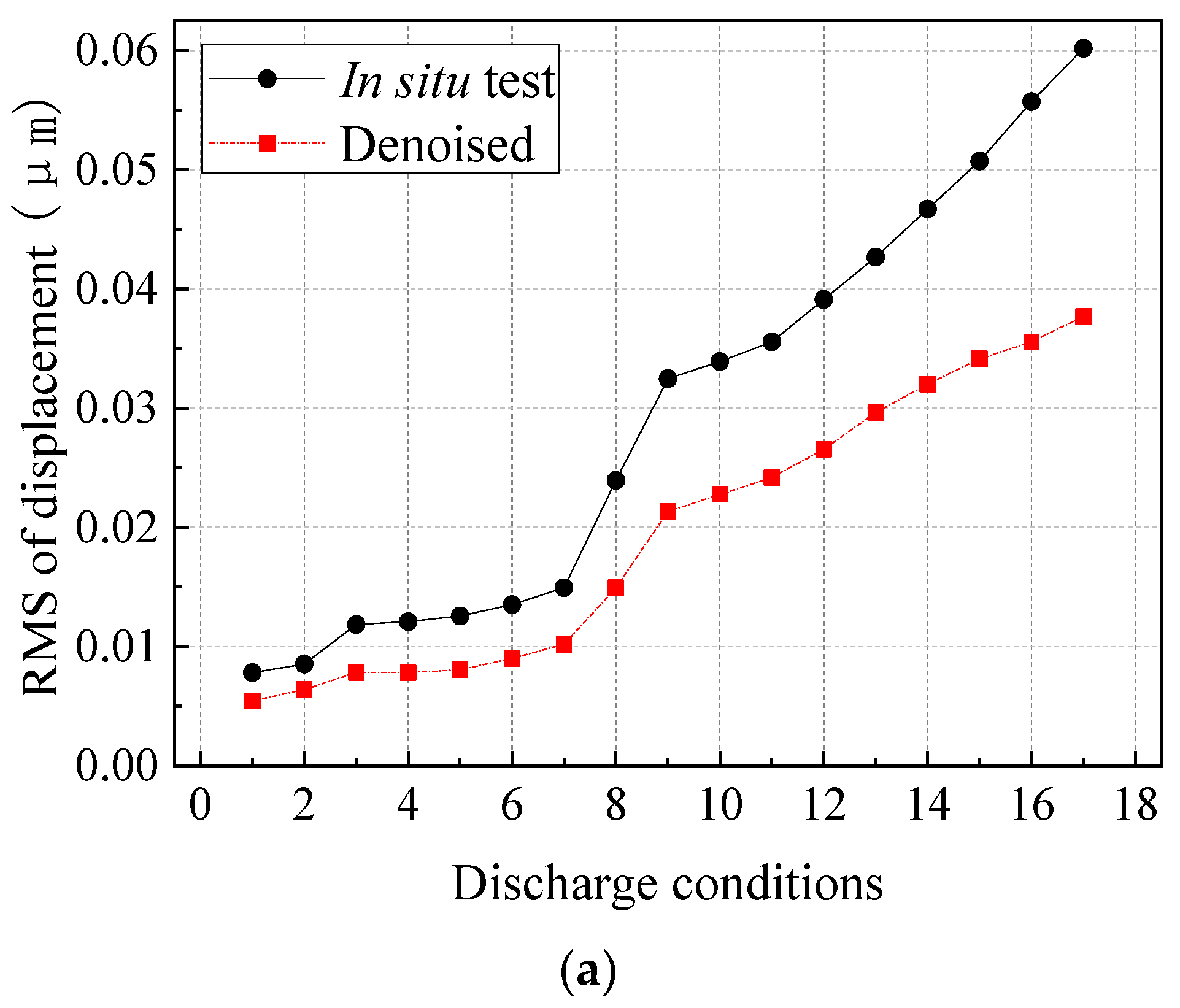
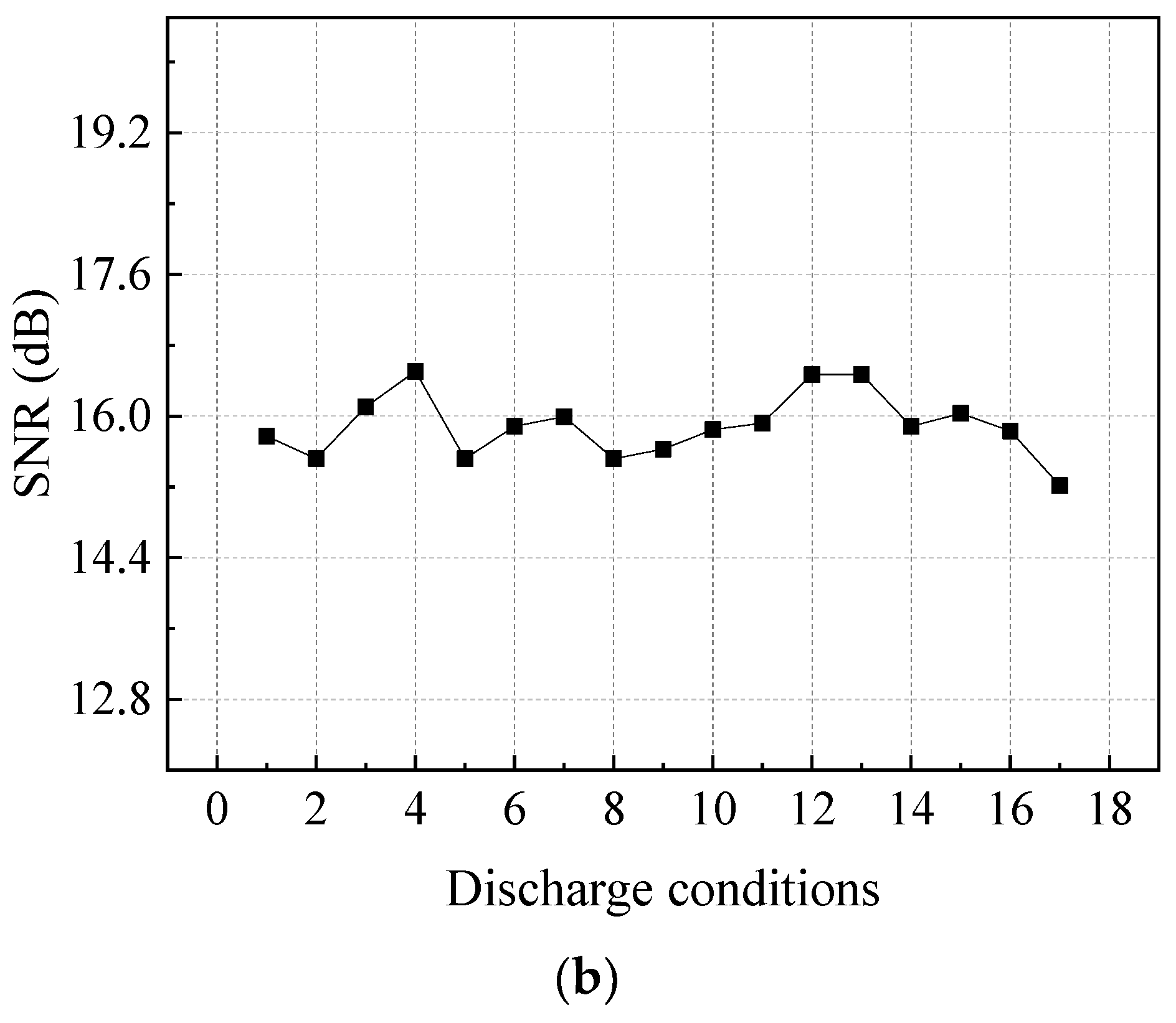
- Signal denoising: A modified ensemble empirical mode decomposition (EEMD) and a wavelet threshold filtering method [32] are applied to filter the noise of the main source signals and the ground vibration signals.
- MP-FRF estimation: The CS of the input and output () and the averaged AS of the input () are calculated. The same is done for other similar discharge conditions. All CSs and ASs are averaged separately, the MP-FRF is estimated using Equation (9).
- Vibration prediction: The Fourier spectrum of the ground vibration can be obtained by multiplying the Fourier spectrum of the vibration source and the MP-FRF. The time history curve of the ground vibration can be obtained using an inverse Fourier transform.
- Noise correction: A noise signal calculated using Equation (11) is added to the predicted time history curve to correct the vibration energy loss due to filtering.
4. Application to Ground Vibration Downstream of Xiangjiaba Dam
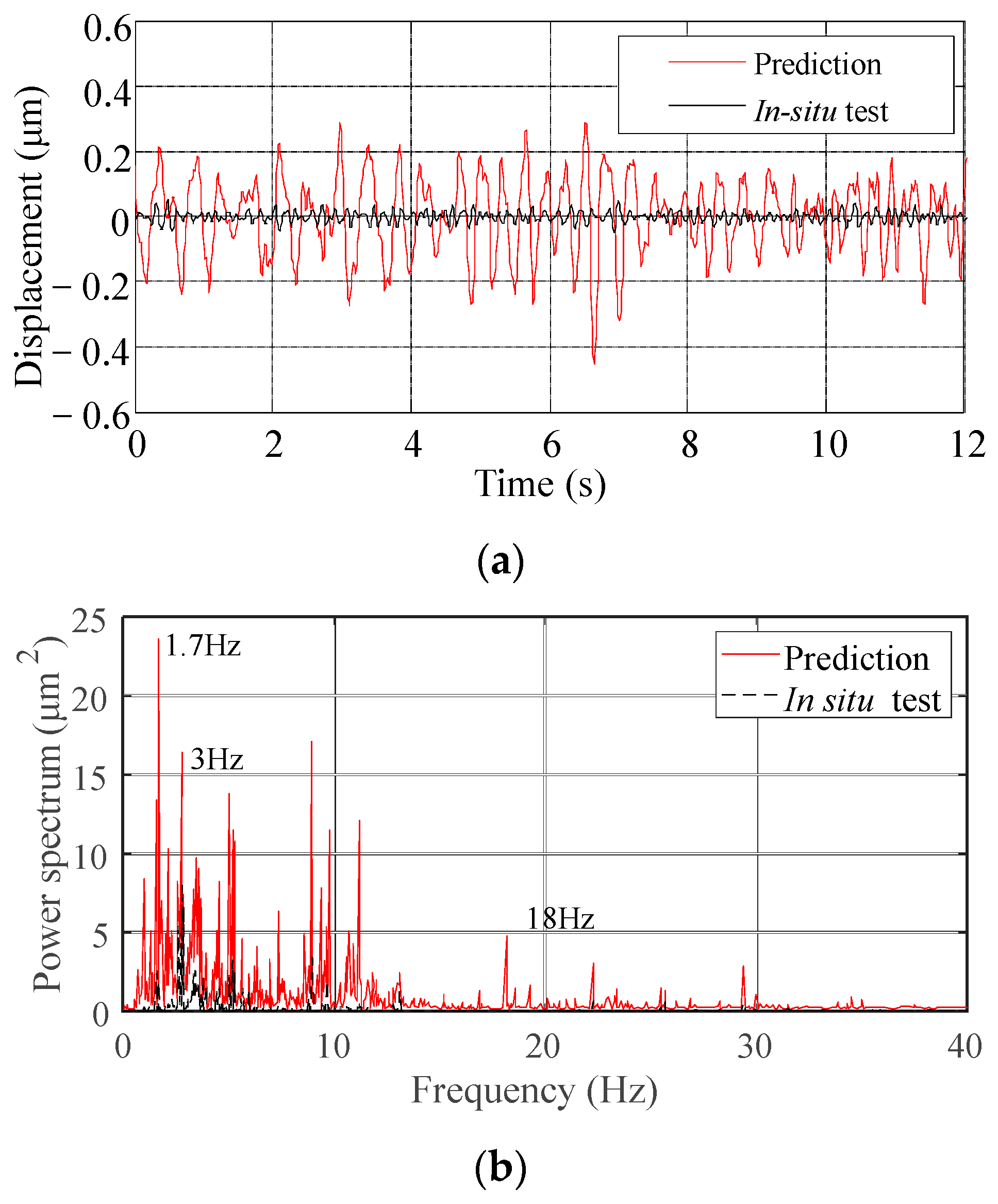
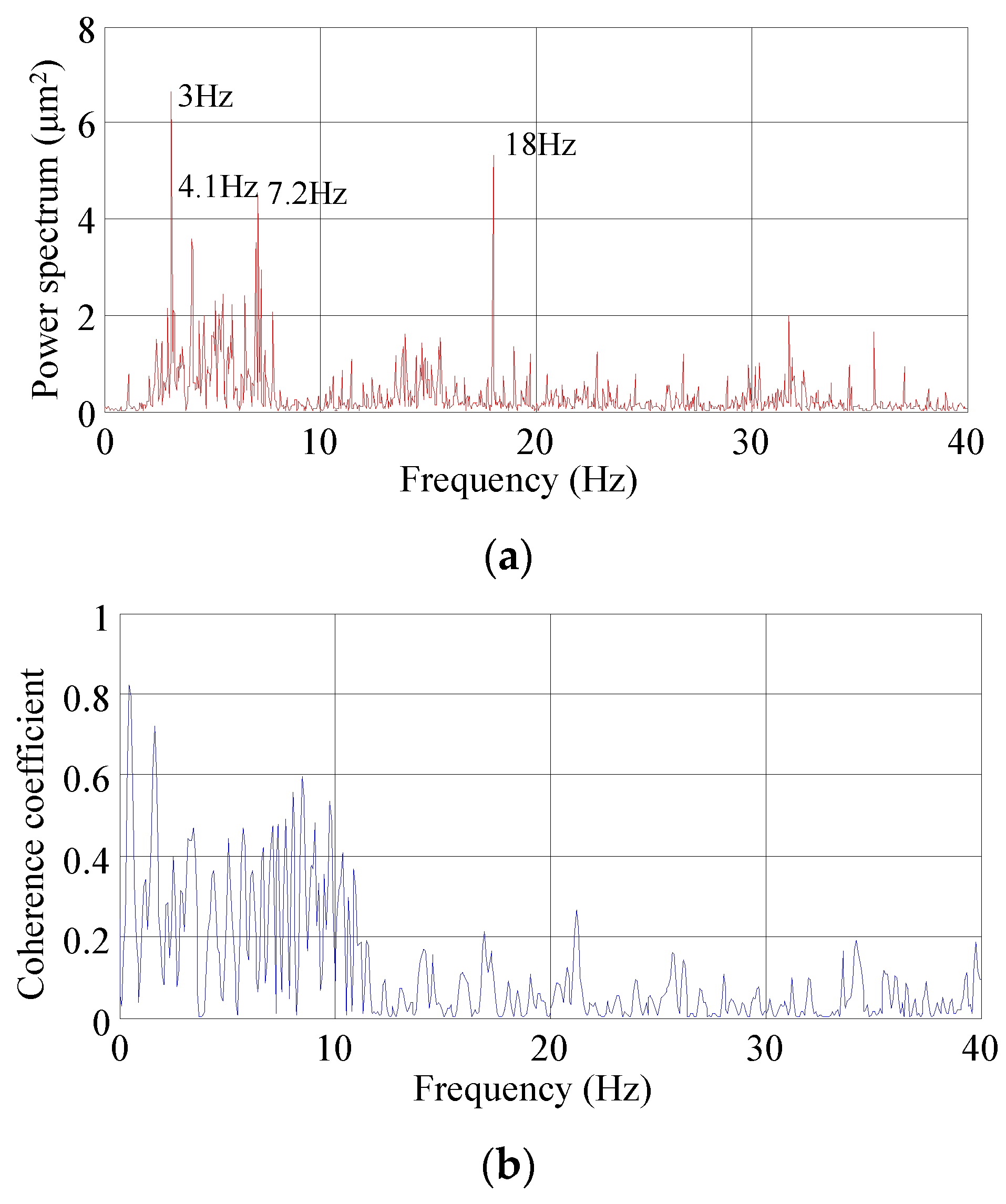
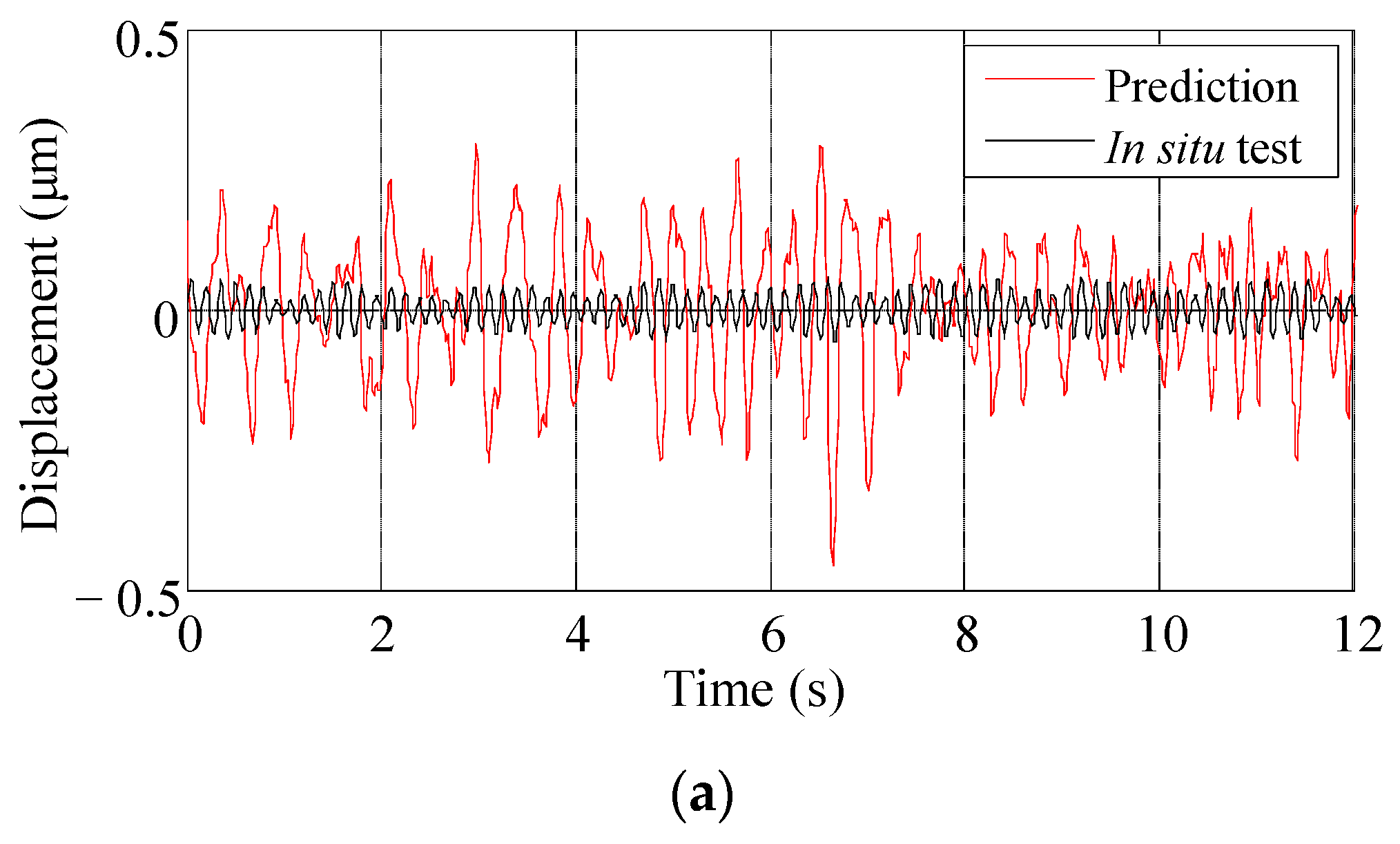
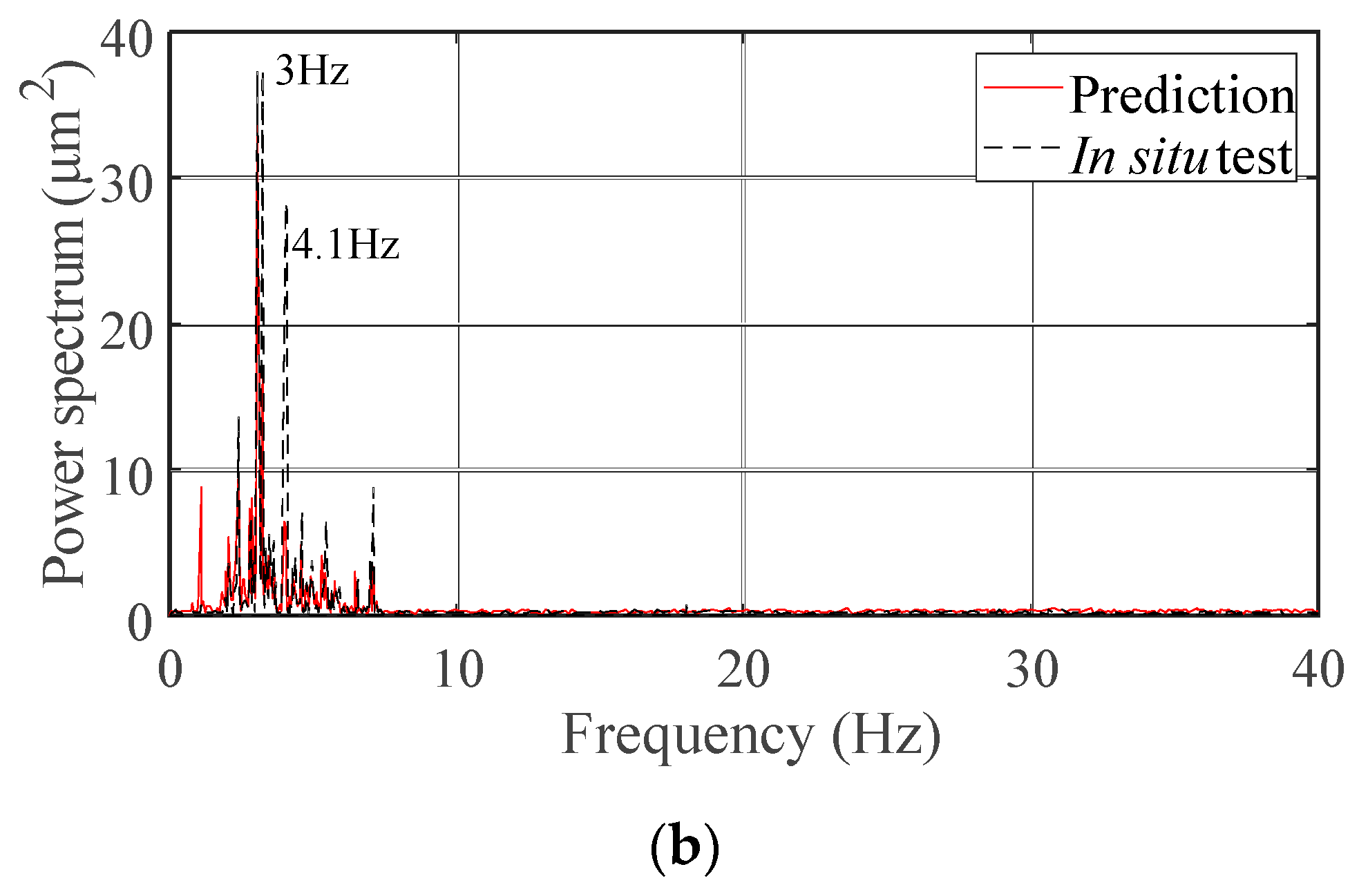
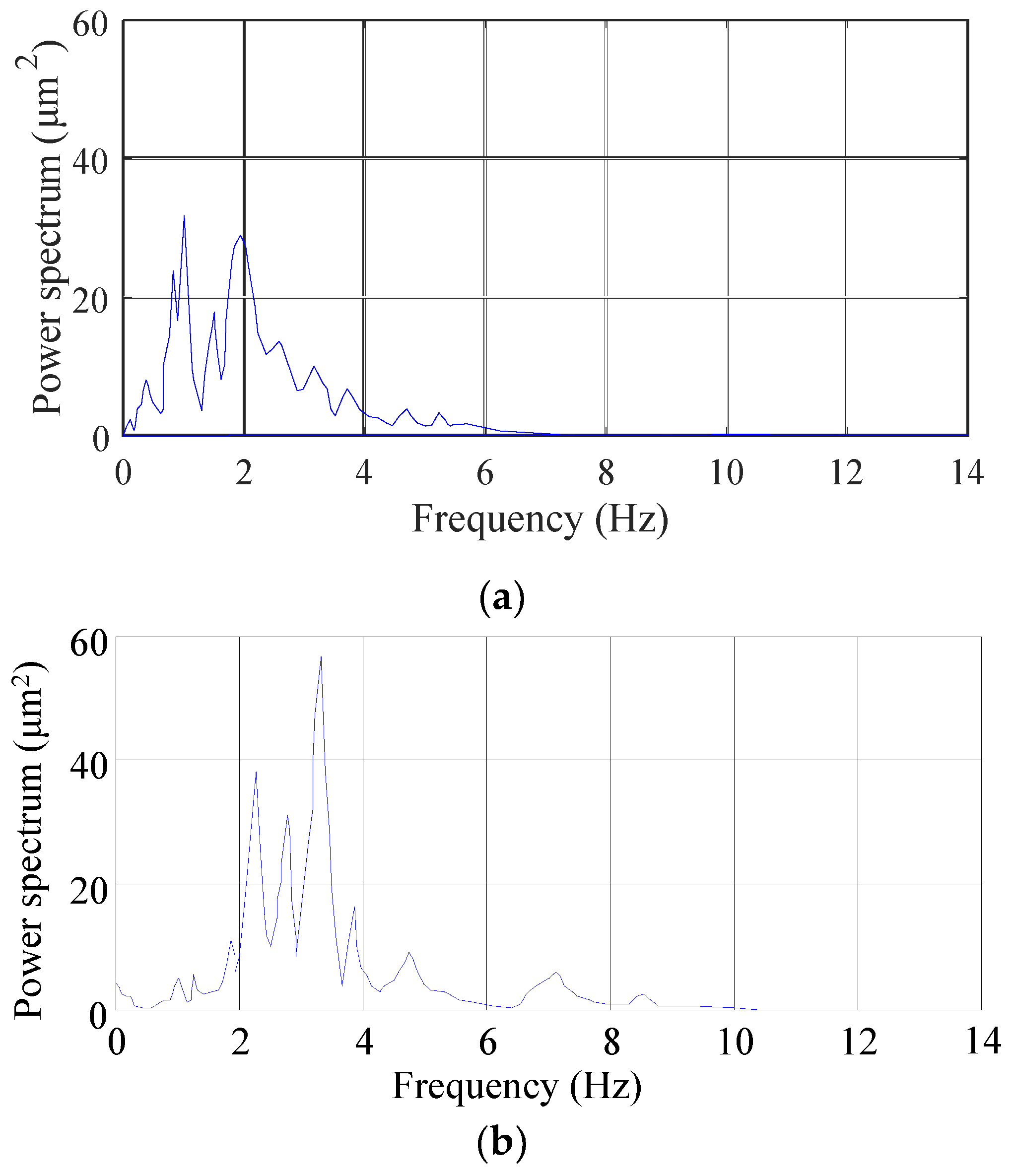
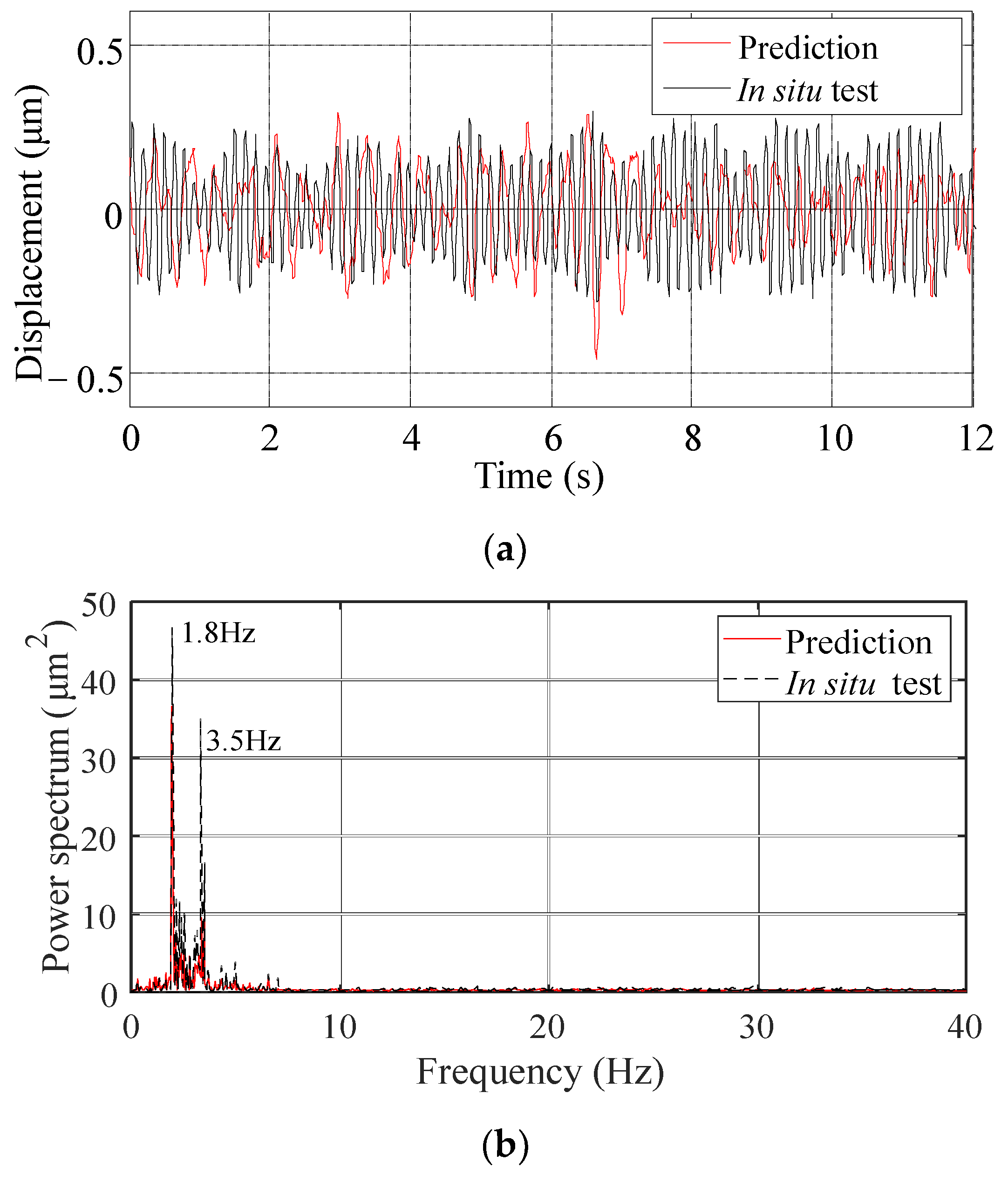
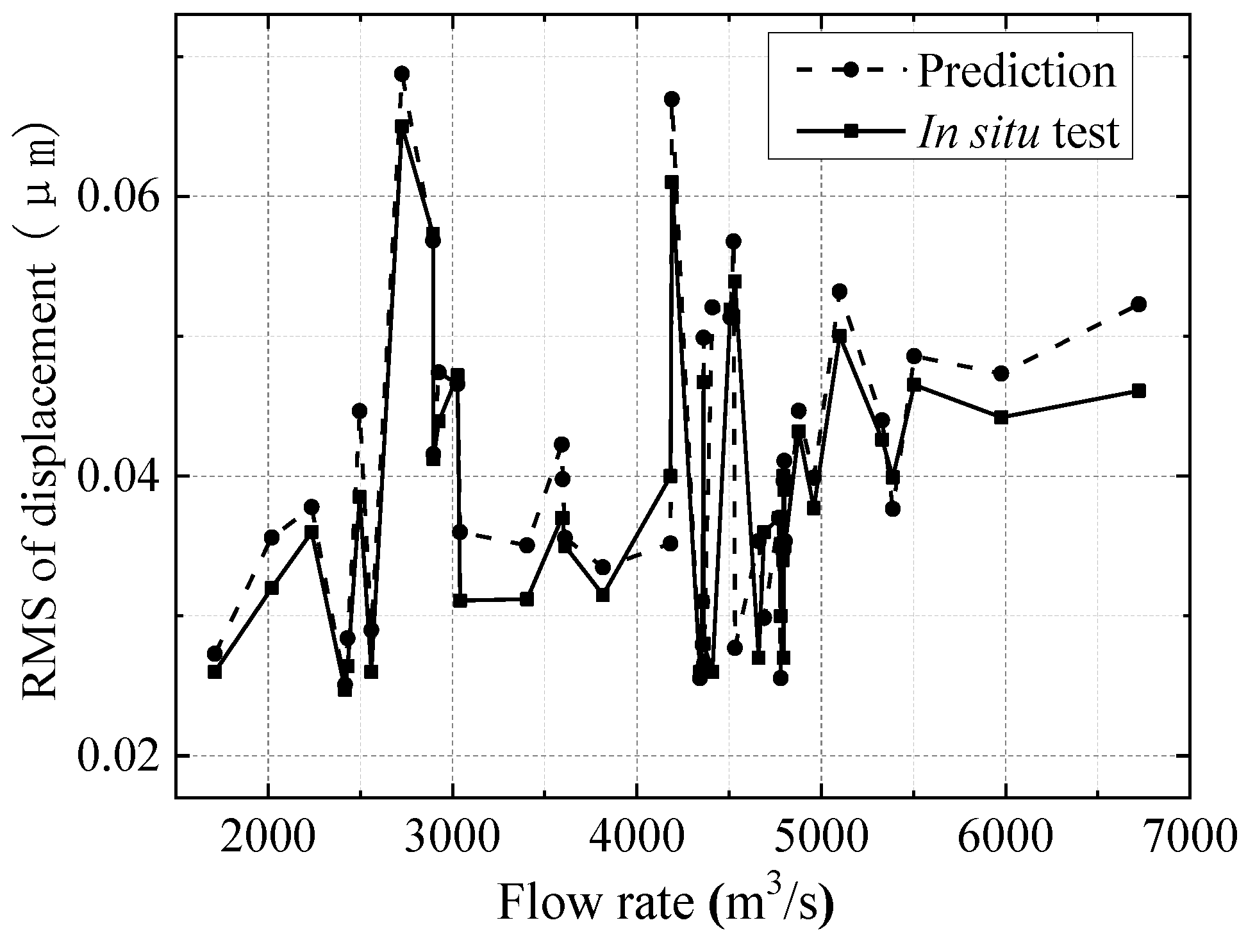
Prediction Results
5. Concluding Remarks
- As the MP-FRF is used to predict vibrations with a broadband frequency and two or more frequency bands with relative high energies, the prediction results show some frequencies caused by non-vibration sources, and the vibration amplitude is amplified. Therefore, the input and output signals need to be filtered, and the amplitude prediction loss caused by filtering can be corrected by adding a constructed white noise signal to the prediction result.
- Compared with using the signal at multiple vibration sources after superimposed as the input, using the main source (displacement at the orifice) as the input improves the accuracy of the predicted frequency distribution, and the predicted signals have fewer frequency peaks.
- The predicted amplitude errors for the downstream area of Xiangjiaba Dam are less than 10%. The predicted results, like the in-situ measurements, are sensitive to factors that affect the ground vibration intensity, such as the flow rate and different discharge modes. The proposed method can predict the dominant frequency and the frequency bands with relative high energies of the downstream ground vibration. The main vibration propagation band is 1.0–10.0 Hz. The MP-FRF remains stable when the vibration source (input) and the vibration response (output) are selected, and the amplitude of the MP-FRF decreases as the distance increases in both the ancient watercourse area and the east town. Therefore, it can be used to predict some other conditions when the inputs are known and the outputs are unknown.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zarfl, C.; Lumsdon, A.E.; Berlekamp, J.; Tydecks, L.; Tockner, K. A global boom in hydropower dam construction. Aquat. Sci. 2015, 77, 161–170. [Google Scholar] [CrossRef]
- Lian, J.J.; Zhang, Y.; Liu, F.; Zhao, Q.H. Analysis of the characteristics for ground vibration induced by flood discharge of high dam using cross wavelet transform. J. Renew. Sustain. Energy 2015, 7, 043146. [Google Scholar] [CrossRef]
- Kotlyakov, A.V.; Shumakova, E.M.; Artemev, S.A. Dynamics of the coastal zone of the Kuibyshev and Saratov reservoirs in the Tolyatti area and its correlation with the operation regime of the Zhigulevskaya HPP. Water Resour. 2007, 34, 657–662. [Google Scholar] [CrossRef]
- Shumakova, E.M.; Kotlyakov, A.V.; Shumakov, G.V. The effect of vibrations in the Zhigulevskii hydropower structure on soils in the nearby territories of Tolyatti city. Water Resour. 2010, 37, 306–310. [Google Scholar] [CrossRef]
- Yin, R.G.; Zhang, J.H. Vibrations source and shock absorption scheme research of near-field vibrations caused by flood discharge and energy dissipation of a stilling pool. In Proceedings of the Geo Shanghai International Congress, Tongji University, Shanghai, China, 26–28 May 2014; pp. 107–116. [Google Scholar]
- Lian, J.J. The roport of related structures vibration monitoring under bottom outlet discharging condition of Xiluodu Hydropower Station in Jinsha River. In State Key Laboratory of Hydraulic Engineering Simulation and Safety; Tianjin University: Tianjin, China, 2013. (In Chinese) [Google Scholar]
- Chen, F.; Takemiya, H.; Huang, M. Prediction and mitigation analyses of ground vibrations induced by high speed train with 3-dimensional finite element method and substructure method. J. Vib. Control 2011, 17, 1703–1720. [Google Scholar] [CrossRef]
- Kouroussis, G.; Florentin, J.; Verlinden, O. Ground vibrations induced by InterCity/InterRegion trains: A numerical prediction based on the multibody/finite element modeling approach. J. Vib. Control 2016, 22, 4192–4210. [Google Scholar] [CrossRef]
- Lombaert, G.; Degrande, G.; François, S.; Thompson, D.J. Ground-borne vibration due to railway traffic: A review of excitation mechanisms, prediction methods and mitigation measures. In Noise and Vibration Mitigation for Rail Transportation Systems; Springer: Berlin/Heidelberg, Germany, 2015; Volume 126, pp. 253–287. [Google Scholar]
- Zhang, J.; Peng, Y.; Xu, W. Hydraulic prediction of near-field vibrations induced by releasing flood. J. Hydraul. Eng. 2017, 143, 05017002. [Google Scholar] [CrossRef]
- Tang, X.; Peng, F.; Yan, R.; Gong, Y.H.; Li, X. An effective time domain model for milling stability prediction simultaneously considering multiple modes and cross-frequency response function effect. Int. J. Adv. Manuf. Technol. 2016, 86, 1037–1054. [Google Scholar] [CrossRef]
- Wang, Z.W.; Zhu, P. Response prediction for modified mechanical systems based on in-situ frequency response functions: Theoretical and numerical studies. J. Sound Vib. 2017, 400, 417–441. [Google Scholar] [CrossRef]
- McKelvey, T.; Guérin, G. Non-parametric frequency response estimation using a local rational model 16th IFAC Symposium on System Identification. In Proceedings of the International Federation of Automatic Control, Brussels, Belgium, 1 July 2012. [Google Scholar]
- Jalali, H.; Bonab, B.T. Nonlinearity identification using sensitivity of frequency response functions. J. Vib. Control 2013, 19, 787–800. [Google Scholar] [CrossRef]
- Wang, J.T.; Wang, C.J.; Zhao, J.P. Frequency response function-based model updating using Kriging model. Mech. Syst. Signal Process. 2017, 87, 218–228. [Google Scholar] [CrossRef]
- Bandara, R.P.; Chan, T.H.T.; Thambiratnam, D.P. Frequency response function based damage identification using principal component analysis and pattern recognition technique. Eng. Struct. 2014, 66, 116–128. [Google Scholar] [CrossRef]
- Limongelli, M.P. Frequency response function interpolation for damage detection under changing environment. Mech. Syst. Signal Process. 2010, 24, 2898–2913. [Google Scholar] [CrossRef]
- U.S. Federal Transit Administration (FTA). Transit Noise and Vibration Impact Assessment; FTA-VA-90-91003-06; U.S. Federal Transit Administration (FTA): Washington, DC, USA, 2006.
- With, C.; Bodare, A. Prediction of train-induced vibrations inside buildings using transfer functions Soil Dynamics & Earthquake. Engineering 2007, 27, 93–98. [Google Scholar]
- Lang, Z.Q.; Billings, S.A.; Yue, R.; Li, J. Output frequency response function of nonlinear Volterra systems. Automatica 2007, 43, 805–816. [Google Scholar] [CrossRef]
- Maia, N.M.M.; Silva, J.M.M.; Almas, E.A.M.; Sampaio, R.P.C. Damage detection in structures: From mode shape to frequency response function methods. Mech. Syst. Signal Process. 2003, 17, 489–498. [Google Scholar] [CrossRef]
- El-Khatib, A.; Guillon, F.; Dômont, A. Vertical vibration transmission through the lumbar spine of the seated subject-First results. J. Sound Vib. 1998, 215, 763–773. [Google Scholar] [CrossRef]
- Fritz, O. Fourier Transforms of Distributions and Their Inverses: A Collection of Tables; Academic Press Inc.: New York, NY, USA; A Subsidiary of Harourt Brace Jovanovich Publicatiuon: New York, NY, USA; London, UK, 1973. [Google Scholar]
- Germain, B.; Daniel, S.G. Synthesis of gradient-index profiles corresponding to spectral reflectance derived by inverse Fourier transform. Appl. Opt. 1987, 26, 4209–4213. [Google Scholar]
- Madsen, C.K.; Zhao, J.H. Optical Filter Design and Analysis; Wiley-Interscience Publication: New York, NY, USA, 1999. [Google Scholar]
- Vanhoenacker, K.; Schoukens, J.; Swevers, J.; Vaes, D. Summary and comparing overview of techniques for the detection of non-linear distortions. Die Pharm. 2004, 57, 1241–1256. [Google Scholar]
- Brandt, A. Noise and Vibration Analysis: Signal Analysis and Experimental Procedures; A John Wiley and Sons Ltd. Publication: Hoboken, NJ, USA, 2011. [Google Scholar]
- Solomou, M.; Rees, D. Frequency domain analysis of nonlinear distortions on linear frequency response function measurements. IEEE Trans. Instrum. Meas. 2005, 54, 1313–1320. [Google Scholar] [CrossRef]
- Bendat, J.S. Statistical errors in measurement of coherence functions and input/output quantities. J. Sound Vib. 1978, 59, 405–421. [Google Scholar] [CrossRef]
- Schoukens, J.; Rolain, Y.; Pintelon, R. Leakage reduction in frequency response function measurements. In Proceedings of the IEEE Transactions on Instrumentation and Measurement, Ottawa, ON, Canada, 20 November 2006; Volume 55, pp. 2286–2291. [Google Scholar]
- Ugryumova, D.; Pintelon, R.; Vandersteen, G. Frequency response function estimation in the presence of missing output data. IEEE Trans. Instrum. Meas. 2015, 64, 541–553. [Google Scholar] [CrossRef]
- Zhang, Y.; Lian, J.J.; Liu, F. An improved filtering method based on EEMD and wavelet-threshold for modal parameter identification of hydraulic structure. Mech. Syst. Signal Process. 2016, 68, 316–329. [Google Scholar] [CrossRef]
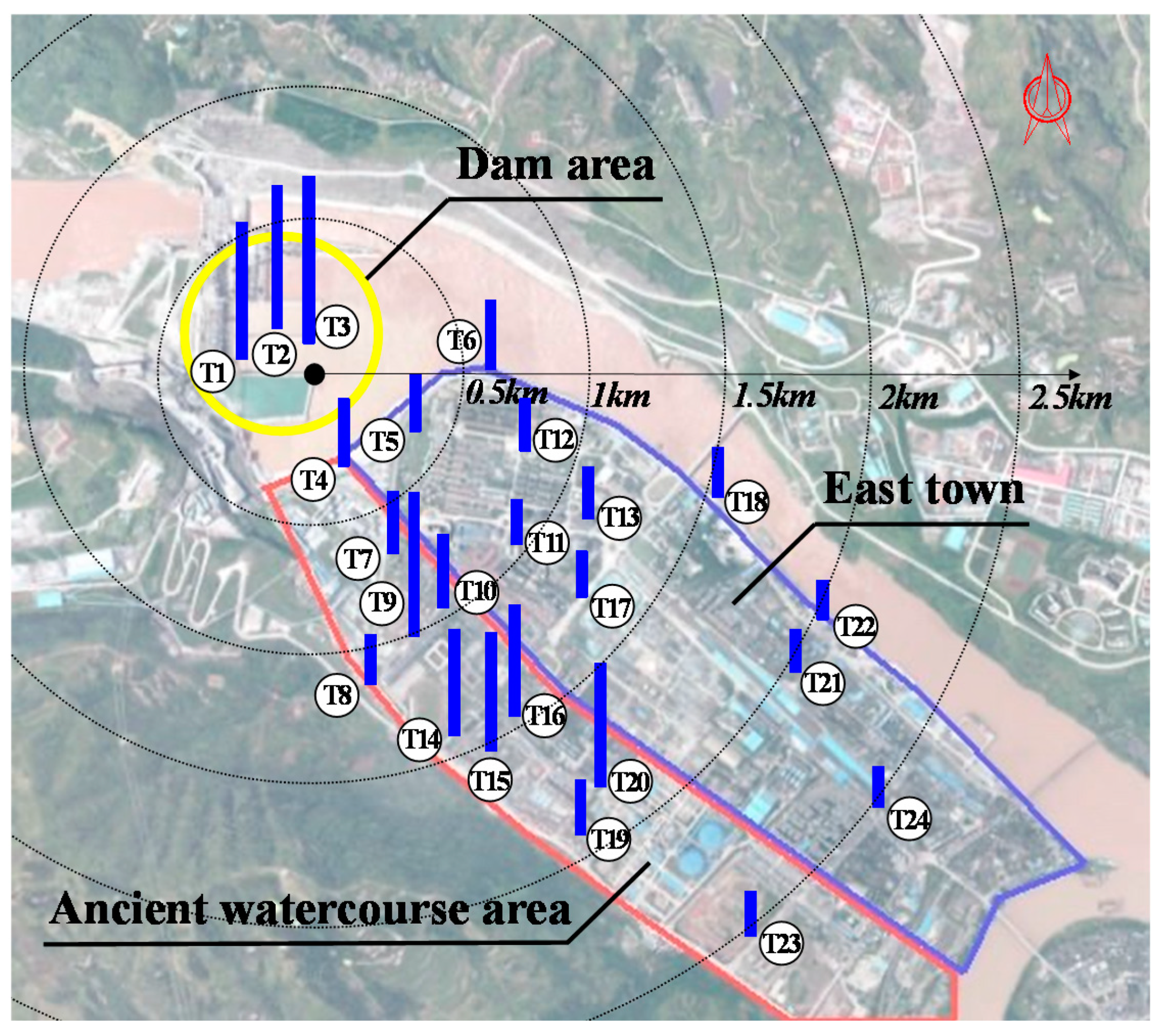


| Measurement Point | RMS of the Vertical Displacement (μm) | Measurement Point | RMS of the Vertical Displacement (μm) | Measurement Point | RMS of the Vertical Displacement (μm) |
|---|---|---|---|---|---|
| T1 | 1.33 | T9 | 1.24 | T17 | 0.34 |
| T2 | 1.48 | T10 | 0.53 | T18 | 0.37 |
| T3 | 1.81 | T11 | 0.33 | T19 | 0.40 |
| T4 | 0.50 | T12 | 0.38 | T20 | 0.89 |
| T5 | 0.40 | T13 | 0.38 | T21 | 0.31 |
| T6 | 0.50 | T14 | 0.76 | T22 | 0.29 |
| T7 | 0.46 | T15 | 0.85 | T23 | 0.33 |
| T8 | 0.36 | T16 | 0.81 | T24 | 0.29 |
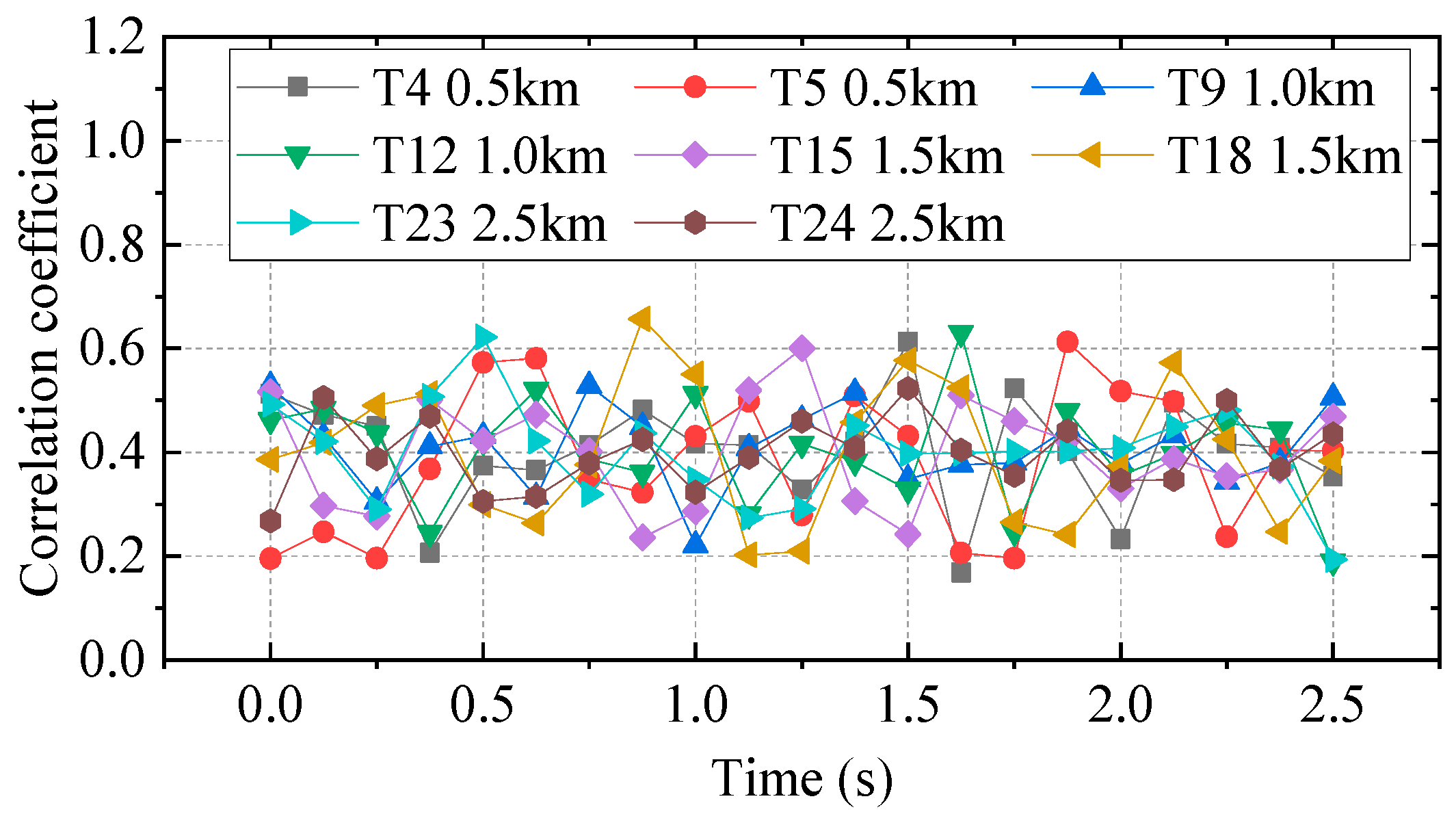
| Measurement Point | T4 | T5 | T9 | T12 | T15 | T18 | T23 | T24 | |
|---|---|---|---|---|---|---|---|---|---|
| Phase Difference (s) | |||||||||
| 0 | 0.513 | 0.195 | 0.528 | 0.462 | 0.516 | 0.386 | 0.492 | 0.268 | |
| 0.125 | 0.473 | 0.247 | 0.431 | 0.484 | 0.297 | 0.419 | 0.421 | 0.506 | |
| 0.25 | 0.451 | 0.196 | 0.306 | 0.437 | 0.277 | 0.490 | 0.290 | 0.388 | |
| 0.375 | 0.207 | 0.368 | 0.411 | 0.245 | 0.501 | 0.513 | 0.507 | 0.470 | |
| 0.5 | 0.374 | 0.573 | 0.431 | 0.421 | 0.422 | 0.299 | 0.622 | 0.306 | |
| 0.625 | 0.366 | 0.581 | 0.314 | 0.520 | 0.472 | 0.264 | 0.422 | 0.315 | |
| 0.75 | 0.414 | 0.348 | 0.529 | 0.387 | 0.402 | 0.376 | 0.319 | 0.379 | |
| 0.875 | 0.482 | 0.323 | 0.450 | 0.361 | 0.236 | 0.657 | 0.437 | 0.425 | |
| 1 | 0.417 | 0.431 | 0.221 | 0.512 | 0.286 | 0.550 | 0.348 | 0.323 | |
| 1.125 | 0.414 | 0.498 | 0.408 | 0.280 | 0.520 | 0.202 | 0.273 | 0.390 | |
| 1.25 | 0.328 | 0.279 | 0.463 | 0.416 | 0.600 | 0.209 | 0.291 | 0.460 | |
| 1.375 | 0.420 | 0.509 | 0.515 | 0.382 | 0.306 | 0.458 | 0.451 | 0.408 | |
| 1.5 | 0.613 | 0.431 | 0.349 | 0.328 | 0.242 | 0.577 | 0.397 | 0.523 | |
| 1.625 | 0.168 | 0.206 | 0.376 | 0.630 | 0.510 | 0.524 | 0.398 | 0.404 | |
| 1.75 | 0.523 | 0.196 | 0.379 | 0.247 | 0.460 | 0.266 | 0.402 | 0.355 | |
| 1.875 | 0.402 | 0.613 | 0.446 | 0.479 | 0.423 | 0.241 | 0.402 | 0.441 | |
| 2 | 0.233 | 0.518 | 0.378 | 0.355 | 0.330 | 0.372 | 0.408 | 0.346 | |
| 2.125 | 0.496 | 0.498 | 0.433 | 0.397 | 0.387 | 0.572 | 0.449 | 0.347 | |
| 2.25 | 0.416 | 0.238 | 0.343 | 0.456 | 0.354 | 0.425 | 0.481 | 0.500 | |
| 2.375 | 0.409 | 0.405 | 0.380 | 0.444 | 0.367 | 0.247 | 0.373 | 0.368 | |
| 2.5 | 0.354 | 0.403 | 0.505 | 0.190 | 0.469 | 0.384 | 0.193 | 0.435 | |
| Measurement Points | T4 | T5 | T9 | T12 | T15 | T18 | T19 | T21 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Flow Rate (m3/s) | I (μm) | P (μm) | I (μm) | P (μm) | I (μm) | P (μm) | I (μm) | P (μm) | I (μm) | P (μm) | I (μm) | P (μm) | I (μm) | P (μm) | I (μm) | P (μm) | |
| 1711 | 0.010 | 0.011 | 0.008 | 0.009 | 0.026 | 0.027 | 0.008 | 0.008 | 0.018 | 0.019 | 0.008 | 0.008 | 0.005 | 0.007 | 0.007 | 0.007 | |
| 2020 | 0.014 | 0.014 | 0.012 | 0.011 | 0.032 | 0.036 | 0.010 | 0.011 | 0.022 | 0.024 | 0.010 | 0.013 | 0.007 | 0.009 | 0.008 | 0.009 | |
| 2236 | 0.015 | 0.017 | 0.012 | 0.012 | 0.036 | 0.038 | 0.011 | 0.012 | 0.028 | 0.031 | 0.013 | 0.012 | 0.010 | 0.011 | 0.009 | 0.009 | |
| 2417 | 0.010 | 0.013 | 0.008 | 0.013 | 0.025 | 0.025 | 0.010 | 0.008 | 0.017 | 0.017 | 0.007 | 0.007 | 0.008 | 0.011 | 0.006 | 0.006 | |
| 2431 | 0.018 | 0.014 | 0.012 | 0.009 | 0.026 | 0.028 | 0.008 | 0.010 | 0.022 | 0.019 | 0.008 | 0.011 | 0.009 | 0.009 | 0.007 | 0.007 | |
| 2497 | 0.016 | 0.018 | 0.012 | 0.014 | 0.039 | 0.045 | 0.012 | 0.014 | 0.026 | 0.031 | 0.014 | 0.013 | 0.012 | 0.012 | 0.010 | 0.011 | |
| 2560 | 0.013 | 0.012 | 0.014 | 0.017 | 0.026 | 0.029 | 0.008 | 0.009 | 0.018 | 0.020 | 0.008 | 0.009 | 0.008 | 0.009 | 0.007 | 0.007 | |
| 2726 | 0.024 | 0.028 | 0.021 | 0.022 | 0.065 | 0.069 | 0.020 | 0.021 | 0.045 | 0.047 | 0.019 | 0.021 | 0.018 | 0.022 | 0.016 | 0.017 | |
| 2894 | 0.027 | 0.023 | 0.018 | 0.018 | 0.057 | 0.057 | 0.020 | 0.017 | 0.041 | 0.039 | 0.012 | 0.016 | 0.020 | 0.018 | 0.014 | 0.016 | |
| 2896 | 0.017 | 0.021 | 0.013 | 0.016 | 0.041 | 0.042 | 0.013 | 0.013 | 0.028 | 0.028 | 0.012 | 0.012 | 0.013 | 0.013 | 0.010 | 0.010 | |
| 2925 | 0.018 | 0.019 | 0.018 | 0.015 | 0.044 | 0.047 | 0.012 | 0.015 | 0.030 | 0.034 | 0.013 | 0.014 | 0.014 | 0.015 | 0.011 | 0.012 | |
| 3027 | 0.019 | 0.019 | 0.015 | 0.015 | 0.047 | 0.047 | 0.014 | 0.014 | 0.037 | 0.032 | 0.012 | 0.015 | 0.015 | 0.015 | 0.012 | 0.012 | |
| 3041 | 0.017 | 0.015 | 0.010 | 0.012 | 0.031 | 0.036 | 0.010 | 0.011 | 0.026 | 0.025 | 0.009 | 0.011 | 0.009 | 0.012 | 0.008 | 0.009 | |
| 3404 | 0.013 | 0.017 | 0.013 | 0.011 | 0.031 | 0.035 | 0.013 | 0.011 | 0.021 | 0.026 | 0.013 | 0.010 | 0.010 | 0.011 | 0.008 | 0.009 | |
| 3593 | 0.018 | 0.020 | 0.012 | 0.014 | 0.037 | 0.042 | 0.011 | 0.013 | 0.028 | 0.029 | 0.011 | 0.013 | 0.012 | 0.014 | 0.009 | 0.011 | |
| 3597 | 0.015 | 0.016 | 0.012 | 0.013 | 0.037 | 0.040 | 0.014 | 0.012 | 0.025 | 0.027 | 0.011 | 0.012 | 0.015 | 0.017 | 0.009 | 0.012 | |
| 3610 | 0.014 | 0.017 | 0.015 | 0.014 | 0.035 | 0.036 | 0.011 | 0.014 | 0.028 | 0.033 | 0.013 | 0.011 | 0.011 | 0.011 | 0.009 | 0.009 | |
| 3816 | 0.011 | 0.014 | 0.010 | 0.011 | 0.032 | 0.033 | 0.010 | 0.010 | 0.022 | 0.023 | 0.009 | 0.013 | 0.010 | 0.011 | 0.008 | 0.008 | |
| 4182 | 0.016 | 0.019 | 0.013 | 0.011 | 0.040 | 0.035 | 0.012 | 0.011 | 0.032 | 0.024 | 0.012 | 0.010 | 0.017 | 0.014 | 0.010 | 0.009 | |
| 4190 | 0.025 | 0.027 | 0.020 | 0.022 | 0.061 | 0.067 | 0.019 | 0.021 | 0.042 | 0.046 | 0.018 | 0.020 | 0.015 | 0.019 | 0.015 | 0.017 | |
| 4342 | 0.016 | 0.010 | 0.016 | 0.013 | 0.026 | 0.026 | 0.015 | 0.008 | 0.018 | 0.018 | 0.013 | 0.008 | 0.008 | 0.012 | 0.007 | 0.009 | |
| 4355 | 0.013 | 0.013 | 0.010 | 0.010 | 0.031 | 0.031 | 0.010 | 0.013 | 0.021 | 0.025 | 0.009 | 0.012 | 0.013 | 0.010 | 0.008 | 0.008 | |
| 4356 | 0.013 | 0.011 | 0.014 | 0.016 | 0.031 | 0.028 | 0.013 | 0.009 | 0.025 | 0.022 | 0.009 | 0.008 | 0.010 | 0.012 | 0.008 | 0.007 | |
| 4361 | 0.019 | 0.020 | 0.015 | 0.016 | 0.047 | 0.050 | 0.014 | 0.015 | 0.032 | 0.034 | 0.014 | 0.015 | 0.015 | 0.016 | 0.012 | 0.012 | |
| 4363 | 0.014 | 0.011 | 0.009 | 0.009 | 0.028 | 0.027 | 0.009 | 0.008 | 0.019 | 0.018 | 0.012 | 0.008 | 0.009 | 0.009 | 0.007 | 0.007 | |
| 4410 | 0.010 | 0.017 | 0.012 | 0.017 | 0.026 | 0.052 | 0.010 | 0.016 | 0.028 | 0.036 | 0.008 | 0.012 | 0.008 | 0.014 | 0.007 | 0.013 | |
| 4507 | 0.017 | 0.021 | 0.017 | 0.017 | 0.052 | 0.051 | 0.016 | 0.018 | 0.036 | 0.035 | 0.015 | 0.015 | 0.017 | 0.017 | 0.013 | 0.013 | |
| 4524 | 0.019 | 0.023 | 0.015 | 0.018 | 0.051 | 0.057 | 0.016 | 0.017 | 0.035 | 0.039 | 0.012 | 0.017 | 0.014 | 0.018 | 0.013 | 0.014 | |
| 4532 | 0.022 | 0.028 | 0.017 | 0.019 | 0.054 | 0.028 | 0.017 | 0.019 | 0.037 | 0.029 | 0.016 | 0.018 | 0.017 | 0.019 | 0.013 | 0.007 | |
| 4660 | 0.016 | 0.014 | 0.009 | 0.011 | 0.027 | 0.035 | 0.014 | 0.011 | 0.019 | 0.024 | 0.008 | 0.011 | 0.009 | 0.011 | 0.007 | 0.009 | |
| 4690 | 0.015 | 0.012 | 0.012 | 0.010 | 0.036 | 0.030 | 0.011 | 0.009 | 0.025 | 0.026 | 0.011 | 0.009 | 0.012 | 0.010 | 0.009 | 0.007 | |
| 4770 | 0.015 | 0.015 | 0.016 | 0.020 | 0.037 | 0.037 | 0.011 | 0.011 | 0.025 | 0.025 | 0.011 | 0.011 | 0.012 | 0.012 | 0.009 | 0.009 | |
| 4780 | 0.012 | 0.010 | 0.010 | 0.008 | 0.030 | 0.026 | 0.012 | 0.012 | 0.021 | 0.028 | 0.009 | 0.008 | 0.010 | 0.008 | 0.008 | 0.006 | |
| 4792 | 0.014 | 0.014 | 0.011 | 0.013 | 0.034 | 0.035 | 0.010 | 0.011 | 0.023 | 0.024 | 0.012 | 0.015 | 0.013 | 0.011 | 0.009 | 0.009 | |
| 4794 | 0.017 | 0.014 | 0.017 | 0.015 | 0.040 | 0.035 | 0.012 | 0.011 | 0.027 | 0.022 | 0.012 | 0.017 | 0.015 | 0.014 | 0.010 | 0.009 | |
| 4796 | 0.011 | 0.016 | 0.012 | 0.013 | 0.027 | 0.040 | 0.012 | 0.012 | 0.024 | 0.027 | 0.008 | 0.012 | 0.009 | 0.012 | 0.007 | 0.010 | |
| 4800 | 0.016 | 0.017 | 0.013 | 0.013 | 0.039 | 0.041 | 0.012 | 0.013 | 0.027 | 0.028 | 0.012 | 0.012 | 0.013 | 0.013 | 0.010 | 0.010 | |
| 4803 | 0.014 | 0.014 | 0.011 | 0.011 | 0.035 | 0.035 | 0.011 | 0.011 | 0.024 | 0.029 | 0.014 | 0.017 | 0.014 | 0.011 | 0.009 | 0.009 | |
| 4878 | 0.017 | 0.022 | 0.014 | 0.014 | 0.043 | 0.045 | 0.013 | 0.014 | 0.030 | 0.031 | 0.013 | 0.013 | 0.012 | 0.014 | 0.011 | 0.011 | |
| 4960 | 0.018 | 0.016 | 0.016 | 0.013 | 0.038 | 0.040 | 0.012 | 0.012 | 0.026 | 0.027 | 0.011 | 0.013 | 0.012 | 0.013 | 0.009 | 0.010 | |
| 5100 | 0.020 | 0.021 | 0.016 | 0.017 | 0.050 | 0.053 | 0.015 | 0.016 | 0.034 | 0.038 | 0.016 | 0.016 | 0.016 | 0.017 | 0.013 | 0.013 | |
| 5330 | 0.017 | 0.018 | 0.014 | 0.018 | 0.043 | 0.044 | 0.013 | 0.014 | 0.029 | 0.030 | 0.013 | 0.013 | 0.014 | 0.014 | 0.011 | 0.011 | |
| 5388 | 0.014 | 0.015 | 0.013 | 0.012 | 0.040 | 0.038 | 0.012 | 0.012 | 0.029 | 0.026 | 0.016 | 0.018 | 0.013 | 0.012 | 0.010 | 0.009 | |
| 5504 | 0.019 | 0.020 | 0.018 | 0.016 | 0.047 | 0.049 | 0.016 | 0.017 | 0.032 | 0.037 | 0.014 | 0.015 | 0.017 | 0.016 | 0.012 | 0.014 | |
| 5976 | 0.018 | 0.024 | 0.018 | 0.020 | 0.044 | 0.047 | 0.014 | 0.015 | 0.034 | 0.036 | 0.013 | 0.015 | 0.014 | 0.015 | 0.011 | 0.012 | |
| 6722 | 0.023 | 0.021 | 0.015 | 0.017 | 0.046 | 0.052 | 0.016 | 0.018 | 0.038 | 0.043 | 0.017 | 0.019 | 0.017 | 0.017 | 0.012 | 0.015 | |
| Prediction error (%) | 7.07 | 5.67 | 9.26 | 3.09 | 5.36 | 9.43 | 9.12 | 8.08 | |||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Lian, J.; Li, S.; Zhao, Y.; Zhang, G.; Liu, Y. Predicting Dam Flood Discharge Induced Ground Vibration with Modified Frequency Response Function. Water 2021, 13, 144. https://doi.org/10.3390/w13020144
Zhang Y, Lian J, Li S, Zhao Y, Zhang G, Liu Y. Predicting Dam Flood Discharge Induced Ground Vibration with Modified Frequency Response Function. Water. 2021; 13(2):144. https://doi.org/10.3390/w13020144
Chicago/Turabian StyleZhang, Yan, Jijian Lian, Songhui Li, Yanbing Zhao, Guoxin Zhang, and Yi Liu. 2021. "Predicting Dam Flood Discharge Induced Ground Vibration with Modified Frequency Response Function" Water 13, no. 2: 144. https://doi.org/10.3390/w13020144
APA StyleZhang, Y., Lian, J., Li, S., Zhao, Y., Zhang, G., & Liu, Y. (2021). Predicting Dam Flood Discharge Induced Ground Vibration with Modified Frequency Response Function. Water, 13(2), 144. https://doi.org/10.3390/w13020144






