Physiological Changes and Elemental Ratio of Scrippsiella trochoidea and Heterosigma akashiwo in Different Growth Phase
Abstract
1. Introduction
2. Material and Methods
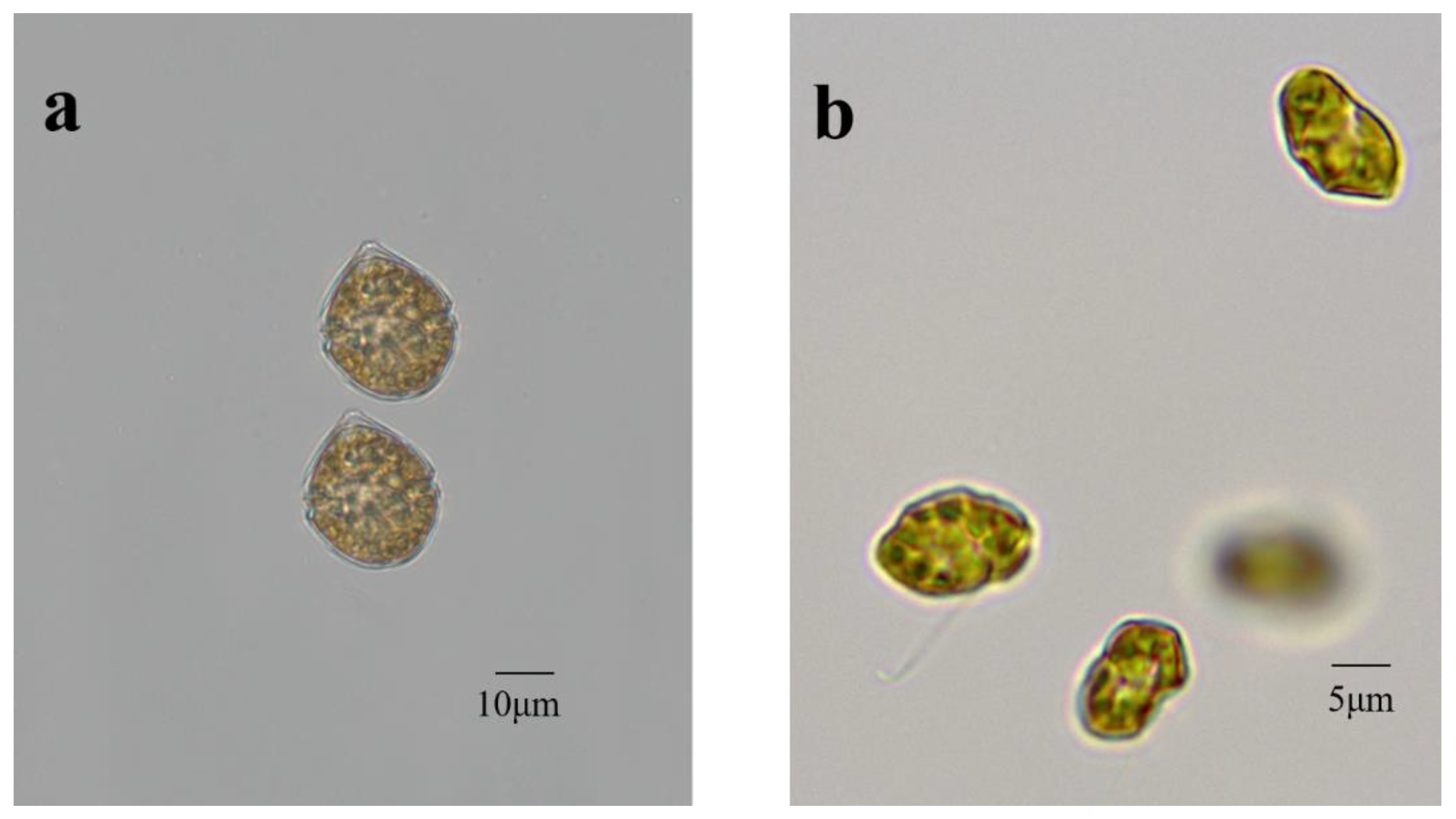
2.1. Microalgal Species and Pre-Culture Conditions
2.2. Determination of Microalgal Growth
2.3. Sample Analyses
2.4. Date Analyses
3. Results
3.1. Growth Profiles of Scrippsiella trochoidea and Heterosigma akashiwo
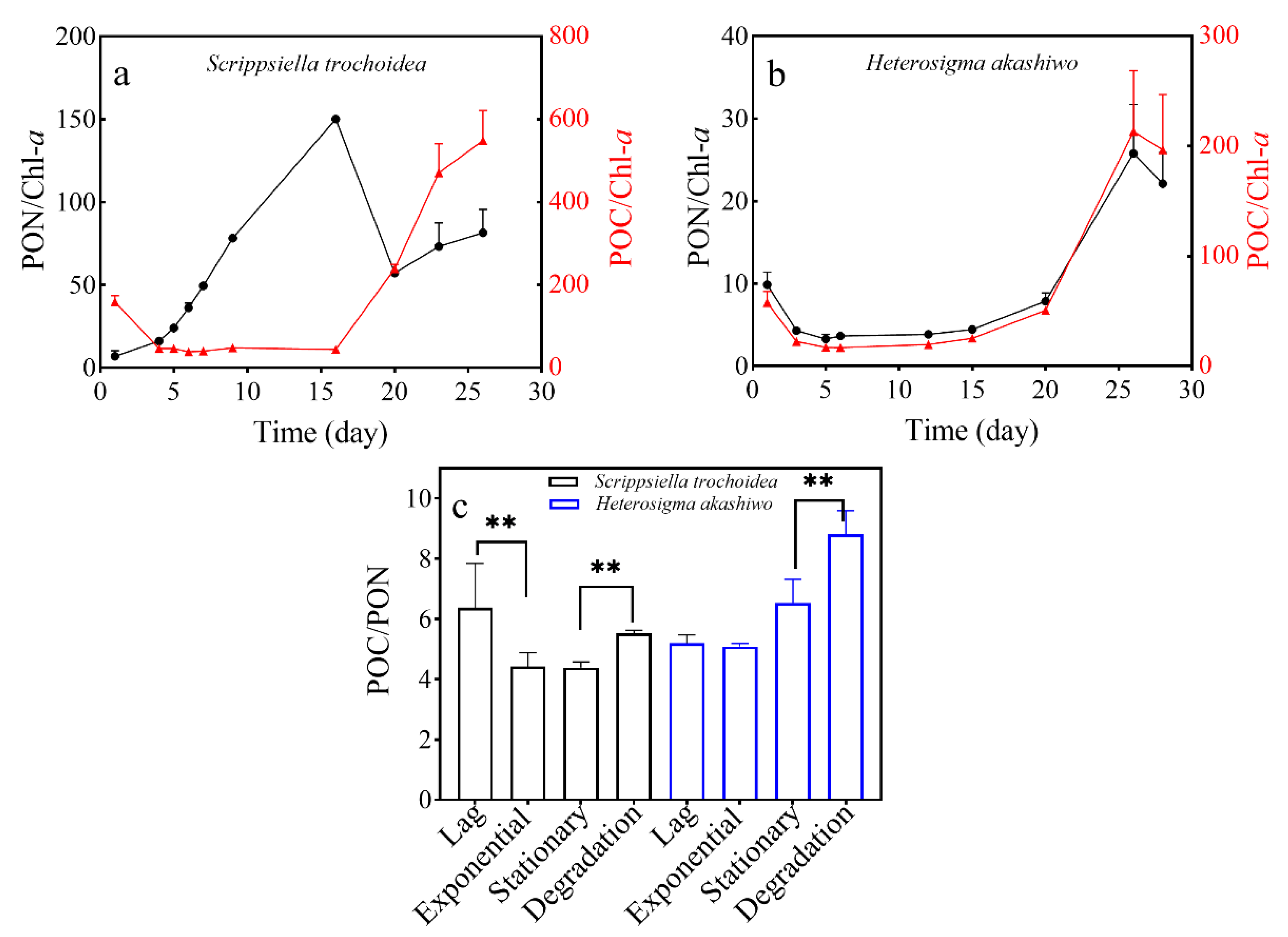
3.2. Chlorophyll-a Content of Two Microalgal Species
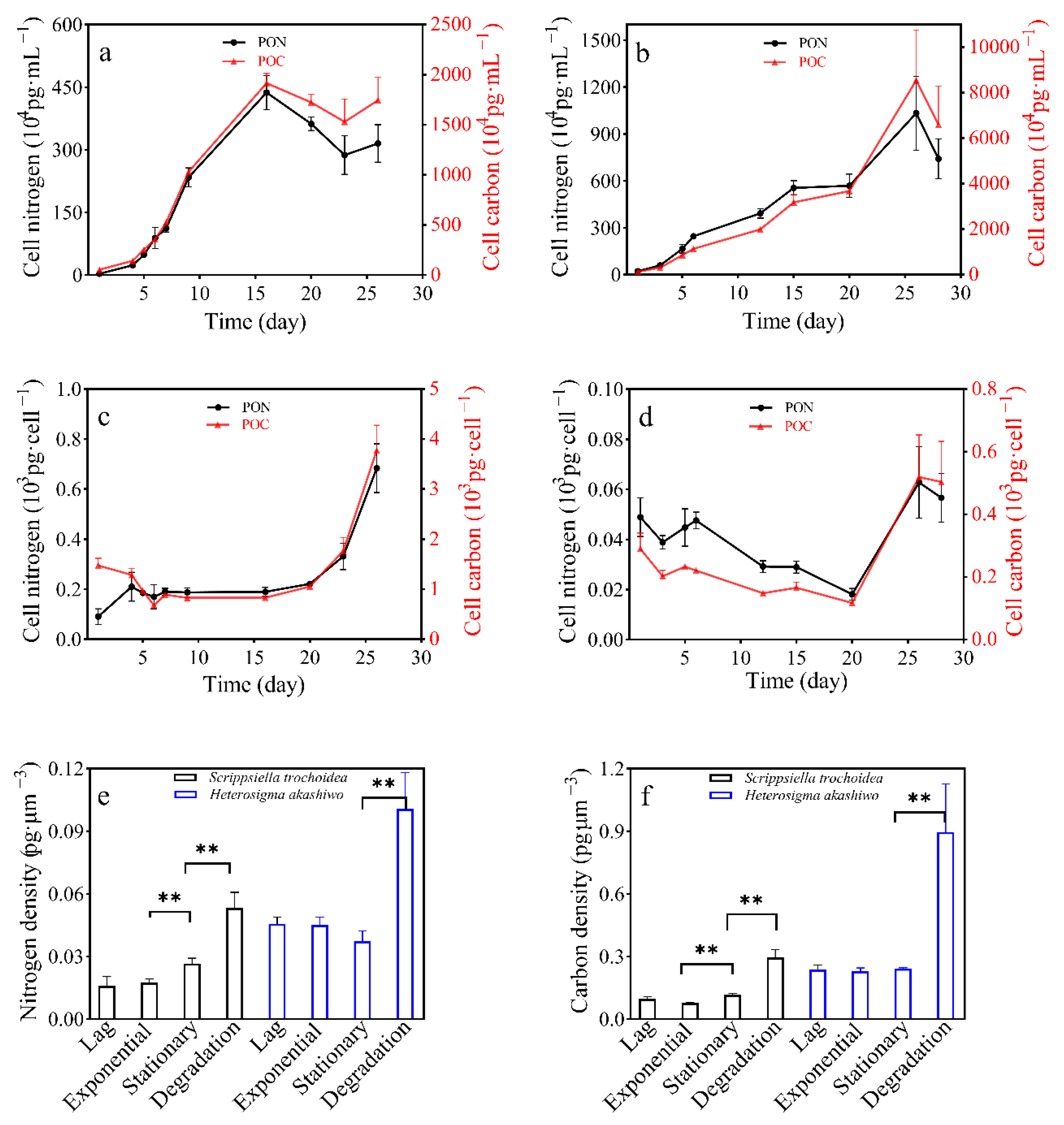
3.3. POC and PON Content in Two Microalgal Species
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sun, J. Marine phytoplankton and biological carbon sink. Acta Ecol. Sin. 2011, 31, 5372–5378. [Google Scholar]
- Marañón, E. Cell size as a key determinant of phytoplankton metabolism and community structure. Ann. Rev. Mar. 2014, 7, 241–264. [Google Scholar] [CrossRef]
- Duarte, C.M.; Conley, D.J.; Carstensen, J.; Sánchez-Camacho, M. Return to neverland: Shifting baselines affect eutrophication restoration targets. Estuaries Coast 2009, 2, 29–36. [Google Scholar] [CrossRef]
- Longhurst, A.R.; Harrison, W.G. The biological pump: Profiles of plankton production and consumption in the upper ocean. Prog. Oceanogr. 1989, 22, 47–123. [Google Scholar] [CrossRef]
- Jakobsen, H.H.; Markager, S. Carbon-to-chlorophyll ratio for phytoplankton in temperate coastal waters: Seasonal patterns and relationship to nutrients. Limnol. Oceanogr. 2016, 61, 1853–1868. [Google Scholar] [CrossRef]
- Vidoudez, C.; Pohnert, G. Comparative metabolomics of the diatom Skeletonema marinoi in different growth phases. Metabolomics 2012, 8, 654–669. [Google Scholar] [CrossRef]
- Laws, E.A.; Falkowski, P.G.; Smith, W.O., Jr.; Ducklow, H.; McCarthy, J.J. Temperature effects on export production in the open ocean. Glob. Biogeochem. Cycles 2000, 14, 1231–1246. [Google Scholar] [CrossRef]
- Armstrong, R.A.; Lee, C.; Hedges, J.I.; Honjo, S.; Wakeham, S.G. A new, mechanistic model for organic carbon fluxes in the ocean based on the quantitative association of POC with ballast minerals. Deep Sea Res. Part II 2001, 49, 219–236. [Google Scholar] [CrossRef]
- Vrede, K.; Heldal, M.; Norland, S.; Bratbak, G. Elemental composition (C, N, P) and cell volume of exponentially growing and nutrient-limited bacterioplankton. Appl. Environ. Microbiol. 2002, 68, 2965–2971. [Google Scholar] [CrossRef]
- Markou, G.; Depraetere, O.; Muylaert, K. Effect of ammonia on the photosynthetic activity of Arthrospira and Chlorella: A study on chlorophyll fluorescence and electron transport. Algal Res. 2016, 16, 449–457. [Google Scholar] [CrossRef]
- Bopaiah, B.; Benner, R. Carbon, nitrogen, and carbohydrate fluxes during the production of particulate and dissolved organic matter by marine phytoplankton. Limnol. Oceanogr. 1997, 42, 506–518. [Google Scholar] [CrossRef]
- Liang, C.J.; Wang, J.T.; Tan, L.J. Distribution of particulate organic carbon in Qingdao coastal waters in summer and winter. Mar. Environ. Sci. 2010, 29, 12–16. [Google Scholar] [CrossRef]
- Mongin, M.; Nelson, D.M.; Pondaven, P.; Tréguer, P. Simulation of upper-ocean biogeochemistry with a flexible-composition phytoplankton model: C, N and Si cycling and Fe limitation in the Southern Ocean. Deep Sea Res. Part II 2006, 53, 601–619. [Google Scholar] [CrossRef]
- Eppley, R.W.; Chavez, F.P.; Barber, R.T. Standing stocks of particulate carbon and nitrogen in the equatorial Pacific at 150 W. J. Geophys. Res. C: Ocean. 1992, 97, 655–661. [Google Scholar] [CrossRef]
- Oubelkheir, K.; Claustre, H.; Sciandra, A.; Babin, M. Bio-optical and biogeochemical properties of different trophic regimes in oceanic waters. Limnol. Oceanogr. 2005, 50, 1795–1809. [Google Scholar] [CrossRef]
- Behrenfeld, M.J.; Boss, E.; Siegel, D.A.; Shea, D.M. Carbon-based ocean productivity and phytoplankton physiology from space. Glob. Biogeochem. 2005, 19, GB1006. [Google Scholar] [CrossRef]
- Platt, T.; Sathyendranath, S.; Forget, M.H.; White, G.N., III; Caverhill, C.; Bouman, H. Operational estimation of primary production at large geographical scales. Remote Sens. Environ. 2008, 112, 3437–3448. [Google Scholar] [CrossRef]
- Terry, K.L.; Hirata, J.; Laws, E.A. Light-limited growth of two strains of the marine diatom Phaeodactylum tricornutum Bohlin-Chemical composition, carbon partitioning and the diel periodicity of physiological processes. J. Exp. Mar. Biol. Ecol. 1983, 68, 209–227. [Google Scholar] [CrossRef]
- Markager, S.; Sand-Jensen, K. Implications of thallus thickness for growth-irradiance relationships of marine macroalgae. Eur. J. Phycol. 1996, 31, 79–87. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Stuart, V.; Nair, A.; Oka, K.; Nakane, T.; Bouman, H.; Platt, T. Carbon-to chlorophyll ratio and growth rate of phytoplankton in the sea. Mar. Ecol. Prog. Ser. 2009, 383, 73–84. [Google Scholar] [CrossRef]
- Massie, T.M.; Blasius, B.; Weithoff, G.; Gaedke, U.; Fussmann, G.F. Cycles, phase synchronization, and entrainment in single-species phytoplankton populations. Proc. Natl. Acad. Sci. USA 2010, 107, 4236–4241. [Google Scholar] [CrossRef]
- Qi, Y.Z.; Zheng, L.; Wang, R. The life cycle of Scrippsiella trochoidea and its physiol-ecological control. Chin. J. Oceanol. Limnol 1997, 28, 588–593. [Google Scholar]
- Xiao, Y.Z. The relationship between Scrippsiella trochoidea red tide and cysts in the Daya Bay. Mar. Sci. 2001, 25, 50–54. [Google Scholar]
- Wang, Z.H.; Liang, W.B.; Guo, X.; Liu, L. Inactivation of Scrippsiella trochoidea cysts by different physical and chemical methods: Application to the treatment of ballast water. Mar. Pollut. Bull. 2018, 126, 150–158. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Lou, Y.D.; Wang, H.X.; Liu, Q. Effects of carbon source restricted on pH chang during growth of red tides algae. Mar. Environ. Sci. 2019, 38, 286–293. [Google Scholar]
- Zhou, C.X.; Wang, F.X.; Yan, X.J. Effects of temperature, salinity and irradiance on the cell stability of Heterosigma akashiwo Hada. Mar. Environ. Sci. 2008, 27, 17–20. [Google Scholar] [CrossRef]
- Qin, X.M.; Qin, P.Y.; Zou, J.Z. Effects of nitrogen and phosphorus on the growth of a red tide dinoflagellate Scrippsiella trochoidea (stein) loeblch III. Chin. J. Oceanol. Limnol. 1999, 17, 212–218. [Google Scholar] [CrossRef]
- Guillard, R.R.L.; Hargraves, P.E. Stichochrysis immobilis is a diatom, not a chrysophyte. Phycologia 1993, 32, 234–236. [Google Scholar] [CrossRef]
- Liu, Y.; Lv, J.P.; Feng, J.; Liu, Q.; Nan, F.R.; Xie, S.L. Treatment of real aquaculture wastewater from a fishery utilizing phytoremediation with microalgae. J. Chem. Technol. Biotechnol. 2019, 94, 900–901. [Google Scholar] [CrossRef]
- Sun, J.; Ning, X.R. Marine phytoplankton specific growth rate. Adv. Earth Sci. 2005, 20, 939–945. [Google Scholar] [CrossRef]
- Sun, J.; Liu, D.Y. Geometric models for calculating cell biovolume and surface area for phytoplankton. J. Plankton Res. 2003, 25, 1331–1346. [Google Scholar] [CrossRef]
- Welschmeyer, N.A. Fluorometric analysis of chlorophyll a in the presence of chlorophyll b and pheopigments. Limnol. Oceanogr. 1994, 39, 1985–1992. [Google Scholar] [CrossRef]
- Liu, H.J.; Xue, B.; Feng, Y.; Zhang, R.; Chen, M.; Sun, J. Size-fractionated Chlorophyll a biomass in the northern South China Sea in summer 2014. Chin. J. Oceanol. Limnol. 2016, 34, 672–682. [Google Scholar] [CrossRef]
- Xu, N.; Lv, S.H.; Chen, J.F.; He, L.S.; Xie, L.C.; Qi, Y.Z. The influence of water temperature and salinity on the growth of Scrippsiella trochoidea. Mar. Environ. Sci. 2004, 23, 36–38. [Google Scholar] [CrossRef]
- Ono, K.; Khan, S.; Onoue, Y. Effects of temperature and light intensity on the growth and toxicity of Heterosigma akashiwo (Raphidophyceae). Aquacult. Res. 2000, 31, 427–433. [Google Scholar] [CrossRef]
- Guo, Y.J. Studies on heterosigma akashiwo (HADA) in the Dalian bight, Liaoning, China. Oceanol. Limnol. Sin. 1994, 25, 211–215. [Google Scholar]
- Wang, Z.H.; Qi, Y.Z.; Chen, J.F.; Xu, N.; Yang, Y.F. Phytoplankton abundance, community structure and nutrients in cultural areas of Daya Bay, South China Sea. J. Mar. Syst. 2006, 62, 85–94. [Google Scholar] [CrossRef]
- Wang, H.Q. The Heterosigma Akashiwo red tide and ecological characteristics in Dalian Bight. Res. Environ. Sci. 1991, 4, 53–59. [Google Scholar]
- Finkel, Z.V.; Beardall, J.; Flynn, K.J.; Quigg, A.; Rees, T.A.V.; Raven, J.A. Phytoplankton in a changing world: Cell size and elemental stoichiometry. J. Plankton Res. 2009, 1, 119–137. [Google Scholar] [CrossRef]
- Sun, J.; Liu, D.Y.; Chen, Z.T.; Wei, T.D. Growth of Platymonas helgolandica var. tsingtaoensis, Cylindrotheca closterium and Karenia mikimotoi and their survival strategies under different N/P ratios. J. Appl. Ecol. 2004, 15, 2122–2126. [Google Scholar] [CrossRef]
- Goldman, J.C.; Hansell, D.A.; Dennett, M.R. Chemical characterization of three large oceanic diatoms: Potential impact on water column chemistry. Mar. Ecol. Prog. Ser. 1992, 88, 257–270. [Google Scholar] [CrossRef]
- Beardall, J.; Allen, D.; Bragg, J.; Finkel, Z.V.; Flynn, K.J.; Quigg, A.; Raven, J.A. Allometry and stoichiometry of unicellular, colonial and multicellular phytoplankton. New Phytol. 2009, 181, 295–309. [Google Scholar] [CrossRef]
- Riegman, R.; Mur, L.R. Theoretical considerations on growth kinetics and physiological adaptation of nutrient-limited phytoplankton. Arch. Microbiol. 1984, 140, 96–100. [Google Scholar] [CrossRef]
- Huete-Ortega, M.; Cermeno, P.; Calvo-Díaz, A.; Marañón, E. Isometric size-scaling of metabolic rate and the size abundance distribution of phytoplankton. Proc. R. Soc. Lond. Ser. B 2012, 279, 1815–1823. [Google Scholar] [CrossRef]
- Sunda, W.G.; Hardison, D.R. Evolutionary tradeoffs among nutrient acquisition, cell size, and grazing defense in marine phytoplankton promote ecosystem stability. Mar. Ecol. Prog. Ser. 2010, 401, 63–76. [Google Scholar] [CrossRef]
- Bian, M.M.; Song, J.L.; Feng, J.Y.; Liu, Z.L. Occurrence and ananlysis of red tides in Qinhuangdao sea area. Heibei Fish. 2019, 8, 26–28. [Google Scholar]
- Viličić, D. An examination of cell volume in dominant phytoplankton species of the central and southern Adriatic Sea. Int. Rev. Gesamten Hydrobiol. 1985, 70, 829–843. [Google Scholar] [CrossRef]
- Parsons, T.R.; Stephens, K.; Strickland, J.D.H. On the chemical composition of eleven species of marine phytoplankters. J. Fish. Res. Board Can. 1961, 18, 1001–1016. [Google Scholar] [CrossRef]
- Marañón, E.; Cermeño, P.; López-Sandoval, D.C.; Rodríguez-Ramos, T.; Sobrino, C.; Huete-Ortega, M.; Maria Blanco, J.; Rodríguez, J. Unimodal size scaling of phytoplankton growth and the size dependence of nutrient uptake and use. Ecol. Lett. 2013, 16, 371–379. [Google Scholar] [CrossRef]
- Geider, R.; La Roche, J. Redfield revisited: Variability of C: N: P in marine microalgae and its biochemical basis. Eur. J. Phycol. 2002, 37, 1–17. [Google Scholar] [CrossRef]
- Klausmeier, C.A.; Litchman, E.; Levin, S.A. Phytoplankton growth and stoichiometry under multiple nutrient limitation. Limnol. Oceanogr. 2004, 49, 1463–1470. [Google Scholar] [CrossRef]
- Arrigo, K.R. Marine microorganisms and global nutrient cycles. Nature 2005, 437, 349–355. [Google Scholar] [CrossRef] [PubMed]
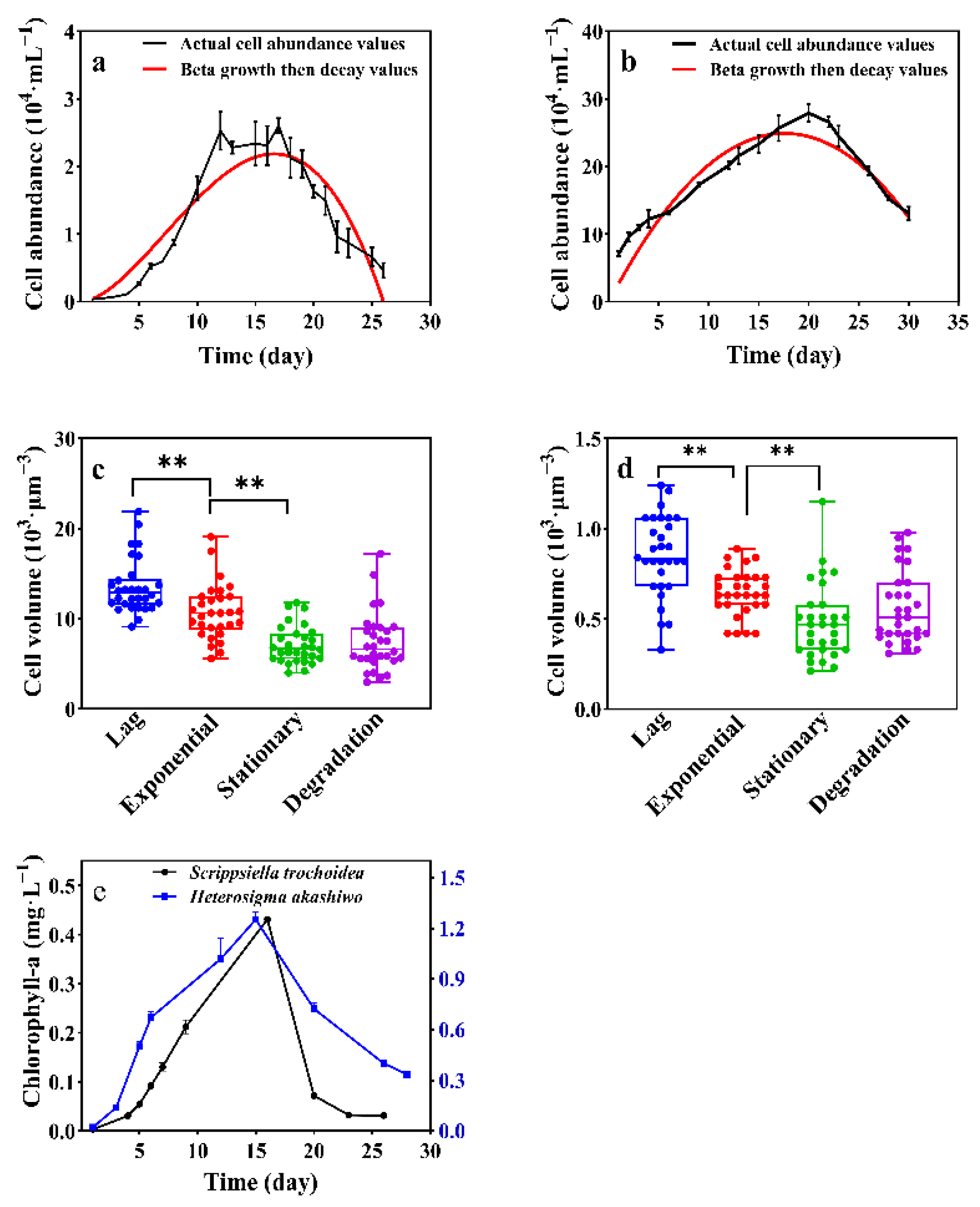
| Species | Model | Formula | R-Squared | K (104·mL−1) | T (d) | Tm (d) |
|---|---|---|---|---|---|---|
| Scrippsiella trochoidea | Beta growth then decay | Yt = K × (1+ (Tm − t)/(Tm − T)) × (t/Tm)^(Tm/(Tm − T)) | 0.872 | 2.185 | 7.21 | 24.09 |
| Heterosigma akashiwo | 0.970 | 25.88 | 9.55 | 16.60 |
| POC Quotas (Average ± SD) /pg·Cell−1 | PON Quotas (Average ± SD) /pg·Cell−1 | POC Densities (Average ± SD) /pg·μm−3 | PON Densities (Average ± SD) /pg·μm−3 | ||
|---|---|---|---|---|---|
| S. trochoidea | lag | 1285.3 ± 126.55 a | 210.21 ± 57.92 a | 0.0947 ± 0.0093 a | 0.0159 ± 0.0043 a |
| exponential | 825.98 ± 21.70 b | 187.65 ± 18.50 b | 0.0768 ± 0.0020 a | 0.0175 ± 0.0017 a | |
| stationary | 830.35 ± 41.80 b | 189.60 ± 17.71 b | 0.1168 ± 0.0058 b | 0.0267 ± 0.0023 b | |
| degradation | 3778.90 ± 497.56 c | 683.53 ± 97.55 c | 0.5101 ± 0.0671 c | 0.0532 ± 0.0076 c | |
| H. akashiwo | lag | 202.18 ± 18.73 a | 38.86 ± 2.73 a | 0.2376 ± 0.0220 a | 0.0457 ± 0.0032 a |
| exponential | 148.46 ± 10.00 b | 29.20 ± 2.33 b | 0.2298 ± 0.0155 a | 0.0452 ± 0.0036 a | |
| stationary | 116.92 ± 2.06 b | 18.09 ± 2.36 c | 0.2415 ± 0.0043 a | 0.0374 ± 0.0049 a | |
| degradation | 503.83 ± 129.22 c | 56.66 ± 9.69 a | 0.8958 ± 0.2297 b | 0.1007 ± 0.0172 b | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Liu, Y.; Noman, M.A.; Thangaraj, S.; Sun, J. Physiological Changes and Elemental Ratio of Scrippsiella trochoidea and Heterosigma akashiwo in Different Growth Phase. Water 2021, 13, 132. https://doi.org/10.3390/w13020132
Liu X, Liu Y, Noman MA, Thangaraj S, Sun J. Physiological Changes and Elemental Ratio of Scrippsiella trochoidea and Heterosigma akashiwo in Different Growth Phase. Water. 2021; 13(2):132. https://doi.org/10.3390/w13020132
Chicago/Turabian StyleLiu, Xiaofang, Yang Liu, Md Abu Noman, Satheeswaran Thangaraj, and Jun Sun. 2021. "Physiological Changes and Elemental Ratio of Scrippsiella trochoidea and Heterosigma akashiwo in Different Growth Phase" Water 13, no. 2: 132. https://doi.org/10.3390/w13020132
APA StyleLiu, X., Liu, Y., Noman, M. A., Thangaraj, S., & Sun, J. (2021). Physiological Changes and Elemental Ratio of Scrippsiella trochoidea and Heterosigma akashiwo in Different Growth Phase. Water, 13(2), 132. https://doi.org/10.3390/w13020132







