Study on the Dynamic Responses of a Large Caisson during Wet-Towing Transportation
Abstract
1. Introduction
2. Caisson Model and Towing System
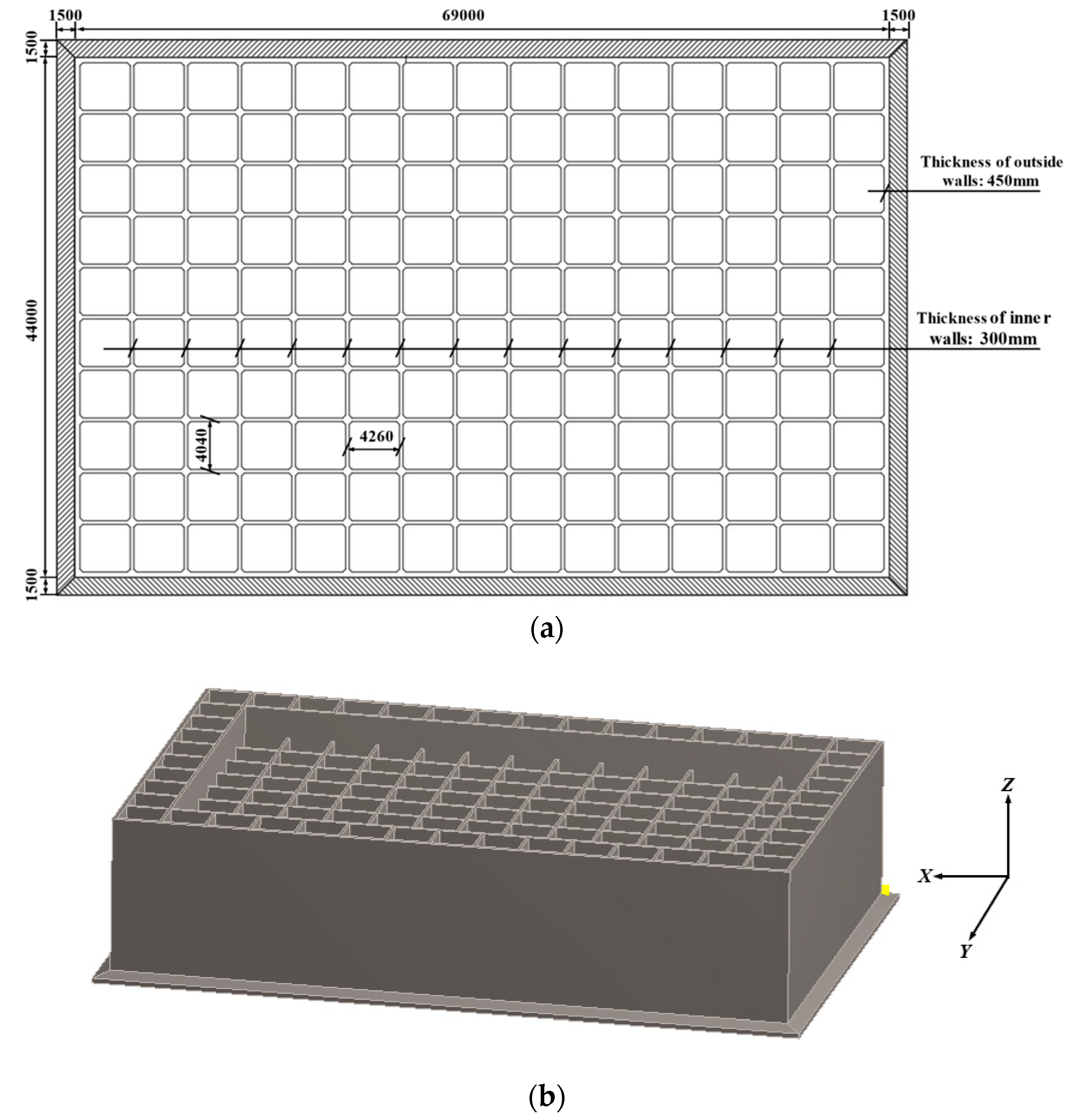
2.1. Caisson Model
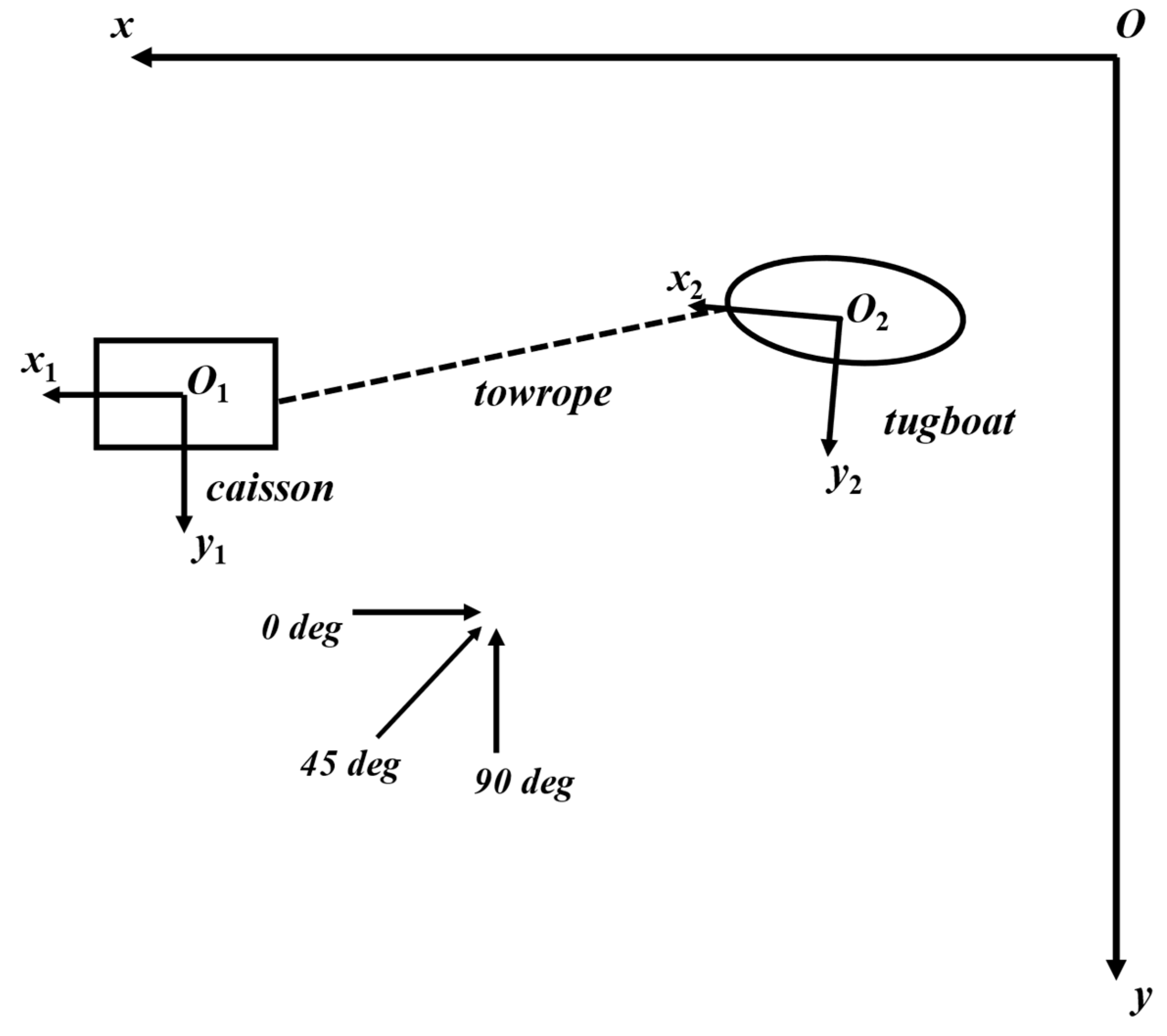
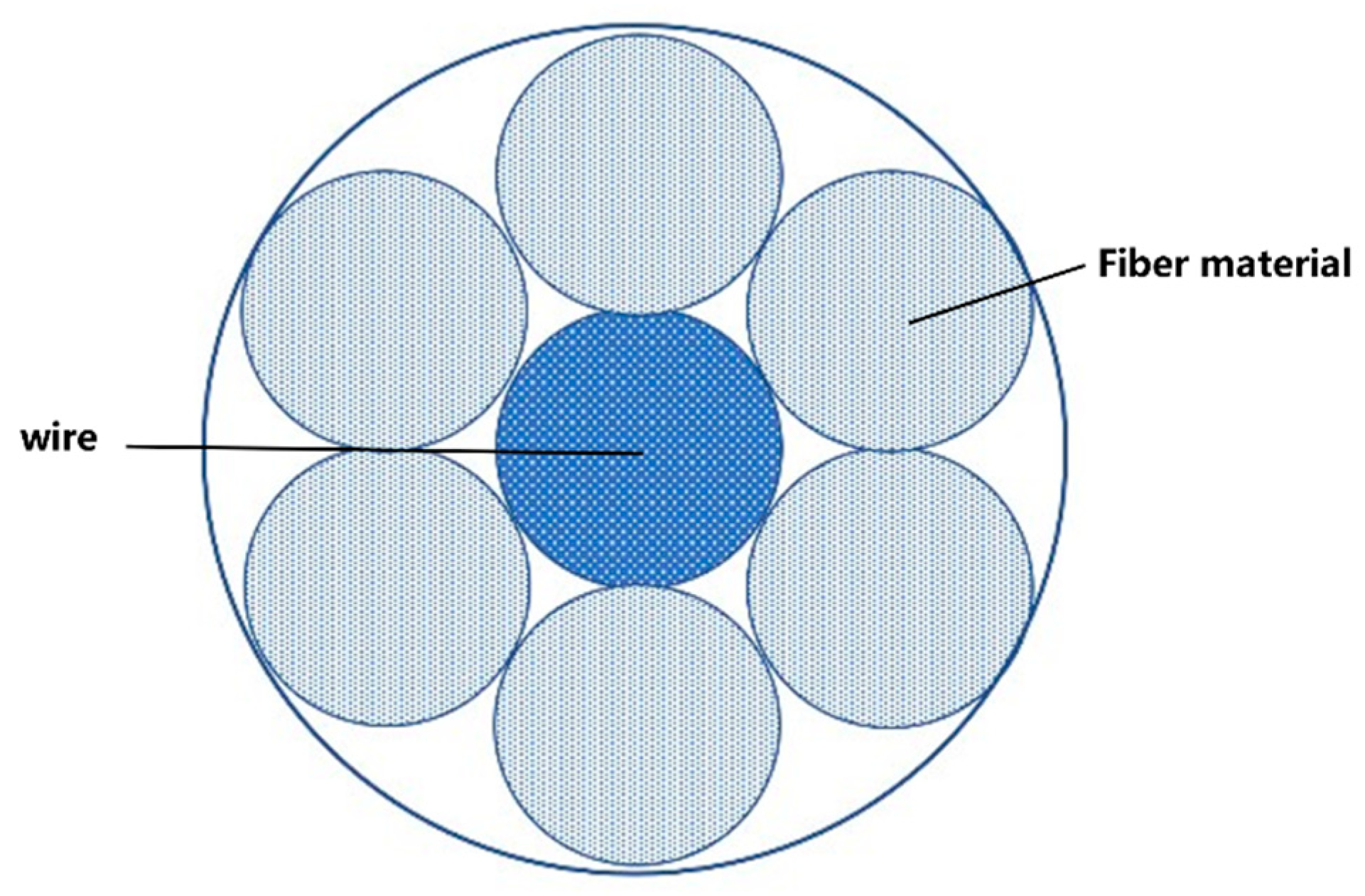
2.2. Towing System
3. Numerical Method
3.1. Intact Stability Analysis
3.2. Hydrodynamics Analysis
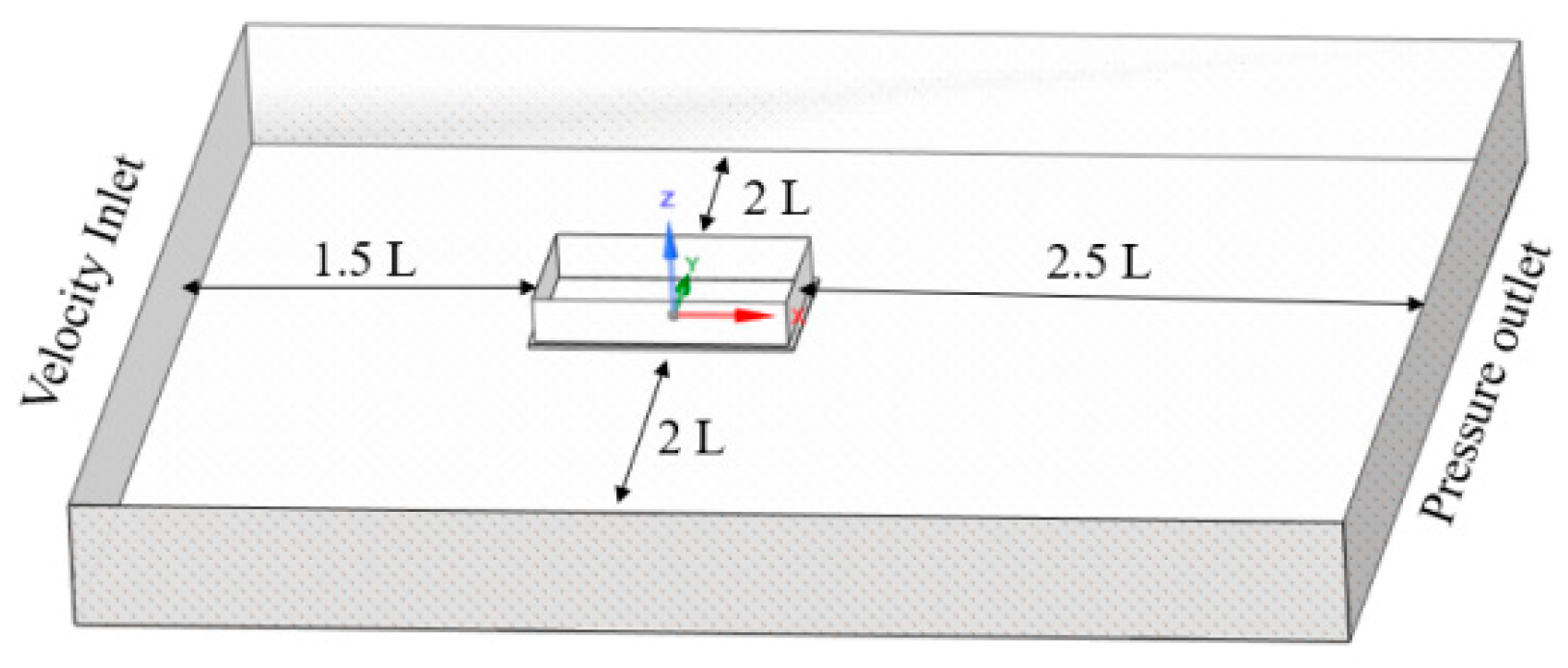
3.3. Mesh Convergence Analyses
3.4. Estimation of CO2 Emissions
4. Numerical Results
4.1. Stability Analysis Results
4.2. Results of Dynamic Response
4.2.1. Drift Depth and Towing Speed
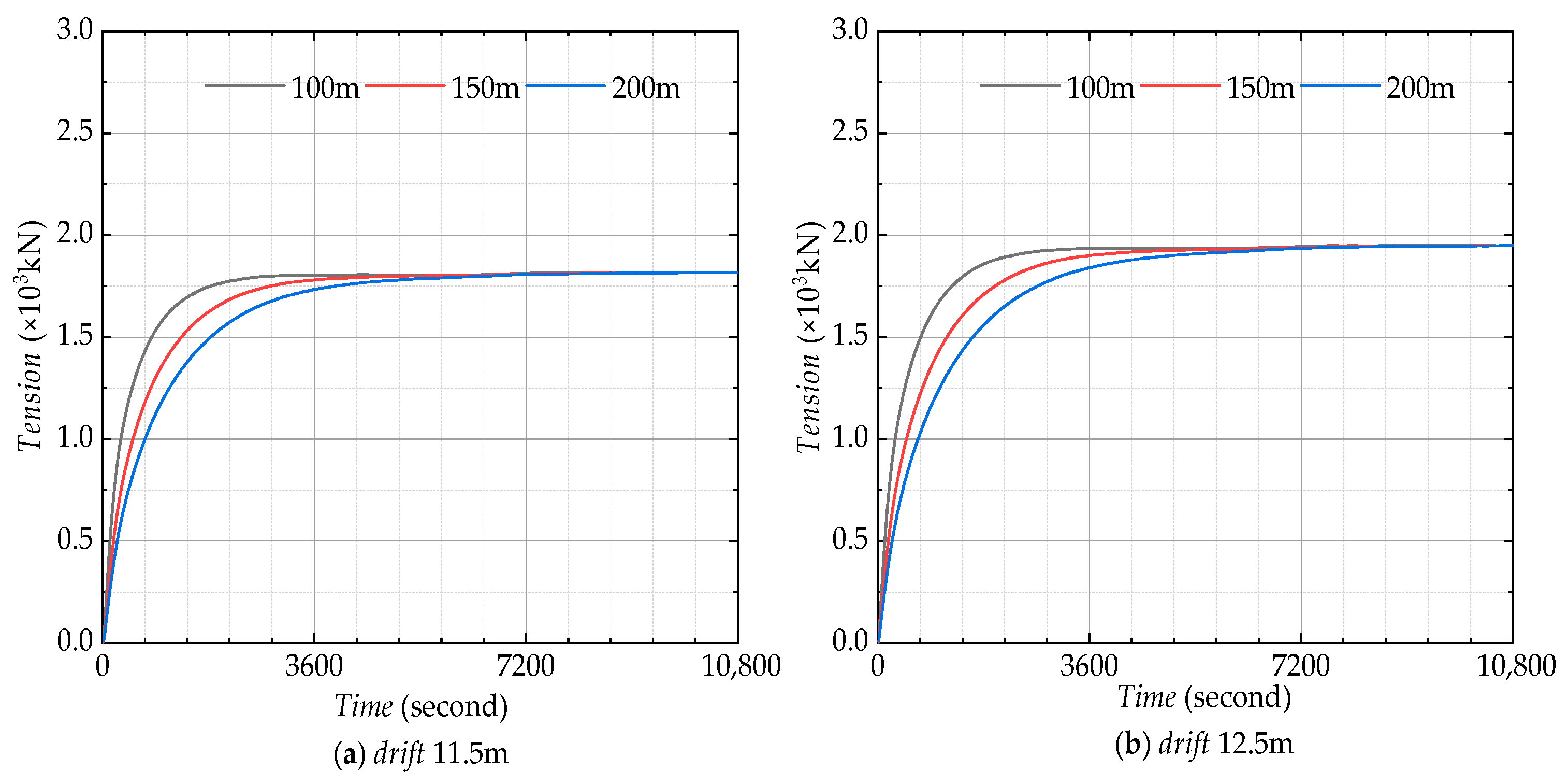
4.2.2. Drift Depth and Towrope Length
4.3. Extmated of CO2 Emissions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Y.; Miao, W.; Ding, Q.; Li, C.; Xiang, B. Numerical investigations on control strategies of wake deviation for large wind turbines in an offshore wind farm. Ocean Eng. 2019, 173, 794–801. [Google Scholar] [CrossRef]
- Algaze, G. Ancient Mesopotamia at the Dawn of Civilization: The Evolution of an Urban Landscape; The University of Chicago Press: Chicago, IL, USA, 2008. [Google Scholar]
- Kim, B.; Kim, T.W. Scheduling and cost estimation simulation for transport and installation of floating hybrid generator platform. Renew. Energy 2017, 111, 131–146. [Google Scholar] [CrossRef]
- Kim, B.; Kim, T.W. Monte Carlo simulation for offshore transportation. Ocean Eng. 2017, 129, 177–190. [Google Scholar] [CrossRef]
- Sinibaldi, M.; Bulian, G. Towing simulation in wind through a nonlinear 4-dof model: Bifurcation analysis and occurrence of fishtailing. Ocean Eng. 2014, 88, 366–392. [Google Scholar] [CrossRef]
- Marine Accident Investigation Branch (MAIB). Report on the Investigation of the Loss of the Tug Flying Phantom While Towing Red Jasmine on the River Clyde on 19 December 2007. Resulting in 3 Fatalities and 1 Injury; Report No. 17/2008; Marine Accident Investigation Branch (MAIB): Southampton, UK, 2008. Available online: https://assets.publishing.service.gov.uk/media/547c7010ed915d4c0d000073/FlyingPhantom.pdf (accessed on 4 January 2021).
- Transportation Safety Board of Canada (TSB). Marine Investigation Report M09W0141. Tug Girding and Capsizing. Tug North Arm Venture While Towing the Barge North Arm Express, Entrance to the Sechelt Rapids, British Columbia, 19 July 2009; Transportation Safety Board of Canada (TSB): Gatineau, QC, Canada, 2009. Available online: https://www.bst-tsb.gc.ca/eng/rapports-reports/marine/2009/m09w0141/m09w0141.pdf (accessed on 4 January 2021).
- Lyng, I.; Andreassen, D.; Fiksdal, G.; Loken, G.; Skolvy, Y.; Petternsen, T. The Loss of the Bourbon Dolphin on 12 April 2007; Official Norwegian Reports; Government Administration Services: Oslo, Norwegian, 2008; Volume 8, ISBN 987-82-583-0965-6.
- Berg, P. A Discussion of Technical Challenges and Operational Limits for Towing Operations. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2017. [Google Scholar]
- Berbitsas, M.M.; Kekridis, N.S. Nonlinear Stability Analysis of Ship Towed by Elastic Rope. J. Ship Res. 1986, 30, 136–146. [Google Scholar]
- Bernitsas, M.M.; Kekridis, N.S. Simulation and Stability of Ship Towing. Int. Shipbuild. Prog. 1985, 32, 112–123. [Google Scholar] [CrossRef]
- Fitriadhy, A.; Yasukawa, H.; Koh, K.K. Course stability of a ship towing system in wind. Ocean Eng. 2013, 64, 135–145. [Google Scholar] [CrossRef]
- Fitriadhy, A.; Yasukawa, H. Course stability of a ship towing system. Ship Technol. Res. Schiffstechnik. 2011, 58, 4–23. [Google Scholar] [CrossRef]
- Jurewicz, J.M. Design and Construction of an Offshore Floating Nuclear Power Plant. Doctoral Dissertation, Massachusetts Institute of Technology, Cambridge, MA, USA, 2015. [Google Scholar]
- Kang, W.; Zhang, C.; Yu, J.X. Stochastic extreme motion analysis of jack-up responses during wet towing. Ocean Eng. 2016, 111, 56–66. [Google Scholar] [CrossRef]
- Zhao, Z.; Tang, Y.; Wu, Z.; Li, Y.; Wang, Z. Towing Analysis of Multi-Cylinder Platform for Offshore Marginal Oil Field Development. In Proceedings of the ASME 2016 35th International Conference on Ocean, Offshore and Arctic Engineering, Busan, Korea, 19–24 June 2016. [Google Scholar]
- Ding, H.; Han, Y.; Le, C.; Zhang, P. Dynamic analysis of a floating wind turbine in wet tows based on multi-body dynamics. J. Renew. Sustain. Energy 2017, 9, 033104. [Google Scholar] [CrossRef]
- Zhang, P.; Peng, Y.; Ding, H.; Hu, R.; Shi, J. Numerical analysis of offshore integrated meteorological mast for wind farms during wet towing transportation. Ocean Eng. 2019, 188, 106271. [Google Scholar] [CrossRef]
- JIAN FENG SLING CO., LTD. Available online: http://www.jian-feng.com/page85.html?article_id=9 (accessed on 13 December 2020).
- Rawson, K.J.; Tupper, E.C. Basic Ship Theory; Longman: London, UK, 2001. [Google Scholar]
- Lee, S.; Hong, C. Study on the course stability of very large vessels in shallow water using CFD. Ocean Eng. 2017, 145, 395–405. [Google Scholar] [CrossRef]
- Liu, Y.; Zou, Z.; Zou, L.; Fan, S. Cfd-based numerical simulation of pure sway tests in shallow water towing tank. Ocean Eng. 2019, 189, 106311. [Google Scholar] [CrossRef]
- Jin, Y.; Duffy, J.; Chai, S.; Chin, C.; Bose, N. URANS study of scale effects on hydrodynamic manoeuvering coefficients of KVLCC2. Ocean Eng. 2016, 118, 93–106. [Google Scholar] [CrossRef]
- He, R.; Zhang, Z.Z.; Wang, X.Z.; Feng, D.K. Numerical simulation of the ship bottom interaction DTC container carrier for different keel clearance in pure sway motion. In Proceedings of the 4th International Conference on Ship Manoeuvering in Shallow and Confined Water (MASHCON): Ship-Bottom interaction, Hamburg, Germany, 23–25 May 2016; pp. 65–72. [Google Scholar]
- Tang, S. Flow Friction of Pile and Pile Group and Its Application on the Tidal Numerical Modelling. Doctoral Dissertation, Dalian University of Technology, Dalian, China, 2002. [Google Scholar]
- Jürgen, W. Handbook of Terminal Planning, 2nd ed.; Springer: Suderburg, Germany, 2011. [Google Scholar]
- Karimirad, M.; Moan, T. Wave-and wind-induced dynamic response of a spar-type offshore wind turbine. J. Waterw. Port Coast. Ocean Eng. 2012, 138, 9–20. [Google Scholar] [CrossRef]
- CCS. Guidelines for Towage at Sea; CCS: Beijing, China, 2011. [Google Scholar]
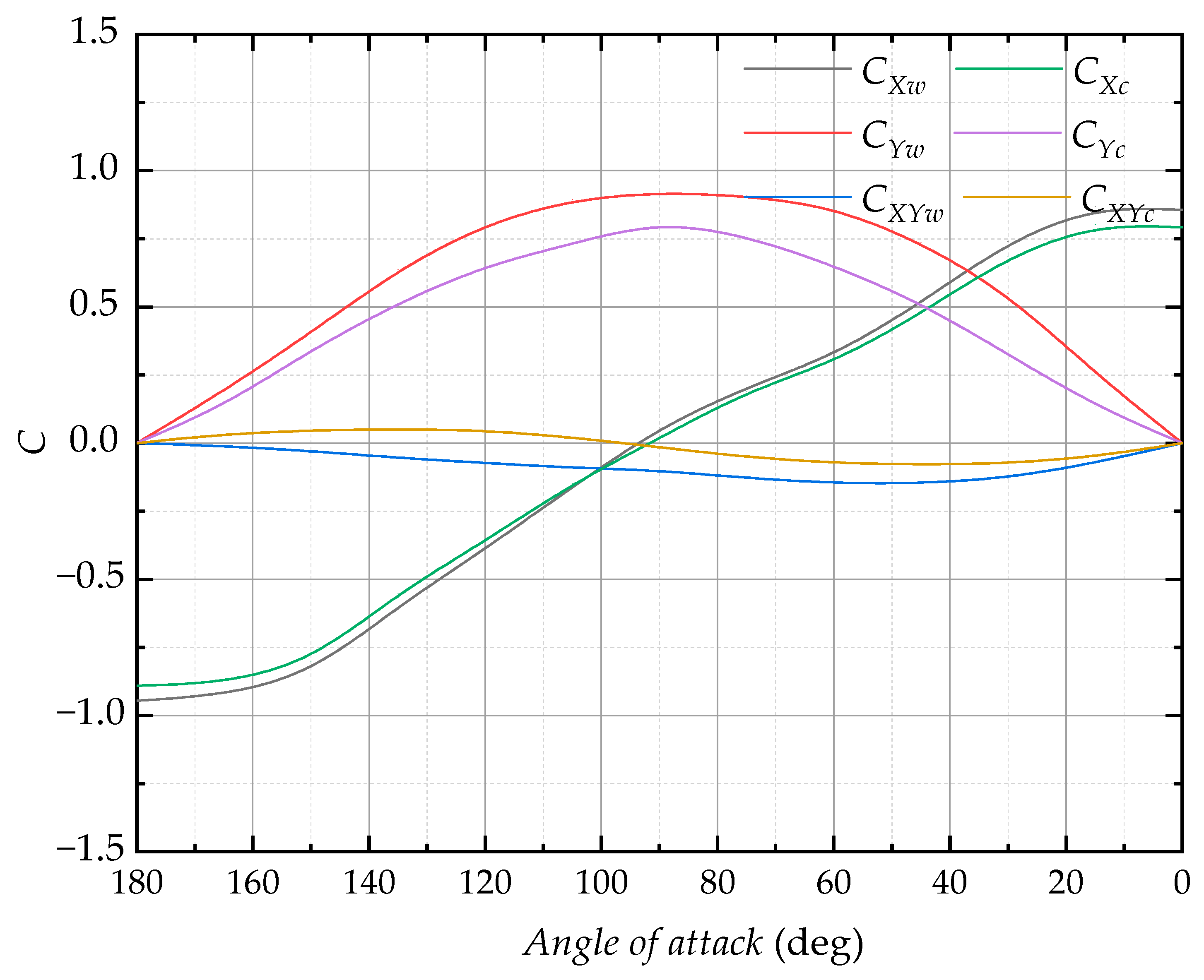
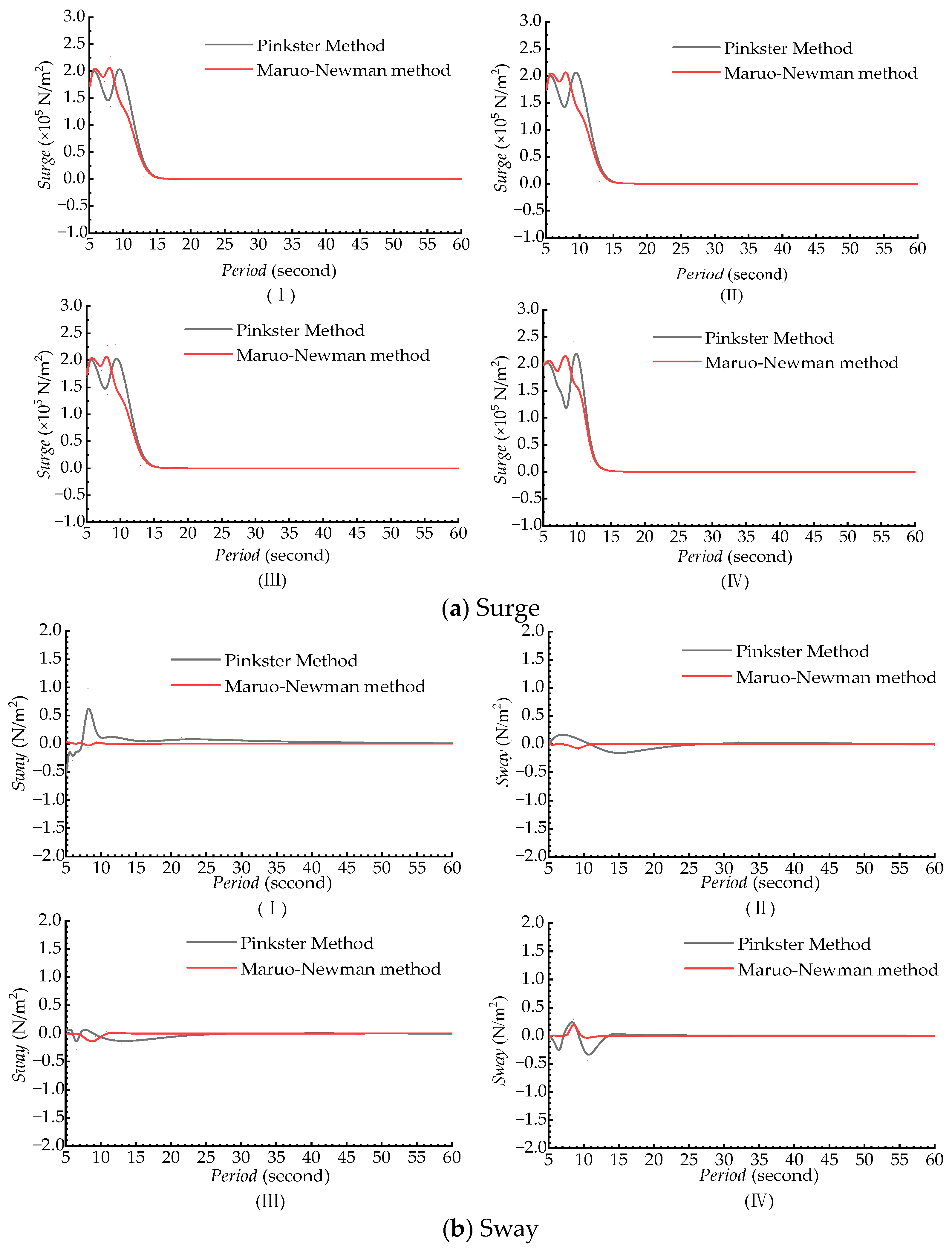
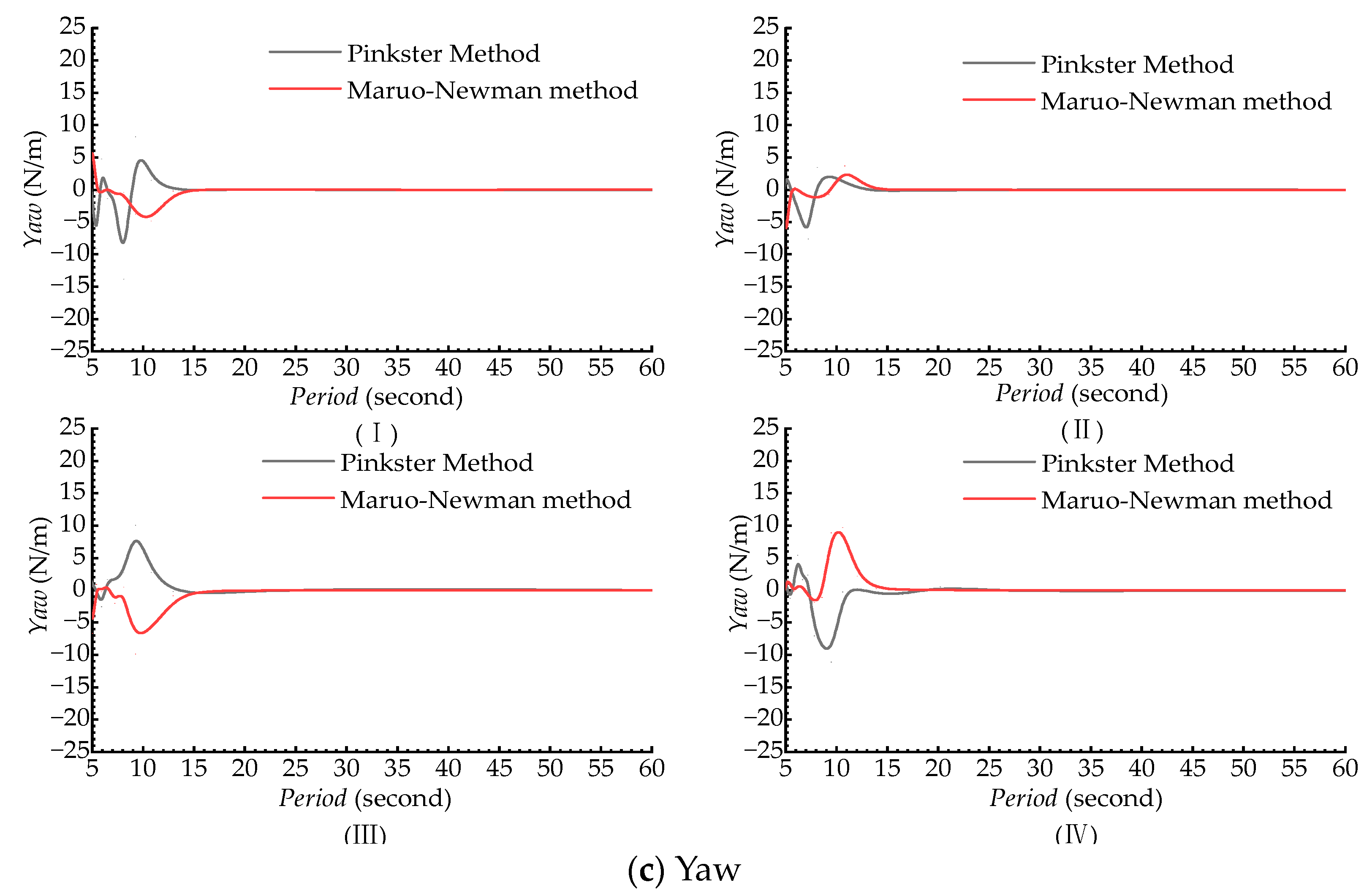
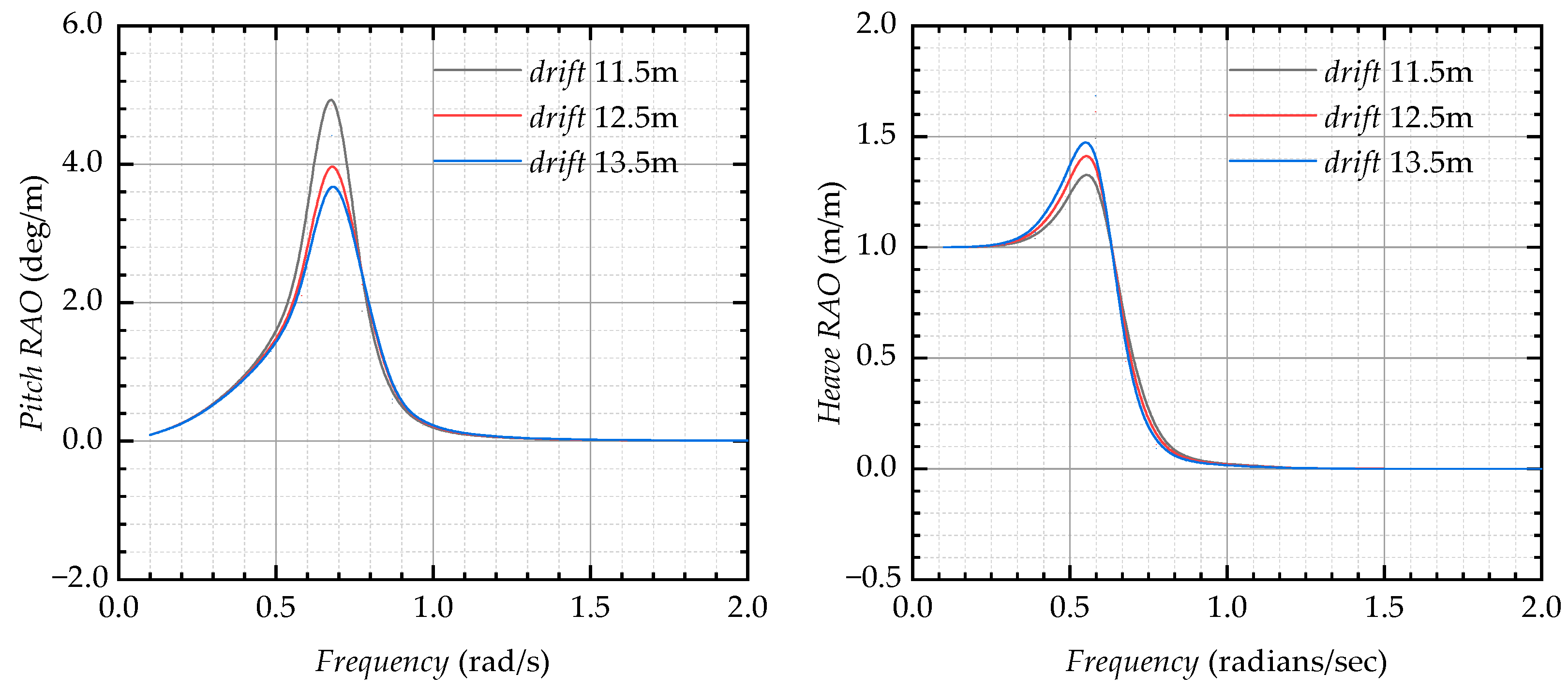

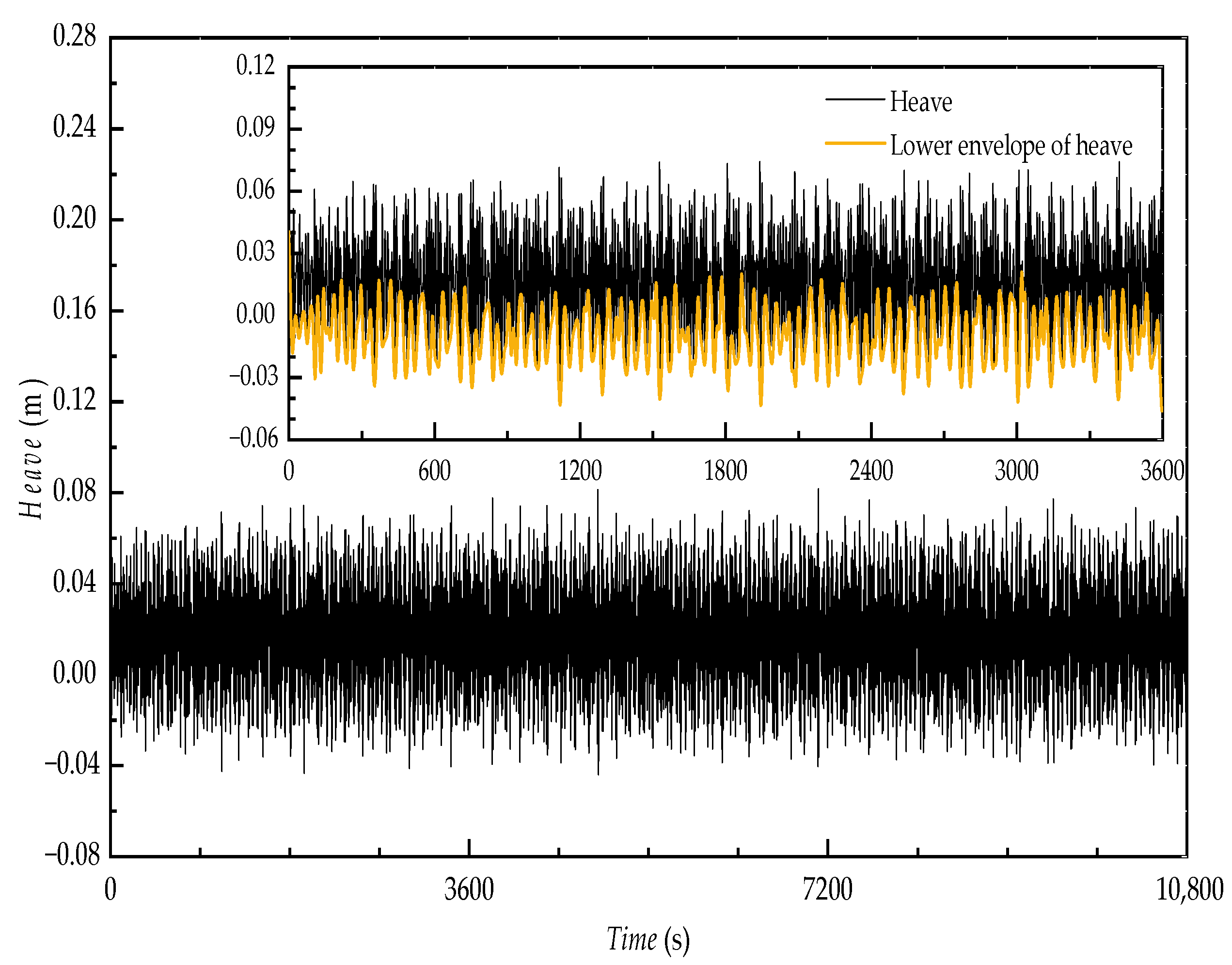
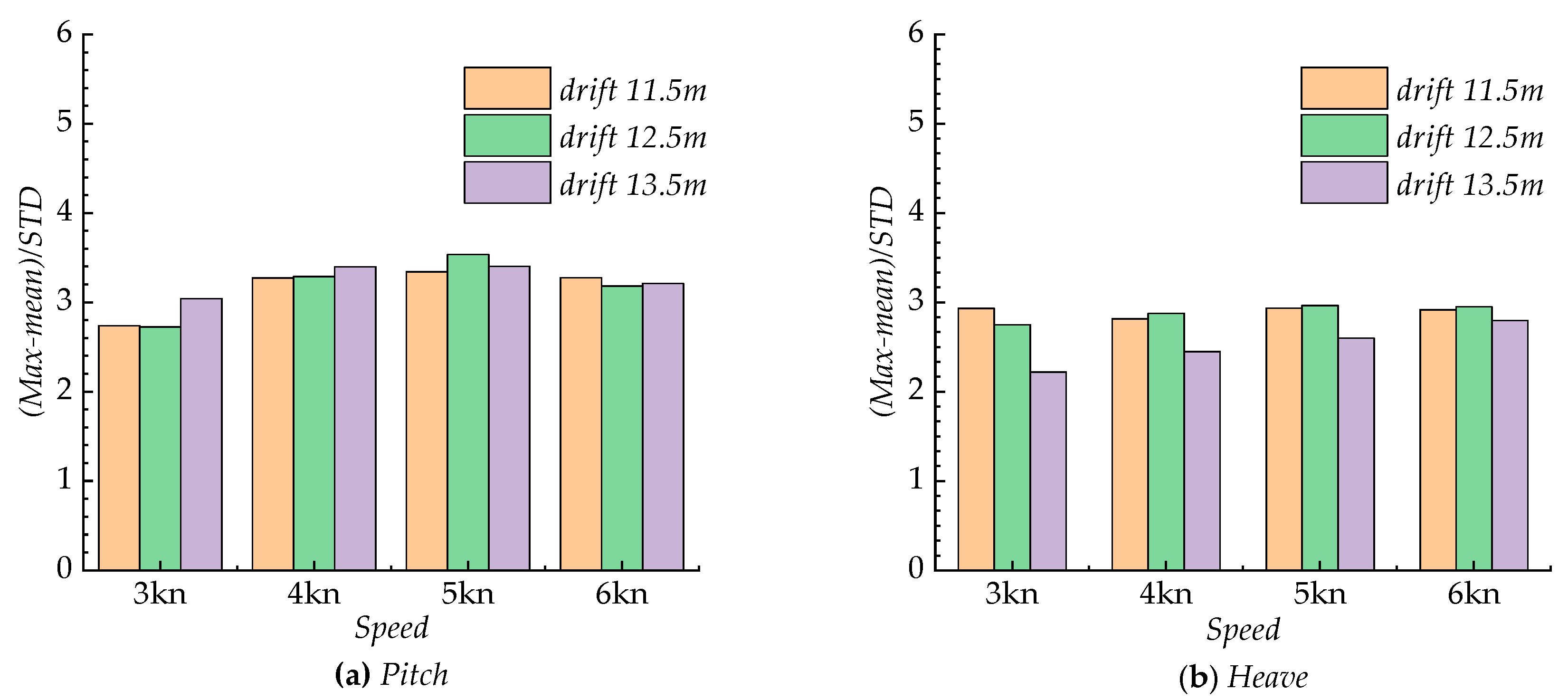
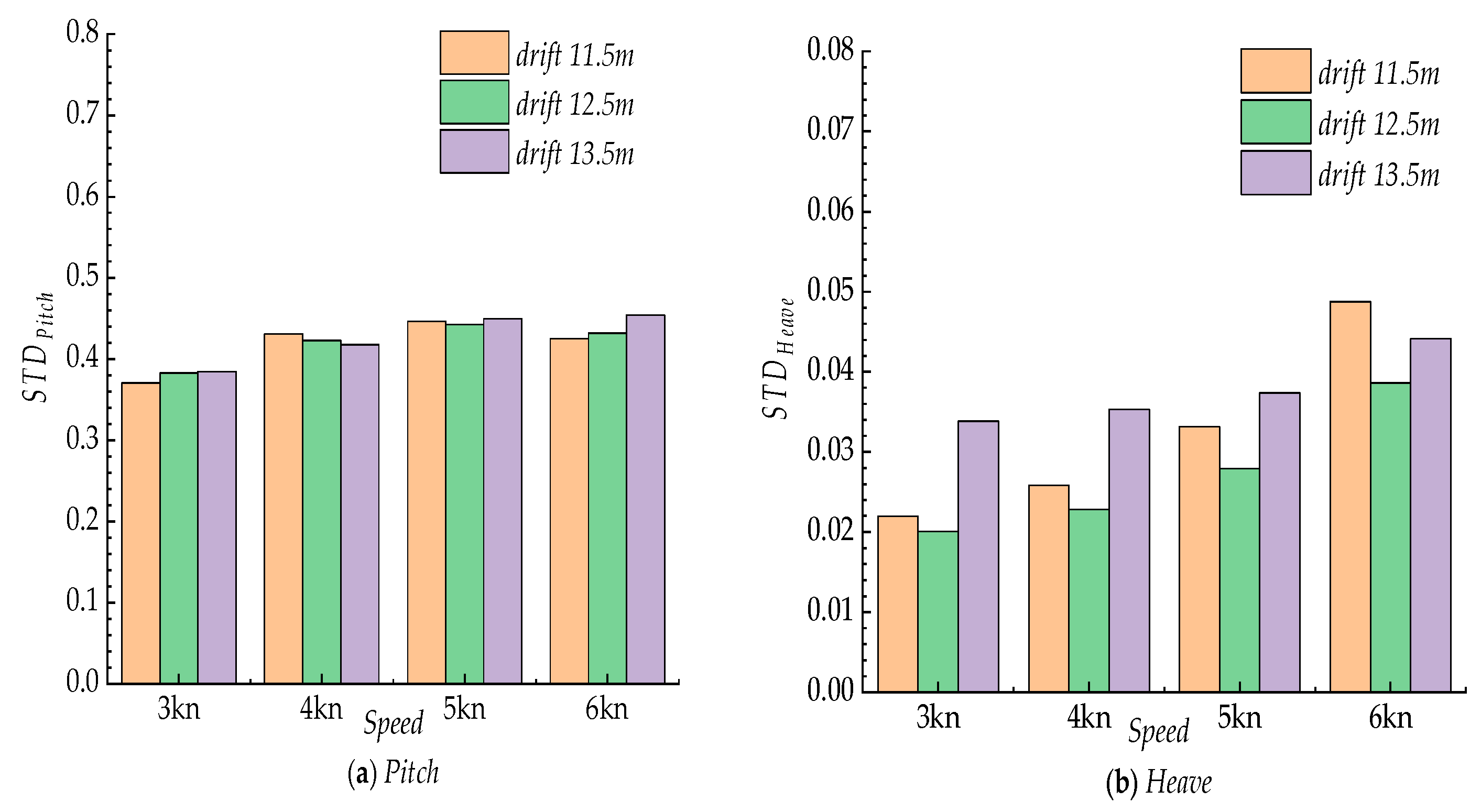
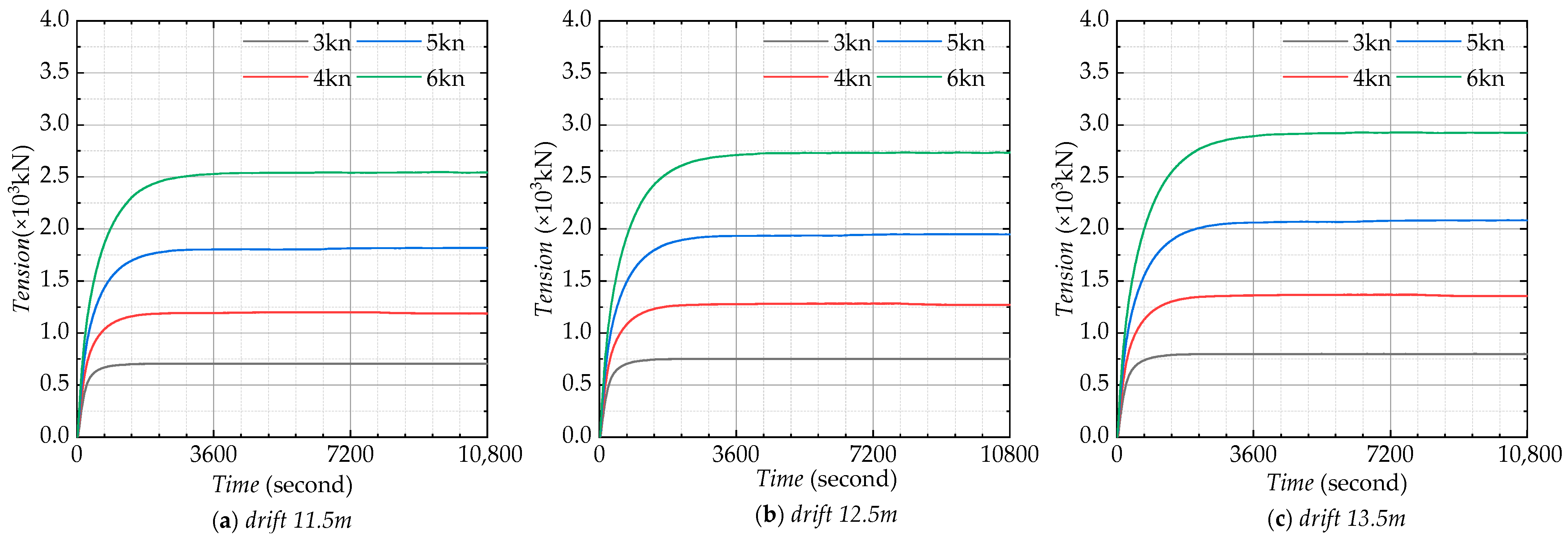
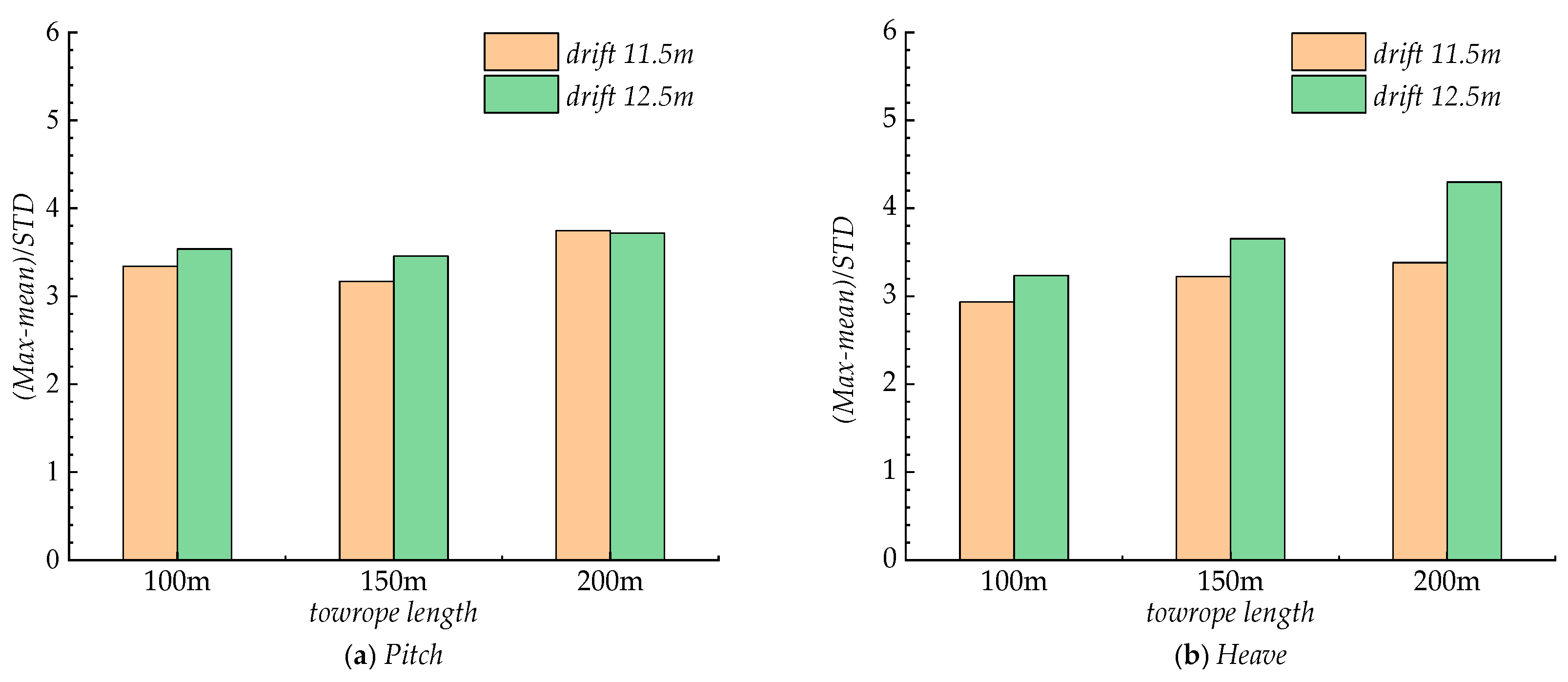
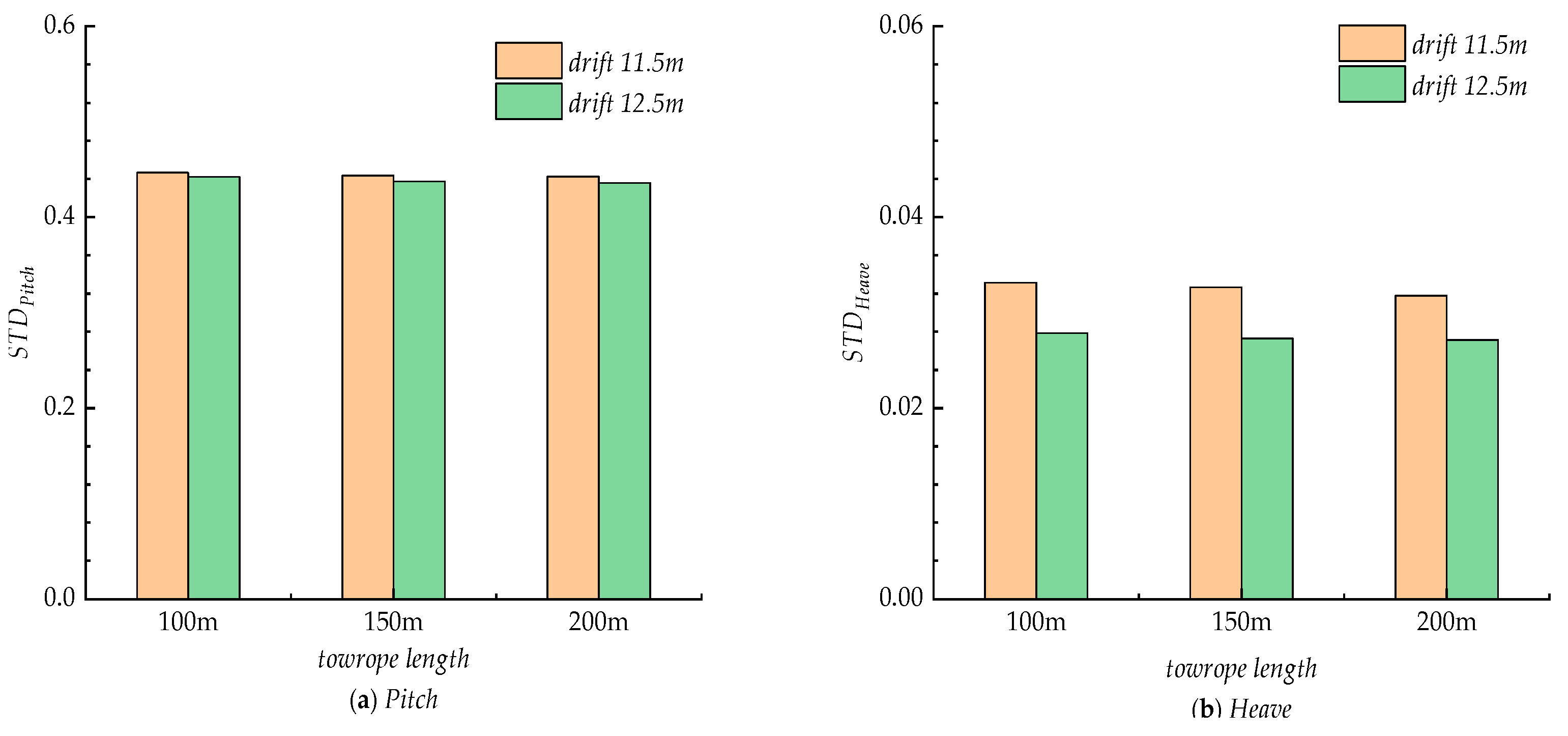
| Items | Value |
|---|---|
| Length/m | 69 |
| Width/m | 44 |
| Height/m | 16.8 |
| Initial draft/m | 8.2 |
| Center of gravity/m | (0, 0, 5.58) |
| Radius of gyration (COG)/m | (5, 7, 8) |
| Angle/deg | CTang’s | Cfluent | Error |
|---|---|---|---|
| 0 | 1.88 | 1.931 | 2.71% |
| 10 | 1.26 | 1.294 | 2.70% |
| 20 | 1.26 | 1.276 | 1.27% |
| 30 | 1.33 | 1.351 | 1.58% |
| 45 | 1.42 | 1.464 | 3.10% |
| Drift/m | - | IXX/m4 | ▽/m3 | BM/m | ZB/m | ZG/m | GM/m | Error |
|---|---|---|---|---|---|---|---|---|
| 11.50 | AQWA | 489,807.00 | 35,122.00 | 13.95 | −5.79 | −6.76 | 14.92 | 4.65% |
| 11.50 | Theoretical | 506,950.25 | 34,914.00 | 14.52 | −5.79 | −6.91 | 15.64 | |
| 12.50 | AQWA | 489,807.00 | 38,209.40 | 12.82 | −6.29 | −7.66 | 14.19 | 3.82% |
| 12.50 | Theoretical | 506,950.25 | 37,950.00 | 13.36 | −6.29 | −7.68 | 14.75 | |
| 13.50 | AQWA | 489,807.00 | 41,247.10 | 11.87 | −6.79 | −8.50 | 13.58 | 4.28% |
| 13.50 | Theoretical | 506,950.25 | 40,986.00 | 12.37 | −6.79 | −8.61 | 14.19 |
| Drift/m | Speed/kn | STD | Error | Mean/m | Error | Normalized Max | Error | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 h | 3 h | 1 h | 3 h | 1 h | 3 h | |||||
| 11.5 m | 3 kn | 0.022 | 0.022 | 1.25% | 0.017 | 0.017 | 0.10% | 2.635 | 2.934 | 10.20% |
| 11.5 m | 4 kn | 0.025 | 0.026 | 2.53% | 0.017 | 0.017 | 0.13% | 2.723 | 2.816 | 3.29% |
| 11.5 m | 5 kn | 0.031 | 0.033 | 6.17% | 0.017 | 0.017 | 0.07% | 2.807 | 2.935 | 4.36% |
| 11.5 m | 6 kn | 0.043 | 0.049 | 12.43% | 0.017 | 0.017 | 0.27% | 2.880 | 2.916 | 1.24% |
| 12.5 m | 3 kn | 0.020 | 0.020 | 0.49% | −0.011 | −0.011 | 0.04% | 2.635 | 2.749 | 4.12% |
| 12.5 m | 4 kn | 0.022 | 0.023 | 2.08% | −0.011 | −0.011 | 0.00% | 2.660 | 2.876 | 7.51% |
| 12.5 m | 5 kn | 0.026 | 0.028 | 5.24% | −0.011 | −0.011 | 0.05% | 2.837 | 2.965 | 4.30% |
| 12.5 m | 6 kn | 0.034 | 0.039 | 11.09% | −0.011 | −0.011 | 0.00% | 3.033 | 2.952 | 2.76% |
| 13.5 m | 3 kn | 0.034 | 0.034 | 0.33% | −0.039 | −0.039 | 0.05% | 2.068 | 2.221 | 6.88% |
| 13.5 m | 4 kn | 0.035 | 0.035 | 0.44% | −0.039 | −0.039 | 0.05% | 2.264 | 2.447 | 7.47% |
| 13.5 m | 5 kn | 0.037 | 0.037 | 1.00% | −0.039 | −0.039 | 0.04% | 2.463 | 2.599 | 5.23% |
| 13.5 m | 6 kn | 0.041 | 0.044 | 7.01% | −0.039 | −0.039 | 0.04% | 2.585 | 2.795 | 7.50% |
| Drift/m | Speed/kn | STD | Error | Mean/deg | Error | Normalized Max | Error | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 h | 3 h | 1 h | 3 h | 1 h | 3 h | |||||
| 11.5 m | 3 kn | 0.355 | 0.371 | 4.21% | 0.023 | 0.024 | 5.41% | 2.818 | 2.736 | 2.96% |
| 11.5 m | 4 kn | 0.420 | 0.431 | 2.56% | 0.037 | 0.040 | 7.47% | 2.915 | 3.273 | 10.94% |
| 11.5 m | 5 kn | 0.438 | 0.447 | 1.95% | 0.055 | 0.061 | 9.53% | 3.422 | 3.343 | 2.38% |
| 11.5 m | 6 kn | 0.427 | 0.424 | 0.73% | 0.075 | 0.084 | 11.10% | 2.877 | 3.276 | 12.18% |
| 12.5 m | 3 kn | 0.367 | 0.383 | 4.16% | 0.026 | 0.028 | 6.51% | 2.716 | 2.724 | 0.29% |
| 12.5 m | 4 kn | 0.412 | 0.423 | 2.59% | 0.044 | 0.047 | 7.45% | 3.078 | 3.289 | 6.41% |
| 12.5 m | 5 kn | 0.430 | 0.442 | 2.74% | 0.064 | 0.072 | 10.33% | 3.653 | 3.536 | 3.31% |
| 12.5 m | 6 kn | 0.429 | 0.431 | 0.55% | 0.088 | 0.099 | 11.43% | 2.867 | 3.183 | 9.93% |
| 13.5 m | 3 kn | 0.370 | 0.384 | 3.75% | 0.030 | 0.032 | 5.66% | 2.718 | 3.043 | 10.70% |
| 13.5 m | 4 kn | 0.406 | 0.418 | 2.72% | 0.050 | 0.055 | 8.86% | 3.127 | 3.398 | 7.96% |
| 13.5 m | 5 kn | 0.432 | 0.449 | 3.88% | 0.073 | 0.082 | 11.06% | 3.560 | 3.402 | 4.66% |
| 13.5 m | 6 kn | 0.450 | 0.454 | 0.90% | 0.100 | 0.115 | 13.15% | 2.985 | 3.211 | 7.06% |
| Drift/m | Speed/kn | Tensions/KN | Number of Tugboats | MCR | LF | A | EF | Emissions of CO2/kg |
|---|---|---|---|---|---|---|---|---|
| 11.5 | 3 | 704.5426 | 1 | 4500 | 0.68 | 10 | 0.744 | 22,766.4 |
| 11.5 | 4 | 1187.94 | 2 | 9000 | 0.68 | 7.5 | 0.744 | 34,149.6 |
| 11.5 | 5 | 1816.56 | 3 | 13,500 | 0.68 | 6 | 0.744 | 40,979.52 |
| 11.5 | 6 | 2541.9 | 3 | 13,500 | 0.68 | 5 | 0.744 | 34,149.6 |
| 12.5 | 3 | 751.4154 | 1 | 4500 | 0.68 | 10 | 0.744 | 22,766.4 |
| 12.5 | 4 | 1272.13 | 2 | 9000 | 0.68 | 7.5 | 0.744 | 34,149.6 |
| 12.5 | 5 | 1947.65 | 3 | 13,500 | 0.68 | 6 | 0.744 | 40,979.52 |
| 12.5 | 6 | 2734.05 | 3 | 13,500 | 0.68 | 5 | 0.744 | 34,149.6 |
| 13.5 | 3 | 799.2422 | 1 | 4500 | 0.68 | 10 | 0.744 | 22,766.4 |
| 13.5 | 4 | 1356.29 | 2 | 9000 | 0.68 | 7.5 | 0.744 | 34,149.6 |
| 13.5 | 5 | 2083.59 | 3 | 13,500 | 0.68 | 6 | 0.744 | 40,979.52 |
| 13.5 | 6 | 2922.2 | 3 | 13,500 | 0.68 | 5 | 0.744 | 34,149.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, H.; Wang, H.; Zhai, Q.; Feng, W.; Cao, J. Study on the Dynamic Responses of a Large Caisson during Wet-Towing Transportation. Water 2021, 13, 126. https://doi.org/10.3390/w13020126
Gu H, Wang H, Zhai Q, Feng W, Cao J. Study on the Dynamic Responses of a Large Caisson during Wet-Towing Transportation. Water. 2021; 13(2):126. https://doi.org/10.3390/w13020126
Chicago/Turabian StyleGu, Haoyang, Huakun Wang, Qiu Zhai, Weibing Feng, and Jiaxiu Cao. 2021. "Study on the Dynamic Responses of a Large Caisson during Wet-Towing Transportation" Water 13, no. 2: 126. https://doi.org/10.3390/w13020126
APA StyleGu, H., Wang, H., Zhai, Q., Feng, W., & Cao, J. (2021). Study on the Dynamic Responses of a Large Caisson during Wet-Towing Transportation. Water, 13(2), 126. https://doi.org/10.3390/w13020126







