Multiple-Depth Soil Moisture Estimates Using Artificial Neural Network and Long Short-Term Memory Models
Abstract
:1. Introduction
2. Materials and Methods
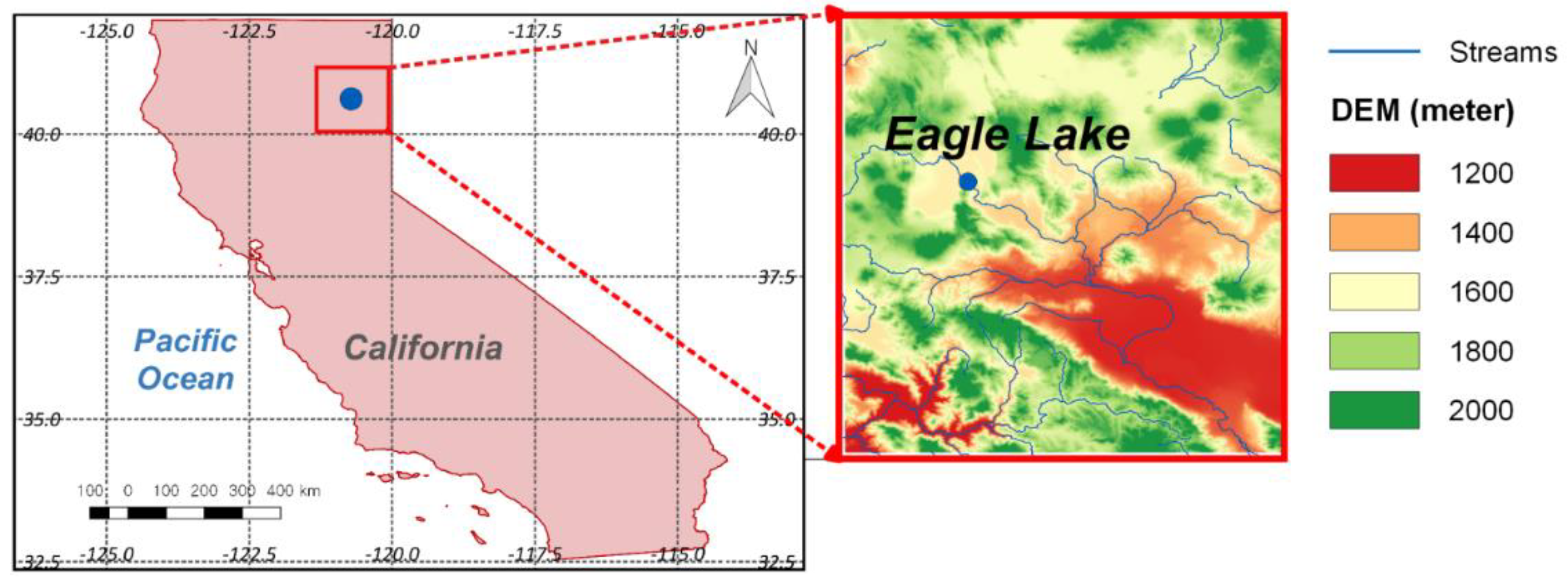
2.1. Study Area and Data
2.2. Methods
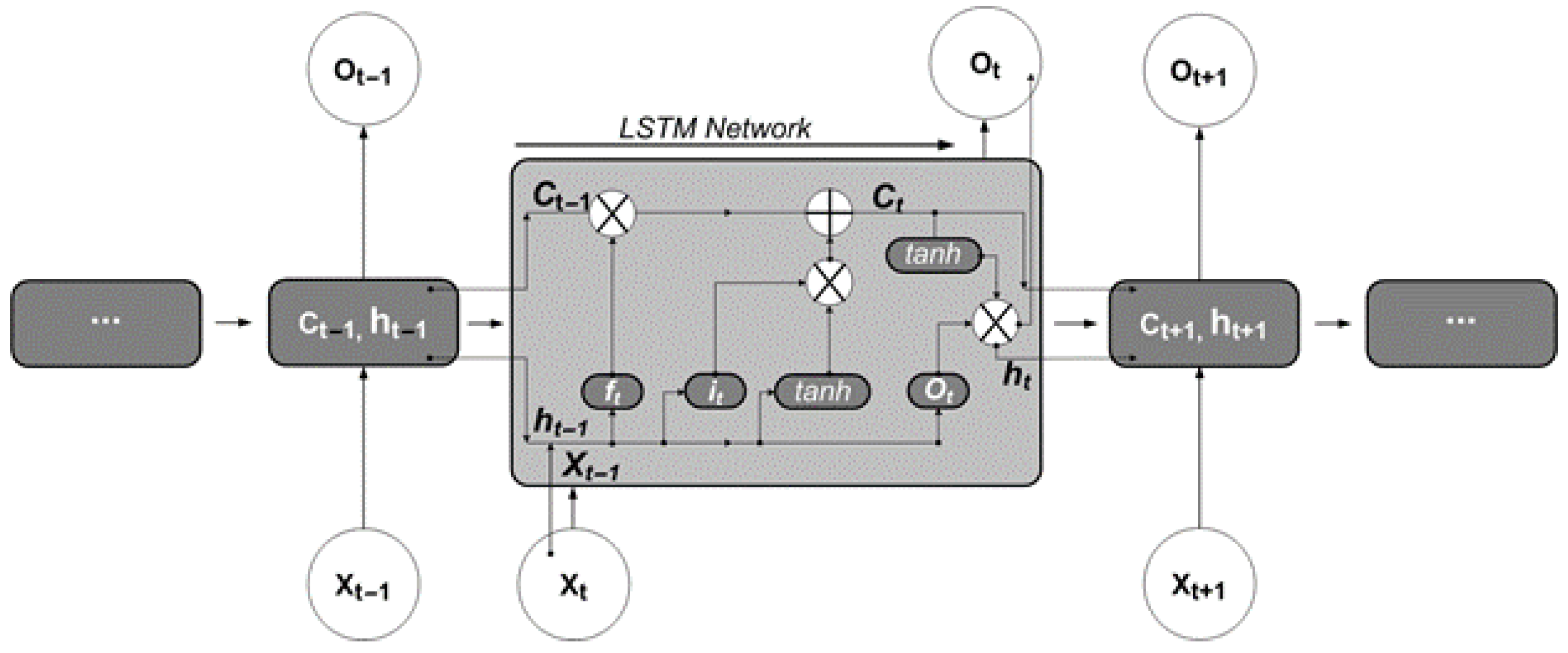
2.2.1. Long Short-Term Memory Model (LSTM)
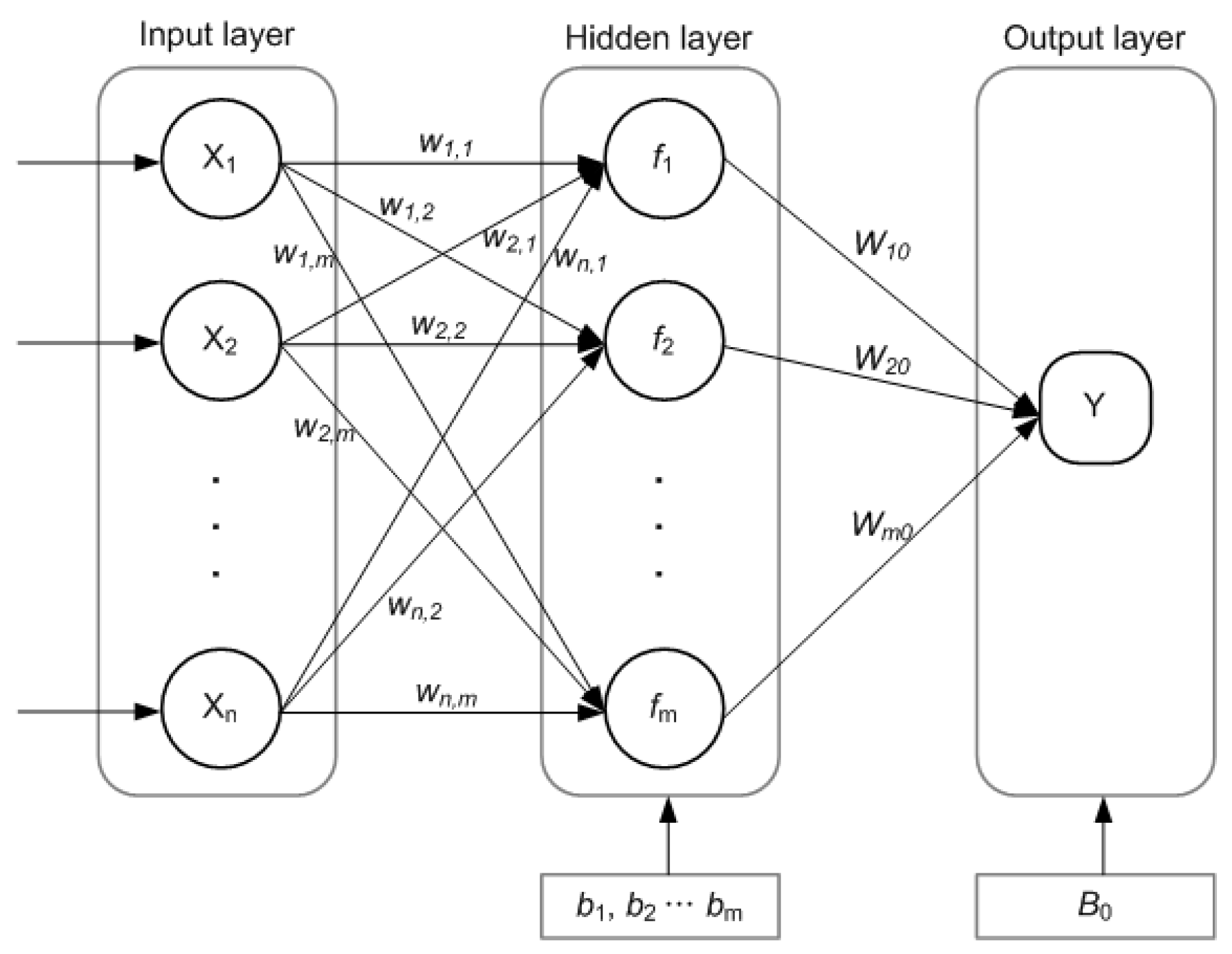
2.2.2. Artificial Neural Network (ANN)
2.3. Model Development
2.4. Evaluation Methods
3. Results
3.1. Comparison with Observations at Four Layers
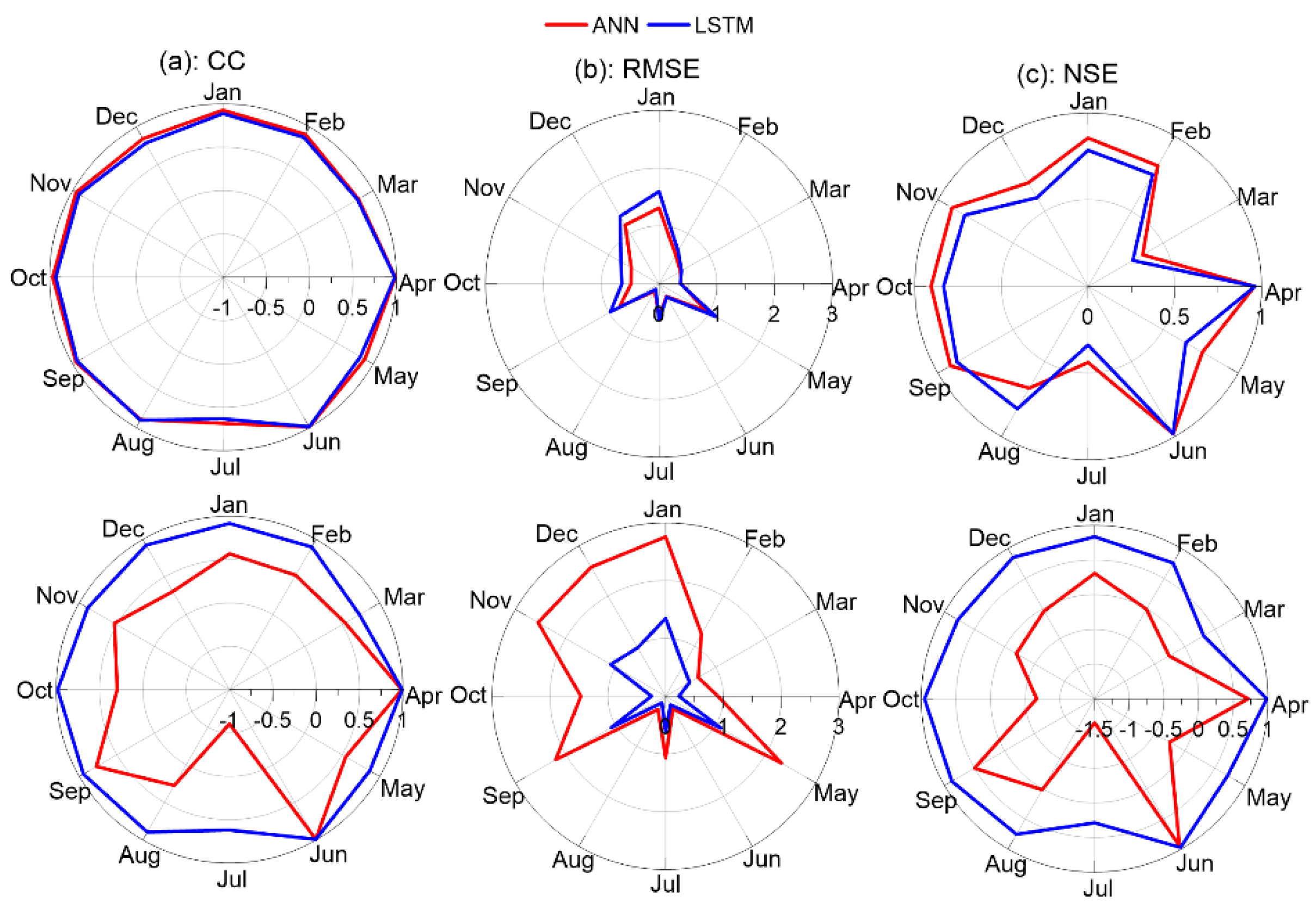
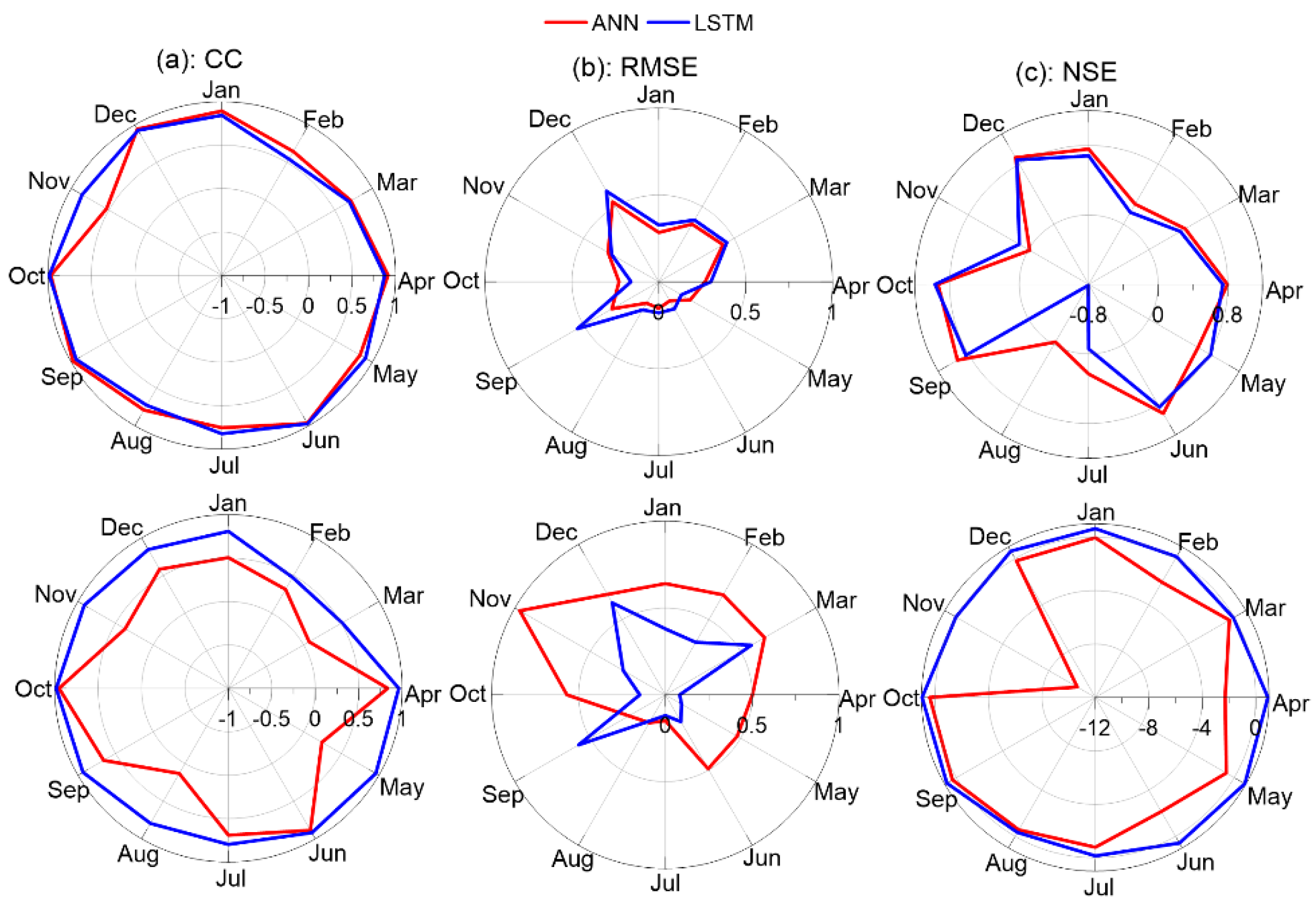
3.2. Monthly Based Evaluation
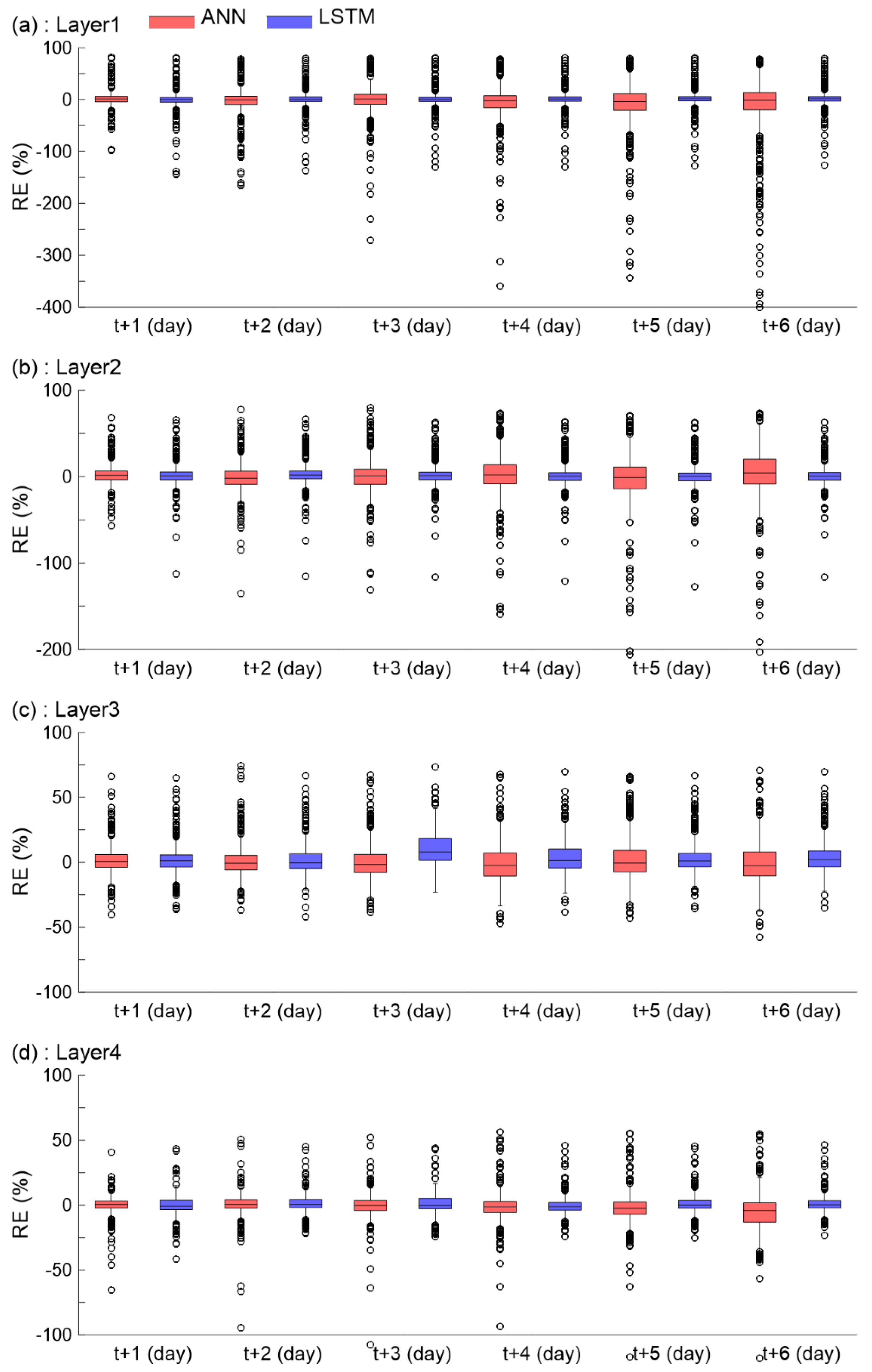
3.3. Errors in Predicted Soil Moisture
4. Discussions and Conclusions
4.1. Limitations of the Data-Driven Models
4.2. Implications for Hydrological Analysis Using Soil Moisture
Author Contributions
Funding
Conflicts of Interest
References
- Islam, S.; Engman, T. Why bother for 0.0001% of Earth’s water? Challenges for soil moisture research. Eos Trans. Am. Geophys. Union 1996, 77, 420. [Google Scholar] [CrossRef]
- Corradini, C.; Morbidelli, R.; Melone, F. On the interaction between infiltration and Hortonian runoff. J. Hydrol. 1998, 204, 52–67. [Google Scholar] [CrossRef]
- Koster, R.D.; Dirmeyer, P.A.; Guo, Z.; Bonan, G.; Chan, E.; Cox, P.; Gordon, C.T.; Kanae, S.; Kowalczyk, E.; Lawrence, D.; et al. Regions of strong coupling between soil moisture and precipitation. Science 2004, 305, 1138–1140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Komma, J.; Blöschl, G.; Reszler, C. Soil moisture updating by ensemble Kalman filtering in real-time flood forecasting. J. Hydrol. 2008, 357, 228–242. [Google Scholar] [CrossRef]
- Beck, H.K.; de Jeu, R.A.; Schellekens, J.; van Dijk, A.I.; Bruijnzeel, L.A. Improving curve number based storm runoff estimates using soil moisture proxies. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2009, 2, 250–259. [Google Scholar] [CrossRef]
- Brocca, L.; Melone, F.; Moramarco, T.; Wagner, W.; Naeimi, V.; Bartalis, Z.; Hasenauer, S. Improving runoff prediction through the assimilation of the ASCAT soil moisture product. Hydrol. Earth Syst. Sci. 2010, 14, 1881–1893. [Google Scholar] [CrossRef] [Green Version]
- Hirschi, M.; Seneviratne, S.I.; Alexandrov, V.; Boberg, F.; Boroneant, C.; Christensen, O.B.; Formayer, H.; Orlowsky, B.; Stepanek, P. Observational evidence for soil-moisture impact on hot extremes in southeastern Europe. Nat. Geosci. 2011, 4, 17–21. [Google Scholar] [CrossRef]
- Li, J.; Islam, S. On the estimation of soil moisture profile and surface fluxes partitioning from sequential assimilation of surface layer soil moisture. J. Hydrol. 1999, 220, 86–103. [Google Scholar] [CrossRef]
- Evans, R.O.; Sneed, R.E. Measuring Soil Water for Irrigation Scheduling: Monitoring Methods and Devices; AG-North Carolina Agricultural Extension Service, North Carolina State University (USA): Raleigh, NC, USA, 1991; Volume 455, 5p. [Google Scholar]
- Ling, P. A review of soil moisture sensors. Assn. Flor. Prof. Bull 2004, 886, 22–23. [Google Scholar] [CrossRef]
- Saxton, K.E.; Johnson, H.P.; Shaw, R.H. Modeling Evapotranspiration and Soil Moisture. Trans. ASAE 1974, 17, 673–677. [Google Scholar] [CrossRef]
- Holtan, H.N. USDAHL-74 Revised Model of Watershed Hydrology; Tech. Bull. 1518; Agricultural Research Service, US Department of Agriculture: Washington, DC, USA, 1975. [Google Scholar]
- Peck, E.L. Catchment Modeling and Initial Parameter Estimation for the National Weather Service River Forecast System; NOAA Technical Memorandum; NWS Hydo-31; National Weather Service: Silver Spring, MD, USA, 1976. [Google Scholar]
- Njoku, E.G.; Jackson, T.J.; Lakshmi, V.; Chan, T.K.; Nghiem, S.V. Soil moisture retrieval from AMSR-E. IEEE Trans. Geosci. Remote Sens. 2003, 41, 215–229. [Google Scholar] [CrossRef]
- Moran, M.S.; Peters-Lidard, C.F.; Watts, J.M.; McElroy, S. Estimating soil moisture at the watershed scale with satellite-based radar and land surface models. Can. J. Remote Sens. 2004, 30, 805–826. [Google Scholar] [CrossRef] [Green Version]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.C.; Bizzarri, B.; Wigneron, J.P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Hydrol. Res. 2007, 38, 1–20. [Google Scholar] [CrossRef]
- Peng, J.; Loew, A. Recent advances in soil moisture estimation from remote sensing. Water 2017, 9, 530. [Google Scholar] [CrossRef] [Green Version]
- Parinussa, R.M.; Yilmaz, M.T.; Anderson, M.C.; Hain, C.R.; de Jeu, R.A.M. An intercomparison of remotely sensed soil moisture products at various spatial scales over the Iberian Peninsula. Hydrol. Process. 2014, 28, 4865–4876. [Google Scholar] [CrossRef]
- Chauhan, N.S.; Miller, S.; Ardanuy, P. Spaceborne soil moisture estimation at high resolution: A microwave-optical/IR synergistic approach. Int. J. Remote Sens. 2003, 24, 4599–4622. [Google Scholar] [CrossRef]
- Ray, R.L.; Jacobs, J.M.; Cosh, M.H. Landslide susceptibility mapping using downscaled AMSR-E soil moisture: A case study from Cleveland Corral, California, US. Remote Sens. Environ. 2010, 114, 2624–2636. [Google Scholar] [CrossRef]
- Solomatine, D.P.; Ostfeld, A. Data-driven modelling: Some past experiences and new approaches. J. Hydroinf. 2008, 10, 3–22. [Google Scholar] [CrossRef] [Green Version]
- James, T.; Schillaci, C.; Lipani, A. Convolutional neural networks for water segmentation using sentinel-2 red, green, blue (RGB) composites and derived spectral indices. Int. J. Remote Sens. 2021, 42, 5342–5369. [Google Scholar] [CrossRef]
- Kim, S.; Singh, V.P. Modeling daily soil temperature using data-driven models and spatial distribution. Theor. Appl. Climatol. 2014, 118, 465–479. [Google Scholar] [CrossRef]
- Feng, Y.; Cui, N.; Hao, W.; Gao, L.; Gong, D. Estimation of soil temperature from meteorological data using different machine learning models. Geoderma 2019, 338, 67–77. [Google Scholar] [CrossRef]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. Adv. Neural Inf. Process. Syst. 2014, 27, 3104–3112. [Google Scholar]
- Baghdadi, N.; Gaultier, S.; King, C. Retrieving Surface Roughness and Soil Moisture from Synthetic Aperture Radar (SAR) Data Using Neural Networks. Can. J. Remote Sens. 2002, 28, 701–711. [Google Scholar] [CrossRef]
- Zaman, B.; McKee, M.; Neale, C.M. Fusion of remotely sensed data for soil moisture estimation using relevance vector and support vector machines. Int. J. Remote Sens. 2012, 33, 6516–6552. [Google Scholar] [CrossRef]
- Shukla, A.; Panchal, H.; Mishra, M.; Patel, P.R.; Srivastava, H.S.; Patel, P.; Shukla, A.K. Soil moisture estimation using gravimetric technique and FDR probe technique: A comparative analysis. Am. Int. J. Res. Form. Appl. Nat. Sci 2014, 8, 89–92. [Google Scholar]
- Gill, M.K.; Asefa, T.; Kemblowski, M.W.; McKee, M. Soil moisture prediction using support vector machines. JAWRA J. Am. Water Resour. Assoc. 2006, 42, 1033–1046. [Google Scholar] [CrossRef]
- Prakash, S.; Sharma, A.; Sahu, S.S. Soil moisture prediction using machine learning. In Proceedings of the 2018 Second International Conference on Inventive Communication and Computational Technologies (ICICCT), Coimbatore, India, 20–21 April 2018; pp. 1–6. [Google Scholar]
- Achieng, K.O. Modelling of soil moisture retention curve using machine learning techniques: Artificial and deep neural networks vs support vector regression models. Comput. Geosci. 2019, 133, 104320. [Google Scholar] [CrossRef]
- Adeyemi, O.; Grove, I.; Peets, S.; Domun, Y.; Norton, T. Dynamic neural network modelling of soil moisture content for predictive irrigation scheduling. Sensors 2018, 18, 3408. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, S.; Kalra, A.; Stephen, H. Estimating soil moisture using remote sensing data: A machine learning approach. Adv. Water Resour. 2010, 33, 69–80. [Google Scholar] [CrossRef]
- Gorthi, S.; Dou, H. Prediction models for the estimation of soil moisture content. In Proceedings of the ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Washington, DC, USA, 28 August 2011; pp. 945–953. [Google Scholar]
- Ali, I.; Greifeneder, F.; Stamenkovic, J.; Neumann, M.; Notarnicola, C. Review of machine learning approaches for biomass and soil moisture retrievals from remote sensing data. Remote Sens. 2015, 7, 16398–16421. [Google Scholar] [CrossRef] [Green Version]
- Efremova, N.; Zausaev, D.; Antipov, G. Prediction of Soil Moisture Content Based on Satellite Data and Sequence-to-Sequence Networks. arXiv 2019, arXiv:1907.03697. [Google Scholar]
- Norbiato, D.; Borga, M.; Degli Esposti, S.; Gaume, E.; Anquetin, S. Flash flood warning based on rainfall thresholds and soil moisture conditions: An assessment for gauged and ungauged basins. J. Hydrol. 2018, 362, 274–290. [Google Scholar] [CrossRef]
- Kim, J.; Han, H.; Kim, B.; Chen, H.; Lee, J. Use of a high-resolution-satellite-based precipitation product in mapping continental-scale rainfall erosivity: A case study of the United States. Catena 2020, 193, 104602. [Google Scholar] [CrossRef]
- Ralph, F.M.; Neiman, P.J.; Wick, G.A.; Gutman, S.I.; Dettinger, M.D.; Cayan, D.R.; White, A.B. Flooding on California’s Russian River: Role of atmospheric rivers. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Han, H.; Kim, J.; Chandrasekar, V.; Choi, J.; Lim, S. Modeling Streamflow Enhanced by Precipitation from Atmospheric River Using the NOAA National Water Model: A Case Study of the Russian River Basin for February 2004. Atmosphere 2019, 10, 466. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Hu, C.; Wu, Q.; Jian, S.; Li, N.; Lou, Z. Deep learning with a long short-term memory networks approach for rainfall-runoff simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef] [Green Version]
- Fan, H.; Jiang, M.; Xu, L.; Zhu, H.; Cheng, J.; Jiang, J. Comparison of Long Short Term Memory Networks and the Hydrological Model in Runoff Simulation. Water 2020, 12, 175. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Tran, Q.K.; Song, S.K. Water level forecasting based on deep learning: A use case of Trinity river-Texas-The United States. J. KIISE 2017, 44, 607–612. [Google Scholar] [CrossRef]
- Lee, G.H.; Jung, S.H.; Lee, D.E. Comparison of physics-based and data-driven models for streamflow simulation of the Mekong river. J. Kor. Water Resour. Assoc. 2018, 51, 503–514. [Google Scholar] [CrossRef]
- Tanty, R.; Desmukh, T.S. Application of artificial neural network in hydrology—A review. Int. J. Eng. Res. Tech. 2015, 4, 184–188. [Google Scholar]
- Jung, J.; Han, H.; Kim, K.; Kim, H.S. Machine Learning-Based Small Hydropower Potential Prediction under Climate Change. Energies 2021, 14, 3643. [Google Scholar] [CrossRef]
- Han, H.; Morrison, R.R. Data-driven approaches for runoff prediction using distributed data. Stoch. Environ. Res. Risk Assess. 2021, 35, 1–19. [Google Scholar] [CrossRef]

| Layers | Lead Time (days) | ANN | LSTM | ||||
|---|---|---|---|---|---|---|---|
| CC | RMSE | NSE | CC | RMSE | NSE | ||
| 1 | 1 | 0.97 | 0.76 | 0.94 | 0.96 | 0.91 | 0.91 |
| 2 | 0.93 | 1.10 | 0.87 | 0.96 | 0.88 | 0.92 | |
| 3 | 0.89 | 1.42 | 0.78 | 0.96 | 0.88 | 0.92 | |
| 4 | 0.86 | 1.59 | 0.73 | 0.96 | 0.87 | 0.92 | |
| 5 | 0.82 | 1.78 | 0.66 | 0.96 | 0.84 | 0.92 | |
| 6 | 0.80 | 1.89 | 0.62 | 0.96 | 0.84 | 0.93 | |
| 2 | 1 | 0.97 | 0.68 | 0.93 | 0.96 | 0.75 | 0.91 |
| 2 | 0.93 | 0.96 | 0.86 | 0.95 | 0.79 | 0.90 | |
| 3 | 0.89 | 1.19 | 0.78 | 0.96 | 0.76 | 0.91 | |
| 4 | 0.85 | 1.35 | 0.71 | 0.95 | 0.76 | 0.91 | |
| 5 | 0.83 | 1.42 | 0.68 | 0.95 | 0.78 | 0.90 | |
| 6 | 0.82 | 1.51 | 0.64 | 0.96 | 0.75 | 0.91 | |
| 3 | 1 | 0.93 | 0.51 | 0.85 | 0.91 | 0.58 | 0.81 |
| 2 | 0.87 | 0.65 | 0.75 | 0.90 | 0.58 | 0.80 | |
| 3 | 0.85 | 0.68 | 0.73 | 0.90 | 0.66 | 0.74 | |
| 4 | 0.85 | 0.70 | 0.72 | 0.90 | 0.58 | 0.80 | |
| 5 | 0.83 | 0.74 | 0.67 | 0.90 | 0.58 | 0.80 | |
| 6 | 0.80 | 0.79 | 0.63 | 0.90 | 0.59 | 0.80 | |
| 4 | 1 | 0.98 | 0.32 | 0.97 | 0.98 | 0.36 | 0.96 |
| 2 | 0.97 | 0.45 | 0.93 | 0.98 | 0.36 | 0.96 | |
| 3 | 0.95 | 0.53 | 0.90 | 0.98 | 0.38 | 0.95 | |
| 4 | 0.94 | 0.60 | 0.88 | 0.98 | 0.37 | 0.95 | |
| 5 | 0.93 | 0.63 | 0.87 | 0.98 | 0.38 | 0.95 | |
| 6 | 0.91 | 0.74 | 0.82 | 0.98 | 0.37 | 0.95 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Choi, C.; Kim, J.; Morrison, R.R.; Jung, J.; Kim, H.S. Multiple-Depth Soil Moisture Estimates Using Artificial Neural Network and Long Short-Term Memory Models. Water 2021, 13, 2584. https://doi.org/10.3390/w13182584
Han H, Choi C, Kim J, Morrison RR, Jung J, Kim HS. Multiple-Depth Soil Moisture Estimates Using Artificial Neural Network and Long Short-Term Memory Models. Water. 2021; 13(18):2584. https://doi.org/10.3390/w13182584
Chicago/Turabian StyleHan, Heechan, Changhyun Choi, Jongsung Kim, Ryan R. Morrison, Jaewon Jung, and Hung Soo Kim. 2021. "Multiple-Depth Soil Moisture Estimates Using Artificial Neural Network and Long Short-Term Memory Models" Water 13, no. 18: 2584. https://doi.org/10.3390/w13182584
APA StyleHan, H., Choi, C., Kim, J., Morrison, R. R., Jung, J., & Kim, H. S. (2021). Multiple-Depth Soil Moisture Estimates Using Artificial Neural Network and Long Short-Term Memory Models. Water, 13(18), 2584. https://doi.org/10.3390/w13182584









