Retrofitting of Pressurized Sand Traps in Hydropower Plants
Abstract
:1. Introduction
Scope of Work
2. Methods and Materials
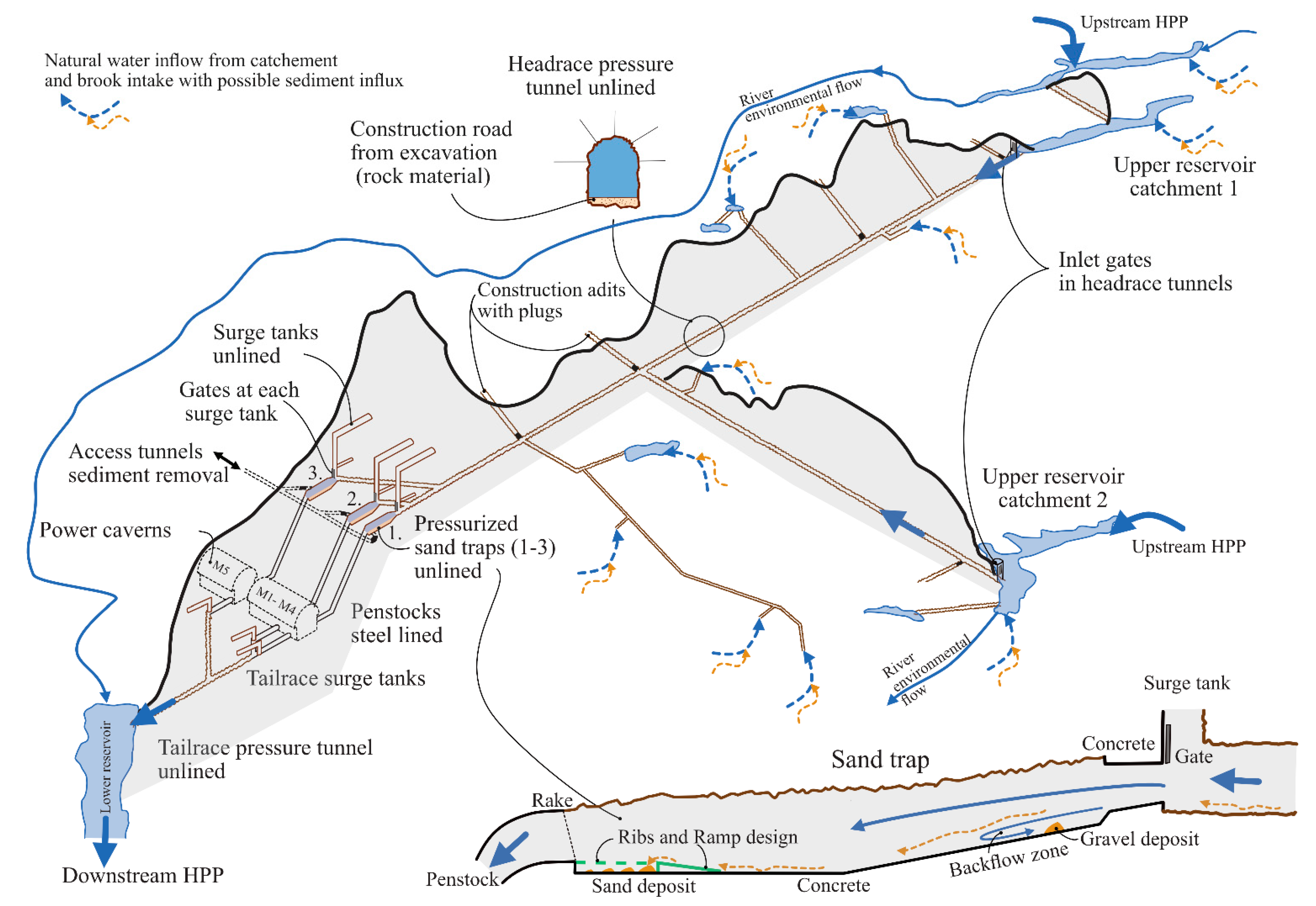
2.1. General Description of the Methodology
2.2. Prototype Observations
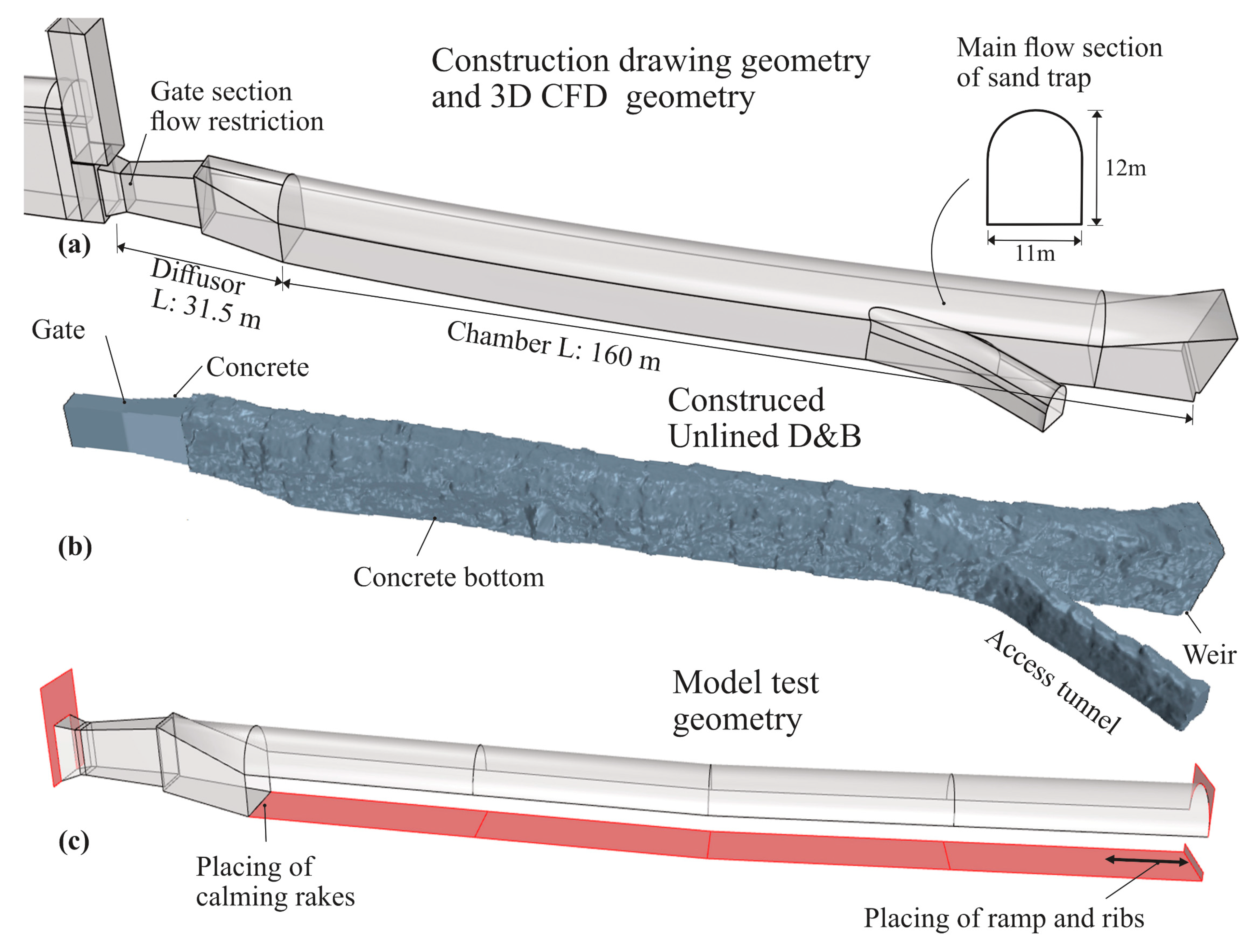
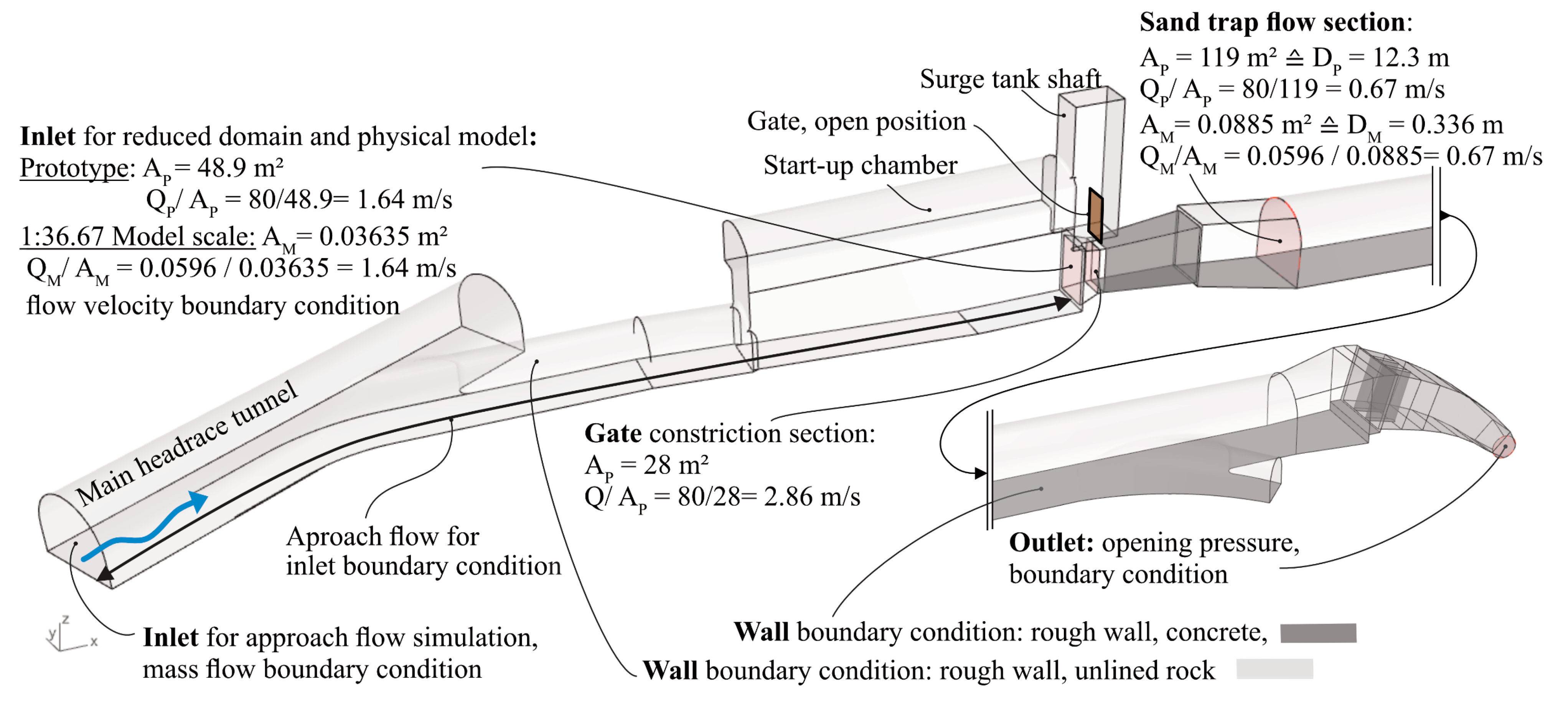
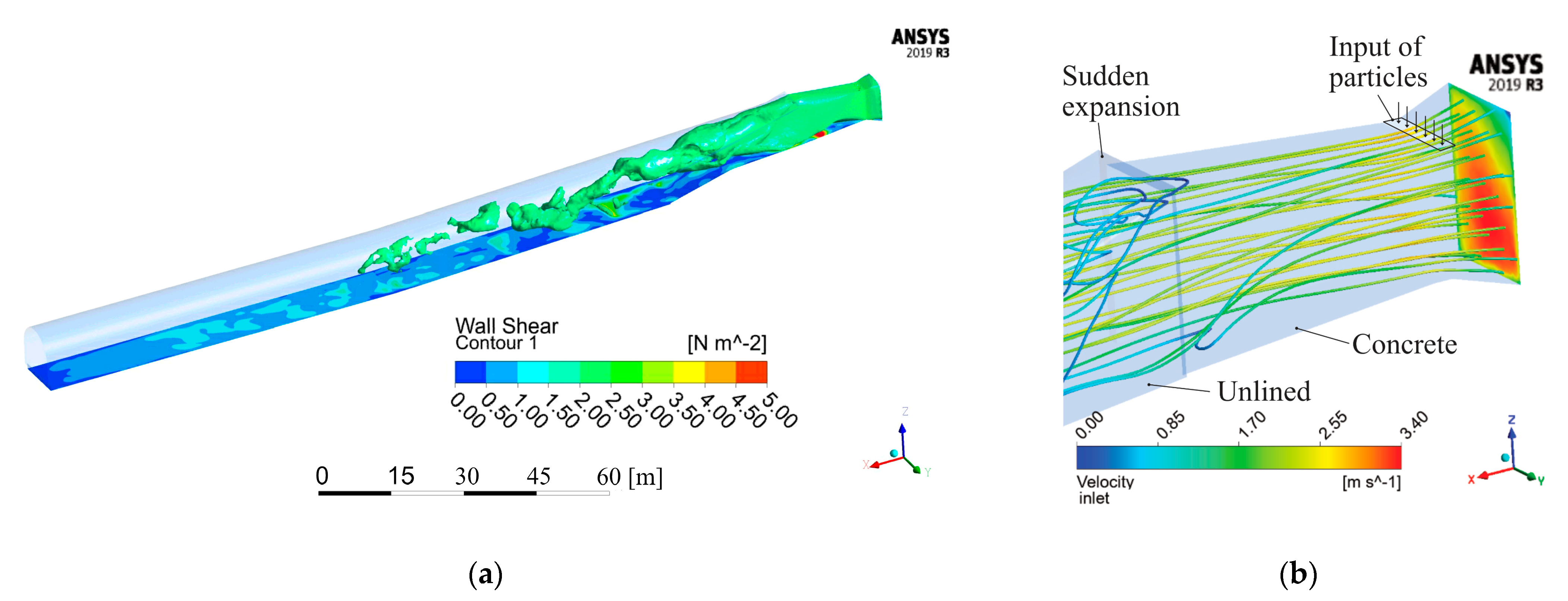
2.3. Numerical Simulations with 3D CFD
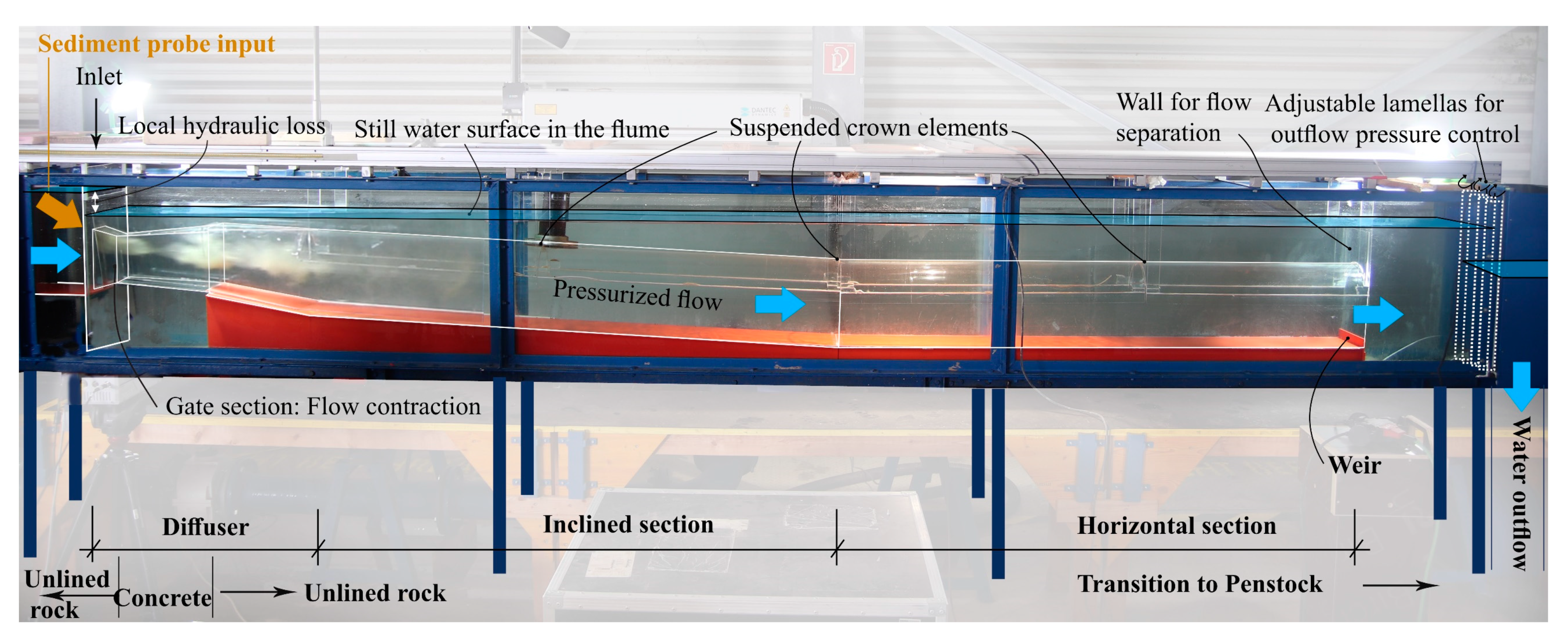
2.4. Physical Scale Model Test
2.5. Tested Retrofitting Options
3. Results
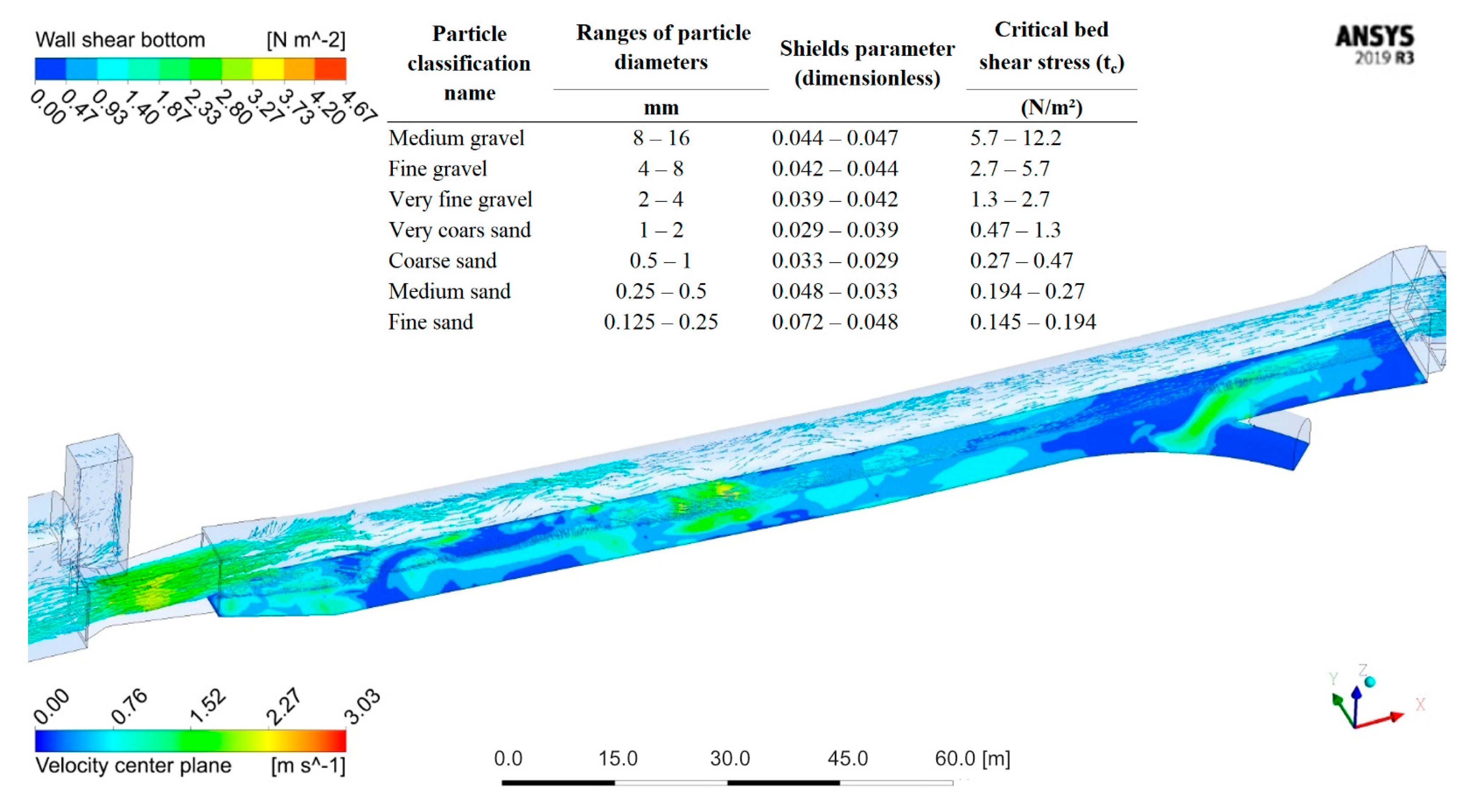
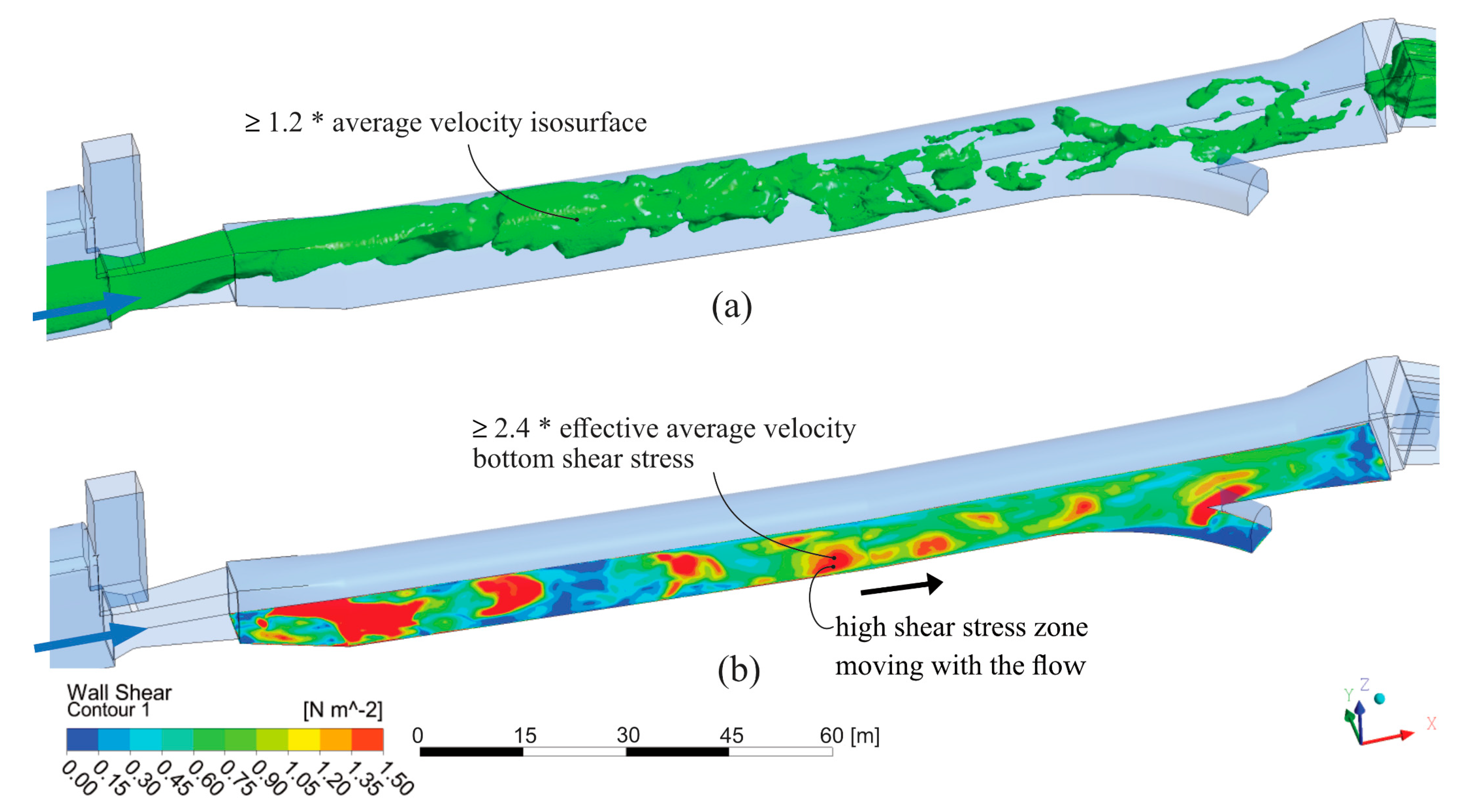
3.1. 3D CFD Simulations of the Flow and Wall Shear Stress
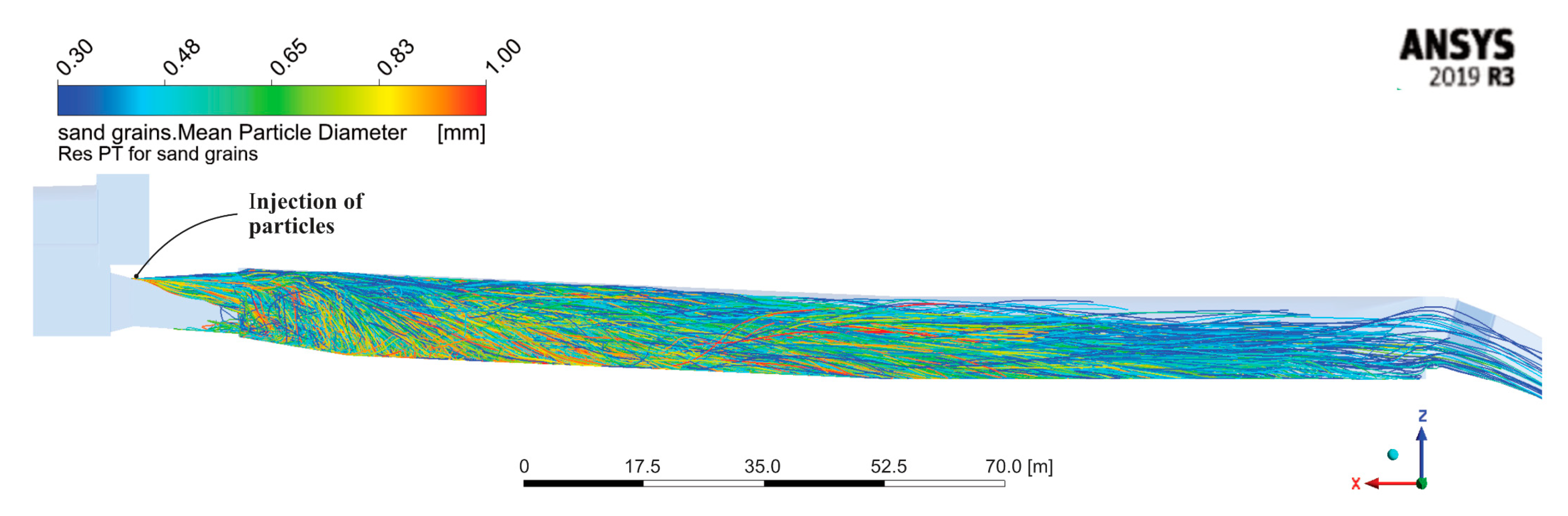
3.2. 3D CFD Simulations with Particle Tracking Modelling
3.3. Physical Scale Model Tests
4. Discussion
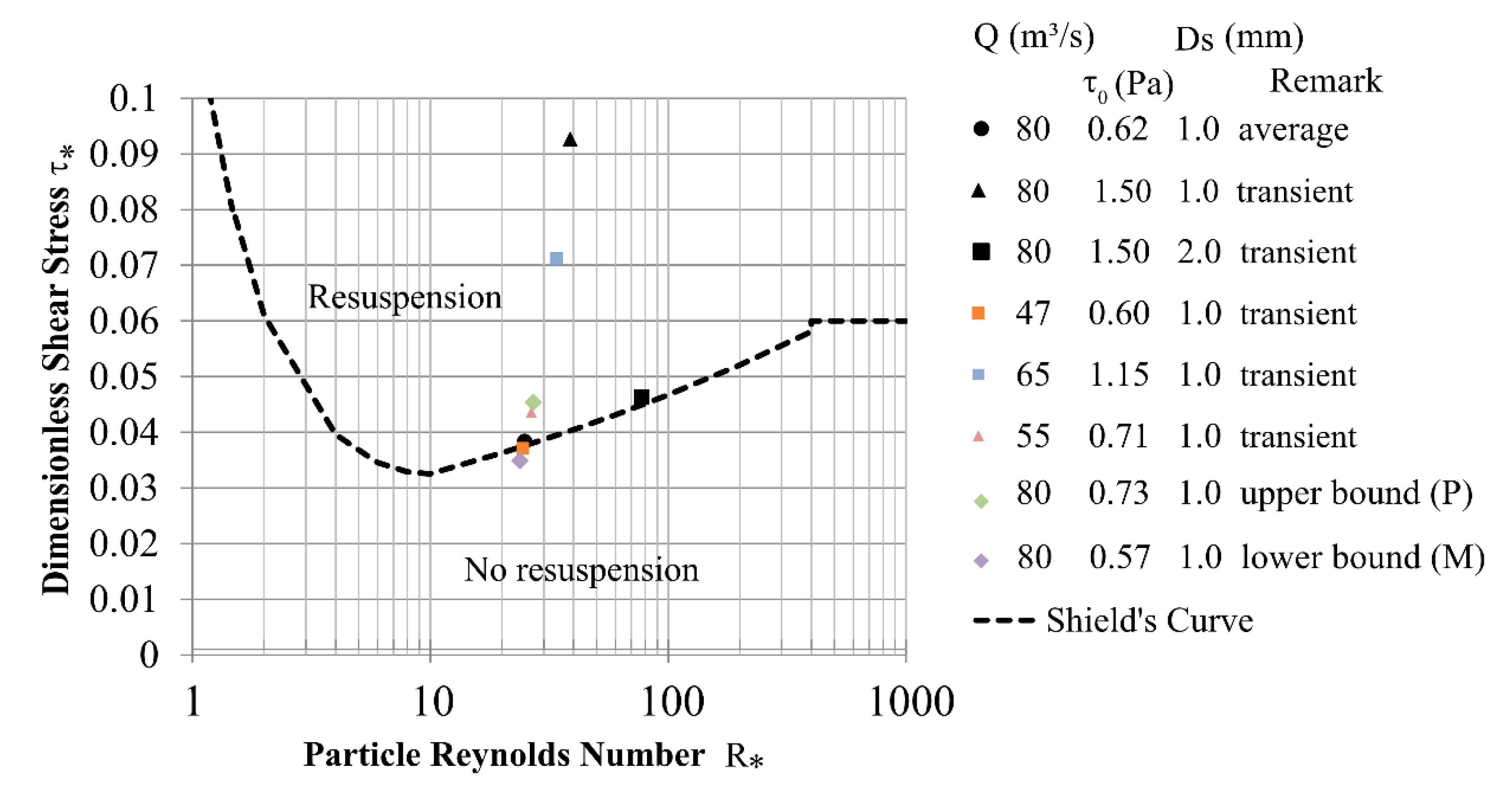
4.1. Comparison with Shields Diagram
4.2. 3D CFD Simulations
4.3. Physical Model Tests
4.4. Retrofitting Solutions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| sand grain particle diameter (mm) | |
| FQd | Factor of design discharge (-), (80 m3/s = 1.0) |
| f | Darcy-Weisbach friction factor (-) |
| Local head loss (m) | |
| HPP | Hydropower plant |
| Equivalent sand grain roughness (mm) | |
| M | Machine for hydraulic energy generation (turbine) |
| Q | discharge (m3/s) |
| Qd | Design discharge = 80 (m3/s) |
| P | Pressure (Pa) |
| Particle Reynolds Number (-) | |
| Velocity (m/s) | |
| Shear velocity (m/s) | |
| Volume sediment (m3, l) | |
| SCF | Scale factor (-) |
| ηtrap | Trap efficiency |
| Kinematic viscosity (m2/s) | |
| Density (kg/m3) | |
| Boundary shear stress (Pa) | |
| Critical Shields shear stress (-) | |
| Dimensionless shear stress respectively Shields parameter (-) | |
| ζ | Local hydraulic loss factor (-) |
| Indices | |
| M | Model test |
| P | Prototype |
References
- Brekke, T.L.; Rippley, B.D. Design Guidelines for Pressure Tunnels and Shafts; Final Report No. 1745-17; EPRI—Electric Power Research Institute, University of California at Berkley: Palo Alto, CA, USA, 1987. [Google Scholar]
- Brox, D. Practical Guide to Rock Tunneling; CRC Press/Balkema: EH Leiden, The Netherlands, 2017; ISBN 978-1-315-21011-7. [Google Scholar]
- Huval, C.J. Hydraulic Design of Unlined Rock Tunnels. J. Hydraul. Eng. ASCE 1969, 4, 1235–1246. [Google Scholar] [CrossRef]
- Lysne, D.K. Sand transport and Sand Traps in Hydro Power Tunnels, in International Conference on Pumped Storage Development and Its Environmental Effects; University of Wisconsin: Milwaukee, WI, USA, 1971. [Google Scholar]
- Mattimoe, J.J.; Tinney, E.R.; Wolcott, W.W. Rock Trap Experience in Unlined Tunnels. ASCE Power J. 1964, 90, 29–45. [Google Scholar]
- Brox, D. DIC, Design and Functional Requirements for Rock Traps for Hydropower Pressure Tunnels. Int. J. Hydropower Dams 2016, 23, 4386–4396. [Google Scholar]
- Solvik, Ø.; Tesaker, E. Floor Paving in Unlined Hydropower Tunnels. In Hydropower’97; A. A. Balkema: Rotterdam, The Netherlands, 1997; ISBN 9054108886. [Google Scholar]
- Vereide, K.; Richter, W.; Havrevoll, O.H.; Betete, K.; Shrestha, U.; Navaratnam, U.; Mauko, G.; Lia, L. Flexible Sand Traps; HydroCen Report 20; Norwegian Research Centre for Hydropower Technology: Trondheim, Norway, 2021. [Google Scholar]
- Vereide, K.; Bjørnar, S.; Rolv, G. Case Study: Damaging Effects of Increasing the Installed Capacity in an Existing Hydropower Plant; BHR Pressure Surges: Dublin, Ireland, 2015. [Google Scholar]
- Bråtveit, K.; Olsen, N.R. Calibration of Horizontal Acoustic Doppler Current profilers by three dimensional CFD simulations. Eng. Appl. Comput. Fluid Mech. 2015, 9, 41–45. [Google Scholar] [CrossRef] [Green Version]
- Almeland, S.K.; Olsen, N.R.B.; Bråveit, K.; Aryal, P.R. Multiple solutions of the Navier-Stokes equations computing water flow in sand traps. Eng. Appl. Comput. Fluid Mech. 2019, 13, 199–219. [Google Scholar] [CrossRef]
- Belete, K.; Shrestha, U.; Vereide, K. Physical Model Study of Tonstad Sand Trap III, Report; NTNU: Trondheim, Norway, 2020; ISBN 978-82-8289-018-2(e). [Google Scholar]
- Gabl, R.; Gems, B.; Birkner, F.; Hofer, B.; Aufleger, M. Adaptation of an Existing Intake Structure Caused by Increased Sediment Level. Water 2018, 10, 1066. [Google Scholar] [CrossRef] [Green Version]
- Seyfeddine, M.; Vorlet, S.; Adam, N.; De Cesare, G. Holistic Design Approach of a Throttled Surge Tank: The Case of Refurbishment of Gondo High-Head Power Plant in Switzerland. Water 2020, 12, 3440. [Google Scholar] [CrossRef]
- Andersson, L.R.; Hellström, J.G.I.; Andreasson, P.; Lundström, T.S. Numerical Investigation of a Hydropower Tunnel: Estimating Localised Head-Loss Using the Manning Equation. Water 2019, 11, 1562. [Google Scholar] [CrossRef] [Green Version]
- de Jong, R.; Perdijk, H.; Develay, D.; Gautier, J.; Binquet, J. Hydraulic Model Studies of Desilting Basins of a Hydro-electric Project. In Proceedings of the 5th International Symposium on River Sedimentation, Karlsruhe, Germany, 6–10 April 1992. [Google Scholar]
- Brevik, O. 3D Numerisk Modellering av Deler av Vassvegen til Tonstad Kraftverk. Master’s Thesis, NTNU, Trondheim, Norway, 2013. [Google Scholar]
- Havrevoll, O.H.; Vereide, K.; Lia, L. Efficiency of Pressurized Rock Traps for Unlined Hydropower Tunnels. Energies 2021, 14, 4344. [Google Scholar] [CrossRef]
- Richter, W.; Vereide, K.; Zenz, G. Upgrading of a Norwegian pressurized sand trap combined with an open air surge tank. Geomech. Tunn. 2017, 10, 620–624. [Google Scholar] [CrossRef]
- Ansys, CFX 2019 R3 Documentation; Ansys Inc.: Canonsburg, PA, USA, 2021.
- U.S. Geological Survey. Scientific Investigations Report 2008–5093, 10 January 2013. Available online: https://pubs.usgs.gov/sir/2008/5093/table7.html (accessed on 21 August 2019).
- Schiller, L.; Naumann, A. Über die Grundlegenden Berechnungen bei der Schwerkraftaufbereitung. In Zeitschrift des Vereines Deutscher Ingenieure; Z. Vereines Deutscher Inge: Leipzig, Germany, 1933. [Google Scholar]
- Richter, W.; Zenz, G. Hydraulic Investigations, Numerical Simulations, Flexible Sand Trap 1.0; Technical Report; Graz University of Technology: Graz, Austria, 2020. [Google Scholar]
- Richter, W.; Mauko, G.; Zenz, G. Hydraulic Investigation, Numerical and Physical Model Test, Flexible sand trap 2.0; Technical Report; Graz University of Technology: Graz, Austria, 2020. [Google Scholar]
- Vanoni, V.A. Sedimentation Engineering; ASCE Manuals and Reports on Engineering Practice No. 54; American Society of Civil Engineers: Reston, VA, USA, 1977. [Google Scholar]
- Idel’cik, I.E. Handbook of Hydraulic Resistance, 3rd ed.; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Alfadhli, I.; Yang, S.-Q.; Sivakumar, M. Influence of Vertical Motion on Initiation of Sediment Movement. J. Water Resour. Prot. 2014, 6, 1666–1681. [Google Scholar] [CrossRef] [Green Version]
- Pugh, C.A. Sediment Transport Scaling for Physical Models, in Appendix C. In Sedimentation Engineering: Processes, Measurements, Modeling, and Practice; No. 110; ASCE: New York, NY, USA, 2008. [Google Scholar]
- Camp, T.R. Sedimentation and the Design of Settling Tanks. Trans. Am. Soc. Civ. Eng. 1946, 111, 146. [Google Scholar] [CrossRef]
- Ivarson, M.M.; Trivedi, C.; Vereide, K. Investigations of Rake and Rib Structures in Sand Traps to Prevent Sediment Transport in Hydropower Plants. Energies 2021, 14, 3882. [Google Scholar] [CrossRef]
- Jacobsen, T. Sediment Problems in Reservoirs: Control of Sediment Deposits. Ph.D. Thesis, Norwegian Technical University, Trondheim, Norway, 1997. [Google Scholar]
- Beheshti, A.A.; Ataie-Ashtiani, B. Analysis of threshold and incipient conditions for sediment movement. Coast. Eng. 2008, 55, 423–430. [Google Scholar] [CrossRef]
- Shields, A. Anwendung der Aehnlichkeitsmechanik und der Turbulenzforschung auf die Geschiebebewegung. Doctoral Dissertation, Mitteilungen der Preussischen Versuchsanstalt für Wasserbau und Schiffbau, Berlin, Germany, 1936. [Google Scholar]
- Chanson, H. Hydraulics of Open Channel Flow; Elsevier Ltd.: Amsterdam, The Netherlands, 2004; ISBN 978-0-7506-5978-9. [Google Scholar] [CrossRef]
- Ching, E.; Christian, J.; Ho, C. Shields Diagram Calculator for Determining the Onset of Particle Movement at the Bottom of a Fluid-Filled Tank; Sandia National Laboratories: Albuquerque, NM, USA, 2013. [Google Scholar]
- Shahmohammadi, R.; Afzalimehr, H.; Sui, J. Assessment of Critical Shear Stress and Threshold Velocity in Shallow Flow with and Particles. Water 2021, 13, 994. [Google Scholar] [CrossRef]






| 3D CFD | Physical Scale Model | Prototype | |
|---|---|---|---|
| Geometry scale | 1:1 | 1:36.67 | |
| Water Velocity scale | 1:1 | 1:1 | |
| Discharge scale | 1:1 | 1:36.672 | |
| Sediment size scale | 1:1 | 1:1 | |
| Time scale (-) | 1:1 | 1 × 36.67 | |
| Sediment sizescale (-) | 1:1 | 1:1 | |
| Sediment volume scale (-) | - | 1:36.673 | |
| Re (-) | 8.2 × 106 | 2.2 × 105 | 8.2 × 106 |
| Particle diameters (mm) | 0.3–1.0 | 0.3–1.0/5–30 | 0.01–100 1 |
| Density of particles kg/m3 | 2650 | 2650 | 2650 |
| Wall roughness, rock, ks concrete, ks (mm) | 300 1 | 0.1 0.1 | 300 0.76 |
| Materials/software | Ansys CFX, 2019 R3 | 30 cm wide flume in glass, acrylic glass crown | Real structure |
| Fluid | Water—RANS | Water | Water |
| Modelling strength | Transient flow conditions, bottom wall shear, hydrodynamic & particle settling | Transient particle transportation, settling- and resuspension processes, utilization of the flume | Observations |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Scale | 1:1 | Geometry | Prototype |
| Particles diameter | 0.3–1.0 mm | Particle injection | Gate crown surface |
| Simulation time, Discharge | 240–300 s 80 m3/s | Roughness unlined wall, concrete | 300 mm, f: 0.052 1 mm |
| Timestep | 0.2 s | Particle roughness | No |
| Particle coupling | One-way | ||
| Particles injection | 1.0 kg/s 0.1 m/s 150 1/s | Restitution coefficient of particles on wall; perp., parallel | 0.9 (-), 0.9 (-) |
| Particles density | 2650 kg/m3 | Bottom roughness | 1.0 mm |
| Particle roughness | no | Material | Unlined Rock |
| Particle drag | sphere | Mesh | 0.35 cm, no inflation, refinements concrete |
| Turbulence modelling | RANS SAS-SST | Water temperature | 10 °C |
| Mesh size | >4 mill. elements | Wall boundary | Rough wall |
| Inlet boundary | Mass flow rate, resp. normal flow velocity | Outlet boundary | Opening pressure, 0 Pa |
| Prototype | Model Test | |
| Inlet flow area (m2) | 48.9 | 0.036 |
| Gate flow area (m2) | 28 | 0.02 |
| Sand trap flow area (m2) | 119 | 0.089 |
| Discharge, Inlet flow velocity | 80 m3/s, 1.64 m/s | 59.6 l/s, 1.64 m/s |
| Discharge, average velocity | 80 m3/s, 0.67 m/s 65 m3/s, 0.55 m/s 55 m3/s, 0.46 m/s | 59.6 l/s, 0.67 m/s 48 l/s, 0.55 m/s 41 l/s, 0.46 m/s |
| Sand particles diameter | 0.01–100 mm | 0.3–1.0 mm |
| Gravel particles diameter | 5–30 mm | |
| Reynolds number (-) for Q = 80/65/55) in sand trap | 8.27/6.72/5.68 × 106 | 2.25/1.83/1.55 × 105 |
| Euler number (-) for Q = 80/65/55) in sand trap | 7.78/6.47/5.4 × 10−2 | 7.78/6.47/5.4 × 10−2 |
| Froude number (-) for Q = 80/65/55) in sand trap | 3.37/2.51/1.75 × 10−3 | 1.36/9.1/6.4 × 10−2 |
| Roughness of rock ks (mm) | 300 | 0.1 |
| Roughness of invert ks (mm) | 0.76 | 0.015 |
| Friction of invert f (-) | 0.011 | 0.011 |
| at Q = 80 m3/s | 0.038 | 0.038 |
| at Q = 80 m3/s | 24.93 | 24.93 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Richter, W.; Vereide, K.; Mauko, G.; Havrevoll, O.H.; Schneider, J.; Zenz, G. Retrofitting of Pressurized Sand Traps in Hydropower Plants. Water 2021, 13, 2515. https://doi.org/10.3390/w13182515
Richter W, Vereide K, Mauko G, Havrevoll OH, Schneider J, Zenz G. Retrofitting of Pressurized Sand Traps in Hydropower Plants. Water. 2021; 13(18):2515. https://doi.org/10.3390/w13182515
Chicago/Turabian StyleRichter, Wolfgang, Kaspar Vereide, Gašper Mauko, Ola H. Havrevoll, Josef Schneider, and Gerald Zenz. 2021. "Retrofitting of Pressurized Sand Traps in Hydropower Plants" Water 13, no. 18: 2515. https://doi.org/10.3390/w13182515






