Hydrological Similarity-Based Parameter Regionalization under Different Climate and Underlying Surfaces in Ungauged Basins
Abstract
:1. Introduction
2. Study Area, Data, and Methodology
2.1. Study Area
2.2. Data
2.3. Methods
2.3.1. GR Hydrological Model
2.3.2. Parameter Regionalization
2.3.3. Correlation and Regression Analysis
3. Results
3.1. Hydrological Changes in the Hulan River Basin and Poyang Lake Basin
3.2. Hydrological Simulation Using the GR Model
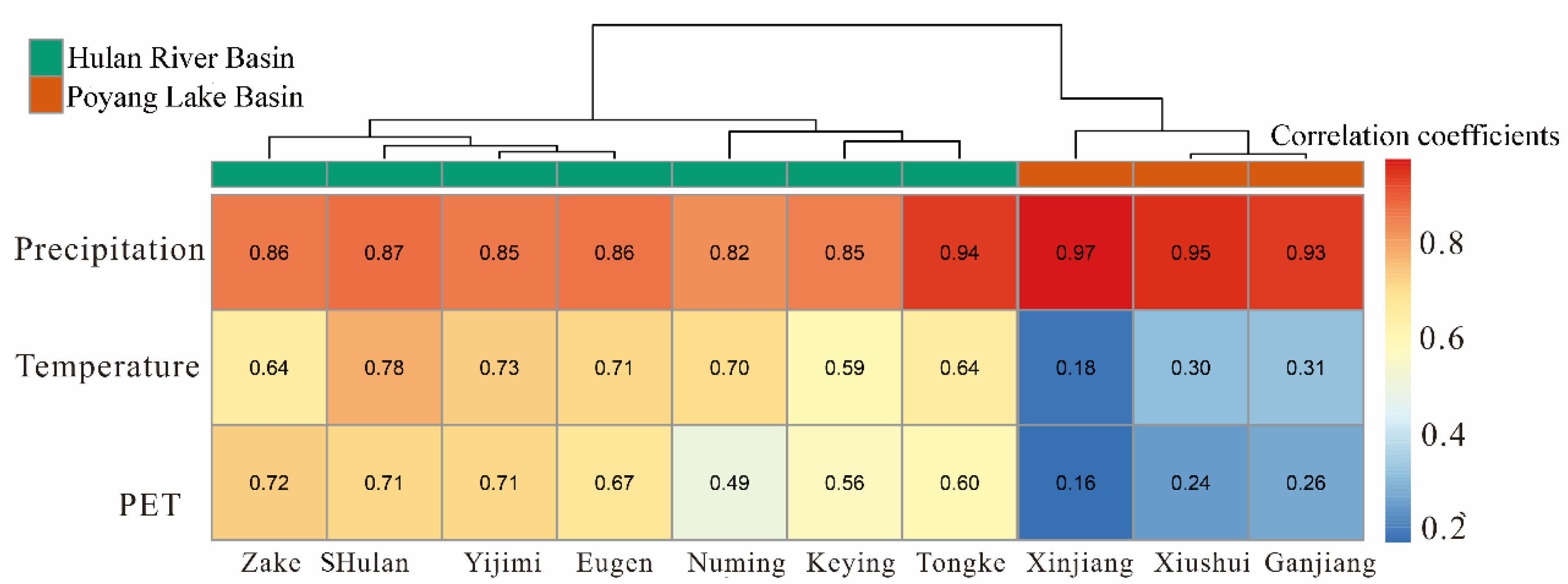
3.3. Hydrological Model Parameter Relationships with Climate and Underlying Surface Factors
3.4. Hydrological Similarity and Parameter Regionalization
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jiang, L.L.; Wu, H.A.; Lorenzo, A. Review of regionalization and remote sensing based method for hydrological model parameters calibration in ungauged basins. Acta Sci. Nat. Univ. Pekin. 2020, 56, 1152–1164. (In Chinese) [Google Scholar]
- Kiran, K.G.; Srinivas, V.V. Fuzzy ensemble clustering approach to address regionalization uncertainties in flood frequency analysis. Water Resour. Res. 2021, 57, e2020WR028412. [Google Scholar] [CrossRef]
- De Souza, G.R.; Merwade, V.; Coutinho de Oliveira, L.F.; Viola, M.R.; Farias, M.d.S. Regional flood frequency analysis and uncertainties: Maximum streamflow estimates in ungauged basins in the region of Lavras, MG, Brazil. Catena 2021, 197, 104970. [Google Scholar] [CrossRef]
- Dobler, C.C.; Hagemann, S.; Wilby, R.L.; Stotter, J. Quantifying different sources of uncertainty in hydrological projections in an Alpine watershed. Hydrol. Earth Syst. Sci. 2012, 16, 4343–4360. [Google Scholar] [CrossRef] [Green Version]
- Hrachowitz, M.; Savenije, H.; Bloschl, G.; Mcdonnell, J.; Sivapalan, M.; Pomeroy, J.; Arheimer, B.; Blume, T.; Clark, M.; Ehret, U.; et al. A decade of Predictions in Ungauged Basins (PUB)—A review. Hydrol. Sci. J. 2013, 58, 1198–1255. [Google Scholar] [CrossRef]
- Jafarzadegan, K.; Moradkhani, H. Regionalization of stage-discharge rating curves for hydrodynamic modeling in ungauged basins. J. Hydrol. 2020, 589, 125165. [Google Scholar] [CrossRef]
- Wagener, T.; Montanari, A. Convergence of approaches toward reducing uncertainty in predictions in ungauged basins. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef] [Green Version]
- Parajka, J.; Viglione, A.; Rogger, M.; Salinas, J.L.; Sivapalan, M.; Blöschl, G. Comparative assessment of predictions in ungauged basins—Part 1: Runoff-hydrograph studies. Hydrol. Earth Syst. Sci. 2013, 17, 1783–1795. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.; Magnusson, J.; Rizzi, J.; Xu, C.-Y. Runoff prediction in ungauged catchments in Norway: Comparison of regionalization approaches. Hydrol. Res. 2017, 49, 487–505. [Google Scholar] [CrossRef]
- Oudin, L.; Kay, A.; Andréassian, V.; Perrin, C. Are seemingly physically similar catchments truly hydrologically similar? Water Resour. Res. 2010, 46, 11558. [Google Scholar] [CrossRef]
- Samuel, J.; Coulibaly, P.; Metcalfe, R.A. Estimation of continuous streamflow in Ontario Ungauged Basins: Comparison of regionalization methods. J. Hydrol. Eng. 2011, 16, 447–459. [Google Scholar] [CrossRef]
- Yang, X.; Magnusson, J.; Xu, C.-Y. Transferability of regionalization methods under changing climate. J. Hydrol. 2018, 568, 67–81. [Google Scholar] [CrossRef]
- Tegegne, G.; Kim, Y.-O. Modelling ungauged catchments using the catchment runoff response similarity. J. Hydrol. 2018, 564, 452–466. [Google Scholar] [CrossRef]
- Parajka, J.; Merz, R.; Blöschl, G. A comparison of regionalisation methods for catchment model parameters. Hydrol. Earth Syst. Sci. 2005, 9, 157–171. [Google Scholar] [CrossRef] [Green Version]
- Yadav, M.; Wagener, T.; Gupta, H. Regionalization of constraints on expected watershed response behavior for improved predictions in ungauged basins. Adv. Water Resour. 2007, 30, 1756–1774. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Perrin, C.; Michel, C.; le Moine, N. Spatial proximity, physical similarity, regression and ungaged catchments: A comparison of regionalization approaches based on 913 French catchments. Water Resour. Res. 2008, 44, 03413. [Google Scholar] [CrossRef]
- Razavi, T.; Coulibaly, P. Streamflow prediction in ungauged basins: Review of regionalization methods. J. Hydrol. Eng. 2013, 18, 958–975. [Google Scholar] [CrossRef]
- Grimaldi, S.; Petroselli, A.; Salvadori, G.; de Michele, C. Catchment compatibility via copulas: A non-parametric study of the dependence structures of hydrological responses. Adv. Water Resour. 2016, 90, 116–133. [Google Scholar] [CrossRef]
- Betterle, A.; Schirmer, M.; Botter, G. Flow dynamics at the continental scale: Streamflow correlation and hydrological similarity. Hydrol. Process. 2019, 33, 627–646. [Google Scholar] [CrossRef] [Green Version]
- Loritz, R.; Gupta, H.; Jackisch, C.; Westhoff, M.; Kleidon, A.; Ehret, U.; Zehe, E. On the dynamic nature of hydrological similarity. Hydrol. Earth Syst. Sci. 2018, 22, 3663–3684. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Zhang, Y.; Zhang, L.; Wang, Z. Regionalization of hydrological modeling for predicting streamflow in ungauged catchments: A comprehensive review. Wiley Interdiscip. Rev. Water 2021, 8, 1487. [Google Scholar] [CrossRef]
- Rianna, M.; Ridolfi, E.; Napolitano, F. Comparison of different hydrological similarity measures to estimate flow quantiles. In Proceedings of the International Conference of Numerical Analysis and Applied Mathematics (ICNAAM 2016), Rhodes, Greece, 19–25 September 2016; AIP Publishing: College Park, MD, USA, 2017; Volume 1863. [Google Scholar]
- Yang, X.; Magnusson, J.; Huang, S.; Beldring, S.; Xu, C.-Y. Dependence of regionalization methods on the complexity of hydrological models in multiple climatic regions. J. Hydrol. 2020, 582, 124357. [Google Scholar] [CrossRef]
- Ragettli, S.; Zhou, J.; Wang, H. Modeling flash floods in ungauged mountain catchments of China: A decision tree learning approach for parameter regionalization. J. Hydrol. 2017, 555, 330–346. [Google Scholar] [CrossRef]
- Zhou, G.T. Study on the intra-annual runoff distribution characteristics in Hulan River Basin. Int. J. Hydroelectr. Energy 2018, 36, 39–43. (In Chinese) [Google Scholar]
- Wang, R.; Li, X.H.; Xue, C.Y.; Zhang, D. Spatio-temporal variations of the drought-flood abrupt alternation events in the Lake Poyang Basin from 1960 to 2012. J. Lake Sci. 2020, 32, 209–224. (In Chinese) [Google Scholar]
- Yang, W.J.; Liu, T.H.; Luan, H.L.; Cheng, D.B.; XU, X.F. Key techniques and demonstration of comprehensive control of ecological water conservancy in the Poyang Lake region and its five major tributaries. J. Sichuan Univ. Eng. Sci. Ed. 2019, 51, 1–12. (In Chinese) [Google Scholar]
- Zhang, L.; Meng, X.; Wang, H.; Yang, M.; Cai, S. Investigate the applicability of CMADS and CFSR reanalysis in Northeast China. Water 2020, 12, 996. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Zhang, X.; Yang, M.; Wang, H.; Chen, J.; Pan, Z.; Wu, Y. Application and evaluation of the China meteorological assimilation driving datasets for the SWAT model (CMADS) in poorly gauged regions in western China. Water 2019, 11, 2171. [Google Scholar] [CrossRef] [Green Version]
- Deng, P.X.; Wang, Y.T.; Hu, Q.F. Application of GR4J in daily runoff simulation for Ganjiang River Basin. J. China Hydrol. 2014, 34, 60–65. (In Chinese) [Google Scholar]
- Deng, P.X.; Hu, Q.F.; Wang, Y.T. Comparison of GR model, Xin’anjiang model, and WBM-DP model in rainfall-runoff simulation in Gangjiang River Basin. J. Hohai Univ. Nat. Sci. 2014, 42, 382–387. (In Chinese) [Google Scholar]
- Wang, H.J.; Zhang, J.Y.; Wang, G.Q. Relationships between runoff yield and flow concentration processes and climate and underlying surface in China’s middle and small river. Sci. Geogr. Sin. 2021, 41, 1–12. (In Chinese) [Google Scholar]
- Coron, L.; Thirel, G.; Delaigue, O.; Perrin, C.; Andréassian, V. The suite of lumped GR hydrological models in an R package. Environ. Model. Softw. 2017, 94, 166–171. [Google Scholar] [CrossRef]
- Valéry, A.; Andréassian, V.; Perrin, C. ‘As simple as possible but not simpler’: What is useful in a temperature-based snow-accounting routine? Part 1—Comparison of six snow accounting routines on 380 catchments. J. Hydrol. 2014, 517, 1166–1175. [Google Scholar] [CrossRef]
- Sauquet, E.; Richard, B.; Devers, A.; Prudhomme, C. Water restrictions under climate change: A Rhone–Mediterranean perspective combining bottom-up and top-down approaches. Hydrol. Earth Syst. Sci. 2019, 23, 3683–3710. [Google Scholar] [CrossRef] [Green Version]
- Burn, D.H.; Boorman, D.B. Estimation of hydrological parameters at ungauged catchments. J. Hydrol. 1993, 143, 429–454. [Google Scholar] [CrossRef]
- Kay, A.L.; Jones, D.A.; Crooks, S.M.; Kjeldsen, T.R.; Fung, C.F. An investigation of site-similarity approaches to generalisation of a rainfall–runoff model. Hydrol. Earth Syst. Sci. 2007, 11, 500–515. [Google Scholar] [CrossRef] [Green Version]
- He, Y.; Bárdossy, A.; Zehe, E. A review of regionalisation for continuous streamflow simulation. Hydrol. Earth Syst. Sci. 2011, 15, 3539–3553. [Google Scholar] [CrossRef] [Green Version]
- Petheram, C.; Rustomji, P.; Chiew, F.; Vleeshouwer, J. Rainfall–runoff modelling in northern Australia: A guide to modelling strategies in the tropics. J. Hydrol. 2012, 462–463, 28–41. [Google Scholar] [CrossRef]
- Merz, R.; Parajka, J.; Bloschl, G. Scale effects in conceptual hydrological modeling. Water Resour. Res. 2009, 45, 09405. [Google Scholar] [CrossRef]
- Nester, T.; Kirnbauer, R.; Gutknecht, D.; Blöschl, G. Climate and catchment controls on the performance of regional flood simulations. J. Hydrol. 2011, 402, 340–356. [Google Scholar] [CrossRef]
- Salinas, J.L.; Laaha, G.; Rogger, M.; Parajka, J.; Viglione, A.; Sivapalan, M.; Bloschl, G. Comparative assessment of predictions in ungauged basins—Part 2: Flood and low flow studies. Hydrol. Earth Syst. Sci. 2013, 17, 2637–2652. [Google Scholar] [CrossRef] [Green Version]
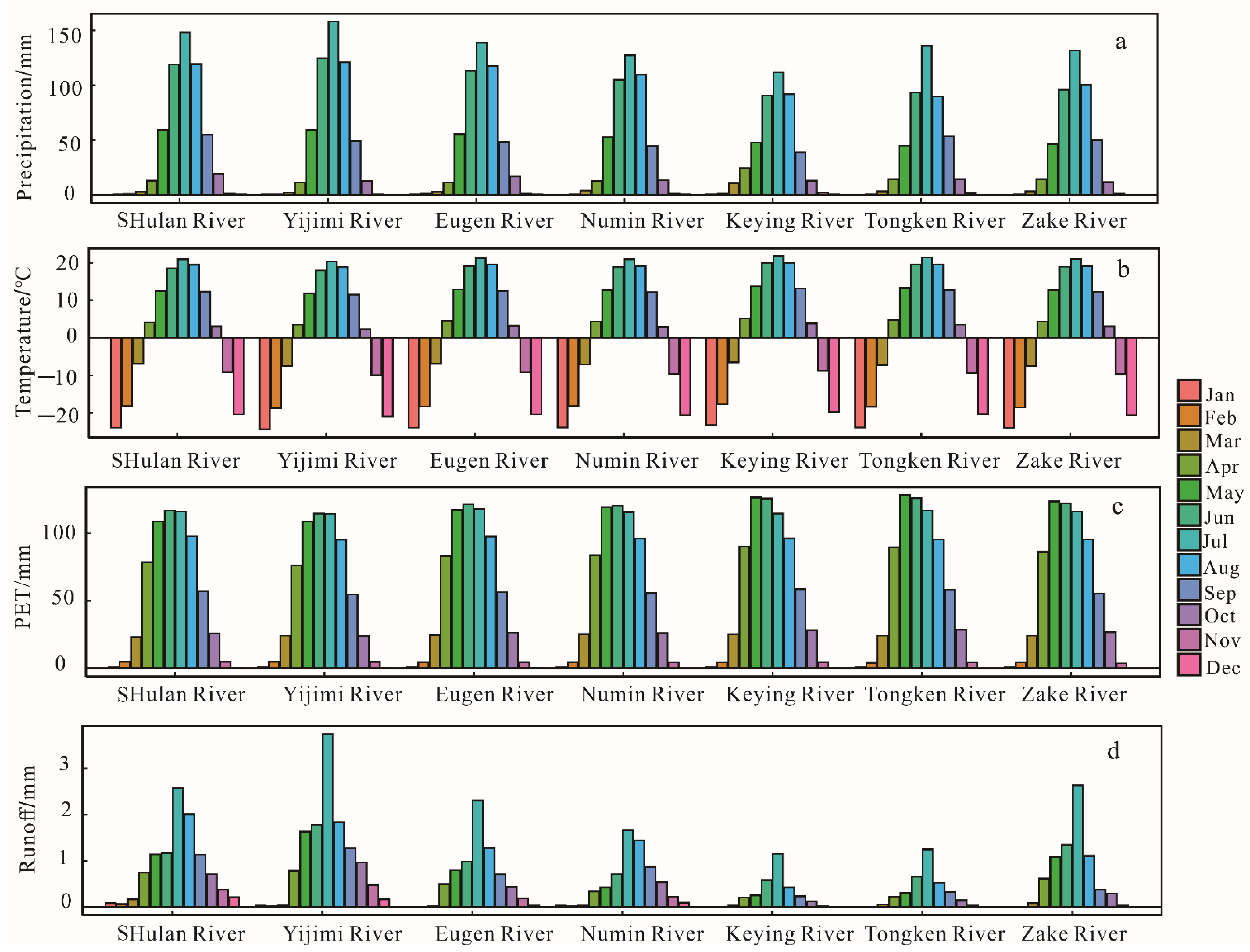
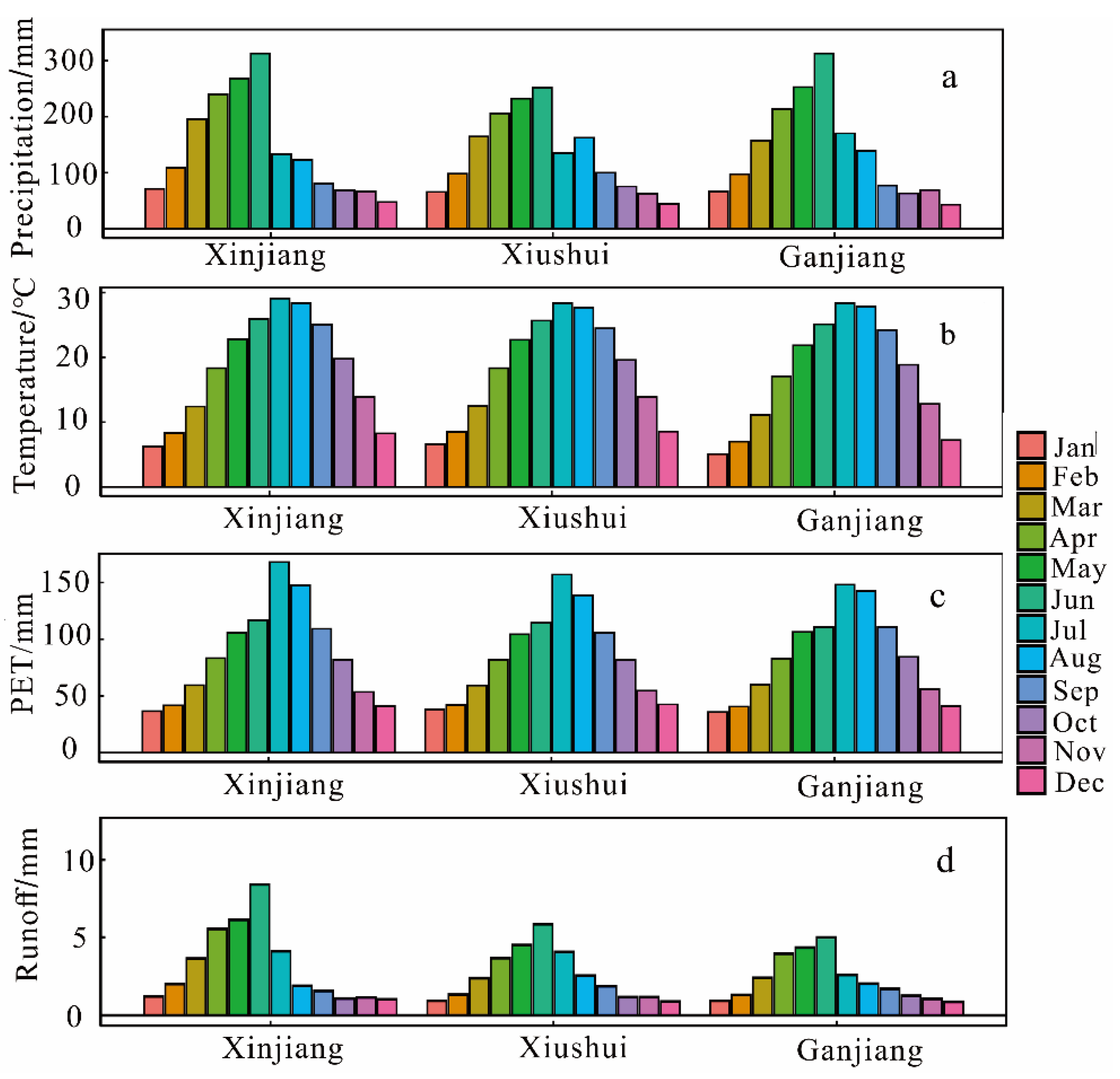
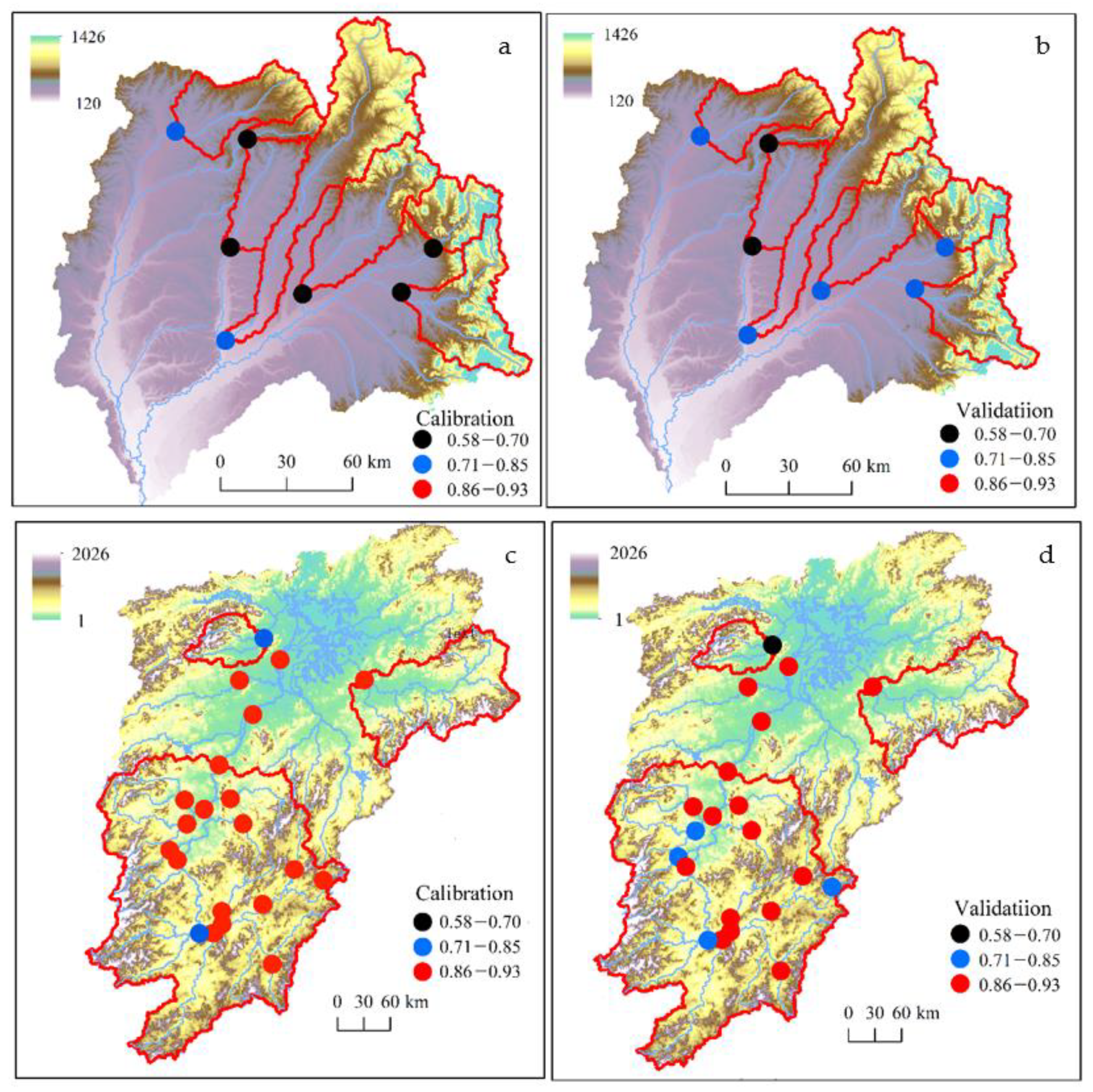
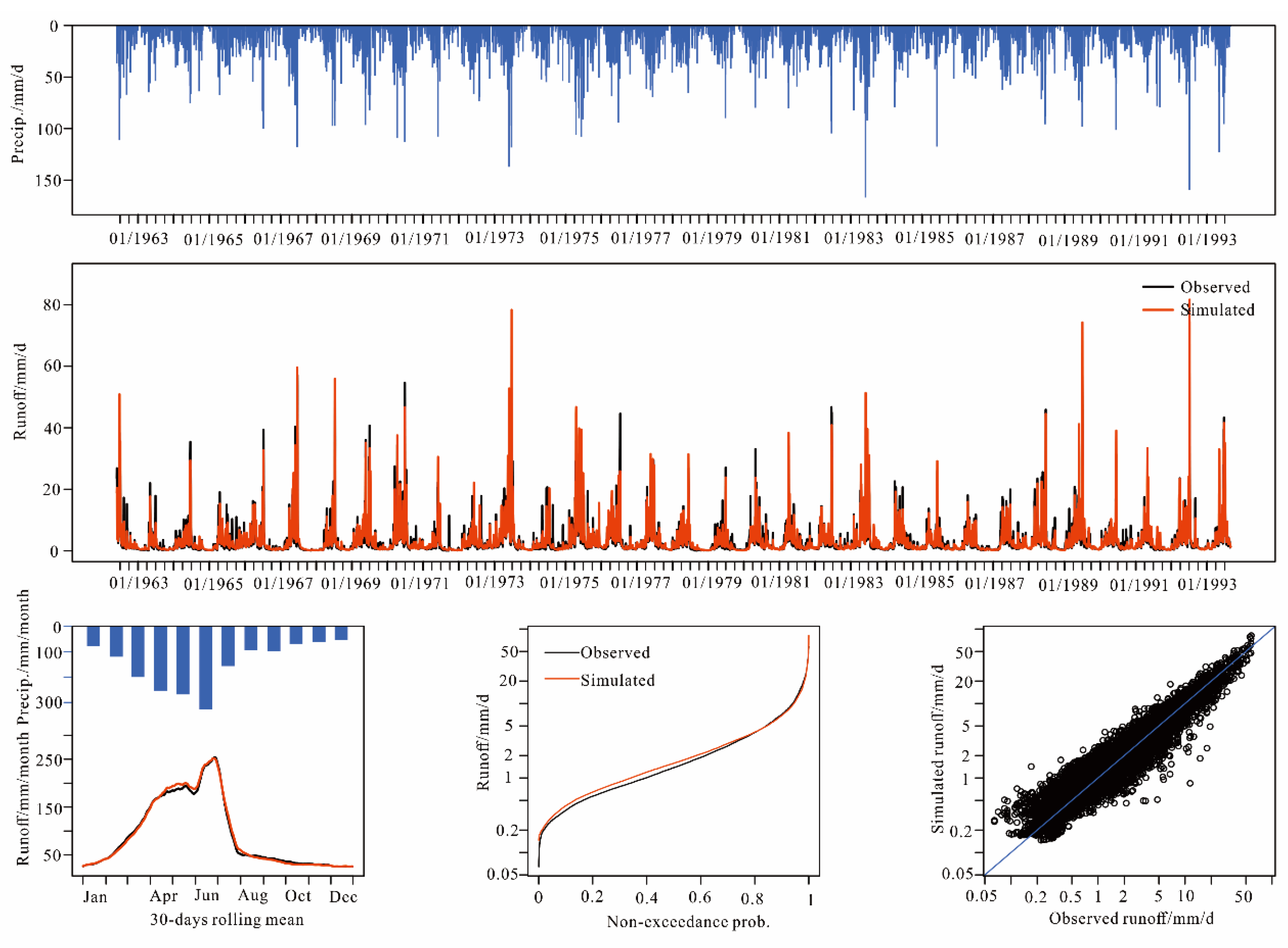
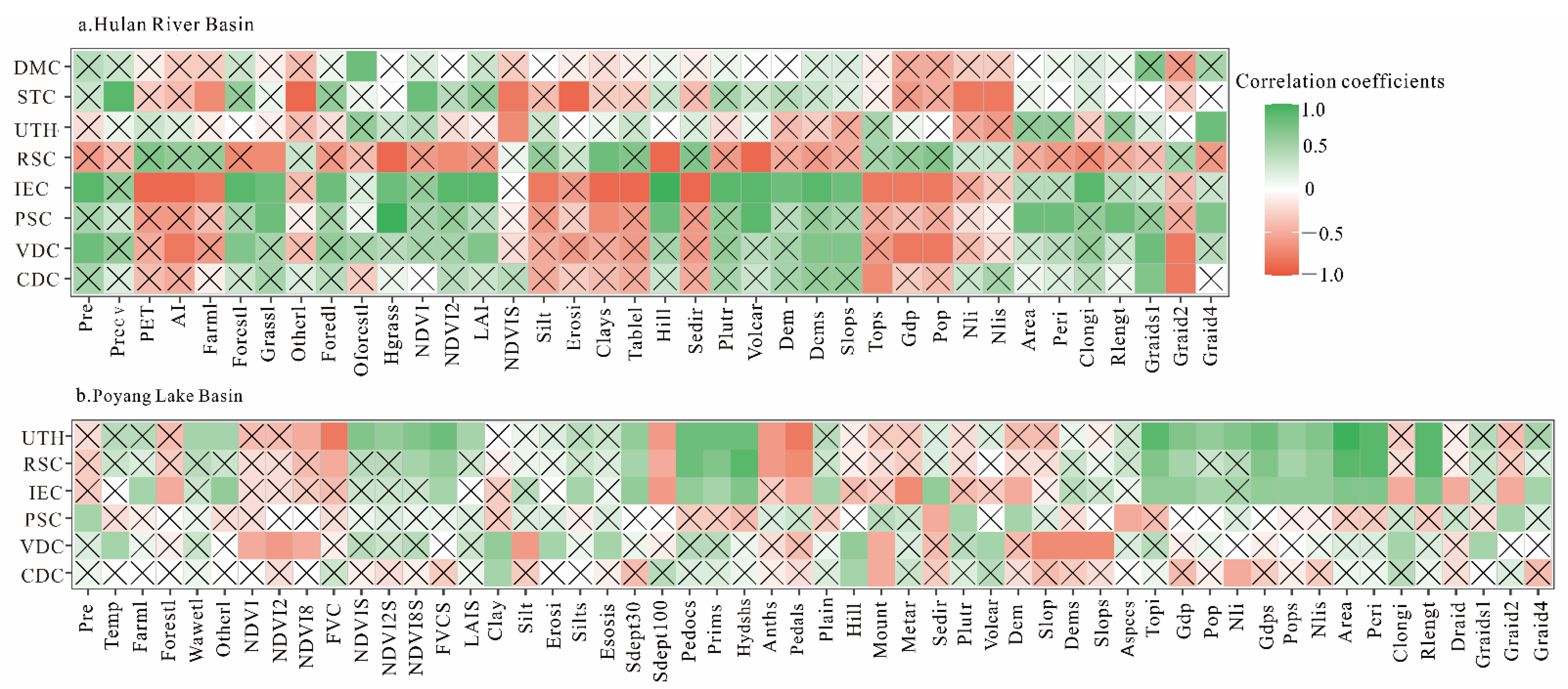
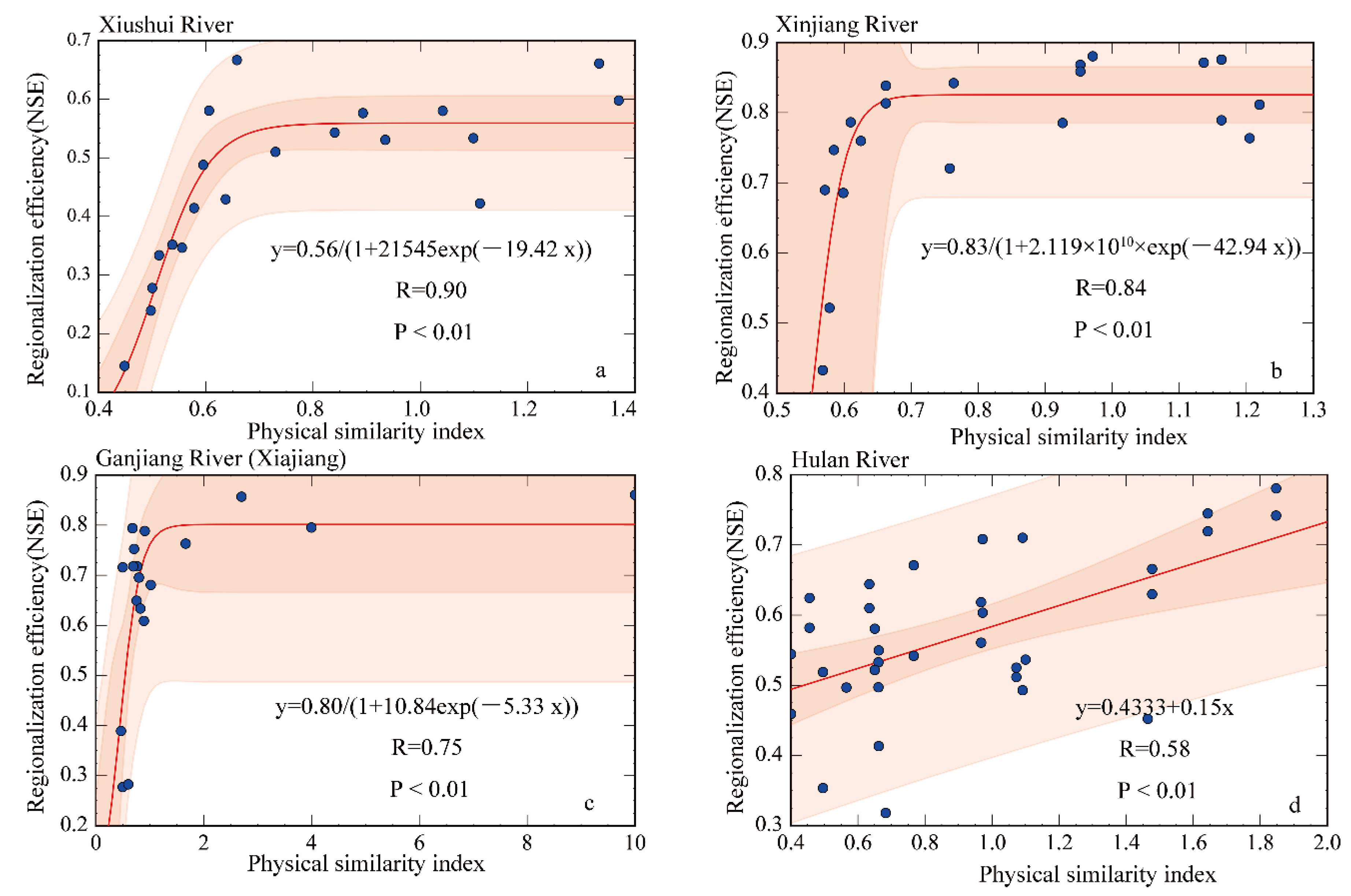
| River | Hydrological Station | Abbreviate of Hydrological Station | Latitude | Longitude | |
|---|---|---|---|---|---|
| Hulan River Basin | Small Hulan River (SHulan River) | Tieli | TL | 128.0197 | 46.97139 |
| Yijimi River | Beiguan | BG | 128.2441 | 47.12867 | |
| Eugen River | Eugen River | EGH | 127.44 | 47.01839 | |
| Numin River | Sifangtai | SFT | 126.9511 | 46.87278 | |
| Keyin River | Suileng | SL | 127.0503 | 47.24528 | |
| Tongken River | Haibei | HB | 126.8137 | 47.7403 | |
| Zake River | Chenjiadian | CJD | 127.2367 | 47.67111 | |
| Poyang Lake Basin | Xiushui River | Wanjiabu | WJF | 115.6479 | 28.85572 |
| Xinjiang River | Maygang | MG | 116.8175 | 28.43833 | |
| Ganjiang River | Xiajiang | XJ | 115.1512 | 27.54625 | |
| Ganjiang River | Shicheng | SC | 116.3567 | 26.37833 | |
| Ganjiang River | Ningdu | ND | 116.0233 | 26.48667 | |
| Ganjiang River | Mazhou | MZ | 115.7833 | 25.515 | |
| Ganjiang River | Hanlinqiao | HLQ | 115.2044 | 26.04876 | |
| Ganjiang River | Julongtan | JLT | 115.1175 | 25.82709 | |
| Ganjiang River | Bashang | BAS | 114.9554 | 25.82062 | |
| Ganjiang River | Linkeng | LK | 114.6022 | 26.66611 | |
| Ganjiang River | Shangshalan | SSL | 114.7925 | 26.93833 | |
| Ganjiang River | Saitang | ST | 114.7633 | 27.18183 | |
| Ganjiang River | Baisha | BS | 115.4333 | 26.95 | |
| Ganjiang River | Xintian | XT | 115.2856 | 27.20222 | |
| Ganjiang River | Gaoan | GA | 115.371 | 28.41717 | |
| Ganjiang River | Fenkeng | FK | 115.667 | 26.12772 | |
| Ganjiang River | Waizhou | WZ | 115.8404 | 28.63267 | |
| Ganjiang River | Xiashan | XS | 115.2117 | 25.91667 | |
| Ganjiang River | Dongbei | DB | 114.6921 | 26.56842 | |
| Ganjiang River | Jian | JA | 114.9862 | 27.09176 | |
| Ganjiang River | Zhangshu | ZS | 115.533 | 28.067 |
| Types | Indices |
|---|---|
| Climate | Annual average precipitation (Pre), coefficient of variation in average precipitation (Precv), annual mean potential evapotranspiration (Evap), coefficient of variation in annual potential evapotranspiration (Evapcv), aridity index(AI), temperature (Temp) |
| Vegetation and land use | Proportion of farmland (Farml), proportion of forest (Forestl), proportion of grassland (Grassl), proportion of water and wetland (Wawetl), proportion of other land uses (Otherl), proportion of forested land (Foredl), proportion of shrub (Shrub), proportion of other forest land (Oforestl), proportion of high-coverage grassland (Hgrass), proportion of medium-coverage grassland (Mgrass), proportion of low-coverage grassland (Lgrass), mean Normalized Difference Vegetation Index (NDVI), monthly minimum NDVI (NDVI2), monthly maximum NDVI (NDVI8), vegetation coverage (FVC), leaf area index (LAI), standard deviation of spatial NDVI (NDVIS), standard deviation of spatial minimum NDVI (NDVI2S), standard deviation of spatial maximum NDVI (NDVI8S), standard deviation of spatial vegetation coverage (FVCS), standard deviation of spatial leaf area index (LAIS) |
| Soil | Percentage of sand (Sand), percentage of silt (Silt), percentage of clay (Clay), soil erosion (Erosi), standard deviation of spatial sand (Sands), standard deviation of spatial silt (Silts), standard deviation of spatial clay (Clays), standard deviation of spatial soil erosion (Erosis), proportion of soil reference depth (30 cm) (Sdept30), proportion of soil reference depth (100 cm) (Sdept100), proportion of soil available water content (>100 mm/m) (Awc1), proportion of soil available water content (<100 mm/m) (Awc2), proportion of luvisol and semi-luvisols (lusimlus), proportion of pedocal (Pedocs), proportion of arid soil and desert soil (Aridests), proportion of primitive soil (Prims), proportion of hydromorphic soil and semi-hydromorphic soil (Hydshs), proportion of anthropic soils (Anths), proportion of alpine soil (Alpis), proportion of pedalfer (Pedals) |
| Landform and geology | Proportion of plain (Plain), proportion of tableland (Tablel), proportion of hilly land (Hill), proportion of mountainous land (Mount), proportion of metamorphic rock (Metar), proportion of sedimentary rock (Sedir), proportion of plutonic rock (Plutr), proportion of volcanic rock (Volcar) |
| Terrain | Elevation (Dem), slope (Slop), aspect (Aspec), standard deviation of spatial elevation (Dems), standard deviation of spatial slope (Slops), standard deviation of spatial aspect (Aspecs), topographic index (Topi), wetness index (Weti) |
| Human activity | Annual mean Gross Domestic Product (GDP), Annual mean population (Pop), Annual mean night light intensity (Nli), standard deviation of spatial GPD (GDPs), standard deviation of spatial population (Pops), standard deviation of night light intensity (Nlis) |
| Watershed morphology | Basin area (Area), basin perimeter (Peri), centroid longitude (Clongi), centroid latitude (Clati), river length (Rlengt), coefficient of basin shape (Bshac), drainage density (Draid), proportion of level 1 of Strahler stream ordering of drainage density (Draid1), proportion of level 2 of Strahler stream ordering of drainage density (Draid2), proportion of level 3 of Strahler stream ordering of drainage density (Draid3), proportion of level 4 of Strahler stream ordering of drainage density (Draid4) |
| Basin | Climate | Vegetation and Land Use | Soil | Landform and Geology | Terrain | Human Activity | Watershed Morphology |
|---|---|---|---|---|---|---|---|
| SHulan River | −1.9039 | −2.6856 | −2.7654 | −2.3337 | −3.9161 | −0.7298 | −0.4336 |
| Yijimi River | −3.1684 | −2.9296 | −5.3405 | −3.8697 | −3.3713 | −2.3611 | 0.9909 |
| Eugen River | −0.4310 | −0.2504 | 1.6002 | −0.0845 | 0.4899 | −1.8270 | −2.1255 |
| Numin River | −0.0444 | −1.9447 | 0.6299 | −0.5110 | 0.6204 | 1.4776 | −3.2721 |
| Keyin River | 2.9795 | 4.7161 | 3.5410 | 2.7547 | 1.9544 | 2.9993 | 1.0706 |
| Tongken River | 1.7442 | 2.1156 | 1.5983 | 2.2794 | 2.0931 | 1.0289 | −0.4684 |
| Zake River | 0.8240 | 0.9787 | 0.7365 | 1.7649 | 2.1295 | −0.5877 | 4.2381 |
| Weight | 0.1216 | 0.2200 | 0.1005 | 0.1177 | 0.1368 | 0.1643 | 0.1390 |
| Hulan River | Yijimi River | Eugen River | Numin River | Keyin River | Tongken River | Zake River | ||
|---|---|---|---|---|---|---|---|---|
| Physical similarity | SHulan River | - | 1.85 | 0.77 | 0.66 | 0.40 | 0.50 | 0.57 |
| Yijimi River | 1.85 | - | 0.97 | 1.64 | 0.63 | 1.09 | 1.10 | |
| Eugen River | 0.97 | 0.77 | - | 0.97 | 0.66 | 1.07 | 0.86 | |
| Numin River | 0.97 | 0.66 | 1.64 | - | 0.46 | 1.48 | 0.88 | |
| Keyin River | 0.46 | 0.40 | 0.63 | 0.66 | - | 0.65 | 1.53 | |
| Tongken River | 0.65 | 0.50 | 1.09 | 1.07 | 1.48 | - | 0.68 | |
| Zake River | 0.68 | 0.57 | 1.10 | 0.86 | 0.88 | 1.53 | - | |
| Spatial similarity/m | SHulan River | - | 44,658 | 62,456 | 93,509 | 10,6676 | 13,9106 | 11,5220 |
| Yijimi River | 44,658 | - | 37,722 | 58,260 | 85,381 | 10,8254 | 82,863 | |
| Eugen River | 62,456 | 37,722 | - | 32,950 | 48,265 | 76,759 | 52,808 | |
| Numin River | 93,509 | 58,260 | 32,950 | - | 40,125 | 50,379 | 24,972 | |
| Keyin River | 10,6676 | 85,381 | 48,265 | 40,125 | - | 40,083 | 30,291 | |
| Tongken River | 13,9106 | 10,8254 | 76,759 | 50,379 | 40,083 | - | 25,440 | |
| Zake River | 11,5220 | 82,863 | 52,808 | 24,972 | 30,291 | 25,440 | - |
| Calibration Period | Validation Period | Reference Basin | Similarity Index | Rank | ||
|---|---|---|---|---|---|---|
| Spatial similarity | SHulan River | 0.76 | 0.79 | Yijimi River | 44,658.44 | 1/6 |
| Yijimi River | 0.57 | 0.53 | Eugen River | 37,721.69 | 3/6 | |
| Eugen River | 0.75 | 0.74 | Numin River | 32,950.20 | 1/6 | |
| Numin River | 0.10 | 0.29 | Zake River | 24,972.11 | 6/6 | |
| Keyin River | 0.02 | 0.23 | Zake River | 30,290.81 | 6/6 | |
| Tongken River | 0.28 | 0.51 | Zake River | 25,440.49 | 6/6 | |
| Zake River | 0.42 | 0.34 | Eugen River | 24,972.11 | 5/6 | |
| physical similarity | SHulan River | 0.76 | 0.79 | Yijimi River | 1.85 | 1/6 |
| Yijimi River | 0.79 | 0.73 | Hulan River | 1.85 | 1/6 | |
| Eugen River | 0.75 | 0.74 | Numin River | 1.64 | 1/6 | |
| Numin River | 0.75 | 0.71 | Eugen River | 1.64 | 1/6 | |
| Keyin River | 0.73 | 0.64 | Tongken River | 1.48 | 1/6 | |
| Tongken River | 0.73 | 0.60 | Keyin River | 1.53 | 1/6 | |
| Zake River | 0.46 | 0.40 | Tongken River | 1.53 | 4/6 |
| Ungauged Basin | Calibration Period | Validation Period | Reference Basin | Similarity Index | Rank | |
|---|---|---|---|---|---|---|
| Physical similarity | Xiushui River | 0.51 | 0.56 | Ganjiang River (Gaoan) | 75,879.00 | 6/20 |
| Xinjiang River | 0.87 | 0.85 | Ganjiang River (Xintian) | 147,975.00 | 5/20 | |
| Ganjiang River (Xiajiang) | 0.86 | 0.86 | Ganjiang River (Jian) | 13,824.00 | 1/20 | |
| physical similarity | Xiushui River | 0.64 | 0.68 | Xinjiang River | 1.36 | 1/20 |
| Xinjiang River | 0.88 | 0.87 | Ganjiang River (Saitang) | 1.33 | 1/20 | |
| Ganjiang River (Xiajiang) | 0.86 | 0.86 | Ganjiang River (Jian) | 9.56 | 1/20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Cao, L.; Feng, R. Hydrological Similarity-Based Parameter Regionalization under Different Climate and Underlying Surfaces in Ungauged Basins. Water 2021, 13, 2508. https://doi.org/10.3390/w13182508
Wang H, Cao L, Feng R. Hydrological Similarity-Based Parameter Regionalization under Different Climate and Underlying Surfaces in Ungauged Basins. Water. 2021; 13(18):2508. https://doi.org/10.3390/w13182508
Chicago/Turabian StyleWang, Huaijun, Lei Cao, and Ru Feng. 2021. "Hydrological Similarity-Based Parameter Regionalization under Different Climate and Underlying Surfaces in Ungauged Basins" Water 13, no. 18: 2508. https://doi.org/10.3390/w13182508






