Theoretical Description of the Hydrodynamic Process after Barrier Lake Formation and Emergency Responses Implementation
Abstract
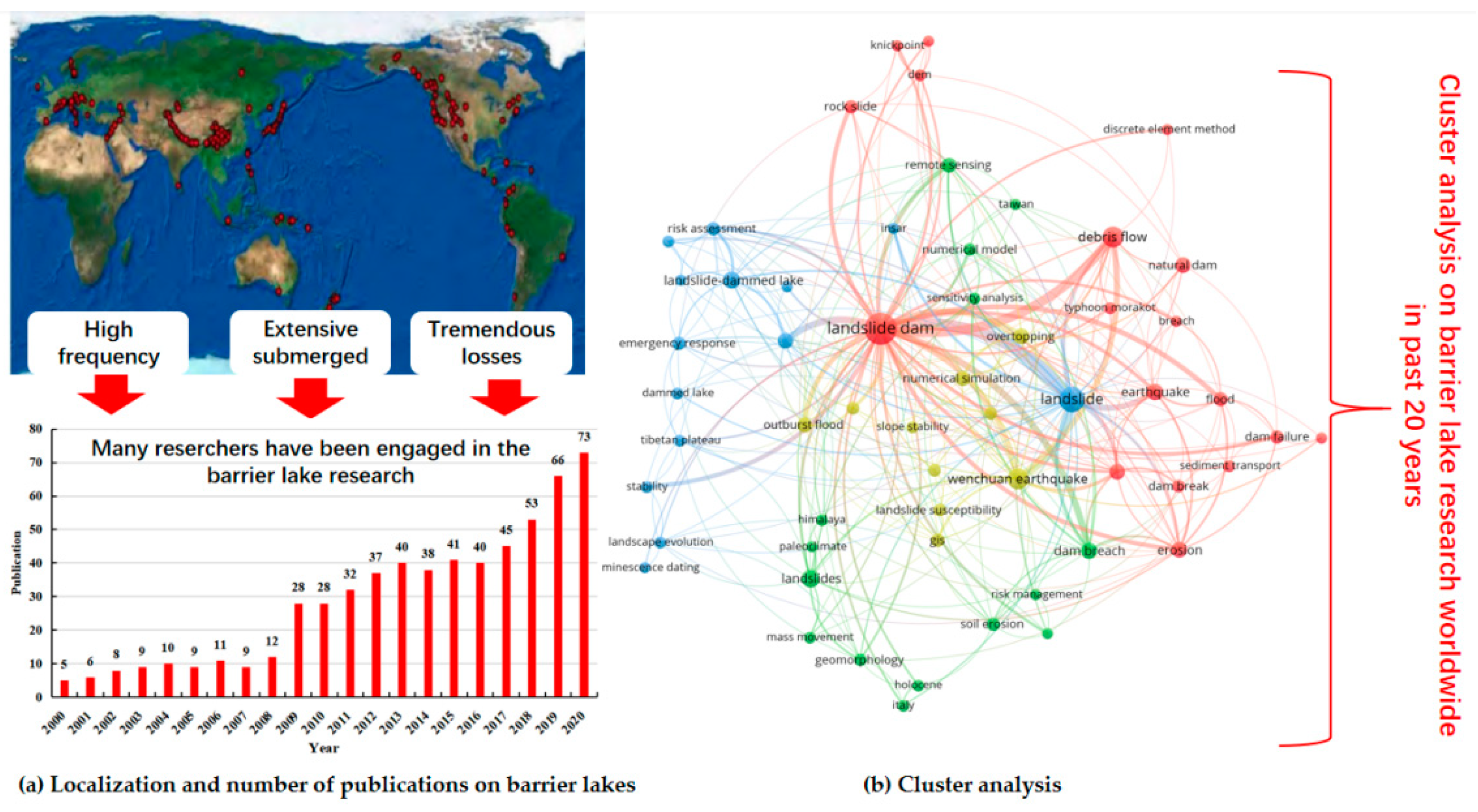
:1. Introduction
2. Materials and Methods
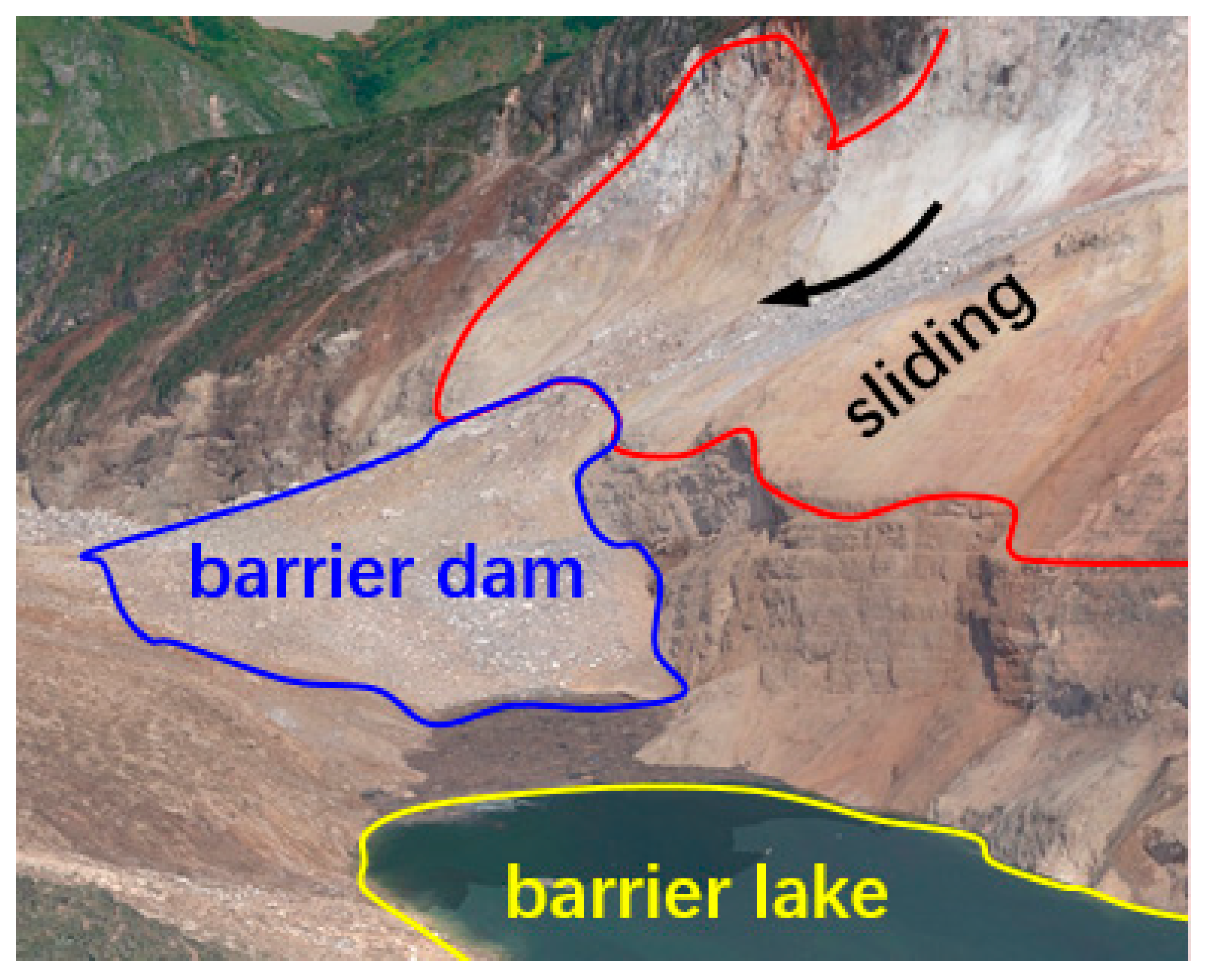
2.1. Tremendous Yigong Landslide
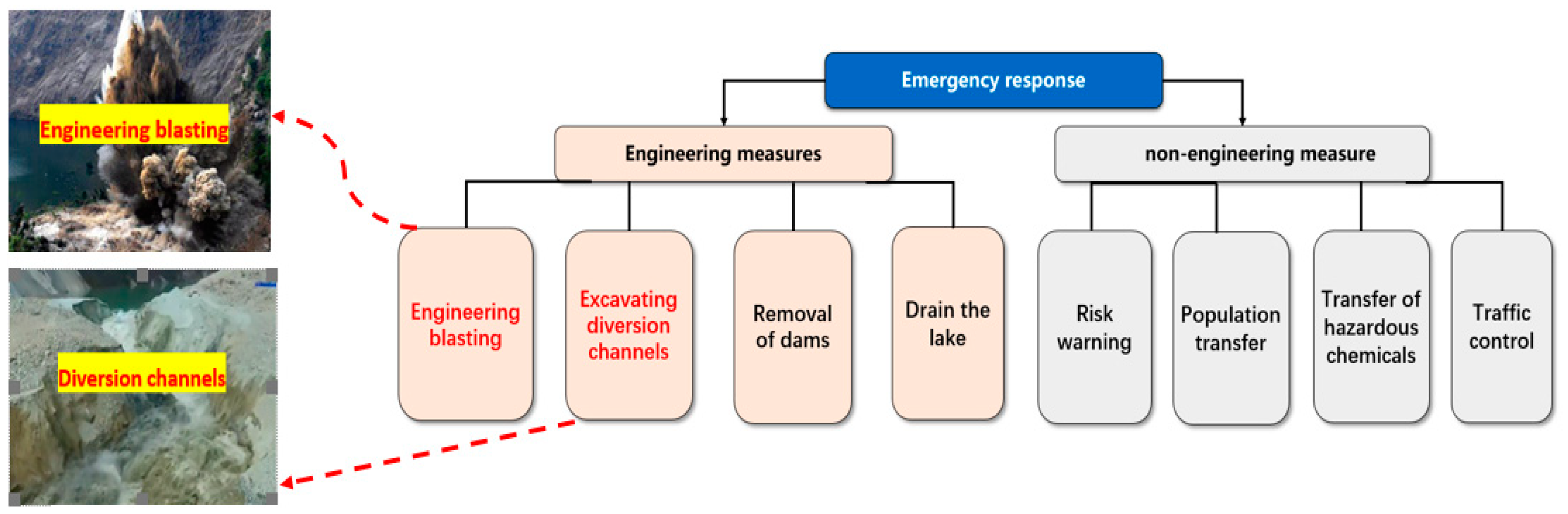
2.2. Emergency Responses of Yigong Landslide
2.3. Calculus Application
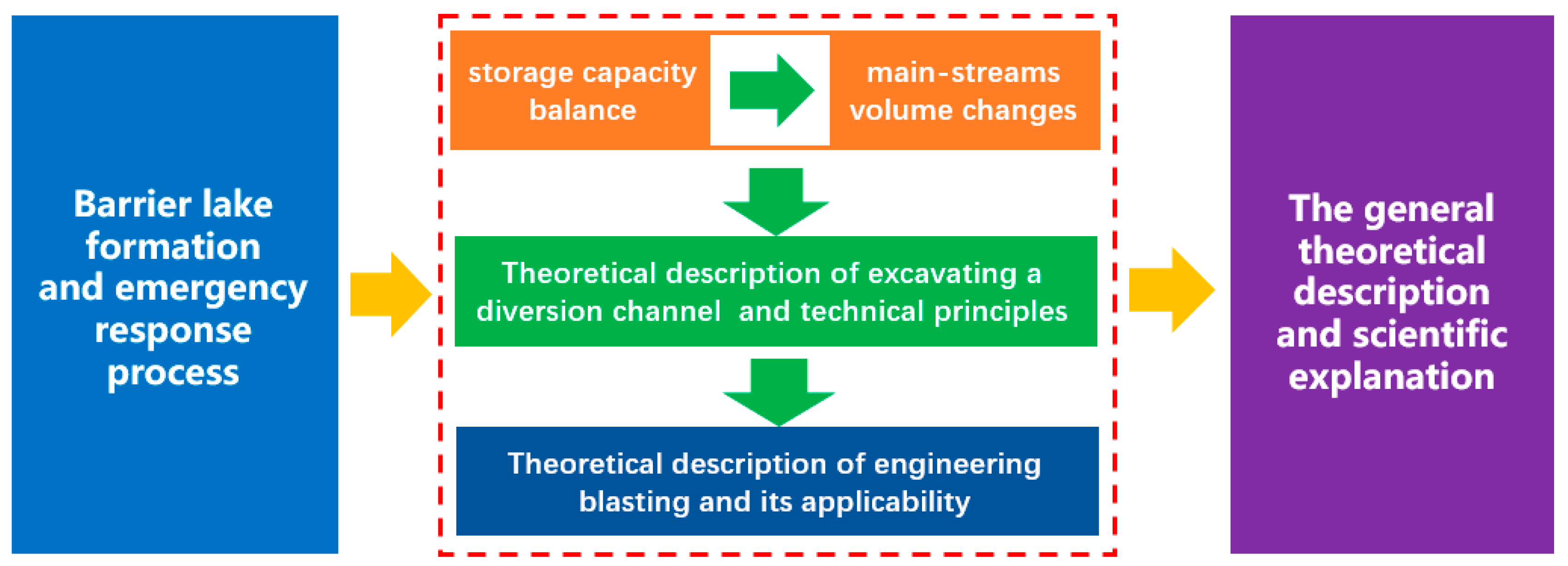
3. Results and Analysis
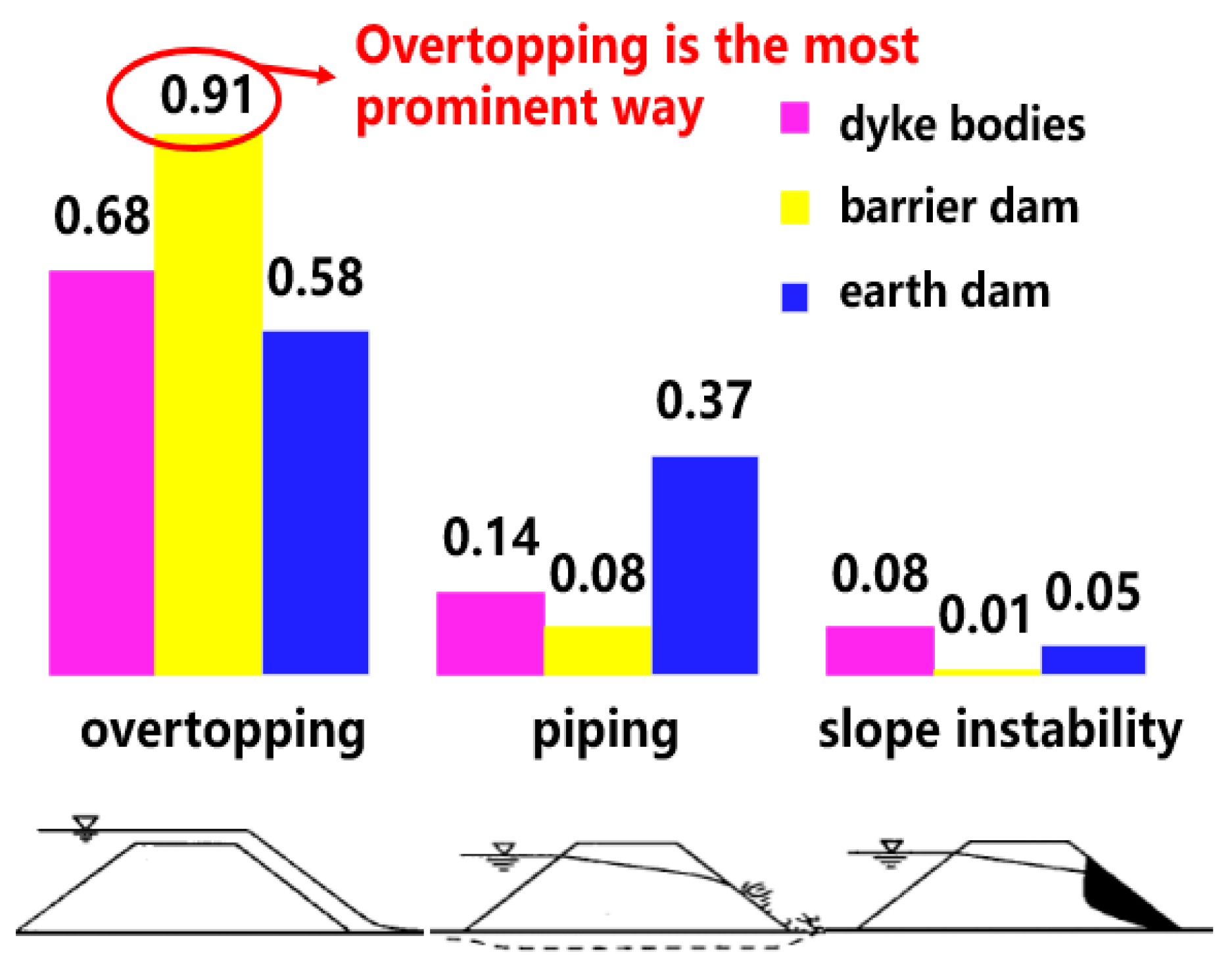
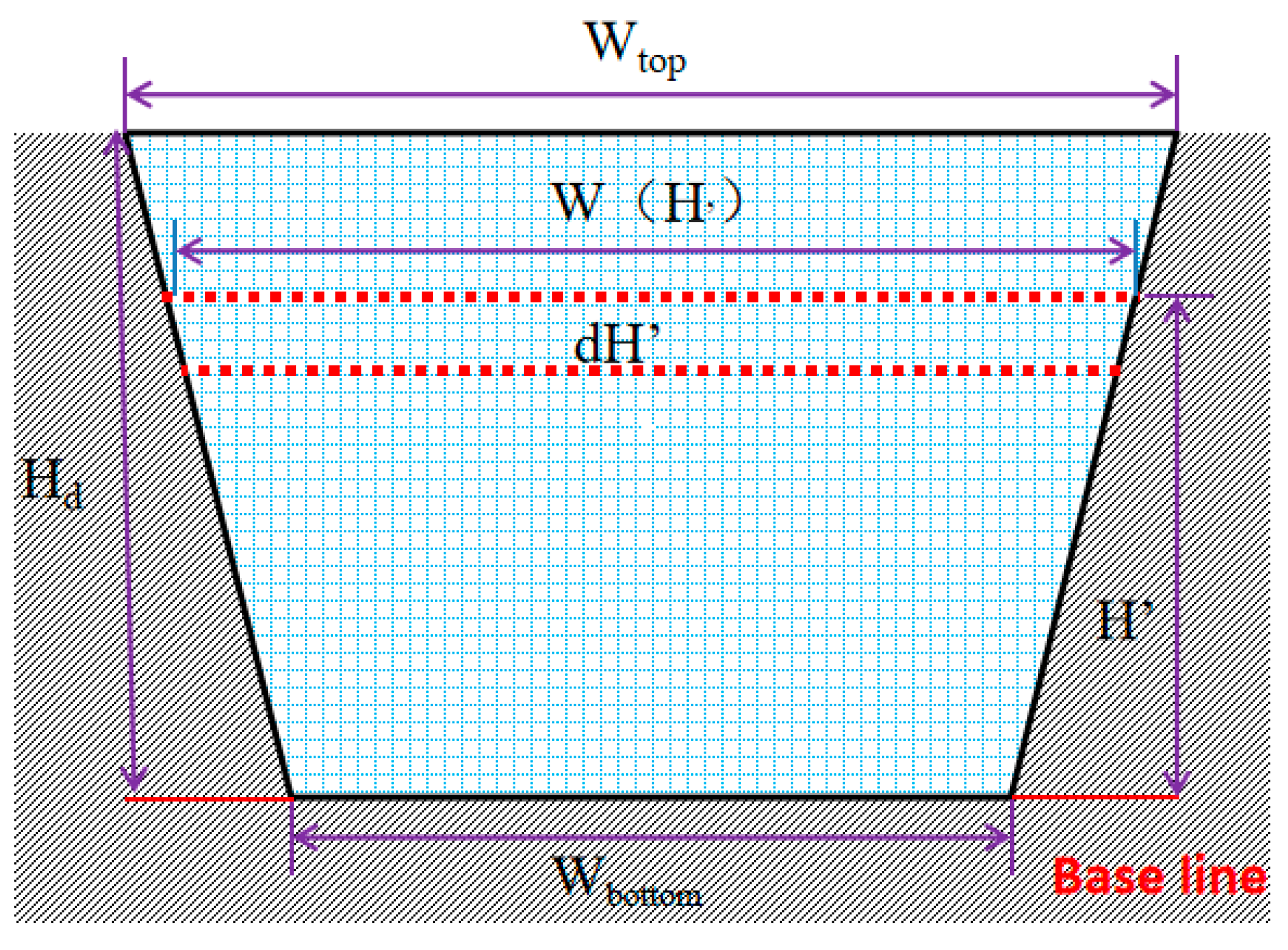
3.1. Theoretical Analysis of Barrier Lake Formation
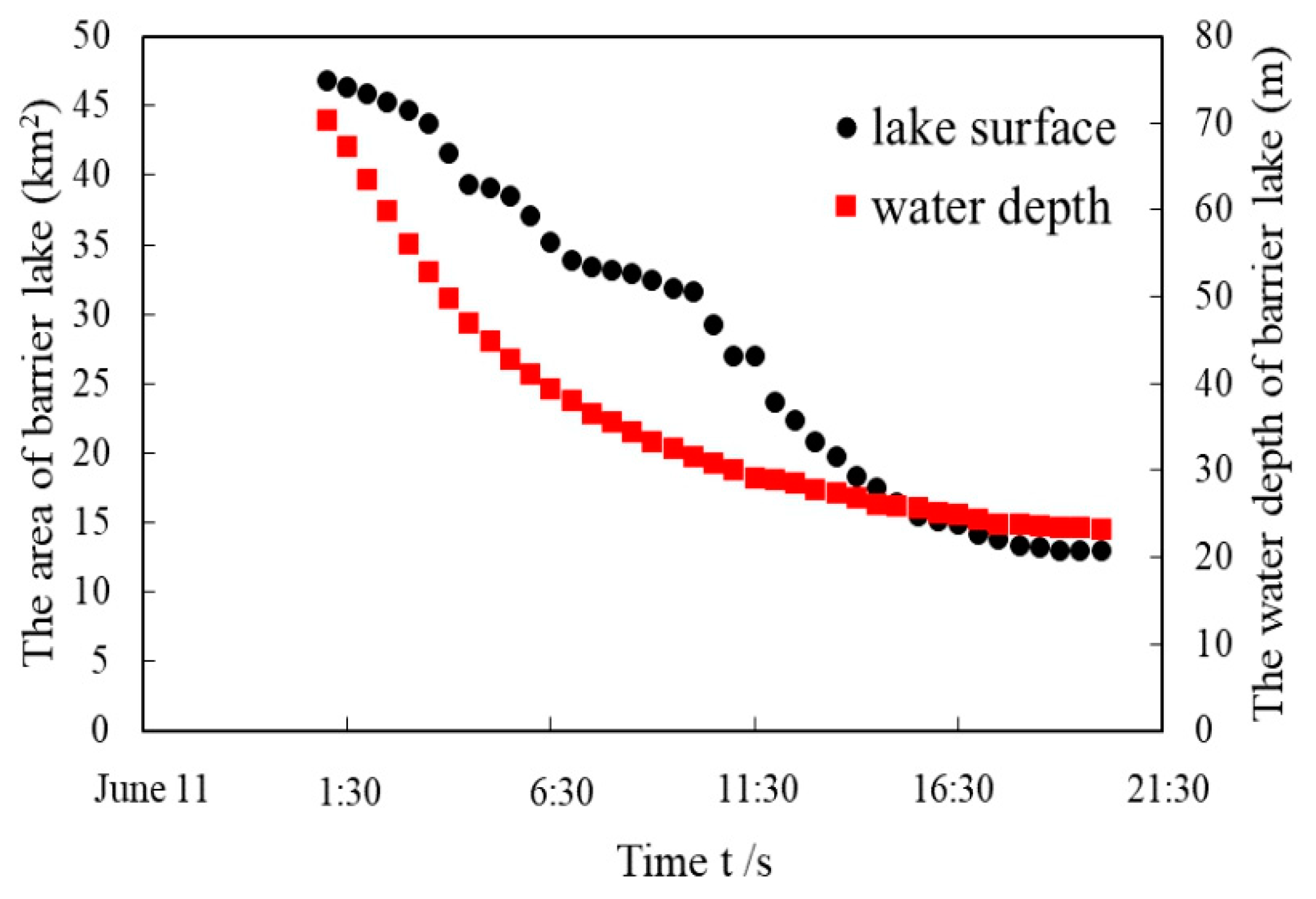
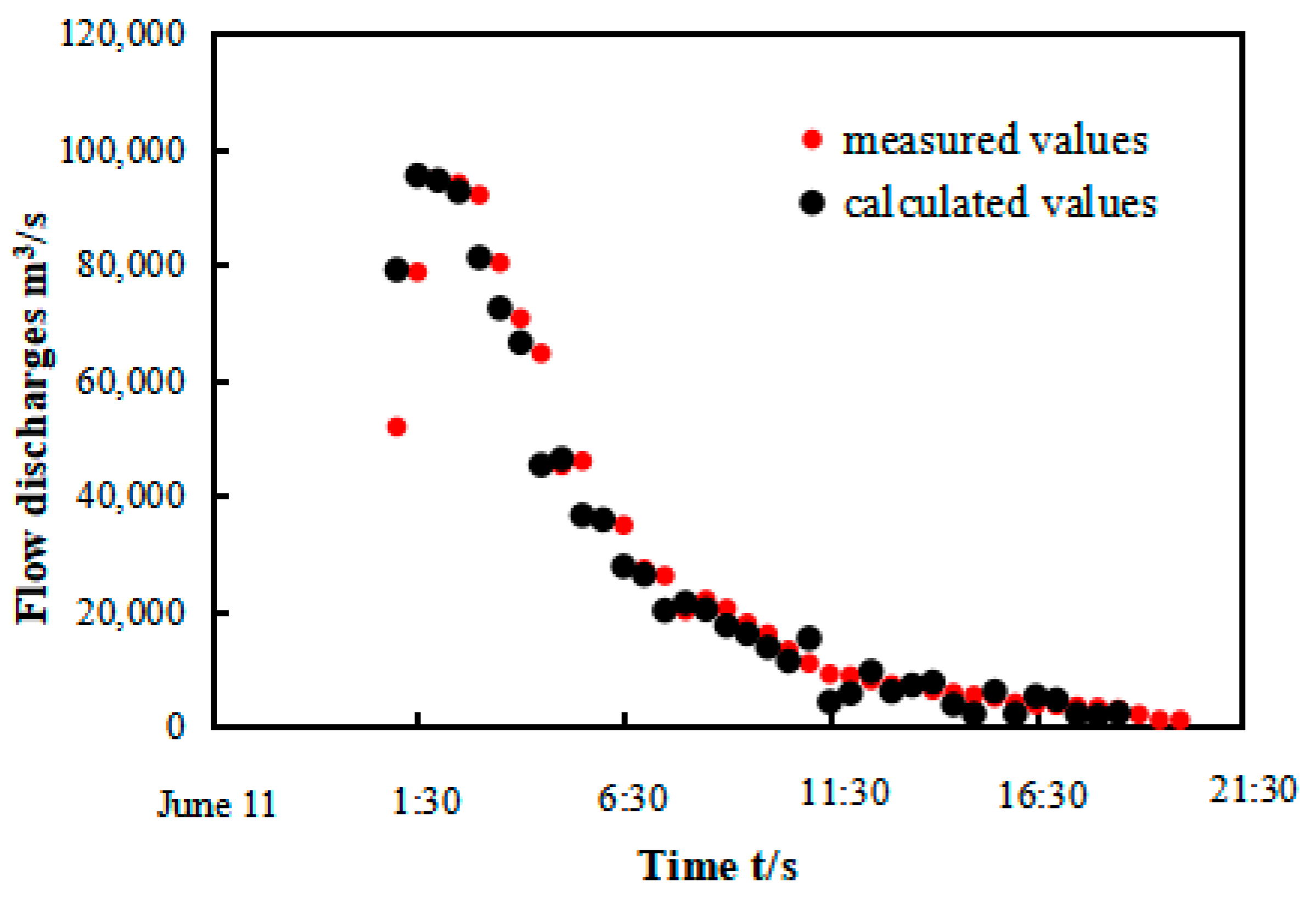
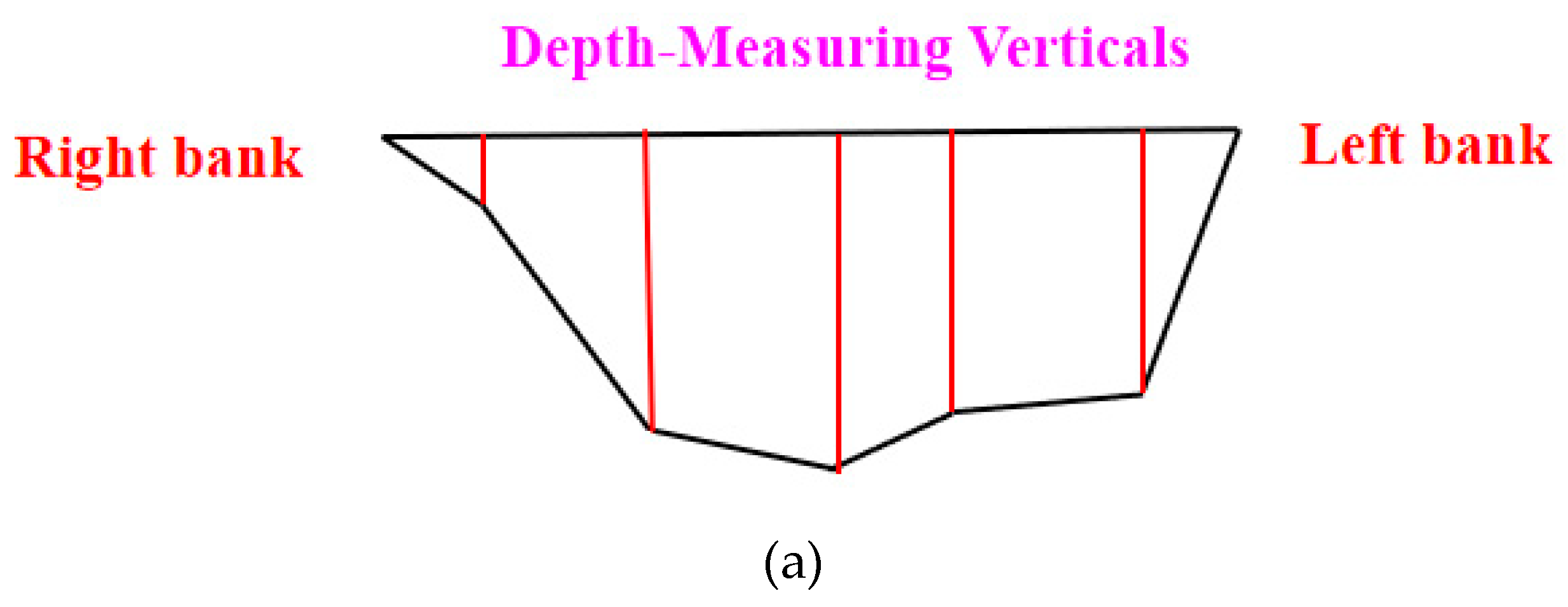
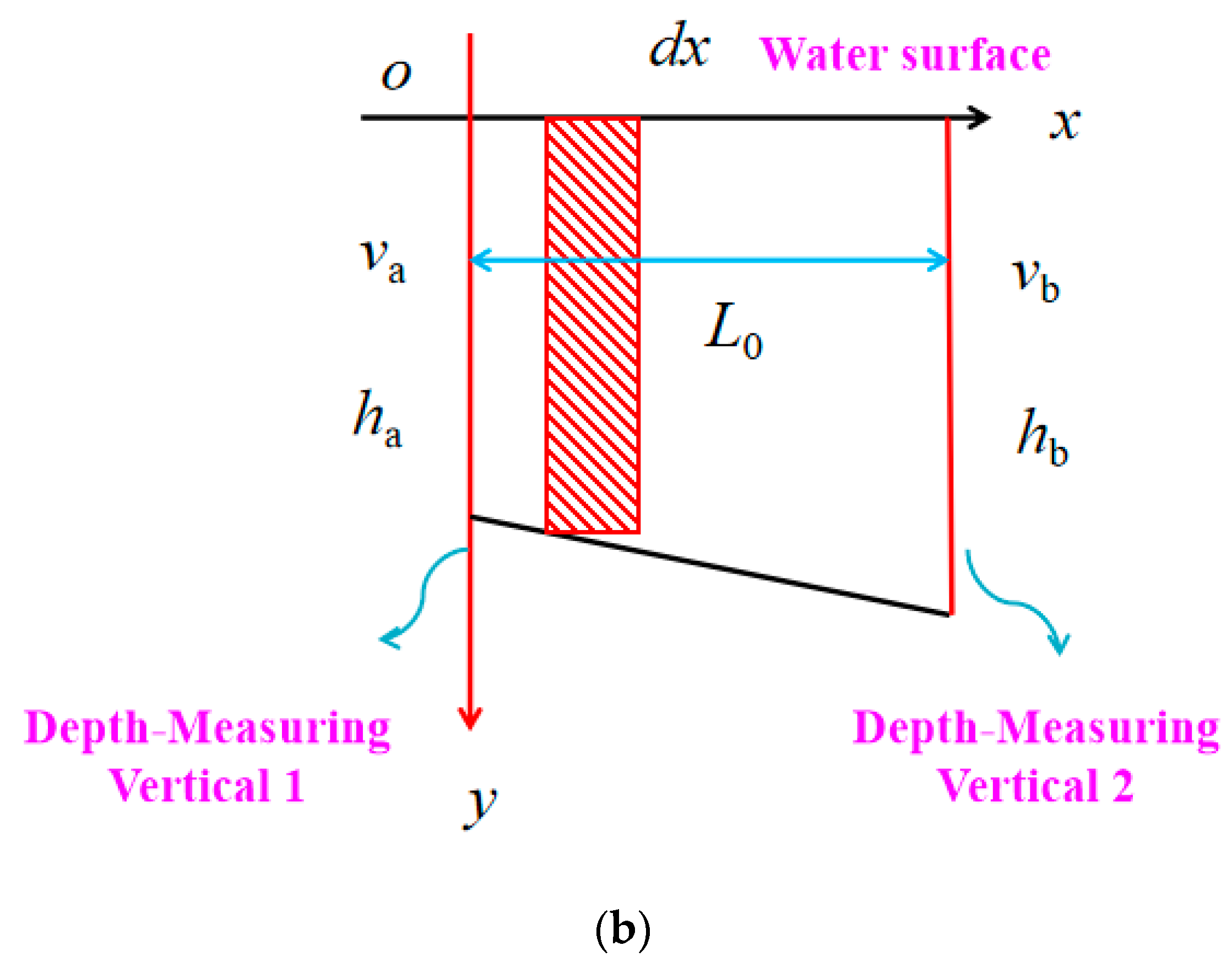
3.2. Theoretical Description of Main-Stream Volume Variation
3.3. Theoretical Description of Emergency Measures
3.3.1. Excavation of Diversion Channels
3.3.2. Implementation of Engineering Blasting
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, S.J.; Chen, Z.Y.; Tao, R.; Yu, S.; Xu, W.J.; Zhou, X.B.; Zhou, Z.D. Emergency Response and Back Analysis of the Failures of Earthquake Triggered Cascade Landslide Dams on the Mianyuan River, China. Nat. Hazards Rev. 2018, 19, 05018005. [Google Scholar] [CrossRef]
- Shi, Z.M.; Wang, Y.Q.; Peng, M.; Guan, S.G.; Chen, J.F. Landslide dam de-formation analysis under aftershocks using large-scale shaking table tests measured by video grammetric technique. Eng. Geol. 2015, 186, 68–78. [Google Scholar] [CrossRef]
- Zhou, G.G.D.; Zhou, M.J.; Shrestha, M.S.; Song, D.R.; Choi, C.E.; Cui, K.F.E.; Peng, M.; Shi, Z.M.; Zhu, X.H.; Chen, H.Y. Experimental investigation on the longitudinal evolution of landslide dam breaching and outburst floods. Geomorphology 2019, 334, 29–43. [Google Scholar] [CrossRef]
- Cao, Z.; Yue, Z.; Pender, G. Landslide dam 1failure and flood hydraulics. Part-II: Coupled theoretical modeling. Nat. Hazards 2011, 59, 1021–1045. [Google Scholar] [CrossRef]
- Zhang, L.M.; Peng, M.; Xu, Y. Assessing risks of breaching of earth dams and natural landslide dams. In Proceedings of the Indian Geotechnical Conference-2010, Mumbai, India, 16–18 December 2010. [Google Scholar]
- Zhao, W.Y.; Chen, X.Q.; You, Y.; Chen, J.G. Dam-break characteristics of landslide dams with different types of open channel discharge sections. Environ. Earth Sci. 2015, 74, 1–10. [Google Scholar] [CrossRef]
- Clague, J.J.; Evans, S.G. A review of catastrophic drainage of moraine-dammed lakes in British Columbia. Quat. Sci. Rev. 2000, 19, 1763–1783. [Google Scholar] [CrossRef]
- Liu, M.; Zhang, Y.; Tian, S.F.; Chen, N.S.; Rahman, M.M.; Iqbal, J. The effects of loose deposits on debris flow processes in the Aizi Valley, southwest China. J. Mt. Sci. Engl. 2019, 17, 156–172. [Google Scholar] [CrossRef]
- Zhang, L.; Xiao, T.; Jian, H.; Chen, C. Erosion-based analysis of breaching of Baige landslide dams on the Jinsha River, China, in 2018. Landslides 2019, 16, 1965–1979. [Google Scholar] [CrossRef]
- Wu, L.; Deng, H.; Huang, R.; Zhang, L.M.; Guo, X.G.; Zhou, Y. Evolution of lakes created by landslide dams and the role of dam erosion: A case study of the Jiajun landslide on the Dadu River, China. Quatern. Int. 2019, 503A, 41–50. [Google Scholar] [CrossRef]
- Sassa, K.; Tsuchiya, S.; Fukuoka, H.; Mikos, M.; Doan, L. Landslides: Review of achievements in the second 5-year period (2009–2013). Landslides 2015, 12, 213–223. [Google Scholar] [CrossRef]
- Van, T.P.; Sassa, K.; Takara, K.; Dang, K.; Luong, L.H.; Ha, N.D. Formation process of two massive dams following rainfall-induced deep-seated rapid landslide failures in the Kii Peninsula of Japan. Landslides 2018, 15, 1761–1778. [Google Scholar]
- Paliaga, G.; Faccini, F.; Luino, F.; Turconi, L.; Bobrowsky, P. Geomorphic processes and risk related to a large landslide dam in a highly urbanized Mediterranean catchment (Genova, Italy). Geomorphology 2019, 327, 48–61. [Google Scholar] [CrossRef]
- Korup, O. Geomorphic hazard assessment of landslide dams in South Westland, New Zealand: Fundamental problems and approaches. Geomorphology 2005, 66, 167–188. [Google Scholar] [CrossRef]
- Costa, J.E.; Schuster, R.L. The formation and failure of natural dams. Geol. Soc. Am. Bull. 1988, 100, 1054–1068. [Google Scholar] [CrossRef]
- Wang, F.; Dai, Z.; Okeke, C.A.U.; Mitani, Y.; Yang, H. Experimental study to identify premonitory factors of landslide dam failures. Eng. Geol. 2018, 232, 123–134. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, J.M.; Chen, Y.L.; Peng, Y.; Liu, X.; Liu, W.J. Comparison of measured dam-break flood waves in triangular and rectangular channels. J. Hydrol. 2019, 575, 690–703. [Google Scholar] [CrossRef]
- Zhou, G.G.; Cui, P.; Zhu, X.H. A preliminary study of the failure mechanisms of cascading landslide dams. Int. J. Sediment. Res. 2016, 30, 223–234. [Google Scholar] [CrossRef]
- Nian, T.K.; Wu, H.; Li, D.Y. Experimental investigation on the formation process of landslide dams and a criterion of river blockage. Landslides 2020, 17, 2547–2562. [Google Scholar] [CrossRef]
- Li, D.; Nian, T.; Wu, H.; Wang, F.W.; Zheng, L. A predictive model for the geometry of landslide dams in V-shaped valleys. Bull. Eng. Geol. Environ. 2020, 79, 1–14. [Google Scholar] [CrossRef]
- Shrestha, B.B.; Nakagawa, H. Hazard assessment of the formation and failure of the Sunkoshi landslide dam in Nepal. Nat. Hazards 2016, 82, 2029–2049. [Google Scholar] [CrossRef]
- Gong, X.L.; Chen, K.T.; Chen, X.Q.; You, Y.; Chen, J.G.; Zhao, W.Y.; Liang, J. Characteristics of a Debris Flow Disaster and Its Mitigation Countermeasures in Zechawa Gully, Jiuzhaigou Valley, China. Water 2020, 12, 1256. [Google Scholar] [CrossRef]
- Jiang, X.; Wei, Y. Erosion characteristics of outburst floods on channel beds under the conditions of different natural dam downstream slope angles. Landslides 2020, 17, 1823–1834. [Google Scholar] [CrossRef]
- Xu, Q.; Fan, X.M.; Huang, R.Q.; Westen, C.V. Landslide dams triggered by the wenchuan earthquake, Sichuan Province, south west China. Bull. Eng. Geol. Environ. 2009, 68, 373–386. [Google Scholar] [CrossRef]
- Zhao, T.; Dai, F.; Xu, N.W. Coupled DEM-CFD investigation on the formation of landslide dams in narrow rivers. Landslides 2017, 14, 189–201. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Chen, G.; Zhang, Y.; Zheng, L.; Zhang, H. Dynamic simulation of landslide dam behavior considering kinematic characteristics using a coupled DDA-SPH method. Eng. Anal. Bound. Elem. 2017, 80, 172–183. [Google Scholar] [CrossRef]
- Seyedashraf, O.; Mehrabi, M.; Akhtari, A. Novel approach for dam break flow modeling using computational Intelligence. J. Hydrol. 2018, 559, 1028–1038. [Google Scholar] [CrossRef]
- Stefanelli, C.T.; Casagli, N.; Catani, F. Landslide damming hazard susceptibility maps: A new GIS-based procedure for risk management. Landslides 2020, 17, 1635–1648. [Google Scholar] [CrossRef] [Green Version]
- Rohan, T.J.; Wondolowski, N.; Shelef, E. Landslide susceptibility analysis based on citizen reports. Earth. Surf. Proc. Land. 2021, 46, 791–803. [Google Scholar] [CrossRef]
- Wu, H.; Nian, T.K.; Chen, G.Q.; Zhao, W.; Li, D.Y. Laboratory-scale investigation of the 3-D geometry of landslide dams in a U-shaped valley. Eng. Geol. 2020, 265, 105428. [Google Scholar] [CrossRef]
- Dabiri, Z.; Hlbling, D.; Abad, L.; Helgason, K.J.; Samundsson, P.; Tiede, D. Assessment of Landslide-Induced Geomorphological Changes in Hítardalur Valley, Iceland, Using Sentinel-1 and Sentinel-2 Data. Appl. Sci. 2020, 10, 5848. [Google Scholar] [CrossRef]
- Chen, L.C.; Yang, H.Q.; Song, K.L.; Huang, W.; Ren, X.H.; Xu, H. Failure mechanisms and characteristics of the Zhongbao landslide at Liujing Village, Wulong, China. Landslides 2021, 18, 1445–1457. [Google Scholar] [CrossRef]
- Wang, H.; Liu, S.; Xu, W. Numerical investigation on the sliding process and deposit feature of an earthquake-induced landslide: A case study. Landslides 2020, 17, 2671–2682. [Google Scholar] [CrossRef]
- Guo, X.J.; Cui, P.; Li, Y.; Zou, Q.; Kong, Y.D. The formation and development of debris flows in large watersheds after the 2008 Wenchuan Earthquake. Landslides 2016, 13, 25–37. [Google Scholar] [CrossRef]
- Tian, S.; Chen, N.; Wu, H.; Yang, C.Y.; Zhong, Z.; Rahman, M. New insights into the occurrence of the baige landslide along the jinsha river in tibet. Landslides 2020, 17, 1207–1216. [Google Scholar] [CrossRef]
- Xu, C.; Cui, Y.; Xu, X.; Bao, P.P.; Fu, G.; Jiang, W.L. An anthropogenic landslide dammed the songmai river, a tributary of the jinsha river in southwestern china. Nat. Hazards 2019, 99, 599–608. [Google Scholar] [CrossRef]
- Song, K.; Wang, F.W.; Zuo, Q.J.; Huang, B.L.; Mao, W.W.; Zheng, H. Successful disaster management of the July 2020 Shaziba landslide triggered by heavy rainfall in Mazhe Village, Enshi City, Hubei Province, China. Landslides 2020, 1–5. [Google Scholar] [CrossRef]
- Junichi, K.; Naoki, I. Outline of measures for sediment disaster by the sabo department of mlit, japan. Landslides 2020, 17, 2503–2513. [Google Scholar] [CrossRef]
- Fan, X.; Xu, Q.; Alonso-Rodriguez, A.; Subramanian, S.S.; Li, W.L.; Zheng, G.; Dong, X.J.; Huang, R.Q. Successive landsliding and damming of the Jinsha river in eastern Tibet, China: Prime investigation, early warning, and emergency response. Landslides 2019, 16, 1003–1020. [Google Scholar] [CrossRef]
- Xu, Y.; He, L.J.; Zhang, L.X. Engineering measures for emergency disposal and analysis on typical cases of barrier lakes. Eps. Water Res. Hydropwer. Info. 2021, 42, 49–54. (In Chinese) [Google Scholar]
- Lanzoni, S.; Gregoretti, C.; Stancanelli, L.M. Coarse-grained debris flow dynamics on erodible beds. J. Geophys. Res. 2017, 122, 592–614. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, L.M.; Xiao, T.; He, J. Barrier lake bursting and flood routing in the Yarlung Tsangpo Grand Canyon in October 2018. J. Hydrol. 2020, 583, 124603. [Google Scholar] [CrossRef]
- Abdedou, A.; Soulaïmania, A.; Tchamen, G.W. Uncertainty propagation of dam break flow using the stochastic nonintrusive B-splines Bézier elements-based method. J. Hydrol. 2020, 590, 125342. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, Y.; Wang, S.X.; Wang, F.T. Coupled model constructed to simulate the landslide dam flood discharge: A case study of baige landslide dam, jinsha river. Front. Earth Sci. 2020, 14, 63–76. [Google Scholar] [CrossRef]
- Liang, G.; Wang, Z.; Zhang, G.G.; Wang, L.L. Two huge landslides that took place in quick succession within a month at the same location of Jinsha River. Landslides 2019, 16, 1059–1062. [Google Scholar] [CrossRef]
- Liu, N.; Ysng, Q.G.; Chen, Q.G. Hazard Mitigation for Barrier Lakes; Changjiang Press: Wuhan, China, 2016; pp. 240–266. [Google Scholar]
- Begam, S.; Sen, D.; Dey, S. Moraine dam breach and glacial lake outburst flood generation by physical and numerical models. J. Hydrol. 2018, 563, 694–710. [Google Scholar] [CrossRef]
- Hardesty, S.; Shen, X.; Nikolopoulos, E.; Anagnostou, E. A numerical framework for evaluating flood inundation hazard under different dam operation scenarios—A case study in Naugatuck river. Water 2018, 10, 1798. [Google Scholar] [CrossRef] [Green Version]
- Evans, S.G.; Hermanns, R.L.; Schuster, R.L.; Strom, A. Natural and Artificial Rockslide Dams; Springer: Berlin, Germany, 2011. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Tan, G.; Shu, C.; Zhang, C.; Wang, R.; Han, S.; Yang, Q. Theoretical Description of the Hydrodynamic Process after Barrier Lake Formation and Emergency Responses Implementation. Water 2021, 13, 2506. https://doi.org/10.3390/w13182506
Wang J, Tan G, Shu C, Zhang C, Wang R, Han S, Yang Q. Theoretical Description of the Hydrodynamic Process after Barrier Lake Formation and Emergency Responses Implementation. Water. 2021; 13(18):2506. https://doi.org/10.3390/w13182506
Chicago/Turabian StyleWang, Jingwen, Guangming Tan, Caiwen Shu, Chong Zhang, Rui Wang, Shasha Han, and Qigui Yang. 2021. "Theoretical Description of the Hydrodynamic Process after Barrier Lake Formation and Emergency Responses Implementation" Water 13, no. 18: 2506. https://doi.org/10.3390/w13182506





