Transpiration and Water Use of an Irrigated Traditional Olive Grove with Sap-Flow Observations and the FAO56 Dual Crop Coefficient Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Site Description and Crop Characterization
2.2. Sap Flow and Transpiration Data
2.3. The SIMDualKc Model and Simulation of Transpiration Fluxes
- (a)
- Soil data: soil depth (m); the soil water content at field capacity (θFC, m3 m−3) and at the permanent wilting point (θWP, m3 m−3), the values of which were measured; the depth of the soil evaporation layer (Ze, m) and the total and readily evaporable water (TEW and REW, mm), which were estimated based on [12]; and the measured values of the initial soil water available in the root zone and the Ze soil layer, expressed as a percentage of TAW and TEW, respectively.
- (b)
- Climatic forcing at the daily time-step: rainfall (P, mm), reference crop evapotranspiration (ETo, mm d−1), minimum and maximum air temperature (Tmin and Tmax, °C), minimum relative air humidity (RHmin, %), and wind speed measured at a 2 m height (u2, m s−1).
- (c)
- Crop data: dates for the start of the crop stages (non-growing, initial, crop development, mid-season, late-season and end-season); initial values of Kcb for the considered crop stages; the soil water depletion fraction p for no stress for the same stages; root depth (Zr, m); tree height (h, m); the fraction of ground covered by vegetation (fc) at the same stages; and the row orientation and spacing.
- (d)
- Irrigation data: fraction of soil wetted (fw); applied depths (Ii, mm) and the respective dates.
- (e)
2.4. Estimation of Kcb Values from Observations of the Fraction of Ground Cover and Crop Height: The A&P Approach
2.5. SIMDualKc Model Calibration and Validation; Goodness-of-Fit Indicators
- (a)
- The regression coefficient (b0, dimensionless) of the linear regression forced to the origin between the measured and simulated variables; the target value is b0 = 1.0, which indicates that the predicted values are statistically equal to the observed ones;
- (b)
- The coefficient of determination (R2, dimensionless) of the ordinary least-squares regression between the simulated and observed values; its value should be close to 1.0, indicating that most of the variance of the observed values is explained by the model;
- (c)
- The root mean square error (RMSE, mm d−1), the target value of which is zero, indicating a perfect match between simulated and observed variables, the value of which must be quite smaller than the mean of the observed values;
- (d)
- The average absolute error (AAE, mm d−1), expressing the average error associated with the estimations and which should also be much smaller than the mean of the observed values;
- (e)
- The percent bias (PBIAS, %), measuring the average tendency of the predicted values to be larger or smaller than the corresponding measured pair; positive values correspond to an overestimation bias, whereas negative values indicate under-estimation bias; and
- (f)
- The Nash and Sutcliffe efficiency of modelling (EF, dimensionless) [54], obtained as the ratio between the mean square error (MSE) and the variance of the observed variable (s2obs), the target value of which, equal to 1.0, indicates that MSE is negligible with respect to s2obs;
3. Results and Discussion
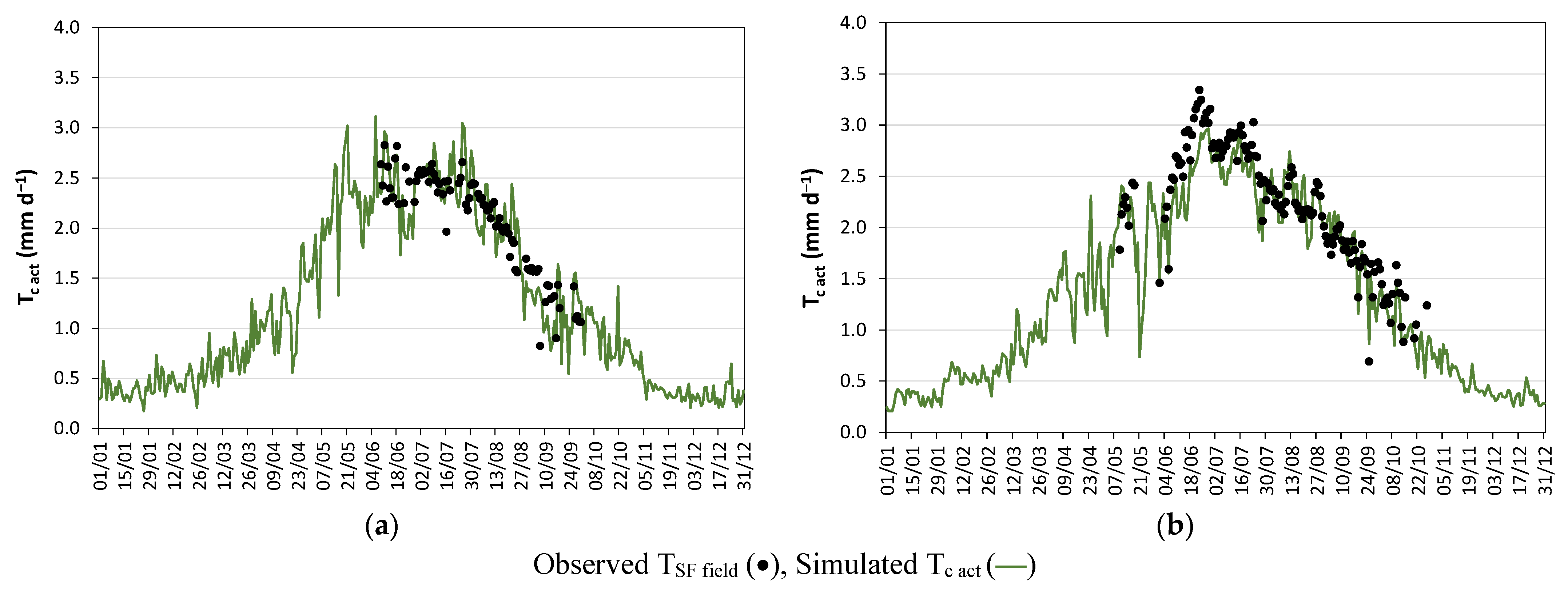
3.1. Model Calibration and Validation Using Transpiration Measurements
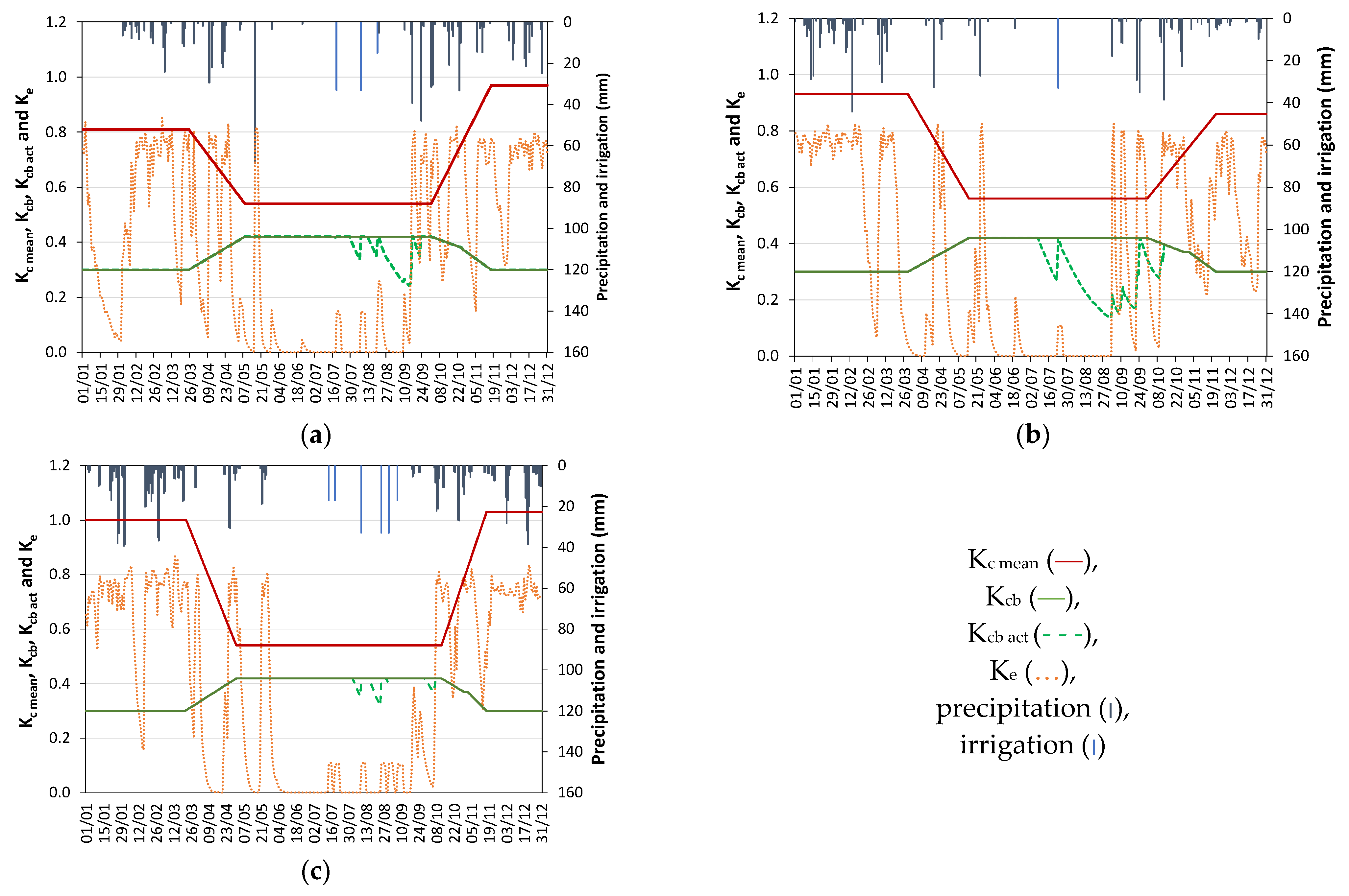
3.2. Dynamics of the Single and Basal Crop Coefficients throughout the Season
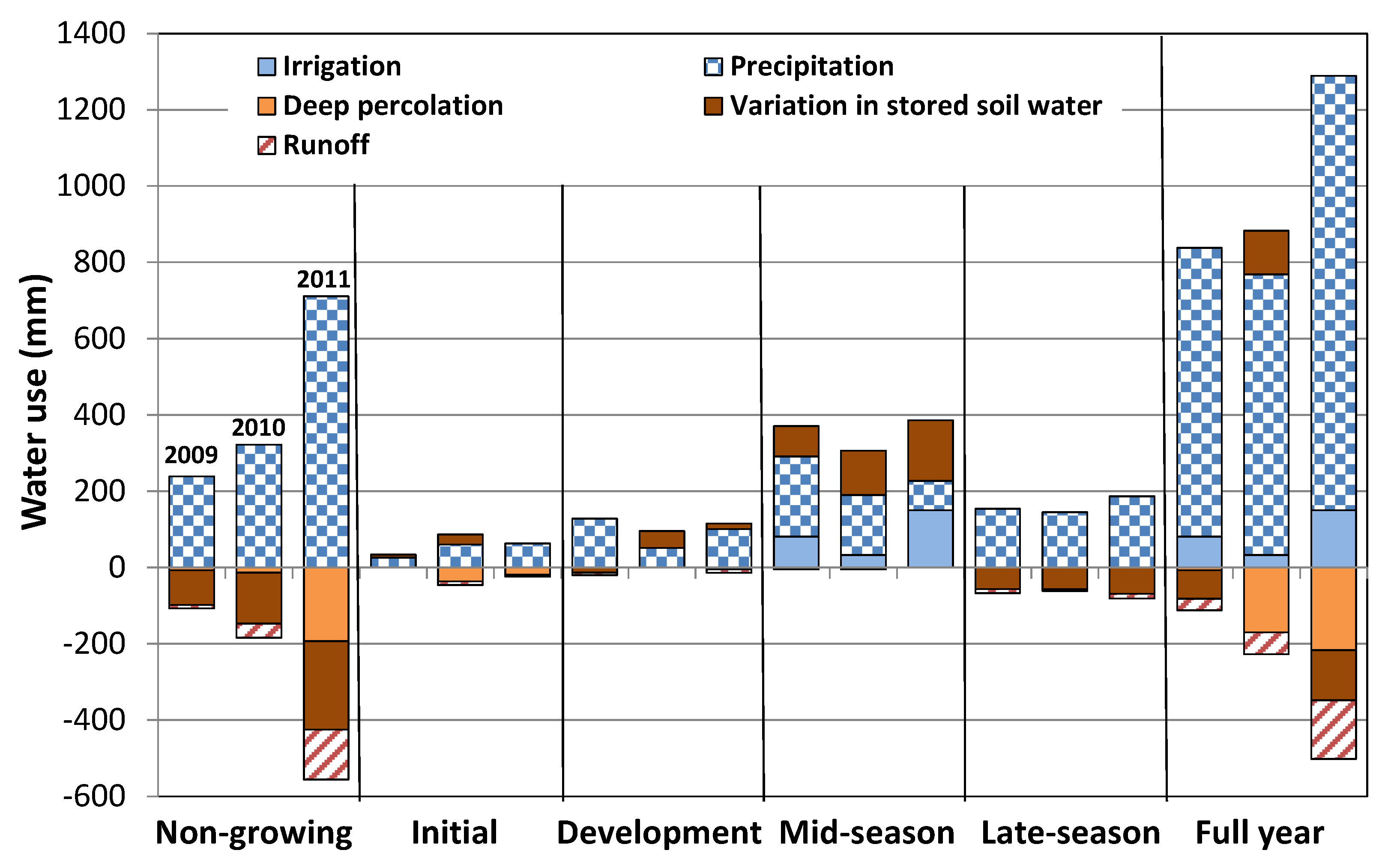
3.3. Soil Water Balance and Water Use
3.4. Assessing the Applicability of the A&P Approach
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Symbols and Abbreviations
| A | Area (m2) |
| AAE | Average Absolute Error (units of the variable) |
| A&P | Allen and Pereira approach (see [31]) |
| aD | Parameter of the deep percolation equation related with the available soil water at saturation and field capacity (mm) |
| bD | Parameter of the deep percolation equation related with drainage characteristics of the soil (mm) |
| b0 | Regression coefficient of the linear regression forced to the origin (-) |
| CN | Curve Number (dimensionless) |
| CR | Capillary Rise (mm) |
| Dr | Depth of cumulative evapotranspiration (depletion) from the root zone (mm) |
| DP | Deep Percolation (mm) |
| Es | Evaporation from the soil (mm d−1 or mm h−1) |
| EF | Efficiency of modelling (dimensionless) |
| ETc | Crop evapotranspiration under standard conditions (mm d−1 or mm h−1) |
| ETc act | Actual crop evapotranspiration, i.e., under non-standard conditions (mm d−1 or mm h−1) |
| ETo | (Grass) Reference crop evapotranspiration (mm d−1 or mm h−1) |
| fc | Fraction of soil surface covered by vegetation (dimensionless) |
| few | Fraction of soil that is both exposed and wetted (dimensionless) |
| fw | Fraction of soil surface wetted by rain or irrigation (dimensionless) |
| F | Sap flux (m3 s−1) |
| Fr | Resistance correction factor (dimensionless) |
| h | Crop height (m) |
| I | Irrigation depth (mm) |
| Kc | (Standard) crop coefficient (dimensionless) |
| Kc act | Actual crop coefficient (under non-standard conditions) (dimensionless) |
| Kc ini | Crop coefficient during the initial growth stage (dimensionless) |
| Kc mid | Crop coefficient during the mid-season growth stage (dimensionless) |
| Kc end | Crop coefficient at end of the late-season growth stage (dimensionless) |
| Kc max | Maximum value of crop coefficient (dimensionless) |
| Kc min | Minimum value of crop coefficient (dimensionless) |
| Kc non-growing | Crop coefficient during the non-growing crop stage (dimensionless) |
| Kcb | Basal crop coefficient (dimensionless) |
| Kcb cover | Basal crop coefficient of the ground cover in the absence of tree foliage (dimensionless) |
| Kcb full | Basal crop coefficient during mid-season (at peak plant size or height) for vegetation with full ground cover or LAI > 3 (dimensionless) |
| Kcb ini | Basal crop coefficient during the initial growth stage (dimensionless) |
| Kcb mid | Basal crop coefficient during the mid-season growth stage (dimensionless) |
| Kcb end | Basal crop coefficient at end of the late-season growth stage (dimensionless) |
| Kcb non-growing | Basal crop coefficient during the non-growing crop stage (dimensionless) |
| Kd | Crop density coefficient (dimensionless) |
| Ke | Soil evaporation coefficient (dimensionless) |
| Ke max | Maximum value of Ke coefficient (following rain or irrigation) (dimensionless) |
| Kr | Soil evaporation reduction coefficient (dimensionless) |
| Ks | Water stress coefficient (dimensionless) |
| LAI | Leaf area index (m2 (leaf area) m−2 (soil surface)) |
| LAIfield | Field leaf area index (m2 m−2) |
| LAIplant | Plant leaf area index (m2 m−2) |
| ML | Multiplier on fc describing the effect of canopy density (dimensionless) |
| MSE | Mean square error (units of the variable) |
| P | Precipitation (mm) |
| PBIAS | Percent bias (%) |
| p | Soil water depletion fraction for no stress (dimensionless) |
| R2 | Coefficient of determination (dimensionless) |
| RAW | Readily available soil water of the root zone (mm) |
| REW | Readily evaporable water from the soil surface layer (mm) |
| RHmin | Daily minimum relative humidity (%) |
| RMSE | Root mean square error (units of the variable) |
| RO | Surface runoff (mm) |
| rl | (Bulk) mean stomatal resistance of well-illuminated leaf (s m−1) |
| rtyp | (Bulk) typical stomatal resistance of well-illuminated leaf (s m−1) |
| Tc | Crop transpiration (mm d−1 or mm h−1) |
| Tc act | Actual crop transpiration (mm d−1 or mm h−1) |
| Tmax | Daily maximum air temperature (°C) |
| Tmin | Daily minimum air temperature (°C) |
| TSF field | Field daily transpiration (mm d−1) |
| TSF plant | Plant daily transpiration depth (mm d−1) |
| TAW | Total available soil water in the root zone (mm) |
| TEW | Total evaporable water from the soil surface layer (mm) |
| t | Time (h or d) |
| u2 | Wind speed observed, or adjusted to 2 m above ground surface (m s−1) |
| Ze | Depth of the surface soil layer subjected to drying by evaporation (m) |
| γ | Psychrometric constant (kPa °C−1) |
| ΔT | Difference of temperature (°C) |
| ΔTmax | Maximum difference of temperatures (°C) |
| θFC | Soil water content at field capacity (m3 m−3) |
| θWP | Soil water content at the permanent wilting point (m3 m−3) |
| ν | Sap flow density (m3 m−2 s−1) |
References
- Duarte, F.; Jones, N.; Fleskens, L. Traditional olive orchards on sloping land: Sustainability or abandonment? Environ. Manag. 2007, 89, 86–98. [Google Scholar] [CrossRef] [PubMed]
- Tanasijevic, L.; Todorovic, M.; Pizzigalli, C.; Lionello, P.; Pereira, L.S. Impacts of climate change on olives crop evapotranspiration and irrigation water requirements in the Mediterranean Region. Agric. Water Manag. 2014, 144, 54–68. [Google Scholar] [CrossRef]
- Freixa, E.; Gil, J.M.; Tous, J.; Hermoso, J.F. Comparative study of the economic viability of high- and super-high-density olive orchards in Spain. Acta Hortic. 2011, 924, 247–254. [Google Scholar] [CrossRef]
- Paço, T.A.; Pôças, I.; Cunha, M.; Silvestre, J.C.; Santos, F.L.; Paredes, P.; Pereira, L.S. Evapotranspiration and crop coefficients for a super intensive olive orchard. An application of SIMDualKc and METRIC models using ground and satellite observations. J. Hydrol. 2014, 519, 2067–2080. [Google Scholar] [CrossRef] [Green Version]
- Paço, T.A.; Paredes, P.; Pereira, L.S.; Silvestre, J.; Santos, F.L. Crop coefficients and transpiration of a super intensive Arbequina olive orchard using the dual Kc approach and the Kcb computation with the fraction of ground cover and height. Water 2019, 11, 383. [Google Scholar] [CrossRef] [Green Version]
- De Gennaro, B.; Notarnicola, B.; Roselli, L.; Tassielli, G. Innovative olive-growing models: An environmental and economic assessment. J. Clean. Prod. 2011, 28, 70–80. [Google Scholar] [CrossRef]
- Paço, T.A.; Ferreira, M.I.; Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Conceição, N.; Pacheco, C.A.; Pereira, L.S. The dual crop coefficient approach using a density factor to simulate the evapotranspiration of a peach orchard: SIMDualKc model versus eddy covariance measurements. Irrig. Sci. 2012, 30, 115–126. [Google Scholar] [CrossRef]
- Russo, C.; Cappelletti, G.M.; Nicoletti, G.M.; Di Noia, A.E.; Michalopoulos, G. Comparison of European olive production systems. Sustainability 2016, 8, 825. [Google Scholar] [CrossRef] [Green Version]
- Iniesta, F.; Testi, L.; Orgaz, F.; Villalobos, F.J. The effects of regulated and continuous deficit irrigation on the water use, growth and yield of olive trees. Eur. J Agron. 2009, 30, 258–265. [Google Scholar] [CrossRef]
- Trentacoste, E.R.; Puertas, C.M.; Sadras, V.O. Effect of irrigation and tree density on vegetative growth, oil yield and water use efficiency in young olive orchard under arid conditions in Mendoza, Argentina. Irrig. Sci. 2015, 33, 429–440. [Google Scholar] [CrossRef]
- Pereira, L.S. Water, agriculture and food: Challenges and issues. Water Resour. Manag. 2017, 31, 2985–2999. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration, Guidelines for Computing Crop Water Requirements. In FAO Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998; 300p. [Google Scholar]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop evapotranspiration estimation with FAO56: Past and future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Rallo, G.; Paço, T.A.; Paredes, P.; Puig-Sirera, À.; Massai, R.; Provenzano, G.; Pereira, L.S. Updated single and dual crop coefficients for tree and vine fruit crops. Agric. Water Manag. 2021, 250, 106645. [Google Scholar] [CrossRef]
- Testi, L.; Villalobos, F.J.; Orgaz, F. Evapotranspiration of a young irrigated olive orchard in southern Spain. Agric. For. Meteorol. 2004, 121, 1–18. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Smith, M.; Raes, D.; Wright, J.L. FAO-56 dual crop coefficient method for estimating evaporation from soil and application extensions. J. Irrig. Drain. Eng. 2005, 131, 2–13. [Google Scholar] [CrossRef] [Green Version]
- Er-Raki, S.; Chehbouni, A.; Boulet, G.; Williams, D.G. Using the dual approach of FAO-56 for partitioning ET into soil and plant components for olive orchards in a semi-arid region. Agric. Water Manag. 2010, 97, 1769–1778. [Google Scholar] [CrossRef] [Green Version]
- Rallo, G.; Baiamonte, G.; Juárez, J.M.; Provenzano, G. Improvement of FAO-56 model to estimate transpiration fluxes of drought tolerant crops under soil water deficit: Application for olive groves. J. Irrig. Drain. Eng. 2014, 140, A4014001. [Google Scholar] [CrossRef] [Green Version]
- Cammalleri, C.; Anderson, M.C.; Ciraolo, G.; D’Urso, G.; Kustas, W.P.; La Loggia, G.; Minacapilli, M. Applications of a remote sensing-based two-source energy balance algorithm for mapping surface fluxes without in situ air temperature observations. Remote Sens. Environ. 2012, 124, 502–515. [Google Scholar] [CrossRef]
- Conceição, N.; Tezza, L.; Häusler, M.; Lourenço, S.; Pacheco, C.; Ferreira, I. Three years of monitoring evapotranspiration components and crop and stress coefficients in a deficit irrigated intensive olive orchard. Agric. Water Manag. 2017, 191, 138–152. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Jovanovic, N. Soil water balance models for determining crop water and irrigation requirements and irrigation scheduling focusing on the FAO56 method and the dual Kc approach. Agric. Water Manag. 2020, 241, 106357. [Google Scholar] [CrossRef]
- Santos, C.; Lorite, I.J.; Allen, R.G.; Tasumi, M. Aerodynamic parameterization of the satellite-based energy balance (METRIC) model for ET estimation in rainfed olive orchards of Andalusia, Spain. Water Resour. Manag. 2012, 26, 3267–3283. [Google Scholar] [CrossRef]
- Cammalleri, C.; Rallo, G.; Agnese, C.; Ciraolo, G.; Minacapilli, M.; Provenzano, G. Combined use of eddy covariance and sap flow techniques for partition of ET fluxes and water stress assessment in an irrigated olive orchard. Agric. Water Manag. 2013, 120, 89–97. [Google Scholar] [CrossRef] [Green Version]
- Pôças, I.; Paço, T.A.; Cunha, M.; Andrade, J.A.; Silvestre, J.; Sousa, A.; Santos, F.L.; Pereira, L.S.; Allen, R.G. Satellite based evapotranspiration of a super-intensive olive orchard: Application of METRIC algorithm. Biosyst. Eng. 2014, 128, 69–81. [Google Scholar] [CrossRef] [Green Version]
- Pôças, I.; Paço, T.A.; Paredes, P.; Cunha, M.; Pereira, L.S. Estimation of actual crop coefficients using remotely sensed vegetation indices and soil water balance modelled data. Remote Sens. 2015, 7, 2373–2400. [Google Scholar] [CrossRef] [Green Version]
- Autovino, D.; Rallo, G.; Provenzano, G. Predicting soil and plant water status dynamic in olive orchards under different irrigation systems with Hydrus-2D: Model performance and scenario analysis. Agric. Water Manag. 2018, 203, 225–235. [Google Scholar] [CrossRef]
- Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Alves, I.; Fernando, R.M.; Pereira, L.S.; Allen, R.G. Implementing the dual crop coefficient approach in interactive software. 1. Background and computational strategy. Agric. Water Manag. 2012, 103, 8–24. [Google Scholar] [CrossRef]
- Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Fernando, R.M.; Alves, I.; Pereira, L.S.; Allen, R.G. Implementing the dual crop coefficient approach in interactive software: 2. Model testing. Agric. Water Manag. 2012, 103, 62–77. [Google Scholar] [CrossRef]
- Fandiño, M.; Cancela, J.J.; Rey, B.J.; Martínez, E.M.; Rosa, R.G.; Pereira, L.S. Using the dual-Kc approach to model evapotranspiration of Albariño vineyards (Vitis vinifera L. cv. Albariño) with consideration of active ground cover. Agric. Water Manag. 2012, 112, 75–87. [Google Scholar] [CrossRef]
- Cancela, J.J.; Fandiño, M.; Rey, B.J.; Martínez, E.M. Automatic irrigation system based on dual crop coefficient, soil and plant water status for Vitis vinifera (cv Godello and cv Mencía). Agric. Water Manag. 2015, 151, 52–63. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S. Estimating crop coefficients from fraction of ground cover and height. Irrig. Sci. 2009, 28, 17–34. [Google Scholar] [CrossRef] [Green Version]
- Pereira, L.S.; Paredes, P.; Melton, F.; Johnson, L.; Wang, T.; López-Urrea, R.; Cancela, J.J.; Allen, R. Prediction of crop coefficients from fraction of ground cover and height. Background and validation using ground and remote sensing data. Agric. Water Manag. 2020, 241, 106197. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Melton, F.; Johnson, L.; Mota, M.; Wang, T. Prediction of crop coefficients from fraction of ground cover and height. Practical application to vegetable, field and fruit crops with focus on parameterization. Agric. Water Manag. 2021, 252, 106663. [Google Scholar] [CrossRef]
- Provenzano, G.; Rallo, G.; Ghazouani, H. Assessing field and laboratory calibration protocols for the diviner 2000 probe in a range of soils with different textures. J. Irr. Drain. Eng. 2016, 142, 04015040. [Google Scholar] [CrossRef]
- Rallo, G.; Provenzano, G.; Castellini, M.; Puig-Sirera, À. Application of EMI and FDR sensors to assess the fraction of transpirable soil water over an olive grove. Water 2018, 10, 168. [Google Scholar] [CrossRef] [Green Version]
- Rallo, L.; Torreño, P.; Vargas, A.; Alvarado, J. Dormancy and alternative bearing in olive. Acta Hortic. 1994, 356, 127–136. [Google Scholar] [CrossRef]
- Sanz-Cortés, F.; Martinez-Calvo, J.; Badenes, M.L.; Bleiholder, H.; Hack, H.; LLácer, G.; Meier, U. Phenological growth stages of olive trees (Olea europaea). Ann. Appl. Biol. 2002, 140, 151–157. [Google Scholar] [CrossRef]
- Orlandi, F.; Garcia-Mozo, H.; Vazquez Ezquerra, L.; Romano, B.; Dominguez, E.; Galan, C.; Fornaciari, M. Phenological olive chilling requirements in Umbria (Italy) and Andalusia (Spain). Plant Biosyst. 2004, 138, 111–116. [Google Scholar] [CrossRef]
- Orlandi, F.; Sgromo, C.; Bonofiglio, T.; Ruga, L.; Romano, B.; Fornaciari, M. A comparison among olive flowering trends in different Mediterranean areas (south-central Italy) in relation to meteorological variations. Theor. Appl. Climatol. 2009, 97, 339–347. [Google Scholar] [CrossRef]
- Rallo, G.; Provenzano, G. Modelling eco-physiological response of table olive trees (Olea europaea L.) to soil water deficit conditions. Agric. Water Manag. 2013, 120, 79–88. [Google Scholar] [CrossRef] [Green Version]
- Granier, A. Evaluation of transpiration in a Douglas-fir stand by means of sap flow measurements. Tree Physiol. 1987, 3, 309–320. [Google Scholar] [CrossRef]
- González-Altozano, P.; Pavel, E.W.; Oncins, J.A.; Doltra, J.; Cohen, M.; Gonza, P.; Paço, T.A.; Massai, R.; Castel, J.R. Comparative assessment of five methods of determining sap flow in peach trees. Agric. Water Manag. 2008, 95, 503–515. [Google Scholar] [CrossRef]
- Siqueira, J.M.; Paço, T.A.; Silvestre, J.C.; Santos, F.L.; Falcão, A.O.; Pereira, L.S. Generating fuzzy rules by learning from olive tree transpiration measurement—An algorithm to automatize Granier sap flow data analysis. Comput. Electron. Agric. 2014, 101, 1–10. [Google Scholar] [CrossRef]
- Valancogne, C.; Granier, A. Mesures de flux de sève brut. In L’eau Dans L’espace Rural. Production Végétale et Qualité de L’eau; Riou, C., Bonhomme, R., Chassin, P., Neveu, A., Papy, F., Eds.; INRA: Paris, France, 1997; pp. 153–160. [Google Scholar]
- Motisi, A.; Rossi, F.; Consoli, S.; Papa, R.; Minacapilli, M.; Rallo, G.; Cammalleri, C.; D‘Urso, G. Eddy covariance and sap flow measurements of energy and mass exchanges of woody crops in a Mediterranean environment. Acta Hortic. 2012, 951, 121–127. [Google Scholar] [CrossRef] [Green Version]
- Villalobos, F.J.; Orgaz, F.; Mateos, L. Non-destructive measurement of leaf area in olive (Olea europaea L.) trees using a gap inversion method. Agric. For. Meteorol. 1995, 73, 29–42. [Google Scholar] [CrossRef]
- Allen, R.G.; Wright, J.L.; Pruitt, W.O.; Pereira, L.S.; Jensen, M.E. Water requirements. In Design and Operation of Farm Irrigation Systems, 2nd ed.; Hoffman, G.J., Evans, R.G., Jensen, M.E., Martin, D.L., Elliot, R.L., Eds.; ASABE: St. Joseph, MI, USA, 2007; pp. 208–288. [Google Scholar]
- Liu, Y.; Pereira, L.S.; Fernando, R.M. Fluxes through the bottom boundary of the root zone in silty soils: Parametric approaches to estimate groundwater contribution and percolation. Agric. Water Manag. 2006, 84, 27–40. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef] [Green Version]
- Pereira, L.S.; Paredes, P.; Rodrigues, G.C.; Neves, M. Modeling malt barley water use and evapotranspiration partitioning in two contrasting rainfall years. Assessing AquaCrop and SIMDualKc models. Agric. Water Manag. 2015, 159, 239–254, Corrigendum in 2016, 163, 408. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, Y.; Xu, D.; Zhao, N.; Lei, B.; Rosa, R.D.; Paredes, P.; Paço, T.A.; Pereira, L.S. The dual crop coefficient approach to estimate and partitioning evapotranspiration of the winter wheat—Summer maize crop sequence in North China Plain. Irrig. Sci. 2013, 31, 1303–1316. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Liew, M.W.; Van Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Wang, X.; Williams, J.; Gassman, P.W.; Baffaut, C.; Izaurralde, R.; Jeong, J.; Kiniry, J.R. EPIC and APEX: Model use, calibration, and validation. Trans. ASABE 2012, 55, 1447–1462. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Villalobos, F.J.; Testi, L.; Orgaz, F.; García-Tejera, O.; Lopez-Bernal, A.; González-Dugo, M.V.; Ballester-Lurbe, C.; Castel, J.R.; Alarcón-Cabañero, J.J.; Nicolás-Nicolás, E.; et al. Modelling canopy conductance and transpiration of fruit trees in Mediterranean areas: A simplified approach. Agric. For. Meteorol. 2013, 171–172, 93–103. [Google Scholar] [CrossRef]
- Martínez-Cob, A.; Faci, J.M. Evapotranspiration of an hedge-pruned olive orchard in a semiarid area of NE Spain. Agric. Water Manag. 2010, 97, 410–418. [Google Scholar] [CrossRef] [Green Version]
- Villalobos, F.J.; Orgaz, F.; Testi, L.; Fereres, E. Measurement and modeling of evapotranspiration of olive (Olea europaea L.) orchards. Eur. J. Agron. 2000, 13, 155–163. [Google Scholar] [CrossRef]
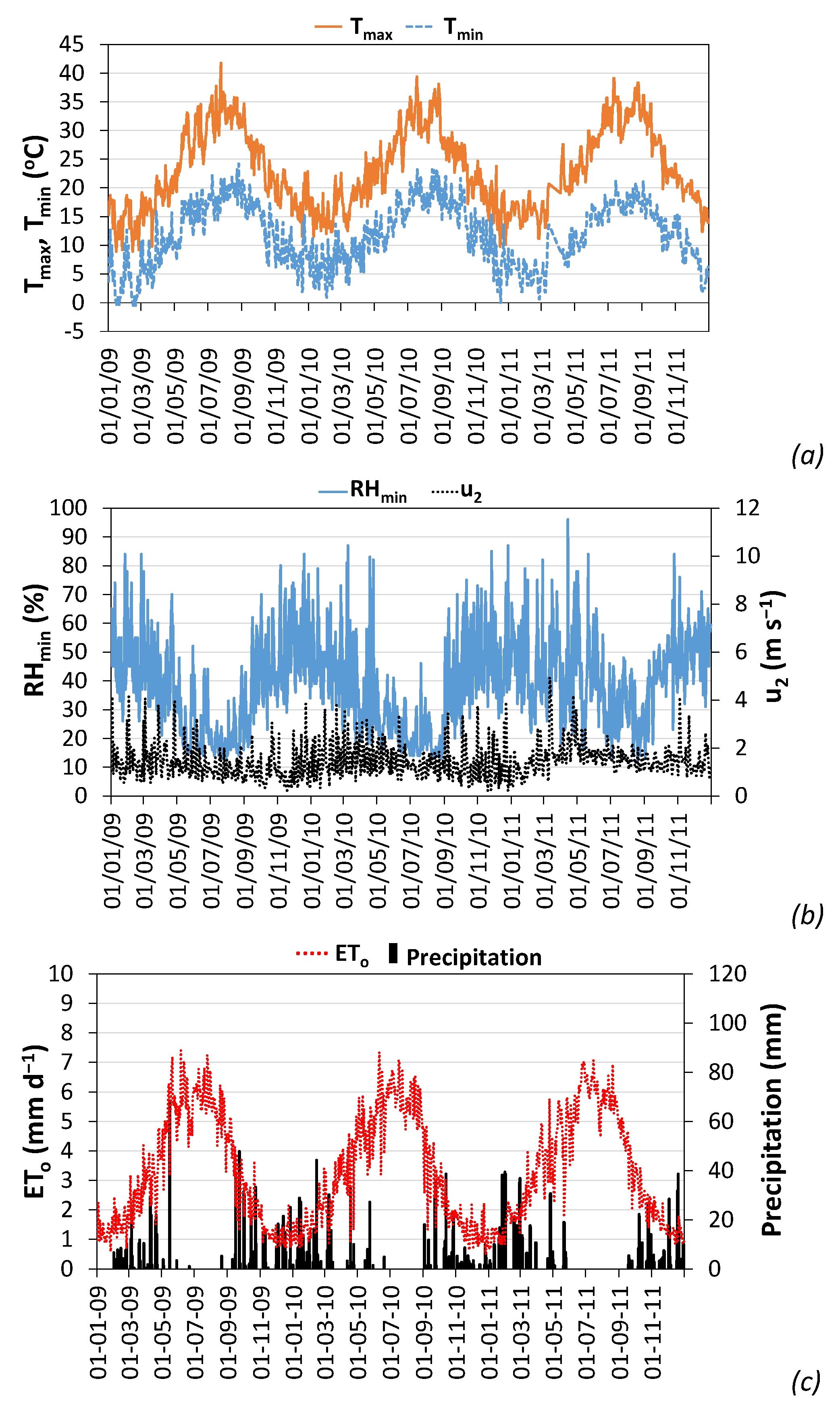
| Crop Growth Stages | ||||||
|---|---|---|---|---|---|---|
| Season | Non-Growing | Initial | Crop Development | Mid-Season | Late Season | Non-Growing |
| 2009 | 01/01–09/03 | 10/03–24/03 | 25/03–07/05 | 08/05–30/09 | 01/10–15/11 | 16/11–31/12 |
| 2010 | 01/01–08/03 | 09/03–28/03 | 29/03–14/05 | 15/05–29/09 | 30/09–22/11 | 23/11–31/12 |
| 2011 | 01/01–07/03 | 08/03–20/03 | 21/03–30/04 | 1/05–11/10 | 12/10–17/11 | 18/11–31/12 |
| Crop Growth Stages | 2009 | 2010 | 2011 | |||
|---|---|---|---|---|---|---|
| Precipitation (mm) | Irrigation (mm) | Precipitation (mm) | Irrigation (mm) | Precipitation (mm) | Irrigation (mm) | |
| Non-growing * | 239 | 0 | 323 | 0 | 711 | 0 |
| Initial | 26 | 0 | 60 | 0 | 63 | 0 |
| Development | 128 | 0 | 51 | 0 | 101 | 0 |
| Mid-season | 210 | 81 | 157 | 33 | 77 | 150 |
| Late-season | 154 | 0 | 145 | 0 | 187 | 0 |
| Total | 757 | 81 | 736 | 33 | 1139 | 150 |
| Parameters | Initial Values | Calibrated Values | |
|---|---|---|---|
| Crop | Kcb non-growing | 0.25 | 0.30 |
| Kcb ini | 0.25 | 0.30 | |
| Kcb mid | 0.40 | 0.42 | |
| Kcb end | 0.30 | 0.37 | |
| p ini | 0.65 | 0.65 | |
| p dev | 0.65 | 0.65 | |
| p mid | 0.65 | 0.65 | |
| p maturity | 0.65 | 0.65 | |
| p end | 0.65 | 0.65 | |
| Soil evaporation | TEW | 28 | 28 |
| REW | 10 | 10 | |
| Ze | 0.10 | 0.10 | |
| Runoff and deep percolation | CN | 72 | 75 |
| aD | 320 | 330 | |
| bD | −0.0175 | −0.0175 |
| n | b0 | R2 | PBIAS (%) | RMSE (mm d−1) | AAE (mm d−1) | EF | |
|---|---|---|---|---|---|---|---|
| Calibration, 2009 | 104 | 1.00 | 0.76 | 0.6 | 0.27 | 0.22 | 0.71 |
| Validation, 2011 | 145 | 0.94 | 0.84 | −5.2 | 0.26 | 0.20 | 0.81 |
| Crop Growth Stages | 2009 | 2010 | 2011 | Average |
|---|---|---|---|---|
| Non-growing * | 0.87 | 0.90 | 1.01 | 0.93 |
| Initial | 0.81 | 0.93 | 1.00 | 0.92 |
| Mid-season | 0.54 | 0.56 | 0.54 | 0.55 |
| End season | 0.97 | 0.86 | 1.03 | 0.95 |
| Year | Non-Growing | Initial | Development | Mid-Season | Late-Season | Whole Year | |
|---|---|---|---|---|---|---|---|
| ETc act (mm) | 2009 | 132 | 34 | 108 | 366 | 87 | 726 |
| 2010 | 138 | 41 | 96 | 301 | 83 | 656 | |
| 2011 | 155 | 39 | 101 | 386 | 106 | 787 | |
| Es (mm) | 2009 | 87 | 22 | 56 | 65 | 53 | 283 |
| 2010 | 93 | 26 | 29 | 72 | 47 | 264 | |
| 2011 | 109 | 28 | 47 | 61 | 61 | 305 | |
| Tc act (mm) | 2009 | 45 | 12 | 52 | 301 | 34 | 443 |
| 2010 | 45 | 15 | 67 | 229 | 36 | 392 | |
| 2011 | 46 | 11 | 54 | 325 | 45 | 482 | |
| Es/ETc act (%) | 2009 | 66 | 65 | 52 | 18 | 61 | 39 |
| 2010 | 67 | 63 | 30 | 24 | 57 | 40 | |
| 2011 | 70 | 72 | 47 | 16 | 58 | 39 | |
| Tc act/ETc act (%) | 2009 | 34 | 35 | 48 | 82 | 39 | 61 |
| 2010 | 33 | 37 | 70 | 76 | 43 | 60 | |
| 2011 | 30 | 28 | 53 | 84 | 42 | 61 | |
| ETc act/ETc (%) | 2009 | 100 | 100 | 100 | 96 | 100 | 98 |
| 2010 | 100 | 100 | 100 | 84 | 98 | 91 | |
| 2011 | 100 | 100 | 100 | 99 | 100 | 99 |
| n | b0 | R2 | PBIAS (%) | RMSE (mm d−1) | AAE (mm d−1) | EF | ||
|---|---|---|---|---|---|---|---|---|
| A&P, 2009 | Central value | 104 | 1.01 | 0.68 | 2.5 | 0.28 | 0.21 | 0.67 |
| Upper value | 1.13 | 0.68 | 15.3 | 0.43 | 0.35 | 0.26 | ||
| A&P, 2011 | Central value | 145 | 0.91 | 0.81 | −8.1 | 0.31 | 0.25 | 0.71 |
| Upper value | 1.02 | 0.81 | 3.3 | 0.27 | 0.21 | 0.78 |
| Approach | Growth Stage | ||
|---|---|---|---|
| Mid-Season | End-Season | ||
| 2009 | A&P central value | 0.40 | 0.30 |
| A&P upper value | 0.45 | 0.35 | |
| SIMDualKc | 0.39 | 0.37 | |
| 2011 | A&P central value | 0.40 | 0.30 |
| A&P upper value | 0.45 | 0.35 | |
| SIMDualKc | 0.41 | 0.37 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puig-Sirera, À.; Rallo, G.; Paredes, P.; Paço, T.A.; Minacapilli, M.; Provenzano, G.; Pereira, L.S. Transpiration and Water Use of an Irrigated Traditional Olive Grove with Sap-Flow Observations and the FAO56 Dual Crop Coefficient Approach. Water 2021, 13, 2466. https://doi.org/10.3390/w13182466
Puig-Sirera À, Rallo G, Paredes P, Paço TA, Minacapilli M, Provenzano G, Pereira LS. Transpiration and Water Use of an Irrigated Traditional Olive Grove with Sap-Flow Observations and the FAO56 Dual Crop Coefficient Approach. Water. 2021; 13(18):2466. https://doi.org/10.3390/w13182466
Chicago/Turabian StylePuig-Sirera, Àngela, Giovanni Rallo, Paula Paredes, Teresa A. Paço, Mario Minacapilli, Giuseppe Provenzano, and Luis S. Pereira. 2021. "Transpiration and Water Use of an Irrigated Traditional Olive Grove with Sap-Flow Observations and the FAO56 Dual Crop Coefficient Approach" Water 13, no. 18: 2466. https://doi.org/10.3390/w13182466
APA StylePuig-Sirera, À., Rallo, G., Paredes, P., Paço, T. A., Minacapilli, M., Provenzano, G., & Pereira, L. S. (2021). Transpiration and Water Use of an Irrigated Traditional Olive Grove with Sap-Flow Observations and the FAO56 Dual Crop Coefficient Approach. Water, 13(18), 2466. https://doi.org/10.3390/w13182466











