Towards a Comprehensive Assessment of Statistical versus Soft Computing Models in Hydrology: Application to Monthly Pan Evaporation Prediction
Abstract
:1. Introduction
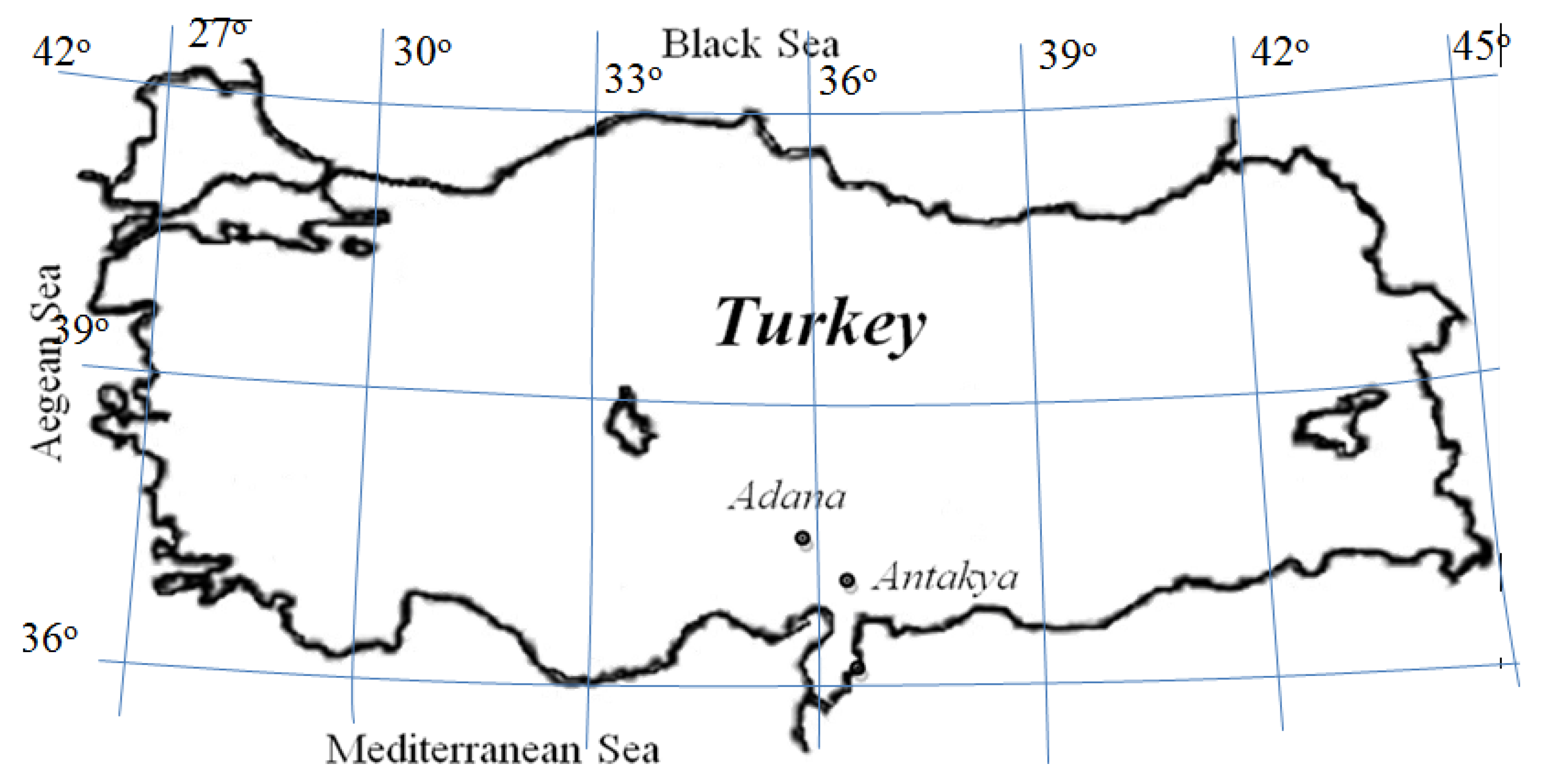
2. Case Study and Dataset
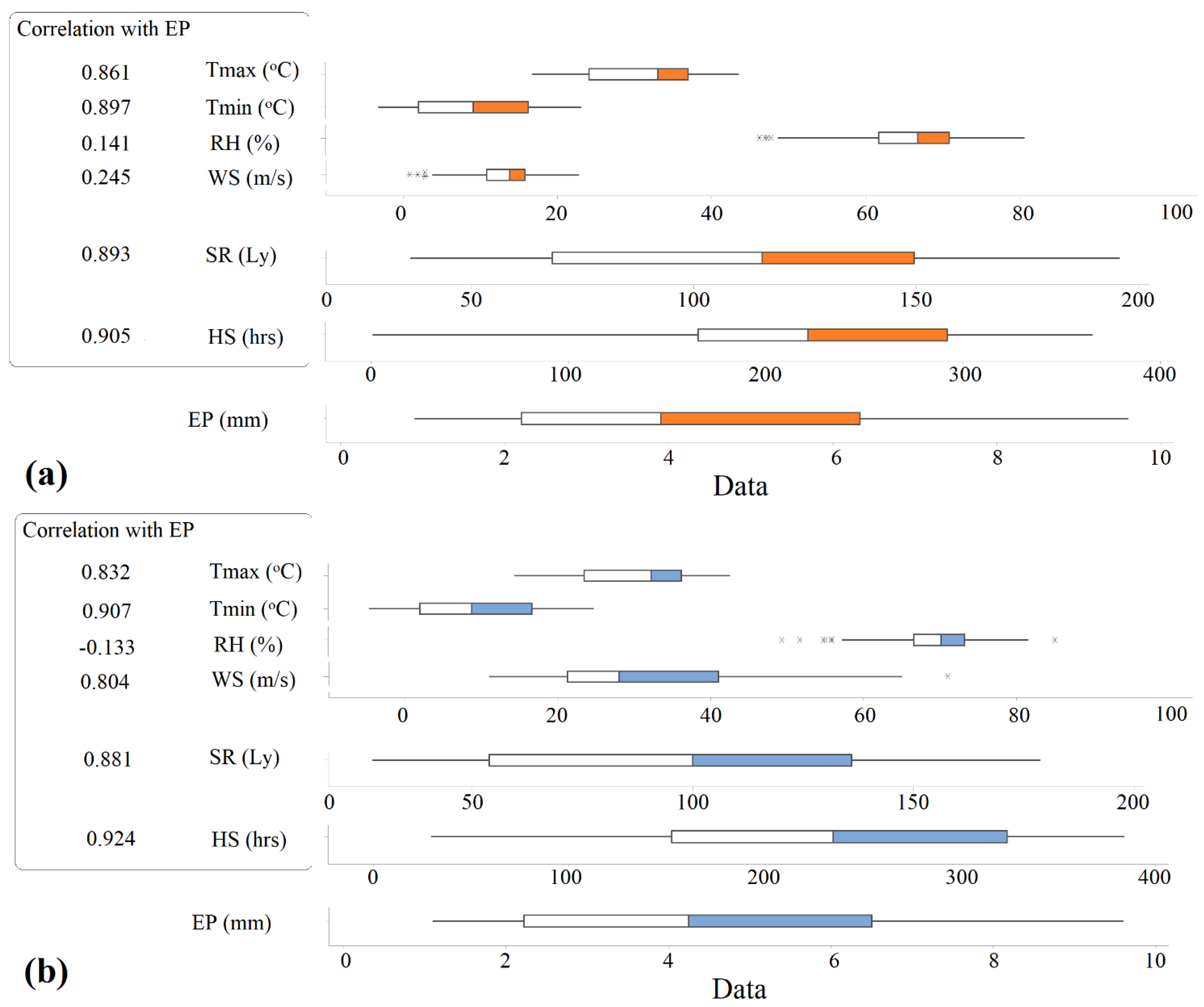
- Antakya Station: HS, Tmin, SR, WS, Tmax, and RH.
- Adana Station: HS, Tmin, SR, Tmax, WS, and RH.
3. Methods
3.1. Artificial Neural Networks: MLP-LM, MLP-CG, RBFNN
3.2. Support Vector Regression (SVR)
3.3. Multivariate Regression Spline (MARS)
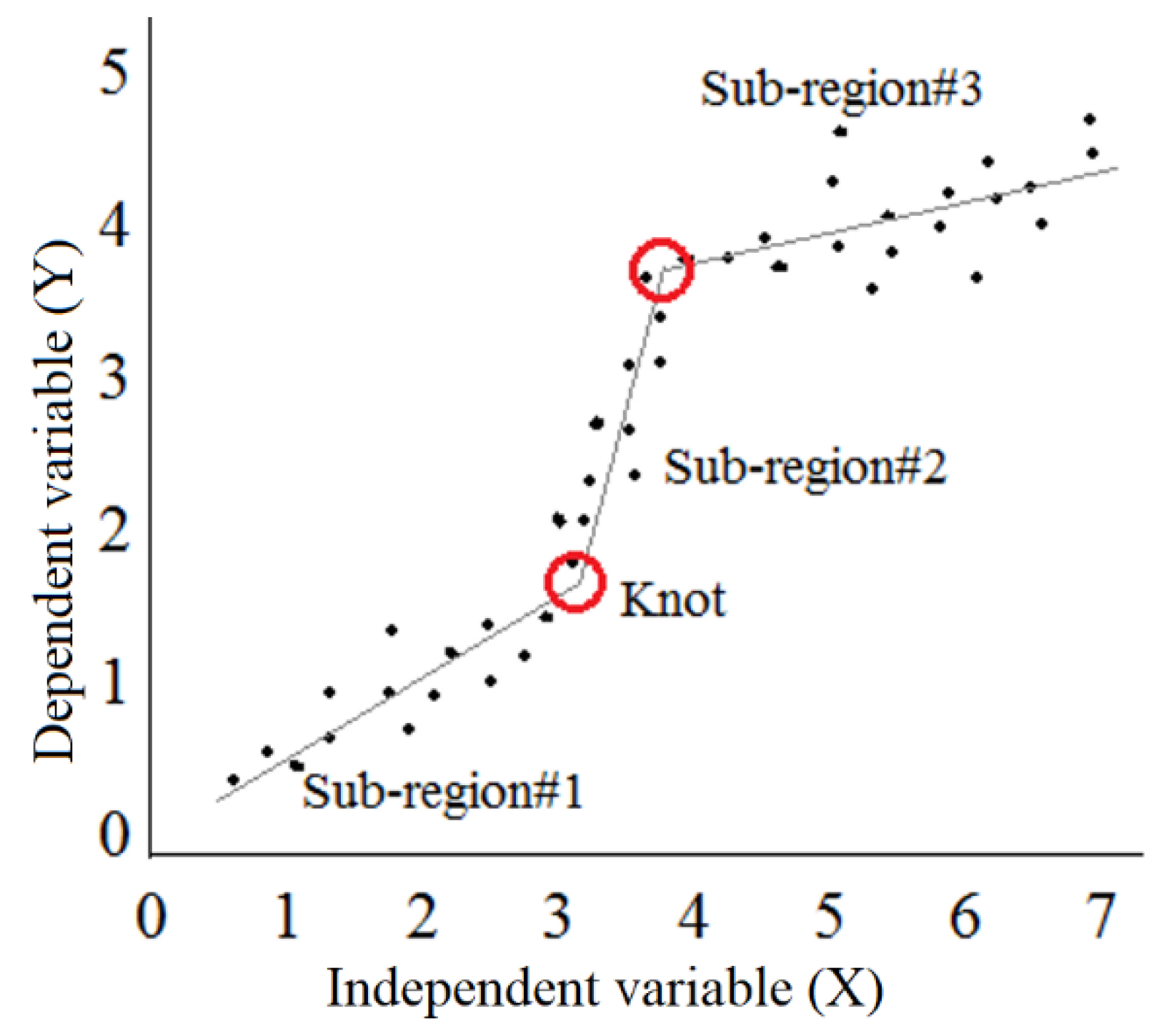
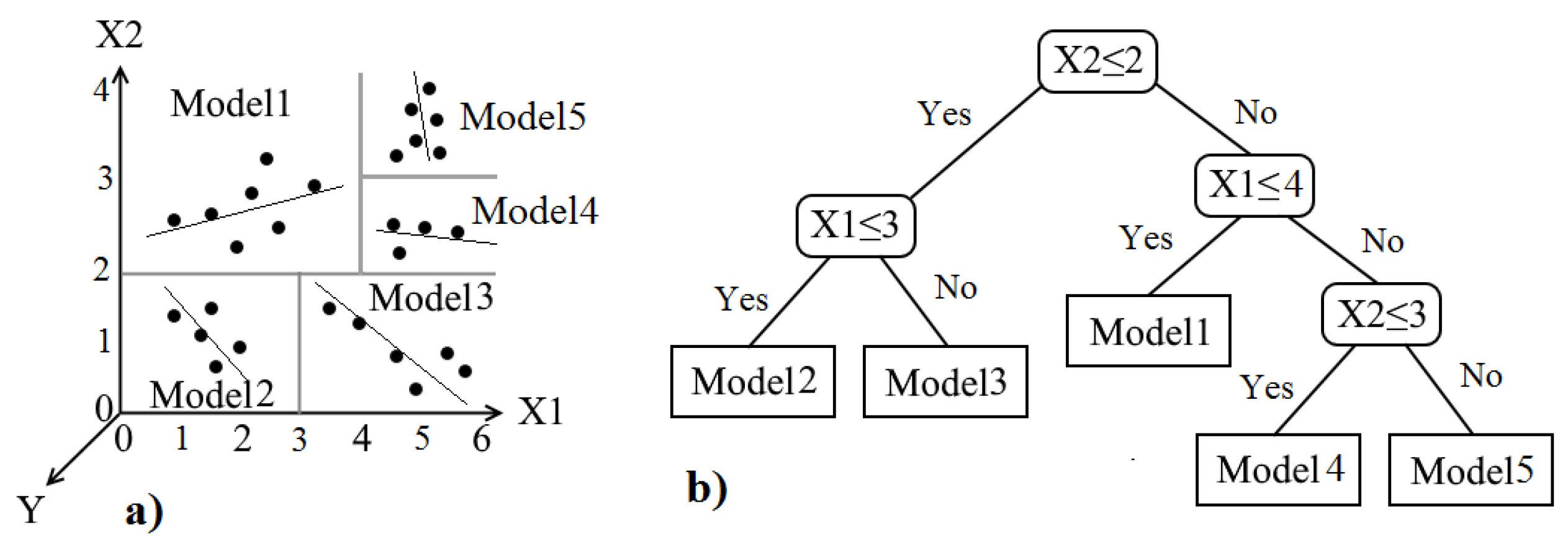
3.4. M5 Model Tree
3.5. Response Surface Methodology
3.6. Kriging Interpolation Approach
3.7. Improved Kriging
3.8. Methodology and Models Evaluation
- Scenario I (without periodicity):
- Scenario II, (with periodicity):
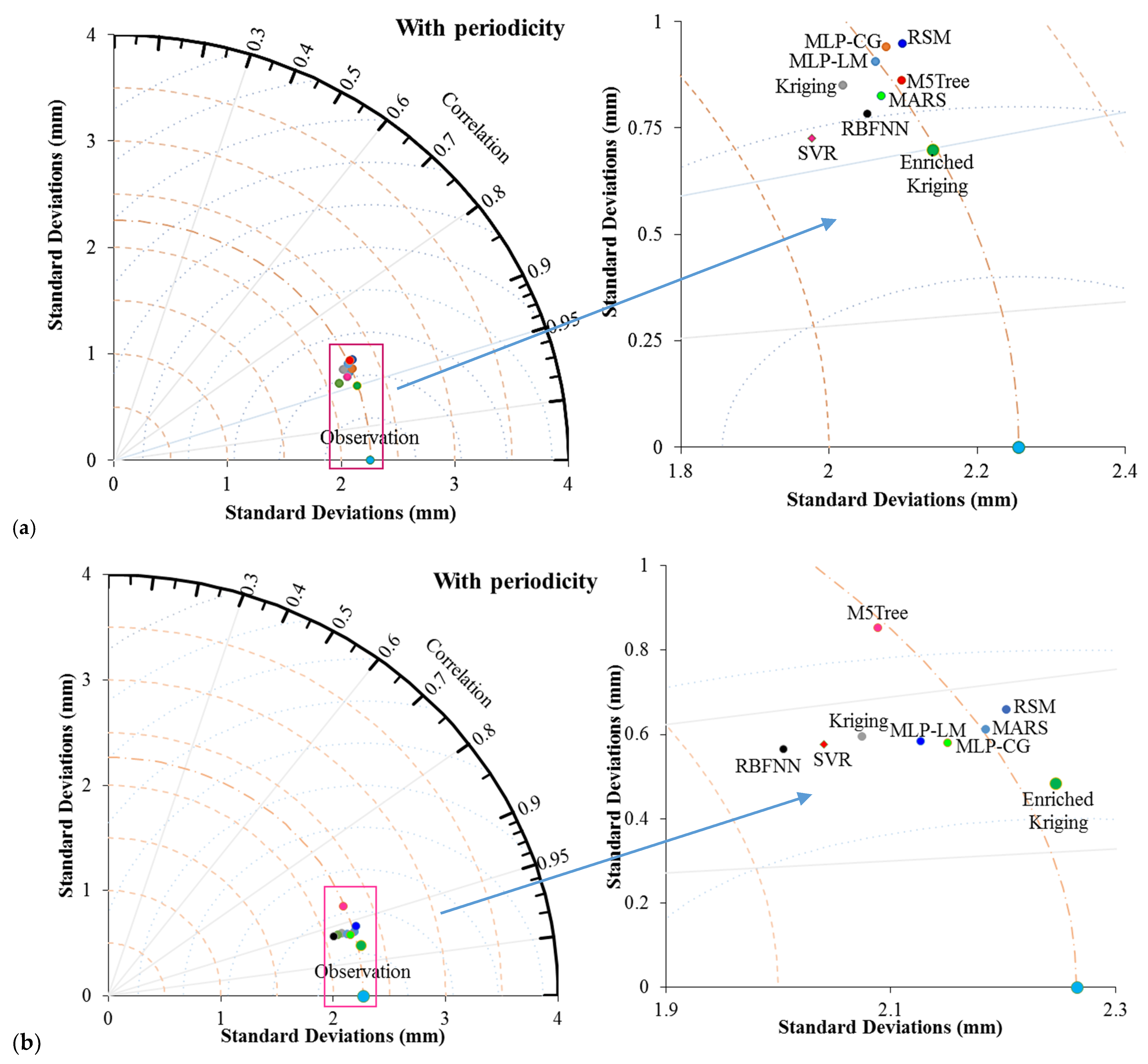
4. Comparison and Results
4.1. Evaluation of the Applied Models
4.2. Hypothesis Testing
5. Discussion
6. Conclusions
- Soft computing using machine learning models such as the SVR, MARS, MLP-ML, and RBNN provided more accurate predictions than the M5Tree and RSM.
- The kriging model, as well as the SVR, RBFNN and MLP-ML, provided better performances compared to the RSM and M5Tree.
- It was found that the developed improved kriging model performed better than the other applied models, including the soft computing (SVR, RBNN, MLP-ML, and MARS) and standard statistical (kriging and RSM) models.
- By comparing the performances of the improved kriging method with six other applied models, it can be concluded that the proposed kriging framework can be successfully applied for this current hydrological challenge while its performances for other hydrological stations and other complex, sophisticated problems should be discussed in future.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BF | Basis functions |
| ANFIS | Adaptive neuro-fuzzy inference systems |
| ANN | Artificial neural networks |
| d | Willmott index |
| ELM | Extreme learning machine |
| LSSVM | Least square support vector machine |
| m | Number basis functions |
| MAE | Mean absolute error |
| MAPE | Mean absolute percentage error |
| MARS | Multivariate adaptive regression spline |
| MBE | Mean bias error |
| MLPNN | Multilayer perceptron artificial neural networks |
| MLR | Multiple linear regression |
| MNLR | Multivariate nonlinear regression |
| Correlation matrix | |
| RBFNN | Radial basis function neural networks |
| RMSE | Root mean square error |
| SVM | Support vector machine |
| SVR | Support vector regression |
| wj, wij | Weights |
| NV | Number of input variables |
| K(x,xi) | Kernel function |
| β | Unknown coefficients |
References
- Kişi, Ö. Daily pan evaporation modelling using a neuro-fuzzy computing technique. J. Hydrol. 2006, 329, 636–646. [Google Scholar] [CrossRef]
- Li, D.; Pan, M.; Cong, Z.; Zhang, L.; Wood, E. Vegetation control on water and energy balance within the budyko framework. Water Resour. Res. 2013, 49, 969–976. [Google Scholar] [CrossRef]
- Yan, D.; Lai, Z.; Ji, G. Using budyko-type equations for separating the impacts of climate and vegetation change on runoff in the source area of the yellow river. Water 2020, 12, 3418. [Google Scholar] [CrossRef]
- Almorox, J.; Grieser, J. Calibration of the hargreaves–samani method for the calculation of reference evapotranspiration in different köppen climate classes. Hydrol. Res. 2016, 47, 521–531. [Google Scholar] [CrossRef] [Green Version]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Chatterjee, C. Modelling the dynamics of evapotranspiration using variable infiltration capacity model and regionally calibrated hargreaves approach. Irrig. Sci. 2018, 36, 289–300. [Google Scholar] [CrossRef]
- Srivastava, A.; Sahoo, B.; Raghuwanshi, N.S.; Singh, R. Evaluation of variable-infiltration capacity model and modis-terra satellite-derived grid-scale evapotranspiration estimates in a river basin with tropical monsoon-type climatology. J. Irrig. Drain. Eng. 2017, 143, 04017028. [Google Scholar] [CrossRef] [Green Version]
- Kisi, O.; Zounemat-Kermani, M. Comparison of two different adaptive neuro-fuzzy inference systems in modelling daily reference evapotranspiration. Water Resour. Manag. 2014, 28, 2655–2675. [Google Scholar] [CrossRef]
- Dong, L.; Zeng, W.; Wu, L.; Lei, G.; Chen, H.; Srivastava, A.K.; Gaiser, T. Estimating the pan evaporation in northwest china by coupling catboost with bat algorithm. Water 2021, 13, 256. [Google Scholar] [CrossRef]
- Majhi, B.; Naidu, D. Pan evaporation modeling in different agroclimatic zones using functional link artificial neural network. Inf. Process. Agric. 2021, 8, 134–147. [Google Scholar] [CrossRef]
- Duan, Z.; Bastiaanssen, W. Evaluation of three energy balance-based evaporation models for estimating monthly evaporation for five lakes using derived heat storage changes from a hysteresis model. Environ. Res. Lett. 2017, 12, 024005. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Fu, Z.-Y.; Chen, H.-S.; Nie, Y.-P.; Wang, K.-L. Modeling daily reference et in the karst area of northwest Guangxi (China) using gene expression programming (gep) and artificial neural network (ann). Theor. Appl. Climatol. 2016, 126, 493–504. [Google Scholar] [CrossRef]
- Sudheer, K.; Gosain, A.; Mohana Rangan, D.; Saheb, S. Modelling evaporation using an artificial neural network algorithm. Hydrol. Process. 2002, 16, 3189–3202. [Google Scholar] [CrossRef]
- Kisi, O. Pan evaporation modeling using least square support vector machine, multivariate adaptive regression splines and m5 model tree. J. Hydrol. 2015, 528, 312–320. [Google Scholar] [CrossRef]
- Keskin, M.E.; Terzi, Ö. Artificial neural network models of daily pan evaporation. J. Hydrol. Eng. 2006, 11, 65–70. [Google Scholar] [CrossRef]
- Moghaddamnia, A.; Gousheh, M.G.; Piri, J.; Amin, S.; Han, D. Evaporation estimation using artificial neural networks and adaptive neuro-fuzzy inference system techniques. Adv. Water Resour. 2009, 32, 88–97. [Google Scholar] [CrossRef]
- Kim, S.; Shiri, J.; Kisi, O. Pan evaporation modeling using neural computing approach for different climatic zones. Water Resour. Manag. 2012, 26, 3231–3249. [Google Scholar] [CrossRef]
- Gao, B.; Xu, X. Derivation of an exponential complementary function with physical constraints for land surface evaporation estimation. J. Hydrol. 2021, 593, 125623. [Google Scholar] [CrossRef]
- Wang, H.; Yan, H.; Zeng, W.; Lei, G.; Ao, C.; Zha, Y. A novel nonlinear arps decline model with salp swarm algorithm for predicting pan evaporation in the arid and semi-arid regions of china. J. Hydrol. 2020, 582, 124545. [Google Scholar] [CrossRef]
- Wu, L.; Huang, G.; Fan, J.; Ma, X.; Zhou, H.; Zeng, W. Hybrid extreme learning machine with meta-heuristic algorithms for monthly pan evaporation prediction. Comput. Electron. Agric. 2020, 168, 105115. [Google Scholar] [CrossRef]
- Singh, A.; Singh, R.; Kumar, A.S.; Kumar, A.; Hanwat, S.; Tripathi, V. Evaluation of soft computing and regression-based techniques for the estimation of evaporation. J. Water Clim. Chang. 2021, 12, 32–43. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Sabziparvar, A.-A. Estimation of daily pan evaporation using artificial neural network and multivariate non-linear regression. Irrig. Sci. 2010, 28, 399–406. [Google Scholar] [CrossRef]
- Kisi, O.; Genc, O.; Dinc, S.; Zounemat-Kermani, M. Daily pan evaporation modeling using chi-squared automatic interaction detector, neural networks, classification and regression tree. Comput. Electron. Agric. 2016, 122, 112–117. [Google Scholar] [CrossRef]
- Tezel, G.; Buyukyildiz, M. Monthly evaporation forecasting using artificial neural networks and support vector machines. Theor. Appl. Climatol. 2016, 124, 69–80. [Google Scholar] [CrossRef]
- Keshtegar, B.; Kisi, O. Modified response-surface method: New approach for modeling pan evaporation. J. Hydrol. Eng. 2017, 22, 04017045. [Google Scholar] [CrossRef]
- Wang, L.; Niu, Z.; Kisi, O.; Yu, D. Pan evaporation modeling using four different heuristic approaches. Comput. Electron. Agric. 2017, 140, 203–213. [Google Scholar] [CrossRef]
- Wang, L.; Kisi, O.; Hu, B.; Bilal, M.; Zounemat-Kermani, M.; Li, H. Evaporation modelling using different machine learning techniques. Int. J. Climatol. 2017, 37, 1076–1092. [Google Scholar] [CrossRef]
- Ghorbani, M.; Deo, R.C.; Yaseen, Z.M.; Kashani, M.H.; Mohammadi, B. Pan evaporation prediction using a hybrid multilayer perceptron-firefly algorithm (mlp-ffa) model: Case study in north iran. Theor. Appl. Climatol. 2018, 133, 1119–1131. [Google Scholar] [CrossRef]
- Majhi, B.; Naidu, D.; Mishra, A.P.; Satapathy, S.C. Improved prediction of daily pan evaporation using deep-lstm model. Neural Comput. Appl. 2020, 32, 7823–7838. [Google Scholar] [CrossRef]
- Sebbar, A.; Heddam, S.; Djemili, L. Predicting daily pan evaporation (e pan) from dam reservoirs in the mediterranean regions of algeria: Opelm vs oselm. Environ. Process. 2019, 6, 309–319. [Google Scholar] [CrossRef]
- Al-Mukhtar, M. Modeling the monthly pan evaporation rates using artificial intelligence methods: A case study in iraq. Environ. Earth Sci. 2021, 80, 1–14. [Google Scholar] [CrossRef]
- Mohamadi, S.; Ehteram, M.; El-Shafie, A. Accuracy enhancement for monthly evaporation predicting model utilizing evolutionary machine learning methods. Int. J. Environ. Sci. Technol. 2020, 17, 3373–3396. [Google Scholar] [CrossRef]
- Yaseen, Z.M.; Al-Juboori, A.M.; Beyaztas, U.; Al-Ansari, N.; Chau, K.-W.; Qi, C.; Ali, M.; Salih, S.Q.; Shahid, S. Prediction of evaporation in arid and semi-arid regions: A comparative study using different machine learning models. Eng. Appl. Comput. Fluid Mech. 2020, 14, 70–89. [Google Scholar] [CrossRef] [Green Version]
- Keshtegar, B.; Mert, C.; Kisi, O. Comparison of four heuristic regression techniques in solar radiation modeling: Kriging method vs rsm, mars and m5 model tree. Renew. Sustain. Energy Rev. 2018, 81, 330–341. [Google Scholar] [CrossRef]
- Heddam, S.; Keshtegar, B.; Kisi, O. Predicting total dissolved gas concentration on a daily scale using kriging interpolation, response surface method and artificial neural network: Case study of columbia river basin dams, USA. Nat. Resour. Res. 2020, 29, 1801–1818. [Google Scholar] [CrossRef]
- Gupta, A.K. Predictive modelling of turning operations using response surface methodology, artificial neural networks and support vector regression. Int. J. Prod. Res. 2010, 48, 763–778. [Google Scholar] [CrossRef]
- Ladlani, I.; Houichi, L.; Djemili, L.; Heddam, S.; Belouz, K. Estimation of daily reference evapotranspiration (et 0) in the north of algeria using adaptive neuro-fuzzy inference system (anfis) and multiple linear regression (mlr) models: A comparative study. Arab. J. Sci. Eng. 2014, 39, 5959–5969. [Google Scholar] [CrossRef]
- Zounemat-Kermani, M.; Mahdavi-Meymand, A. Hybrid meta-heuristics artificial intelligence models in simulating discharge passing the piano key weirs. J. Hydrol. 2019, 569, 12–21. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Keshtegar, B.; Thai, D.-K.; Troung, N.-T. An ann-adaptive dynamical harmony search algorithm to approximate the flyrock resulting from blasting. Eng. Comput. 2020, 1–13. [Google Scholar] [CrossRef]
- Johansson, E.M.; Dowla, F.U.; Goodman, D.M. Backpropagation learning for multilayer feed-forward neural networks using the conjugate gradient method. Int. J. Neural Syst. 1991, 2, 291–301. [Google Scholar] [CrossRef]
- Yu, Q.; Hou, Z.; Bu, X.; Yu, Q. Rbfnn-based data-driven predictive iterative learning control for nonaffine nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2019, 31, 1170–1182. [Google Scholar] [CrossRef]
- Esfe, M.H. Designing an artificial neural network using radial basis function (rbf-ann) to model thermal conductivity of ethylene glycol–water-based tio 2 nanofluids. J. Therm. Anal. Calorim. 2017, 127, 2125–2131. [Google Scholar] [CrossRef]
- Santamaría-Bonfil, G.; Reyes-Ballesteros, A.; Gershenson, C. Wind speed forecasting for wind farms: A method based on support vector regression. Renew. Energy 2016, 85, 790–809. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, M.; Gao, L.; Chu, S. Probability and interval hybrid reliability analysis based on adaptive local approximation of projection outlines using support vector machine. Comput. Aided Civ. Infrastruct. Eng. 2019, 34, 991–1009. [Google Scholar] [CrossRef]
- Zhang, J.; Xiao, M.; Gao, L.; Chu, S. A combined projection-outline-based active learning kriging and adaptive importance sampling method for hybrid reliability analysis with small failure probabilities. Comput. Methods Appl. Mech. Eng. 2019, 344, 13–33. [Google Scholar] [CrossRef]
- Chiogna, G.; Marcolini, G.; Liu, W.; Ciria, T.P.; Tuo, Y. Coupling hydrological modeling and support vector regression to model hydropeaking in alpine catchments. Sci. Total Environ. 2018, 633, 220–229. [Google Scholar] [CrossRef]
- Chen, J.-L.; Yang, H.; Lv, M.-Q.; Xiao, Z.-L.; Wu, S.J. Estimation of monthly pan evaporation using support vector machine in three gorges reservoir area, china. Theor. Appl. Climatol. 2019, 138, 1095–1107. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 19, 1–67. [Google Scholar] [CrossRef]
- Jalali-Heravi, M.; Asadollahi-Baboli, M.; Mani-Varnosfaderani, A. Shuffling multivariate adaptive regression splines and adaptive neuro-fuzzy inference system as tools for qsar study of sars inhibitors. J. Pharm. Biomed. Anal. 2009, 50, 853–860. [Google Scholar] [CrossRef]
- Zhang, J.; Gao, L.; Xiao, M. A new hybrid reliability-based design optimization method under random and interval uncertainties. Int. J. Numer. Methods Eng. 2020, 121, 4435–4457. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, L.; Xiao, M. Maximizing natural frequencies of inhomogeneous cellular structures by kriging-assisted multiscale topology optimization. Comput. Struct. 2020, 230, 106197. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T. Evaluating seismic liquefaction potential using multivariate adaptive regression splines and logistic regression. Geomech. Eng. 2016, 10, 269–284. [Google Scholar] [CrossRef]
- Keshtegar, B.; Kisi, O. Rm5tree: Radial basis m5 model tree for accurate structural reliability analysis. Reliab. Eng. System Saf. 2018, 180, 49–61. [Google Scholar] [CrossRef]
- Kisi, O.; Keshtegar, B.; Zounemat-Kermani, M.; Heddam, S.; Trung, N.-T. Modeling reference evapotranspiration using a novel regression-based method: Radial basis m5 model tree. Theor. Appl. Climatol. 2021, 145, 639–659. [Google Scholar] [CrossRef]
- Pal, M.; Deswal, S. M5 model tree based modelling of reference evapotranspiration. Hydrol. Process. Int. J. 2009, 23, 1437–1443. [Google Scholar] [CrossRef]
- Sattari, M.T.; Pal, M.; Apaydin, H.; Ozturk, F. M5 model tree application in daily river flow forecasting in sohu stream, turkey. Water Resour. 2013, 40, 233–242. [Google Scholar] [CrossRef]
- Seghier, M.E.A.B.; Keshtegar, B.; Correia, J.A.; Lesiuk, G.; De Jesus, A.M. Reliability analysis based on hybrid algorithm of m5 model tree and monte carlo simulation for corroded pipelines: Case of study x60 steel grade pipes. Eng. Fail. Anal. 2019, 97, 793–803. [Google Scholar] [CrossRef]
- Kowsar, R.; Keshtegar, B.; Miyamoto, A. Understanding the hidden relations between pro-and anti-inflammatory cytokine genes in bovine oviduct epithelium using a multilayer response surface method. Sci. Rep. 2019, 9, 1–17. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keshtegar, B.; Seghier, M.e.A.B. Modified response surface method basis harmony search to predict the burst pressure of corroded pipelines. Eng. Fail. Anal. 2018, 89, 177–199. [Google Scholar] [CrossRef]
- Bezerra, M.A.; Santelli, R.E.; Oliveira, E.P.; Villar, L.S.; Escaleira, L.A. Response surface methodology (rsm) as a tool for optimization in analytical chemistry. Talanta 2008, 76, 965–977. [Google Scholar] [CrossRef]
- Keshtegar, B.; Gholampour, A.; Thai, D.-K.; Taylan, O.; Trung, N.-T. Hybrid regression and machine learning model for predicting ultimate condition of frp-confined concrete. Compos. Struct. 2021, 262, 113644. [Google Scholar] [CrossRef]
- Keshtegar, B.; Bagheri, M.; Fei, C.-W.; Lu, C.; Taylan, O.; Thai, D.-K. Multi-extremum-modified response basis model for nonlinear response prediction of dynamic turbine blisk. Eng. Comput. 2021, 1–12. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to testing the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Gao, L.; Xiao, M.; Shao, X.; Jiang, P.; Nie, L.; Qiu, H. Analysis of gene expression programming for approximation in engineering design. Struct. Multidiscip. Optim. 2012, 46, 399–413. [Google Scholar] [CrossRef]
- Keshtegar, B.; Heddam, S.; Sebbar, A.; Zhu, S.-P.; Trung, N.-T. Svr-rsm: A hybrid heuristic method for modeling monthly pan evaporation. Environ. Sci. Pollut. Res. 2019, 26, 35807–35826. [Google Scholar] [CrossRef] [PubMed]
- Fei, C.-W.; Lu, C.; Liem, R.P. Decomposed-coordinated surrogate modeling strategy for compound function approximation in a turbine-blisk reliability evaluation. Aerosp. Sci. Technol. 2019, 95, 105466. [Google Scholar] [CrossRef]
- Echard, B.; Gayton, N.; Lemaire, M. Ak-mcs: An active learning reliability method combining kriging and monte carlo simulation. Struct. Saf. 2011, 33, 145–154. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, J.; Gao, L. A system active learning kriging method for system reliability-based design optimization with a multiple response model. Reliab. Eng. Syst. Saf. 2020, 199, 106935. [Google Scholar] [CrossRef]
- Xiao, M.; Zhang, J.; Gao, L.; Lee, S.; Eshghi, A.T. An efficient kriging-based subset simulation method for hybrid reliability analysis under random and interval variables with small failure probability. Struct. Multidiscip. Optim. 2019, 59, 2077–2092. [Google Scholar] [CrossRef]
- Zhu, S.-P.; Keshtegar, B.; Tian, K.; Trung, N.-T. Optimization of load-carrying hierarchical stiffened shells: Comparative survey and applications of six hybrid heuristic models. Arch. Comput. Methods Eng. 2021, 28, 4153–4166. [Google Scholar] [CrossRef]
- Lu, C.; Feng, Y.-W.; Fei, C.-W.; Bu, S.-Q. Improved decomposed-coordinated kriging modeling strategy for dynamic probabilistic analysis of multicomponent structures. IEEE Trans. Reliab. 2019, 69, 440–457. [Google Scholar] [CrossRef]
- Keshtegar, B.; Hao, P. A hybrid descent mean value for accurate and efficient performance measure approach of reliability-based design optimization. Comput. Methods Appl. Mech. Eng. 2018, 336, 237–259. [Google Scholar] [CrossRef]
- Keshtegar, B.; Nehdi, M.L.; Kolahchi, R.; Trung, N.-T.; Bagheri, M. Novel hybrid machine leaning model for predicting shear strength of reinforced concrete shear walls. Eng. Comput. 2021, 1–12. [Google Scholar] [CrossRef]
- El Amine Ben Seghier, M.; Keshtegar, B.; Tee, K.F.; Zayed, T.; Abbassi, R.; Trung, N.T. Prediction of maximum pitting corrosion depth in oil and gas pipelines. Eng. Fail. Anal. 2020, 112, 104505. [Google Scholar] [CrossRef]
- Malik, A.; Kumar, A. Pan evaporation simulation based on daily meteorological data using soft computing techniques and multiple linear regression. Water Resour. Manag. 2015, 29, 1859–1872. [Google Scholar] [CrossRef]
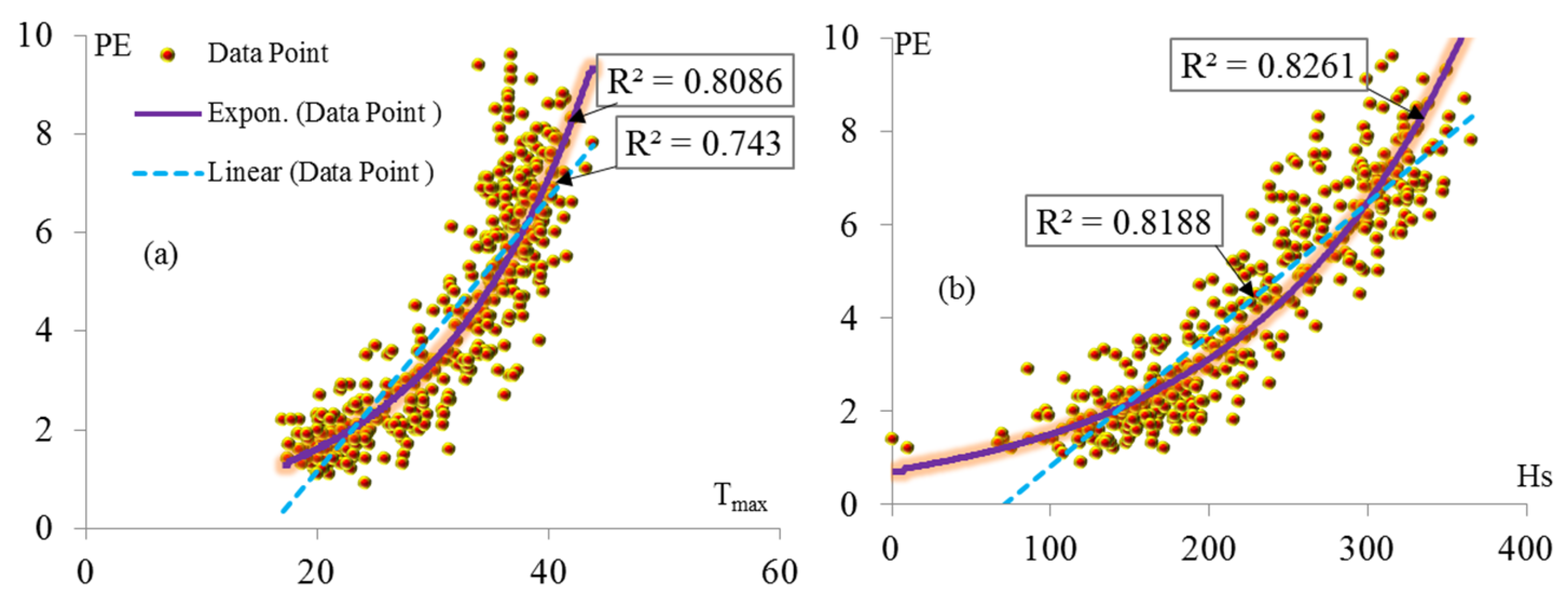
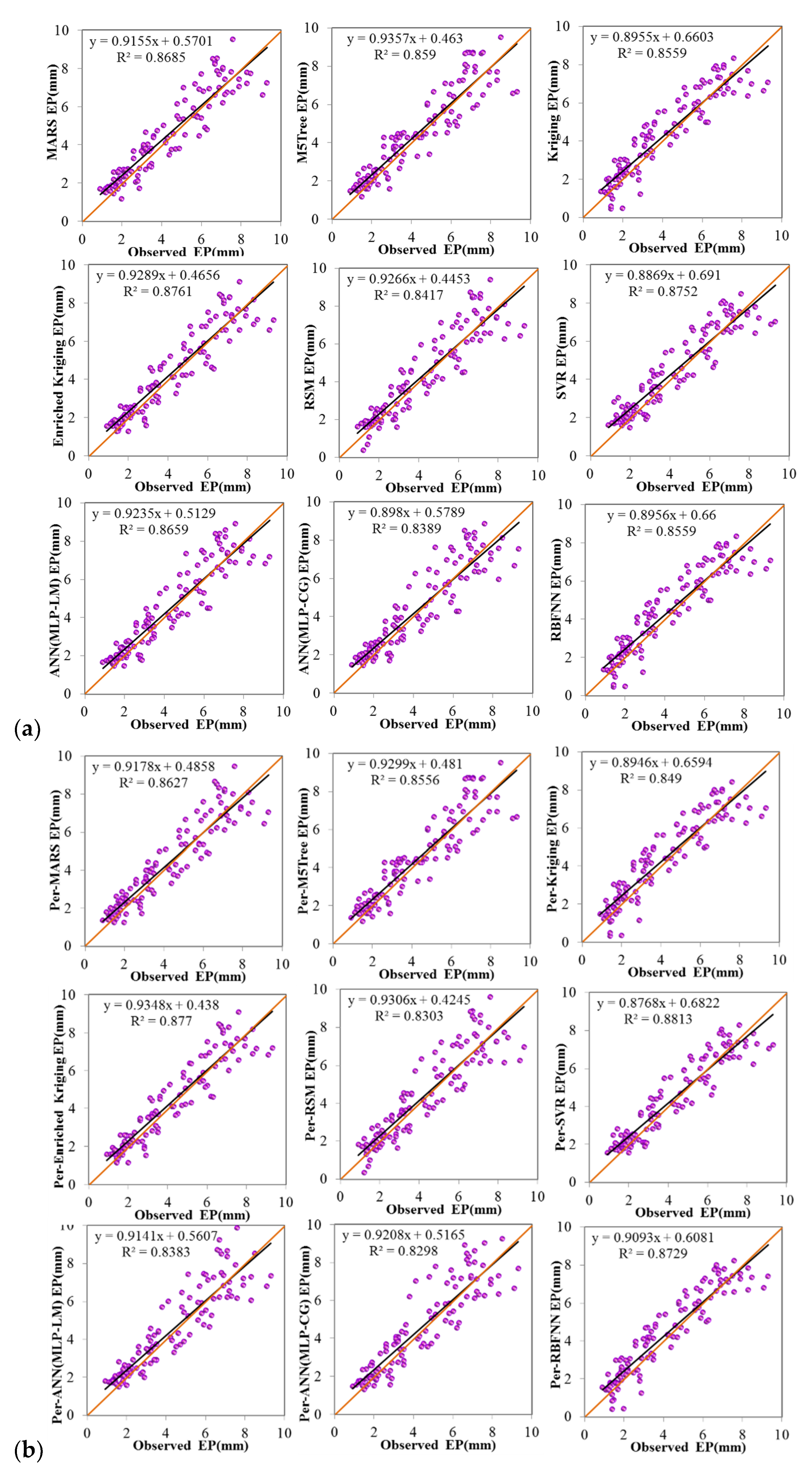
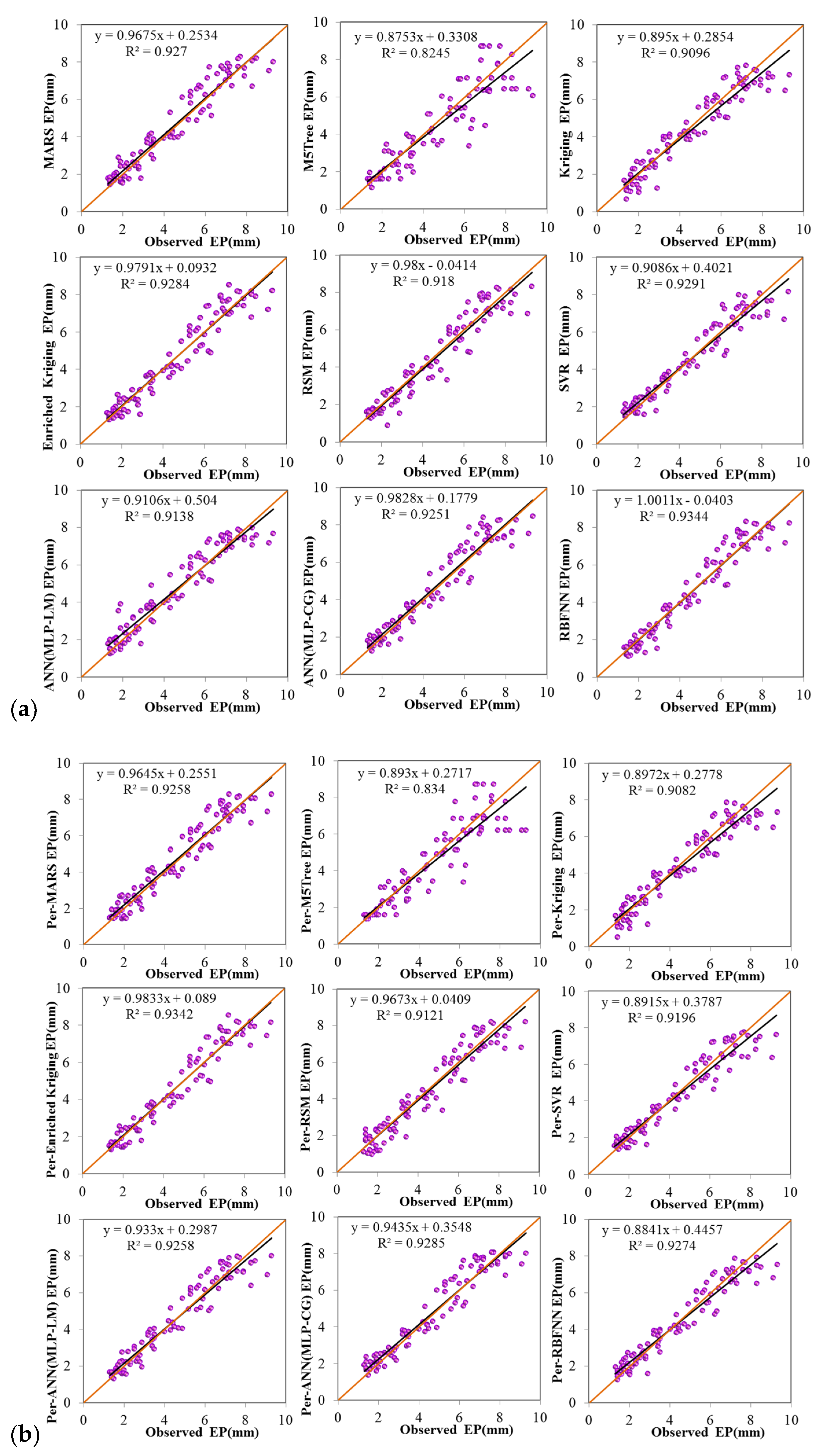
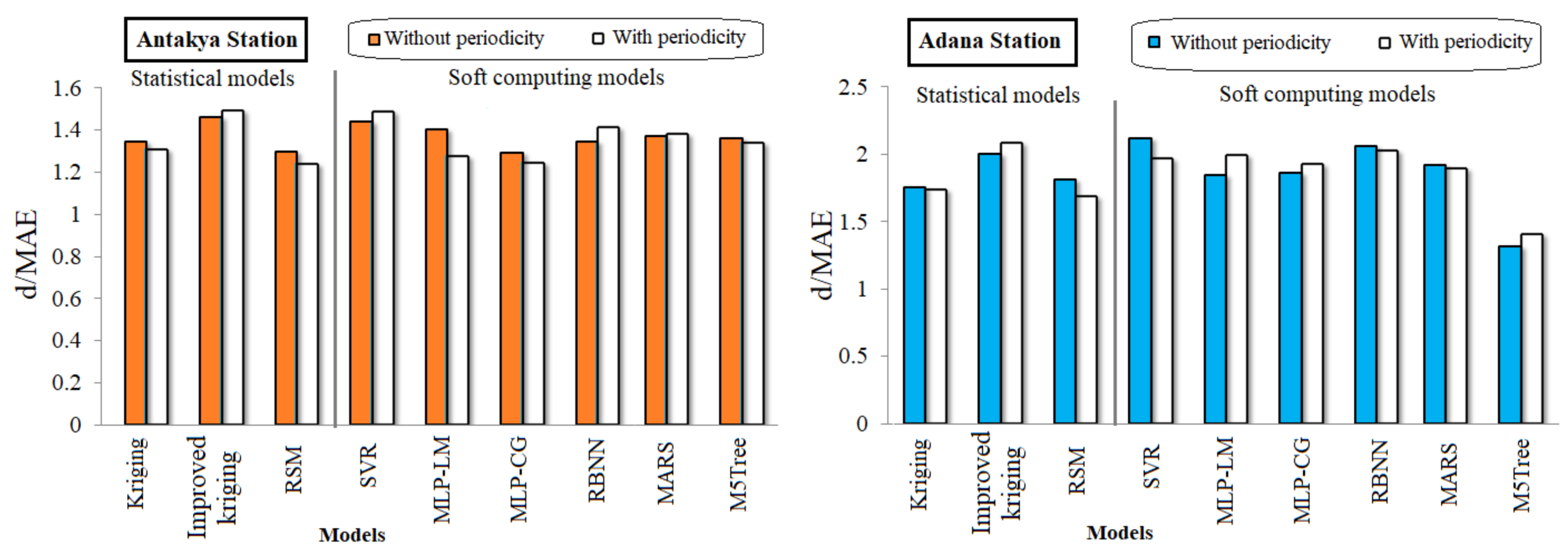
| Category | Model | MAE (mm) | RMSE (mm) | MBE (mm) | d | Max (RE) | Mean * (mm) | STD * (mm) | Tot-EP * (mm) | MAPE |
|---|---|---|---|---|---|---|---|---|---|---|
| Statistical | kriging | 0.712 | 0.891 | 0.228 | 0.958 | 86.31 | 4.36 | 2.19 | 501.63 | 0.213 |
| Improved kriging | 0.659 | 0.843 | 0.172 | 0.964 | 72.89 | 4.31 | 2.26 | 495.13 | 0.184 | |
| RSM | 0.736 | 0.933 | 0.142 | 0.956 | 79.08 | 4.28 | 2.29 | 491.71 | 0.205 | |
| Soft computing models | MARS | 0.701 | 0.855 | 0.221 | 0.962 | 87.78 | 4.35 | 2.23 | 500.78 | 0.203 |
| M5Tree | 0.704 | 0.890 | 0.197 | 0.960 | 80.77 | 4.33 | 2.29 | 498.11 | 0.190 | |
| SVR | 0.668 | 0.828 | 0.223 | 0.964 | 135.32 | 4.36 | 2.15 | 501.08 | 0.208 | |
| ANN(LM) | 0.685 | 0.861 | 0.197 | 0.962 | 83.32 | 4.33 | 2.25 | 498.01 | 0.195 | |
| ANN(CG) | 0.739 | 0.930 | 0.157 | 0.955 | 66.74 | 4.29 | 2.22 | 493.49 | 0.207 | |
| RBFNN | 0.712 | 0.892 | 0.229 | 0.958 | 86.31 | 4.36 | 2.19 | 501.68 | 0.213 |
| Category | Structures | MAE (mm) | RMSE (mm) | MBE (mm) | d | Max (RE) | Mean * (mm) | STD * (mm) | Tot-EP * (mm) | MAPE |
|---|---|---|---|---|---|---|---|---|---|---|
| Statistical | kriging | 0.730 | 0.912 | 0.224 | 0.957 | 88.79 | 4.36 | 2.20 | 501.11 | 0.220 |
| Improved kriging | 0.646 | 0.821 | 0.168 | 0.966 | 76.97 | 4.30 | 2.26 | 494.75 | 0.181 | |
| RSM | 0.768 | 0.972 | 0.138 | 0.953 | 100.96 | 4.27 | 2.31 | 491.22 | 0.210 | |
| Soft computing models | MARS | 0.697 | 0.859 | 0.146 | 0.962 | 63.13 | 4.28 | 2.24 | 492.19 | 0.193 |
| M5Tree | 0.715 | 0.897 | 0.192 | 0.959 | 80.77 | 4.33 | 2.28 | 497.45 | 0.197 | |
| SVR | 0.648 | 0.796 | 0.173 | 0.966 | 106.42 | 4.31 | 2.12 | 495.30 | 0.200 | |
| MLP-LM | 0.746 | 0.949 | 0.206 | 0.954 | 99.85 | 4.34 | 2.26 | 499.06 | 0.205 | |
| MLP-CG | 0.764 | 0.976 | 0.189 | 0.952 | 71.22 | 4.32 | 2.29 | 497.16 | 0.208 | |
| RBNN | 0.682 | 0.842 | 0.233 | 0.963 | 85.82 | 4.37 | 2.21 | 502.21 | 0.214 |
| Scenario I, without Periodicity | Scenario II, with Periodicity | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Category | Model | Accuracy | Precision | Tendency | Best Model(s) | Accuracy | Precision | Tendency | Best Model(s) |
| Statistical | Kriging | M | L | + | M | L | + | ||
| Improved kriging | H | H | + | * | H | H | + | * | |
| RSM | L | M | + | L | L | + | |||
| Soft computing models | MARS | H | H | + | * | M | H | + | |
| M5Tree | M | M | + | M | M | + | |||
| SVR | H | L | + | H | L | + | |||
| MLP-LM | M | H | + | L | H | + | |||
| MLP-CG | L | M | + | L | M | + | |||
| RBNN | L | L | + | H | M | + | |||
| Category | Model | MAE (mm) | RMSE (mm) | MBE (mm) | d | Max (RE) | Mean * (mm) | STD * (mm) | Tot-EP * (mm) | MAPE |
|---|---|---|---|---|---|---|---|---|---|---|
| Statistical | kriging | 0.555 | 0.717 | −0.190 | 0.974 | 56.81 | 4.34 | 2.17 | 399.39 | 0.142 |
| Improved kriging | 0.489 | 0.626 | −0.001 | 0.981 | 48.06 | 4.53 | 2.35 | 416.77 | 0.119 | |
| RSM | 0.540 | 0.687 | −0.132 | 0.978 | 60.99 | 4.40 | 2.36 | 404.77 | 0.129 | |
| Soft computing models | MARS | 0.510 | 0.637 | 0.107 | 0.981 | 60.01 | 4.64 | 2.32 | 426.71 | 0.130 |
| M5Tree | 0.722 | 0.998 | −0.234 | 0.949 | 58.18 | 4.30 | 2.22 | 395.33 | 0.158 | |
| SVR | 0.463 | 0.613 | −0.012 | 0.981 | 54.12 | 4.52 | 2.18 | 415.77 | 0.115 | |
| MLP-LM | 0.528 | 0.681 | 0.099 | 0.976 | 105.46 | 4.63 | 2.20 | 426.01 | 0.145 | |
| MLP-CG | 0.525 | 0.651 | 0.100 | 0.980 | 49.28 | 4.63 | 2.36 | 426.11 | 0.126 | |
| RBFNN | 0.476 | 0.610 | −0.035 | 0.983 | 47.64 | 4.50 | 2.39 | 413.67 | 0.117 |
| Category | Model | MAE (mm) | RMSE (mm) | MBE (mm) | d | Max (RE) | Mean * (mm) | STD * (mm) | Tot-EP * (mm) | MAPE |
|---|---|---|---|---|---|---|---|---|---|---|
| Statistical | kriging | 0.560 | 0.721 | −0.188 | 0.973 | 62.26 | 4.55 | 2.35 | 418.14 | 0.145 |
| Improved kriging | 0.471 | 0.601 | 0.014 | 0.983 | 43.68 | 4.42 | 2.34 | 407.02 | 0.114 | |
| RSM | 0.579 | 0.701 | −0.107 | 0.976 | 67.19 | 4.42 | 2.15 | 406.53 | 0.155 | |
| Soft computing models | MARS | 0.517 | 0.638 | 0.094 | 0.980 | 48.89 | 4.32 | 2.26 | 397.37 | 0.132 |
| M5Tree | 0.677 | 0.970 | −0.212 | 0.953 | 49.04 | 4.34 | 2.17 | 399.62 | 0.142 | |
| SVR | 0.496 | 0.664 | −0.113 | 0.977 | 49.49 | 4.53 | 2.24 | 416.47 | 0.117 | |
| MLP-LM | 0.492 | 0.625 | −0.005 | 0.981 | 44.51 | 4.63 | 2.26 | 425.98 | 0.118 | |
| MLP-CG | 0.508 | 0.623 | 0.099 | 0.981 | 68.50 | 4.45 | 2.12 | 409.60 | 0.132 | |
| RBFNN | 0.483 | 0.632 | −0.079 | 0.979 | 48.67 | 4.32 | 2.26 | 397.37 | 0.122 |
| Scenario I, without Periodicity | Scenario II, with Periodicity | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Category | Model | Accuracy | Precision | Tendency | Best Model(s) | Accuracy | Precision | Tendency | Best Model(s) |
| Statistical | Kriging | L | H | − | L | L | − | ||
| Improved kriging | H | H | N | * | H | M | + | * | |
| RSM | L | L | − | L | M | − | |||
| Soft computing models | MARS | M | H | + | M | H | + | ||
| M5Tree | L | M | − | L | L | − | |||
| SVR | H | L | − | M | M | − | |||
| MLP-LM | M | M | + | H | H | N | * | ||
| MLP-CG | M | M | + | H | H | + | * | ||
| RBNN | H | L | − | M | L | − | |||
| Soft Computing Models | |||||||
|---|---|---|---|---|---|---|---|
| M5Tree | RBNN | MLP-LM | MLP-CG | SVR | MARS | ||
| Statistical models | RSM | 0.792 | 0.899 | 0.865 | 0.654 | 0.970 | 0.720 |
| Kriging | 0.878 | 0.844 | 0.984 | 0.964 | 0.970 | 0.977 | |
| Improved kriging | 0.988 | 0.724 | 0.870 | 0.918 | 0.886 | 0.895 | |
| Soft Computing Models | |||||||
|---|---|---|---|---|---|---|---|
| M5Tree | RBNN | MLP-LM | MLP-CG | SVR | MARS | ||
| Statistical models | RSM | 0.824 | 0.873 | 0.626 | 0.631 | 0.786 | 0.638 |
| kriging | 0.904 | 0.722 | 0.478 | 0.532 | 0.648 | 0.518 | |
| Improved kriging | 0.709 | 0.997 | 0.757 | 0.785 | 0.910 | 0.778 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zounemat-Kermani, M.; Keshtegar, B.; Kisi, O.; Scholz, M. Towards a Comprehensive Assessment of Statistical versus Soft Computing Models in Hydrology: Application to Monthly Pan Evaporation Prediction. Water 2021, 13, 2451. https://doi.org/10.3390/w13172451
Zounemat-Kermani M, Keshtegar B, Kisi O, Scholz M. Towards a Comprehensive Assessment of Statistical versus Soft Computing Models in Hydrology: Application to Monthly Pan Evaporation Prediction. Water. 2021; 13(17):2451. https://doi.org/10.3390/w13172451
Chicago/Turabian StyleZounemat-Kermani, Mohammad, Behrooz Keshtegar, Ozgur Kisi, and Miklas Scholz. 2021. "Towards a Comprehensive Assessment of Statistical versus Soft Computing Models in Hydrology: Application to Monthly Pan Evaporation Prediction" Water 13, no. 17: 2451. https://doi.org/10.3390/w13172451
APA StyleZounemat-Kermani, M., Keshtegar, B., Kisi, O., & Scholz, M. (2021). Towards a Comprehensive Assessment of Statistical versus Soft Computing Models in Hydrology: Application to Monthly Pan Evaporation Prediction. Water, 13(17), 2451. https://doi.org/10.3390/w13172451








