CFD Model of the Density-Driven Bidirectional Flows through the West Crack Breach in the Great Salt Lake Causeway
Abstract
:1. Introduction
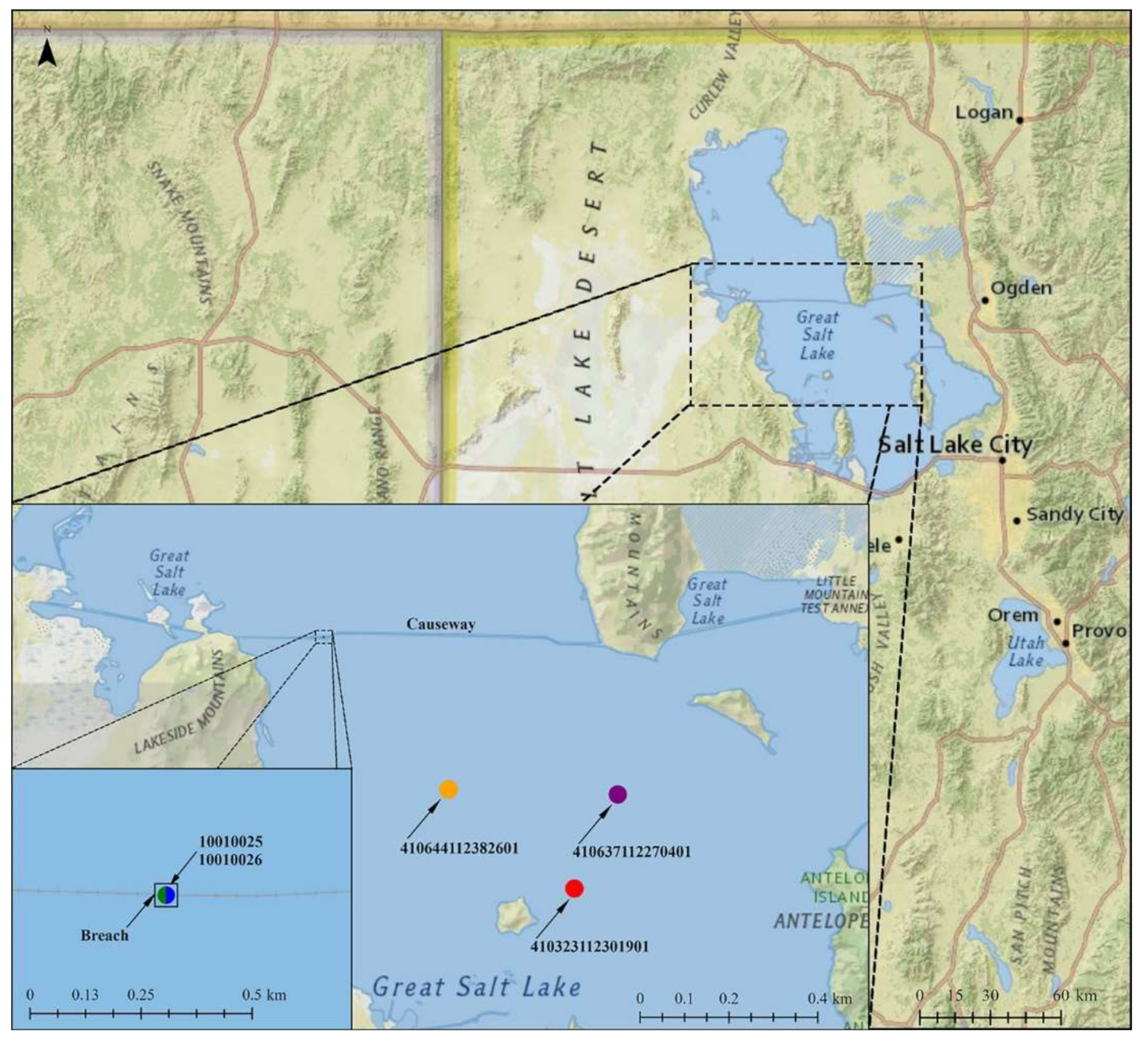
2. Great Salt Lake and the West Crack Breach
3. Materials and Methods
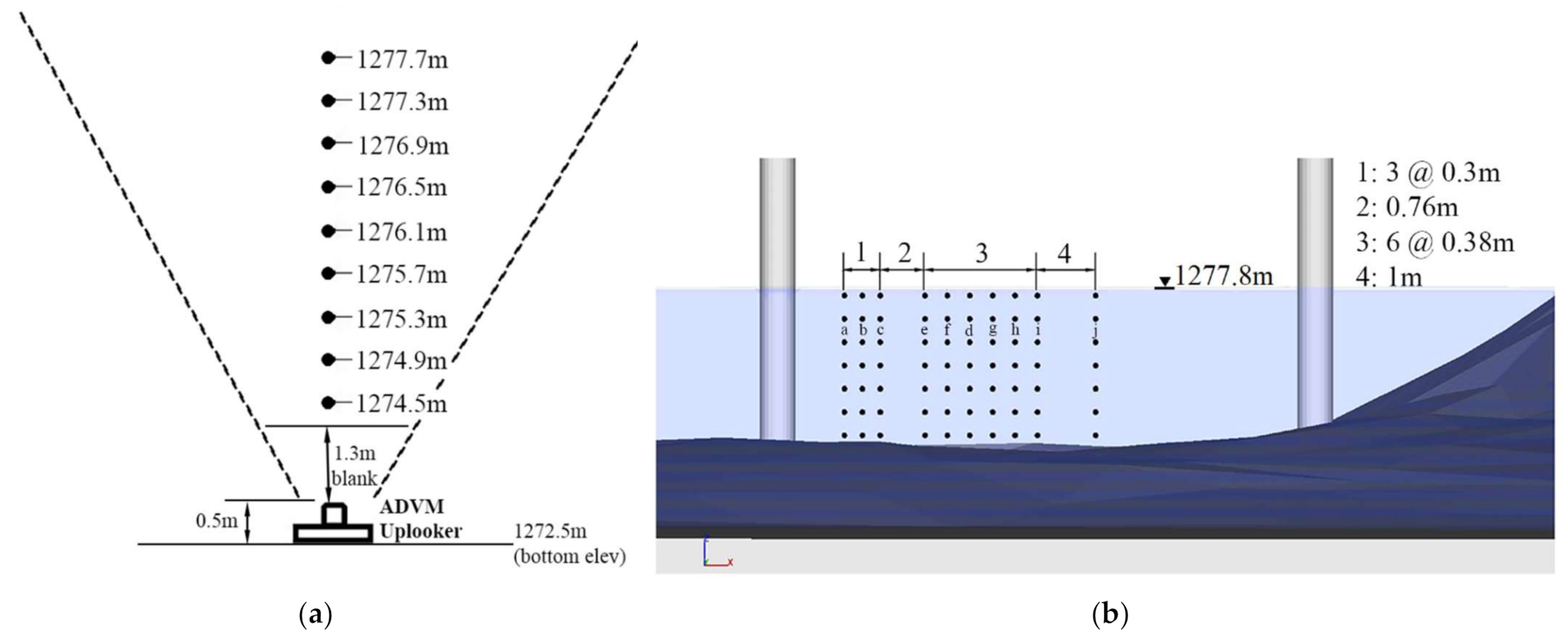
3.1. Field Campaign
3.2. Numerical Model
3.2.1. Model Overview and Flow Equations
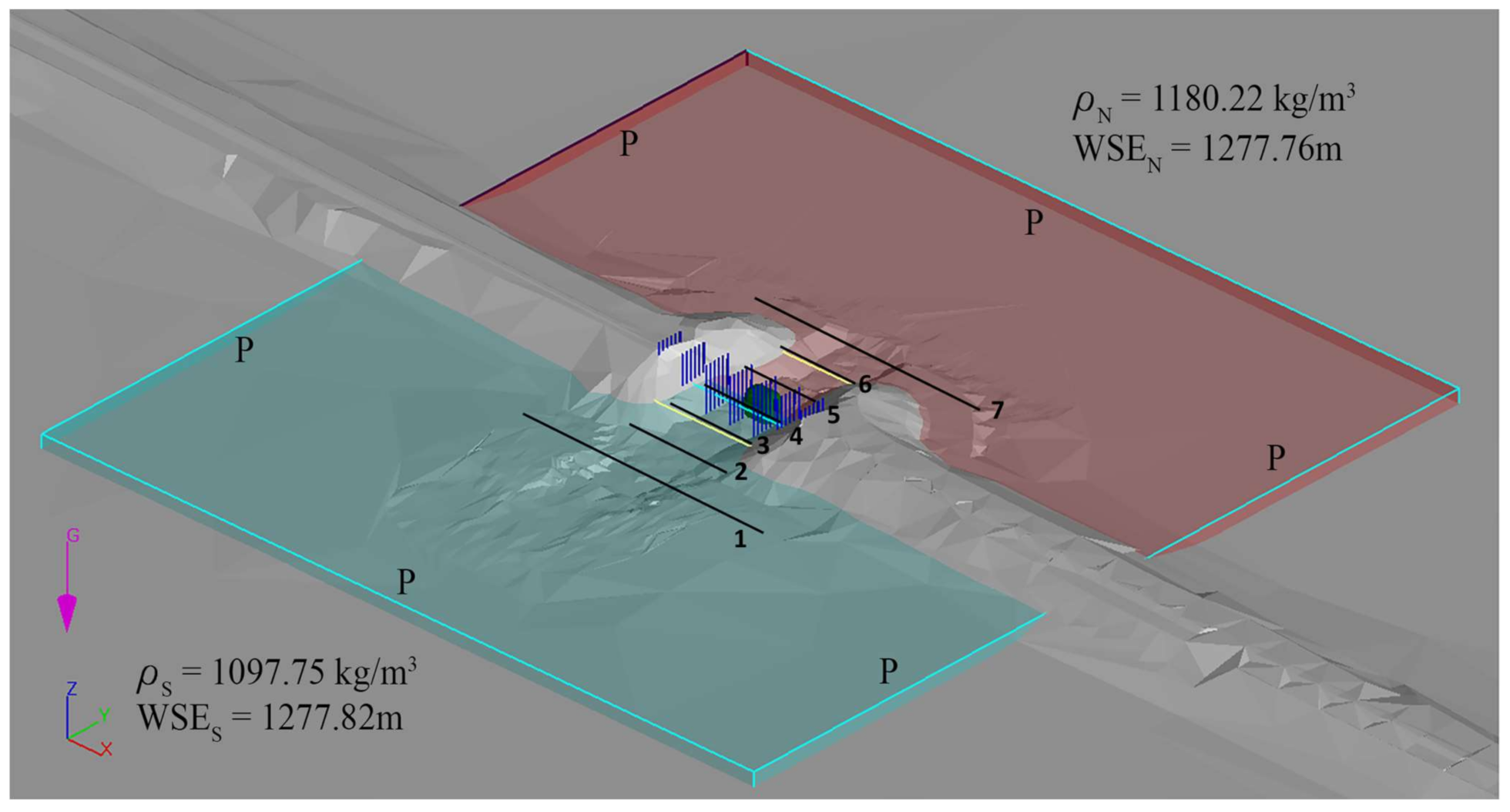
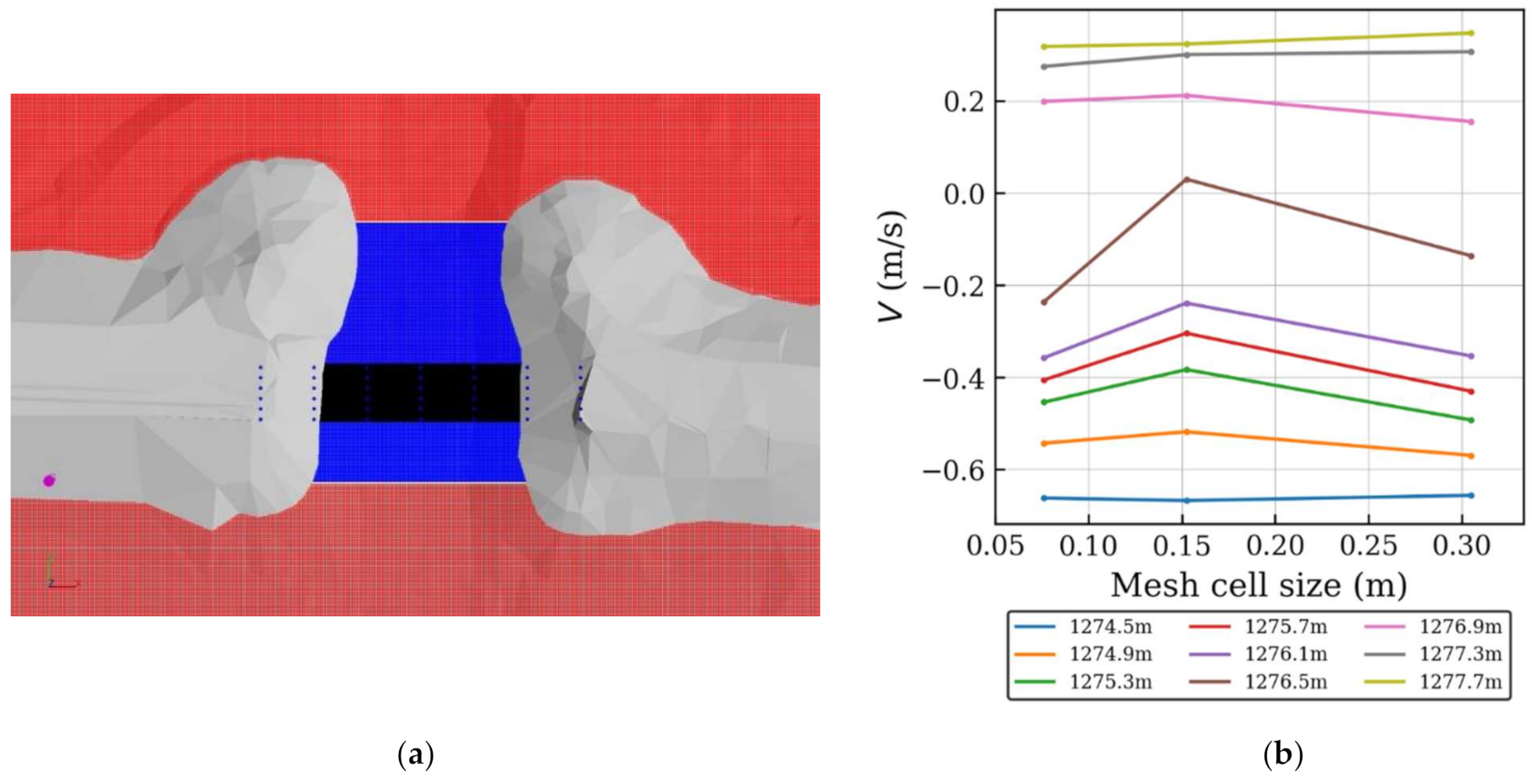
3.2.2. Model Domain and Boundary Conditions
4. Results and Discussion
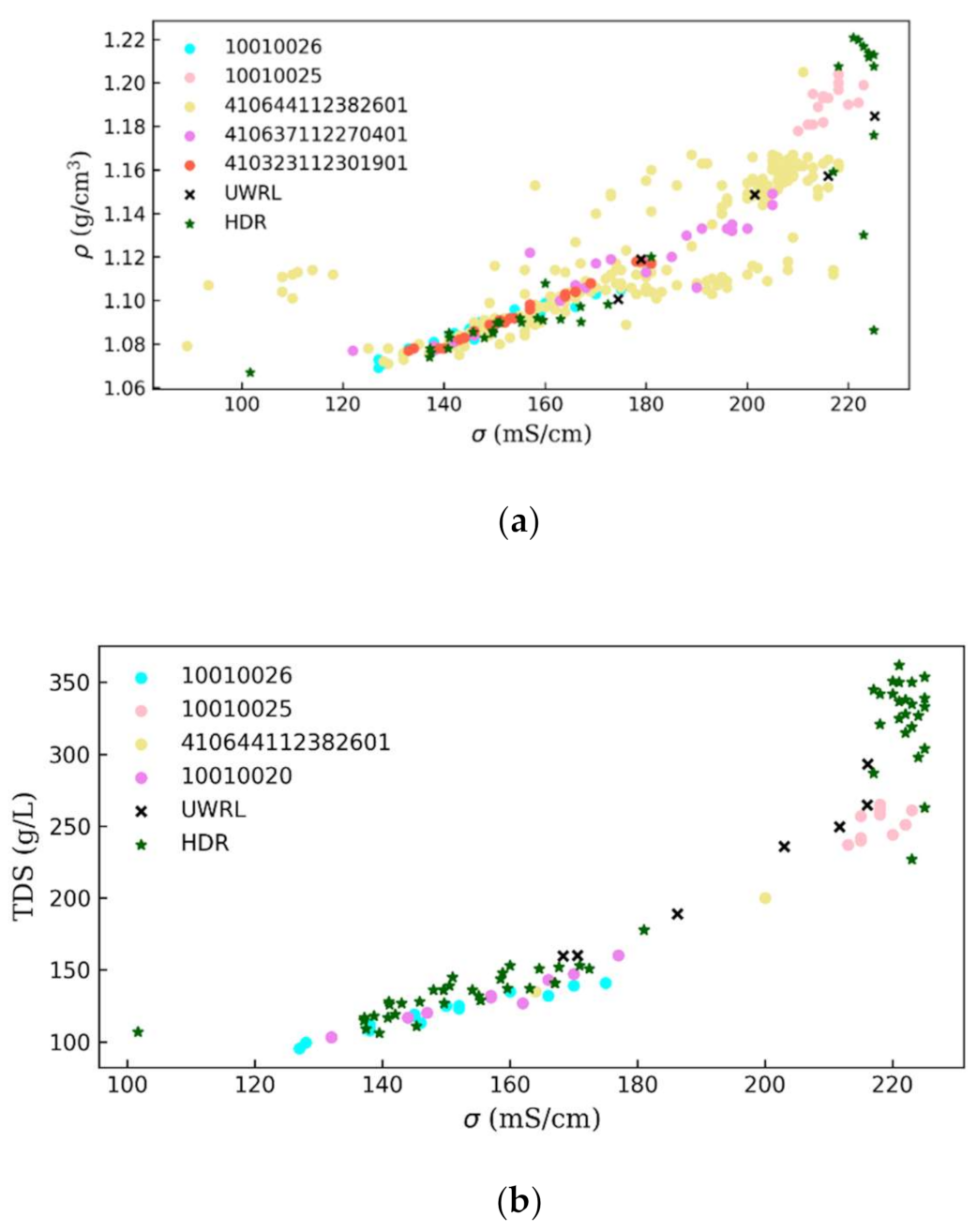
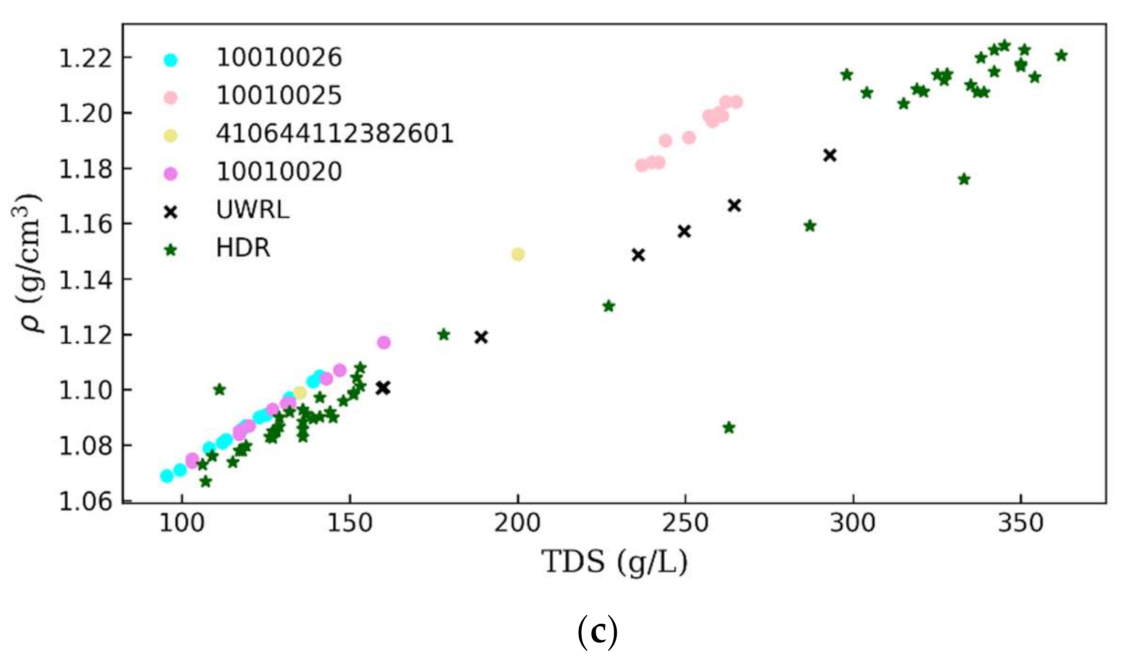
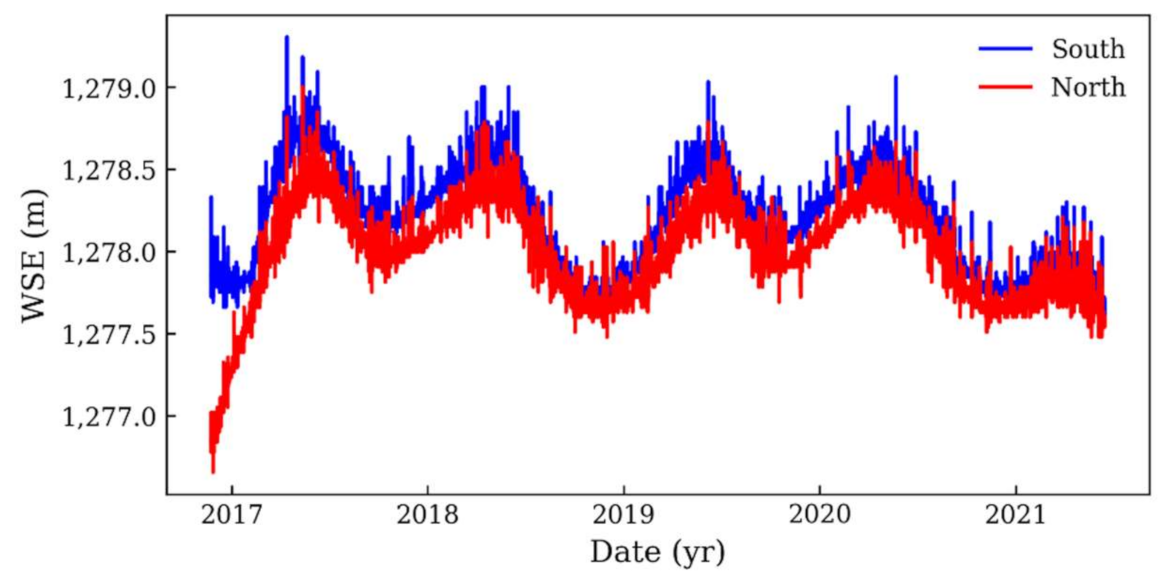
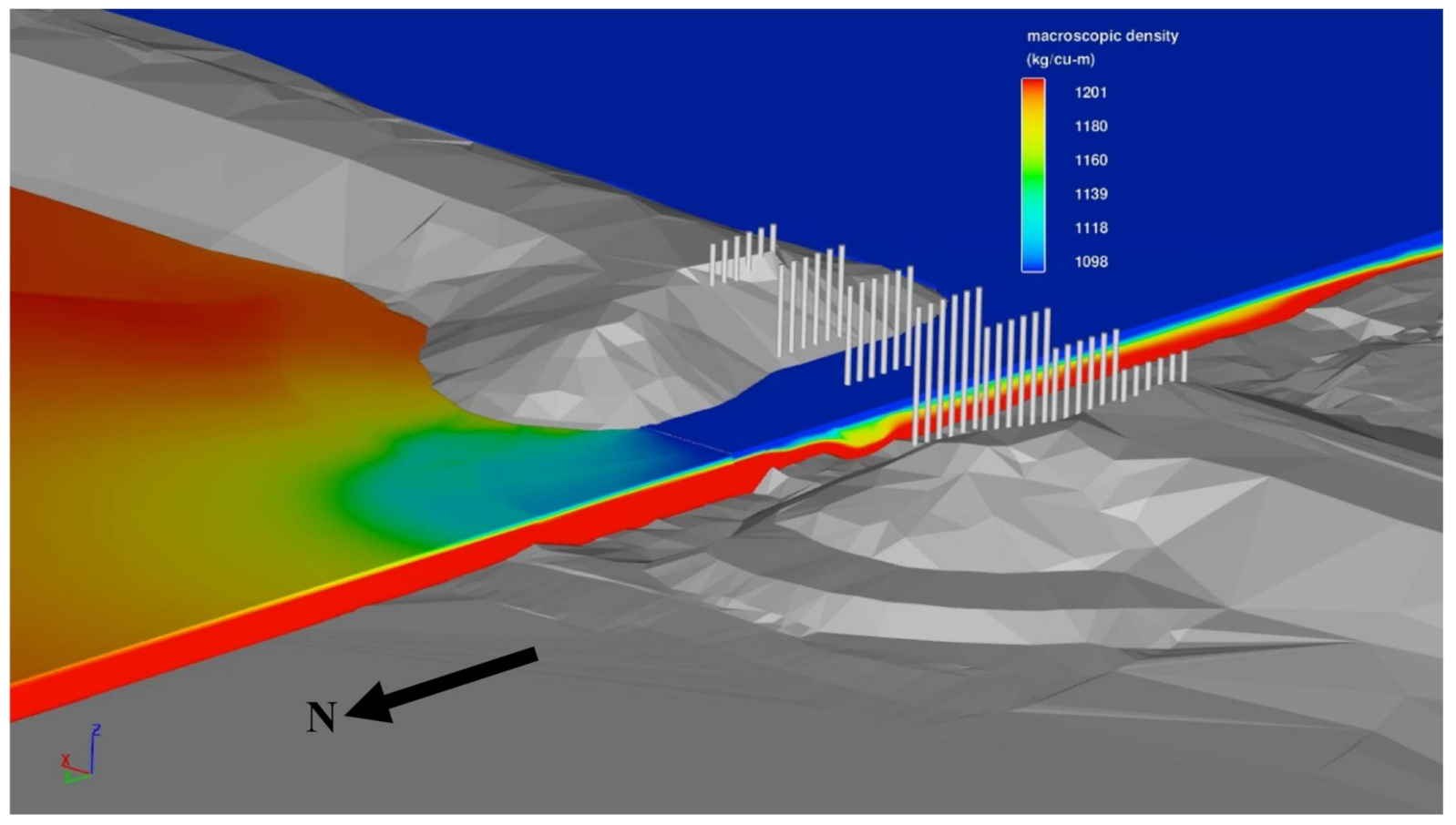
4.1. Density and Water Surface Elevations
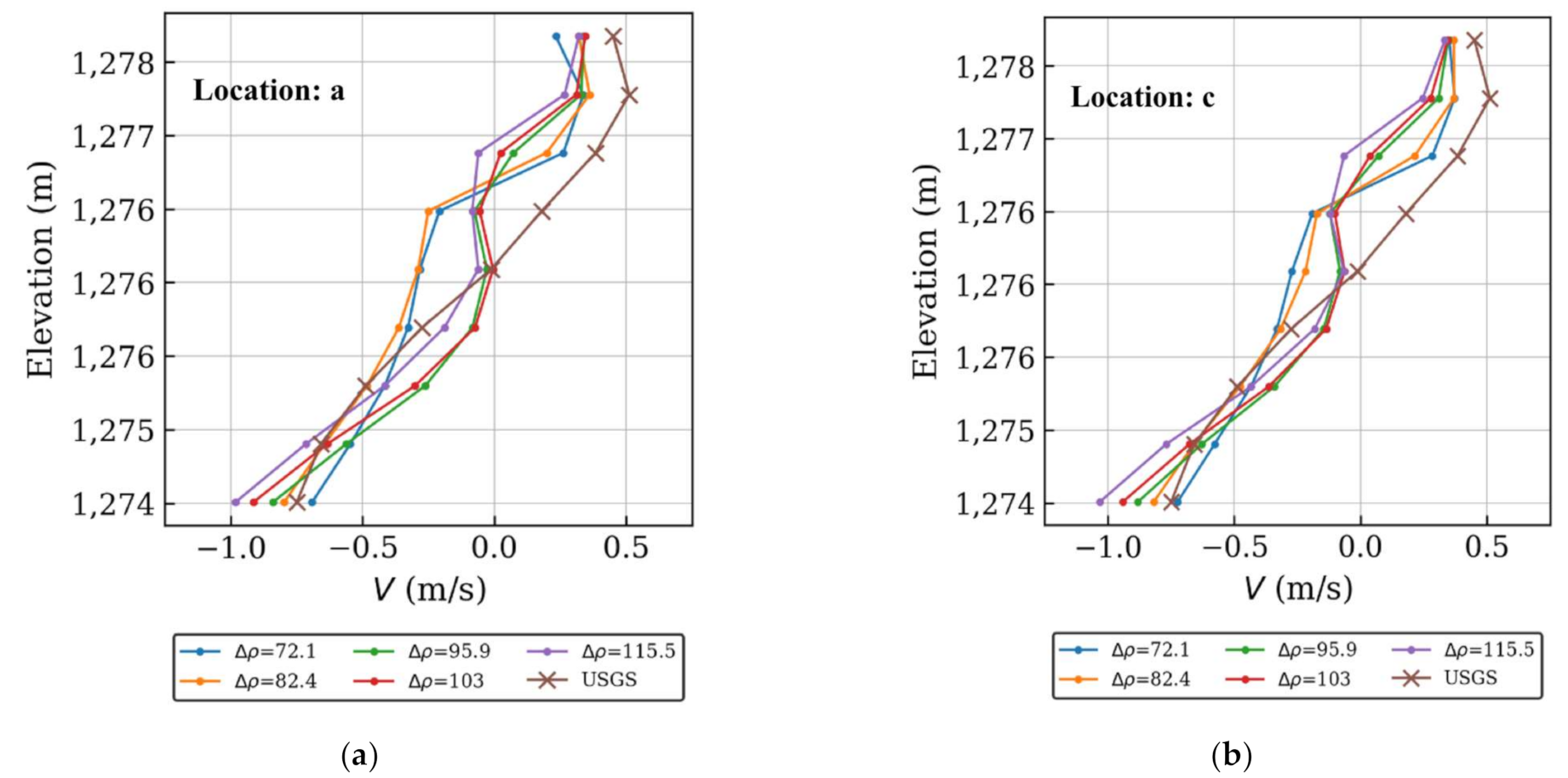
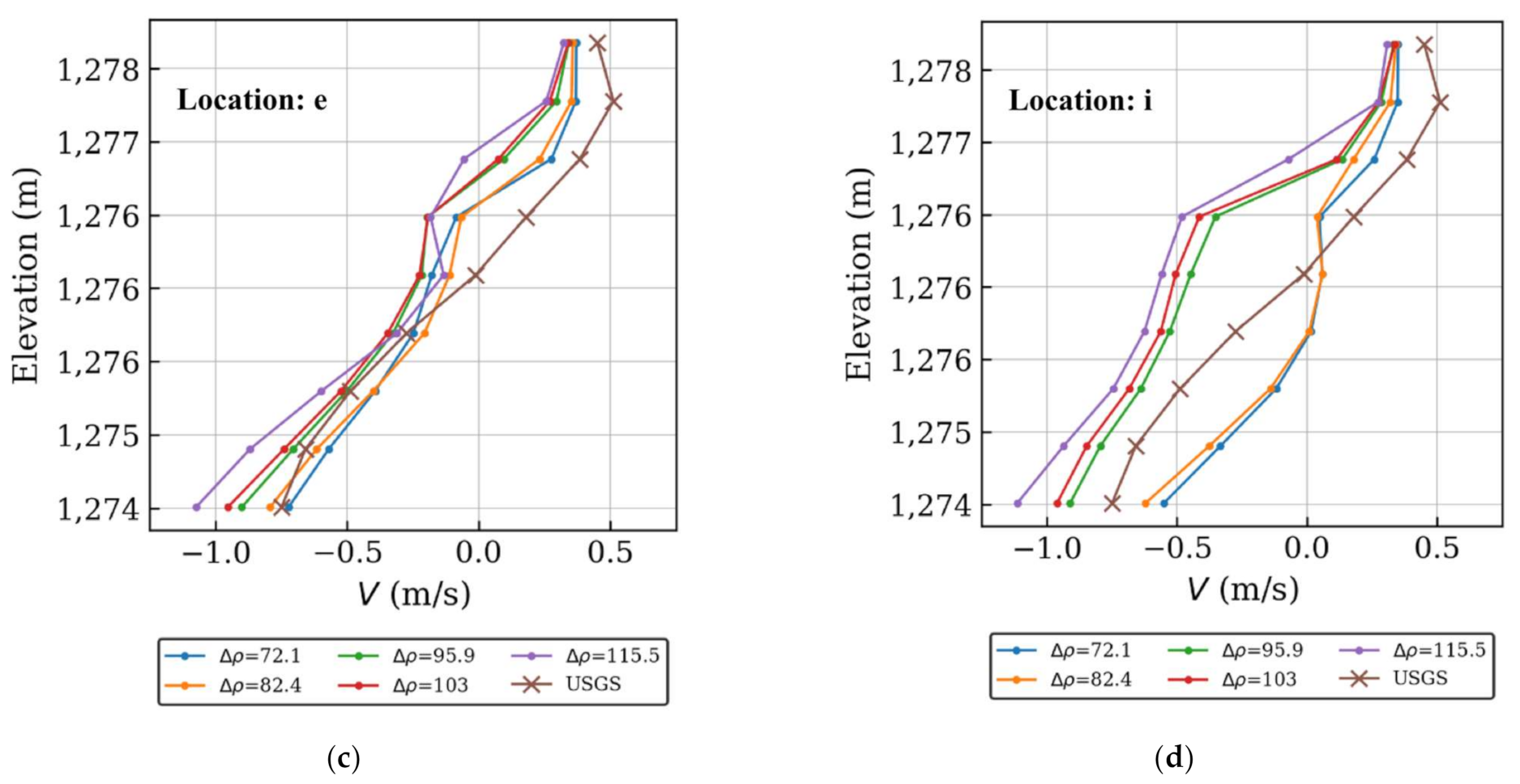
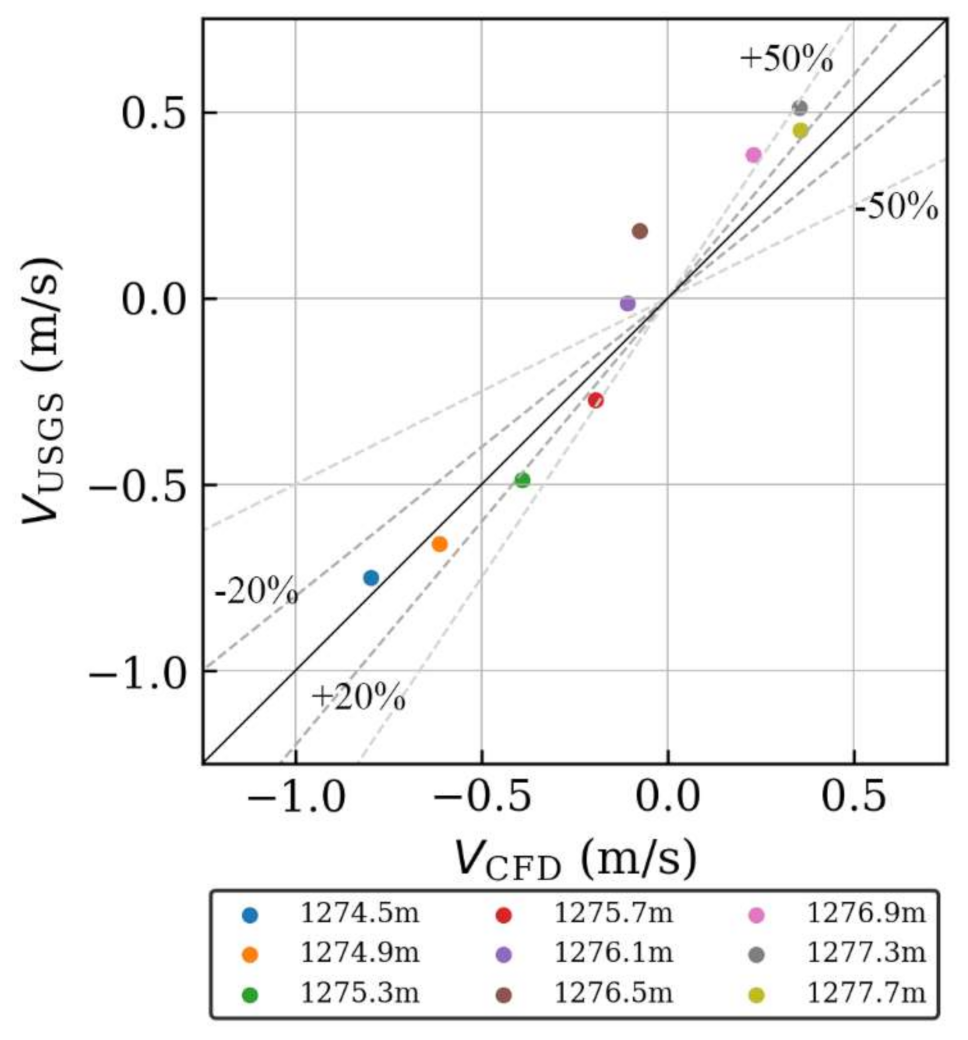
4.2. Model Comparison with Field Measurements
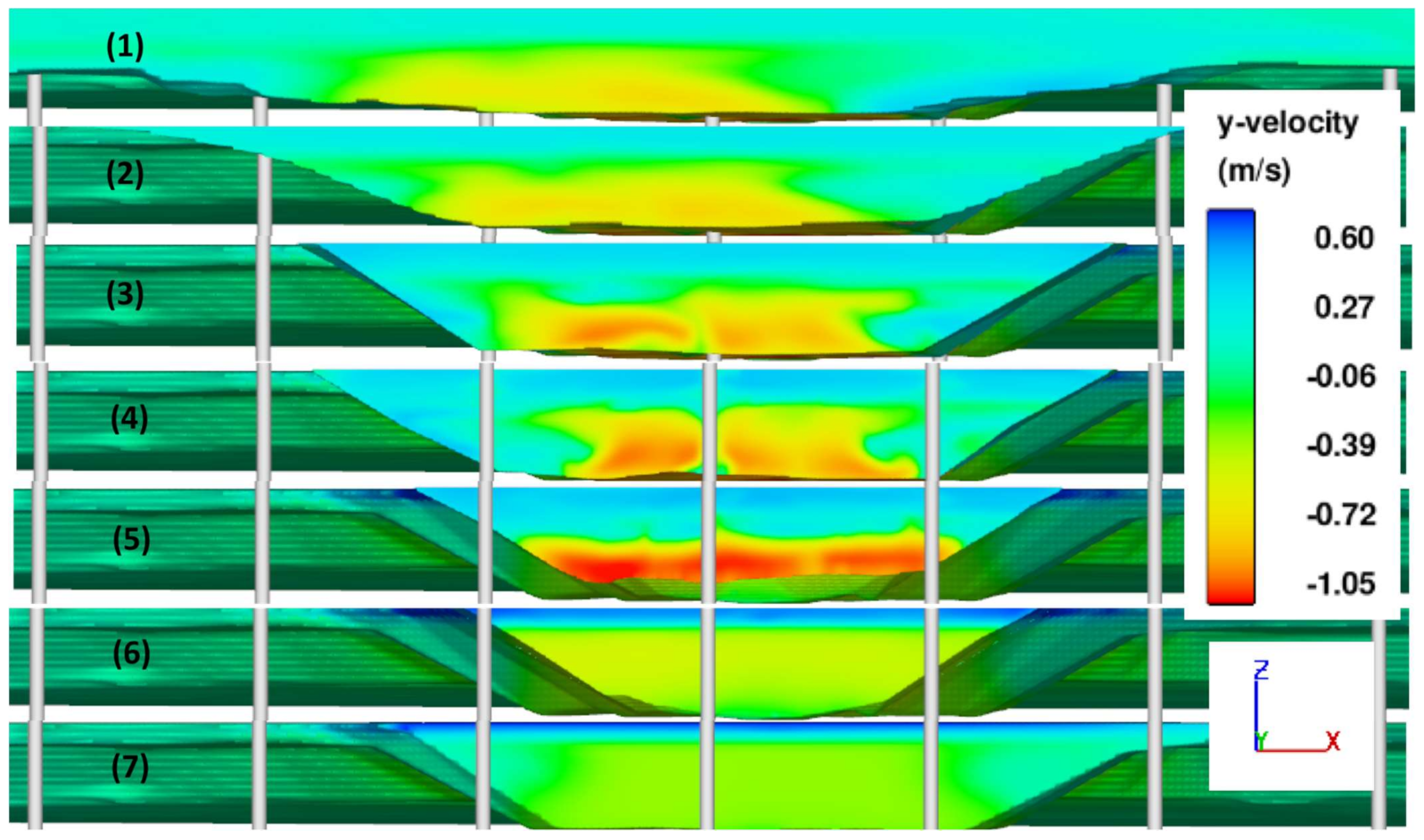
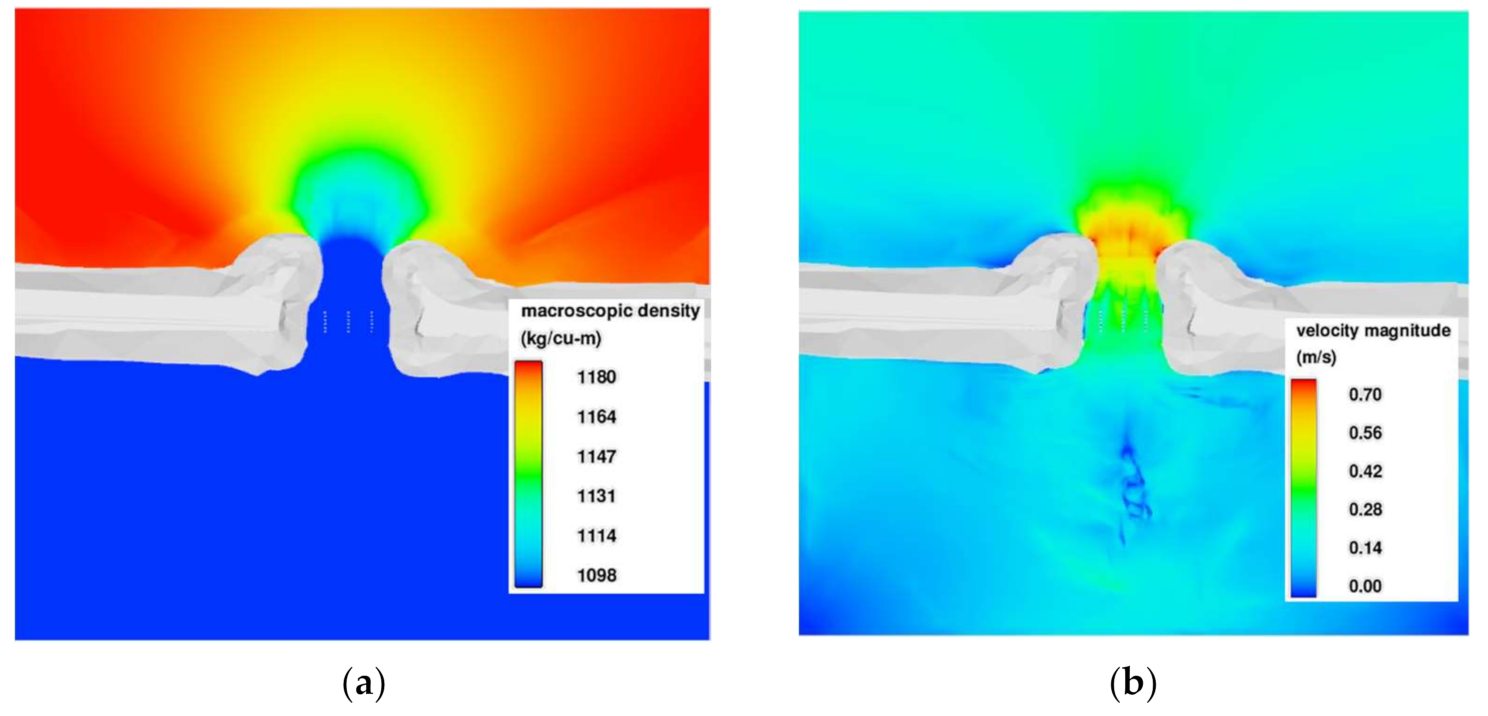
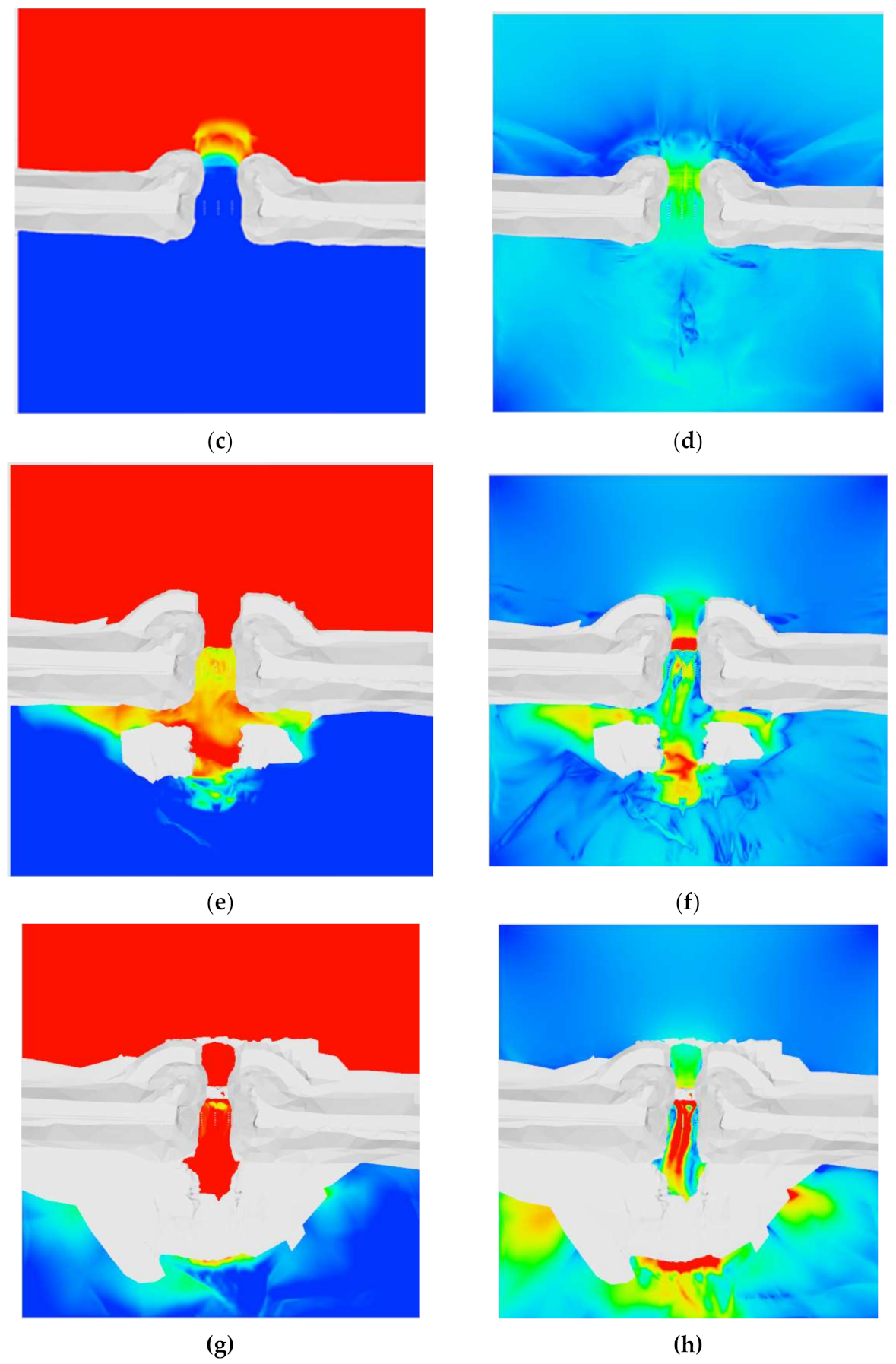
4.3. Simulated Flow Field
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Messager, M.L.; Lehner, B.; Grill, G.; Nedeva, I.; Schmitt, O. Estimating the volume and age of water stored in global lakes using a geo-statistical approach. Nat. Commun. 2016, 7, 13603. [Google Scholar] [CrossRef]
- Pendleton, M.C.; Sedgwick, S.; Kettenring, K.M.; Atwood, T.B. Ecosystem functioning of Great Salt Lake wetlands. Wetlands 2020, 40, 2163–2177. [Google Scholar] [CrossRef]
- Conover, M.R.; Bell, M.E. Importance of Great Salt Lake to pelagic birds: Eared grebes, phalaropes, gulls, ducks, and white pelicans. In Great Salt Lake Biology; Springer: Cham, Switzerland, 2020; pp. 239–262. [Google Scholar]
- Wurtsbaugh, W.A.; Miller, C.; Null, S.E.; DeRose, R.J.; Wilcock, P.; Hahnenberger, M.; Moore, J. Decline of the world’s saline lakes. Nat. Geosci. 2017, 10, 816–821. [Google Scholar] [CrossRef]
- Mischke, S.; Liu, C.; Zhang, J.; Zhang, C.; Zhang, H.; Jiao, P.; Plessen, B. The world’s earliest Aral-Sea type disaster: The decline of the Loulan Kingdom in the Tarim Basin. Sci. Rep. 2017, 7, 43102. [Google Scholar] [CrossRef] [PubMed]
- AghaKouchak, A.; Norouzi, H.; Madani, K.; Mirchi, A.; Azarderakhsh, M.; Nazemi, A.; Hasanzadeh, E. Aral Sea syndrome desiccates Lake Urmia: Call for action. J. Great Lakes Res. 2015, 41, 307–311. [Google Scholar] [CrossRef]
- Gross, M. The world’s vanishing lakes. Curr. Biol. 2017, 27, 43–46. [Google Scholar] [CrossRef]
- Jellison, R.; Williams, W.D.; Timms, B.; Alocer, J.; Aladin, N.V. Aquatic Ecosystems: Trends and Global Prospects; Polunin, N.V.C., Ed.; Cambridge University Press: Cambridge, UK, 2008; pp. 94–112. [Google Scholar]
- Case, H.L.I. Salton Sea Ecosystem Monitoring and Assessment Plan Open-File Report 2013–1133; United States Geological Survey: Reston, VA, USA, 2013.
- Barnes, B.D.; Wurtsbaugh, W.A. The effects of salinity on plankton and benthic communities in the Great Salt Lake, Utah, USA: A microcosm experiment. Can. J. Fish. Aquat. Sci. 2015, 72, 807–817. [Google Scholar] [CrossRef]
- Naftz, D.L.; Cederberg, J.R.; Krabbenhoft, D.P.; Beisner, K.R.; Whitehead, J.; Gardberg, J. Diurnal trends in methylmercury concentration in a wetland adjacent to Great Salt Lake, Utah, USA. Chem. Geol. 2011, 283, 78–86. [Google Scholar] [CrossRef]
- White, J.S.; Null, S.E.; Tarboton, D.G. How do changes to the railroad causeway in Utah’s Great Salt Lake affect water and salt flow? PLoS ONE 2015, 10, e0144111. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Null, S.E.; Wurtsbaugh, W.A.; Miller, C. Can the causeway in the Great Salt Lake be used to manage salinity? Friends Great Salt Lake Newsl. 2013, 19, 14. [Google Scholar]
- Bioeconomics, Inc. Economic Significance of the Great Salt Lake to the State of Utah. Prepared for State of Utah Great Salt Lake Advisory Council. 2012. Available online: http://www.gslcouncil.utah.gov/docs/GSL_FINAL_REPORT-1-26-12.PDF (accessed on 1 June 2021).
- Wurtsbaugh, W.; Miller, C.; Null, S.; Wilcock, P.; Hahnenberger, M.; Howe, F. Impacts of Water Development on Great Salt Lake and the Wasatch Front. In White Paper to the Utah State Legislature. Prepared by Utah State University; Utah State University: Salt Lake City, UT, USA, 2016. [Google Scholar]
- WHSRN. Western Hemisphere Shorebird Reserve Network. 2016. Available online: www.whsrn.org (accessed on 1 May 2021).
- Loving, B.L.; Waddell, K.M.; Miller, C.W. Water and Salt Balance of Great Salt Lake, Utah, and Simulation of Water and Salt Movement through the Causeway, 1987–1998; U.S.G.S Water-Resources Investigations Report 00-4221; U.S. Geologic Survey: Salt Lake City, UT, USA, 2000.
- Waddell, K.M.; Bolke, E.L. The Effects of Restricted Circulation on the Salt Balance of Great Salt Lake, Utah; Bulletin 18; Utah Geological Survey Water Resources: Salt Lake City, UT, USA.
- Stephens, D.W. Changes in lake levels, salinity and the biological community of Great Salt Lake (Utah, USA), 1847–1987. Hydrobiologia 1990, 197, 139–146. [Google Scholar] [CrossRef]
- Rupke, A.L.; McDonald, A. Great Salt Lake Brine Chemistry Database, 1966–2011; Open-File Report 596, compact disk; Utah Geological Survey: Reston, VA, USA, 2012.
- Baxter, B.K. Great Salt Lake microbiology: A historical perspective. Int. Microbiol. 2018, 21, 79–95. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.; Johnson, W.P.; Black, F.J.; Rowland, R.; Rumsey, C.; Piskadlo, A. Response of density stratification, aquatic chemistry, and methylmercury to engineered and hydrologic forcings in an endorheic lake (Great Salt Lake, USA). Limnol. Oceanogr. 2020, 65, 915–926. [Google Scholar] [CrossRef]
- Holley, E.R.; Waddell, K.M. Stratified Flow in Great Salt Lake Culvert. J. Hydraul. Div. 1976, 102, 969–985. [Google Scholar] [CrossRef]
- Spall, R.E. A Hydrodynamic Model of the Circulation within the South Arm of the Great Salt Lake. Int. J. Model. Simul. 2009, 29, 181–190. [Google Scholar]
- Spall, R.E. Basin-Scale Internal Waves within the South Arm of the Great Salt Lake. Int. J. Model. Simul. 2011, 31, 25–31. [Google Scholar] [CrossRef]
- Dutta, S.; Tokyay, T.E.; Cataño-Lopera, Y.A.; Serafino, S.; Garcia, M.H. Application of computational fluid dynamic modelling to improve flow and grit transport in Terrence J. O’Brien Water Reclamation Plant, Chicago, Illinois. J. Hydraul. Res. 2014, 52, 759–774. [Google Scholar] [CrossRef]
- Crookston, B.M.; Anderson, R.M.; Tullis, B.P. Free-flow discharge estimation method for Piano Key weir geometries. J. Hydro-Environ. Res. 2018, 19, 160–167. [Google Scholar] [CrossRef]
- Standard Methods. 2540 C, 2540 D, 2540 E, APHA, AWWA, and WEF 2014. Standard Methods for the Analysis of Water and Wastewater Online. Available online: www.standardmethods.org (accessed on 1 July 2021).
- In-Situ. Aqua TROLL ® 600 Multiparameter Sonde 2020. Available online: https://in-situ.com/pub/media/support/documents/AquaTROLL600_Spec-Sheet.pdf (accessed on 1 August 2021).
- Levesque, V.A.; Oberg, K.A. Computing Discharge Using the Index Velocity Method; U.S. Geological Survey: Reston, VA, USA, 2012; 148p.
- U.S. Geological Survey (USGS). National Water Information System Data for the Nation. 2020. Available online: https://waterdata.usgs.gov/nwis/ (accessed on 15 June 2021).
- HDR 2019 Annual Data Monitoring Report 2020. Available online: https://documents.deq.utah.gov/water-quality/standards-technical-services/gsl-website-docs/uprr-causeway/DWQ-2020-003963.pdf (accessed on 15 November 2020).
- HDR 2020 Annual Data Monitoring Report 2021. Available online: https://documents.deq.utah.gov/water-quality/standards-technical-services/gsl-website-docs/uprr-causeway/DWQ-2021-002902.pdf (accessed on 15 November 2020).
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Stancanelli, L.M.; Musumeci, R.E.; Foti, E. Computational fluid dynamics for modeling gravity currents in the presence of oscillatory ambient flow. Water 2018, 10, 635. [Google Scholar] [CrossRef] [Green Version]
- Smagorinsky, J. General circulation experiments with the primitive equations: I. The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef] [Green Version]
- Pope, S.B. Turbulent Flows; Cambridge: Cambridge, UK, 2001. [Google Scholar]
- Yeh, T.H.; Cantero, M.; Cantelli, A.; Pirmez, C.; Parker, G. Turbidity current with a roof: Success and failure of RANS modeling for turbidity currents under strongly stratified conditions. J. Geophys. Res. Earth Surf. 2013, 118, 1975–1998. [Google Scholar] [CrossRef] [Green Version]
- An, S.; Julien, P.Y.; Venayagamoorthy, S.K. Numerical simulation of particle-driven gravity currents. Environ. Fluid Mech. 2012, 12, 495–513. [Google Scholar] [CrossRef]
- Roache, P.J. Verification and Validation in Computational Science and Engineering; Hermosa: Albuquerque, NM, USA, 1998; p. 895. [Google Scholar]
- Naftz, D.L.; Millero, F.J.; Jones, B.F.; Green, W.R. An equation of state for hypersaline water in Great Salt Lake, Utah, USA. Aquat. Geochem. 2011, 17, 809–820. [Google Scholar] [CrossRef]




| Sim (#) | ρS (g/cm3) | ρN (g/cm3) | Δρ (kg/m3) | ΔWSE (m) |
|---|---|---|---|---|
| 1 | 1.0978 | 1.1699 | 72.1 | 0.061 |
| 2 | 1.0978 | 1.1802 | 82.4 | 0.061 |
| 3 | 1.0998 | 1.1957 | 95.9 | 0.061 |
| 4 | 1.0978 | 1.2008 | 103.0 | 0.061 |
| 5 | 1.09782 | 1.2127 | 115.5 | 0.061 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rasmussen, M.; Dutta, S.; Neilson, B.T.; Crookston, B.M. CFD Model of the Density-Driven Bidirectional Flows through the West Crack Breach in the Great Salt Lake Causeway. Water 2021, 13, 2423. https://doi.org/10.3390/w13172423
Rasmussen M, Dutta S, Neilson BT, Crookston BM. CFD Model of the Density-Driven Bidirectional Flows through the West Crack Breach in the Great Salt Lake Causeway. Water. 2021; 13(17):2423. https://doi.org/10.3390/w13172423
Chicago/Turabian StyleRasmussen, Michael, Som Dutta, Bethany T. Neilson, and Brian Mark Crookston. 2021. "CFD Model of the Density-Driven Bidirectional Flows through the West Crack Breach in the Great Salt Lake Causeway" Water 13, no. 17: 2423. https://doi.org/10.3390/w13172423






