An Improved Techno-Economic Approach to Determination of More Precise Installed Parameter for Small Hydropower Plants
Abstract
1. Introduction
2. Materials and Methods
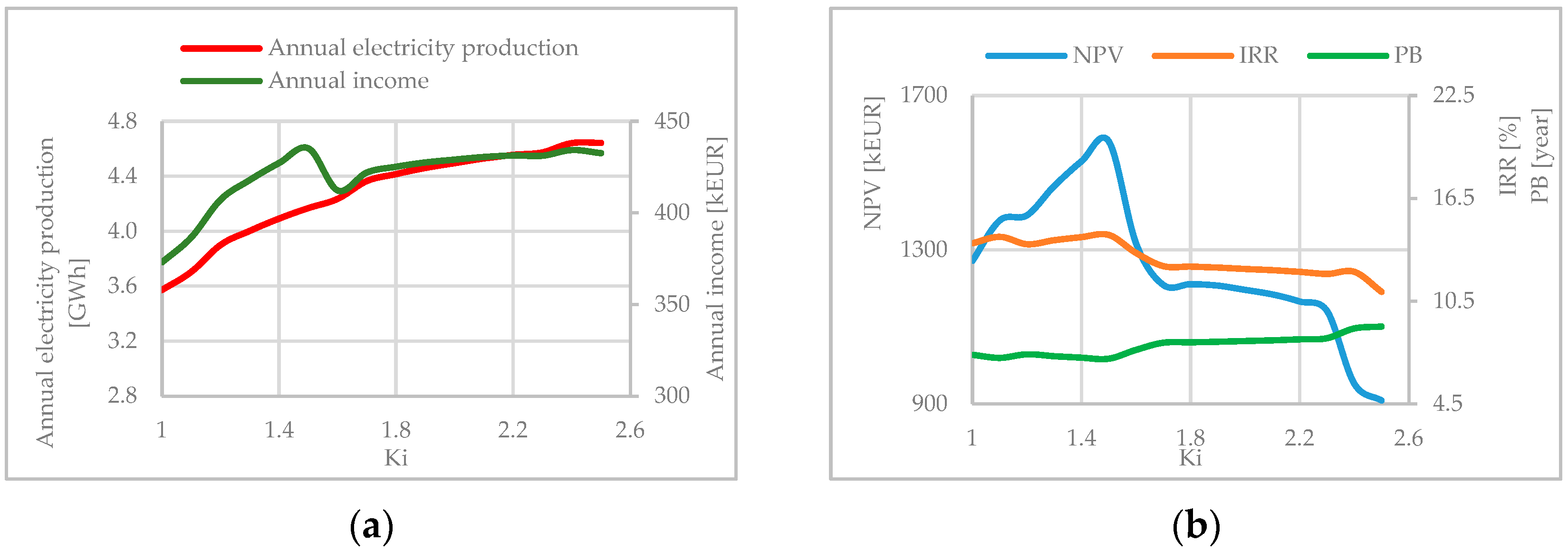
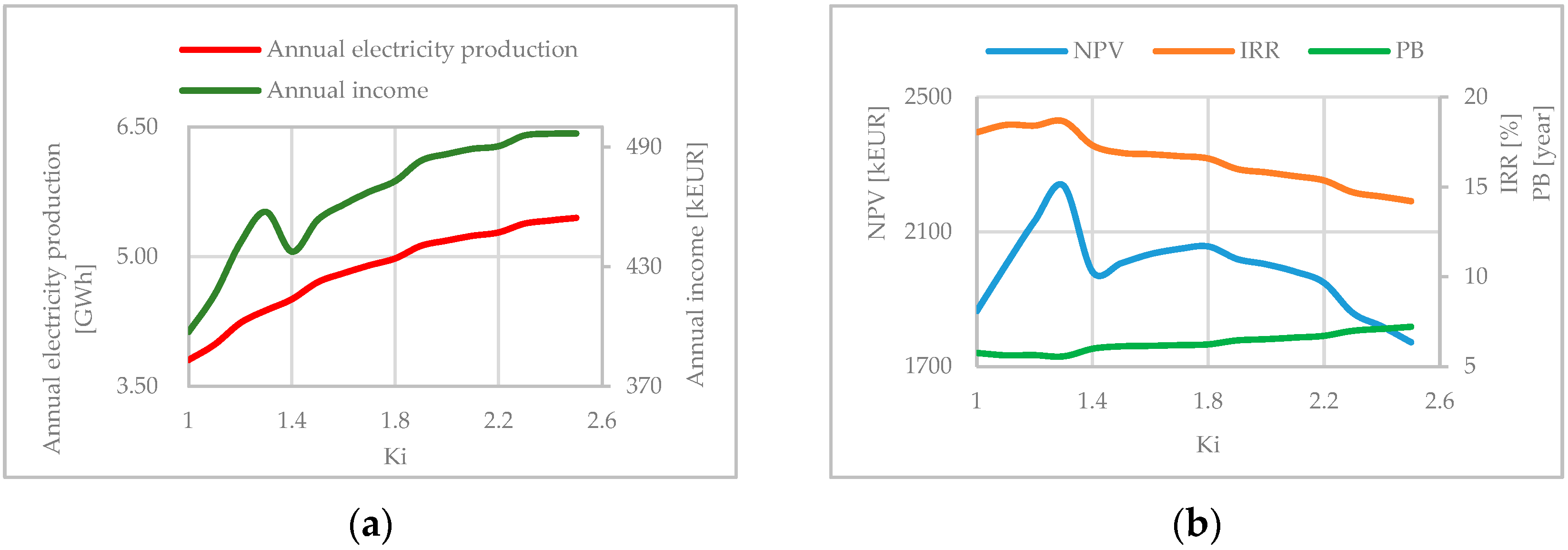
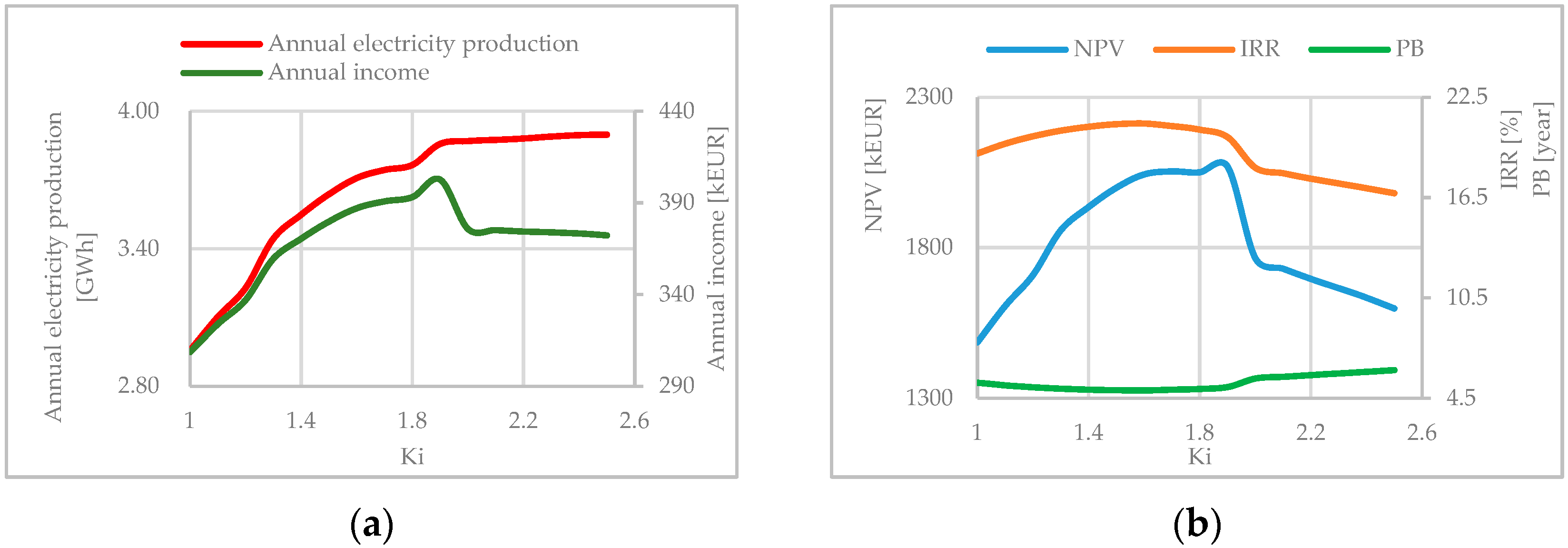
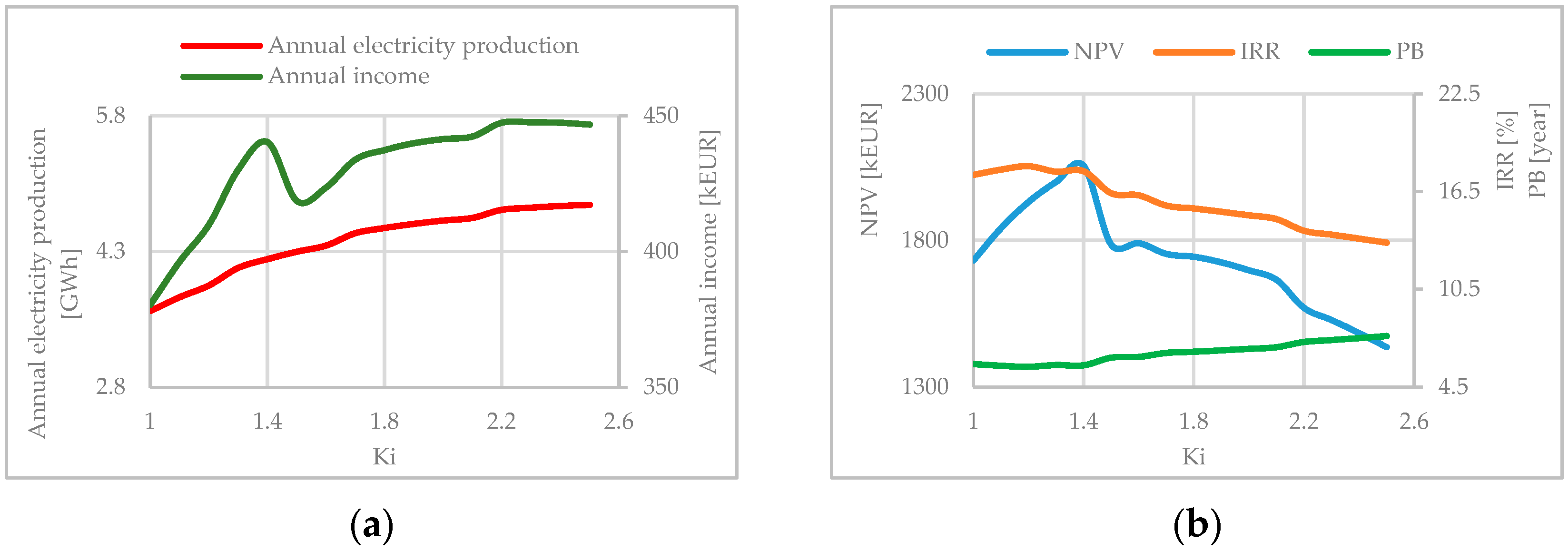
3. Results
4. Conclusions
- 1.
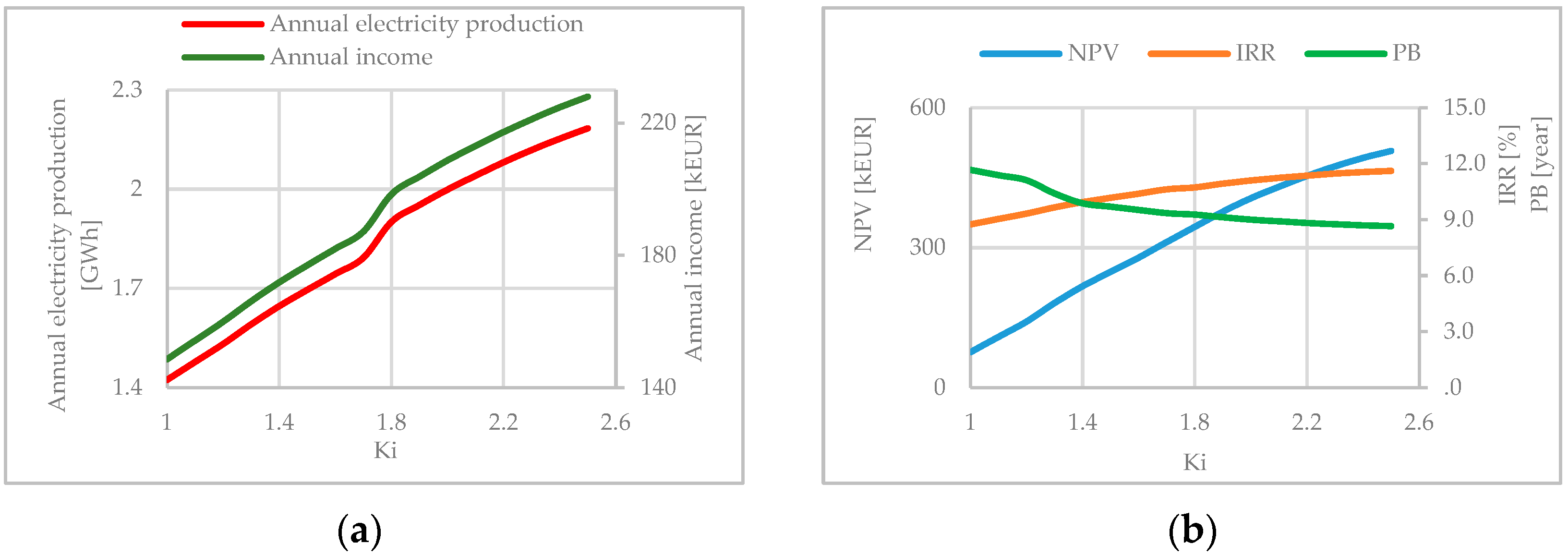
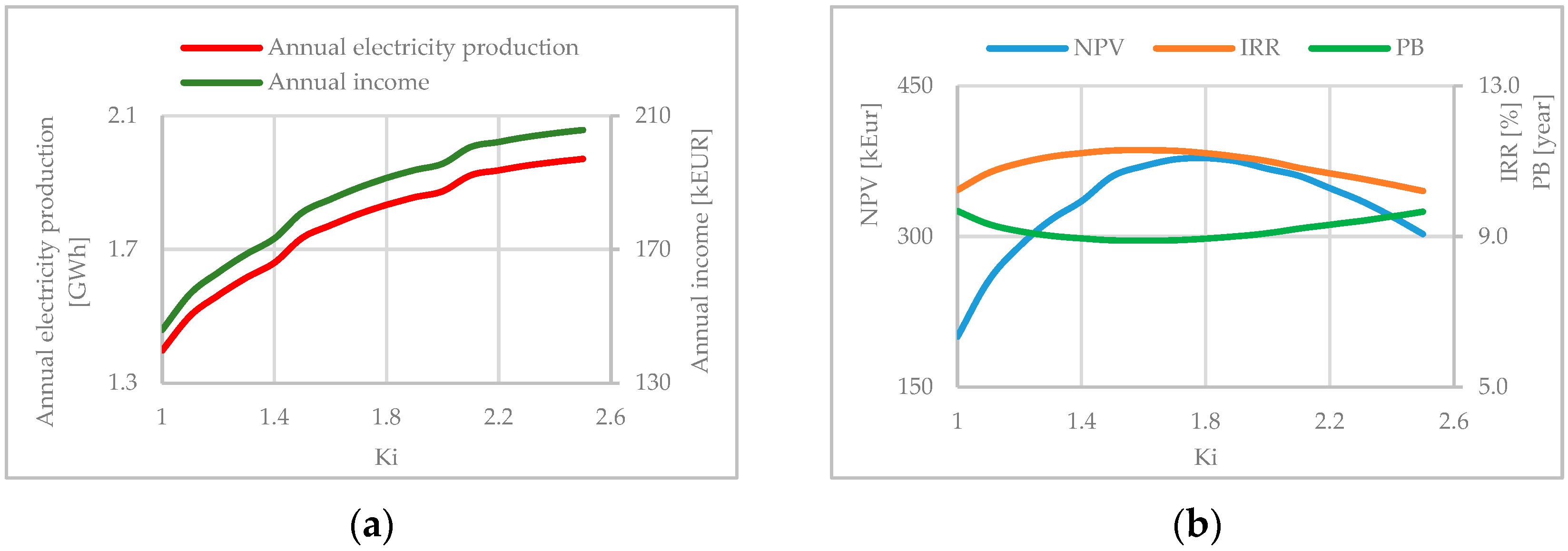
- Annual electricity production and annual income give the highest examined value of Ki = 2.5 as the optimal solution for all considered plants.
- 2.
- The economic parameters NPV and IRR narrowed the initial value of SHPP installed parameter range to Ki = (1.6 ÷ 2.5).
- 3.
- By studying a few typical examples, it can be noticed that NPV and IRR have more influence on the choice of SHPP installed parameter compared to annual electricity production and income.
- 4.
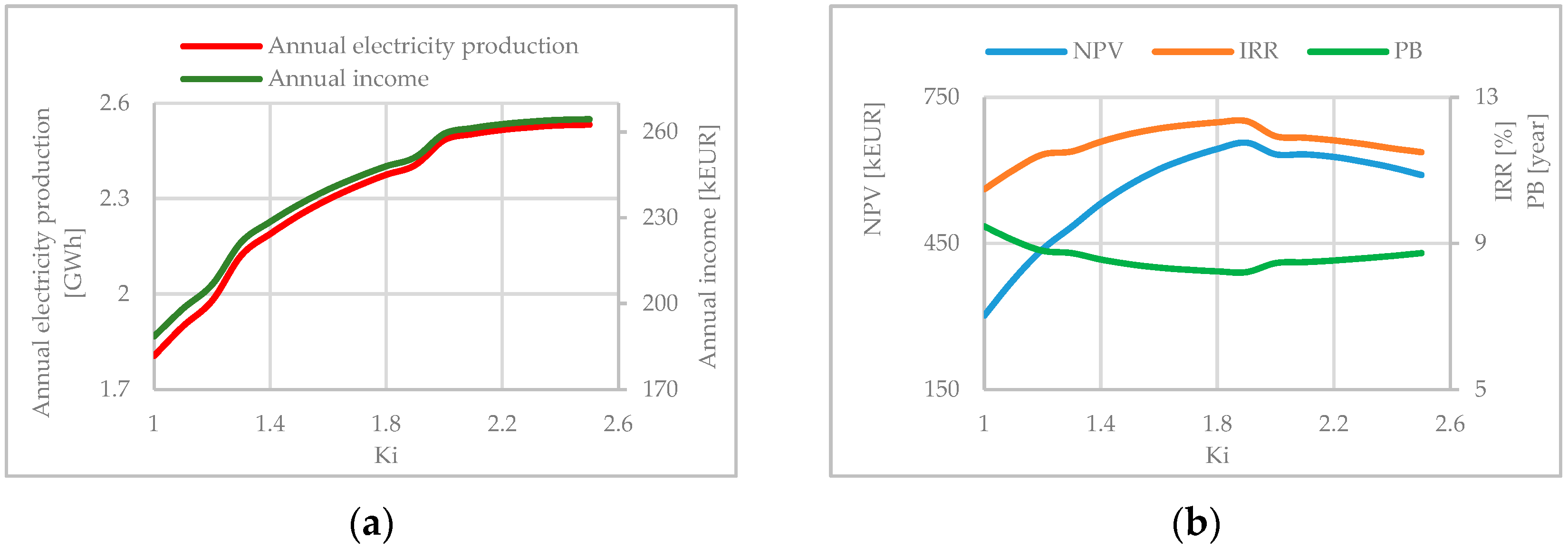
- Annual electricity production for any case gives chosen upper limit of Ki = 2.5 as the optimal solution.
- 5.
- The highest annual income gives the range of SHPP installed parameter range of Ki = (2.0 ÷ 2.5).
- 6.
- NPV and IRR also narrow the range of the Ki, but from the upper limit, and for this group of plants it is Ki = (1.0 ÷ 2.1).
- 7.
- Examination of several typical examples shows that NPV and IRR are more influential parameters for choosing Ki compared to annual electricity production and income.
- 8.
- Due to higher and constant incentive price, the SHPP installed parameter which gives capacity below 1 MW can always be chosen as the optimal solution.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- IHA (International Hydropower Association). Hydropower Status Report: Sector Trends and Insights. 2020. Available online: https://www.hydropower.org/status2020 (accessed on 5 June 2020).
- Besharat, M.; Dadfar, A.; Viseu, M.T.; Brunone, B.; Ramos, H.M. Transient-flow induced compressed air energy storage (TI-CAES) system towards new energy concept. Water 2020, 12, 601. [Google Scholar] [CrossRef]
- Okot, D.K. Review of small hydropower technology. Renew. Sustain. Energy Rev. 2013, 26, 515–520. [Google Scholar] [CrossRef]
- Cirić, R. Review of techno-economic and environmental aspects of building small hydroelectric plants—A case study in Serbia. Renew. Energy 2019, 80, 715–721. [Google Scholar] [CrossRef]
- Hadad, O.B.; Jalal, M.M.; Marino, M.A. Design-operation optimization of run-of-river power plants. Proc. Inst. Civ. Eng.-Water Manag. 2011, 164, 463–475. [Google Scholar] [CrossRef]
- Lopes de Almeida, J.P.P.G.; Nenri Lejeune, A.G.; Sa Marques, J.A.A.; Conceição Cunha, M. OPAH a model for optimal design of multipurpose small hydropower plants. Adv. Eng. Softw. 2006, 37, 236–247. [Google Scholar] [CrossRef]
- Anagnostopoulos, J.S.; Papantonis, D.E. Optimal sizing of a run-of river small hydropower plant. Energy Convers. Manag. 2007, 48, 2663–2670. [Google Scholar] [CrossRef]
- Ardizzon, G.; Cavazzini, G.; Pavesi, G. A new generation of small hydro and pumped hydro power plants: Advances and future challenges. Renew. Sustain. Energy Rev. 2014, 31, 746–761. [Google Scholar] [CrossRef]
- Hosseini, S.; Forouzbakhsh, F.; Rahimpoor, M. Determination of the optimal installation capacity of small hydro-power plants through the use of technical economic and reliability indices. Energy Policy 2005, 33, 1948–1956. [Google Scholar] [CrossRef]
- Najmaii, M.; Movaghar, A. Optimal design of run-of-river power plants. Water Resour. Res. 1992, 28, 991–997. [Google Scholar] [CrossRef]
- Eliasson, J.; Jensson, P.; Ludvigsson, G. Opimal design of hydropower plants. In Hydropower 97, Proceedings of the 3rd International Conference, Trondheim, Norway, 30 June–2 July 1997; Broch, E., Lysne, D.K., Flatabo, N., Helland-Hansen, E., Eds.; Balkema: Rotterdam, The Netherlands, 1997. [Google Scholar]
- Voros, N.G.; Kiranoudis, C.T.; Maroulis, Z.B. Short-cut design of small hydroelectric plants. Renew. Energy 2000, 19, 545–563. [Google Scholar] [CrossRef]
- Karlis, A.D.; Papadopoulos, D.P. A systematic assessment of the technical feasibility and economic viability of small hydroelectric system installations. Renew. Energy 2000, 20, 253–262. [Google Scholar] [CrossRef]
- Paish, O. Small hydro power: Technology and current status. Renew. Sustain. Energy Rev. 2002, 6, 537–556. [Google Scholar] [CrossRef]
- Montanari, R. Criteria for the economic planning of a low power hydroelectric plant. Renew. Energy 2003, 28, 2129–2145. [Google Scholar] [CrossRef]
- Kaldellis, J.K.; Vlachou, D.S.; Korbakis, G. Techno-economic evaluation of small hydro power plants in Greece: A complete sensitivity analysis. Energy Policy 2005, 33, 1969–1985. [Google Scholar] [CrossRef]
- Andaroodi, M. Standardization of Civil Engineering Works of Small High-Head Hydropower Plants and Development of an Optimization Tool; Laboratoire de Constructions Hydrauliques: Lausanne, Switzerland, 2006. [Google Scholar]
- Forouzbakhsha, F.; Hosseinib, S.M.H.; Vakilianc, M. An approach to the investment analysis of small and medium hydro-power plants. Energy Policy 2007, 35, 1013–1024. [Google Scholar] [CrossRef]
- Anagnostopoulos, J.S.; Papantonis, D.E. Pumping station design for a pumped-storage wind-hydro power plant. Energy Convers. Manag. 2007, 48, 3009–3017. [Google Scholar] [CrossRef]
- Bhat, V.I.K.; Prakash, R. Life cycle analysis of run-of river small hydro power plants in India. Open Renew. Energy J. 2008, 1, 11–16. [Google Scholar] [CrossRef][Green Version]
- Bockman, T.; Fleten, S.K.; Juliussen, E.; Langhammer Havard, J.; Revdal, I. Investment timing and optimal capacity choice for small hydropower projects. Eur. J. Oper. Res. 2008, 190, 255–267. [Google Scholar] [CrossRef]
- Alexander, K.V.; Giddens, E.P. Optimum penstocks for low head microhydro schemes. Renew. Energy 2008, 33, 507–519. [Google Scholar] [CrossRef]
- Pena, R.; Medina, A.; Anaya-Lara, O.; McDonald, J. Capacity estimation of a mini hydro plant based on time series forecasting. Renew. Energy 2009, 34, 1204–1209. [Google Scholar] [CrossRef]
- Ogayar, B.; Vidal, P.G. Cost determination of the electro-mechanical equipment of a small hydro-power plant. Renew. Energy 2009, 34, 6–13. [Google Scholar] [CrossRef]
- Aggidis, G.A.; Luchinskaya, E.; Rothschild, R.; Howard, D.C. The costs of small-scale hydro power production: Impact on the development of existing potential. Renew. Energy 2010, 35, 2632–2638. [Google Scholar] [CrossRef]
- Mishra, S.; Singal, S.K.; Khatod, D.K. Approach for cost determination of electro-mechanical equipment in RoR SHP projects. Renew. Energy 2011, 2, 63–67. [Google Scholar] [CrossRef]
- Santolin, A.; Cavazzini, G.; Pavesi, G.; Ardizzon, G.; Rosetti, A. Techno-economical method for the capacity sizing of a small hydropower plant. Water Resour. Manag. 2011, 52, 2533–2541. [Google Scholar] [CrossRef]
- Mishra, S.; Singal, S.K.; Khatod, D.K. A review on electromechanical equipment applicable to small hydropower plants. Int. J. Energy Res. 2012, 36, 553–571. [Google Scholar] [CrossRef]
- Basso, S.; Botter, G. Streamflow variability and optimal capacity of run-of-river hydropower plants. Water Resour. Res. 2012, 48, W10527. [Google Scholar] [CrossRef]
- Barelli, L.; Liucci, L.; Ottaviano, A.; Valigi, D. Mini-hydro: A design approach in case of torrential rivers. Energy 2013, 58, 695–706. [Google Scholar] [CrossRef]
- Carapellucci, R.; Giordano, L.; Pierguidi, F. Techno-economic evaluation of small-hydro power plants: Modelling and characterisation of the Abruzzo region in Italy. Renew. Energy 2015, 75, 395–406. [Google Scholar] [CrossRef]
- Nicotra, A.; Zema, D.A.; D’Agostino, D.; Zimbone, S.M. Equivalent small hydro power: A simple method to evaluate energy production by small turbines in collective irrigation systems. Water 2018, 10, 1390. [Google Scholar] [CrossRef]
- Tiago Filho, G.L.; dos Santos, I.F.S.; Barros, R.M. Cost estimate of small hydroelectric power plants based on the aspect factor. Renew. Sustain. Energy Rev. 2017, 77, 229–238. [Google Scholar] [CrossRef]
- Mamo, G.E.; Marence, M.; Hurtao, J.C.C.; Franca, M.J. Optimization-of-river hydropower plant capacity. Int. Water Power Dam Constr. 2018, XXIX. Available online: https://www.researchgate.net/publication/326942666_Optimization_of_Run-of-River_Hydropower_Plant_Capacity (accessed on 22 July 2021).
- Hounnou, A.H.J.; Dubas, F.; Fifatin, F.X.; Chamagne, D.; Vianou, A. Multi-objective optimization of run-of-river small-hydropover plants considering both investment cost and annual energy generation. Int. J. Energy Power Eng. 2019, 13, 17–21. [Google Scholar]
- Yildiz, V.; Vrugt, J.A. A Toolbox for the optimal design of run-of-river hydropower plants. Environ. Model. Softw. 2019, 111, 134–152. [Google Scholar] [CrossRef]
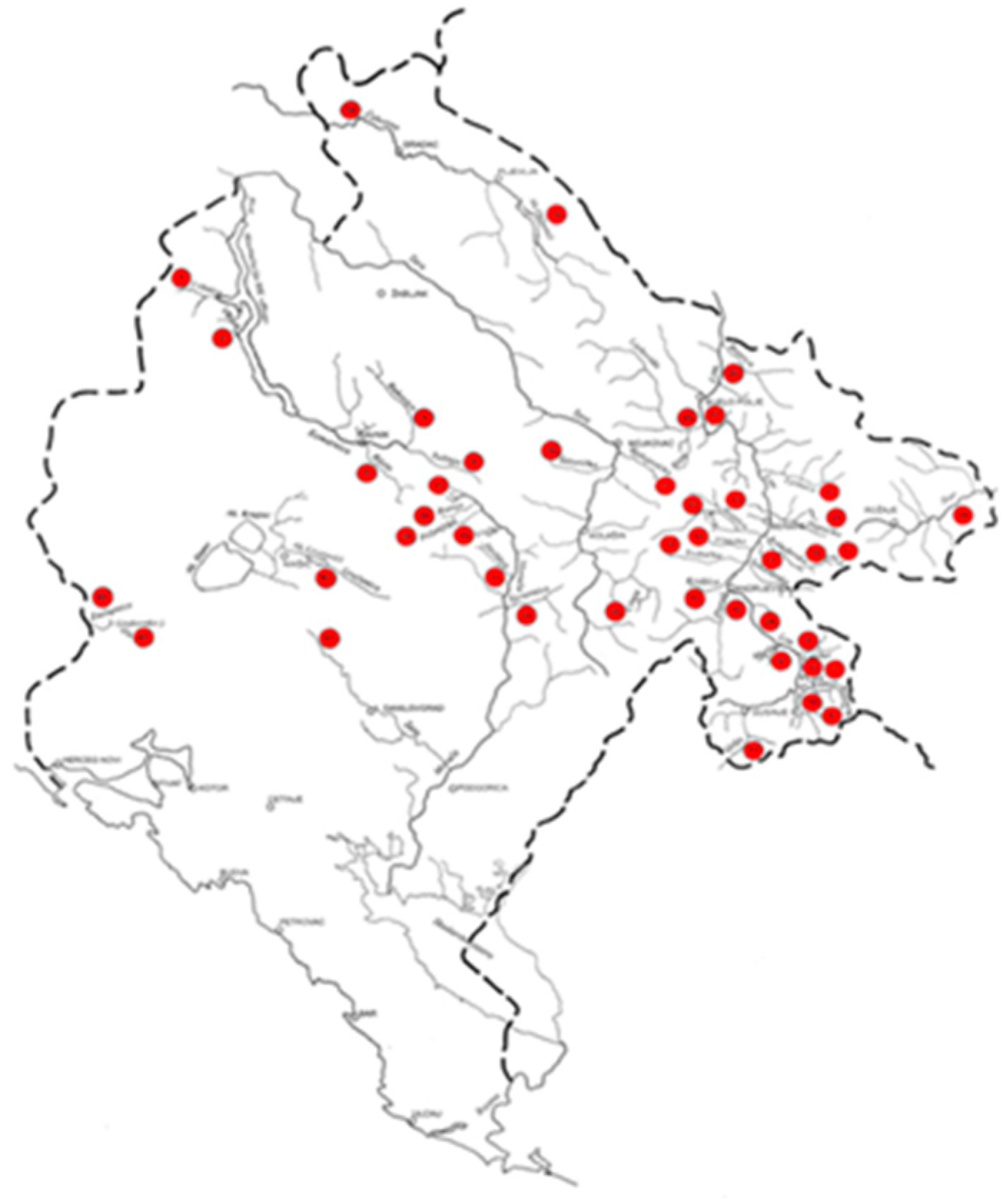
- Sekulić, G. The utilization of the hydropower potential of rivers in Montenegro. In The Rivers of Montenegro; The Handbook of Environmental Chemistry; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Ministry of Economy, Sector for Energetics. Renewable Energy Sources in Montenegro, Podgorica, Montenegro. Available online: http://oie-res.me/ (accessed on 31 May 2021).
- Ministry of Economy. Strategy for Development of Small Hydropower Plants in Montenegro; Ministry of Economy: Podgorica, Montenegro, 2006.
- Vodni Zdroje, A.S.; Blom; Sweco Hydroprojekt CZ, A.S.; Sistem doo; Hydrometeorological Institute of Montenegro. Registry of Small Rivers and Potential Locations of SHPPs at Municipality Level for Central and Northern Montenegro; European Bank for Reconstruction and Development (EBRD): London, UK; Ministry of Economy: Podgorica, Montenegro, 2011. [Google Scholar]
- Vodni Zdroje, A.S.; Sweco Hydroprojekt, C.Z. Enhancement of Registry of Small Rivers for Small Hydropower Projects tential of up to 10 MW, European Bank for Reconstruction and Development (EBRD) and Ministry of Economy, Podgorica, Montenegro. 2019. Available online: https://www.ebrd.com/work-with-us/projects/tcpsd/enhancement-of-the-registry-of-small-rivers-in-central-and-northern-montenegro-to-cover-small-hydropower-projects-shpp-potential-of-up-to-10-mw.html (accessed on 10 June 2021).
- Government of Montenegro. Strategy for Montenegro’s Energetics Development until 2030; Government of Montenegro: Podgorica, Montenegro, 2014.
- Government of Montenegro. Montenegro’s National Action Plan for Renewable Energy Sources until 2020; Government of Montenegro: Podgorica, Montenegro, 2014.
- Hydrometeorological Institute of Montenegro. Hydrology Analysis of Profiles of Small (Mini, Micro) Hydro Power Plants (SHPPs) on Tributaries of Main Watercourses in Montenegro; Institute of Hydrometeorology and Seismology of Montenegro: Podgorica, Montenegro, 2011. [Google Scholar]
- Ministry of Agriculture and Rural Development. Regulation on the Approach of Estimating the Ecologically Acceptable Surface Water Flow; Ministry of Agriculture and Rural Development: Podgorica, Montenegro, 2015.
- Vilotijević, V.; Karadžić, U.; Vušanović, I. Determination of the degree of installed flow in small hydropower plants. In Proceedings of the International Conference Energy and Ecology Industry, Belgrade, Serbia, 10–13 October 2018. [Google Scholar]
- Vilotijević, V.; Karadžić, U.; Božić, I.; Ilić, J. Design discharge determination for SHPPs with capacity below 1 MW. In Proceedings of the 14th International Conference on Accomplishments in Mechanical and Industrial Engineering, Banja Luka, Bosnia and Herzegovina, 24–25 May 2019. [Google Scholar]
- Karadžić, U.; Kovijanić, V.; Vujadinović, R. Possibility for hydro energetic utilization of relatively researched water streams. Water Resour. 2014, 41, 774–781. [Google Scholar] [CrossRef]
- Vilotijević, V. Determination of the Installed Flow in Small Hydropower Plants. Master’s Thesis, University of Montenegro, Faculty of Mechanical Engineering, Podgorica, Montenegro, 2018. (In Serbian). [Google Scholar]
- Kovijanić, V. Functional Application for Calculation of Basic Parameters of Small Hydropower Plants. Master’s Thesis, University of Montenegro, Faculty of Mechanical Engineering, Podgorica, Montenegro, 2019. (In Montenegrin). [Google Scholar]
- Niadas, I.A.; Mentzelopoulos, P. Probabilistic flow duration curves for small hydro plant design and performance evaluation. Water Resour. Manag. 2008, 22, 509–523. [Google Scholar] [CrossRef]
- Government of Montenegro. Regulation on the Tariff System for Determining the Feed Cost of Electricity from Renewable Energy Sources and High-Efficiency Cogeneration; Government of Montenegro: Podgorica, Montenegro, 2015.
- Yildiza, V. Numerical Simulation Model of Run of River Hydropower Plants: Concepts, Numerical Modeling, Turbine System and Selection, and Design Optimization. Master’s Thesis, University of California, Irvine, CA, USA, 2015. [Google Scholar]
| Hydro Power Plant Capacity (MW) | Incentive Price (cEUR/kWh) |
|---|---|
| PSHPP < 1 MW | 10.44 |
| 1 ≤ PSHPP 3 MW | 10.44 − 0.7·PSHPP |
| 3 ≤ PSHPP 5 MW | 8.87 − 0.24·PSHPP |
| 5 ≤ PSHPP 8 MW | 8.35 − 0.18·PSHPP |
| 8 ≤ PSHPP 10 MW | 6.8 |
| River Group | Capacity Range | Remark |
|---|---|---|
| I | PSHPP < 1 MW | fits with incentive price range |
| II | 0.4 MW ≤ PSHPP ≤ 2.4 MW |
| No | SHPP Name | Annual Electricity Production (GWh) | Annual Income (kEUR) | Ki for Max Electricity Production | Ki for Max Income | Current Ki for (*) |
|---|---|---|---|---|---|---|
| 1 | Jasičje | 2.53 | 264.4 | 2.5 | 2.5 | |
| 2 | Štitarička 1 | 2.65 | 276.6 | 2.5 | 2.5 | |
| 3 | Bijela 1 | 2.12 | 221.7 | 2.5 | 2.5 | |
| 4 | Mišnića * | 0.77 | 81.3 | 2.5 | 2.5 | 1.0 |
| 5 | Slatina | 0.90 | 94.2 | 2.5 | 2.5 | |
| 6 | Šeremet * | 2.25 | 235.5 | 2.5 | 2.5 | 2.3 |
| 7 | Bukovičko | 1.97 | 205.8 | 2.5 | 2.5 | |
| 8 | Rupočajski | 2.34 | 244.8 | 2.5 | 2.5 | |
| 9 | Lazanska | 2.09 | 218.7 | 2.5 | 2.5 | |
| 10 | Kozička | 2.42 | 253.1 | 2.5 | 2.5 | |
| 11 | Bukeljka | 1.98 | 207.1 | 2.5 | 2.5 | |
| 12 | Rmuš * | 1.59 | 166.8 | 2.5 | 2.5 | 1.8 |
| 13 | Spaljevići * | 2.35 | 246.2 | 2.5 | 2.5 | 1.7 |
| 14 | Umski * | 3.01 | 314.4 | 2.5 | 2.5 | 1.1 |
| 15 | Javorski | 2.74 | 286.7 | 2.5 | 2.5 | |
| 16 | Hridska * | 2.18 | 228.0 | 2.5 | 2.5 | 1.5 |
| No | SHPP Name | IRR (%) | NPV (kEUR) | PB for Max IRR (year) | Ki for Max IRR (%) | Ki for Max NPV |
|---|---|---|---|---|---|---|
| 1 | Jasičje | 12.35 | 656.9 | 8.2 | 1.9 | 1.9 |
| 2 | Štitarička 1 | 10.18 | 399.4 | 9.7 | 2.0 | 2.1 |
| 3 | Bijela 1 | 8.78 | 118.2 | 11.6 | 2.0 | 2.0 |
| 4 | Mišnića | 5.37 | 163.9 | 16.0 | 1.9 | 1.8 |
| 5 | Slatina | 7.09 | 58.8 | 13.6 | 1.9 | 1.8 |
| 6 | Šeremet | 14.11 | 745.3 | 7.3 | 1.8 | 2.1 |
| 7 | Bukovičko | 11.30 | 378.2 | 8.9 | 1.6 | 1.8 |
| 8 | Rupočajski | 15.42 | 876.4 | 6.7 | 1.9 | 2.5 |
| 9 | Lazanska | 7.67 | 58.2 | 12.8 | 2.5 | 2.5 |
| 10 | Kozička | 6.07 | 377.1 | 14.8 | 1.8 | 1.3 |
| 11 | Bukeljka | 6.51 | 247.4 | 14.2 | 2.5 | 1.6 |
| 12 | Rmuš | 6.38 | 225.1 | 14.4 | 2.5 | 2.5 |
| 13 | Spaljevići | 10.19 | 369.2 | 9.7 | 2.5 | 2.5 |
| 14 | Umski | 18.94 | 1466.4 | 5.4 | 1.7 | 2.3 |
| 15 | Javorski | 14.05 | 958.1 | 7.3 | 2.5 | 2.5 |
| 16 | Hridska | 11.63 | 507.9 | 8.7 | 2.5 | 2.5 |
| SHPP Name | Ki for Max Electricity Production and Max Income | Ki for Max IRR (%) | Ki for Max NPV | PB for Max IRR (year) |
|---|---|---|---|---|
| Hridska | 2.5 | 2.5 | 2.5 | 8.7 |
| Jasičje | 2.5 | 1.9 | 1.9 | 8.2 |
| Bukovičko | 2.5 | 1.6 | 1.8 | 8.9 |
| No | SHHP Name | Annual Electricity Production (GWh) | Annual Income (kEUR) | Ki for Max Electricity Production | Ki for Max Income | Current Ki for (*) |
|---|---|---|---|---|---|---|
| 1 | Kaludarska | 4.64 | 435.2 | 2.5 | 1.5 | |
| 2 | Stožernica | 4.81 | 447.7 | 2.5 | 2.3 | |
| 3 | Vrelo * | 3.89 | 402.7 | 2.5 | 1.9 | 1.3 |
| 4 | Skrbuša | 4.46 | 417.6 | 2.5 | 2.5 | |
| 5 | Radmanska | 3.76 | 359.6 | 2.5 | 1.7 | |
| 6 | Bistrica Lipovska * | 5.44 | 496.7 | 2.5 | 2.5 | 1.3 |
| 7 | Pecka * | 3.32 | 331.7 | 2.5 | 2.1 | 2.0 |
| 8 | Trnovačka | 5.97 | 534.2 | 2.5 | 2.4 | |
| 9 | Hotska | 4.50 | 412.7 | 2.5 | 2.5 | |
| 10 | Jasenička | 4.72 | 429.6 | 2.5 | 2.4 | |
| 11 | Bukovica 2 | 6.35 | 559.9 | 2.5 | 2.5 | |
| 12 | Požnja | 4.95 | 454.2 | 2.5 | 2.5 | |
| 13 | Ljevak * | 4.65 | 433.0 | 2.5 | 2.5 | 1.0 |
| 14 | Koložun | 3.90 | 357.7 | 2.5 | 2.5 | |
| 15 | Rzački | 3.21 | 322.9 | 2.5 | 2.0 | |
| 16 | Meteška | 2.59 | 255.8 | 2.5 | 2.0 | |
| 17 | Bjelojevićka | 3.23 | 321.3 | 2.5 | 2.0 | |
| 18 | Crnja | 2.65 | 258.4 | 2.5 | 2.1 | |
| 19 | Bukovica 1 | 2.78 | 282.7 | 2.5 | 2.3 | |
| 20 | Vinicka | 2.73 | 276.7 | 2.5 | 2.0 | |
| 21 | Paljevinska * | 2.28 | 230.5 | 2.5 | 2.3 | 1.4 |
| 22 | Štitska * | 2.78 | 264.9 | 2.5 | 2.5 | 2.0 |
| No | SHHP Name | IRR (%) | NPV (kEUR) | PB for Max IRR (year) | Ki for Max IRR | Ki for Max NPV |
|---|---|---|---|---|---|---|
| 1 | Kaludarska | 14.37 | 1580.9 | 7.2 | 1.5 | 1.5 |
| 2 | Stožernica | 18.07 | 2055.5 | 5.7 | 1.2 | 1.4 |
| 3 | Vrelo | 20.93 | 2069.6 | 5.0 | 1.6 | 1.9 |
| 4 | Skrbuša | 20.80 | 2185.6 | 5.0 | 1.5 | 1.6 |
| 5 | Radmanska | 15.80 | 1421.5 | 6.5 | 1.2 | 1.7 |
| 6 | Bistrica Lipovska | 18.65 | 2237.1 | 5.6 | 1.3 | 1.3 |
| 7 | Pecka | 11.99 | 808.8 | 8.4 | 1.7 | 2.1 |
| 8 | Trnovačka | 24.45 | 2892.4 | 4.3 | 1.1 | 1.7 |
| 9 | Hotska | 13.85 | 1342.6 | 7.4 | 1.3 | 1.3 |
| 10 | Jasenička | 15.69 | 16555 | 6.6 | 1.2 | 1.2 |
| 11 | Bukovica 2 | 11.01 | 961.2 | 9.0 | 1.0 | 1.0 |
| 12 | Požnja | 19.91 | 2161.6 | 5.2 | 1.2 | 1.3 |
| 13 | Ljevak | 19.65 | 2097.6 | 5.3 | 1.5 | 1.5 |
| 14 | Koložun | 13.90 | 1041.2 | 7.4 | 1.3 | 1.3 |
| 15 | Rzački | 17.80 | 1436.4 | 5.8 | 1.7 | 2.0 |
| 16 | Meteška | 9.85 | 316.9 | 9.9 | 2.0 | 2.0 |
| 17 | Bjelojevićka | 16.08 | 1292.3 | 6.4 | 1.7 | 2.0 |
| 18 | Crnja | 8.27 | 55.5 | 12.1 | 2.1 | 2.1 |
| 19 | Bukovica 1 | 7.07 | 192.2 | 13.5 | 1.5 | 1.5 |
| 20 | Vinicka | 13.05 | 792.3 | 7.8 | 1.5 | 1.8 |
| 21 | Paljevinska | 13.05 | 125.7 | 11.6 | 1.5 | 1.5 |
| 22 | Štitska | 12.31 | 679.1 | 8.2 | 1.9 | 1.9 |
| SHPP Name | Ki for Max Electricity Production | Ki for Max Income | Ki for Max IRR (%) | Ki for Max NPV | PB for Max IRR (year) |
|---|---|---|---|---|---|
| Kaludarska | 2.5 | 1.5 | 1.5 | 1.5 | 7.2 |
| Bistrica Lipovska | 2.5 | 2.5 | 1.3 | 1.3 | 5.6 |
| Vrelo | 2.5 | 1.9 | 1.6 | 1.9 | 5.0 |
| Stožernica | 2.5 | 2.3 | 1.2 | 1.4 | 5.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vilotijević, V.; Karadžić, U.; Vujadinović, R.; Kovijanić, V.; Božić, I. An Improved Techno-Economic Approach to Determination of More Precise Installed Parameter for Small Hydropower Plants. Water 2021, 13, 2419. https://doi.org/10.3390/w13172419
Vilotijević V, Karadžić U, Vujadinović R, Kovijanić V, Božić I. An Improved Techno-Economic Approach to Determination of More Precise Installed Parameter for Small Hydropower Plants. Water. 2021; 13(17):2419. https://doi.org/10.3390/w13172419
Chicago/Turabian StyleVilotijević, Vidosava, Uroš Karadžić, Radoje Vujadinović, Vuko Kovijanić, and Ivan Božić. 2021. "An Improved Techno-Economic Approach to Determination of More Precise Installed Parameter for Small Hydropower Plants" Water 13, no. 17: 2419. https://doi.org/10.3390/w13172419
APA StyleVilotijević, V., Karadžić, U., Vujadinović, R., Kovijanić, V., & Božić, I. (2021). An Improved Techno-Economic Approach to Determination of More Precise Installed Parameter for Small Hydropower Plants. Water, 13(17), 2419. https://doi.org/10.3390/w13172419









