1. Introduction
Dams are an essential element in our way of living, since they provide fundamental services to our society, including drinking water, irrigation, navigation, flood protection, and recreation. In addition, they are a decisive element in hydroelectric generation schemes. According to the International Commission on Large Dams (ICOLD), there are around 60,000 large dams in operation worldwide, 6100 of which are in Europe [
1]. Many of them were built decades ago and are close to, or even exceeded, their service life. This results in an increasing relevance of predictive maintenance and safety assessment of dams, as was highlighted in a recent report published by the United Nations University [
2]. Similar figures were also reported in the USA [
3].
Dam failures are rare, but safe dam operation requires significant resources for monitoring and repair. In this context, the early detection of anomalies allows increasing the effectiveness of investments in maintenance and, therefore, reduces the cost of operation.
The conventional approach to anomaly detection involves the use of some predictive model to estimate the dam response under a given combination of loads. Models based on the finite element method (FEM) can be used for such a purpose, once properly calibrated. Nonetheless, there is a tendency towards the use of machine-learning (ML) models, which are solely based on monitoring data [
4,
5].
In both cases, a set of monitoring devices is typically selected, and the measurements are compared to the predictions of the model. This is done separately for each response variable, then results are interpreted together with the knowledge about the dam properties, past behaviour, and other relevant information. In case some deviation is detected between the expected response and the observed behaviour, engineering judgement is employed to make decisions regarding dam safety. In particular, the comparison shall be interpreted to identify the probable origin of the observed deviations, which requires an additional effort.
In this work, ML is applied to jointly analyse the records of a set of relevant monitoring devices and to associate them either to normal operation or to some anomaly scenario. This approach has two potential benefits:
Increased efficiency of the overall process: it directly provides an interpretation of the dam response, without the need for analysing each device separately.
Reduction of the occurrence of false alerts: deviations of measurements from predictions due to measurement errors in isolated devices are not compatible with serious anomaly scenarios and therefore would be considered as normal behaviour with this approach.
In spite of the increasing interest of the community in applying ML methods in dam safety, the joint analysis has been much less explored. Mata et al. [
6] applied linear discriminant analysis (LDA) to classify a group of observations into two classes: normal operation and potential failure scenario. They used DEM/FEM to generate the data corresponding to both situations. In a previous work, we used random forests (RF) as classifiers to associate a set of records to six potential scenarios (normal and five different potential anomalies) [
7]. Although the results showed the potential of such an approach, a relevant drawback was also highlighted: anomaly scenarios need to be simulated with accuracy to generate the training set. This raises doubts on the capability for anomaly detection when the actual behaviour is not considered among the simulated scenarios. This relevant issue, specially from a practical viewpoint, is addressed in this work: a methodology is proposed for detecting unforeseen anomalies, i.e., scenarios which were not used for training the ML classifier. A similar approach was applied by Fischer et al. for detecting internal erosion in earth dams and levees, based on experimental laboratory data [
8,
9]. We further explore the possibilities of such approach for anomaly detection in arch dams, with the addition of the following elements:
A real arch dam in operation is considered as the case study, and the dataset used is based on the actual recorded monitoring data.
Realistic anomaly scenarios are analysed, correspondent to crack opening in typical locations in arch dams.
Time is considered when analysing the predictions of the model, so that part of the false negatives are eliminated and the final method is more robust.
The predictions of the model are further analysed, which provides additional information on the reliability of anomaly detection.
The rest of the paper is organised as follows: the methods used are introduced in
Section 2, including the FEM model used for generating the database, the ML algorithms and their calibration; results are presented and described in
Section 3: model calibration, performance analysis, exploration of errors and evaluation on the validation set.
Section 4 includes the conclusions and ideas for future research.
2. Methods
The overall workflow includes the following steps:
A thermo-mechanical FEM model of the dam was created and its results compared to available monitoring data.
Transient analyses were run on the FEM model for the scenarios considered: normal operation and different crack openings.
The time series of results of the FEM model in terms of radial and tangential displacements were exported, together with a label correspondent to the scenario from which they were obtained.
ML classifiers were fitted to a fraction of the data available and they were later evaluated in terms of prediction accuracy on an independent dataset.
In view of the results for the test set, a new criterion for anomaly detection was defined, based on the model predictions, which was applied to the validation set.
The details of each step are described in the next subsections.
2.1. Case Study
The proposed methodology was applied to a Spanish double curvature arch dam with a height of 81 m above foundation and 20 cantilevers, with the material properties specified in
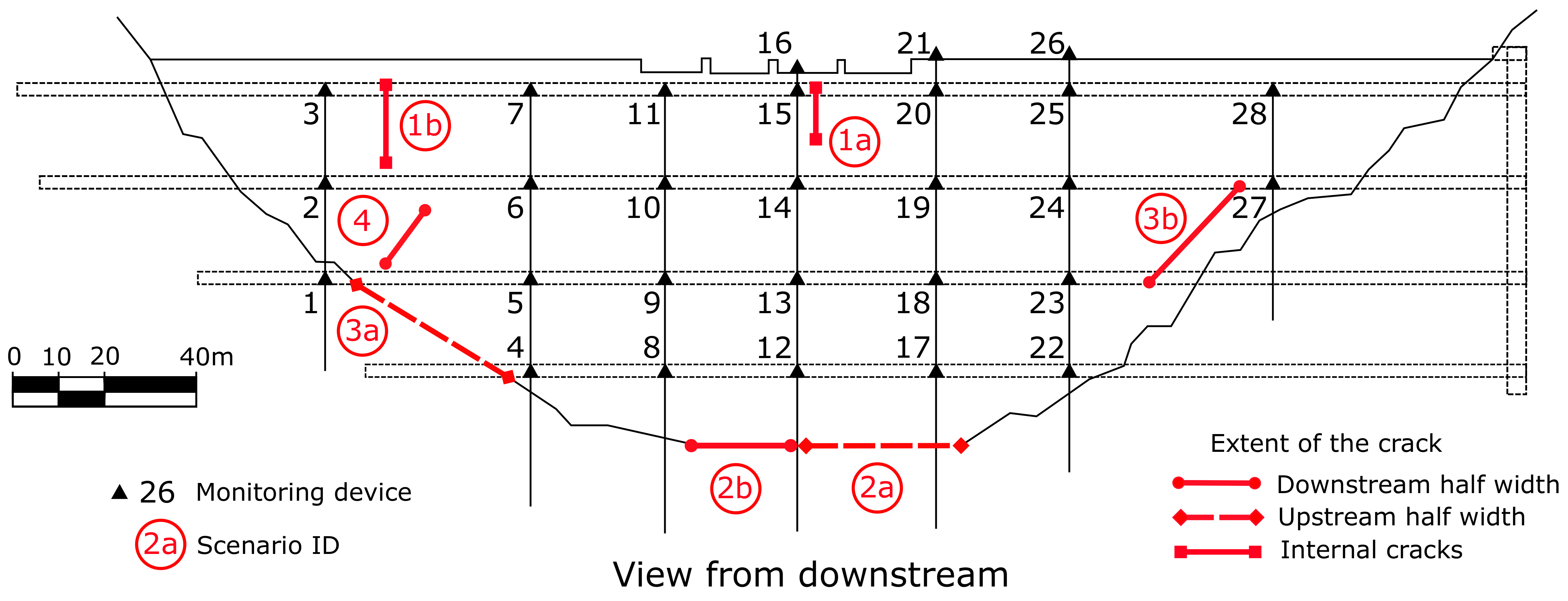
Table 1. Five years of monitoring data were considered for this work (corresponding to the period from March 1999 to March 2004), which included the reservoir level and the air temperature, as well as the displacements at 28 monitoring stations corresponding to seven pendulums located as shown in
Figure 1.
2.2. FEM Model
For the construction of the 3D model, the designed mesh was formed by linear tetrahedra of variable size (
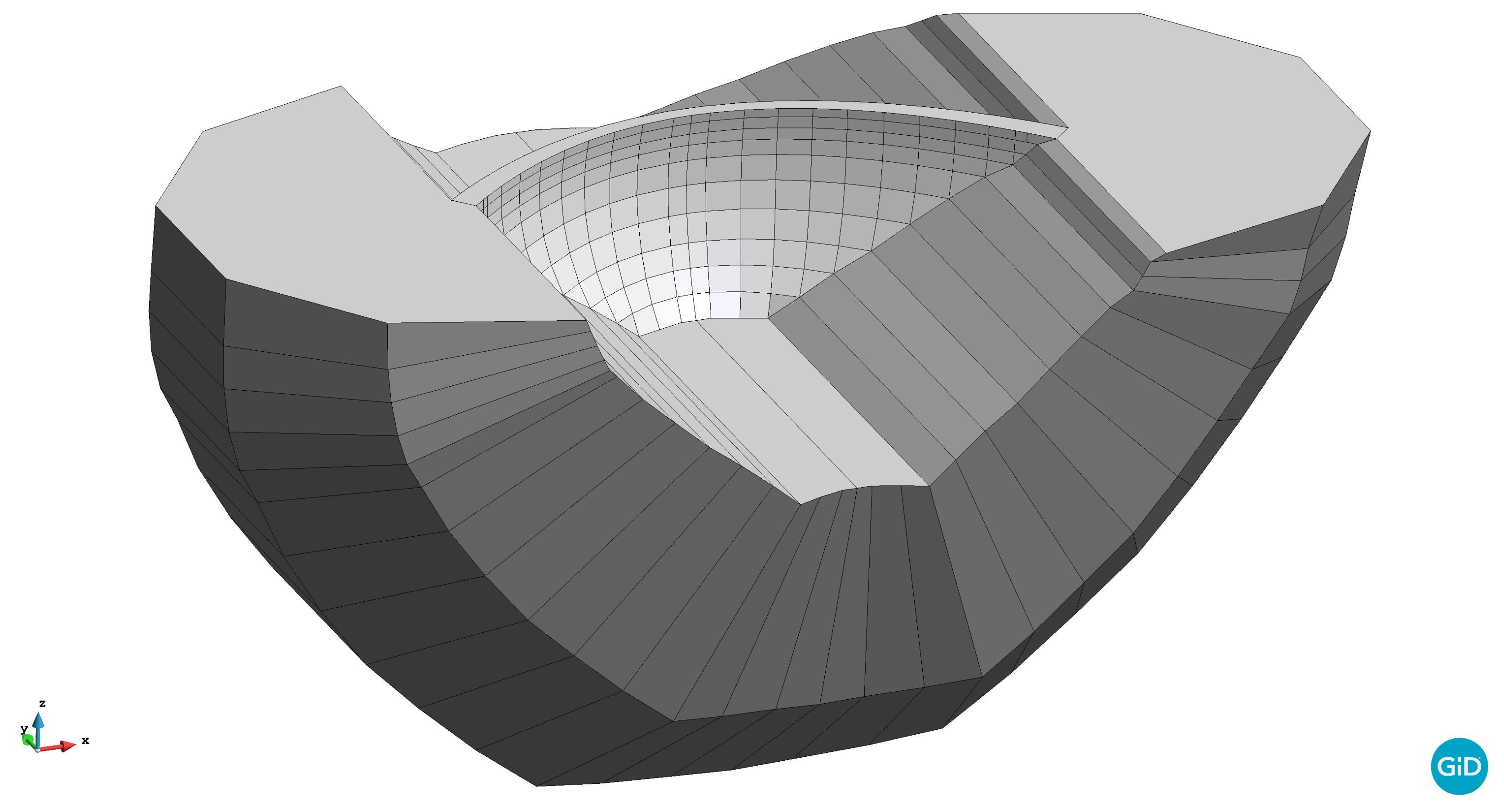
Figure 2). A portion of the foundation was included in the 3D model with the conventional dimensions for structural analyses: foundation domain of two heights of the dam in depth, upstream and downstream directions and more than half the length of the dam on the left and right sides (
Figure 3). The geometry was generated using a tool developed by the authors [
10], which assists in creating the 3D model of arch dams from the geometrical definition of the arches and cantilevers. The mesh size in the dam body was chosen to ensure at least three elements along the radial direction, while the size of the elements of the foundation was increased gradually up to 25 m. This resulted in a mesh of 33,000 nodes forming 173,000 tetrahedra, generated with the GiD software [
11].
The final goal of this study is to identify behaviour patterns associated to certain structural anomalies in arch dams and, in particular, those due to crack openings. After a literature review, four categories of cracks frequently observed in arch dams were identified (
Table 2). Two anomaly scenarios were defined for each category (
Figure 1).
The cracks are considered in the FEM model by duplicating the faces of the corresponding elements and eliminating the tensile strength. This is basically equivalent to using no-tension interface elements. The location and dimensions of the cracks introduced and the associated scenarios are shown in
Figure 1.
Since the temperature field in the dam body influences the deformations of the dam and depends on the initial temperature considered, we performed a preliminary analysis to obtain a realistic thermal field to be used as the reference temperature in the body of the dam. This is a relevant issue, since thermal displacements are computed on the basis of the difference between these values and the thermal field at each time step of the simulation [
16]. For this purpose, we performed a 12-year transitory analysis with a fixed value of the initial temperature (8 ℃) and a time step of 12 h. The resulting thermal field at the end of this preliminary calculation was taken as the initial temperature for all the scenarios considered. A similar approach was used by Santillan et al. [
17] and by the authors in previous studies [
18].
A transient analysis was performed for a 5-year period on the Scenario 0 (normal operation, no crack opening). Since actual records for air temperature and reservoir level were applied, the results are realistic and can be considered representative of the actual behaviour of the dam. A one-way coupling between the thermal and the mechanical problem was applied: the thermal field at the end of the preliminary transient analysis was taken as reference temperature, i.e., deviations from such a value results in thermal deformations; the hydrostatic load is applied and the stress and deformation are computed assuming elastic behaviour; the deformation field is computed as the sum of the thermal and the mechanical deformations. The numerical implementation was developed by the authors and described in detail in [
16].
The results of this model in terms of radial and tangential displacements at the location of the monitoring stations (see
Figure 1) were extracted and compared to the actual measurements recorded.
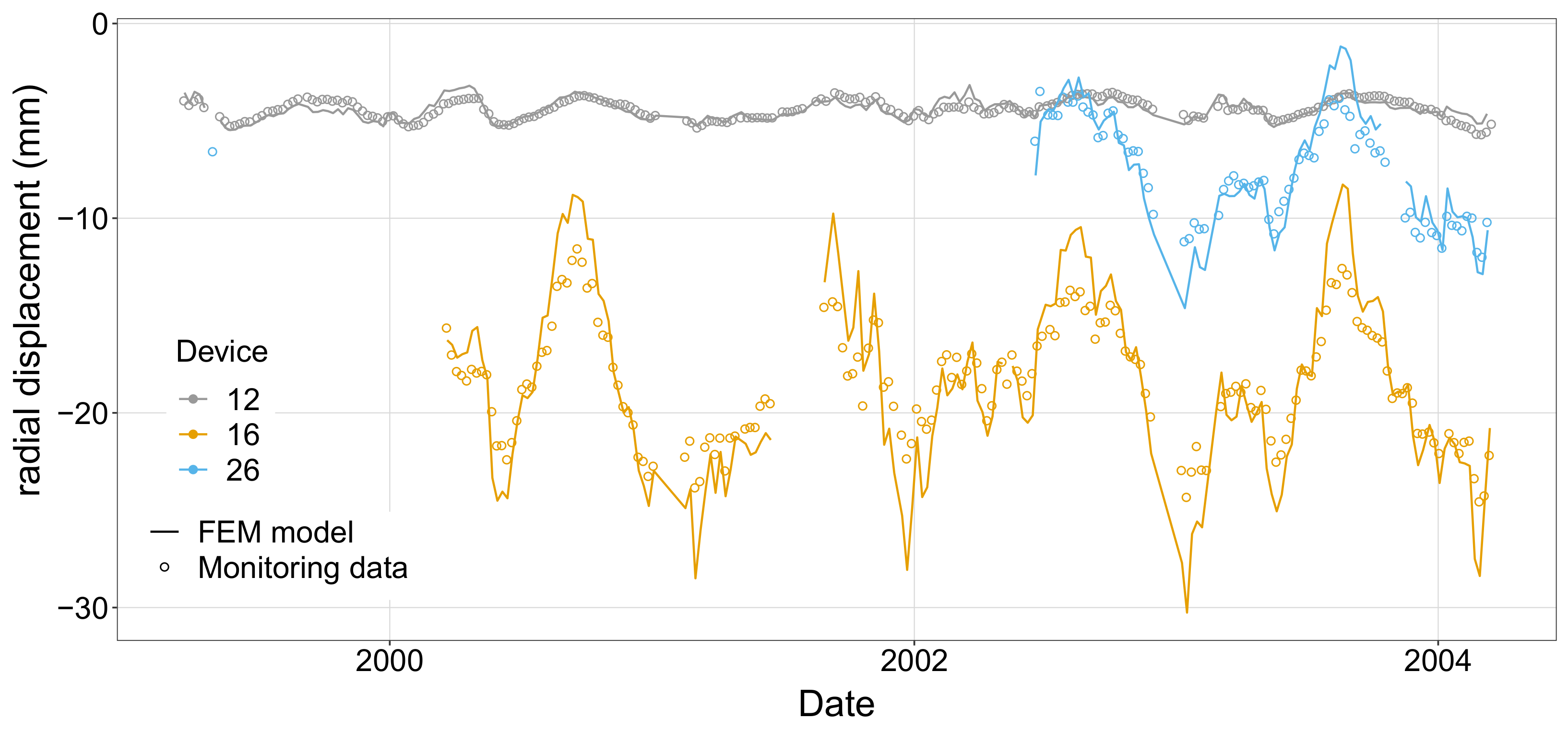
Figure 4 shows this comparison for three of the measuring stations. Results show that the simulated behaviour is representative of the actual evolution of dam displacements as a function of the variation of the thermal and hydrostatic loads.
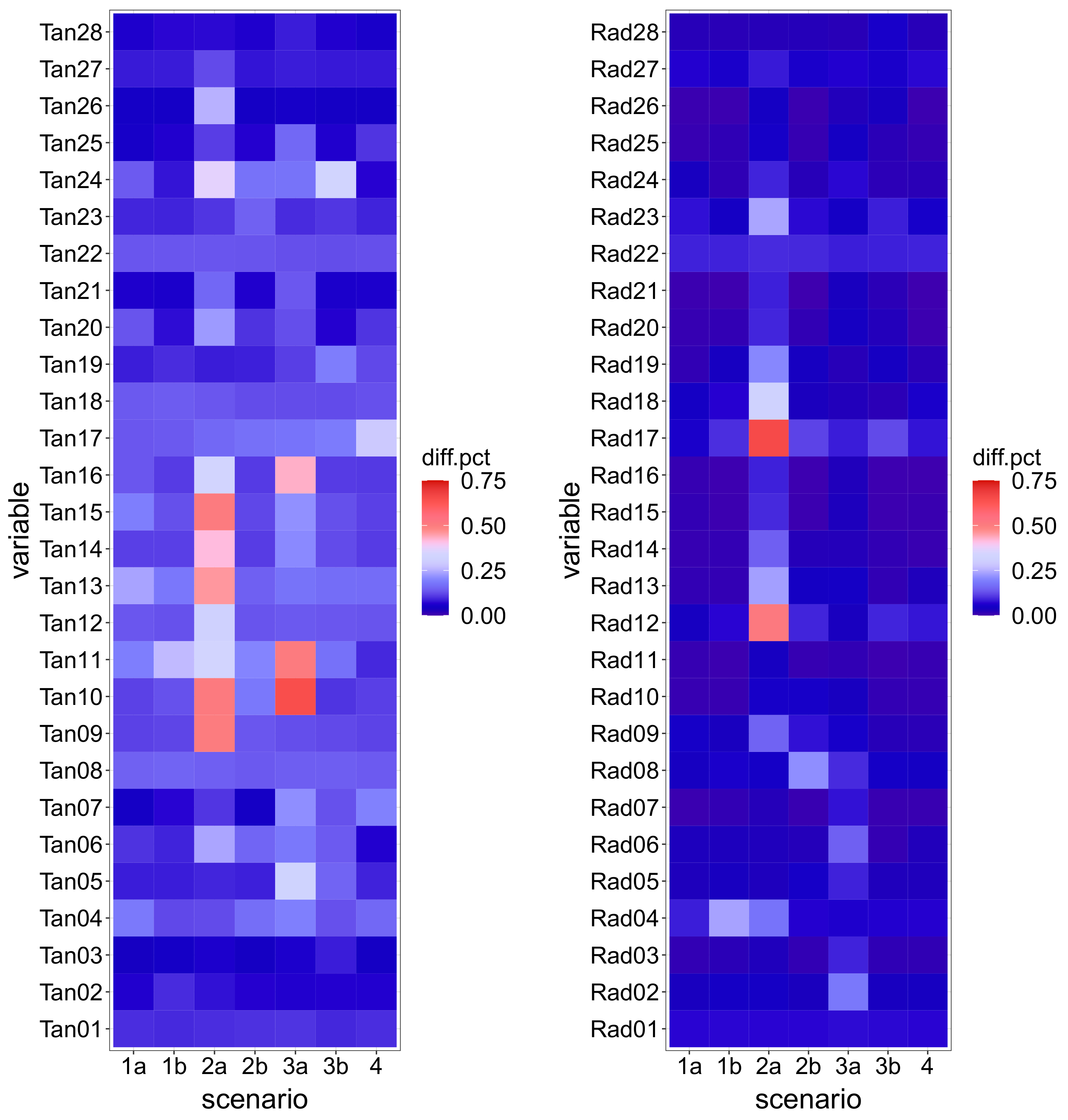
Afterwards, seven FEM simulations were run for the same 5-year period on the modified models, correspondent to the anomaly scenarios defined. The tile plots in
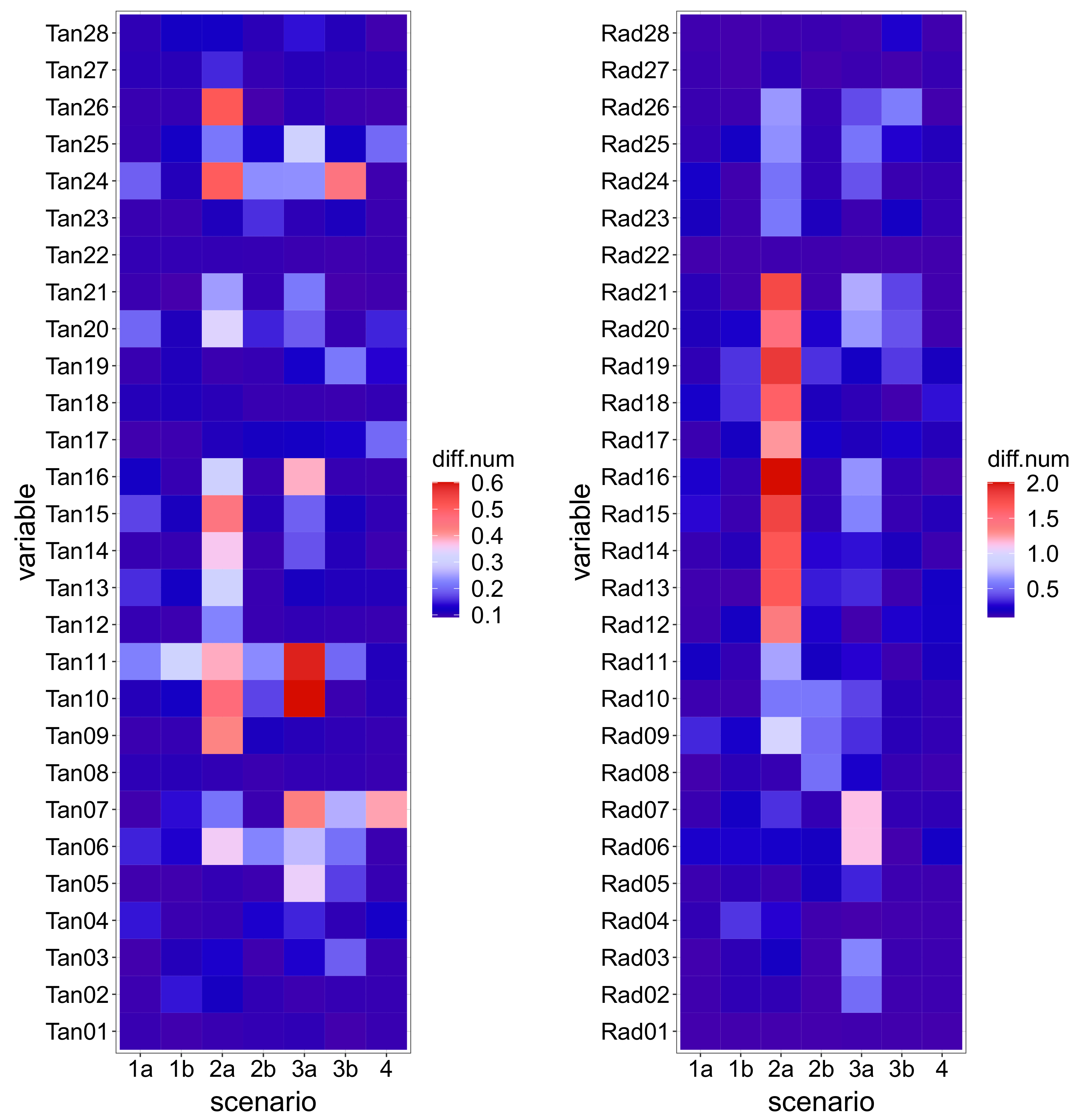
Figure 5 show the magnitude of the difference to Scenario 0: each tile corresponds to a monitoring variable and a particular scenario. The colour of the tile is a function of the median difference on the 5-year period between the records of the corresponding device for the scenario considered and those for Scenario 0, normalized with respect to the range of variation of the variable. Although this allows for comparison among devices and scenarios, the denormalized value (
Figure 6) is also relevant, since deviations in variables with low fluctuation may be of the same order of magnitude of the measuring error, thus hard to distinguish.
The plots show that Scenario 2a features the greatest deviation from normal operation. This is due to the nature of the anomaly: a crack opening in the dam heel. The combined effect of hydrostatic load and low temperatures generates tensile stresses in that area, which result in high displacements when the crack opens. The deviation from the reference case is greater for the lower station of the closest pendulum (Rad17), and decays progressively along such vertical (Rad18 to Rad21). The effect is similar, though lower, for the adjacent pendulum line (Rad12 to Rad16).
By contrast, the crack simulated in Scenario 2b, located in the downstream toe, has a minor effect on the records because such an area is compressed most of the time, thus the crack is closed and the behaviour is similar to the reference case.
The deviations in other scenarios are in general lower, with more impact on the tangential displacements in relative terms.
2.3. Data Preparation
As a result of the numerical calculations, a database is created including 8 scenarios: normal operation (Scenario 0) and 7 different anomalous behaviours (Scenarios 1a, 1b, 2a, 2b, 3a, 3b and 4). For each scenario, the database includes one record per day, corresponding to the actual recorded reservoir level and air temperature for the period 18 March 1999–15 March 2004, i.e., 1825 records per scenario.
This database reasonably approximates the dam response to the variation of thermal and mechanical loads in a realistic situation. However, the numerical model excludes the measuring errors which exist in actual devices. These errors were considered by adding a noise with normal distribution to the simulated displacements.
Such data are divided into three subsets as a function of the date: the training set includes data for the period 18 March 1999–17 March 2002, the test set ranges from 18 March 2002 to 17 March 2003 and the validation set goes from 18 March 2003 to 15 March 2004.
2.4. Classification Tasks
2.4.1. Multi-Class (MC) Classification
The conventional problem of supervised classification requires a training set with a set of inputs (also called features or predictors) and the corresponding labels. Those data are supplied to the algorithm, which learns the structure of the data and defines rules for assigning some classes to a set of inputs. In our case, the fitted model will be supplied with a set of monitoring records for a given load combination and will generate a prediction in terms of the scenario to which it corresponds. More precisely, the model differentiates between normal operation (Scenario 0) and each of the anomalies (other 7 scenarios).
In practice, ML classification models compute a probability of belonging to each of the classes defined during training for each set of input values. By default, the predicted class is that with the highest probability. However, the raw probabilities can be explored to draw more information regarding model predictions.
The prediction of this model corresponds to one of the 8 classes used for training. This approach has the advantage of distinguishing among different anomalies, but requires availability of samples corresponding to all possible situations, which need to be generated with numerical models. It is not clear if such a model would be useful in case some anomaly not included in the training set occurs.
2.4.2. Two-Class (TC) Classification
To overcome such limitation, an alternative approach is proposed. Part of the anomalies considered were eliminated from the training set. As a result, models were fitted on a modified training set, which only includes Scenarios 0, 1a, 2a, 3a and 4. A new label was created with two classes: 0 for normal operation (former Scenario 0) and 1 for all other scenarios. To avoid the problem of imbalanced data [
19], a random sample of records for anomalous scenarios was taken, so that this modified training set includes 1825 samples for class 0 and the same amount of records for class 1 (equally distributed among the original scenarios 1a, 2a, 3a and 4). The test set included both Scenario 0 and those anomalies not used for training (Scenarios 1b, 2b and 3b). Again, the class label was modified to include only two classes (0 and 1), as in the training set. This classification task is more challenging, since part of the test set corresponds to situations not used for training (Scenarios 1b, 2b and 3b). However, it is more realistic: anomalies in the test set may represent real scenarios, i.e., actual behaviour patterns not considered during model training.
2.4.3. One-Class (OC) Classification
The third alternative explored makes use of the ‘One-Class Classification’ approach [
20,
21]. This technique was developed for problems in which the information available for training only corresponds to the normal operation. It is therefore applied for novelty detection. The training set in this case is limited to the samples corresponding to Scenario 0 within the original training set. The model fitted with this procedure is only capable of predicting two classes: that used for training and some other (it is thus useless to differentiate among different types of anomalies). This method was developed for cases in which information on the response of the system for abnormal operation is not available or is costly or impossible to obtain. That is the case in dam safety, and that was the limitation of previous approaches: in the best setting, some anomalies could be simulated, but they do not necessarily correspond to the behaviour patterns that may occur.
2.5. Algorithms
Machine learning (ML) problems can be classified into two main categories in accordance to the nature of the target variable: while in regression problems the goal is predicting the value of some numerical variable, in classification tasks the objective is assigning some label to a set of input values.
The vast majority of applications of statistical and ML methods to the analysis of dam monitoring data make use of the regression approach: some model is fitted to the available monitoring data with the aim of predicting some dam response such as the radial displacement at a given location within the dam body. Decisions regarding dam safety are made on the basis of the comparison between the model predictions and the observations.
By contrast, this work is based on classification: we define a set of response patterns, or classes, associated to the scenarios considered. They are provided to the model together with the values of the monitoring variables. The objective of model fitting is identifying patterns in the input data useful to distinguish between classes. The output of the model is thus a categorical variable (label).
Many ML algorithms can be applied both to regression and classification tasks, though their capabilities and performance often vary. In this work, two of the most popular ML algorithms available for classification were considered as described in the next sections: random forests (RF) and support vector machines (SVM).
2.5.1. Random Forests (RF)
RFs [
22] are known to be appropriate for environments with many highly interrelated input variables [
23]. Although the amount of samples in our database is relatively large, as compared to the number of inputs, these are highly correlated by nature (they have a strong association since they are linked in the numerical model).
This same algorithm was previously used in regression problems in different applications, e.g., to build regression models to predict dam behaviour [
24], to interpret the response of dams to seismic loads [
25] and to better understand the behaviour of labyrinth spillways [
26]. Other fields of application in the water sector include dam safety [
27], water quality [
28], classification of water bodies [
29] or urban flood mapping [
30].
A random forest model is a group of classification trees, each of which is fitted on an altered version (a bootstrap sample) of the training set [
31]. Since they were first proposed by Breiman [
22], RFs have been used in multiple fields both for regression and classification tasks. The main ingredients of the algorithm can be summarized as follows:
For each tree in the final model (ntree), a bootstrap sample from the training set is drawn.
A tree model is fitted to each sample. Instead of all the available inputs, a random subsample of size mtry is taken for each split.
The prediction of the forest is taken by averaging the outcomes of all individual trees. For classification, the label with higher proportion of predictions is taken.
This process includes randomness in two steps (in bootstrap sample generation, and in taking predictors at each split) with the aim of capturing as many patterns as possible from the training data.
One of the advantages of RF is the existence of the out-of-bag data (OOB), i.e., the part of the observations excluded from each bootstrap sample. The prediction accuracy for each observation can be computed from the trees grown on samples where such observation was not included. This can be considered as an implicit cross validation, which allows for obtaining a good estimate of the prediction error without the need to explicitly separate a subset of the available data.
Extensive application of this algorithm showed high prediction accuracy and robustness, i.e., the effect of the model parameters is low [
31,
32]. In addition, the algorithm performs implicit variable selection while fitting each tree, which simplifies pre-process [
33].
As mentioned above, RF classifiers are robust in the sense that the model parameters typically have low influence on the results. Nonetheless, a calibration process was followed in this work based on the OOB error: all possible combinations of mtry (4, 6, 8 and 10), ntree (400, 600, 800 and 1000) and nodesize (1, 3, 5 and 7) were considered to fit RF models, and the prediction accuracy for the OOB data was assessed. The combination of parameters with the lowest error was chosen to fit the final RF model. The same procedure was followed for multi-class and two-class tasks.
2.5.2. Support Vector Machines (SVM)
Although SVM can be applied to regression problems, the algorithm was originally created for classification [
34]. The model fitting process not only aims at increasing classification accuracy on the training set, but also at maximizing the margin to improve separation of the classes [
35]. This results in greater generalization capability. In addition, SVM is also among the most appropriate algorithms for one-class classification [
20] and has already been used for this purpose in the water field [
21]. Applications of SVM both for regression and classification are numerous in different sectors. In hydraulics and hydrology, examples include pipe failure detection in water distribution networks [
36], prediction of urban water demand [
37] rainfall-runoff modelling [
38], flood forecasting [
39], as well as reliability analysis [
40,
41,
42] and dam safety [
4,
5,
8,
9,
43,
44].
SVM make use of a non-linear transformation of the inputs into a high dimensional space, where a linear function is used for classification. The theoretical fundamentals of the algorithm are described in many publications (see, for instance [
34,
35,
45]).
Since SVM models are more sensitive to the training parameters than RFs, calibration is more important than for RFs. Five-fold cross-validation (CV) was applied to the training set to obtain reliable estimates of prediction error and thus to select the best training parameters. In this work, we used radial basis kernels, defined as a function of two parameters: C (cost) and . For MC and TC, all possible combinations of C (0.1, 1, 10) and (0.001, 0.01, 0.1) were considered and the best combination from CV was later applied to fit the final model.
The process is similar for one-class classification (see
Section 2.4), with the addition of the parameter
, which controls the size of the margin between the class used for training and the outliers (anomalies in our case) [
20]. We considered all possible combinations of
(0.01, 0.04, 0.05, 0.06, 0.1),
C (0.1, 1, 10) and
(0.01, 0.025, 0.05, 0.075, 0.1). The results were evaluated in terms of the BA on a test set including both the anomalous situations in the training period and all the cases for the test period.
2.6. Measures of Accuracy
Henceforth, anomalies are considered as positive experiments (correctly predicted cracked cases are thus true positives, TP), while Scenario 0 corresponds to negative experiments (correct predictions for Scenario 0 are true negatives, TN). Consequently, false positives (FP) will be cases where the model predicted a crack on data from a crack-free case, and false negatives (FN) those when the model predicted no crack with data from a cracked case. In this work, the following measures of accuracy were considered:
Two error measures were used that take into account both false positives and false negatives: balanced accuracy (BA) is computed as the mean of sensitivity and specificity. In turn, the F1 score [
46] also considers both, but more relevance is given to the false positives. This is in accordance to the nature of the phenomenon to be considered: in dam safety, overseeing an anomaly is more important than predicting a false crack.
where:
3. Results and Discussion
3.1. Multi-Class Classification
3.1.1. Calibration
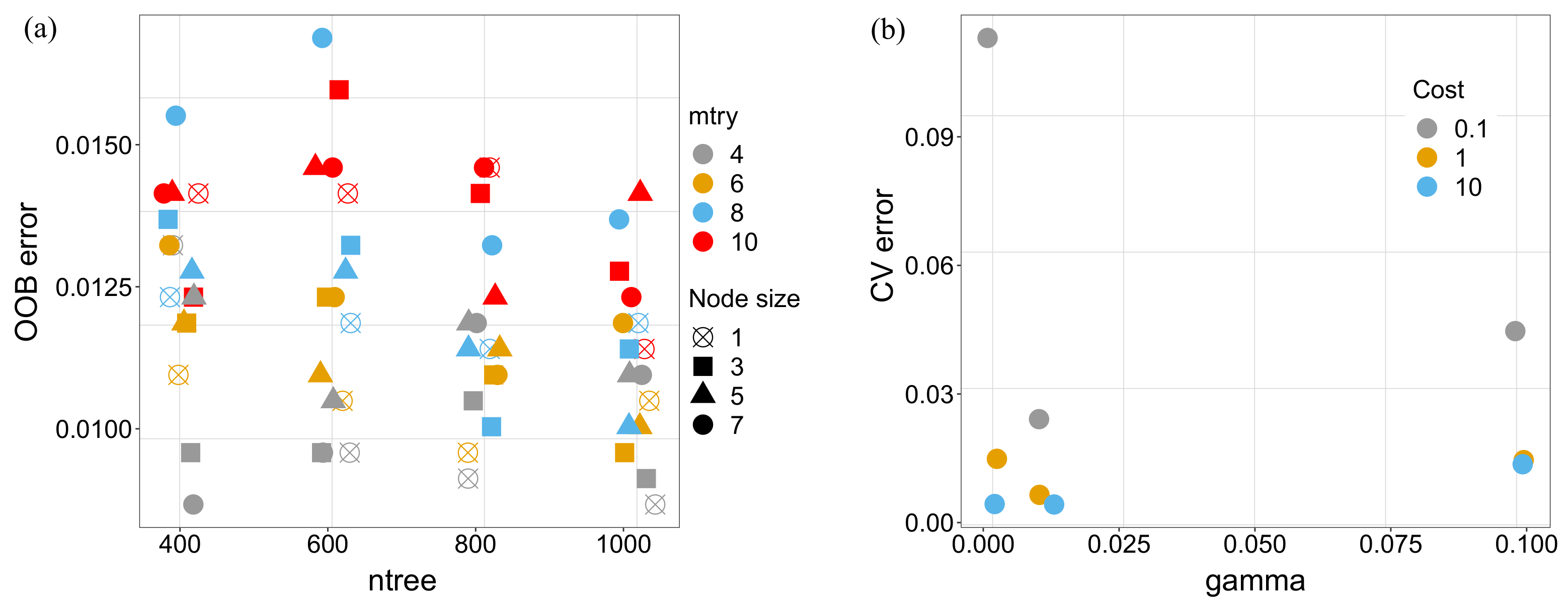
Figure 7a shows the median of OOB class error for all combinations of parameters tested for RF models. It can be observed that the effect of the model parameters on the results is low. Nonetheless, we took the values from the best combination of those considered:
ntree = 1000,
mtry = 4,
nodesize = 1. The same result of the calibration process is shown for the SVM model also in
Figure 7. In this case, the best performance was obtained with
C = 10 and
= 0.001.
3.1.2. Evaluation
Although OOB error is often a good estimate for the generalization error, the RF model was evaluated using the test set, so that it can be compared to the SVM model. The confusion matrix is the main result, showing the predictions versus the real values.
Table 3 and
Table 4 include the results both for the RF and the SVM model, in addition to the F1 and balanced accuracy for each class.
The results of both algorithms show high accuracy in identifying all scenarios, being the performance of SVM model slightly better. This confirms the benefits of these techniques for supervised classification.
Both models show more accurate results than those obtained in a previous work based on RF [
7], in which different anomalies were considered. This may be due to the calibration process, more detailed in this case, but also to the nature of the anomalies introduced. While they affected the mechanical boundary conditions in the former study, more realistic situations are considered here, representative of crack formation in different areas of the dam body. The effect of these modifications on the dam response have a more local effect, easier to identify by ML models.
The high accuracy demonstrates the soundness of the approach and the usefulness of the algorithms. However, it still has the limitation of the need for identifying and modelling the anomalies to be detected, which is highly relevant for its practical implementation.
3.2. Two-Class Classification
3.2.1. Calibration
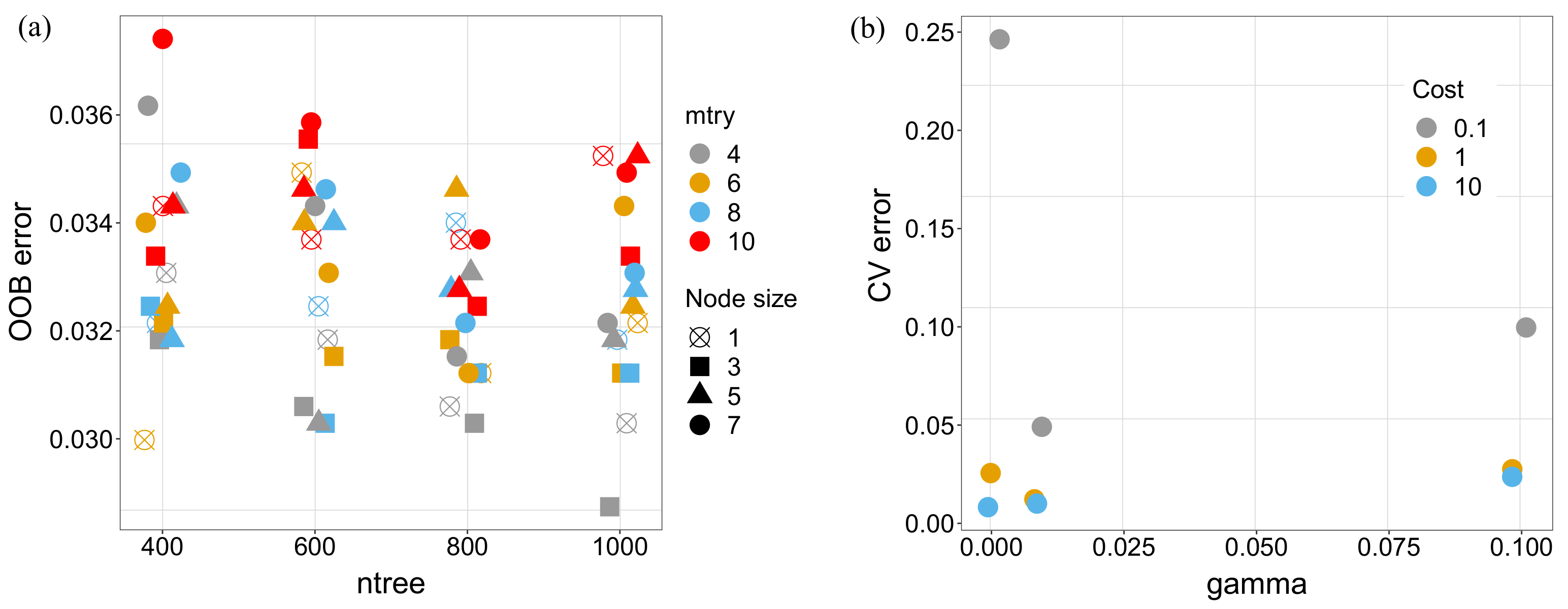
The same process was followed for calibration of both models for the case of two classes. The result is shown in
Figure 8. As before, the combinations of parameters with best performance for the OOB error (RF) and the 5-folds cross-validation error (SVM) were later used for evaluation.
3.2.2. Evaluation
The evaluation of classification models for this task can be done in the first instance by means of the confusion matrix, as before.
Table 5 shows the result for the RF model, which featured an F1 of 0.820 and a balanced accuracy of 0.846. In this case, there is a clear difference between classes. The model is highly accurate for identifying anomalies: the rate of false positives is 0.3%. This results in a specificity of 0.995. By contrast, the rate of false negatives is relatively high (48%), and thus sensitivity is lower (0.697).
The features of the training set need to be considered for the analysis of these results. The problem was posed in an unconventional manner, since samples labelled as anomalies in the training set (Class 1) are indeed different from those with the same label in the test set. They are both anomalous and different from Class 0, which corresponds to normal operation in both the training and the test sets, but they were computed from different numerical models. In conventional classification problems, classes defined in the training set are the same as in the evaluation or test sets. When the model is applied to a new set of input values, these are classified according to their similarity to each of the classes. In this case, the test scenarios are in fact different from either of the two classes defined during training. The model determines which of the two classes is more closely related to the new input. The relatively high proportion of anomalous cases that the model considers as normal is therefore explained by the nature of the classification task. This can be further explored by separating the samples for class 1 into the original scenarios (
Table 6). There is a clear difference among anomalies: accuracies or Scenarios 1b, 2b and 3b are 52%, 67% and 90%, respectively.
This conclusion is confirmed by the results of the SVM model (
Table 7). Although the overall accuracy is again slightly higher than for the RF model (F1 0.822; balanced accuracy 0.847), the same imbalance is observed, with specificity of 0.997 and sensitivity of 0.698.
The same difference among scenarios is observed for the SVM model (
Table 8). While Scenario 3b is again well identified (98% accuracy), results are poorer for Scenarios 1b and 2b (57% and 54%, respectively).
3.3. One-Class Classification
3.3.1. Calibration
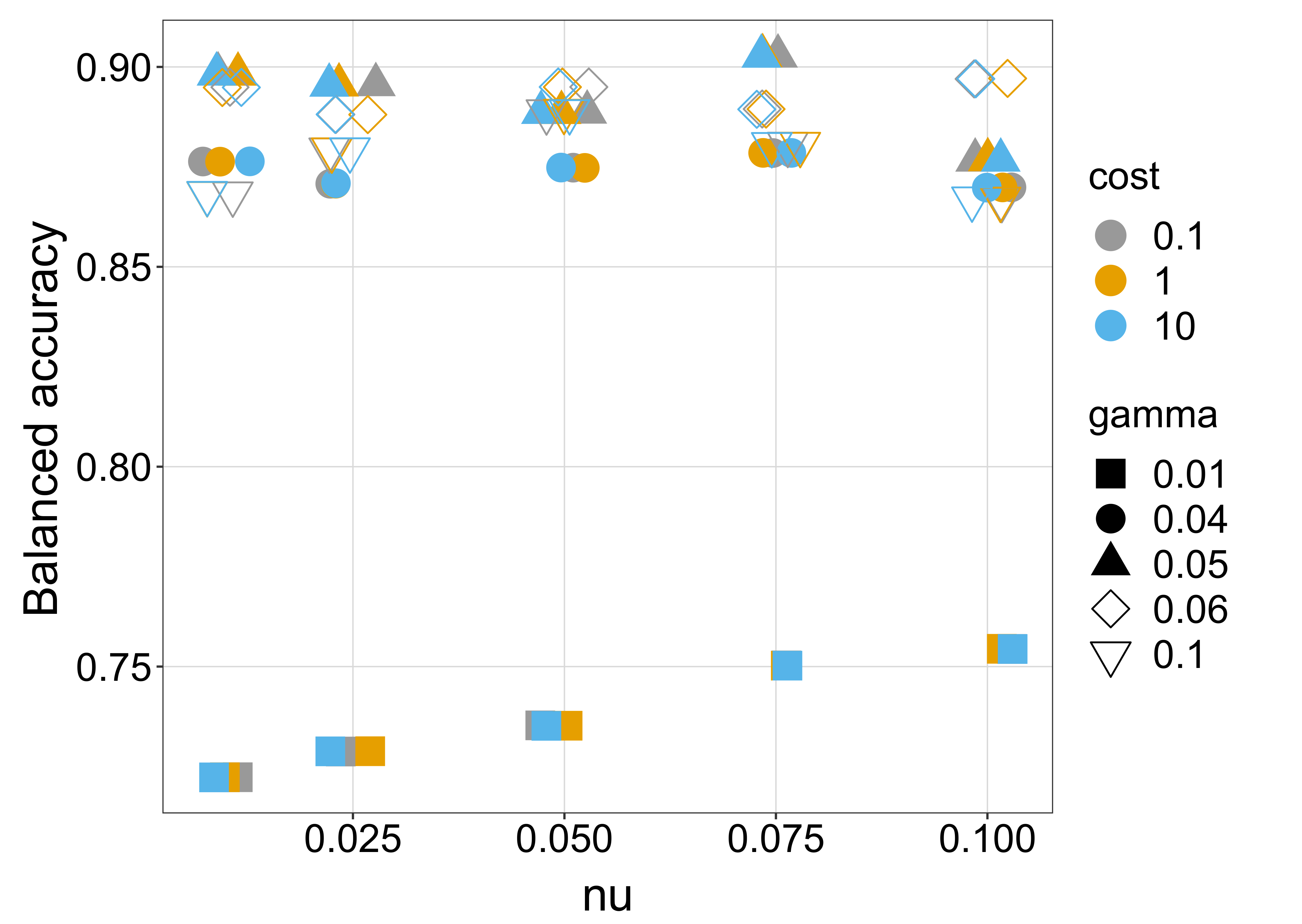
Three different combinations of parameters featured the highest accuracy, one of which (
= 0.075, C = 0.1,
= 0.05) was taken to fit the final model.
Figure 9 shows the results of the calibration process.
3.3.2. Evaluation
The results of the one-class classifier on the test set show similar general figures than for the two-class models (F1 0.920; BA 0.903), but they are more balanced between ability to detect normal operation and anomalies. The figures from the confusion matrix (
Table 9) result in a sensitivity of 0.858 and a specificity of 0.948.
Again, these results can be further explored by separating the anomalies into the original scenarios (
Table 10). In this case, all classes are predicted with higher accuracy (from 75% for Scenario 4 up to 100% for Scenarios 2a and 3a), at the cost of a higher proportion of false positives, which nonetheless is low (5 %).
Results are better for Scenarios 2a and 3a because their deviation from the reference pattern (Scenario 0) is higher, as can be observed in
Figure 5.
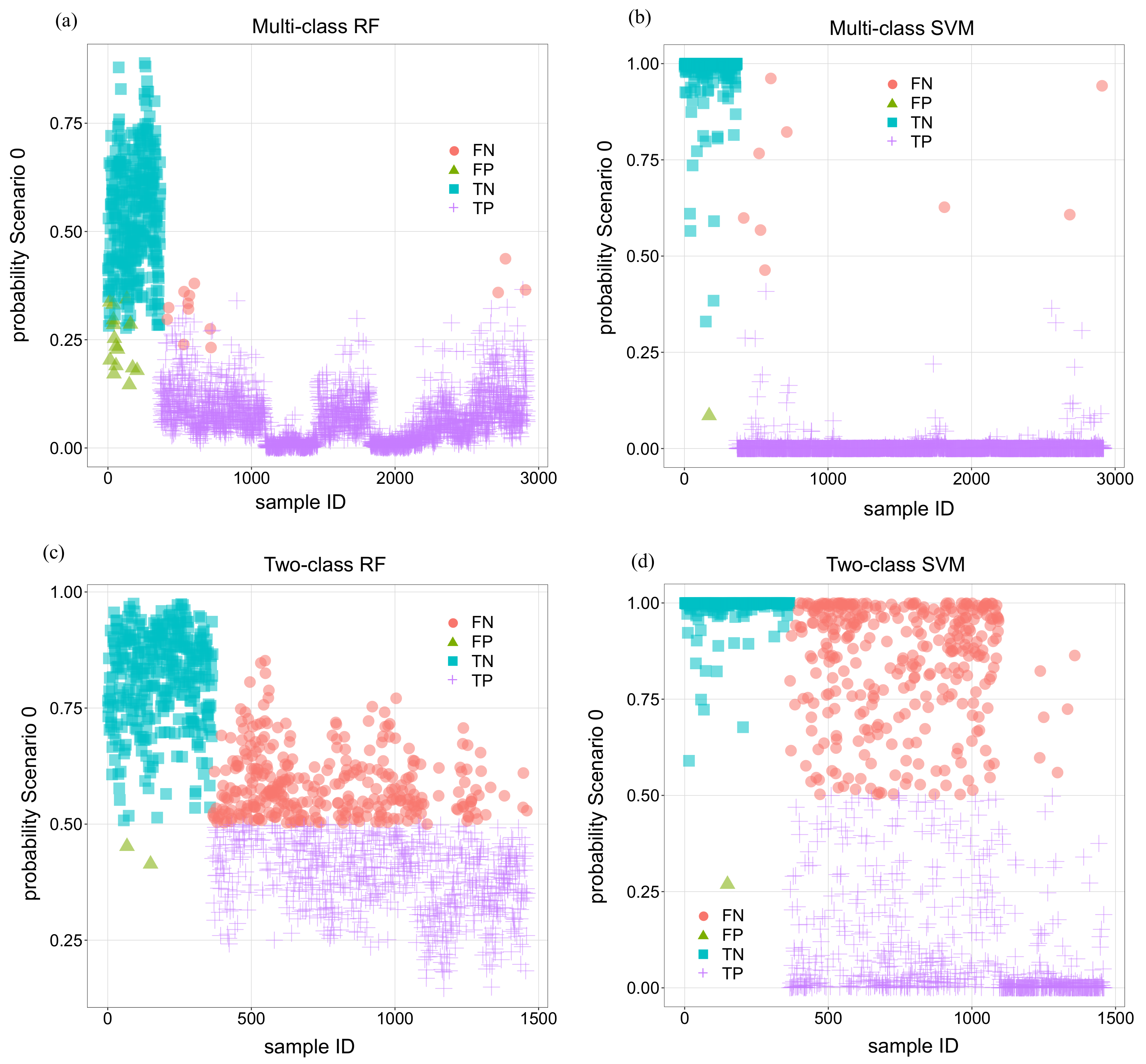
3.4. Class Probability
The previous analyses are based on the raw predictions of the ML models. In this section, we discuss the class probability. For example, RF models include a large number of classification trees, each of which generates a predicted class. The overall prediction is taken as the majority vote for all trees. The value of the predicted probability can be explored to draw more detailed information on the behaviour of the system and make decisions. The prediction of a class with high probability can be expected to be more reliable than others for which two or more classes feature similar probabilities.
Following this idea, the predicted probabilities of the calibrated models for the test set were computed for all scenarios.
Figure 10 includes the results for all 4 calibrated models with the classification of the outcome into TN, FN, TP and FP.
This analysis was made with the aim of exploring the possibility of defining some practical criterion to improve the results of the raw predictions. This could be the case for the multi-class RF model: all wrong predictions, both FPs and FNs, correspond to relatively low probabilities for Scenario 0. In other words, predicted probabilities for TN are in general high, and those for TP are low in the vast majority of the cases. This may suggest that an intermediate category of uncertain predictions might be defined including all cases with predicted probability for Scenario 0 in an intermediate range (e.g., 0.2 to 0.4). This would eliminate the FPs and FNs, at the cost of converting a proportion of TPs and TNs into this intermediate category.
The analysis of the plot for multi-class SVM shows the capability of the algorithm to maximise the margin between categories. Probabilities of Scenario 0 in correct predictions are close to 1 for TNs and close to 0 for TPs. The criterion mentioned for RFs is not useful to eliminate the FNs because the few errors feature probabilities above 0.5.
In any case, the main reason for not defining this practical criterion for multi-class models is that their default accuracy is already very high, in addition to the aforementioned limitation of the need to identify a priori and accurately model the anomalies to be detected.
As for the two-class models, the plots show that the separation between classes is less clear. Interestingly, the predicted probabilities of the SVM model for FNs are farther from the 0.5 limit than for the RF model. Again, there is not a clear benefit in using the predicted probabilities for practical purposes.
3.5. Time Evolution of Predictions
In previous sections, the model predictions were evaluated separately: both false positives and false negatives were assessed in terms of the amount of occurrences as compared to the size of the test set. From a practical viewpoint, the persistence of predictions is relevant when it comes to make decisions regarding dam safety. Anomalies in dam behaviour generally occur progressively, starting by a small deviation from normal operation and increasing in time. In such event, an accurate model would predict anomalous behaviour with persistence in time. In other words, no major decision will be made from a single prediction of anomaly if the subsequent sets of records are considered as normal by the model.
As a result, isolated prediction errors can be considered affordable from a practical point of view. Since the test set corresponds to realistic evolution of external loads and dam response over time (one year of actual measurements), draw relevant conclusions can be drawn from the exploration of the location of errors in time.
This was done for all five models (three prediction tasks and two algorithms). More precisely, the number of consecutive errors—at least two—were computed (either false positives or false negatives) and included in
Table 11 together with the overall miss-classifications. The results show a large reduction in miss-classifications in all cases as the time window grows. It should be noted that for multi-class models, errors between anomalous scenarios are considered TPs.
3.6. Practical Criterion
As a result of the previous analysis, a procedure was defined to generate predictions for its application to the validation set. A homologous process was followed for all alternatives used (RF and SVM models for multi-class and two-class classification, and SVM model for one-class):
A new model was fitted using a dataset including both the training and the test set, i.e., for the period 1999–2003. In all cases, the parameters of the model were taken from the previous calibration.
A new classification is generated, based on the results of the previous analyses. The rationale is that true anomalies in dam behaviour are persistent in time, at least until some remediation measure is adopted. Hence, model predictions should be stable over short periods of time. In accordance, shifts in model predictions, from normal to anomaly or vice versa, are considered with caution and termed as “soft predictions”, whereas stable outcomes are classified as “hard predictions”. Therefore, four categories are defined as follows:
- (a)
If the model prediction is Normal and equal to previous prediction, i.e., at least two consecutive predictions of no-crack, it is classified as “Hard negative” (HN).
- (b)
If the model prediction is Normal, but the previous prediction was Anomaly, it is considered “Soft negative” (SN).
- (c)
If the model prediction is Anomaly, but the previous prediction was Normal, it is considered “Soft positive” (SP).
- (d)
If the model prediction is Anomaly and equals the previous prediction, it is termed as “Hard positive” (HP).
The evaluation of the results is made on the basis of the errors defined in
Table 12.
3.7. Validation
3.7.1. Multi-Class Classification
The confusion matrix for the RF model is included in
Table 13. It shows 5 hard errors (all of them HP) out of 2912 cases (0.2%). The proportion of soft predictions is below 5%, which implies that the model can be useful for practical application.
The results for the SVM model are similar, as can be observed in
Table 14. As in previous analysis, the performance is slightly better. In particular, only one hard error is registered, and the amount of soft predictions is lower (37; 1%).
These results demonstrate the capability of both algorithms for identifying behaviour patterns. The SVM model consistently outperformed RF in all analyses, though the difference is small. The calibration effort and required computational time is also similar. In other settings, SVM may require more detailed calibration and some variable selection. It shall be remembered that the amount of inputs is relatively high and that all inputs are highly correlated by their nature. In such a setting, the performance of some classification algorithms may degrade. This was not expected to affect the RF model, which is known to perform well even with many correlated variables, but SVM also provided accurate results without performing variable selection.
The main benefit of this approach is the capability of distinguishing response patterns, not only between normal and anomalous behaviour, but also among different anomalies. By contrast, it has the limitation of requiring the identification and modelling of the expected anomalies. It is thus unclear what the effect of the application of these models would be in practice when some unforeseen anomaly scenario occurs.
3.7.2. Two-Class Classification
The confusion matrix for the RF model and the two-class classification task is included in
Table 15. The format of this matrix is unconventional, not only because of the particular definition of the soft predictions, but also because the anomalous situations, which were provided to the model as belonging to a unique Class with label 1, are disaggregated here in accordance with the actual scenario from which they were obtained with the FEM (classes 1a to 4). It should be reminded that the models used for this task were fitted on a training sample including Scenarios 0, 1a, 2a, 3a and 4, and that the anomalous situations in the validation set comprise different anomalies (Scenarios 1b, 2b and 3b) in addition to the normal situation. The prediction task is thus more challenging, but also more realistic, since unforeseen response patterns can be expected to occur in practice.
It can be seen that no HFP are registered for the RF model and the ad hoc criterion defined. The amount of HFN is higher due to the difference in nature of Class 1 samples between the training and the validation set.
In this case, the results for the SVM model is poorer (
Table 16), especially for Scenarios 1b and 2b. This may be the effect of the maximization of the margin between categories when applied to samples of different nature. In this case, no HFP are obtained and the amount of soft predictions is 332 (23%).
The results of this approach for Scenario 3b suggest that it can be useful to detect anomalies only in case they resemble the situations considered for training. By contrast, the model tends to consider as normal those patterns not included in the training data. This is a similar limitation as that described for the MC model, and confirms the conclusions drawn in the previous section.
These classification models fitted with data involving some situations and applied to different anomalies, predict on the basis of the degree of similarity between the new, observed behaviour and those provided for training. Good performance can be expected in terms of anomaly detection when the actual pattern is more similar to some of the foreseen anomalies than to the normal scenario. This is the case of Scenario 3b.
3.7.3. One-Class Classification
The new criterion showed to be useful for OC model.
Table 17 shows the confusion matrix for the validation set. The ratio of HFP is low (0.1%). A higher proportion of HFN is observed, though still better than for the TC models (3.8%). It should be reminded that the OC model was fitted using exclusively data from normal operation. This is relevant from a practical viewpoint, since this approach avoids the need for identifying and modelling the anomaly scenarios for model fitting.
3.7.4. Summary of Validation
The models examined include relevant differences in terms of the information used for training and evaluation. Those differences need to be considered when comparing performances. Furthermore, although the anomalous scenarios are initially the same for all tasks, they are included different ways: as different classes (MC), grouped into one single anomalous class with different scenarios in training and testing (TC) or plainly grouped into a global category for all situations different from Scenario 0 (OC).
Keeping these differences in mind, results are summarised and compared in
Table 18. It can be seen that the error rates in this case (adding soft and hard errors) are similar than those for the test set (
Table 11). This confirms that the model accuracy is representative of the models used and the case study.
The proposed criterion is beneficial for the OC model, in the sense that the majority of raw miss-classifications are turned into soft errors.
4. Conclusions
Both RF and SVM showed high prediction accuracy for the multi-class classification task (miss-classification rate below 0.5%), with SVM slightly better than RF. These models have the advantage of being capable of distinguishing between anomalies of different kind, which can be useful when potential failure modes can be well defined and modelled. However, this need may be a relevant limitation in many settings for their practical application. Their capability to detect anomalous patterns not considered for model fitting is unclear.
Two-class classification models can only distinguish between two classes—normal and anomalous behaviour—but they are incapable of differentiating among different anomalies. This approach is more representative of the practical application, where unforeseen patterns, not considered for model fitting, may occur. The results for the TC models show their limitations in real settings. Their capability for identifying anomalies is strongly dependent on the nature of the actual pattern and its relation to the situations used for model fitting. While high accuracy was obtained for Scenario 3b, the proportion of miss-classifications for Scenarios 1b and 2b is too high for considering this approach in practice.
The one-class classifier based on SVM is fitted exclusively on data for normal operation. This is the typical situation in many dams which performed correctly for long periods, and thus the approach can be applied in practice using monitoring data. The results were better than TC models, and overall suggest that this model can be useful in practice. Although the accuracy also depends on the properties of the situation to identify, the model is not biased by the decisions of the modeller regarding which scenario to consider: the ability for anomaly detection of this model depends on the magnitude of the anomaly, i.e., serious anomalies can be detected with higher accuracy. The process is simpler because no anomalous data are required for model fitting: there is no need to create a numerical model and the probable anomaly scenarios need to be neither defined nor modelled. This also enlarges the scope of application to any dam typology and response variable, since some phenomena are difficult to simulate with the FEM. The model can be fitted solely with monitoring data in dams with long series of high-quality records for a relevant number of response variables. In general, a FEM model can be created to complement the time series—e.g., fill periods with missing values.
A practical criterion was defined to classify patterns on the basis of the model outcomes to differentiate predictions as a function of their consistency over time. This resulted in a decrease in miss-classification rate for all approaches. Although the overall conclusions hold for all prediction tasks and algorithms, the utility of the one-class classifier is clearer. This criterion is specific to the case study considered, and thus should be adapted to other situations in accordance with the amount of data available, the reading frequency and other problem-specific properties such as the nature of the potential failure scenario. The work also showed that the time window applied has a relevant effect on the performance of the mode. Engineering judgment and knowledge on dam history should be the fundamentals for setting up a procedure for each specific case.
The main drawback of this approach is that no information is obtained regarding the kind of anomaly identified: the outcome of the model is limited to the probability of belonging to the pattern used for model fitting or some other, without further specification. The combination of this approach with engineering knowledge and some other model—either a multi-class classifier or a set of regression models—may result in a more complete pattern identification. The authors are exploring this possibility in an open research line. This involves the need for analysing each output separately, but its application to a set of selected variables can be beneficial to take advantage of the benefits of both approaches, and alleviate their limitations.
Another limitation of these approaches is that high-quality data is needed for model fitting. In this analysis, training data was generated by a FEM model, which ensured that the resulting time series are complete and—in principle—of arbitrary length. By contrast, databases of monitoring data in many dams include periods of missing values, variable reading frequency and other issues. FEM models can be useful for improving the monitoring data to some extent, but still have limitations for some dam typologies, certain failure scenarios and determined response variables. The performance of ML classifiers when fitted with low-quality databases is also the topic of ongoing research.
Author Contributions
Conceptualization, F.S. and A.C.; methodology, F.S., A.C., J.I. and D.J.V.; validation, A.C. and J.I.; data curation, A.C.; writing—original draft preparation, F.S.; writing—review and editing, F.S., A.C., J.I. and D.J.V.; funding acquisition, F.S. and J.I. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially funded by the Spanish Ministry of Science, Innovation and Universities through the Project TRISTAN (RTI2018-094785-B-I00). The authors also acknowledge financial support from the Spanish Ministry of Economy and Competitiveness, through the “Severo Ochoa Programme for Centres of Excellence in R & D” (CEX2018-000797-S), and from the Generalitat de Catalunya through the CERCA Program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- European ICOLD Club. Manifesto “Dams and Reservoirs”. 2016. Available online: https://cnpgb.apambiente.pt/IcoldClub/documents/Manifesto/Manifesto_v_Nov_2016.pdf (accessed on 27 August 2021).
- Perera, D.; Smakhtin, V.; Williams, S.; North, T.; Curry, A. Ageing Water Storage Infrastructure: An Emerging Global Risk; UNU-INWEH Report Series, Issue 11; United Nations University Institute for Water, Environment and Health: Hamilton, ON, Canada, 2021.
- Hariri-Ardebili, M.A. Risk, Reliability, Resilience (R3) and beyond in dam engineering: A state-of-the-art review. Int. J. Disaster Risk Reduct. 2018, 31, 806–831. [Google Scholar] [CrossRef]
- Salazar, F.; Morán, R.; Toledo, M.A.; Oñate, E. Data-Based Models for the Prediction of Dam Behaviour: A Review and Some Methodological Considerations. Arch. Comput. Methods Eng. 2017, 24, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Salazar, F. A Machine Learning Based Methodology for Anomaly Detection in Dam Behaviour. Ph.D. Thesis, Universitat Politecnica de Catalunya, Barcelona, Spain, 2017. [Google Scholar]
- Mata, J.; Leitão, N.S.; de Castro, A.T.; da Costa, J.S. Construction of decision rules for early detection of a developing concrete arch dam failure scenario. A discriminant approach. Comput. Struct. 2014, 142, 45–53. [Google Scholar] [CrossRef] [Green Version]
- Salazar, F.; Conde, A.; Vicente, D.J. Identification of dam behavior by means of machine learning classification models. In Lecture Notes in Civil Engineering, Proceedings of the ICOLD International Benchmark Workshop on Numerical Analysis of Dams, ICOLD-BW, Milan, Italy, 9–11 September 2019; Springer: Cham, Switzerland, 2019; pp. 851–862. [Google Scholar]
- Fisher, W.D.; Camp, T.K.; Krzhizhanovskaya, V.V. Anomaly detection in earth dam and levee passive seismic data using support vector machines and automatic feature selection. J. Comput. Sci. 2017, 20, 143–153. [Google Scholar] [CrossRef]
- Fisher, W.D.; Camp, T.K.; Krzhizhanovskaya, V.V. Crack detection in earth dam and levee passive seismic data using support vector machines. Procedia Comput. Sci. 2016, 80, 577–586. [Google Scholar] [CrossRef] [Green Version]
- Vicente, D.J.; San Mauro, J.; Salazar, F.; Baena, C.M. An Interactive Tool for Automatic Predimensioning and Numerical Modeling of Arch Dams. Math. Probl. Eng. 2017, 2017, 9856938. [Google Scholar] [CrossRef]
- Ribó, R.; Pasenau, M.; Escolano, E.; Pérez, J.; Coll, A.; Melendo, A.; González, S. GiD the Personal Pre and Postprocessor; Reference Manual, Version 9; CIMNE: Barcelona, Spain, 2008.
- Ghanaat, Y. Failure modes approach to safety evaluation of dams. In Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, BC, Canada, 1–6 August 2004. [Google Scholar]
- Lin, P.; Wei, P.; Wang, W.; Huang, H. Cracking Risk and Overall Stability Analysis of Xulong High Arch Dam: A Case Study. Appl. Sci. 2018, 8, 2555. [Google Scholar] [CrossRef] [Green Version]
- Lin, P.; Zhou, W.; Liu, H. Experimental Study on Cracking, Reinforcement, and Overall Stability of the Xiaowan Super-High Arch Dam. Rock Mech. Rock Eng. 2015, 48, 819–841. [Google Scholar] [CrossRef]
- Hamedian, S.; Koltuniuk, R. Cracking In Thin Arch Concrete Dam – Nonlinear Dynamic Structural Analysis. In Proceedings of the Annual USSD Conference, Anaheim, CA, USA, 3–7 April 2017. [Google Scholar]
- Salazar, F.; Vicente, D.J.; Irazábal, J.; de Pouplana, I.; San Mauro, J. A Review on Thermo-mechanical Modelling of Arch Dams During Construction and Operation: Effect of the Reference Temperature on the Stress Field. Arch. Comput. Methods Eng. 2020, 27, 1681–1707. [Google Scholar] [CrossRef]
- Santillán, D.; Salete, E.; Vicente, D.J.; Toledo, M.A. Treatment of Solar Radiation by Spatial and Temporal Discretization for Modeling the Thermal Response of Arch Dams. J. Eng. Mech. 2014, 140, 05014001. [Google Scholar] [CrossRef]
- Salazar, F.; Toledo, M.A.; González, J.M.; Oñate, E. Early detection of anomalies in dam performance: A methodology based on boosted regression trees. Struct. Control Health Monit. 2017, 24, e2012. [Google Scholar] [CrossRef]
- Krawczyk, B. Learning from imbalanced data: Open challenges and future directions. Prog. Artif. Intell. 2016, 5, 221–232. [Google Scholar] [CrossRef] [Green Version]
- Shin, H.J.; Eom, D.H.; Kim, S.S. One-class support vector machines—an application in machine fault detection and classification. Comput. Ind. Eng. 2005, 48, 395–408. [Google Scholar] [CrossRef]
- Tan, F.H.S.; Park, J.R.; Jung, K.; Lee, J.S.; Kang, D.K. Cascade of One Class Classifiers for Water Level Anomaly Detection. Electronics 2020, 9, 1012. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Díaz-Uriarte, R.; Alvarez de Andrés, S. Gene selection and classification of microarray data using random forest. BMC Bioinform. 2006, 7, 3. [Google Scholar] [CrossRef] [Green Version]
- Salazar, F.; Toledo, M.A.; Oñate, E.; Morán, R. An empirical comparison of machine learning techniques for dam behaviour modelling. Struct. Saf. 2015, 56, 9–17. [Google Scholar] [CrossRef] [Green Version]
- Salazar, F.; Hariri-Ardebili, M. Machine Learning based Seismic Stability Assessment of Dams with Heterogeneous Concrete. In Proceedings of the 3rd Meeting of EWG Dams and Earthquakes. An International Symposium, Lisbon, Portugal, 6–8 May 2019. [Google Scholar]
- Salazar, F.; Crookston, B. A Performance Comparison of Machine Learning Algorithms for Arced Labyrinth Spillways. Water 2019, 11, 544. [Google Scholar] [CrossRef] [Green Version]
- Dai, B.; Gu, C.; Zhao, E.; Qin, X. Statistical model optimized random forest regression model for concrete dam deformation monitoring. Struct. Control Health Monit. 2018, 25, e2170. [Google Scholar] [CrossRef]
- Singh, B.; Sihag, P.; Singh, K. Modelling of impact of water quality on infiltration rate of soil by random forest regression. Model. Earth Syst. Environ. 2017, 3, 999–1004. [Google Scholar] [CrossRef]
- Ko, B.C.; Kim, H.H.; Nam, J.Y. Classification of potential water bodies using Landsat 8 OLI and a combination of two boosted random forest classifiers. Sensors 2015, 15, 13763–13777. [Google Scholar] [CrossRef] [Green Version]
- Feng, Q.; Liu, J.; Gong, J. Urban flood mapping based on unmanned aerial vehicle remote sensing and random forest classifier—A case of Yuyao, China. Water 2015, 7, 1437–1455. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and Regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Genuer, R.; Poggi, J.M.; Tuleau-Malot, C. Variable selection using random forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H.; Meulman, J.J. Multiple additive regression trees with application in epidemiology. Stat. Med. 2003, 22, 1365–1381. [Google Scholar] [CrossRef]
- Moguerza, J.M.; Muñoz, A. Support vector machines with applications. Stat. Sci. 2006, 21, 322–336. [Google Scholar] [CrossRef] [Green Version]
- Bennett, K.P.; Campbell, C. Support vector machines: Hype or hallelujah? ACM SIGKDD Explor. Newsl. 2000, 2, 1–13. [Google Scholar] [CrossRef]
- Giraldo-González, M.M.; Rodríguez, J.P. Comparison of Statistical and Machine Learning Models for Pipe Failure Modeling in Water Distribution Networks. Water 2020, 12, 1153. [Google Scholar] [CrossRef] [Green Version]
- Herrera, M.; Torgo, L.; Izquierdo, J.; Pérez-García, R. Predictive models for forecasting hourly urban water demand. J. Hydrol. 2010, 387, 141–150. [Google Scholar] [CrossRef]
- Granata, F.; Gargano, R.; De Marinis, G. Support Vector Regression for Rainfall-Runoff Modeling in Urban Drainage: A Comparison with the EPA’s Storm Water Management Model. Water 2016, 8, 69. [Google Scholar] [CrossRef]
- Chang, M.J.; Chang, H.K.; Chen, Y.C.; Lin, G.F.; Chen, P.A.; Lai, J.S.; Tan, Y.C. A Support Vector Machine Forecasting Model for Typhoon Flood Inundation Mapping and Early Flood Warning Systems. Water 2018, 10, 1734. [Google Scholar] [CrossRef] [Green Version]
- Hariri-Ardebili, M.A.; Pourkamali-Anaraki, F. Support vector machine based reliability analysis of concrete dams. Soil Dyn. Earthq. Eng. 2018, 104, 276–295. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Pourkamali-Anaraki, F. Simplified reliability analysis of multi hazard risk in gravity dams via machine learning techniques. Arch. Civ. Mech. Eng. 2018, 18, 592–610. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Salazar, F. Engaging soft computing in material and modeling uncertainty quantification of dam engineering problems. Soft Comput. 2020, 24, 11583–11604. [Google Scholar] [CrossRef]
- Ranković, V.; Grujović, N.; Divac, D.; Milivojević, N. Development of support vector regression identification model for prediction of dam structural behaviour. Struct. Saf. 2014, 48, 33–39. [Google Scholar] [CrossRef]
- Cheng, L.; Zheng, D. Two online dam safety monitoring models based on the process of extracting environmental effect. Adv. Eng. Softw. 2013, 57, 48–56. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Jung, I.S.; Berges, M.; Garrett, J.H.; Poczos, B. Exploration and evaluation of AR, MPCA and KL anomaly detection techniques to embankment dam piezometer data. Adv. Eng. Inform. 2015, 29, 902–917. [Google Scholar] [CrossRef] [Green Version]
Figure 1.
Location of pendulums and cracks considered for each scenario. View from downstream.
Figure 1.
Location of pendulums and cracks considered for each scenario. View from downstream.
Figure 2.
Close view of the dam body and the mesh elements.
Figure 2.
Close view of the dam body and the mesh elements.
Figure 3.
Overall view of the computational model for the dam body and foundation.
Figure 3.
Overall view of the computational model for the dam body and foundation.
Figure 4.
Comparison between the observed radial displacements in stations 12, 16 and 26 and the results of the numerical model of Scenario 0.
Figure 4.
Comparison between the observed radial displacements in stations 12, 16 and 26 and the results of the numerical model of Scenario 0.
Figure 5.
Median difference between anomaly scenarios and Scenario 0 for all tangential (left) and radial (right) displacements considered. Results are normalized to the range of variation of each input in Scenario 0.
Figure 5.
Median difference between anomaly scenarios and Scenario 0 for all tangential (left) and radial (right) displacements considered. Results are normalized to the range of variation of each input in Scenario 0.
Figure 6.
Median difference between anomaly scenarios and Scenario 0 for all tangential (left) and radial (right) displacements considered. Colour scales differ as corresponds to the typical higher variation of radial displacements.
Figure 6.
Median difference between anomaly scenarios and Scenario 0 for all tangential (left) and radial (right) displacements considered. Colour scales differ as corresponds to the typical higher variation of radial displacements.
Figure 7.
Results of the calibration process. (a) RF model. The mean of the OOB error for all classes is plotted as a function of the number of trees (ntree), nodesize and the mtry parameter. (b) SVM model results for 5-folds cross validation.
Figure 7.
Results of the calibration process. (a) RF model. The mean of the OOB error for all classes is plotted as a function of the number of trees (ntree), nodesize and the mtry parameter. (b) SVM model results for 5-folds cross validation.
Figure 8.
Result of the calibration process for the two-class classification task. (a) RF model. (b) SVM model.
Figure 8.
Result of the calibration process for the two-class classification task. (a) RF model. (b) SVM model.
Figure 9.
Result of the calibration process for the one-class SVM model with 5-folds cross-validation.
Figure 9.
Result of the calibration process for the one-class SVM model with 5-folds cross-validation.
Figure 10.
Predicted probability of belonging to Scenario 0. (a) RF multi-class. (b) SVM multi-class. (c) RF two-class. (d) SVM two-class.
Figure 10.
Predicted probability of belonging to Scenario 0. (a) RF multi-class. (b) SVM multi-class. (c) RF two-class. (d) SVM two-class.
Table 1.
Material properties.
Table 1.
Material properties.
| Material Properties | Concrete | Soil | Units |
|---|
| Young Modulus | 3 | 4.9 | Pa |
| Poisson coefficient | 0.2 | 0.25 | [-] |
| Density | 2400 | 3000 | Kg/m |
Table 2.
Classification according to the type of crack.
Table 2.
Classification according to the type of crack.
| Nomenclature | Type of Crack |
|---|
| Case 1 (a & b) | Vertical crosswise [12,13,14] |
| Case 2 (a & b) | Horizontal at the base [13,14] |
| Case 3 (a & b) | Parallel to the dam-foundation contact, mid-height [13,14,15] |
| Case 4 | Perpendicular to the dam-foundation contact, downstream mid-height [13,14] |
Table 3.
Confusion matrix for multi-class classification for the RF model.
Table 3.
Confusion matrix for multi-class classification for the RF model.
| | | Observed Class | | |
|---|
| Predicted class | | 0 | 1a | 1b | 2a | 2b | 3a | 3b | 4 | F1 | BA |
| 0 | 350 | 10 | 0 | 0 | 0 | 0 | 0 | 3 | 0.962 | 0.977 |
| 1a | 5 | 333 | 0 | 0 | 1 | 0 | 0 | 1 | 0.945 | 0.955 |
| 1b | 1 | 17 | 365 | 0 | 1 | 0 | 0 | 1 | 0.973 | 0.996 |
| 2a | 0 | 0 | 0 | 365 | 0 | 0 | 0 | 0 | 1 | 1 |
| 2b | 0 | 0 | 0 | 0 | 360 | 0 | 0 | 0 | 0.993 | 0.993 |
| 3a | 0 | 0 | 0 | 0 | 0 | 365 | 0 | 0 | 1 | 1 |
| 3b | 2 | 4 | 0 | 0 | 2 | 0 | 365 | 0 | 0.989 | 0.998 |
| 4 | 7 | 1 | 0 | 0 | 1 | 0 | 0 | 360 | 0.981 | 0.991 |
Table 4.
Confusion matrix for multi-class classification for the SVM model.
Table 4.
Confusion matrix for multi-class classification for the SVM model.
| | | Observed Class | | |
|---|
| Predicted class | | 0 | 1a | 1b | 2a | 2b | 3a | 3b | 4 | F1 | BA |
| 0 | 364 | 6 | 0 | 0 | 1 | 0 | 0 | 2 | 0.986 | 0.997 |
| 1a | 0 | 356 | 0 | 0 | 0 | 0 | 0 | 2 | 0.985 | 0.987 |
| 1b | 1 | 2 | 365 | 0 | 0 | 0 | 0 | 0 | 0.996 | 0.999 |
| 2a | 0 | 0 | 0 | 365 | 0 | 0 | 0 | 0 | 1 | 1 |
| 2b | 0 | 0 | 0 | 0 | 364 | 0 | 0 | 0 | 0.999 | 0.999 |
| 3a | 0 | 0 | 0 | 0 | 0 | 365 | 0 | 0 | 1 | 1 |
| 3b | 0 | 0 | 0 | 0 | 0 | 0 | 365 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 361 | 0.993 | 0.994 |
Table 5.
Confusion matrix for the RF model on the test set in the two-class classification problem.
Table 5.
Confusion matrix for the RF model on the test set in the two-class classification problem.
| | | Observed Class |
|---|
| | | 0 | 1 |
| Predicted class | 0 | 363 | 332 |
| 1 | 2 | 763 |
Table 6.
Detailed confusion matrix for the RF model and the two-class classification. All anomalous samples are separated into the original scenarios.
Table 6.
Detailed confusion matrix for the RF model and the two-class classification. All anomalous samples are separated into the original scenarios.
| | | Observed Class |
|---|
| | | 0 | 1a | 1b | 2a | 2b | 3a | 3b | 4 |
| Predicted class | 0 | 363 | 0 | 176 | 0 | 120 | 0 | 35 | 0 |
| 1 | 2 | 0 | 189 | 0 | 245 | 0 | 330 | 0 |
Table 7.
Confusion matrix for the SVM model on the test set in the two-class classification problem.
Table 7.
Confusion matrix for the SVM model on the test set in the two-class classification problem.
| | | Observed Class |
|---|
| Predicted class | | 0 | 1 |
| 0 | 364 | 331 |
| 1 | 1 | 764 |
Table 8.
Detailed confusion matrix for the SVM model and the two-class classification. All anomalous samples are separated into the original scenarios.
Table 8.
Detailed confusion matrix for the SVM model and the two-class classification. All anomalous samples are separated into the original scenarios.
| | | Observed Class |
|---|
| | | 0 | 1a | 1b | 2a | 2b | 3a | 3b | 4 |
| Predicted class | 0 | 364 | 0 | 157 | 0 | 168 | 0 | 6 | 0 |
| 1 | 1 | 0 | 208 | 0 | 197 | 0 | 359 | 0 |
Table 9.
Confusion matrix for the SVM model on the test set in the one-class classification problem.
Table 9.
Confusion matrix for the SVM model on the test set in the one-class classification problem.
| | | Observed Class |
|---|
| Predicted class | | 0 | 1 |
| 0 | 346 | 364 |
| 1 | 19 | 2191 |
Table 10.
Detailed confusion matrix for the one-class model separated by the original scenarios considered.
Table 10.
Detailed confusion matrix for the one-class model separated by the original scenarios considered.
| | | Observed Class |
|---|
| | | 0 | 1a | 1b | 2a | 2b | 3a | 3b | 4 |
| Predicted class | 0 | 346 | 96 | 70 | 0 | 48 | 0 | 33 | 117 |
| 1 | 19 | 269 | 295 | 365 | 317 | 365 | 332 | 248 |
Table 11.
Number of consecutive errors (both false negatives and false positives) by model and prediction task. All errors are also shown for comparison.
Table 11.
Number of consecutive errors (both false negatives and false positives) by model and prediction task. All errors are also shown for comparison.
| Task | Algorithm | All Errors | 2 Consecutive Errors | 3 Consecutive Errors | 4 Consecutive Errors |
|---|
| MC | RF | 28 (1.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) |
| MC | SVM | 10 (0.3%) | 0 (0.00%) | 0 (0.0%) | 0 (0.0%) |
| TC | RF | 334 (22.9%) | 151 (10.3%) | 77 (5.27%) | 38 (2.60%) |
| TC | SVM | 338 (23.2%) | 157 (10.8%) | 83 (5.68%) | 42 (2.88%) |
| OC | SVM | 383 (13.1%) | 115 (3.9%) | 40 (1.37%) | 17 (0.58%) |
Table 12.
Definition of hard and soft errors for evaluation of the modified predictions.
Table 12.
Definition of hard and soft errors for evaluation of the modified predictions.
| | | Observed |
|---|
| | | Normal | Anomaly |
| Predicted | HN | TN | Hard FN |
| SN | TN | Soft FN |
| SP | Soft FP | TP |
| HP | Hard FP | TP |
Table 13.
Confusion matrix for the validation set and the RF model. Multi-class classification.
Table 13.
Confusion matrix for the validation set and the RF model. Multi-class classification.
| | | Observed Class |
|---|
| | | 0 | 1a | 1b | 2a | 2b | 3a | 3b | 4 |
| Predicted class | HN | 332 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SN | 14 | 1 | 0 | 0 | 0 | 0 | 0 | 5 |
| SP | 13 | 60 | 3 | 1 | 5 | 1 | 5 | 18 |
| HP | 5 | 303 | 361 | 363 | 359 | 363 | 359 | 341 |
Table 14.
Confusion matrix for the validation set and the SVM model. Multi-class classification.
Table 14.
Confusion matrix for the validation set and the SVM model. Multi-class classification.
| | | Observed Class |
|---|
| | | 0 | 1a | 1b | 2a | 2b | 3a | 3b | 4 |
| Predicted class | HN | 347 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SN | 8 | 0 | 0 | 0 | 0 | 0 | 0 | 2 |
| SP | 8 | 9 | 1 | 1 | 1 | 1 | 1 | 5 |
| HP | 1 | 355 | 363 | 363 | 363 | 363 | 363 | 357 |
Table 15.
Confusion matrix for the validation set and the RF model. Two-class classification.
Table 15.
Confusion matrix for the validation set and the RF model. Two-class classification.
| | | Observed Class |
|---|
| | | 0 | 1a | 1b | 2a | 2b | 3a | 3b | 4 |
| Predicted class | HN | 359 | 0 | 90 | 0 | 59 | 0 | 1 | 0 |
| SN | 3 | 0 | 84 | 0 | 86 | 0 | 22 | 0 |
| SP | 2 | 0 | 85 | 0 | 85 | 0 | 23 | 0 |
| HP | 0 | 0 | 105 | 0 | 134 | 0 | 318 | 0 |
Table 16.
Confusion matrix for the validation set and the SVM model. Two-class classification.
Table 16.
Confusion matrix for the validation set and the SVM model. Two-class classification.
| | | Observed Class |
|---|
| | | 0 | 1a | 1b | 2a | 2b | 3a | 3b | 4 |
| Predicted class | HN | 359 | 0 | 180 | 0 | 139 | 0 | 1 | 0 |
| SN | 3 | 0 | 70 | 0 | 85 | 0 | 8 | 0 |
| SP | 2 | 0 | 71 | 0 | 84 | 0 | 9 | 0 |
| HP | 0 | 0 | 43 | 0 | 56 | 0 | 346 | 0 |
Table 17.
Confusion matrix for the validation set and the SVM model. One-class classification.
Table 17.
Confusion matrix for the validation set and the SVM model. One-class classification.
| | | Observed Class |
|---|
| | | 0 | 1a | 1b | 2a | 2b | 3a | 3b | 4 |
| Predicted class | HN | 329 | 30 | 18 | 0 | 11 | 0 | 5 | 48 |
| SN | 17 | 66 | 52 | 0 | 37 | 0 | 28 | 69 |
| SP | 16 | 67 | 53 | 1 | 37 | 1 | 29 | 70 |
| HP | 3 | 202 | 242 | 364 | 280 | 364 | 303 | 178 |
Table 18.
Model comparison for the validation set.
Table 18.
Model comparison for the validation set.
| | RF MC | SVM MC | RF TC | SVM TC | SVM OC |
|---|
| | # | pct | # | pct | # | pct | # | pct | # | pct |
| TN | 346 | 11.9% | 355 | 12.2% | 362 | 24.9% | 362 | 24.9% | 346 | 11.9% |
| Hard FN | 0 | 0.0% | 0 | 0.0% | 150 | 10.3% | 320 | 22.0% | 112 | 3.8% |
| Soft FN | 6 | 0.2% | 2 | 0.1% | 192 | 13.2% | 163 | 11.2% | 252 | 8.7% |
| Hard FP | 5 | 0.2% | 1 | 0.0% | 0 | 0.0% | 0 | 0.0% | 3 | 0.1% |
| Soft FP | 13 | 0.4% | 8 | 0.3% | 2 | 0.1% | 2 | 0.1% | 16 | 0.5% |
| TP | 2542 | 87.3% | 2546 | 87.4% | 750 | 51.5% | 609 | 41.8% | 2191 | 75.2% |
| # samples | 2912 | 100% | 2912 | 100% | 1456 | 100% | 1456 | 100% | 2912 | 100% |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).