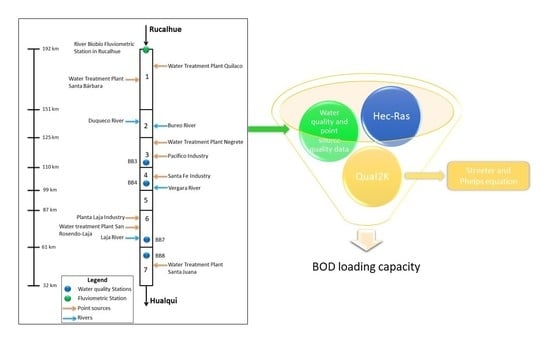
Modeling Biological Oxygen Demand Load Capacity in a Data-Scarce Basin with Important Anthropogenic Interventions
Abstract
:1. Introduction
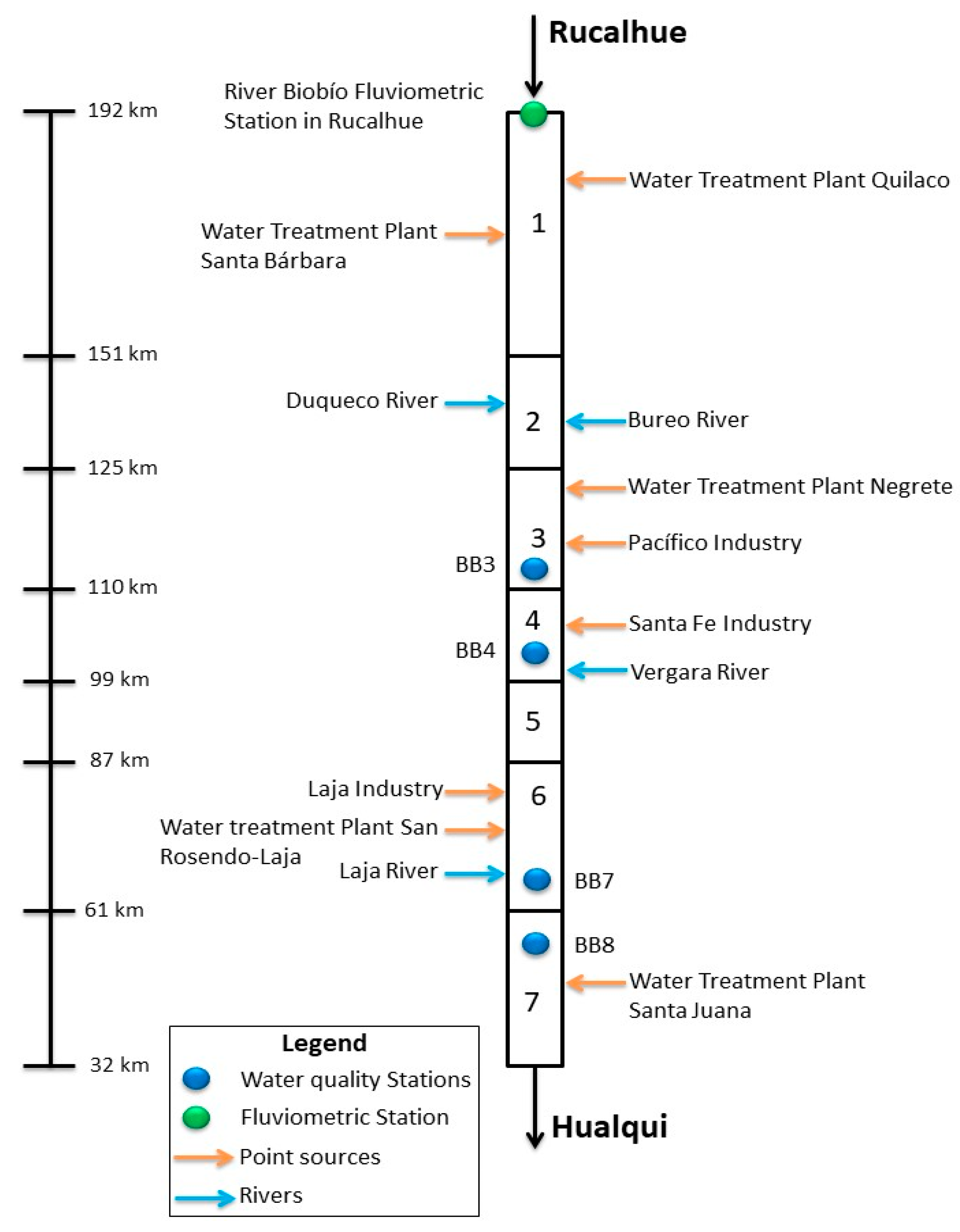
2. Study Area
Study Basin
3. Water Quality Legislation in Chile
4. Water Quality Model
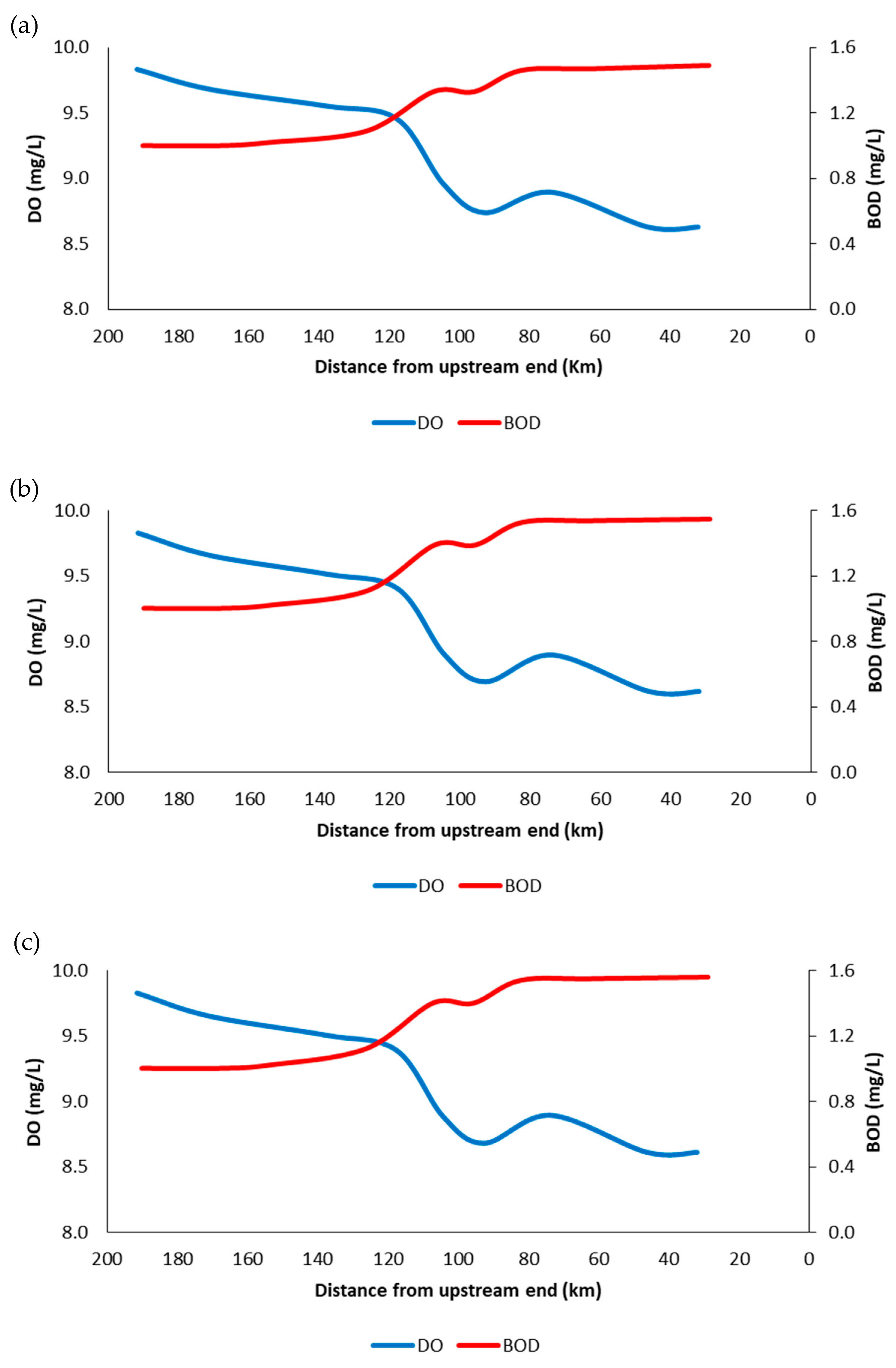
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- WWAP. Informe Mundial de Naciones Unidas Sobre el Desarrollo de los Recursos Hidricos 2019-No Dejar a Nadie Atrás; UNESCO: Paris, Fance, 2019. [Google Scholar]
- Hutchins, M.G.; Abesser, C.; Prudhomme, C.; Elliott, J.A.; Bloomfield, J.P.; Mansour, M.M.; Hitt, O.E. Combined impacts of future land-use and climate stressors on water resources and quality in groundwater and surface waterbodies of the upper Thames river basin, UK. Sci. Total Environ. 2018, 631–632, 962–986. [Google Scholar] [CrossRef]
- Mack, L.; Andersen, H.E.; Beklioglu, M.; Bucak, T.; Couture, R.M.; Cremona, F.; Ferreira, M.T.; Hutchins, M.G.; Mischke, U.; Molina-Navarro, E.; et al. The future depends on what we do today—Projecting Europe’s surface water quality into three different future scenarios. Sci. Total Environ. 2019, 668, 470–484. [Google Scholar] [CrossRef]
- GEO-5. Environment for the Future We Want; UNEP: Nairobi, Kenya, 2012. [Google Scholar]
- GEO-6. Regional Assessment for Latin America and the Caribbean; UNEP: Nairobi, Kenya, 2016. [Google Scholar]
- WWAP. Informe Mundial de las Naciones Unidas sobre el Desarrollo de los Recursos Hídricos 2020: Agua y Cambio Climático; UNESCO: Paris, Fance, 2020. [Google Scholar]
- Guo, D.L.; Lintern, A.; Webb, J.A.; Ryu, D.; Bende-Michl, U.; Liu, S.C.; Western, A.W. A data-based predictive model for spatiotemporal variability in stream water quality. Hydrol. Earth Syst. Sci. 2020, 24, 827–847. [Google Scholar] [CrossRef] [Green Version]
- Hernandez-Ramirez, A.G.; Martinez-Tavera, E.; Rodriguez-Espinosa, P.F.; Mendoza-Perez, J.A.; Tabla-Hernandez, J.; Escobedo-Urias, D.C.; Jonathan, M.P.; Sujitha, S.B. Detection, provenance and associated environmental risks of water quality pollutants during anomaly events in River Atoyac, Central Mexico: A real-time monitoring approach. Sci. Total Environ. 2019, 669, 1019–1032. [Google Scholar] [CrossRef] [PubMed]
- Pejman, A.H.; Bidhendi, G.R.N.; Karbassi, A.R.; Mehrdadi, N.; Bidhendi, M.E. Evaluation of spatial and seasonal variations in surface water quality using multivariate statistical techniques. Int. J. Environ. Sci. Technol. 2009, 6, 467–476. [Google Scholar] [CrossRef] [Green Version]
- Mirauda, D.; Caniani, D.; Colucci, M.T.; Ostoich, M. Assessing the fluvial system resilience of the river Bacchiglione to point sources of pollution in Northeast Italy: A novel Water Resilience Index (WRI) approach. Environ. Sci. Pollut. Res. 2021, 28, 36775–36792. [Google Scholar] [CrossRef]
- Mukundan, R.; Acharya, N.; Gelda, R.K.; Frei, A.; Owens, E.M. Modeling streamflow sensitivity to climate change in New York City water supply streams using a stochastic weather generator. J. Hydrol. Reg. Stud. 2019, 21, 147–158. [Google Scholar] [CrossRef]
- Montes, R.T.; Navarro, I.; Domínguez, R.; Jiménez, B. Modificación de la capacidad de autodepuración del río Magdalena ante el cambio climático. Tecnol. Cienc. Agua 2013, 4, 71–83. [Google Scholar]
- Bailey, R.T.; Ahmadi, M. Spatial and temporal variability of in-stream water quality parameter influence on dissolved oxygen and nitrate within a regional stream network. Ecol. Model. 2014, 277, 87–96. [Google Scholar] [CrossRef]
- Bhargava, D.S. Models for Polluted Streams Subject to Fast Purification. Water Res. 1986, 20, 1–8. [Google Scholar] [CrossRef]
- Katyal, D. Water quality indices used for surface water vulnerability assessment. Int. J. Environ. Sci. 2011, 2, 154–173. [Google Scholar]
- Fan, C.; Ko, C.H.; Wang, W.S. An innovative modeling approach using Qual2K and HEC-RAS integration to assess the impact of tidal effect on River Water quality simulation. J. Environ. Manag. 2009, 90, 1824–1832. [Google Scholar] [CrossRef]
- Gurjar, S.K.; Tare, V. Spatial-temporal assessment of water quality and assimilative capacity of river Ramganga, a tributary of Ganga using multivariate analysis and QUEL2K. J. Clean. Prod. 2019, 222, 550–564. [Google Scholar] [CrossRef]
- Streeter, H.W.; Phelps, E.B. A study of the pollution and natural purification of the Ohio River. III Factors concerned in the phenomena of oxidation and reaeration. Public Realt. Bull. 1925, 146, 75. [Google Scholar]
- Ji, X.L.; Shang, X.; Dahlgren, R.A.; Zhang, M.H. Prediction of dissolved oxygen concentration in hypoxic river systems using support vector machine: A case study of Wen-Rui Tang River, China. Environ. Sci. Pollut. Res. 2017, 24, 16062–16076. [Google Scholar] [CrossRef]
- Nagisetty, R.M.; Flynn, K.F.; Uecker, D. Dissolved oxygen modeling of effluent-dominated macrophyte-rich Silver Bow Creek. Ecol. Model. 2019, 393, 85–97. [Google Scholar] [CrossRef]
- Xu, J.; Jin, G.Q.; Tang, H.W.; Mo, Y.M.; Wang, Y.G.; Li, L. Response of water quality to land use and sewage outfalls in different seasons. Sci. Total Environ. 2019, 696. [Google Scholar] [CrossRef]
- Vaideliene, A.; Michailov, N. Dam influence on the river self-purification. In Proceedings of the 7th International Conference Environmental Engineering, Vilnius, Lithuania, 22–23 May 2008; pp. 748–757. [Google Scholar]
- VishnuRadhan, R.; Zainudin, Z.; Sreekanth, G.B.; Dhiman, R.; Salleh, M.N.; Vethamony, P. Temporal water quality response in an urban river: A case study in peninsular Malaysia. Appl. Water Sci. 2017, 7, 923–933. [Google Scholar] [CrossRef] [Green Version]
- Zubaidah, T.; Karnaningroem, N.; Slamet, A. The Self-Purification Ability in the Rivers of Banjarmasin, Indonesia. J. Ecol. Eng. 2019, 20, 177–182. [Google Scholar] [CrossRef]
- Diego, C.A. Modelo de Calidad de Aguas Para Determinar la Capacidad Autodepurativa del Río BioBío de las Descargas de la Industria de la Celulosa y Papel; Universidad de Concepción: Concepción, Chile, 2001. [Google Scholar]
- Gonzalez, S.O.; Almeida, C.A.; Calderon, M.; Mallea, M.A.; Gonzalez, P. Assessment of the water self-purification capacity on a river affected by organic pollution: Application of chemometrics in spatial and temporal variations. Environ. Sci. Pollut. Res. 2014, 21, 10583–10593. [Google Scholar] [CrossRef]
- Chi, M.; Zhang, D.; Fan, G.; Zhang, W.; Liu, H. Prediction of water resource carrying capacity by the analytic hierarchy process-fuzzy discrimination method in a mining area. Ecol. Indic. 2019, 96, 647–655. [Google Scholar] [CrossRef]
- Darmian, M.D.; Khodabandeh, F.; Azizyan, G.; Giesy, J.P.; Hashemi Monfared, S.A. Analysis of assimilation capacity for conservation of water quality: Controllable discharges of pollutants. Arab. J. Geosci. 2020, 13, 888. [Google Scholar] [CrossRef]
- Camacho, R.A.; Martin, J.L.; Wool, T.; Singh, V.P. A framework for uncertainty and risk analysis in Total Maximum Daily Load applications. Environ. Model. Softw. 2018, 101, 218–235. [Google Scholar] [CrossRef]
- Chang, C.L.; Hong, T.Y. Applying environmental models to determine total maximum daily loads for reservoir watershed management. Int. J. Environ. Sci. Technol. 2019, 16, 5635–5642. [Google Scholar] [CrossRef]
- Xu, Y.L.; Bosch, D.J.; Wagena, M.B.; Collick, A.S.; Easton, Z.M. Meeting Water Quality Goals by Spatial Targeting of Best Management Practices under Climate Change. Environ. Manag. 2019, 63, 173–184. [Google Scholar] [CrossRef]
- Fan, C.H.; Chen, K.H.; Huang, Y.Z. Model-based carrying capacity investigation and its application to total maximum daily load (TMDL) establishment for river water quality management: A case study in Taiwan. J. Clean. Prod. 2021, 291, 125251. [Google Scholar] [CrossRef]
- Patil, A.; Deng, Z.Q.; Malone, R.F. Temporal scale-induced uncertainty in load duration curves for instream-dissolved oxygen. Environ. Monit. Assess. 2013, 185, 1939–1949. [Google Scholar] [CrossRef]
- Wang, X.Y.; Pang, S.J.; Yang, L.; Melching, C.S. A framework for determining the maximum allowable external load that will meet a guarantee probability of achieving water quality targets. Sci. Total Environ. 2020, 735, 139421. [Google Scholar] [CrossRef]
- Zhang, R.B.; Gao, H.L.; Zhu, W.T.; Hu, W.; Ye, R. Calculation of permissible load capacity and establishment of total amount control in the Wujin River Catchment-a tributary of Taihu Lake, China. Environ. Sci. Pollut. Res. 2015, 22, 11493–11503. [Google Scholar] [CrossRef]
- Antunes, I.M.H.R.; Albuquerque, M.T.D.; Oliveira, S.F.; Sánz, G. Predictive scenarios for surface water quality simulation—A watershed case study. Catena 2018, 170, 283–289. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Hong Quan, N.; Quang, N.X.; Hieu, N.D.; Thang, L.V. Spatio-temporal pattern of water quality in the Saigon-Dong Nai river system due to waste water pollution sources. Int. J. River Basin Manag. 2021, 19, 221–243. [Google Scholar] [CrossRef]
- Fajardo, M.I.A.D.; Agudelo, V.M.S.R.N. Simulación de calidad del agua en un tramo de la sub-cuenca río alto Bogotá en el periodo 2014–2016 a partir del modelo HEC-RAS. Rev. Colomb. Cienc. Anim. Recia 2019, 11, 43–55. [Google Scholar]
- Halaj, P.; Barek, V.; Veliskova, Y.P.; Barekova, A.P.; Pechacova, K.; Stredanska, A. Longitudinal Dispersion Coefficient Impact Assessment On HEC-RAS Water Quality Model Outputs. In Proceedings of the International Multidisciplinary Scientific GeoConference: SGEM, Albena, Bulgaria, 16–22 June 2013; pp. 213–220. [Google Scholar]
- Olaoye, I.A.; Confesor, R.B.; Ortiz, J.D. Impact of Seasonal Variation in Climate on Water Quality of Old Woman Creek Watershed Ohio Using SWAT. Climate 2021, 9, 50. [Google Scholar] [CrossRef]
- Woo, S.-Y.; Kim, S.-J.; Lee, J.-W.; Kim, S.-H.; Kim, Y.-W. Evaluating the impact of interbasin water transfer on water quality in the recipient river basin with SWAT. Sci. Total Environ. 2021, 776, 145984. [Google Scholar] [CrossRef]
- Bui, H.H.; Ha, N.H.; Nguyen, T.N.D.; Nguyen, A.T.; Pham, T.T.H.; Kandasamy, J.; Nguyen, T.V. Integration of SWAT and QUAL2K for water quality modeling in a data scarce basin of Cau River basin in Vietnam. Ecohydrol. Hydrobiol. 2019, 19, 210–223. [Google Scholar] [CrossRef]
- Arriagada, P.; Dieppois, B.; Sidibe, M.; Link, O. Impacts of Climate Change and Climate Variability on Hydropower Potential in Data-Scarce Regions Subjected to Multi-Decadal Variability. Energies 2019, 12, 2747. [Google Scholar] [CrossRef] [Green Version]
- Bolinches, A.; De Stefano, L.; Paredes-Arquiola, J. Designing river water quality policy interventions with scarce data: The case of the Middle Tagus Basin, Spain. Hydrol. Sci. J. 2020, 65, 749–762. [Google Scholar] [CrossRef]
- Shah, M.I.; Javed, M.F.; Abunama, T. Proposed formulation of surface water quality and modelling using gene expression, machine learning, and regression techniques. Environ. Sci. Pollut. Res. 2021, 28, 13202–13220. [Google Scholar] [CrossRef]
- Yevenes, M.A.; Figueroa, R.; Parra, O. Seasonal drought effects on the water quality of the Biobio River, Central Chile. Environ. Sci. Pollut. Res. 2018, 25, 13844–13856. [Google Scholar] [CrossRef]
- Parra, O.; Figueroa, R.; Valdovinos, C.; Habit, E.; Díaz, M.E. Programa de Monitoreo de la Calidad del Agua del Sistema río Biobío 1994-2012: Aplicación del Anteproyecto de Norma de la Calidad del Agua del río Biobío, Concepción; Universidad de Concepción: Concepción, Chile, 2013. [Google Scholar]
- EULA-Chile, C. Centro EULA-Chile: Evolución y Perspectivas a 30 Años de su Creación; Universidad de Concepción (Chile); EULA-CHILE. Centro de Ciencias Ambientales: Concepción, Chile, 2020. [Google Scholar]
- Díaz, M.E.; Figueroa, R.; Alonso, M.L.S.; Vidal-Abarca, M.R. Exploring the complex relations between water resources and social indicators: The Biobío Basin (Chile). Ecosyst. Serv. 2018, 31, 84–92. [Google Scholar] [CrossRef]
- DGA. Dirección General de Aguas. Información Oficial Hidrometeorológica y de Calidad de Aguas en Línea. Available online: https://snia.mop.gob.cl/BNAConsultas/reportes (accessed on 1 September 2014).
- Melo, O.; Perez, J. Water Quality Policy. In Water Policy in Chile; Donoso, G., Ed.; Springer International Publishing: Cham, Switzerland, 2018; pp. 87–102. [Google Scholar]
- Decree-Decreto N°9. Norma Secundaria de Calidad Ambiental para la Protección de las Aguas Continentales Superficiales de la Cuenca del Río Biobío; Ministerio de Medio Ambiente, Gobierno de Chile: Santiago, Chile, 2015.
- Long, B.T. Inverse algorithm for Streeter-Phelps equation in water pollution control problem. Math. Comput. Simul. 2020, 171, 119–126. [Google Scholar] [CrossRef]
- Churchill, M.A. Analysis of a Stream’s Capacity for Assimilating Pollution. Sew. Ind. Wastes 1954, 26, 887–904. [Google Scholar]
- Kannel, P.R.; Kanel, S.R.; Lee, S.; Lee, Y.S.; Gan, T.Y. A Review of Public Domain Water Quality Models for Simulating Dissolved Oxygen in Rivers and Streams. Environ. Model. Assess. 2011, 16, 183–204. [Google Scholar] [CrossRef]
- Khorashadizadeh, M.; Azizyan, G.; Monfared, S.A.H.; Akbarpour, A.; Shabani, A. A timetable and spatial planning for pollutant entrance to the river. Int. J. Environ. Sci. Technol. 2020, 17, 4171–4188. [Google Scholar] [CrossRef]
- Mcbride, G.B. Nomographs for Rapid Solutions for the Streeter-Phelps Equations. J. Water Pollut. Control Fed. 1982, 54, 378–384. [Google Scholar]
- Nuruzzaman, M.; Al-Mamun, A.; Bin Salleh, M.N. A Modified Laboratory Approach to Determine Reaeration Rate for River Water. Arab. J. Sci. Eng. 2018, 43, 2037–2051. [Google Scholar] [CrossRef]
- Reckhow, K.H. Water-Quality Simulation Modeling and Uncertainty Analysis for Risk Assessment and Decision-Making. Ecol. Model. 1994, 72, 1–20. [Google Scholar] [CrossRef]
- Sharma, D.; Kansal, A.; Pelletier, G. Water quality modeling for urban reach of Yamuna river, India (1999–2009), using QUAL2Kw. Appl. Water Sci. 2017, 7, 1535–1559. [Google Scholar] [CrossRef] [Green Version]
- Zhang, R.B.; Qian, X.; Li, H.M.; Yuan, X.C.; Ye, R. Selection of optimal river water quality improvement programs using QUAL2K: A case study of Taihu Lake Basin, China. Sci. Total Environ. 2012, 431, 278–285. [Google Scholar] [CrossRef]
- Abdeveis, S.; Sedghi, H.; Hassonizadeh, H.; Babazadeh, H. Application of Water Quality Index and Water Quality Model QUAL2K for Evaluation of Pollutants in Dez River, Iran. Water Resour. 2020, 47, 892–903. [Google Scholar] [CrossRef]
- Chapra, S.C.; Pelletier, G.J.; Tao, H. QUAL2K: A Modeling Framework for Simulating River and Stream Water Quality, Version 2.11: Documentation and Users Manual; Civil and Environmental Engineering Dept., Tufts University: Medford, MA, USA, 2008. [Google Scholar]
- Cho, J.H.; Ha, S.R. Parameter optimization of the QUAL2K model for a multiple-reach river using an influence coefficient algorithm. Sci. Total Environ. 2010, 408, 1985–1991. [Google Scholar] [CrossRef]
- Walling, B.; Chaudhary, S.; Dhanya, C.T.; Kumar, A. Estimation of environmental flow incorporating water quality and hypothetical climate change scenarios. Environ. Monit. Assess. 2017, 189, 861. [Google Scholar] [CrossRef]
- U.S. Department of the Interior. U.S.G.S. Earth Explorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 1 September 2014).
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. Asabe 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. Asabe 2015, 58, 1763–1785. [Google Scholar] [CrossRef] [Green Version]
- Parajuli, P.B.; Nelson, N.O.; Frees, L.D.; Mankin, K.R. Comparison of AnnAGNPS and SWAT model simulation results in USDA-CEAP agricultural watersheds in south-central Kansas. Hydrol. Process. 2009, 23, 748–763. [Google Scholar] [CrossRef]
- Hadiani, M.; Asl, S.J.; Banafsheh, M.R.; Dinpajouh, Y. Investigation on the Effect of the Season in Determination of Manning Roughness Coefficient in Predicting Drought Hydraulic Behavior (Case Study: Haraz River). World Appl. Sci. J. 2013, 22, 307–312. [Google Scholar]
- Norma Chilena Oficial. NCh 1333/1987. Requisitos de calidad de agua para diferentes usos. Available online: https://ciperchile.cl/pdfs/11-2013/norovirus/NCh1333-1978_Mod-1987.pdf (accessed on 20 October 2014).
- Langbein, W.B.; Durum, W.H. The Aeration Capacity of Streams; US Department of the Interior, Geological Survey: Washington, DC, USA, 1967; Volume 542.
- Bowie, G.L.; Mills, W.B.; Porcella, D.B.; Campbell, C.L.; Pagenkopf, J.R.; Rupp, G.L.; Johnson, K.M.; Chan, P.; Gherini, S.A.; Chamberlin, C. Rates, constants, and kinetics formulations in surface water quality modeling. Environ. Prot. Agency 1985, 600, 3–85. [Google Scholar]
- Link, O. Estimación de la capacidad de Reaireación en Ríos, Aplicación al Río Bío Bío, Informe Memoria de Título Para Optar al Título de Ingeniero Civil; Universidad de Concepción: Concepción, Chile, 1998. [Google Scholar]
- Anderson, T.W.; Darling, D.A. Asymptotic Theory of Certain “Goodness of Fit” Criteria Based on Stochastic Processes. Ann. Math. Stat. 1952, 23, 193–212. [Google Scholar] [CrossRef]
- Valdovinos, C.; Parra, O. La cuenca del río Biobío: Historia natural de un ecosistema de uso múltiple. Publ. Cent. EULA 2006, 1–25. [Google Scholar]
| Statistical Indicators | Calibration | Validation | Correlation |
|---|---|---|---|
| R2 | 0.999 | 0.845 | Optimum value 1 |
| NSE | 0.987 | 0.832 | Optimum value 1 |
| PBIAS | 0.225 | −0.291 | Optimum value 0 |
| d | 0.998 | 0.985 | Optimum value 1 |
| Section | ka (d−1) | kd (d−1) | θa | θd |
|---|---|---|---|---|
| 1 | 0.51 | 0.34 | 1.024 | 1.047 |
| 2 | 0.47 | 0.32 | 1.024 | 1.047 |
| 3 | 0.20 | 0.32 | 1.024 | 1.047 |
| 4 | 6.90 | 0.25 | 1.024 | 1.047 |
| 5 | 5.96 | 0.23 | 1.024 | 1.047 |
| 6 | 5.54 | 0.38 | 1.024 | 1.047 |
| 7 | 1.56 | 0.31 | 1.024 | 1.047 |
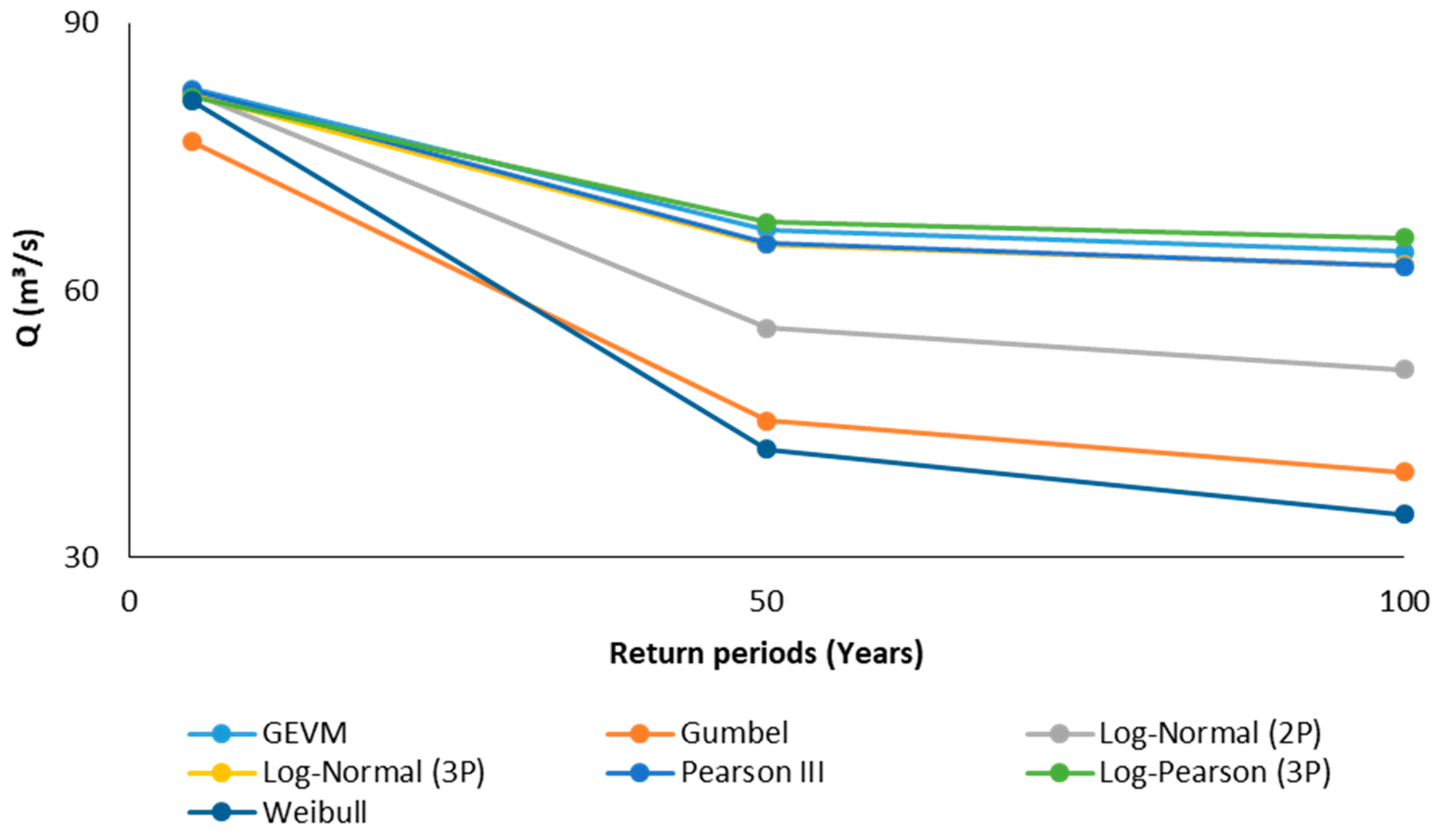
| Distribution | |||||||
|---|---|---|---|---|---|---|---|
| GEVM | Pearson III | Log-Normal (3P) | Log-Pearson (3P) | Weibull | Log-Normal (2P) | Gumbel | |
| A2 | 0.36 | 0.36 | 0.44 | 0.57 | 1.03 | 1.04 | 1.63 |
| Critical Value | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 | 2.50 |
| Approve | Yes | Yes | Yes | Yes | Yes | Yes | Yes |
| T (Years) | Q (m3/s) | BODmax (mg/L) | Distance (km) |
|---|---|---|---|
| 5 | 82.59 | 2078 | 104 |
| 50 | 66.82 | 1679 | 104 |
| 100 | 64.32 | 1580 | 104 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zurita, A.; Aguayo, M.; Arriagada, P.; Figueroa, R.; Díaz, M.E.; Stehr, A. Modeling Biological Oxygen Demand Load Capacity in a Data-Scarce Basin with Important Anthropogenic Interventions. Water 2021, 13, 2379. https://doi.org/10.3390/w13172379
Zurita A, Aguayo M, Arriagada P, Figueroa R, Díaz ME, Stehr A. Modeling Biological Oxygen Demand Load Capacity in a Data-Scarce Basin with Important Anthropogenic Interventions. Water. 2021; 13(17):2379. https://doi.org/10.3390/w13172379
Chicago/Turabian StyleZurita, Alejandra, Mauricio Aguayo, Pedro Arriagada, Ricardo Figueroa, María Elisa Díaz, and Alejandra Stehr. 2021. "Modeling Biological Oxygen Demand Load Capacity in a Data-Scarce Basin with Important Anthropogenic Interventions" Water 13, no. 17: 2379. https://doi.org/10.3390/w13172379
APA StyleZurita, A., Aguayo, M., Arriagada, P., Figueroa, R., Díaz, M. E., & Stehr, A. (2021). Modeling Biological Oxygen Demand Load Capacity in a Data-Scarce Basin with Important Anthropogenic Interventions. Water, 13(17), 2379. https://doi.org/10.3390/w13172379