Forecasting of Debris Flow Using Machine Learning-Based Adjusted Rainfall Information and RAMMS Model
Abstract
:1. Introduction
2. Theoretical Background
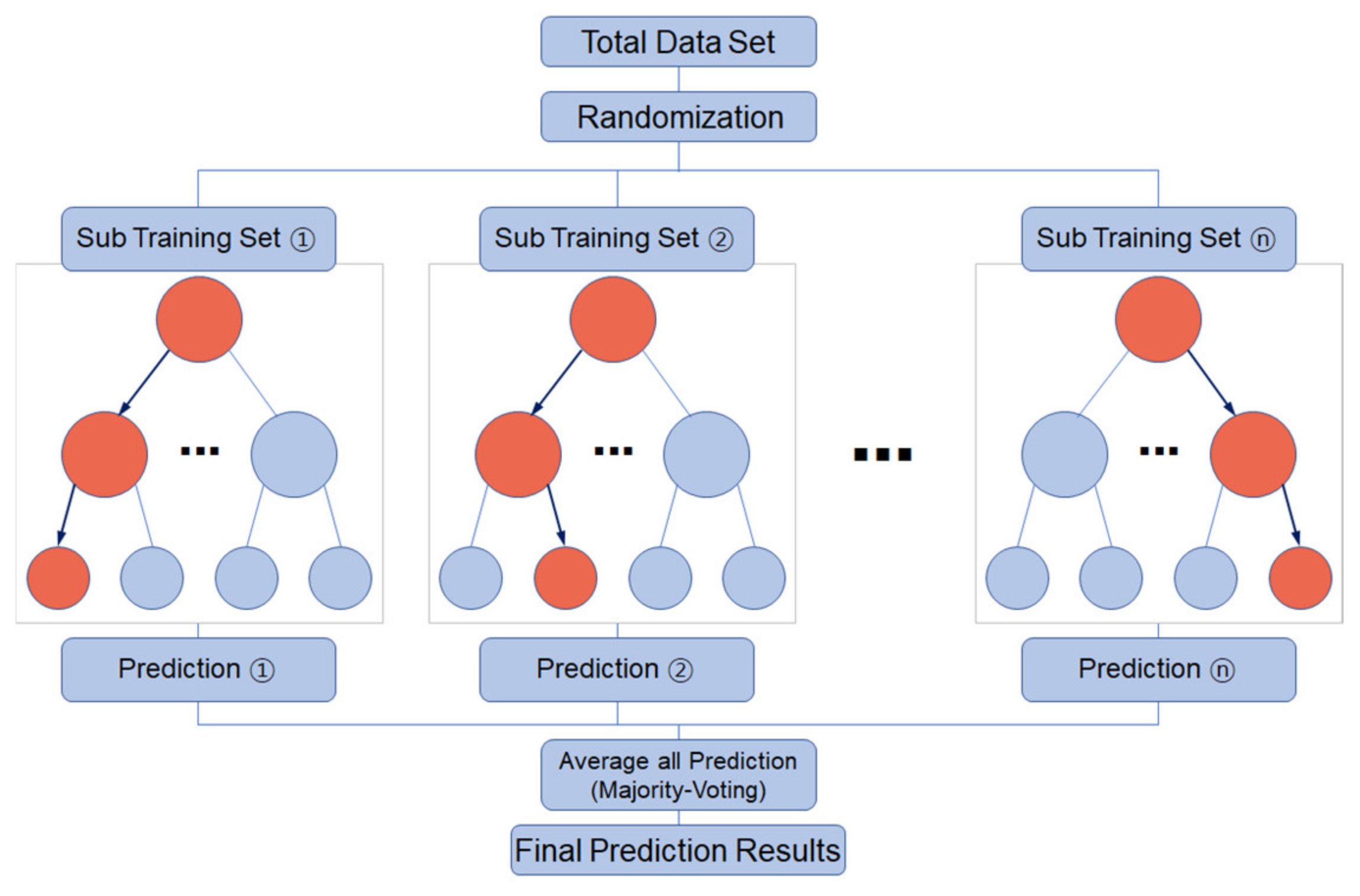
2.1. Machinge Learning (Random Forest)
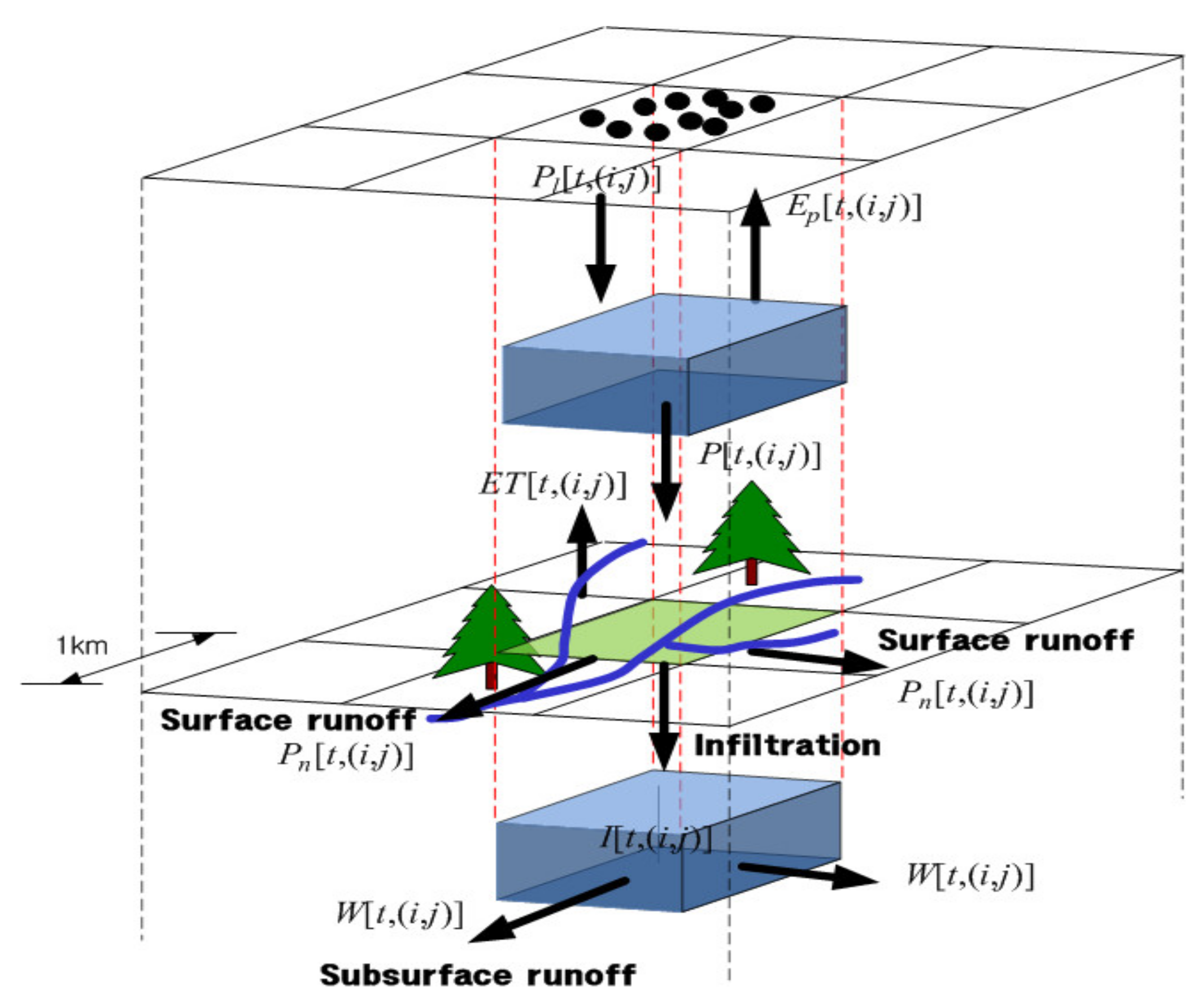
2.2. Spatial Runoff Assessment Tool (S-RAT)
2.3. Debris Flow Simulation
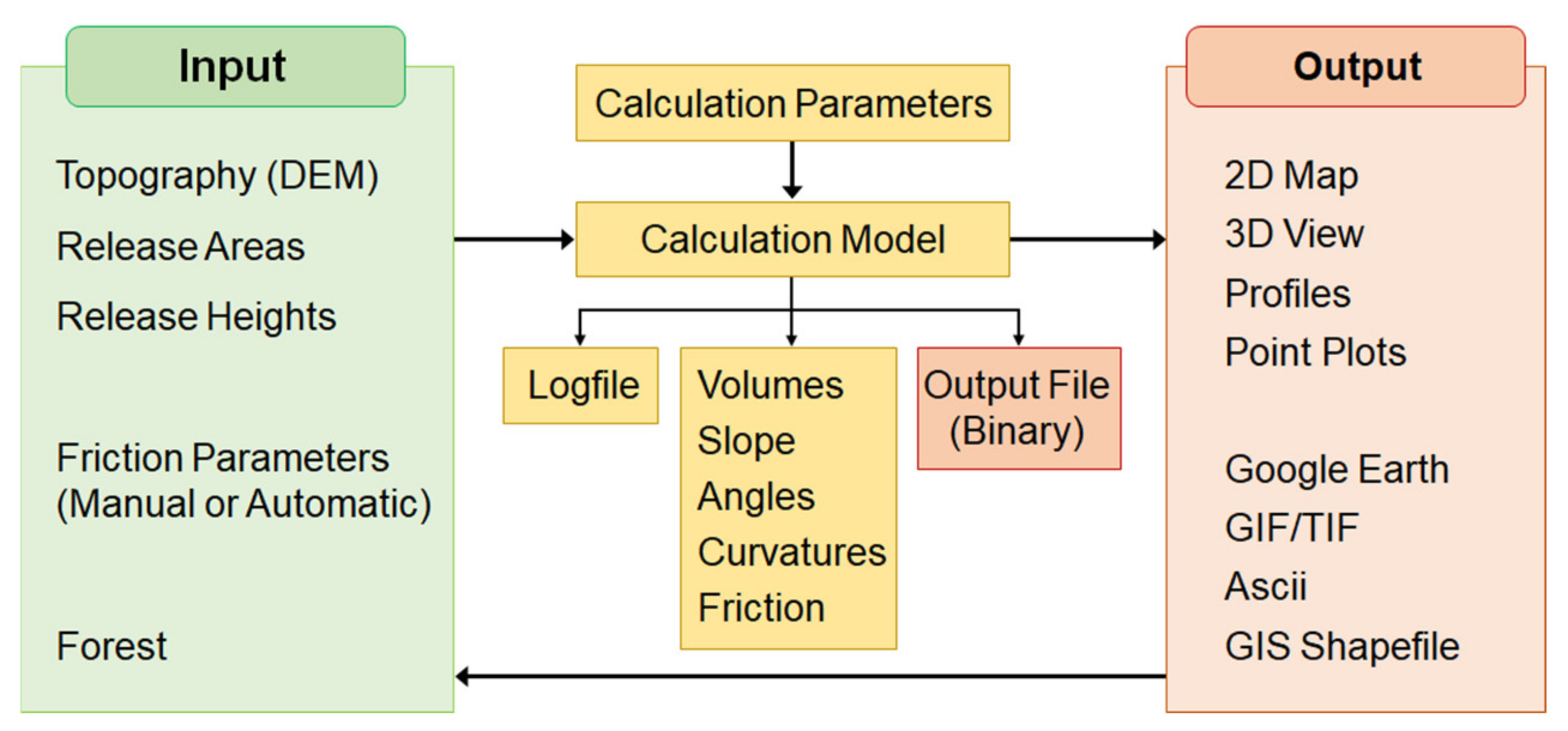
2.3.1. Two-Dimensional Rapid Mass Movements (RAMMS) Model
2.3.2. Calculation of Soil Volume
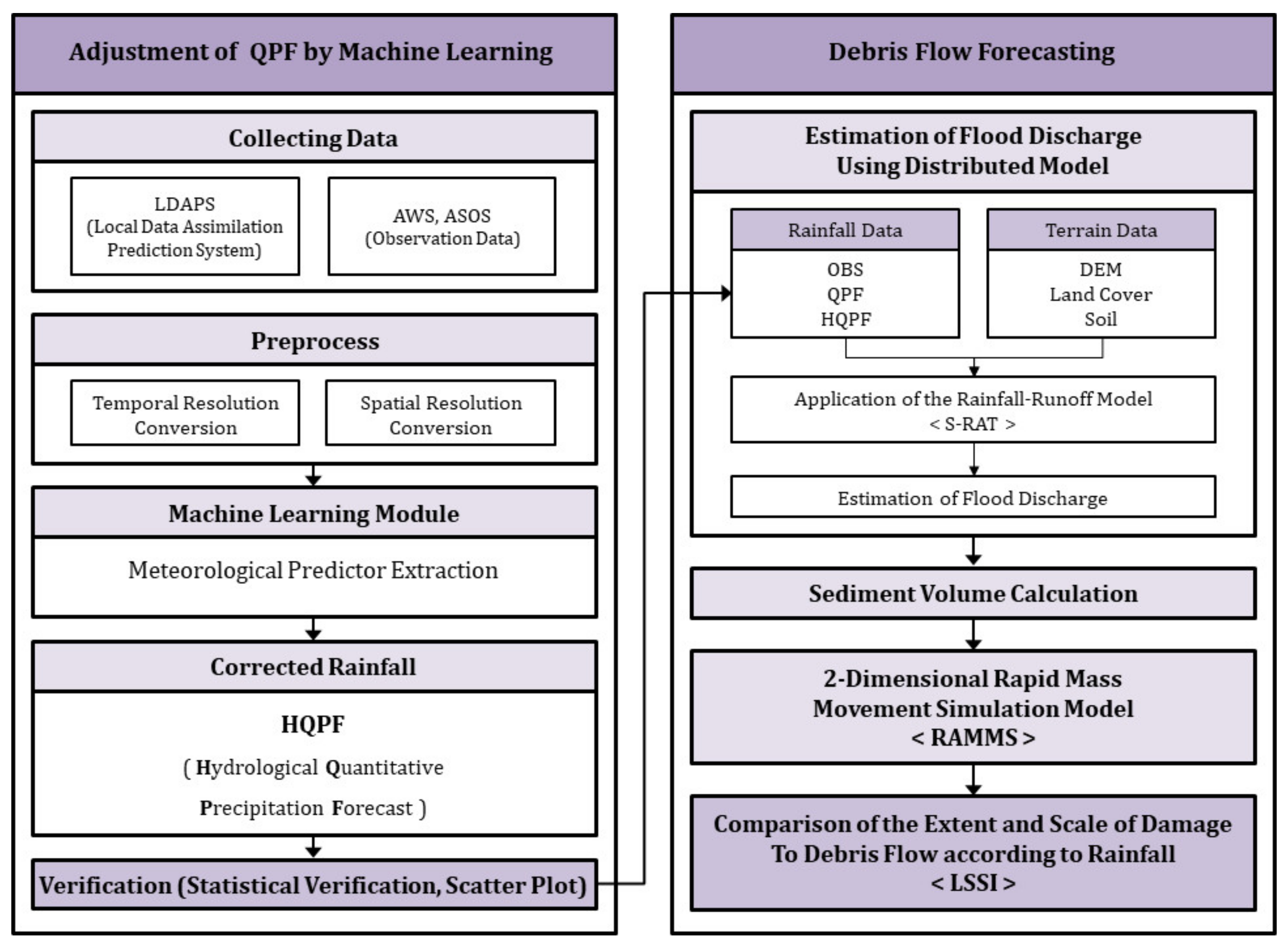
3. Analysis and Results
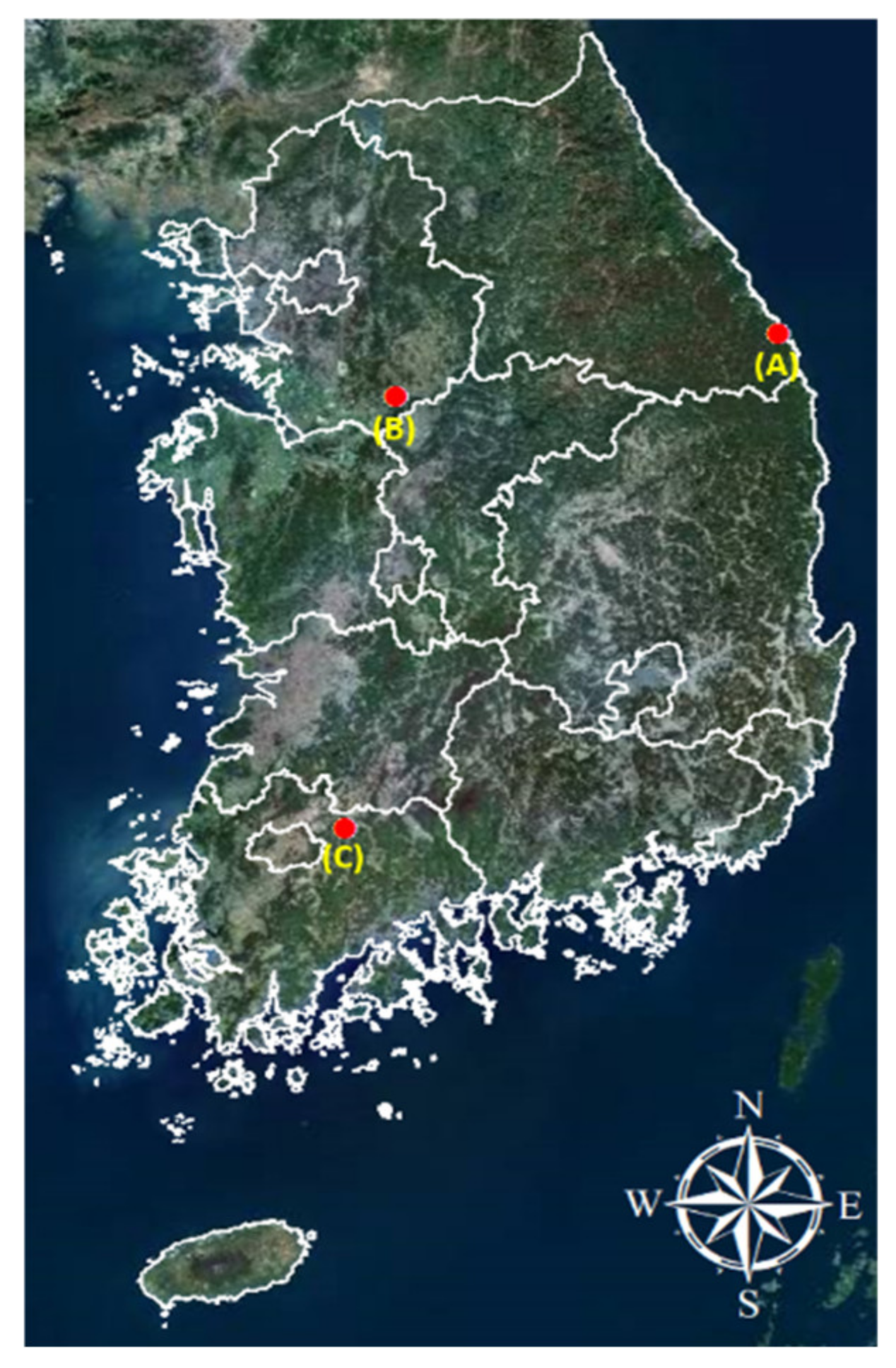
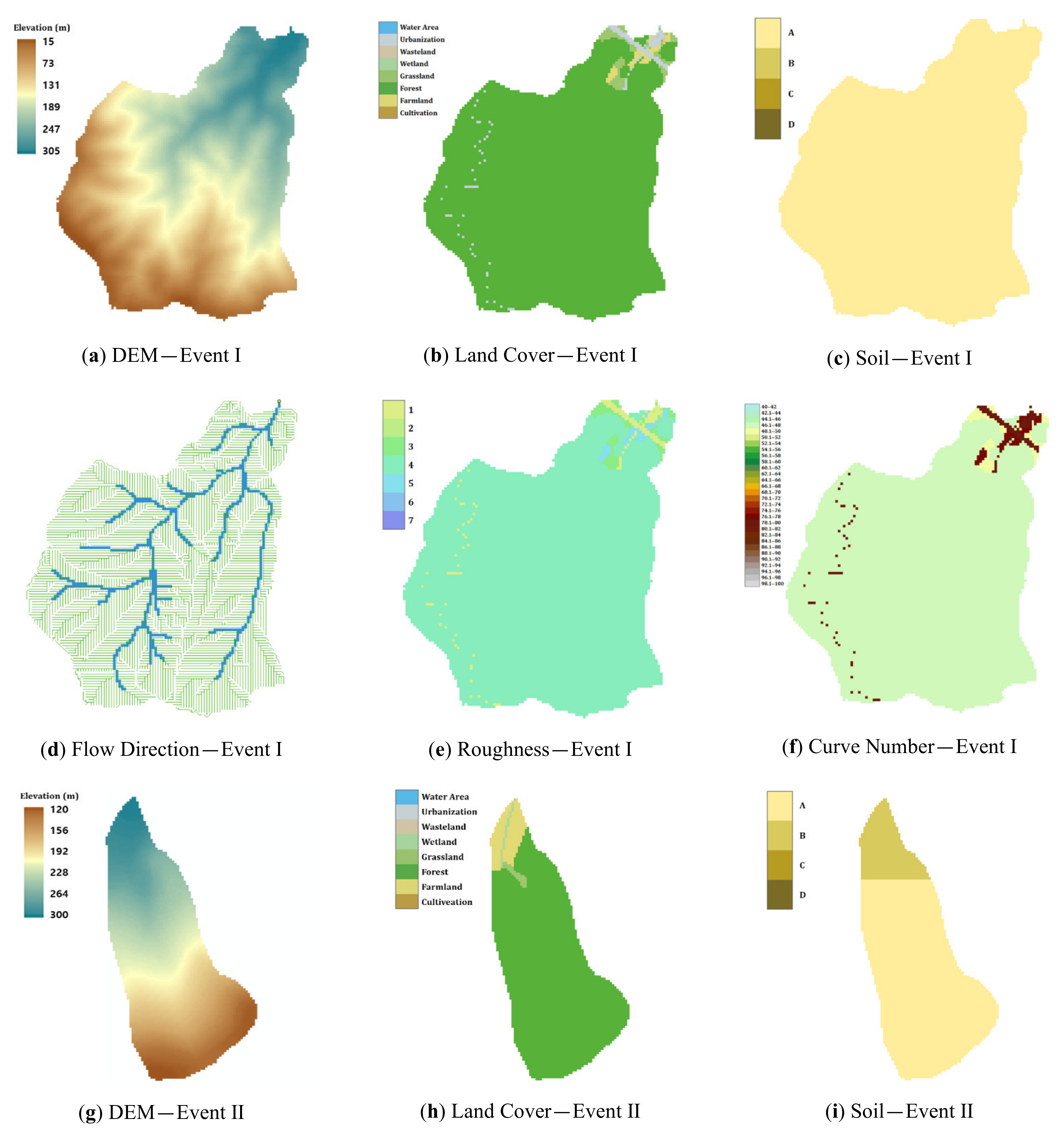
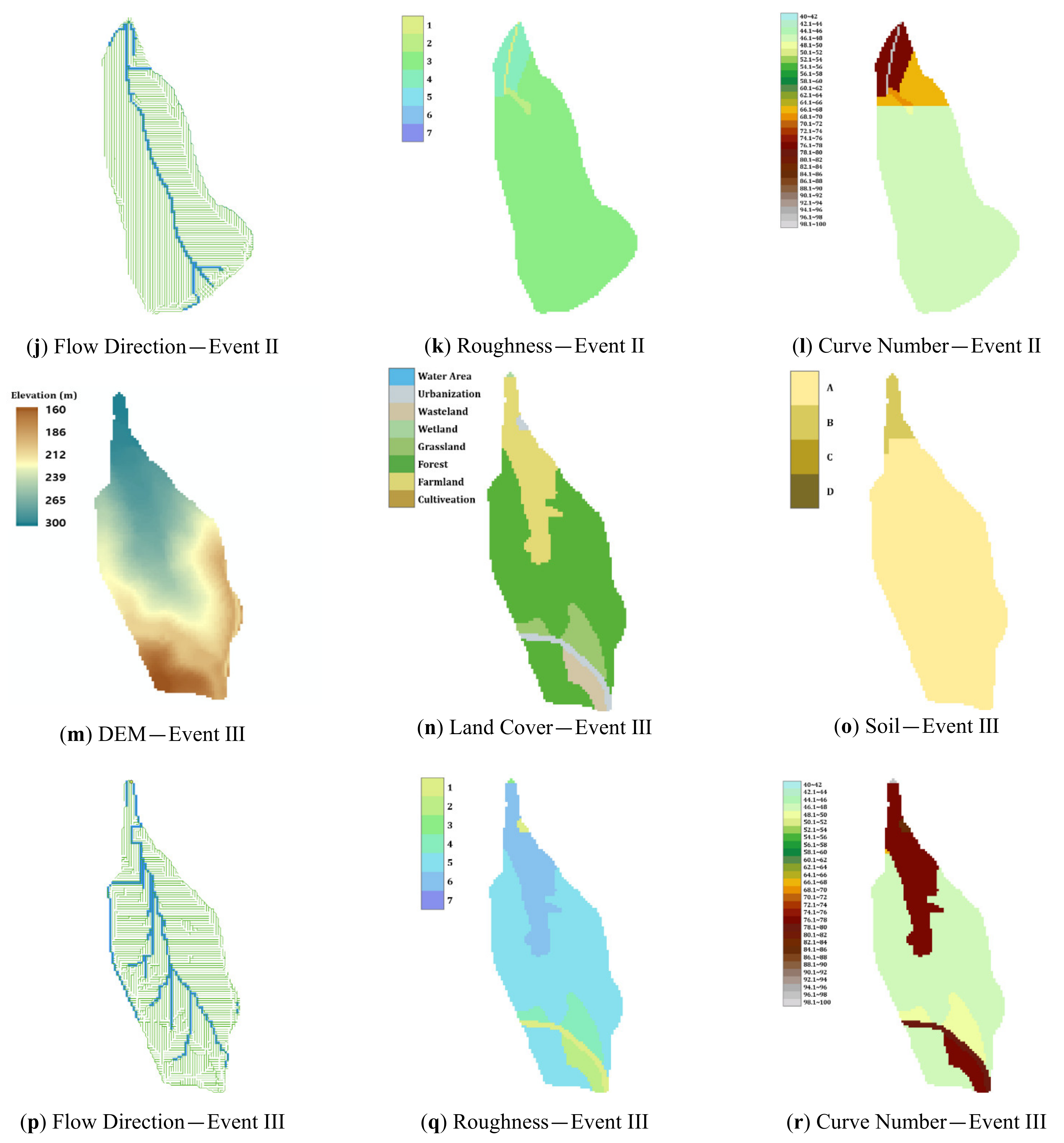
3.1. Selection of Analysis Areas
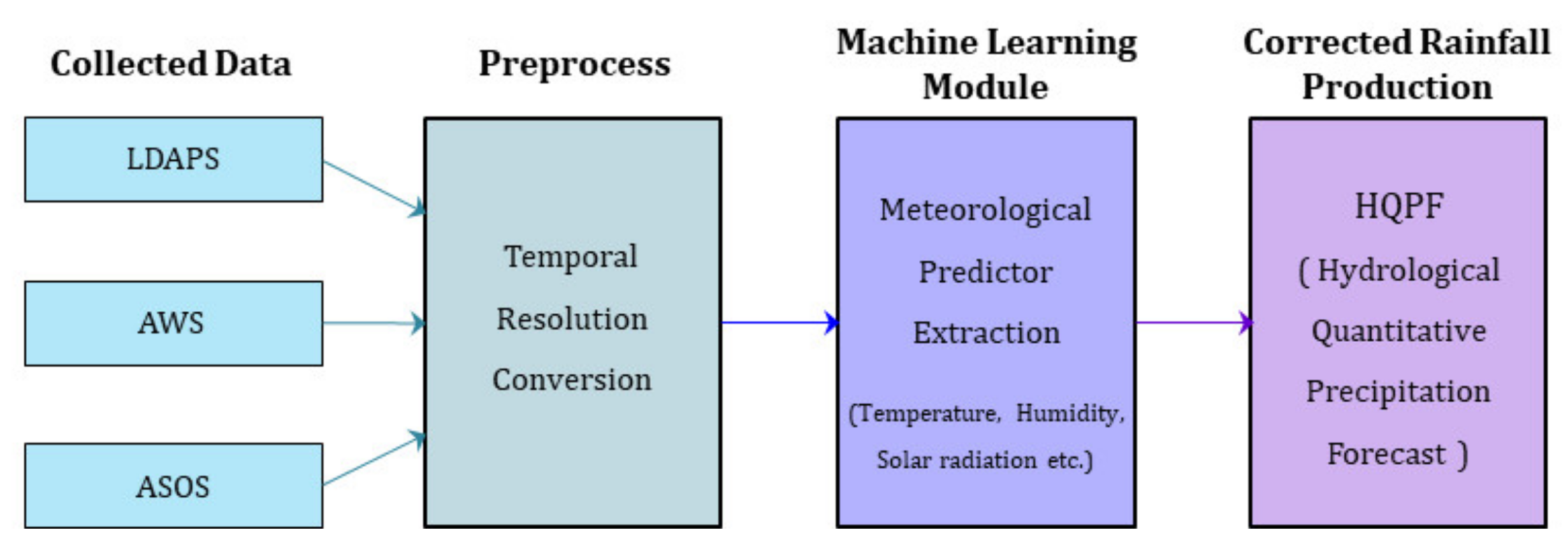
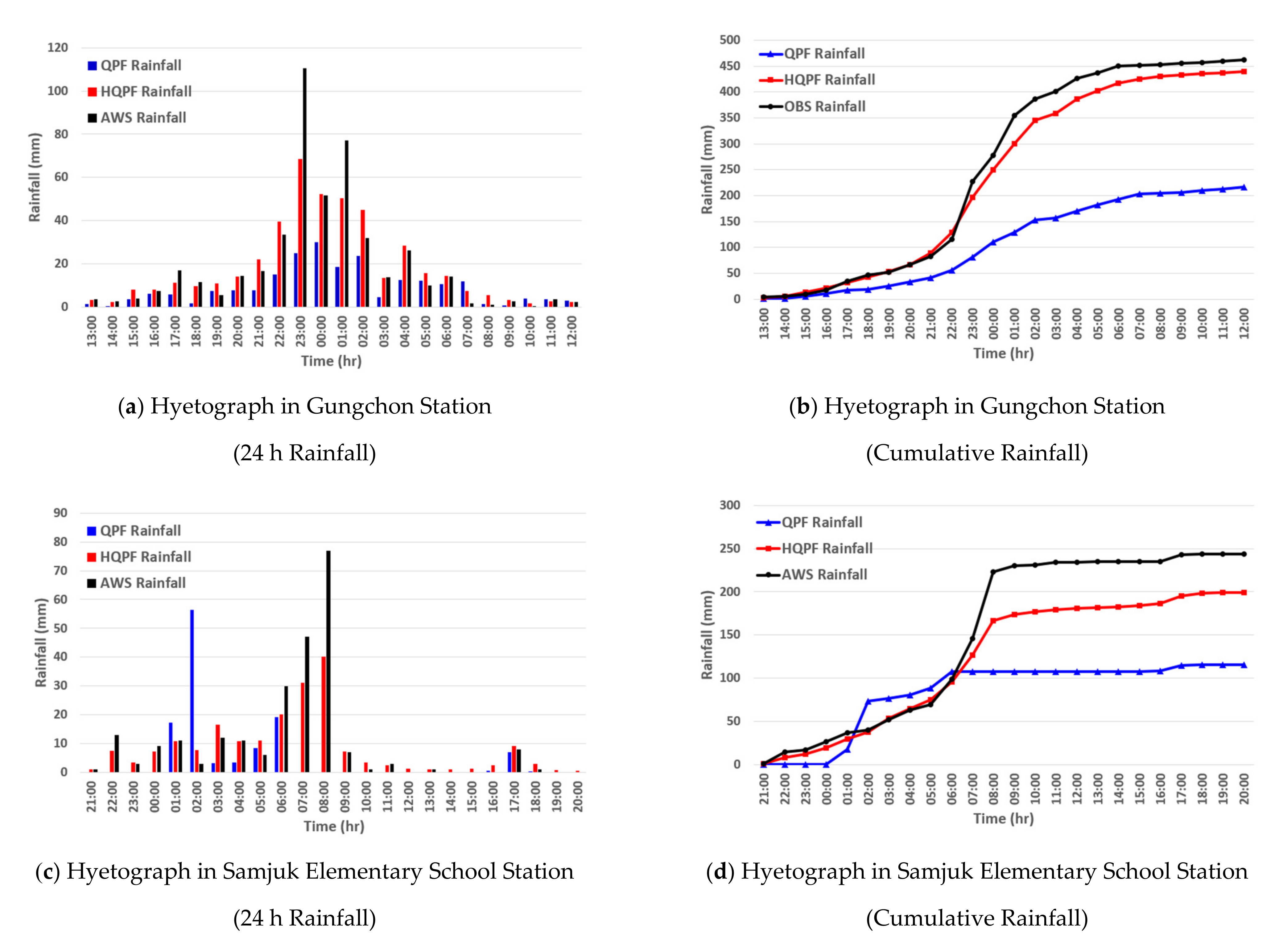
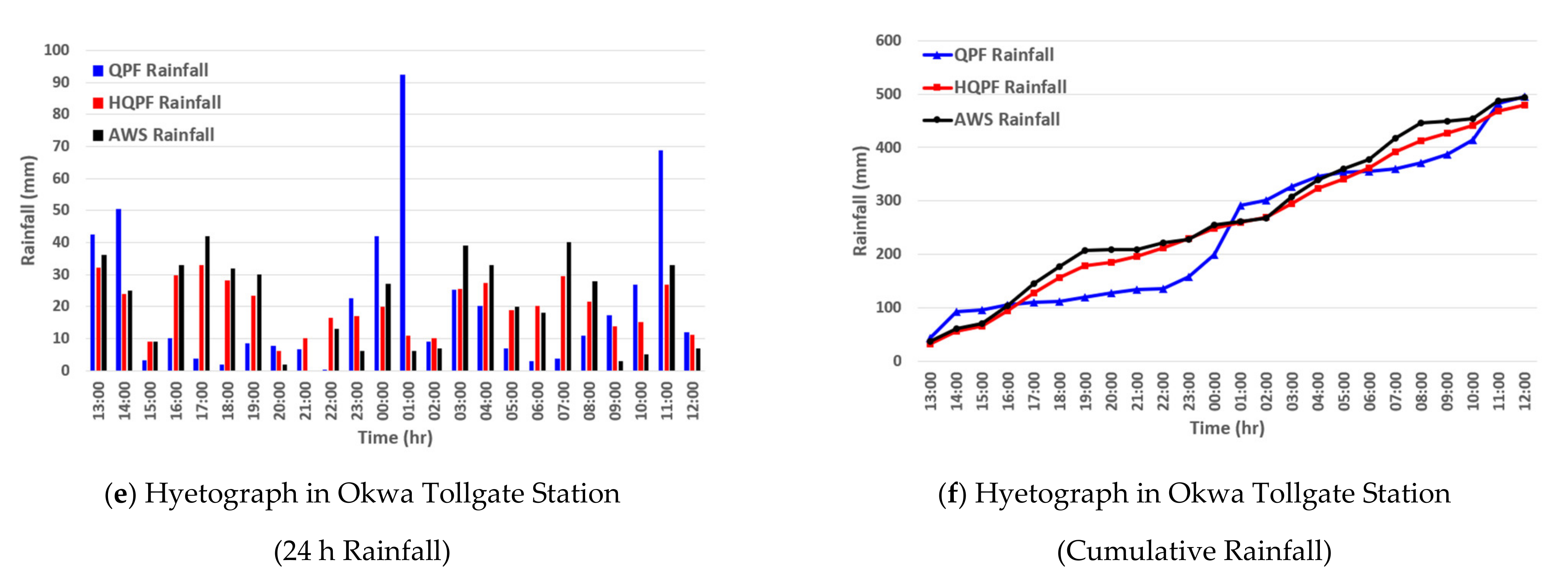
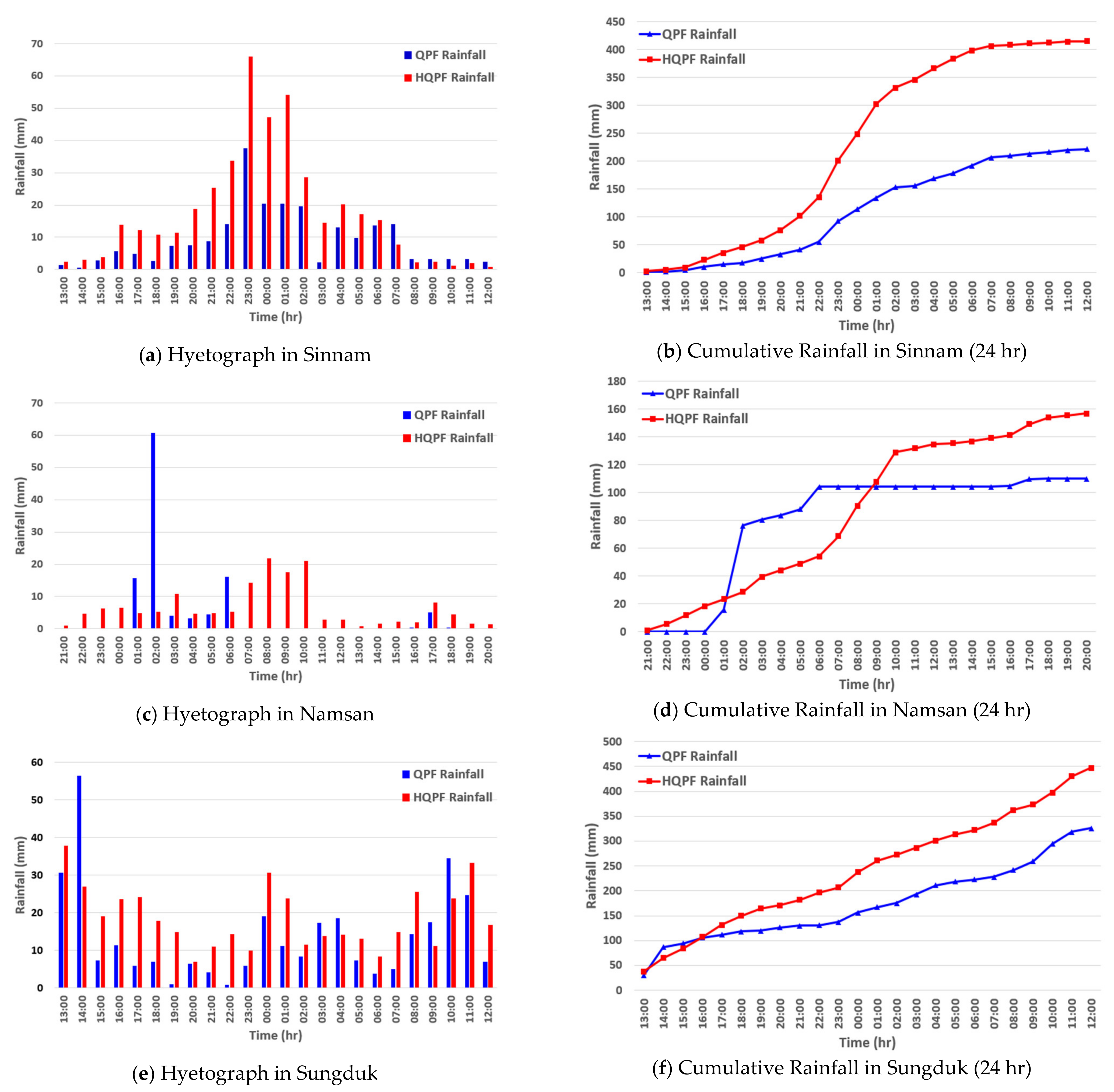
3.2. Correction and Verification of Precipitation Forecast Using Machine Learning
3.3. Debris Flow Prediction Using Debris Flow Simulation
3.3.1. The Collection and Input Data Construction of Runoff Simulation
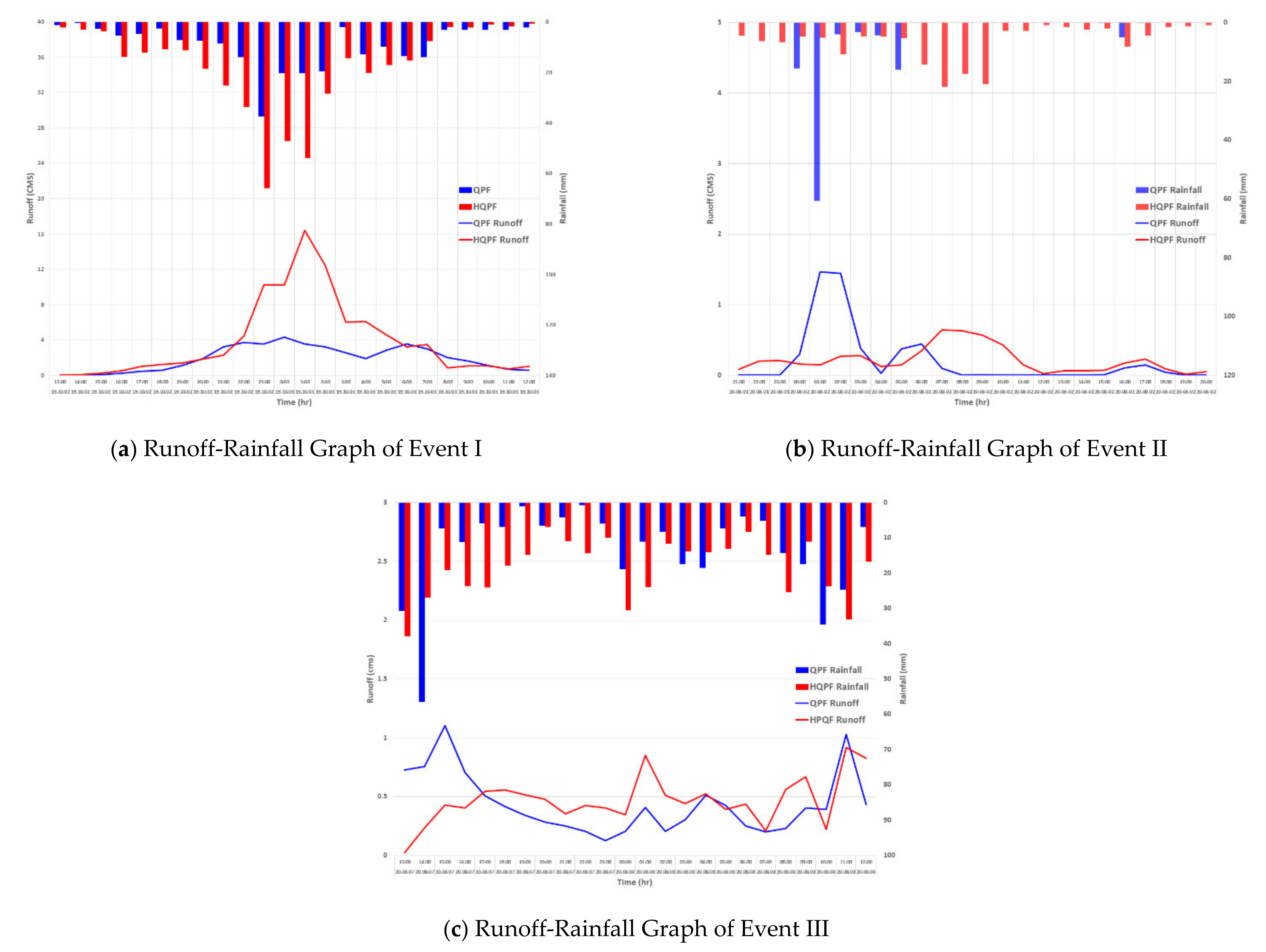
3.3.2. Runoff Volume Calculation (S-RAT)
3.3.3. Calculation of Soil Volume
3.3.4. Debris Flow Simulation
3.4. Verification of the Applicability of the HQPF Data Using Actual Damage Data
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, S. Long-term Comprehensive Water Resources Plan (2001~2020): Report = Water Vision 2020; Ministry of Construction and Transportation: Sejong City, Korea, 2000.
- National Institute of Forest Science. Things to Know About Landslides; National Institute of Forest Science Research Data No. 584. 2014. Available online: http://know.nifos.go.kr/book/search/DetailView.ax?sid=1&cid=163018 (accessed on 1 August 2021).
- Nam, D.H.; Lee, S.H.; Jeon, G.W.; Kim, B.S. A Study on the Debris Flow Movement and the Run-out Calculation Using the Coupling of Flood Runoff Model and Debris Flow Model. Crisisonomy 2016, 12, 131–143. [Google Scholar] [CrossRef]
- Choi, Y.N.; Lee, H.H. Characteristic Analysis and Prediction of Debris Flow-Prone Area at Daeryongsan. J. Korean Assoc. Geogr. Inf. Stud. 2018, 21, 48–62. [Google Scholar]
- Kim, S.E.; Baek, J.C.; Kim, G.S. Run-out Modeling of Debris Flows in Mt. Umyeon using FLO-2D. J. Civ. Environ. Eng. Res. 2013, 33, 965–974. [Google Scholar]
- Jun, G.W.; Oh, C.Y. Study on Risk Analysis of Debris Flow Occurrence Basin Using GIS. J. Korean Soc. Saf. 2011, 26, 83–88. [Google Scholar]
- Yun, W.J.; Kim, J.H.; Bae, D.H. Application on the Coupled Short-Term Precipitation-Stream Flow Forecast. J. Korea Water Resour. Assoc. 2004, 2004, 308–312. [Google Scholar]
- Lee, J.D.; Bae, D.H. A Study on the Short-term Forecast Method Using Land-Gauge Data. J. Korea Water Resour. Assoc. 2009, 2009, 1167–1171. [Google Scholar]
- Jung, J.S.; Kim, K.S. Rainfall Nowcasting with Multi-later Neural Network. J. Kroean Soc. Environ. Technol. 2000, 1, 95–100. [Google Scholar]
- Kim, G.S. Forecast of Areal Average Rainfall Using Radiosonde Data and Neural Networks. J. Korea Water Resour. Assoc. 2006, 39, 717–726. [Google Scholar] [CrossRef] [Green Version]
- Kim, G.S.; Kim, J.P. Development of a Short-term Rainfall Forecast Model Using Sequential CAPPI Data. J. Civ. Environ. Eng. Res. 2009, 29, 543–550. [Google Scholar]
- Yoon, S.S.; Bae, D.H.; Choi, Y.J. Urban Inundation Forecasting Using Predicted Radar Rainfall: Case Study. J. Korean Soc. Hazard. Mitig. 2014, 14, 117–126. [Google Scholar] [CrossRef] [Green Version]
- Kim, B.S.; Yun, S.G.; Yang, D.M.; Gwon, H.H. Development of Conceptually Grid Based Hydrological Model. J. Korea Water Resour. Assoc. 2010, 43, 667–679. [Google Scholar] [CrossRef]
- Jung, S.H.; Lee, D.E.; Lee, K.S. Prediction of River Water Level Using Deep-Learning Open Library. J. Korean Soc. Hazard. Mitig. 2018, 18, 1–11. [Google Scholar] [CrossRef]
- Choi, C.H.; Kim, J.S.; Kim, D.H.; Lee, J.H.; Kim, D.H.; Kim, H.S. Development of Heavy Rain Damage Prediction Functions in the Seoul Capital Area Using Machine Learning Techniques. J. Korean Soc. Hazard. Mitig. 2018, 18, 435–447. [Google Scholar] [CrossRef] [Green Version]
- Ham, Y.G.; Kim, J.H.; Luo, J.J. Deep Learning for ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef] [PubMed]
- Fox, J.T.; Magoulick, D.D. Predicting hydrologic disturbance of streams using species occurrence data. J. Sci. Total Environ. 2019, 686, 254–263. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.M.; Ko, C.M.; Shin, S.C.; Kim, B.S. The Development of a Rainfall Correction Technique based on Machine Learning for Hydrological Applications. J. Environ. Sci. Int. 2019, 28, 125–135. [Google Scholar] [CrossRef]
- Yen, M.H.; Liu, D.W.; Hsin, Y.C.; Lin, C.E.; Chen, C.C. Application of the deep learning for the prediction of rainfall in Southern Taiwan. Sci. Rep. 2019, 9, 12774. [Google Scholar] [CrossRef] [Green Version]
- Korea Meteorological Administration. Forecast Technologies in Your Hands; Korea Meteorological Administration Forecast Bureau: Seoul, Korea, 2012; p. 17. Available online: http://www.kma.go.kr/down/e-learning/hands/hands_17.pdf (accessed on 15 August 2021).
- Yoo, J.E. Random forests: An alternative data mining technique to decision tree. J. Educ. Eval. 2015, 28, 427–448. [Google Scholar]
- Choi, C.H.; Park, K.H.; Park, H.K.; Lee, M.J.; Kim, J.S.; Kim, H.S. Development of Heavy Rain Damage Prediction Function for Public Facility Using Machine Learning. J. Korean Soc. Hazard. Mitig. 2017, 17, 443–450. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Houtao, D.; Runger, G.; Tuv, E. System monitoring with real-time contrasts. J. Qual. Technol. 2012, 44, 9–27. [Google Scholar]
- Nam, D.H.; Ha, H.J.; Kim, B.S. Validation of Flood Runoff Sumulation Using Distributed Hydrologic Models. J. Korean Soc. Hazard. Mitig. 2020, 20, 173–184. [Google Scholar] [CrossRef] [Green Version]
- Nam, D.H.; Kim, M.I.; Kang, D.H.; Kim, B.S. Debris Flow Damage Assessment by Considering Debris Flow Direction and Direction Angle of Structure in South Korea. Water 2019, 11, 328. [Google Scholar] [CrossRef] [Green Version]
- Hussin, H.Y.; Quan Luna, B.; Van Westen, C.J.; Christen, M.; Malet, J.-P.; Van Asch, T.H.W.J. Parameterization of a numerical 2-D debris flow model with entrainment: A Event study of the Faucon catchment, Southern French Alps. Nat. Hazards Earth Syst. Sci. 2012, 12, 3075–3090. [Google Scholar] [CrossRef]
- Takahashi, T.; Nakagawa, H.; Satofuka, Y.; Kawaike, K. Flood and sediment disasters triggered by 1999 rainfall in VeneZuela: A river restoration plan for an alluvial fan. J. Nat. Disaster Sci. 2001, 23, 65–82. [Google Scholar]
- Hutter, K.; Svendsen, B.; Rickenmann, D. Debris flow modeling:A review. Contin. Mech. Thermodyn. 1994, 8, 1–35. [Google Scholar] [CrossRef]
- National Institute for Land and Infrastructure Management (NILIM). Manual of Technical Standard for Establishing Sabo Master Plan for Debris Flow and Driftwood; Technical Note of National Institute for Land Infrastructure Management No. 364; NILIM: Tsukuba, Japan, 2016; pp. 25–32. Available online: http://www.nilim.go.jp/lab/bcg/siryou/tnn/tnn0904pdf/ks0904.pdf (accessed on 1 August 2021).
- Chae, B.G.; Song, Y.S.; Choi, J.H.; Kim, G.S. The Current Methods of Landslide Monitoring Using Observation Sensors for Geologic Property. J. Sens. Sci. Technol. 2015, 24, 291–298. [Google Scholar] [CrossRef] [Green Version]
- Jung, G.H.; Jun, C.M.; Ko, J.H.; Park, Y.R. A Study on the Error Detection of Attached Cadastral Maps Using GIS. Proc. Korean Soc. Surv. Geod. Photogramm. Cartogr. Conf. 2007, 12, 47–55. Available online: https://www.koreascience.or.kr/article/CFKO200716419439853.jsp-kj=SSMHB4&py=2012&vnc=v27n6&sp=588 (accessed on 15 August 2021).
- Hua, L.; Tang, L.; Cui, S.; Yun, K. Simulating Urban Growth Using the SLEUTH Model in a Coastal Peri-Urban District in China. Sustainability 2014, 6, 3899–3914. [Google Scholar] [CrossRef] [Green Version]
- Choi, J.H.; Jeon, J.H.; Kim, T.H.; Kim, B.S. Comparison of inundation patterns of urban inundation model and flood tracking model based on inundation traces. J. Korea Water Resour. Assoc. 2021, 54, 71–80. [Google Scholar]
- Korea Forest Service. 2019 Landslide Cause Investigation Results Report; Korea Forest Service: Daejeon, Korea, 2019; pp. 28–53.
- Kwon, W.S. Oh My Photo 2020. The Scene of the ‘Disastrous Anseong Juksan-Myeon Landslide’ Seen with a Drone. Available online: http://www.ohmynews.com/NWS_Web/OhmyPhoto/2020/at_pg.aspx?CNTN_CD=A0002664401 (accessed on 15 August 2021).
- Jin, C.I. JoongAng Ilbo. Gokseong Landslide Disastrous for 5 People… Residents: “Soil Collapsed at the National Road Expansion Construction Site”. Available online: https://www.joongang.co.kr/article/23844086#home (accessed on 15 August 2021).






| Verification | Event I | Event II | Event III | |||
|---|---|---|---|---|---|---|
| QPF-AWS | HQPF-AWS | QPF-AWS | HQPF-AWS | QPF-AWS | HQPF-AWS | |
| MAE | 11.78 | 5.65 | 10.57 | 4.1 | 20.03 | 5.93 |
| NPE | −0.73 | −0.38 | 0.27 | 0.47 | 1.2 | 0.2 |
| PTE | 0 | 0 | −6 | 0 | 8 | 4 |
| Event I | Event II | Event III | |
|---|---|---|---|
| Solid density () | |||
| Liquid density () | |||
| Internal friction angle () | |||
| Average slope () | |||
| Equilibrium sediment concen-tration () | 0.32 | 0.41 | 0.31 |
| Porosity () | 0.45 | 0.45 | 0.45 |
| Cumulative rainfall () | |||
| Basin Area () | |||
| Runoff correction rate () | 0.26 | 0.439 | 0.493 |
| Soil runoff volume () |
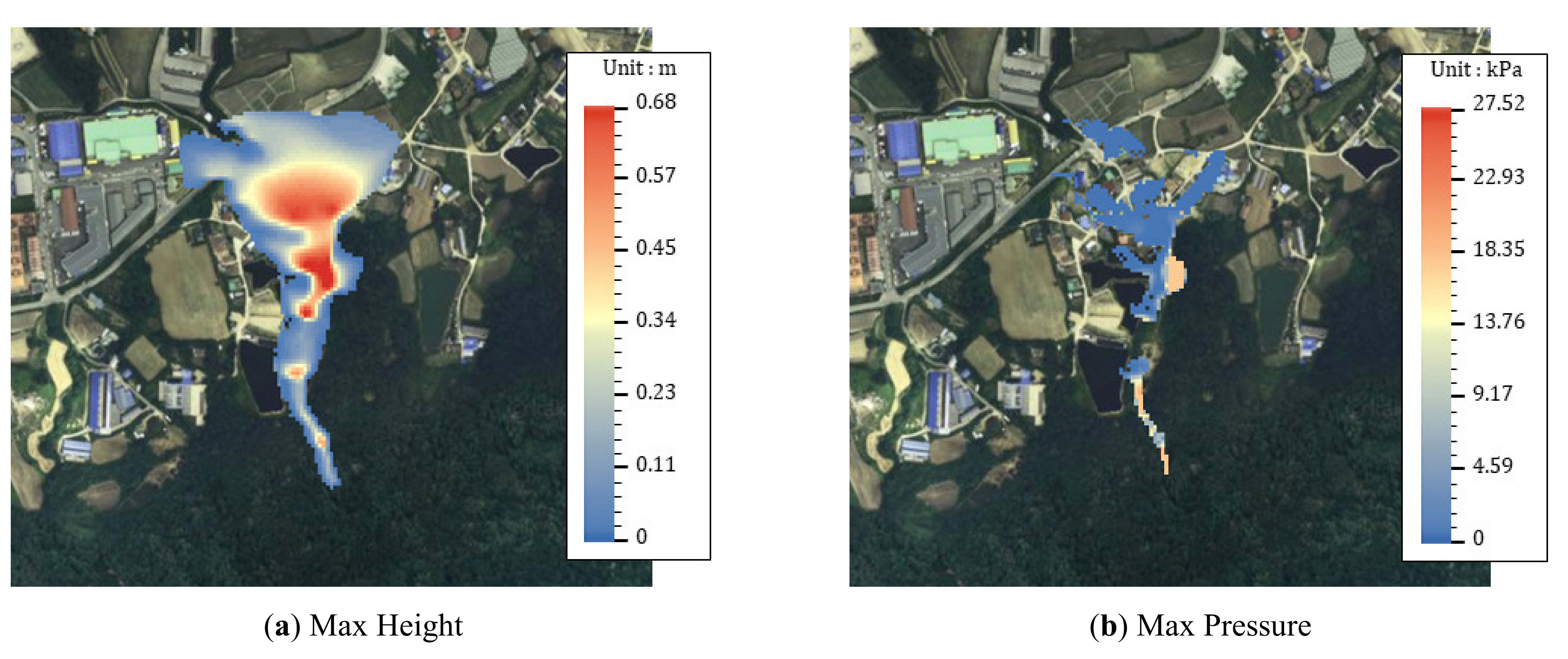
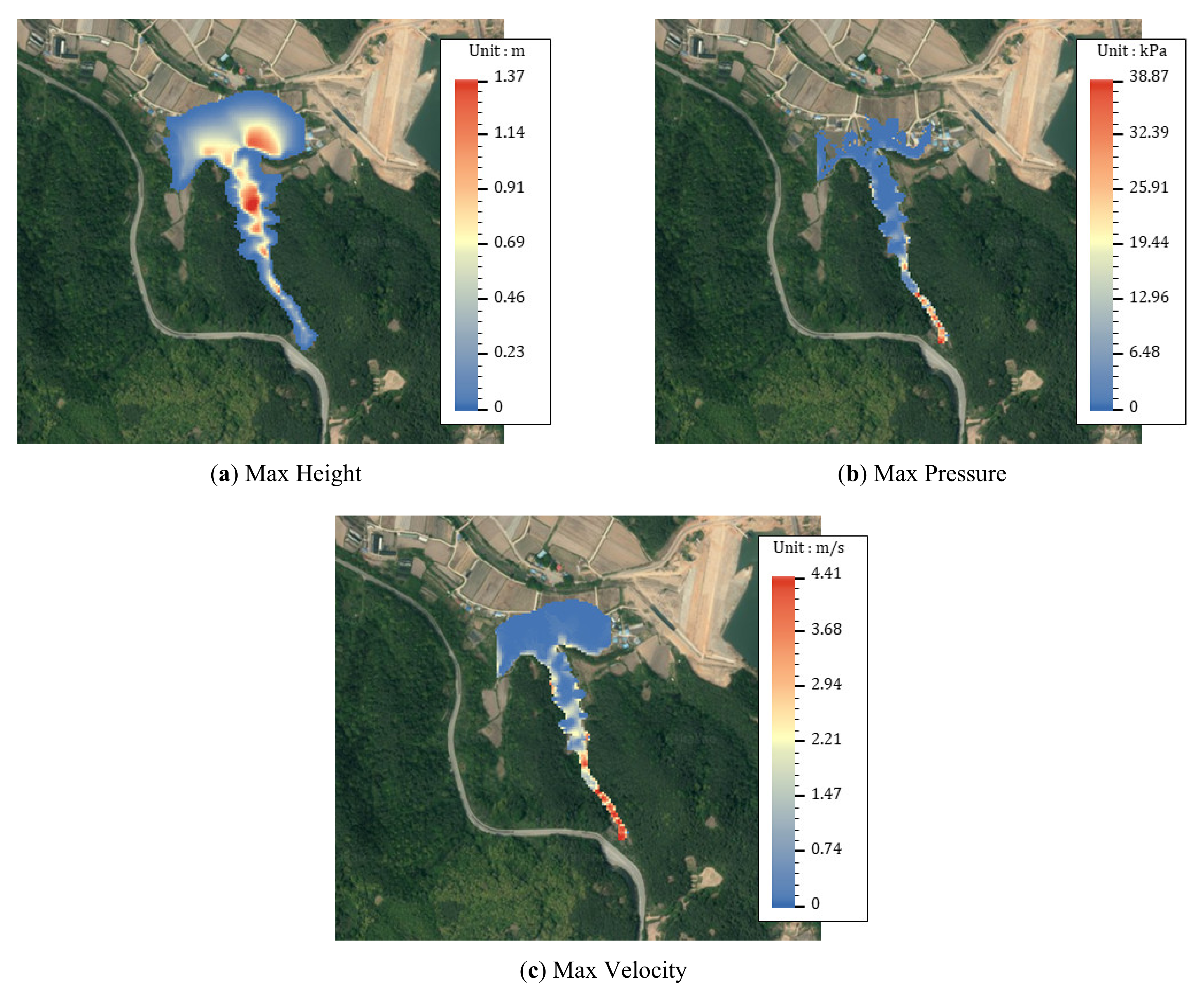
| Event I | Event II | Event III | |
|---|---|---|---|
| Max Height | |||
| Max Pressure | |||
| Max Velocity | |||
| Damage Area |
| Event I | Event II | Event III | |
|---|---|---|---|
| Actual Damage Area (A) | |||
| Analysis Damage Area (B) | |||
| 48.55% | 44.70% | 44.88% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Oh, C.-H.; Choo, K.-S.; Go, C.-M.; Choi, J.-R.; Kim, B.-S. Forecasting of Debris Flow Using Machine Learning-Based Adjusted Rainfall Information and RAMMS Model. Water 2021, 13, 2360. https://doi.org/10.3390/w13172360
Oh C-H, Choo K-S, Go C-M, Choi J-R, Kim B-S. Forecasting of Debris Flow Using Machine Learning-Based Adjusted Rainfall Information and RAMMS Model. Water. 2021; 13(17):2360. https://doi.org/10.3390/w13172360
Chicago/Turabian StyleOh, Cheong-Hyeon, Kyung-Su Choo, Chul-Min Go, Jung-Ryel Choi, and Byung-Sik Kim. 2021. "Forecasting of Debris Flow Using Machine Learning-Based Adjusted Rainfall Information and RAMMS Model" Water 13, no. 17: 2360. https://doi.org/10.3390/w13172360






