The Phenomenological Theory of Turbulence and the Scour Evolution Downstream of Grade-Control Structures under Steady Discharges
Abstract
:1. Introduction
- (1)
- the basic assumptions of the PTT-theory are still valid, notwithstanding the fact that such structures are partially submerged in general.
- (2)
- the scour evolution is consistent with that of plunging jets, unsubmerged vertical weirs, and Piano Key weirs, that are non-linear weirs often used for stream rehabilitation projects [18].
- (3)
- two different phases can be distinguished, i.e., the developing and the developed phases. (It is worth remarking that this result was not obvious a priori. In fact, according to Tregnaghi et al. [19], generally scour processes are characterized by an “affine transformation of a scour hole profile into another” during scour evolution, but this does not imply that a homothetic expansion may occur (geometric similitude). Namely, the affine transformation is a necessary but not sufficient condition for a homothetic expansion of the scour hole.)
- (4)
- (5)
- the scour evolution equation developed by Bombardelli et al. [16] furnishes reasonably good estimations of the scour evolution, without tuning the coefficients and exponents derived for scour processes caused by jets.
2. PTT Approach: Literature Background
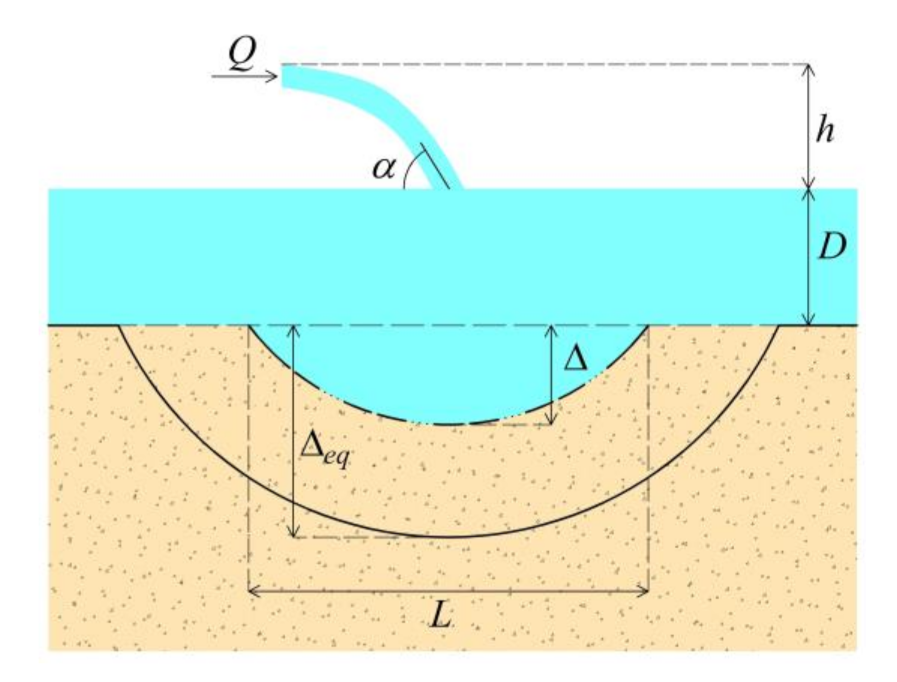
3. On the Applicability of the PTT to Grade-Control Structures
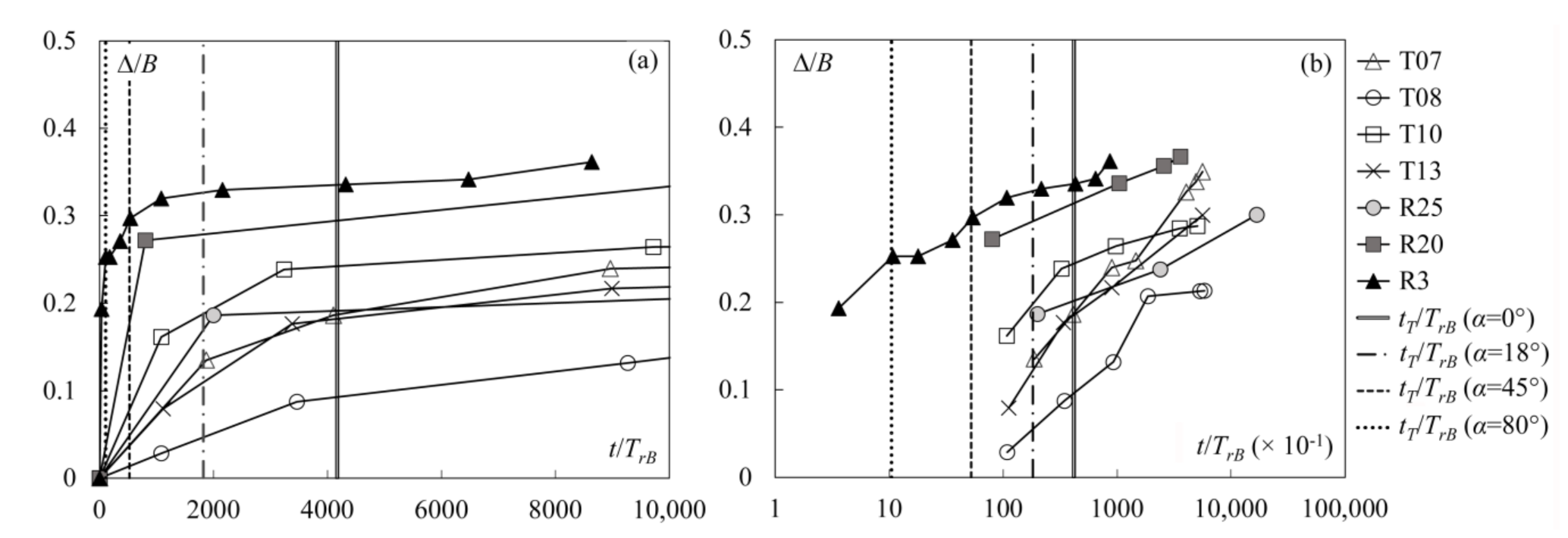
3.1. Developing and Developed Phases
3.2. Homothetic Expansion of the Scour Hole
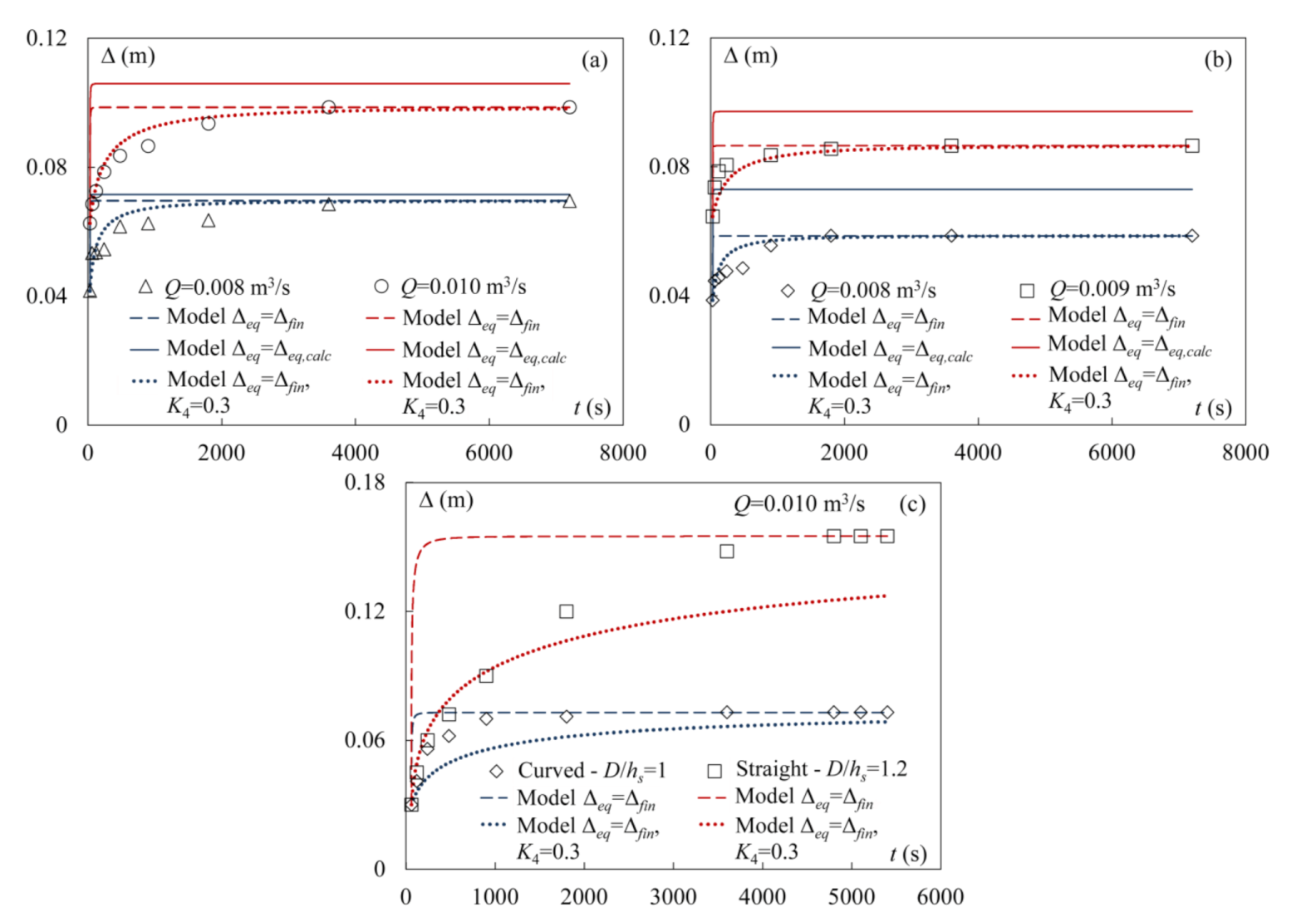
4. Validation of the PTT-Evolution Model
4.1. Generalities on the PTT-Evolution Model and Its Applicability to Grade-Control Structures
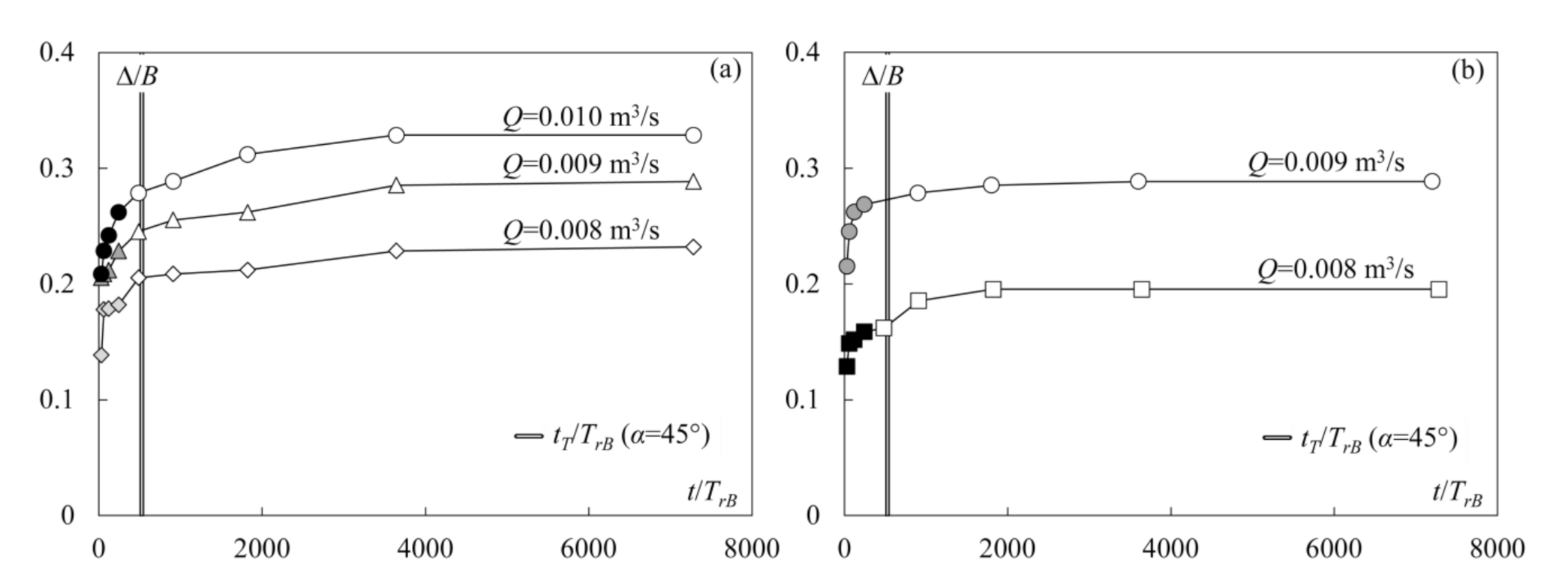
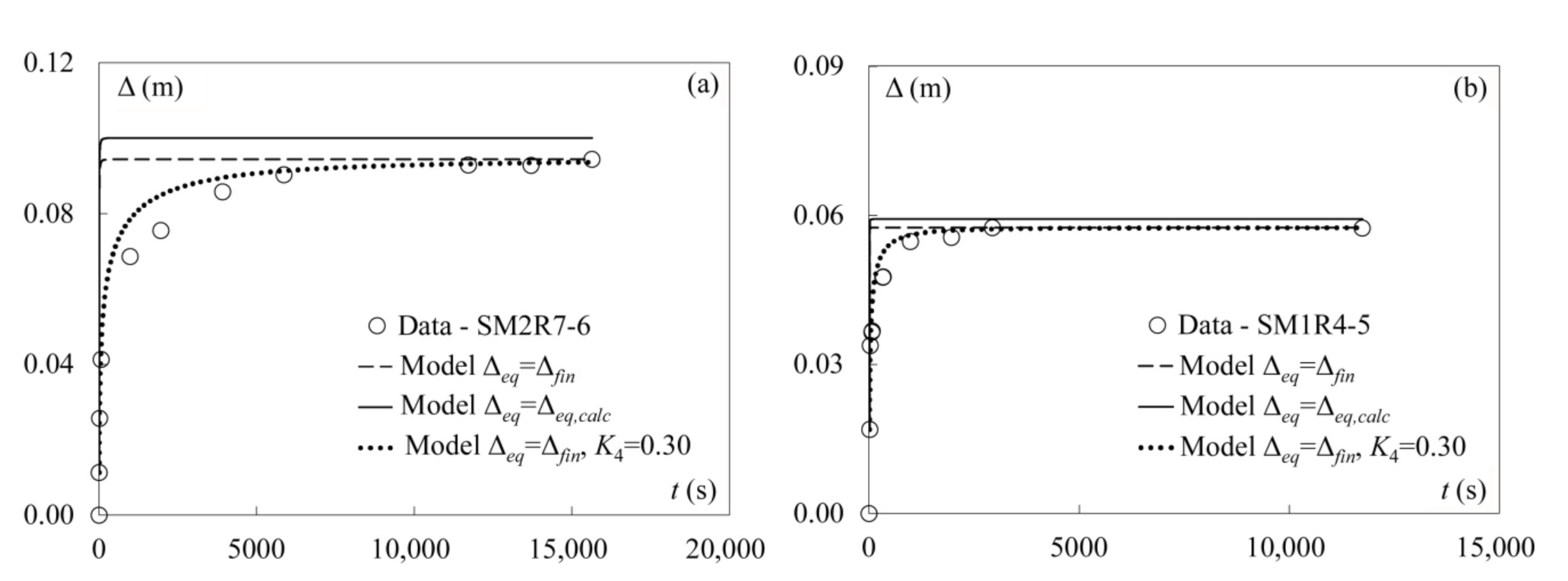
4.2. Validation with Data of Gaudio and Marion [1]
4.3. Validation with Scour Evolution Data Not Included in Pagliara and Palermo [7] and Data of Palermo and Pagliara [27]
4.4. Validation with Data of Lu et al. [25]
5. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gaudio, R.; Marion, A. Time evolution of scouring downstream of bed sills. J. Hydraul. Res. 2003, 41, 271–284. [Google Scholar] [CrossRef]
- Lenzi, M.A.; Marion, A.; Comiti, F.; Gaudio, R. Local scouring in low and high gradient streams at bed sills. J. Hydraul. Res. 2002, 40, 731–739. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. Scour holes downstream of bed sills in low-gradient channels. J. Hydraul. Res. 2006, 44, 497–509. [Google Scholar] [CrossRef]
- Guan, D.; Melville, B.W.; Friedrich, H. Live-bed scour at submerged weirs. J. Hydraul. Eng. 2015, 141, 04014071. [Google Scholar] [CrossRef]
- Wang, L.; Melville, B.W.; Guan, D.; Whittaker, C.N. Local scour at downstream sloped submerged weirs. J. Hydraul. Eng. 2018, 144, 04018044. [Google Scholar] [CrossRef]
- Wang, L.; Melville, B.W.; Whittaker, C.N.; Guan, D. Temporal evolution of clear-water scour depth at submerged weirs. J. Hydraul. Eng. 2020, 146, 06020001. [Google Scholar] [CrossRef]
- Pagliara, S.; Palermo, M. Rock grade control structures and stepped gabion weirs: Scour analysis and flow features. Acta Geophys. 2013, 61, 126–150. [Google Scholar] [CrossRef]
- Pagliara, S.; Palermo, M.; Kurdistani, S.M.; Hassanabadi, L.S. Erosive and hydrodynamic processes downstream of low-head control structures. J. Appl. Water Eng. Res. 2015, 3, 122–131. [Google Scholar] [CrossRef]
- Bormann, E.; Julien, P.Y. Scour downstream of grade control structures. J. Hydraul. Eng. 1991, 117, 579–594. [Google Scholar] [CrossRef] [Green Version]
- Beltaos, S.; Rajaratnam, N. Plane turbulent impinging jets. J. Hydraul. Res. 1973, 11, 29–59. [Google Scholar] [CrossRef]
- Hoffmans, G.J.C.M. Jet scour in equilibrium phase. J. Hydraul. Eng. 1998, 124, 430–437. [Google Scholar] [CrossRef]
- Hoffmans, G.J.C.M. Closure problem to jet scour. J. Hydraul. Res. 2009, 47, 100–109. [Google Scholar] [CrossRef]
- Bombardelli, F.A.; Gioia, G. Towards a theoretical model for scour phenomena. In River, Coastal, and Estuarine Morphodynamics, Proceedings of the RCEM 2005, 4th IAHR Symposium on River, Coastal and Estuarine Morphodynamics, Urbana, IL, USA, 4–7 October 2005; Parker, G., Garcìa, M., Eds.; CRC Press: Boca Raton, FL, USA, 2005; Volume 2, pp. 931–936. [Google Scholar]
- Bombardelli, F.A.; Gioia, G. Scouring of granular beds by jet-driven axisymmetric turbulent cauldrons. Phys. Fluids 2006, 18, 088101. [Google Scholar] [CrossRef] [Green Version]
- Gioia, G.; Bombardelli, F.A. Localized turbulent flows on scouring granular beds. Phys. Rev. Lett. 2005, 95, 014501. [Google Scholar] [CrossRef] [Green Version]
- Bombardelli, F.A.; Palermo, M.; Pagliara, S. Temporal evolution of jet induced scour depth in cohesionless granular beds and the phenomenological theory of turbulence. Phys. Fluids 2018, 30, 085109. [Google Scholar] [CrossRef]
- Palermo, M.; Bombardelli, F.A.; Pagliara, S.; Kuroiwa, J. Time-dependent scour processes on granular beds at large scale. Environ. Fluid Mech. 2021, 21, 791–816. [Google Scholar] [CrossRef]
- Palermo, M.; Crookston, B.; Pagliara, S. Analysis of Equilibrium Morphologies Downstream of a PK Weir Structure. Proccedings of the World Environmental and Water Resources Congress 2020, Henderson, NV, USA, 17–21 2020; pp. 43–51. [Google Scholar] [CrossRef]
- Tregnaghi, M.; Marion, A.; Gaudio, R. Affinity and similarity of local scour holes at bed sills. Water Resour. Res. 2007, 43, W11417. [Google Scholar] [CrossRef]
- Pagliara, S.; Hager, W.H.; Unger, J. Temporal evolution of plunge pool scour. J. Hydraul. Eng. 2008, 134, 1630–1638. [Google Scholar] [CrossRef] [Green Version]
- Pagliara, S.; Amidei, M.; Hager, W.H. Hydraulics of 3D plunge pool scour. J. Hydraul. Eng. 2008, 134, 1275–1284. [Google Scholar] [CrossRef]
- Oliveto, G.; Hager, W.H. Temporal Evolution of Clear-Water Pier and Abutments Scour. J. Hydraul. Eng. 2002, 128, 811–820. [Google Scholar] [CrossRef]
- Foster, G.; Meyer, L.; Onstad, C. An erosion equation derived from basic erosion principles. Trans. ASAE 1977, 20, 678–682. [Google Scholar] [CrossRef]
- Palermo, M.; Pagliara, S.; Bombardelli, F. Theoretical Approach for Shear-Stress Estimation at 2D Equilibrium Scour Holes in Granular Material due to Subvertical Plunging Jets. J. Hydraul. Eng. 2020, 146. [Google Scholar] [CrossRef]
- Lu, J.-Y.; Hong, J.-H.; Chang, K.-P.; Lu, T.-F. Evolution of scouring process downstream of grade-control structures under steady and unsteady flows. Hydrol. Process. 2013, 27, 2699–2709. [Google Scholar] [CrossRef]
- Ben Meftah, M.; Mossa, M. New Approach to Predicting Local Scour Downstream of Grade-Control Structure. J. Hydraul. Eng. 2020, 146, 04019058. [Google Scholar] [CrossRef]
- Palermo, M.; Pagliara, S. Effect of unsteady flow conditions on scour features at low-head hydraulic structures. J. Hydro-Environ. Res. 2018, 19, 168–178. [Google Scholar] [CrossRef]
- Pagliara, S. Influence of sediment gradation on scour downstream of block ramps. J. Hydraul. Eng. 2007, 133, 1241–1248. [Google Scholar] [CrossRef]
- Guan, D.; Melville, B.W.; Friedrich, H. Local scour at submerged weirs in sand bed channels. J. Hydraul. Res. 2016, 54, 172–184. [Google Scholar] [CrossRef]
- Ben Meftah, M.; De Serio, F.; De Padova, D.; Mossa, M. Hydrodynamic structure with scour hole downstream of bed sills. Water 2020, 12, 186. [Google Scholar] [CrossRef] [Green Version]
- Yalin, M.S. The Mechanics of Sediment Transport; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Julien, P.Y. Erosion and Sedimentation, 2nd ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Gaudio, R.; Marion, A.; Bovolin, V. Morphological effects of bed sills in degrading rivers. J. Hydraul. Res. 2000, 38, 89–96. [Google Scholar] [CrossRef]
- Marion, A.; Tregnaghi, M.; Tait, S.J. Sediment supply and local scouring at bed sills in high-gradient streams. Water Resour. Res. 2006, 42, W06416. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Nardi, J.; Palermo, M.; Bombardelli, F.A.; Pagliara, S. The Phenomenological Theory of Turbulence and the Scour Evolution Downstream of Grade-Control Structures under Steady Discharges. Water 2021, 13, 2359. https://doi.org/10.3390/w13172359
Di Nardi J, Palermo M, Bombardelli FA, Pagliara S. The Phenomenological Theory of Turbulence and the Scour Evolution Downstream of Grade-Control Structures under Steady Discharges. Water. 2021; 13(17):2359. https://doi.org/10.3390/w13172359
Chicago/Turabian StyleDi Nardi, Jessica, Michele Palermo, Fabián A. Bombardelli, and Stefano Pagliara. 2021. "The Phenomenological Theory of Turbulence and the Scour Evolution Downstream of Grade-Control Structures under Steady Discharges" Water 13, no. 17: 2359. https://doi.org/10.3390/w13172359







