Multifractal Analysis of River Networks under the Background of Urbanization in the Yellow River Basin, China
Abstract
:1. Introduction
2. Materials and Methods
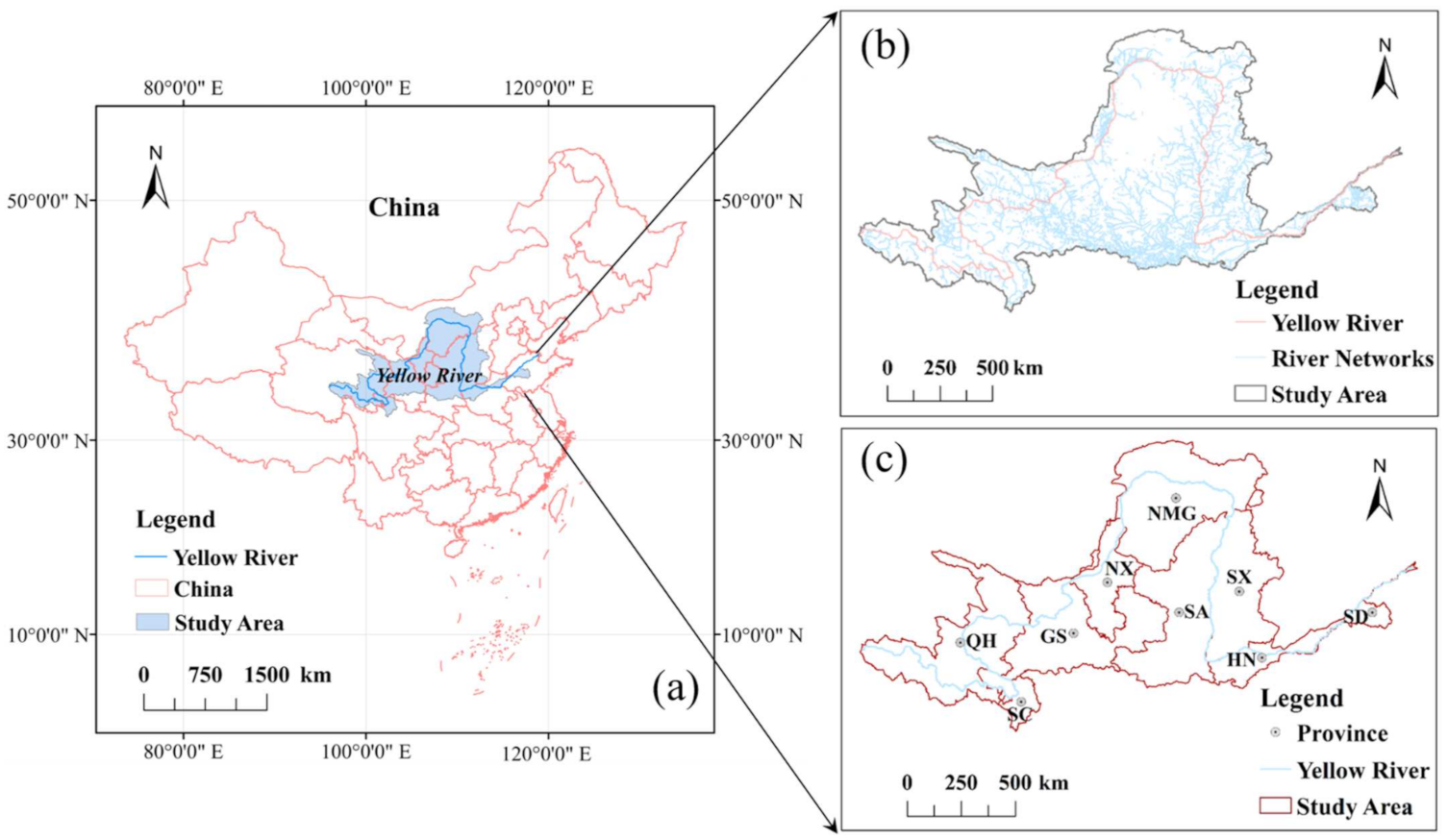
2.1. Study Area
2.2. Data Description
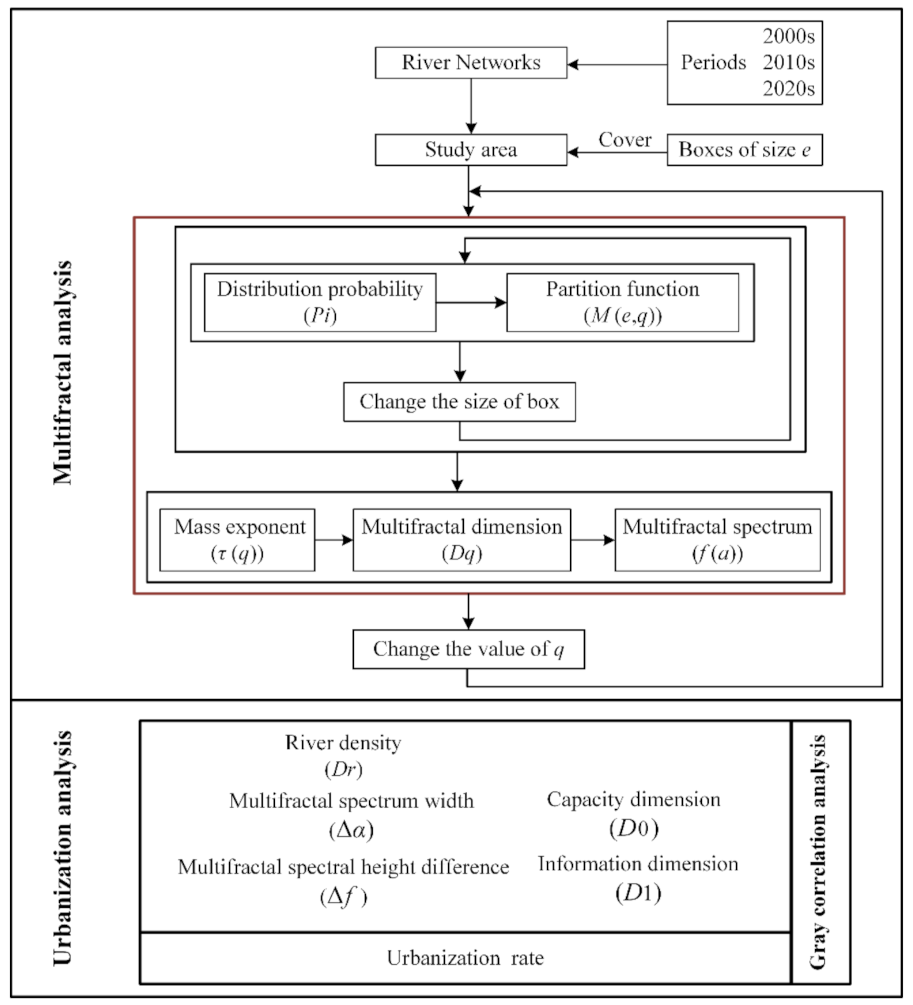
2.3. Method
- (1)
- The study area F is covered with boxes of size , and the total number of non-empty boxes is denoted . is the probability measure of the region contained in each box; that is, the distribution probability of the characteristic information. differs for different units. and e are related via Equation (1):where α is a singular exponent that corresponds to different units and is determined by the probability measure (). can be computed using Equation (2):where is the characteristic information of the river network in box i (e.g., river length), and is the total characteristic information of the study area under the scale of e, which reflects the overall morphological features of the studied basin. In this study, is the sum of the river lengths in box i, and is the total length of the study area.
- (2)
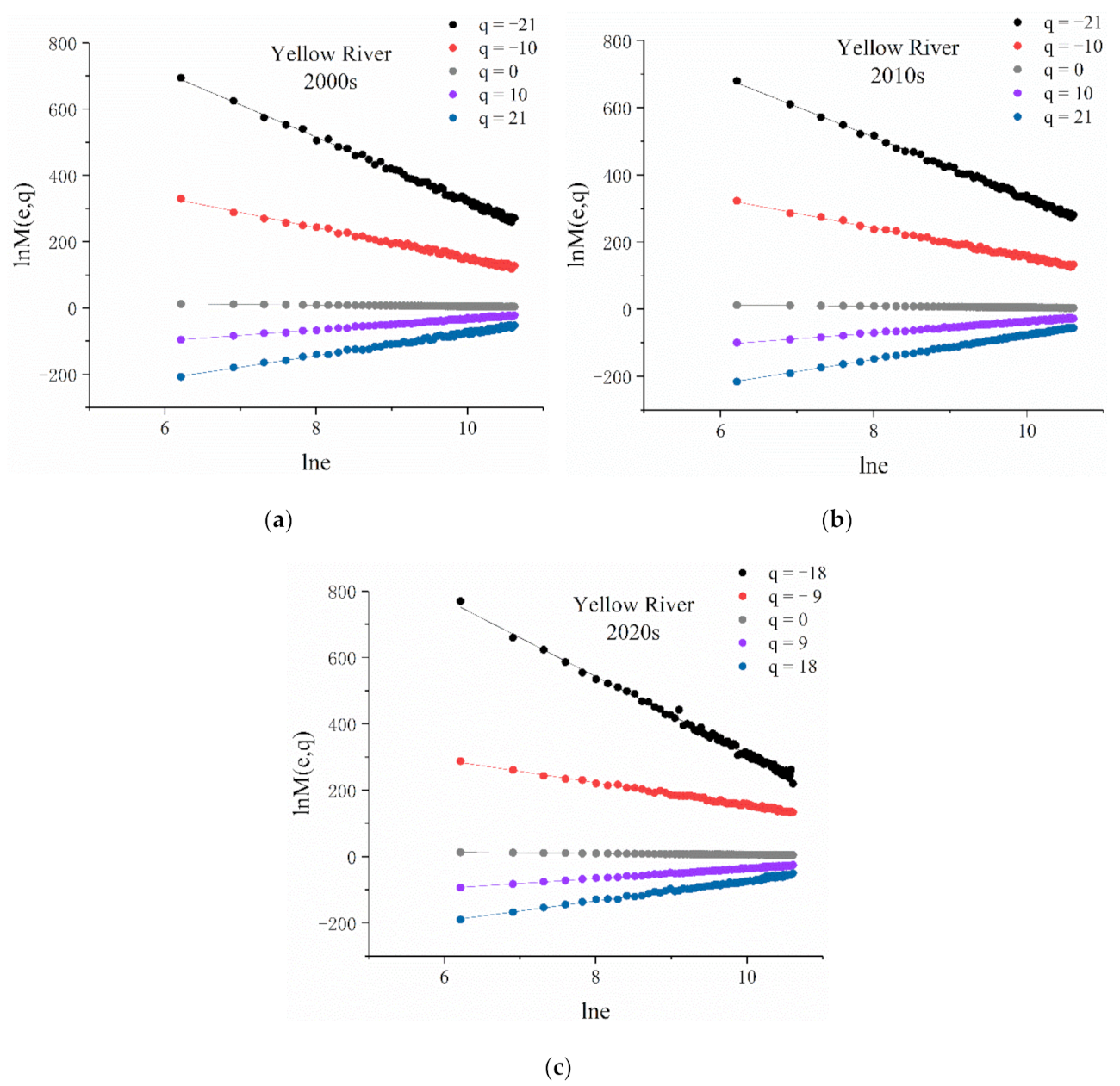
- The partition function is defined as the weighted sum of the slope distribution probability to power q (Equation (3)):where q is the order of the statistical moment, , and is used to describe the magnitude of the singularity in the multifractal analysis, and a different q represents the important role played by different river network probability subsets in the partition function. In the calculation, we took different q values and calculated the partition function under the corresponding q value. There is a good linear relationship between the logarithm of the partition function and the logarithm of the box size when the networks are multifractal in nature. This is an important basis for judging whether a research object has multifractal properties.
- (3)
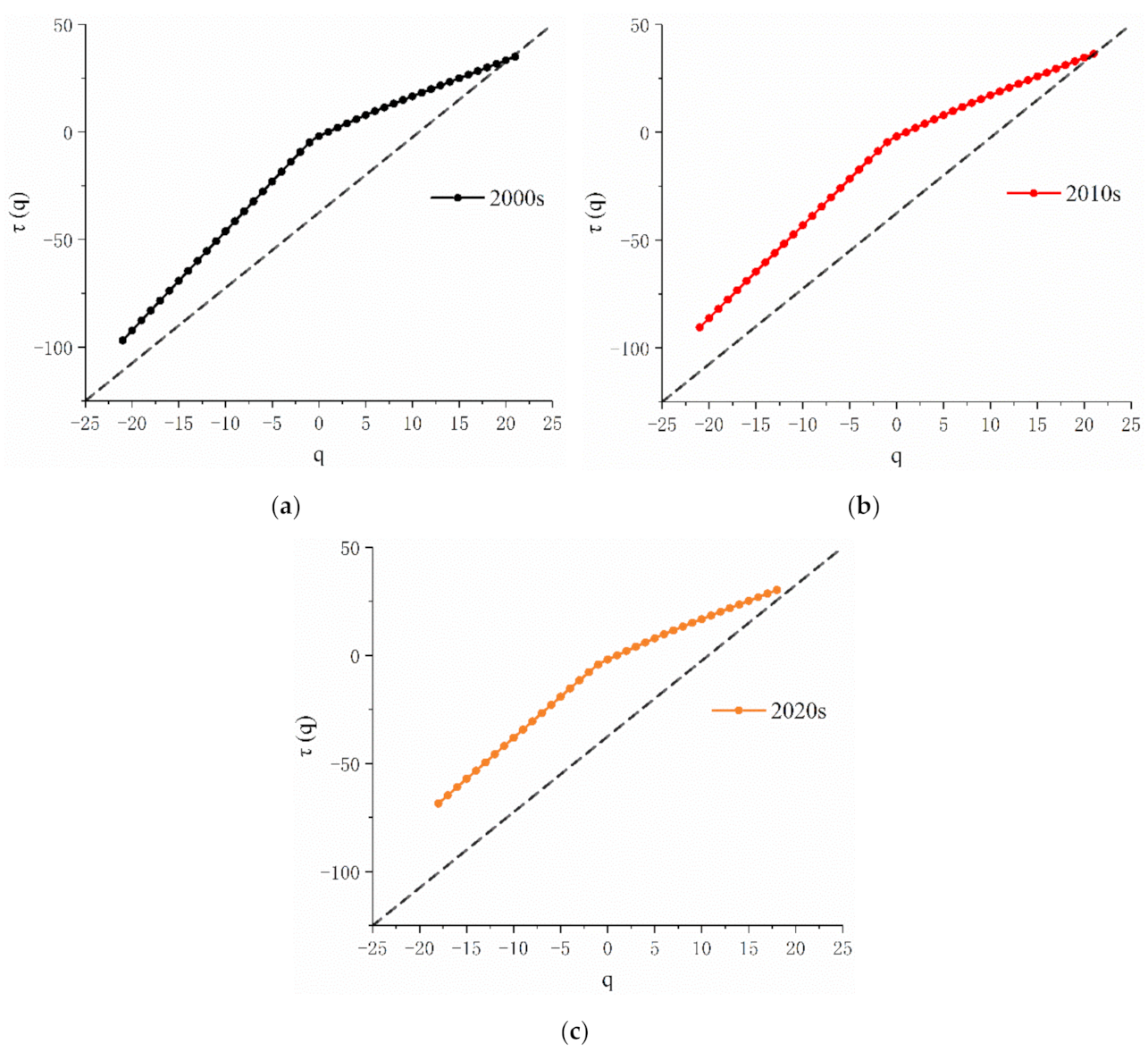
- For a given moment q, the relationship between the mass exponential function and is given by Equation (4). In the calculation, the size of the box under the corresponding q value is changed, and the partition function under the corresponding box size is computed. Then, can be computed through the coefficient of the straight line fit of ~ (Equation (5)). With the change in q, the corresponding can be calculated using the above procedure.where is the eigenvalue of the multifractal behavior. When is a convex function with respect to q, the research object exhibits multifractal features. This is another important criterion for judging whether a research object has a multifractal property.
- (4)
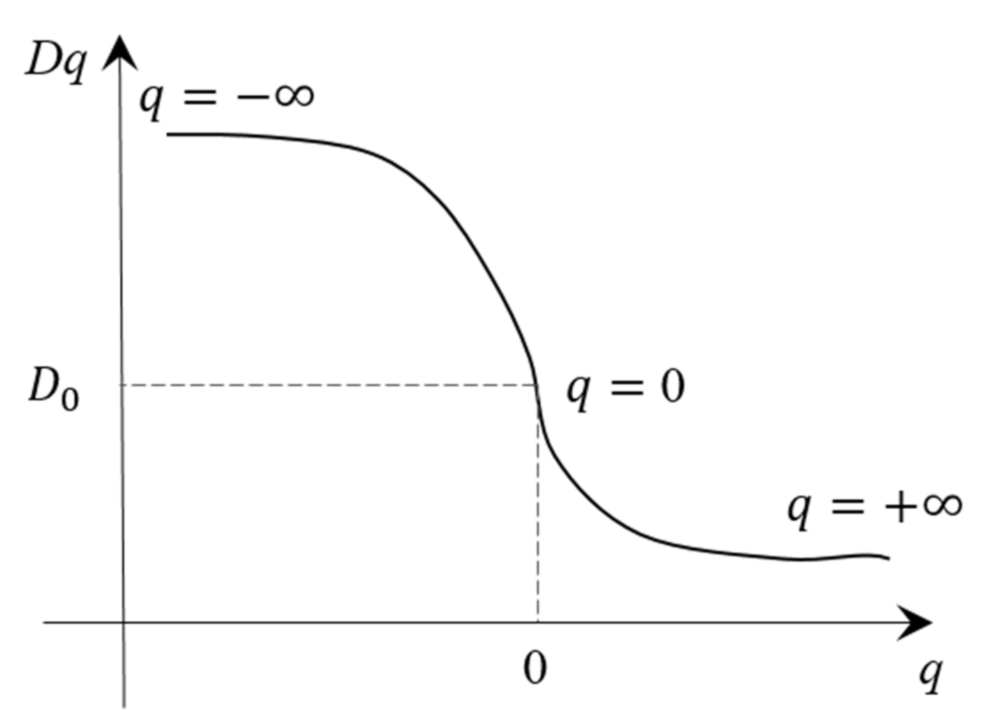
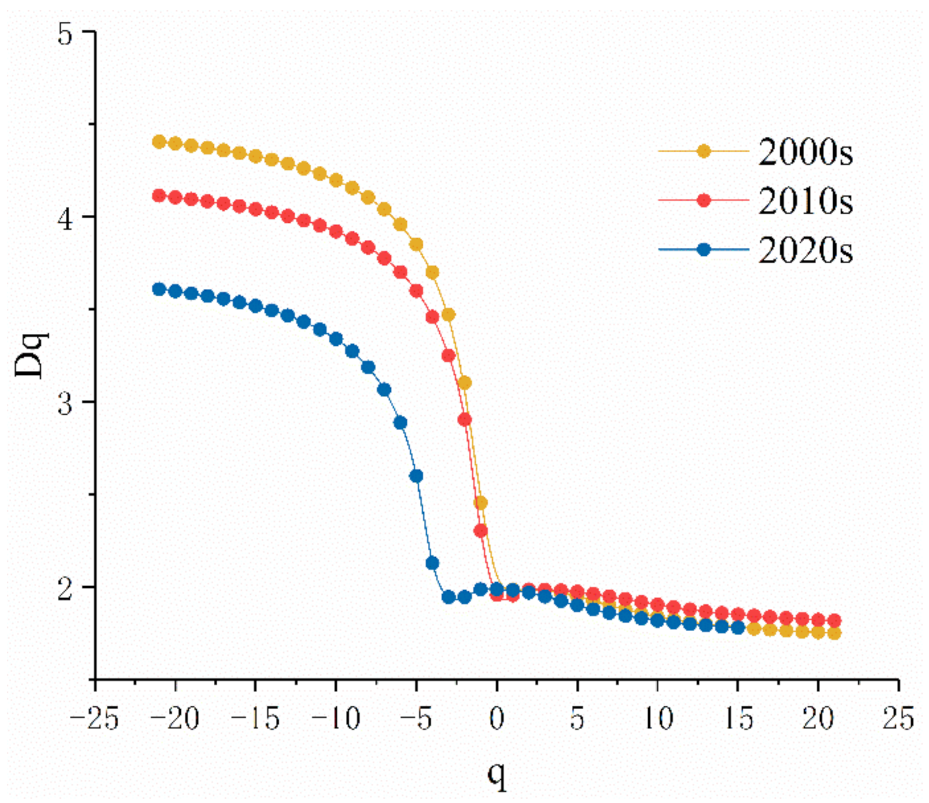
- The generalized fractal dimension is defined by Equation (6) and varies with q. can reflect the singularity of each subset of the research object from an overall perspective, so there is the relationship between and α in Equations (7) and (8).
- (5)
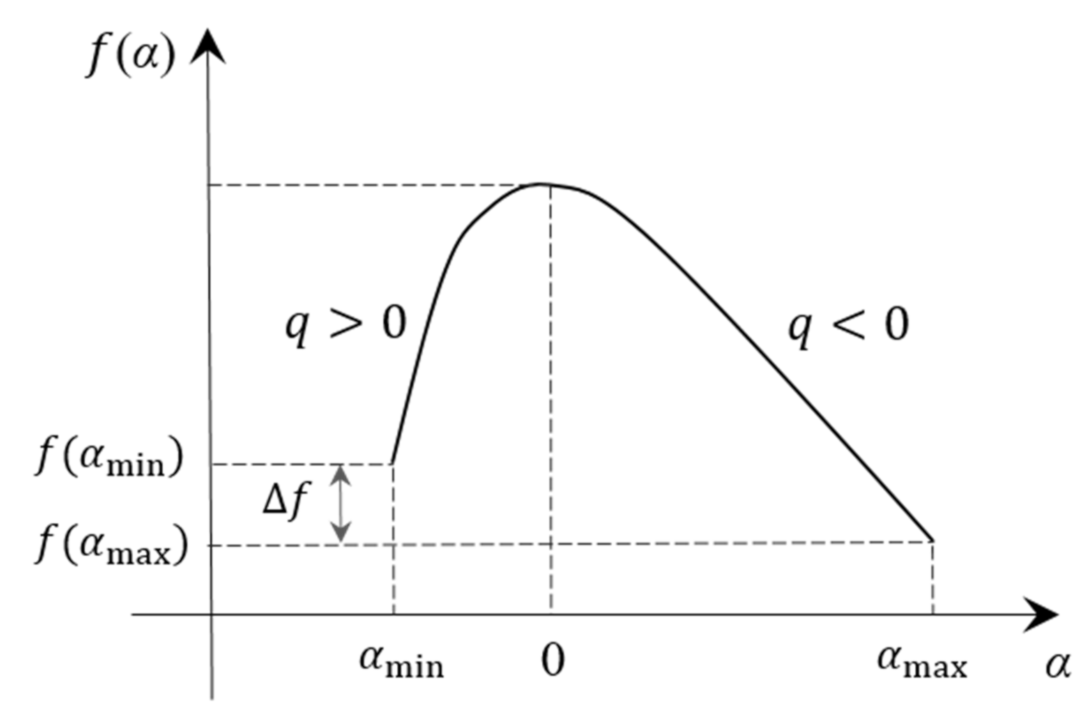
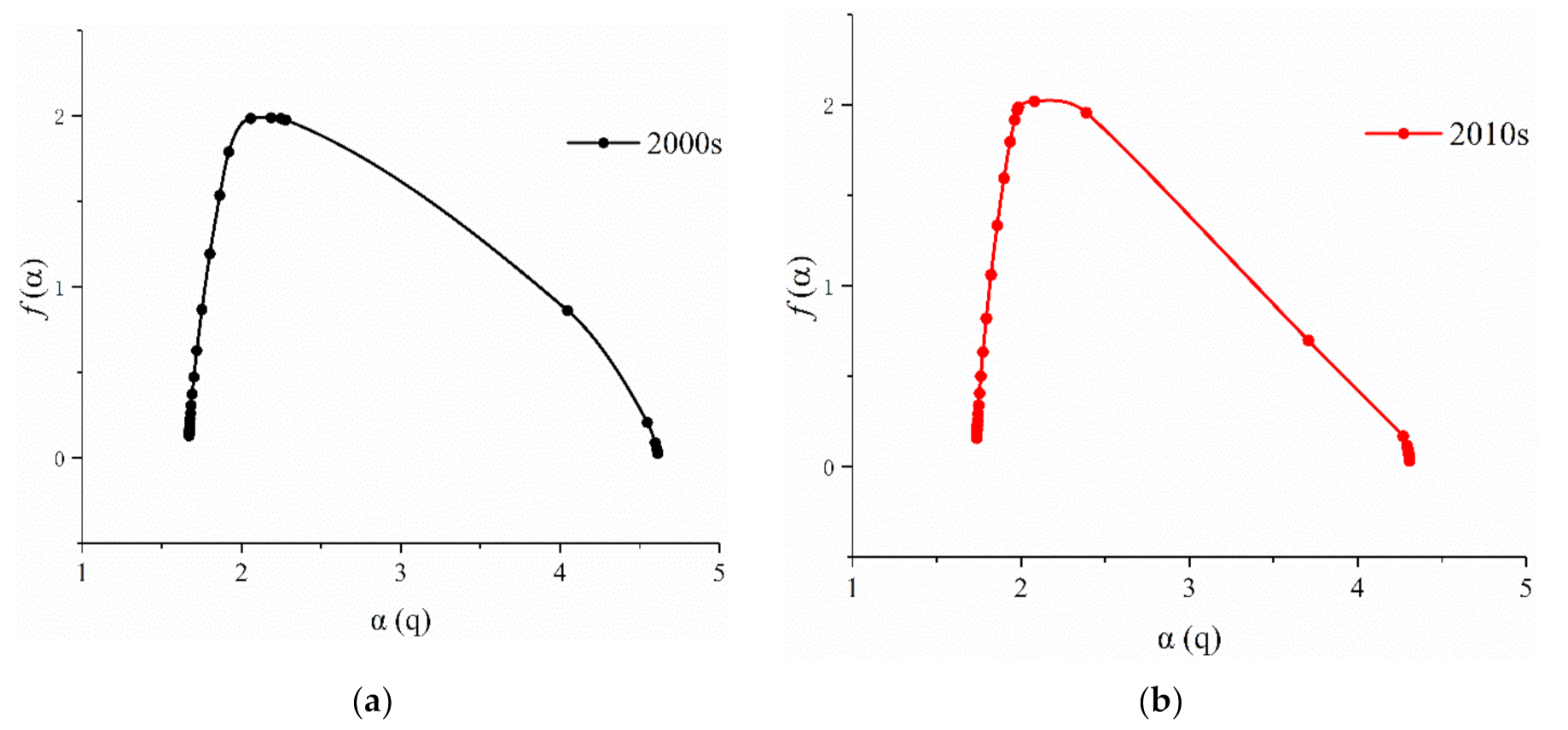
- When is differentiable, the multifractal spectrum and singular exponent can be obtained by the Legendre transformation of Equation (9).
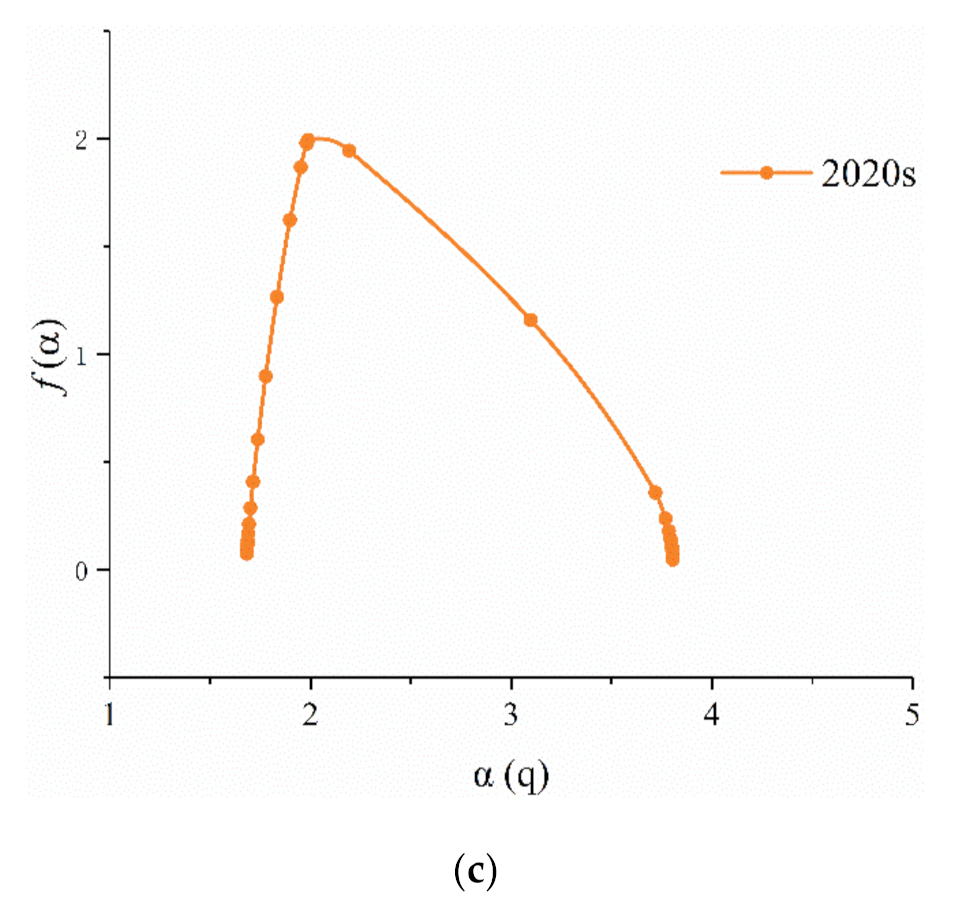
- The span of the singular exponent is the width of the multifractal spectrum, (Equation (10)). indicates the degree of fluvial inhomogeneity, irregularity, and complexity in each sub-region within the basin. and (Equations (7) and (8)), respectively, indicate the singular exponent of the distribution probability of the maximum characteristic information and the distribution probability of the minimum characteristic information with the change in e. The smaller the , the larger is the . Therefore, we can use the span of the singular exponent to describe the unevenness in the distribution probability of the river network. A larger indicates that the distribution of characteristic information in the basin is less uniform, the internal difference in the research object is greater, and the polarization trend of each subset probability is clearer. In contrast, a smaller indicates that the difference is smaller inside the fractal body, and the distribution of subsets tends to be concentrated and uniform.
- The difference between the maximum and minimum values of the multifractal spectrum is (Equation (11)). and represent the number of subsets of the maximum and minimum probabilistic characteristic information, respectively. The difference in can be used to calculate the difference between the maximum and minimum distribution probability subset numbers of the basin characteristic information. When , the curve ~ is hooked to the right, and the number of grid points contained in the maximum characteristic information distribution probability subset is less than the minimum probability subset number. The river network is densely distributed. In contrast, when , the curve is hooked to the left. When , the curve ~ is symmetrical and bell-shaped.
- Symmetry of curve ~. The multifractal spectrum is more symmetrical, which indicates that the fluvial distribution proportion is more uniform in the study area.
- (6)
- When calculating the generalized fractal dimension and the multifractal spectrum , the value of q plays an important role in the accuracy of the calculation results [32,33,34]. Theoretically,, but in the actual calculation, only a limited range can be selected as the value of q. According to the research of [35], when the convergence coefficient , the resulting changes to and are very small. The multifractal spectrum calculated within this range can be considered as a multifractal spectrum that reflects the characteristics of the research object. The value range of can be calculated using (12):
3. Results
3.1. Determination of Multifractal Characteristics
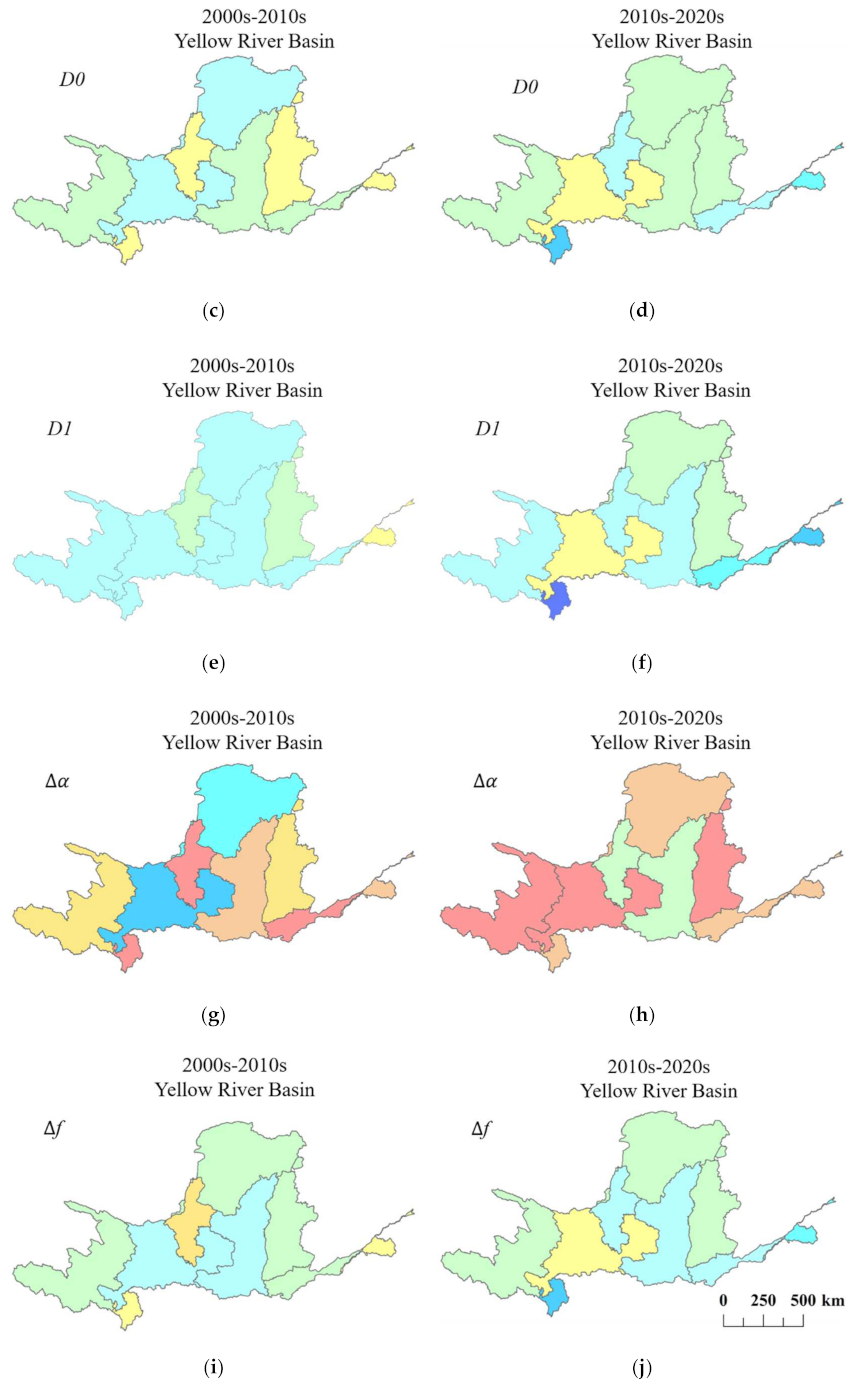
3.2. Multifractal Dimension Analysis
3.3. Multifractal Spectrum Analysis
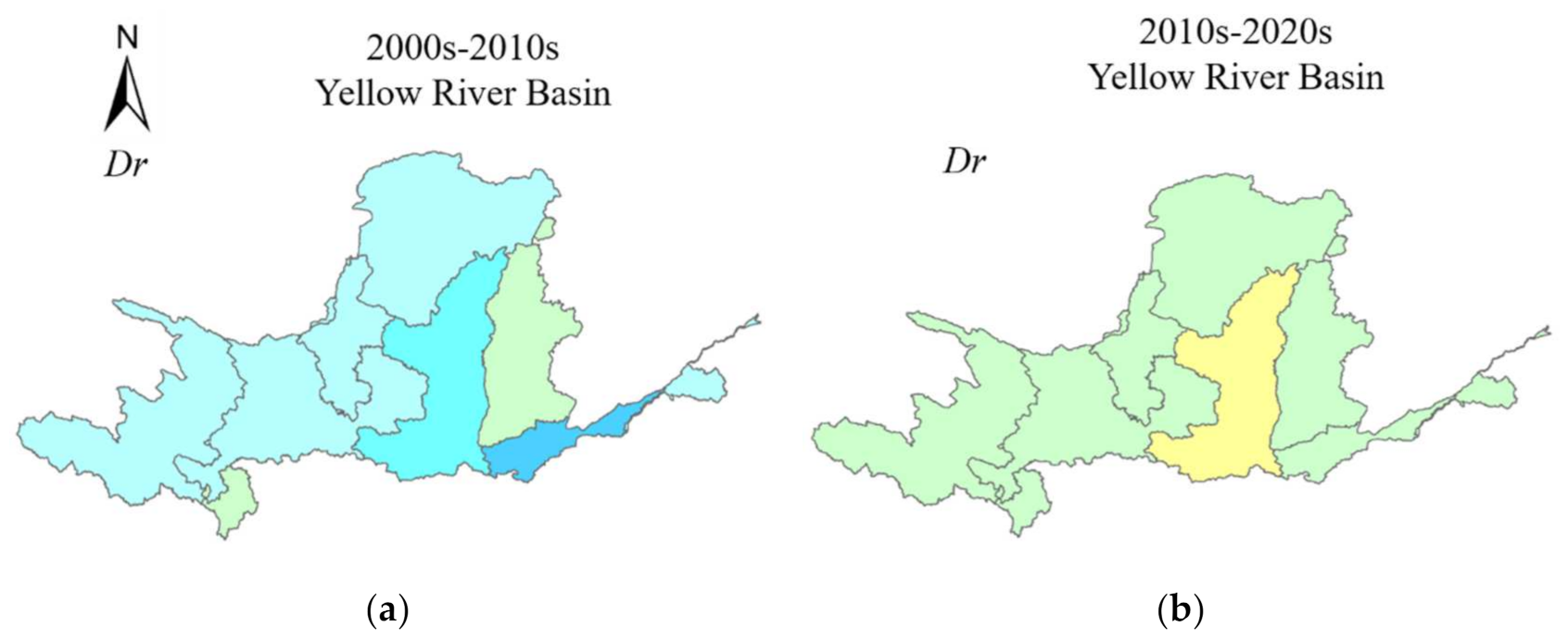
3.4. Correlation Analysis of Multifractal Indicators and the Urbanization Process
4. Discussion
5. Conclusions
- During the period of 2000–2020, the river network of the Yellow River Basin has clear multifractal properties. It was found that the river network structure of the Yellow River Basin is greatly affected by areas of higher river density. The river network structure (the number and density of the rivers in the network, etc.) has shown a decreasing trend over the past 20 years, and the degree of the impact of dense rivers has also decreased.
- The changes in river networks were significantly affected by urbanization. Changes in river network structure were significantly correlated with the urbanization process. The average Gray correlation values between the changes in river networks and urbanization were greater than 0.7, which was greater than the resolution coefficient of the Gray correlation analysis (0.5). Their order was . This result indicates that the greater the urbanization rate, the greater the impact on the river network structure.
- To better study the spatiotemporal characteristics of river network changes in the Yellow River Basin in the context of urbanization, we calculated the fluvial characteristic parameters of provinces in the study area during periods of slow urbanization (2000–2010) and rapid urbanization (2010–2020). Moreover, we analyzed the degree of variation and temporal and spatial differences in these parameters. The results show that the changes in the river network structure are more affected by urbanization during the rapid urbanization stage. The multifractal spectrum width is more sensitive to changes in the river network structure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Czuba, J.A.; Foufoula-Georgiou, E.; Gran, K.B.; Belmont, P.; Wilcock, P.R. Interplay between spatially explicit sediment sourcing, hierarchical river-network structure, and in-channel bed material sediment transport and storage dynamics. J. Geophys. Res. Earth Surf. 2017, 122, 1090–1120. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Zabalza-Martínez, J.; Borràs, G.; López-Moreno, J.; Pla, E.; Pascual, D.; Savé, R.; Biel, C.; Funes, I.; Azorin-Molina, C. Extreme hydrological events and the influence of reservoirs in a highly regulated river basin of northeastern Spain. J. Hydrol. Reg. Stud. 2017, 12, 13–32. [Google Scholar] [CrossRef]
- Fox, C.A. River Basin Development. In International Encyclopedia of Human Geography; Elservier: Amsterdam, The Netherlands, 2009; Volume 90, pp. 414–422. [Google Scholar]
- Horton, R.E. Drainage-basin characteristics. Eos Trans. Am. Geophys. Union 1932, 13, 350–361. [Google Scholar] [CrossRef]
- Tucker, G.E.; Catani, F.; Rinaldo, A.; Bras, R.L. Statistical analysis of drainage density from digital terrain data. Geomorphology 2001, 36, 187–202. [Google Scholar] [CrossRef]
- Perron, J.T.; Richardson, P.W.; Ferrier, K.L.; Laptre, M. The root of branching river networks. Nature 2012, 492, 100–103. [Google Scholar] [CrossRef]
- Angeles, G.R.; Perillo, G.; Piccolo, M.C.; Pierini, J.O. Fractal analysis of tidal channels in the Baha Blanca Estuary (Argentina). Geomorphology 2004, 57, 263–274. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Krupiński, M.; Wawrzaszek, A.; Drzewiecki, W.; Jenerowicz, M.; Aleksandrowicz, S. What Can Multifractal Analysis Tell Us about Hyperspectral Imagery? Remote Sens. 2020, 12, 4077. [Google Scholar]
- Qin, Z.L.; Wang, J.X.; Lu, Y. Multifractal Characteristics Analysis Based on Slope Distribution Probability in the Yellow River Basin, China. ISPRS Int. J. Geo-Inf. 2021, 10, 337. [Google Scholar]
- Parisi, G.; Frisch, U. On the singularity structure of fully developed turbulence in Turbulence and predictability in geophysical fluid dynamics and climate dynamics. Am. J. Theol. Philos. 1985, 88, 71–88. [Google Scholar]
- Chen, Y.; Liu, J. Frantals and Fractal Dsimensions of Structure of River Systems: Models Reconstruction and Parameters Interpretation of Horton’s Laws of Network Composition. Adv. Earth Sci. 2001, 16, 178–183. [Google Scholar]
- Bartolo, S.; Veltri, M.; Primavera, L. Estimated generalized dimensions of river networks. J. Hydrol. 2006, 322, 181–191. [Google Scholar] [CrossRef]
- Bartolo, S.D.; Gabriele, S.; Gaudio, R. Multifractal behaviour of river networks. Hydrol. Earth Syst. Sci. 2000, 4, 105–112. [Google Scholar] [CrossRef] [Green Version]
- Ariza-Villaverde, A.B.; Jiménez-Hornero, F.; Gutiérrez, d. Influence of DEM resolution on drainage network extraction: A multifractal analysis. Geomorphology 2015, 241, 243–254. [Google Scholar] [CrossRef]
- Zhang, H.; Loáiciga, H.; Feng, L.; He, J.; Du, Q. Setting the Flow Accumulation Threshold Based on Environmental and Morphologic Features to Extract River Networks from Digital Elevation Models. Int. J. Geo-Inf. 2021, 10, 186. [Google Scholar] [CrossRef]
- Gaudio, R.; Bartolo, S.; Primavera, L.; Veltri, M.; Gabriele, S. Procedures in multifractal analysis of river networks: A state of the art review. Water Energy Abstr. 2005, 15, 5. [Google Scholar]
- Gaudio, R.; Bartolo, S.; Primavera, L.; Gabriele, S.; Veltri, M. Lithologic control on the multifractal spectrum of river networks. J. Hydrol. 2006, 327, 365–375. [Google Scholar] [CrossRef]
- Bartolo, S.D.; Gaudio, R.; Gabriele, S. Multifractal analysis of river networks: Sandbox approach. Water Resour. Res. 2004, 40, 2201. [Google Scholar] [CrossRef] [Green Version]
- Gregory, K.J. The human role in changing river channels. Geomorphology 2006, 79, 172–191. [Google Scholar] [CrossRef]
- Chin, A. Urban transformation of river landscapes in a global context. Geomorphology 2006, 79, 460–487. [Google Scholar] [CrossRef]
- Deng, X.; Xu, Y.; Han, L.; Song, S.; Liu, Y.; Li, G.; Wang, Y. Impacts of Urbanization on River Systems in the Taihu Region, China. Water 2015, 7, 1340–1358. [Google Scholar] [CrossRef]
- Elmore, A.J.; Kaushal, S.S. Disappearing headwaters: Patterns of stream burial due to urbanization. Front. Ecol. Environ. 2008, 6, 308–312. [Google Scholar] [CrossRef]
- Kalantari, Z.; Ferreira, C.S.; Walsh, R.P.; Ferreira, A.J.; Destouni, G. Urbanization Development under Climate Change: Hydrological Responses in a Peri-Urban Mediterranean Catchment. Land Degrad. Dev. 2017, 28, 2207–2221. [Google Scholar] [CrossRef] [Green Version]
- Fotherby, L.M. Valley confinement as a factor of braided river pattern for the Platte River. Geomorphology 2009, 103, 562–576. [Google Scholar] [CrossRef]
- Xu, S.; Yu, Z.; Yang, C.; Ji, X.; Ke, Z. Trends in evapotranspiration and their responses to climate change and vegetation greening over the upper reaches of the Yellow River Basin. Agric. For. Meteorol. 2018, 263, 118–129. [Google Scholar] [CrossRef]
- Aharony, A. Measuring multifractals. Phys. D Nonlinear Phenom. 1989, 38, 1–4. [Google Scholar] [CrossRef]
- Rolph, S. Fractal Geometry: Mathematical Foundations and Applications. Math. Gaz. 1990, 74, 288–317. [Google Scholar]
- Halsey, T.; Jensen, M.; Kadanoff, L.; Procaccia, I.; Shraiman, B. Fractal measures and their singularities: The characterization of strange sets. Phys. Rev. A Third 1986, 33, 1141–1151. [Google Scholar] [CrossRef]
- Wawrzaszek, A.; Echim, M.; Bruno, R. Multifractal Analysis of Heliospheric Magnetic Field Fluctuations observed by Ulysses. Astrophys. J. 2019, 876, 153. [Google Scholar] [CrossRef] [Green Version]
- Wawrzaszek, A.; Echim, M.; Macek, W.M.; Bruno, R. Evolution of Intermittency in the Slow and Fast Solar Wind Beyond the Ecliptic Plane. Astrophys. J. 2016, 814, L19. [Google Scholar] [CrossRef] [Green Version]
- Almqvist, N. Fractal analysis of scanning probe microscopy images. Surf. Sci. 1996, 355, 221–228. [Google Scholar] [CrossRef]
- Lee, J.; Stanley, H.E. Phase transition in the multifractal spectrum of diffusion-limited aggregation. Phys. Rev. Lett. 1988, 61, 2945–2948. [Google Scholar] [CrossRef] [PubMed]
- Malcai, O.; Lidar, D.A.; Biham, O.; Avnir, D. Scaling Range and Cutoffs in Empirical Fractals. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1998, 56, 2817–2828. [Google Scholar] [CrossRef] [Green Version]
- Sun, X.; Fu, Z.X.; Wu, Z.Q. Multifractal calculation of thin film growth. Chin. J. Comput. Phys. 2001, 18, 247–252. [Google Scholar]
- Song, S.; Zeng, L.; Wang, Y.; Li, G.; Deng, X. The response of river network structure to urbanization: A multifractal perspective. J. Clean. Prod. 2019, 221, 377–388. [Google Scholar] [CrossRef]
- Huang, J.P.; Zhang, G.L.; Yu, H.P.; Wang, S.S.; Guan, X.D.; Ren, Y. Characteristics of climate change in the Yellow River basin during recent 40 years. J. Hydraul. Eng. 2020, 51, 1048–1058. [Google Scholar]
- Huang, Y.L.; Wang, Y.L.; Liu, Z.H.; Zeng, X.K.; Chen, L. Stream construction characteristics in rapid urbanization area: Shenzhen city as a case. Geogr. Res. 2008, 27, 1212–1220. [Google Scholar]
- Chin, A. 9.39 Urbanization and River Channels. Treatise Geomorphol. 2013, 809–827. [Google Scholar] [CrossRef]
- Wang, J.J.; Wu, Z.Q. Delimiting the Stages of Urbanization Growth Process: A Method Based on Northam’s Theory and Logistic Growth Mode. Acta Geogr. Sin. 2009, 64, 177–188. [Google Scholar]
- Wang, R.L.; Liu, Y.; Wang, C.X.; Li, M.C.; Tang, Y.C.; Xue, M.Y. Study on the economic connection and network structure evolution of the Yellow River Basin. World Reg. Stud. 2021, 3, 1–11. [Google Scholar]
- Chen, Y.P.; Fu, B.J.; Zhao, Y.; Wang, K.B.; Wang, H. Sustainable development in the Yellow River Basin: Issues and strategies. J. Clean. Prod. 2020, 263, 121223. [Google Scholar] [CrossRef]
- Xie, J.; Xu, Y.-P.; Wang, Y.; Gu, H.; Wang, F. Influences of climatic variability and human activities on terrestrial water storage variations across the Yellow River basin in the recent decade-ScienceDirect. J. Hydrol. 2019, 579, 124218. [Google Scholar] [CrossRef]

| Periods | ||||||
|---|---|---|---|---|---|---|
| 2000s | 1.6720 | 4.6134 | 0.1286 | 0.0262 | 2.9414 | 0.1024 |
| 2010s | 1.7376 | 4.3076 | 0.1568 | 0.0324 | 2.5700 | 0.1243 |
| 2020s | 1.6836 | 3.8057 | 0.0746 | 0.0474 | 2.1220 | 0.0272 |
| Urbanization Rate | Provinces | Parameters | ||||
|---|---|---|---|---|---|---|
| Gray correlation | QH | 0.7900 | 0.7870 | 0.7935 | 0.7317 | 0.7843 |
| GS | 0.7384 | 0.7380 | 0.7397 | 0.7355 | 0.7424 | |
| NX | 0.7417 | 0.7343 | 0.7391 | 0.7882 | 0.7303 | |
| SA | 0.7453 | 0.7417 | 0.7469 | 0.6977 | 0.7472 | |
| NMG | 0.7189 | 0.7239 | 0.7217 | 0.7193 | 0.7171 | |
| SX | 0.7698 | 0.7653 | 0.7615 | 0.7211 | 0.7634 | |
| HN | 0.7494 | 0.7481 | 0.7543 | 0.7055 | 0.7464 | |
| SD | 0.7783 | 0.7664 | 0.7701 | 0.7322 | 0.7657 | |
| SC | 0.8896 | 0.8563 | 0.8865 | 0.9326 | 0.8778 | |
| YRB | 0.7041 | 0.7159 | 0.7169 | 0.7967 | 0.7086 | |
| Average | 0.7626 | 0.7577 | 0.7630 | 0.7561 | 0.7583 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Qin, Z.; Shi, Y.; Yao, J. Multifractal Analysis of River Networks under the Background of Urbanization in the Yellow River Basin, China. Water 2021, 13, 2347. https://doi.org/10.3390/w13172347
Wang J, Qin Z, Shi Y, Yao J. Multifractal Analysis of River Networks under the Background of Urbanization in the Yellow River Basin, China. Water. 2021; 13(17):2347. https://doi.org/10.3390/w13172347
Chicago/Turabian StyleWang, Jinxin, Zilong Qin, Yan Shi, and Jing Yao. 2021. "Multifractal Analysis of River Networks under the Background of Urbanization in the Yellow River Basin, China" Water 13, no. 17: 2347. https://doi.org/10.3390/w13172347
APA StyleWang, J., Qin, Z., Shi, Y., & Yao, J. (2021). Multifractal Analysis of River Networks under the Background of Urbanization in the Yellow River Basin, China. Water, 13(17), 2347. https://doi.org/10.3390/w13172347





