A Systematic Analysis of the Interaction between Rain-on-Grid-Simulations and Spatial Resolution in 2D Hydrodynamic Modeling
Abstract
1. Introduction
Motivation and Research Gap
- Zeiger & Hubbart (2021) [3] evaluated an integrated modeling approach, using a coupled-modeling routine. The river basin model SWAT (‘Soil and Water Assessment Tool’) was used to determine effective rainfall rates and HEC-RAS 2D was used as for the rain-on-grid simulations. The Hinkson Creek Watershed (232 km2) was discretized with 10 m mesh and 1 m DEM as underlying subgrid.
- Krvavica & Rubinić (2020) [4] applied HEC-RAS with direct precipitation in a small ungauged catchment of 3.08 km2. The focus of the research project was the evaluation of the influence of different storm designs and rainfall durations on the catchment outflow. A mesh with an average grid size of 10 m and local refinements of 5 m was used with a 2 m subgrid DEM for topographic details.
- Rangari et al. (2019) [16] applied HEC-RAS as HDRRM for different storm events in the highly urbanized area of Hyderabad. The model was set up for an area with 47.08 km2, a fixed mesh resolution and underlying DEM of each 10 m and 139,487 computational cells.
- Caviedes-Voullième et al. (2020) [17] compared the impact of the application of zero-inertia (‘ZI’) and shallow-water (‘SW’) models. The results of six different benchmarking test cases were analyzed. One of the test cases included the application in an urban area in Glasgow with a catchment size of 0.4 km2. The study was conducted for four different (1. ‘very-coarse’—4 m, 2. ‘coarse’—3 m, 3. ‘medium’—2 m, 4.‘fine’—1 m) model-set-ups.
- Tyrna et al. (2018) [8] applied the 2D hydraulic model FloodArea in an ungauged urban area with a study area of 144 km2 to provide “large-scale high-resolution fluvial flood hazard mapping”. They presented a method that involves a precipitation model, a hydrological model, a digital elevation model and a hydraulic model component. The model set-up consisted of a 1 m raster-based model.
- Pina et al. (2016) [18] used two case studies to compare a semi (‘SD’)—and a fully (‘FD’)—distributed model. The study consists of two model set-ups with the focus of the comparison of the SD and FD approaches and the integration of a sewer-system network. The first FD model has an average resolution of 61 m2 with a catchment size of 8.5 km2. The second FD model has a size of 1.5 km2 with an average cell size of 89 m2. The focus of the modeling processes is the comparison of the two different model types.
- Cea & Rodriguez (2016) [19] present the development of a 2D distributed hydrologic-hydraulic model (‘GUAD-2D’) with the objective to model the rainfall–runoff process within a catchment. The presented model was tested in a 12.97 km2 large urban catchment, an ungauged area with a cell size of 4 m and a 500 year storm event. The model was evaluated against a model-set up without DRM.
- Fraga et al. (2016) [20] conducted a global sensitivity and uncertainty analysis for a 2d-1d dual drainage model [21] using the GLUE (‘Generalized Likelihood Uncertainty Estimation’, compare Beven & Binley (1992) [22]) method which is developed for distributed models. For the surface model the sensitivity of the Manning’s n coefficient and the infiltration parameters were analyzed. The study was conducted in a motorway section with an area of 0.049 km2. The model geometry consists of an unstructured mesh with a fixed mesh resolution of circa 3 m.
- Leandro et al. (2016) [23] introduced a methodology that stepwise increases the model complexity in different modeling levels to evaluate the impact of ‘spatial heterogeneity of urban key features’. The 2D overland flow model P-DWave [24] was set-up for a catchment area (‘Borbecker Mühlenbach’, 4.9 km2). The model was systematically extended in five stages with focus on the representation of buildings and land surfaces. The model geometry was created with a fixed grid with 2 m resolution.
- Yu et al. (2015) [2] applied the hydro-inundation model FloodMap in an urbanized area in Kingston upon Hull (UK). The influence of improved urban and rural drainage and storage capacity was investigated in a stepwise manner. During the modeling process the model sensitivity to roughness and mesh resolution was determined.
- Néelz & Pender (2013) [25] analyzed various 2D hydrodynamic model in eight different benchmark test cases. The last test case includes an application of the 2D models by direct precipitation in a small urban area in Glasgow with a total size of 0.384 km2. The same test case was further evaluated for various models in [26] and for HEC-RAS in [27]. For most of the models, a fixed spatial resolution and roughness values were used with a 2 m grid. For HEC-RAS two different mesh resolution (2 m, 4 m) were evaluated, which showed minor sensitivity on model run times and sensitivity on water level time series [27].
- Chen et al. (2010) [28] applied the integrated 1D sewer and 2D overland flow model SIPSON/UIM in a small urban catchment area (‘Stockbridge’, ca. 0.18 km2) close to a riverside. The model is set-up with a fixed resolution of 2 m. The focus of the study is given on the impact of different design storms and floods for an area which is affected by combined pluvial and fluvial flooding.
- David & Schmalz (2020) [5] evaluated the application of the modeling software HEC-RAS in a low mountain-range study area with a catchment size of 38 km2. Various model settings were tested for the specific application of DRM and a model calibration was carried out based on the Manning’s n roughness. It has been shown that internal model parameters are sensitive for the application of hydrodynamic rainfall–runoff modeling and must be adapted to a different value range. Due to the size of the area and the resulting extensive computing times, no detailed sensitivity analysis was carried out.
- Jia et al. (2019) [7] developed the model system for surface and channel runoff CCHE2D. It was applied to a subcatchment of the Mississippi River, with a catchment size of 18 km2. In the study a local sensitivity analysis for the Manning’s n roughness was carried out. The evaluated values were in a range between 0.03 and 0.3 s × m−1/3. The model was set up with a fixed mesh resolution between 3.8 and 5 m.
- Broich et al. (2019) [6] developed an approach for the implementation of the DRM in the 2D hydrodynamic model TELEMAC-2D. They applied the extended model to the catchment areas of Simbach (45.9 km2) and Triftern (90.1 km2). Furthermore, alternative approaches for the roughness calculation for sheet water flow were implemented as new calculation routines. Additionally the impact of model intern (‘hidden’) parameters on the modeling results were evaluated. The model geometry was based on a 5 m DEM with 1 s timestep.
- Hall (2015) [29] conducted a DRM application in the Birrega catchment with an area of ca. 185 km2. For the model application, the 2D model MIKE from the Danish Hydraulic Institute (‘DHI’) was used. The model geometry consists of a grid with a constant resolution of 20 m. In the modeling process, design floods with different return periods were evaluated. In a simplified local sensitivity analysis of the impact of 1. rainfall, 2. Manning’s roughness, 3. infiltration and 4. groundwater inundation. Each model set-up was tested for a large- (176 km2) and small- (7 km2) scale catchment area.
- Cea & Bladé (2015) [30] developed a discretization scheme (‘Decoupled hydrological discretization’, DHD) to solve the 2D SWE for hydrodynamic rainfall–runoff applications. They applied the model to five test cases, where two test cases involved application in small rural basins. The first catchment has a size of 4 km2 with an average cell size of 15.5 m. The second catchment has a size of 5 km2 with an average cell size of 20 m. The model was calibrated by the infiltration rate and the Manning’s n values. In the study, the alternative discretization scheme is evaluated against three other methods.
- Clark et al. (2008) [31] compares the two 2D models TUFlow and SOBEK with a traditional lumped hydrological rainfall runoff model. In a 11.85 km2 large catchment area a local sensitivity analysis is performed considering various parameters. The spatial resolution is evaluated for mesh resolution between 10 m and 100 m (TUFlow) and 5 m and 100 m (SOBEK). It has shown that both models are sensitive towards the mesh resolution.
2. Objectives
- To introduce a stepwise methodology which allows a systematic analysis of model behavior and parameter sensitivity when applying HEC-RAS and the DRM in a small rural catchment.
- To reduce the number of model runs in order to manually execute the methodology.
- To evaluate the parameter sensitivity of: 1. mesh resolution, 2. subgrid topographical data, 3. laminar depth, 4. Manning’s n values, 5. model-specific filter settings and 6. precipitation data.
- To give recommendations on suitable spatial resolution and identify sensitive model settings when applying the 2D model HEC-RAS for storm hazard analysis in small catchments of low mountain range areas.
3. Materials and Methods
3.1. Model Behavior, Sensitivity Analysis and Model Uncertainty
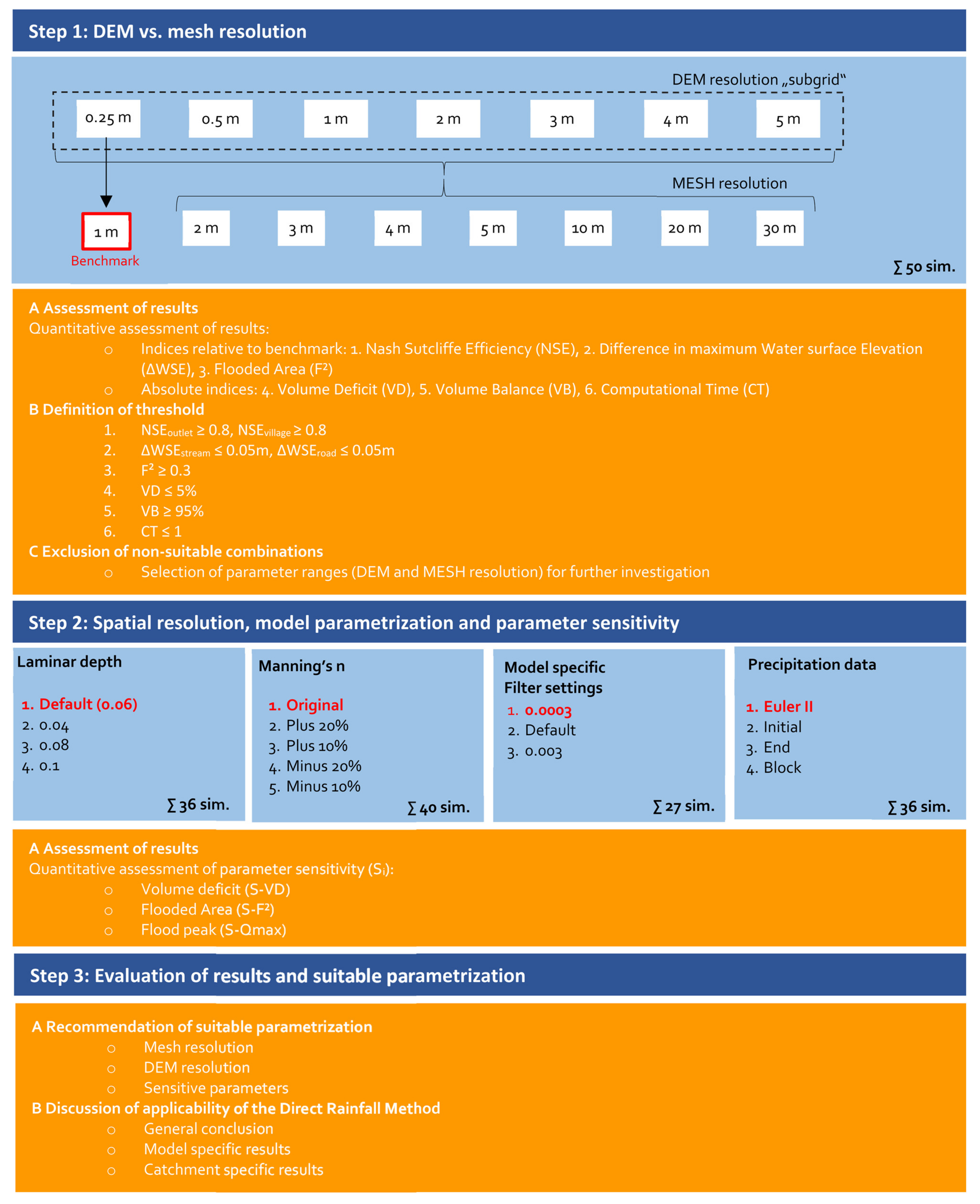
3.2. Systematic Analysis of Model Behavior
3.3. Hardware
3.4. Evaluation of Results
3.4.1. Nash–Sutcliffe Efficiency (NSE)
3.4.2. Difference in Maximum Water-Surface Elevation (ΔWSE)
3.4.3. Flooded Area (F2)
3.4.4. Volume Deficit (VD)
3.4.5. Volume Balance (VB)
3.4.6. Computational Time (CT)
3.4.7. Local Model Sensitivity (e)
3.5. 2D Hydrodynamic Model: HEC-RAS
4. Case Study, Data and Model Set-up
4.1. Messbach Catchment
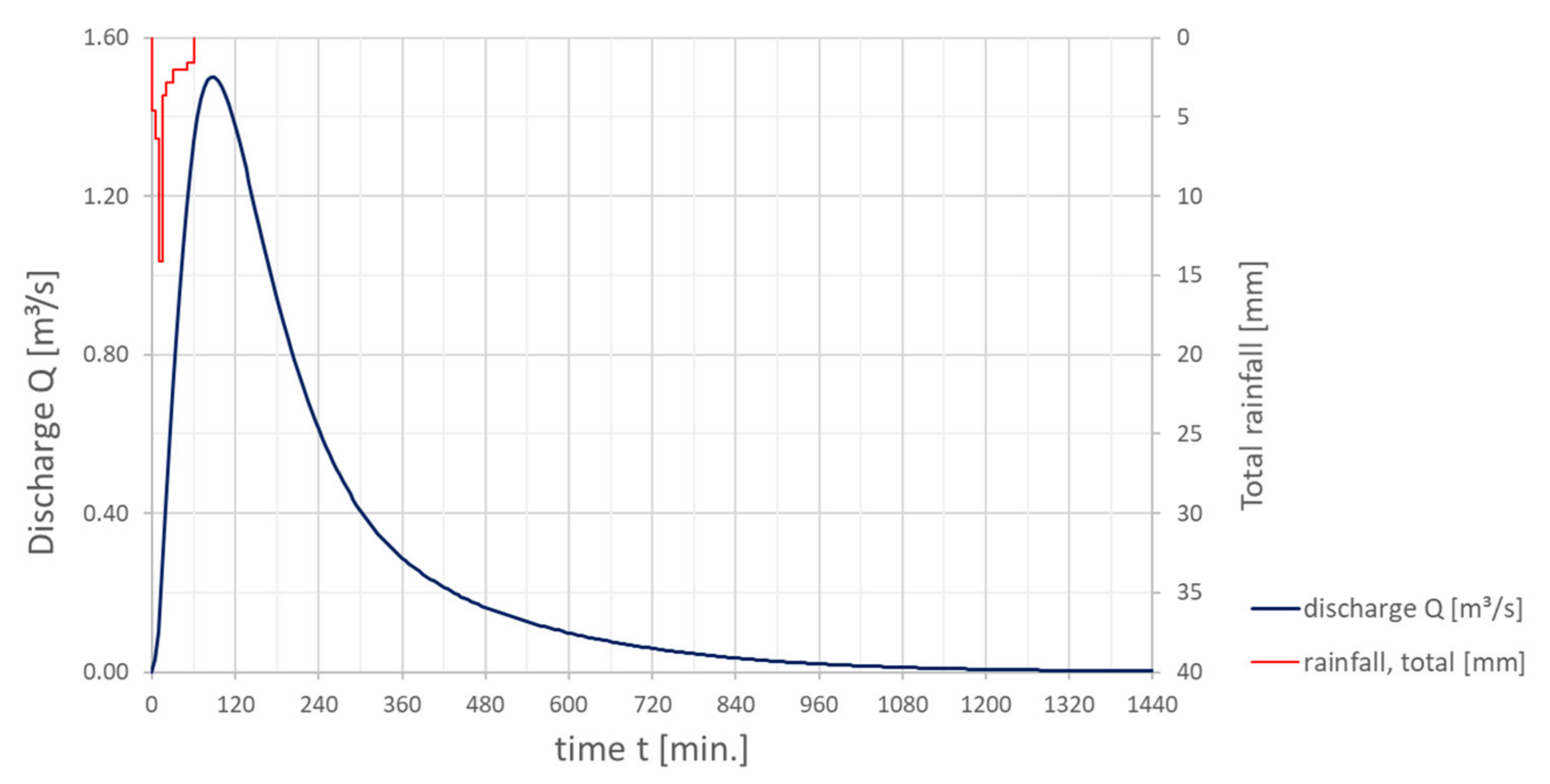
4.2. Model Set-up
5. Results and Discussion
5.1. Pre-Study: Comparison of HEC-RAS 5.0.7 and 6.0
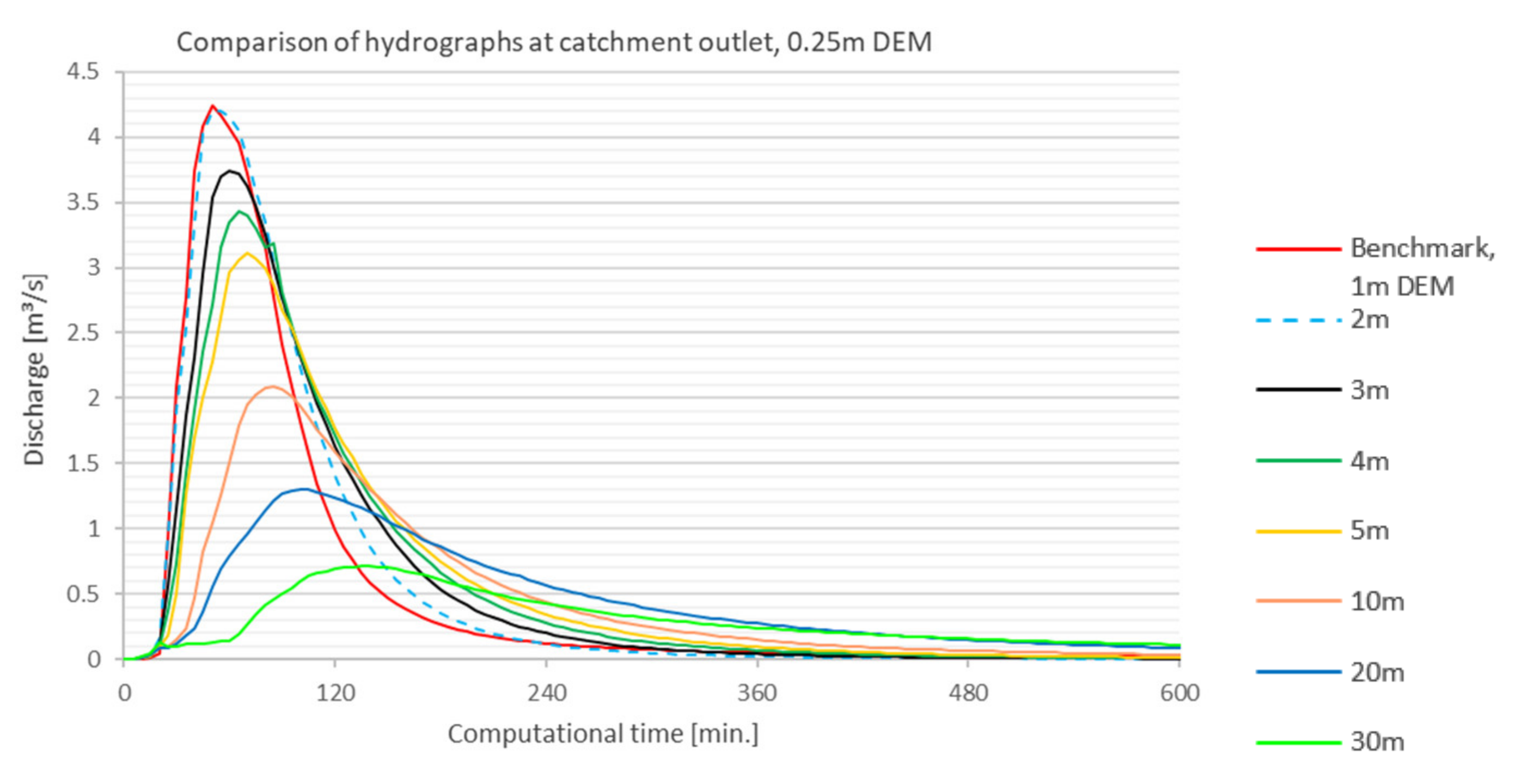
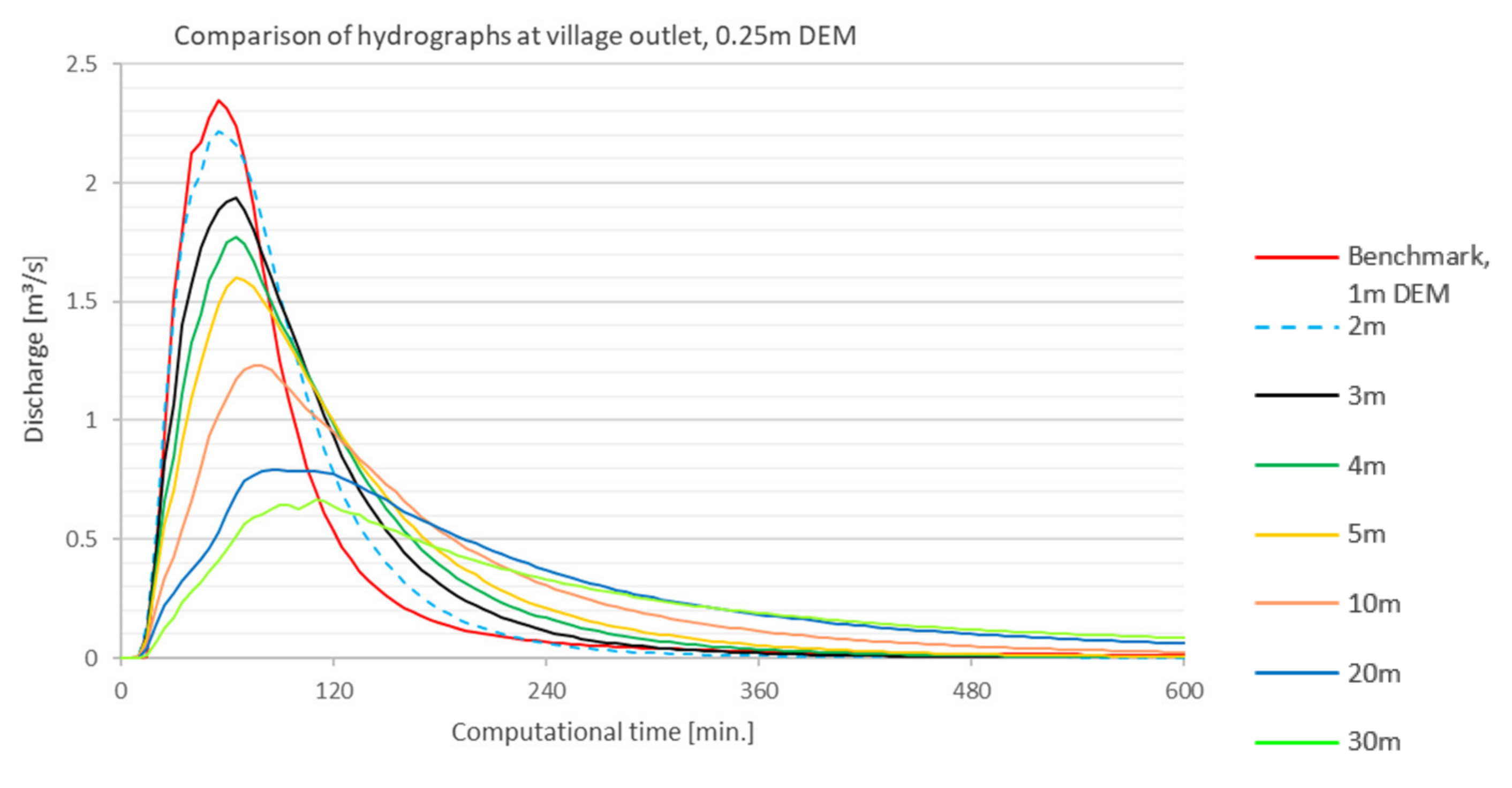
5.2. Step 1—DEM vs. Mesh Resolution
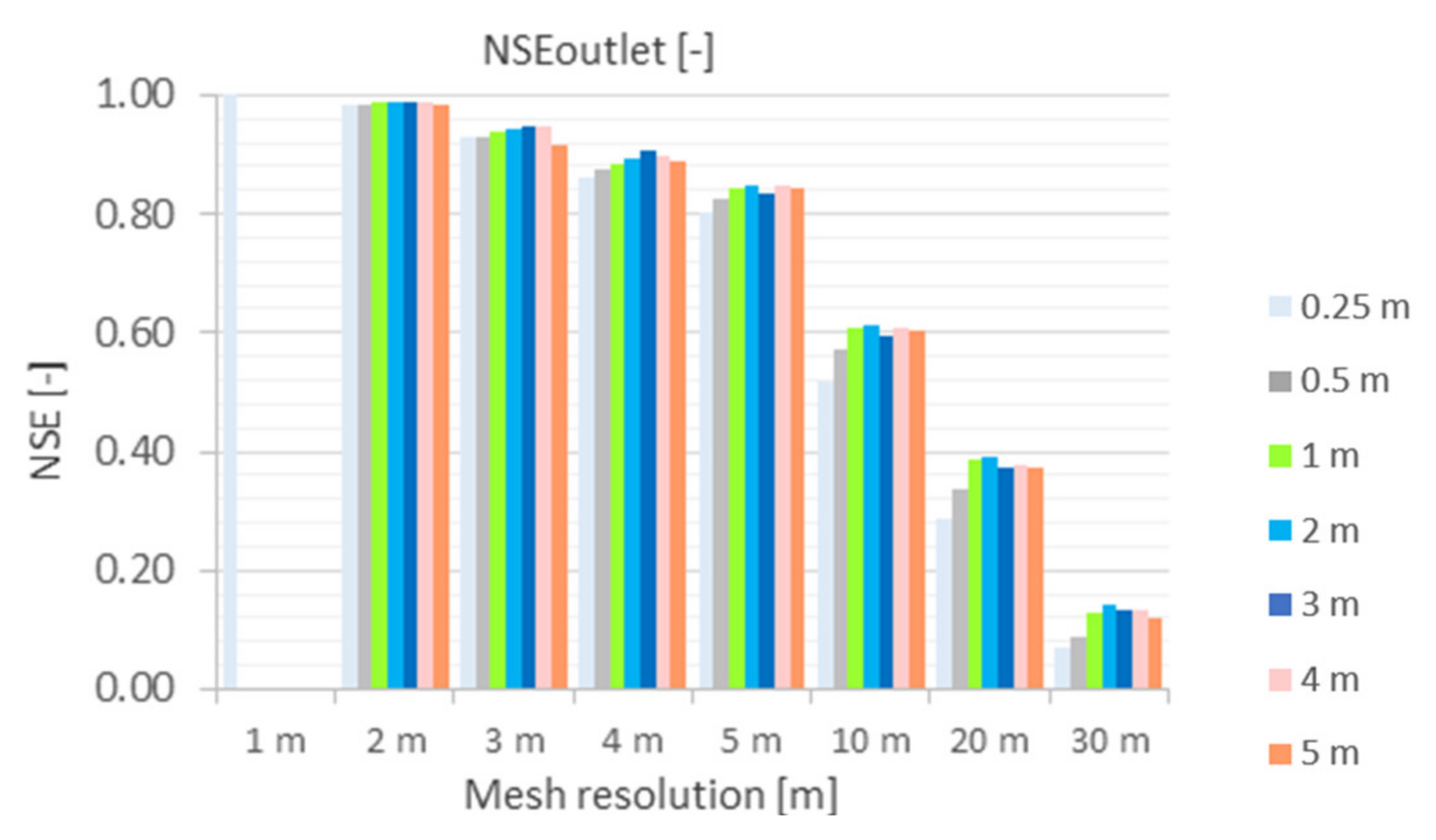
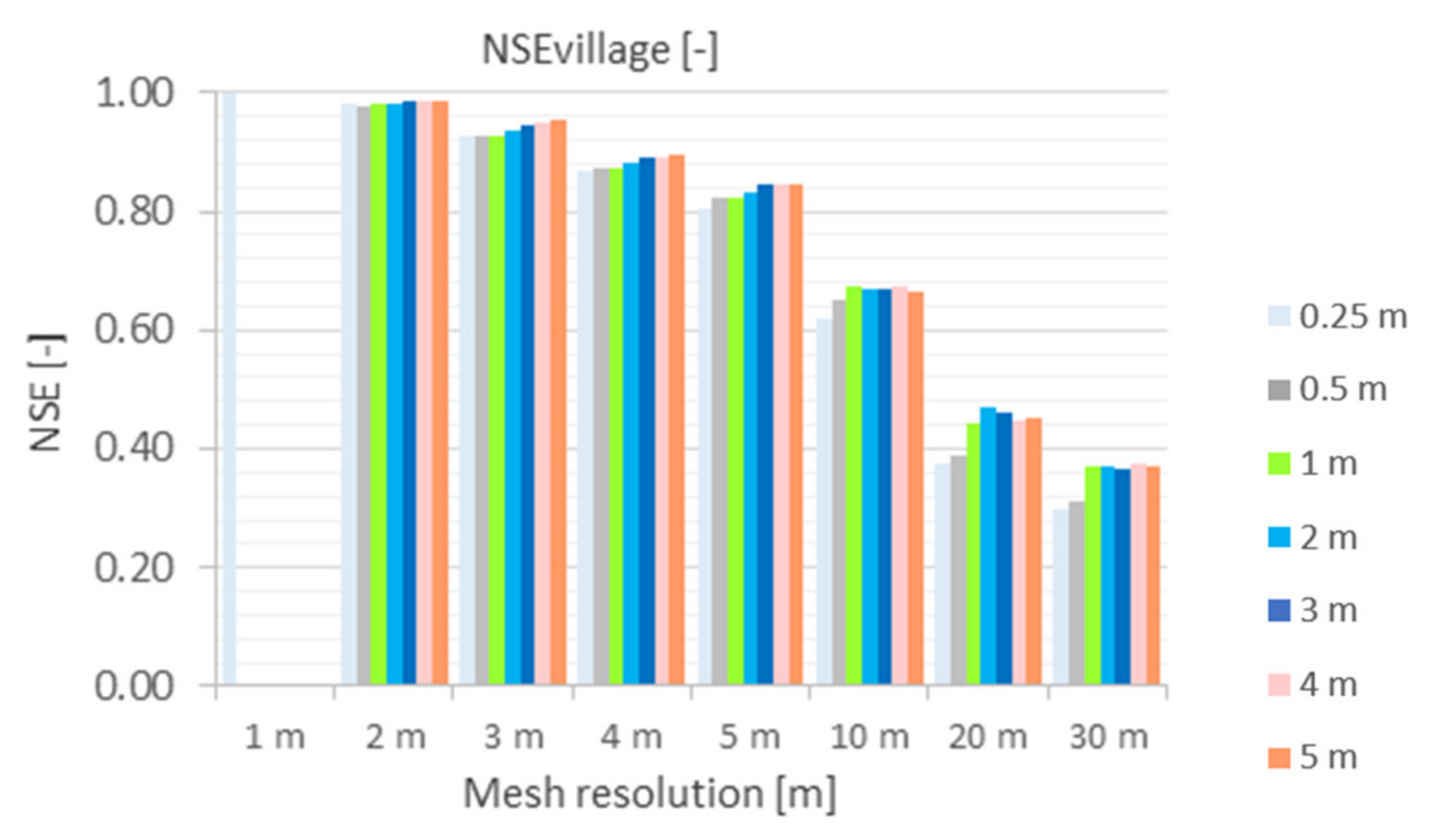
5.2.1. Nash–Sutcliffe Efficiency (NSE)
- a.
- NSEoutlet
- b.
- NSEvillage
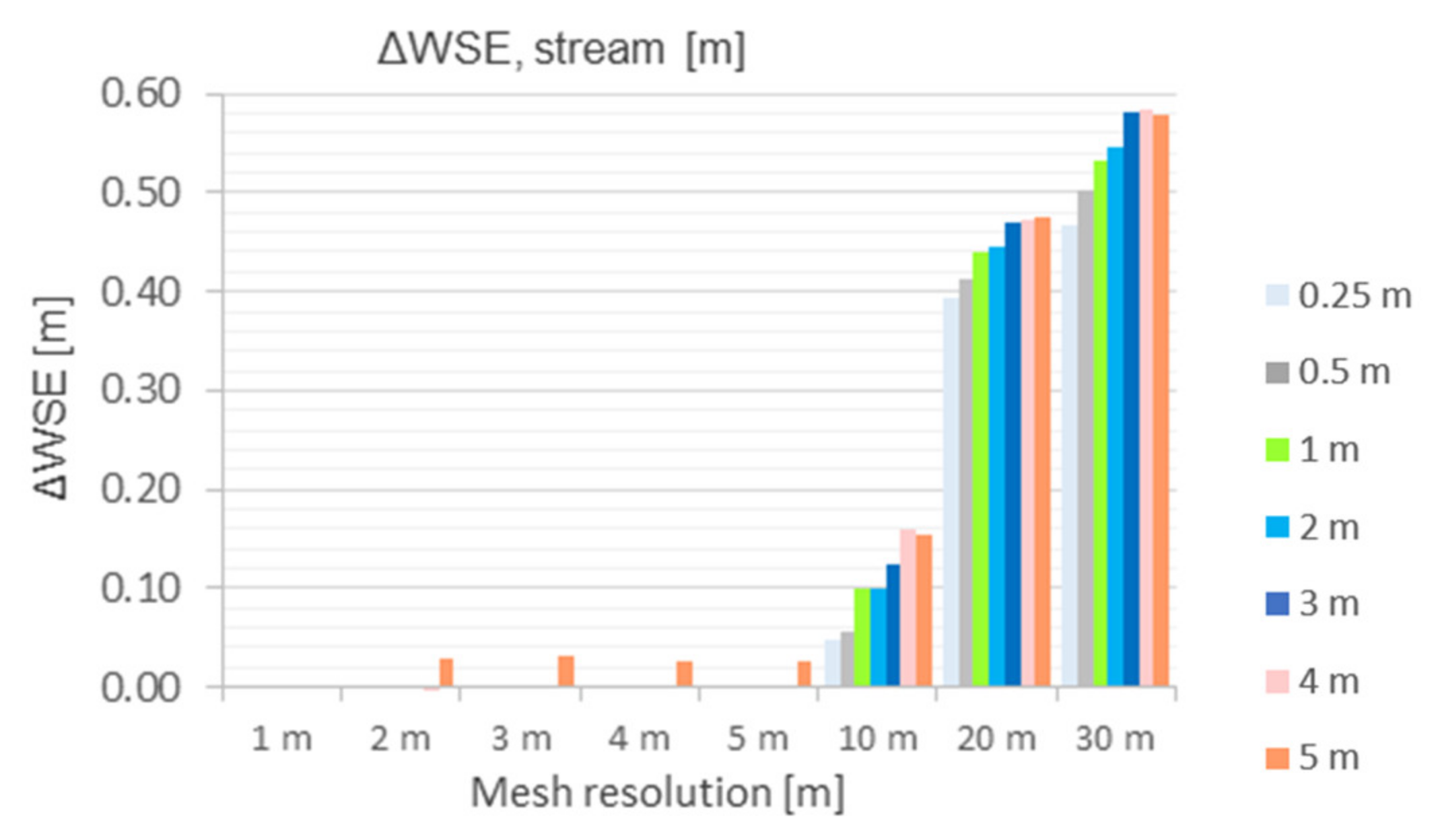
5.2.2. Difference in Maximum Water-Surface Elevation (ΔWSE)
- a.
- ΔWSEstream
- b.
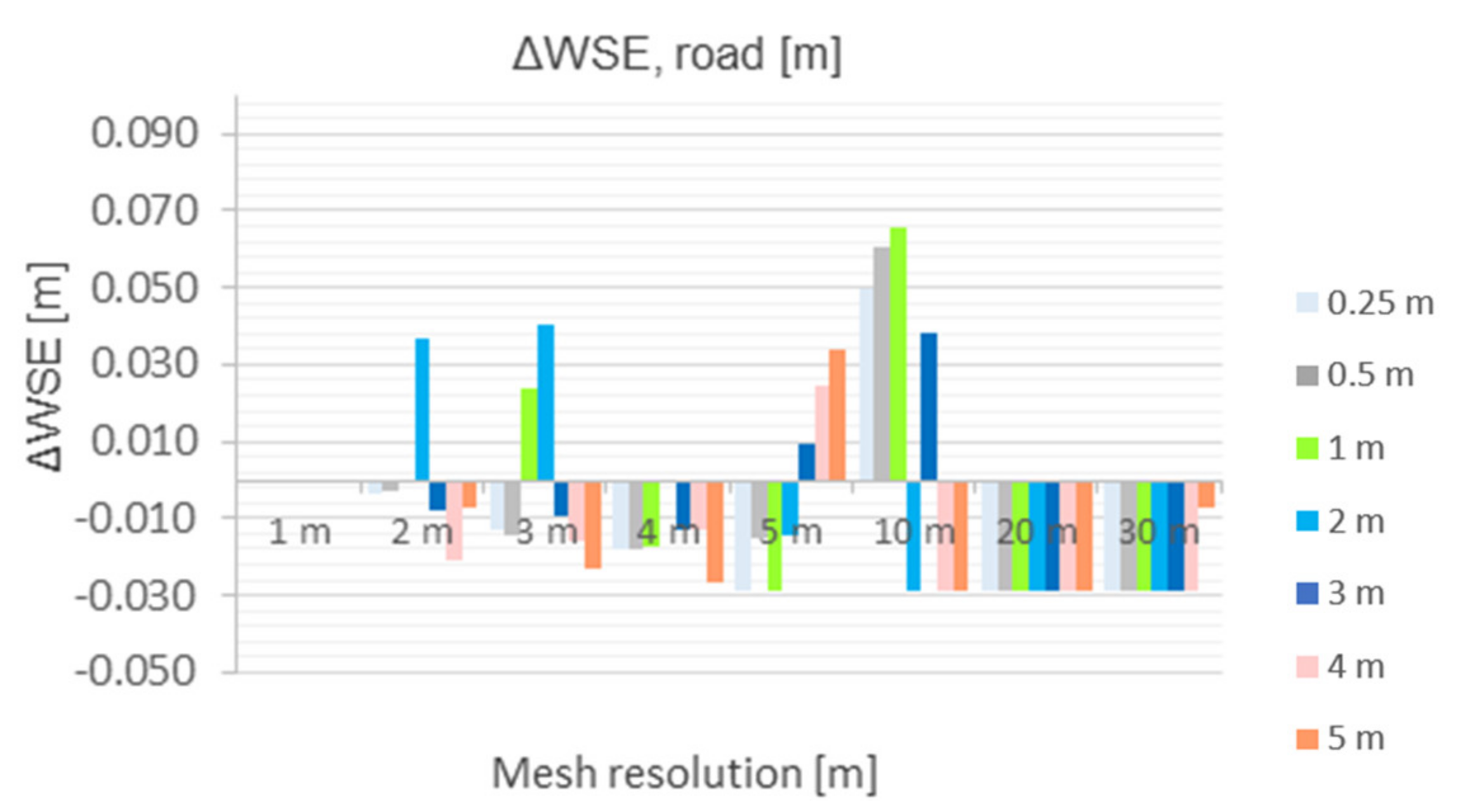
- ΔWSEroad
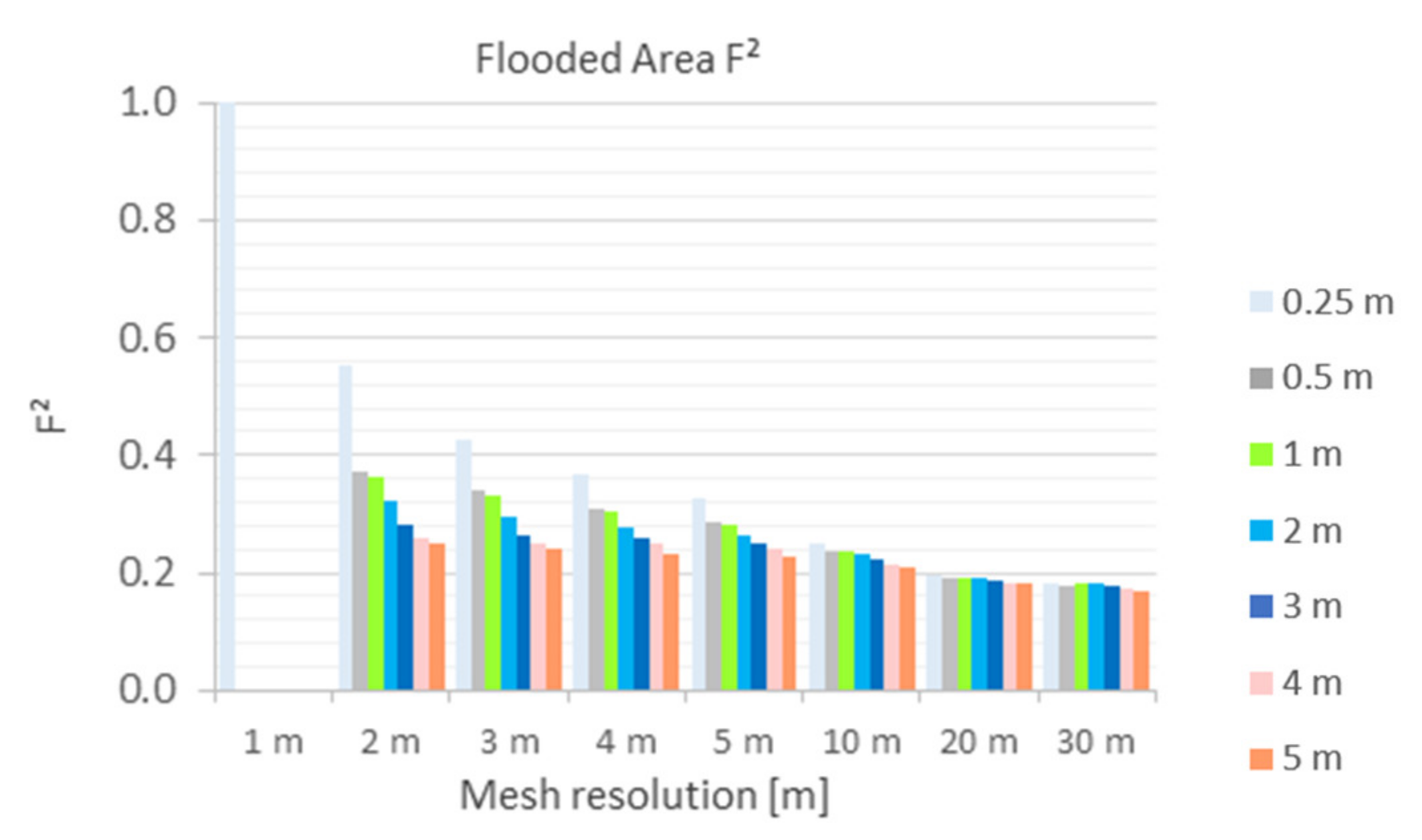
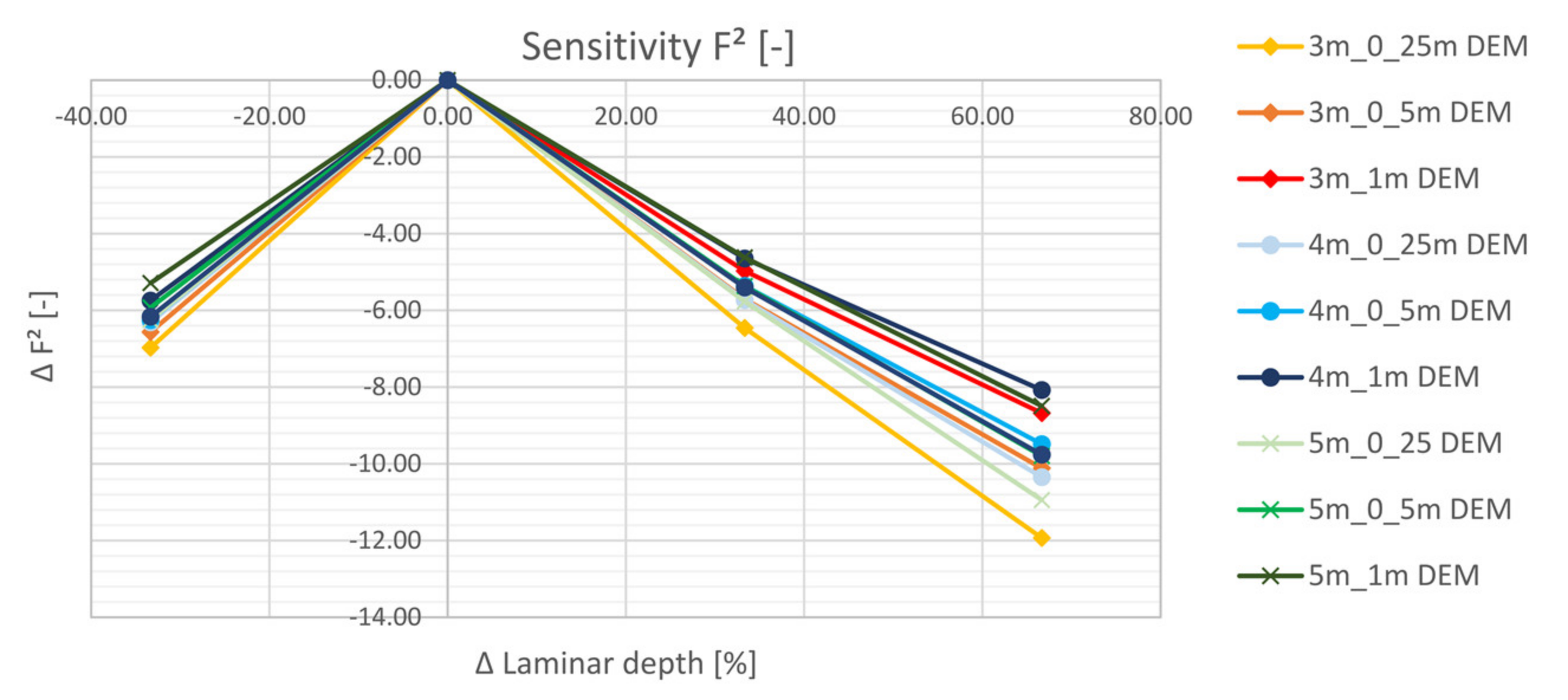
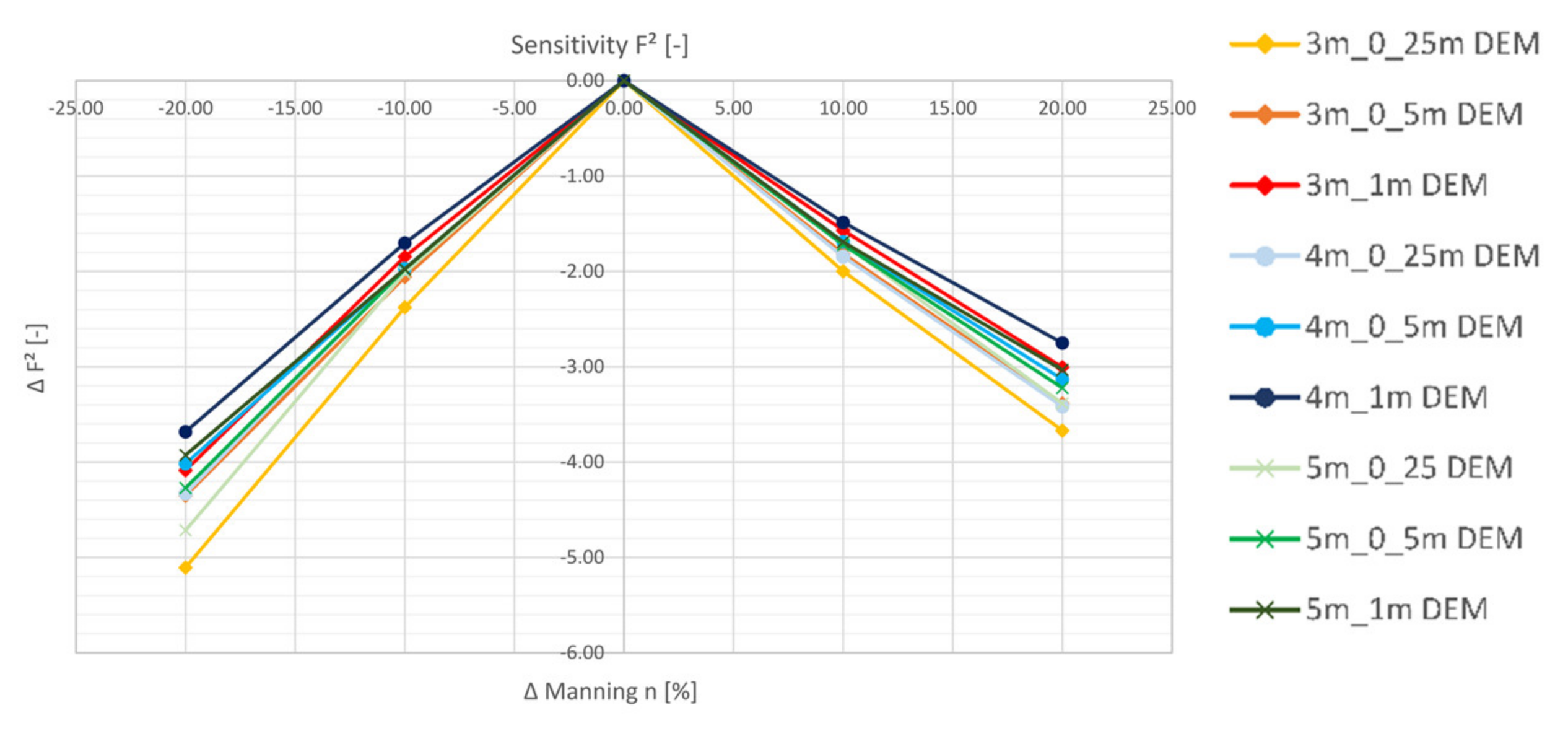
5.2.3. Flooded Area (F2)
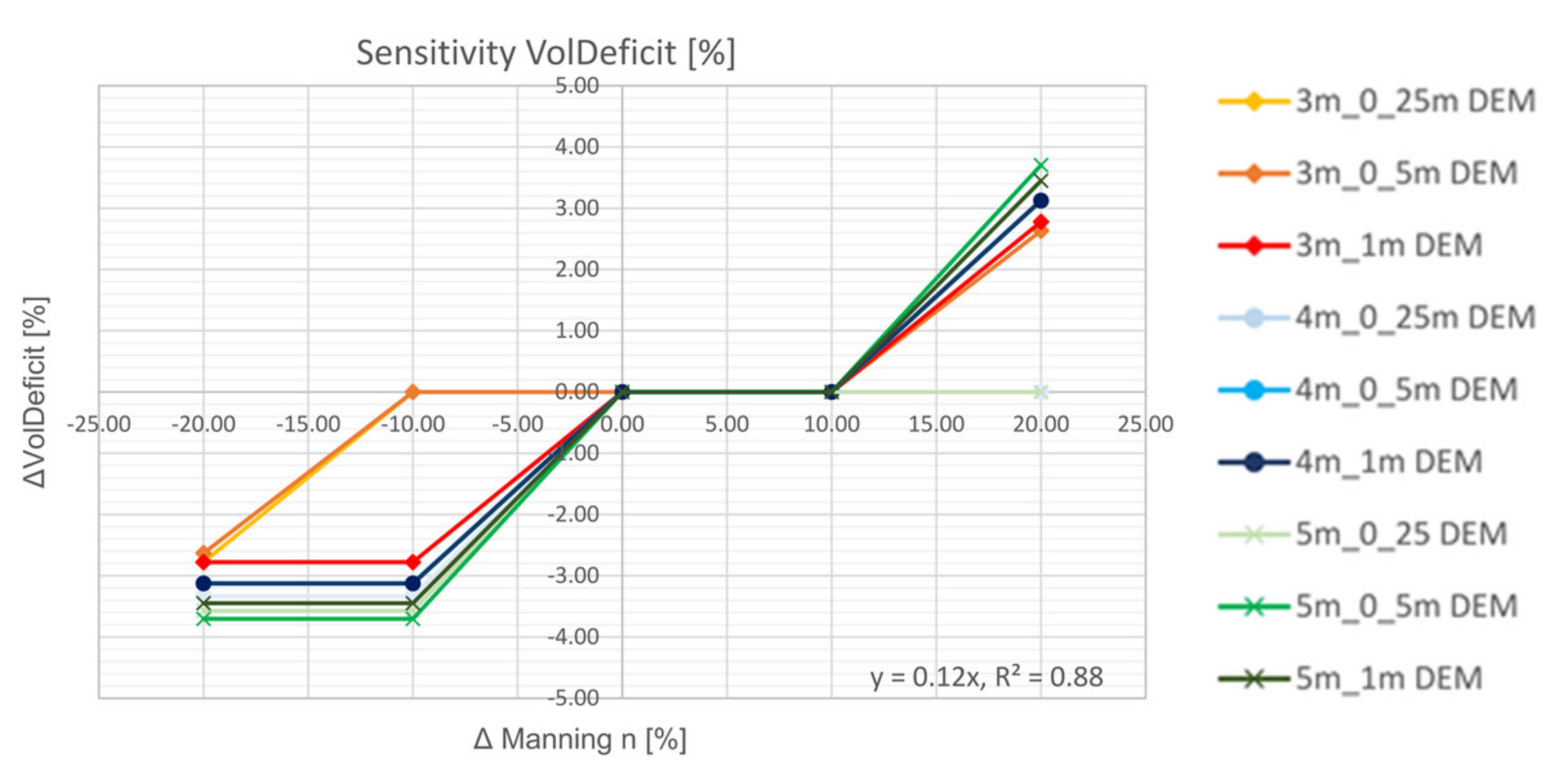
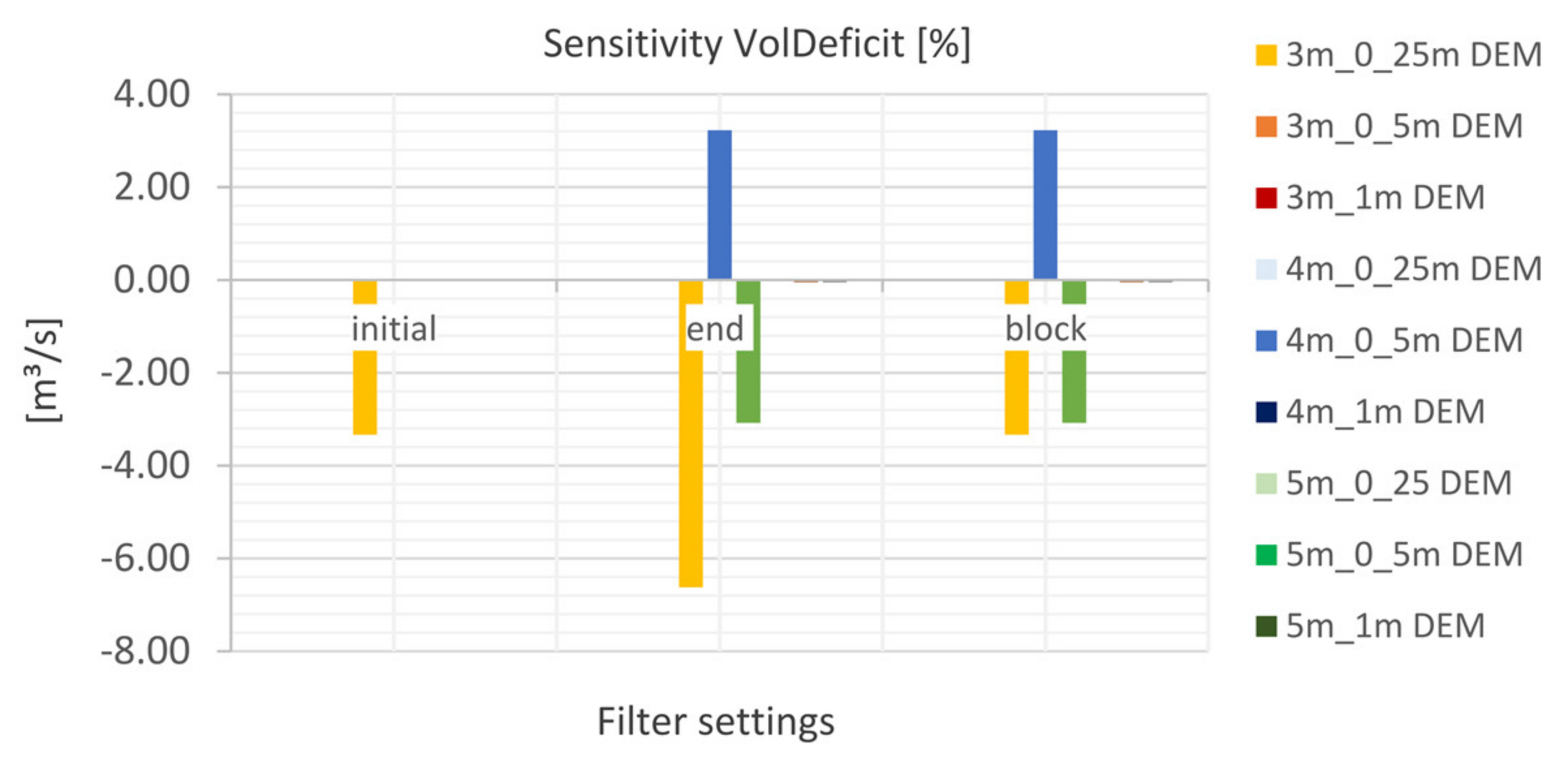
5.2.4. Volume Deficit (VD)
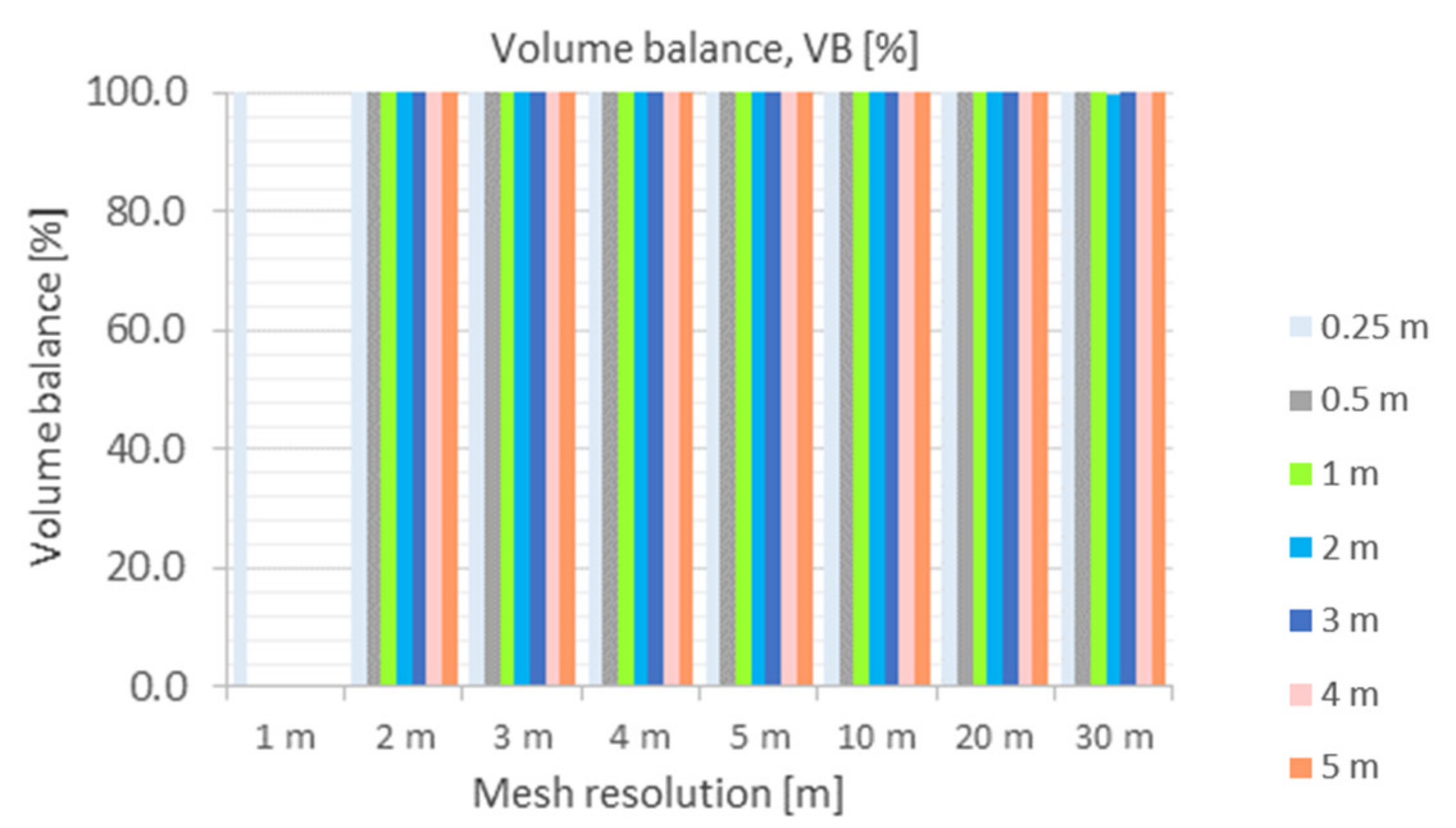
5.2.5. Volume Balance (VB)
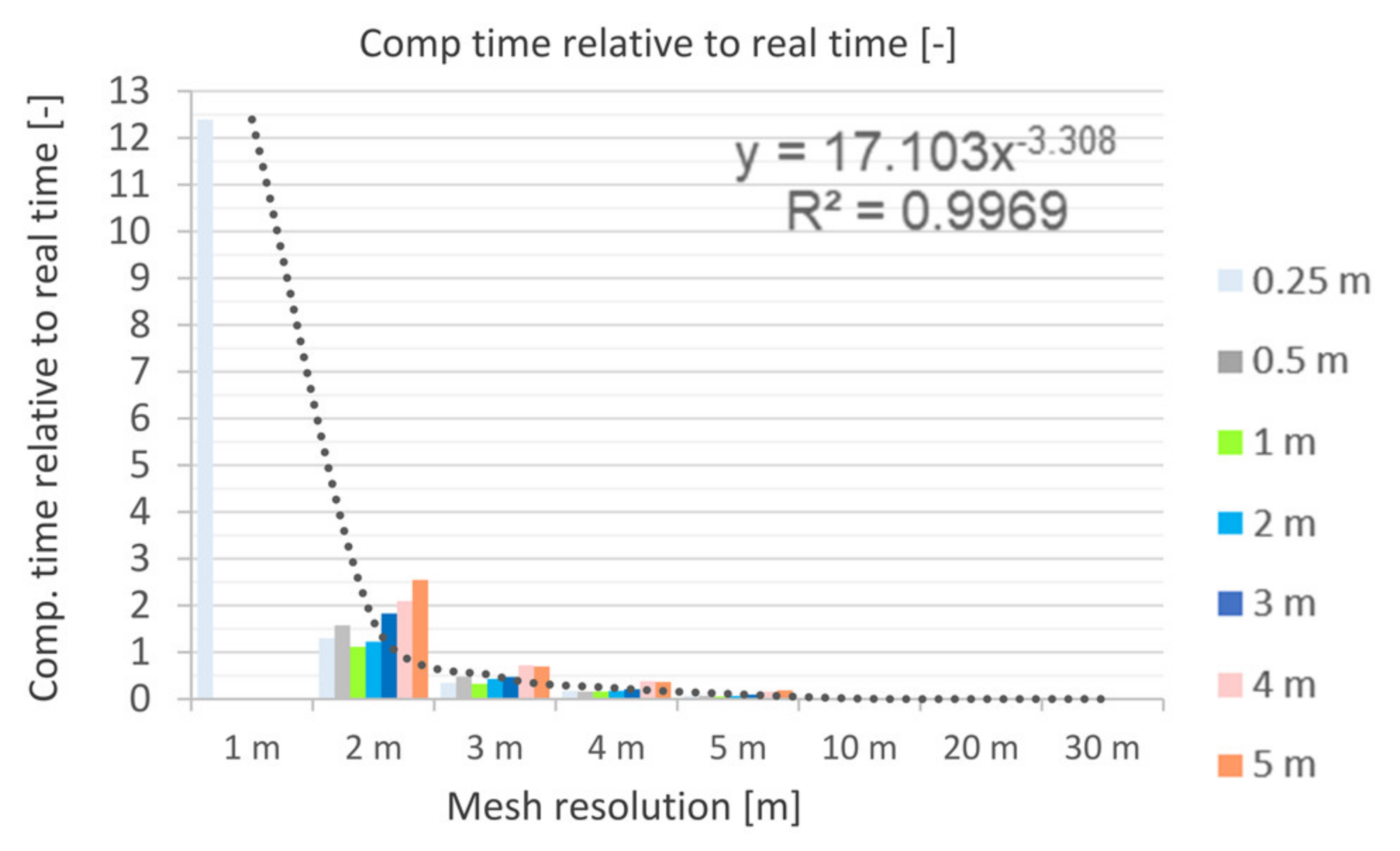
5.2.6. Computational Time in Comparison to Real Time (CT)
5.3. Criteria for the Selection of Suitable Model Configurations
- NSEvillage/outlet = 0.8,
- ΔWSEroad = 0.03 cm,
- Δ WSEstream = 0.05 cm,
- VD = 5%, VB = 95%,
- CT = 1
- 3 m mesh with 0.25 m, 0.5 m, 1 m terrain model,
- 4 m mesh with 0.25 m, 0.5 m, 1 m terrain model,
- 5 m mesh with 0.25 m, 0.5 m, 1 m terrain model.
5.4. Step 2—Further Parameter Sensitivity
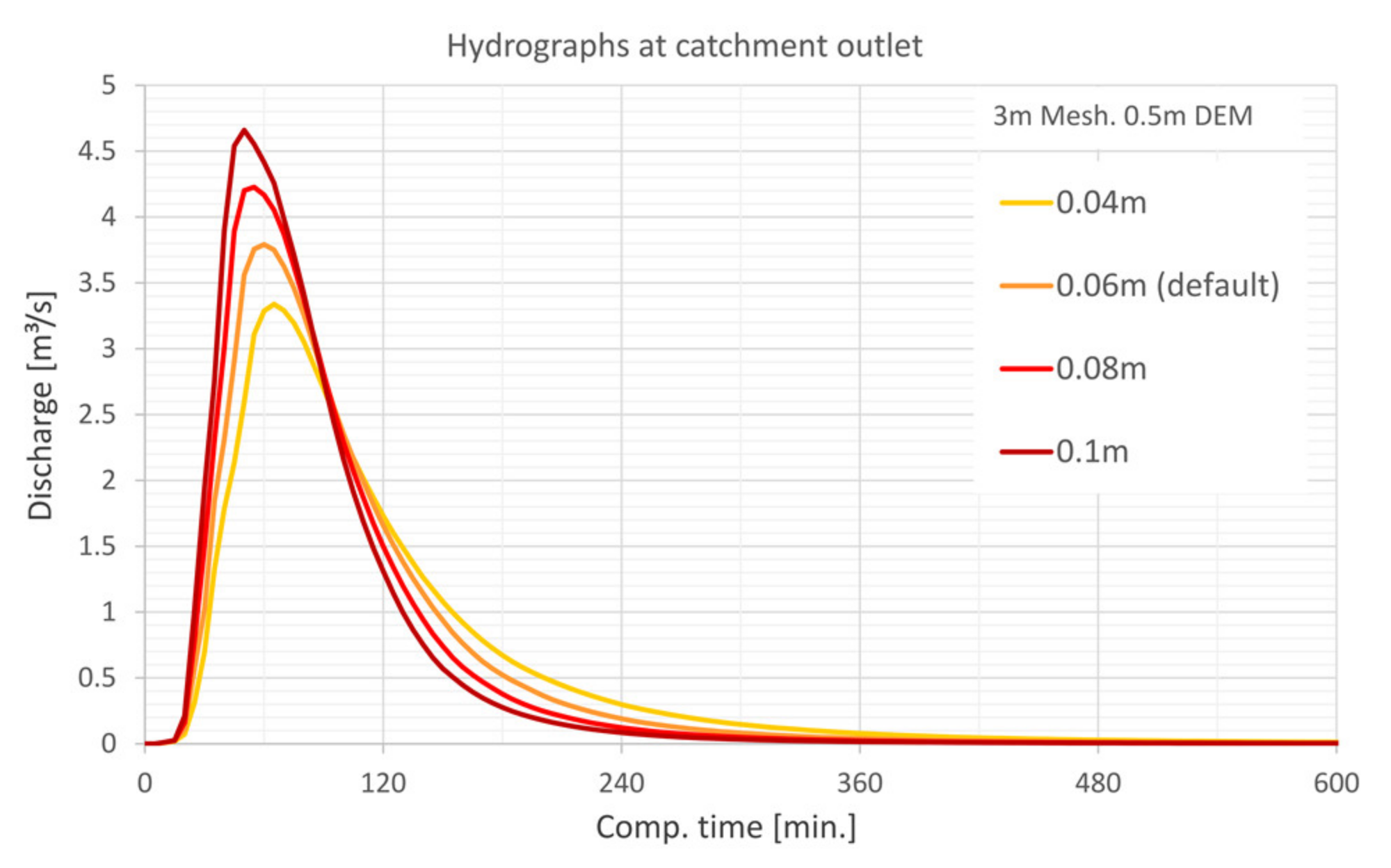
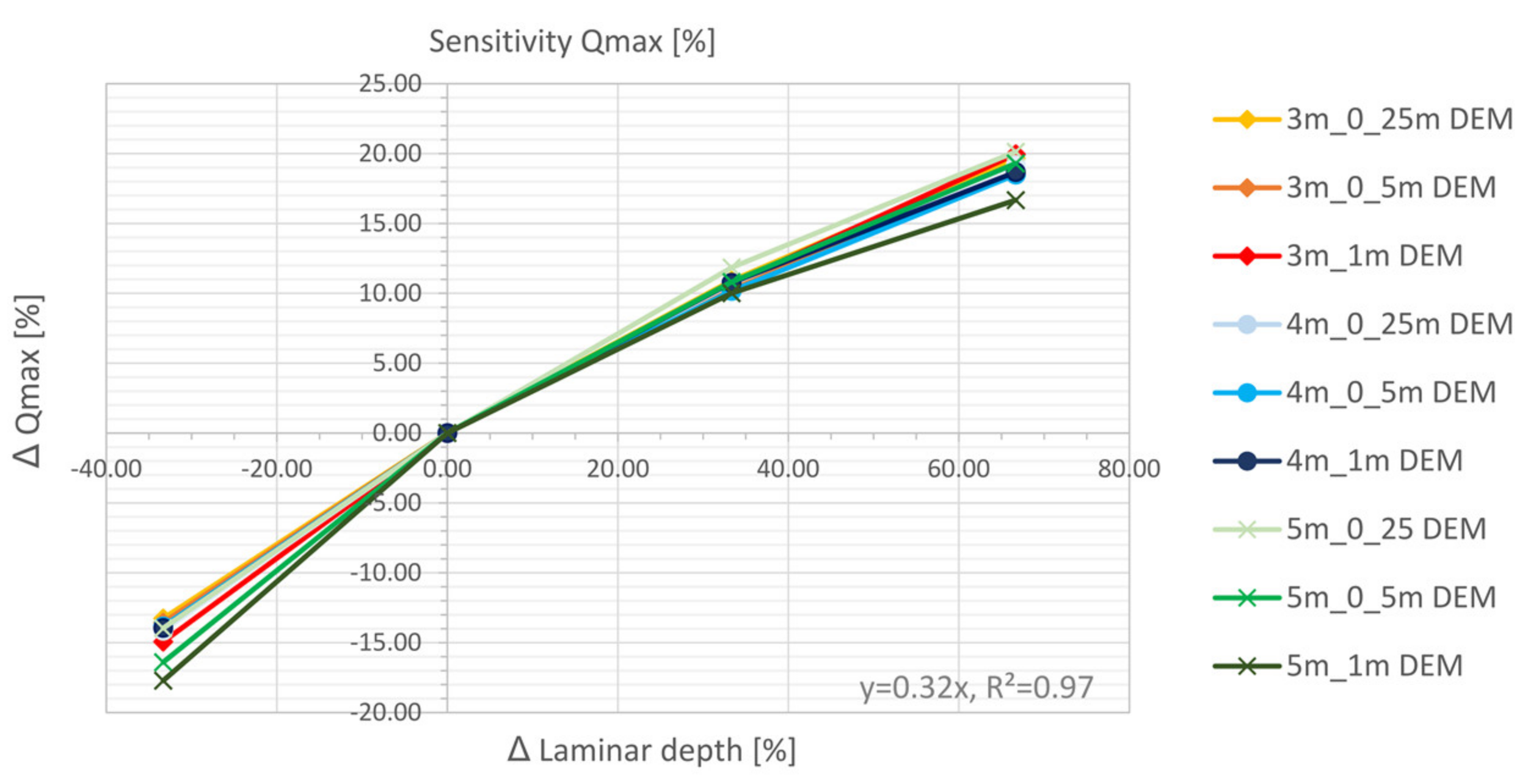
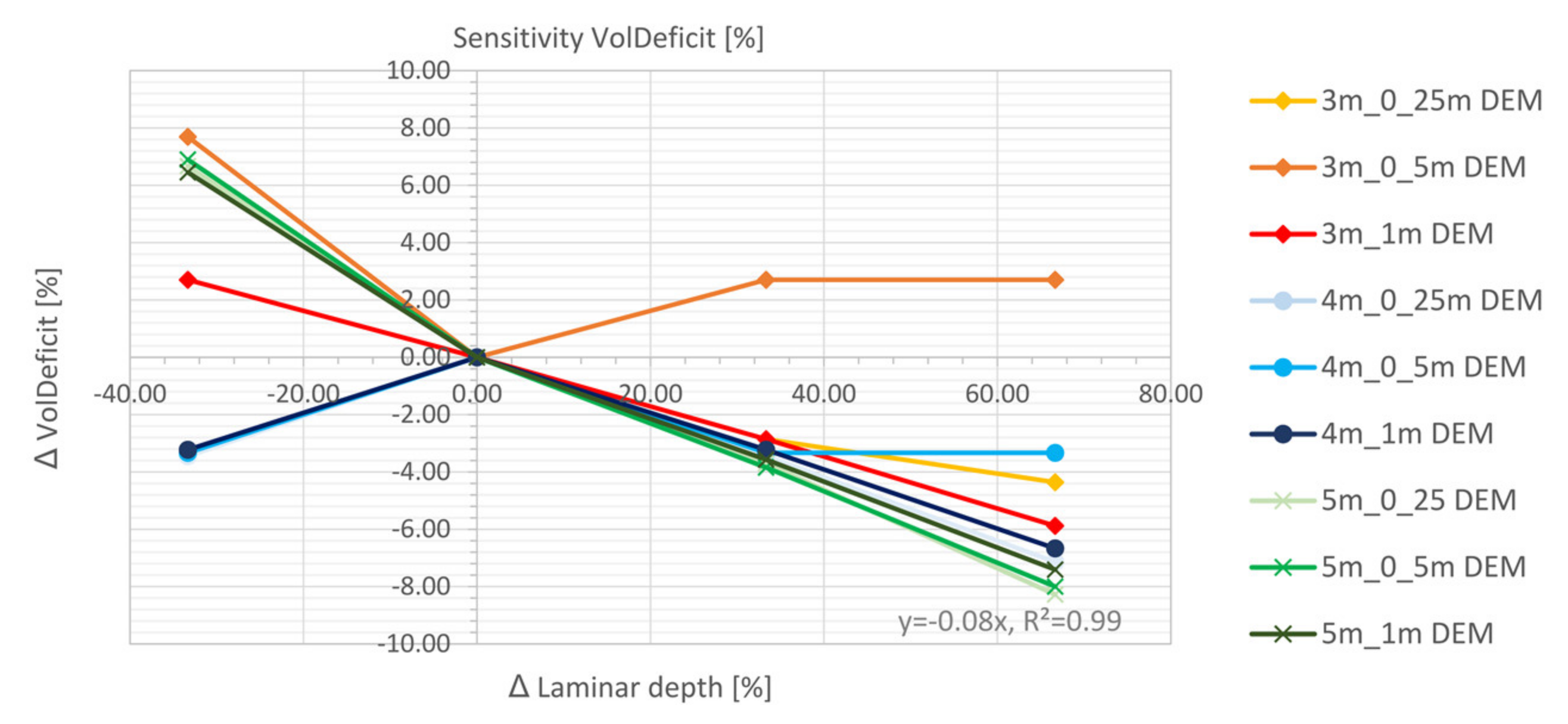
5.4.1. Laminar Depth
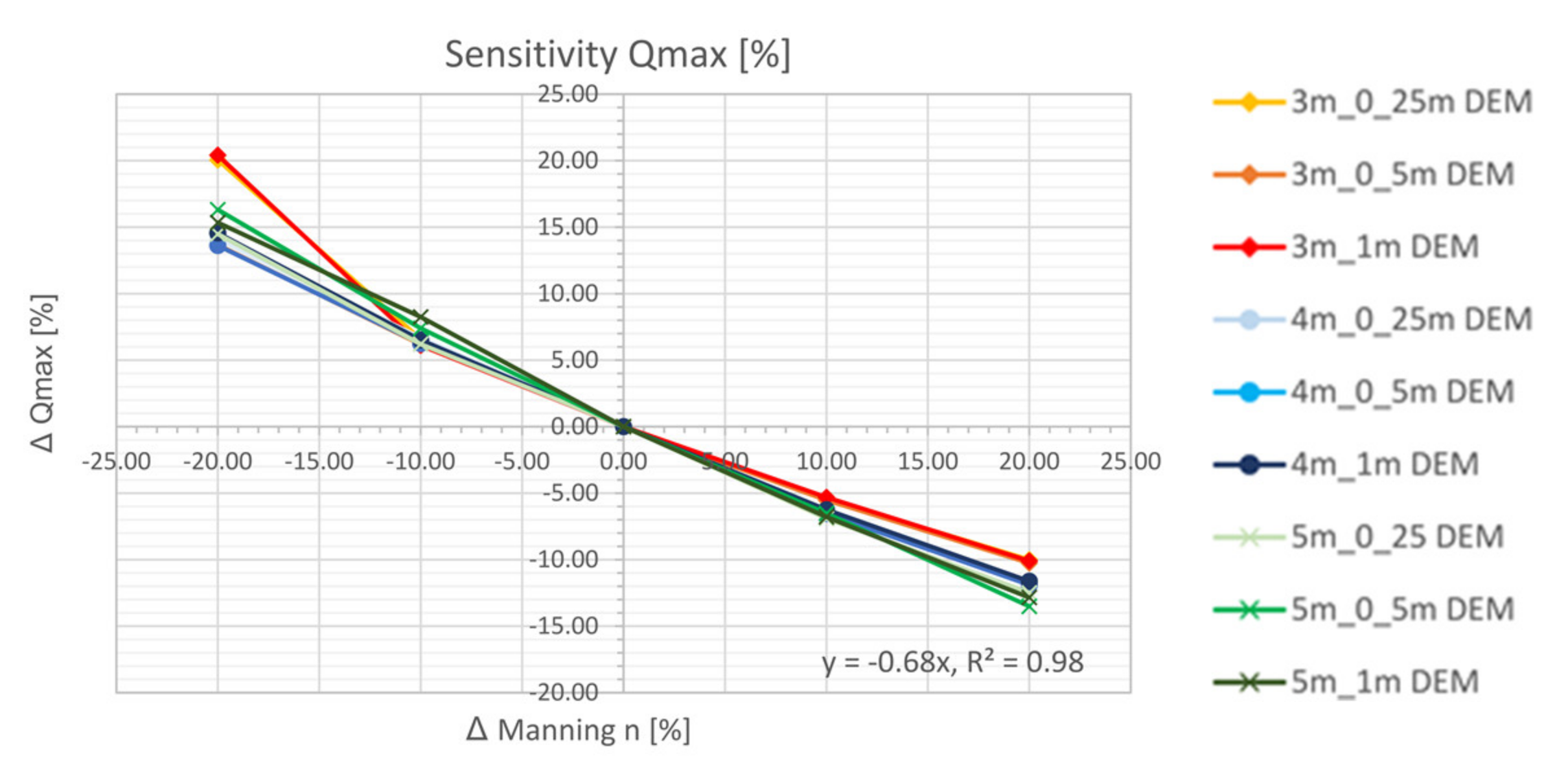
5.4.2. Manning’s n Roughness Values
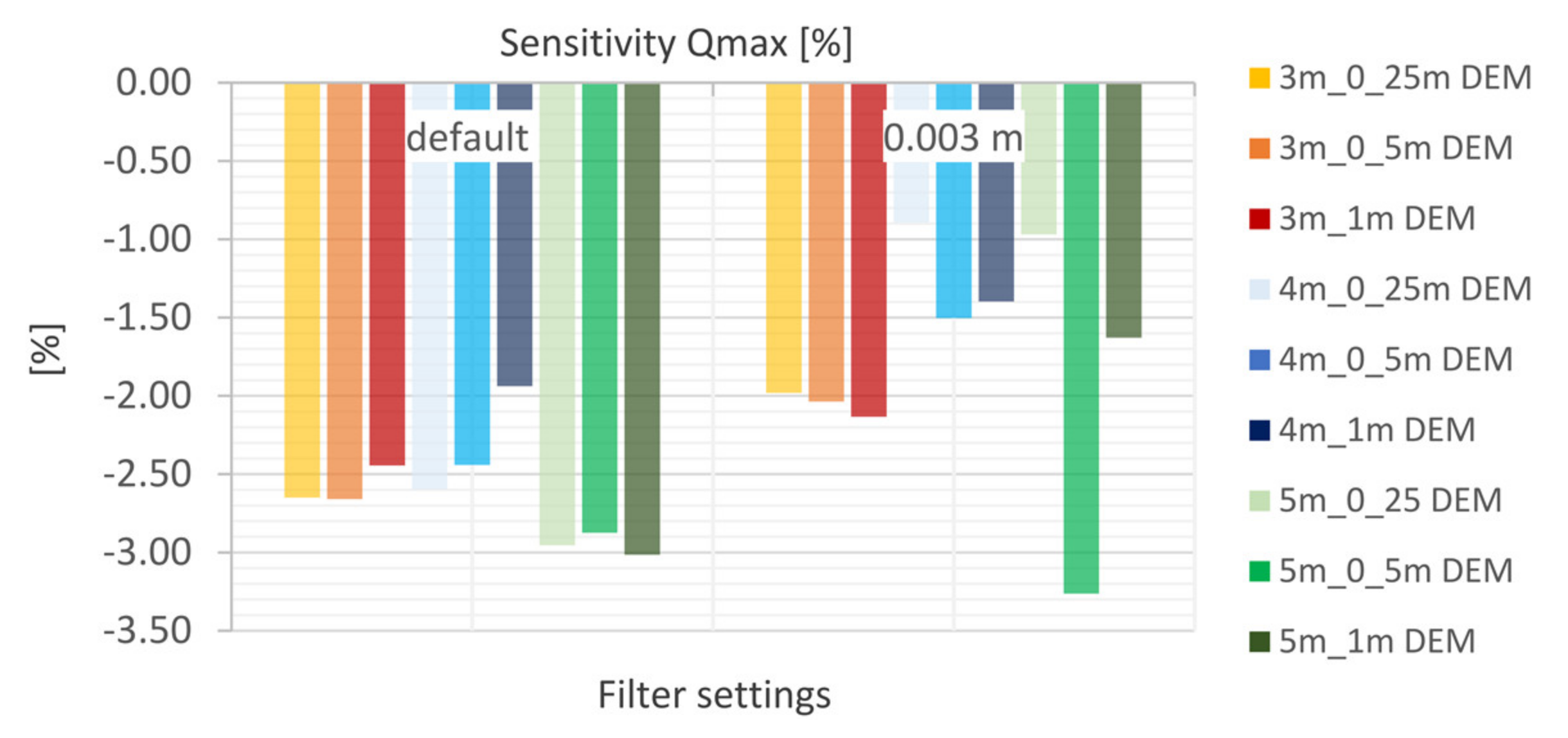
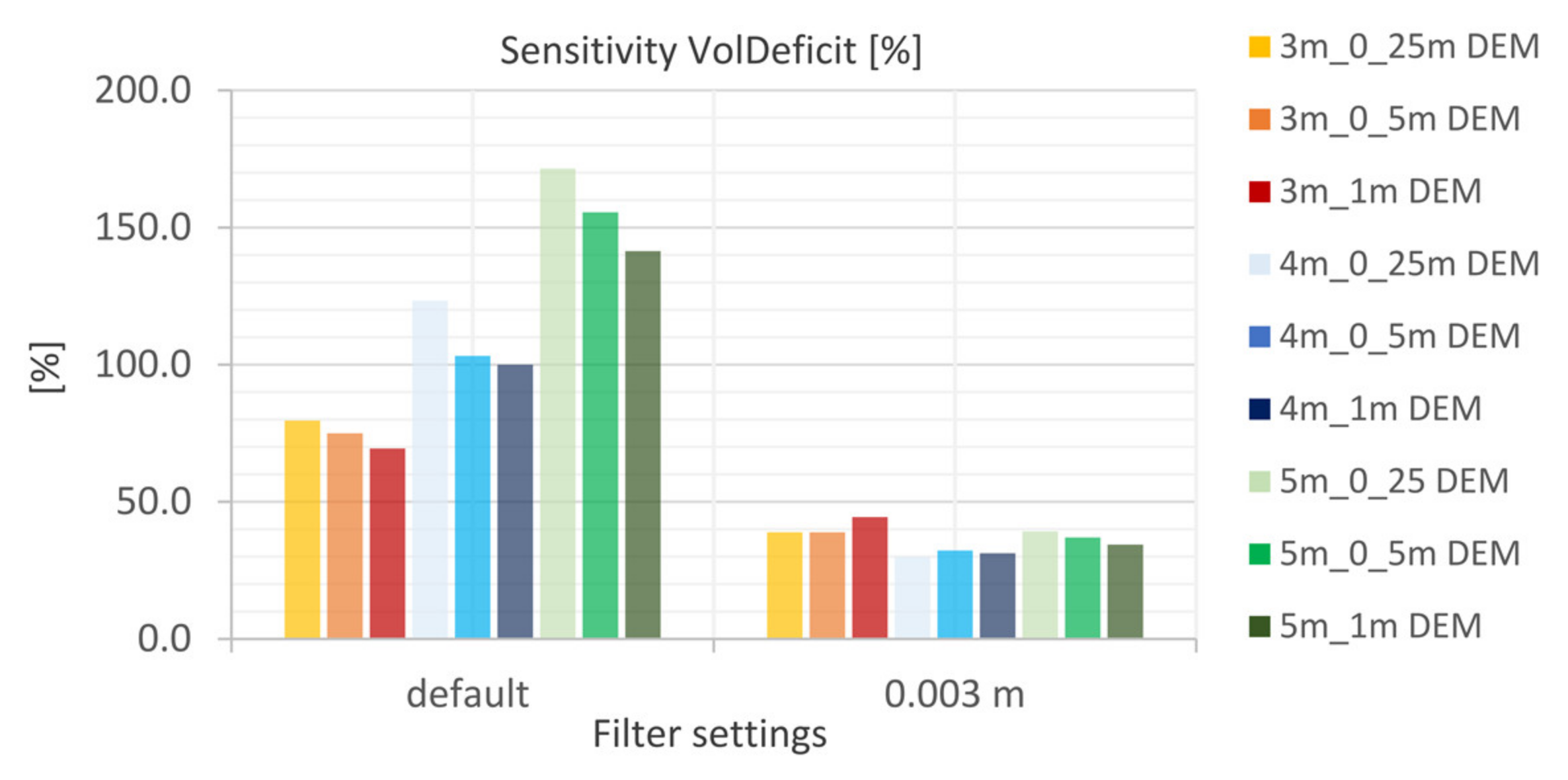
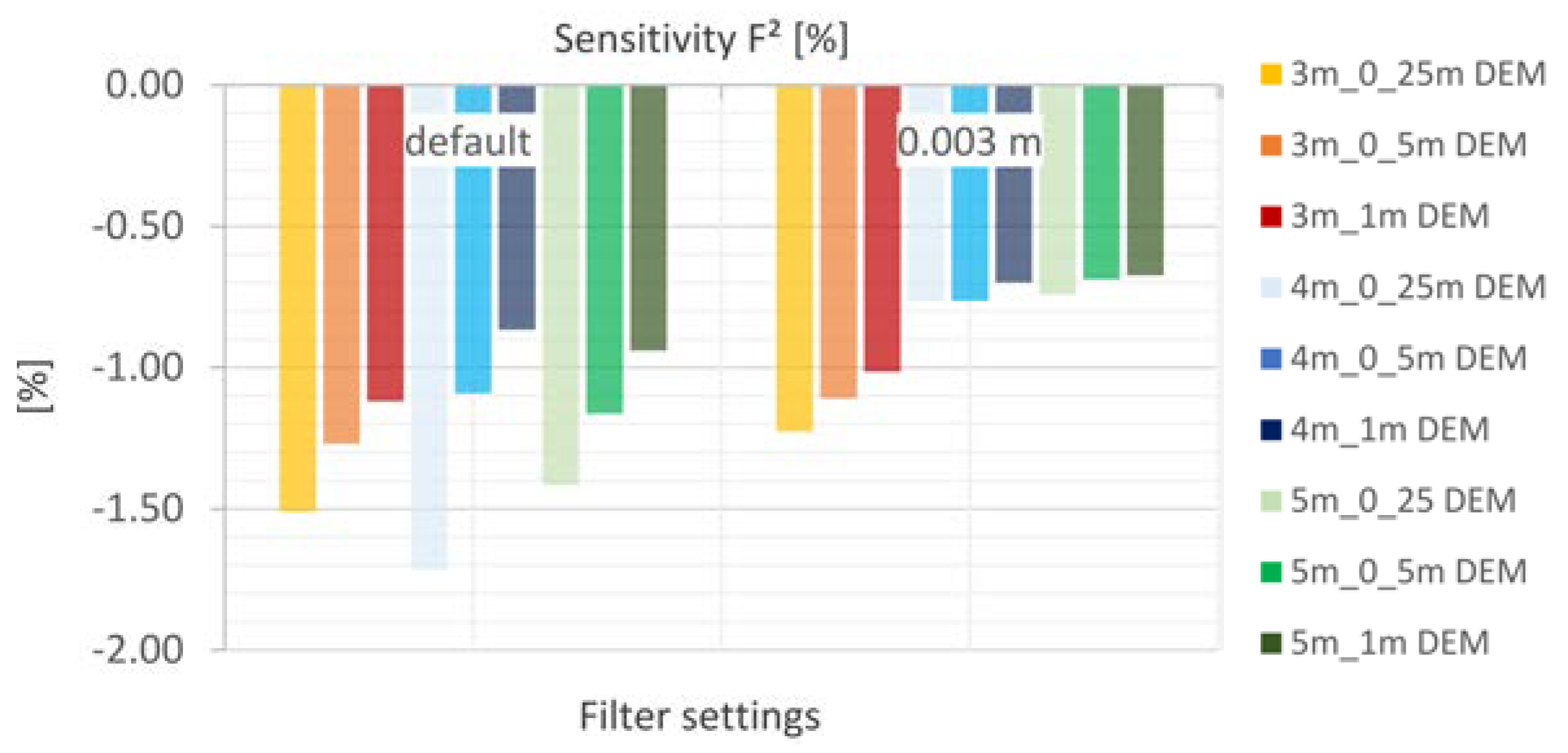
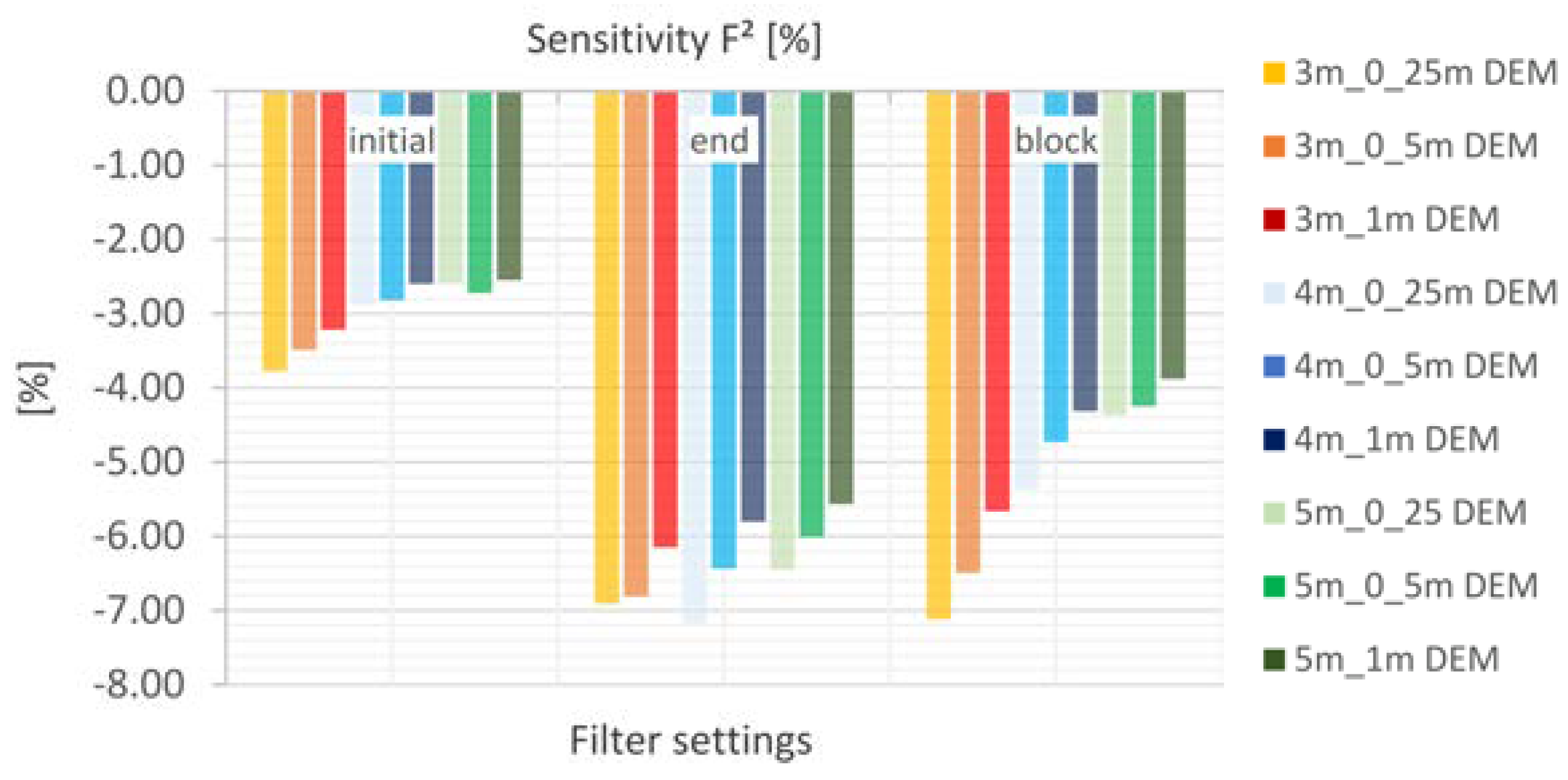
5.4.3. Filter Settings
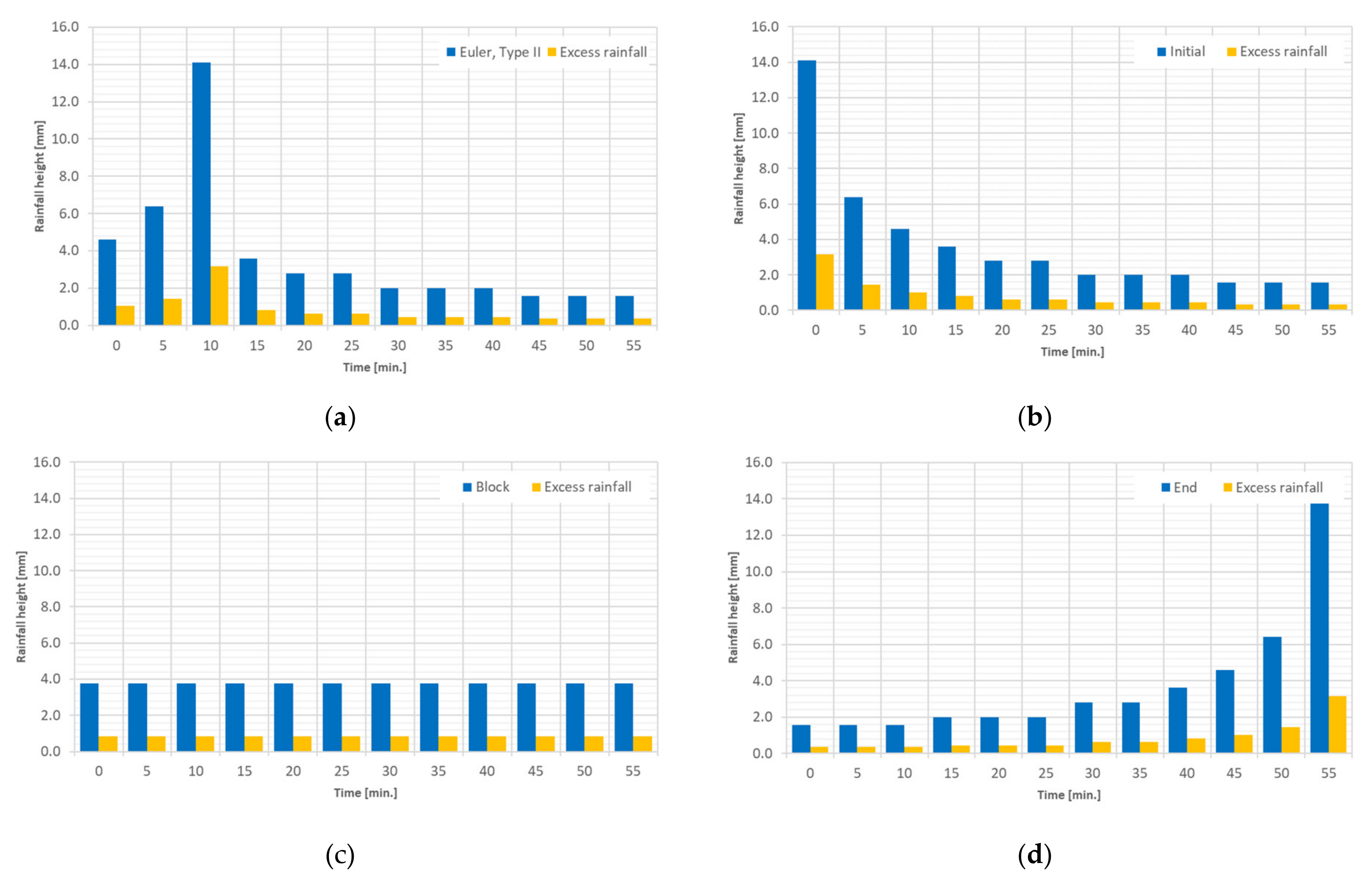
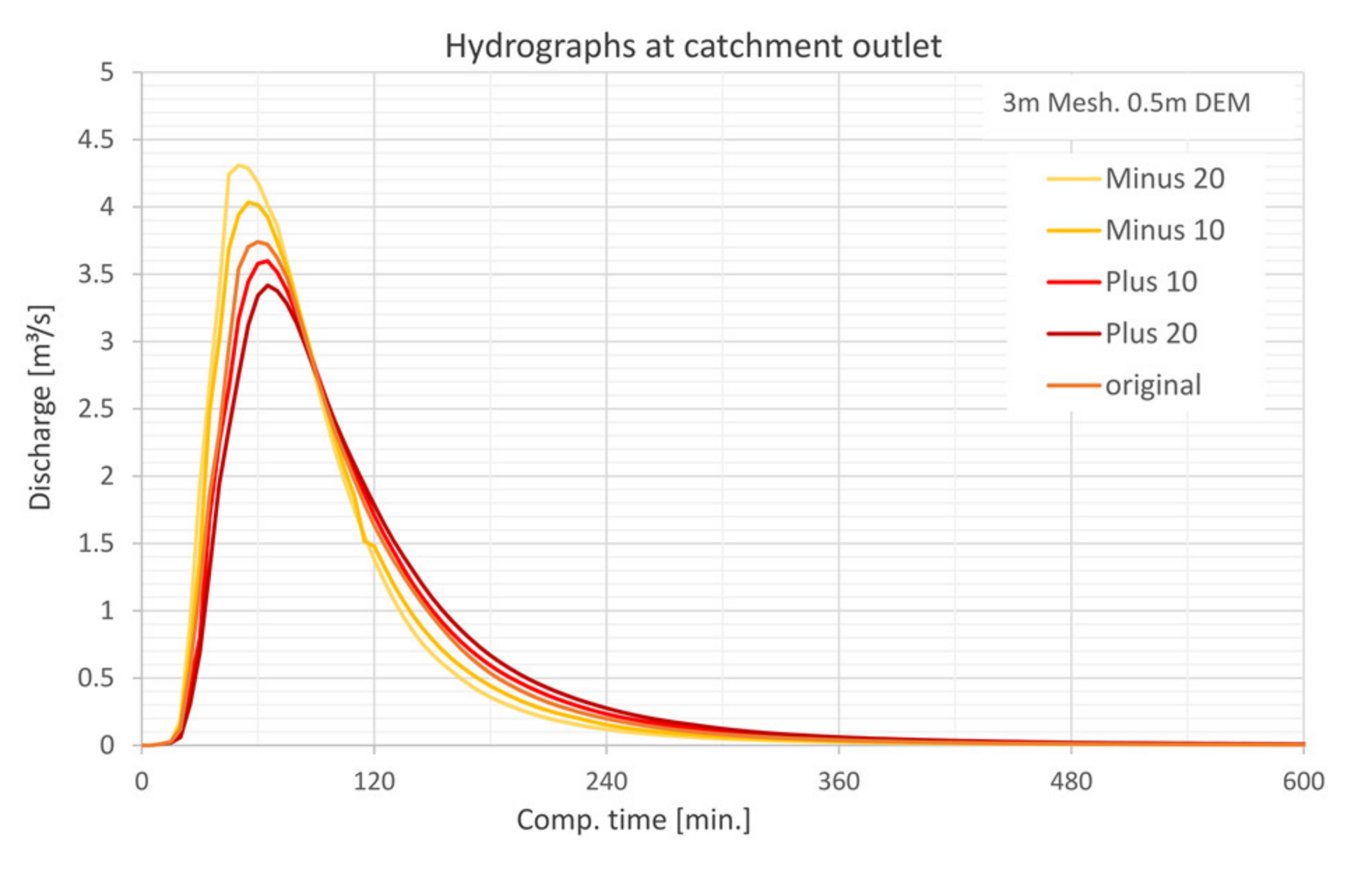
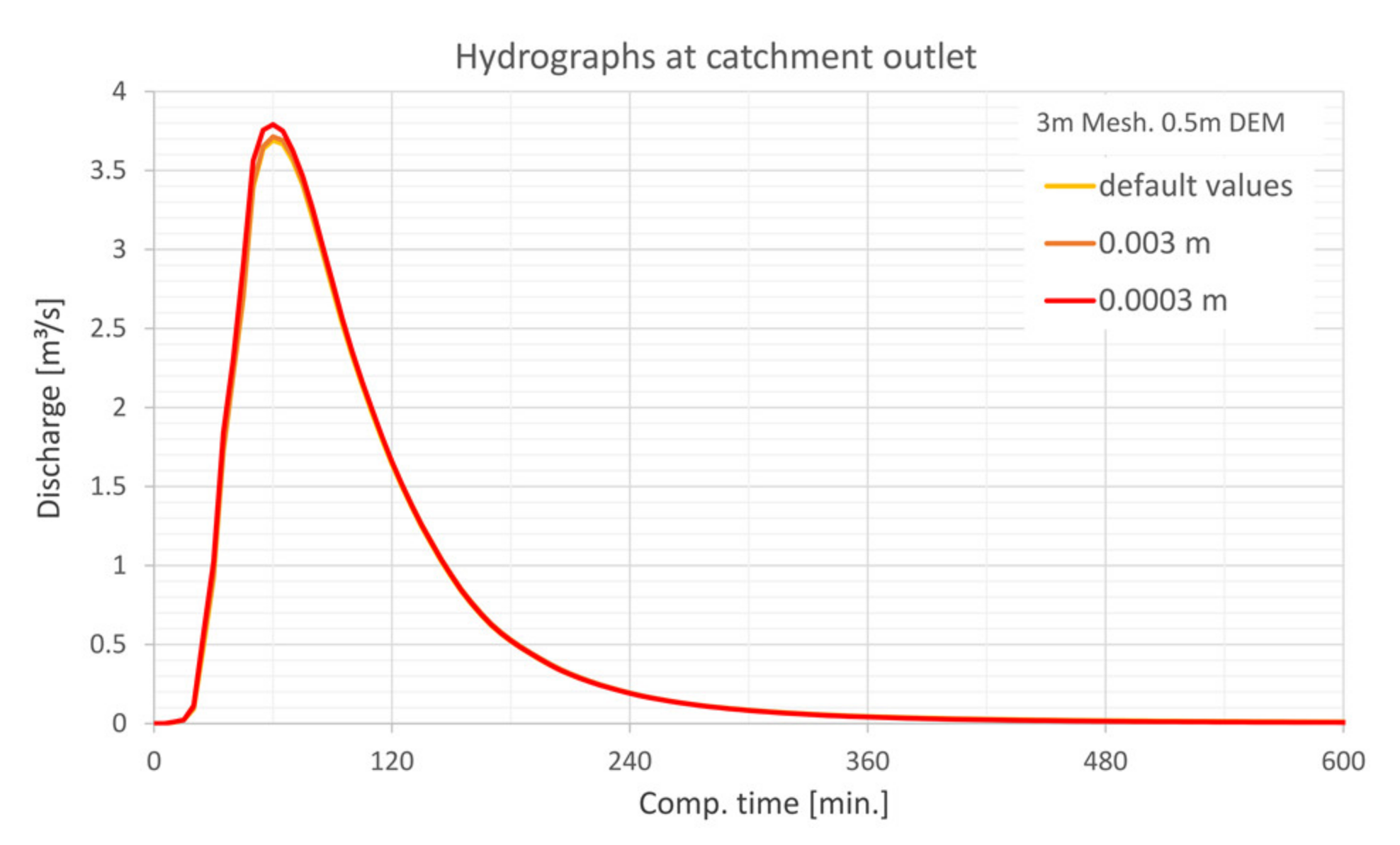
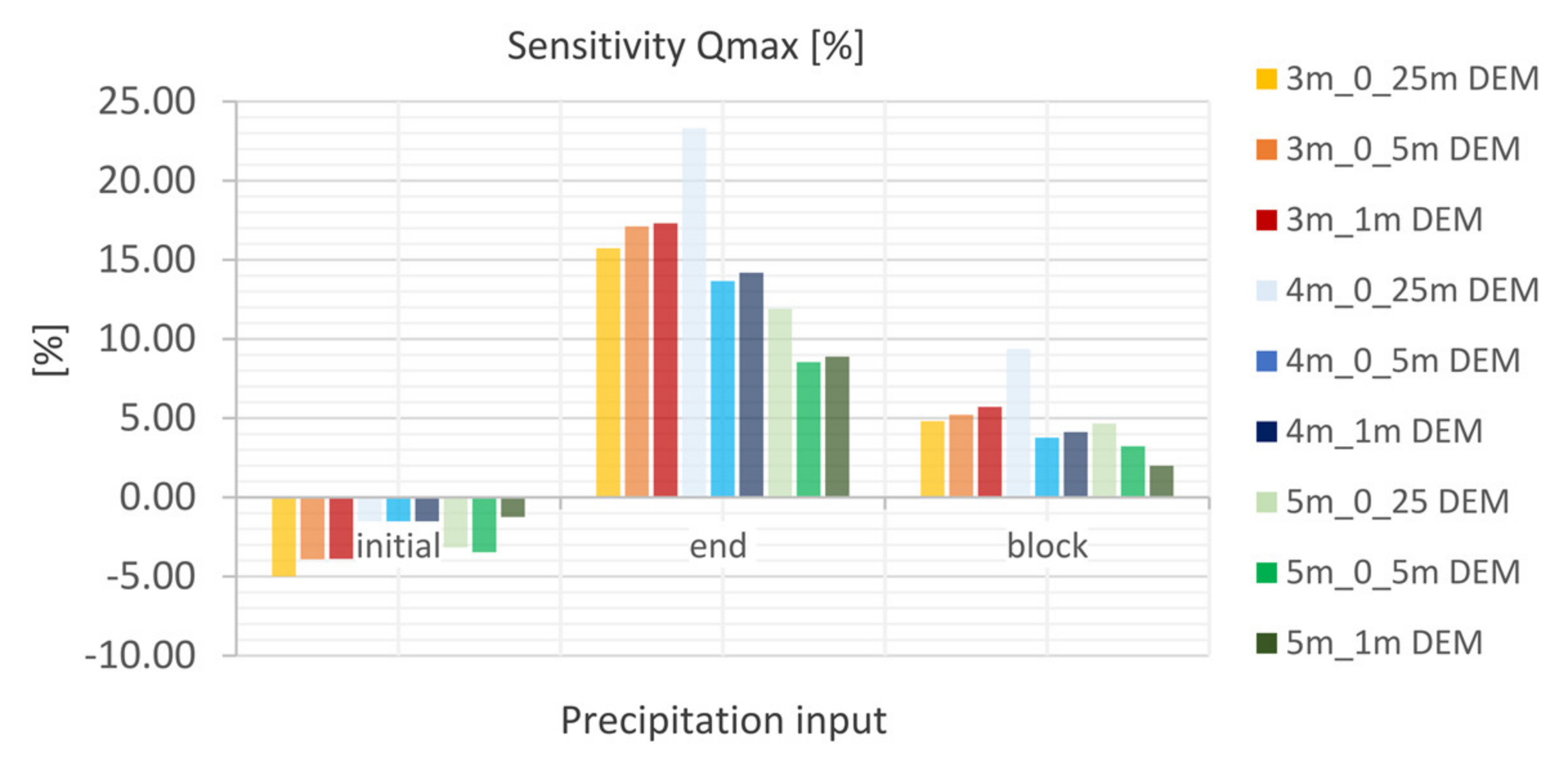
5.4.4. Precipitation Input
5.5. Discussion of the Results in the Context of Rain-on-Grid Simulations
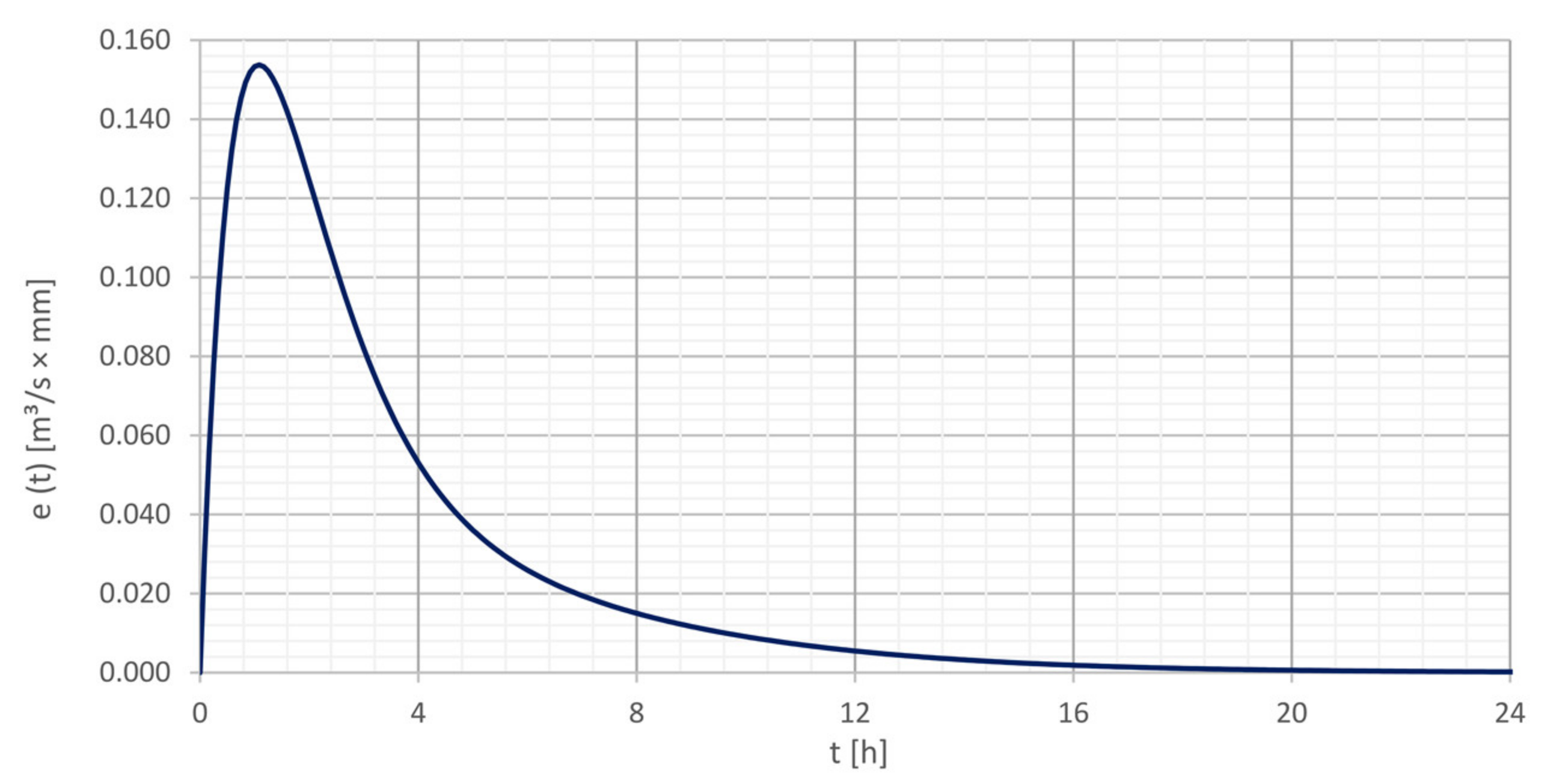
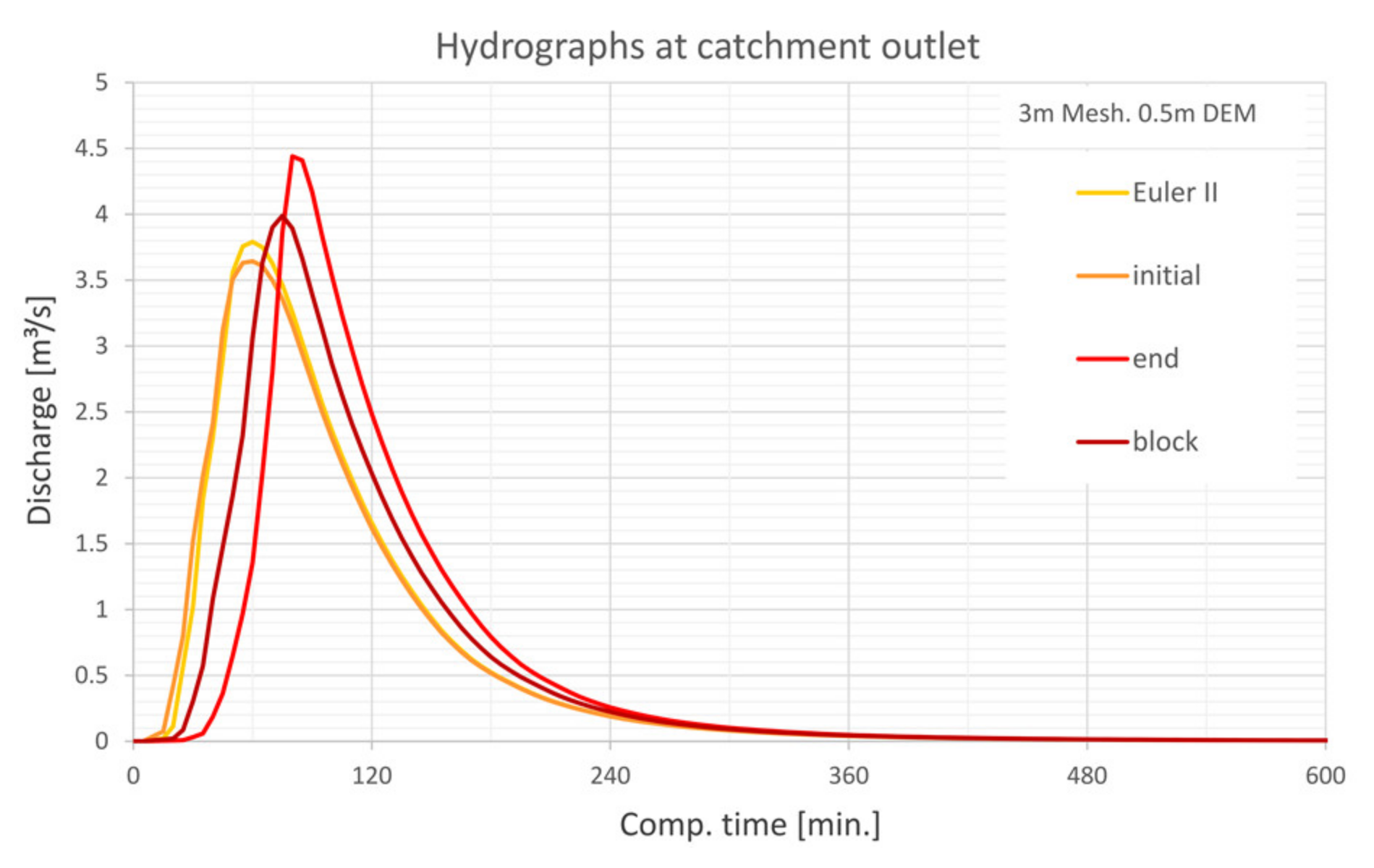
5.6. Comparison with Determined Unit—Hydrograph
6. Conclusions
- For the coarser grids from 10 m mesh, the runoff is significantly delayed at the catchment outlet. The results showed that this effect is caused by a very low water layer that is computationally kept in the cells. The comparison with the benchmark run showed that comparable results could be achieved up to a mesh resolution of 5 m and a terrain model up to 1 m (NSE ≥ 0.8).
- For the water levels in the channel, there is very good agreement (Δ WSE ≤ 0.03 m) with the benchmark run up to a spatial resolution of 5 m mesh.
- The area-based index F2 shows large deviations from the benchmark for all simulations. The study has made evident that deviations are sourcing mainly from a large number of microsinks in the 0.25 m DEM. The latter are mapped well using a 1 m mesh. The detailed display of microsinks reduces with increasing DEM and mesh resolutions.
- The study emphasized that the volume deficit as indicator was only partially meaningful. A qualitative analysis was additionally necessary to interpret the results adequately. It is shown that artificial depressions are detected for the mesh resolution coarser than 10 m. These are caused due to the very low water levels (<10 cm) in comparison to changes in topography.
- With regard to the computing time, model resolutions in the order of 3 m or higher are considered acceptable for a catchment area of this size (A = 2.13 km2, CT < 1 and thus smaller than 24 h of computing time).
- The laminar flow depth is viewed as weakly sensitive with regard to the maximum discharge height. The roughness values are considered sensitive with respect to the discharge height. The filter settings show only a very low sensitivity for the calculated resolutions with respect to the runoff height and the floodplains. For the precipitation distributions, it is shown that the initially stressed precipitation event has only a very small effect on the runoff height. For the 1 h-event, the end distributed rainfall event results in the highest peak flow.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ball, J.; Barton, C.; Bishop, W.; Gray, S.; Jones, R.; McCowan, A.; Murtagh, J.; Peirson, B.; Phillips, B.; Rigby, T.; et al. Australian Rainfall & Runoff Revision Projects (Project 15)—Two Dimensional Modelling in Urban and Rural Floodplains; Engineers Australia: Barton, KS, USA, 2012; pp. 184–202. [Google Scholar]
- Yu, D.; Coulthard, T. Evaluating the Importance of Catchment Hydrological Parameters for Urban Surface Water Flood Modelling Using a Simple Hydro-Inundation Model. J. Hydrol. 2015, 524, 385–400. [Google Scholar] [CrossRef]
- Zeiger, S.; Hubbart, J. Measuring and Modeling Event-Based Environmental Flows: An Assessment of HEC-RAS 2D Rain-on-Grid Simulations. J. Environ. Manag. 2021, 285, 112125. [Google Scholar] [CrossRef]
- Krvavica, N.; Rubinić, J. Evaluation of Design Storms and Critical Rainfall Durations for Flood Prediction in Partially Urbanized Catchments. Water 2020, 12, 2044. [Google Scholar] [CrossRef]
- David, A.; Schmalz, B. Flood Hazard Analysis in Small Catchments: Comparison of Hydrological and Hydrodynamic Approaches by the Use of Direct Rainfall. J. Flood Risk Manag. 2020, 13, e12639. [Google Scholar] [CrossRef]
- Broich, K.; Pflugbeil, T.; Disse, M.; Nguyen, H. Using TELEMAC-2D for Hydrodynamic Modeling of Rainfall–runoff. In Proceedings of the 26th TELEMAC-MASCARET User Conference 2019, Toulouse, France, 15–17 October 2019; Zenodo CERFACS: Toulouse, France, 2019. [Google Scholar]
- Jia, Y.; Shirmeen, T.; Locke, M.A.; Lizotte, E.R., Jr.; Shields, D.F., Jr. Simulation of Surface Runoff and Channel Flows Using a 2D Numerical Model. In Soil Erosion—Rainfall Erosivity and Risk Assessment; Hrissanthou, V., Kaffas, K., Eds.; IntechOpen: London, UK, 2019; ISBN 978-1-78985-195-3. [Google Scholar]
- Tyrna, B.; Assmann, A.; Fritsch, K.; Johann, G. Large-Scale High-Resolution Pluvial Flood Hazard Mapping Using the Raster-Based Hydrodynamic Two-Dimensional Model FloodAreaHPC. J. Flood Risk Manag. 2018, 11, 1024–1037. [Google Scholar] [CrossRef]
- Cea, L.; Garrido, M.; Puertas, J.; Jácome, A.; Del Río, H.; Suárez, J. Overland Flow Computations in Urban and Industrial Catchments from Direct Precipitation Data Using a Two-Dimensional Shallow Water Model. Water Sci. Technol. 2010, 62, 1998–2008. [Google Scholar] [CrossRef]
- Hunter, N.; Bates, P.; Neelz, S.; Pender, G.; Villanueva, I.; Wright, N.; Liang, D.; Falconer, R.; Lin, B.; Waller, S.; et al. Benchmarking 2D Hydraulic Models for Urban Flooding. Proc. Inst. Civ. Eng.-Water Manag. 2008, 161, 13–30. [Google Scholar] [CrossRef]
- Mandlburger, G.; Höfle, B.; Briese, C.; Ressl, C.; Otepka, J.; Hollaus, M.; Pfeifer, N. Topographische Daten Aus Laserscanning Als Grundlage Für Hydrologie Und Wasserwirtschaft. Österreichische Wasser Abfallwirtsch. 2009, 61, 89–97. [Google Scholar] [CrossRef][Green Version]
- Schanze, J. Pluvial Flood Risk Management: An Evolving and Specific Field: Editorial. J. Flood Risk Manag. 2018, 11, 227–229. [Google Scholar] [CrossRef]
- Oberle, P.; Kron, A.; Kerlin, T.; Nestmann, F.; Ruiz Rodriguez, E. Diskussionsbeitrag Zur Fließwiderstandsparametrisierung Zur Simulation Der Oberflächenabflüsse Bei Starkregen. Wasserwirtschaft 2021, 2021, 12–21. [Google Scholar] [CrossRef]
- Grismer, M. Surface Runoff in Watershed Modeling—Turbulent or Laminar Flows? Hydrology 2016, 3, 18. [Google Scholar] [CrossRef]
- Djordjević, S.; Prodanović, D.; Maksimović, Č. An Approach to Simulation of Dual Drainage. Water Sci. Technol. 1999, 39, 95–103. [Google Scholar] [CrossRef]
- Rangari, V.; Umamahesh, N.; Bhatt, C. Assessment of Inundation Risk in Urban Floods Using HEC RAS 2D. Model. Earth Syst. Environ. 2019, 5, 1839–1851. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; Fernández-Pato, J.; Hinz, C. Performance Assessment of 2D Zero-Inertia and Shallow Water Models for Simulating Rainfall–runoff Processes. J. Hydrol. 2020, 584, 124663. [Google Scholar] [CrossRef]
- Pina, R.; Ochoa-Rodriguez, S.; Simões, N.; Mijic, A.; Marques, A.; Maksimović, Č. Semi- vs. Fully-Distributed Urban Stormwater Models: Model Set Up and Comparison with Two Real Case Studies. Water 2016, 8, 58. [Google Scholar] [CrossRef]
- Cea, M.; Rodriguez, M. Two-Dimensional Coupled Distributed Hydrologic–Hydraulic Model Simulation on Watershed. Pure Appl. Geophys. 2016, 173, 909–922. [Google Scholar] [CrossRef]
- Fraga, I.; Cea, L.; Puertas, J.; Suárez, J.; Jiménez, V.; Jácome, A. Global Sensitivity and GLUE-Based Uncertainty Analysis of a 2D-1D Dual Urban Drainage Model. J. Hydrol. Eng. 2016, 21, 04016004. [Google Scholar] [CrossRef]
- Fraga, I.; Cea, L.; Puertas, J. Validation of a 1D-2D Dual Drainage Model under Unsteady Part-Full and Surcharged Sewer Conditions. Urban Water J. 2015, 14, 74–84. [Google Scholar] [CrossRef]
- Beven, K.; Binley, A. The Future of Distributed Models: Model Calibration and Uncertainty Prediction. Hydrol. Process. 1992, 6, 279–298. [Google Scholar] [CrossRef]
- Leandro, J.; Schumann, A.; Pfister, A. A Step towards Considering the Spatial Heterogeneity of Urban Key Features in Urban Hydrology Flood Modelling. J. Hydrol. 2016, 535, 356–365. [Google Scholar] [CrossRef]
- Leandro, J.; Chen, A.; Schumann, A. A 2D Parallel Diffusive Wave Model for Floodplain Inundation with Variable Time Step (P-DWave). J. Hydrol. 2014, 517, 250–259. [Google Scholar] [CrossRef]
- Néelz, S.; Pender, G. Benchmarking the Latest Generation of 2D Hydraulic Modelling Packages—Report; Environment Agency: Bristol, UK, 2013; p. 194. [Google Scholar]
- Broich, K.; Kaiser, M.; Lin, Q.; Mitterer, J.; Nguyen, H.; Pflugbeil, T.; von Trentini, F.; Willkofer, F.; Disse, M.; Ludwig, R. Das Projekt HiOS—Erstellung einer Hinweiskarte für Oberflächenabfluss und Sturzfluten für bayerische Gemeinden. In Proceedings of the Starkregen und Sturzfluten—Erfassen, Erforschen, Evaluieren Beiträge zum Seminar am 6. Juni 2018 an der Technischen Universität München, Erforschen, Germany, 18 June 2018; Fachgemeinschaft Hydrologische Wissenschaften: Munich, Germany, 2018; Volume 40.18. [Google Scholar]
- Brunner, G. Benchmarking of the HEC-RAS Two-Dimensional Hydraulic Modeling Capabilities; U.S. Army Corps of Engineers: Davis, CA, USA, 2018.
- Chen, A.; Djordjević, S.; Leandro, J.; Savić, D. An Analysis of the Combined Consequences of Pluvial and Fluvial Flooding. Water Sci. Technol. 2010, 62, 1491–1498. [Google Scholar] [CrossRef]
- Hall, J. Direct Rainfall Flood Modelling: The Good, the Bad and the Ugly. Australas. J. Water Resour. 2015, 19, 74–85. [Google Scholar] [CrossRef]
- Cea, L.; Bladé, E. A Simple and Efficient Unstructured Finite Volume Scheme for Solving the Shallow Water Equations in Overland Flow Applications: The Shallow Water Equations for Overland Flow Applications. Water Resour. Res. 2015, 51, 5464–5486. [Google Scholar] [CrossRef]
- Clark, K.; Ball, J.; Babister, M. Can Fixed Grid 2D Hydraulic Models Be Used as Hydrologic Models? Engineers Australia: Modbury, SA, Australia, 2008; pp. 2496–2507. [Google Scholar]
- Hydrologic Engineering Center (‘HEC’). HEC-RAS River Analysis System Hydraulic Reference Manual—Version 6.0 Beta; US Army Corps of Engineers—HEC: Davis, CA, USA, 2020.
- Zaiß, H. Simulation Ereignisspezifischer Einflüsse Des Niederschlag-Abfluß-Prozesses von Hochwasserereignissen Kleiner Einzugsgebiete Mit N-A-Modellen; TH Darmstadt—Institut für Wasserbau: Darmstadt, Germany, 1989. [Google Scholar]
- Deutsche Vereinigung für Wasserwirtschaft, Abwasser und Abfall (‘DWA’). Merkblatt DWA-M 524—Hydraulische Berechnung von Fließgewässern Mit Vegetation; DWA: Hennef, Germany, 2020. [Google Scholar]
- Machiels, O.; Erpicum, S.; Dewals, B.; Archambeau, P.; Pirotton, M. Continuous Formulation for Bottom Friction in Free Surface Flows Modelling. In River Basin Management V; WIT Press: Hampshire, UK, 2009; pp. 81–92. [Google Scholar]
- Lawrence, D. Macroscale Surface Roughness and Frictional Resistance in Overland Flow. Earth Surf. Process. Landf. 1996, 22, 365–382. [Google Scholar] [CrossRef]
- Lindner, K. Der Strömungswiderstand von Pflanzenbeständen; Leichtweiß-Institut für Wasserbau, TU Braunschweig: Braunschweig, Germany, 1982. [Google Scholar]
- Casulli, V. A High-Resolution Wetting and Drying Algorithm for Free-Surface Hydrodynamics. Int. J. Numer. Methods Fluids 2009, 60, 391–408. [Google Scholar] [CrossRef]
- Schmalz, B.; Kruse, M. Impact of Land Use on Stream Water Quality in the German Low Mountain Range Basin Gersprenz. Landsc. Online 2019, 72, 1–17. [Google Scholar] [CrossRef]
- Kissel, M.; Schmalz, B. Comparison of Baseflow Separation Methods in the German Low Mountain Range. Water 2020, 12, 1740. [Google Scholar] [CrossRef]
- Grosser, P.; Schmalz, B. Low Flow and Drought in a German Low Mountain Range Basin. Water 2021, 13, 316. [Google Scholar] [CrossRef]
- Savage, J.; Pianosi, F.; Bates, P.; Freer, J.; Wagener, T. Quantifying the Importance of Spatial Resolution and Other Factors through Global Sensitivity Analysis of a Flood Inundation Model: GSA of a flood inundation model. Water Resour. Res. 2016, 52, 9146–9163. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models; Wiley: Hoboken, NJ, USA, 2004; ISBN 978-0-470-87093-8. [Google Scholar]
- Beven, K. Rainfall–Runoff Modelling: The Primer, 2nd ed.; Wiley-Blackwell: Chichester, UK; Hoboken, NJ, USA, 2012; ISBN 978-0-470-71459-1. [Google Scholar]
- Saltelli, A. Global Sensitivity Analysis: The Primer; John Wiley: Chichester, UK; Hoboken, NJ, USA, 2008; ISBN 978-0-470-05997-5. [Google Scholar]
- Willis, T.; Wright, N.; Sleigh, A. Systematic Analysis of Uncertainty in 2D Flood Inundation Models. Environ. Model. Softw. 2019, 122, 104520. [Google Scholar] [CrossRef]
- Willems, P. Model Uncertainty Analysis by Variance Decomposition. Phys. Chem. Earth Parts ABC 2012, 42–44, 21–30. [Google Scholar] [CrossRef]
- Hornberger, G.; Spear, R. An Approach to the Preliminary Analysis of Environmental Systems. J. Environ. Manag. USA 1981, 12, 7–18. [Google Scholar]
- Pappenberger, F.; Beven, K.; Ratto, M.; Matgen, P. Multi-Method Global Sensitivity Analysis of Flood Inundation Models. Adv. Water Resour. 2008, 31, 1–14. [Google Scholar] [CrossRef]
- Bates, P.D.; De Roo, A.P.J. A Simple Raster-Based Model for Flood Inundation Simulation. J. Hydrol. 2000, 236, 54–77. [Google Scholar] [CrossRef]
- Aronica, G.; Bates, P.; Horritt, M. Assessing the Uncertainty in Distributed Model Predictions Using Observed Binary Pattern Information within GLUE. Hydrol. Process. 2002, 16, 2001–2016. [Google Scholar] [CrossRef]
- Maidment, D.; Hoogerwerf, T. Parameter Sensitivity in Hydrologic Modeling; The University of Texas at Austin: Austin, TX, USA, 2002. [Google Scholar]
- Walega, A.; Rutkowska, A.; Policht-Latawiec, A. Sensitivity of Beta and Weibull Synthetic Unit Hydrographs to Input Parameter Changes. Pol. J. Environ. Stud. 2014, 23, 221–229. [Google Scholar]
- Ouédraogo, W.; Raude, J.; Gathenya, J. Continuous Modeling of the Mkurumudzi River Catchment in Kenya Using the HEC-HMS Conceptual Model: Calibration, Validation, Model Performance Evaluation and Sensitivity Analysis. Hydrology 2018, 5, 44. [Google Scholar] [CrossRef]
- Echo Zeitungen GmbH Gewitter Bringt Starkregen Nach Südhessen—Vollgelaufene Keller in Seeheim-Jugenheim, Fischbachtal Und Modautal; Echo Online: Darmstadt, Germany, 2018.
- HVBG. Luftgestütztes Messverfahren Airborne Laserscanning (ALS); Hessische Verwaltung für Bodenmanagement und Geoinformation (HVBG): Wiesbaden, Germany, 2019. [Google Scholar]
- HVBG. Amtliches Topographisch-Kartographisches Informationssystem (ATKIS®); Hessische Verwaltung für Bodenmanagement und Geoinformation (HVBG): Wiesbaden, Germany, 2017. [Google Scholar]
- HLNUG. Digitale Bodenflächendaten 1:50.000 Hessen (BFD50); Hessisches Landesamt für Naturschutz, Umwelt und Geologie (HLNUG): Wiesbaden, Germany, 2017. [Google Scholar]
- Deutscher Wetterdienst (‘DWD’). KOSTRA-DWD-2010R—Starkniederschlagshöhen Für Deutschland (Bezugszeitraum 1951 Bis 2010). Available online: ftp://ftp-cdc.dwd.de/pub/CDC/grids_germany/return_periods/precipitation/KOSTRA/KOSTRA_DWD_2010R/ (accessed on 20 August 2017).
- Wackermann, R. Eine Einheitsganglinie Aus Charakteristischen Systemwerten Ohne Niederschlags-Abfluß-Messungen—A Unit Hydrograph Developed from Characteristic Parameters without the Aid of Rainfall–runoff Readings. Wasser Boden 1981, 1981, 23–28. [Google Scholar]
- Deutsche Vereinigung für Wasserwirtschaft, Abwasser und Abfall (‘DWA’). Abflüsse Aus Außengebieten Der Kanalisation. Korresp. Abwasser Abfall 2008, 2008, 850–859. [Google Scholar] [CrossRef]
- Schröder, W.; Euler, G. (Eds.) Grundlagen des Wasserbaus: Hydrologie, Hydraulik, Wasserrecht; Werner-Ingenieur-Texte, WIT Wasserbau; 4., völlig überarb. und erw. Aufl; Werner: Düsseldorf, Germany, 1999; ISBN 978-3-8041-3475-1. [Google Scholar]
- ESRI Inc. LAS-Dataset in Raster (Conversion). Available online: https://pro.arcgis.com/de/pro-app/tool-reference/conversion/las-dataset-to-raster.htm (accessed on 2 August 2021).
- ESRI Inc. An Overview of the TIN Dataset Toolset. Available online: https://pro.arcgis.com/en/pro-app/2.6/tool-reference/3d-analyst/an-overview-of-the-tin-dataset-toolset.htm (accessed on 2 August 2021).
- Engman, E. Roughness Coefficients for Routing Surface Runoff. J. Irrig. Drain. Eng. 1986, 112, 39–53. [Google Scholar] [CrossRef]
- Downer, C.; Ogden, F. Gridded Surface Subsurface Hydrologic Analysis (GSSHA) User’s Manual, Version 1.43 for Watershed Modeling System 6.1; System-Wide Water Resources Program; U.S. Army Engineer Research and Development Center: Vicksburg, MS, USA, 2006.
- Patt, H.; Jüpner, R. (Eds.) Hochwasser-Handbuch; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-28190-7. [Google Scholar]
- Deutsche Vereinigung für Wasserwirtschaft, Abwasser und Abfall (DWA) (Ed.) Hydraulische Bemessung und Nachweis von Entwässerungssystemen; DWA-Regelwerk; DWA: Hennef, Germany, 2006; ISBN 978-3-939057-15-4. [Google Scholar]
- Hydrologic Engineering Center (‘HEC’). HEC-GeoHMS—Geospatial Hydrological Modeling Extension—Version 10.1; US Army Corps of Engineers—HEC: Davis, CA, USA, 2012.
- Veneziano, D.; Villani, P. Best Linear Unbiased Design Hyetograph. Water Resour. Res. 1999, 35, 2725–2738. [Google Scholar] [CrossRef]
- Savage, J.; Bates, P.; Freer, J.; Neal, J.; Aronica, G. When Does Spatial Resolution Become Spurious in Probabilistic Flood Inundation Predictions? Hydrol. Process. 2016, 30, 2014–2032. [Google Scholar] [CrossRef]
- Ozdemir, H.; Sampson, C.; De Almeida, G.; Bates, P. Evaluating Scale and Roughness Effects in Urban Flood Modelling Using Terrestrial LIDAR Data. Hydrol. Earth Syst. Sci. Discuss. 2013, 10, 5903–5942. [Google Scholar] [CrossRef]
- Chow, V.; Maidment, D.; Mays, L. Applied Hydrology; McGraw-Hill Series in Water Resources and Environmental Engineering; McGraw-Hill: New York, NY, USA, 1988; ISBN 978-0-07-010810-3. [Google Scholar]
- Chifflard, P.; Fohrer, N.; Bormann, H.; Miegel, K.; Casper, M.; Bronstert, A.; Schumann, A.; Weiler, N. Hydrologie der Mittelgebirge. In Hydrologie; Fohrer, N., Bormann, H., Miegel, K., Casper, M., Bronstert, A., Schumann, A., Weiler, N., Eds.; Utb Hydrologie, Physische Geographie; Haupt Verlag: Bern, Switzerland, 2016; pp. 275–285. ISBN 978-3-8252-4513-9. [Google Scholar]





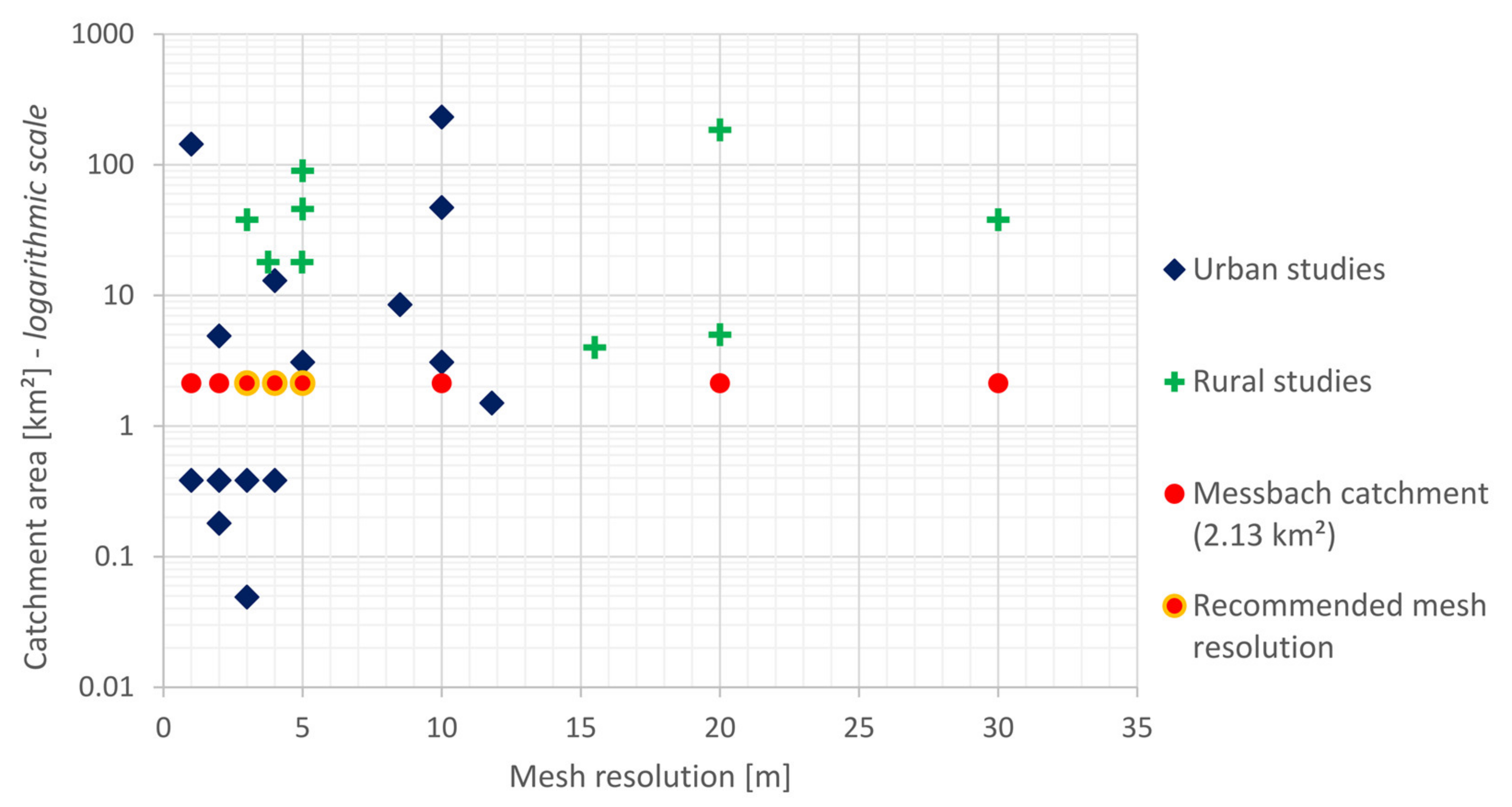
| Reference | 2D Model (s) | Catchment: Size | Spatial Resolution (Number of Cells) | Rainfall Input | Rainfall Loss Approach | Roughness Values [s×m−1/3] | Sensitivity Analysis | Calibration Data |
|---|---|---|---|---|---|---|---|---|
| Zeiger & Hubbart (2021) [3] | SWAT/ HEC-RAS | Hinkson Creek, MO: 232 km2 | DEM: 1 m Mesh: 10 m | 10 historical storm events | long term hydrological modeling (SWAT) SCS CN approach | Manning formula n from 0.003 (barren land) to 0.092 (Herbaceous); calibrated values | Computational interval | gauging stations |
| Krvavica & Rubinić (2020) [4] | HEC-RAS | Novigrad: 3.08 km2 | DEM: 2 m Mesh: 10 m, 5 m refinement (38,499 cells) | 2 historical events 6 statistical events | SCS CN approach | Manning formula n = 0.015 (roads) n = 0.2 (agriculture) | 6 different design storms 4 different rainfall durations | none |
| Caviedes-Voullième et al. (2020) [17] | in-house development | Glasgow: 0.384 km2 | 4 m (24,100) 3 m (42,693) 2 m (96,400) 1 m (384,237) | 1 rainfall event | none | Manning formula n = 0.02 (roads) n = 0.05 (other) | SWE and ZI (‘zero inertia’) solver mesh resolution | none |
| Rangari et al. (2019) [16] | HEC-RAS | Hyderabad: 47.08 km2 | DEM: 10 m Mesh: 10 m (139,487) | 3 historical events 3 statistical events | no information | Manning formula n = 0.025 | none | none |
| Tyrna et al. (2018) [8] | FloodArea | Unna: 144 km2 | 1 m (144,000,000) | 1 statistical event 1 fictional event | simplified physical approach based on Green and Ampt and Darcy | Manning formula from n = 0.013 (roads) to n = 0.250 (forest) | none | none |
| Pina et al. (2016) [18] | Infoworks ICM v.5.5 | Cranbrook: 8.5 km2 Zona central: ca. 1.5 km2 | Cranbrook: avrg. 8.5 m (117,712) Zona central: avrg. 11.8 m (10,741) | Cranbrook: 3 historical events, 5 statistical events Zona central: 4 historical events, 6 statistical events | fixed runoff coefficient | no information | SD/FD approach different design storms | gauging station |
| Cea & Rodriguez (2016) [19] | GUAD-2D | Alginet: 12.97 km2 | 4 m (ca. 810,625) | 500-year event | SCS CN approach Green-Ampt Horton Philip | Manning formula | hydraulic-hydrological calculation | none |
| Fraga et al. (2016) [20] | in-house development | Motorway section: 0.049 km2 | avrg. 3 m (ca. 5444) | 7 historical events | initial- constant approach | Manning formula n = 0.02–0.1 (impervious surface) n = 0.02–0.5 (pervious surface) n = 0.008–0.025 (conduits) | Manning’s n Infiltration rates Discharge coefficients | discharge data |
| Leandro et al. (2016) [23] | P-DWave | Borbecker Mühlenbach: 4.9 km2 | 2 m (ca. 1,225,000) | 1 historical event | Green-Ampt | Manning formula | 5 modeling levels, increasing complexity of key urban features | none |
| Yu et al. (2015), [2] | FloodMap | City of Kingston/Hull: - | 10 m 20 m | 1 historical event | Green-Ampt | Manning formula | Mesh resolution Manning’s n Hydraulic conductivity | inundation areas |
| Néelz & Pender (2013) [25] Karl Broich et al. (2018) [26] Brunner (2018) [27] | Various | Glasgow: 0.384 km2 | 2 m (ca. 97,000) HEC-RAS: DEM: 0.5 m Mesh: 2 m, 4 m | 1 event | none | Manning formula 0.02 (roads) 0.05 (area) | HEC-RAS: mesh resolution | none |
| Chen et al. (2010) [28] | Sipson/UIM | Stockbridge: ca. 0.18 km2 | 2 m (ca. 45,000) | statistical events | no information | no information | design storms flood types | none |
| Reference | 2D Model (s) | Catchment: Size | Spatial Resolution (Number of Cells) | Rainfall Input | Rainfall Loss Approach | Roughness Values [s×m−1/3] | Sensitivity Analysis | Calibration Data |
|---|---|---|---|---|---|---|---|---|
| David & Schmalz (2020), [5] | HEC-RAS | Fischbach: 38 km2 | DEM: 1 m Mesh: 100 m, 5 m refinement (246,100) 30 m, 3 m refinement (687,800) | 3 historical events | constant psi SCS CN approach with modification [33] | Manning formula final range from n = 0.07 for pastures to n = 0.11 for forest-covered areas | Manning’s n model specific parameters: computational and filter tolerances | gauging station |
| Jia et al. (2019), [7] | CCHE2D | Howden Lake: 18 km2 | from 3.76 to 4.98 m (ca. 942,600) | historical events | no loss (clayey soils) | Manning formula initial value from 0.03 to 0.3 final value n = 0.3 (catchment area), n = 0.16 (channel) | Manning’s n | gauging station |
| Broich et al. (2019), [6] | TELEMAC 2D | Simbach a. Inn: 45.9 km2 Triftern: 90.1 km2 | 5 m (ca. 1,836,000) 5 m (ca. 3,604,000) | 1 historical event | SCS CN approach | DWA, (2020), [34] Machiels et al. (2009), [35] Lawrence, (1996), [36] Lindner, (1982), [37] | model specific parameters: fricti.f (H0), steep slope correction (SSC) | gauging station |
| Hall (2015), [29] | MIKE Flood | Birrega: 185 km2 | 20 m (ca. 462,500) | 2 historical events 5 statistical events | constant infiltration rate | Manning formula calibrated n from n = 0.022 (roads) to n = 0.059 (urban/native vegetation) | rainfall depth Manning’s n Infiltration rate Groundwater inundation | gauging station |
| Cea & Bladé (2015), [30] | in-house development | Solivella: 4 km2 Maior River: 5 km2 | Solivella: avrg. ca. 15.5 m (17,926) Maior River: avrg. ca. 20 m (24,676) | Solivella: 1 fictional storm event Maior River: 1 historical event | Solivella: no infiltration (fully saturated soil) Maior river: constant infiltration rate | Manning formula Solivella: n = 0.15 Maior river: from n = 0.3 to n = 0.5 | four different discretization schemes | none |
| Clark et al. (2008), [31] | TUFLOW, SOBEK | Boembee Valley: 11.85 km2 | 5 m, 10 m, 20 m, 50 m, 100 m | design storm: 100-year event, 2 h | constant infiltration rate | constant n-values: 0.04, 0.06, 0.08 | timestep Manning’s n mesh resolution run length slope return period | none |
| PC-1 | PC-2 | PC-3 | PC-4 | |
|---|---|---|---|---|
| System | ThinkStation P330 | ThinkStation P520c | ThinkStation P330 | ThinkStation P520c |
| CPU | I9-9900, 3.10 GHz | Xeon W-2125, 4.00 GHz | i7-9700, 3.00 GHz | Xeon W-2125, 4.00 GHz |
| GPU | Nvidia Quadro P2000 | Nvidia Quadro P2000 | Nvidia Quadro P620 | Nvidia Quadro P2000 |
| RAM | 16 GB | 16 GB | 16 GB | 32 GB |
| Used for | DEM vs. Mesh resolution Precipitation data | Filter parameters | Manning’s n | Laminar depth |
| Landuse Classification [57] | Soil Classification [58] | ||||
|---|---|---|---|---|---|
| Description | Area [km2] | Percentage [%]* | Description | Area [km2] | Percentage [%]* |
| Wooded area | 1.15 | 54.0 | sandy loamy silt | 1.25 | 58.7 |
| Farmland: field crops | 0.40 | 18.8 | medium clayey silt | 0.69 | 32.4 |
| Farmland: grassland | 0.39 | 18.3 | clayey silt | 0.13 | 6.1 |
| Trails | 0.09 | 4.2 | Not classified | 0.06 | 2.8 |
| Settlements Thereof buildings | 0.04 0.01 | 1.9 0.5 | |||
| Roads | 0.03 | 1.4 | |||
| Water bodies | 0.02 | 0.9 | |||
| # | File Name* | Mesh Resolution | Number of Cells |
|---|---|---|---|
| 1 | 0_25 m_1 m | 1 m | 2,128,354 |
| 2 | 0_25 m_2 m | 2 m | 531,489 |
| 3 | 0_25 m_3 m | 3 m | 236,035 |
| 4 | 0_25 m_4 m | 4 m | 132,652 |
| 5 | 0_25 m_5 m | 5 m | 84,810 |
| 6 | 0_25 m_10 m | 10 m | 21,102 |
| 7 | 0_25 m_20 m | 20 m | 5236 |
| 8 | 0_25 m_30 m | 30 m | 2299 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
David, A.; Schmalz, B. A Systematic Analysis of the Interaction between Rain-on-Grid-Simulations and Spatial Resolution in 2D Hydrodynamic Modeling. Water 2021, 13, 2346. https://doi.org/10.3390/w13172346
David A, Schmalz B. A Systematic Analysis of the Interaction between Rain-on-Grid-Simulations and Spatial Resolution in 2D Hydrodynamic Modeling. Water. 2021; 13(17):2346. https://doi.org/10.3390/w13172346
Chicago/Turabian StyleDavid, Amrei, and Britta Schmalz. 2021. "A Systematic Analysis of the Interaction between Rain-on-Grid-Simulations and Spatial Resolution in 2D Hydrodynamic Modeling" Water 13, no. 17: 2346. https://doi.org/10.3390/w13172346
APA StyleDavid, A., & Schmalz, B. (2021). A Systematic Analysis of the Interaction between Rain-on-Grid-Simulations and Spatial Resolution in 2D Hydrodynamic Modeling. Water, 13(17), 2346. https://doi.org/10.3390/w13172346






