A Tool for the Automatic Aggregation and Validation of the Results of Physically Based Distributed Slope Stability Models
Abstract
:1. Introduction
2. Materials and Methods
2.1. Test Site
2.2. Previous Slope Stability Modeling in the Test Site
2.3. Input Data Needed
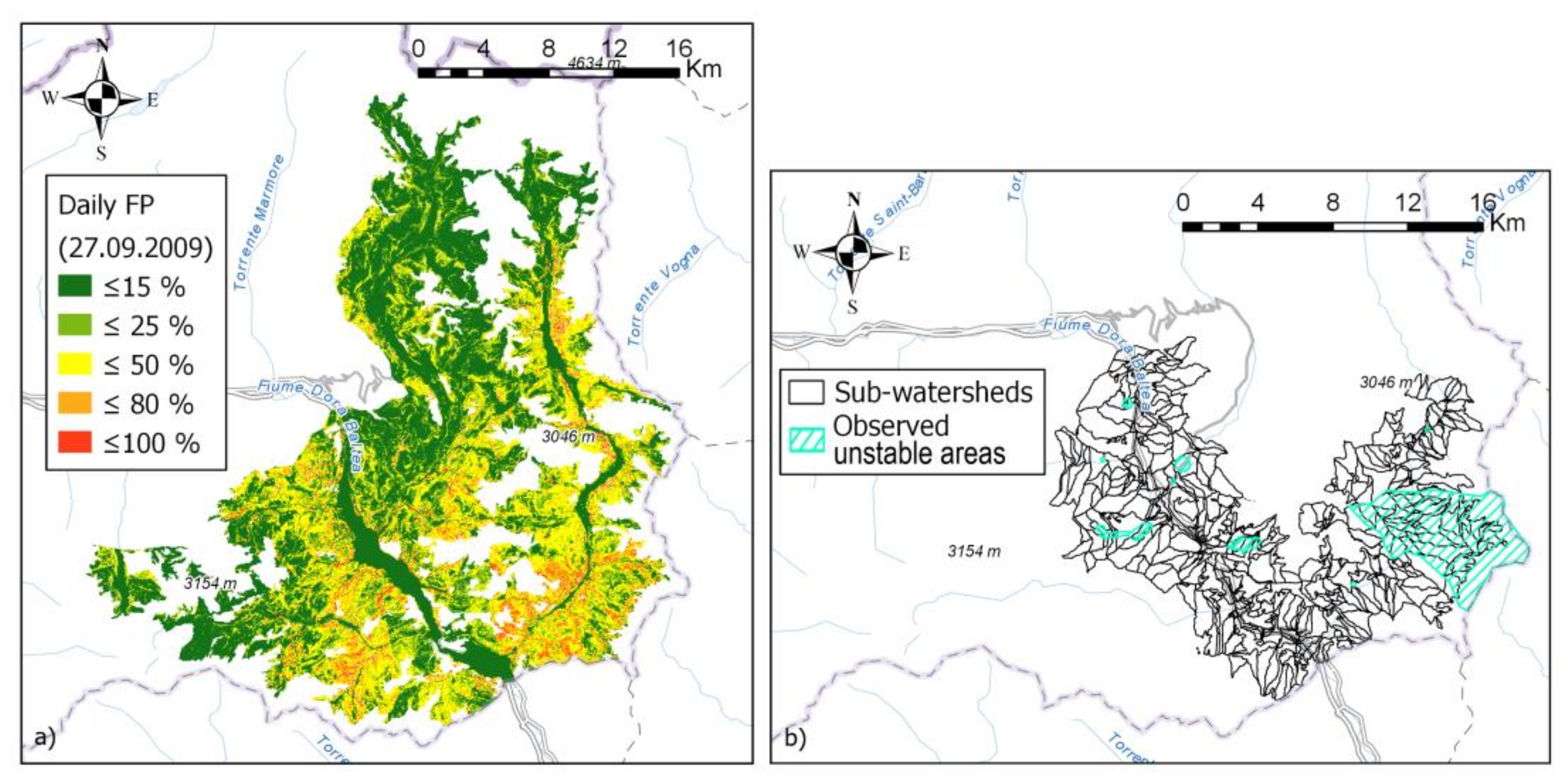
- Pixel-based failure probability raster maps: raster maps describe the failure probability distribution of a certain area (in a specific time) obtained using a distributed slope stability model (i.e., raster maps, in which every pixel reports the probability to have factor of safety below one) (Figure 2a). In this work, we used raster outputs of HIRESSS [45] with 10 m resolution, consisting in a summarizing raster map computed by the model in which each pixel was associated with the highest probability value calculated during each hour of that day.
- Reaggregation units: a polygonal shapefile of territorial units identifying the elements in which the user needs to spatially aggregate the pixel-based information, to be used for hazard management. In our case, as reaggregation units, we used sub-watersheds (Figure 2b) with 0.37 km2 average areal extension and extracted starting from a DEM of the study area using ArcMap. Other possible reaggregation units could be municipal areas, alert areas, and sub-areas used by civil protection centers.
- Landslide dataset: this is the inventory of the landslides that occurred in the modeled events. In this case study, it is represented by a shapefile of landslides including all landslides triggered by the meteorological event described in the previous section, as reported by the local authorities to the regional Civil Protection offices (Figure 2b, “observed unstable areas”). Most of these landslides were originally mapped as polygons. In this case, they were just imported in the shapefile. Other landslides were registered less accurately: only the approximated location (e.g., name of the locality, road trait hit by the slide, and address of a damaged infrastructure) was noted and thus they were represented only as points. The points were transformed into circles with a radius corresponding to the associated uncertainty in the location. Only landslides with a small spatial uncertainty that would allow the triggering point into a precise watershed to be located (a total of 10 landslides) were included. Moreover, on the basis of the reports and of a field survey, all landslide types not compatible with the triggering mechanism encompassed by HIRESSS (e.g., rockfalls) were discarded.
2.4. Instability Diffusion Threshold—Tool Development
Step 1: Set up the Failure Probability Threshold (FPT)
Step 2: Set up the Instability Diffusion Threshold (IDT)
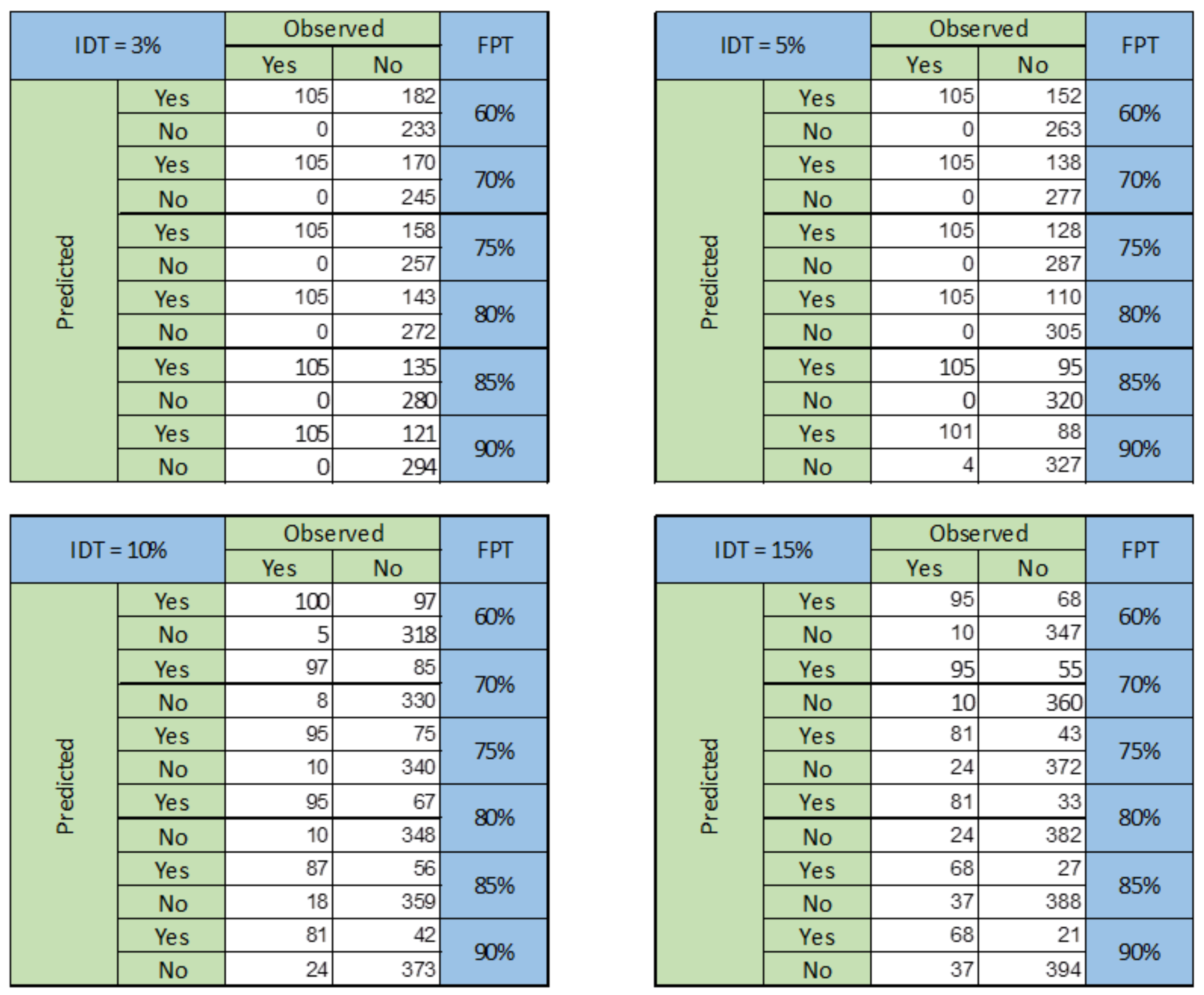
Step 3: Create Validation Maps (Output #1)
Step 4: Create Contingency Table (Output #2)
Step 5: Reset the Model
2.5. Tool Application
3. Results
3.1. DTVT Outputs and Sensitivity Analysis
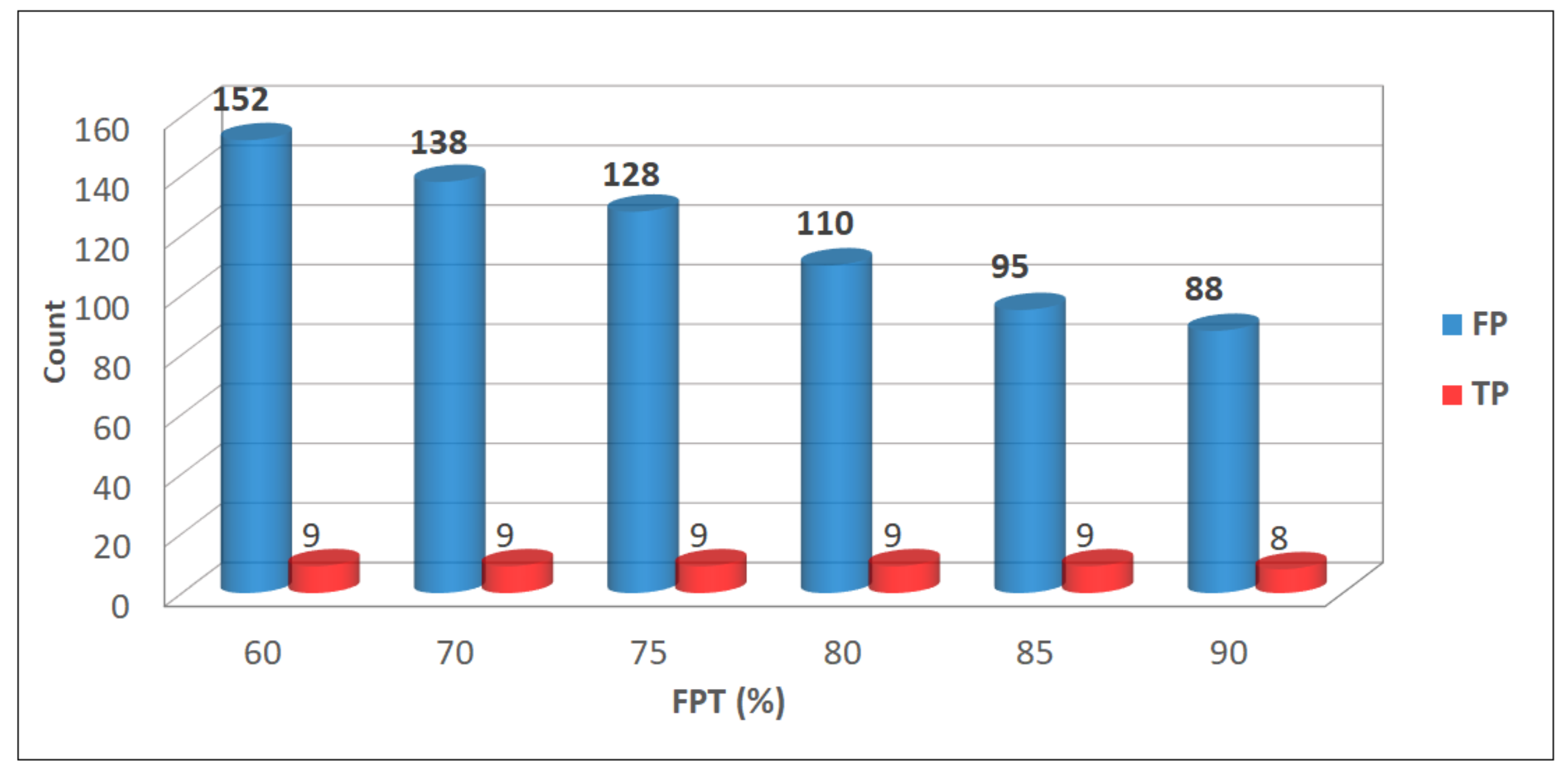
3.2. Identification of the Most Balanced Prediction
3.3. Identification of the Operational Warning Criterion
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- 2009 UNISDR Terminology on Disaster Risk Reduction|UNDRR. Available online: https://www.undrr.org/publication/2009-unisdr-terminology-disaster-risk-reduction (accessed on 7 April 2021).
- Intrieri, E.; Gigli, G.; Casagli, N.; Nadim, F. Landslide Early Warning System: Toolbox and general concepts. Hazards Earth Syst. Sci. 2013, 13, 85–90. [Google Scholar] [CrossRef] [Green Version]
- Michoud, C.; Bazin, S.; Blikra, L.H.; Derron, M.H.; Jaboyedoff, M. Experiences from site-specific landslide early warning systems. Nat. Hazards Earth Syst. Sci. 2013, 13, 2659–2673. [Google Scholar] [CrossRef] [Green Version]
- Piciullo, L.; Calvello, M.; Cepeda, J.M. Territorial early warning systems for rainfall-induced landslides. Earth-Sci. Rev. 2018, 179, 228–247. [Google Scholar] [CrossRef]
- Baum, R.L.; Godt, J.W.; Savage, W.Z. Estimating the timing and location of shallow rainfall-induced landslides using a model for transient, unsaturated infiltration. J. Geophys. Res. 2010, 115, F03013. [Google Scholar] [CrossRef]
- Rosi, A.; Segoni, S.; Canavesi, V.; Monni, A.; Gallucci, A.; Casagli, N. Definition of 3D rainfall thresholds to increase opera-tive landslide early warning system performances. Landslides 2021, 18, 1045–1057. [Google Scholar] [CrossRef]
- Aleotti, P. A warning system for rainfall-induced shallow failures. Eng. Geol. 2004, 73, 247–265. [Google Scholar] [CrossRef]
- Lagomarsino, D.; Segoni, S.; Fanti, R.; Catani, F. Updating and tuning a regional-scale landslide early warning system. Landslides 2013, 10, 91–97. [Google Scholar] [CrossRef]
- Devoli, G.; Tiranti, D.; Cremonini, R.; Sund, M.; Boje, S. Comparison of landslide forecasting services in Piedmont (Italy) and Norway, illustrated by events in late spring 2013. Nat. Hazards Earth Syst. Sci. 2018, 18, 1351–1372. [Google Scholar] [CrossRef] [Green Version]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Gariano, S.L.; Sarkar, R.; Dikshit, A.; Dorji, K.; Brunetti, M.T.; Peruccacci, S.; Melillo, M. Automatic calculation of rainfall thresholds for landslide occurrence in Chukha Dzongkhag, Bhutan. Bull. Eng. Geol. Environ. 2019, 78, 4325–4332. [Google Scholar] [CrossRef]
- Tiranti, D.; Nicolò, G.; Gaeta, A.R. Shallow landslides predisposing and triggering factors in developing a regional early warning system. Landslides 2019, 16, 235–251. [Google Scholar] [CrossRef]
- Yang, H.; Wei, F.; Ma, Z.; Guo, H.; Su, P.; Zhang, S. Rainfall threshold for landslide activity in Dazhou, southwest China. Landslides 2020, 17, 61–77. [Google Scholar] [CrossRef]
- Dikshit, A.; Sarkar, R.; Pradhan, B.; Segoni, S.; Alamri, A.M. Rainfall induced landslide studies in indian himalayan region: A critical review. Appl. Sci. 2020, 10, 2466. [Google Scholar] [CrossRef] [Green Version]
- Bordoni, M.; Corradini, B.; Lucchelli, L.; Meisina, C. Preliminary results on the comparison between empirical and physically-based rainfall thresholds for shallow landslides occurrence. Ital. J. Eng. Geol. Environ. 2019, 1, 5–10. [Google Scholar]
- Dietrich, W.M.; Montgomery, D.R. Shalstab: A Digital Terrain Model for Mapping Shallow Landslide Potential; Technical Report; University of California: Berkley, CA, USA, 1998. [Google Scholar]
- Aristizábal, E.; Vélez, J.I.; Martínez, H.E.; Jaboyedoff, M. SHIA_Landslide: A distributed conceptual and physically based model to forecast the temporal and spatial occurrence of shallow landslides triggered by rainfall in tropical and mountainous basins. Landslides 2016, 13, 497–517. [Google Scholar] [CrossRef]
- Chae, B.-G.; Park, H.-J.; Catani, F.; Simoni, A.; Berti, M. Landslide prediction, Monitoring and early warning: A concise review of state-of-the-art. Geosci. J. 2017, 21, 1033–1070. [Google Scholar] [CrossRef]
- Ho, J.Y.; Lee, K.T. Performance evaluation of a physically based model for shallow landslide prediction. Landslides 2017, 14, 961–980. [Google Scholar] [CrossRef]
- Salciarini, D.; Fanelli, G.; Tamagnini, C. A probabilistic model for rainfall—induced shallow landslide prediction at the regional scale. Landslides 2017, 14, 1731–1746. [Google Scholar] [CrossRef]
- Reder, A.; Rianna, G.; Pagano, L. Physically based approaches incorporating evaporation for early warning predictions of rainfall-induced landslides. Hazards Earth Syst. Sci 2018, 18, 613–631. [Google Scholar] [CrossRef] [Green Version]
- Pack, R.T.; Tarboton, D.G.; Goodwin, C.N. Assessing Terrain Stability in a GIS using SINMAP. In Proceedings of the 8th Congress of the International Association of Engineering Geology, Vancouver, BC, Canada, 21–25 September 1998. [Google Scholar]
- Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS-A Fortran Program for Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Analysis; US Geological Survey: Reston, VA, USA, 1988. [Google Scholar]
- Baum Jonathan, W.; Godt, R.L. Early warning of rainfall-induced shallow landslides and debris flows in the USA. Landslides 2010, 7, 259–272. [Google Scholar] [CrossRef]
- Simoni, S.; Zanotti, F.; Bertoldi, G.; Rigon, R. Modelling the probability of occurrence of shallow landslides and channelized debris flows using GEOtop-FS. Hydrol. Process. 2008, 22, 532–545. [Google Scholar] [CrossRef]
- Ren, D.; Leslie, L.M.; Fu, R.; Dickinson, R.E.; Xin, X. A storm-triggered landslide monitoring and prediction system: Formulation and case study. Earth Interact. 2010, 14, 1–24. [Google Scholar] [CrossRef]
- Arnone, E.; Noto, L.V.; Lepore, C.; Bras, R.L. Physically-based and distributed approach to analyze rainfall-triggered landslides at watershed scale. Geomorphology 2011, 133, 121–131. [Google Scholar] [CrossRef] [Green Version]
- Mercogliano, P.; Segoni, S.; Rossi, G.; Sikorsky, B.; Tofani, V.; Schiano, P.; Catani, F.; Casagli, N. Brief communication A prototype forecasting chain for rainfall induced shallow landslides. Nat. Hazards Earth Syst. Sci. 2013, 13, 771–777. [Google Scholar] [CrossRef] [Green Version]
- Rossi, G.; Catani, F.; Leoni, L.; Segoni, S.; Tofani, V. HIRESSS: A physically based slope stability simulator for HPC applications. Nat. Hazards Earth Syst. Sci. 2013, 13, 151–166. [Google Scholar] [CrossRef] [Green Version]
- Fusco, F.; De Vita, P.; Mirus, B.B.; Baum, R.L.; Allocca, V.; Tufano, R.; Clemente, E.D.; Calcaterra, D. Physically based estimation of rainfall thresholds triggering shallow landslides in volcanic slopes of Southern Italy. Water 2019, 11, 1915. [Google Scholar] [CrossRef] [Green Version]
- Palazzolo, N.; Peres, D.J.; Bordoni, M.; Meisina, C.; Creaco, E.; Cancelliere, A. Improving spatial landslide prediction with 3d slope stability analysis and genetic algorithm optimization: Application to the oltrepò pavese. Water 2021, 13, 801. [Google Scholar] [CrossRef]
- Crosta, G.B.; Frattini, P. Distributed modelling of shallow landslides triggered by intense rainfall. Nat. Hazards Earth Syst. Sci. 2003, 3, 81–93. [Google Scholar] [CrossRef] [Green Version]
- Fusco, F.; Mirus, B.B.; Baum, R.L.; Calcaterra, D.; De Vita, P. Incorporating the effects of complex soil layering and thickness local variability into distributed landslide susceptibility assessments. Water 2021, 13, 713. [Google Scholar] [CrossRef]
- Tofani, V.; Bicocchi, G.; Rossi, G.; Segoni, S.; DAmbrosio, M.; Casagli, N.; Catani, F. Soil characterization for shallow landslides modeling: A case study in the Northern Apennines (Central Italy). Landslides 2017, 14, 755–770. [Google Scholar] [CrossRef] [Green Version]
- Bicocchi, G.; Tofani, V.; Tacconi-Stefanelli, C.; Vannocci, P.; Casagli, N.; Lavorini, G.; Trevisani, M.; Catani, F. Geotechnical and hydrological characterization of hillslope deposits for regional landslide prediction modeling. Bull. Eng. Geol. Environ. 2019, 78, 4875–4891. [Google Scholar] [CrossRef] [Green Version]
- Schmaltz, E.M.; Van Beek, L.P.H.; Bogaard, T.A.; Kraushaar, S.; Steger, S.; Glade, T. Strategies to improve the explanatory power of a dynamic slope stability model by enhancing land cover parameterisation and model complexity. Earth Surf. Process. Landf. 2019, 44, 1259–1273. [Google Scholar] [CrossRef]
- Bregoli, F.; Medina, V.; Chevalier, G.; Hürlimann, M.; Bateman, A. Debris-flow susceptibility assessment at regional scale: Validation on an alpine environment. Landslides 2015, 12, 437–454. [Google Scholar] [CrossRef]
- Vasseur, J.; Wadsworth, F.B.; Lavallée, Y.; Bell, A.F.; Main, I.G.; Dingwell, D.B. Heterogeneity: The key to failure forecasting. Sci. Rep. 2015, 5, 1–7. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhou, G.L.; Xu, T.; Heap, M.J.; Meredith, P.G.; Mitchell, T.M.; Sesnic, A.S.Y.; Yuan, Y. A three-dimensional numerical meso-approach to modeling time-independent deformation and fracturing of brittle rocks. Comput. Geotech. 2020, 117, 103274. [Google Scholar] [CrossRef]
- Canavesi, V.; Segoni, S.; Rosi, A.; Ting, X.; Nery, T.; Catani, F.; Casagli, N. Different approaches to use morphometric attributes in landslide susceptibility mapping based on meso-scale spatial units: A case study in Rio de Janeiro (Brazil). Remote Sens. 2020, 12, 1826. [Google Scholar] [CrossRef]
- Domènech, G.; Alvioli, M.; Corominas, J. Preparing first-time slope failures hazard maps: From pixel-based to slope unit-based. Landslides 2020, 17, 249. [Google Scholar] [CrossRef] [Green Version]
- Palau, R.M.; Hürlimann, M.; Berenguer, M.; Sempere-Torres, D. Influence of the mapping unit for regional landslide early warning systems: Comparison between pixels and polygons in Catalonia (NE Spain). Landslides 2020, 17, 2067–2083. [Google Scholar] [CrossRef]
- Crosta, G.B.; Frattini, P. Rainfall-induced landslides and debris flows. Hydrol. Process. 2008, 22, 473–477. [Google Scholar] [CrossRef]
- Kuriakose, S.L.; van Beek, L.P.H.; van Westen, C.J. Parameterizing a physically based shallow landslide model in a data poor region. Earth Surf. Process. Landf. 2009, 34, 867–881. [Google Scholar] [CrossRef]
- Salvatici, T.; Tofani, V.; Rossi, G.; D’Ambrosio, M.; Tacconi Stefanelli, C.; Benedetta Masi, E.; Rosi, A.; Pazzi, V.; Vannocci, P.; Petrolo, M.; et al. Application of a physically based model to forecast shallow landslides at a regional scale. Nat. Hazards Earth Syst. Sci. 2018, 18, 1919–1935. [Google Scholar] [CrossRef] [Green Version]
- Canli, E.; Mergili, M.; Thiebes, B.; Glade, T. Probabilistic landslide ensemble prediction systems: Lessons to be learned from hydrology. Nat. Hazards Earth Syst. Sci. 2018, 18, 2183–2202. [Google Scholar] [CrossRef] [Green Version]
- Richards, L.A. Capillary conduction of liquids through porous mediums. J. Appl. Phys. 1931, 1, 318–333. [Google Scholar] [CrossRef]
- Beguería, S. Validation and evaluation of predictive models in hazard assessment and risk management. Nat. Hazards 2006, 37, 315–329. [Google Scholar] [CrossRef] [Green Version]
- Martelloni, G.; Segoni, I.S.; Fanti, I.R.; Catani, I.F. Rainfall thresholds for the forecasting of landslide occurrence at regional scale. Landslides 2012, 9, 485–495. [Google Scholar] [CrossRef] [Green Version]
- Segoni, S.; Tofani, V.; Rosi, A.; Catani, F.; Casagli, N. Combination of rainfall thresholds and susceptibility maps for dynamic landslide hazard assessment at regional scale. Front. Earth Sci. 2018, 6, 85. [Google Scholar] [CrossRef] [Green Version]
- Abraham, M.T.; Satyam, N.; Bulzinetti, M.A.; Pradhan, B.; Pham, B.T.; Segoni, S. Using field-based monitoring to enhance the performance of rainfall thresholds for landslide warning. Water 2020, 12, 1–21. [Google Scholar] [CrossRef]

| Efficiency | FPT 60% | FPT 70% | FPT 75% | FPT 80% | FPT 85% | FPT 90% |
|---|---|---|---|---|---|---|
| IDT 3% | 0.650 | 0.673 | 0.696 | 0.725 | 0.740 | 0.767 |
| IDT 5% | 0.708 | 0.735 | 0.754 | 0.788 | 0.817 | 0.823 |
| IDT 10% | 0.804 | 0.821 | 0.837 | 0.852 | 0.858 | 0.873 |
| IDT 15% | 0.850 | 0.875 | 0.871 | 0.890 | 0.877 | 0.888 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulzinetti, M.A.; Segoni, S.; Pappafico, G.; Masi, E.B.; Rossi, G.; Tofani, V. A Tool for the Automatic Aggregation and Validation of the Results of Physically Based Distributed Slope Stability Models. Water 2021, 13, 2313. https://doi.org/10.3390/w13172313
Bulzinetti MA, Segoni S, Pappafico G, Masi EB, Rossi G, Tofani V. A Tool for the Automatic Aggregation and Validation of the Results of Physically Based Distributed Slope Stability Models. Water. 2021; 13(17):2313. https://doi.org/10.3390/w13172313
Chicago/Turabian StyleBulzinetti, Maria Alexandra, Samuele Segoni, Giulio Pappafico, Elena Benedetta Masi, Guglielmo Rossi, and Veronica Tofani. 2021. "A Tool for the Automatic Aggregation and Validation of the Results of Physically Based Distributed Slope Stability Models" Water 13, no. 17: 2313. https://doi.org/10.3390/w13172313
APA StyleBulzinetti, M. A., Segoni, S., Pappafico, G., Masi, E. B., Rossi, G., & Tofani, V. (2021). A Tool for the Automatic Aggregation and Validation of the Results of Physically Based Distributed Slope Stability Models. Water, 13(17), 2313. https://doi.org/10.3390/w13172313








