HydroMet: A New Code for Automated Objective Optimization of Hydrometeorological Thresholds for Landslide Initiation
Abstract
:1. Introduction
2. Theoretical Basis
2.1. Optimizing with Receiver Operating Characteristics
2.2. Threshold Formulation
3. Implementation
3.1. System Requirements
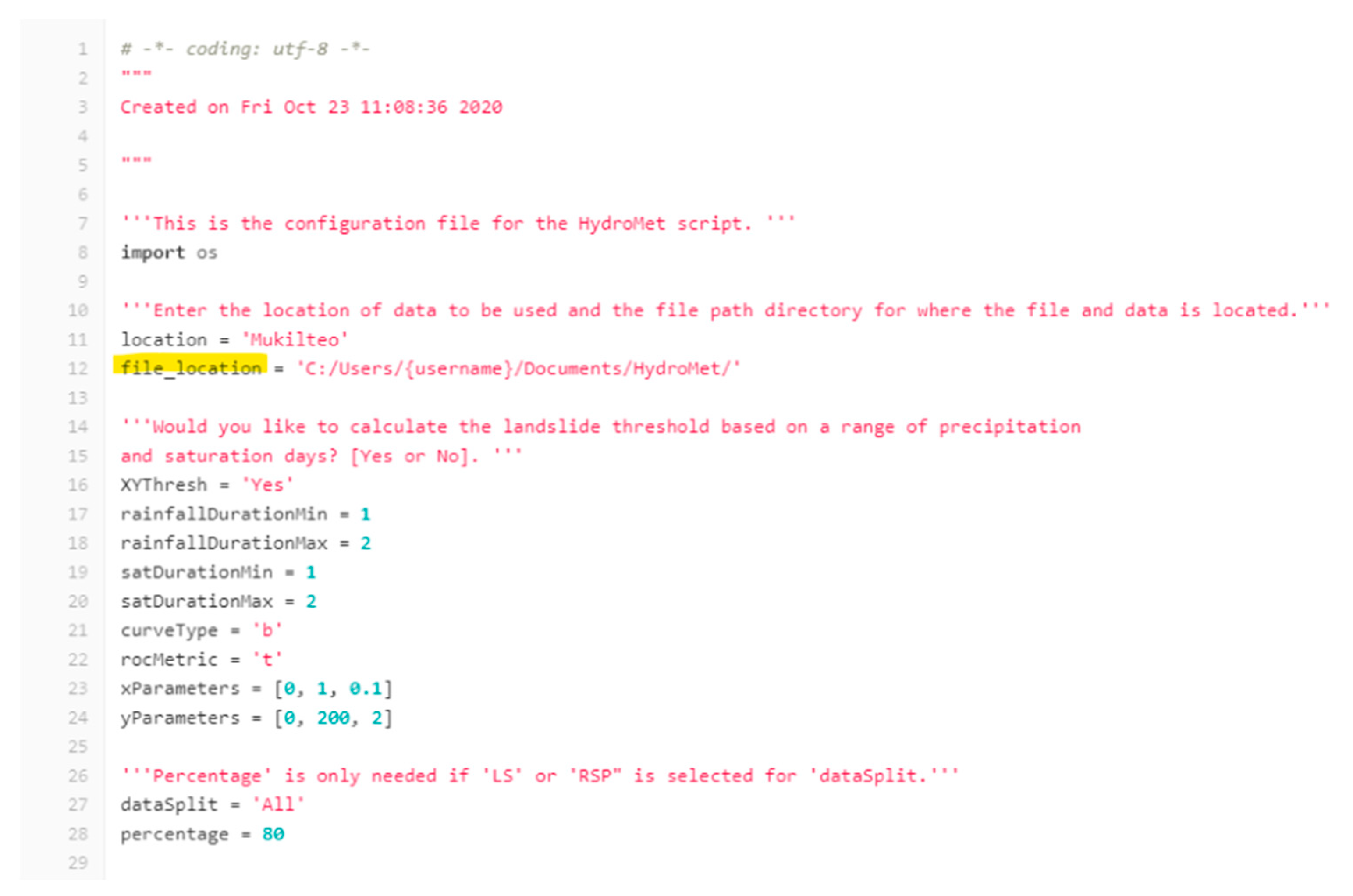
3.2. Input Requirements
- Rainfall, saturation, pressure (RSP) files are four-column, header-less files
- ○
- Column 1: time of data recording, as a date number, (e.g., number of days since January 1, 0001)
- ○
- Column 2: rainfall measurement, in length (e.g., mm)
- ○
- Column 3: saturation measurement, unitless
- ○
- Column 4: pressure measurement, in ML−1T −2 (e.g., kPa)
- LandslideTimes files are single column, header-less files
- ○
- Column 1: time of landslide recording, as a date number
3.3. Additional Options
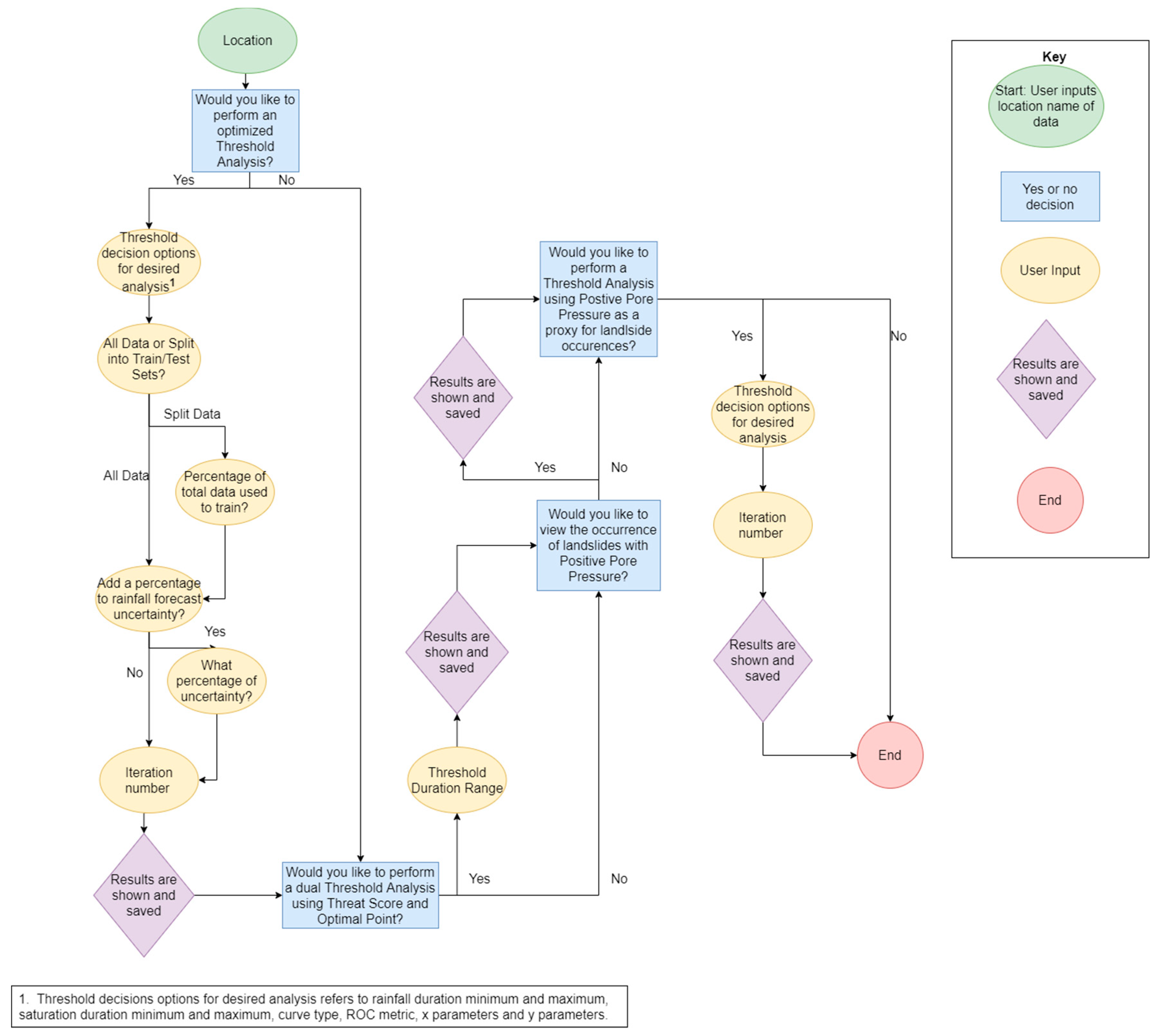
3.4. Operational Instructions
4. Output Files
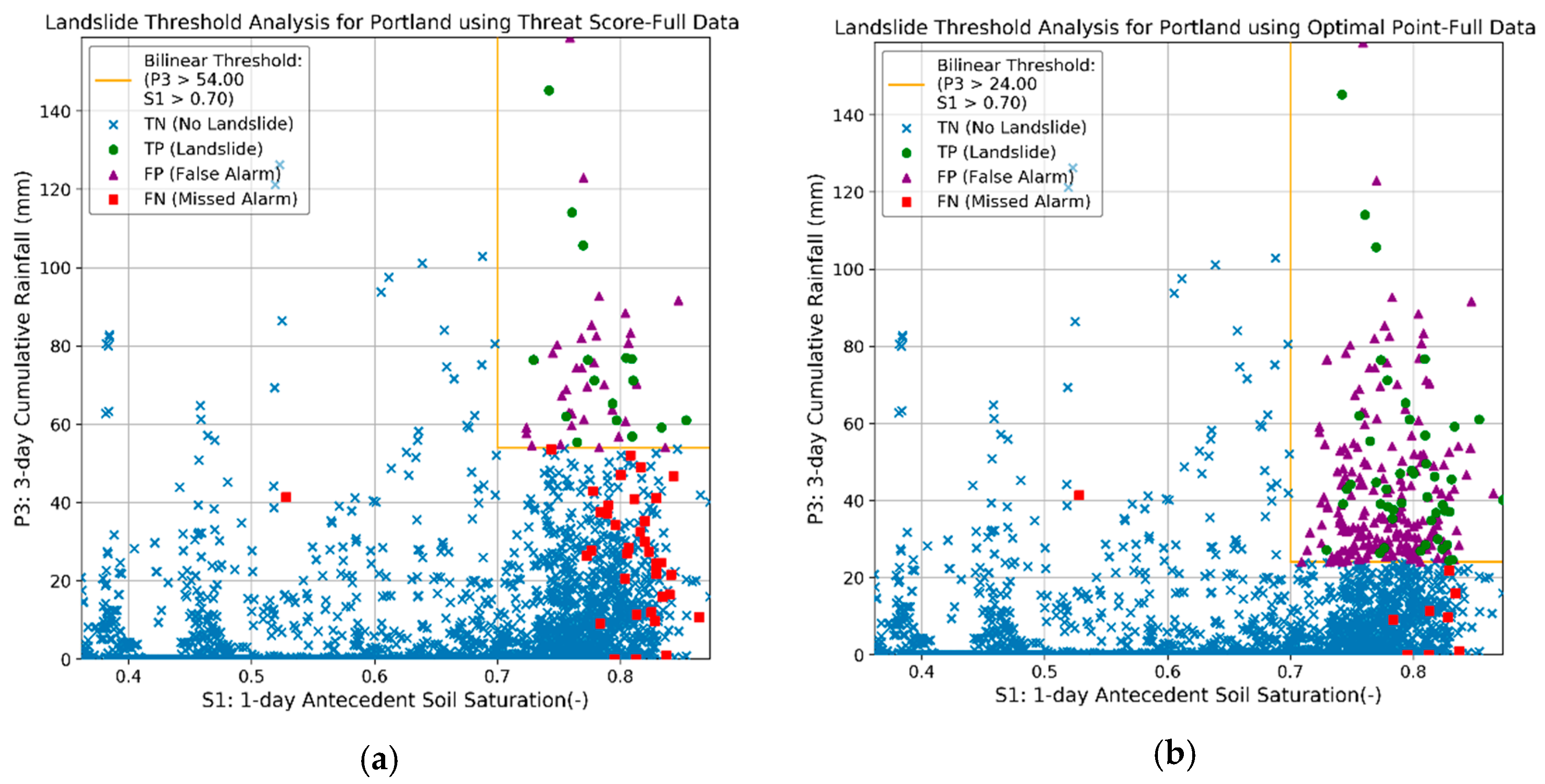
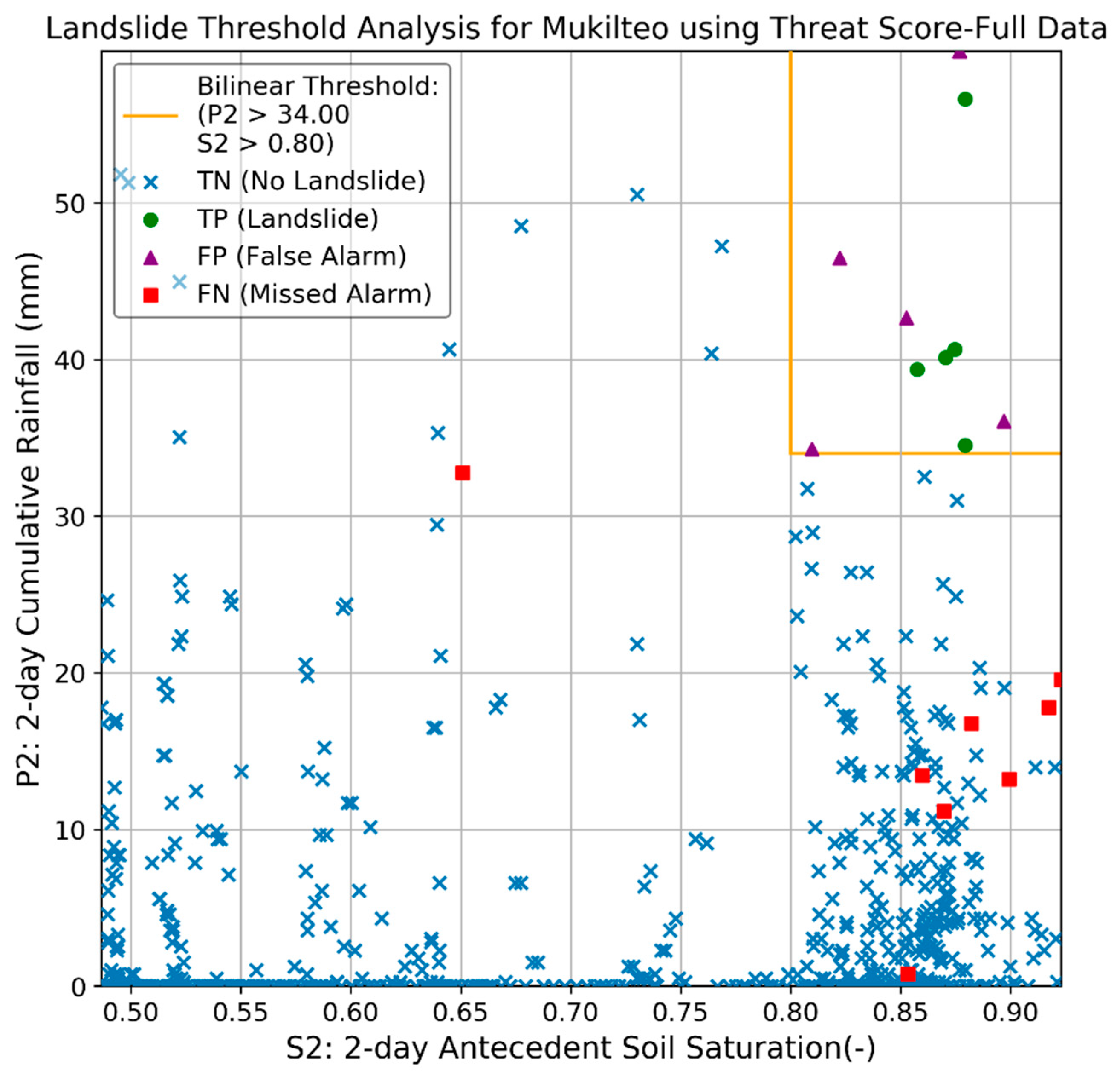
5. Example Applications
6. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Caine, N. The rainfall intensity-duration control of shallow landslides and debris flows. Geogr. Ann A Phys. Geogr. 1980, 62, 23–27. [Google Scholar]
- Keefer, D.K.; Wilson, R.C.; Mark, R.K.; Brabb, E.E.; Brown, W.M.; Ellen, S.D.; Harp, E.L.; Wieczorek, G.F.; Alger, C.S.; Zatkin, R.S. Real-time landslide warning during heavy rainfall. Science 1987, 238, 921–925. [Google Scholar] [CrossRef] [PubMed]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Mirus, B.B.; Morphew, M.D.; Smith, J.B. Developing hydro-meteorological thresholds for shallow landslide initiation and early warning. Water 2018, 10, 1274. [Google Scholar] [CrossRef] [Green Version]
- Mirus, B.B.; Becker, R.; Baum, R.L.; Smith, J.B. Integrating real-time subsurface hydrologic monitoring with empirical rainfall thresholds to improve landslide early warning. Landslides 2018, 15, 1909. [Google Scholar] [CrossRef]
- Thomas, M.A.; Mirus, B.B.; Collins, B.D. A physics-based approach to identify thresholds for rainfall-induced shallow landsliding. Geophys. Res. Lett. 2018, 45, 9651–9661. [Google Scholar] [CrossRef]
- Thomas, M.A.; Collins, B.D.; Mirus, B.B. Assessing the feasibility of satellite-based thresholds for hydrologically driven landsliding. Water Resour. Res. 2019, 55, 9006–9023. [Google Scholar] [CrossRef]
- Thomas, M.A.; Mirus, B.B.; Smith, J.B. Hillslopes in humid-tropical climates aren’t always wet: Implications for hydrologic response and landslide initiation in Puerto Rico. Hydrol. Processes 2020, 34, 4307–4318. [Google Scholar] [CrossRef]
- Segoni, S.; Rosi, A.; Lagomarsino, D.; Fanti, R.; Casagli, N. Brief communication: Using averaged soil moisture estimates to improve the performances of a regional-scale landslide early warning system. Nat. Hazards Earth Syst. Sci. 2018, 18, 807–812. [Google Scholar] [CrossRef] [Green Version]
- Wicki, A.; Lehmann, P.; Hauck, C.; Seneviratne, S.I.; Waldner, P.; Stähli, M. Assessing the potential of soil moisture measurements for regional landslide early warning. Landslides 2020, 17, 1881–1896. [Google Scholar] [CrossRef] [Green Version]
- Segoni, S.; Rosi, A.; Rossi, G.; Catani, F.; Casagli, N. Analysing the relationship between rainfalls and landslides to define a mosaic of triggering thresholds for regional-scale warning systems. Nat. Hazards Earth Syst. Sci. 2014, 14, 2637–2648. [Google Scholar] [CrossRef] [Green Version]
- Piciullo, L.; Gariano, S.L.; Melillo, M.; Brunetti, M.; Peruccacci, S.; Guzzetti, F. Definition and performance of a threshold-based regional early warning model for rainfall-induced landslides. Landslides 2017, 14, 995–1008. [Google Scholar] [CrossRef]
- Baum, R.L.; Fischer, S.J.; Vigil, J.C. THRESH—Software for Tracking Rainfall Thresholds for Landslide and Debris-Flow Occurrence, User Manual: U.S. Geological Survey Techniques and Methods, Book 14. 2018. Available online: https://doi.org/10.3133/tm14A2 (accessed on 23 June 2021).
- Melillo, M.; Brunetti, M.T.; Peruccacci, S.; Gariano, S.L.; Roccati, A.; Guzzetti, F. A tool for the automatic calculation of rainfall thresholds for landslide occurrence. Environ. Modell. Softw. 2018, 105, 230–243. [Google Scholar] [CrossRef]
- Bogaard, T.; Greco, R. Invited perspectives: Hydrological perspectives on precipitation intensity-duration thresholds for landslide initiation: Proposing hydrometeorological thresholds. Nat. Hazards Earth Syst. Sci. 2018, 18, 31–39. [Google Scholar] [CrossRef] [Green Version]
- Swets, J.A. Measuring the accuracy of diagnostic systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Chleborad, A.F.; Baum, R.L.; Godt, J.W.; Powers, P.S. A prototype system for forecasting landslides in the Seattle, Washington, area. Rev. Eng. Geol. 2008, 20, 103–120. [Google Scholar]
- Baum, R.L.; Godt, J.W. Early warning of rainfall-induced shallow landslides and debris flows in the USA. Landslides 2010, 7, 259–272. [Google Scholar] [CrossRef]
- Smith, J.B.; Baum, R.L.; Mirus, B.B.; Michel, A.R.; Stark, B. Results of Hydrologic Monitoring on Landslide-Prone Coastal Bluffs near Mukilteo, Washington, U.S. Geological Survey Data Release. 2017. Available online: https://doi.org/10.5066/F7NZ85WX (accessed on 23 June 2021).




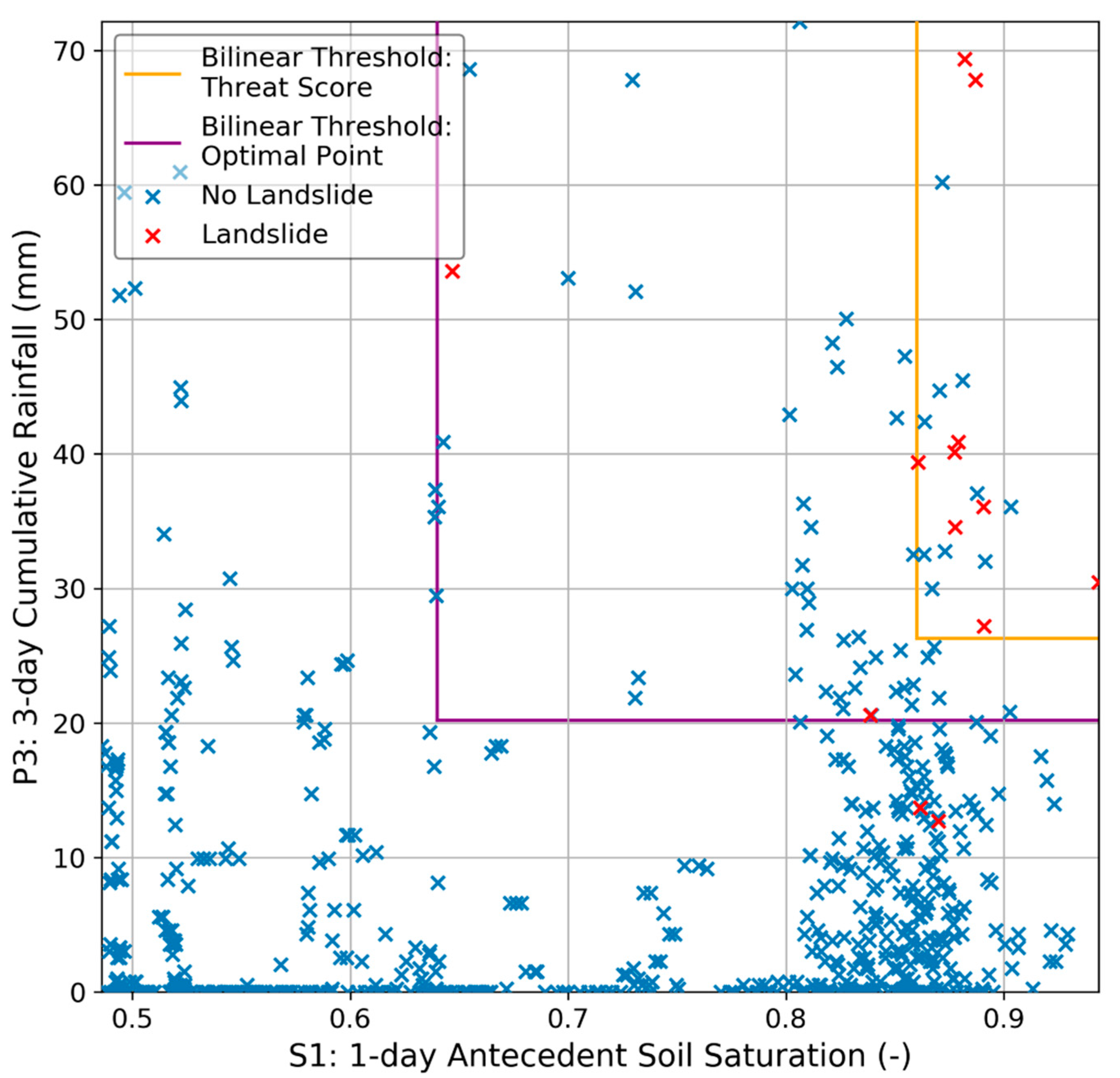
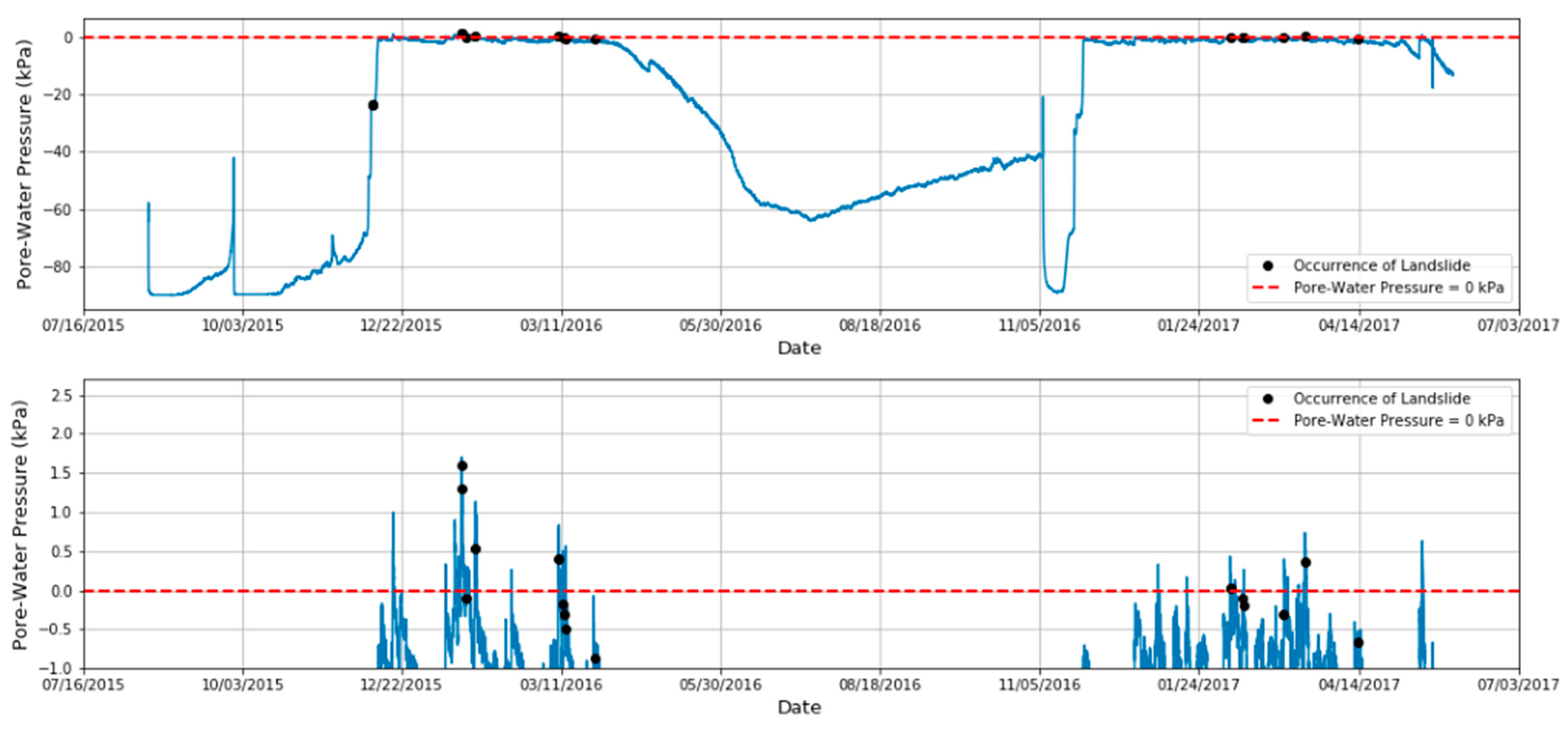
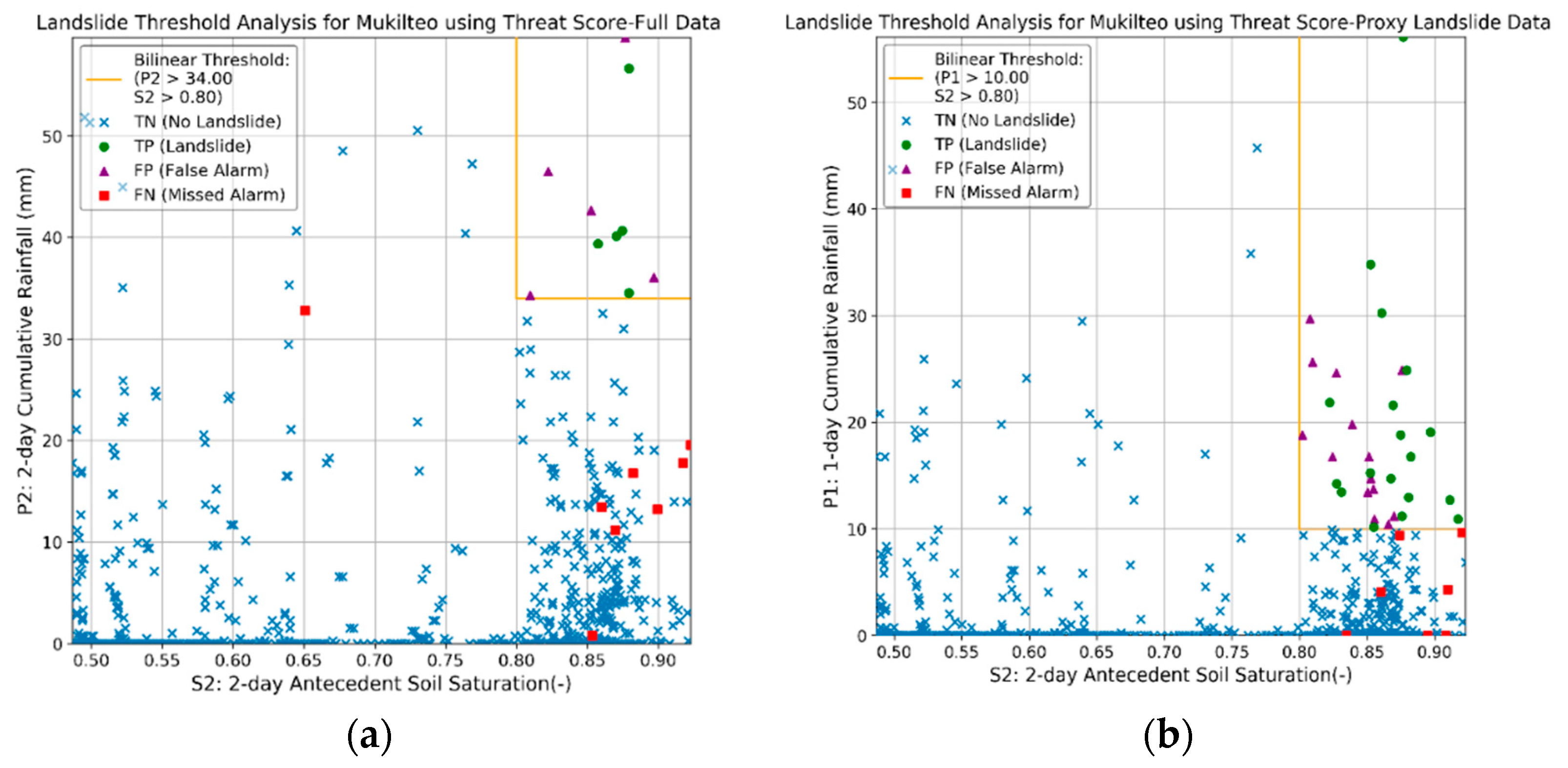
| Optimized Skill Statistic | Optimal Threshold TPR | Optimal Threshold FPR | Formula P (mm), S (unitless) |
|---|---|---|---|
| threat score | 0.5333 | 0.0155 | P3 > 54, S1 > 0.70 |
| optimal point | 0.9000 | 0.0918 | P3 > 24, S1 > 0.70 |
| precision | 0.3222 | 0.0009 | P3 > 100, S1 > 0.70 |
| true skill statistic | 0.9000 | 0.0918 | P3 > 24, S1 > 0.70 |
| Round{Value} | ROCRound{Value} | BestThresholdRound{Value} | |
|---|---|---|---|
| Range of precipitation days to evaluate | • | ||
| Range of saturation days to evaluate | • | ||
| Threshold curve ROC Metric used to optimize threshold | • | ||
| X intercept range | • | ||
| Y intercept range | • | ||
| Optimal cumulative rainfall days | • | • | |
| Optimal antecedent saturation days | • | • | |
| Optimal threshold y intercept | • | • | |
| Optimal threshold x intercept | • | • | |
| FPR | • | • | • |
| TPR | • | • | • |
| Threat score | • | • | |
| Precision score | • | • | |
| True skill statistic | • | • | |
| Optimal Point score | • | • | |
| Percent of landslides exceeding threshold | • | • | |
| AUC | • | • | |
| Best threshold from each P:S day combination | • | ||
| Single Optimal Threshold | • |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Conrad, J.L.; Morphew, M.D.; Baum, R.L.; Mirus, B.B. HydroMet: A New Code for Automated Objective Optimization of Hydrometeorological Thresholds for Landslide Initiation. Water 2021, 13, 1752. https://doi.org/10.3390/w13131752
Conrad JL, Morphew MD, Baum RL, Mirus BB. HydroMet: A New Code for Automated Objective Optimization of Hydrometeorological Thresholds for Landslide Initiation. Water. 2021; 13(13):1752. https://doi.org/10.3390/w13131752
Chicago/Turabian StyleConrad, Jacob L., Michael D. Morphew, Rex L. Baum, and Benjamin B. Mirus. 2021. "HydroMet: A New Code for Automated Objective Optimization of Hydrometeorological Thresholds for Landslide Initiation" Water 13, no. 13: 1752. https://doi.org/10.3390/w13131752
APA StyleConrad, J. L., Morphew, M. D., Baum, R. L., & Mirus, B. B. (2021). HydroMet: A New Code for Automated Objective Optimization of Hydrometeorological Thresholds for Landslide Initiation. Water, 13(13), 1752. https://doi.org/10.3390/w13131752






