Abstract
Integrated water management has become a priority for cropping systems where subirrigation is possible. Compared to conventional sprinkler irrigation, the controlling water table can lead to a substantial increase in yield and water use efficiency with less pumping energy requirements. Knowing the spatiotemporal distribution of water table depth (WTD) and soil properties should help perform intelligent, integrated water management. Observation wells were installed in cranberry fields with different water management systems: Bottom, with good drainage and controlled WTD management; Surface, with good drainage and sprinkler irrigation management; Natural, without drainage, or with imperfectly drained and conventional sprinkler irrigation. During the 2017–2020 growing seasons, WTD was monitored on an hourly basis, while precipitation was measured at each site. Multi-frequential periodogram analysis revealed a dominant periodic component of 40 days each year in WTD fluctuations for the Bottom and Surface systems; for the Natural system, periodicity was heterogeneous and ranged from 2 to 6 weeks. Temporal cross correlations with precipitation show that for almost all the sites, there is a 3 to 9 h lag before WTD rises; one exception is a subirrigation site. These results indicate that automatic water table management based on continuously updated knowledge could contribute to integrated water management systems, by using precipitation-based models to predict WTD.
1. Introduction
Agricultural water management faces more and more challenges, having to cope with changing climate conditions including more occurrences of extreme droughts and precipitation. One way to adapt is to implement integrated water management through agricultural hydroinformatics [1]. The use of such tools actively relies on developing and incorporating real-time predictive and adaptive models of distribution patterns of water table depth (WTD). This kind of real-time water management has been studied widely through monitoring or modelling of soil water content or status [2,3], soil matric potential [4,5,6], crop parameters [7], and water table depth (WTD) [8,9].
Cranberry farms are good candidates for integrated water management based on real-time monitoring of WTD through controlled drainage or subirrigation. Optimal cranberry farm water management usually has four basic elements: (i) an infrastructure for storing water, (ii) a network of channels and ditches to route water in and out of fields, (iii) a network of subsurface drains and water level controllers for subirrigation or controlled drainage, and (iv) reutilisation of water in an almost closed-circuit system. The soil can be considered a reservoir to ensure water supply to plants by controlling the WTD using the subsurface drainage system. By doing so at the right place and time, cranberries can be more resilient to droughts at a lower cost of energy [4,10] than with a water management system based solely on sprinkler irrigation for instance. On the other hand, when extreme precipitation events are forecasted, proactive management of WTD is needed to lower the level ahead of time.
For an intelligent and integrated system to work in predictive and adaptive modes, the detection of periodic components and the recognition of patterns in time series of WTD associated with an appropriate water management system that anticipates hydrometeorological conditions are of crucial importance. Multi-frequential periodogram analysis (MFPA) [11,12] is a statistical method for the detection of periodic components in time series, in particular overlapping signals that may correspond to fractional frequencies. Such WTD patterns may be specific to a water management system (i.e., controlled drainage, sprinkler irrigation) or a location (i.e., type of soil, site conditions). In this study, the focus is on the water management system rather than the soil conditions, as these are assumed to be comparable. The detection of periodic components is of great interest in water management because WTD fluctuations are subjected, for example, to evapotranspiration cycles, precipitation events, and water supply through subsurface drains. These processes may operate simultaneously and with noninteger frequencies. A temporal cross-correlation analysis performed after removal of the fitted periodic components can help quantify and interpret WTD fluctuations subjected to external time-dependent processes such as precipitation events.
Autoregressive models are identified for time series forecasting based on simple and partial autocorrelation functions that characterise them and are used for process prediction from correlated variables and study of heterogeneous patterns in discrete space and time [12] (pp. 297–306) [13,14]. Autoregressive modelling has been applied in state-space representation to predict WTD fluctuations in relation to precipitation or evapotranspiration in systems with subsurface drainage [15]. A simpler way to assess the association between time series at successive lags is by temporal cross-correlation analysis or temporal cross correlograms. For instance, this approach was used to study the association through time between soil water storage, precipitation, and cumulative crop evapotranspiration [16]. Sample cross-correlation coefficients can represent correlations in time and space-time [12].
The objective of this study was to analyse the impact of three water management systems on the temporal heterogeneities of WTD submitted to precipitation events during four growing seasons (2017–2020) of cranberries in Québec, Canada. To our knowledge, only a few studies have considered the impacts of water management on the temporal heterogeneity of WTD [17]. To achieve this objective, MFPA was first used to describe the temporal structure of time series. Then, using residuals, an autoregressive modelling approach was used to (i) analyse the temporal autocorrelation of WTD during each growing season and (ii) describe the spatiotemporal cross correlations between WTD and precipitation events for each year and each type of irrigation. The outcome of this study will contribute to the implementation of beneficial water management practices based on a predictive and adaptive tool to obtain optimum soil water conditions.
2. Materials and Methods
2.1. Soils, Sites, and Data
Cranberry farms in Québec, Canada, are mostly established on sandy soils and most of the time by removing the first 30 cm of topsoil and replacing it with local sand. The sand used varies from very fine to coarse. Under the sand, subsurface drains are usually installed, along the length of the field (one field corresponding to one polygon in Figure 1), with depths between 60 and 90 cm from one field extremity to the other. These drains, 2 to 14 per field (fields being generally 45 m wide and between 175 and 500 m long), are connected to either the main subsurface collector, a water level control structure, or directly to a surface ditch or channel. However, some older fields (more than 30 years) may not have this type of drainage system. In all cases, dams and channels are parts of the farm water management, namely, for inundation during harvest and routing excess water towards retention basins.
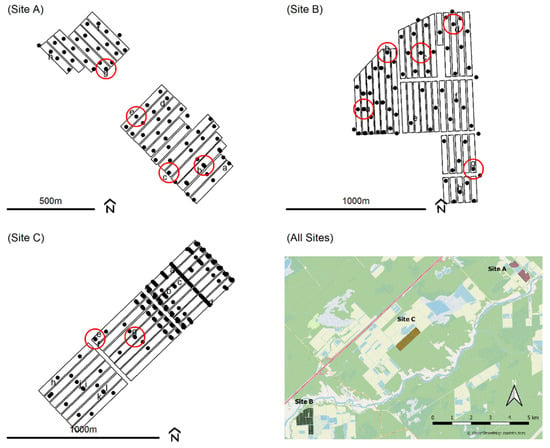
Figure 1.
Observation wells of the three cranberry farms: Site A, Site B, Site C, and a geographical representation of all Sites. Circles are the instrumented wells for years 2017, 2018, 2019, and 2020.
For this study, WTD was monitored in observation wells that were installed at three different cranberry farms (Sites A, B, and C; Figure 1) in Québec, Canada, from May 2017 throughout 2018, 2019, and 2020. Site A is about 7 km far from Site C and 14 km far from Site B, with Site C between the two others (Figure 1). At some locations (black dots with a letter on Figure 1), water levels were measured and recorded every hour from June to September of each year using dipperLog NANO (Heron Instruments, ON, Canada) or HOBO water level (U20L-04, Onset, MA, USA) data loggers. Among these instrumented wells, some were chosen (red circles on Figure 1) to cover different types of water table management: (1) good drainage and either controlled drainage or subirrigation (i.e., Bottom); (2) good drainage and sprinkler irrigation management based on optimum soil matric potential thresholds (i.e., Surface); (3) no drainage or imperfect drainage with sprinkler irrigation management (i.e., Natural). Five observation wells were located within the Bottom type of water table management, two with subirrigation (Wells A-b and A-c at Site A, Figure 1) and three with controlled drainage (Well B-a at Site B; Wells C-e and C-g at Site C, Figure 1). Three observations wells were located within the Surface type (Wells B-b, B-c, and B-d at Site B, Figure 1), and three within the Natural type (Wells A-e and A-g at Site A; Well B-g at Site B, Figure 1). Over the 4 years, a total of 24 time series of WTDs met the characteristics of water table management required to be classified Bottom (8), Surface (8), or Natural (8). On an annual basis, 10 time series were kept for 2017, 7 for 2018, 3 for 2019, and 4 for 2020. Other time series were discarded because some sites were not under subirrigation or controlled drainage (for Bottom), i.e., the water table management was not applied, or level loggers were not functioning properly (faulty batteries, errors).
Each site was also equipped with a meteorological station (Hortau Inc., Lévis, QC, Canada) monitoring hourly cumulative precipitation (Figure 2). Technical problems with the rain gauge in Site A during growing seasons 2018 and 2020 (Figure 2) resulted in almost no precipitation records; these series were not used for the cross-correlation analyses.
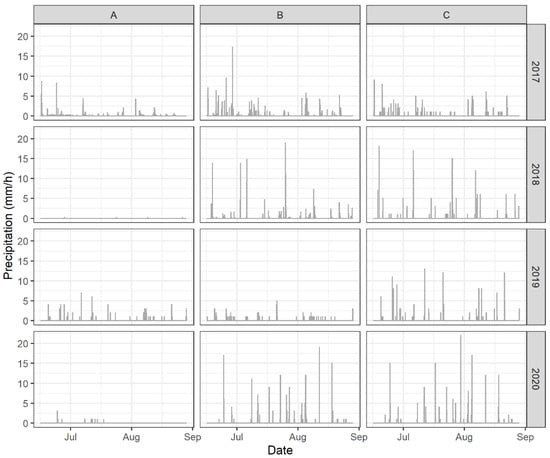
Figure 2.
Hourly precipitation at each site (A, B, C) of each year (2017–2020) between 16 June, 0:00, and 28 August, 23:00.
2.2. Statistical Methods
The 24 WTD time series were examined for outliers and filtered to keep the section over which water management took place to meet plant requirements (i.e., removal of the beginning of growing seasons and the harvest flooding parts). That left 1776 h from 16 June, 0:00, to 28 August, 23:00. An MFPA [11] was performed on each time series to assess the structure and detect two main periodic components, using the adespatial package [18] in R [19]. For all the time series, but one, two frequency components having a joint coefficient of determination (R2) greater than 0.30 were fitted with a trigonometric model. For two Natural time series, a linear trend was incorporated to make a polynomial–trigonometric model. Estimated periods were calculated by dividing the length of time series (1776 h) by the nonangular frequencies (number of cycles) found by the MFPA. Residuals ε(t) were then calculated for each time series U(t) based on an intercept (a), cosine and sine coefficients (cf and df) for each frequency component (ωf, with f = 1, …, F = 2):
Note that when there is a large-scale trend component (i.e., the fitted model being polynomial–trigonometric), .
Residual WTD time series were submitted to cross-correlation analysis with precipitation time series for the same 1776 h at each site in each year, using the ARIMA procedure of SAS 9.4 (SAS Institute Inc., Cary, NC, USA). Sample simple and partial autocorrelation coefficients, together with the Akaike information criterion, were used to identify the autoregressive order for prewhitening (i.e., removal of autocorrelation to avoid bias in cross-correlation estimation) in a preliminary step of cross-correlation analysis; an autoregressive model of second order, or AR(2), was identified for residual WTD time series. The first positive lag at which the WTD time series became positively and significantly cross-correlated with the corresponding precipitation time series was noted.
3. Results and Discussion
3.1. Observed and Modelled Time Series
The observed and modelled Bottom time series are presented in Figure 3. In 2017, the Bottom 4 and 5 series present a temporal pattern similar to those expected with optimum water table management in cranberry production. That is, WTD remains in the −35 to −70 cm depth range, which was found optimal for maximum cranberry production [4,10,20]. The risk of highest vegetative growth and shallowest rooting depth is increased for WTD above −35 cm. Hall [21] observed shallow rooting depth at −6 cm WTD, while roots were going deeper at −35 cm. Baumann et al. [22] drew similar conclusions from the comparison of WTD values of −13, −39, and −57 cm, i.e., having deeper rooting and less vegetative growth as WTD went deeper. Caron et al. [23] set the lower limit of WTD to −80 cm, which was related to a high plant water stress risk. When controlled water table management is the primary source of irrigation, as for the Bottom type, Pelletier et al. [10] observed that the highest cranberry yields corresponded to a WTD of −60 cm. In 2017, the WTD was mostly kept within an optimum range of −35 to −70 cm at Bottom 2 and 3 (Figure 3), as at Surface 2 and 3 in 2017, and a majority of sites in 2018 (Figure 4).
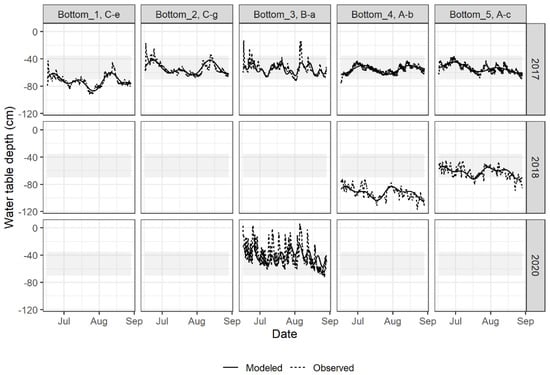
Figure 3.
Observed and modelled time series of WTDs using multi-frequential periodogram for the Bottom sites and years meeting the required water management conditions (controlled drainage or subirrigation).
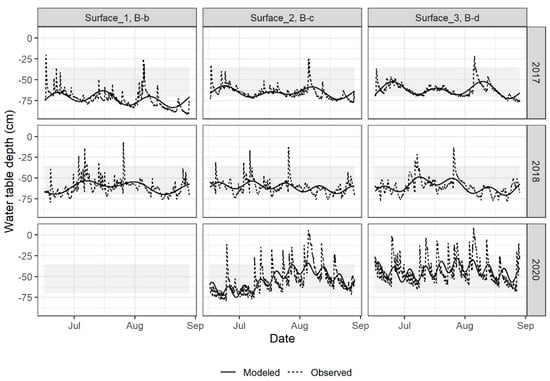
Figure 4.
Observed and modelled time series of WTDs using multi-frequential periodogram for the Surface sites and years meeting the required water management conditions.
The observation of time series suggests that the WTD patterns for the Natural type of water management (Figure 5) were different from those of the Bottom and Surface types (Figure 3 and Figure 4). Some time series of the Natural type present a downward trend, which could be related to a regional water table drawdown. Natural 1 (Well B-g) is near a wetland area (east of Site B; Figure 1), whereas Natural 2 (Well A-e) is close to a raised retention basin (northwest; Figure 1). This regional trend had to be included in the MFPA for Natural 1 in 2019 and Natural 2 in 2018.
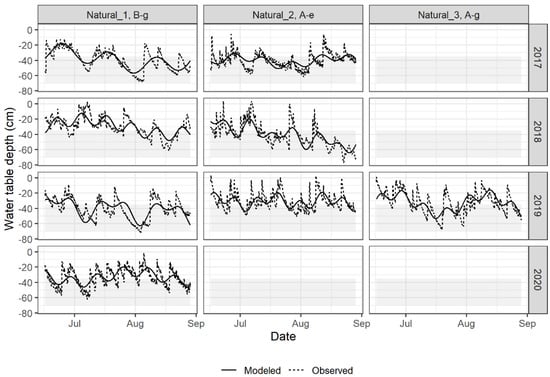
Figure 5.
Observed and modelled time series of WTDs using multi-frequential periodogram for the Natural sites and years meeting the required water management conditions.
Each time series was modelled with a maximum of two frequency components (i.e., two periodic components) because weekly or monthly periods were physically expected for local WTD variations: (i) weekly, based on meteorological depression regimes at the location and (ii) monthly because water table control devices stay in place for months. In the case of sprinkler irrigation, it is expected that the optimum management (Surface type) would result in periods of at least one week and possibly up to one month of adequate WTD control, because of ideal conditions. For the Natural type, even though sprinkler irrigation was practiced, drainage was poor, and changes in WTD were expected to be smooth over one week or more. The MFPA results (Figure 6) show that (i) there are differences in the estimated periods among years; (ii) Bottom and Surface time series present similar estimated periods overall; (iii) some of the periodic components of Natural time series are much shorter than those of the other types. In 2017, all three types had similar estimated periods, ranging from 38 to 52 days, but heterogeneity appeared in 2018 and further increased in 2020, with periods then ranging from 8 to 58 days (Figure 6). Peaks were more frequent and of greater magnitude in the 2020 WTD time series than for the other years. Compared to the Natural type, Bottom and Surface types generally show periods between one month and one and a half months, reflecting a higher homogeneity of the annual WTD fluctuations over years. For the Natural type, periods range between two weeks and one month (Figure 6). Condon and Maxwell [17] showed that irrigation changes the temporal dynamics of natural systems, decreasing interannual variability on farm sites. Even if observation wells of the Natural type received irrigation, they were closer to natural conditions of the water table than those of the Bottom and Surface types.
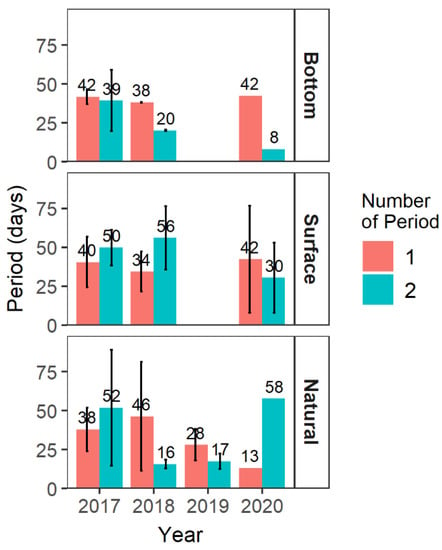
Figure 6.
Average periods with standard deviation calculated from the multi-frequential periodogram analysis at frequencies 1 and 2 for the 24 sites (8 Bottom, 8 Surface, 8 Natural) and years meeting the required water management conditions.
3.2. Cross-Correlation Analyses
3.2.1. The Year 2017
Bottom 3, Surface 1, and Surface 2 time series show the same positive and significant cross-correlated relationship after 4 h in 2017, with the highest coefficient after 6 h (B3/B = 0.191, S1/B = 0.222, S2/B = 0.202; Table 1). This result means that 4 h after a precipitation event, and with a maximum of 6 h, the WTD responded similarly, regardless of the irrigation management. It also suggests that soil drainage conditions were the same. The Bottom and Surface types of water management had similar fluctuation patterns of water level in 2017, in particular, at Site B where three main peaks were observed, namely, (i) in June, (ii) at the beginning of July, and (iii) early August (Figure 3 and Figure 4). Interestingly, precipitation at Site B (Figure 2) showed three similar peaks in 2017. In the case of Surface 3, still at Site B, the WTD responded positively 5 h after a rainfall event, with a maximum at 15 h (S3/B = 0.167; Table 1). This response is similar to that for Natural 1 at Site B (N1/B = 0.101; Table 1). Even though the drainage at Surface 3 (Well B-d) was more efficient than at Natural 1 (Well B-g), both were at the shortest distance from the natural wetlands located east of Site B, and the regional WTD could have damped the fluctuations caused by precipitation. In addition, the cross-correlation coefficients between prewhitened WTD time series of Bottom 3 and Surface 1, 2, and 3 reveal maximum values at the 0- and 1-h lags, with coefficients of 0.5 or higher for B3 and S3 (Table 2). This is likely due to the fact that sprinkler irrigation operations on the farm were not performed everywhere at the same time, as growers irrigated blocks of fields one after the other. Wells B-b and B-c may be managed simultaneously but not Well B-d which is located farther (Figure 1). Even though irrigation management in Well B-a was different from Wells B-b, B-c, and B-d, temporal WTD fluctuations follow the same pattern. In fact, sprinkler irrigation could have been used in controlled drainage management against heat (or frost) in cranberry production, and this may be another explanation for the temporal similarity of patterns. In hot summer, it may happen often, yet not systematically.

Table 1.
Significant (p < 0.05) cross-correlation coefficients at a selection of lags (in hours) between prewhitened time series of water table depth and precipitation events at each site in the years 2017, 2018, 2019, and 2020.

Table 2.
Significant (≥0.05) cross-correlation coefficients for time lag (hours) between prewhitened (p = 2) time series of water table management at site B (Bottom 3 vs. Surfaces 1, 2, 3) for 2017.
The three main peaks of precipitation at Site B in 2017 are observed at Site C in that year (Figure 2), and the temporal pattern of WTD, as modelled from MFPA results, reproduces these peaks for Bottom 1 and 2 (Wells C-e and C-g in 2017, Figure 3). Simply, the cross-correlation coefficients become positive and significant after 6 and 7 h with maximum values at 8 and 9 at Bottom 2 and Bottom 1, respectively (Table 1).
At Site A, the patterns that can be recognised are similar to a lesser degree (i.e., with lower values of cross-correlation coefficients), the precipitation events being less important (<5 mm/h) during most of the growing season (Figure 2). Bottom 5 and Natural 2 both show cross-correlation coefficients significantly positive at 5 h, with a maximum value at 8 h for Bottom 5 instead of 5 h for Natural 2 (B5/A = 0.076, N2/A = 0.137; Table 1). Bottom 5 in 2017 also has smaller positive cross-correlation coefficient values than other WTD series in that year. Bottom 4 was the only WTD series with negative cross-correlation coefficients with precipitation, suggesting that rainfall did not have the anticipated effect on WTD. This is a particular case of subirrigation. For controlled drainage, the channels maintaining water in the system are fluctuating in accordance with rainfall. However, under subirrigation conditions, water is pumped into the control box which can freely drain any overflow of water coming from the soil and the drainage system. Overall in 2017, the local maxima and minima of WTD as modelled by the MFPA were associated with the precipitation regime at a lag varying between 4 and 7 h, with one exception due to subirrigation.
3.2.2. Years 2018–2020
In 2018, the main focus was on Surface WTD maintained within the optimum range (Figure 4). The few peaks rising above −35 cm (mid-June, beginning of July, end of July; Figure 4) were related to the peaks of precipitation at the same site (Site B-2018, Figure 2). Cross-correlation coefficients confirmed this effect with significant values occurring at a time lag of 8 or 9 h (Table 1). This relationship between WTD and precipitation can also be found at Natural 1 (Well B-g, Figure 5), but with a WTD almost always too close to the soil surface. This situation was probably due to inadequate subsurface drainage conditions and the presence of adjacent wetlands. These conditions contributed to a high regional water table for a part of Site B. As in 2017, Natural 1 shows in 2018 a maximum cross correlation with precipitation after 15 h (N1/B = 0.096; Table 1).
In 2019, WTD data were available only for the Natural type and patterns of temporal WTD fluctuations for it were similar to those in the previous two years (Wells B-g and A-e; Figure 5), i.e., generally above the optimum water table management range. Natural 2 (Well A-e) showed almost the same cross-correlation pattern with precipitation as in 2017 (N2/A = 0.204 at 5 h; Table 1). Overall, the temporal association between WTD and precipitation was positive at lags of 3 to 5 h (Table 1).
In 2020, precipitation was more frequent, and occasionally torrential (e.g., the occurrence of precipitation ≥5 mm/h with 19 and 21 h events at Sites B and C, respectively; Figure 2). This likely explains the heterogeneity of WTD temporal patterns and MFPA results for Site B (Figure 3, Figure 4 and Figure 5). Temporal cross-correlation coefficients are unambiguous at all the sites in 2020: their values are positive and significant after 4 h and the maximum is at 5 h (Table 1).
3.2.3. Discussion
Associations between WTD and precipitation temporal patterns for each year are strong indicators that water management should be implemented by anticipating important precipitation events. Studies performed by Pelletier et al. [24] suggest that root zone submergence lasting more than 24 h could cause important cranberry yield losses. For three different sites and over four years, our study showed that producers have between 3 to 9 h to react before precipitation had an effect on the WTD. In real life, it is a short lead time considering the area covered by each farm and the manipulations required for lowering the water table. The other option that seems to be promising is subirrigation—Bottom 4 showed negative or nonsignificant cross-correlation coefficients with precipitation events, suggesting this management system is better adapted to evacuate overflow, compared with controlled drainage. Of course, more sites and years under adequate subirrigation systems would be needed to further substantiate this recommendation. Automatic infrastructures for water table management and adequate hydroinformatics [1], that is, the combined use of predictive models [8,25] and remotely controlled subirrigation systems [26], represent a promising avenue towards real-time water table management.
4. Conclusions
Over the four years of this study (2017–2020), Bottom and Surface types of water management were found to have similar temporal WTD patterns, with a dominant periodicity of about 40 days. The Natural type was more heterogeneous with a dominant estimated period ranging from two weeks to six weeks. After prewhitening of WTD time series of residuals (after periodicity analysis and trigonometric model fitting), the cross-correlation function showed that 3 to 9 h were needed to observe a significant effect on WTD after a precipitation event at almost all sites. The Natural time series appear to be slower, with up to 15 h for maximum correlation with precipitation. The exception was Bottom 4 in 2017, which was under subirrigation management and where precipitation was not positively associated with WTD, suggesting that the system is more adapted to evacuate overflow. However, more sites and years under adequate subirrigation are needed to confirm this latest recommendation. The core message of this study is that no matter what type of water management, producers have 3 to 9 h in reaction to a precipitation event before noticing an effect on the WTD. This represents a short lead-time interval, considering the area covered by each farm and the required operations to lower the water table. The results of this study strongly suggest that a complete integrated water management system should rely on the combined use of a hydrometeorological forecasting system and automatic structures for water table control, in essence, on a hydroinformatics framework.
Author Contributions
J.A.L. wrote the first draft of the manuscript. J.A.L. and V.V. worked on figures and R coding. J.A.L. and P.D. made statistical analyses. J.A.L., S.J.G., A.N.R., P.D., V.V., and J.G. reviewed and edited the manuscript. All authors contributed to the article and approved the submitted version. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Sciences and Engineering Research Council (NSERC) of Canada, Grant Number RDCPJ 477937-14–Gestion intégrée des ressources en eau dans la production de canneberges.
Data Availability Statement
The datasets for this study are subject to protection under a research agreement with the industry; every inquiry can be directed to the corresponding author.
Acknowledgments
We thank all partners of this project for their participation and excellent collaboration, namely, Pampev, Atocas Blandford, Canneberges Bieler, Groupe Nadeau (Mont Atocas), Ferme Daniel Coutu, and Hortau. We also acknowledge the work of many summer students who participated in the installation of equipment and data collection.
Conflicts of Interest
The authors declare the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Celicourt, P.; Rousseau, A.N.; Gumiere, S.J.; Camporese, M. Agricultural hydroinformatics: A blueprint for an emerging framework to foster water management-centric sustainability transitions in farming systems. Front. Water 2020, 2, 1–19. [Google Scholar] [CrossRef]
- Hedley, C.B.; Yule, I.J. Soil water status mapping and two variable-rate irrigation scenarios. Precis. Agric. 2009, 10, 342–355. [Google Scholar] [CrossRef]
- McDonough, K.R.; Hutchinson, S.L.; Hutchinson, J.M.S.; Case, J.L.; Rahmani, V. Validation and assessment of sport-lis surface soil moisture estimates for water resources management applications. J. Hydrol. 2018, 566, 43–54. [Google Scholar] [CrossRef]
- Caron, J.; Pelletier, V.; Kennedy, C.D.; Gallichand, J.; Gumiere, S.; Bonin, S.; Bland, W.; Pepin, S. Guidelines of irrigation and drainage management strategies to enhance cranberry production and optimize water use in north america. Can. J. Soil Sci. 2017, 97, 82–91. [Google Scholar] [CrossRef] [Green Version]
- Masseroni, D.; Facchi, A.; Depoli, E.V.; Renga, F.M.; Gandolfi, C. Irrig-oh: An open-hardware device for soil water potential monitoring and irrigation management. Irrig. Drain. 2016, 65, 750–761. [Google Scholar] [CrossRef]
- Pelletier, V.; Gallichand, J.; Caron, J. Effect of soil water potential threshold for irrigation on cranberry yield and water productivity. Trans. ASABE 2013, 56, 1325–1332. [Google Scholar] [CrossRef]
- Li, M.; Sui, R.; Meng, Y.; Yan, H. A real-time fuzzy decision support system for alfalfa irrigation. Comput. Electron. Agric. 2019, 163. [Google Scholar] [CrossRef]
- Brédy, J.; Gallichand, J.; Celicourt, P.; Gumiere, S.J. Water table depth forecasting in cranberry fields using two decision-tree-modeling approaches. Agric. Water Manag. 2020, 233. [Google Scholar] [CrossRef]
- Knotters, M.; Bierkens, M.F.P. Predicting water table depths in space and time using a regionalised time series model. Geoderma 2001, 103, 51–77. [Google Scholar] [CrossRef]
- Pelletier, V.; Gallichand, J.; Gumiere, S.; Pepin, S.; Caron, J. Water table control for increasing yield and saving water in cranberry production. Sustainability 2015, 7, 10602–10619. [Google Scholar] [CrossRef] [Green Version]
- Dutilleul, P. Multi-frequential periodogram analysis and the detection of periodic components in time series. Commun. Stat. Theory Method 2001, 30, 1063–1098. [Google Scholar] [CrossRef]
- Dutilleul, P.R.L. Spatio-Temporal Heterogeneity: Concepts Analyses; Cambridge University Press: Cambridge. UK, 2011; ISBN 978-0-521-79127-4. [Google Scholar]
- Wendroth, O.; Reuter, H.I.; Kersebaum, K.C. Predicting yield of barley across a landscape: A state-space modeling approach. J. Hydrol. 2003, 272, 250–263. [Google Scholar] [CrossRef]
- Yang, Y.; Wendroth, O. State-space approach to analyze field-scale bromide leaching. Geoderma 2014, 217–218, 161–172. [Google Scholar] [CrossRef]
- Berendrecht, W.L.; Heemink, A.W.; van Geer, F.C.; Gehrels, J.C. State-space modeling of water table fluctuations in switching regimes. J. Hydrol. 2004, 292, 249–261. [Google Scholar] [CrossRef]
- Awe, G.O.; Reichert, J.M.; Timm, L.C.; Wendroth, O. Temporal processes of soil water status in a sugarcane field under residue management. Plant Soil 2015, 387, 395–411. [Google Scholar] [CrossRef]
- Condon, L.E.; Maxwell, R.M. Groundwater-fed irrigation impacts spatially distributed temporal scaling behavior of the natural system: A spatio-temporal framework for understanding water management impacts. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef]
- Dray, S.; Bauman, D.; Blanchet, G.; Borcard, D.; Clappe, S.; Guenard, G.; Thibaut, J.; Larocque, G.; Legendre, P.; Madi, N.; et al. Adespatial: Multivariate Multiscale Spatial Analysis, R package version 0.3-8; 2020. Available online: https://CRAN.R-project.org/package=adespatial (accessed on 13 July 2021).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019; Available online: https://www.R-project.org/ (accessed on 13 July 2021).
- Handyside, P.E. Water Table Management for Cranberry Production on Sandy and Peat Soils in Québec; McGill University: Montréal, QC, Canada, 2003. [Google Scholar]
- Hall, I.V. Cranberry growth as related to water levels in the soil. Can. J. Plant Sci. 1971, 51, 237–238. [Google Scholar] [CrossRef]
- Baumann, D.L.; Workmaster, B.A.; Kosola, K.R. ‘Ben lear’ and ‘stevens’ cranberry root and shoot growth response to soil water potential. HortScience 2005, 40, 795–798. [Google Scholar] [CrossRef]
- Caron, J.; Bonin, S.; Pepin, S.; Kummer, L.; Vanderleest, C.; Bland, W.L. Determination of irrigation set points for cranberries from soil- and plant-based measurements. Can. J. Soil Sci. 2016, 96, 37–50. [Google Scholar] [CrossRef] [Green Version]
- Pelletier, V.; Pepin, S.; Laurent, T.; Gallichand, J.; Caron, J. Cranberry gas exchange under short-term hypoxic soil conditions. HortScience 2016, 51, 910–914. [Google Scholar] [CrossRef] [Green Version]
- Gumiere, S.J.; Camporese, M.; Botto, A.; Lafond, J.A.; Paniconi, C.; Gallichand, J.; Rousseau, A.N. Machine learning vs. Physics-based modeling for real-time irrigation management. Front. Water 2020, 2. [Google Scholar] [CrossRef] [Green Version]
- Celicourt, P.; Gumiere, S.J.; Lafond, J.A.; Gumiere, T.; Gallichand, J.; Rousseau, A.N. Automated mapping of water table for cranberry subirrigation management: Comparison of three spatial interpolation methods. Water 2020, 12, 3322. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).