Monitoring Crop Evapotranspiration and Transpiration/Evaporation Partitioning in a Drip-Irrigated Young Almond Orchard Applying a Two-Source Surface Energy Balance Model
Abstract
:1. Introduction
- Evaluate the performance of the STSEB approach, combined to radiometric temperature measurements, in almond orchard using an eddy-covariance system. Ground measurements of the surface energy fluxes were used as a basis for the assessment.
- Derive single and dual crop coefficients of the drip-irrigated young almond orchard using STSEB and ETo estimates.
- Explore relationships between crop coefficients and biophysical variables and vegetation indices that can be further applied to almond orchards under a range of growing stage and environmental conditions.
2. Materials and Methods
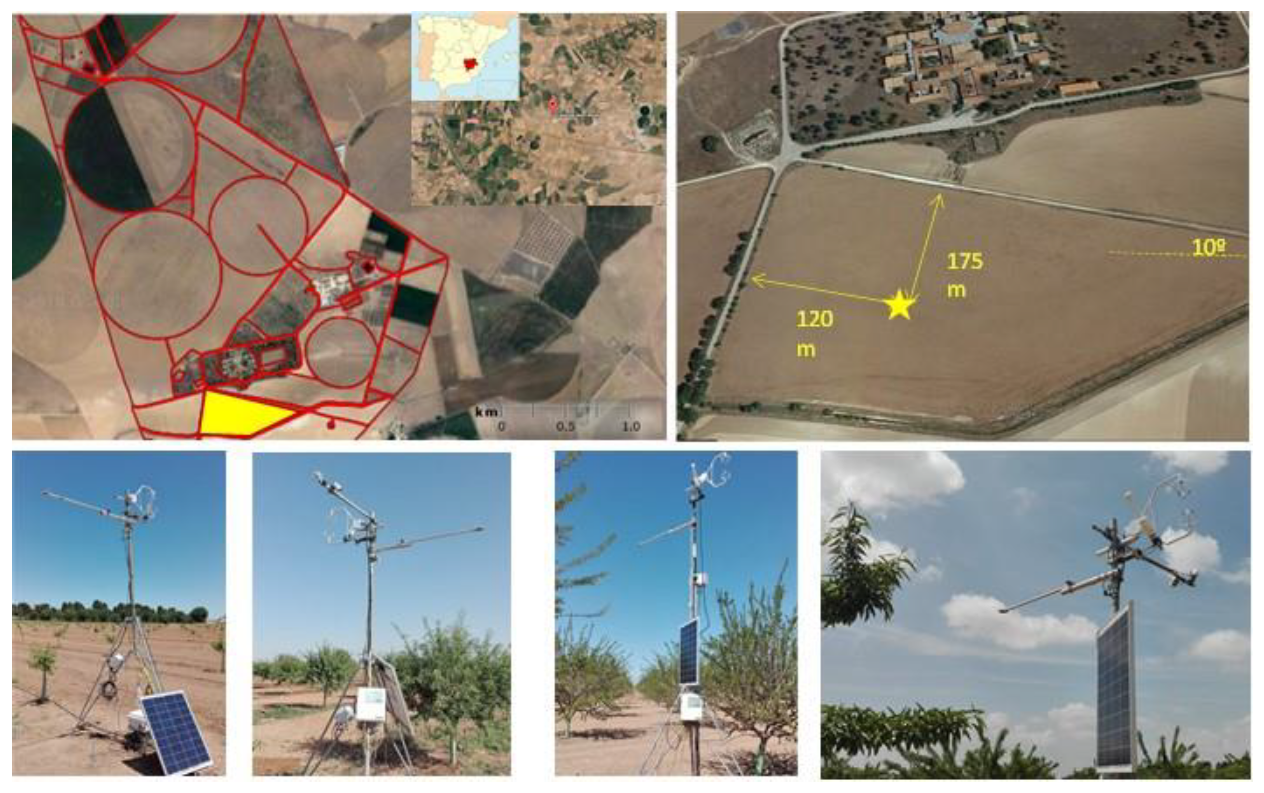
2.1. Study Site
2.2. Orchard Description
2.3. Eddy-Covariance and Meteorological Instrumentation
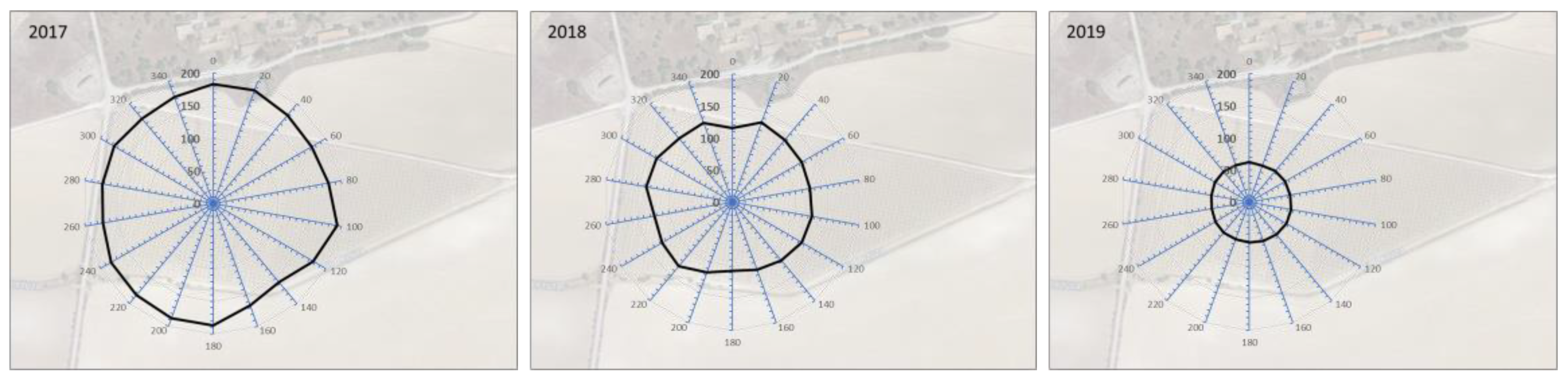
2.4. Footprint Analysis and Adjustment of Turbulent Fluxes
2.5. The STSEB Approach Combined with Ground Radiometric Thermal Measurements
2.6. Satellite-Based ETc Approaches Supported on VI-Kc Relationships
3. Results and Discussion
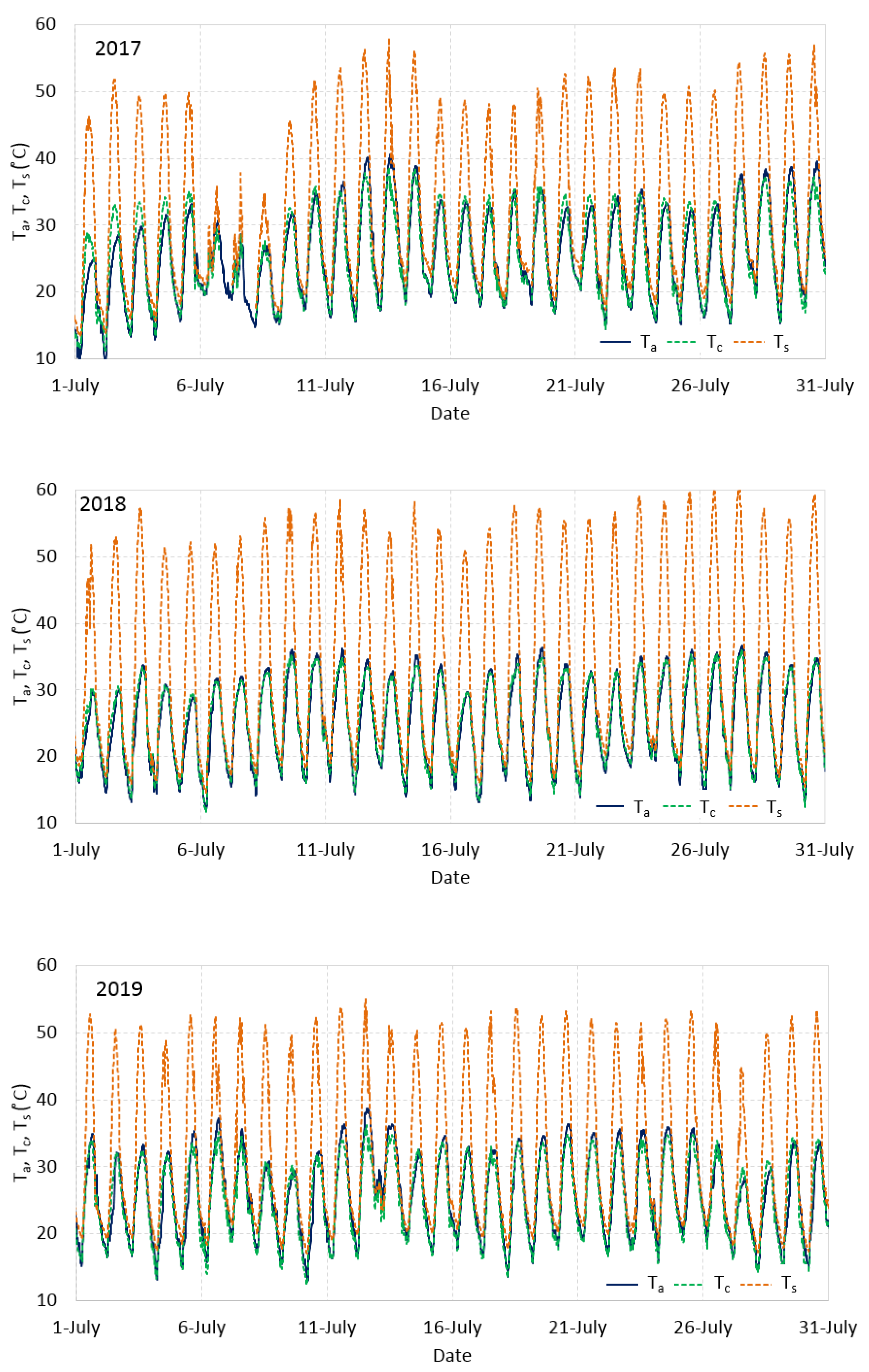
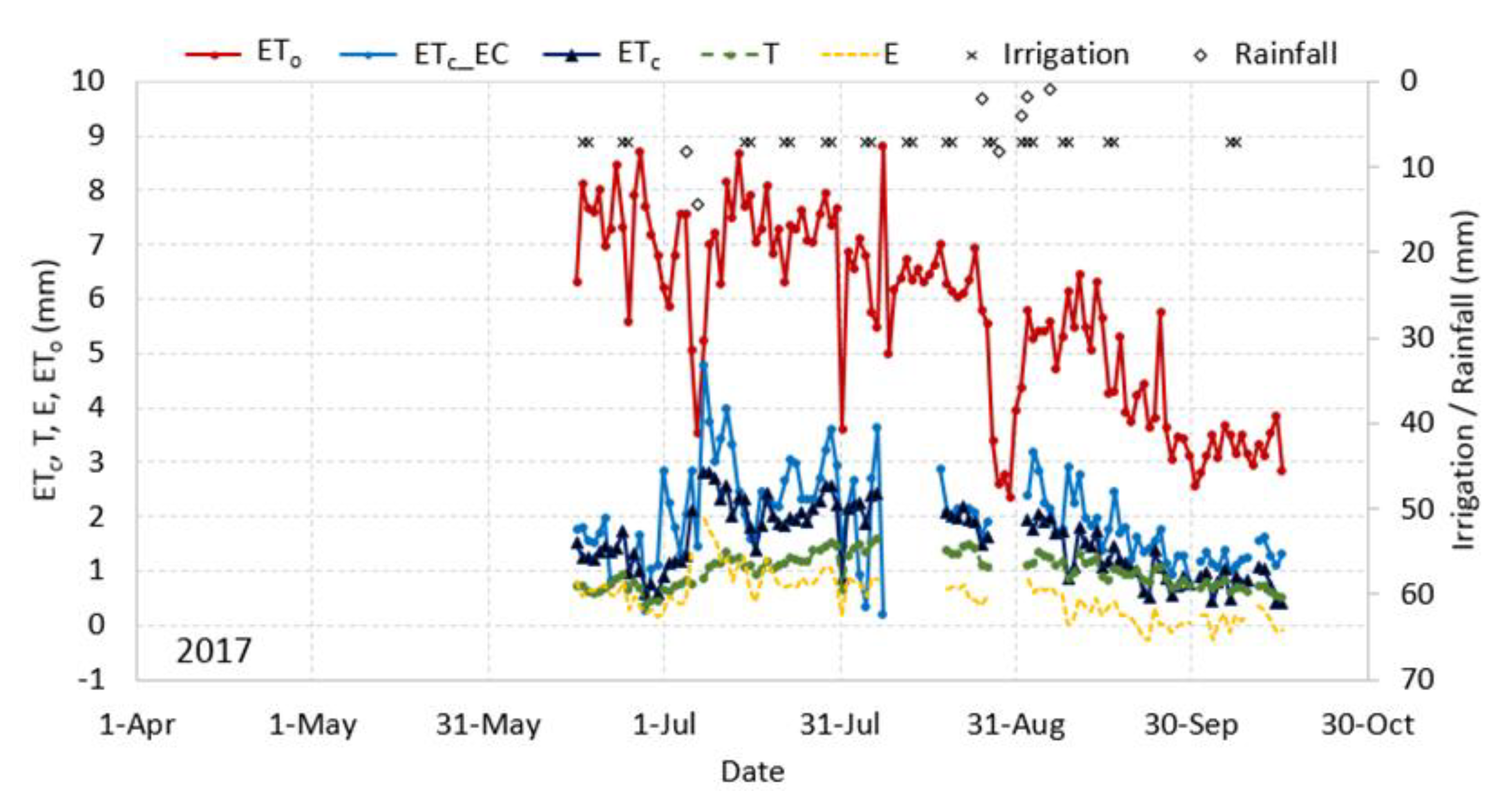
3.1. Weather Conditions and Reference Evapotranspiration
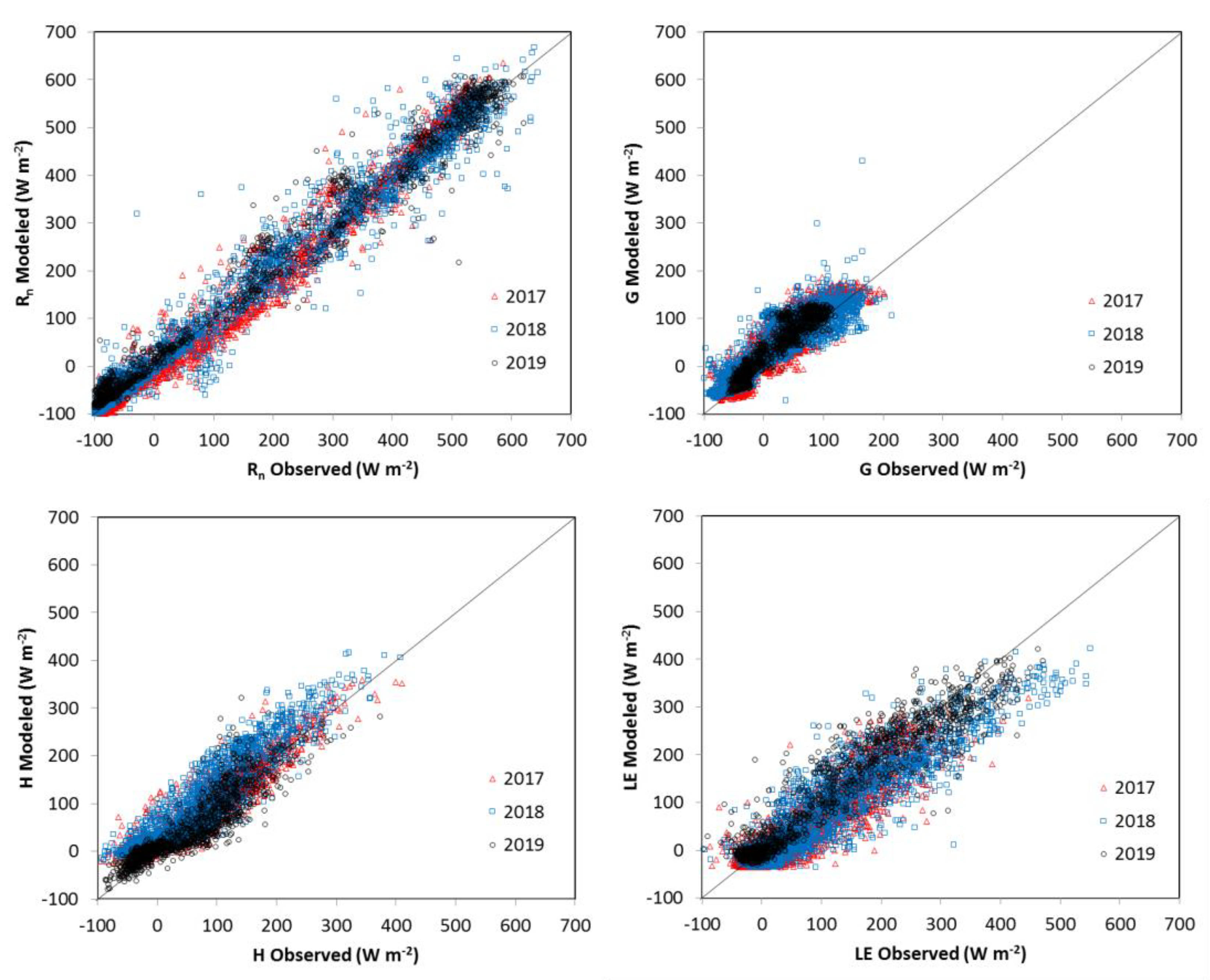
3.2. Energy Balance Closure
3.3. Assessment of the STSEB Model
| Model | Crop | N Days | LEi (W m−2) | Hourly ETc (mm h−1) | Daily ETc (mm d−1) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Bias | RMSE | Bias | RMSE | Bias | RMSE | ||||
| Kustas et al. [22] | TSEB | Cotton | 5 | 5 | 47 | - | - | - | - |
| Sánchez et al. [29] | STSEB | Maize | 50 | −6 | 51 | - | - | - | - |
| Sánchez et al. [51] | STSEB | Sorghum | 73 | - | - | −0.004 | 0.14 | −0.3 | 1.0 |
| Colaizzi et al. [27] | TSEB | Cotton | 170 | 5/−3 | 67/86 | - | - | 0.2/−0.1 | 0.6/1.1 |
| Sánchez et al. [52] | STSEB | Sunflower | 61 | - | - | 0.03 | 0.16 | 0.05 | 1.0 |
| Canola | 90 | - | - | 0.04 | 0.20 | 0.18 | 1.1 | ||
| Sánchez et al. [53] | STSEB | Wheat | 138 | - | - | −0.010 | 0.11 | −0.18 | 0.8 |
| Song et al. [31] | TSEB | Maize | 98 | 12/41 | 50/59 | - | - | 0.2/−0.6 | 0.4/0.7 |
| Cotton | 28 | −33/21 | 95/166 | - | - | - | - | ||
| Sánchez et al. [30] | STSEB | Vineyard | 288 | −10 | 53 | - | - | –0.04 | 0.6 |
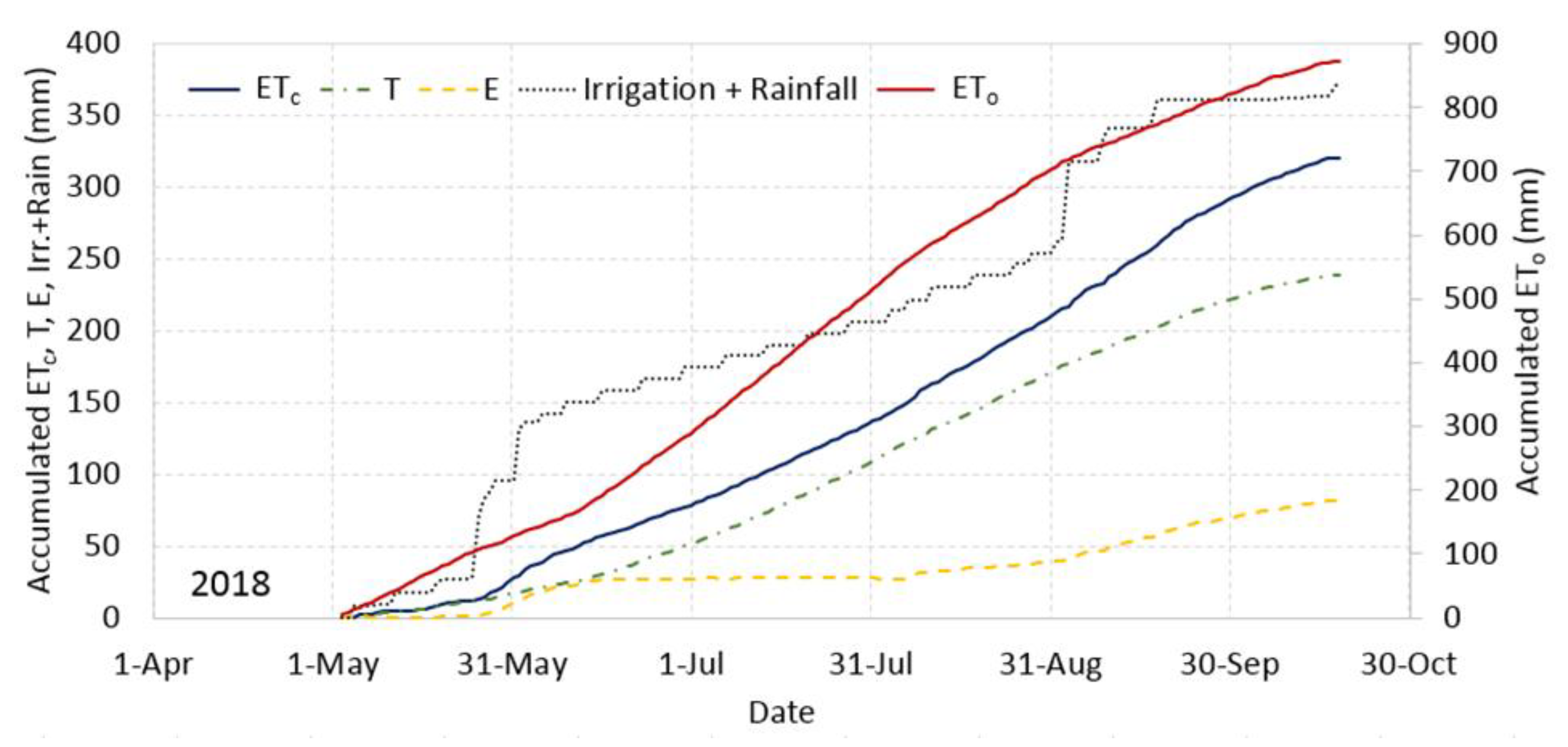
3.4. Crop Evapotranspiration Estimates
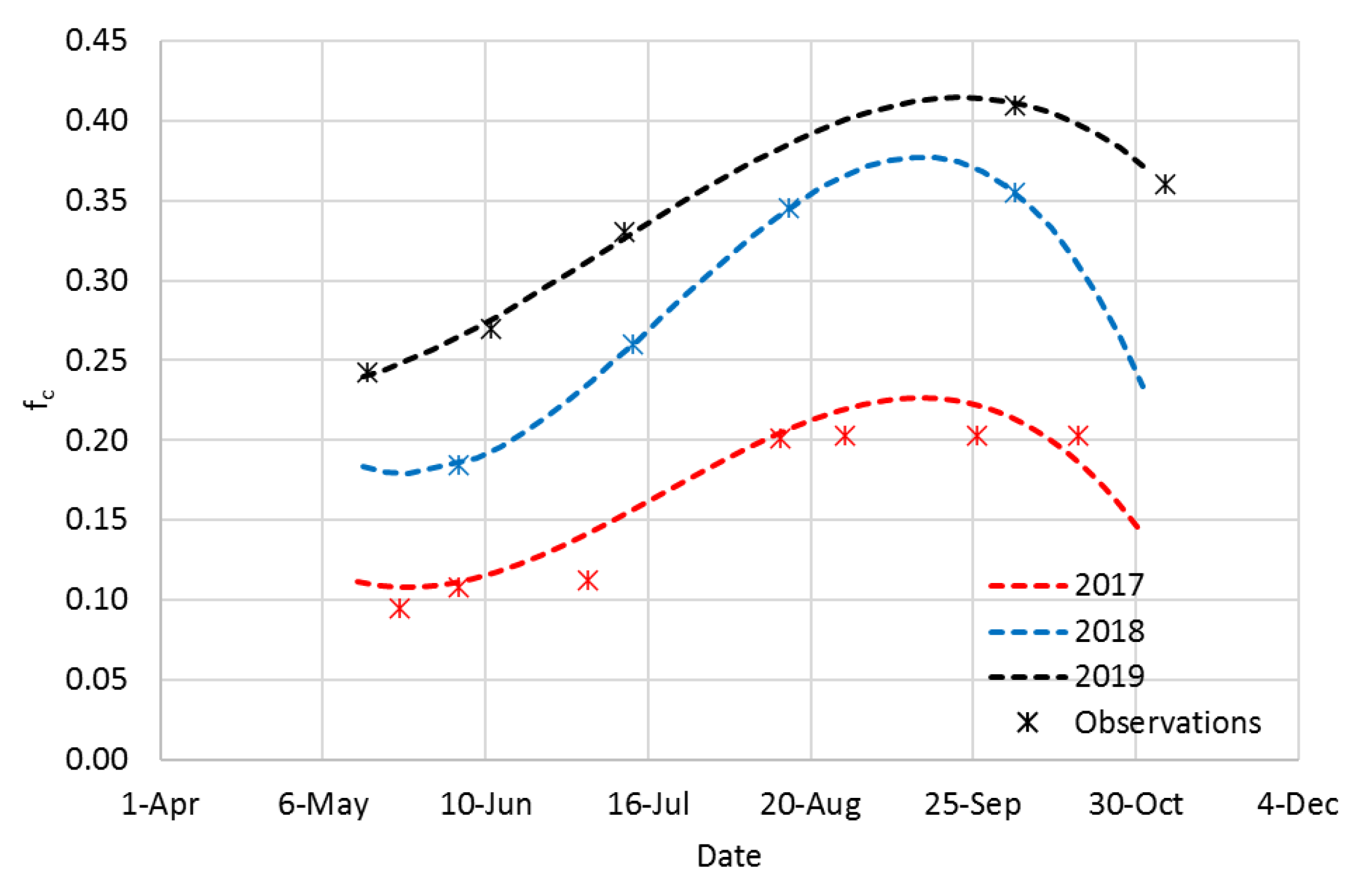
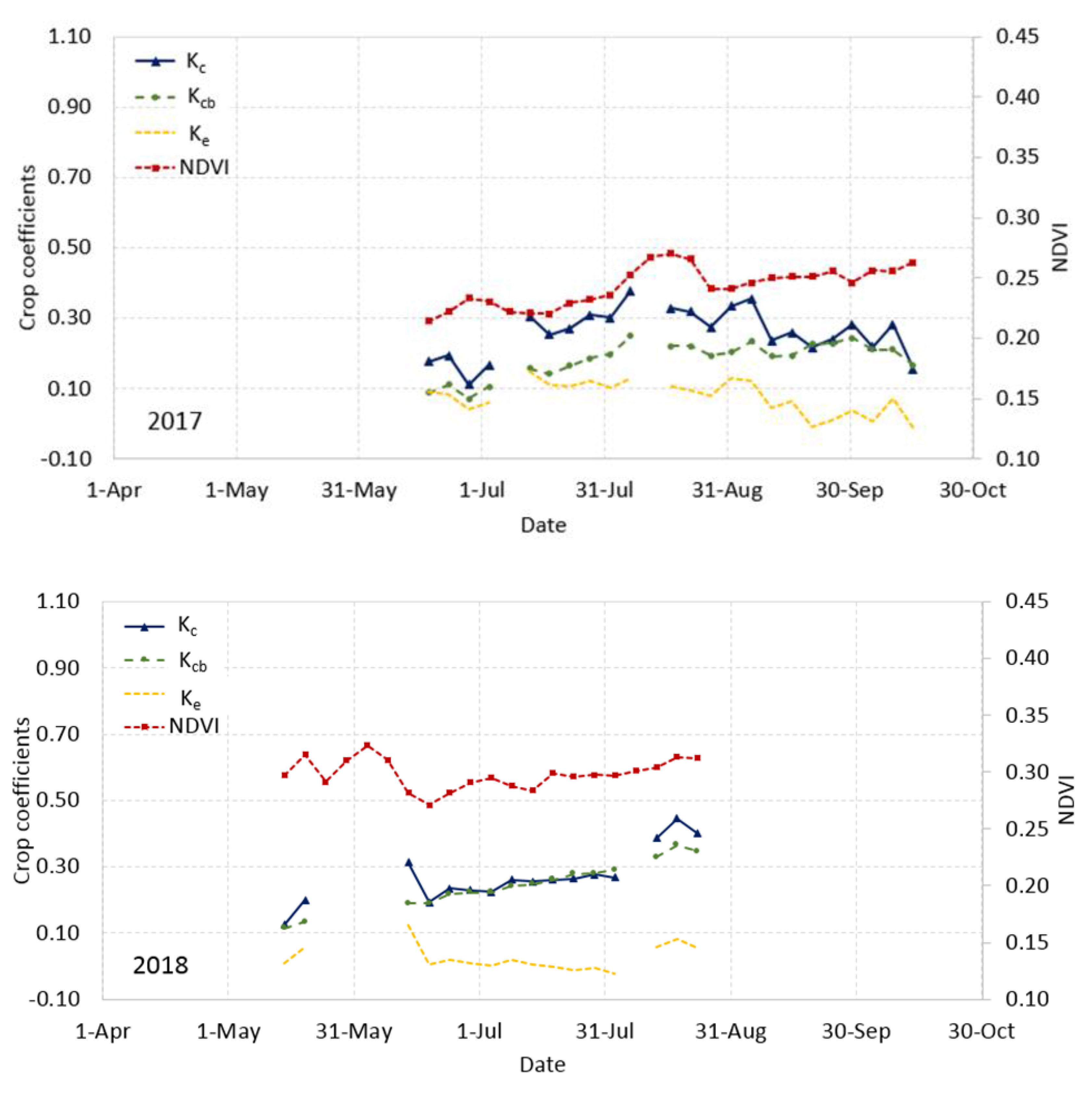
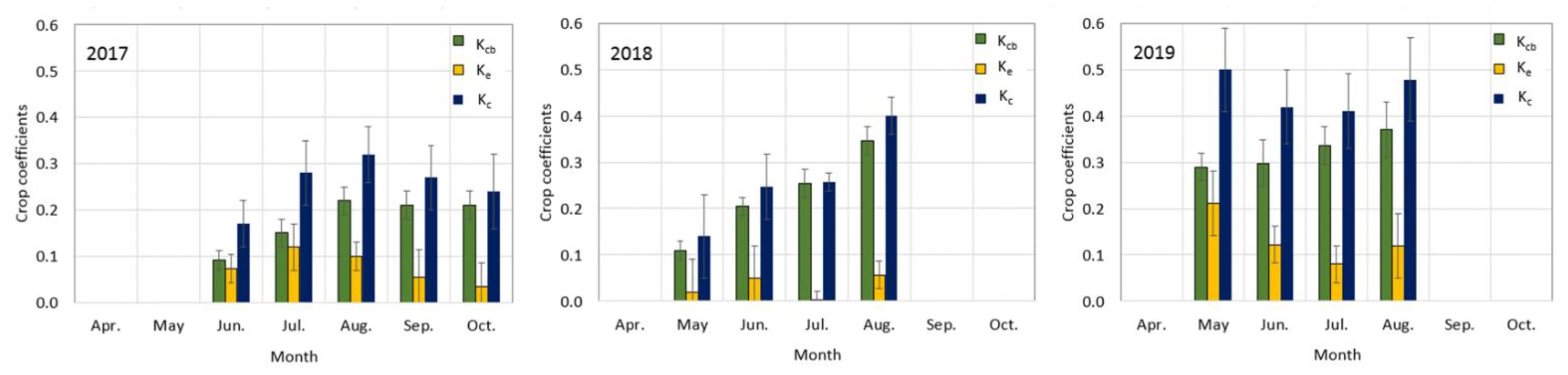
3.5. Crop Coefficients for Young Almond Trees
3.6. Relationships between Crop Coefficients and Biophysical Variables
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- FAOSTAT. FAO Statistical Database. 2018. Available online: http://www.fao.org/faostat/en/#data/QC (accessed on 26 October 2020).
- INC. International Nut & Dried Fruit. Nuts & Dried Fruits Statistical Yearbook 2019/2020. 2019. Available online: https://www.nutfruit.org/industry/statistics (accessed on 27 October 2020).
- MAPA. Anuario de Estadística Agraria. 2019. Available online: https://www.mapa.gob.es/es/estadistica/temas/publicaciones/anuario-de-estadistica/2019/ (accessed on 27 October 2020).
- Mañas, F.; López-Fuster, P.; López-Urrea, R. Effects of Different Regulated and Sustained Deficit Irrigation Strategies in Almond Production. Acta Hortic. 2014, 1028, 391–394. [Google Scholar] [CrossRef]
- IPCC. Summary for Policymakers. In Global Warming of 1.5 °C. An IPCC Special Report on the Impacts of Global Warming of 1.5 °C Above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; World Meteorological Organization: Geneva, Switzerland, 2018; p. 32. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration. Guidelines for Computing Crop Water Requirements, FAO Irrig. Drain. Paper 56; FAO: Rome, Italy, 1998; 300p. [Google Scholar]
- Pereira, L.S.; Paredes, P.; López-Urrea, R.; Hunsaker, D.J.; Mota, M.; Mohammadi Shad, Z. Standard single and basal crop coefficients for vegetable crops, an update of FAO56 crop water requirements approach. Agric. Water Manag. 2021, 243. [Google Scholar] [CrossRef]
- Pereira, L.S.; Paredes, P.; Hunsaker, D.J.; López-Urrea, R.; Mohammadi Shad, Z. Standard single and basal crop coefficients for field crops. Updates and advances to the FAO56 crop water requirements method. Agric. Water Manag. 2021, 243, 106466. [Google Scholar] [CrossRef]
- Bellvert, J.; Adeline, K.; Baram, S.; Pierce, L.; Sanden, B.L.; Smart, D.R. Monitoring crop evapotranspiration and crop coefficients over an almond and pistachio orchard throughout remote sensing. Remote Sens. 2018, 10, 2001. [Google Scholar] [CrossRef] [Green Version]
- Rallo, G.; Paço, T.; Paredes, P.; Puig, A.; Provenzano, G.; Massai, R.; Pereira, L.S. Updated single and dual crop coefficients for trees and vine crops. Agric. Water Manag. 2021, 250, 106645. [Google Scholar] [CrossRef]
- Espadafor, M.; Orgaz, F.; Testi, L.; Lorite, I.J.; Villalobos, F.J. Transpiration of young almond trees in relation to intercepted radiation. Irrig. Sci. 2015, 33, 265–275. [Google Scholar] [CrossRef] [Green Version]
- García-Tejero, I.F.; Hernández, A.; Rodríguez, V.M.; Ponce, J.R.; Ramos, V.; Muriel, J.L.; Durán-Zuazo, V.H. Estimating almond crop coefficients and physiological response to water stress in semiarid environments (SW Spain). J. Agric. Sci. Technol. 2015, 17, 1255–1266. [Google Scholar]
- López-Urrea, R.; Simón, L.L.; Sánchez, J.M.; Martínez, L.; Valentín, F. Surface energy flux measurements over a drip-irrigated young almond orchard. Acta Hortic. 2021, in press. [Google Scholar]
- Goldhamer, D.A.; Girona, J. Almond. Crop Yield Response to Water. Irrigation and Drainage; Steduto, P., Hsiao, T.C., Fereres, E., Raes, D., Eds.; Paper no. 66; FAO: Rome, Italy, 2012. [Google Scholar]
- Fereres, E.; Puech, I. Irrigation Scheduling Guide; A Reference Manual Containing 11 Sections on Irrigation Scheduling; California Department of Water Resources, Office of Water Conservation: Sacramento, CA, USA, 1981; 307p.
- Girona, J. La respuesta del cultivo del almendro al riego. Vida Rural. 2006, 234, 12–16. [Google Scholar]
- Sanden, B. Fall Irrigation Management in a Drought Year for Almonds, Pistachios and Citrus. Kern Soil and Water Newsletter, September 2007; University of California Cooperative Extension: Kern County, CA, USA, 2007; Available online: http://cekern.ucdavis.edu/files/64007.pdf (accessed on 28 July 2021).
- Stevens, R.M.; Ewenz, C.M.; Grigson, G.; Conner, S.M. Water use by an irrigated almond orchard. Irrig. Sci. 2012, 30, 189–200. [Google Scholar] [CrossRef]
- López-López, M.; Espadafor, M.; Testi, L.; Lorite, I.J.; Orgaz, F.; Fereres, E. Water requirements of mature almond trees in response to atmospheric demand. Irrig. Sci. 2018, 36, 271–280. [Google Scholar] [CrossRef]
- Kustas, W.P. Estimates of evapotranspiration with a one- and two-layer model of heat transfer over partial canopy cover. J. Appl. Meteorol. 1990, 29, 704–715. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.; Humes, K. A two-source approach for estimating soil and vegetation energy fluxes from observations of directional radiometric surface temperature. Agric. For. Meteorol. 1995, 77, 263–293. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Evaluation of soil and vegetation heat flux predictions using a simple two-source model with radiometric temperatures for partial canopy cover. Agric. For. Meteorol. 1999, 94, 13–29. [Google Scholar] [CrossRef]
- Su, H.; McCabe, M.F.; Wood, E.F.; Su, Z.; Prueger, J.H. Modeling evapotranspiration during SMACEX: Comparing two approaches for local- and regional-scale prediction. J. Hydrometeorol. 2005, 6, 910–922. [Google Scholar] [CrossRef]
- French, A.N.; Jacob, F.; Anderson, M.C.; Kustas, W.P.; Timmermans, W.; Gieske, A. Surface energy fluxes with the Advanced Spaceborne Thermal Emission and Reflection radiometer (ASTER) at the Iowa 2002 SMACEX site (USA). Remote Sens. Environ. 2005, 99, 55–65. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1 Model formulation. J. Geophys. Res. 2007, 112, D10117. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Colaizzi, P.; Kustas, W.P.; Anderson, M.C.; Agam, N.; Tolk, J.A.; Evett, S.R.; Howel, T.A.; Gowda, P.H.; O’Shaughnessy, S.A. Two-source energy balance model estimates of evapotranspiration using component and composite surface temperatures. Adv. Water Res. 2012, 50, 134–151. [Google Scholar] [CrossRef] [Green Version]
- Tang, R.; Li, Z.L. An end-member-based two-source approach for estimating land surface evapotranspiration from remote sensing data. IEEE Trans. Geosci. Remote. Sens. 2017, 55, 5818–5832. [Google Scholar] [CrossRef]
- Sánchez, J.M.; Kustas, W.P.; Caselles, V.; Anderson, M. Modelling surface energy fluxes over maize using a two-source patch model and radiometric soil and canopy temperature observations. Remote Sens. Environ. 2008, 112, 1130–1143. [Google Scholar] [CrossRef]
- Sánchez, J.M.; López-Urrea, R.; Valentín, F.; Caselles, V.; Galve, J.M. Lysimeter assessment of the Simplified Two-Source Energy Balance model and eddy covariance system to estimate vineyard evapotranspiration. Agric. For. Meteorol. 2019, 274, 172–183. [Google Scholar] [CrossRef]
- Song, L.; Kustas, W.P.; Liu, S.; Colaizzi, P.D.; Nieto, H.; Xu, Z.; Ma, Y.; Mingsong, L.; Xu, T.; Agam, N.; et al. Applications of a thermal-based two-source energy balance model using Priestley-Taylor approach for surface temperature partitioning under advective conditions. J. Hydrol. 2016, 540, 574–587. [Google Scholar] [CrossRef] [Green Version]
- Valentín, F.; Nortes, P.A.; Domínguez, A.; Sánchez, J.M.; Intrigliolo, D.S.; Alarcón, J.J.; López-Urrea, R. Comparing evapotranspiration and yield performance of maize under sprinkler, superficial and subsurface drip irrigation in a semi-arid environment. Irrig. Sci. 2020, 38, 105–115. [Google Scholar] [CrossRef]
- Soil Survey Staff. Keys to Soil Taxonomy, 12th ed.; USDA-Natural Resources Conservation Service: Washington, DC, USA, 2014.
- Fereres, E.; Goldhamer, D.; Sadras, V. Yield response to water of fruit trees and vines: Guidelines. In Crop Yield Response to Water. Irrigation and Drainage; Steduto, P., Hsiao, T.C., Fereres, E., Raes, D., Eds.; Paper no. 66; FAO: Rome, Italy, 2012; pp. 246–295. [Google Scholar]
- López-Urrea, R.; Martín de Santa Olalla, F.; Fabeiro, C.; Moratalla, A. Testing evapotranspiration equations using lysimeter observations in a semiarid climate. Agric. Water Manag. 2006, 85, 15–26. [Google Scholar] [CrossRef]
- Trigo, I.F.; de Bruin, H.; Beyrich, F.; Bosveld, F.C.; Gavilán, P.; Groh, J.; López-Urrea, R. Validation of reference evapotranspiration from Meteosat Second Generation (MSG) observations. Agric. For. Meteorol. 2018, 259, 271–285. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple parameterization for flux footprint predictions. Bound. Layer Meteorol. 2004, 112, 503–523. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. Forest Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef] [Green Version]
- Choudhury, B.J.; Idso, S.B.; Reginato, R.J. Analysis of an empirical model for soil heat flux under a growing wheat crop for estimating evaporation by an infrared-temperature based energy balance equation. Agric. For. Meteorol. 1987, 39, 283–297. [Google Scholar] [CrossRef]
- Friedl, M.A. Relationships among remotely sensed data, surface energy balance, and area-averaged fluxes over partially vegetated land surfaces. J. Appl. Meteor. 1996, 35, 2091–2103. [Google Scholar] [CrossRef]
- Sánchez, J.M.; French, A.N.; Mira, M.; Hunsaker, D.J.; Thorp, K.R.; Valor, E.; Caselles, V. Thermal Infrared Emissivity Dependence on Soil Moisture in Field Conditions. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4652–4659. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef] [Green Version]
- Garrido-Rubio, J.; González-Piqueras, J.; Campos, I.; Osann, A.; González-Gómez, L.; Calera, A. Remote sensing–based soil water balance for irrigation water accounting at plot and water user association management scale. Agric. Water Manag. 2020, 238, 106236. [Google Scholar] [CrossRef]
- Calera, A.; Campos, I.; Osann, A.; D’Urso, G.; Menenti, M. Remote sensing for crop water management: From ET modelling to services for the end users. Sensors 2017, 17, 1104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pôças, I.; Calera, A.; Campos, I.; Cunha, M. Remote sensing for estimating and mapping single and basal crop coefficients: A review on spectral vegetation indices approaches. Agric. Water Manag. 2020, 233, 106081. [Google Scholar] [CrossRef]
- Campos, I.; Neale, C.M.U.; Calera, A.; Balbontín, C.; González-Piqueras, J. Assessing satellite-based basal crop coefficients for irrigated grapes (Vitis vinifera L.). Agric. Water Manag. 2010, 98, 45–54. [Google Scholar] [CrossRef]
- Campos, I.; Villodre, J.; Carrara, A.; Calera, A. Remote sensing-based soil water balance to estimate Mediterranean holm oak savanna (dehesa) evapotranspiration under water stress conditions. J. Hydrol. 2013, 494, 1–9. [Google Scholar] [CrossRef]
- Wilson, K.B.; Hanson, P.J.; Mulholland, P.J.; Baldocchi, D.D.; Wullschleger, S.D. A comparison of methods for determining forest evapotranspiration and its components: Sap-flow, soil water budget, eddy covariance and catchment water balance. Agric. Forest Meteorol. 2002, 106, 153–168. [Google Scholar] [CrossRef]
- Kustas, W.P.; Alfieri, J.G.-P.; Evett, S.; Agam, N. Quantifying variability in field-scale evapotranspiration measurements in an irrigated agricultural region under advection. Irrig. Sci. 2015, 33, 325–338. [Google Scholar] [CrossRef]
- Xue, J.; Bali, K.M.; Light, S.; Hessels, T.; Kisekka, I. Evaluation of remote sensing-based evapotranspiration models against surface renewal in almonds, tomatoes and maize. Agric. Water Manag. 2020, 238, 106228. [Google Scholar] [CrossRef]
- Sánchez, J.M.; López-Urrea, R.; Rubio, E.; Caselles, V. Determining water use of sorghum from two-source energy balance and radiometric temperatures. Hydrol. Earth Syst. Sci. 2011, 15, 3061–3070. [Google Scholar] [CrossRef] [Green Version]
- Sánchez, J.M.; López-Urrea, R.; Rubio, E.; González-Piqueras, J.; Caselles, V. Assessing crop coefficients of sunflower and canola using two-source energy balance and thermal radiometry. Agric. Water Manag. 2014, 137, 23–29. [Google Scholar] [CrossRef]
- Sánchez, J.M.; López-Urrea, R.; Doña, C.; Caselles, V.; González-Piqueras, J.; Niclós, R. Modeling evapotranspiration in a spring wheat from termal radiometry: Crop coefficients and E/T partitioning. Irrig. Sci. 2015, 33, 399–410. [Google Scholar] [CrossRef]
- Golhamer, D.A.; Fereres, E. Establishing an almond water production function for California using long-term yield response to variable irrigation. Irrig. Sci. 2017, 35, 169–179. [Google Scholar] [CrossRef]
- López-López, M.; Espadafor, M.; Testi, L.; Lorite, I.J.; Orgaz, F.; Fereres, E. Yield response of almond trees to transpiration deficits. Irrig. Sci. 2018, 36, 111–120. [Google Scholar] [CrossRef]
- Er-Raki, S.; Rodriguez, J.C.; Garatuza-Payan, J.; Watts, C.J.; Chehbouni, A. Determination of crop evapotranspiration of table grapes in a semi-arid region of Northwest Mexico using multi-spectral vegetation index. Agric. Water Manag. 2013, 122, 12–19. [Google Scholar] [CrossRef]
- Odi-Lara, M.; Campos, I.; Neale, C.M.U.; Ortega-Farías, S.; Poblete-Echeverría, C.; Balbontín, C.; Calera, A. Estimating evapotranspiration of an apple orchard using a remote sensing-based soil water balance. Remote Sens. 2016, 8, 253. [Google Scholar] [CrossRef] [Green Version]
- Johnson, L.F.; Trout, T.J. Satellite NDVI Assisted monitoring of vegetable crop evapotranspiration in California’s San Joaquin Valley. Remote Sens. 2012, 4, 439–455. [Google Scholar] [CrossRef] [Green Version]





| Ta mean | RHmin | u2 | S | Rainfall * | ETo | |
|---|---|---|---|---|---|---|
| (°C) | (%) | (m s−1) | (MJ m−2 d−1) | (mm) | (mm d−1) | |
| 2017 | ||||||
| March | 9.5 (9.3) | 40.1 | 3.1 | 18.1 | 60.0 (26.6) | 2.8 |
| April | 12.2 (11.6) | 34.2 | 2.7 | 22.3 | 22.3 (39.3) | 3.8 |
| May | 16.7 (15.6) | 28.6 | 2.7 | 26.1 | 8.9 (40.8) | 5.3 |
| June | 22.9 (21.0) | 20.7 | 2.9 | 29.0 | 0.0 (24.4) | 6.4 |
| July | 24.2 (24.6) | 19.5 | 2.4 | 27.7 | 25.4 (7.0) | 7.0 |
| August | 23.7 (24.2) | 25.5 | 2.5 | 23.3 | 6.1 (9.7) | 5.8 |
| September | 19.3 (19.2) | 24.4 | 2.4 | 20.7 | 1.2 (32.4) | 4.8 |
| October | 15.6 (14.3) | 32.7 | 1.7 | 14.7 | 8.4 (32.6) | 2.6 |
| November | 8.2 (8.6) | 33.6 | 2.1 | 10.5 | 10.7 (32.8) | 1.5 |
| 2018 | ||||||
| March | 8.2 (9.3) | 47.9 | 5.4 | 15.2 | 63.5 (26.6) | 2.5 |
| April | 11.5 (11.6) | 40.0 | 3.7 | 19.7 | 19.9 (39.3) | 3.4 |
| May | 14.6 (15.6) | 35.6 | 2.4 | 24.7 | 64.0 (40.8) | 4.3 |
| June | 19.6 (21.0) | 33.2 | 2.4 | 25.3 | 46.4 (24.4) | 5.3 |
| July | 24.1 (24.6) | 16.1 | 2.5 | 28.7 | 0.0 (7.0) | 7.3 |
| August | 24.4 (24.2) | 24.7 | 2.6 | 24.0 | 15.3 (9.7) | 6.3 |
| September | 20.3 (19.2) | 37.7 | 2.0 | 18.7 | 99.3 (32.4) | 3.9 |
| October | 13.4 (14.3) | 42.9 | 2.4 | 13.3 | 23.3 (32.6) | 2.5 |
| November | 9.1 (8.6) | 63.2 | 3.1 | 8.1 | 69.2 (32.8) | 1.2 |
| 2019 | ||||||
| March | 9.3 (9.3) | 29.9 | 2.6 | 18.8 | 18.0 (26.6) | 3.0 |
| April | 10.5 (11.6) | 44.8 | 3.5 | 18.5 | 123.7 (39.3) | 3.0 |
| May | 16.0 (15.6) | 29.1 | 2.7 | 26.4 | 16.3 (40.8) | 4.9 |
| June | 20.5 (21.0) | 20.4 | 2.8 | 29.2 | 0.0 (24.4) | 6.7 |
| July | 24.7 (24.6) | 20.6 | 2.8 | 27.5 | 0.0 (7.0) | 7.4 |
| August | 23.7 (24.2) | 21.6 | 2.2 | 24.5 | 17.5 (9.7) | 6.2 |
| September | 19.6 (19.2) | 37.5 | 2.6 | 17.4 | 38.3 (32.4) | 4.0 |
| October | 15.0 (14.3) | 38.8 | 2.4 | 13.9 | 18.9 (32.6) | 3.1 |
| November | 9.2 (8.6) | 56.4 | 5.0 | 8.8 | 38.5 (32.8) | 1.8 |
| Year (N) | Slope | Intercept (W m−2) | r2 | Bias (W m−2) | RMSE * (W m−2) | |
|---|---|---|---|---|---|---|
| 2017 (2526) | Rn | 1.03 | −7 | 0.975 | −4 | 34 |
| G | 1.03 | 14 | 0.834 | 15 | 31 | |
| H | 0.87 | 20 | 0.892 | 13 | 29 | |
| LE | 0.82 | −10 | 0.828 | −22 | 44 | |
| 2018 (3675) | Rn | 0.98 | 5 | 0.975 | 2 | 36 |
| G | 0.80 | 15 | 0.815 | 14 | 32 | |
| H | 0.99 | 24 | 0.872 | 24 | 37 | |
| LE | 0.79 | −7 | 0.871 | −23 | 48 | |
| 2019 (1568) | Rn | 0.98 | 16 | 0.982 | 13 | 35 |
| G | 1.12 | 15 | 0.890 | 16 | 25 | |
| H | 0.83 | 7 | 0.827 | 1 | 31 | |
| LE | 0.88 | 14 | 0.915 | 3 | 40 |
| N | Slope | Intercept (mm d−1) | r2 | Bias (mm d−1) | RMSE (mm d−1) | |
|---|---|---|---|---|---|---|
| 2017 | 154 | 0.75 (0.50) | −0.07 (0.3) | 0.829 (0.500) | −0.5 (−0.5) | 0.6 (0.9) |
| 2018 | 161 | 0.71 (0.62) | 0.02 (0.3) | 0.775 (0.581) | −0.7 (−0.6) | 0.9 (1.0) |
| 2019 | 80 | 0.89 (0.69) | 0.4 (0.6) | 0.840 (0.725) | 0.08 (−0.3) | 0.4 (0.7) |
| N | ETc | T | E | Kc | Kcb | Ke | |
|---|---|---|---|---|---|---|---|
| (mm d−1) | (mm d−1) | (mm d−1) | |||||
| 2017 | |||||||
| May | - | - | - | - | - | - | - |
| June | 15 | 1.18 | 0.66 | 0.53 | 0.17 | 0.09 | 0.07 |
| July | 29 | 2.01 | 1.10 | 0.92 | 0.28 | 0.15 | 0.12 |
| August | 20 | 1.96 | 1.32 | 0.64 | 0.32 | 0.22 | 0.10 |
| September | 28 | 1.27 | 1.01 | 0.26 | 0.27 | 0.21 | 0.05 |
| October | 14 | 0.77 | 0.68 | 0.09 | 0.24 | 0.21 | 0.03 |
| 2018 | |||||||
| May | 22 | 0.53 | 0.49 | 0.04 | 0.14 | 0.11 | 0.02 |
| June | 20 | 1.51 | 1.25 | 0.26 | 0.25 | 0.20 | 0.05 |
| July | 30 | 1.87 | 1.85 | 0.02 | 0.26 | 0.25 | 0.00 |
| August | 17 | 2.33 | 2.01 | 0.33 | 0.40 | 0.35 | 0.06 |
| September | - | - | - | - | - | - | - |
| October | - | - | - | - | - | - | - |
| 2019 | |||||||
| May | 25 | 2.5 | 1.44 | 1.07 | 0.5 | 0.29 | 0.21 |
| June | 29 | 2.82 | 2.00 | 0.82 | 0.42 | 0.3 | 0.12 |
| July | 30 | 3.03 | 2.48 | 0.55 | 0.41 | 0.34 | 0.08 |
| August | 19 | 3.33 | 2.54 | 0.78 | 0.48 | 0.37 | 0.12 |
| September | - | - | - | - | - | - | - |
| October | - | - | - | - | - | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez, J.M.; Simón, L.; González-Piqueras, J.; Montoya, F.; López-Urrea, R. Monitoring Crop Evapotranspiration and Transpiration/Evaporation Partitioning in a Drip-Irrigated Young Almond Orchard Applying a Two-Source Surface Energy Balance Model. Water 2021, 13, 2073. https://doi.org/10.3390/w13152073
Sánchez JM, Simón L, González-Piqueras J, Montoya F, López-Urrea R. Monitoring Crop Evapotranspiration and Transpiration/Evaporation Partitioning in a Drip-Irrigated Young Almond Orchard Applying a Two-Source Surface Energy Balance Model. Water. 2021; 13(15):2073. https://doi.org/10.3390/w13152073
Chicago/Turabian StyleSánchez, Juan M., Llanos Simón, José González-Piqueras, Francisco Montoya, and Ramón López-Urrea. 2021. "Monitoring Crop Evapotranspiration and Transpiration/Evaporation Partitioning in a Drip-Irrigated Young Almond Orchard Applying a Two-Source Surface Energy Balance Model" Water 13, no. 15: 2073. https://doi.org/10.3390/w13152073
APA StyleSánchez, J. M., Simón, L., González-Piqueras, J., Montoya, F., & López-Urrea, R. (2021). Monitoring Crop Evapotranspiration and Transpiration/Evaporation Partitioning in a Drip-Irrigated Young Almond Orchard Applying a Two-Source Surface Energy Balance Model. Water, 13(15), 2073. https://doi.org/10.3390/w13152073







