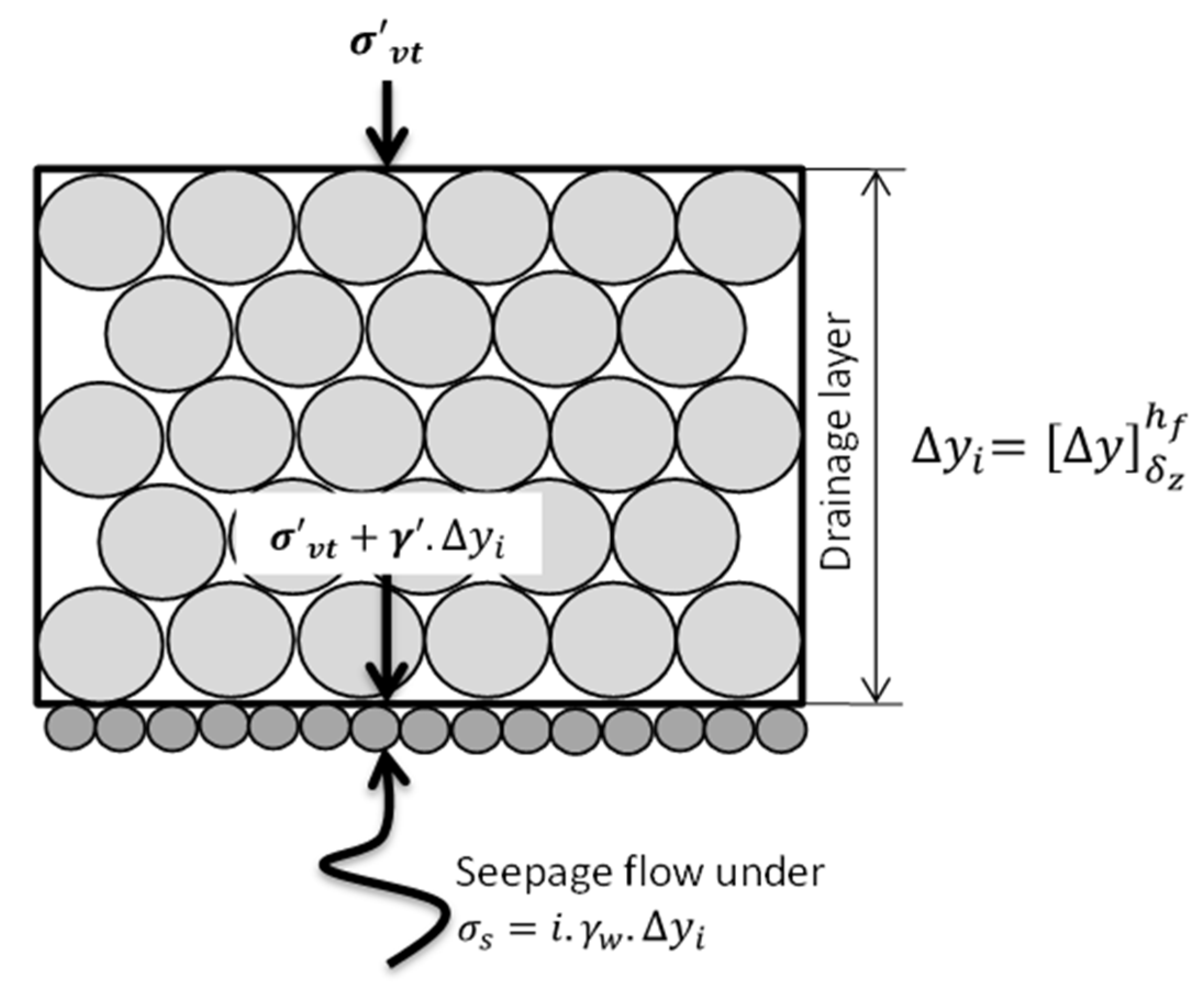
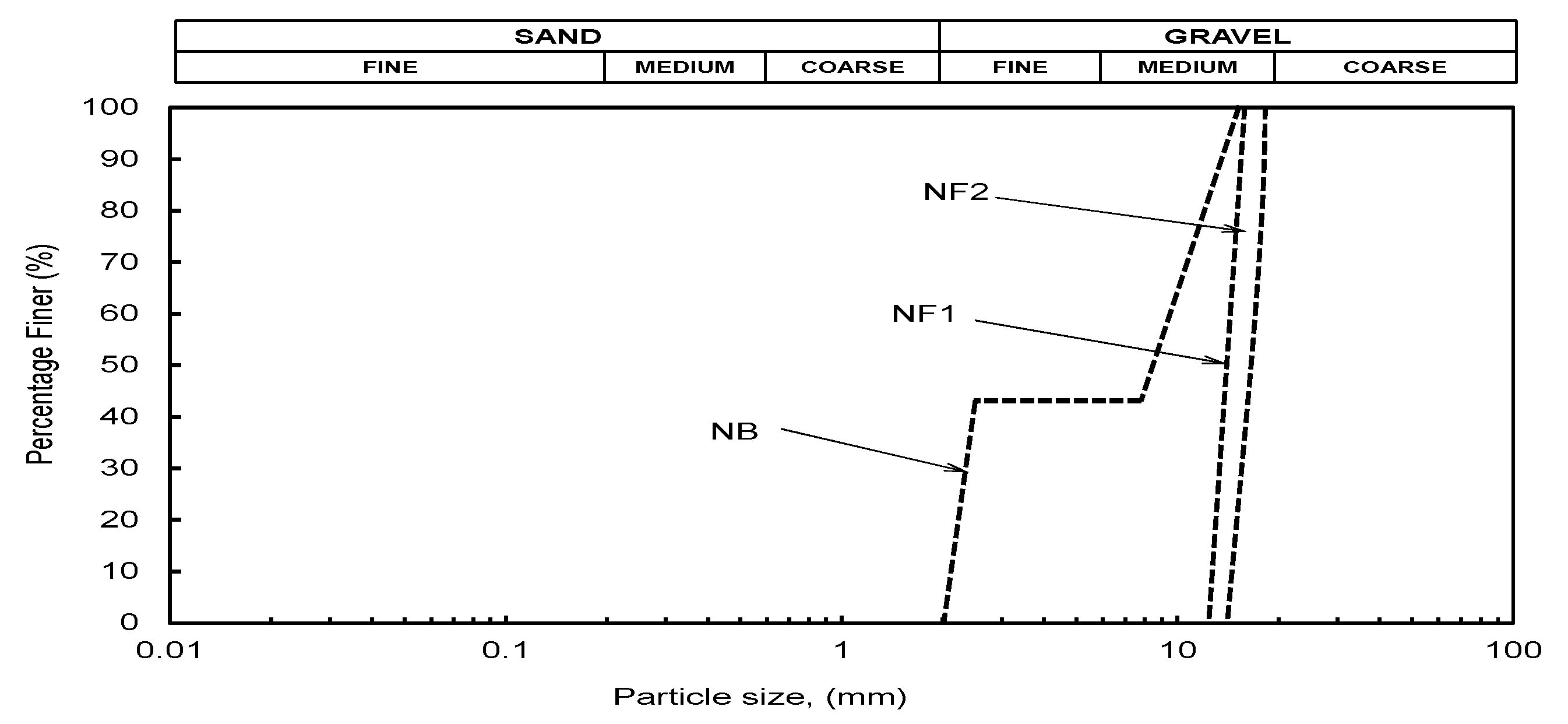
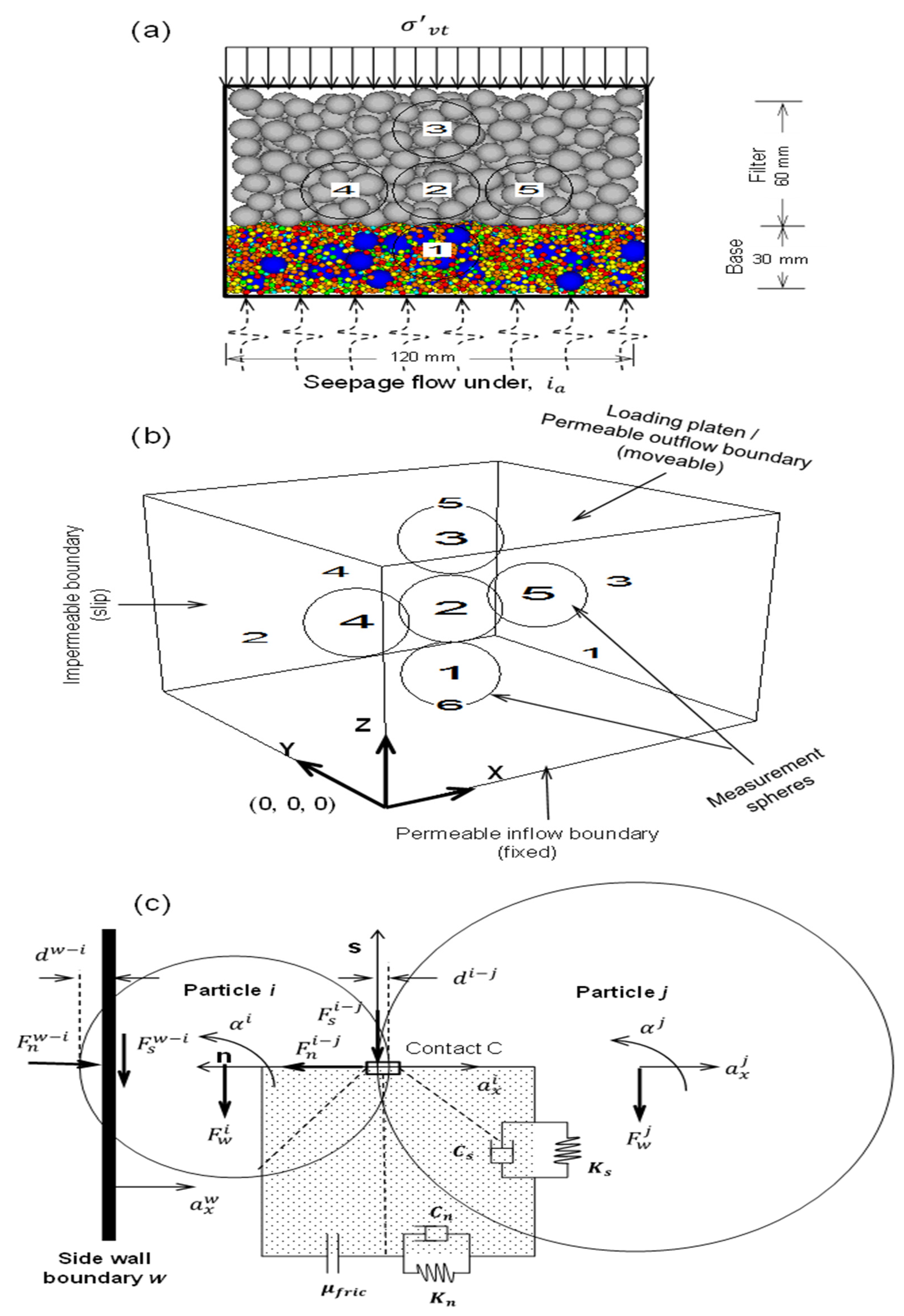
1. Introduction
In practice, granular filters are installed to protect base soils such as dam cores and subgrades from erosion. Recent advances in geotechnical practices have generated an interest in applying granular filters in geo-environmental and transportation engineering [
1,
2,
3], where filtration occurs in the presence of static and cyclic mechanical loading, e.g., railways and highway filters. Unlike large upstream heads in hydropower dams, the hydraulic excitation in railway sub-structures mainly stems from the development of pore pressure at the interface between natural and engineered fills. The filters within these structures function under complex stress states, which significantly influence the erosion-capture mechanism of fine particles such as base soil migration, suffusion, and internal erosion [
4,
5]. Thus far, various researchers have studied these processes and proposed numerous concepts and definitions of governing threshold hydraulic gradients, e.g., the critical hydraulic gradient for piping [
6,
7], segregation piping [
8], complete erosion of base soil through filters [
9,
10], and suffusion or washout failure in granular soils [
11,
12,
13]. The erosion of base soils may occasionally favor the development of self-filtering layers that helps prevent any further erosion and increases the longevity of filters. However, the strong upward seepage could incur significant structural instabilities in the forms of piping, suffusion, and heave development. Alternatively, the reduction in permeability due to base soil eroding into the overlying filter layers would result in progressive clogging, especially under cyclic loading conditions [
14].
In this study, the results of filtration tests simulated using a coupled CFD-DEM model are reported, based on which we propose a semi-empirical model governing the migration of base particles into loaded filters to quantify filter effectiveness in retaining base particles while avoiding piping. Following its development, the proposed model is compared with the existing theories, and the results are presented. The results of numerical simulations from the current study plus those adopted from published DEM studies on the topic are used to validate the proposed model. Notably, this study focuses on the analysis of loaded granular filters subject to one-dimensional upward seepage and the erosion of base particles from the horizontal interface between base and filter layers, e.g., drainage layers in transportation embankments (sub-ballast and subbase) and inverted filters at the downstream of embankment dams. The scales of the laboratory and numerical simulations reported here are not comparable with the practical dimensions of the field problems, and this is always a limitation in the modeling of most geotechnical processes.
3. Results and Discussion
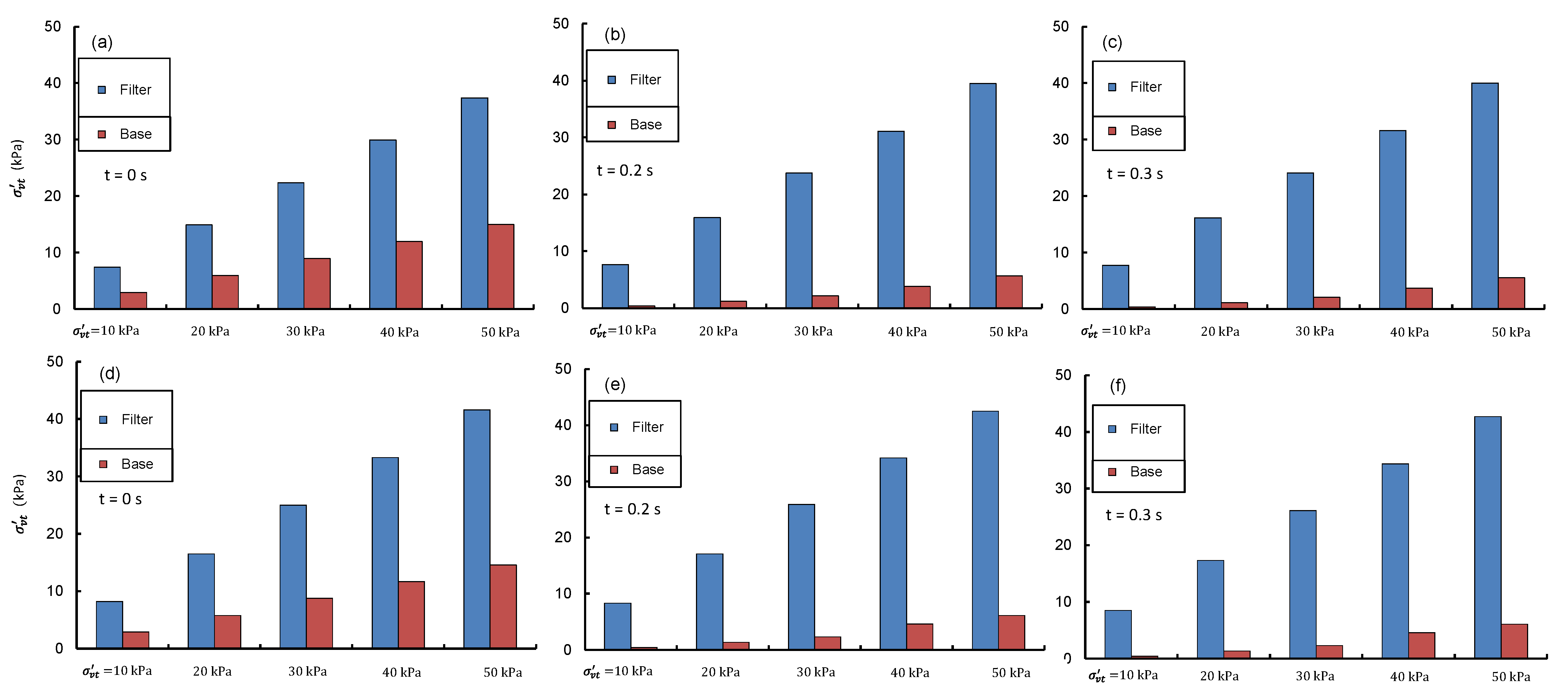
Figure 3 shows the initial and final effective stress magnitudes in the base and filter at simulation times
t = 0, 0.2, and 0.3 s. The base soil exhibited significant stress reduction due to seepage that could eventually neutralize to approximately zero (i.e., piping) for the cases with
≤ 30 kPa. This observation endorsed the previous experimental observations that a relatively higher magnitude of seepage stress would be required to induce any disturbance to the base soil (e.g., piping) when a greater magnitude of
is applied on the upper filter layer. Notably, the stress distributions in base and filter soils for both samples NF1-NB and NF2-NB almost remained unchanged when the simulation time increased from 0.2 to 0.3 s. This clearly depicts that a simulation time of 0.2 s would be sufficient, beyond which the stress conditions become steady.
Figure 4 shows the contact force
fc distributions for specimen NF1-NB when subjected to
= 10–50 kPa. The initial contact force,
fc, and hence the contact stress
distribution within the filter layer is almost uniform for the given
, but it is reduced significantly inside the base soil layer, although there too it remained uniform. This substantial
reduction during transfer from the filter to the base soil clearly indicated that the magnitudes of stress reduction factor (
) in
Appendix B for the current base-filter systems were less than unity. Similarly, the magnitudes of
inside both the base and the filter layers markedly increased with the corresponding increase in
. The final f
c distributions (at
t = 0.2 s) in the filter remained almost the same compared to the base, wherein the seepage stresses markedly reduced the base particle contact stresses.
In this study, the hydraulic gradients
= 20 and 35 were applied on both specimens NF1-NB and NF2-NB. Notably, these high hydraulic gradients were chosen to ensure that the base particles are fully mobilized. For no external loading, the magnitude of minimum hydraulic gradient for the complete erosion of base soil through an ineffective granular filter could be computed using model of Indraratna and Radampola [
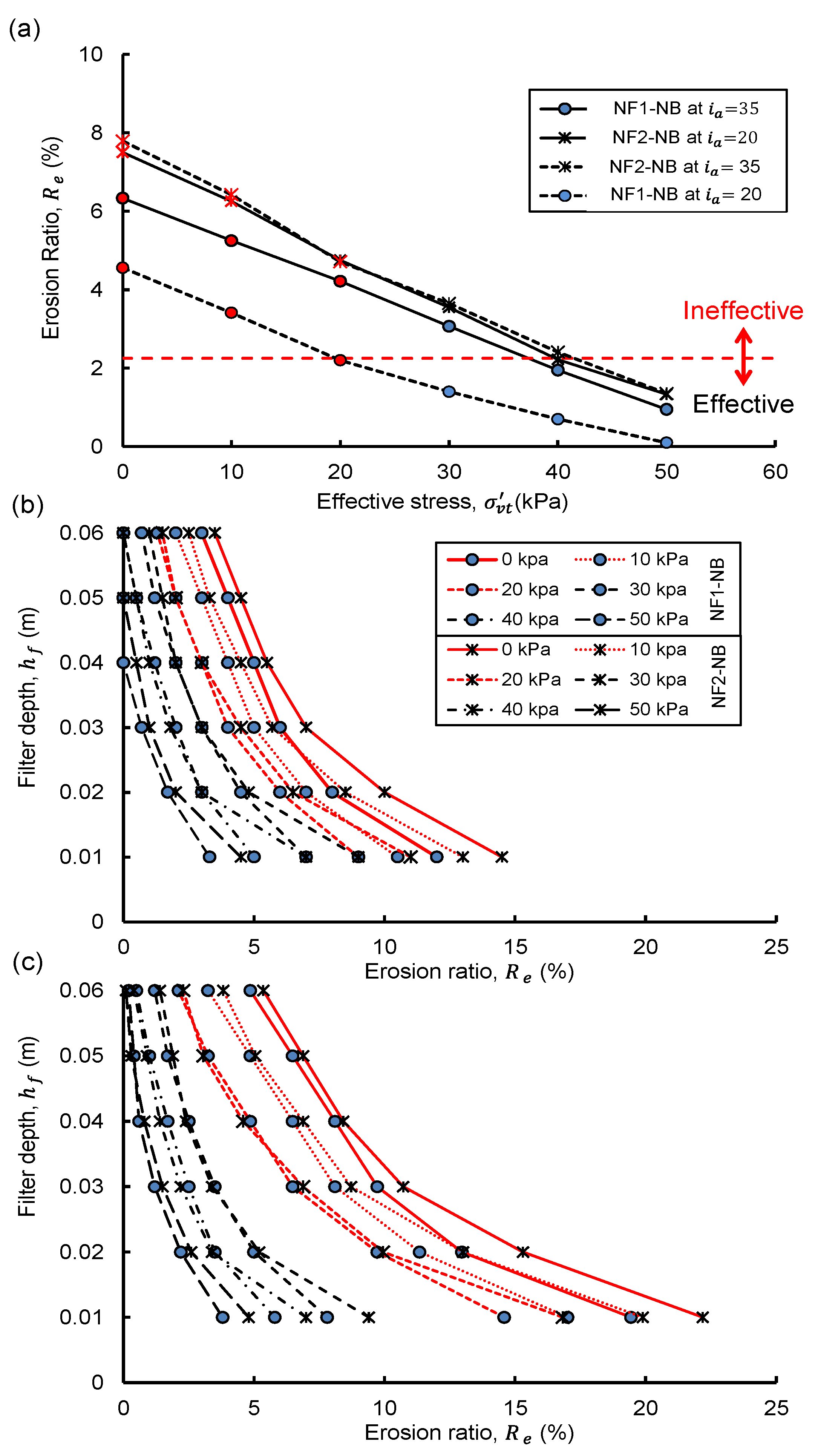
10] and the current magnitudes have been kept slightly larger. The erosion ratio
was computed to quantify the extent of base soil erosion and hence the filter effectiveness [
23]:
where
define the number of eroded and original base particles and their respective radii. The filter was divided into six equal layers of 0.01 m each, and the quantities of eroded base fines and their respective
values were calculated. Based on the published DEM studies, a filter exhibiting
< 2.25% could be considered effective [
24].
Figure 5a presents the correlation between
and
, NF1-NB exhibited relatively smaller
compared to NF2-NB at
= 0 and their
magnitudes decreased significantly with the increase in the magnitudes of
. For instance, at
= 35, the specimen NF1-NB exhibited reductions in
from 6.3% (ineffective) at
= 0 to 2.0% (effective) at
= 40 kPa, which reduced further to almost 0.95% (effective) at
= 50 kPa. Similarly, at
= 20, NF2-NB showed reductions in
from 7.5% (ineffective) at
= 0 to 1.4% (effective) at
= 50 kPa. Notably, when sample NF2-NB was subjected to
= 35, a subtle increase in the magnitude of
was observed. However, subjecting NF1-NB to a relatively smaller
= 20 at the same stress levels could substantially reduce the
values to almost half of that at
= 35. It clearly depicted that the erosion and hence the effectiveness of a base-filter system would be significantly influenced by the magnitude of applied hydraulic gradient.
Figure 5b,c show the spatial distributions of eroded base fines captured at various depths inside the filters at
t = 0.2 s and 0.3 s, respectively. In both cases, the computed
values were higher near the interface, because the hydraulic gradients were higher at the interface than elsewhere, and
gradually decreased with the filter depth. Notably for the given
values, a significant amount of base fines could reach the downstream filter boundary at relatively smaller magnitudes of applied effective stresses, i.e.,
≤ 20 kPa. These fines could have eroded further had either the magnitude of
increased or that of
reduced. Interestingly, the magnitudes of eroded fines (
values) for effective base-filter systems were insensitive to the simulation time because the steady-state conditions could be reached until
t = 0.2 s. In contrast, the continuous erosion from ineffective base-filter systems at
t > 0.2 s resulted in markedly increased
values, as shown by red lines in
Figure 5b,c.
The expressions of hydraulic gradients for a unit displacement of a base particle inside the filter layer and for complete erosion through the entire filter layer read [
10]:
where
and
represent unit weights of soil and water, respectively,
is the soil’s angle of internal friction in degrees,
is the particle contact factor,
is the base particle size,
is the unit displacement of base particle,
is the mean constriction size, and
is the filter depth.
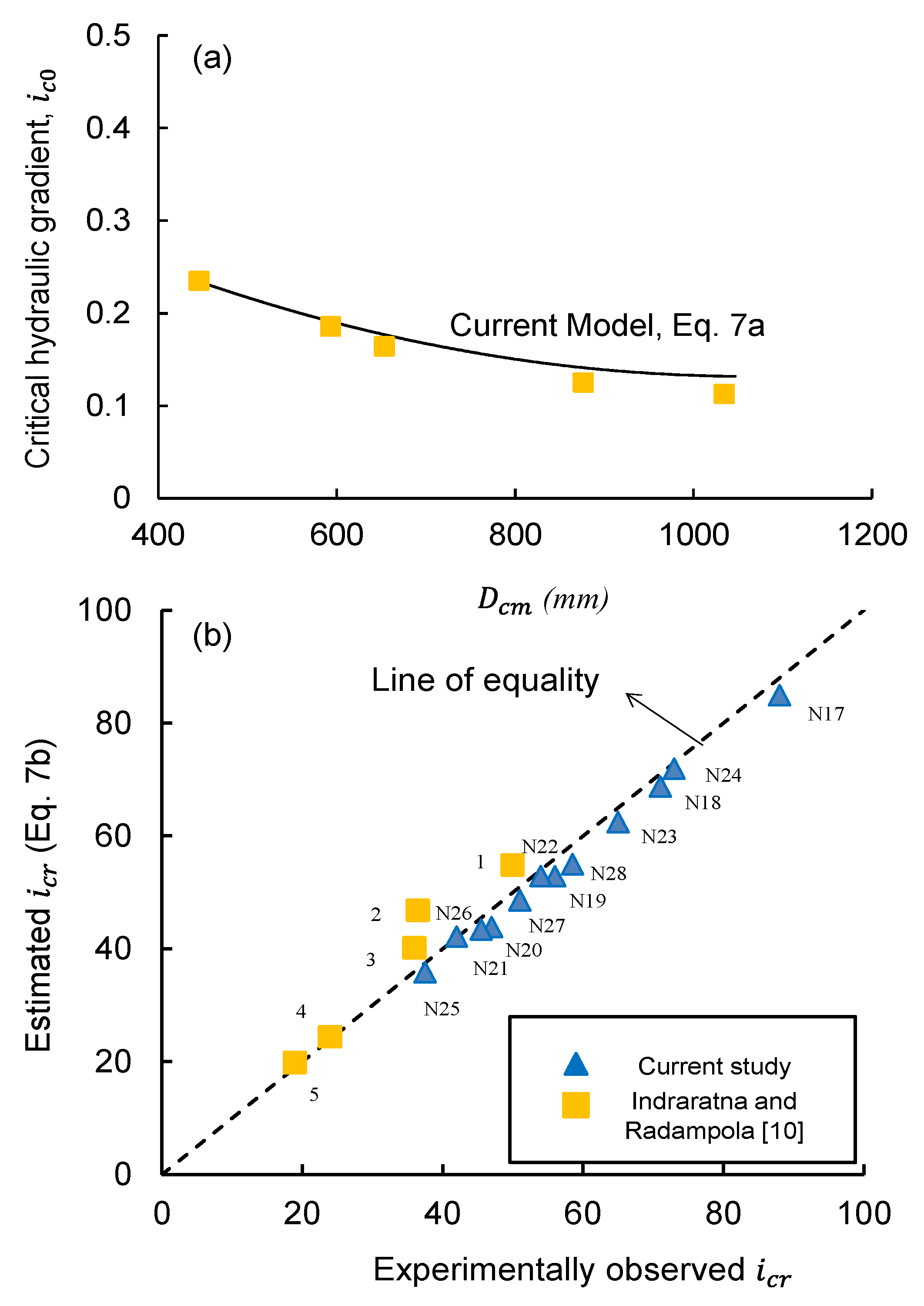
Figure 6a,b plot the critical hydraulic gradient values for unit displacement and complete erosion of base particles versus those predicted by the above Equation (7), respectively. Not surprisingly, the magnitudes of
computed through Equation (7) agree closely with those recorded during the numerical simulations of this study, and it may be because both models consider the particles to be spheres. Nevertheless, the values of the critical hydraulic gradients would be expectedly higher for actual granular soil particles (i.e., non-spheres). It clearly establishes that the values of
obtained from Equation (7) would be conservative when applied to the actual field conditions. Therefore, this study adopts both Equation (7) to capture the unit displacement and the complete erosion of base particles through the filter layer (i.e., unit displacement approaching
), respectively. Furthermore, the additional hydraulic gradient (
) arising due to the normal loading needs to be overcome for once by hydrodynamic forces to dislodge an erodible fine and induce unit displacement (i.e., initiation of erosion) and can be given by (
Appendix B):
Thus, the expression for the complete erosion of base particles (i.e., both initiation and development) from the filter layer can be given by:
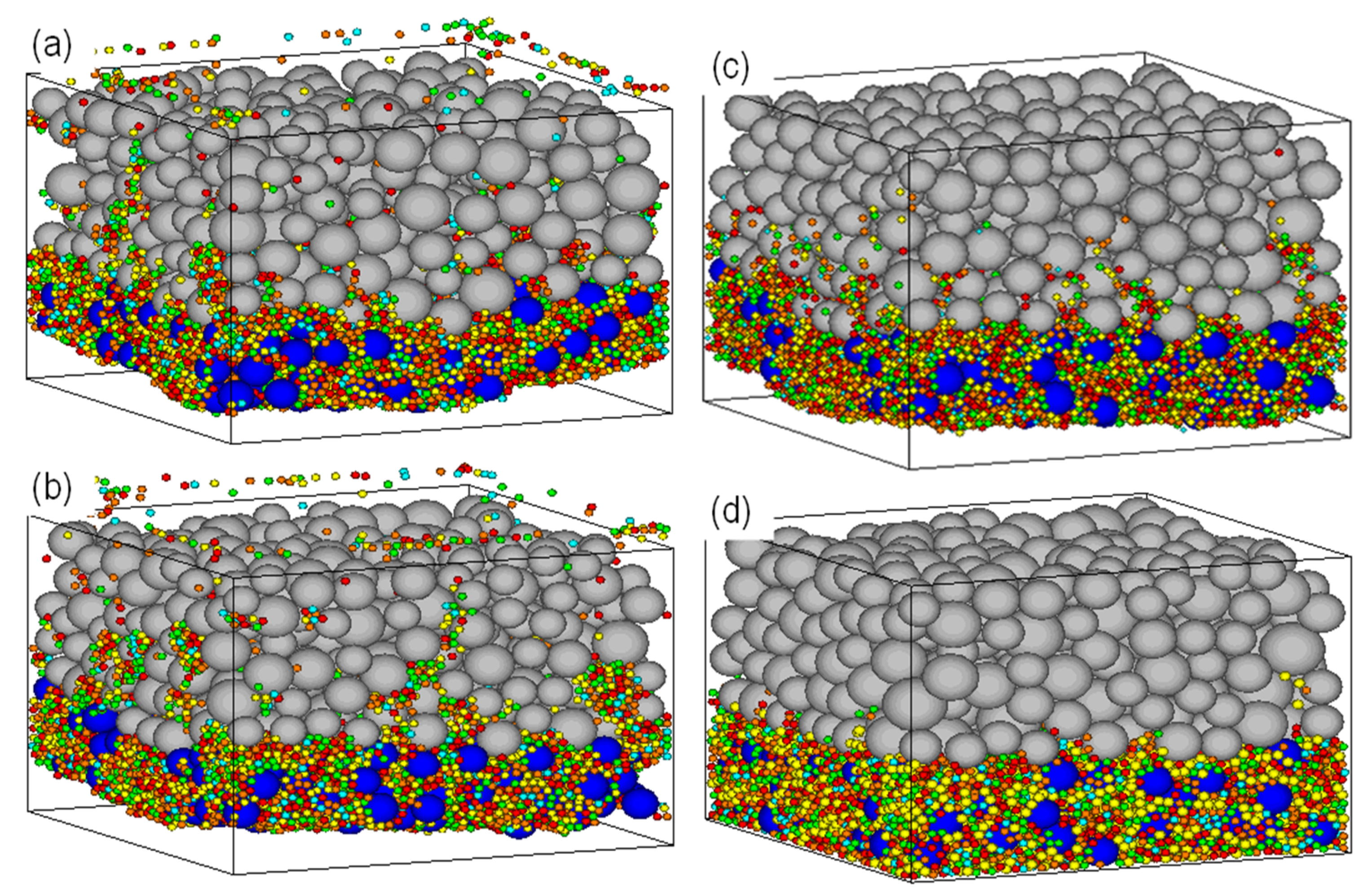
Figure 7 presents the base-filter particle distributions for select specimens at the end of simulations i.e., at
t = 0.2 s for filter NF2 subjected to 0, 10 kPa, 30 kPa, and 50 kPa. As shown, the magnitude of erosion has been significantly reduced with the increase in the magnitude of normal stress. Similarly, the filter’s ability of capturing the eroded fines has been markedly enhanced with the increase in stress magnitude. This clearly depicts that the filter effectiveness could be increased under higher stress magnitudes. Nevertheless, it is fully consistent with our understanding of increasing the stability and effectiveness of inverted filters by constructing berms and providing additional surcharge at downstream of hydraulic structures.
4. Validation of Proposed Model
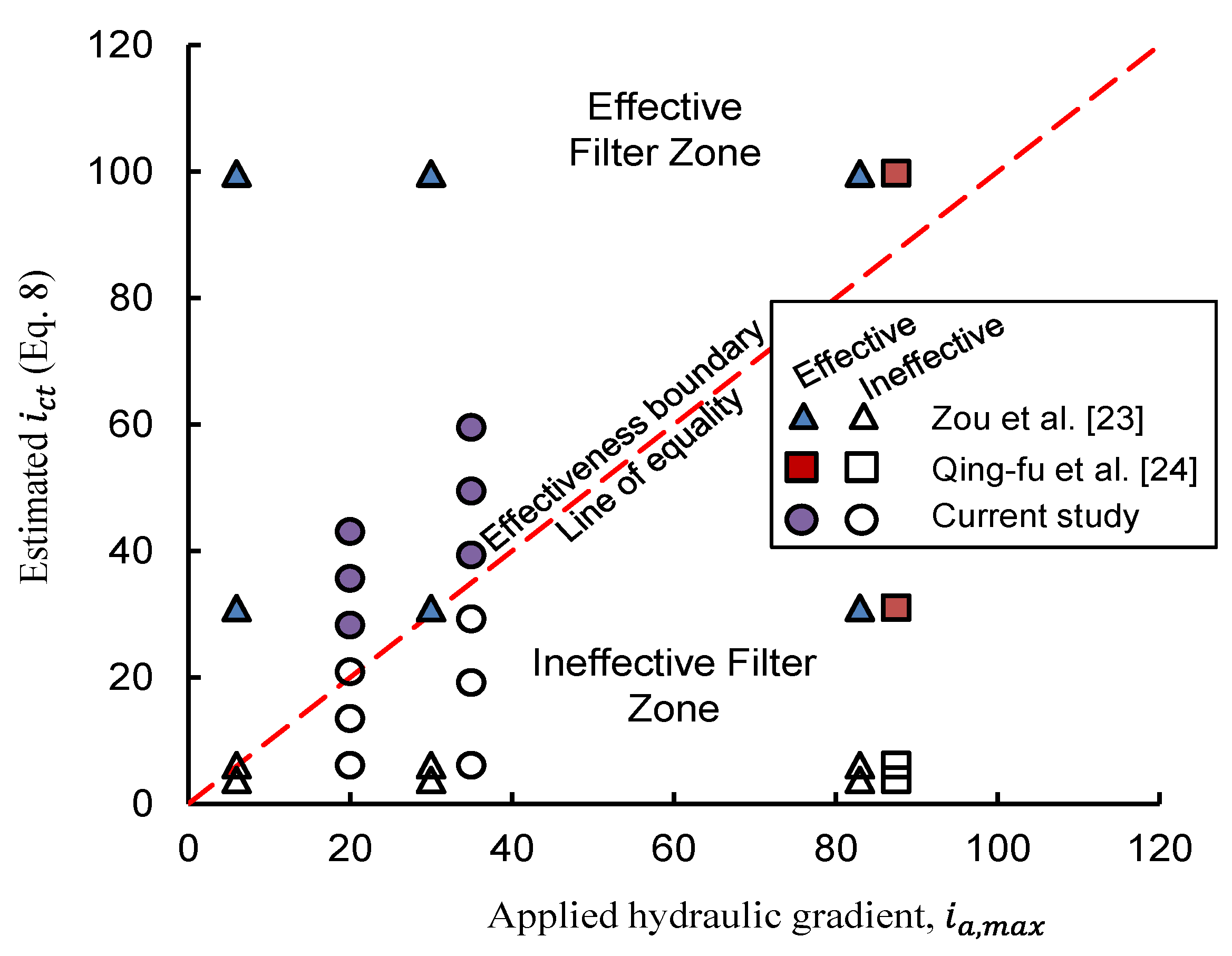
Table 2 presents the results of numerical data of this study plus those adopted from the published DEM studies for validation. In
Figure 8, the magnitudes of maximum applied hydraulic gradients during DEM simulations,
, and those predicted by the proposed model,
(Equation (8)), were plotted. The line of equality demarcates a visible boundary between effective and ineffective base-filter systems, whereby the ones plotting on its right were deemed ineffective and vice versa. The assessment results of filter effectiveness shown in
Figure 8 have been quantified in
Table 2 in the form of effectiveness of a filter in fully protecting the base soil. For brevity, the current model assesses a filter as ineffective should the applied hydraulic gradient be greater than its anticipated
value (Equation (8)). Then, this assessment is compared with the actual DEM response observed in this study or that reported in the adopted works. As
Table 2 shows, out of 40 simulation results from three independent DEM studies including the current work, only five incorrect assessments (i.e., two conservative assessments including N3 and N10 and three unsafe including N11, N25, and N39) are obtained by the currently proposed theoretical model. This acceptably smaller discrepancy in numerical results and theoretical assessments of this study could be because the proposed model is an explicit solution using a continuum approach, while CCFD-DEM simulations of this study capture micro-mechanical responses at the fluid–particle level.
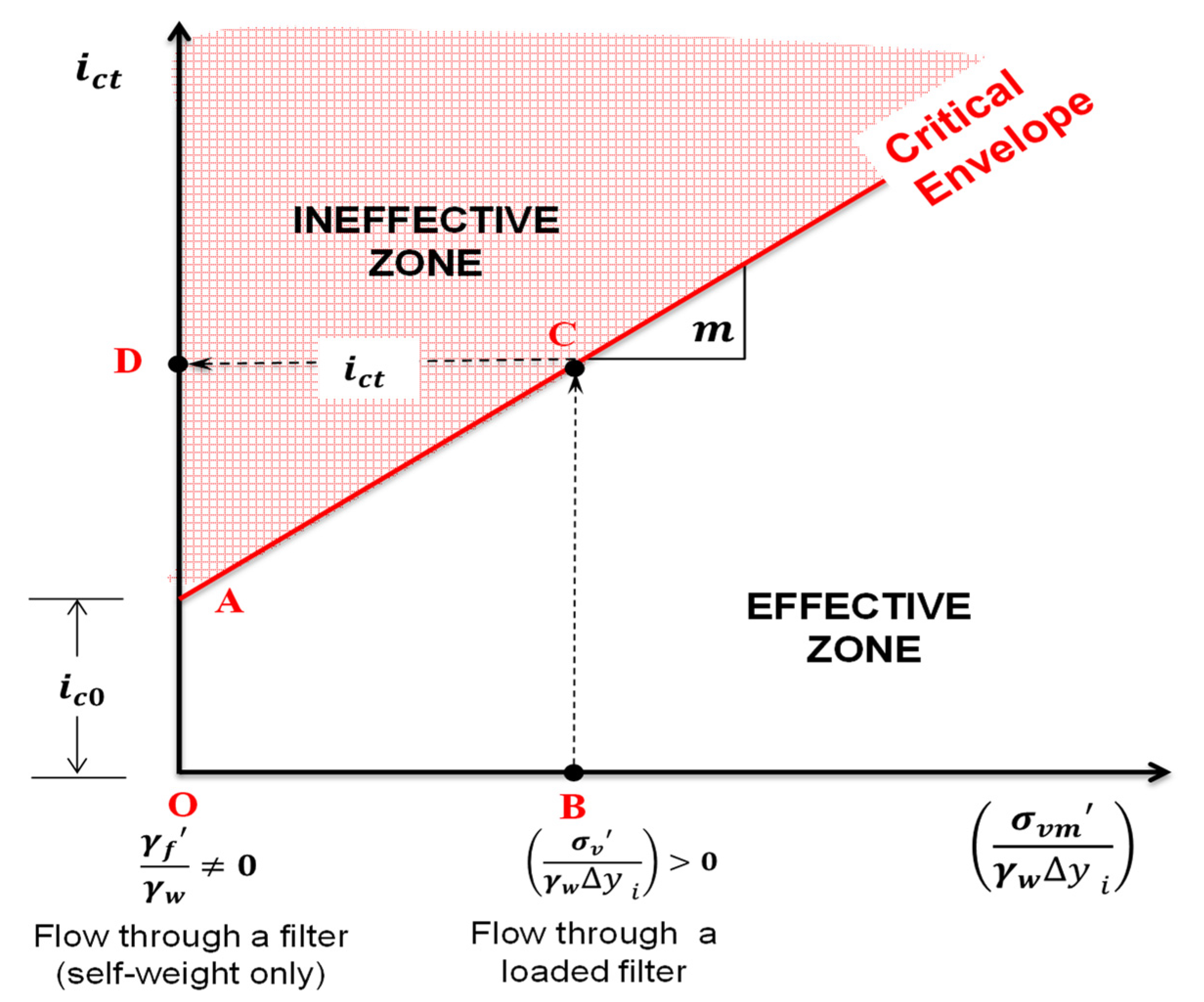
Theoretical Envelope
A graphical illustration of the proposed theoretical hydro-mechanical envelopes (Equation (8)) governing the migration of base particles in loaded filters is presented in
Figure 9. It followed a straight-line relationship with the dimensionless mechanical constraint
(
), having a slope equal to the unit
(Equation (7)). This definition of slope is more realistic because the proposed envelope for a given base-filter system tends to be unique by the virtue of its physical properties. For an internally stable filter under
= 0 (i.e., with no additional surcharge on the filter layer except the self-weight), the
can be estimated by the ordinate intercept (OA) of the theoretical envelope in
Figure 9. Almost all the inter-particle contacts are mechanically active in an internally stable soil [
25]; thus, any value of
> 0 can help a filter resist the erosion of particles by virtue of the increased mechanical and frictional constraints. In turn, this requires larger
values to trigger the migration of base particles (path BCD), thus imitating Terzaghi’s [
6] recommendation of using inverted loaded filters to avoid quicksand conditions at the toe of embankment dams.
Nevertheless, a different response would be expected with internally unstable soils whereby the inter-particle contacts are not mechanically significant, and hence, the load transfer is not efficient. This would not increase the inter-particle friction sufficiently, and hence the theoretical envelope tends not to obey the proposed law. The seepage forces accompany erodible finer fractions from the filter itself, which progressively increases its porosity (thus, the constriction sizes), and then, the base particles require less for erosion through the filter. Hence, a prior assessment of internal stability through an acceptable geometrical criterion is imperative to select internally stable and effective filters.
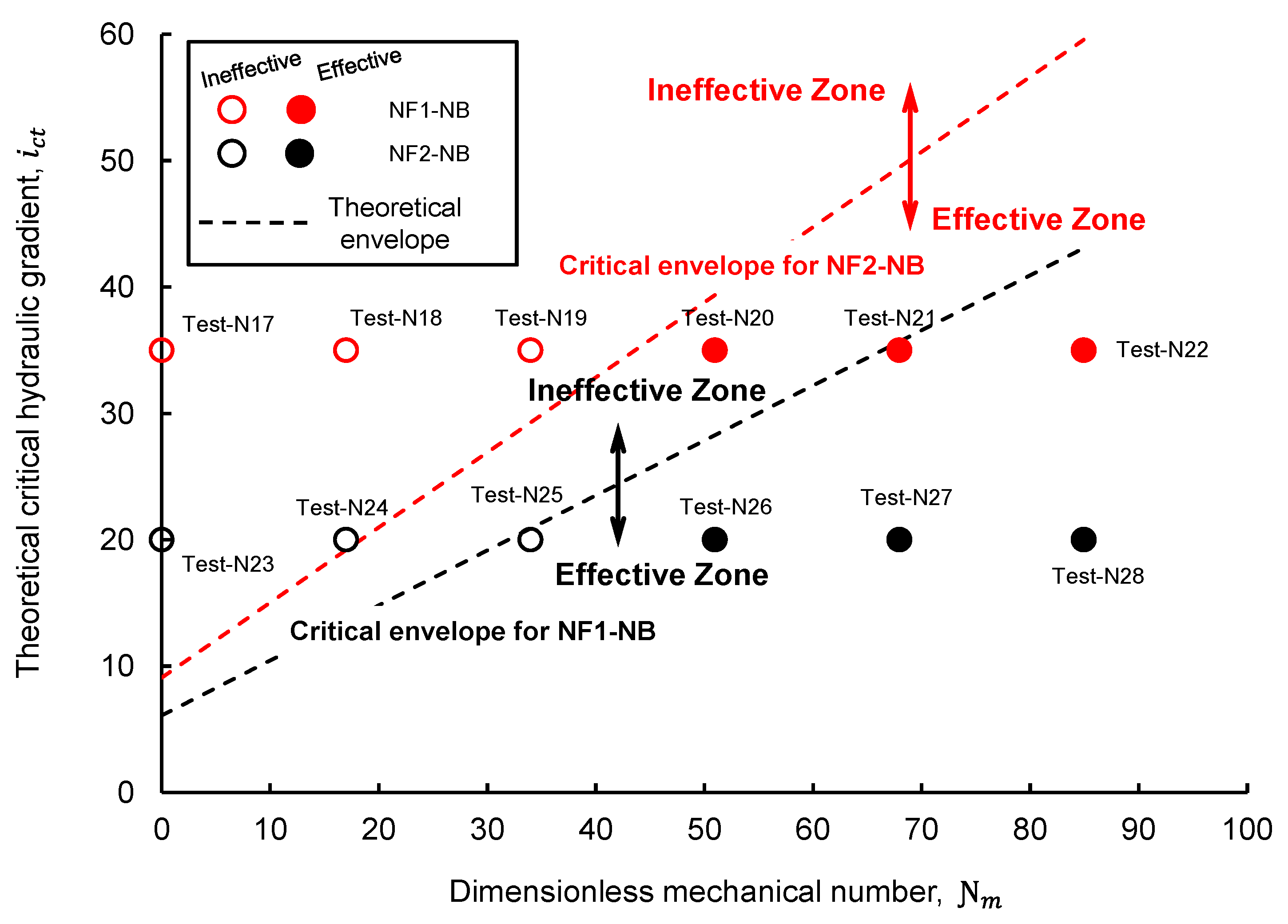
In
Figure 10, the applied
and the
values for the numerical simulation results of this study are plotted with the corresponding theoretical envelopes for the base-filter systems NF1-NB and NF2-NB. Apart from a single incorrect assessment NF1-NB-30 (i.e., test N20 in
Table 2), the rest of the base-filter systems are correctly plotted in their respective effective and ineffective zones by the proposed model. Nonetheless, based on the geometrical and mechanical factors, the proposed theoretical envelopes governing base particle erosion for a given base-filter system should be unique.
5. Conclusions
The following conclusions could be drawn from this study.
The results of CCFD-DEM numerical modeling of this study plus those adopted from the published literature showed good agreements with both the experimental observations and the model predictions. Unlike the available particle size distribution (PSD)-based geometrical criteria for assessing the effectiveness of filters, a performance-based hydro-geo-mechanical approach that considers the level of hydro-mechanical excitation (ia and ) and the geometrical and physical characteristics of filter media (e.g., PSD, Rd, and ∅’ etc.) was presented.
No significant erosion occurs from an effective base-filter system at extended simulation times (t = 0.2 s to t = 0.3 s), whereby steady-state conditions prevail due to the formation of self-filtering layers inside the filter. In contrast, the erosion of base particles continues through an ineffective filter should the simulation time increase. Furthermore, the changes in the magnitudes of applied hydraulic gradients markedly affect the magnitude of erosion.
An enhanced alternative method for quantifying filter effectiveness through the factor of safety against base particle erosion instead of traditional “effective or ineffective” bifurcation may be more efficient and cost effective in practice; for instance, designing filters for properly monitored low-risk structures such as drainage layers subject to low magnitude hydraulic excitation in slopes, embankments, levees, railway, and highway sub-structures.
A novel theoretical model has been proposed to quantify filter effectiveness under static loading condition that could also be presented graphically. Nevertheless, the current simulation results and those adopted from the published literature could sufficiently verify the proposed model, thus enhancing the user confidence in adopting it for various preliminary analyses and assessment purposes.
Needless to mention, the findings from this study only govern internally stable and non-cohesive base-filter systems, but the authors do envisage extending the scope to internally unstable granular filters and cohesive base soils.