Simulations of the Soil Evaporation and Crop Transpiration Beneath a Maize Crop Canopy in a Humid Area
Abstract
:1. Introduction
2. Materials and Methods
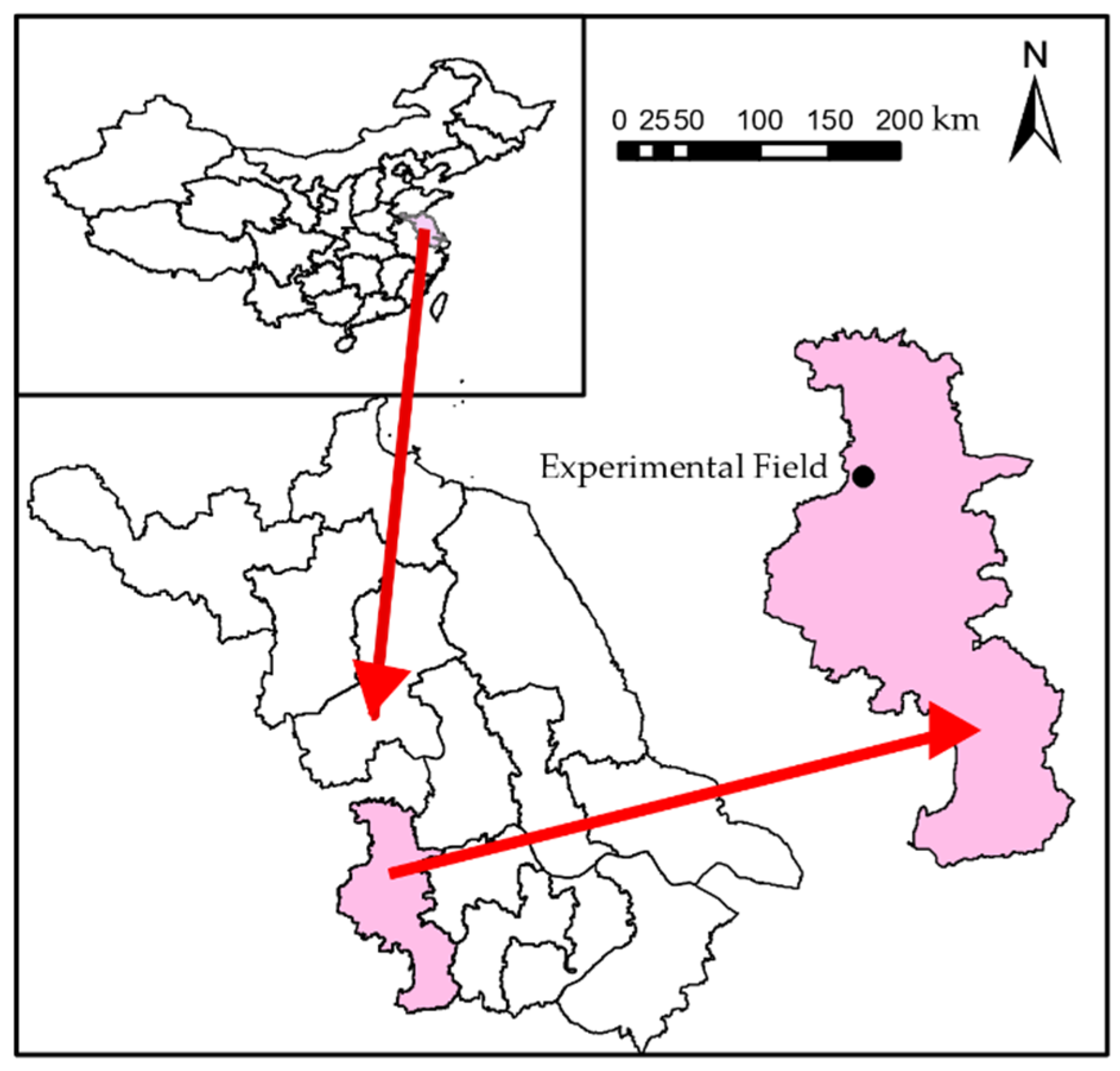
2.1. Measurement Field
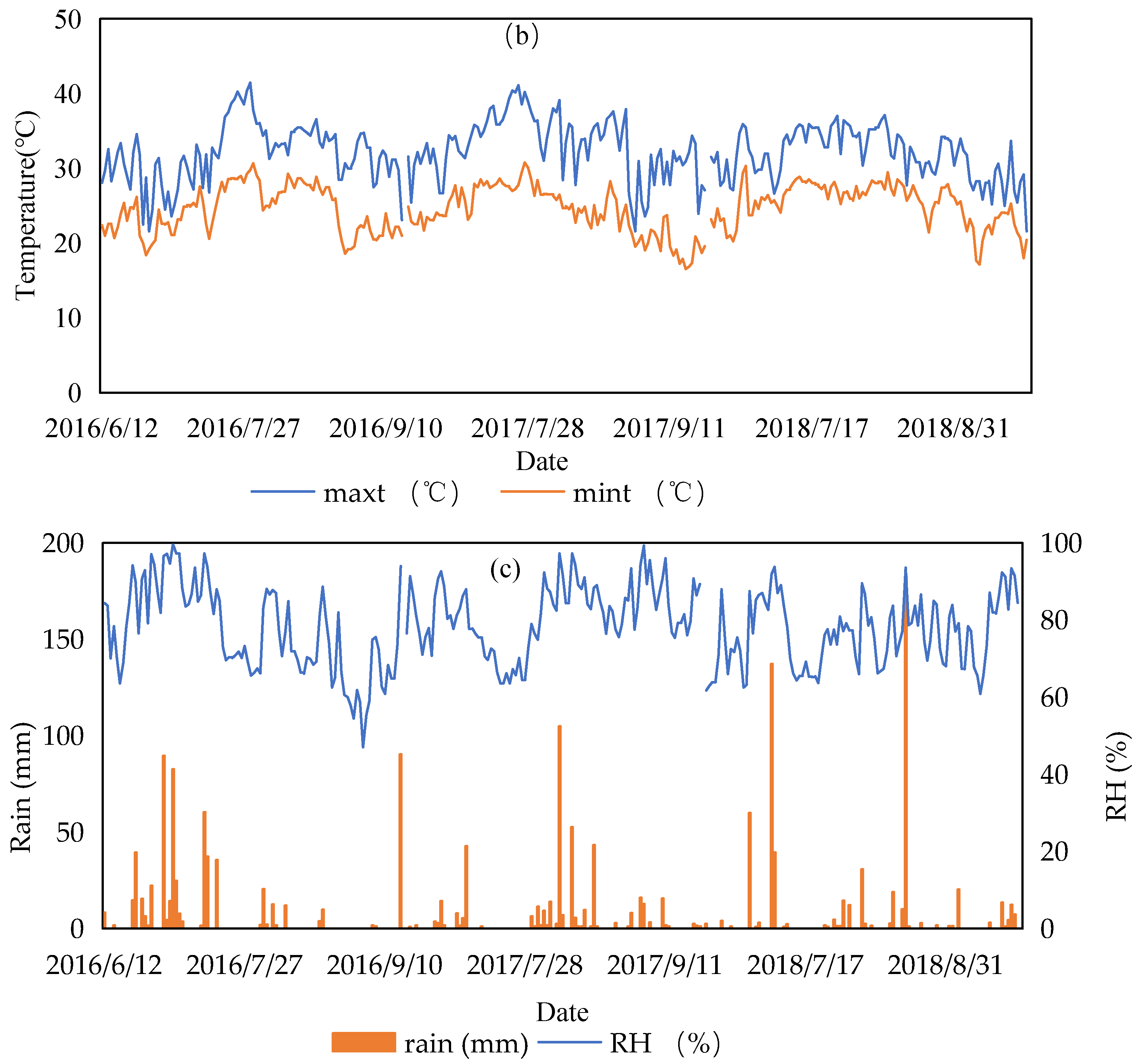
2.2. Measurements and Variations of Meteorological Factors in Maize Growing Periods
2.3. APSIM Model
2.3.1. Es Model in APSIM
2.3.2. Tc Model in APSIM
2.4. Methods for Parameters Tuning and Model Evaluation
2.4.1. Parameters Calibration of Es
2.4.2. Determination of Stemflow
2.4.3. Methods of Model Evaluation
3. Results
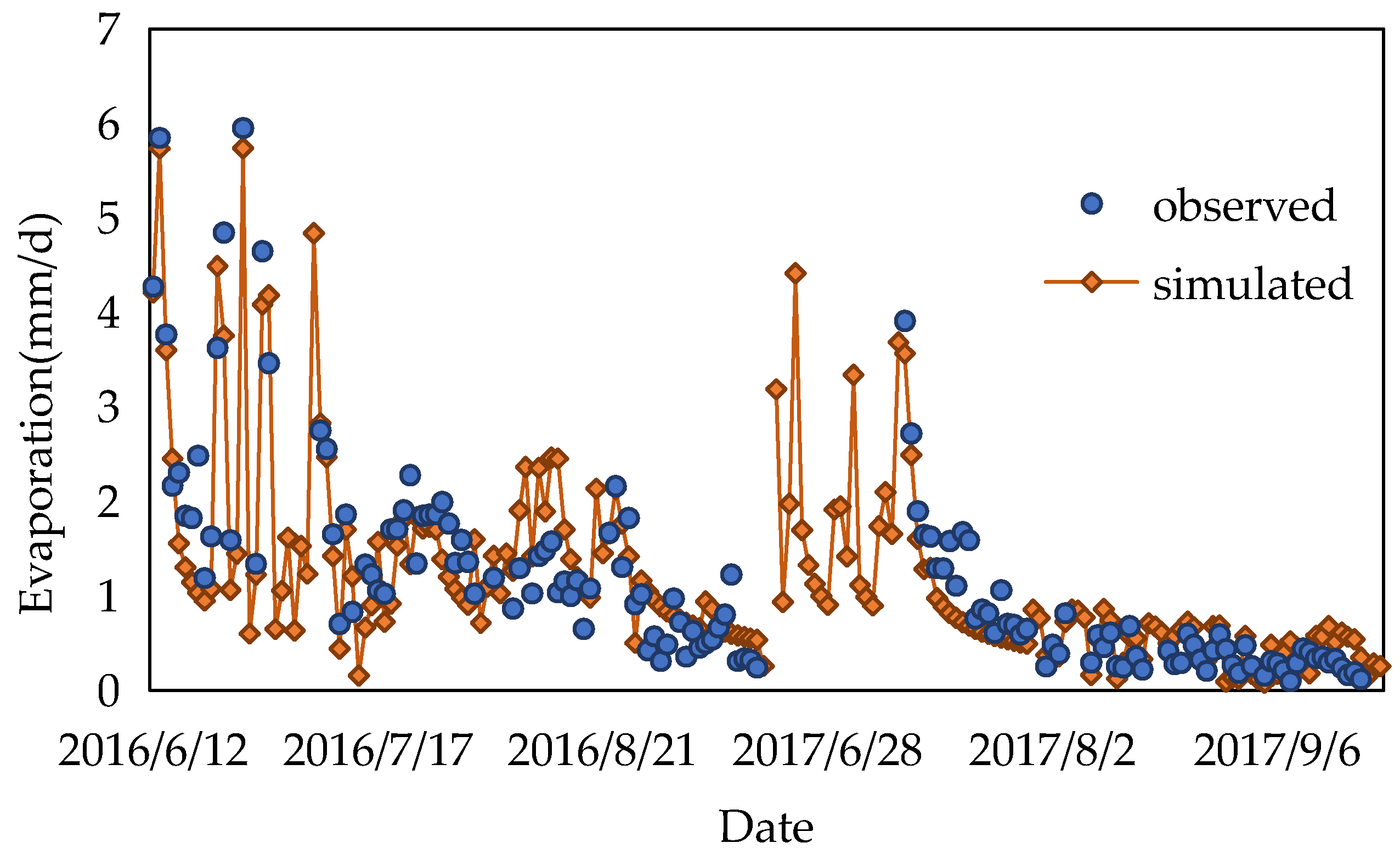
3.1. Simulated and Observed Es from Maize
3.1.1. Es Variation in the Maize Growth Periods
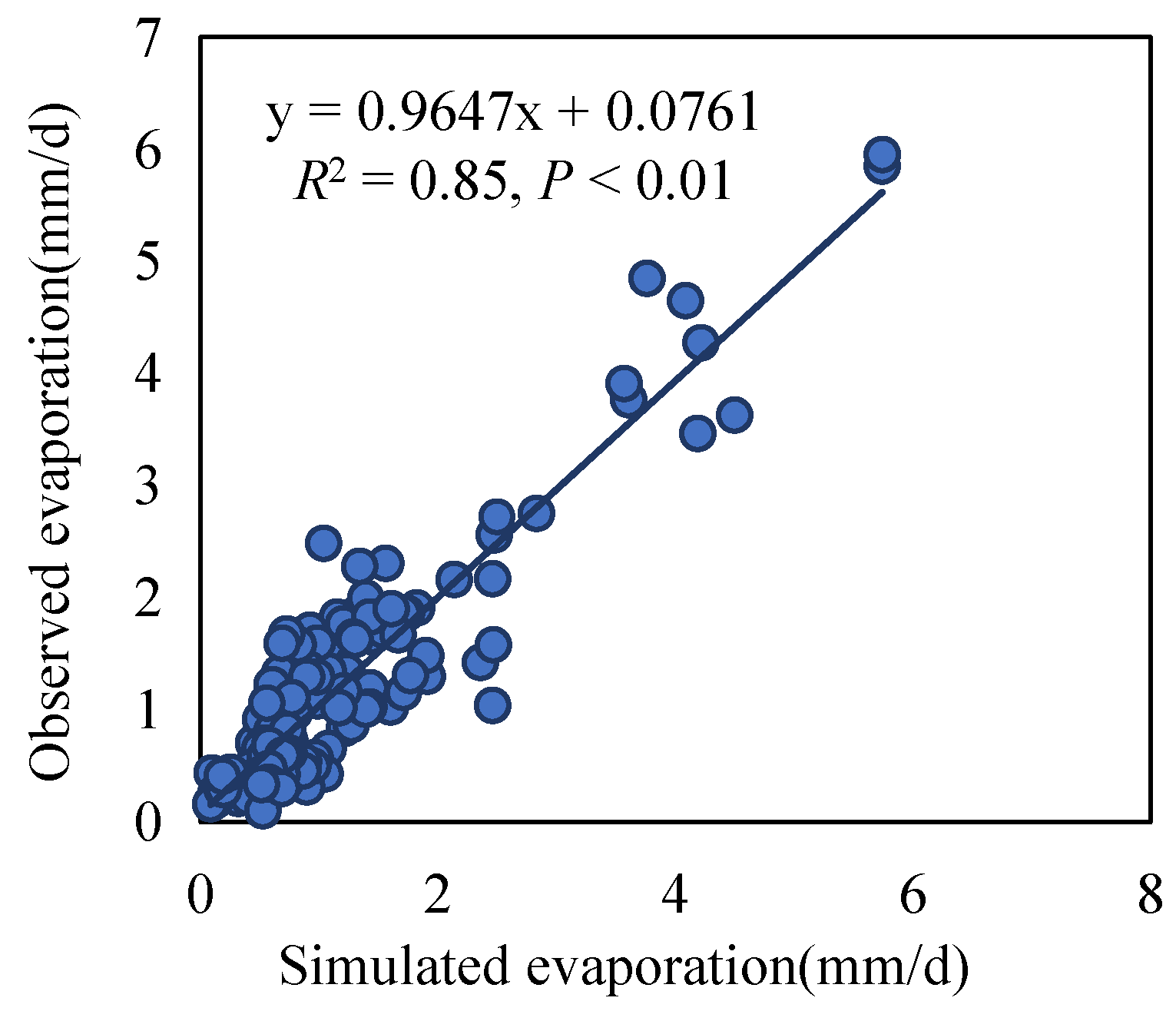
3.1.2. Comparison of Simulated and Observed Es
3.2. Simulated and Observed Tc from Maize
3.2.1. Tc Variation in the Maize Growth Periods
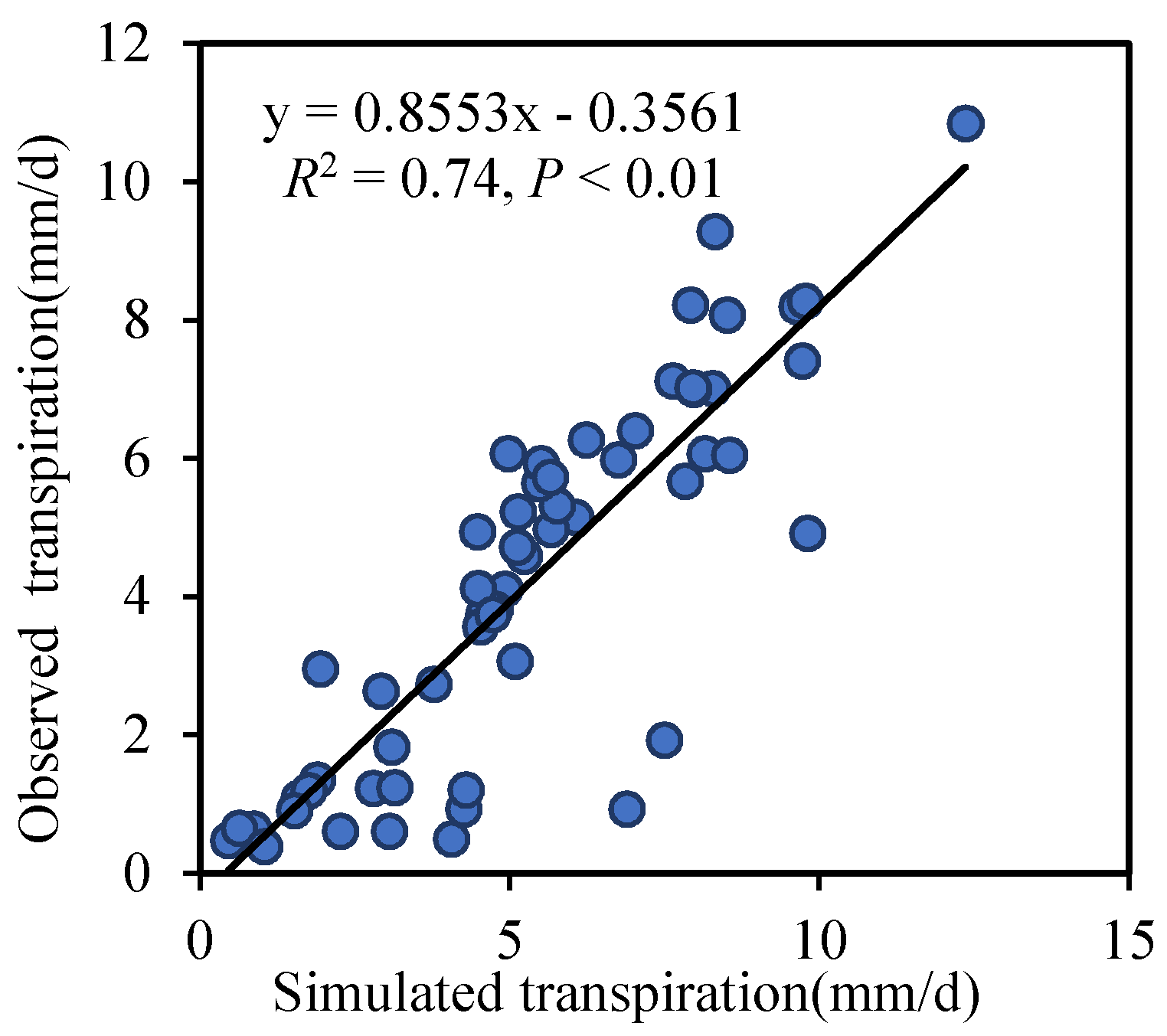
3.2.2. Comparison of Simulated and Observed Tc
4. Discussions
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, F.X.; Ma, Y.J. Evapotranspiration Estimation of Summer Maize with Plastic Mulched Drip Irrigation Based on Dual Crop Coefficient Approach in Xinjiang. Trans. Chin. Soc. Agric. Mach. 2018, 49, 268–274. [Google Scholar]
- Wang, J.; Wang, J.L.; Liu, J.B.; Jiang, W.; ZHao, C.X. Parameters modification and evaluation of two evapotranspiration models based on Penman-Monteith model for summer maize. Chin. J. Appl. Ecol. 2017, 28, 1917–1924. [Google Scholar]
- Qiu, R.J.; Katul, G.G.; Wang, J.T.; Xu, J.Z.; Kang, S.D.; Liu, C.W.; Zhang, B.Z.; Li, L.A.; Cajucom, P.E. Differential response of rice evapotranspiration to varying patterns of warming. Agric. For. Meteorol. 2021, 298–299, 108293. [Google Scholar] [CrossRef]
- Dhillon, R.; Rojo, F.; Upadhyaya, S.K.; Roach, J.; Delwiche, M. Prediction of plant water status in almond and walnut trees using a continuous leaf monitoring system. Precis. Agric. 2019, 20, 723–745. [Google Scholar] [CrossRef]
- Balwinder-Singh; Eberbach, P.L.; Humphreys, E. Simulation of the evaporation of soil water beneath a wheat crop canopy. Agric. Water Manag. 2014, 135, 19–26. [Google Scholar] [CrossRef]
- Leuning, R.; Condon, A.G.; Dunin, F.X.; Zegelin, S.; Denmead, O.T. Rainfall inter ception and evaporation from soil below a wheat canopy. Agric. For. Meteorol. 1994, 67, 221–238. [Google Scholar] [CrossRef]
- Boast, C.; Robertson, T. A “micro-lysimeter” method for determining evaporation from bare soil: Description and laboratory evaluation. Soil Sci. Soc. Am. J. 1982, 46, 689–696. [Google Scholar] [CrossRef]
- Kool, D.; Agam, N.; Lazarovitch, N.; Heitman, J.; Sauer, T.; Ben-Gal, A.J. A review of approaches for evapotranspiration partitioning. Agric. For. Meteorol. 2014, 184, 56–70. [Google Scholar] [CrossRef]
- Gao, X.F.; Shi, H.Z.; Yang, J.; Wang, X.L. Advances in soil evaporation measured by micro-lysimeter. Adv. Sci. Technol. Water Resour. 2010, 30. [Google Scholar] [CrossRef]
- Allen, S.J. Measurement and Estimation of Evaporation from Soil under Sparse Barley Crops in Northern Syria. Agric. For. Meteorol. 1990, 49, 291–309. [Google Scholar] [CrossRef]
- Liu, X.F.; Sun, J.S.; Liu, Z.G.; Wang, S.S.; Wang, J.L.; NaTian, C. Soil Evaporation of Summer Corn under Alternate-furrow Irrigation Condition. Water Sav. Irrig. 2007, 6, 10–12. [Google Scholar]
- Moran, M.; Scott, R.; Keefer, T.; Emmerich, W.; Hernandez, M.; Nearing, G.; Paige, G.; Cosh, M.; O’Neill, P. Partitioning evapotranspiration in semiarid grassland and shrubland ecosystems using time series of soil surface temperature. Agric. For. Meteorol. 2009, 149, 59–72. [Google Scholar] [CrossRef]
- Liu, Y.T. Evaporation Test and Model Study of Saline-Alkalne Soil. Master’s Thesis, Xi’an University of Technology, Xi’an, China, 2019. [Google Scholar]
- Ma, L.; Wei, G.H. Fitness-for-service of evaporatranspiration model in Tarim Basin, Xinjing. J. Arid. Land Resour. Environ. 2015, 29, 132–137. [Google Scholar]
- Tan, G.Y. The Application of APSIM Model and the Measurement of Soil Evaporation Parameters in the Qingyang Loess Plateau, Gansu. Master’s Thesis, Lanzhou University, Lanzhou, China, 2007. [Google Scholar]
- Didari, S.; Ahmadi, S.H. Calibration and evaluation of the FAO56-Penman-Monteith, FAO24-radiation, and Priestly-Taylor reference evapotranspiration models using the spatially measured solar radiation across a large arid and semi-arid area in southern Iran. Theor. Appl. Climatol. 2019, 136, 441–455. [Google Scholar] [CrossRef]
- Li, Q.; Jing, Y.S.; Li, K. Comparation of rice field evaporatranspiration models in two time scales. Jiangsu Agric. Sci. 2019, 47, 238–243. [Google Scholar]
- Mi, N.; Chen, P.S.; Zhang, Y.S.; Ji, R.P.; Zhou, G.S.; Li, R.P. Applications and Comparations of evaportranspiration models in maize field. Resour. Sci. 2009, 31, 1599–1606. [Google Scholar]
- Zheng, Z.; Cai, H.J.; Yu, L.Y.; Wang, J. Comparison of Two Crop Evapotranspiration Calculating Approaches in CSM-CERES-Wheat Model. Trans. Chin. Soc. Agric. Mach. 2016, 47, 179–191. [Google Scholar] [CrossRef]
- Qiu, R.; Liu, C.; Cui, N.; Wu, Y.; Wang, Z.; Li, G. Evapotranspiration estimation using a modified Priestley-Taylor model in a rice-wheat rotation system. Agric. Water Manag. 2019, 224, 105755. [Google Scholar] [CrossRef]
- Qiu, R.; Du, T.; Wu, L.; Chen, R.; Kang, S. Assessing the SIMDualKc model for estimating evapotranspiration of hot pepper grown in a solar greenhouse in Northwest China. Agric. Syst. 2015, 138, 1–9. [Google Scholar] [CrossRef]
- Snow, V.; Huth, N. The APSIM-MICROMET Module; HortResearch: Auckland, New Zealand, 2004; pp. 1–18. [Google Scholar]
- Zhang, J.H.; Wag, X.Y.; Zhou, D.M.; Wang, G.Y. Simulation on water-saving optimization irrigation schedule of winter wheat-summer maize double cropping system in Haihe Plain. J. Hebei Agric. Univ. 2018, 41, 24–30. [Google Scholar] [CrossRef]
- Dai, T.; Wang, J.; He, D.; Wang, N. Modeling the impacts of climate change on spring maize yield in Southwest China using the APSIM model. Resour. Sci. 2016, 38, 155–165. [Google Scholar] [CrossRef]
- Ru, X.Y.; Li, G.; Yan, L.J.; Chen, G.P.; Nie, Z.G. Effect of precipitation and nitrogen application on spring wheat yield in dryland based on APSIM model. Pratacultural Sci. 2019, 36, 2342–2350. [Google Scholar] [CrossRef]
- Li, L. Analysis of Evolutionary Law and Control Measures of Magan Soil. J. Anhui Agric. Sci. 1964, 29–36. (In Chinese) [Google Scholar] [CrossRef]
- Liu, C.; Wu, X.; QIU, R. Evaluation of Evapotranspiration of Maize With Crop Coefficient and Penman-Monteith Methods in Nanjing. Water Sav. Irrig. 2016, 09, 12–17. [Google Scholar]
- Holzworth, D.; Huth, N.I.; Fainges, J.; Brown, H.; Zurcher, E.; Cichota, R.; Verrall, S.; Herrmann, N.I.; Zheng, B.; Snow, V. APSIM Next Generation: Overcoming challenges in modernising a farming systems model. Environ. Model. Softw. 2018, 103, 43–51. [Google Scholar] [CrossRef]
- Carberry, P.S.; Liang, W.-L.; Twomlow, S.; Holzworth, D.P.; Dimes, J.P.; McClelland, T.; Huth, N.I.; Chen, F.; Hochman, Z.; Keating, B.A. Scope for improved eco-efficiency varies among diverse cropping systems. Proc. Natl. Acad. Sci. USA 2013, 110, 8381–8386. [Google Scholar] [CrossRef] [Green Version]
- Ritchie, J.T. Model for predicting evaporation from a row crop with incomplete cover. Water Resour. Res. 1972, 8, 1204–1213. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Duan, A.W.; Chen, J.P.; Shen, X.J.; Liu, Z.D. Modeling soil evaporation in maize/soybean strip intercropping systems. In Proceedings of the Fifth National Conference Collected Paper of Chinese Society of Agricultural Engineering Agricultural Water Soil Energeering, Shihezi, China, 1 July 2008; pp. 87–91. [Google Scholar]
- Kang, S.Z.; Xiong, Y.Z.; Liu, X.M. A Study of Penman-Monteith model to estimate transpiration from crops. J. Northwest A F Univ. 1991, 19, 13–20. [Google Scholar]
- Sun, J.S.; Chen, Y.M.; Kang, S.Z.; Xiong, Y.Z. Study on estimation of crop transpiration and soil evaporation in summer corn field. J. Maize Sci. 1996, 4, 76–80. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. FAO Irrigation and drainage paper. Rome Food Agric. Organ. United Nations 1998, 56, e156. [Google Scholar]
- Penman, H.L. Vegetation and hydrology. Soil Sci. 1963, 96, 357. [Google Scholar] [CrossRef]
- Ao, H.W.; Xie, Y.Z.; Li, Y.H.; Ma, J.L. Adaptability of APSIM Model in Simulating Lucerne-Wheat-Millet Crop Rotation System in Haiyuan Region of Ningxia. Acta Agrestia Sin. 2016, 24, 146–155. [Google Scholar]
- Inman-Bamber, N.; Jackson, P.; Stokes, C.; Verrall, S.; Lakshmanan, P.; Basnayake, J. Sugarcane for water-limited environments: Enhanced capability of the APSIM sugarcane model for assessing traits for transpiration efficiency and root water supply. Field Crop. Res. 2016, 196, 112–123. [Google Scholar] [CrossRef]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63, 1309–1313. [Google Scholar] [CrossRef] [Green Version]
- Willmott, C.J. On the validation of models. Phys. Geogr. 1981, 2, 184–194. [Google Scholar] [CrossRef]
- Liu, Z.J.; Yang, X.G.; Wang, J.; LV, S.; LI, K.N.; Xun, X.; Wang, E.L. Adaptability of APSIM Maize Model in Northeast China. Acta Agron. Sin. 2012, 38, 740–746. [Google Scholar] [CrossRef]
- Yang, X.; YangTan, G.; Shen, Y.Y. Soil Moisture Content under Stubble Retention After Dry framing Winter Wheat Harvest Based on APSIM Model. Arid. Zone Res. 2013, 30, 609–614. [Google Scholar]
- Ma, C.Q.; Li, G.; Wang, J.; Ru, X.Y. Effect of farming practices on spring wheat yield by using APSIM model. Trop. Agric. Eng. 2020, 44, 67–71. [Google Scholar]
- Li, G.; Huang, G.B.; Bellotti, W.; Chen, W. Adaptation Research of APSIM Model under Different Tillage Systems in the Loess hill-gullied Region. Acta Ecol. Sin. 2009, 29, 2655–2663. [Google Scholar]
- Lu, X.J. Studies on the Methods of Utilizing Penman-Monteith Equation to Calculate Evapotranspiration of Forest. Master’s Thesis, Beijing Forestry University, Beijing, China, 2008. [Google Scholar]
- Gao, Z.Q.; Li, T.; Zhang, X.C. Dynamic simulation of canopy transpiration in apple tree. J. Fruit Sci. 2009, 26, 775–780. [Google Scholar]
- Li, L.; Dong, X.H.; Zhao, Q.; Fang, Y.; Yao, Z.X.; Su, H. Observation and Simulation of the Outdoors Evapotranspiration for Citrus Trees. J. Irrig. Drain. 2016, 35, 98–104. [Google Scholar]
- Yan, H.F.; Zhao, B.S.; Zhang, C.; Huang, S.; Fu, H.; Yu, J.J.; Acquah, S.J. Estimating cucumber plants transpiration by Penman-Monteith model in Venlo-type greenhouse. Trans. Chin. Soc. Agric. Eng. 2019, 35, 149–157. [Google Scholar]
- Zhang, B.; Xu, D.; Liu, Y.; Chen, H. Review of multi-scale evapotranspiration estimation and spatio-temporal scale expansion. Trans. Chin. Soc. Agric. Eng. 2015, 31, 8–16. [Google Scholar] [CrossRef]


| Soil Depth (cm) | Air Dry (mm/mm) | DUL (mm/mm) | LL15 (mm/mm) | SAT (mm/mm) |
|---|---|---|---|---|
| 0~5 | 0.038 | 0.221 | 0/119 | 0.300 |
| 5~15 | 0.136 | 0.250 | 0.136 | 0.300 |
| 15~25 | 0.150 | 0.268 | 0.160 | 0.322 |
| 25~40 | 0.158 | 0.274 | 0.167 | 0.311 |
| Sub-Models | R2 | D | p-Value | RMSEs (mm/d) | RMSEu (mm/d) |
|---|---|---|---|---|---|
| Es | 0.85 | 0.96 | 0.000 | 0.0783 | 0.4435 |
| Tc | 0.74 | 0.88 | 0.000 | 1.2261 | 1.4197 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, T.; Liu, C.; Xiang, Y.; Zhang, P.; Wang, R. Simulations of the Soil Evaporation and Crop Transpiration Beneath a Maize Crop Canopy in a Humid Area. Water 2021, 13, 1975. https://doi.org/10.3390/w13141975
Guo T, Liu C, Xiang Y, Zhang P, Wang R. Simulations of the Soil Evaporation and Crop Transpiration Beneath a Maize Crop Canopy in a Humid Area. Water. 2021; 13(14):1975. https://doi.org/10.3390/w13141975
Chicago/Turabian StyleGuo, Tianting, Chunwei Liu, Ying Xiang, Pei Zhang, and Ranghui Wang. 2021. "Simulations of the Soil Evaporation and Crop Transpiration Beneath a Maize Crop Canopy in a Humid Area" Water 13, no. 14: 1975. https://doi.org/10.3390/w13141975





