Avocado cv. Hass Needs Water Irrigation in Tropical Precipitation Regime: Evidence from Colombia
Abstract
:1. Introduction
2. Materials and Methods
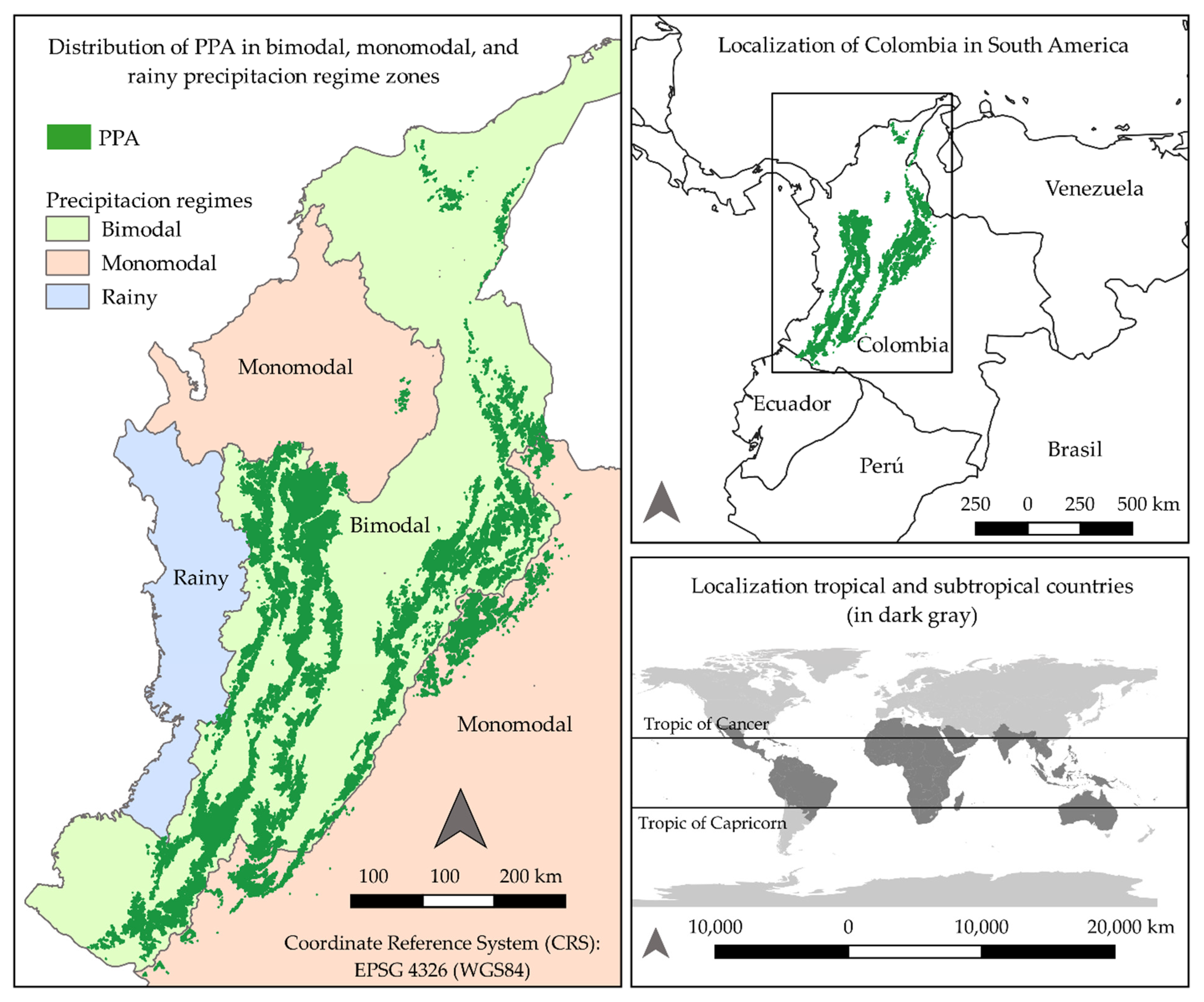
2.1. Localization of the Study
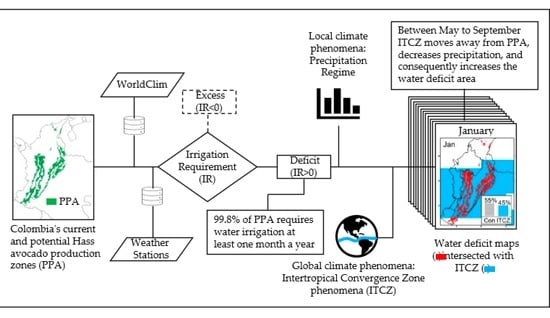
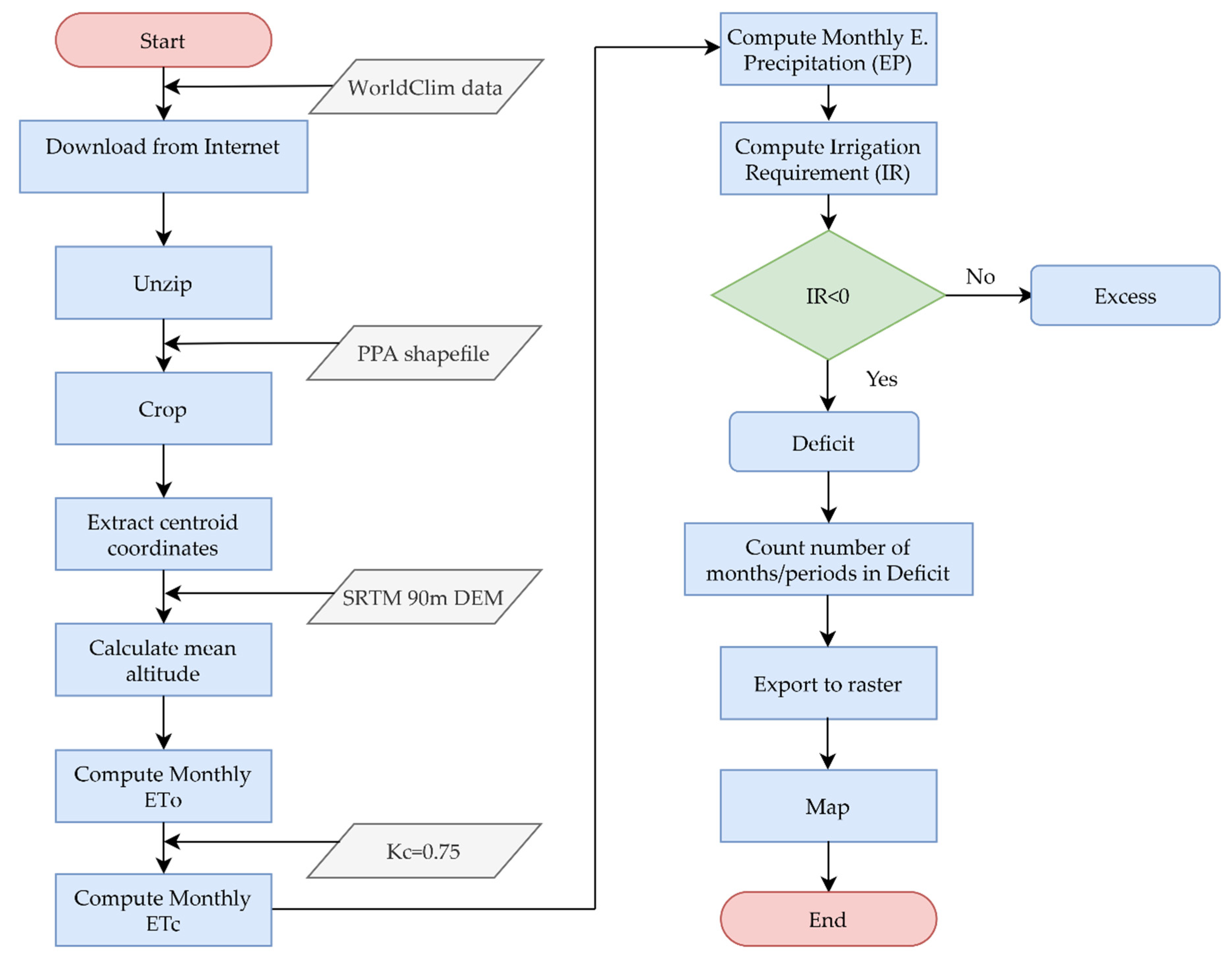
2.2. Model Development of the Irrigation Requirement
2.3. Intertropical Convergence Zone Localization Model
2.4. Description, Acquisition, and Processing of Data
2.5. Model and Data Source Validation
2.6. Computing the Location of Intertropical Convergence Zone and Its Influence on Irrigation Requirement
3. Results
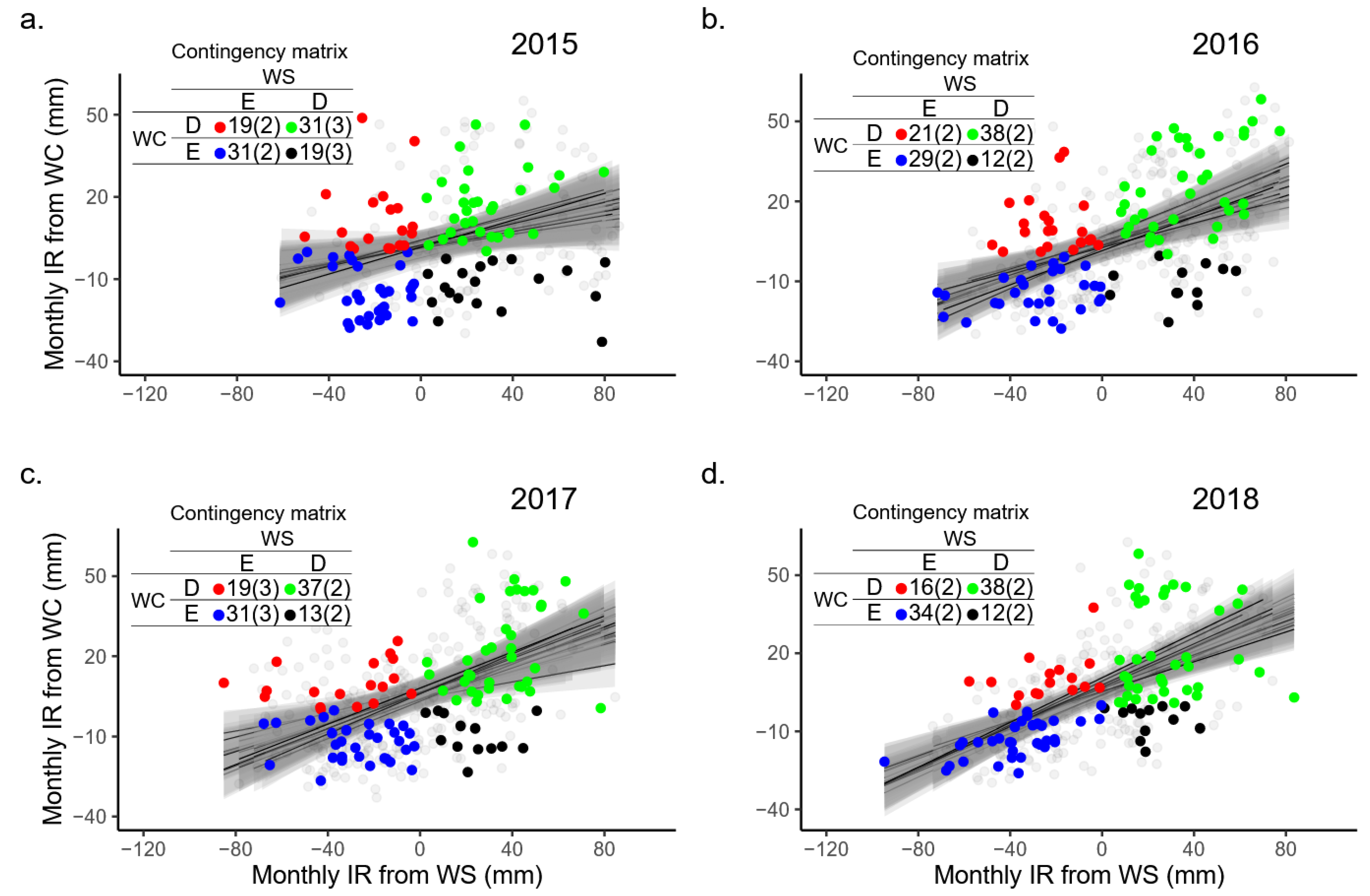
3.1. Model and Data Source Validation
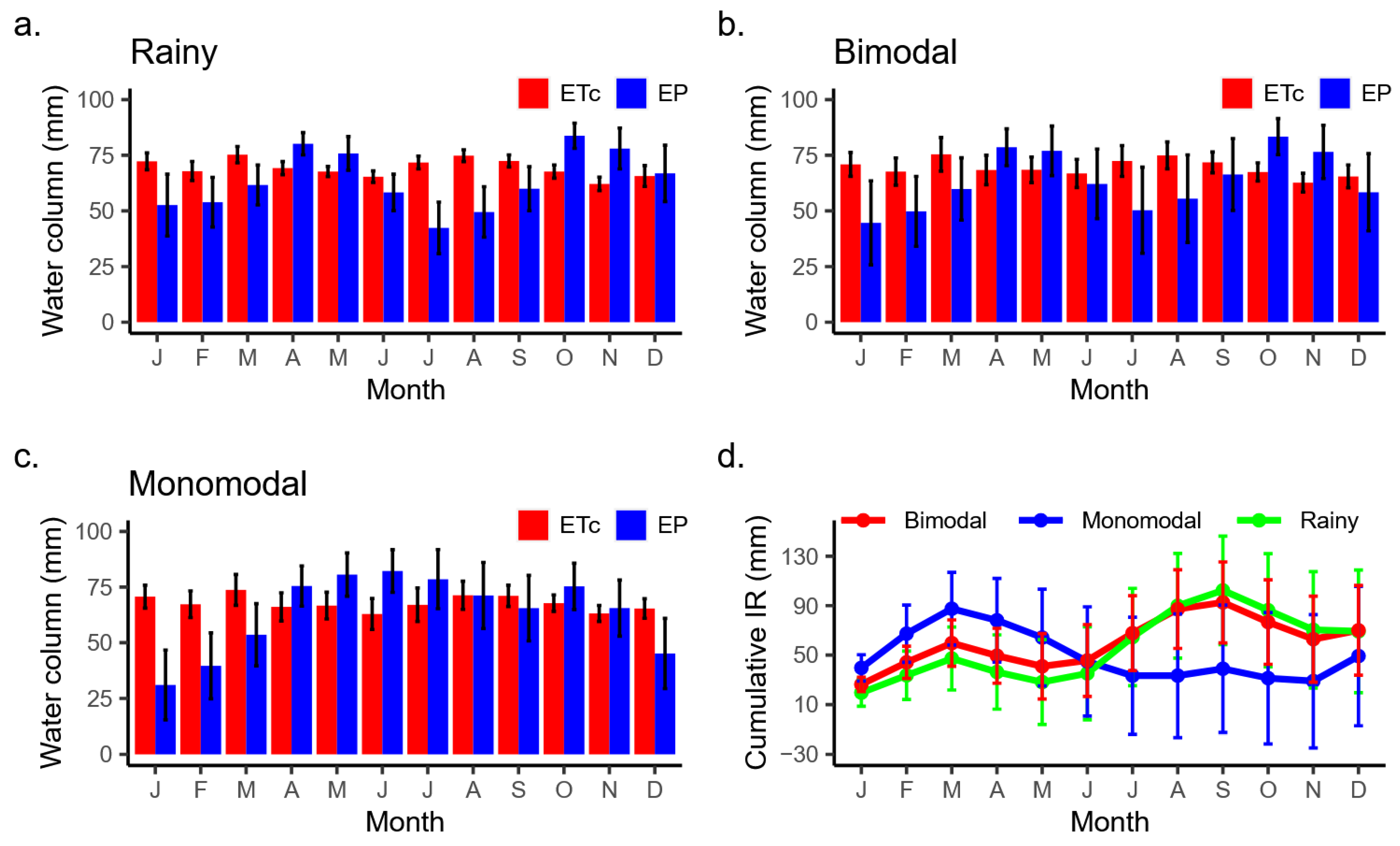
3.2. Annual Distribution of Crop Evapotranspiration and Effective Precipitation
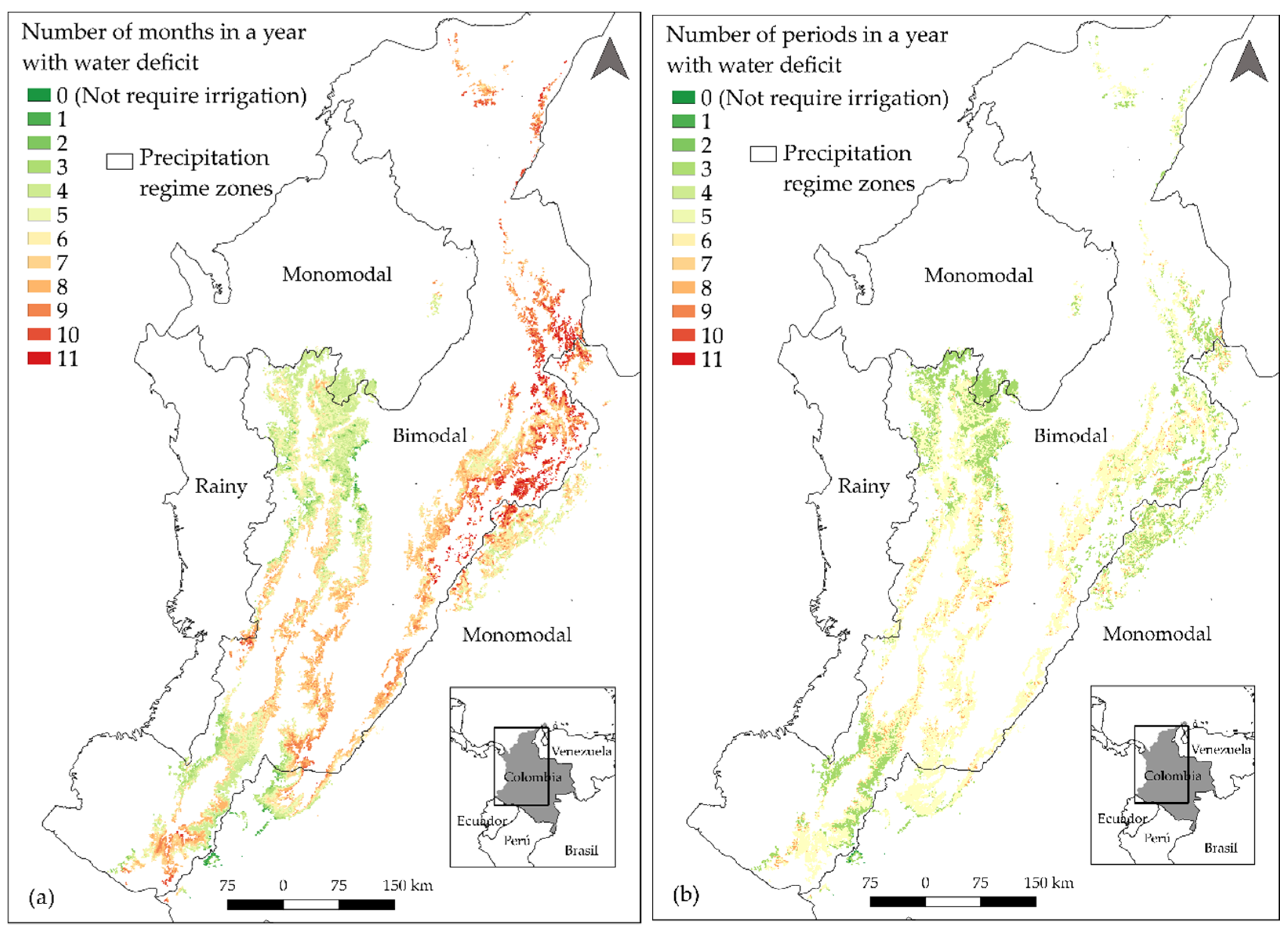
3.3. Water Deficit Visualizations under Geographic Space
3.4. Temporal and Spatial Variation of Irrigation Zones and Computing the Location of Intertropical Convergence Zone and Its Influence on Irrigation Requirement
4. Discussion
4.1. Model and Data Source Validation
4.2. Water Deficit Visualization in Geographic Space
4.3. Influence on Irrigation Requirementof Intertropical Convergence Zone
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- FAOSTAT. Food and Agriculture Data. Available online: http://www.fao.org/faostat/en/#home (accessed on 4 February 2021).
- Serrano, A.; Brooks, A. Who is left behind in global food systems? Local farmers failed by Colombia’s avocado boom. Environ. Plan. E Nat. Space 2019, 2, 348–367. [Google Scholar] [CrossRef] [Green Version]
- Ramírez-Gil, J.G.; Morales, J.G.; Peterson, A.T. Potential geography and productivity of “Hass” avocado crops in Colombia estimated by ecological niche modeling. Sci. Hortic. 2018, 237, 287–295. [Google Scholar] [CrossRef]
- Ramírez-Gil, J.G.; Henao-Rojas, J.C. Mitigation of the Adverse Effects of the El Niño (El Niño, La Niña) Southern Oscillation (ENSO) Phenomenon and the Most Important Diseases in Avocado cv. Hass Crops. Plants 2020, 9, 790. [Google Scholar] [CrossRef]
- Ramírez-Gil, J.G.; Cobos, M.E.; Jiménez-García, D.; Morales-Osorio, J.G.; Peterson, A.T. Current and potential future distributions of Hass avocados in the face of climate change across the Americas. Crop Pasture Sci. 2019, 70, 694–708. [Google Scholar] [CrossRef]
- Nikolaou, G.; Neocleous, D.; Christou, A.; Kitta, E.; Katsoulas, N. Implementing Sustainable Irrigation in Water-Scarce Regions under the Impact of Climate Change. Agronomy 2020, 10, 1120. [Google Scholar] [CrossRef]
- Silva, S.R.D.; Cantuarias-Avilés, T.E.; Chiavelli, B.; Martins, M.A.; Oliveira, M.S. Phenological models for implementing management practices in rain-fed avocado orchards1. Pesqui. Agropecu. Trop. 2017, 47, 321–327. [Google Scholar] [CrossRef] [Green Version]
- Castillo-Argaez, R.; Schaffer, B.; Vazquez, A.; Sternberg, L.D.S.L. Leaf gas exchange and stable carbon isotope composition of redbay and avocado trees in response to laurel wilt or drought stress. Environ. Exp. Bot. 2020, 171. [Google Scholar] [CrossRef]
- Moreno-Ortega, G.; Pliego, C.; Sarmiento, D.; Barceló, A.; Martínez-Ferri, E. Yield and fruit quality of avocado trees under different regimes of water supply in the subtropical coast of Spain. Agric. Water Manag. 2019, 221, 192–201. [Google Scholar] [CrossRef]
- Silber, A.; Naor, A.; Cohen, H.; Bar-Noy, Y.; Yechieli, N.; Levi, M.; Noy, M.; Peres, M.; Duari, D.; Narkis, K.; et al. Irrigation of ‘Hass’ avocado: Effects of constant vs. temporary water stress. Irrig. Sci. 2019, 37, 451–460. [Google Scholar] [CrossRef]
- Ramírez-Gil, J.G.; López, J.H.; Henao-Rojas, J.C. Causes of hass avocado fruit rejection in preharvest, harvest, and packinghouse: Economic losses and associated variables. Agronomy 2020, 10, 8. [Google Scholar] [CrossRef] [Green Version]
- Hernández, I.; Fuentealba, C.; Olaeta, J.A.; Lurie, S.; Defilippi, B.G.; Campos-Vargas, R.; Pedreschi, R. Factors associated with postharvest ripening heterogeneity of “Hass” avocados (Persea americana Mill). Fruits 2016, 71, 259–268. [Google Scholar] [CrossRef] [Green Version]
- Kadbhane, S.J.; Manekar, V.L. Grape production assessment using surface and subsurface drip irrigation methods. J. Water Land Dev. 2021, 49, 169–178. [Google Scholar] [CrossRef]
- Kang, S.; Shin, Y.; Xie, S.-P. Extratropical forcing and tropical rainfall distribution: Energetics framework and ocean Ekman advection. Clim. Atmos. Sci. 2018, 1, 20172. [Google Scholar] [CrossRef] [Green Version]
- Mesa-Sánchez, Ó.J.; Rojo-Hernández, J.D. On the general circulation of the atmosphere around Colombia. Rev. Acad. Colomb. Cienc. Exactas Fis. Nat. 2020, 44, 857–875. [Google Scholar] [CrossRef]
- Takahashi, K.; Battisti, D.S. Processes controlling the mean tropical pacific precipitation pattern. Part I: The Andes and the eastern Pacific ITCZ. J. Clim. 2007, 20, 3434–3451. [Google Scholar] [CrossRef] [Green Version]
- Stephens, G.L.; Smalley, M.A.; Lebsock, M.D. The Cloudy Nature of Tropical Rains. J. Geophys. Res. Atmos. 2019, 124, 171–188. [Google Scholar] [CrossRef]
- Byrne, M.; Pendergrass, A.; Rapp, A.; Wodzicki, K. Response of the Intertropical Convergence Zone to Climate Change: Location, Width, and Strength. Curr. Clim. Chang. Rep. 2018, 4, 355–370. [Google Scholar] [CrossRef] [Green Version]
- Julich, S.; Mwangi, H.; Feger, K.-H. Forest Hydrology in the Tropics. In Tropical Forestry Handbook; Pancel, L., Köhl, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1917–1939. [Google Scholar]
- Mamalakis, A.; Foufoula-Georgiou, E. A Multivariate Probabilistic Framework for Tracking the Intertropical Convergence Zone: Analysis of Recent Climatology and Past Trends. Geophys. Res. Lett. 2018, 45, 13080–13089. [Google Scholar] [CrossRef]
- Richter, M. Precipitation in the Tropics. In Tropical Forestry Handbook; Pancel, L., Köhl, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2016; pp. 363–390. [Google Scholar]
- González-Orozco, C.E.; Porcel, M.; Alzate Velásquez, D.F.; Orduz-Rodríguez, J.O. Extreme climate variability weakens a major tropical agricultural hub. Ecol. Indic. 2020, 111, 106015. [Google Scholar] [CrossRef]
- Grajales, L. Uso Racional del Agua de Riego en Cultivo de Aguacate Hass (Persea Americana) en tres Zonas Productoras de Colombia; Universidad Nacional de Colombia: Bogotá, Colombia, 2017. [Google Scholar]
- NRCS Water Requirements. National Engineering Handbook: Irrigation Guide. Part 652; United States Department of Agriculture: Washington, DC, USA, 1997; p. 754. [Google Scholar]
- Bos, M.; Kselik, R.; Allen, R.; Molden, D. Water Requirements for Irrigation and the Environment; Springer: Dordrecht, The Netherlands, 2009; ISBN 978-1-4020-8947-3. [Google Scholar]
- Allen, R.; Pereira, L.; Raes, D.; Smith, M. FAO Irrigation and Drainage Paper No. 56: Crop Evapotranspiration (Guidelines for Computing Water Requirements); Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Ali, M. Field Water Balance. In Fundamentals of Irrigation and On-Farm Water Management; Springer: Mymensingh, Bangladesh, 2010; Volume 1, pp. 331–372. ISBN 9781441963345. [Google Scholar]
- Carr, M.K.V. The water relations and irrigation requirements of avocado (Persea americana Mill.): A review. Exp. Agric. 2013, 49, 256–278. [Google Scholar] [CrossRef]
- Silber, A.; Israeli, Y.; Levi, M.; Keinan, A.; Shapira, O.; Chudi, G.; Golan, A.; Noy, M.; Levkovitch, I.; Assouline, S. Response of “Hass” avocado trees to irrigation management and root constraint. Agric. Water Manag. 2012, 104, 95–103. [Google Scholar] [CrossRef]
- Holzapfel, E.; de Souza, J.A.; Jara, J.; Guerra, H.C. Responses of avocado production to variation in irrigation levels. Irrig. Sci. 2017, 35, 205–215. [Google Scholar] [CrossRef]
- Fick, S.E.; Hijmans, R.J. WorldClim 2: New 1-km spatial resolution climate surfaces for global land areas. Int. J. Climatol. 2017, 37, 4302–4315. [Google Scholar] [CrossRef]
- UPRA. Zonificación de Aptitud Para el Cultivo Comercial de Aguacate Hass en Colombia, a Escala 1:100.000; Ministerio de Agricultura y Desarrollo Rural: Bogotá, Colombia, 2018. [Google Scholar]
- IDEAM. Consulta y Descarga de Datos Hidrometeorológicos. Available online: http://dhime.ideam.gov.co/atencionciudadano/ (accessed on 4 July 2019).
- Ballabio, C.; Borrelli, P.; Spinoni, J.; Meusburger, K.; Michaelides, S.; Beguería, S.; Klik, A.; Petan, S.; Janeček, M.; Olsen, P.; et al. Mapping monthly rainfall erosivity in Europe. Sci. Total Environ. 2017, 579, 1298–1315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guzmán, D.; Ruíz, J.F.; Cadena, M. Regionalización de Colombia según la Estacionalidad de la Precipitación Media Mensual, a Través Análisis de Componentes Principales (ACP); IDEAM: Bogotá, Colombia, 2014. [Google Scholar]
- Lee, H.-T. Program NOAA CDR NOAA Climate Data Record (CDR) of Monthly Outgoing Longwave Radiation (OLR), Version 2.2-1. Available online: https://data.nodc.noaa.gov/cgi-bin/iso?id=gov.noaa.ncdc:C00809# (accessed on 16 May 2020).
- WorldClim. Historical Climate Data. Available online: https://www.worldclim.org/data/worldclim21.html (accessed on 15 January 2020).
- CGIAR. SRTM 90m Digital Elevation Database. Available online: https://bigdata.cgiar.org/srtm-90m-digital-elevation-database/ (accessed on 8 July 2021).
- R Core Team. R: A Language and Environment for Statistical Computing, Vienna, Austria. 2020. Available online: https://www.R-project.org (accessed on 15 September 2020).
- NOAA. NOAA Interpolated Outgoing Longwave Radiation (OLR). Available online: https://psl.noaa.gov/data/gridded/data.interp_OLR.html (accessed on 14 May 2020).
- QGIS. Development Team QGIS Geographic Information System. 2020. Available online: http://qgis.org (accessed on 1 August 2020).
- Guo, D.; Peterson, T. Package Evapotranspiration: Modelling Actual, Potential and Reference Crop Evapotranspiration. 2020. Available online: https://cran.r-project.org/package=evapotranspiration (accessed on 20 September 2020).
- Agresti, A. Contingency Tables. In An Introduction to Categorical Data Analysis; John Wiley & Sons: Gainesville, FL, USA, 2007; pp. 21–64. [Google Scholar]
- Satizábal, H.; Pérez-Uribe, A. Relevance Metrics to Reduce Input Dimensions in Artificial Neural Networks. In Artificial Neural Networks—ICANN 2007; Marques de Sá, J., Alexandre, L., Duch, W., Mandic, D., Eds.; Springer: Porto, Portugal, 2007; pp. 39–48. ISBN 978-3-540-74690-4. [Google Scholar]
- Galushkin, A. Neural Networks Theory; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-540-48125-6. [Google Scholar]
- Fritsch, S.; Guenther, F.; Wright, M.; Suling, M.; Mueller, S. Package “Neuralnet”: Training of Neural Networks. 2019. Available online: https://cran.r-project.org/package=neuralnet (accessed on 3 July 2019).
- Djaman, K.; Irmak, S.; Sall, M.; Sow, A.; Kabenge, I. Comparison of sum-of-hourly and daily time step standardized ASCE Penman-Monteith reference evapotranspiration. Theor. Appl. Climatol. 2018, 134, 533–543. [Google Scholar] [CrossRef]
- Allen, R.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98, 899–920. [Google Scholar] [CrossRef] [Green Version]
- Elnashar, A.; Wang, L.; Wu, B.; Zhu, W.; Zeng, H. Synthesis of global actual evapotranspiration from 1982 to 2019. Earth Syst. Sci. Data 2021, 13, 447–480. [Google Scholar] [CrossRef]
- Trabucco, A.; Zomer, R. Global High-Resolution Soil-Water Balance. Available online: https://cgiarcsi.community/data/global-high-resolution-soil-water-balance/ (accessed on 8 July 2021).
- Zhuang, W.; Shi, H.; Ma, X.; Cleverly, J.; Beringer, J.; Zhang, Y.; He, J.; Eamus, D.; Yu, Q. Improving Estimation of Seasonal Evapotranspiration in Australian Tropical Savannas using a Flexible Drought Index. Agric. For. Meteorol. 2020, 295, 108203. [Google Scholar] [CrossRef]
- Han, M.; Zhang, H.; Chávez, J.L.; Ma, L.; Trout, T.J.; DeJonge, K.C. Improved soil water deficit estimation through the integration of canopy temperature measurements into a soil water balance model. Irrig. Sci. 2018, 36, 187–201. [Google Scholar] [CrossRef]
- Garrido-Rubio, J.; Sanz, D.; González-Piqueras, J.; Calera, A. Application of a remote sensing-based soil water balance for the accounting of groundwater abstractions in large irrigation areas. Irrig. Sci. 2019, 709–724. [Google Scholar] [CrossRef]
- Mainuddin, M.; Kirby, M.; Chowdhury, R.A.R.; Shah-Newaz, S.M. Spatial and temporal variations of, and the impact of climate change on, the dry season crop irrigation requirements in Bangladesh. Irrig. Sci. 2015, 33, 107–120. [Google Scholar] [CrossRef]
- Steele, D.D.; Thoreson, B.P.; Hopkins, D.G.; Clark, B.A.; Tuscherer, S.R.; Gautam, R. Spatial mapping of evapotranspiration over Devils Lake Basin with SEBAL: Application to flood mitigation via irrigation of agricultural crops. Irrig. Sci. 2015, 33, 15–29. [Google Scholar] [CrossRef]
- Adam, O.; Bischoff, T.; Schneider, T. Seasonal and interannual variations of the energy flux equator and ITCZ. Part I: Zonally averaged ITCZ position. J. Clim. 2016, 29, 3219–3230. [Google Scholar] [CrossRef]
- Barrios-Perez, C.; Okada, K.; Varón, G.G.; Ramirez-Villegas, J.; Rebolledo, M.C.; Prager, S.D. How does El Niño Southern Oscillation affect rice-producing environments in central Colombia? Agric. For. Meteorol. 2021, 306. [Google Scholar] [CrossRef]
- Guimberteau, M.; Laval, K.; Perrier, A.; Polcher, J. Global effect of irrigation and its impact on the onset of the Indian summer monsoon. Clim. Dyn. 2012, 39, 1329–1348. [Google Scholar] [CrossRef]
- Meza, F. Use of ENSO-Driven Climatic Information for Optimum Irrigation under Drought Conditions: Preliminary Assessment Based on Model Results for the Maipo River Basin, Chile. In Climate Prediction and Agriculture: Advances and Challenges; Sivakumar, M., Hansen, J., Eds.; Springer: Berlin/Heidelberg, Germany,, 2007; pp. 79–88. ISBN 9781626239777. [Google Scholar]
- IDEAM. Boletín Hidroclimatológico Mensual. Available online: http://www.ideam.gov.co/web/tiempo-y-clima/climatologico-mensual (accessed on 2 March 2021).
| Variable Name | Units | Format | Source |
|---|---|---|---|
| Hass Avocado’s Potential production area in Colombia | m2 | Shapefile | Datos Abiertos (https://www.datos.gov.co/) (accessed on 10 December 2019) [32] |
| Solar radiation | KJ m−2 day−1 | GeoTIFF | WorldClim (https://www.worldclim.org/) (accessed on 15 January 2020) [37] |
| Maximum temperature | °C | GeoTIFF | WorldClim (https://www.worldclim.org/) |
| Minimum temperature | °C | GeoTIFF | WorldClim (https://www.worldclim.org/) |
| Average temperature | °C | GeoTIFF | WorldClim (https://www.worldclim.org/) |
| Wind speed | m s−1 | GeoTIFF | WorldClim (https://www.worldclim.org/) |
| Water vapor pressure | kPa | GeoTIFF | WorldClim (https://www.worldclim.org/) |
| Precipitation | mm | GeoTIFF | WorldClim (https://www.worldclim.org/) |
| Altitude | m | GeoTIFF | SRTM 90 m (http://srtm.csi.cgiar.org/) (accessed on 8 July 2021) [38] |
| Day of year | DOY | dd-mm-yy | R function lubridate::days_in_month(…) [39] |
| Geographic coordinates | Decimal degrees | dd.ddddd | Centroid of WorldClim pixels |
| Outgoing Longwave Radiation | W m−2 | netCDF | NOAA (https://www.ncdc.noaa.gov/) (accessed on 14 May 2020) [40] |
| Regime | Jan | Feb | Mar | Apr | May | Jun | Jul | Aug | Sep | Oct | Nov | Dec |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bimodal | 58,804 | 54,864 | 53,652 | 7061 | 12,085 | 40,371 | 56,086 | 52,805 | 38,283 | 3174 | 9186 | 42,129 |
| Rainy | 291 | 302 | 304 | 18 | 69 | 290 | 331 | 321 | 304 | 1 | 16 | 161 |
| Monomodal | 13,045 | 12,342 | 10,555 | 1926 | 1070 | 376 | 2455 | 5666 | 8803 | 2772 | 5315 | 11,636 |
| Total | 72,140 | 67,508 | 64,511 | 9005 | 13,224 | 41,037 | 58,872 | 58,792 | 47,390 | 5947 | 14,517 | 53,926 |
| Percentage | 91.1 | 85.3 | 81.5 | 11.4 | 16.7 | 51.9 | 74.4 | 74.3 | 59.9 | 7.5 | 18.3 | 68.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erazo-Mesa, E.; Ramírez-Gil, J.G.; Sánchez, A.E. Avocado cv. Hass Needs Water Irrigation in Tropical Precipitation Regime: Evidence from Colombia. Water 2021, 13, 1942. https://doi.org/10.3390/w13141942
Erazo-Mesa E, Ramírez-Gil JG, Sánchez AE. Avocado cv. Hass Needs Water Irrigation in Tropical Precipitation Regime: Evidence from Colombia. Water. 2021; 13(14):1942. https://doi.org/10.3390/w13141942
Chicago/Turabian StyleErazo-Mesa, Edwin, Joaquín Guillermo Ramírez-Gil, and Andrés Echeverri Sánchez. 2021. "Avocado cv. Hass Needs Water Irrigation in Tropical Precipitation Regime: Evidence from Colombia" Water 13, no. 14: 1942. https://doi.org/10.3390/w13141942
APA StyleErazo-Mesa, E., Ramírez-Gil, J. G., & Sánchez, A. E. (2021). Avocado cv. Hass Needs Water Irrigation in Tropical Precipitation Regime: Evidence from Colombia. Water, 13(14), 1942. https://doi.org/10.3390/w13141942