1. Introduction
Freshwater scarcity has become a pivotal issue in sustainable development [
1,
2,
3], especially in arid and semi-arid regions (ASARs) where communities are encountering water scarcity problems, not only in agricultural and industrial sectors, but also for satisfying domestic water demands [
4,
5,
6,
7]. Most countries in North Africa and the Middle East are facing water scarcity and its related consequences [
8]. Moreover, various factors, such as accelerated climate change, population growth, intensive agricultural activities, and industrialization, as well as continuous pollution of water resources, will exacerbate freshwater scarcity and shortages in the future [
9,
10]. Therefore, more studies are needed in order to focus more specifically on water conservation planning and management, and the sustainable use of potential water resources [
5,
8,
11].
Rainwater harvesting (RWH) can be considered as one of the most cost-effective and environmentally-friendly water conservation methods, especially in ASARs, which simultaneously address water scarcity issues and alleviates groundwater over-extraction [
2,
12,
13,
14]. From a historical perspective, archeological evidence found in Southwest Asia revealed that RWH has been practiced since the Neolithic Age (around 10,000 BC to 4500 BC) [
11,
15]. Moreover, examples of RWH structures were discovered in Tunisia, Greece, China, and historical Palestine, tracing back thousands of years [
2,
16]. In general, all schemes for collecting and storing rainwater to supply safe and inexpensive water for different purposes, such as domestic, industrial, and agricultural purposes are identified as RWHs [
17,
18,
19].
In developing countries, where domestic water utilization is low, RWH can meet a large amount of water demand [
20,
21]. Furthermore, harvested water can be managed and diverted for other purposes, such as groundwater recharge, downstream flood mitigation, soil moisture improvement, irrigation, and livestock purposes [
1,
22,
23]. However, identifying RWH potential areas/zones could be challenging, since several criteria need to be considered, including hydrology, climatic condition, topography, and soil parameters, to maximize water availability, particularly in ASARs [
24,
25].
Many methods have been applied to incorporate contributing RWH factors to locate potential RWH areas. In this regard, the integrated application of multi-criteria decision analysis (MCDA) and geographic information systems (GIS) has been frequently used for a wide range of objectives in water resource research, including potential RWH assessment [
26,
27,
28]. In Saudi Arabia, geospatial and MCDA methods were implemented for identifying potential areas for some RWH structures [
29]. In Egypt, potential RWH and storage areas were determined using remote sensing and decision support systems [
30]. In South Africa, in-field RWH and ex-field RWH suitability maps were developed by combining ecological, physical, and socio-economic factors [
20]. There are other studies that have been done in which assessment of potential RWHs was conducted through the incorporation of biophysical factors (e.g., slope, soil type, land use) [
31,
32].
As a multi-criteria decision-making (MCDM) system, the analytical hierarchy process (AHP) was introduced by Saaty [
33,
34]. It is a favorable decision-supporting technique for solving multiplex problems [
35]. Particularly, it has been recognized as the most applicable decision method for the identification of potential RWH areas, along with the GIS platform [
36]. In the AHP technique, based on the knowledge of experts and mathematics, decisions are organized and analyzed in a structured procedure. The primary idea behind AHP is to use hierarchical symbols to represent the components of any issue and show links between them [
35]. Many studies have made extensive use of AHP in order to identify possible RWH sites [
37].
The majority of related studies indicate that the utilization of practical approaches, as well as the selection of proper/suitable criteria, are the two main factors in the successful implementation of geospatial and MCDA methods in mapping potential RWH areas [
29,
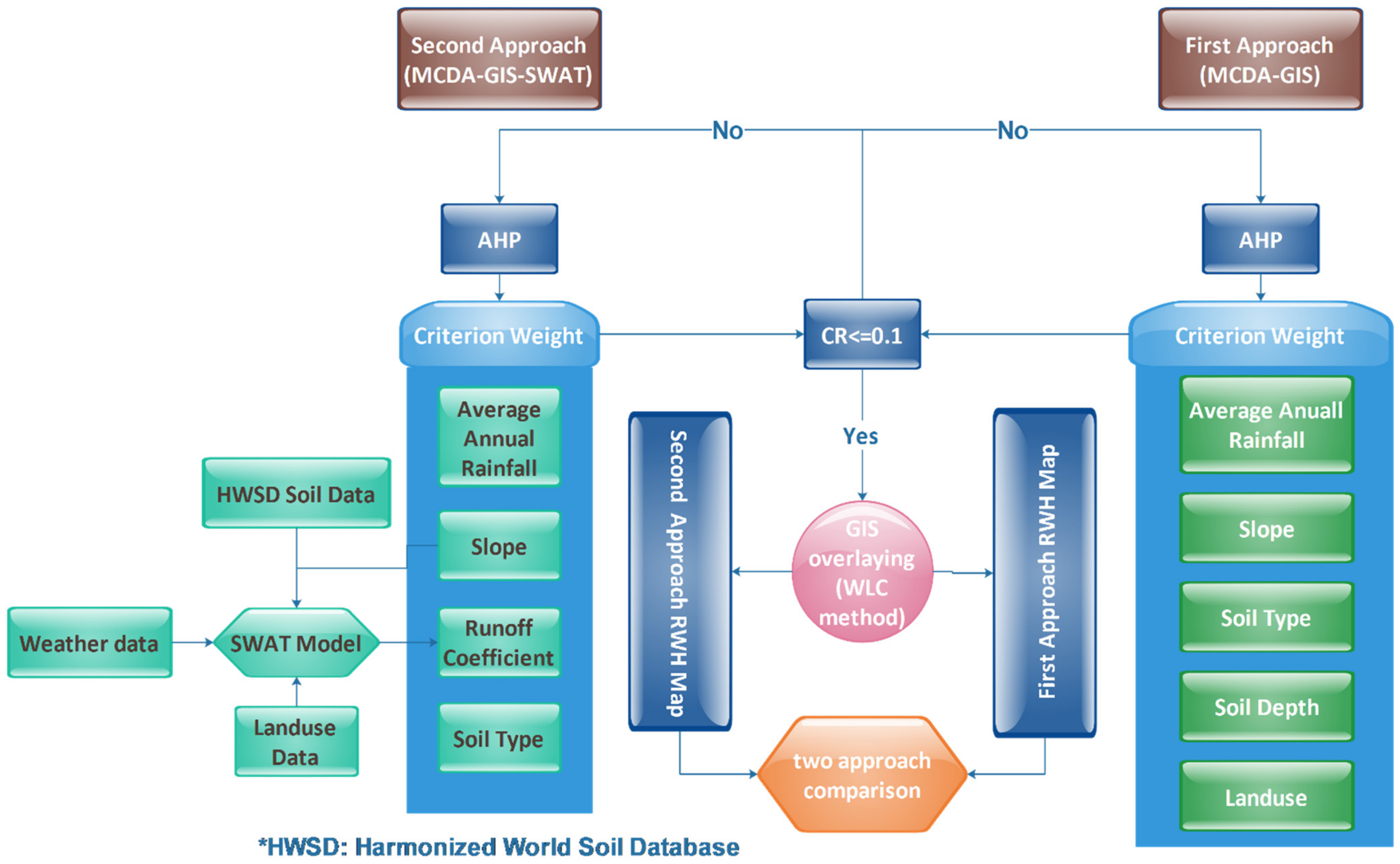
38]. In this study, an assessment of potential RWH through the incorporation of biophysical parameters into MCDA, within a GIS environment, as a frequently used approach, is conducted. Furthermore, the novel approach of integration of SWAT as a hydrological model with MCDA and GIS is adopted to evaluate potential RWHs. The integrated approach of hydrological modeling with MCDA and GIS toward the identification of potential RWH areas in ASARs has already been addressed in numerous studies [
25,
39,
40,
41]. The primary reason for utilizing a hydrological model is to obtain, either the potential runoff generation depth and coefficient map, or to incorporate the obtained layer into MCDA to enhance the RWH site selection criteria. Additionally, studies revealed that the combination of SWAT with GIS and MCDA reduces the likelihood of inherent biases in GIS-based MCDA.
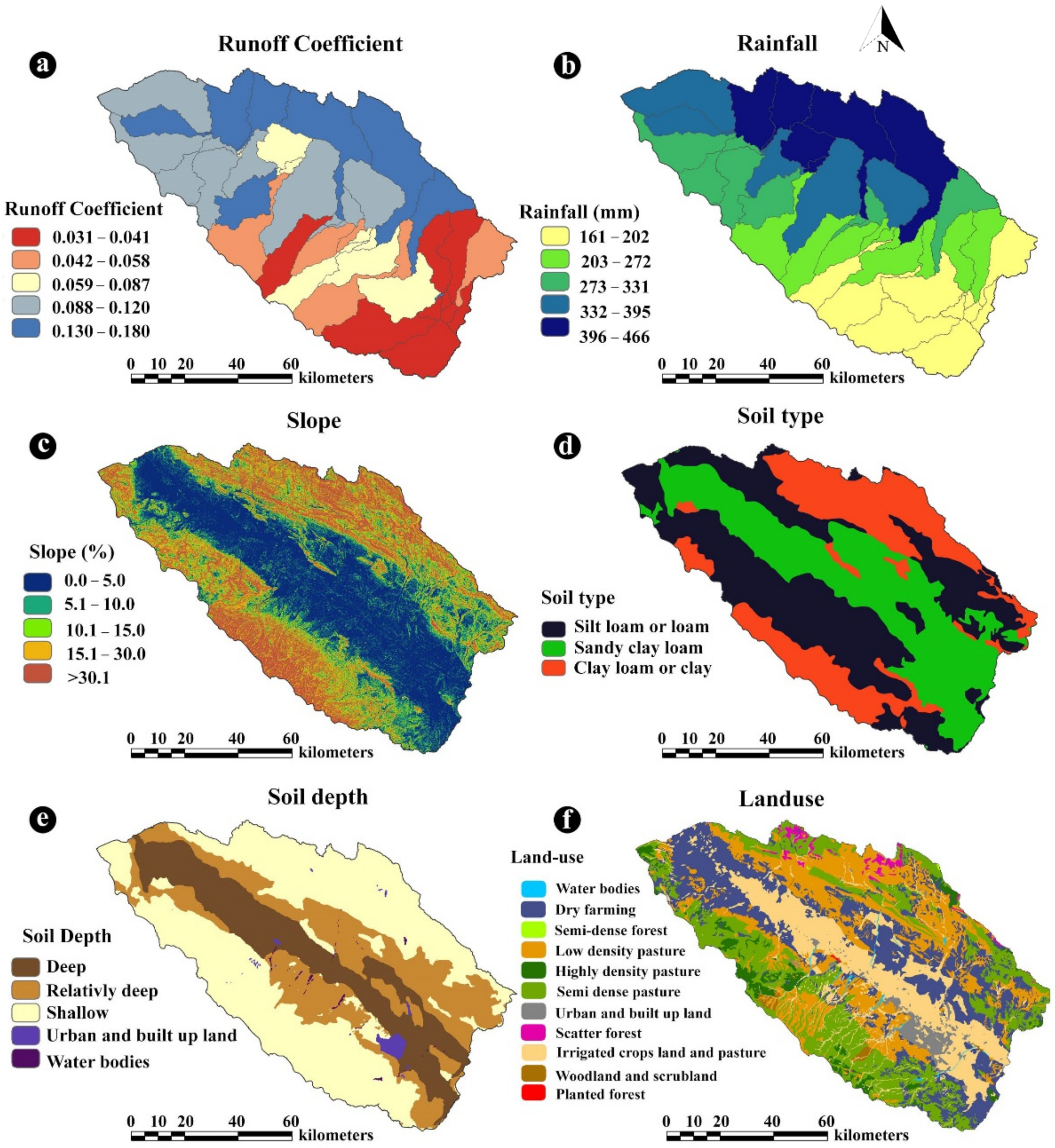
The runoff coefficient is considered as one of the most influential parameters in RWH assessment, accounting for major contributing factors, such as rainfall, topography, land use, and soil texture and structure [
29,
42]. Meanwhile, in most studies, a runoff coefficient map is generated by utilizing the widely-used method known as the soil conservation service-curve number (SCS-CN) method [
43,
44,
45]. The SCS-CN method calculates runoff depth based on land cover, hydrologic soil group, and antecedent soil moisture content. While the SCS-CN method is simple, easily applicable, and conceptually stable, it is constrained by some factors, such as the basin area (less than 8 km
2), low infiltration capacity, and high rainfall depth [
44,
46].
On the other hand, in ungagged basins, the SWAT model [
47] can be considered as a suitable option for hydrological simulations, particularly in developing countries lacking rainfall and runoff records [
48,
49,
50]. Data availability for most parts of the world, along with other advantageous features, including ease of representation, use of spatially available data, and capability of result presentation through GIS, increase the potential of integrating SWAT with the MCDA-GIS approach for the identification of potential RWH areas [
51,
52]. Moreover, the SWAT model, which requires a higher number of inputs, is more comprehensive compared to the SCS-CN, and its application can lead to a more accurate runoff coefficient map. In addition, the SWAT model includes, not only all factors used in the SCS-CN method, but also the independent interaction of influential factors, including infiltration and evaporation in rainfall–runoff modeling, which enables capturing more variability rather than relying on a single CN as a lumped parameter [
48].
This paper evaluates the impact of incorporating a hydrological model on improving the identification of suitable RWH locations. To enable the evaluation, two approaches, one including hydrological model and the other one excluding the hydrological model, are examined. The integrated MCDA-GIS approach was used as the first approach. The second approach, which incorporates hydrological modeling, was the combination of the SWAT model with MCDA and GIS. MPB is located in northeast Iran and struggles with water supply, especially in recent years. A parameters sensitivity analysis was performed to reduce the subjectivity of parameters selected using expert judgment [
48]. In addition, it identified the most sensitive criteria for locating potential RWH zones in MPB. In the end, the most applied RWH structures in ASARs were evaluated for MPB to find the best practices for high-potential areas for RWH.
The inclusive objectives of this research are to: (1) develop and compare the MCDA-GIS approach with the MCDA-GIS integrated with SWAT approach to identify potential RWH zones in the MPB; (2) implement sensitivity analyses on the two approaches to identify the most contributing criteria for potential RWH zone selection; (3) identify the potential location for three conventional RWH techniques (i.e., ponds and pans, terracing, and percolation tank) over MPB. The combined approach of the SWAT model, MCDA, and GIS was evaluated for the first time in ASARs. This paper is categorized as follows: in
Section 2, we describe the study basin and the data and methods used in this study.
Section 3 presents the results of the evaluation.
Section 4 describes conclusions and recommendations for future studies.
4. Conclusions
RWHs are recognized as an applicable and favorable method of water supply, as it conserves existing water resources, while contributes to water scarcity alleviation, particularly in ASARs. Nevertheless, identification of potential RWH areas is challenging due to the inherent uncertainty of input data and the subjectivity involved in selection of influential parameters. In the present study, two approaches for locating potential RWH areas were implemented. In the first approach, a frequently used MCDA-GIS method was utilized, while in the second approach, the SWAT model was included in the analysis in order to examine the effect of incorporating SWAT as a hydrological model into an MCDA-GIS method for RWH assessment. In this study, the SWAT model, as a more comprehensive hydrological model compared to the SCS curve number method was employed for generating the runoff coefficient map.
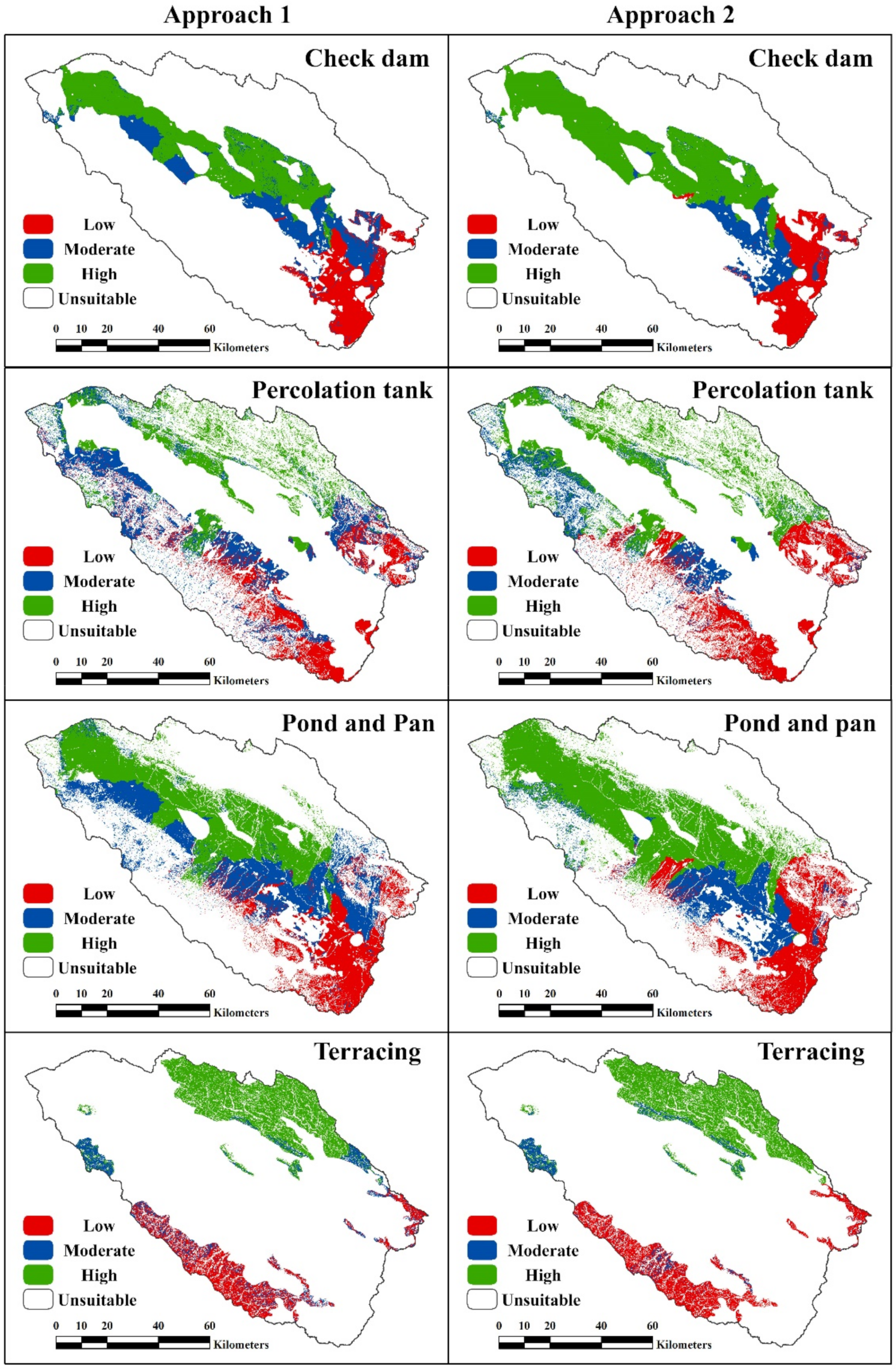
The resultant potential RWH maps of the two approaches indicated a similar pattern for potential RWH areas. In both potential RWH maps, the northern parts of the study area were categorized as the high potential areas, whereas less harvesting potential of rainwater was demonstrated for the southern areas of the case study. In addition, the overlap of the resultant maps of the two approaches indicated that 3394 km2 of the study area is considered a high-potential RWH area. These areas, mainly located in the northern parts of the study area receiving an average annual rainfall of 1366 MCM. Meanwhile, the total capacity of the large dams of Khorasan Razavi Province, where the study area is located, is 1549 MCM. Accordingly, there is high RWH potential in the study area that, if be managed and utilized efficiently, could contribute to water supply and ensure long-term water security.
The high value of the calculated correlation coefficient between the two resultant potential RWH maps (i.e., CC = 0.914), along with provided results, demonstrated that both approaches yield almost identical results. Therefore, it can be stated that the inclusion of SWAT as a hydrological model under the described methodology does not necessarily result in different outputs from conventional MCDA-GIS for RWH evaluation purposes, whereas it demands a higher degree of effort to run the hydrological models. On the other hand, the inclusion of hydrological models can be considered as an efficient strategy to reduce uncertainties embedded in RWH assessment using MCDA. Additionally, there would be less uncertainty associated with the overlapping high-potential RWH areas, since these areas are suggested by a combination of the two approaches, rather than a single conventional MCDA-GIS method.
Moreover, the results of the conducted sensitivity analyses indicate that the rainfall and slope criteria (with weights of 0.329 and 0.243, respectively) have the highest impact on the model in approach 1 whereas the criterion of runoff coefficient (with weights of 0.358) has the highest sensitivity in approach 2. The most-sensitive identified criteria could be ranked as the first priority for future data augmentation to ensure more accurate measurements due to their high weight in the analysis.
Based on the discussed results, a suitability map of the study area from the perspective of three different techniques was developed using various criteria related to each technique for both approaches 1 and 2, and for both models, with and without sensitivity analyses. Results indicate that the ponds and pans technique is the most suitable option for MPB, covering more areas with a high potential of RWH than the two other techniques for both approaches (21% of the study area on average). After that, terracing and percolation tank cover 11.6% and 10.5% of the study area with high potential for RWH on average, respectively.
It should be noted that the modeling cost, data availability and accuracy, and efficiency of these methods can vary significantly from basin to basin. In more developed countries, data can be obtained with minimal effort and have a high accuracy. On the other hand, the cost of developing a hydrologic model may defeat the purpose of integrating the hydrologic model with the MCDA-GIS approach. The abovementioned cost-benefit analysis is clearly beyond the scope of this project. It is recommended that the above approach be considered in other case studies where the flow of data is readily available and the SWAT model parameters can be calibrated. Therefore, the findings of this research can be compared against those of other areas and the reliability of these results can be further investigated.
Moreover, applying hydrologic models as comprehensive as SWAT are usually demanding in terms of data, time, and effort and their advantages need to justify their application. Meanwhile, since in this study generated maps from two approaches that were highly correlated which may not justify its application. This may be because of the fact that we intended to evaluate the efficiency of the model for areas suffering from data scarcity and, consequently, we did not calibrate the SWAT model. Considering this, we recommend applying this approach for areas with sufficient in situ data in order to calibrate the SWAT model and to assess the results from two approaches to check the justification for using a hydrologic model. It is possible that other hydrologic models result in a different conclusion than those drawn in this research and justify the use of hydrologic models for RWH. It is recommended that a group of different hydrologic models be considered to compare two approaches and further evaluate the use of hydrologic modeling in RWH. Moreover, the comparison between the two approaches might be impacted by the utilized MCDA method. It is recommended that a similar analysis be considered using other MCDA methods, such as ANP, and assess possible impacts. In the end, the identified high-potential RWH areas are based on the initial assessment of this study area. More specific and comprehensive studies are required to consider impacts of other hydrological processes, including evapotranspiration, to estimate the actual harvestable rainwater in these areas and fine-tune the water resources management of MPB.
Results of this research can potentially be helpful for further studies for populated areas in a developing country, such as Iran. While there are many technical issues for implementing RWH techniques in a populated area, such as MPB, it is an inevitable need to help satisfy the ever-increasing demand for domestic water. Consequently, it is well within expectations that this approach, or any other comparable one, be considered for application in the near future.