Stochastic Hybrid Event Based and Continuous Approach to Derive Flood Frequency Curve
Abstract
:1. Introduction
2. Data and Methods
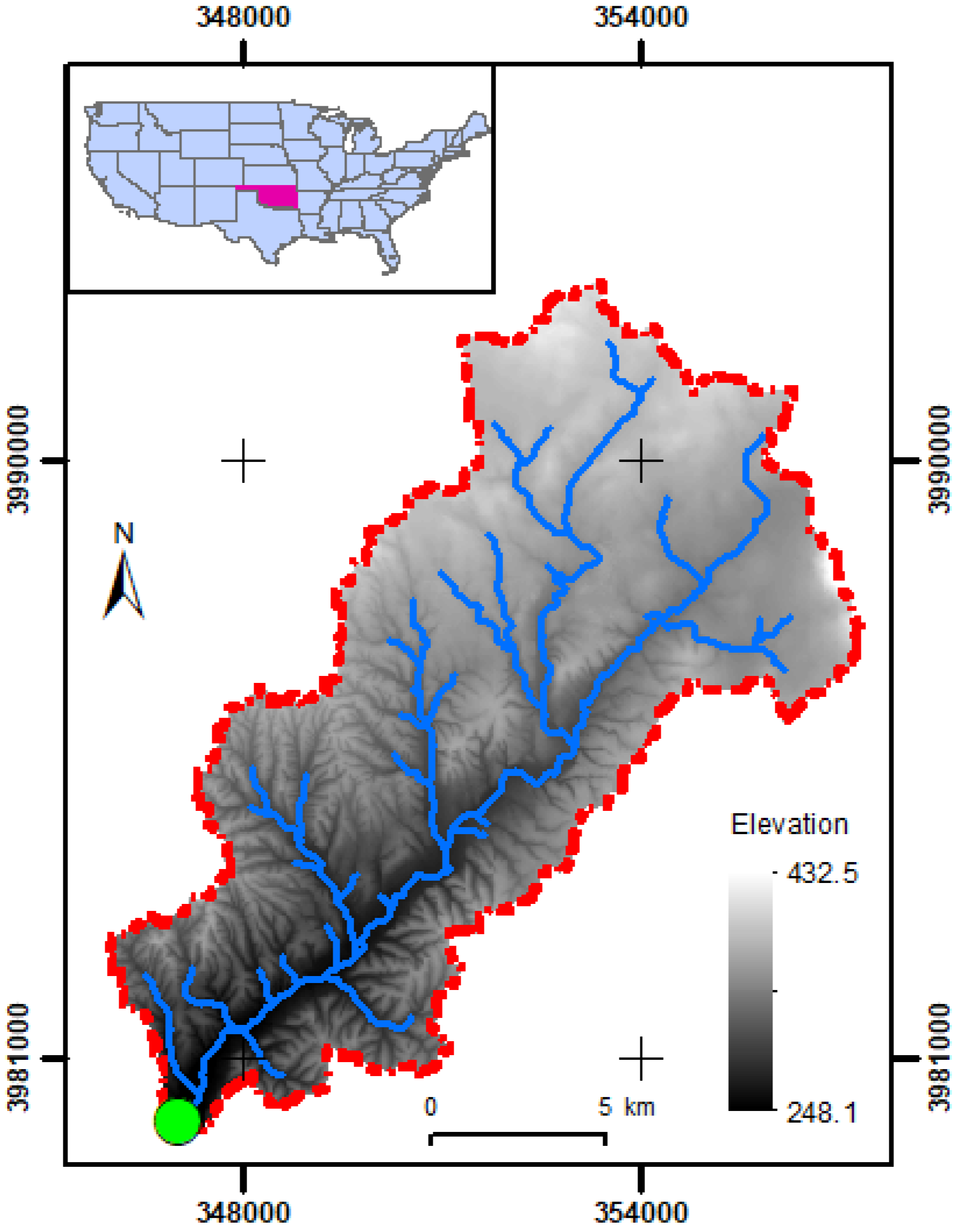
2.1. Case Study
2.2. Set Up of Modelling Experiments
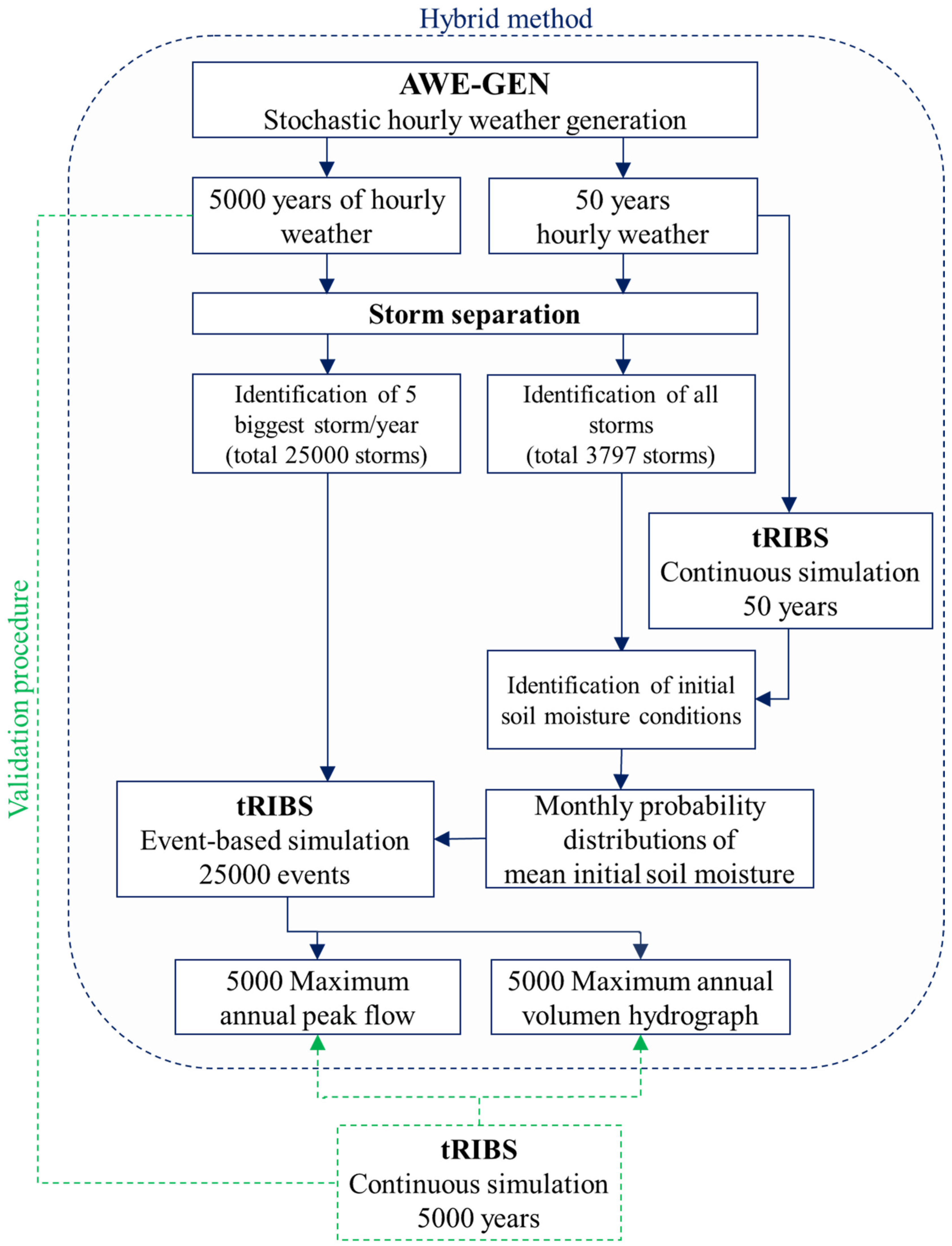
2.3. The Hybrid Method
2.4. Validation of the Method
2.5. Limitations of the Methodology
3. Results and Discussion
3.1. Calibration and Validation of Models
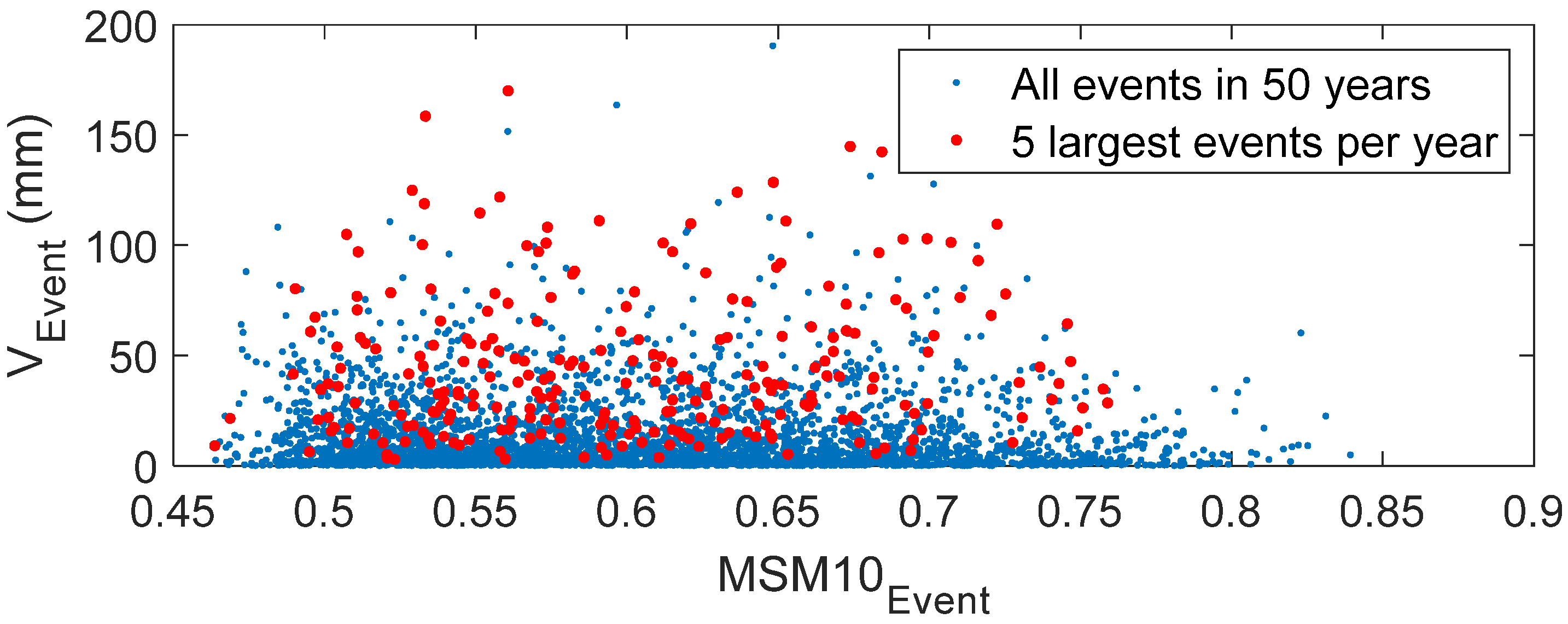
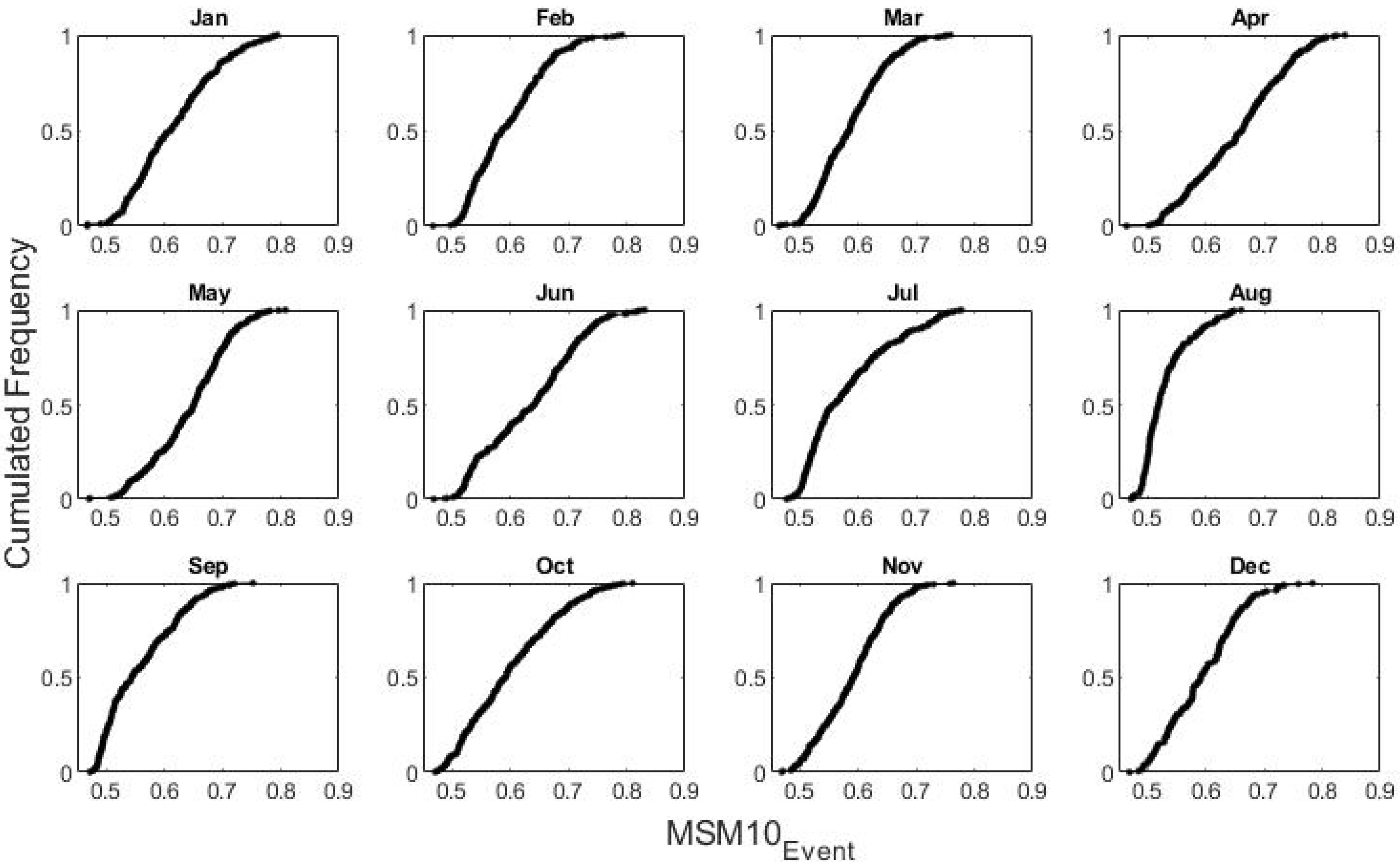
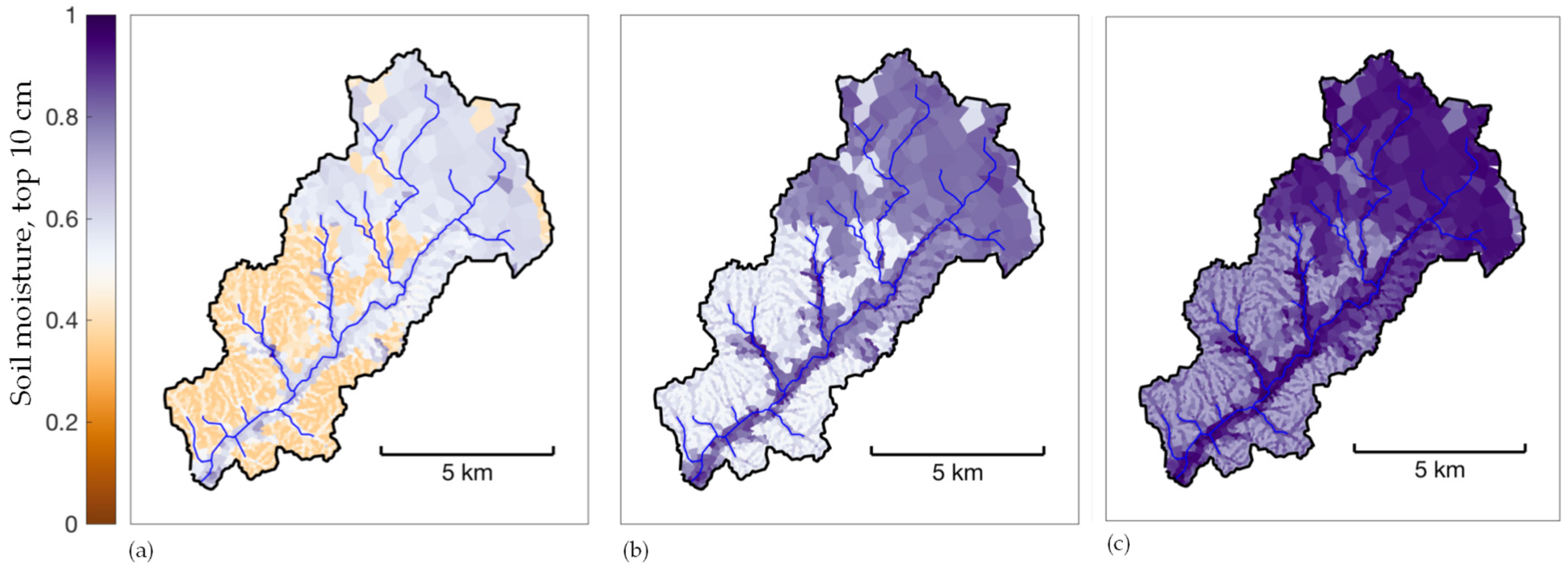
3.2. Initial Soil Moisture Analysis
3.3. Hybrid Method Performance
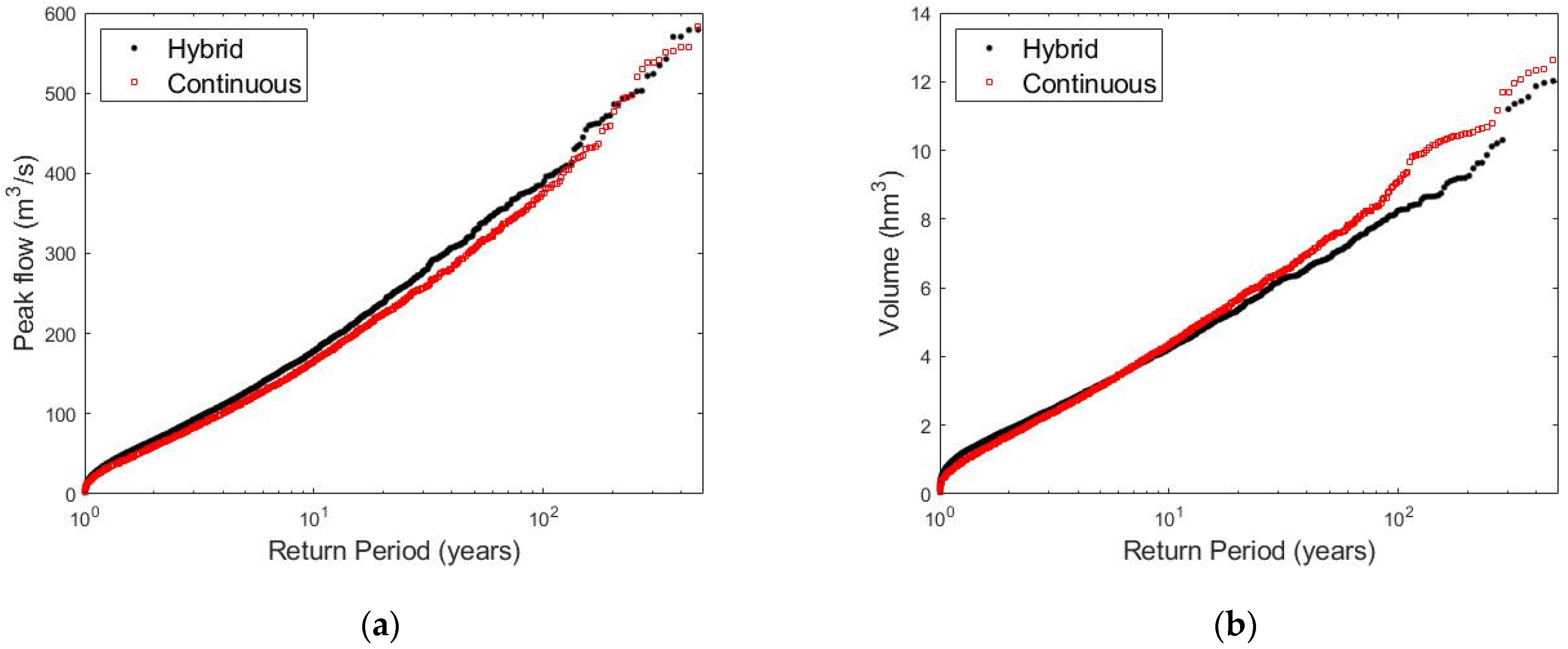
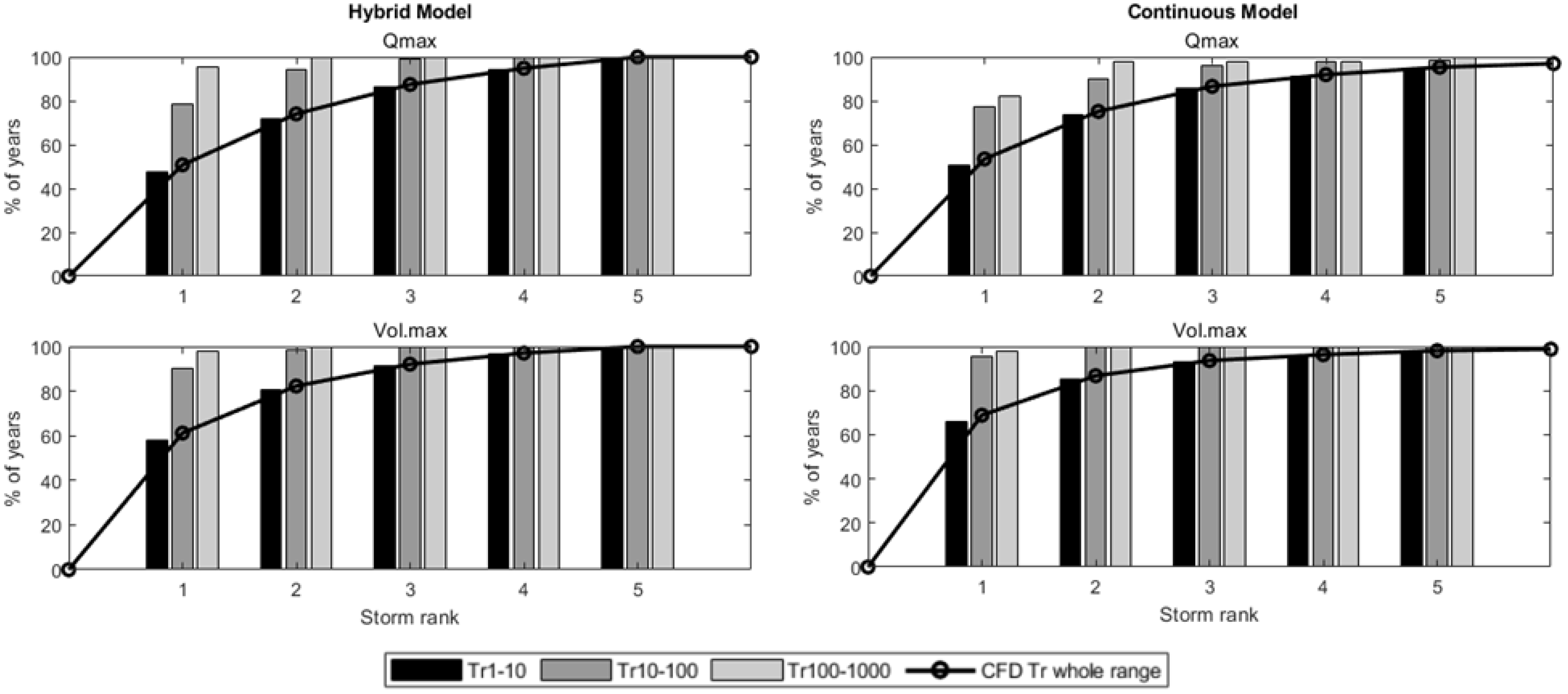
3.3.1. Flood Frequency Distributions
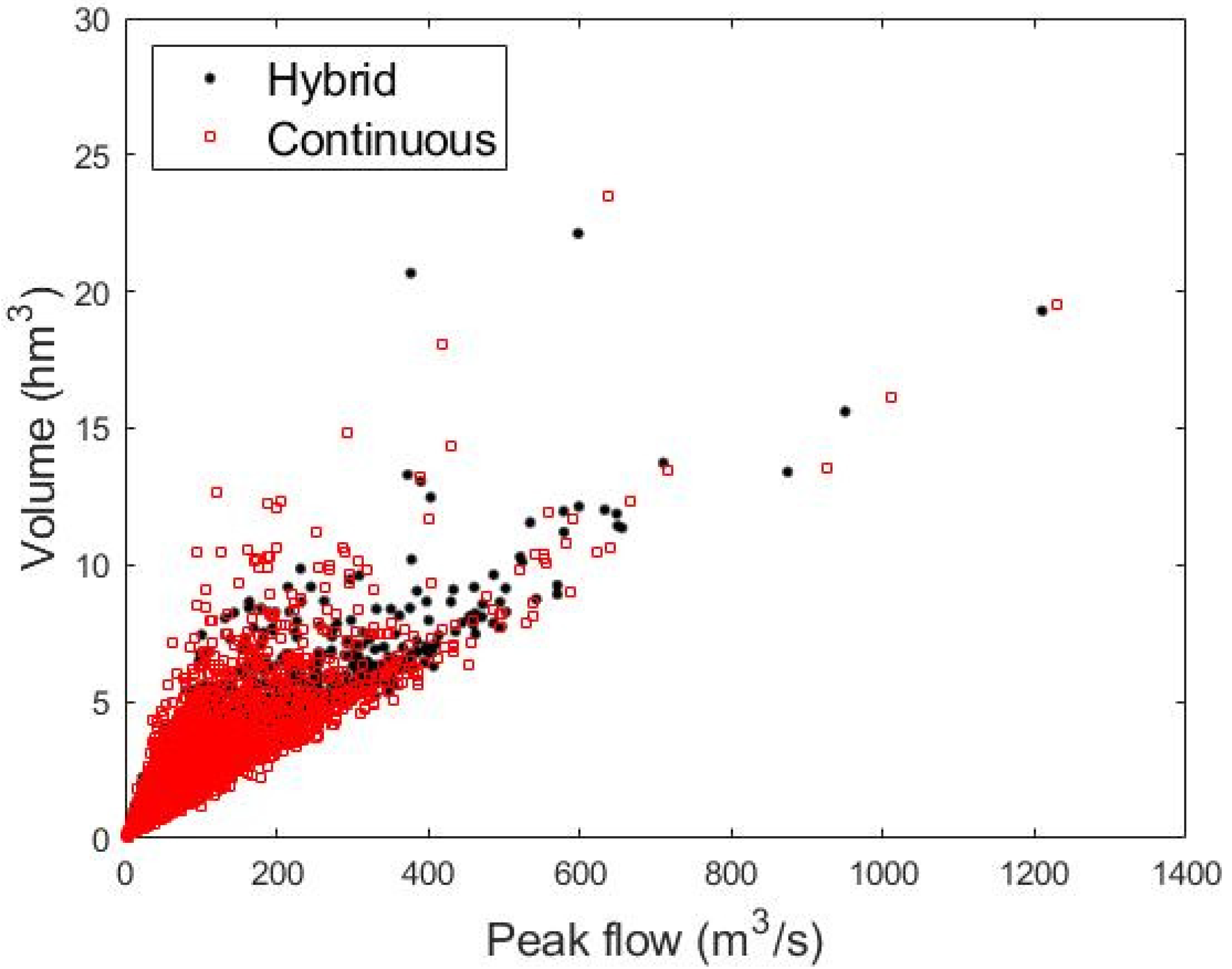
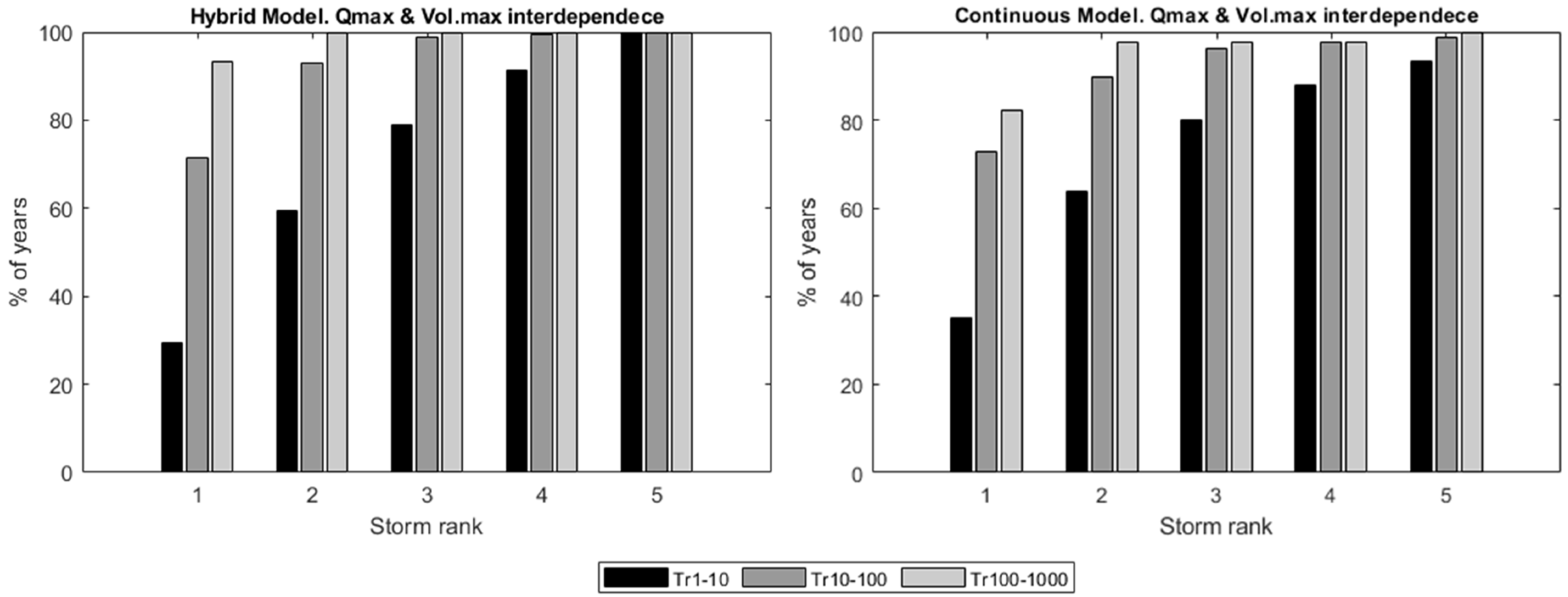
3.3.2. Dependence between the Peak-Flow and Hydrograph Volume
4. Conclusions
- Independence between rainfall events and prior hydrological soil moisture conditions has been proved within the framework of the hybrid method developed.
- The hybrid method reproduces the univariate flood frequency curves with a good agreement to those obtained by the continuous simulation. The maximum annual peak-flow frequency curve is obtained with a Nash–Sutcliffe coefficient of 0.98, whereas the maximum annual volume frequency curve is obtained with a Nash–Sutcliffe value of 0.97.
- The correlation between the occurrence of maximum annual peak-flows and volumes is preserved by the hybrid method similarly to the continuous modelling approach. An error lower than 6 % was estimated (hybrid method and Storm Rank 5) compared to the results obtained through continuous modelling.
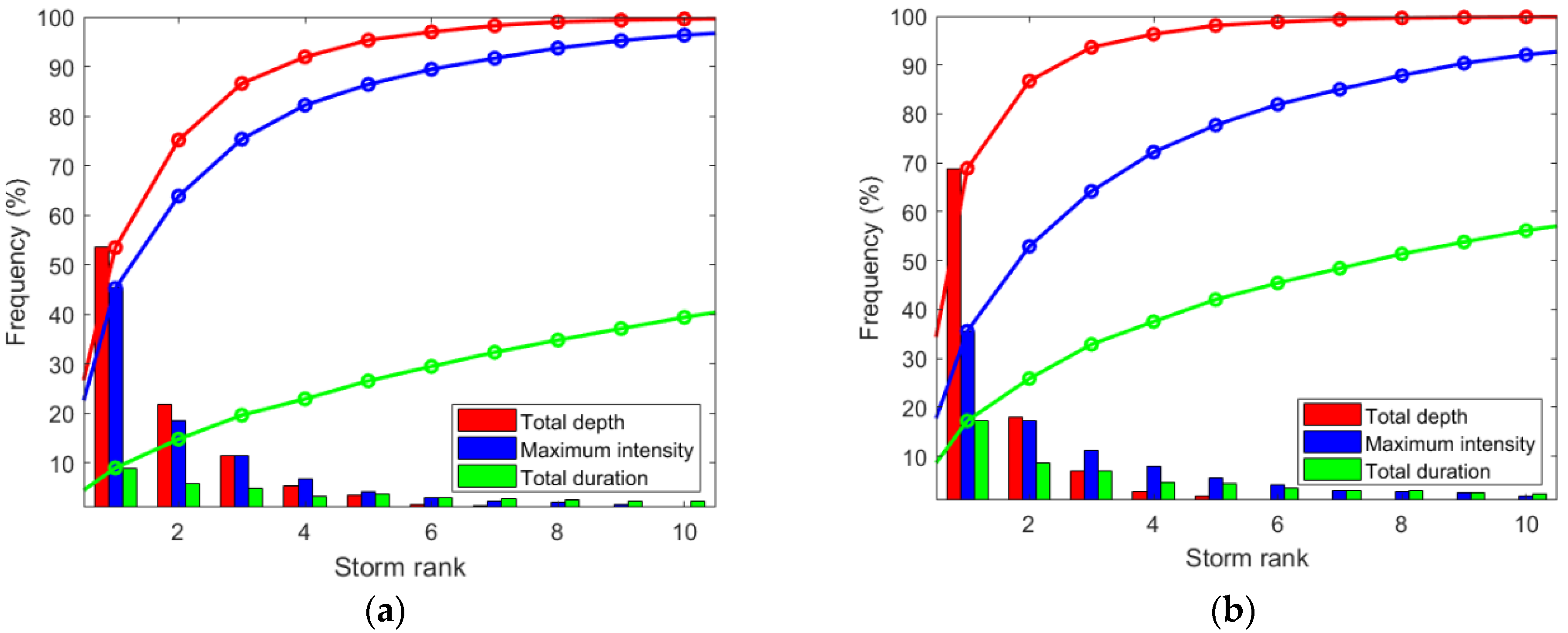
- The higher return period of the events analyzed, the lower storm ranks are needed (number of biggest storm per year considered, total depth criteria) to ensure the inclusion, either the maximum annual peak-flow and/or the maximum annual hydrograph volume.
- The proposed hybrid method reduces the time computation of continuous simulations from 49 days (5000 years, hourly time step, high performance computer) to 27 h of computation (standard computer) for Peacheater Creek basin (64 km2), 18 h to carry out the continuous simulation of 50 years and 9 h to perform the event-based simulations (25,000 events).
- To deepen on the analysis of uncertainty related to the initial moisture determination, analysing the correlation with other variables (basin characteristics, rainfall, other soil moisture variables, etc.).
- To compare the combined flood frequency law (simultaneously considering peak flow and flood volume) obtained with the continuous model and the hybrid approach. To analyse the effect of the proposed approach performance on the derived frequency law of maximum levels achieved in reservoirs, as a measure of the hydrological safety of dams.
- To analyse how flood seasonality is preserved by the proposed approach compared to continuous modelling.
- Accounting for the capabilities of AWE-GEN to be perturbed in order to assess the impact of climate change in flood events.
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fluixá-Sanmartín, J.; Altarejos-García, L.; Morales-Torres, A.; Escuder-Bueno, I. Review article: Climate change impacts on dam safety. Nat. Hazards Earth Syst. Sci. 2018, 18, 2471–2488. [Google Scholar] [CrossRef] [Green Version]
- Carvajal, C.; Peyras, L.; Arnaud, P.; Boissier, D.; Royet, P. Probabilistic Modeling of Floodwater Level for Dam Reservoirs. J. Hydrol. Eng. 2009, 14, 223–232. [Google Scholar] [CrossRef]
- Sordo-Ward, A.; Garrote, L.; Bejarano, M.D.; Castillo, L.G. Extreme flood abatement in large dams with gate-controlled spillways. J. Hydrol. 2013, 498, 113–123. [Google Scholar] [CrossRef]
- Eagleson, P.S. Dynamics of flood frequency. Water Resour. Res. 1972, 8, 878–898. [Google Scholar] [CrossRef]
- Arnaud, P.; Lavabre, J. Coupled rainfall model and discharge model for flood frequency estimation. Water Resour. Res. 2002, 38, 1–11. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G. On the derived flood frequency distribution: Analytical formulation and the influence of antecedent soil moisture condition. J. Hydrol. 2002, 262, 245–258. [Google Scholar] [CrossRef]
- De Michele, C.; Salvadori, G.; Canossi, M.; Petaccia, A.; Rosso, R. Bivariate statistical approach to check adequacy of dam spillway. J. Hydrol. Eng. 2005, 10, 50–57. [Google Scholar] [CrossRef]
- Bianucci, P.; Sordo-Ward, A.; Perez, J.I.; Garcia-Palacios, J.; Mediero, L.; Garrote, L. Risk-based methodology for parameter calibration of a reservoir flood control model. Nat. Hazards Earth Syst. Sci. 2013, 13, 965–981. [Google Scholar] [CrossRef] [Green Version]
- Bianucci, P.; Sordo-Ward, A.; Moralo, J.; Garrote, L. Probabilistic-Multiobjective Comparison of User-Defined Operating Rules. Case Study: Hydropower Dam in Spain. Water 2015, 7, 956–974. [Google Scholar] [CrossRef] [Green Version]
- Flores-Montoya, I.; Sordo-Ward, A.; Garrote, L. Probabilistic methods for hydrologic dam safety analysis. In Dam Protections against Overtopping and Accidental Leakage; Toledo, M.A., Moran, R., Oñate, E., Eds.; Taylor and Francis Group: London, UK, 2015; pp. 261–273. [Google Scholar]
- Flores-Montoya, I.; Sordo-Ward, A.; Mediero, L.; Garrote, L. Fully stochastic distributed methodology for multivariate flood frequency analysis. Water 2016, 8, 6. [Google Scholar] [CrossRef] [Green Version]
- Brigode, P.; Bernardara, P.; Paquet, E.; Gailhard, J.; Garavaglia, F.; Merz, R.; Micovic, Z.; Lawrence, D.; Ribstein, P. Sensitivity analysis of SCHADEX extreme flood estimations to observed hydrometeorological variability. Water Resour. Res. 2014, 50, 353–370. [Google Scholar] [CrossRef] [Green Version]
- Sordo-Ward, A.; Garrote, L.; Martin-Carrasco, F.; Bejarano, M.D. Extreme flood abatement in large dams with fixed-crest spillways. J. Hydrol. 2012, 466, 60–72. [Google Scholar] [CrossRef] [Green Version]
- Paquet, E.; Garavaglia, F.; Garcon, R.; Gailhard, J. The SCHADEX method: A semi-continuous rainfall-runoff simulation for extreme flood estimation. J. Hydrol. 2013, 495, 23–37. [Google Scholar] [CrossRef]
- Loukas, A. Flood frequency estimation by a derived distribution procedure. J. Hydrol. 2002, 255, 69–89. [Google Scholar] [CrossRef]
- Rahman, A.; Weinmann, P.E.; Hoang, T.M.T.; Laurenson, E.M. Monte Carlo simulation of flood frequency curves from rainfall. J. Hydrol. 2002, 256, 196–210. [Google Scholar] [CrossRef]
- Aronica, G.; Candela, A. Derivation of flood frequency curves in poorly gauged Mediterranean catchments using a simple stochastic hydrological rainfall-runoff model. J. Hydrol. 2007, 347, 132–142. [Google Scholar] [CrossRef]
- Sordo-Ward, A.; Bianucci, P.; Garrote, L.; Granados, A. How safe is hydrologic infrastructure design? Analysis of factors affecting extreme flood estimation. J. Hydrol. Eng. 2014, 19, 04014028. [Google Scholar] [CrossRef]
- Sordo-Ward, A.; Bianucci, P.; Garrote, L.; Granados, A. The influence of the annual number of storms on the derivation of the flood frequency curve through event-based simulation. Water 2016, 8, 335. [Google Scholar] [CrossRef] [Green Version]
- Adams, B.J.; Howard, C.D. Design storm pathology. Can. Water Resour. J. 1986, 11, 49–55. [Google Scholar] [CrossRef]
- Alfieri, L.; Laio, F.; Claps, P. A simulation experiment for optimal design hyetograph selection. Hydrol. Process. 2008, 22, 813–820. [Google Scholar] [CrossRef]
- Viglione, A.; Bloschl, G. On the role of storm duration in the mapping of rainfall to flood return periods. Hydrol. Earth. Syst. Sci. 2009, 13, 205–216. [Google Scholar] [CrossRef] [Green Version]
- Chatzichristaki, C.; Stefanidis, S.; Stefanidis, P.; Stathis, D. Analysis of the flash flood in Rodhes Island (South Greece) on November 2013. Silva Balc. 2015, 16, 76–86. [Google Scholar]
- United States Geological Survey (USGS). Guidelines for Determining Flood Flow Frequency; Bulletin N°17B; Hydrology Subcommittee: Washington, DC, USA, 1982. [Google Scholar]
- United States Water Resources Council (USWRC). Guidelines for Determining Flood Flow Frequency; Bulletin 17; Hydrology Subcommittee: Washington, DC, USA, 1976. [Google Scholar]
- Klein, B.; Pahlow, M.; Hundecha, Y.; Schumann, A. Probability analysis of hydrological loads for the design of flood control systems using copulas. J. Hydrol. Eng. 2010, 15, 360–369. [Google Scholar] [CrossRef]
- Zhang, L.; Singh, V.P. Trivariate flood frequency analysis using the Gumbel–Hougaard copula. J. Hydrol. Eng. 2017, 12, 431–439. [Google Scholar] [CrossRef]
- Katz, R.W.; Parlange, M.B.; Naveau, P. Statistics of extremes in hydrology. Adv. Water Resour. 2002, 25, 1287–1304. [Google Scholar] [CrossRef] [Green Version]
- Salinas, J.L.; Laaha, G.; Rogger, M.; Parajka, J.; Viglione, A.; Sivapalan, M.; Blöschl, G. Comparative assessment of predictions in ungauged basins—Part 2: Flood and low flow studies. Hydrol. Earth Syst. Sci. 2013, 17, 2637–2652. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Thyer, M.; Lambert, M.; Kuczera, G.; Metcalfe, A. An efficient causative event-based approach for deriving the annual flood frequency distribution. J. Hydrol. 2014, 510, 412–423. [Google Scholar] [CrossRef] [Green Version]
- Blazkova, S.; Beven, K. Flood frequency estimation by continuous simulation of subcatchment rainfalls and discharges with the aim of improving dam safety assessment in a large basin in the Czech Republic. J. Hydrol. 2004, 292, 153–172. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Ivanov, V.Y.; Bras, R.L.; Entekhabi, D. On the Effects of Triangulated Terrain Resolution on Distributed Hydrologic Model Response. Hydrol. Process. 2005, 19, 2101–2122. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Mascaro, G.; Mniszewski, S.; Fasel, P.; Springer, E.P.; Ivanov, V.Y.; Bras, R.L. Real-world hydrologic assessment of a fully-distributed hydrological model in a parallel computing environment. J. Hydrol. 2011, 409, 483–496. [Google Scholar] [CrossRef]
- Foufoula-Georgiou, E. A probabilistic storm transposition approach for estimating exceedance probabilities of extreme precipitation depths. Water Resour. Res. 1989, 25, 799–815. [Google Scholar] [CrossRef]
- Franchini, M.; Helmlinger, K.R.; Foufoula-Georgiou, E.; Todini, E. Stochastic storm transposition coupled with rainfall-runoff modeling for estimation of exceedance probabilities of design floods. J. Hydrol. 1996, 175, 511–532. [Google Scholar] [CrossRef]
- Flores-Montoya, I. Generación de Hidrogramas de Crecida Mediante Simulación Estocástica Multivariada de Lluvia y Modelación Hidrológica Distribuida: Aplicación a Seguridad de Presas. Ph.D. Thesis, Technical University of Madrid, Madrid, Spain, 2018. (In Spanish) [CrossRef] [Green Version]
- Wright, D.B.; Smith, J.A.; Baeck, M.L. Critical examination of area reduction factors. J. Hydrol. Eng. 2014, 19, 769–776. [Google Scholar] [CrossRef]
- Cea, L.; Fraga, I. Incorporating antecedent moisture conditions and intra-event variability of rainfall on flood frequency analysis in poorly gauged basins. Water Resour. Res. 2018, 54, 8774–8791. [Google Scholar] [CrossRef]
- Brocca, L.; Liersch, S.; Melone, F.; Moramarco, T.; Volk, M. Application of a model-based rainfall-runoff database as efficient tool for flood risk management. Hydrol. Earth Syst. Sci. 1996, 17, 3159–3169. [Google Scholar] [CrossRef] [Green Version]
- Haberlandt, U.; Ebner von Eschenbach, A.D.; Buchwald, I. A space-time hybrid hourly rainfall model for derived flood frequency analysis. Hydrol. Earth Syst. Sci. 2008, 12, 1353–1367. [Google Scholar] [CrossRef] [Green Version]
- Vivoni, E.R.; Di Benedetto, F.; Grimaldi, S.; Eltahir, E.A.B. Hypsometric Control on Surface and Subsurface Runoff. Water Resour. Res. 2008, 44, W12502. [Google Scholar] [CrossRef] [Green Version]
- Stefanidis, S.; Dafis, S.; Stathis, D. Evaluation of Regional Climate Models (RCMs) Performance in Simulating Seasonal Precipitation over Mountainous Central Pindus (Greece). Water 2020, 12, 2750. [Google Scholar] [CrossRef]
- Greve, P.; Roderick, M.L.; Ukkola, A.M.; Wada, Y. The aridity index under global warming. Environ. Res. Lett. 2019, 14, 124006. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, V.Y.; Vivoni, E.R.; Bras, R.L.; Entekhabi, D. Catchment hydrologic response with a fully distributed triangulated irregular network model. Water Resour. Res. 2004, 40, W11102. [Google Scholar] [CrossRef]
- Ivanov, V.Y.; Vivoni, E.R.; Bras, R.L.; Entekhabi, D. Preserving high-resolution surface and rainfall data in operational-scale basin hydrology: A fully-distributed physically-based approach. J. Hydrol. 2004, 298, 80–111. [Google Scholar] [CrossRef]
- Vivoni, E.R.; Entekhabi, D.; Bras, R.L.; Ivanov, V.Y. Controls on runoff generation and scale-dependence in a distributed hydrologic model. Hydrol. Earth Syst. Sci. 2007, 11, 1683–1701. [Google Scholar] [CrossRef] [Green Version]
- Fatichi, S.; Ivanov, V.Y.; Caporali, E. Simulation of future climate scenarios with a weather generator. Adv. Water Resour. 2011, 34, 448–467. [Google Scholar] [CrossRef]
- Gabriel-Martin, I.; Sordo-Ward, A.; Garrote, L.; García, J.T. Dependence Between Extreme Rainfall Events and the Seasonality and Bivariate Properties of Floods. A Continuous Distributed Physically-Based Approach. Water 2019, 11, 1896. [Google Scholar] [CrossRef] [Green Version]
- Vivoni, E.R.; Ivanov, V.Y.; Bras, R.L.; Entekhabi, D. Generation of triangulated irregular networks based on hydrologic similarity. J. Hydrol. Eng. 2004, 9, 288–302. [Google Scholar] [CrossRef]
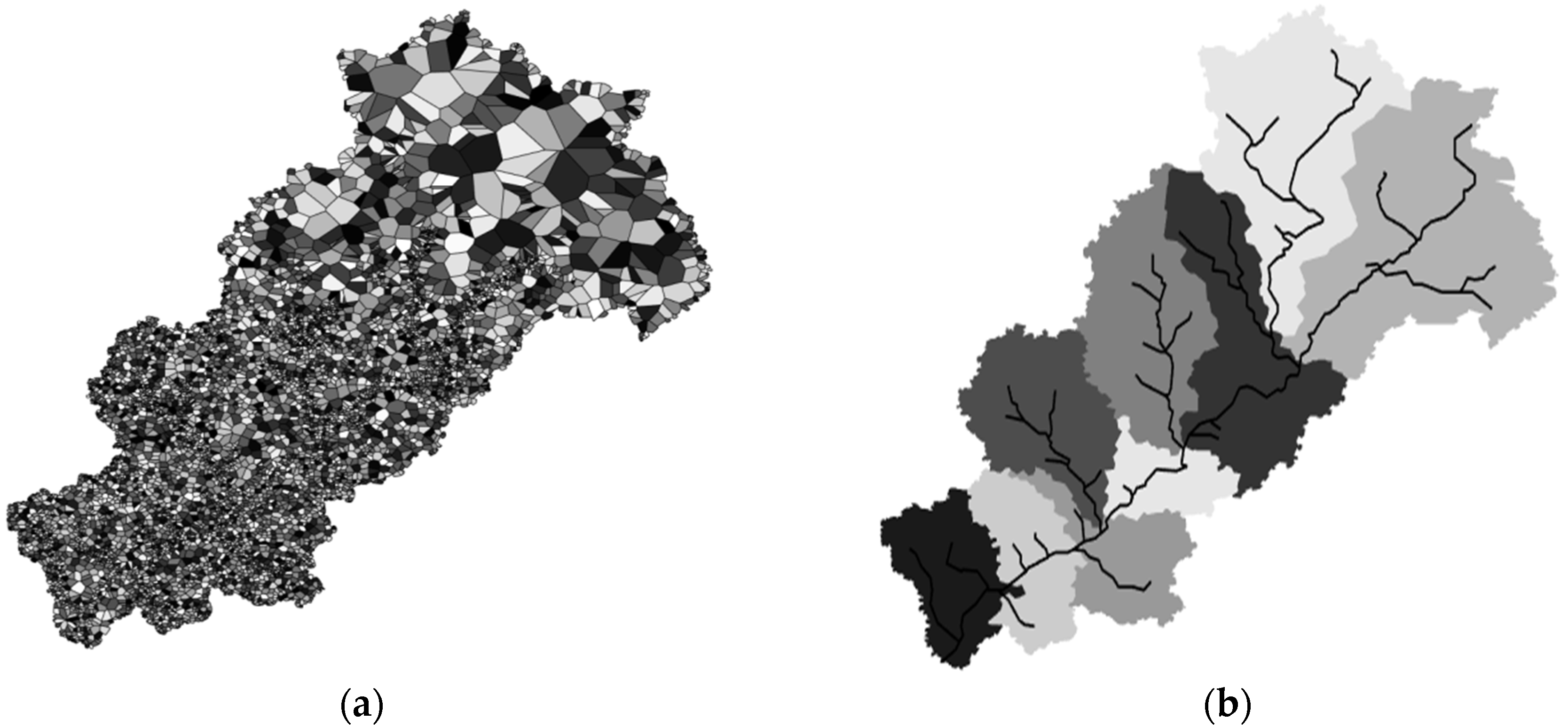
- Karypis, G.; Kumar, V. A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM J. Sci. Comput. 1999, 20, 359–392. [Google Scholar] [CrossRef]
- Restrepo-Posada, P.J.; Eagleson, P.S. Identification of independent rainstorms. J. Hydrol. 1982, 55, 303–319. [Google Scholar] [CrossRef]
- Gringorten, I.I. A plotting rule for extreme probability paper. J. Geophys. Res. 1963, 68, 813. [Google Scholar] [CrossRef]
- Liuzzo, L.; Noto, L.V.; Vivoni, E.R.; La Loggia, G. Basin-scale water resources assessment in Oklahoma under synthetic climate change scenarios using a fully distributed hydrological model. J. Hydrol. Eng. 2010, 15, 107–122. [Google Scholar] [CrossRef]
- Gochis, D.J.; Yu, W.; Yates, D.N. The WRF-Hydro Model Technical Description and User’s Guide, Version 3.0. NCAR Technical Document. 1-120. 2016. Available online: https://www.ral.ucar.edu/projects/wrf_hydro (accessed on 25 May 2021).
- Ivanov, V.Y.; Bras, R.L.; Curtis, D.C. A weather generator for hydrological, ecological, and agricultural applications. Water Resour. Res. 2007, 43, 40. [Google Scholar] [CrossRef] [Green Version]
- Smith, M.B.; Seo, D.J.; Koren, V.I.; Reed, S.M.; Zhang, Z.; Duan, Q.; Moreda, F.; Cong, S. The distributed model intercomparison project (DMIP): Motivation and experiment design. J. Hydrol. 2004, 298, 4–26. [Google Scholar] [CrossRef]
- Sirisena, T.A.J.G.; Maskey, S.; Ranasinghe, R.; Babel, M.S. Effects of different precipitation inputs on streamflow simulation in the Irrawaddy River Basin, Myanmar. J. Hydrol. Reg. Stud. 2018, 19, 265–278. [Google Scholar] [CrossRef]
| Rank | Hybrid Method | Continuous Model | Error | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Number of Years | Number of Years | % | |||||||
| Qmax | Vol. max | (Q and V) max | Qmax | Vol. max | (Q and V) max | Qmax | Vol. max | (Q and V) max | |
| 1 | 2538 | 3060 | 2481 | 2673 | 3442 | 2396 | 5.1 | 11.1 | 3.5 |
| 2 | 3701 | 4115 | 3653 | 3758 | 4337 | 3576 | 1.5 | 5.1 | 2.2 |
| 3 | 4373 | 4604 | 4340 | 4329 | 4681 | 4221 | 1.0 | 1.6 | 2.8 |
| 4 | 4742 | 4853 | 4727 | 4596 | 4815 | 4526 | 3.2 | 0.8 | 4.4 |
| 5 | 5000 | 5000 | 5000 | 4766 | 4905 | 4728 | 4.9 | 1.9 | 5.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sordo-Ward, A.; Gabriel-Martín, I.; Bianucci, P.; Mascaro, G.; Vivoni, E.R.; Garrote, L. Stochastic Hybrid Event Based and Continuous Approach to Derive Flood Frequency Curve. Water 2021, 13, 1931. https://doi.org/10.3390/w13141931
Sordo-Ward A, Gabriel-Martín I, Bianucci P, Mascaro G, Vivoni ER, Garrote L. Stochastic Hybrid Event Based and Continuous Approach to Derive Flood Frequency Curve. Water. 2021; 13(14):1931. https://doi.org/10.3390/w13141931
Chicago/Turabian StyleSordo-Ward, Alvaro, Ivan Gabriel-Martín, Paola Bianucci, Giuseppe Mascaro, Enrique R. Vivoni, and Luis Garrote. 2021. "Stochastic Hybrid Event Based and Continuous Approach to Derive Flood Frequency Curve" Water 13, no. 14: 1931. https://doi.org/10.3390/w13141931






