Assessment of Steady and Unsteady Friction Models in the Draining Processes of Hydraulic Installations
Abstract
:1. Introduction
2. Mathematical Model
2.1. Governing Equations
- Rigid water column model (RWCM):
- : water velocity, m/s;
- : air pocket absolute pressure, Pa;
- : atmospheric pressure, 101,325 Pa;
- : water density, kg m−3;
- : length of a water column, m;
- : head losses using a steady () or unsteady () friction model, m/m;
- : gravitational acceleration, m s−2;
- : difference elevation, m;
- : internal diameter of a pipe, m;
- : resistance coefficient of a valve, s2 m−5;
- : cross-sectional area of a pipe, m2.
- Air–water interface formulation:
- Polytropic law of an air pocket:
- : air pocket length, m;
- : polytropic coefficient;
- : refers to initial conditions.
2.2. Steady Friction Model (SFM)
- : friction factor;
- : the head losses per unit length in the steady flow regime.
- Moody equation:
- : absolute pipe roughness, mm;
- : Reynolds number.
- Wood equation:
- Hazen–Williams equation:
- : Hazen–Williams coefficient.
- Swamee–Jain equation:
2.3. Unsteady Friction Model (UFM)
- : head losses per unit length in the unsteady flow regime;
- : Brunone friction coefficient;
- : wave speed, m s−1;
- : local acceleration;
- : convective acceleration;
- : distance, m.
- : Vardy’s shear decay coefficient.
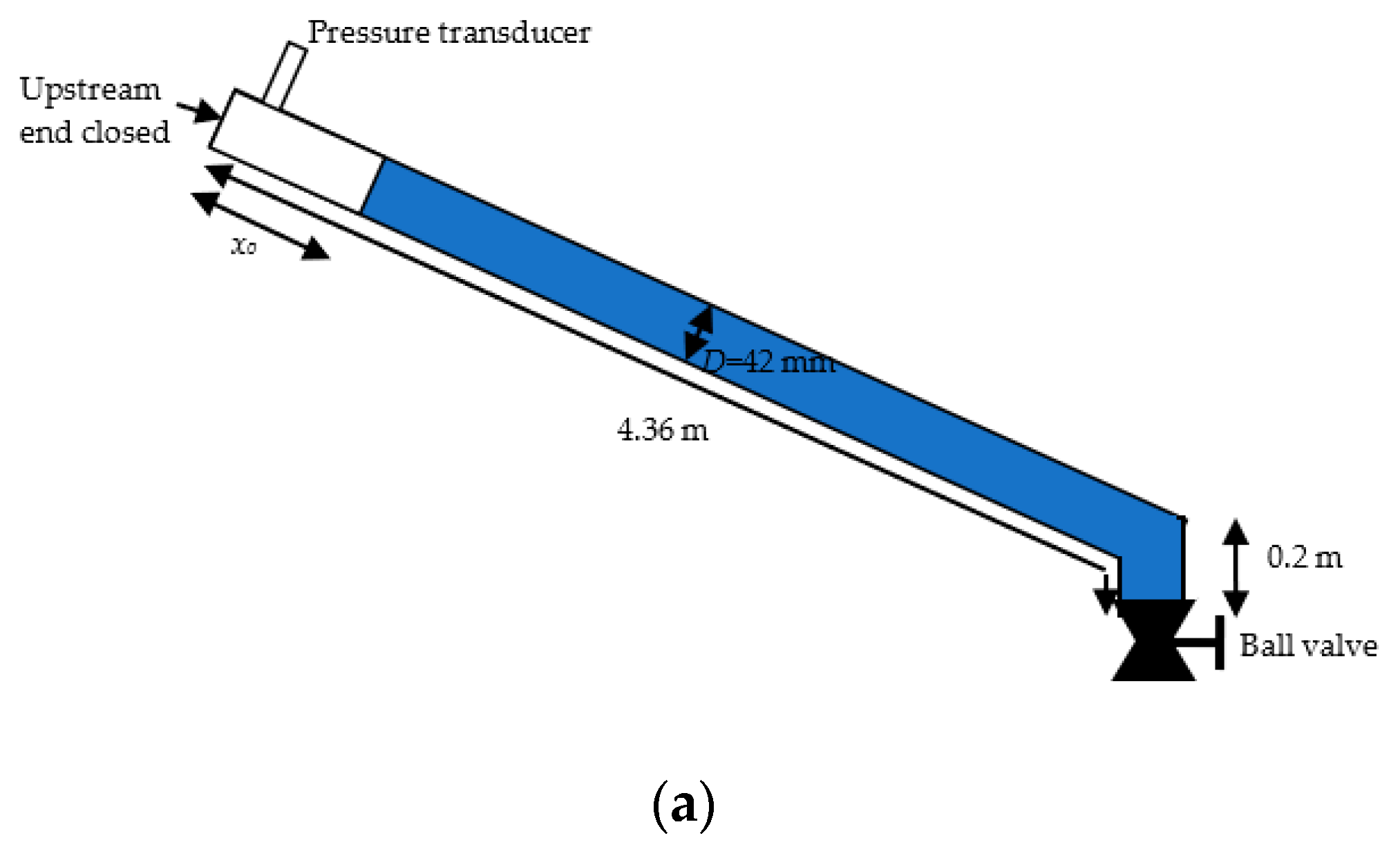
3. Experimental Stage and Numerical Runs
4. Results and Discussions
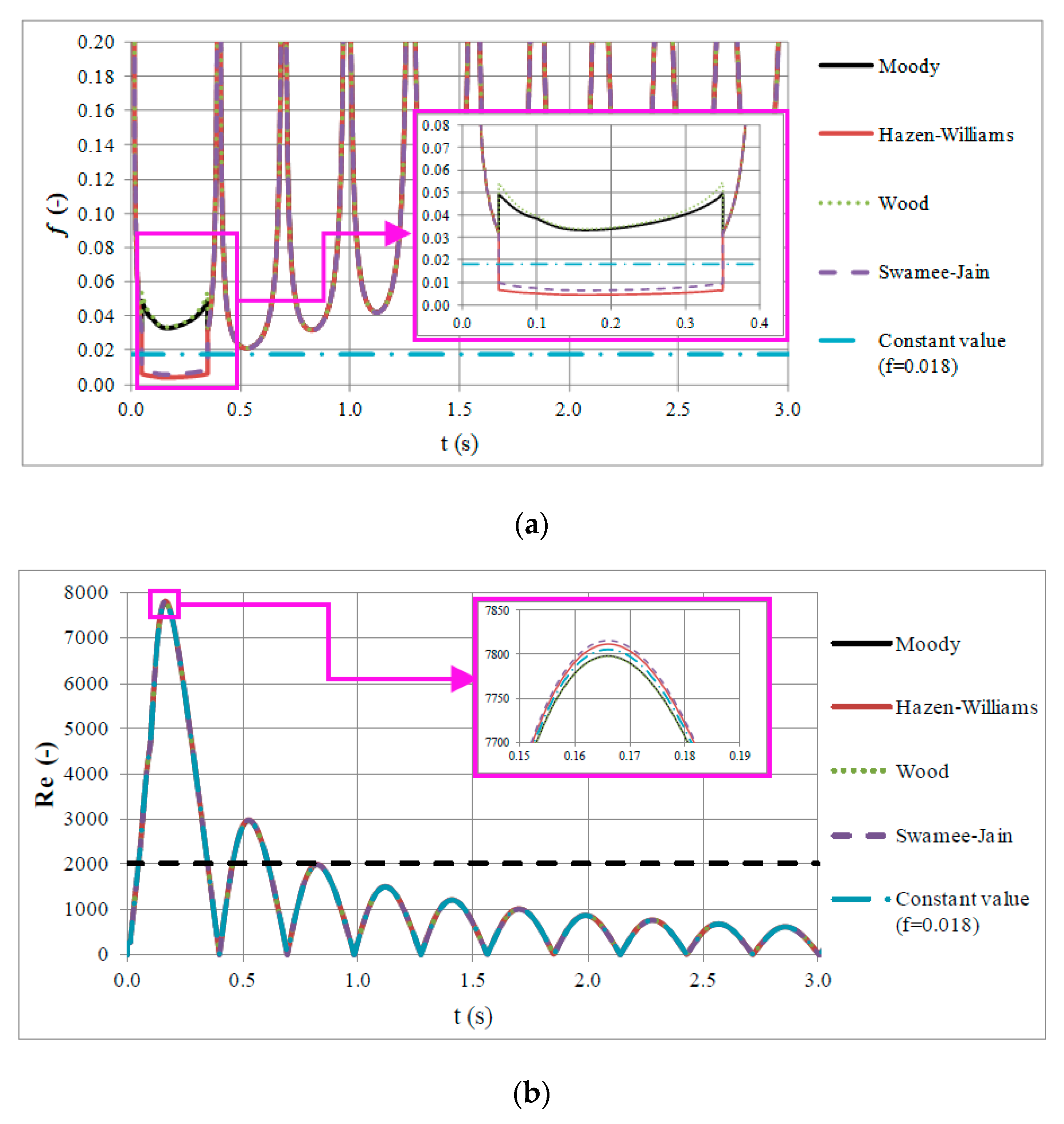
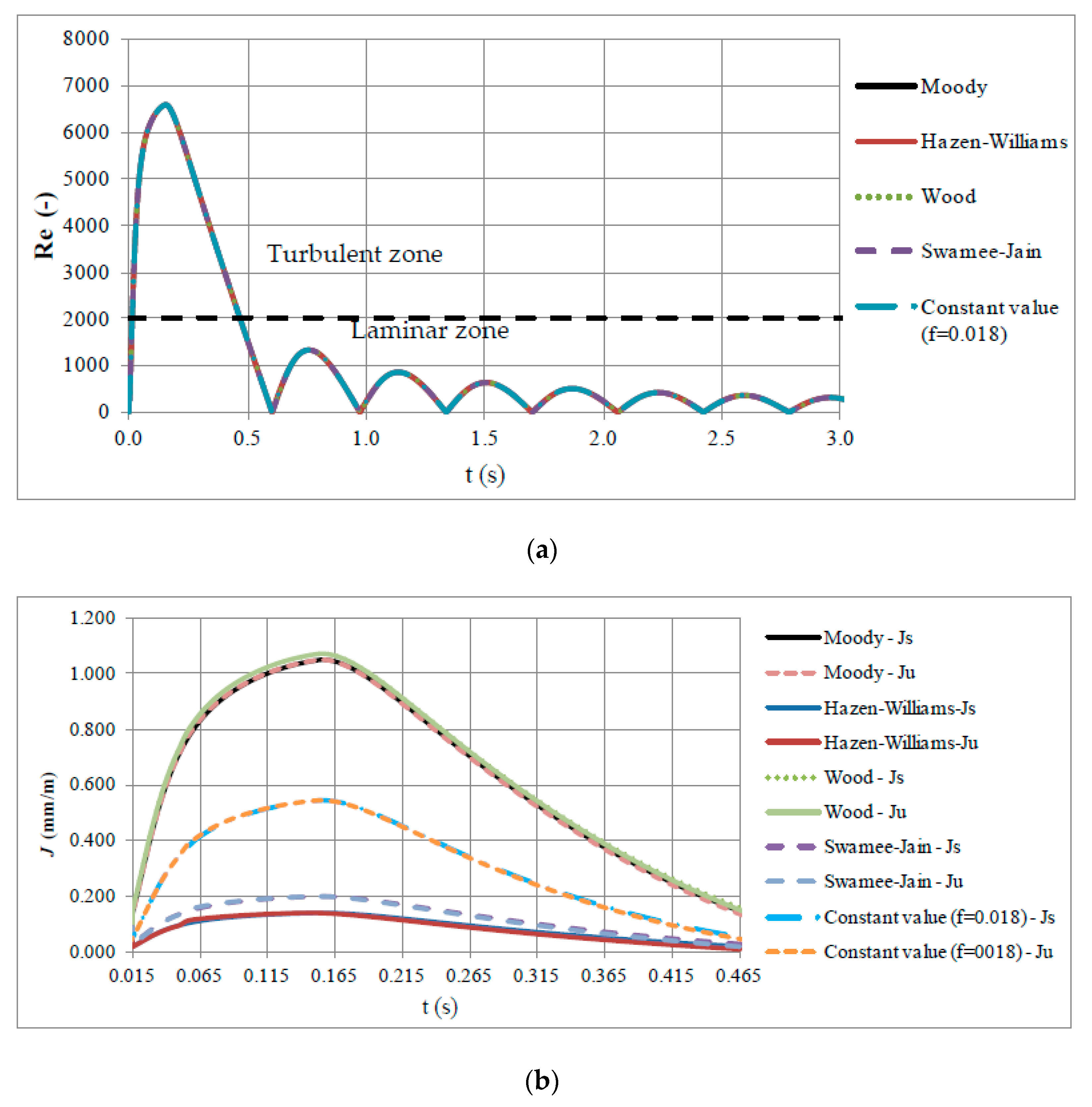
4.1. Steady Friction Model
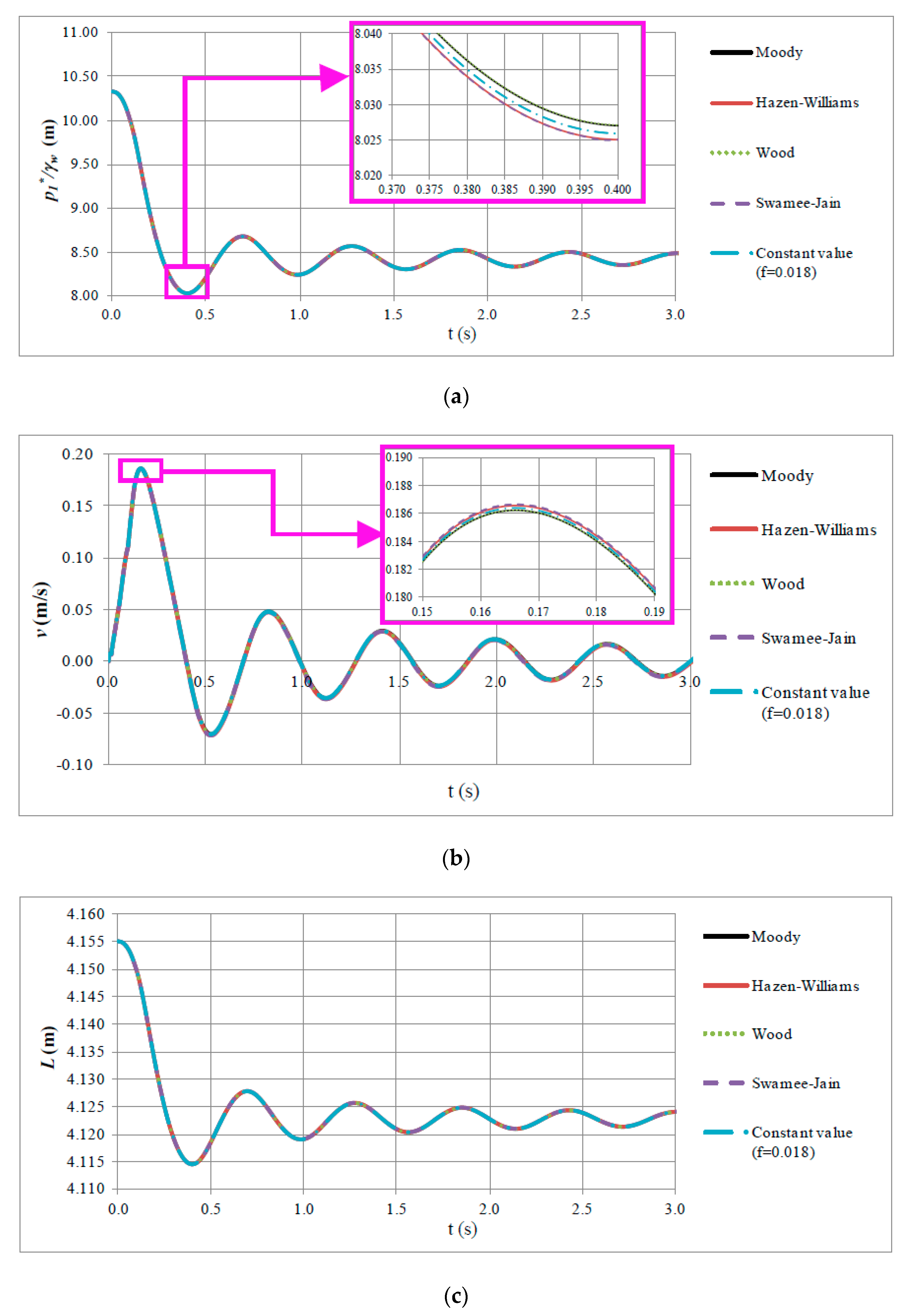
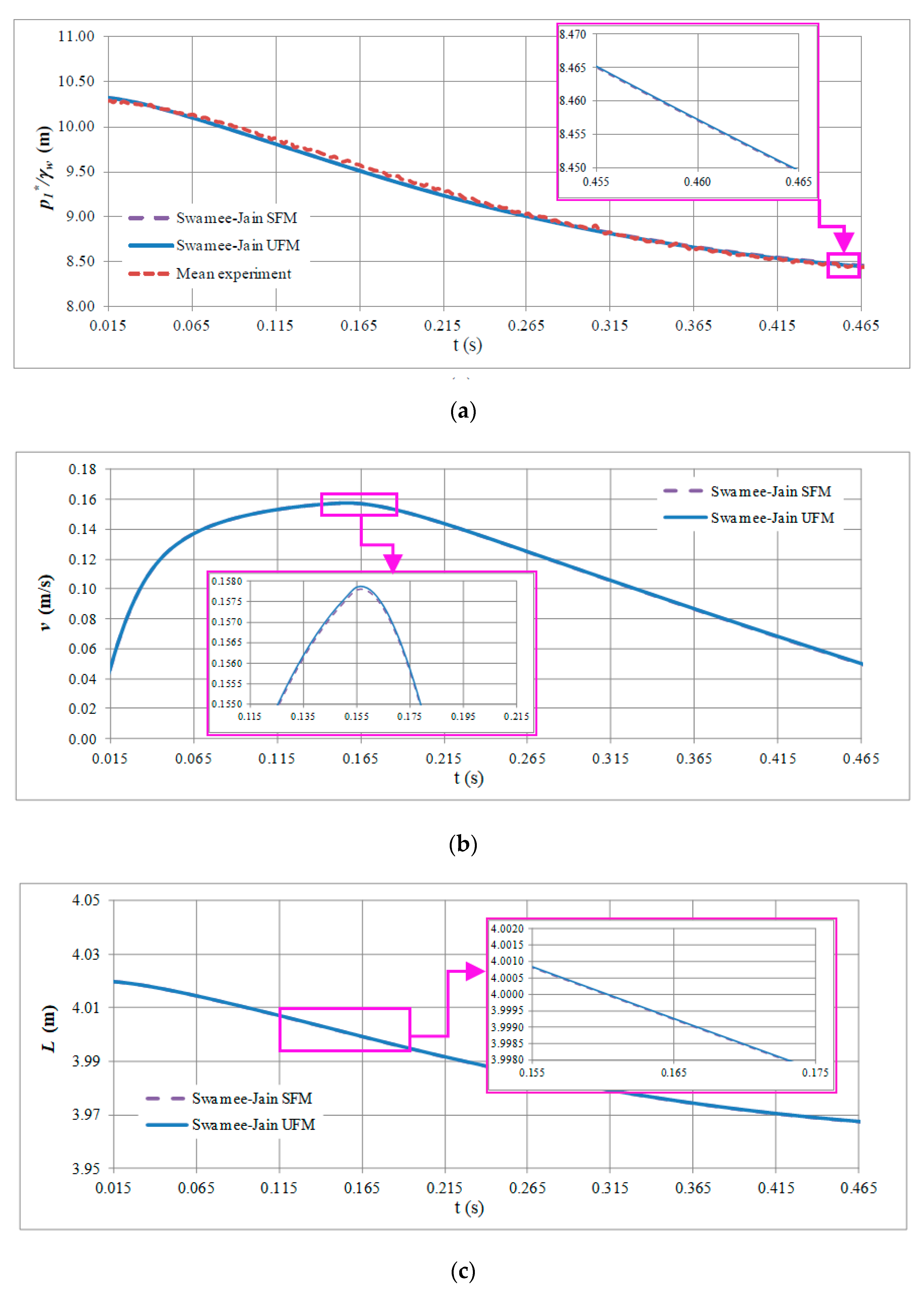
4.2. Unsteady Friction Model
5. Conclusions and Recommendations
- During the emptying process, the air pocket pressure started under atmospheric conditions. When the ball valve located at downstream end was opened, the absolute pressure pattern descended until the lowest value (first drop), after which some oscillations were reached until the water column was again at rest. The length of the water column showed a similar behavior. Regarding the water velocity, it started at rest (0 m s−1), following which it rapidly reached the maximum value, and finally negative and positive values were generated.
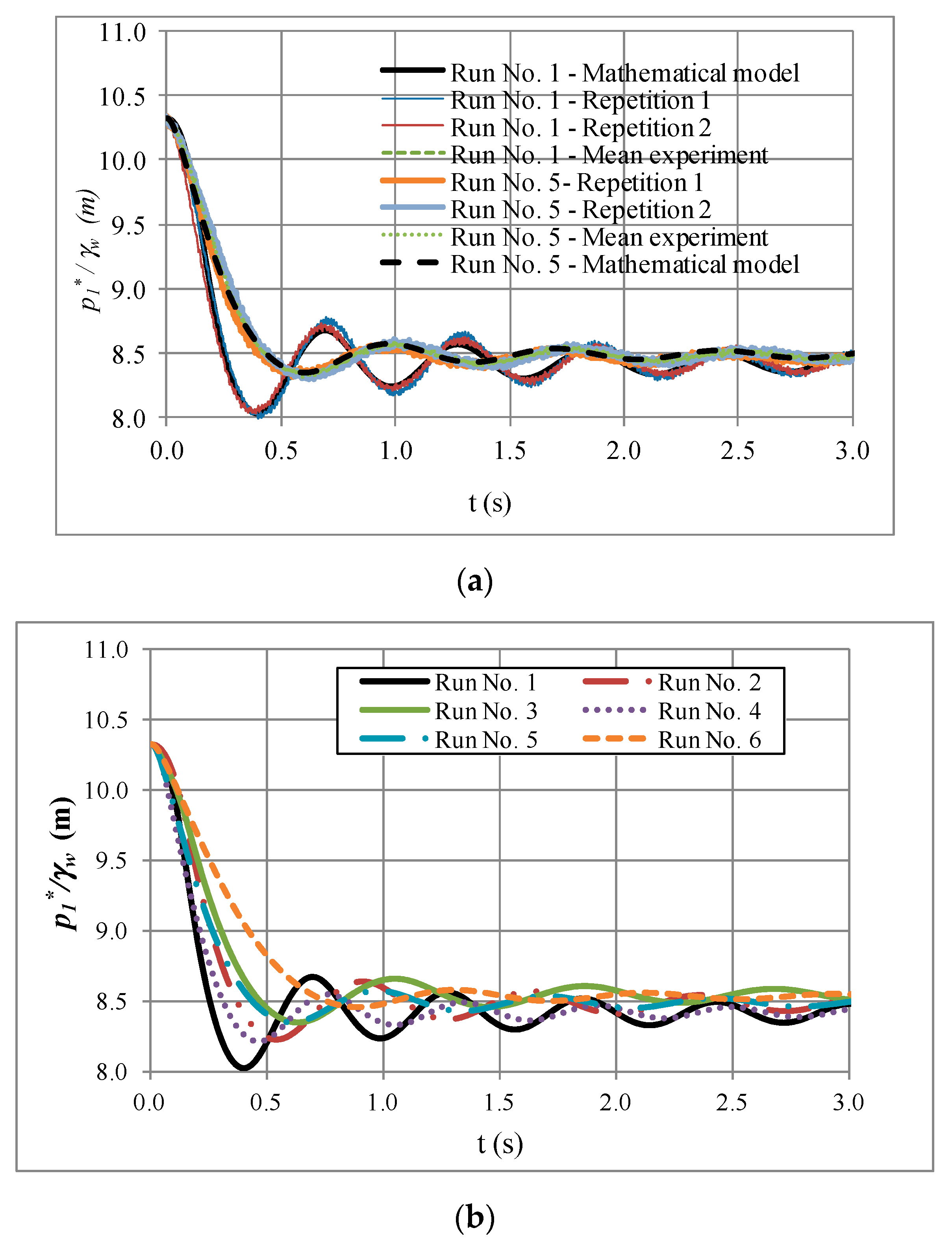
- Considering the six experimental runs, the implementation of the unsteady friction model of Brunone in the simulation of the draining process better fixed the measured air pocket pressure oscillations in the analyzed experimental facility. When the Moody and Wood formulations were implemented with the UFM, the minimum root mean square errors were reached.
- It is important to highlight that both the SFM and the UFM adequately predicted the air pocket pressure oscillations using all of the empirical formulations to compute the friction factor.
- The mathematical model proposed considers the analysis of the laminar and turbulent zone flows. The first drop of sub-atmospheric pressure pattern is the more complex zone to simulate, since it involves the presence of laminar and turbulent flows. After that, the water movement is almost null; consequently, the laminar flow is presented during this part of the transient event.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fuertes-Miquel, V.S.; Coronado-Hernández, Ó.E.; Mora-Melia, D.; Iglesias-Rey, P.L. Hydraulic Modeling during Filling and Emptying Processes in Pressurized Pipelines: A Literature Review. Urban Water J. 2019, 16, 299–311. [Google Scholar] [CrossRef]
- Vasconcelos, J.G.; Klaver, P.R.; Lautenbach, D.J. Flow Regime Transition Simulation Incorporating Entrapped Air Pocket Effects. Urban Water J. 2015, 6, 488–501. [Google Scholar] [CrossRef]
- Fuertes-Miquel, V.S.; Coronado-Hernández, Ó.E.; Iglesias-Rey, P.L.; Mora-Melia, D. Transient Phenomena during the Emptying Process of a Single Pipe with Water-Air Interaction. J. Hydraul. Res. 2019, 57, 318–326. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, D. Experimental Investigation of Entrapped Air Pocket in a Partially Full Water Pipe. J. Hydraul. Res. 2013, 51, 469–474. [Google Scholar] [CrossRef]
- Coronado-Hernández, Ó.E.; Besharat, M.; Fuertes-Miquel, V.S.; Ramos, H.M. Effect of a Commercial Air Valve on the Rapid Filling of a Single Pipeline: A Numerical and Experimental Analysis. Water 2019, 11, 1814. [Google Scholar] [CrossRef] [Green Version]
- Tijsseling, A.; Hou, Q.; Bozkus, Z.; Laanearu, J. Improved One-Dimensional Models for Rapid Emptying and Filling of Pipelines. J. Press. Vessel Technol. 2016, 138, 031301. [Google Scholar] [CrossRef] [Green Version]
- Zhou, L.; Cao, Y.; Karney, B.; Vasconcelos, J.G.; Liu, D.; Wang, P. Unsteady friction in transient vertical-pipe flow with trapped air. J. Hydraul. Res. 2020. [Google Scholar] [CrossRef]
- Vasconcelos, J.G.; Leite, G.M. Pressure Surges Following Sudden Air Pocket Entrapment in Storm-Water Tunnels. J. Hydraul. Eng. 2012, 138, 12. [Google Scholar] [CrossRef] [Green Version]
- Izquierdo, J.; Fuertes, V.S.; Cabrera, E.; Iglesias, P.; García-Serra, J. Pipeline start-up with entrapped air. J. Hydraul. Res. 1999, 37, 579–590. [Google Scholar] [CrossRef]
- Laanearu, J.; Annus, I.; Koppel, T.; Bergant, A.; Vučkovič, S.; Hou, Q.; van’t Westende, J.M.C. Emptying of Large-Scale Pipeline by Pressurized Air. J. Hydraul. Eng. 2012, 138, 1090–1100. [Google Scholar] [CrossRef] [Green Version]
- Laanearu, J.; Annus, I.; Sergejeva, M.; Koppel, T. Semi-empirical method for estimation of energy losses in a large-scale Pipeline. Procedia Eng. 2014, 70, 969–977. [Google Scholar] [CrossRef] [Green Version]
- Coronado-Hernández, Ó.E.; Fuertes-Miquel, V.S.; Besharat, M.; Ramos, H.M. Subatmospheric Pressure in a Water Draining Pipeline with an Air Pocket. Urban Water J. 2018, 15, 346–352. [Google Scholar] [CrossRef]
- Colebrook, C.F. Turbulent Flow in Pipes, with Particular Reference to the Transition Region between the Smooth and Rough Pipe Laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Moody, L.F. Friction Factors for Pipe Flow. Trans. Am. Soc. Mech. Eng. 1994, 66, 671–684. [Google Scholar]
- Wood, D.J. An Explicit Friction Factor Relationship. Civ. Eng. Am. Soc. Civ. Eng. 1972, 383–390. [Google Scholar]
- Travis, Q.; Mays, L.W. Relationship between Hazen–William and Colebrook–White Roughness Values. J. Hydraul. Eng. 2007, 133, 11. [Google Scholar] [CrossRef]
- Swamee, D.K.; Jain, A.K. Explicit Equations for Pipe Flow Problems. J. Hydraul. Div. 1976, 102, 657–664. [Google Scholar] [CrossRef]
- Brunone, B.; Golia, U.M.; Greco, M. Some remarks on the momentum equation for fast transients. In Meeting on Hydraulic Transients with Column Separation; 9th Round Table; IAHR: Valencia, Spain, 1991; pp. 140–148. [Google Scholar]
- Brunone, B.; Karney, B.W.; Mecarelli, M.; Ferrante, M. Velocity profiles and unsteady pipe friction in transient flow. J. Water Res. Plan. Manag. 2000, 126, 236–244. [Google Scholar] [CrossRef] [Green Version]
- Wylie, E.; Streeter, V. Fluid Transients in Systems; Prentice Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Chaudhry, M.H. Applied Hydraulic Transients, 3rd ed.; Springer: New York, NY, USA, 2014. [Google Scholar]
- Coronado-Hernández, Ó.E.; Fuertes-Miquel, V.S.; Iglesias-Rey, P.L.; Martínez-Solano, F.J. Rigid Water Column Model for Simulating the Emptying Process in a Pipeline Using Pressurized Air. J. Hydraul. Eng. 2018, 144, 06018004. [Google Scholar] [CrossRef]
- American Water Works Association (AWWA). Manual of Water Supply Practices-M51: Air-Release, Air-Vacuum, and Combination Air Valves, 1st ed.; American Water Works Association: Denver, CO, USA, 2001. [Google Scholar]
- Ramezani, L.; Karney, B.; Malekpour, A. Encouraging Effective Air Management in Water Pipelines: A Critical Review. J. Water Resour. Plan. Manag. 2016, 142, 04016055. [Google Scholar] [CrossRef] [Green Version]

| Run No. | ||
|---|---|---|
| 1 | 0.205 | 11.89 |
| 2 | 0.340 | 11.89 |
| 3 | 0.450 | 11.89 |
| 4 | 0.205 | 25.00 |
| 5 | 0.340 | 22.68 |
| 6 | 0.450 | 30.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coronado-Hernández, Ó.E.; Derpich, I.; Fuertes-Miquel, V.S.; Coronado-Hernández, J.R.; Gatica, G. Assessment of Steady and Unsteady Friction Models in the Draining Processes of Hydraulic Installations. Water 2021, 13, 1888. https://doi.org/10.3390/w13141888
Coronado-Hernández ÓE, Derpich I, Fuertes-Miquel VS, Coronado-Hernández JR, Gatica G. Assessment of Steady and Unsteady Friction Models in the Draining Processes of Hydraulic Installations. Water. 2021; 13(14):1888. https://doi.org/10.3390/w13141888
Chicago/Turabian StyleCoronado-Hernández, Óscar E., Ivan Derpich, Vicente S. Fuertes-Miquel, Jairo R. Coronado-Hernández, and Gustavo Gatica. 2021. "Assessment of Steady and Unsteady Friction Models in the Draining Processes of Hydraulic Installations" Water 13, no. 14: 1888. https://doi.org/10.3390/w13141888
APA StyleCoronado-Hernández, Ó. E., Derpich, I., Fuertes-Miquel, V. S., Coronado-Hernández, J. R., & Gatica, G. (2021). Assessment of Steady and Unsteady Friction Models in the Draining Processes of Hydraulic Installations. Water, 13(14), 1888. https://doi.org/10.3390/w13141888









