Differences in Reference Evapotranspiration Variation and Climate-Driven Patterns in Different Altitudes of the Qinghai–Tibet Plateau (1961–2017)
Abstract
:1. Introduction
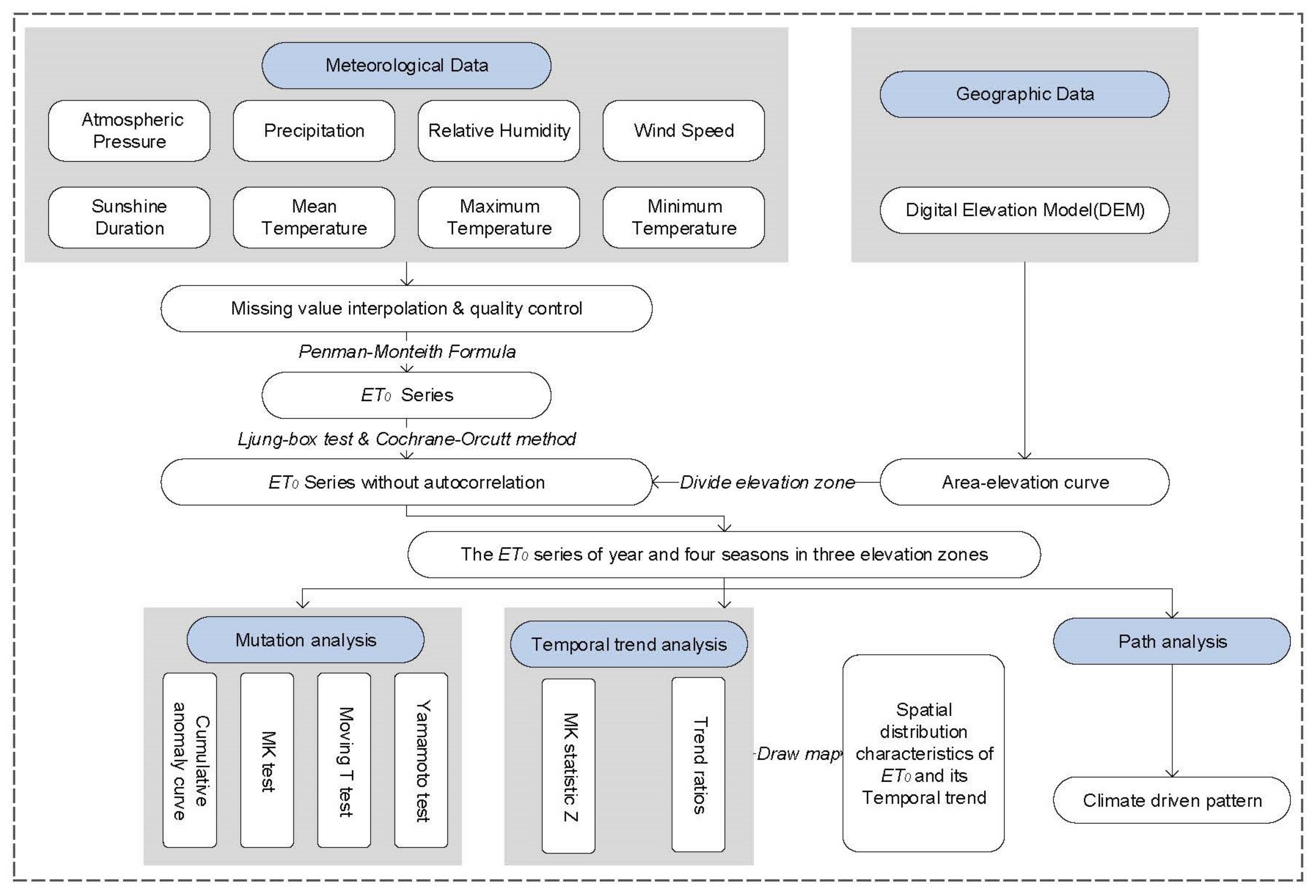
2. Materials and Methods
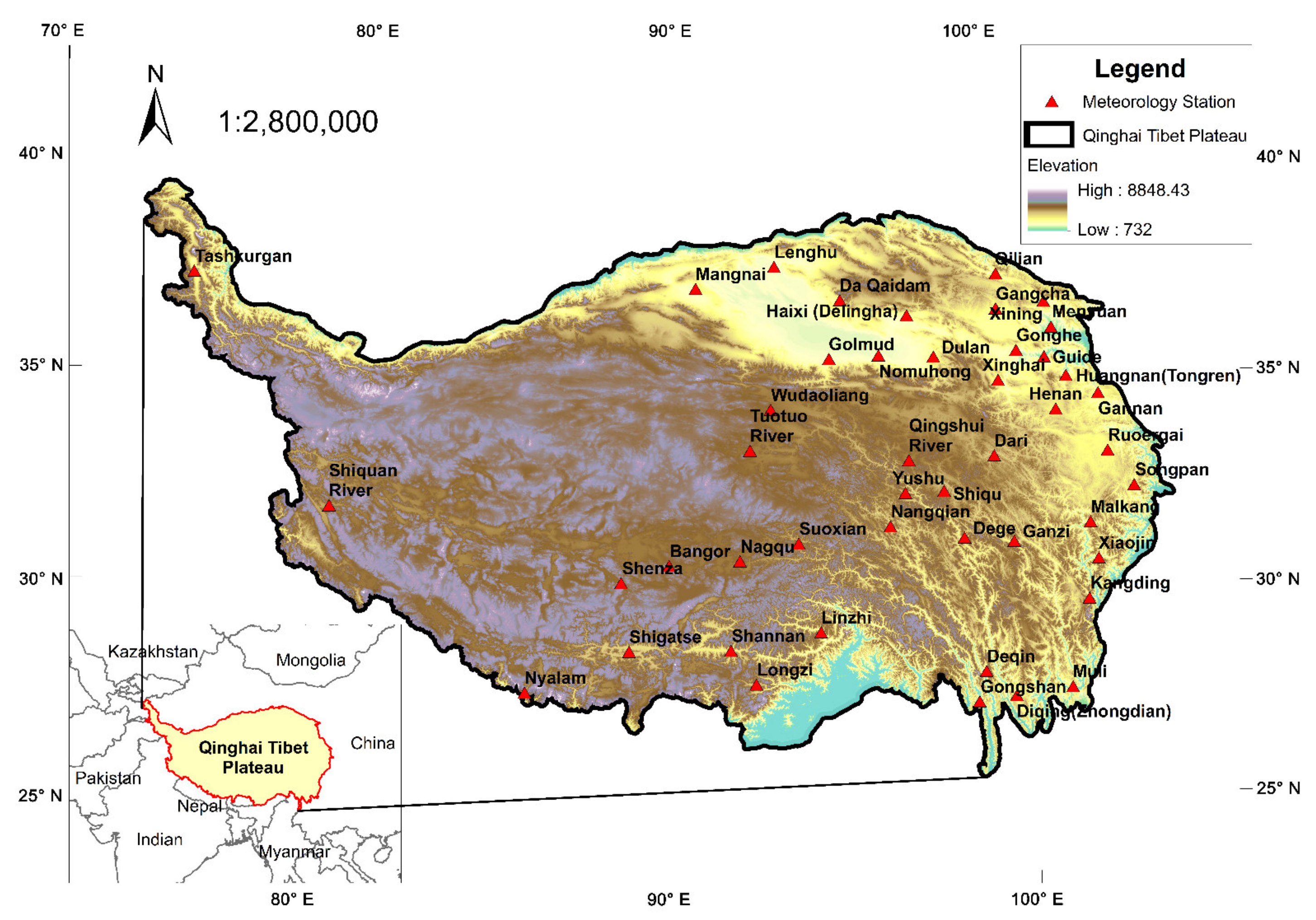
2.1. Study Area and Data
2.2. FAO Penman-Monteith Formula
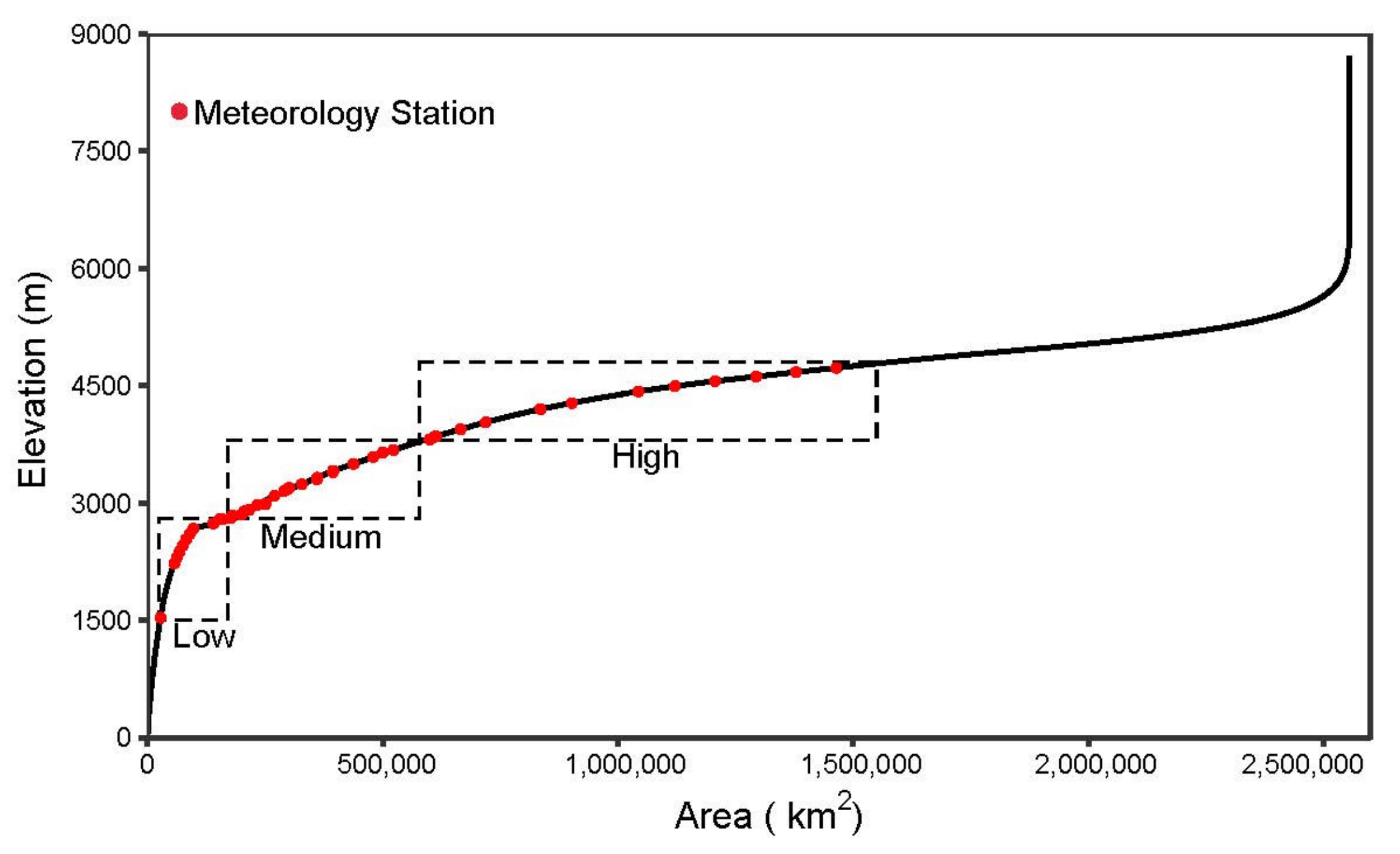
2.3. Data Preprocessing
2.4. Temporal Trend and Mutation Analysis Method
2.4.1. Cumulative Anomaly Curve
2.4.2. Mann–Kendall Test
2.4.3. Moving T-Test
2.4.4. Yamamoto Test
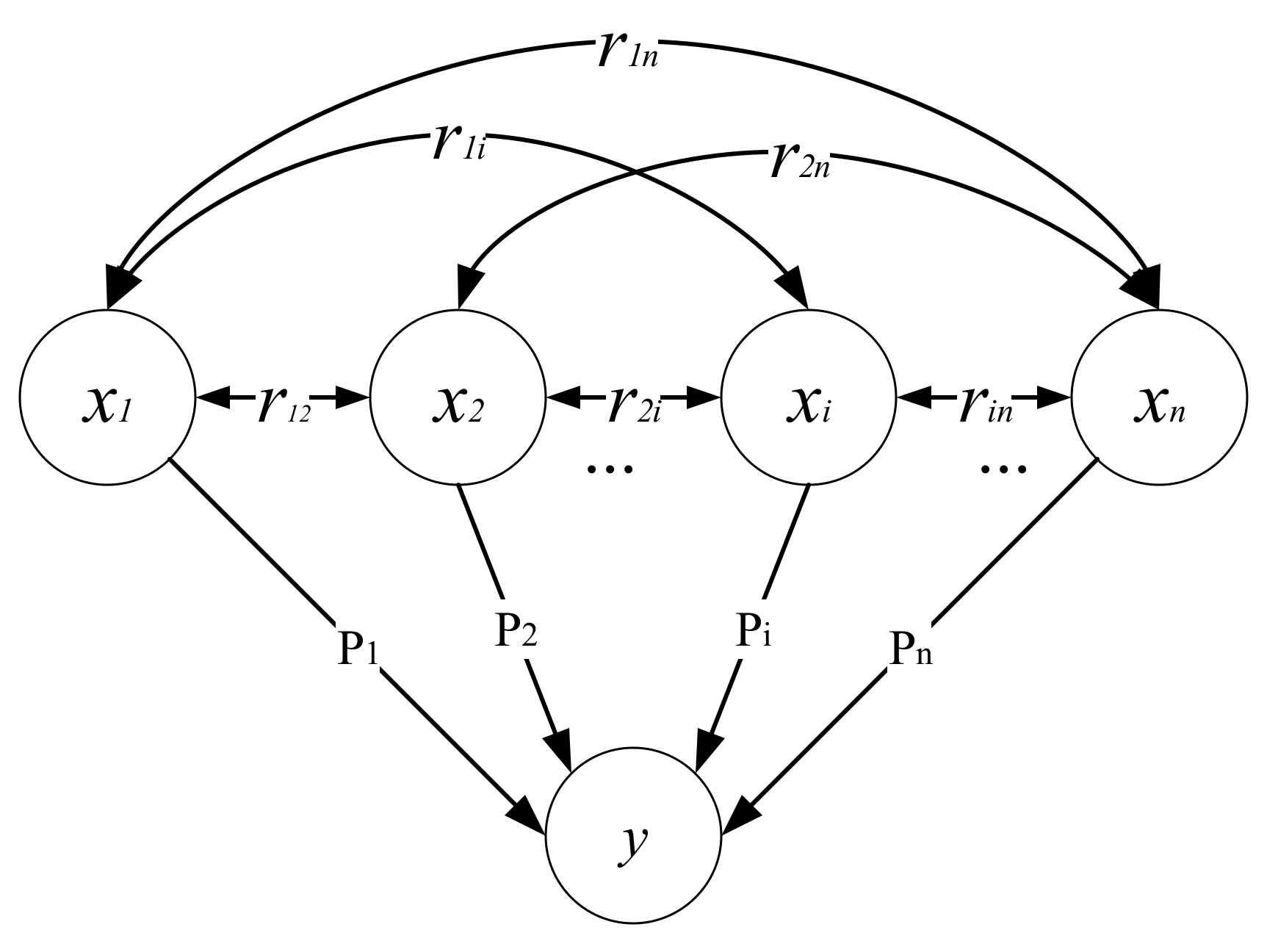
2.5. Path Analysis
3. Results and Discussion
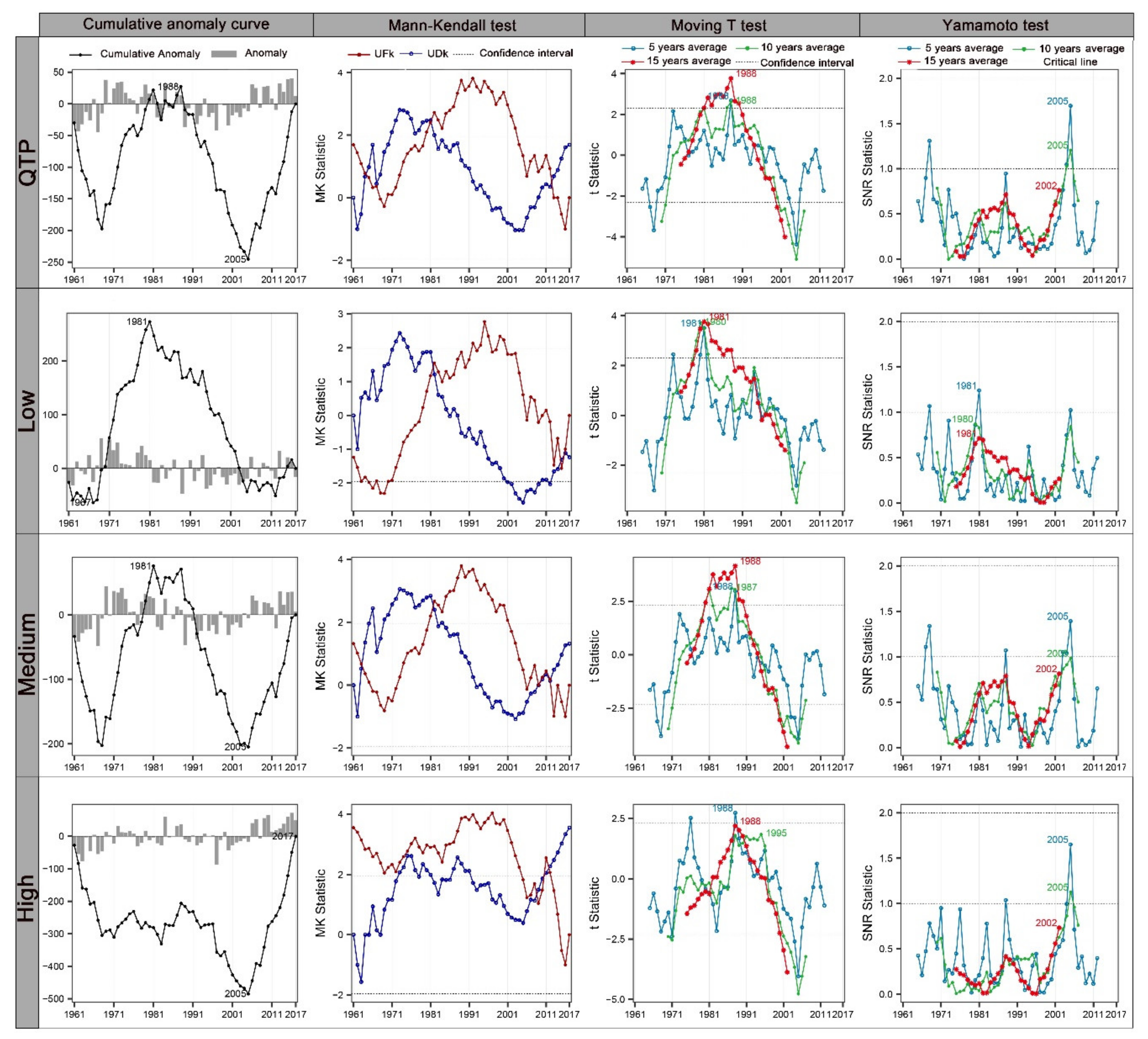
3.1. Mutation Analysis of ET0 in Different Altitudes during 1961–2017
3.1.1. Mutation Analysis of Annual ET0
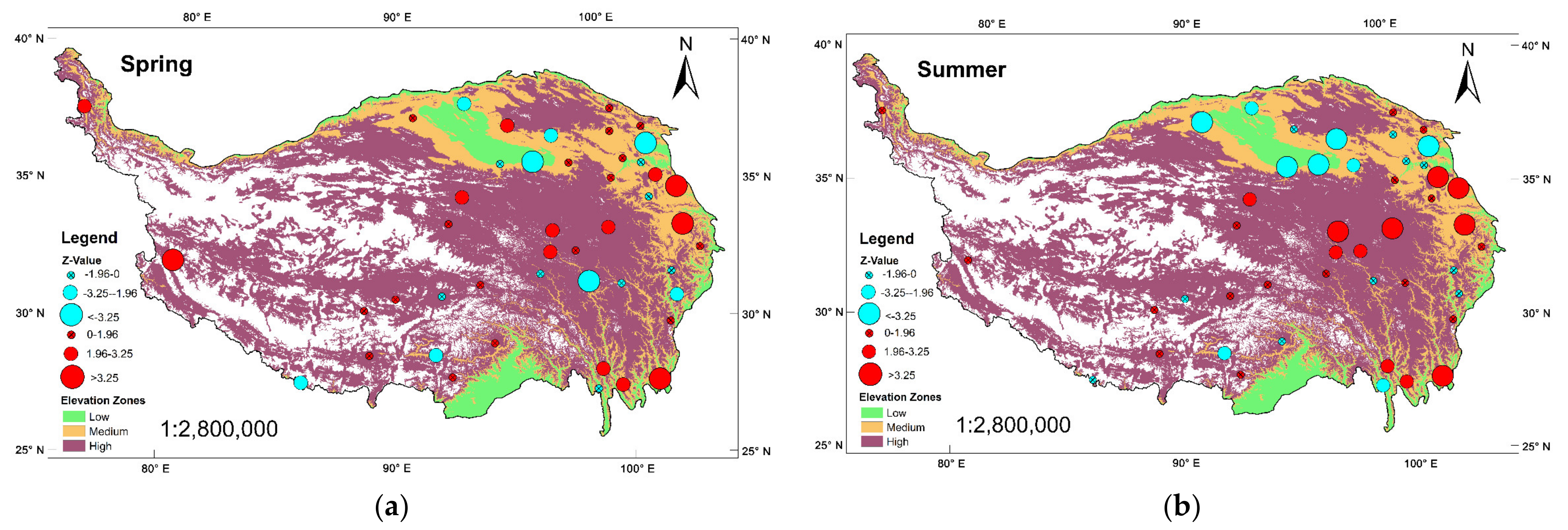
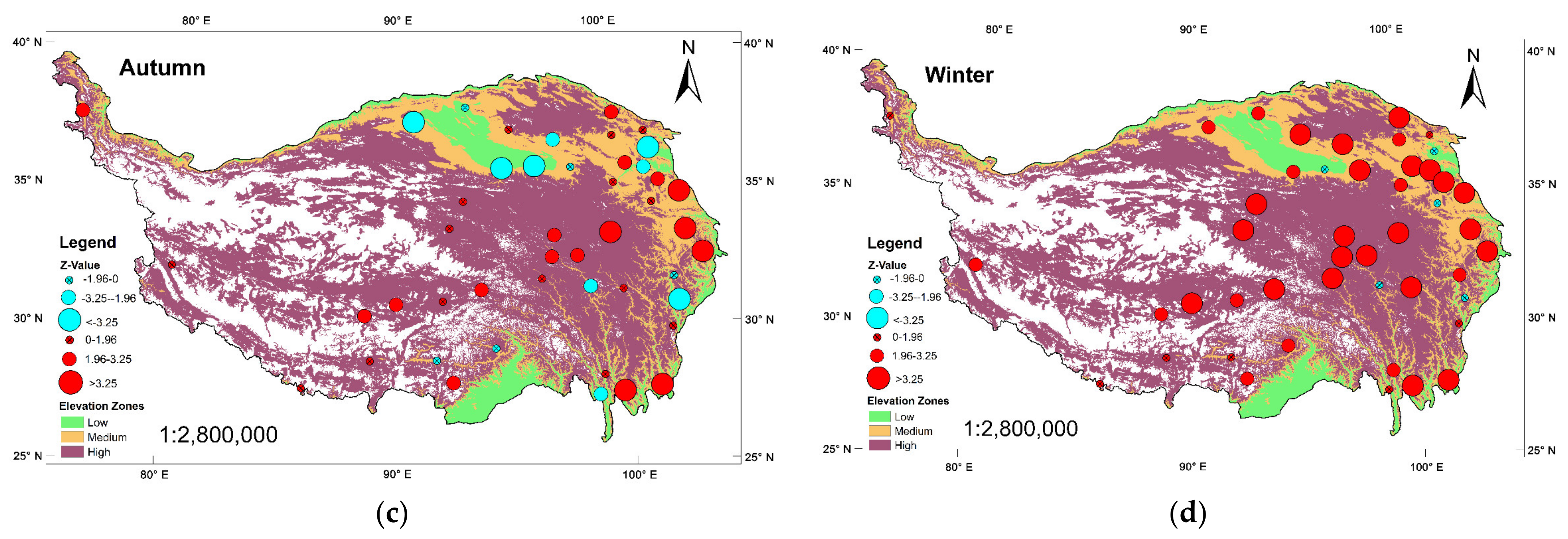
3.1.2. Mutation Analysis of Four Seasons of ET0
3.2. Temporal Trend Analysis of ET0 in Different Altitudes
3.2.1. Temporal Trend of Annual ET0
3.2.2. Temporal Trend of Four Seasons of ET0
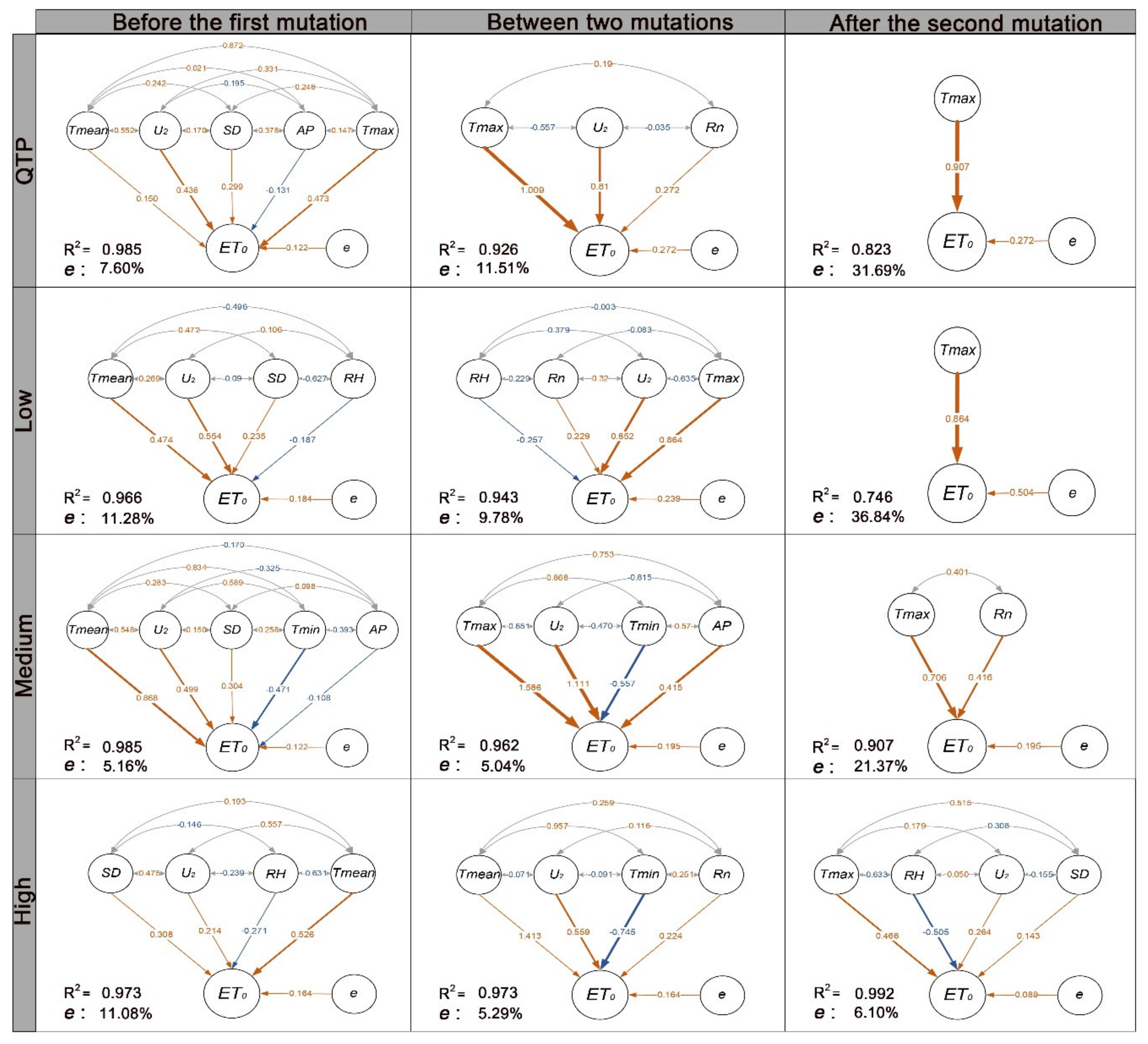
3.3. Climate-Driven Pattern of ET0 in Different Altitudes
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Walther, G.-R.; Post, E.; Convey, P.; Menzel, A.; Parmesan, C.; Beebee, T.J.C.; Fromentin, J.-M.; Hoegh-Guldberg, O.; Bairlein, F. Ecological responses to recent climate change. Nature 2002, 416, 389–395. [Google Scholar] [CrossRef] [PubMed]
- Parmesan, C.; Yohe, G. A globally coherent fingerprint of climate change impacts across natural systems. Nature 2003, 421, 37–42. [Google Scholar] [CrossRef] [PubMed]
- Döll, P. Impact of Climate Change and Variability on Irrigation Requirements: A Global Perspective. Clim. Chang. 2002, 54, 269–293. [Google Scholar] [CrossRef]
- Williamson, C.E.; Saros, J.E.; Schindler, D.W. Sentinels of change. Science 2009, 323, 877–878. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, H.D. Asia’s shrinking glaciers protect large populations from drought stress. Nature 2019, 569, 649–654. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Li, Y.; Chen, A.; Gao, M.; Slette, I.; Piao, S. The impact of the 2009/2010 drought on vegetation growth and terrestrial carbon balance in Southwest China. Agric. For. Meteorol. 2019, 269, 239–248. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Fasullo, J.T.; Kiehl, J. Earth’s Global Energy Budget. Bull. Am. Meteorol. Soc. 2009, 90, 311–324. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.I.; Sheffield, J.; Goulden, M.L.; Bonan, G.; Cescatti, A.; Chen, J.; De Jeu, R.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar] [CrossRef]
- Wang, W.; Li, J.; Yu, Z.; Ding, Y.; Xing, W.; Lu, W. Satellite retrieval of actual evapotranspiration in the Tibetan Plateau: Components partitioning, multidecadal trends and dominated factors identifying. J. Hydrol. 2018, 559, 471–485. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, Z.; Hao, X.; Yue, P. Conversion features of evapotranspiration responding to climate warming in transitional climate regions in northern China. Clim. Dyn. 2018, 52, 3891–3903. [Google Scholar] [CrossRef]
- Howes, D.J.; Fox, P.; Hutton, P. Evapotranspiration from Natural Vegetation in the Central Valley of California: Monthly Grass Reference-Based Vegetation Coefficients and the Dual Crop Coefficient Approach. J. Hydrol. Eng. 2015, 20, 04015004. [Google Scholar] [CrossRef]
- Testa, G.; Gresta, F.; Cosentino, S. Dry matter and qualitative characteristics of alfalfa as affected by harvest times and soil water content. Eur. J. Agron. 2011, 34, 144–152. [Google Scholar] [CrossRef]
- Maček, U.; Bezak, N.; Šraj, M. Reference evapotranspiration changes in Slovenia, Europe. Agric. For. Meteorol. 2018, 260, 183–192. [Google Scholar] [CrossRef]
- Perera, K.C.; Western, A.W.; Nawarathna, B.; George, B. Forecasting daily reference evapotranspiration for Australia using numerical weather prediction outputs. Agric. For. Meteorol. 2014, 194, 50–63. [Google Scholar] [CrossRef]
- Cook, B.I.; Smerdon, J.E.; Seager, R.; Coats, S. Global warming and 21st century drying. Clim. Dyn. 2014, 43, 2607–2627. [Google Scholar] [CrossRef] [Green Version]
- Wu, D.; Fang, S.; Li, X.; He, D.; Zhu, Y.; Yang, Z.; Xu, J.; Wu, Y. Spatial-temporal variation in irrigation water requirement for the winter wheat-summer maize rotation system since the 1980s on the North China Plain. Agric. Water Manag. 2019, 214, 78–86. [Google Scholar] [CrossRef]
- Wurster, P.; Maneta, M.; Beguería, S.; Cobourn, K.; Maxwell, B.; Silverman, N.; Ewing, S.; Jensco, K.; Gardner, P.; Kimball, J.; et al. Characterizing the impact of climatic and price anomalies on agrosystems in the northwest United States. Agric. For. Meteorol. 2020, 280, 107778. [Google Scholar] [CrossRef]
- Xu, C.-Y.; Gong, L.; Jiang, T.; Chen, D.; Singh, V. Analysis of spatial distribution and temporal trend of reference evapotranspiration and pan evaporation in Changjiang (Yangtze River) catchment. J. Hydrol. 2006, 327, 81–93. [Google Scholar] [CrossRef]
- Nam, W.-H.; Hong, E.-M.; Choi, J.-Y. Has climate change already affected the spatial distribution and temporal trends of reference evapotranspiration in South Korea? Agric. Water Manag. 2015, 150, 129–138. [Google Scholar] [CrossRef]
- Wang, Z.; Xie, P.; Lai, C.; Chen, X.; Wu, X.; Zeng, Z.; Li, J. Spatiotemporal variability of reference evapotranspiration and contributing climatic factors in China during 1961–2013. J. Hydrol. 2017, 544, 97–108. [Google Scholar] [CrossRef]
- Ye, L.; Shi, K.; Zhang, H.; Xin, Z.; Hu, J.; Zhang, C. Spatio-Temporal Analysis of Drought Indicated by SPEI over Northeastern China. Water 2019, 11, 908. [Google Scholar] [CrossRef] [Green Version]
- Tran, A.P.; Rungee, J.; Faybishenko, B.; Dafflon, B.; Hubbard, S.S. Assessment of Spatiotemporal Variability of Evapotranspiration and Its Governing Factors in a Mountainous Watershed. Water 2019, 11, 243. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Xiao, W.; Zhao, Y.; Wang, Y.; Hou, B.; Zhou, Y.; Yang, H.; Zhang, X.; Cui, H. The Spatiotemporal Variability of Evapotranspiration and Its Response to Climate Change and Land Use/Land Cover Change in the Three Gorges Reservoir. Water 2019, 11, 1739. [Google Scholar] [CrossRef] [Green Version]
- Cavalcante, R.B.L.; Pontes, P.R.M.; Souza-Filho, P.W.M.; de Souza, E. Opposite Effects of Climate and Land Use Changes on the Annual Water Balance in the Amazon Arc of Deforestation. Water Resour. Res. 2019, 55, 3092–3106. [Google Scholar] [CrossRef]
- Hu, Z.; Chen, X.; Chen, D.; Li, J.; Wang, S.; Zhou, Q.; Yin, G.; Guo, M. “Dry gets drier, wet gets wetter”: A case study over the arid regions of central Asia. Int. J. Clim. 2018, 39, 1072–1091. [Google Scholar] [CrossRef]
- Prăvălie, R.; Sîrodoev, I.; Patriche, C.; Roșca, B.; Piticar, A.; Bandoc, G.; Sfîcă, L.; Tişcovschi, A.; Dumitrascu, M.; Chifiriuc, C.; et al. The impact of climate change on agricultural productivity in Romania. A country-scale assessment based on the relationship between climatic water balance and maize yields in recent decades. Agric. Syst. 2020, 179, 102767. [Google Scholar] [CrossRef]
- Vera, J.F.R.; Mera, Y.E.Z.; Pérez-Martín, M. Adapting water resources systems to climate change in tropical areas: Ecuadorian coast. Sci. Total. Environ. 2020, 703, 135554. [Google Scholar] [CrossRef] [PubMed]
- Dobson, D.; Meredith, P.; Boon, S.A. Simulation of Subduction Zone Seismicity by Dehydration of Serpentine. Science 2002, 298, 1407–1410. [Google Scholar] [CrossRef]
- McVicar, T.; Roderick, M.L.; Donohue, R.J.; Li, L.T.; Van Niel, T.; Thomas, A.; Grieser, J.; Jhajharia, D.; Himri, Y.; Mahowald, N.M.; et al. Global review and synthesis of trends in observed terrestrial near-surface wind speeds: Implications for evaporation. J. Hydrol. 2012, 416–417, 182–205. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, Y.; Qian, Y.; Pan, Z.; Zhu, Y.; Zhang, Y.; Guo, J.; Xu, L. Coincidence of variation in potato yield and climate in northern China. Sci. Total. Environ. 2016, 573, 965–973. [Google Scholar] [CrossRef]
- Lin, P.; He, Z.; Du, J.; Chen, L.; Zhu, X.; Li, J. Impacts of climate change on reference evapotranspiration in the Qilian Mountains of China: Historical trends and projected changes. Int. J. Clim. 2018, 38, 2980–2993. [Google Scholar] [CrossRef]
- Li, Y.; Yao, N.; Chau, H.W. Influences of removing linear and nonlinear trends from climatic variables on temporal variations of annual reference crop evapotranspiration in Xinjiang, China. Sci. Total. Environ. 2017, 592, 680–692. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, S.; Yu, Z.; Yang, C.; Ji, X.; Zhang, K. Trends in evapotranspiration and their responses to climate change and vegetation greening over the upper reaches of the Yellow River Basin. Agric. For. Meteorol. 2018, 263, 118–129. [Google Scholar] [CrossRef]
- Li, M.; Chu, R.; Shen, S.; Islam, A.R.M.T. Dynamic analysis of pan evaporation variations in the Huai River Basin, a climate transition zone in eastern China. Sci. Total. Environ. 2018, 625, 496–509. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Feng, Q.; Adamowski, J.F.; Yin, Z.; Wen, X.; Wu, M.; Jia, B.; Hao, Q. Spatio-temporal variation of reference evapotranspiration in northwest China based on CORDEX-EA. Atmos. Res. 2020, 238, 104868. [Google Scholar] [CrossRef]
- Xing, W.; Wang, W.; Shao, Q.; Yu, Z.; Yang, T.; Fu, J. Periodic fluctuation of reference evapotranspiration during the past five decades: Does Evaporation Paradox really exist in China? Sci. Rep. 2016, 6, 39503. [Google Scholar] [CrossRef]
- Baccour, H.; Slimani, M.; Cudennec, C. Structures spatiales de l’évapotranspiration de référence et des variables climatiques corrélées en Tunisie. Hydrol. Sci. J. 2012, 57, 818–829. [Google Scholar] [CrossRef]
- Li, C.; Wu, P.; Li, X.; Zhou, T.; Sun, S.; Wang, Y.; Luan, X.; Yu, X. Spatial and temporal evolution of climatic factors and its impacts on potential evapotranspiration in Loess Plateau of Northern Shaanxi, China. Sci. Total. Environ. 2017, 589, 165–172. [Google Scholar] [CrossRef]
- Fan, Z.-X.; Thomas, A. Decadal changes of reference crop evapotranspiration attribution: Spatial and temporal variability over China 1960–2011. J. Hydrol. 2018, 560, 461–470. [Google Scholar] [CrossRef]
- Jiang, S.; Liang, C.; Cui, N.; Zhao, L.; Du, T.; Hu, X.; Feng, Y.; Guan, J.; Feng, Y. Impacts of climatic variables on reference evapotranspiration during growing season in Southwest China. Agric. Water Manag. 2019, 216, 365–378. [Google Scholar] [CrossRef]
- Liu, T.; Li, L.; Lai, J.; Liu, C.; Zhuang, W. Reference evapotranspiration change and its sensitivity to climate variables in southwest China. Theor. Appl. Clim. 2015, 125, 499–508. [Google Scholar] [CrossRef]
- Gao, Z.; He, J.; Dong, K.; Li, X. Trends in reference evapotranspiration and their causative factors in the West Liao River basin, China. Agric. For. Meteorol. 2017, 232, 106–117. [Google Scholar] [CrossRef]
- Yao, L. Causative impact of air pollution on evapotranspiration in the North China Plain. Environ. Res. 2017, 158, 436–442. [Google Scholar] [CrossRef]
- Zhao, Z.; Wang, H.; Wang, C.; Li, W.; Chen, H.; Deng, C. Changes in reference evapotranspiration over Northwest China from 1957 to 2018: Variation characteristics, cause analysis and relationships with atmospheric circulation. Agric. Water Manag. 2020, 231, 105958. [Google Scholar] [CrossRef]
- Yao, T.; Liu, X.; Wang, N.; Shi, Y. Amplitude of climatic changes in Qinghai-Tibetan Plateau. Chin. Sci. Bull. 2000, 45, 1236–1243. [Google Scholar] [CrossRef]
- Duan, A.; Xiao, Z. Does the climate warming hiatus exist over the Tibetan Plateau? Sci. Rep. 2015, 5, 13711. [Google Scholar] [CrossRef]
- Gao, Q.; Guo, Y.; Xu, H.; Ganjurjav, H.; Li, Y.; Wan, Y.; Qin, X.; Ma, X.; Liu, S. Climate change and its impacts on vegetation distribution and net primary productivity of the alpine ecosystem in the Qinghai-Tibetan Plateau. Sci. Total. Environ. 2016, 554–555, 34–41. [Google Scholar] [CrossRef]
- Zhao, R.; Li, Z.-W.; Feng, G.-C.; Wang, Q.-J.; Hu, J. Monitoring surface deformation over permafrost with an improved SBAS-InSAR algorithm: With emphasis on climatic factors modeling. Remote Sens. Environ. 2016, 184, 276–287. [Google Scholar] [CrossRef]
- Zhang, G.; Yao, T.; Shum, C.K.; Yi, S.; Yang, K.; Xie, H.; Feng, W.; Bolch, T.; Wang, L.; Behrangi, A.; et al. Lake volume and groundwater storage variations in Tibetan Plateau’s endorheic basin. Geophys. Res. Lett. 2017, 44, 5550–5560. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Cheng, G. Climate warming over the past half century has led to thermal degradation of permafrost on the Qinghai–Tibet Plateau. Cryosphere 2018, 12, 595–608. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.; Li, Z.; Li, J.; Zhao, R.; Ding, X. Glacier mass balance in the Qinghai–Tibet Plateau and its surroundings from the mid-1970s to 2000 based on Hexagon KH-9 and SRTM DEMs. Remote Sens. Environ. 2018, 210, 96–112. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, Y.; Zhu, J.; Liu, Y.; Zu, J.; Zhang, J. The Influences of Climate Change and Human Activities on Vegetation Dynamics in the Qinghai-Tibet Plateau. Remote Sens. 2016, 8, 876. [Google Scholar] [CrossRef] [Green Version]
- Ganjurjav, H.; Gao, Q.; Gornish, E.S.; Schwartz, M.; Liang, Y.; Cao, X.; Zhang, W.; Zhang, Y.; Li, W.; Wan, Y.; et al. Differential response of alpine steppe and alpine meadow to climate warming in the central Qinghai–Tibetan Plateau. Agric. For. Meteorol. 2016, 223, 233–240. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.-L.; Ding, J.-Z.; Peng, Y.-F.; Li, F.; Yang, G.-B.; Liu, L.; Qin, S.-Q.; Fang, K.; Yang, Y.-H. Patterns and drivers of soil microbial communities in Tibetan alpine and global terrestrial ecosystems. J. Biogeogr. 2016, 43, 2027–2039. [Google Scholar] [CrossRef]
- Zhang, Y.; Dong, S.; Gao, Q.; Liu, S.; Zhou, H.; Ganjurjav, H.; Wang, X. Climate change and human activities altered the diversity and composition of soil microbial community in alpine grasslands of the Qinghai-Tibetan Plateau. Sci. Total Environ. 2016, 562, 353–363. [Google Scholar] [CrossRef] [PubMed]
- Ma, Z.; Liu, H.; Mi, Z.; Zhang, Z.; Wang, Y.; Xu, W.; Jiang, L.; He, J.-S. Climate warming reduces the temporal stability of plant community biomass production. Nat. Commun. 2017, 8, 15378. [Google Scholar] [CrossRef]
- Liu, H.; Mi, Z.; Lin, L.; Wang, Y.; Zhang, Z.; Zhang, F.; Wang, H.; Liu, L.; Zhu, B.; Cao, G.; et al. Shifting plant species composition in response to climate change stabilizes grassland primary production. Proc. Natl. Acad. Sci. USA 2018, 115, 4051–4056. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sheng, W.; Zhen, L.; Xiao, Y.; Hu, Y. Ecological and socioeconomic effects of ecological restoration in China’s Three Rivers Source Region. Sci. Total Environ. 2019, 650, 2307–2313. [Google Scholar] [CrossRef]
- Luo, D.; Jin, H.; Marchenko, S.S.; Romanovsky, V.E. Difference between near-surface air, land surface and ground surface temperatures and their influences on the frozen ground on the Qinghai-Tibet Plateau. Geoderma 2018, 312, 74–85. [Google Scholar] [CrossRef]
- Xu, X.; Lu, C.; Shi, X.; Gao, S. World water tower: An atmospheric perspective. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Immerzeel, W.; Droogers, P.; de Jong, S.; Bierkens, M.F. Large-scale monitoring of snow cover and runoff simulation in Himalayan river basins using remote sensing. Remote Sens. Environ. 2009, 113, 40–49. [Google Scholar] [CrossRef]
- Wang, Y.; Spencer, R.G.M.; Podgorski, D.C.; Kellerman, A.M.; Rashid, H.; Zito, P.; Xiao, W.; Wei, D.; Yang, Y.; Xu, Y. Spatiotemporal transformation of dissolved organic matter along an alpine stream flow path on the Qinghai–Tibet Plateau: Importance of source and permafrost degradation. Biogeosciences 2018, 15, 6637–6648. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Song, W.; Yuan, X.; Yin, L. Spatio-Temporal Variations in Farmland Water Conditions in the Yanhe River Basin. Water 2019, 11, 2234. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Liu, L. Analysis of Dry/Wet Variations in the Poyang Lake Basin Using Standardized Precipitation Evapotranspiration Index Based on Two Potential Evapotranspiration Algorithms. Water 2019, 11, 1380. [Google Scholar] [CrossRef] [Green Version]
- Ye, J.; Guo, A.; Sun, G. Statistical Analysis of Reference Evapotranspiration on the Tibetan Plateau. J. Irrig. Drain. Eng. 2009, 135, 134–140. [Google Scholar] [CrossRef]
- Regmi, B.; Lamichhane, S. A dynamic linear model of monthly minimum and maximum temperature changes in three physiographic regions of the Central Himalayas. Clim. Res. 2019, 79, 1–8. [Google Scholar] [CrossRef]
- Drissia, T.K.; Jothiprakash, V.; Anitha, A.B. Statistical classification of streamflow based on flow variability in west flowing rivers of Kerala, India. Theor. Appl. Clim. 2018, 137, 1643–1658. [Google Scholar] [CrossRef]
- Demiroglu, O.C.; Kučerová, J.; Ozcelebi, O. Snow reliability and climate elasticity: Case of a Slovak ski resort. Tour. Rev. 2015, 70, 1–12. [Google Scholar] [CrossRef]
- Peng, D.; Qiu, L.; Fang, J.; Zhang, Z. Quantification of Climate Changes and Human Activities That Impact Runoff in the Taihu Lake Basin, China. Math. Probl. Eng. 2016, 2016, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Misra, V.; Bhardwaj, A. Defining the Northeast Monsoon of India. Mon. Weather Rev. 2019, 147, 791–807. [Google Scholar] [CrossRef]
- Hůnová, I.; Bäumelt, V.; Modlík, M. Long-term trends in nitrogen oxides at different types of monitoring stations in the Czech Republic. Sci. Total Environ. 2020, 699, 134378. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of changes in meteorological variables using Mann-Kendall and Sen’s slope estimator statistical tests in Serbia. Glob. Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Yang, Q.; Zheng, J.; Zhu, H. Influence of spatiotemporal change of temperature and rainfall on major grain yields in southern Jiangsu Province, China. Glob. Ecol. Conserv. 2020, 21, e00818. [Google Scholar] [CrossRef]
- Zhao, F.F.; Xu, Z.X.; Huang, J.X.; Li, J.Y. Monotonic trend and abrupt changes for major climate variables in the headwater catchment of the Yellow River basin. Hydrol. Process. 2008, 22, 4587–4599. [Google Scholar] [CrossRef]
- Mellios, N.; Moe, S.J.; Laspidou, C. Machine Learning Approaches for Predicting Health Risk of Cyanobacterial Blooms in Northern European Lakes. Water 2020, 12, 1191. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Pan, X.; Wang, Z.; Jiang, S.; Liang, L.; Wang, X.; Wang, X. What were the changing trends of the seasonal and annual aridity indexes in northwestern China during 1961–2015? Atmos. Res. 2019, 222, 154–162. [Google Scholar] [CrossRef]
- Li, X.; Chen, Z.; Wang, L. Analysis of the Spatiotemporal Variation Characteristics of Main Extreme Climate Indices in Sichuan Province of China from 1968 to 2017. Appl. Ecol. Environ. Res. 2020, 18, 3211–3242. [Google Scholar] [CrossRef]
- Wang, Z.; Ye, A.; Wang, L.; Liu, K.; Cheng, L. Spatial and temporal characteristics of reference evapotranspiration and its climatic driving factors over China from 1979–2015. Agric. Water Manag. 2019, 213, 1096–1108. [Google Scholar] [CrossRef]
- Thomas, A. Spatial and temporal characteristics of potential evapotranspiration trends over China. Int. J. Climatol. 2000, 20, 381–396. [Google Scholar] [CrossRef]
- Kuang, X.; Jiao, J.J. Review on climate change on the Tibetan Plateau during the last half century. J. Geophys. Res. Atmos. 2016, 121, 3979–4007. [Google Scholar] [CrossRef]
- Kang, S.; Xu, Y.; You, Q.; Flügel, W.-A.; Pepin, N.; Yao, T. Review of climate and cryospheric change in the Tibetan Plateau. Environ. Res. Lett. 2010, 5, 015101. [Google Scholar] [CrossRef]
- Zhang, G.; Xie, H.; Kang, S.; Yi, D.; Ackley, S.F. Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009). Remote Sens. Environ. 2011, 115, 1733–1742. [Google Scholar] [CrossRef]
- Zhang, L.; Traore, S.; Cui, Y.; Luo, Y.; Zhu, G.; Liu, B.; Fipps, G.; Karthikeyan, R.; Singh, V. Assessment of spatiotemporal variability of reference evapotranspiration and controlling climate factors over decades in China using geospatial techniques. Agric. Water Manag. 2019, 213, 499–511. [Google Scholar] [CrossRef]
| Region | 1961–2017 | Before the First Mutation | Between Two Mutations | After the Second Mutation | ||||
|---|---|---|---|---|---|---|---|---|
| Z | Trend | Z | Trend | Z | Trend | Z | Trend | |
| QTP | 1.60 | 3.31 | 1.63 | 11.97 | −0.37 | −4.06 | 1.16 | 15.64 |
| Low | 0.47 | 0.72 | 2.56 * | 28.56 | −1.31 | −8.45 | 0.79 | 10.75 |
| Medium | 1.11 | 2.21 | 1.58 | 13.23 | 0.12 | 3.16 | 0.42 | 12.05 |
| High | 3.42 *** | 9.84 | 1.88 | 17.83 | −0.54 | −12.77 | 1.77 | 32.80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Yao, X.; Wang, Q.; Yu, J.; Jiang, Q.; Jiang, W.; Li, L. Differences in Reference Evapotranspiration Variation and Climate-Driven Patterns in Different Altitudes of the Qinghai–Tibet Plateau (1961–2017). Water 2021, 13, 1749. https://doi.org/10.3390/w13131749
Liu Y, Yao X, Wang Q, Yu J, Jiang Q, Jiang W, Li L. Differences in Reference Evapotranspiration Variation and Climate-Driven Patterns in Different Altitudes of the Qinghai–Tibet Plateau (1961–2017). Water. 2021; 13(13):1749. https://doi.org/10.3390/w13131749
Chicago/Turabian StyleLiu, Yuan, Xiaolei Yao, Qianyang Wang, Jingshan Yu, Qi Jiang, Weiwei Jiang, and Luyi Li. 2021. "Differences in Reference Evapotranspiration Variation and Climate-Driven Patterns in Different Altitudes of the Qinghai–Tibet Plateau (1961–2017)" Water 13, no. 13: 1749. https://doi.org/10.3390/w13131749
APA StyleLiu, Y., Yao, X., Wang, Q., Yu, J., Jiang, Q., Jiang, W., & Li, L. (2021). Differences in Reference Evapotranspiration Variation and Climate-Driven Patterns in Different Altitudes of the Qinghai–Tibet Plateau (1961–2017). Water, 13(13), 1749. https://doi.org/10.3390/w13131749







