Assimilating X- and S-Band Radar Data for a Heavy Precipitation Event in Italy
Abstract
:1. Introduction
2. Materials and Methods
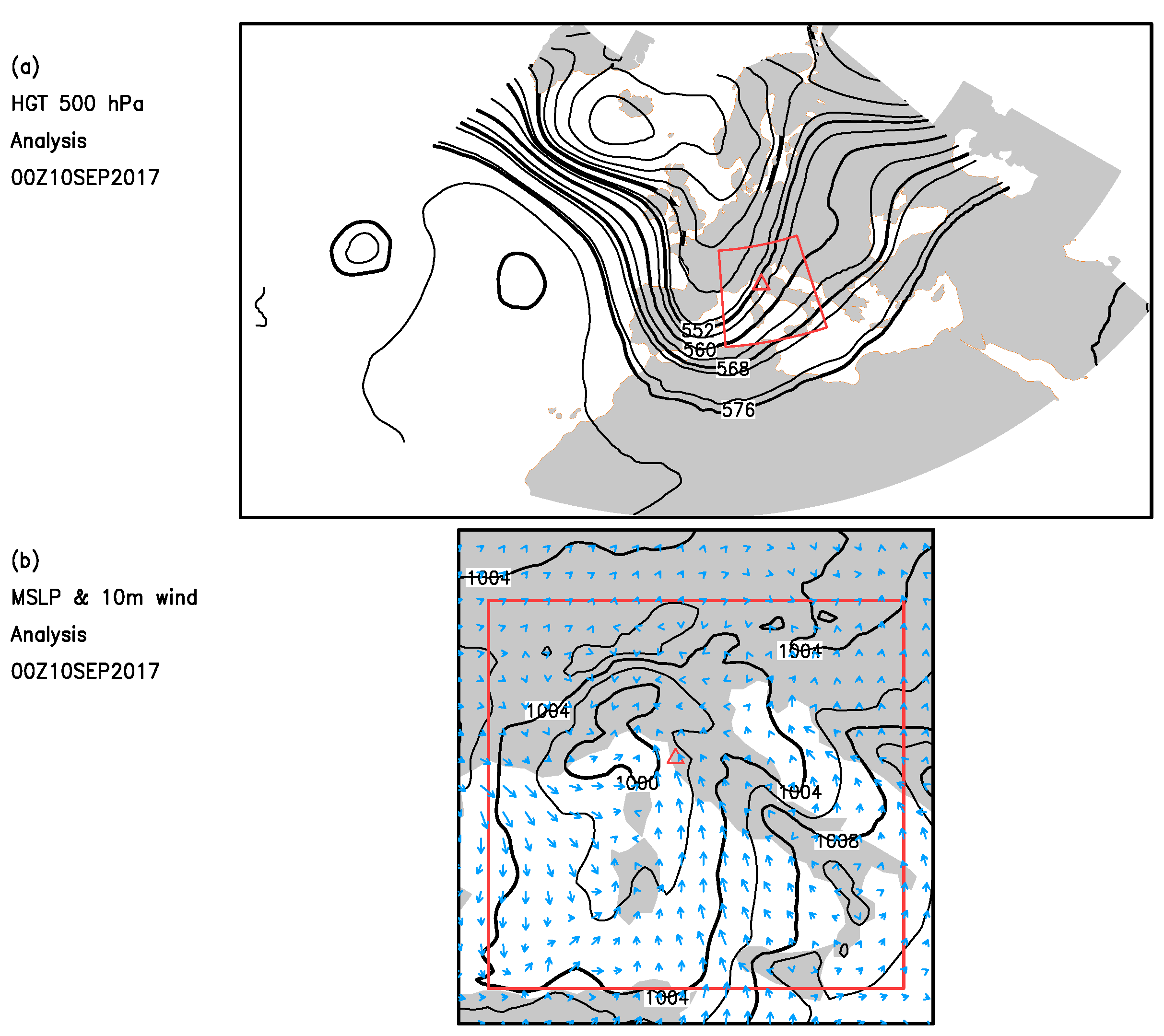
2.1. Synoptic Conditions
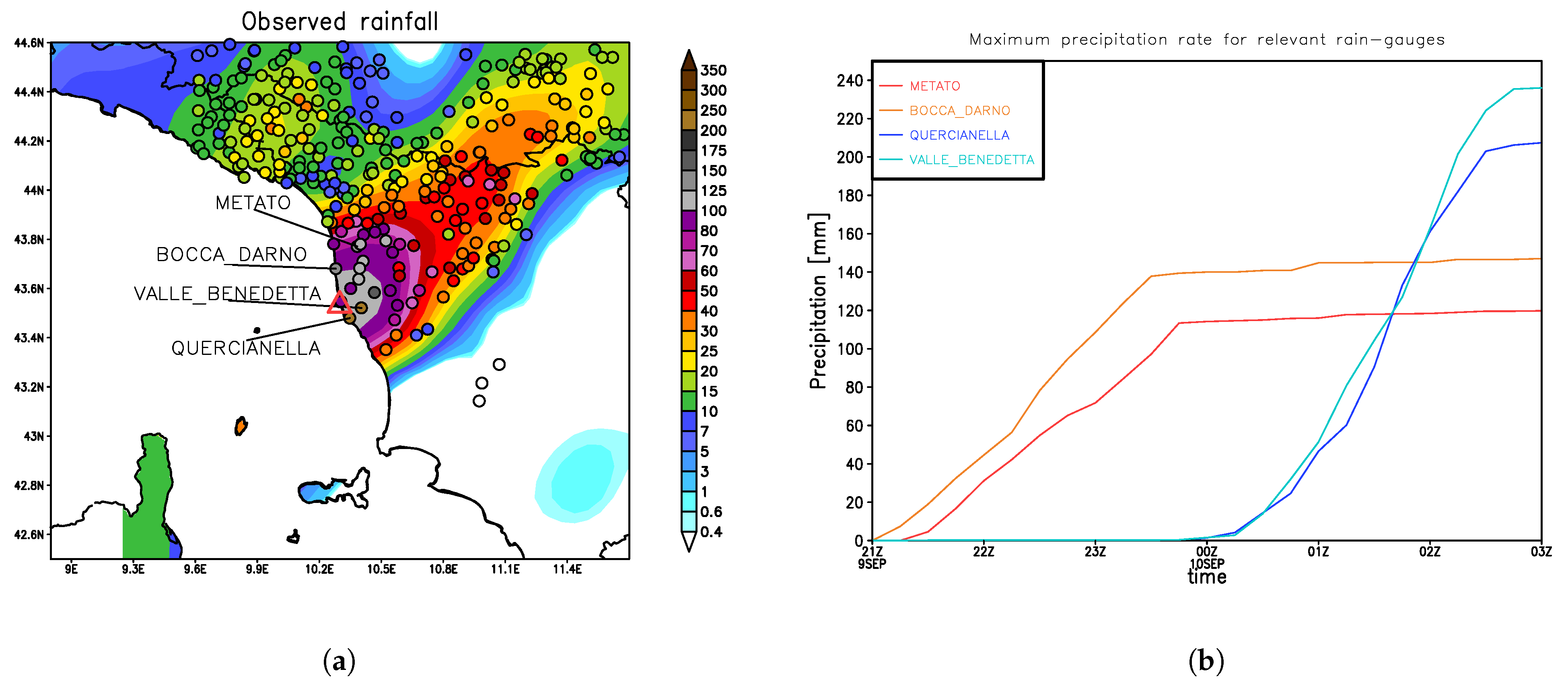
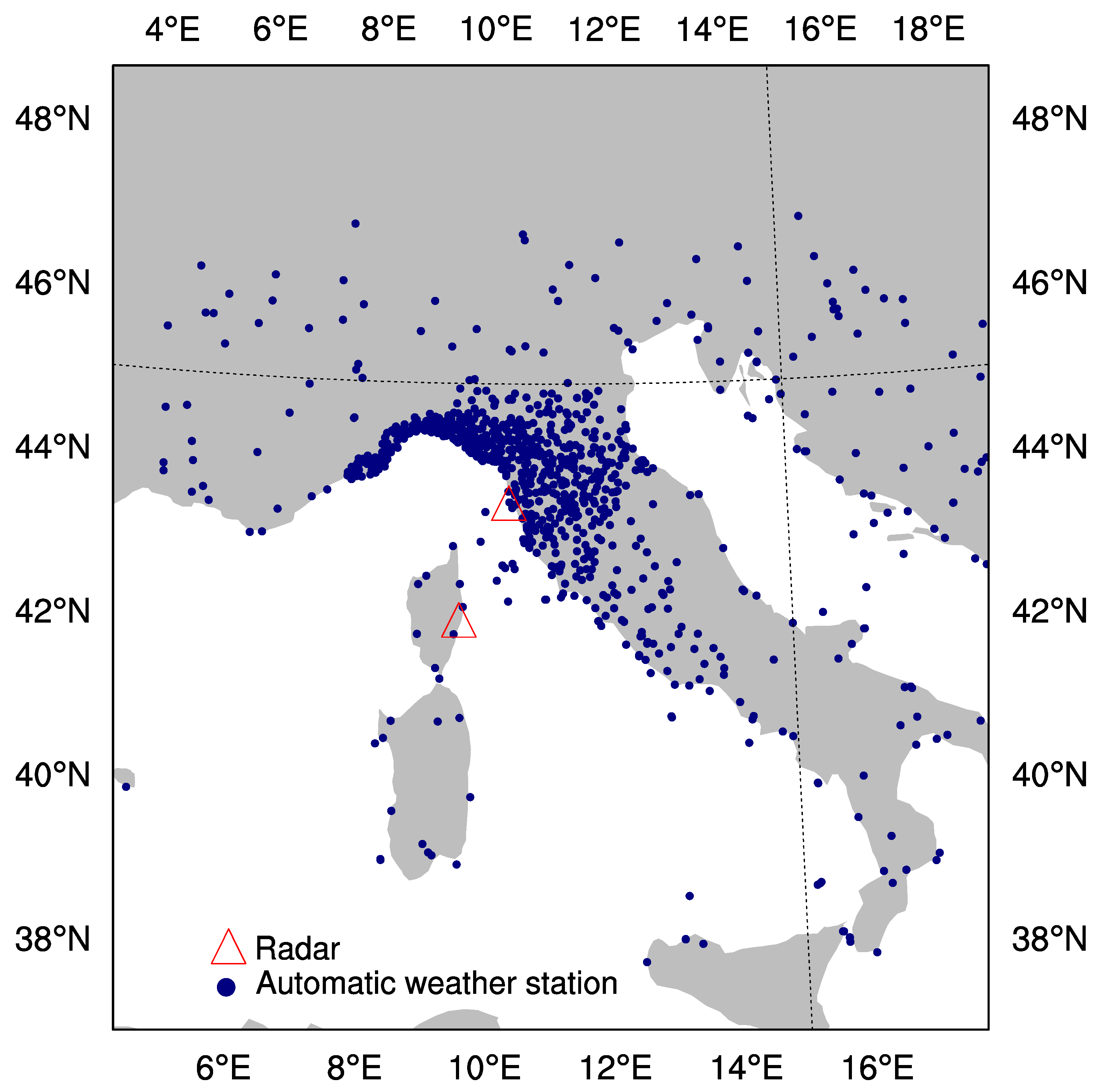
2.2. Observed Precipitation Measurements
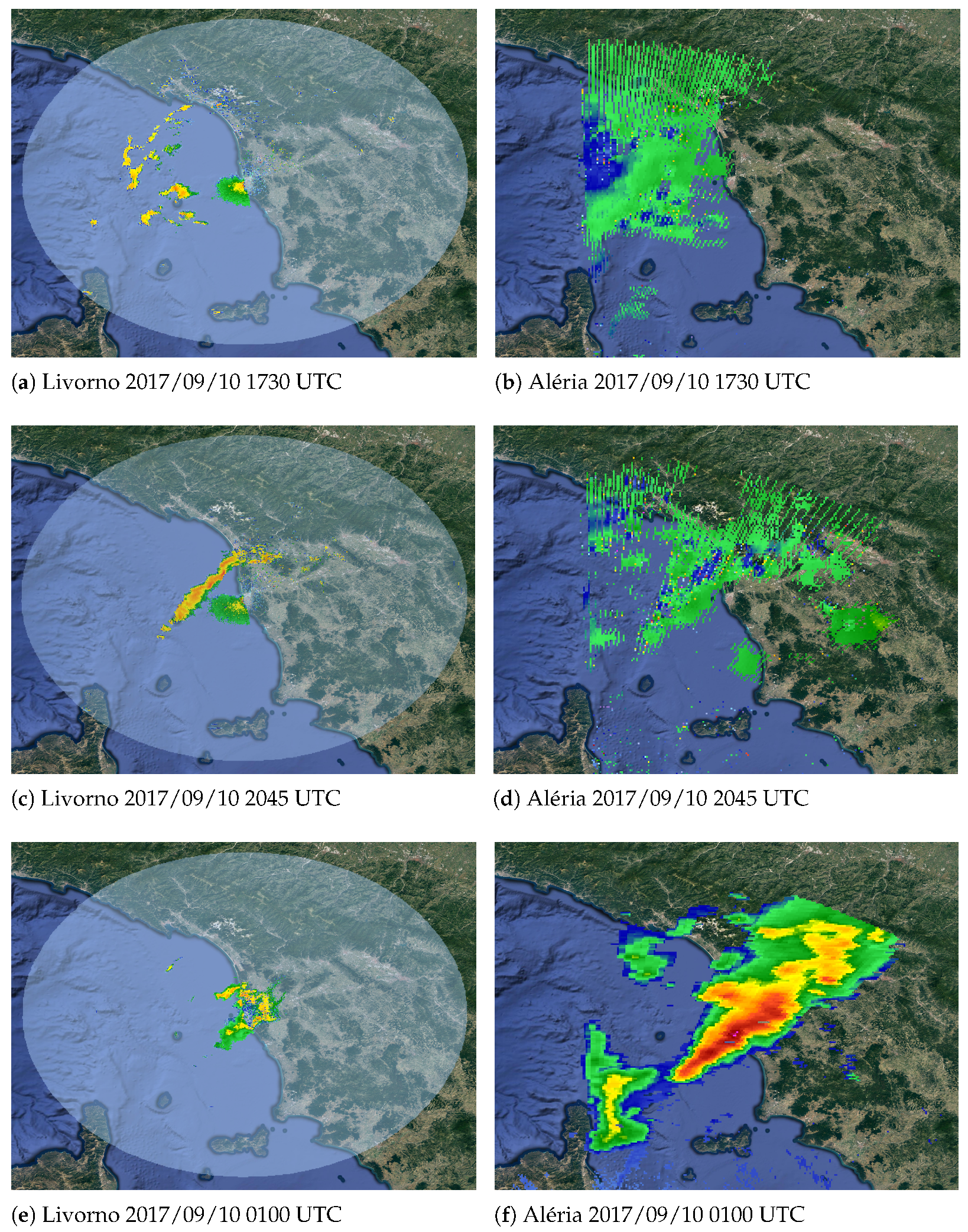
2.3. Radar Data
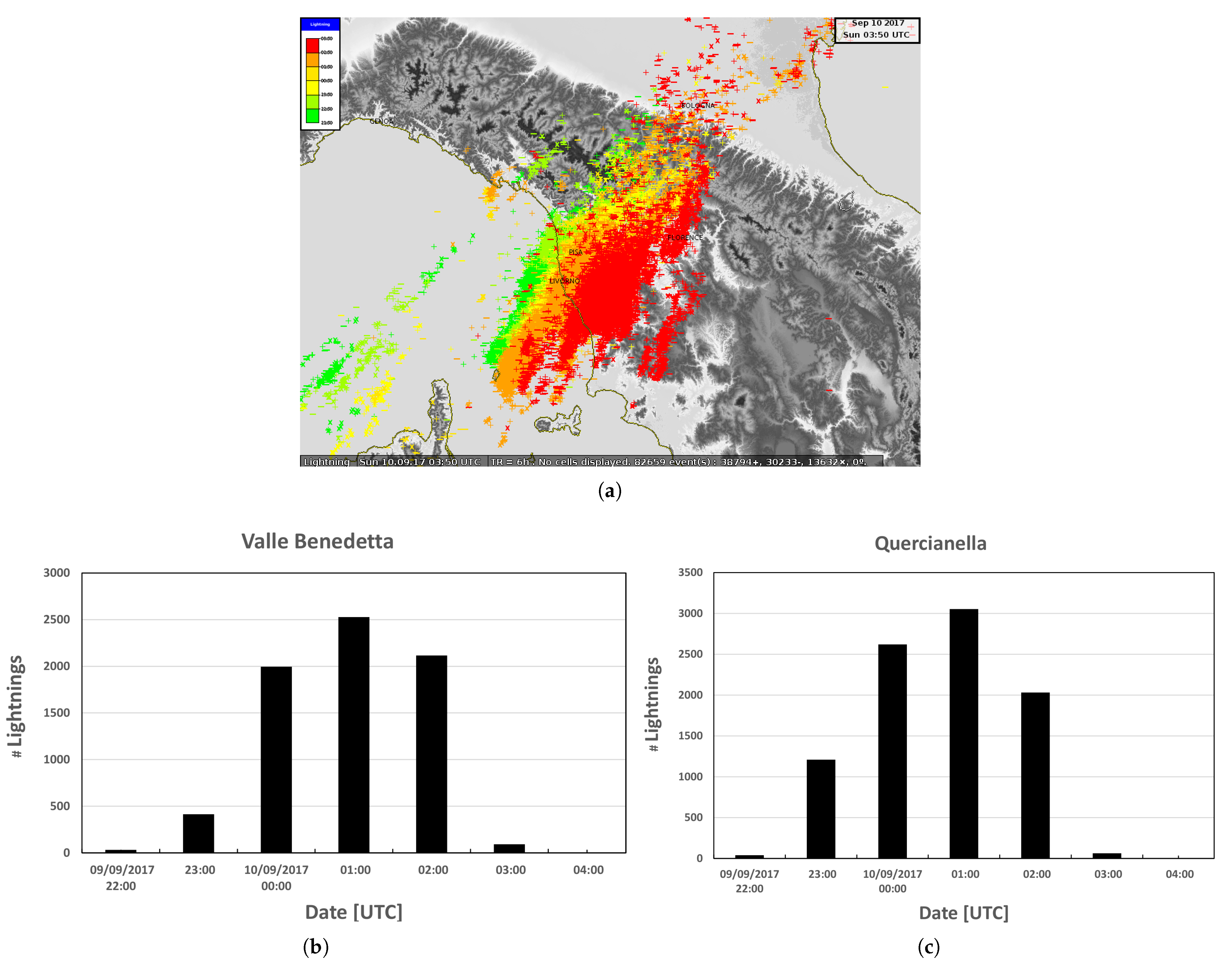
2.4. Satellite and Lighting Data
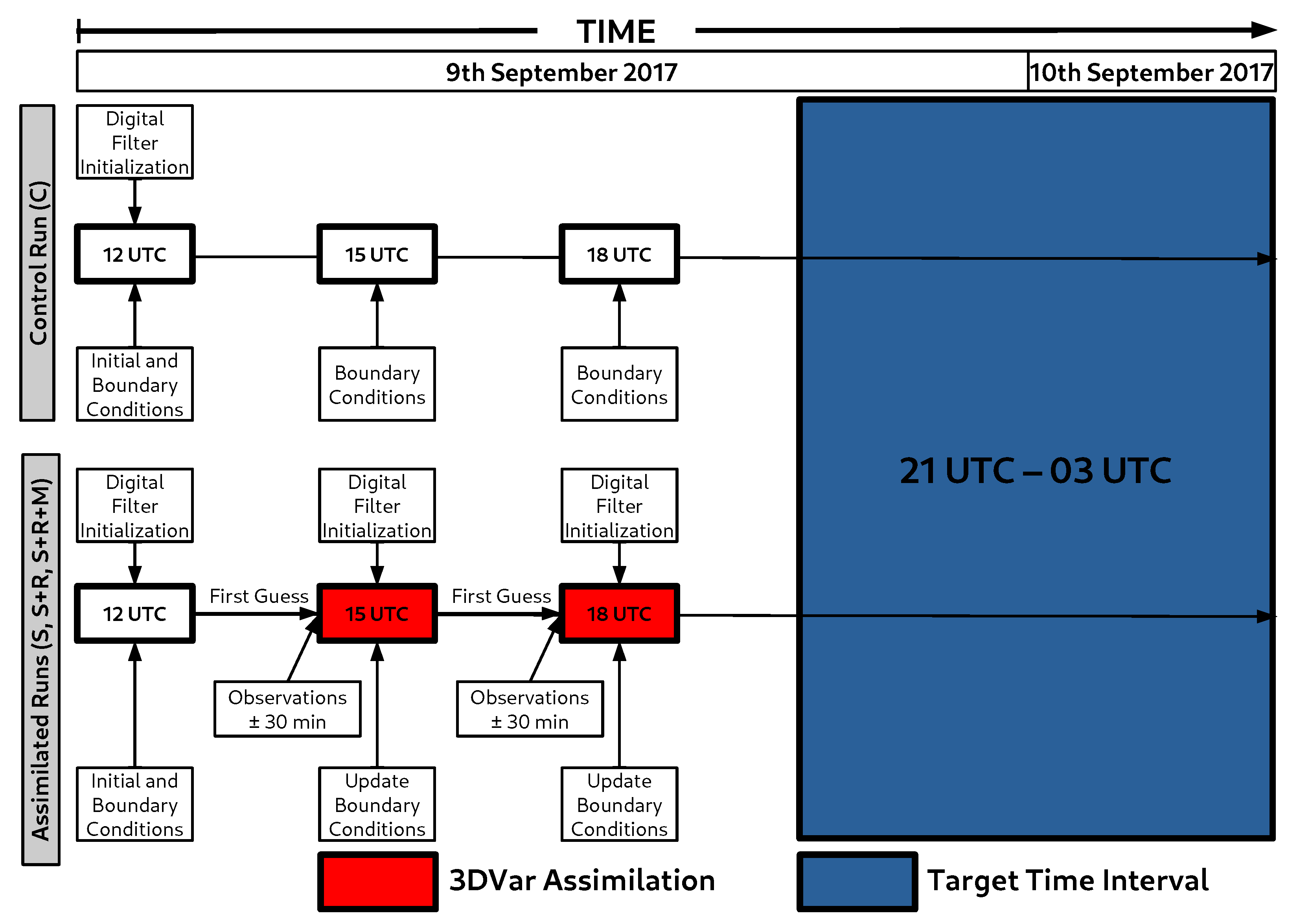
2.5. Modeling Setup
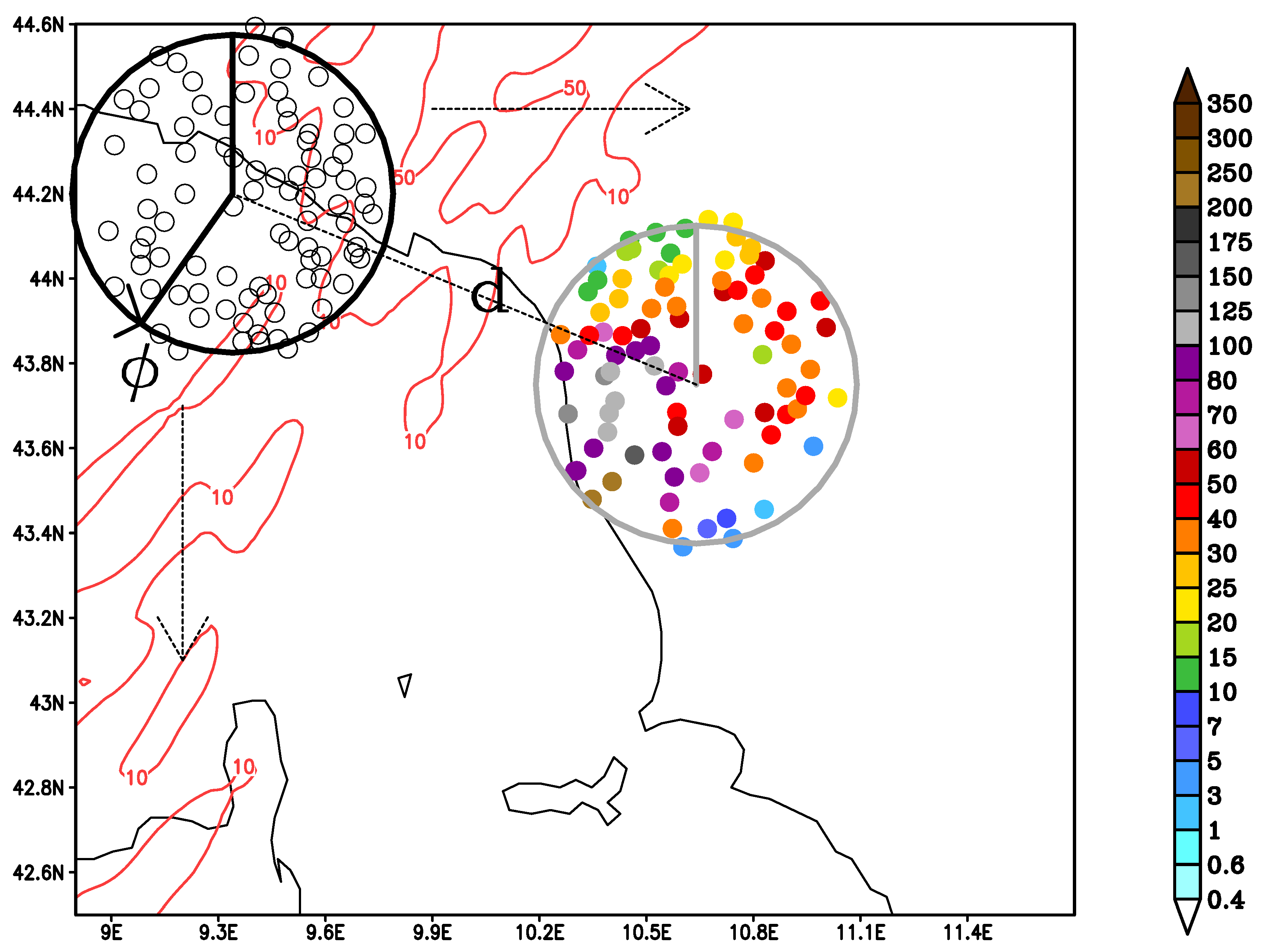
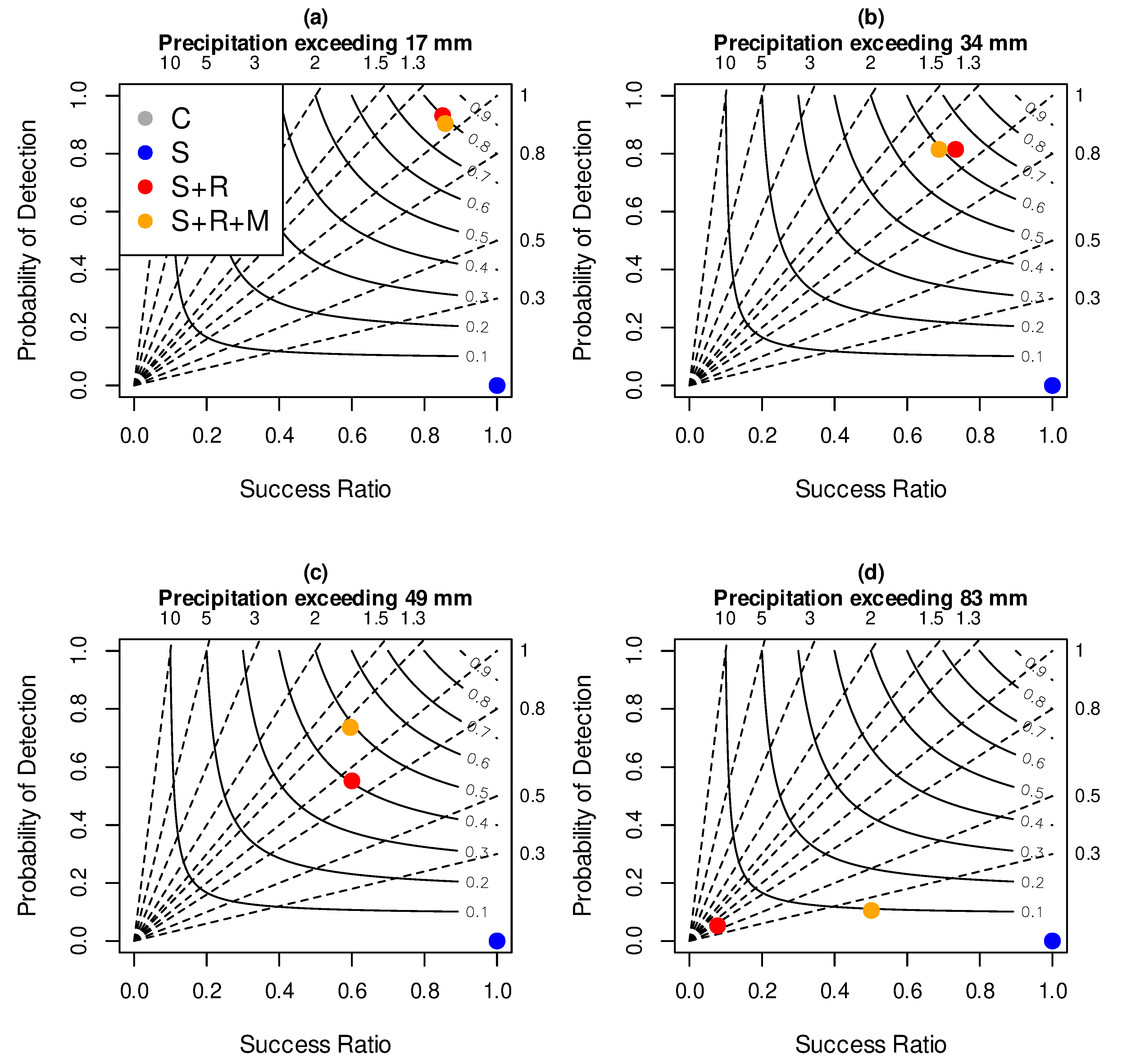
3. Quantitative Precipitation Forecast Verification
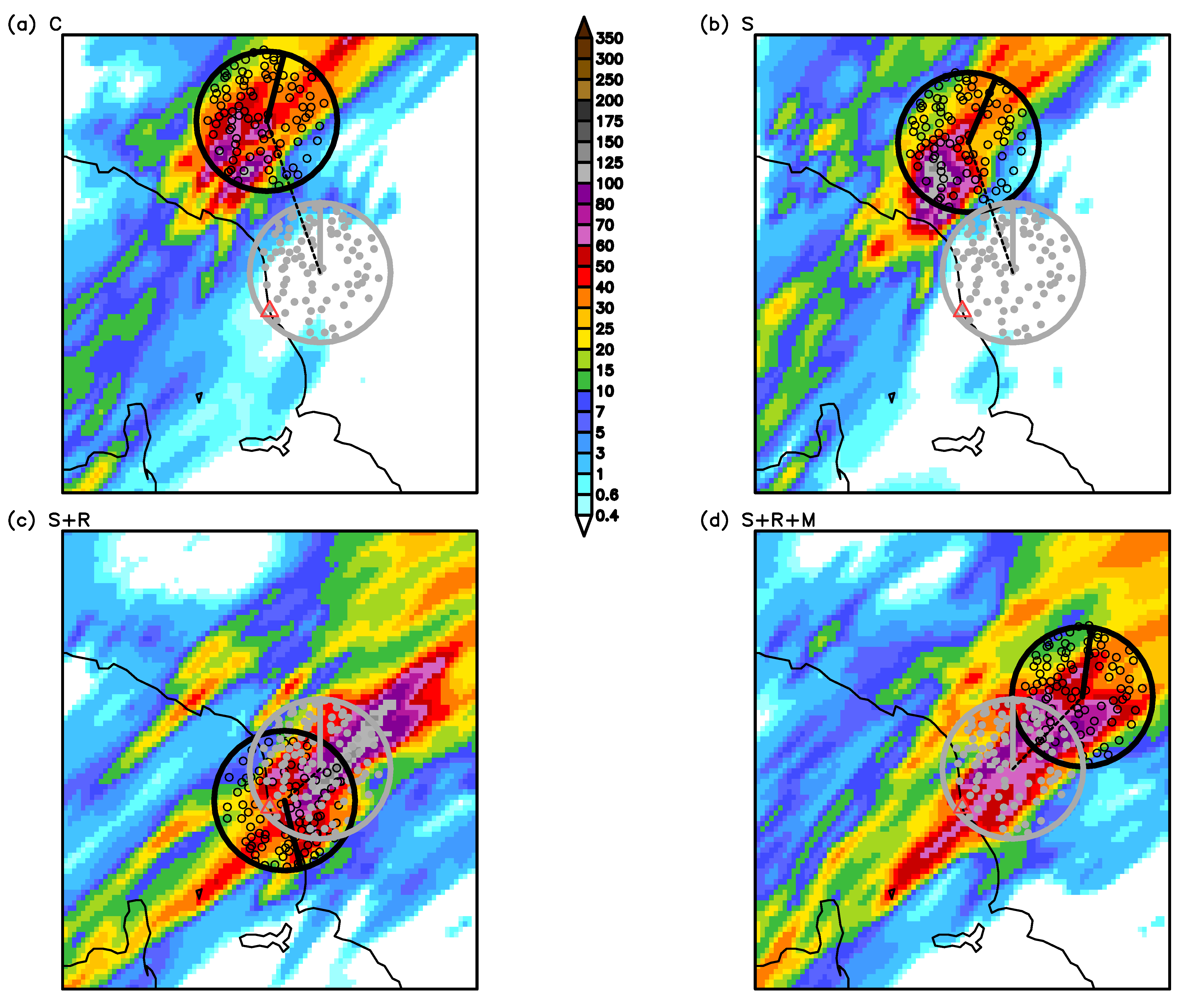
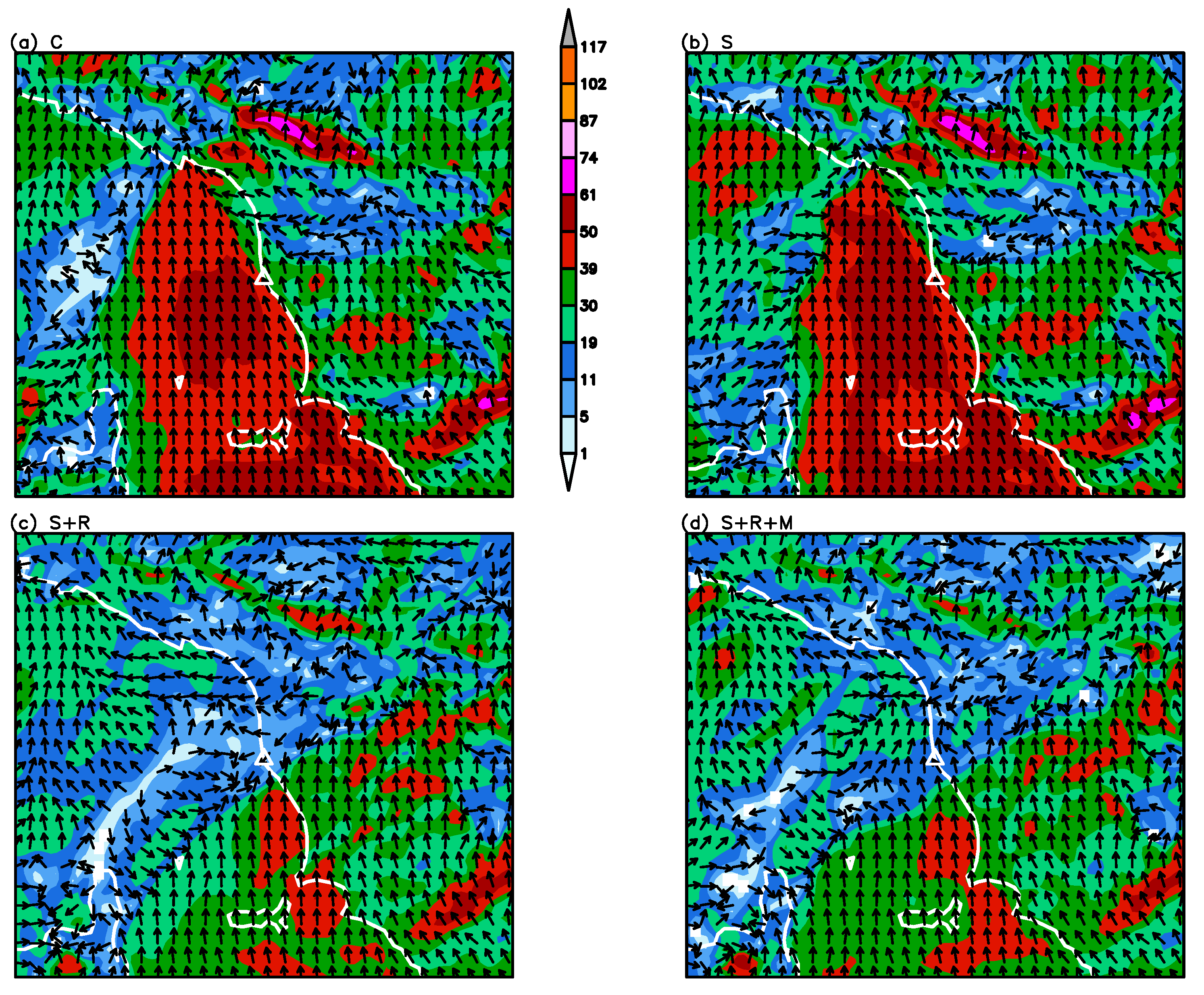
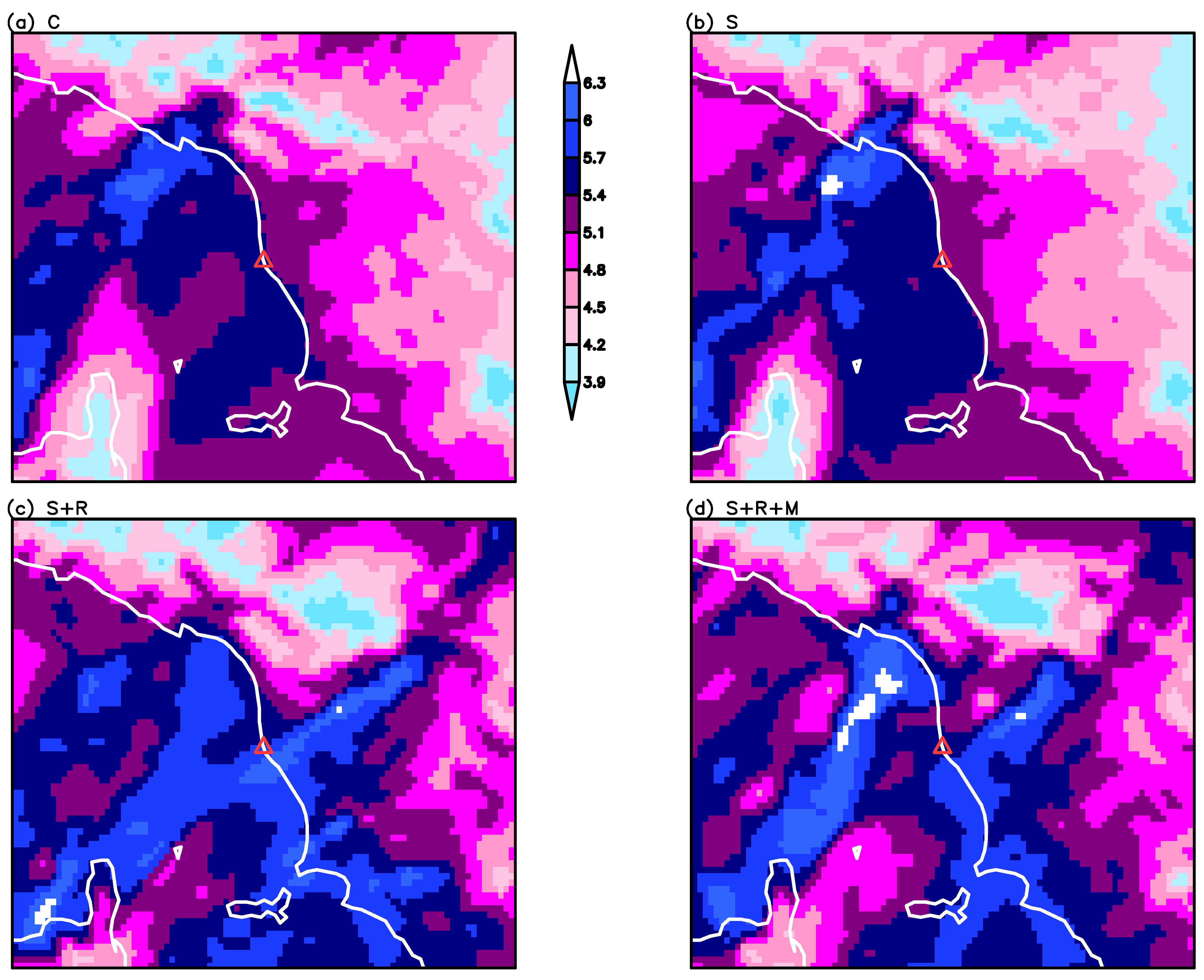
4. Results
5. Discussion
6. Conclusions
- Assimilating reflectivity data from X- and S-band radars and radial velocity data from S-band radar significantly improves the descriptions of atmospheric humidity content and low-level winds, resulting in better QPFs.
- The application of a simplified ocean model, although modifying the low-level jet associated with the event, scarcely impacts the short-range forecast (length shorter than 12 h) of precipitation.
- The novel QPF verification method introduced in this paper, based on roto-translation RMSE-minimisation, confirmed and reinforced the results achieved with standard verification scores, thereby providing more information about the position error of the WRF simulations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gaume, E.; Bain, V.; Bernardara, P.; Newinger, O.; Barbuc, M.; Bateman, A.; Blaškovičová, L.; Blöschl, G.; Borga, M.; Dumitrescu, A.; et al. A compilation of data on European flash floods. J. Hydrol. 2009, 367, 70–78. [Google Scholar] [CrossRef] [Green Version]
- Llasat, M.; Llasat-Botija, M.; Prat, M.; Porcu, F.; Price, C.; Mugnai, A.; Lagouvardos, K.; Kotroni, V.; Katsanos, D.; Michaelides, S.; et al. High-impact floods and flash floods in Mediterranean countries: The FLASH preliminary database. Adv. Geosci. 2010, 23, 47–55. [Google Scholar] [CrossRef] [Green Version]
- Llasat, M.; Llasat-Botija, M.; Petrucci, O.; Pasqua, A.; Rosselló, J.; Vinet, F.; Boissier, L. Towards a database on societal impact of Mediterranean floods within the framework of the HYMEX project. Nat. Hazards Earth Syst. Sci. 2013, 13, 1337. [Google Scholar] [CrossRef] [Green Version]
- Insua-Costa, D.; Lemus-Cánovas, M.; Miguez-Macho, G.; Llasat, M.C. Climatology and ranking of hazardous precipitation events in the western Mediterranean area. Atmos. Res. 2021, 255. [Google Scholar] [CrossRef]
- Malguzzi, P.; Grossi, G.; Buzzi, A.; Ranzi, R.; Buizza, R. The 1966 “century” flood in Italy: A meteorological and hydrological revisitation. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Capecchi, V.; Buizza, R. Reforecasting the Flooding of Florence of 4 November 1966 with Global and Regional Ensembles. J. Geophys. Res. Atmos. 2019, 124, 3743–3764. [Google Scholar] [CrossRef]
- Buzzi, A.; Tartaglione, N.; Malguzzi, P. Numerical simulations of the 1994 Piedmont flood: Role of orography and moist processes. Mon. Weather Rev. 1998, 126, 2369–2383. [Google Scholar] [CrossRef]
- Capecchi, V. Reforecasting the November 1994 flooding of Piedmont with a convection-permitting model. Bull. Atmos. Sci. Technol. 2020, 1–18. [Google Scholar] [CrossRef]
- Nuissier, O.; Ducrocq, V.; Ricard, D.; Lebeaupin, C.; Anquetin, S. A numerical study of three catastrophic precipitating events over southern France. I: Numerical framework and synoptic ingredients. Q. J. R. Meteorol. Soc. 2008, 134, 111–130. [Google Scholar] [CrossRef]
- Ducrocq, V.; Nuissier, O.; Ricard, D.; Lebeaupin, C.; Thouvenin, T. A numerical study of three catastrophic precipitating events over southern France. II: Mesoscale triggering and stationarity factors. Q. J. R. Meteorol. Soc. 2008, 134, 131–145. [Google Scholar] [CrossRef]
- Buzzi, A.; Davolio, S.; Malguzzi, P.; Drofa, O.; Mastrangelo, D. Heavy rainfall episodes over Liguria in autumn 2011: Numerical forecasting experiments. Nat. Hazards Earth Syst. Sci. 2014, 14, 1325. [Google Scholar] [CrossRef] [Green Version]
- Capecchi, V. Reforecasting two heavy-precipitation events with three convection-permitting ensembles. Weather Forecast. 2021. [Google Scholar] [CrossRef]
- Fiori, E.; Comellas, A.; Molini, L.; Rebora, N.; Siccardi, F.; Gochis, D.; Tanelli, S.; Parodi, A. Analysis and hindcast simulations of an extreme rainfall event in the Mediterranean area: The Genoa 2011 case. Atmos. Res. 2014, 138, 13–29. [Google Scholar] [CrossRef] [Green Version]
- Fiori, E.; Ferraris, L.; Molini, L.; Siccardi, F.; Kranzlmueller, D.; Parodi, A. Triggering and evolution of a deep convective system in the Mediterranean Sea: Modelling and observations at a very fine scale. Q. J. R. Meteorol. Soc. 2017, 143, 927–941. [Google Scholar] [CrossRef]
- Chappell, C.F. Quasi-stationary convective events. In Mesoscale Meteorology and Forecasting; Springer: Berlin/Heidelberg, Germany, 1986; pp. 289–310. [Google Scholar]
- Doswell, C.A., III; Brooks, H.E.; Maddox, R.A. Flash flood forecasting: An ingredients-based methodology. Weather Forecast. 1996, 11, 560–581. [Google Scholar] [CrossRef]
- Duffourg, F.; Nuissier, O.; Ducrocq, V.; Flamant, C.; Chazette, P.; Delanoë, J.; Doerenbecher, A.; Fourrié, N.; Di Girolamo, P.; Lac, C.; et al. Offshore deep convection initiation and maintenance during the HyMeX IOP 16a heavy precipitation event. Q. J. R. Meteorol. Soc. 2016, 142, 259–274. [Google Scholar] [CrossRef]
- Romero, R.; Doswell III, C.; Ramis, C. Mesoscale numerical study of two cases of long-lived quasi-stationary convective systems over eastern Spain. Mon. Weather Rev. 2000, 128, 3731–3751. [Google Scholar] [CrossRef]
- Cassola, F.; Ferrari, F.; Mazzino, A.; Miglietta, M. The role of the sea on the flash floods events over Liguria (northwestern Italy). Geophys. Res. Lett. 2016, 43, 3534–3542. [Google Scholar] [CrossRef]
- Ducrocq, V.; Braud, I.; Davolio, S.; Ferretti, R.; Flamant, C.; Jansa, A.; Kalthoff, N.; Richard, E.; Taupier-Letage, I.; Ayral, P.A.; et al. HyMeX-SOP1: The field campaign dedicated to heavy precipitation and flash flooding in the northwestern Mediterranean. Bull. Am. Meteorol. Soc. 2014, 95, 1083–1100. [Google Scholar] [CrossRef]
- Weaver, J.F. Storm motion as related to boundary-layer convergence. Mon. Weather Rev. 1979, 107, 612–619. [Google Scholar] [CrossRef] [Green Version]
- Davolio, S.; Mastrangelo, D.; Miglietta, M.; Drofa, O.; Buzzi, A.; Malguzzi, P. High resolution simulations of a flash flood near Venice. Nat. Hazards Earth Syst. Sci. 2009, 9, 1671–1678. [Google Scholar] [CrossRef]
- Uccellini, L.W.; Johnson, D.R. The coupling of upper and lower tropospheric jet streaks and implications for the development of severe convective storms. Mon. Weather Rev. 1979, 107, 682–703. [Google Scholar] [CrossRef]
- Zipser, E. Use of a conceptual model of the life-cycle of mesoscale convective systems to improve very-short-range forecasts. In Nowcasting; Academic Press: Cambridge, MA, USA, 1982. [Google Scholar]
- Fritsch, J.; Forbes, G. Mesoscale convective systems. In Severe Convective Storms; Springer: Berlin/Heidelberg, Germany, 2001; pp. 323–357. [Google Scholar]
- Houze, R.A. Mesoscale convective systems. Rev. Geophys. 2004, 42. [Google Scholar] [CrossRef] [Green Version]
- Alpert, P.; Ben-Gai, T.; Baharad, A.; Benjamini, Y.; Yekutieli, D.; Colacino, M.; Diodato, L.; Ramis, C.; Homar, V.; Romero, R.; et al. The paradoxical increase of Mediterranean extreme daily rainfall in spite of decrease in total values. Geophys. Res. Lett. 2002, 29. [Google Scholar] [CrossRef] [Green Version]
- Reale, M.; Lionello, P. Synoptic climatology of winter intense precipitation events along the Mediterranean coasts. Nat. Hazards Earth Syst. Sci. 2013, 13, 1707–1722. [Google Scholar] [CrossRef]
- Piervitali, E.; Colacino, M.; Conte, M. Rainfall over the Central-Western Mediterranean basin in the period 1951–1995. Part I: Precipitation trends. Nuovo Cimento C Geophys. Space Phys. C 1998, 21, 331. [Google Scholar]
- Brunetti, M.; Maugeri, M.; Monti, F.; Nanni, T. Changes in daily precipitation frequency and distribution in Italy over the last 120 years. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Scoccimarro, E.; Gualdi, S.; Bellucci, A.; Zampieri, M.; Navarra, A. Heavy precipitation events over the Euro-Mediterranean region in a warmer climate: Results from CMIP5 models. Reg. Environ. Chang. 2016, 16, 595–602. [Google Scholar] [CrossRef]
- Jonkman, S.N. Global perspectives on loss of human life caused by floods. Nat. Hazards 2005, 34, 151–175. [Google Scholar] [CrossRef]
- Doocy, S.; Daniels, A.; Murray, S.; Kirsch, T.D. The human impact of floods: A historical review of events 1980–2009 and systematic literature review. PLoS Curr. 2013, 5. [Google Scholar] [CrossRef]
- Kong, R.; Xue, M.; Liu, C. Development of a hybrid En3DVar data assimilation system and comparisons with 3DVar and EnKF for radar data assimilation with observing system simulation experiments. Mon. Weather Rev. 2018, 146, 175–198. [Google Scholar] [CrossRef]
- Tong, C.C.; Jung, Y.; Xue, M.; Liu, C. Direct Assimilation of Radar Data with Ensemble Kalman Filter and Hybrid Ensemble-Variational Method in the National Weather Service Operational Data Assimilation System GSI for the Stand-Alone Regional FV3 Model at a Convection-Allowing Resolution. Geophys. Res. Lett. 2020, 47, e2020GL090179. [Google Scholar] [CrossRef]
- Kong, R.; Xue, M.; Liu, C.; Jung, Y. Comparisons of Hybrid En3DVar with 3DVar and EnKF for Radar Data Assimilation: Tests with the 10 May 2010 Oklahoma Tornado Outbreak. Mon. Weather Rev. 2021, 149, 21–40. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Ocean. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Gao, J.; Xue, M.; Stensrud, D.J. The development of a hybrid EnKF-3DVAR algorithm for storm-scale data assimilation. Adv. Meteorol. 2013, 2013, 512656. [Google Scholar] [CrossRef] [Green Version]
- Maiello, I.; Ferretti, R.; Gentile, S.; Montopoli, M.; Picciotti, E.; Marzano, F.; Faccani, C. Impact of radar data assimilation for the simulation of a heavy rainfall case in central Italy using WRF–3DVAR. Atmos. Meas. Tech. 2014, 7, 2919–2935. [Google Scholar] [CrossRef]
- Sugimoto, S.; Crook, N.A.; Sun, J.; Xiao, Q.; Barker, D.M. An examination of WRF 3DVAR radar data assimilation on its capability in retrieving unobserved variables and forecasting precipitation through observing system simulation experiments. Mon. Weather Rev. 2009, 137, 4011–4029. [Google Scholar] [CrossRef]
- Xiao, Q.; Sun, J. Multiple-radar data assimilation and short-range quantitative precipitation forecasting of a squall line observed during IHOP_2002. Mon. Weather Rev. 2007, 135, 3381–3404. [Google Scholar] [CrossRef]
- Tian, J.; Liu, J.; Yan, D.; Li, C.; Chu, Z.; Yu, F. An assimilation test of Doppler radar reflectivity and radial velocity from different height layers in improving the WRF rainfall forecasts. Atmos. Res. 2017, 198, 132–144. [Google Scholar] [CrossRef]
- Lagasio, M.; Silvestro, F.; Campo, L.; Parodi, A. Predictive capability of a high-resolution hydrometeorological forecasting framework coupling WRF cycling 3DVAR and Continuum. J. Hydrometeorol. 2019, 20, 1307–1337. [Google Scholar] [CrossRef]
- Sad, H.P.; Kumar, P.; Panda, S.K. Doppler weather radar data assimilation at convective-allowing grid spacing for predicting an extreme weather event in Southern India. Int. J. Remote Sens. 2021, 42, 3681–3707. [Google Scholar] [CrossRef]
- Federico, S.; Torcasio, R.C.; Avolio, E.; Caumont, O.; Montopoli, M.; Baldini, L.; Vulpiani, G.; Dietrich, S. The impact of lightning and radar reflectivity factor data assimilation on the very short-term rainfall forecasts of RAMS@ISAC: Application to two case studies in Italy. Nat. Hazards Earth Syst. Sci. 2019, 19, 1839–1864. [Google Scholar] [CrossRef] [Green Version]
- Cotton, W.R.; Pielke Sr, R.; Walko, R.; Liston, G.; Tremback, C.; Jiang, H.; McAnelly, R.; Harrington, J.Y.; Nicholls, M.; Carrio, G.; et al. RAMS 2001: Current status and future directions. Meteorol. Atmos. Phys. 2003, 82, 5–29. [Google Scholar] [CrossRef]
- Lagasio, M.; Parodi, A.; Pulvirenti, L.; Meroni, A.N.; Boni, G.; Pierdicca, N.; Marzano, F.S.; Luini, L.; Venuti, G.; Realini, E.; et al. A synergistic use of a high-resolution numerical weather prediction model and high-resolution earth observation products to improve precipitation forecast. Remote Sens. 2019, 11, 2387. [Google Scholar] [CrossRef] [Green Version]
- Antonini, A.; Melani, S.; Corongiu, M.; Romanelli, S.; Mazza, A.; Ortolani, A.; Gozzini, B. On the Implementation of a Regional X-Band Weather Radar Network. Atmosphere 2017, 8, 25. [Google Scholar] [CrossRef] [Green Version]
- Bauer, H.S.; Schwitalla, T.; Wulfmeyer, V.; Bakhshaii, A.; Ehret, U.; Neuper, M.; Caumont, O. Quantitative precipitation estimation based on high-resolution numerical weather prediction and data assimilation with WRF—A performance test. Tellus A Dyn. Meteorol. Oceanogr. 2015, 67, 25047. [Google Scholar] [CrossRef]
- Mazzarella, V.; Maiello, I.; Ferretti, R.; Capozzi, V.; Picciotti, E.; Alberoni, P.; Marzano, F.; Budillon, G. Reflectivity and velocity radar data assimilation for two flash flood events in central Italy: A comparison between 3D and 4D variational methods. Q. J. R. Meteorol. Soc. 2020, 146, 348–366. [Google Scholar] [CrossRef]
- Buzzi, A.; Tibaldi, S. Cyclogenesis in the lee of the Alps: A case study. Q. J. R. Meteorol. Soc. 1978, 104, 271–287. [Google Scholar] [CrossRef]
- Buzzi, A.; Davolio, S.; Fantini, M. Cyclogenesis in the lee of the Alps: A review of theories. Bull. Atmos. Sci. Technol. 2020, 1, 433–457. [Google Scholar] [CrossRef]
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Molini, L.; Parodi, A.; Rebora, N.; Craig, G. Classifying severe rainfall events over Italy by hydrometeorological and dynamical criteria. Q. J. R. Meteorol. Soc. 2011, 137, 148–154. [Google Scholar] [CrossRef]
- Capecchi, V.; Crisci, A.; Melani, S.; Morabito, M.; Politi, P. Fractal characterization of rain-gauge networks and precipitations: An application in Central Italy. Theor. Appl. Climatol. 2012, 107, 541–546. [Google Scholar] [CrossRef] [Green Version]
- Cressman, G.P. An operational objective analysis system. Mon. Weather Rev. 1959, 87, 367–374. [Google Scholar] [CrossRef]
- Toscana, R. Report Evento Meteo-Idrologico dei Giorni 9 e 10 Settembre 2017; Technical Report; Regione Toscana: Florence, Italy, 2017. [Google Scholar]
- Vulpiani, G.; Pagliara, P.; Negri, M.; Rossi, L.; Gioia, A.; Giordano, P.; Alberoni, P.P.; Cremonini, R.; Ferraris, L.; Marzano, F.S. The Italian radar network within the national early-warning system for multi-risks management. In Proceedings of the Fifth European Conference on Radar in Meteorology and Hydrology (ERAD 2008), Helsinki, Finland, 30 June–4 July 2008; Volume 184. [Google Scholar]
- Vulpiani, G.; Montopoli, M.; Passeri, L.D.; Gioia, A.G.; Giordano, P.; Marzano, F.S. On the Use of Dual-Polarized C-Band Radar for Operational Rainfall Retrieval in Mountainous Areas. J. Appl. Meteorol. Climatol. 2012, 51, 405–425. [Google Scholar] [CrossRef]
- Tabary, P. The New French Operational Radar Rainfall Product. Part I: Methodology. Weather Forecast. 2007, 22, 393–408. [Google Scholar] [CrossRef]
- Cuccoli, F.; Facheris, L.; Antonini, A.; Melani, S.; Baldini, L. Weather Radar and Rain-Gauge Data Fusion for Quantitative Precipitation Estimation: Two Case Studies. IEEE Trans. Geosci. Remote Sens. 2020, 58, 6639–6649. [Google Scholar] [CrossRef]
- Schmetz, J.; Pili, P.; Tjemkes, S.; Just, D.; Kerkmann, J.; Rota, S.; Ratier, A. An introduction to Meteosat second generation (MSG). Bull. Am. Meteorol. Soc. 2002, 83, 977–992. [Google Scholar] [CrossRef]
- Ricciardelli, E.; Di Paola, F.; Gentile, S.; Cersosimo, A.; Cimini, D.; Gallucci, D.; Geraldi, E.; Larosa, S.; Nilo, S.T.; Ripepi, E.; et al. Analysis of Livorno heavy rainfall event: Examples of satellite-based observation techniques in support of numerical weather prediction. Remote Sens. 2018, 10, 1549. [Google Scholar] [CrossRef] [Green Version]
- Christian, H.J.; Blakeslee, R.J.; Boccippio, D.J.; Boeck, W.L.; Buechler, D.E.; Driscoll, K.T.; Goodman, S.J.; Hall, J.M.; Koshak, W.J.; Mach, D.M.; et al. Global frequency and distribution of lightning as observed from space by the Optical Transient Detector. J. Geophys. Res. Atmos. 2003, 108. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.; Dudhia, J.; Gill, D.; Barker, D.; Wang, W.; Zhiquan, L.; Berner, J.; Powers, J.; Duda, M.; et al. A Description of the Advanced Research WRF Model; Version 4; Technical Report, No. NCAR/TN-556+STR; UCAR: Boulder, CO, USA, 2019. [Google Scholar] [CrossRef]
- Klemp, J.B.; Skamarock, W.C.; Dudhia, J. Conservative split-explicit time integration methods for the compressible nonhydrostatic equations. Mon. Weather Rev. 2007, 135, 2897–2913. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Dudhia, J. Annual Report: WRF Physics; Technical Report 38; Air Force Weather Agency: Bellevue, NE, USA, 2000. [Google Scholar]
- Thompson, G.; Eidhammer, T. A study of aerosol impacts on clouds and precipitation development in a large winter cyclone. J. Atmos. Sci. 2014, 71, 3636–3658. [Google Scholar] [CrossRef]
- Hong, S.Y.; Noh, Y.; Dudhia, J. A new vertical diffusion package with an explicit treatment of entrainment processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef] [Green Version]
- Chen, F.; Mitchell, K.; Schaake, J.; Xue, Y.; Pan, H.L.; Koren, V.; Duan, Q.Y.; Ek, M.; Betts, A. Modeling of land surface evaporation by four schemes and comparison with FIFE observations. J. Geophys. Res. Atmos. 1996, 101, 7251–7268. [Google Scholar] [CrossRef] [Green Version]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
- Barker, D.; Huang, X.Y.; Liu, Z.; Auligné, T.; Zhang, X.; Rugg, S.; Ajjaji, R.; Bourgeois, A.; Bray, J.; Chen, Y.; et al. The weather research and forecasting model’s community variational/ensemble data assimilation system: WRFDA. Bull. Am. Meteorol. Soc. 2012, 93, 831–843. [Google Scholar] [CrossRef] [Green Version]
- Schwitalla, T.; Wulfmeyer, V. Radar data assimilation experiments using the IPM WRF Rapid Update Cycle. Meteorol. Z. 2014, 23, 79–102. [Google Scholar] [CrossRef]
- Barker, D.M.; Huang, W.; Guo, Y.R.; Bourgeois, A.; Xiao, Q. A three-dimensional variational data assimilation system for MM5: Implementation and initial results. Mon. Weather Rev. 2004, 132, 897–914. [Google Scholar] [CrossRef] [Green Version]
- Xiao, Q.; Kuo, Y.H.; Sun, J.; Lee, W.C.; Lim, E.; Guo, Y.R.; Barker, D.M. Assimilation of Doppler radar observations with a regional 3DVAR system: Impact of Doppler velocities on forecasts of a heavy rainfall case. J. Appl. Meteorol. 2005, 44, 768–788. [Google Scholar] [CrossRef]
- Wang, H.; Sun, J.; Fan, S.; Huang, X.Y. Indirect assimilation of radar reflectivity with WRF 3D-Var and its impact on prediction of four summertime convective events. J. Appl. Meteorol. Climatol. 2013, 52, 889–902. [Google Scholar] [CrossRef]
- Courtier, P.; Andersson, E.; Heckley, W.; Vasiljevic, D.; Hamrud, M.; Hollingsworth, A.; Rabier, F.; Fisher, M.; Pailleux, J. The ECMWF implementation of three-dimensional variational assimilation (3D-Var). I: Formulation. Q. J. R. Meteorol. Soc. 1998, 124, 1783–1807. [Google Scholar] [CrossRef]
- Liu, Z.Q.; Rabier, F. The potential of high-density observations for numerical weather prediction: A study with simulated observations. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2003, 129, 3013–3035. [Google Scholar] [CrossRef]
- Bormann, N.; Bauer, P. Estimates of spatial and interchannel observation-error characteristics for current sounder radiances for numerical weather prediction. I: Methods and application to ATOVS data. Q. J. R. Meteorol. Soc. 2010, 136, 1036–1050. [Google Scholar] [CrossRef]
- Bormann, N.; Geer, A.J.; Bauer, P. Estimates of observation-error characteristics in clear and cloudy regions for microwave imager radiances from numerical weather prediction. Q. J. R. Meteorol. Soc. 2011, 137, 2014–2023. [Google Scholar] [CrossRef]
- Parrish, D.F.; Derber, J.C. The National Meteorological Center’s spectral statistical-interpolation analysis system. Mon. Weather Rev. 1992, 120, 1747–1763. [Google Scholar] [CrossRef]
- Sun, J.; Crook, N.A. Dynamical and Microphysical Retrieval from Doppler Radar Observations Using a Cloud Model and Its Adjoint. Part I: Model Development and Simulated Data Experiments. J. Atmos. Sci. 1997, 54. [Google Scholar] [CrossRef]
- Sun, J.; Crook, N.A. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. Part II: Retrieval experiments of an observed Florida convective storm. J. Atmos. Sci. 1998, 55, 835–852. [Google Scholar] [CrossRef]
- Peckham, S.E.; Smirnova, T.G.; Benjamin, S.G.; Brown, J.M.; Kenyon, J.S. Implementation of a digital filter initialization in the WRF Model and its application in the Rapid Refresh. Mon. Weather Rev. 2016, 144, 99–106. [Google Scholar] [CrossRef]
- Foussard, A.; Lapeyre, G.; Plougonven, R. Response of surface wind divergence to mesoscale SST anomalies under different wind conditions. J. Atmos. Sci. 2019, 76, 2065–2082. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Freilich, M.H.; Milliff, R.F. Satellite measurements reveal persistent small-scale features in ocean winds. Science 2004, 303, 978–983. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- O’Neill, L.W.; Chelton, D.B.; Esbensen, S.K. Observations of SST-induced perturbations of the wind stress field over the Southern Ocean on seasonal timescales. J. Clim. 2003, 16, 2340–2354. [Google Scholar] [CrossRef] [Green Version]
- Ricchi, A.; Miglietta, M.M.; Falco, P.P.; Benetazzo, A.; Bonaldo, D.; Bergamasco, A.; Sclavo, M.; Carniel, S. On the use of a coupled ocean–atmosphere–wave model during an extreme cold air outbreak over the Adriatic Sea. Atmos. Res. 2016, 172, 48–65. [Google Scholar] [CrossRef]
- Davis, C.; Wang, W.; Chen, S.S.; Chen, Y.; Corbosiero, K.; DeMaria, M.; Dudhia, J.; Holland, G.; Klemp, J.; Michalakes, J.; et al. Prediction of landfalling hurricanes with the advanced hurricane WRF model. Mon. Weather Rev. 2008, 136, 1990–2005. [Google Scholar] [CrossRef] [Green Version]
- Ebert, E.E. Neighborhood verification: A strategy for rewarding close forecasts. Weather Forecast. 2009, 24, 1498–1510. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100. [Google Scholar]
- Davis, C.; Brown, B.; Bullock, R. Object-based verification of precipitation forecasts. Part I: Methodology and application to mesoscale rain areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef] [Green Version]
- Brown, B.; Jensen, T.; Gotway, J.; Bullock, R.; Gilleland, E.; Fowler, T.; Newman, K.; Adriaansen, D.; Blank, L.; Burek, T.; et al. The Model Evaluation Tools (MET): More than a decade of community-supported forecast verification. Bull. Am. Meteorol. Soc. 2020. [Google Scholar] [CrossRef]
- Roebber, P.J. Visualizing multiple measures of forecast quality. Weather Forecast. 2009, 24, 601–608. [Google Scholar] [CrossRef] [Green Version]
- Lebeaupin, C.; Ducrocq, V.; Giordani, H. Sensitivity of torrential rain events to the sea surface temperature based on high-resolution numerical forecasts. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Mazzarella, V.; Ferretti, R.; Picciotti, E.; Marzano, F.S. Investigating 3D and 4D Variational Rapid-Update-Cycling Assimilation of Weather Radar Reflectivity for a Flash Flood Event in Central Italy. Nat. Hazards Earth Syst. Sci. Discuss. 2021. [Google Scholar] [CrossRef]
| Parameter | Value |
|---|---|
| Rows × Columns | 440 × 400 |
| Grid spacing | 3 km |
| Vertical levels | 50 |
| Time step | 12 s |
| Cumulus convection | explicit (no parameterisation) |
| Micro-physics option | Thompson scheme [68] |
| Boundary-layer option | Yonsei University [69] |
| Land-surface option | Unified Noah model [70] |
| Radiation option | Rapid radiative transfer model [71] |
| Turbulence option | Yonsei University+2D Smagorisnski [69] |
| Forecast Code | Data Assimilated |
|---|---|
| C | none (control run) |
| S | Convectional data from weather stations: |
| pressure, 2-m temperature | |
| 2-m relative humidity | |
| 10-m wind speed and direction | |
| as in S plus reflectivity data from X- and S-band radars, | |
| and radial velocity data from the S-band radar | |
| as in | |
| (it differs from the experiment because | |
| it implements a simplified marine model) |
| Event Observed | |||
|---|---|---|---|
| yes | no | ||
| Event Forecast | yes | A | B |
| no | C | D | |
| Forecast Code | |||
|---|---|---|---|
| C | 65.8 | −50.3 | < |
| S | 65.9 | −50.5 | < |
| 46.3 | −2.5 | 0.95 | |
| 40.4 | −2.9 | 0.94 |
| Forecast Code | |||||
|---|---|---|---|---|---|
| C | 29.7 | −0.36 | +0.87 | 100 | |
| S | 29.0 | −0.30 | +0.75 | 86 | |
| 29.9 | −0.24 | −0.18 | 27 | ||
| 30.1 | +0.48 | +0.41 | 60 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Capecchi, V.; Antonini, A.; Benedetti, R.; Fibbi, L.; Melani, S.; Rovai, L.; Ricchi, A.; Cerrai, D. Assimilating X- and S-Band Radar Data for a Heavy Precipitation Event in Italy. Water 2021, 13, 1727. https://doi.org/10.3390/w13131727
Capecchi V, Antonini A, Benedetti R, Fibbi L, Melani S, Rovai L, Ricchi A, Cerrai D. Assimilating X- and S-Band Radar Data for a Heavy Precipitation Event in Italy. Water. 2021; 13(13):1727. https://doi.org/10.3390/w13131727
Chicago/Turabian StyleCapecchi, Valerio, Andrea Antonini, Riccardo Benedetti, Luca Fibbi, Samantha Melani, Luca Rovai, Antonio Ricchi, and Diego Cerrai. 2021. "Assimilating X- and S-Band Radar Data for a Heavy Precipitation Event in Italy" Water 13, no. 13: 1727. https://doi.org/10.3390/w13131727









