Improved Streamflow Calibration of a Land Surface Model by the Choice of Objective Functions—A Case Study of the Nakdong River Watershed in the Korean Peninsula
Abstract
:1. Introduction
2. Materials and Methods
2.1. Brief Description of the CoLM
2.2. Model Implementation
2.2.1. Study Area
2.2.2. Surface Boundary Conditions
2.2.3. Meteorological Forcing Data
2.2.4. Initialization
2.3. Model Calibration Approach
3. Results and Discussion
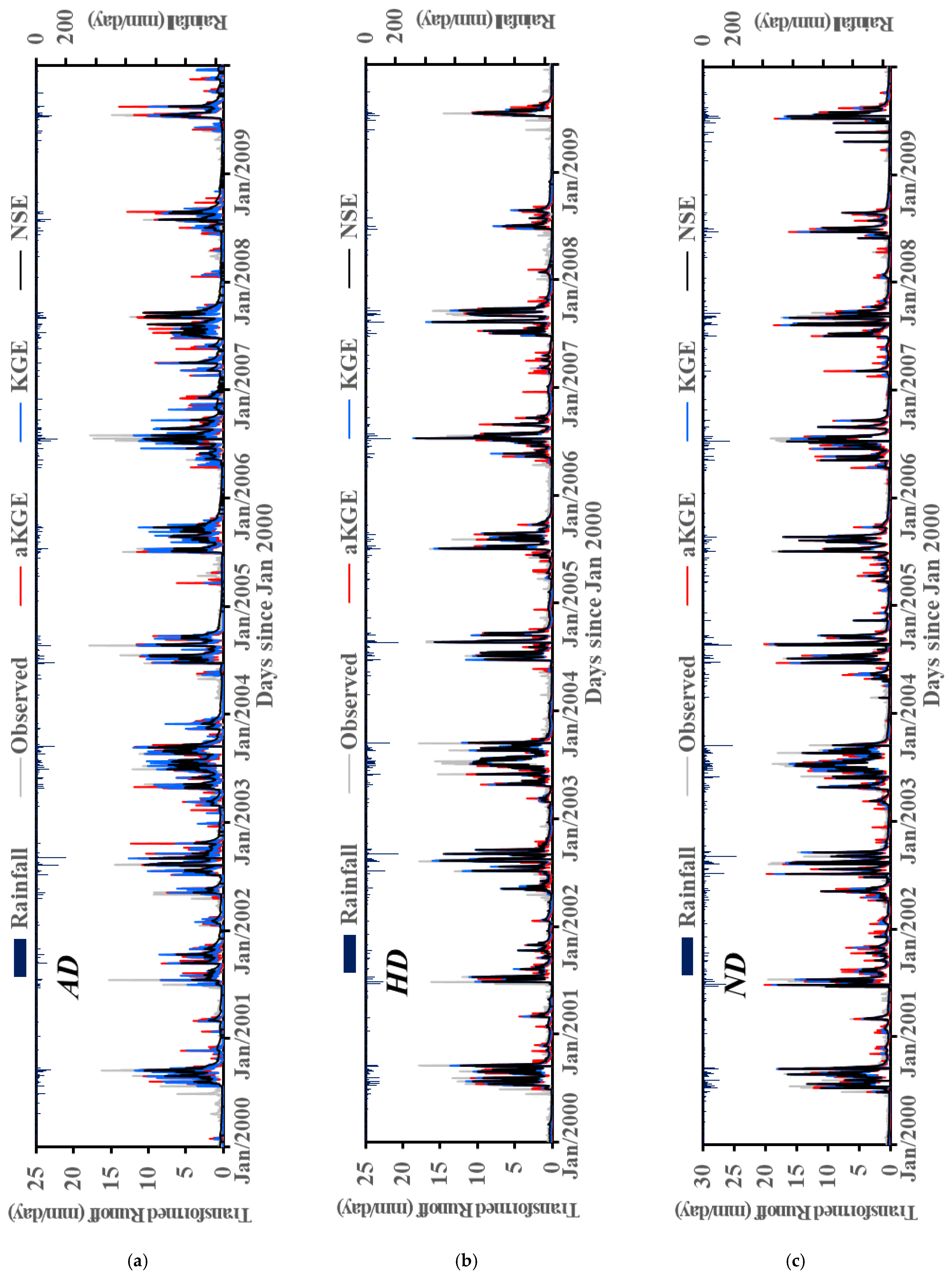
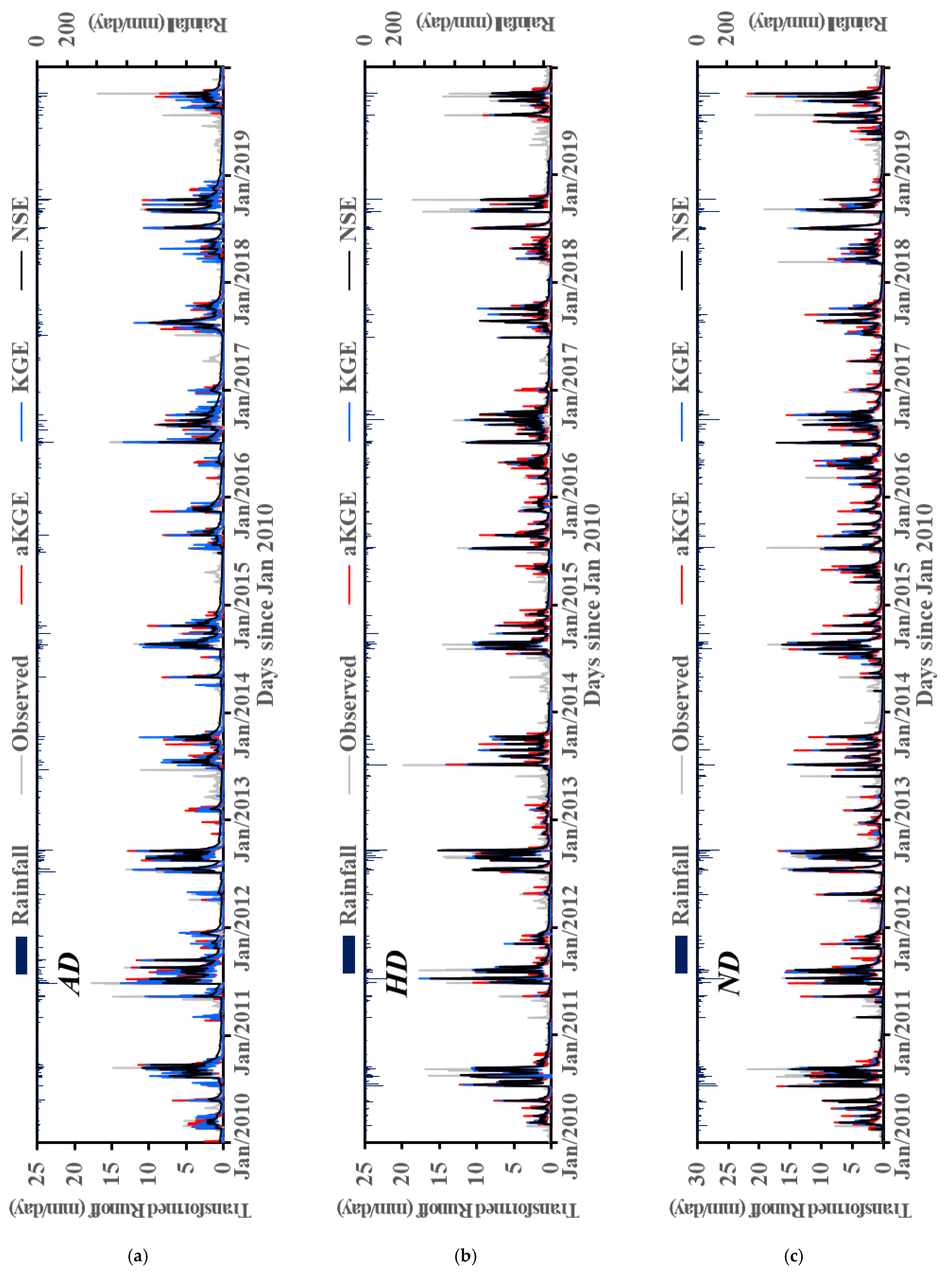
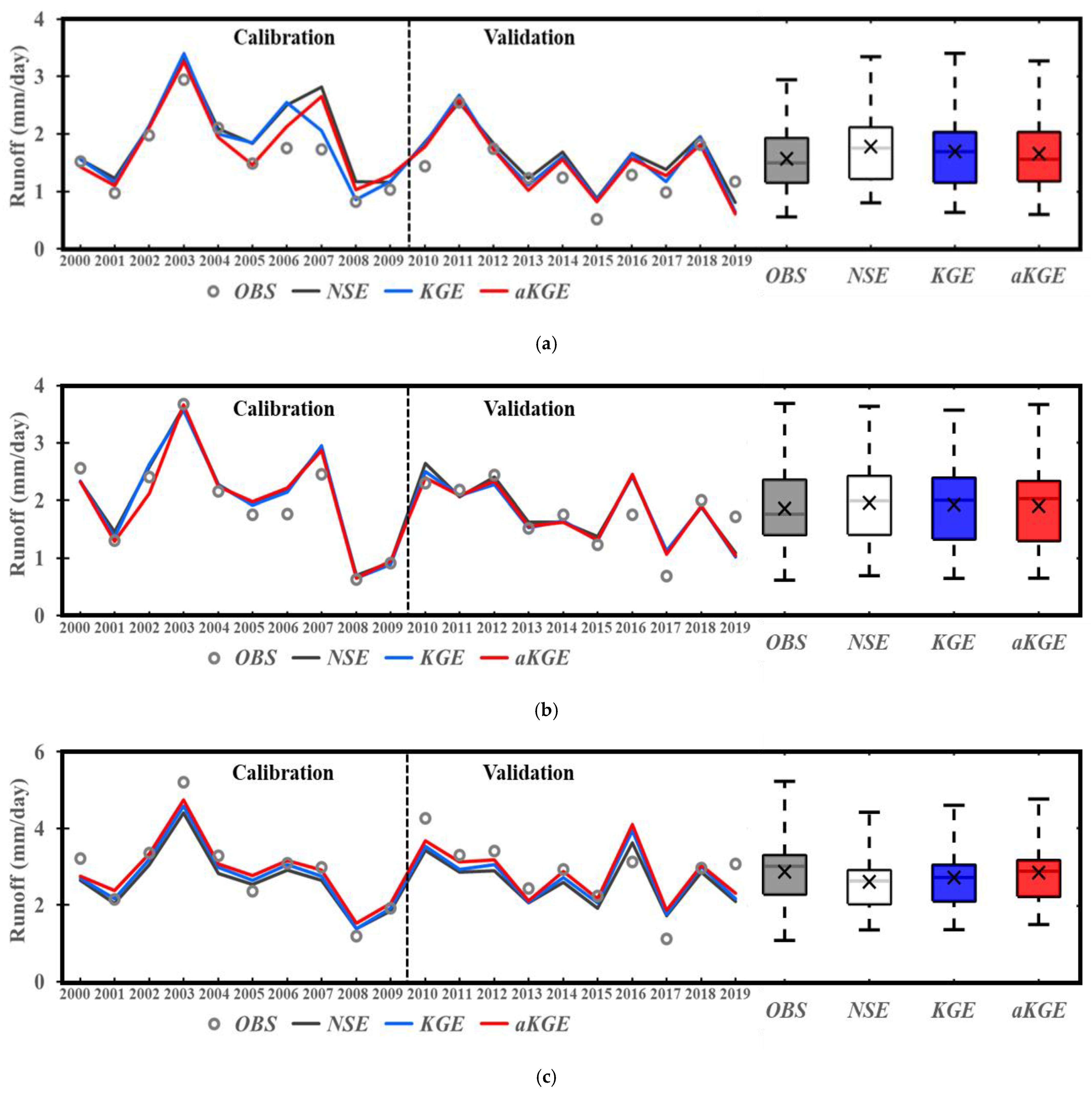
3.1. Calibration and Validation
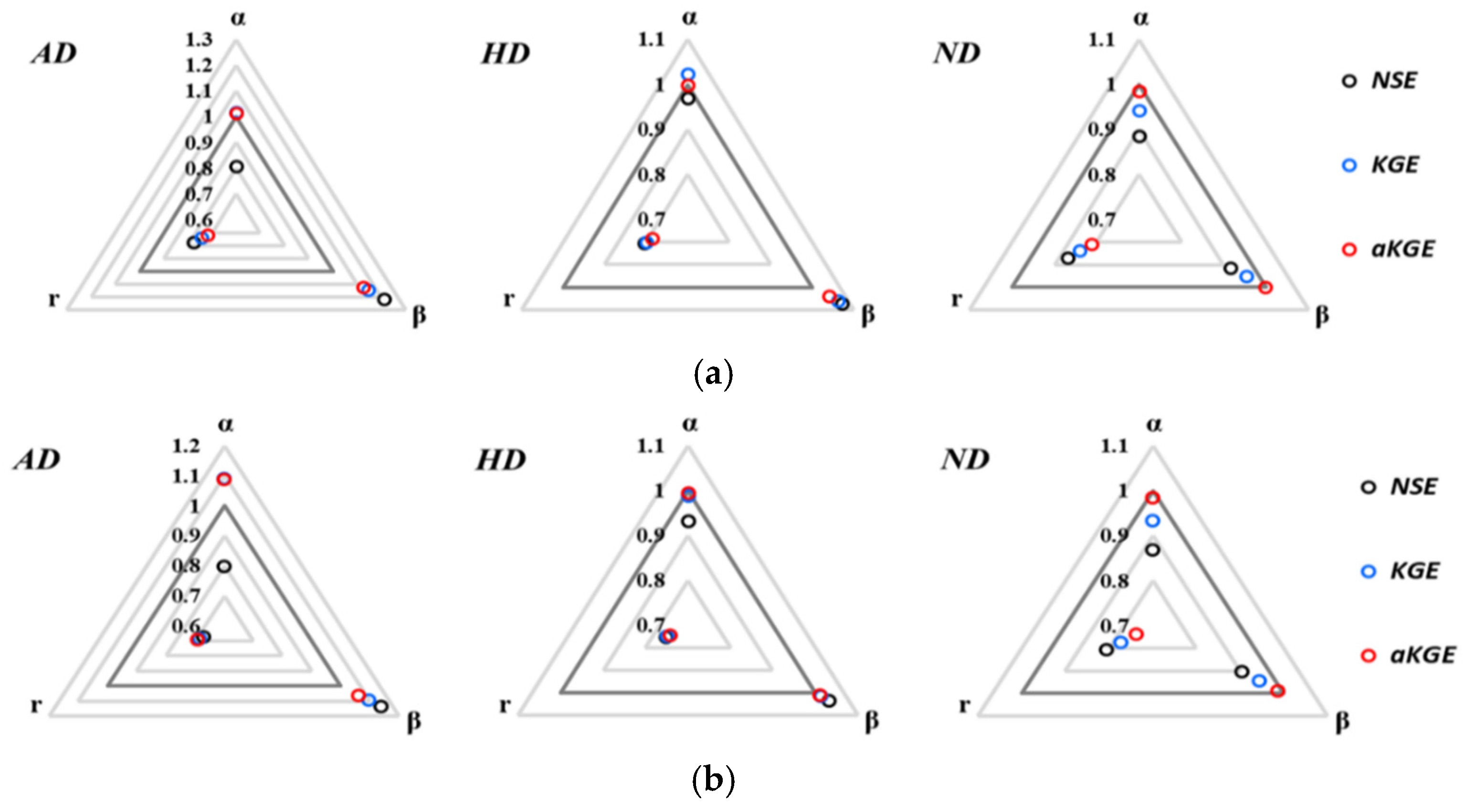
3.2. Evaluation of Streamflow Performance by Objective Functions
4. Summary and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Shao, Q.; Zhang, S.; Zhai, X.; She, D. Multi-metric calibration of hydrological model to capture overall flow regimes. J. Hydrol. 2016, 539, 525–538. [Google Scholar] [CrossRef]
- Panagoulia, D. Artificial neural networks and high and low flows in various climate regimes. Hydrol. Sci. J. 2006, 51, 563–587. [Google Scholar] [CrossRef]
- Panagoulia, D.; Dimou, G. Sensitivity of flood events to global climate change. J. Hydrol. 1997, 191, 208–222. [Google Scholar] [CrossRef]
- Perera, D.; Smakhtin, V.U.; Pischke, F.; Ohara, M.; Findikakis, A.; Werner, M.; Amarnath, G.; Koeppel, S.; Plotnykova, H.; Hulsmann, S. Water-related extremes and risk management. In UNESCO World Water Assessment Programme (WWAP); UN-Water. The United Nations World Water Development Report 2020: Water and Climate Change; UNSECO: Paris, France, 2020; pp. 58–67. [Google Scholar]
- Global Runoff Data Centre. Available online: https://www.bafg.de/ (accessed on 1 May 2021).
- Sivapalan, M.; Yaeger, M.A.; Harman, C.J.; Xu, X.; Troch, P.A. Functional model of water balance variability at the catchment scale: 1. Evidence of hydrologic similarity and space-time symmetry. Water Resour. Res. 2011, 47, W02522. [Google Scholar] [CrossRef]
- Zaman, M.A.; Rahman, A.; Haddad, K. Regional flood frequency analysis in arid regions: A case study for Australia. J. Hydrol. 2012, 475, 74–83. [Google Scholar] [CrossRef]
- Schaller, N.; Sillmann, J.; Müller, M.; Haarsma, R.; Hazeleger, W.; Hegdahl, T.J.; Kelder, T.; van den Oord, G.; Weerts, A.; Whan, K. The role of spatial and temporal model resolution in a flood event storyline approach in western Norway. Weather Clim. Extrem. 2020, 29, 100259. [Google Scholar] [CrossRef]
- Lobligeois, F.; Andréassian, V.; Perrin, C.; Tabary, P.; Loumagne, C. When does higher spatial resolution rainfall information improve streamflow simulation? An evaluation using 3620 flood events. Hydrol. Earth Syst. Sci. 2014, 18, 575–594. [Google Scholar] [CrossRef] [Green Version]
- Fisher, R.A.; Koven, C.D. Perspectives on the Future of Land Surface Models and the Challenges of Representing Complex Terrestrial Systems. J. Adv. Model. Earth Syst. 2020, 12, e2018MS001453. [Google Scholar] [CrossRef] [Green Version]
- Blyth, E.M.; Arora, V.K.; Clark, D.B.; Dadson, S.J.; De Kauwe, M.G.; Lawrence, D.M.; Melton, J.R.; Pongratz, J.; Turton, R.H.; Yoshimura, K.; et al. Advances in Land Surface Modelling. Curr. Clim. Change Rep. 2021, 7, 45–71. [Google Scholar] [CrossRef]
- Muleta, M.K.; Nicklow, J.W. Sensitivity and uncertainty analysis coupled with automatic calibration for a distributed watershed model. J. Hydrol. 2005, 306, 127–145. [Google Scholar] [CrossRef] [Green Version]
- Troy, T.J.; Wood, E.F.; Sheffield, J. An efficient calibration method for continental-scale land surface modeling. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Rouholahnejad, E.; Vaghefi, S.; Srinivasan, R.; Yang, H.; Kløve, B. A continental-scale hydrology and water quality model for Europe: Calibration and uncertainty of a high-resolution large-scale SWAT model. J. Hydrol. 2015, 524, 733–752. [Google Scholar] [CrossRef] [Green Version]
- Parker, S.R.; Adams, S.K.; Lammers, R.W.; Stein, E.D.; Bledsoe, B.P. Targeted hydrologic model calibration to improve prediction of ecologically-relevant flow metrics. J. Hydrol. 2019, 573, 546–556. [Google Scholar] [CrossRef]
- Bates, B.C.; Kundzewicz, Z.W.; Wu, S.; Palutikof, J.P. Climate Change and Water; Technical Paper of Intergovernmental Panel on Climate Change; IPCC Secretariat: Geneva, Switzerland, 2008; p. 210. [Google Scholar]
- IPCC. Climate Change 2013: The Physical Science Basis. Summary for Policymakers. In Working Group I Contribution to the IPCC Fifth Assessment Report; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Sulis, M.; Paniconi, C.; Rivard, C.; Harvey, R.; Chaumont, D. Assessment of climate change impacts at the catchment scale with a detailed hydrological model of surface-subsurface interactions and comparison with a land surface model. Water Resour. Res. 2011, 47. [Google Scholar] [CrossRef]
- Niu, G.Y.; Paniconi, C.; Troch, P.A.; Scott, R.L.; Durcik, M.; Zeng, X.; Huxman, T.; Goodrich, D.C. An integrated modelling framework of catchment-scale ecohydrological processes: 1. Model description and tests over an energy-limited watershed. Ecohydrology 2014, 7, 427–439. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Yang, T.; Liang, K.; Liu, C. Evaluation of streamflow simulation results of land surface models in GLDAS on the Tibetan plateau. J. Geophys. Res. Atmos. 2016, 121, 12180–112197. [Google Scholar] [CrossRef]
- Choi, H.I.; Liang, X.-Z.; Kumar, P. A conjunctive surface–subsurface flow representation for mesoscale land surface models. J. Hydrometeorol. 2013, 14, 1421–1442. [Google Scholar] [CrossRef]
- Lee, J.S.; Choi, H.I. Improvements to Runoff Predictions from a Land Surface Model with a Lateral Flow Scheme Using Remote Sensing and In Situ Observations. Water 2017, 9, 148. [Google Scholar] [CrossRef] [Green Version]
- Lin, P.; Yang, Z.-L.; Gochis, D.J.; Yu, W.; Maidment, D.R.; Somos-Valenzuela, M.A.; David, C.H. Implementation of a vector-based river network routing scheme in the community WRF-Hydro modeling framework for flood discharge simulation. Environ. Model. Softw. 2018, 107, 1–11. [Google Scholar] [CrossRef]
- Dai, Y.; Zeng, X.; Dickinson, R.E.; Baker, I.; Bonan, G.B.; Bosilovich, M.G.; Denning, A.S.; Dirmeyer, P.A.; Houser, P.R.; Niu, G. The common land model. Bull. Am. Meteorol. Soc. 2003, 84, 1013–1024. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.-Z.; Choi, H.I.; Kunkel, K.E.; Dai, Y.; Joseph, E.; Wang, J.X.; Kumar, P. Surface boundary conditions for mesoscale regional climate models. Earth Interact. 2005, 9, 1–28. [Google Scholar] [CrossRef]
- Choi, H.I.; Kumar, P.; Liang, X.Z. Three-dimensional volume-averaged soil moisture transport model with a scalable parameterization of subgrid topographic variability. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Choi, H.I.; Liang, X.-Z. Improved terrestrial hydrologic representation in mesoscale land surface models. J. Hydrometeorol. 2010, 11, 797–809. [Google Scholar] [CrossRef]
- Kim, E.S.; Choi, H.I.; Kim, S. Implementation of a topographically controlled runoff scheme for land surface parameterizations in regional climate models. KSCE J. Civ. Eng. 2011, 15, 1309. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Murphy, A.H. Skill scores based on the mean square error and their relationships to the correlation coefficient. Mon. Weather Rev. 1988, 116, 2417–2424. [Google Scholar] [CrossRef]
- Wȩglarczyk, S. The interdependence and applicability of some statistical quality measures for hydrological models. J. Hydrol. 1998, 206, 98–103. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef] [Green Version]
- Santos, L.; Thirel, G.; Perrin, C. Pitfalls in using log-transformed flows within the KGE criterion. Hydrol. Earth Syst. Sci. 2018, 22, 4583–4591. [Google Scholar] [CrossRef] [Green Version]
- Mizukami, N.; Rakovec, O.; Newman, A.J.; Clark, M.P.; Wood, A.W.; Gupta, H.V.; Kumar, R. On the choice of calibration metrics for “high-flow” estimation using hydrologic models. Hydrol. Earth Syst. Sci. 2019, 23, 2601–2614. [Google Scholar] [CrossRef] [Green Version]
- Kling, H.; Fuchs, M.; Paulin, M. Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios. J. Hydrol. 2012, 424, 264–277. [Google Scholar] [CrossRef]
- Fowler, K.; Peel, M.; Western, A.; Zhang, L. Improved rainfall-runoff calibration for drying climate: Choice of objective function. Water Resour. Res. 2018, 54, 3392–3408. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.Z.; Choi, H.I.; Kunkel, K.E.; Dai, Y.; Joseph, E.; Wang, J.X.L.; Kumar, P. Development of the Regional Climate-Weather Research and Forecasting Model (CWRF): Surface Boundary Conditions; ISWS SR 2005-01; Illinois State Water Survey: Champaign, IL, USA, 2005; p. 32. [Google Scholar]
- Beven, K.J.; Kirkby, M.J. A physically based, variable contributing area model of basin hydrology/Un modèle à base physique de zone d’appel variable de l’hydrologie du bassin versant. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar] [CrossRef] [Green Version]
- Korea Meteorological Administration. Available online: http://www.kma.go.kr (accessed on 1 May 2021).
- Water Management Information System. Available online: http://www.wamis.go.kr/wkd/mn_dammain.aspx (accessed on 1 May 2021).
- Bastidas, L.; Gupta, H.V.; Sorooshian, S.; Shuttleworth, W.J.; Yang, Z. Sensitivity analysis of a land surface scheme using multicriteria methods. J. Geophys. Res. Atmos. 1999, 104, 19481–19490. [Google Scholar] [CrossRef] [Green Version]
- Bastidas, L.A.; Hogue, T.; Sorooshian, S.; Gupta, H.V.; Shuttleworth, W.J. Parameter sensitivity analysis for different complexity land surface models using multicriteria methods. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Van Werkhoven, K.; Wagener, T.; Reed, P.; Tang, Y. Sensitivity-guided reduction of parametric dimensionality for multi-objective calibration of watershed models. Adv. Water Resour. 2009, 32, 1154–1169. [Google Scholar] [CrossRef]
- Neelin, J.D.; Bracco, A.; Luo, H.; McWilliams, J.C.; Meyerson, J.E. Considerations for parameter optimization and sensitivity in climate models. Proc. Natl. Acad. Sci. USA 2010, 107, 21349–21354. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chen, J.; Kumar, P. Topographic influence on the seasonal and interannual variation of water and energy balance of basins in North America. J. Clim. 2001, 14, 1989–2014. [Google Scholar] [CrossRef]
- Kumar, P. Layer averaged Richard’s equation with lateral flow. Adv. Water Resour. 2004, 27, 521–531. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Gupta, H.V.; Wagener, T. A process-based diagnostic approach to model evaluation: Application to the NWS distributed hydrologic model. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef] [Green Version]
- Pfannerstill, M.; Guse, B.; Fohrer, N. Smart low flow signature metrics for an improved overall performance evaluation of hydrological models. J. Hydrol. 2014, 510, 447–458. [Google Scholar] [CrossRef]
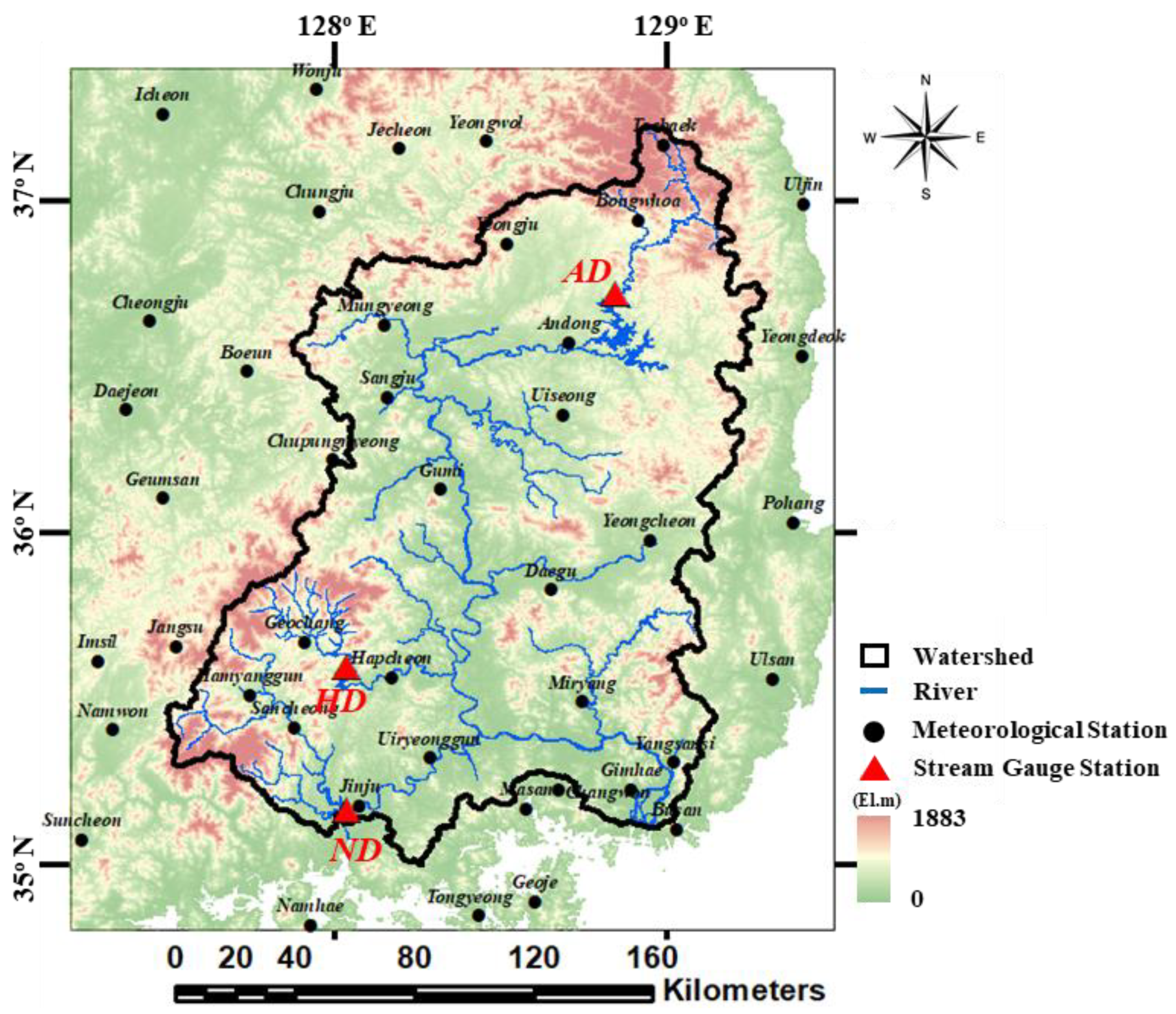
| Station Symbol | Station Name | Latitude (°N) | Longitude (°E) | Upstream Area 1 (km2) |
|---|---|---|---|---|
| AD | Andong Dam | 36.72 | 128.84 | 2474 |
| HD | Hapcheon Dam | 35.53 | 128.03 | 1254 |
| ND | Nam River Dam | 35.16 | 128.03 | 3151 |
| SBCs | AD | HD | ND |
|---|---|---|---|
| Land Cover Category | Savanna, Mixed Forest | Savanna, Mixed Forest | Savanna, Mixed Forest |
| Albedo | 0.13–0.20 | 0.13–0.20 | 0.13–0.20 |
| Fractional Vegetation Cover (%) | 100 | 99 | 100 |
| Leaf Area Index (m2/m2) | 0.5–4.6 | 0.7–4.1 | 0.6–4.3 |
| Surface Elevation (EL.m) | 284.7–887.1 | 379.0–573.3 | 130.5–726.2 |
| Sand/Clay Fraction Profile (%) | 62.3/20.6 | 65.0/20.0 | 61.3/21.0 |
| Bedrock Depth (m) | 80.0–95.8 | 80.0 | 80.0–98.2 |
| Station | Objective Function | Optimal Parameter | Calibration Period | Validation Period | |||||
|---|---|---|---|---|---|---|---|---|---|
| ƒ | ζ | ||||||||
| AD | NSE | 4 | 40,000 | 0.194 | 0.214 | 0.225 | 0.201 | 0.137 | 0.329 |
| KGE | 8 | 8000 | 0.015 | 0.147 | 0.260 | 0.091 | 0.095 | 0.315 | |
| aKGE | 9 | 7000 | 0.013 | 0.127 | 0.283 | 0.087 | 0.062 | 0.309 | |
| HD | NSE | 5 | 20,000 | 0.032 | 0.073 | 0.196 | 0.067 | 0.033 | 0.249 |
| KGE | 6 | 20,000 | 0.022 | 0.062 | 0.200 | 0.011 | 0.012 | 0.251 | |
| aKGE | 7 | 6000 | 0.003 | 0.041 | 0.215 | 0.006 | 0.010 | 0.258 | |
| ND | NSE | 6 | 90,000 | 0.115 | 0.084 | 0.132 | 0.131 | 0.096 | 0.193 |
| KGE | 6 | 30,000 | 0.059 | 0.047 | 0.161 | 0.066 | 0.056 | 0.228 | |
| aKGE | 7 | 6000 | 0.016 | 0.000 | 0.189 | 0.015 | 0.013 | 0.262 | |
| Station | Objective Function | RMSE of Extreme High Flows | RMSE of Extreme Low Flows | ||
|---|---|---|---|---|---|
| Calibration | Validation | Calibration | Validation | ||
| AD | NSE | 0.863 | 0.788 | 0.036 | 0.035 |
| KGE | 0.741 | 0.737 | 0.030 | 0.017 | |
| aKGE | 0.738 | 0.724 | 0.059 | 0.035 | |
| HD | NSE | 0.962 | 0.871 | 0.014 | 0.039 |
| KGE | 0.931 | 0.869 | 0.009 | 0.034 | |
| aKGE | 0.908 | 0.864 | 0.011 | 0.035 | |
| ND | NSE | 1.152 | 1.091 | 0.010 | 0.031 |
| KGE | 1.146 | 1.085 | 0.008 | 0.030 | |
| aKGE | 1.136 | 1.079 | 0.012 | 0.031 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.S.; Choi, H.I. Improved Streamflow Calibration of a Land Surface Model by the Choice of Objective Functions—A Case Study of the Nakdong River Watershed in the Korean Peninsula. Water 2021, 13, 1709. https://doi.org/10.3390/w13121709
Lee JS, Choi HI. Improved Streamflow Calibration of a Land Surface Model by the Choice of Objective Functions—A Case Study of the Nakdong River Watershed in the Korean Peninsula. Water. 2021; 13(12):1709. https://doi.org/10.3390/w13121709
Chicago/Turabian StyleLee, Jong Seok, and Hyun Il Choi. 2021. "Improved Streamflow Calibration of a Land Surface Model by the Choice of Objective Functions—A Case Study of the Nakdong River Watershed in the Korean Peninsula" Water 13, no. 12: 1709. https://doi.org/10.3390/w13121709
APA StyleLee, J. S., & Choi, H. I. (2021). Improved Streamflow Calibration of a Land Surface Model by the Choice of Objective Functions—A Case Study of the Nakdong River Watershed in the Korean Peninsula. Water, 13(12), 1709. https://doi.org/10.3390/w13121709






