1. Introduction
Drip irrigation is one of the most advantageous micro-irrigation systems owing to its low energy cost and high water distribution uniformity. It can significantly reduce soil evaporation and increase water utilization by creating a small wet area in the root zone [
1]. However, emitter clogging in drip irrigation systems is a serious problem that occurs when using re-used water or underground water containing sediments because it reduces the flow of water, the pressure at each emitter, and eventually the crop yield [
2,
3,
4,
5]. To prevent emitter clogging, it is essential to use a water filtration system [
6,
7,
8].
Disc, screen, and sand filters are commonly used in agriculture [
9,
10,
11]. Among them, the disc filter provides high filtration capacity and low energy consumption for large areas compared to other filters [
12]. In this type of filter, a group of cylindrical discs with grooved surfaces on the upper and lower parts are stacked together to effectively trap suspended solids/particles greater than the size of the groove [
13].
When water passes through the disc filter, hydraulic head loss occurs because the fluid path contracts due to filtration. This head loss requires a powerful pump, which eventually increases energy consumption. Moreover, the head loss of the filter usually accounts for more than 40% of the total head loss in an overall drip irrigation system [
14]. Therefore, it is important to minimize head loss when designing the filter, and several studies have analyzed head loss and the geometrical parameters affecting it. Yürdem et al. [
15] proposed the main geometrical parameters, such as the diameter of external inlet and outlet pipes, internal and external diameters of the disc, and the total effective length of the disc filter. Demir et al. [
16] compared the head loss of various disc filters and recommended the curly groove-shaped disc to reduce head loss and energy consumption. Duran-Ros et al. [
17] considered the total concentration of suspended solids, the kinematic viscosity of irrigation water, and the diameter of the inlet and outlet pipes as the parameters related to head loss. Furthermore, Puig-Bargués et al. [
18] and Wu et al. [
14] proposed a method for calculating the head loss of disc filters based on dimensional analysis.
The type of cross section of disc filter grooves varies by manufacturer, such as triangular or trapezoidal. In the case of a triangular cross section, it is easy to design and manufacture the groove, but a large head loss may occur. The trapezoidal shape, which is most commonly used, is a form with an improved corner of the triangle to reduce the head loss. However, if a disc filter is designed to reduce head loss and energy consumption, the filtration performance might degrade. Additionally, based on the disc groove shape, head loss patterns and filtration performance may vary under the same conditions. Hence, it is necessary to determine the comprehensive cross-sectional shape of the disc groove. Therefore, the purpose of this study is to analyze the appropriate cross-sectional shape of the disc groove that reduces the head loss without decreasing the filtration performance.
2. Materials and Methods
2.1. Shape of Disc Groove
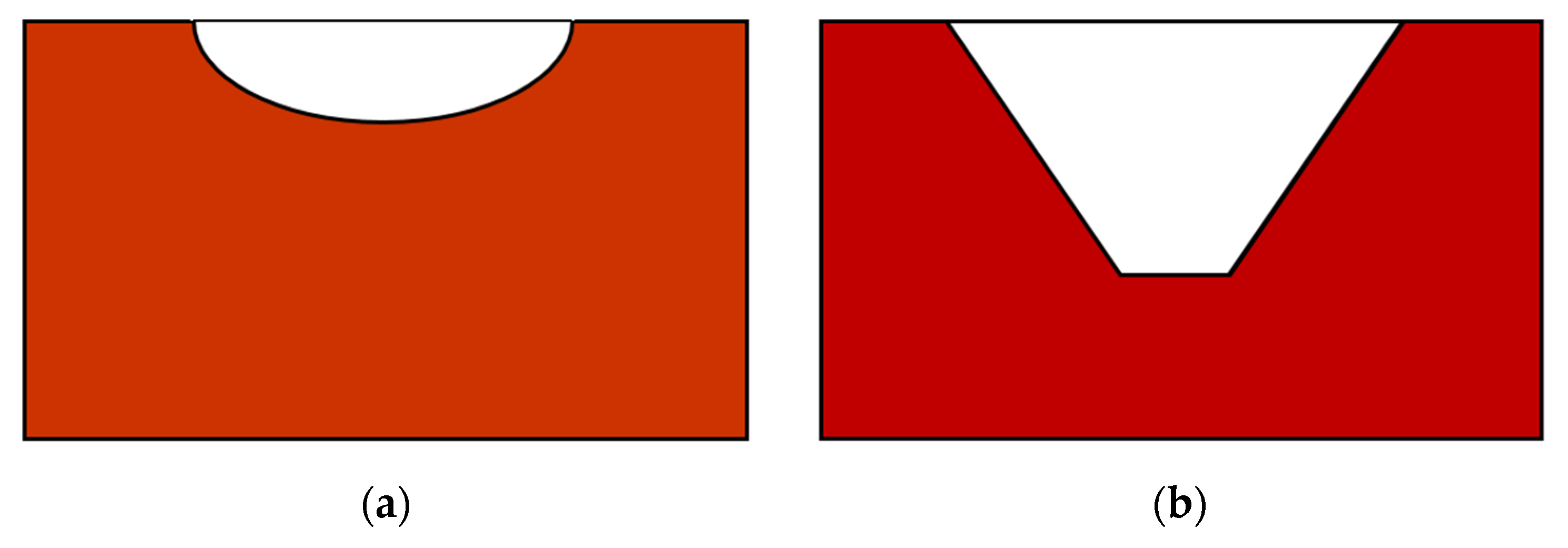
From a hydraulic point of view, the ideal shape of the groove channel is a circular type because it reduces the head loss and friction of passing water. For a constant sectional area, the semi-circular shape minimizes the wetted perimeter where the fluid meets the channel and maximizes the hydraulic diameter, thereby reducing the friction and maximizing the flow rate [
19,
20]. However, a perfect circle is difficult to implement in the manufacturing process and not practical to manufacture [
21]. Therefore, an ellipse type shape such as a semi-elliptical groove is hydraulically advantageous in the design of the disc filter. Nevertheless, most manufacturers have produced disc filters using triangular or trapezoidal grooves without sufficiently considering the hydraulic characteristics. In addition, we believe that a semi-elliptical disc groove shape will have no problem in mass production.
The type of disc filter in actual irrigation systems is selected based on the mesh standard, which is defined as the smallest particle size that can be filtered. The 120 mesh was selected as the standard design in this study because it can filter particles larger than 125 μm in diameter and is commonly used in South Korea. The shape of the disc groove suggested in this research and the widely used trapezoidal disc groove are shown in
Figure 1. The groove size and shape of these disc filters are different depending on the type of groove even if they are designed with the same mesh standard.
Disc specifications, such as the number of stacked discs, disc diameter, and number and length of grooves, were analyzed in this study. The depth, width, and cross-sectional shape of the grooves that were difficult to observe directly were measured through magnified images captured using field emission scanning electron microscopy (FESEM, AURIGA, Carl Zeiss, Oberkochen, Germany). Furthermore, the shapes of the upper and lower grooves were different even on the same disc. Thus, the accurate cross-sectional shape was analyzed using FESEM to calculate the groove sectional area of each disc filter.
2.2. Experimental Set-Up
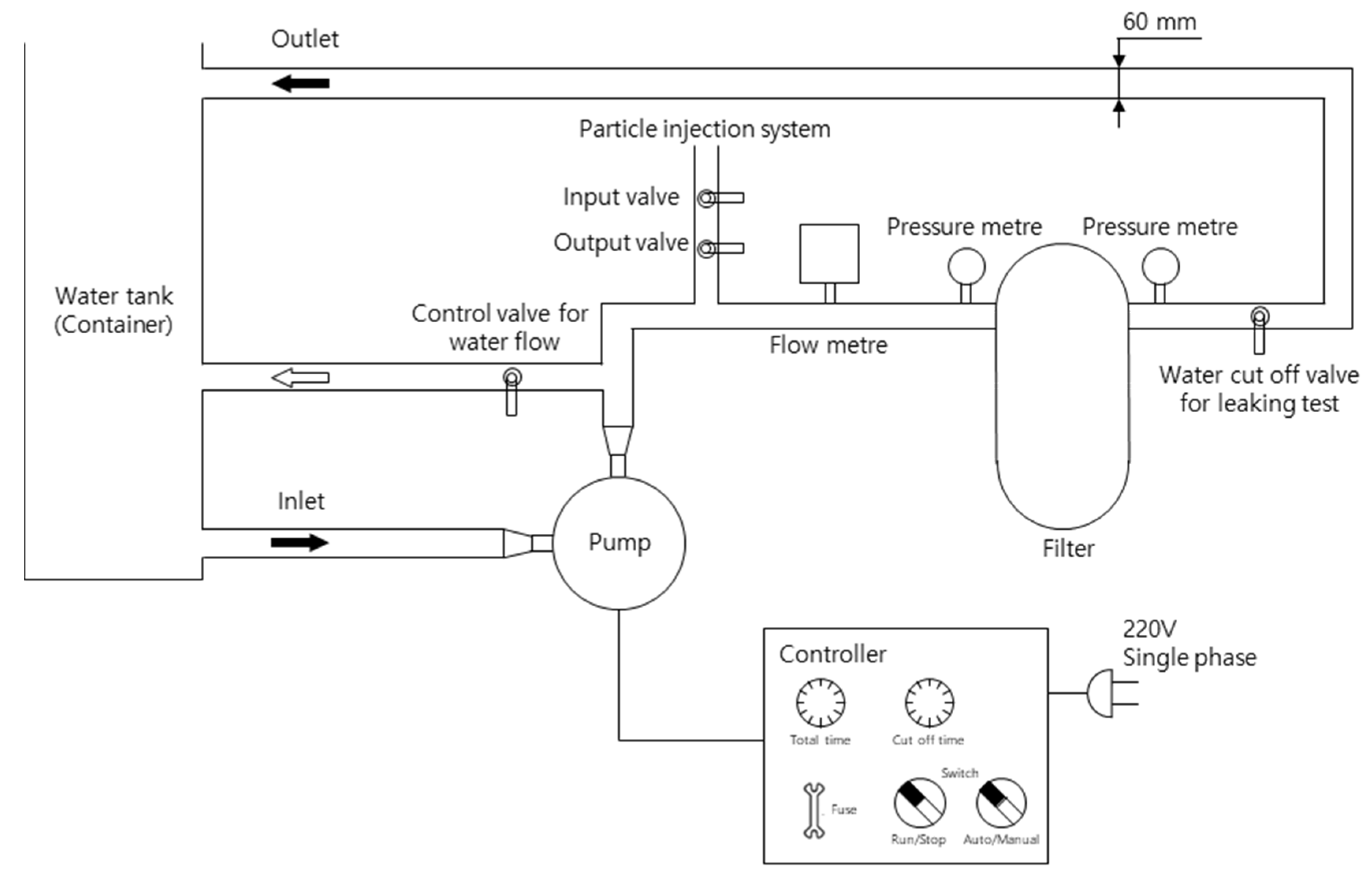
The experimental set-up to analyze the head loss of disc filters is shown in
Figure 2. Tap water was supplied to the filter using a pump (PH-1588W, Hanil, Seoul, South Korea), and the water from the filter was supplied back to the tank to circulate water continuously. The water tank was 1.1 m long, 0.7 m wide, and 0.65 m tall, and filled up to 0.3 m. The intake level of the pump was set at a height of 0.2 m from the bottom of the water tank. The pipes were 60 mm in diameter and manufactured to withstand a pressure of 10 bar.
Additionally, various valves were installed on the pipe to facilitate and control the experiment. The control valve was installed at the outlet of the pump to control the flow rate by changing the amount of water flowing into the filter. A cut-off valve was installed to test water leakage in the pipe and filter before proceeding with the experiment. The input and output valves in the particle injection system were designed to insert soil particles when water is flowing through the pipe to conduct a filtration performance test. A flow meter and two pressure meters were installed in this set-up to observe the state of water flow. The two pressure meters were installed before and after the filter to evaluate the head loss caused by the filter.
2.3. Head Loss Test
The head loss graph from the technical information of the disc filter shows the relationship between pressure head loss and flow rate in a logarithmic scale. Generally, it obeys the following relationship as Equation (1):
where
is the head loss in bar,
is the flow rate in m
3/h, and
and
are empirical constants that are determined by various structural features of the disc filter. In the head loss graph depicted in a logarithmic scale of general disc filters,
is indicated by the slope of a straight line, which varies depending on the type of disc filter.
To obtain the relationship between head loss and flow rate, a test was conducted to measure the head loss for various flow rates. The control valve was used to control the flow rate, which was measured using a flow meter. The head loss was obtained by calculating the difference in the pressure meter readings installed before and after the filter. Then, a regression equation was derived in the form of an exponential function such as Equation (1) for the head loss result according to various flow rates.
2.4. Analysis of Head Loss Considering the Disc Groove Shape
The disc filters used in this study had different groove sectional areas. Generally, a small head loss occurs when the sectional area is large, regardless of the groove shape. Therefore, the head losses for different sectional areas were compared by considering that the grooves have the same sectional area. Hence, the head loss equation () was divided by the total number of grooves to obtain the head loss equation in a single groove (). Then, the head loss in a single groove with the adjusted area () was derived using the relationship between head loss and fluid properties, such as velocity, sectional area, and flow rate.
The head loss that occurs in the groove consists of friction head loss and minor losses, such as inflow and outflow losses. The Darcy–Weisbach friction head loss (
) was calculated using Equation (2):
where
is the Darcy friction factor,
is the length of the channel,
is the hydraulic diameter of the channel,
is the flow velocity, and
is the gravitational acceleration. For a laminar flow, the friction factor can be derived using Equations (3) and (4):
where
is the Reynolds number,
is the density of the fluid,
is the characteristic length or hydraulic diameter,
is the dynamic viscosity, and
is the kinematic viscosity. If the Reynolds number is less than 2100, the flow can be considered to be laminar.
For the constant flow rate, the flow velocity is inversely proportional to the sectional area. In addition, when the channel cross-sectional shapes are the same, the hydraulic diameter is proportional to the square root of the sectional area because the diameter is a term with respect to length. Hence, using these proportional relationships and substituting Equations (3) and (4) into Equation (2), the following relationship between the unit head loss and sectional area can be derived as Equation (5):
Therefore, the head loss in a groove, which is mainly affected by friction loss considering the adjusted sectional area (
), can be calculated using Equation (6):
2.5. Filtration Performance Test
The disc filter based on the 120 mesh standard is designed to filter particles larger than 125 μm in diameter. However, some filters are often manufactured without sufficient particle removal capacity to reduce head loss and energy consumption. Therefore, it is important to ensure adequate filtration performance when designing the disc filter. In this study, a filtration performance test was conducted using soil particles of various sizes to evaluate the particle removal efficiency. The soil particles were classified using 5 types of sieve (No. 70, 80, 100, 120, and 140), and 5 g from each size range was inserted into the particle injection system. The particles that could not be filtered were captured using a No. 200 sieve, and their weights were measured. The removal efficiency was calculated using the ratio of the weight of particles captured by the sieve and the total weight of inserted particles. Additionally, the maximum particle size that could pass through the cross section of the groove of each filter was derived and compared.
3. Results and Discussion
3.1. Analysis of Disc Groove
The disc specifications that can be observed with the naked eye are shown in
Table 1. The total number of grooves was 248,640 and 268,800 in the proposed and traditional disc filters, respectively, which were not significantly different. Additionally, the geometrical features, such as the disc diameter and groove length, showed no significant difference.
The cross-sectional shapes of the grooves were analyzed using FESEM images (
Figure 3). The grooves in the proposed disc filter were semi-elliptical, and the upper and lower parts were symmetrical. In the traditional disc filter, the grooves were trapezoidal, and the upper and lower parts were different. The width, depth, wetted perimeter, sectional area, and hydraulic diameter of both discs are shown in
Table 2. The average width and depth of the semi-elliptic groove were 362.1 μm and 97.0 μm, respectively. In the case of the trapezoidal groove, the upper part was 437.7 μm wide and 243.2 μm deep, whereas the lower part was 409.0 μm wide and 97.3 μm deep.
The average sectional areas of the grooves were calculated to be 27,574.4 μm2 and 49,285.4 μm2 for the semi-elliptic and trapezoidal groove disc filters, respectively. Unlike the geometrical features of discs that could be observed with the naked eye, the shape of the grooves showed a difference of up to 57.6% in their sectional area. Additionally, the shape of the grooves on the upper and lower parts of the semi-elliptic groove disc was similar, whereas in the trapezoidal groove disc filter, the grooves on the upper and lower parts were different. The difference in hydraulic diameter according to the type of disc filter was small compared to the difference in the sectional area because the semi-elliptical groove shape in the proposed disc filter had a relatively large hydraulic diameter even in a small area. In other words, for the same sectional area, the elliptical shape provided a greater hydraulic diameter compared to other shapes.
3.2. Head Loss Test Result
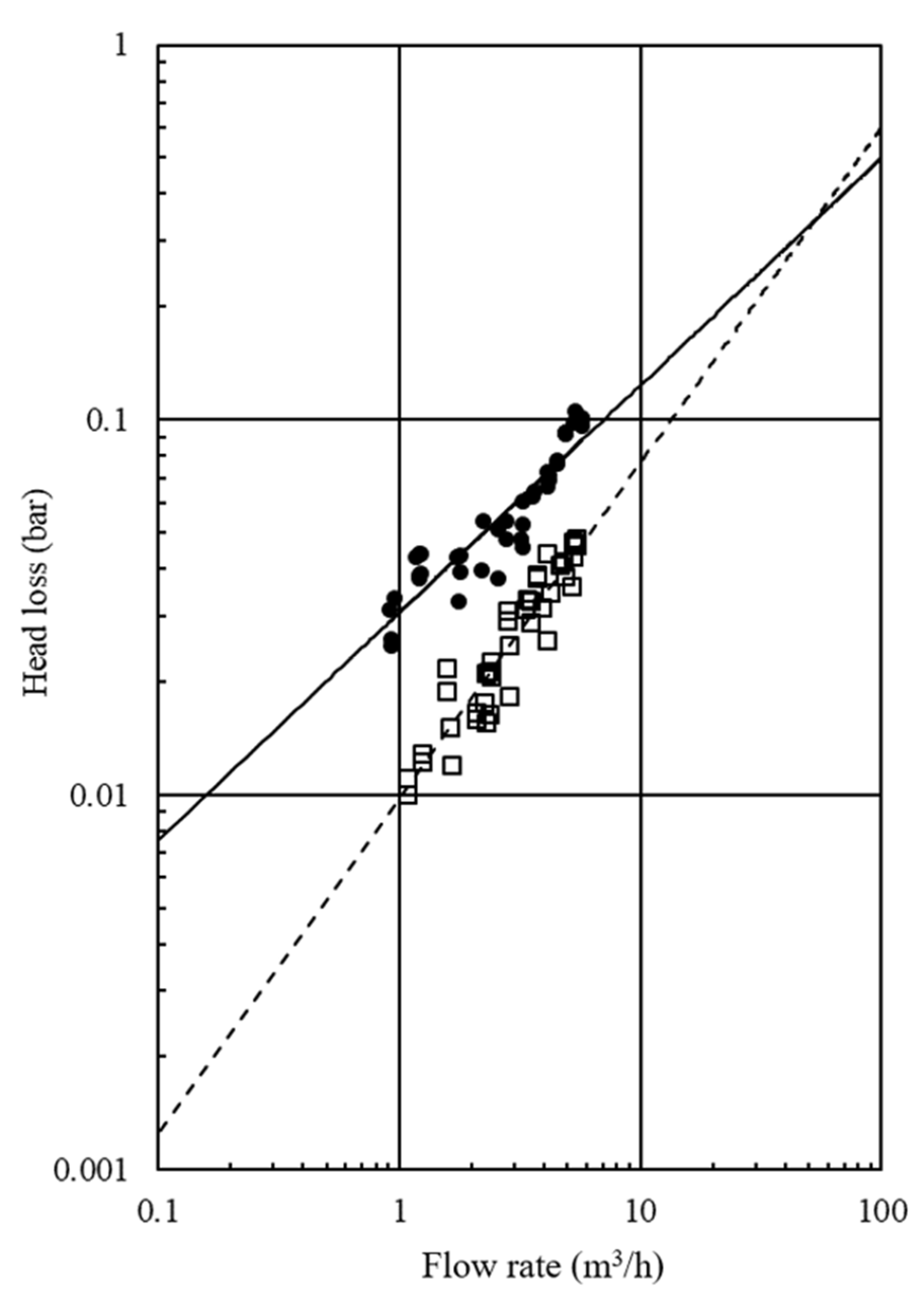
The head loss for different flow rates was measured, as shown in
Figure 4. In the flow range of 0.9–5.7 m
3/h measured in the experiment, the head loss in the semi-elliptic groove filter was greater than that of the trapezoidal groove filter because the total number of grooves in the traditional disc filter was higher, and their average sectional area was approximately 1.8 times larger than that of the proposed disc filter. However, as the flow rate increased, the head loss of the trapezoidal groove filter increased more steeply, and it was estimated to be greater than that of the semi-elliptic groove filter at the flow rates exceeding 52.4 m
3/h.
The friction loss in the trapezoidal groove disc was observed to be less in the flow range used in this experiment. As a result of the head loss test, the head loss equations showing the relationship between the flow rate and head loss were derived as Equations (7) and (8):
3.3. Analysis of Head Loss According to the Groove Type
Using the head loss equations and total number of grooves, the head loss equations for a single groove were derived, as shown in Equations (9) and (10):
The Reynolds number in the single groove was calculated by applying the kinematic viscosity coefficient of 1.01 × 10
−6 m
2/s, as shown in
Table 3. The Reynolds number was less than 2100 in the majority of flow rates less than 63.9 m
3/h and 98.8 m
3/h in the semi-elliptic and trapezoidal groove filters, respectively. Accordingly, the flow inside the disc groove was considered to be laminar.
Therefore, assuming the grooves in the traditional and proposed disc filters have the same sectional area, the head loss in one groove can be derived using Equation (6), as shown in
Table 4. At flow rates above 1.2 m
3/h, the head loss in the trapezoidal disc groove with an adjusted area was greater than that of the semi-elliptic disc groove. In the range of 12–25 m
3/h, which is the recommended flow rate provided in the product manual for disc filters, the head loss in a groove in two filters differed by 48–58%. Although the total head loss of the trapezoidal groove filter was smaller than that of the semi-elliptic groove filter in the head loss test, it was found that the head loss of the semi-elliptic groove filter was smaller when the sectional areas of the grooves were same. In other words, it is estimated that the hydraulically efficient cross section to reduce the head loss is elliptical because it increases the hydraulic diameter.
3.4. Filtration Performance Test Results
The particle removal efficiency of each disc filter was calculated, as shown in
Table 5. The weight of unfiltered particles that passed through the disc filter was calculated by subtracting the weight of the sieve from the weight of the sieve with the captured particles. The removal efficiency of the semi-elliptic groove disc filter was higher than that of the trapezoidal groove disc filter for all size ranges of soil particles. For the particle range of 125–150 μm, the removal efficiency of the trapezoidal groove filter was 90.6%, i.e., 0.47 g of the 5 g of soil particles was unfiltered and captured by the sieve. However, the semi-elliptic groove filter demonstrated a higher removal efficiency of 97.2% for the same soil particle size range. Additionally, for particles smaller than 125 μm, the semi-elliptic groove filter showed a removal efficiency of 95.0%, whereas that of the trapezoidal groove filter was only 79.2%.
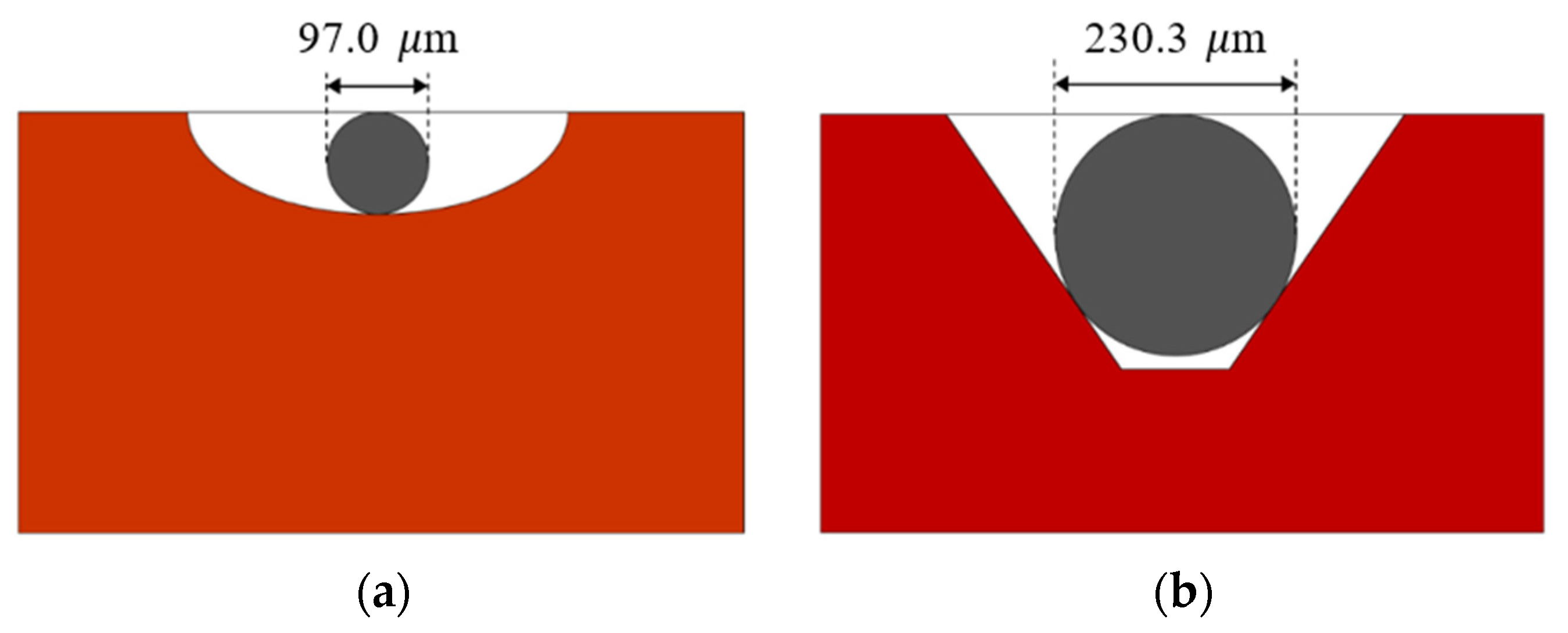
As a result of analyzing the groove cross section, the maximum particle size that can pass through the grooves of semi-elliptic and trapezoidal disc filters was 97.0 μm and 230.3 μm, respectively (
Figure 5). In the case of the trapezoidal groove disc filter, particles larger than 125 μm could pass through without being filtered in the actual disc groove cross section despite being designed using the 120 mesh standard. Therefore, the semi-elliptic groove disc filter performed more effective filtration. Additionally, the semi-elliptic groove filter can perform a stable filtration even when the concentration of suspended solids is high.
4. Conclusions
In this study, the effect of the groove shape of the disc filter on head loss and filtration performance was analyzed through the head loss test and filtration performance test, respectively. The comparative analysis was performed using a disc filter with a semi-elliptical groove shape that is hydraulically advantageous and the existing widely used disc filter. Deriving the relationship between flow rate and head loss revealed that a smaller head loss occurs in disc filters with a larger groove sectional area and a higher number of grooves. As the cross section of the two grooves analyzed in this study could not be similar due to manufacturing limitations, it was not possible to compare the head loss under similar conditions experimentally. However, when the sectional area of the groove was the same, a smaller head loss occurred in the semi-elliptical groove. Additionally, the semi-elliptical-groove-shaped disc filter was found to be suitable for the 120 mesh standard and filtered the soil particles more effectively.
Accordingly, it was determined that the optimum disc filter can be designed by considering the cross-sectional shape of the disc groove. To reduce the head loss and energy consumption of the disc filter, the hydraulically advantageous elliptic type of groove shape should be used. In addition, the larger the sectional area of the groove, the smaller the head loss; however, this can decrease the filtration performance. Therefore, the hydraulically advantageous cross section should be selected in the same sectional area to ensure sufficient filtration performance as well as small head loss. In this study, comparative analysis was conducted on disc filters with the same mesh standard but different sectional areas and different filtration performance due to manufacturing limitations. Therefore, it is expected that the optimal shape can be determined through further studies considering more diverse groove shapes and mesh standards, and detailed conditions. Furthermore, the head loss should be further minimized by considering the sectional area and the number of grooves.
Author Contributions
Conceptualization, J.-Y.C. and W.C.; methodology, S.-i.L. and J.-Y.C.; validation, S.-i.L. and W.C.; formal analysis, S.-i.L., J.-Y.C. and W.C.; investigation, S.-i.L. and W.C.; resources, S.-i.L. and J.-Y.C.; data curation, S.-i.L., J.-Y.C. and W.C.; writing—original draft preparation, S.-i.L.; writing—review and editing, S.-i.L., J.-Y.C. and W.C.; visualization, S.-i.L.; supervision, J.-Y.C. and W.C.; project administration, J.-Y.C.; funding acquisition, J.-Y.C. and W.C. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Korea Institute of Planning and Evaluation for Technology in Food, Agriculture, Forestry and Fisheries (IPET) through Agricultural Foundation and Disaster Response Technology Development Program, funded by Ministry of Agriculture, Food and Rural Affairs (MAFRA) (No. 321066-3) and the National Research Foundation of Korea (NRF) grant funded by the Korea government (Ministry of Science and ICT) (No. 2017R1E1A1A01077413).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Liu, H.; Huang, G. Laboratory experiment on drip emitter clogging with fresh water and treated sewage effluent. Agr. Water Manag. 2009, 96, 745–756. [Google Scholar] [CrossRef]
- Bucks, D.A.; Nakayama, F.S.; Gilbert, R.G. Trickle irrigation water quality and preventive maintenance. Agr. Water Manag. 1979, 2, 149–162. [Google Scholar] [CrossRef]
- Tajrishy, M.A.; Hills, D.J.; Tchobanoglous, G. Pretreatment of secondary effluent for drip irrigation. J. Irrig. Drain. Eng. 1994, 120, 716–731. [Google Scholar] [CrossRef]
- Capra, A.; Scicolone, B. Emitter and filter tests for wastewater reuse by drip irrigation. Agr. Water Manag. 2004, 68, 135–149. [Google Scholar] [CrossRef]
- Duran-Ros, M.; Puig-Bargués, J.; Arbat, G.; Barragán, J.; De Cartagena, F.R. Effect of filter, emitter and location on clogging when using effluents. Agr. Water Manag. 2009, 96, 67–79. [Google Scholar] [CrossRef]
- Yürdem, H.; Demir, V.; Değirmencioğlu, A. Development of a mathematical model to predict clean water head losses in hydrocyclone filters in drip irrigation systems using dimensional analysis. Biosyst. Eng. 2010, 105, 495–506. [Google Scholar] [CrossRef]
- Puig-Bargués, J.; Duran-Ros, M.; Arbat, G.; Barragán, J.; De Cartagena, F.R. Prediction by neural networks of filtered volume and outlet parameters in micro-irrigation sand filters using effluents. Biosyst. Eng. 2012, 111, 126–132. [Google Scholar] [CrossRef]
- Duran-Ros, M.; Puig-Bargués, J.; Arbat, G.; Barragán, J.; De Cartagena, F.R. Performance and backwashing efficiency of disc and screen filters in microirrigation systems. Biosyst. Eng. 2009, 103, 35–42. [Google Scholar] [CrossRef]
- Zong, Q.; Zheng, T.; Liu, H.; Li, C. Development of head loss equations for self-cleaning screen filters in drip irrigation systems using dimensional analysis. Biosyst. Eng. 2015, 133, 116–127. [Google Scholar] [CrossRef]
- Nieto, P.J.G.; García–Gonzalo, E.; Arbat, G.; Duran–Ros, M.; De Cartagena, F.R.; Puig-Bargués, J. Pressure drop modelling in sand filters in micro-irrigation using gradient boosted regression trees. Biosyst. Eng. 2018, 171, 41–51. [Google Scholar] [CrossRef]
- Mesquita, M.; De Deus, F.P.; Testezlaf, R.; Da Rosa, L.M.; Diotto, A.V. Design and hydrodynamic performance testing of a new pressure sand filter diffuser plate using numerical simulation. Biosyst. Eng. 2019, 183, 58–69. [Google Scholar] [CrossRef]
- Liu, G.; Jiang, H.; Liao, D.; Deng, Y. Comparative experiments on the technological performance of disc filters. IOP Conf. Ser. Mat. Sci. 2017, 207, 1–7. [Google Scholar] [CrossRef]
- Puig-Bargués, J.; Arbat, G.; Barragán, J.; De Cartagena, F.R. Effluent particle removal by microirrigation system filters. Span. J. Agric. Res. 2005, 3, 182–191. [Google Scholar] [CrossRef]
- Wu, W.; Chen, W.E.I.; Liu, H.; Yin, S.; Niu, Y. A new model for head loss assessment of screen filters developed with dimensional analysis in drip irrigation systems. Irrig. Drain. 2014, 63, 523–531. [Google Scholar] [CrossRef]
- Yürdem, H.; Demir, V.; Değirmencioğlu, A. Development of a mathematical model to predict head losses from disc filters in drip irrigation systems using dimensional analysis. Biosyst. Eng. 2008, 100, 14–23. [Google Scholar] [CrossRef]
- Demir, V.; Yürdem, H.; Yazgi, A.; Değirmencioğlu, A. Determination of the head losses in metal body disc filters used in drip irrigation systems. Turk. J. Agric. For. 2009, 33, 219–229. [Google Scholar]
- Duran-Ros, M.; Arbat, G.; Barragán, J.; De Cartagena, F.R.; Puig-Bargués, J. Assessment of head loss equations developed with dimensional analysis for micro irrigation filters using effluents. Biosyst. Eng. 2010, 106, 521–526. [Google Scholar] [CrossRef]
- Puig-Bargués, J.; Barragán, J.; De Cartagena, F.R. Development of equations for calculating the head loss in effluent filtration in microirrigation systems using dimensional analysis. Biosyst. Eng. 2005, 92, 383–390. [Google Scholar] [CrossRef]
- Monadjemi, P. General formulation of best hydraulic channel section. J. Irrig. Drain. Eng. 1994, 120, 27–35. [Google Scholar] [CrossRef]
- Jain, A.; Bhattacharjya, R.K.; Sanaga, S. Optimal design of composite channels using genetic algorithm. J. Irrig. Drain. Eng. 2004, 130, 286–295. [Google Scholar] [CrossRef]
- Abdulrahman, A. Best hydraulic section of a composite channel. J. Hydraul. Eng. 2007, 133, 695–697. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).