Study on the Pricing of Water Rights Transaction between Irrigation Water Users Based on Cooperative Game in China
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Data Sources
2.1.1. Study Area
2.1.2. Data Sources
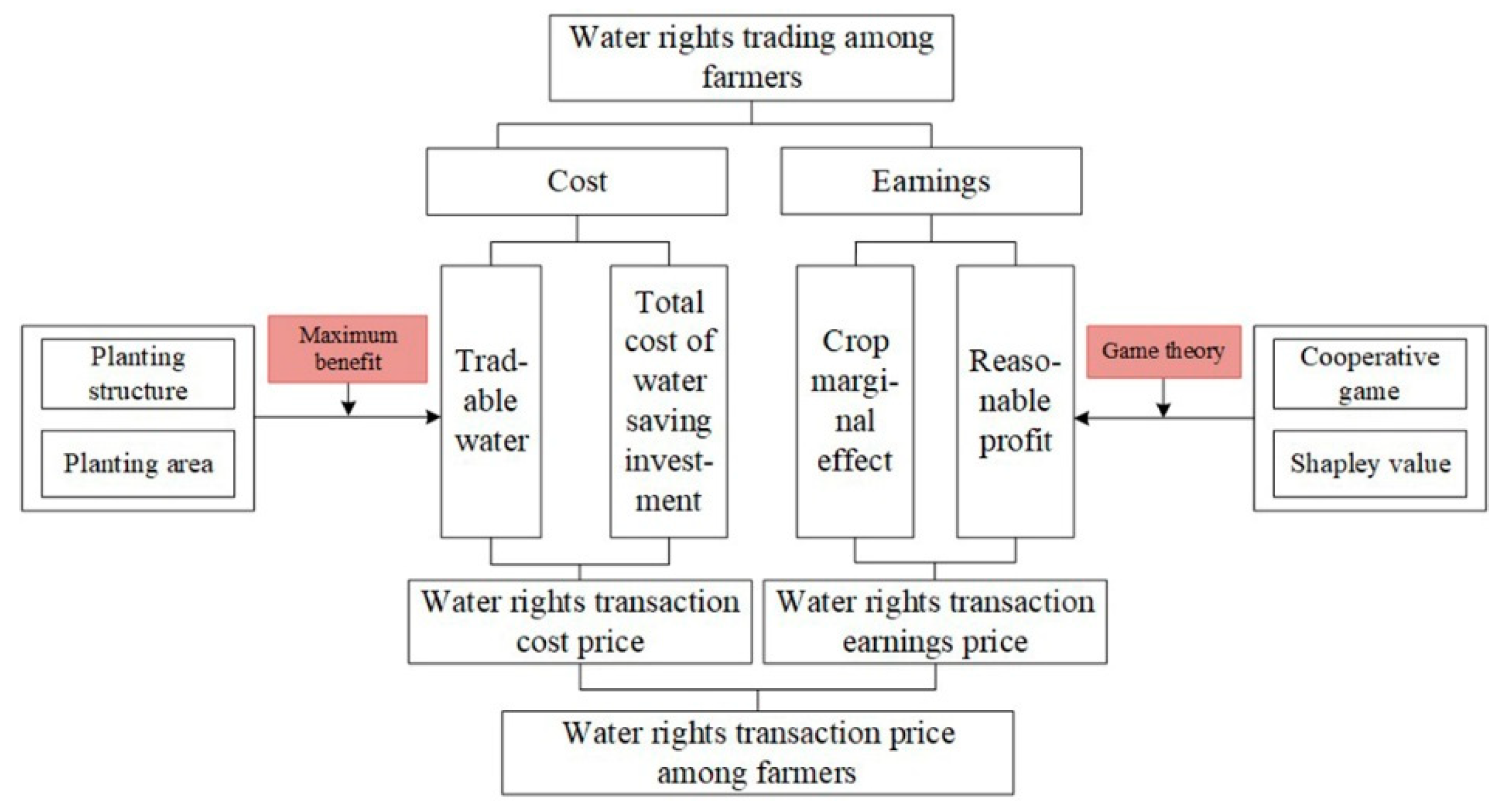
2.2. Methodology
2.2.1. Cost Price of Water Conservation in the Water Rights Transaction between Farmers
2.2.2. Earnings Price of Water Rights Transaction among Farmers Based on the Production Function of Crop Water and Cooperative Game Theory
Marginal Benefit of Crops
Determination of Reasonable Return Coefficient of Water Rights Transaction Based on Game Theory
2.2.3. Tradable Water Volume
2.2.4. Comprehensive Pricing
3. Results
3.1. The Relationship Between Irrigation Water Volume and Marginal Benefit
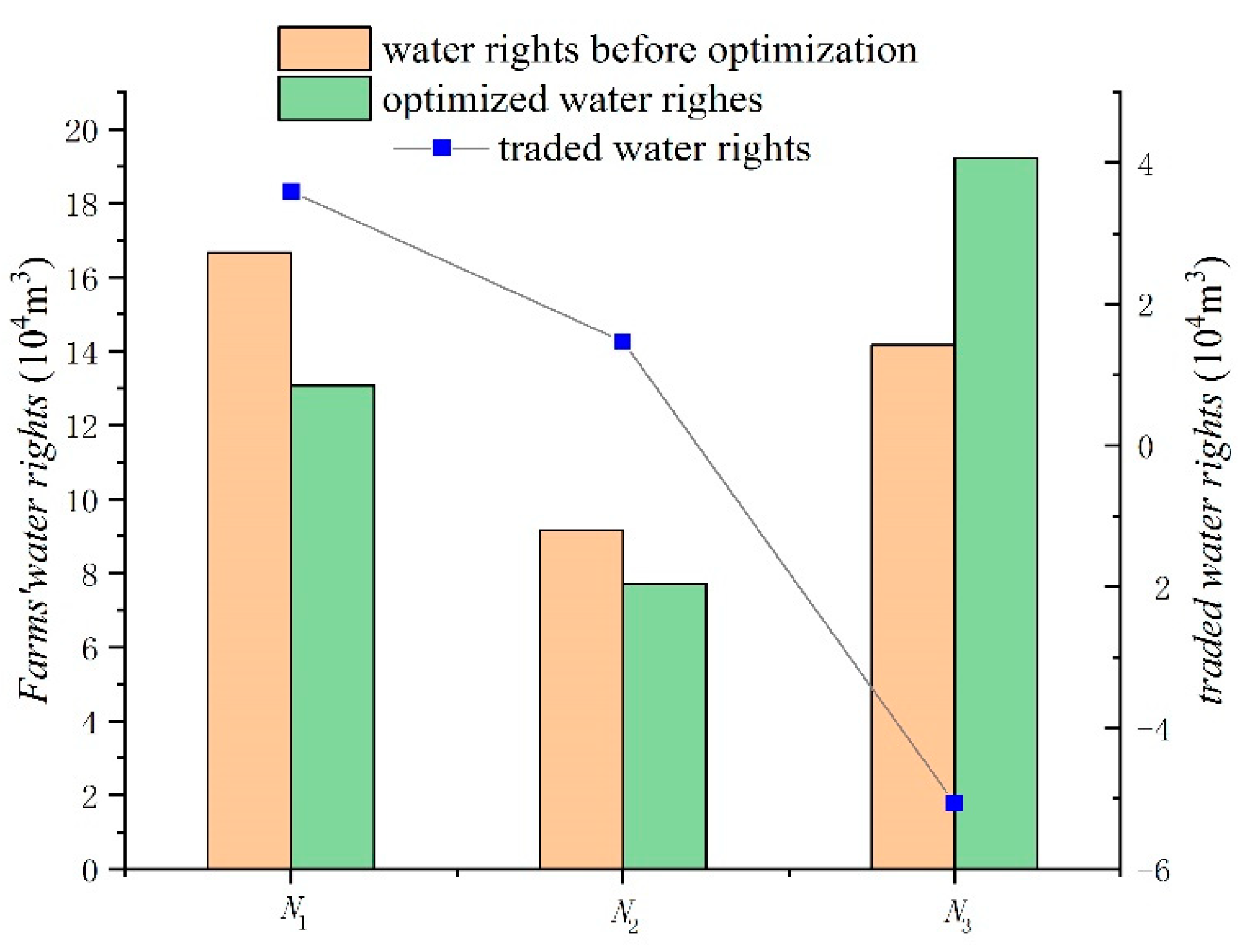
3.2. Tradeable Water Volume Among Farmers
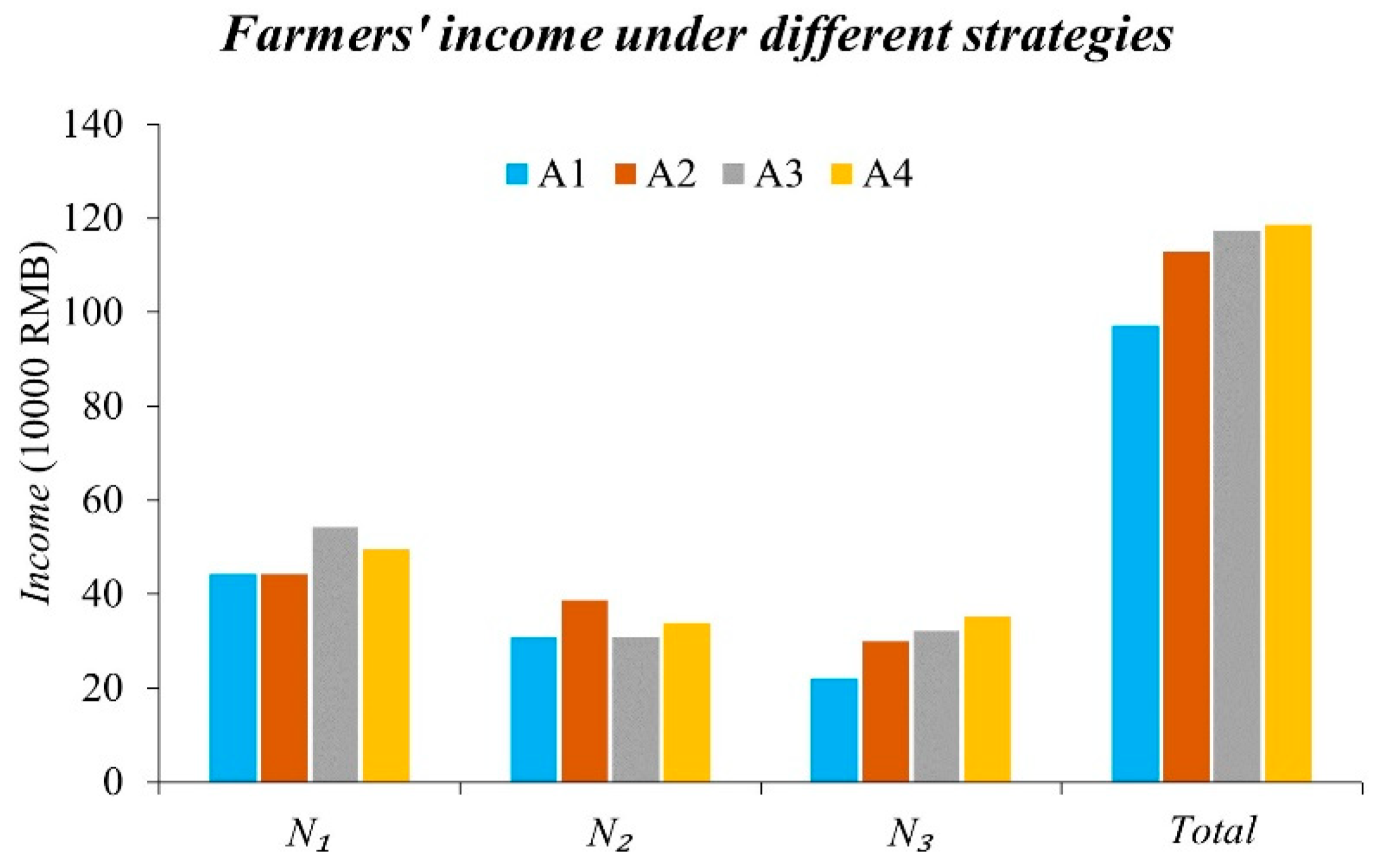
3.3. Farmers’ Income Calculation Results
- (1)
- Farmers’ income after optimizing irrigation quota
- (2)
- Redistribution of farmers’ income based on Shapely Value
3.4. Water Rights Transaction Price
4. Discussion
4.1. Income Analysis Among Farmers
4.2. Analysis on the Price of Water Rights Transaction among Farmers
4.3. Limitation
5. Conclusions
- (1)
- Economically determined irrigation quotas and crop planting patterns can be used to optimize the allocation of water for each crop. If the initial allocation of water rights is inconsistent with the optimal allocation of water, the difference should theoretically be the volume of water to be traded.
- (2)
- The pricing model of water rights transaction proposed in this paper includes cost price and earnings price. The model is not only suitable for water rights transaction between farmers in water-deficient areas, but also suitable for water rights transaction between different industries in water-deficient areas.
- (3)
- The total revenue distribution based on the Shapley value method makes the revenue distribution under each alliance fairer and more reasonable, and the water rights pricing should also be acceptable to farmers, as undertaking a transaction will improve their income.
- (4)
- A reasonable price can encourage transactions, thereby improving the efficiency of the water rights market. The consideration of the earnings price makes the determined price closer to the real value of water resources, and has important theoretical significance for improving the water rights transaction price theory.
- (5)
- This paper mainly focuses on the study of water rights transaction between one buyer and two sellers, providing a basis for future transactions between multiple buyers and multiple sellers.
- (6)
- Because the price of water rights transaction is affected by many factors such as economy, society, and environment, the study of this paper on the price of water rights transaction based on the production function and Game Theory is only a theoretical discussion. In the practical work, it is necessary to determine the final price and tradable water volume of water right transaction based on this theory and considering various factors comprehensively, for example, the bargaining power of both parties to water rights transactions, supply and demand factors, and crop market prices.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, Y.H.; Luo, P.P.; Zhang, S.; Sun, B. Spatiotemporal Analysis of Hydrological Variations and Their Impacts on Vegetation in Semiarid Areas from Multiple Satellite Data. Remote Sens. 2020, 12, 4177. [Google Scholar] [CrossRef]
- Luo, P.P.; Sun, Y.T.; Wang, S.T.; Wang, S.; Lyu, J.; Zhou, M.; Nagakami, K.; Takara, K.; Nover, D. Historical Assessment and Future Sustainability Challenges of Egyptian Water Resources Management. J. Clean. Prod. 2020, 263, 121154. [Google Scholar] [CrossRef]
- Yoo, J.; Simonit, S.; Connors, J.P.; Maliszewski, P.J.; Kinzig, A.P.; Perrings, C. The Value of Agricultural Water Rights in Agricultural Properties in Thepathof Development. Ecol. Econ. 2013, 91, 57–68. [Google Scholar] [CrossRef]
- Rey, D.; Garrido, A.; Calatrava, J. An Innovative Option Contract for Allocating Water in Inter-Basin Transfers: The Case of the Tagus-Segura Transfer in Spain. Water Resour. Manag. 2016, 30, 1165–1182. [Google Scholar] [CrossRef]
- Blanco, M.; Viladrichgrau, M. The Introduction of a Water Rights Trading Scheme in the Segre Basin and the Contribution of Reused Irrigation Water. Itea Inf. Tec. Econ. Ag. 2014, 110, 374–399. [Google Scholar] [CrossRef]
- Rosegrant, M.W.; Ringler, C.; Zhu, T. Water Markets as an Adaptive Response to Climate Change. Glob. Issues Water Policy 2014, 11, 35–55. [Google Scholar] [CrossRef]
- Lu, Q.E.; Luo, P.P.; Yu, W.Q.; Zhang, S.P.; Wang, G.Y.; Zhu, X.; Gao, F.; Zhou, M.M.; Lv, J.Q.; Ren, B.M. Research Progress of Urban Rainwater Utilization. Water Resour. Prot. 2021, 2, 1–10. (In Chinese) [Google Scholar]
- Luo, P.P.; Mu, D.R.; Xue, H.; Duc-Ngo, T.; Dang-Dinh, K.; Takara, K.; Nover, D.; Schladow, G. Flood Inundation Assessment for the Hanoi Central Area, Vietnam under Historical and Extreme Rainfall Conditions. Sci. Total. Environ. 2018, 8, 12623. [Google Scholar] [CrossRef] [PubMed]
- Cao, X.; Wang, Y.B.; Wu, P.T.; Zhao, X.N.; Wang, J. An Evaluation of the Water Utilization and Grain Production of Irrigated and Rain-Fed Croplands in China. Sci. Total Environ. 2015, 529, 10–20. [Google Scholar] [CrossRef] [PubMed]
- Bekchanov, M.; Bhaduri, A.; Ringler, C. Potential Gains from Water Rights Trading in the Aral Sea Basin. Agric. Water Manag. 2015, 152, 41–56. [Google Scholar] [CrossRef]
- Li, Y.P.; Liu, J.; Huang, G.H. A Hybrid Fuzzy-Stochastic Programming Method for Water Trading within an Agricultural System. Agric. Syst. 2014, 123, 71–83. [Google Scholar] [CrossRef]
- Wang, Y.B.; Liu, D.; Cao, X.C.; Yang, Z.Y.; Song, J.F.; Chen, D.Y.; Sun, S.K. Agricultural Water Rights Trading and Virtual Water Export Compensation Coupling Model: A Case Study of an Irrigation District in China. Agric. Water Manag. 2017, 180, 99–106. [Google Scholar] [CrossRef]
- Shao, D.G.; Wu, Z.; Gu, W.Q.; Chen, S. Water Use Right Trading Model of Irrigation Area Based on Supply-Demand Relation and Production Function. Hydraul. Eng. 2017, 48, 61–69. [Google Scholar] [CrossRef]
- Zhu, T.; Marques, G.F.; Lund, J.R. Hydroeconomic Optimization of Integrated Water Management and Transfers under Stochastic Surface Water Supply. Water Resour. Res. 2015, 51, 3568–3587. [Google Scholar] [CrossRef]
- Yue, G.; Fu, Q.; Zhao, K.; Li, T.X. Research on water Rights Trading Model Based on Interval Programming. J. Northeast Agric. Univ. 2016, 3, 102–108. (In Chinese) [Google Scholar] [CrossRef]
- Li, W. Analysis on the Present Situation, Shortages and Measures of Water Right Trading Price Formation Mechanism. Mod. Econ. Inf. 2020, 10, 156–158. [Google Scholar]
- Deng, X.H.; Xu, Z.M. A Laboratory Study of Auctions for Water Rights Transactions in Inland River Basin: A Case Study of Irrigation Areas of Heihe River Basin. Acta Ecol. Sin. 2012, 2, 1587–1595. (In Chinese) [Google Scholar] [CrossRef][Green Version]
- Tian, G.L.; Gui, S.W.; Wei, D.; Shuai, M.D. A Study on the Influence of Comprehensive Reform of Agricultural Water Price on the Price of Water Rights in the Process of Transaction. Price Theory Pract. 2017, 2, 66–69. (In Chinese) [Google Scholar]
- Michelsen, A.M.; Person, P.; Young, R.A.; Michelse, A.M. Determinants and Trends in Water Right Market Prices. In Water Policy and Management: Solving the Problems, Proceedings of the 21st Annual Conference, Water Resources Planning and Management Division, Denver, CO, USA, 23–26 May 1994; American Society of Civil Engineers: Reston, VA, USA, 1994; pp. 165–168. Available online: Library.wrds.uwyo.edu/wrp/94-32/94-32.pdf (accessed on 18 April 2021).
- Wu, F.P.; Cheng, M.B. Research on the Pricing Method of Secondary Water Rights Trading Market Based on Cooperative Game Perspective. Price Theory Pract. 2018, 5, 43–46. [Google Scholar]
- Liu, G.; Yang, L.; Shi, Y.B.; Fang, Z.; Wang, S. An Empirical Study on the Two-tier Dynamic Game Pricing Mechanism of Water Rights Transaction under Quasi-market Conditions. China Popul. Resour. Environ. 2017, 27, 151–159. [Google Scholar]
- Han, Z.Q.; Zhang, X.H.; Tong, H.J.; Wang, L.P. Application Research of Crop Water Production Function in the Yellow River Basin. Yellow River 1994, 11, 45–49. (In Chinese) [Google Scholar]
- Yin, Y.S.; Meng, L.J. Alliance Game Analysis of “Win-Win” Outcomes in Water Rights Trading. Water Resour. Econ. 2008, 26, 14–15. (In Chinese) [Google Scholar]
- Do, K.H.P. Special Issue on Game Theory and Water Resource. Manag. Water Econ. Policy 2019, 1802005, 1–6. [Google Scholar] [CrossRef]
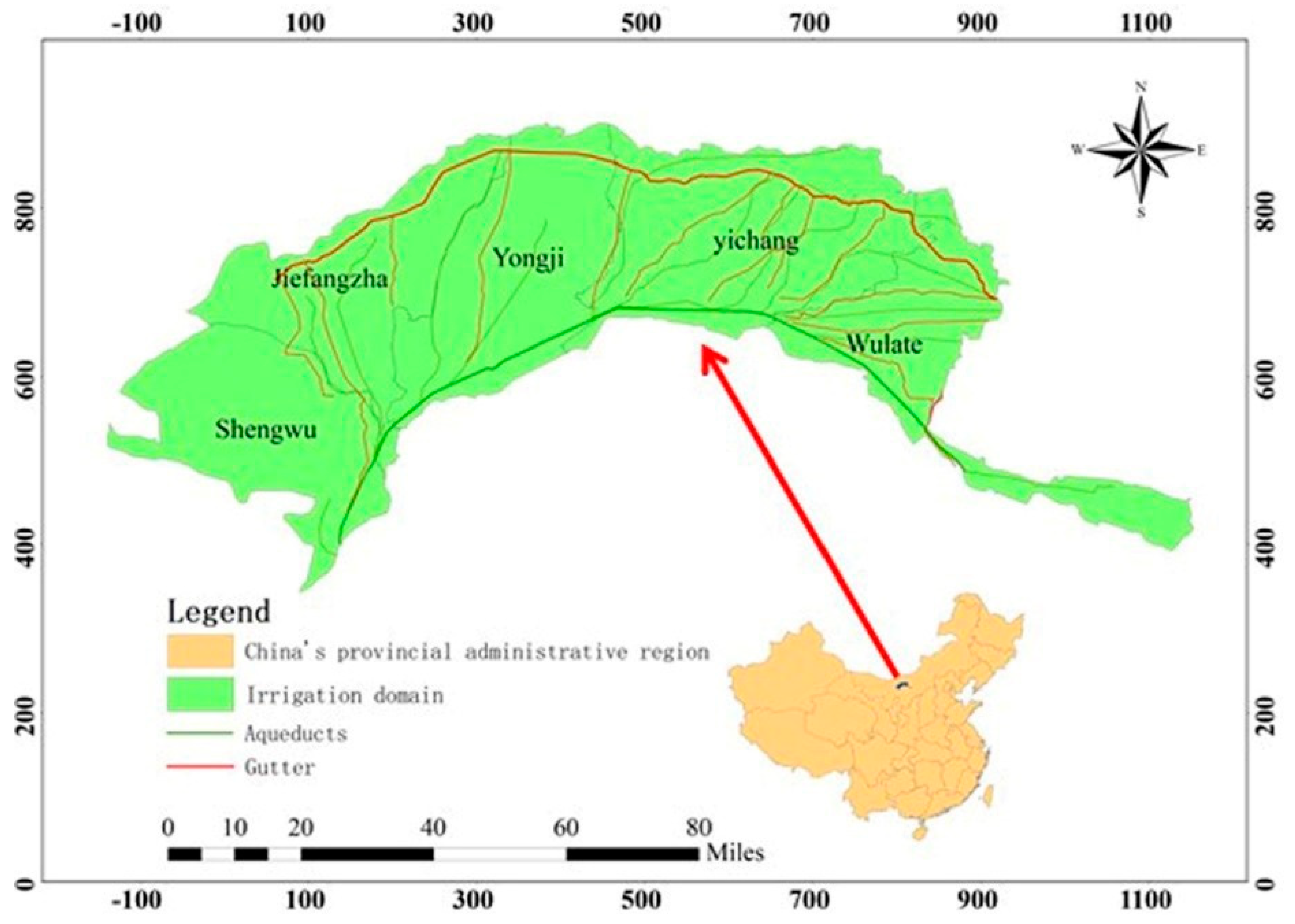
| Farmer | Crop | Total Water (104 m3) | Irrigation Water Use Coefficient | Total Water for Irrigation (104 m3) | Initial Water Rights (104 m3) | Initial Irrigation Quota (m3/hm2) | Crop Price ($/kg) |
|---|---|---|---|---|---|---|---|
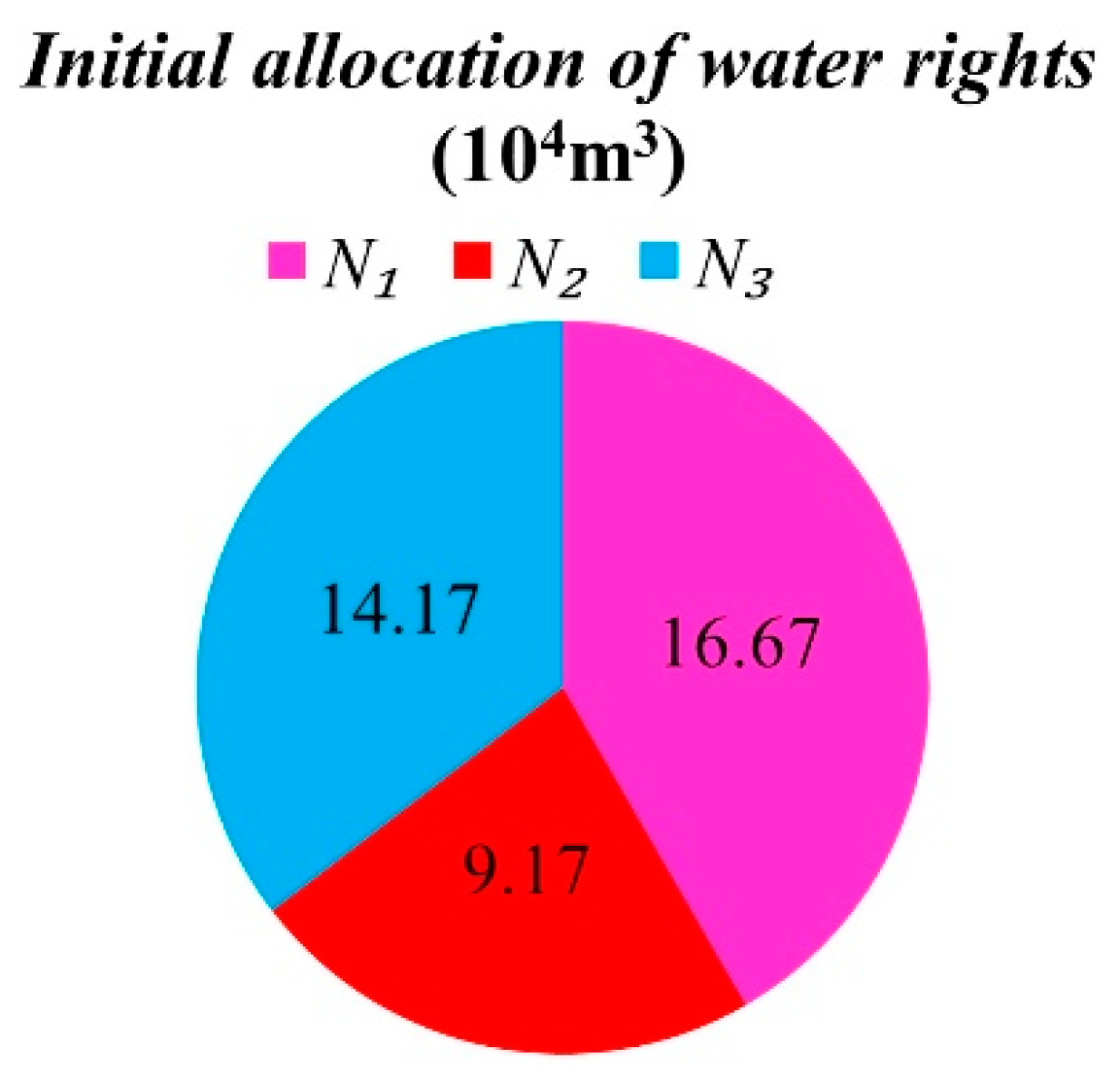
| N1 | Wheat | 57 | 0.7 | 40 | 16.67 9.17 14.17 | 4168 4168 4168 | 0.264 |
| N2 | Maize | 0.300 | |||||
| N3 | Cotton | 2.331 |
| Crop | Constant Term of Water Production Function | ||
|---|---|---|---|
| a | b | c | |
| Wheat | −0.0059474 | 3.9260908 | −197.94 |
| Maize | −0.0077347 | 4.7880120 | −248.42 |
| Cotton | −0.0024283 | 1.9811347 | −334.08 |
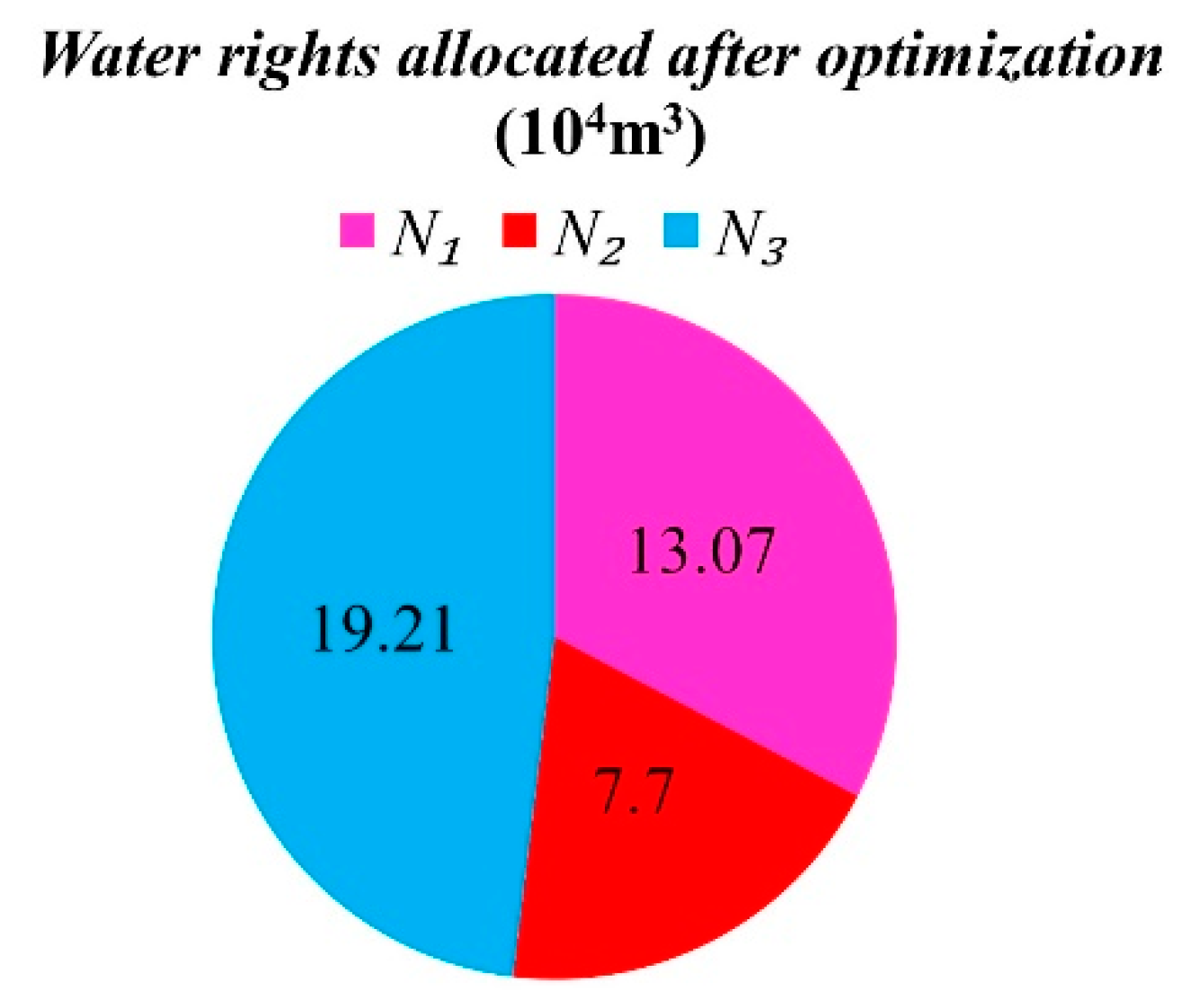
| Farmer | Crop | Initial Irrigation Quota (m3/hm2) | Initial Allocation of Water (Ten Thousand m3) | Optimized Economic Irrigation Quota (m3/hm2) | Water Demand after Optimization (Ten Thousand m3) | Water Savings (Ten Thousand m3) |
|---|---|---|---|---|---|---|
| N1 | wheat | 4168 | 16.67 | 3267 | 13.07 | 3.6 |
| N2 | corn | 4168 | 9.17 | 3502 | 7.7 | +1.47 |
| N3 | cotton | 4168 | 14.17 | 5651 | 19.21 | −5.07 |
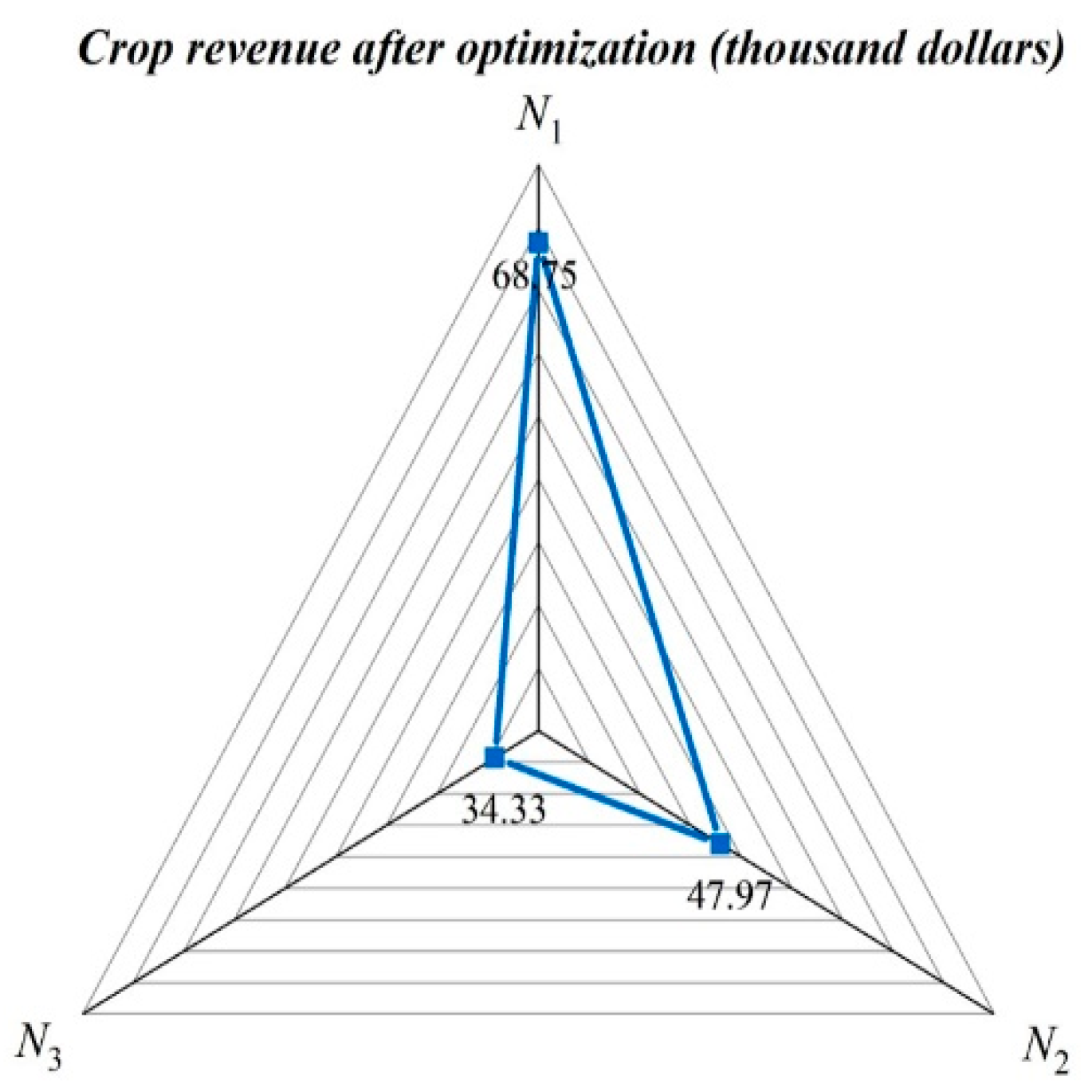
| Farmer | Revenue before Optimization (Thousand Dollars) | Revenue after Optimization (Thousand Dollars) | Revenue Per Unit Area before Optimization (1000 $/hm2) | Revenue Per Unit Area after Optimization (1000 $/hm2) |
|---|---|---|---|---|
| N1 | 68.75 | 59.44 | 1.72 | 1.49 |
| N2 | 47.97 | 44.32 | 2.18 | 2.01 |
| N3 | 34.33 | 80.40 | 1.01 | 2.36 |
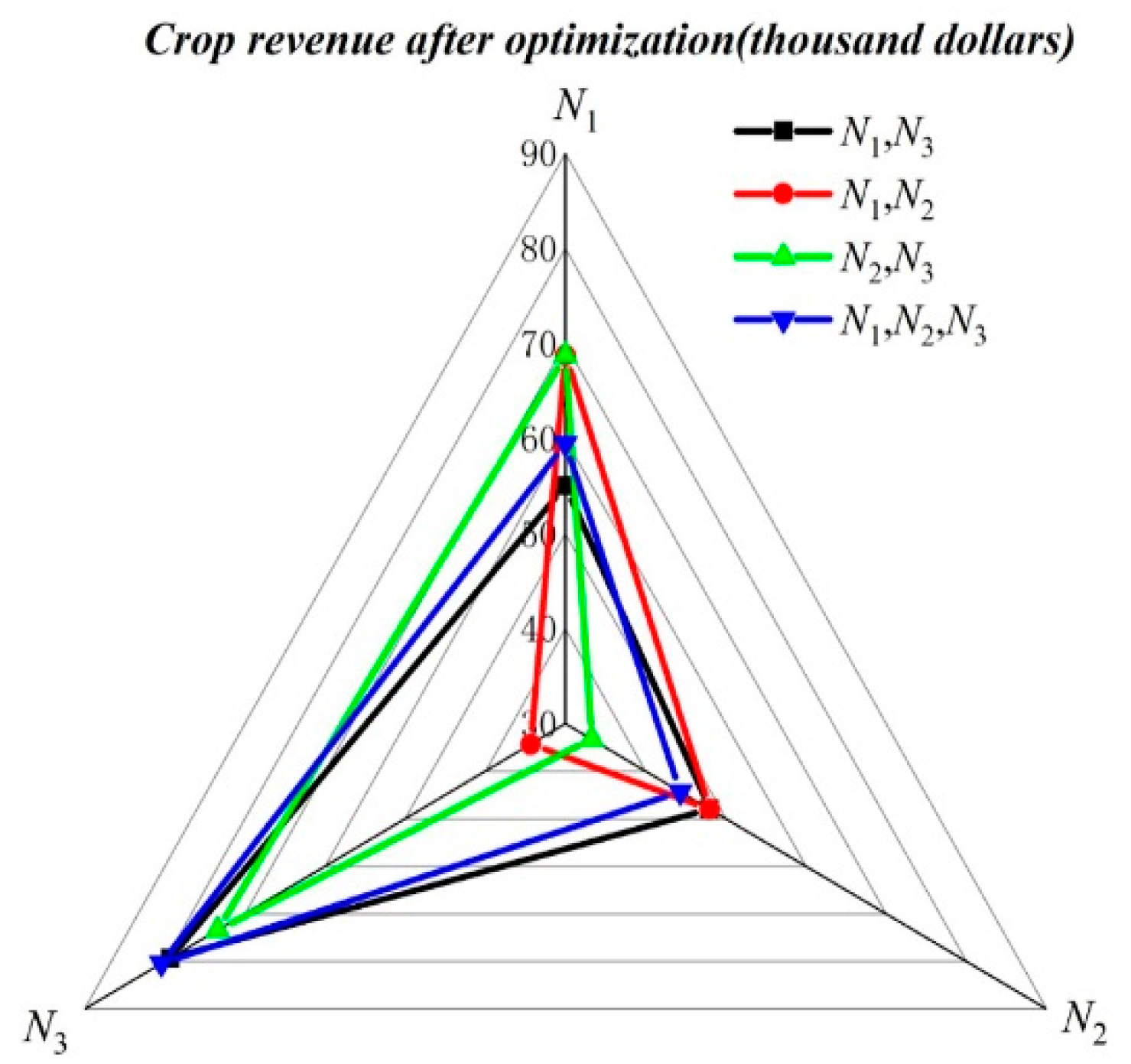
| No. | Alliance Form | Revenue |
|---|---|---|
| 1 | 68.75 | |
| 2 | 47.97 | |
| 3 | 34.33 | |
| 4 | 116.72 | |
| 5 | 134.37 | |
| 6 | 106.64 | |
| 7 | 184.16 |
| S | ||
|---|---|---|
| υ(S) | 68.75 | 134.37 |
| υ(S\{M}) | 0 | 34.33 |
| υ(s) − υ(S\{M}) | 68.75 | 100.04 |
| |S| | 1 | 2 |
| w(|S|) | 1/2 | 1/2 |
| w(|S|)[υ(s) − υ(S\{M})] | 34.37 | 50.02 |
| S | ||||
|---|---|---|---|---|
| υ(S) | 68.75 | 116.72 | 134.37 | 184.16 |
| υ(S\{M}) | 0 | 47.97 | 34.33 | 106.64 |
| υ(s) − υ(S\{M}) | 68.75 | 68.75 | 100.04 | 77.52 |
| |S| | 1 | 2 | 2 | 3 |
| w(|S|) | 1/3 | 1/6 | 1/6 | 1/3 |
| w(|S|)[υ(s) − υ(S\{M})] | 22.92 | 11.46 | 16.67 | 25.84 |
| Strategy | Tradable Water (104 m3) | Revenue under Alliances (Thousand Dollars) | Crop Revenue after Optimization (Thousand Dollars) | Increase Revenue Value (Thousand Dollars) | Pricing of Water Rights Transactions ($/m3) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| N1 | N2 | |||||||||
| A1 | - | - | - | - | - | - | - | - | - | - |
| A2 | 0 | +3.65 | 0 | 60.14 | - | 33.24 | - | +26.9 | - | 0.737 |
| A3 | +4.76 | 0 | 84.40 | 0 | 55.01 | - | +29.39 | 0.617 | - | |
| A4 | +3.60 | +1.47 | 76.89 | 52.63 | 59.44 | 44.32 | +17.45 | +8.31 | 0.485 | 0.565 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guan, X.; Du, Q.; Zhang, W.; Wang, B. Study on the Pricing of Water Rights Transaction between Irrigation Water Users Based on Cooperative Game in China. Water 2021, 13, 1672. https://doi.org/10.3390/w13121672
Guan X, Du Q, Zhang W, Wang B. Study on the Pricing of Water Rights Transaction between Irrigation Water Users Based on Cooperative Game in China. Water. 2021; 13(12):1672. https://doi.org/10.3390/w13121672
Chicago/Turabian StyleGuan, Xinjian, Qiongying Du, Wenge Zhang, and Baoyong Wang. 2021. "Study on the Pricing of Water Rights Transaction between Irrigation Water Users Based on Cooperative Game in China" Water 13, no. 12: 1672. https://doi.org/10.3390/w13121672
APA StyleGuan, X., Du, Q., Zhang, W., & Wang, B. (2021). Study on the Pricing of Water Rights Transaction between Irrigation Water Users Based on Cooperative Game in China. Water, 13(12), 1672. https://doi.org/10.3390/w13121672





