1. Introduction
Smoothed particle hydrodynamics (SPH) is a mesh-free Lagrangian particle method originally designed for continuum scale applications. The method was first introduced in the late seventies independently by [
1,
2] for astrophysical problems in the three-dimensional open space. Initially, the method’s main feature uses statistical techniques to describe the physical variables quantities from a known distribution of fluid elements. In the 1990s, the method was extended to the simulation of free surface flow by [
3]. The method has been improved throughout the years, and now it is attracting more researchers and has been successfully used in many engineering areas [
4,
5]. With the development of the SPH method and its application to a wide range of problems in hydraulics [
6,
7], more attractive features have been demonstrated while some drawbacks have also been identified. Among the advantages listed in [
8], SPH can handle very large deformations of a continuum body given that the connectivity between particles describing the continuum are updated every computational time step. Furthermore, the resolution can be changed with particle position and time.
The SPH method obtains approximate numerical solution of the fluid flow equations using the notion of representing the fluid by unconnected and unrestrained particles carrying fluid properties such as mass, density, pressure, velocity, position, etc. The particle properties can change over time due to the interaction with the other surrounding particles using a smoothing function. In SPH method, the function and its spatial derivatives are approximated by the interaction between particles using the so-called kernel and particle approximation. Kernel approximation is obtained by choosing a kernel smoothing function to define the interaction with the surrounding particles and to determine the extent of the influence area of a particle. The kernel smoothing function introduced and published in literature [
4] is radial symmetric (gaussian, quadratic, spline, etc.); however, the choice of the smoothing function and the smoothing length has a significant importance in accuracy and speed. Most often, the smoothing function is chosen as a compact function because of the good performance [
3,
4,
5]. The particle approximation is the integration over the nearest neighbor particles, such that the properties variables on a particle are approximated by a summation of the values over the particles within the concern particle support domain. The particle position and the magnitude of the individual fluid properties are updated every computational time step. The particle approximation for functions and their derivatives reduces the set of PDEs to ODEs discretized only with respect to time and solved using explicit numerical schemes [
9].
The numerical simulations of different natural phenomena such as flood waves due to dam breaks [
10], river flood waves, and tidal flows are important for flood risk analysis [
4]. These types of simulations have been conducted using solution of shallow water equations (SWEs) on classical grid-based discretization of the computational domain. Recently, SPH has been used to approximate the SWEs with the so-called SPH-SWEs numerical scheme. The SPH-SWEs scheme shows promising results using different formulations [
11,
12]. The Lagrangian formulation of the problem where no mesh generation is needed enables the SPH method to describe the wet-dry interface without any special treatment, making SPH particularly suitable for SWEs.
In the SPH-SWEs solution, special consideration is given to aspects such as closed and open boundary conditions, stabilization terms, source terms, and convergence where poor resolution is present. Different methods have been proposed to simulate the closed boundary condition, with each method having its own advantages and drawbacks [
13]. An open boundary algorithm is proposed by [
14] based on a simplified version of the characteristic method, to simulate both subcritical and supercritical inflow and outflow. In order to avoid numerical oscillation in the presence of shock waves, viscosity is added as a stabilization term to the momentum equation formulation.
A new stabilization term approach based on the idea of Lax–Friedrichs flux is introduced by [
11], with the main advantage of having no parameters. This term is to be calibrated in comparison with the artificial viscosity term, which is based on the necessary level of viscosity. As an alternative way to handle shock waves, Riemann solvers are used. A two-shock Riemann solver for the SPH-SWEs scheme is defined by [
15]. To reduce the overall numerical viscosity error using both the Lax–Friedrichs and the two-shock Riemann solver, the Monotone Upwind-Centred Scheme for Conservation Laws (MUSCL) is used as shown in [
16]. The MUSCL scheme is a non-upwind procedure to reconstruct the viscosity term of the Lax–Friedrichs flux, as well as velocities and water depths in the two-shock Riemann solver. In the momentum equation, the bed gradient source term is addressed in two ways; [
17] describes the bed gradient using an analytical function whereas [
15] introduces an approach to address irregular bathymetries. In this last technique, the bed is discretized into a new set of interpolation points called bottom particles over which an SPH-based interpolation is performed to calculate the bed gradient and tensor. The method uses two different formulations of the momentum equation to deal with the imbalance associated with the bed discontinuity. The first one obtains a fully conservative formulation using the variational formulation of the SWEs while the second one is based on a non-conservative form of the free-surface gradient. The issue of poor resolution when the flow enters an area with very shallow depths is addressed by using a conservative particle splitting procedure, which improves the method convergence [
18]. In this procedure, the resolution is increased by splitting the particle in the region of poor resolution to seven daughter particles given that the mass and the momentum are conserved.
The SPH-SWEs has been validated in literature using different test cases like dam break [
9], Tsunami [
19], Thacker basin, and flow in a parabolic channel. Except for dam break cases, most of the validation cases were restricted to small scale simulations. Research presented herein examined the applicability of the SPH-SWEs in hydraulic engineering using different practical cases varying from simple non-uniform flow water profile and wave propagation to flood inundation cases with complex geometries in practical scales. The simulations were done using the recent SPH-SWEs improvements. This research includes comparison with semi-analytical solutions and results obtained by using several Eulerian modeling approaches. The simulations were conducted using the SWE-SPHysics solver [
20,
21,
22,
23], which incorporates most of the up-to-date improvements. SPHysics is a platform of open source SPH codes to simulate free-surface flows developed by a group of researchers from several universities around the world: the Johns Hopkins University (U.S.A.), the University of Vigo (Spain), the University of Manchester (U.K.), and the University of Rome La Sapienza (Italy). The SWE-SPHysics solver is based on the SPH-SWEs formulations with the option of particle splitting, in which the closed boundary conditions are represented using modified virtual boundary particle method (MVBP), and the open boundary conditions are simulated [
14,
15]. SWE-SPHysics is an open source and freely downloadable code from SPHysics website,
http://www.sphysics.org (accessed on 1 February 2021).
This paper is structured in five parts. After this introduction, the method theoretical formulations are presented followed by the SPH-SWEs models descriptions. Subsequently, the models’ results are analyzed and discussed, and finally, conclusions are drawn.
3. Materials and Methods
In order to test the suitability of the SPH-SWEs approach to solve Saint-Venant equations describing hydraulic problems, a number of theoretical and practical cases were considered: the non-uniform water profiles, wave propagation, and flooding. The first set of test cases are the non-uniform flow water profile (M1 and M2) for which the SPH-SWEs model results were compared with the semi-analytical results using the direct step method. The second set of tests simulate the wave propagation. Results of second tests were analyzed and discussed based on the general understanding of the wave behavior. Finally, two cases of flood inundation over an initially dry bed were conducted, and the results were compared with the results obtained using several Eulerian modeling approaches.
A common setup is adopted for all the SPH-SWEs considered models. The Lax–Friedrichs flux with MUSCL reconstruction is used as a stabilization term. The initial smoothing length is taken to be 1.2 times the initial particles spacing; however, the simulations were marched using variable time step with Courant number equal to 0.4. The inflow and outflow open boundary conditions were chosen as discharge hydrographs. In SWE-SPHysics, particles can only have properties in terms of velocities and water depths; therefore, Manning formula was used to transform the discharge hydrographs into velocities and water depths.
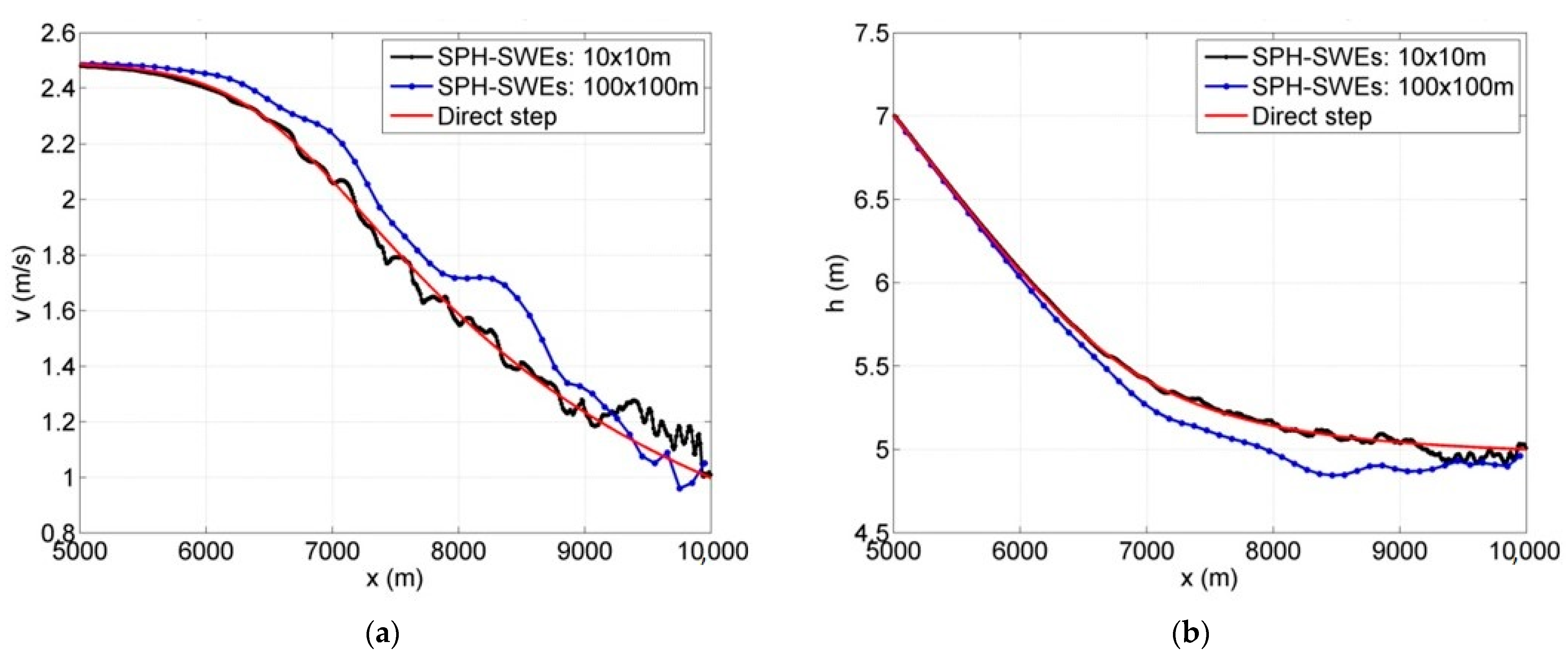
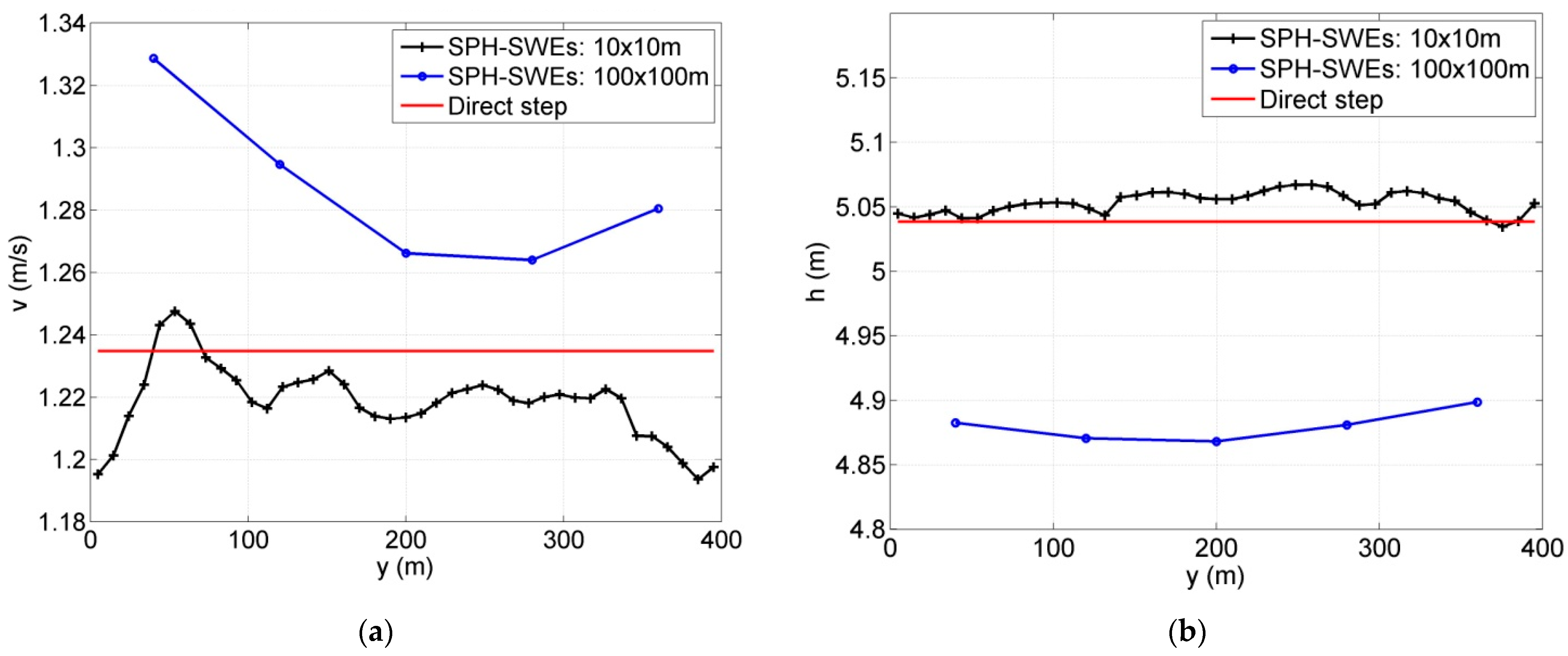
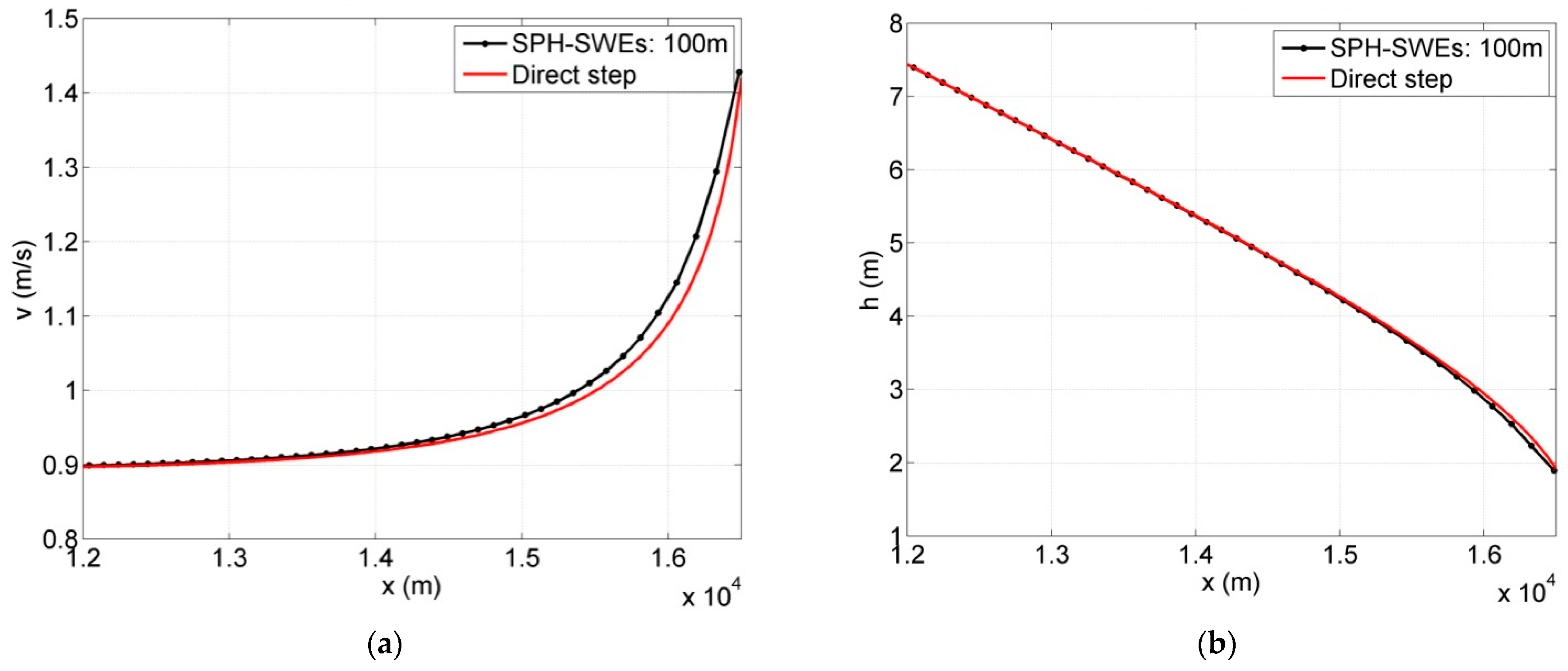
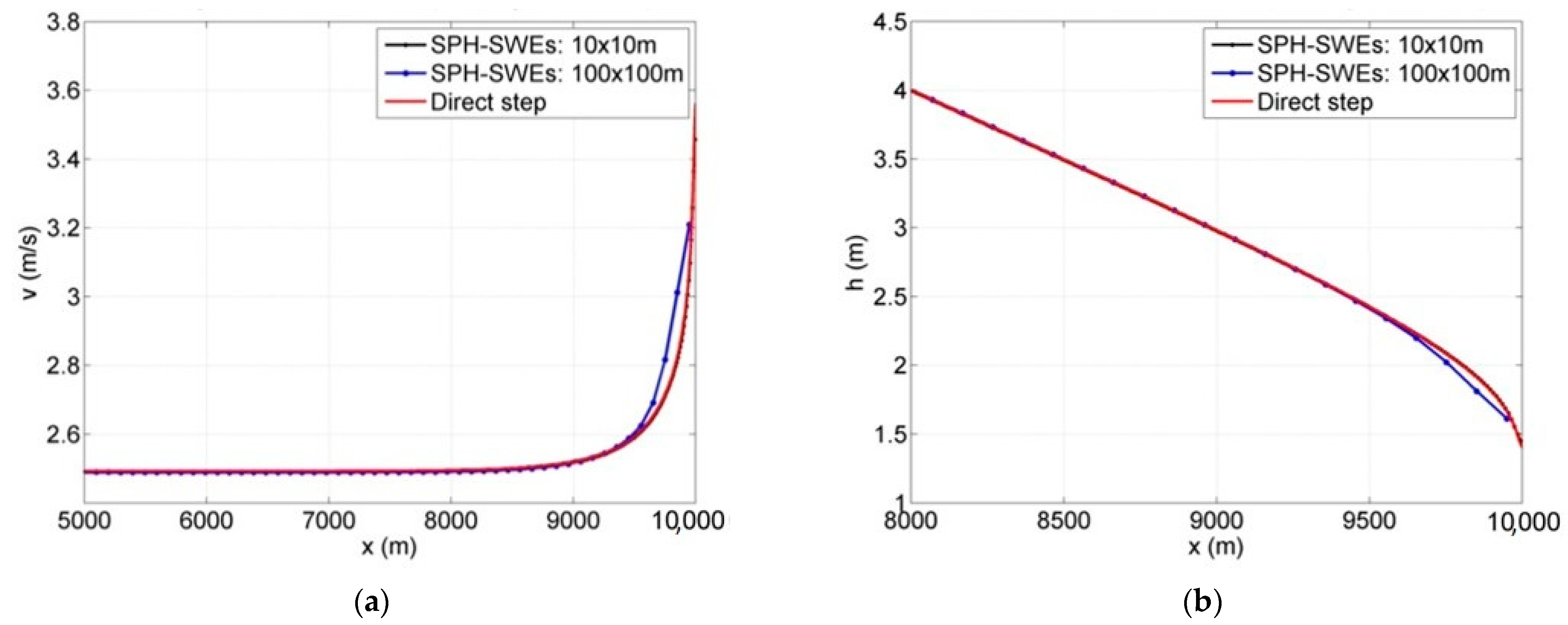
3.1. Non-Uniform Steady State Profiles
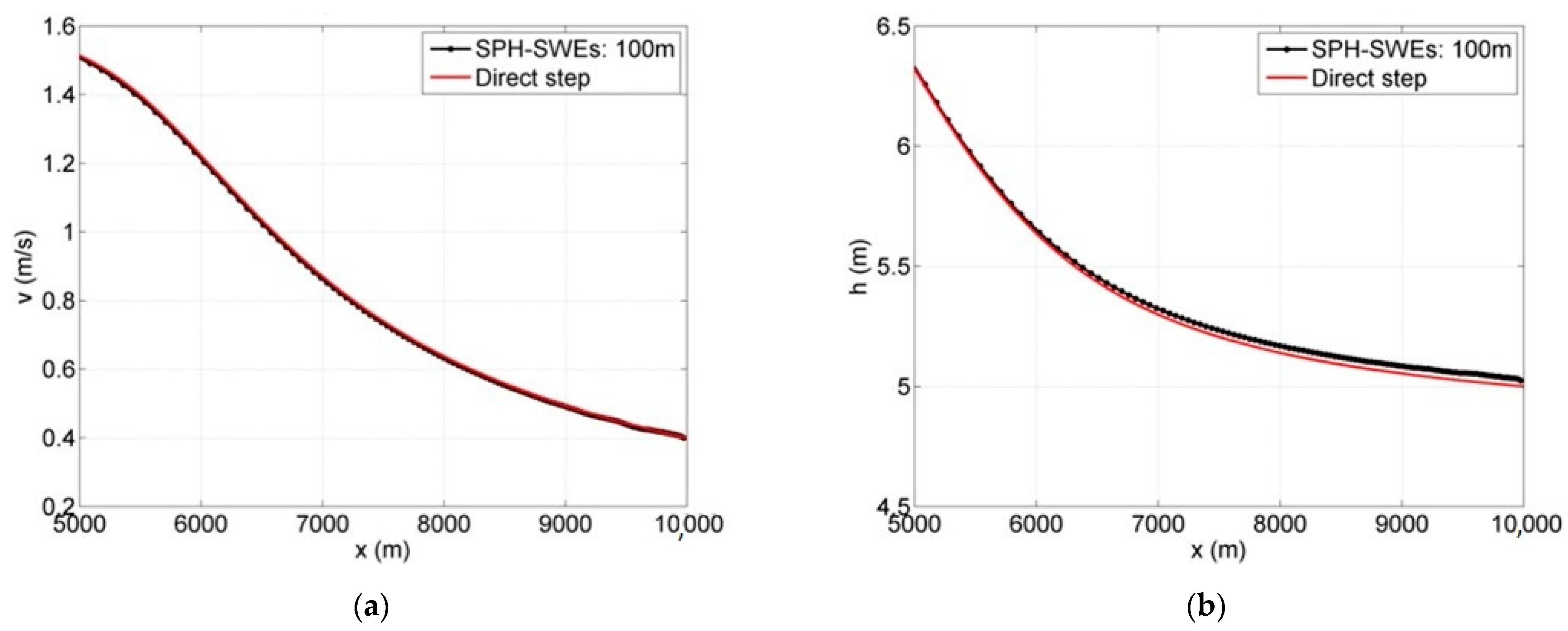
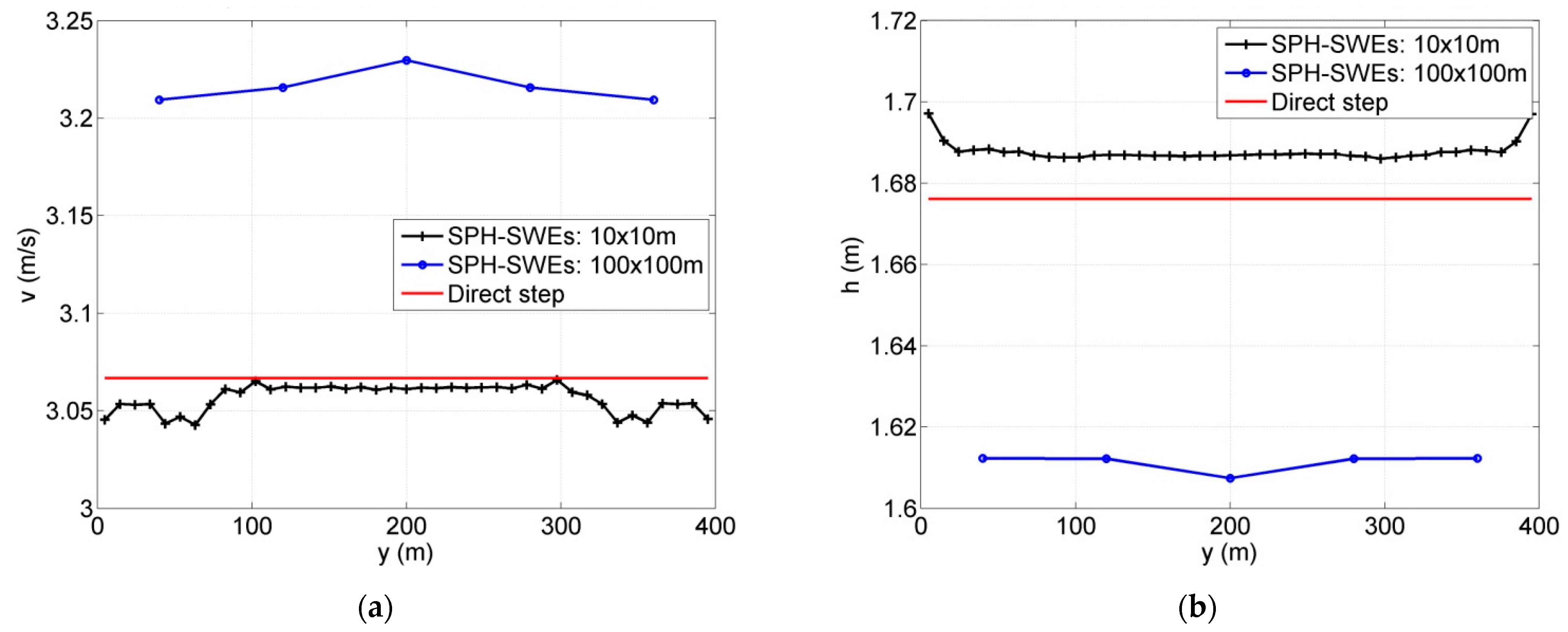
Two simple shallow water cases, water surface profiles M1 and M2, for mild slope channels are represented and solved using SPH-SWEs formulation. The results obtained were compared with the ones obtained by applying the semi-analytical direct step method. In order to evaluate the effect of wall boundary in a 2D simulation domain, both 1D and 2D simulations were conducted. Details of the considered models in terms of channel physical properties (length, width, slope, roughness), boundary conditions, and numerical parameters (number of particles and their spacing) are summarized in
Table 1. The models are run until the simulation reaches the steady state. The maximum non-dimensional errors were calculated using Equations (10)–(12).
where the superscript
sa is for the result obtained with the semi-analytically solution using the direct step method, and
and
are velocities in
x and
y directions, respectively.
3.2. Wave Propagation
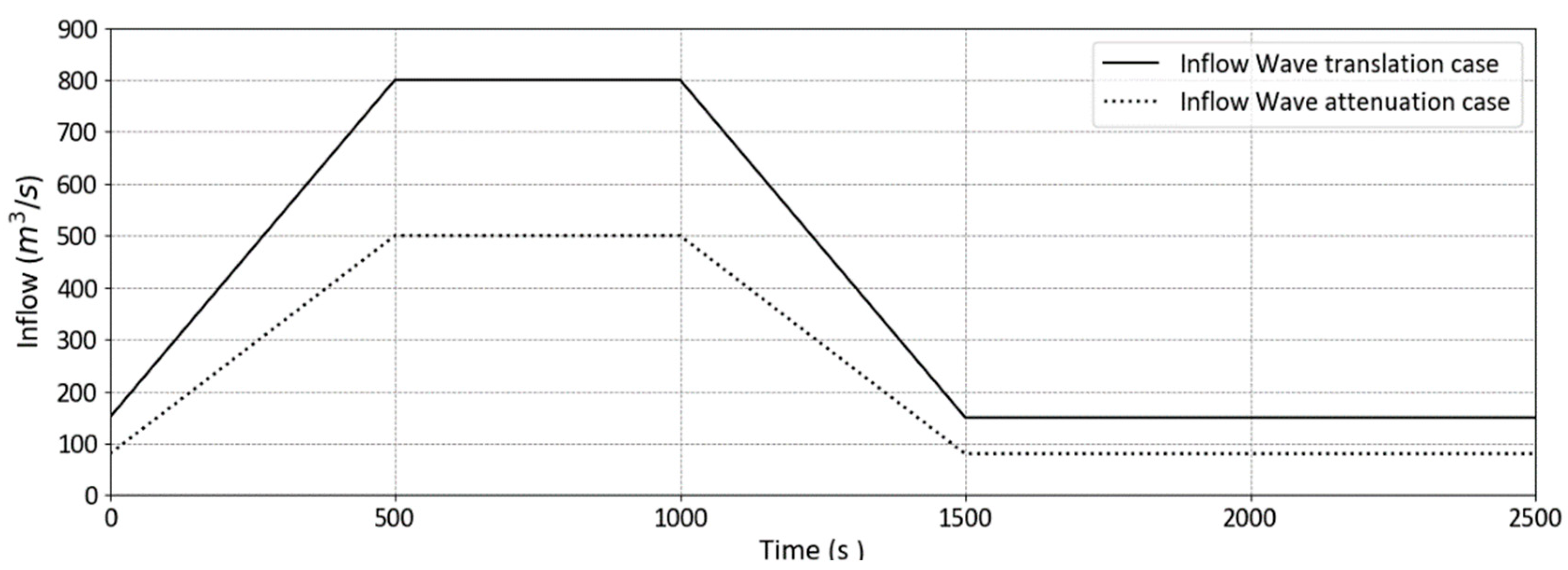
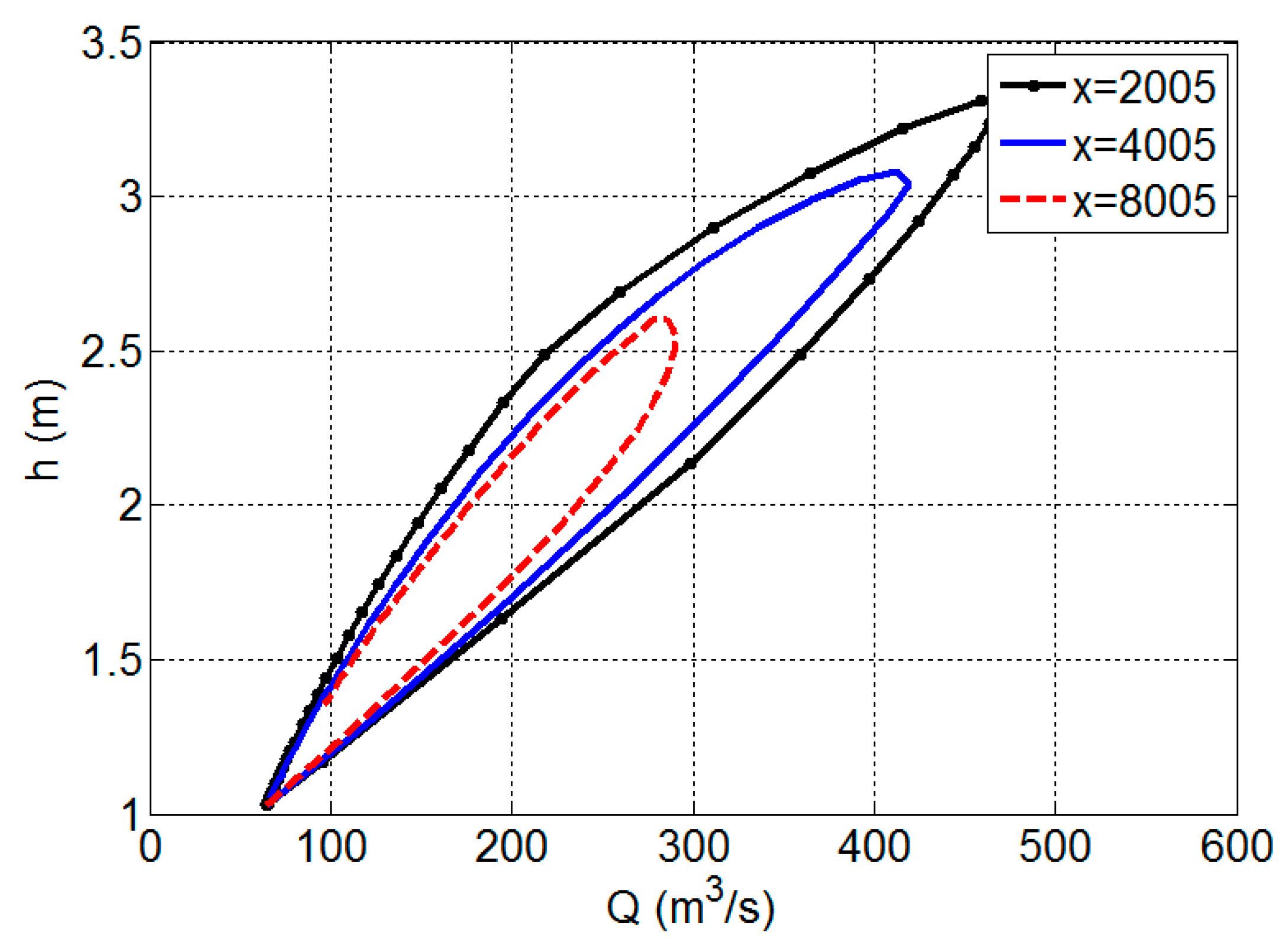
Wave propagation behavior was studied by simulating its behavior in a straight channel. The main objective is to assess the method’s ability to represent the attenuation and translation of the wave.
3.2.1. Wave Attenuation
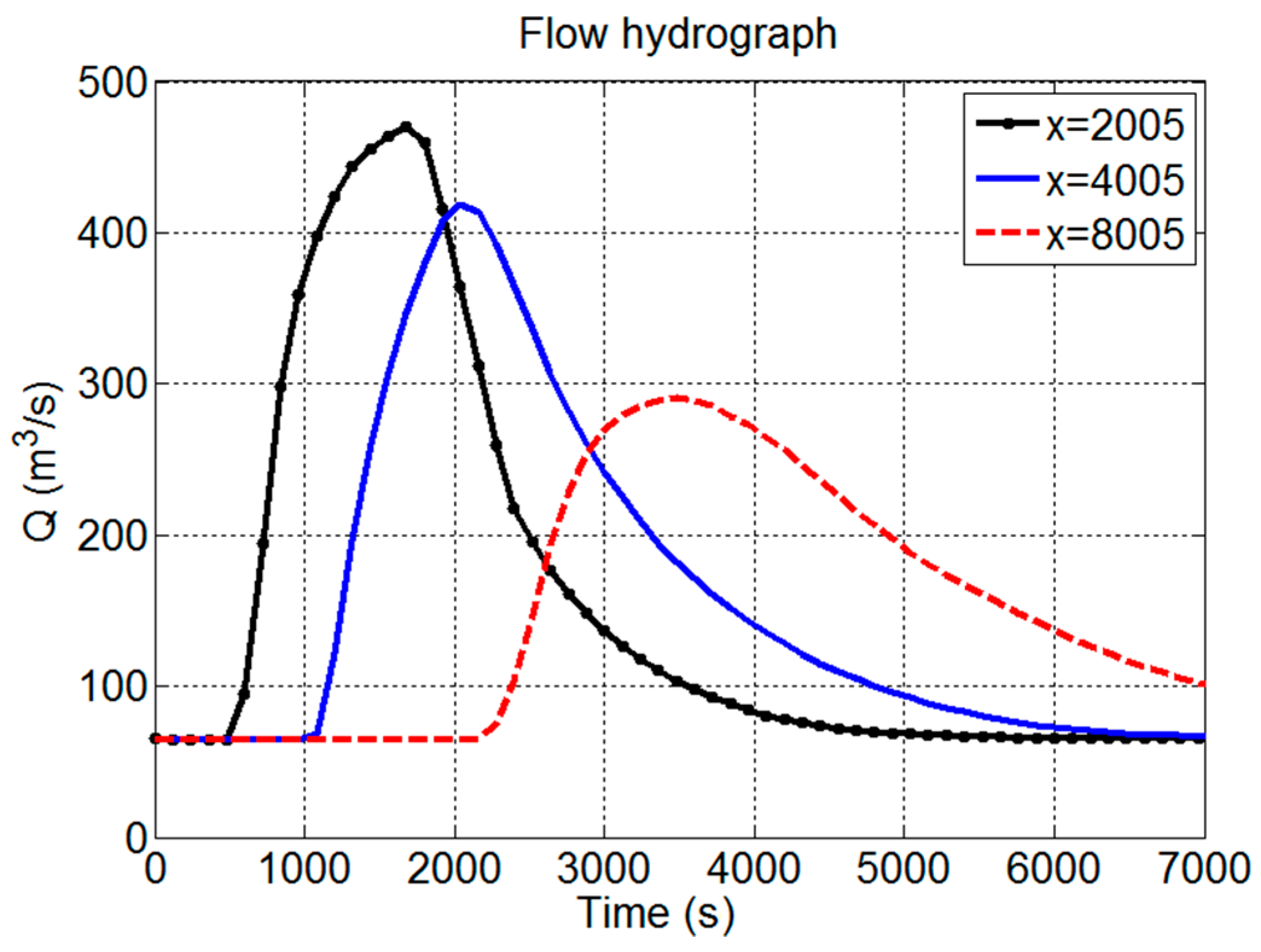
Wave attenuation takes place when the channel has the capacity to reduce the peak of the wave, as it is translated towards downstream. This is checked in the downstream part of a river, in regions with flat topography. Such a wave is referred to as diffusive wave. To simulate wave attenuation, the considered model consists of a channel with a relatively small slope of 0.001. The channel has a rectangular cross-section of 60 m width with a uniform Manning coefficient of 0.03. An initial discharge of 80 m
3/s is applied, and the upstream boundary condition represents an inflow flood hydrograph with a flood peak of 500 m
3/s over 2000 s as shown in
Figure 1. A constant outflow discharge of 80 m
3/s was set as the downstream boundary condition.
3.2.2. Wave Translation
The considered wave translation was the one of kinematic wave when the flood hydrograph travels downstream with its shape unchanged. This phenomenon occurs when the gravitational force is the dominant one as compared to the frictional force; therefore, the wave propagates downstream with almost no attenuation. This situation is seen during flash floods in a steep channel. The SPH-SWEs test model is set-up as a rectangular cross-sectional channel with 60 m width and a steep slope of 0.01. The friction parameter uses a uniform Manning coefficient 0.02. The initial discharge is 150 m
3/s, and the inflow hydrograph is applied upstream with 800 m
3/s peak discharge over a time base of 1500 s (
Figure 1). A constant outflow discharge of 150 m
3/s was set as the downstream boundary condition.
Detailed model set-up for the wave propagation tests is given in
Table 2.
3.3. Flooding
In 2009, UK Environment Agency (EA) carried out a benchmarking study of several 2D hydraulic modeling packages [
18]. Selected studies cover flooding cases with detailed discussion and models’ evaluations and provides an insight of the latest 2D hydraulic modeling tools capabilities. An updated report was published in 2013 [
24], and the data are available to use for comparison. Same benchmarking tests were used by [
23,
24,
25,
26] to investigate the capability of XBeach software. These cases offer an opportunity to weigh SPH method against the other grid-based methods implemented in the hydraulic modeling packages used in the EA report. Two test cases of the EA report were chosen for the simulation of floods using SPH-SWA: momentum conservation over a hump and filling of floodplain depressions. The comparisons were carried out using InfoWorks RS 2D, Flood Modeller 2D component, and XBeach software. The InfoWorks RS 2D algorithm is based on solving the shallow water equations using finite volume scheme while Flood Modeller 2D and XBeach use different finite difference schemes.
3.3.1. Momentum Conservation over a Hump
The main objective of this test case is to examine SPH-SWEs capability to conserve momentum over a hump. It also shows the method’s ability to simulate advancing of a wave front over an initially dry bed and to handle disconnected water bodies simulation. Momentum conservation is an essential property in the case of sewer or pluvial flooding in urban floodplain areas.
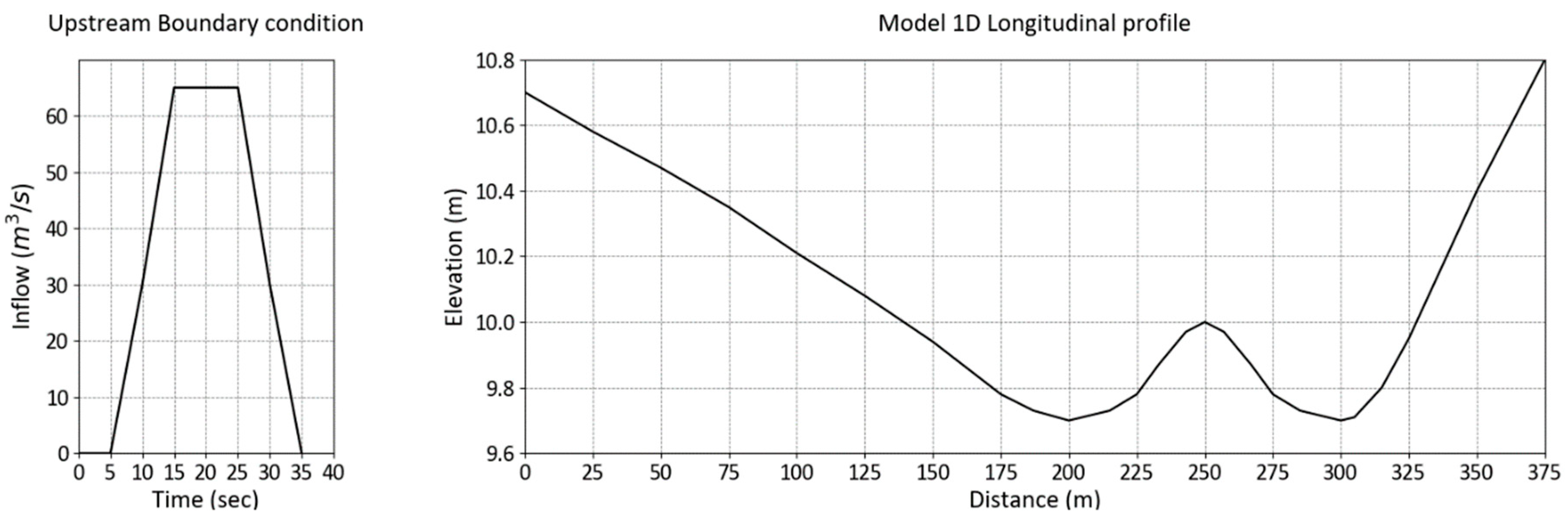
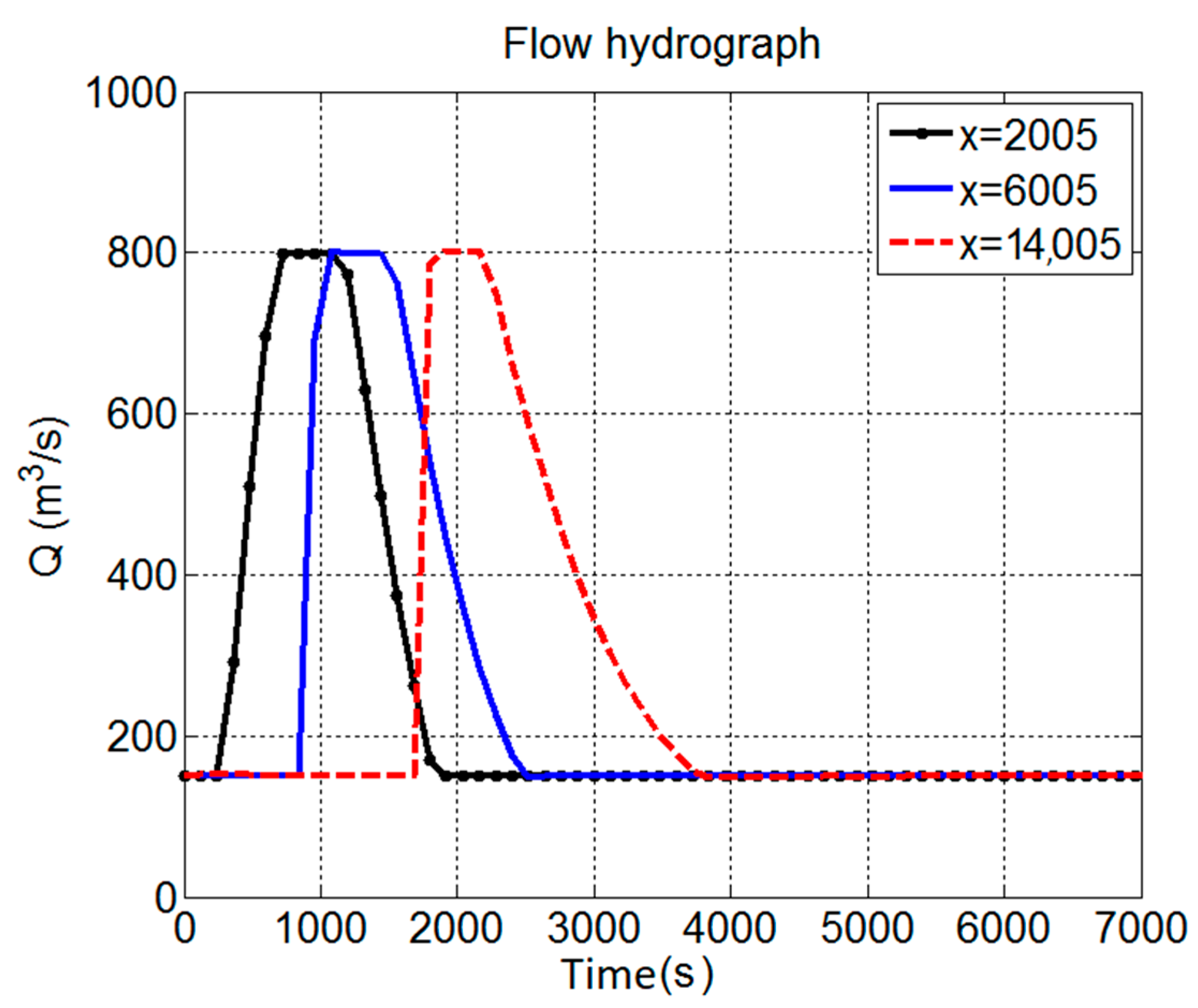
As described in [
24], the test topography consists of two depressions separated by a hump, with a longitudinal profile as shown in
Figure 2. The domain is initially fully dry where a varying inflow hydrograph is applied at the left boundary. The inflow hydrograph has a peak flow of 65.5 m
3/s and a time base of 30 s (
Figure 2). The flow travels downhill with a steep slope of 1:200. The total volume of the inflow hydrograph is just sufficient to fill in the left depression, and some of the volume is expected to overtop the hump as a result of the flow inertia. The total simulation time is 15 min to allow the water to settle. The channel friction is represented by a uniform Manning coefficient value of 0.01.
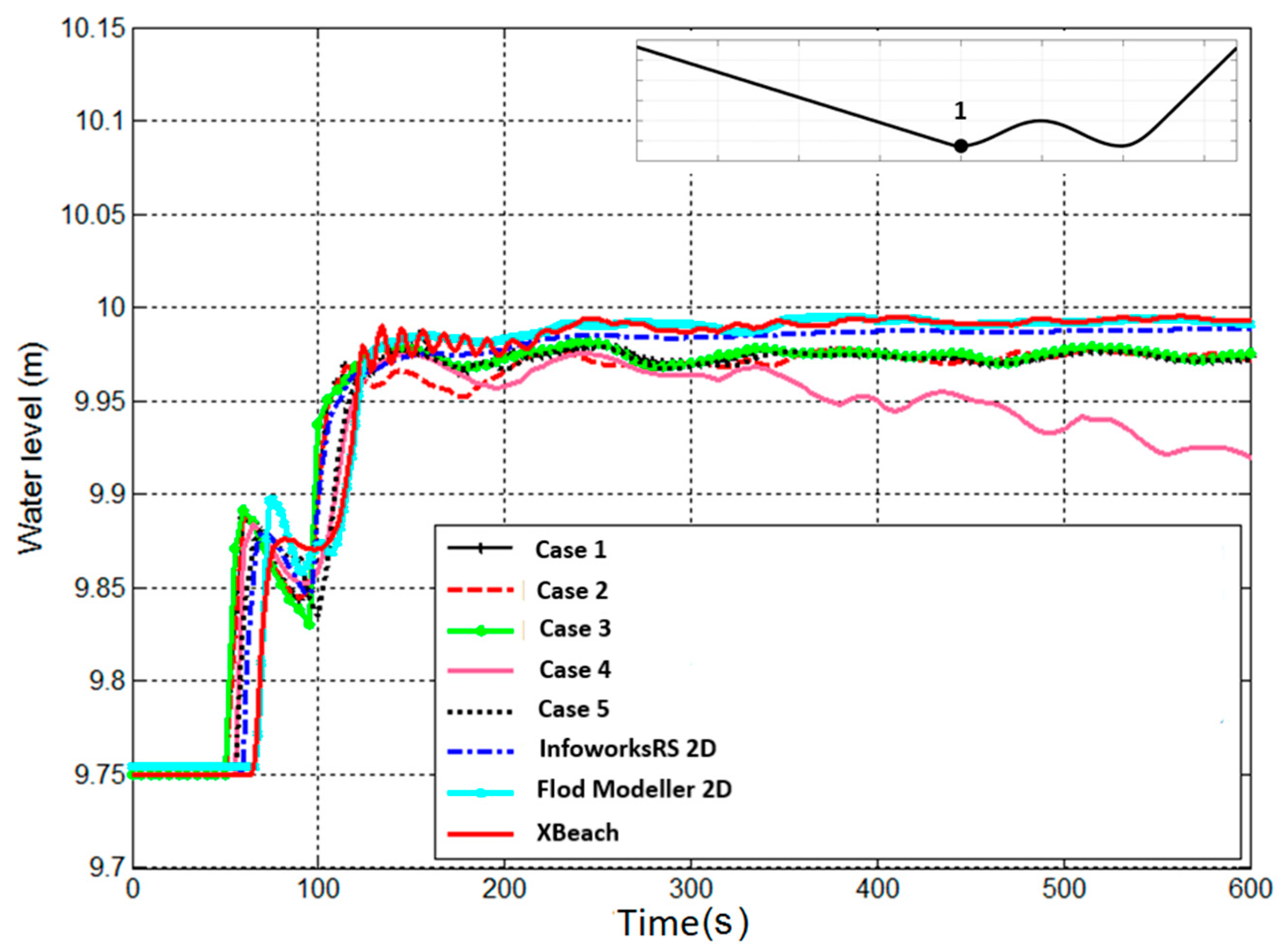
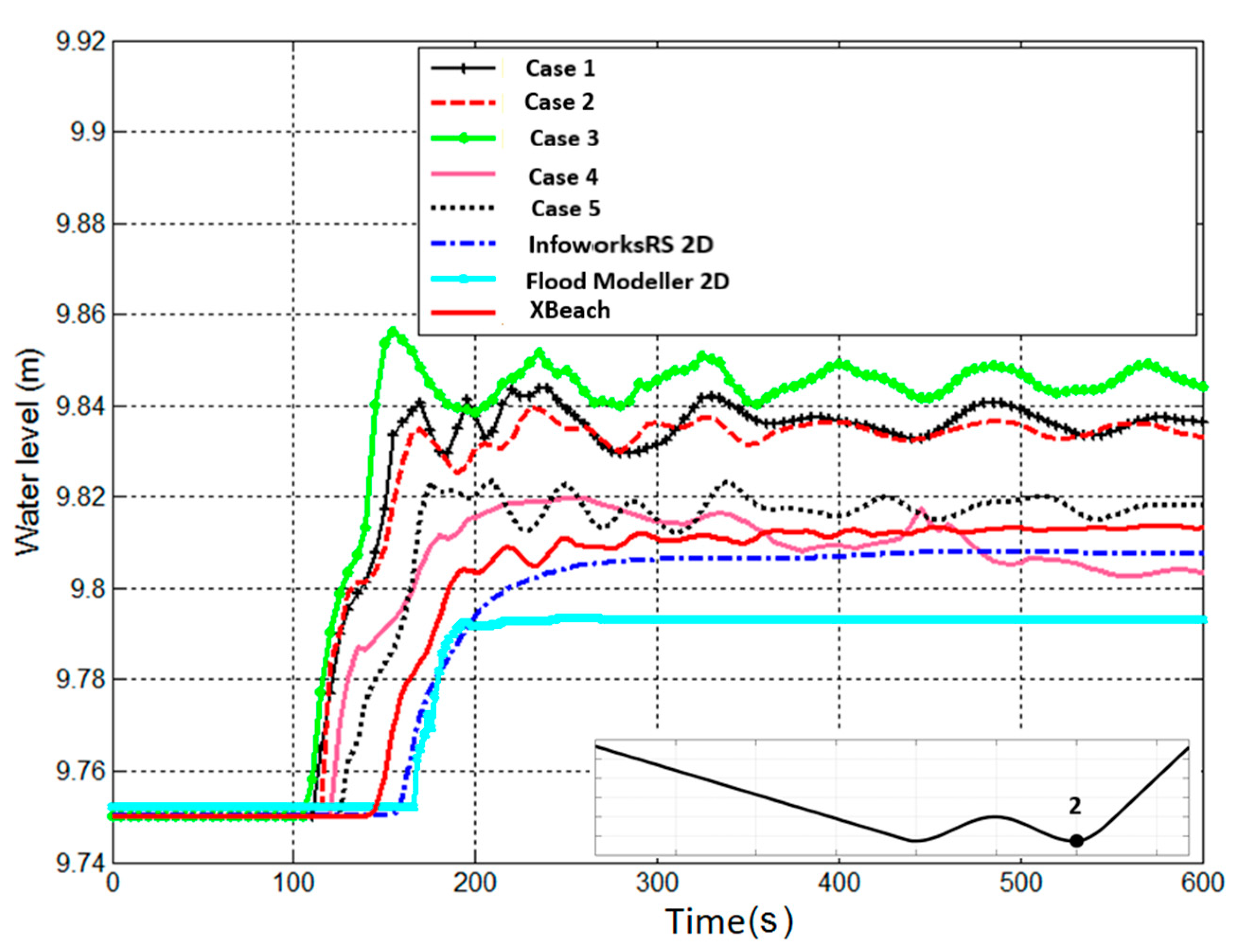
Five cases were simulated with different values of minimum friction depth, inflow velocity, water depth, and particle spacing as presented in
Table 3. Particle splitting procedure was applied in Case 4. The domain was initially empty, and therefore, starting to split the particle as it enters the domain causes some of the daughter particles to be located outside. Thus, the splitting process was set to take place at enough distance from the boundary; however, this resulted in having the particle travel without split until it reaches the splitting region.
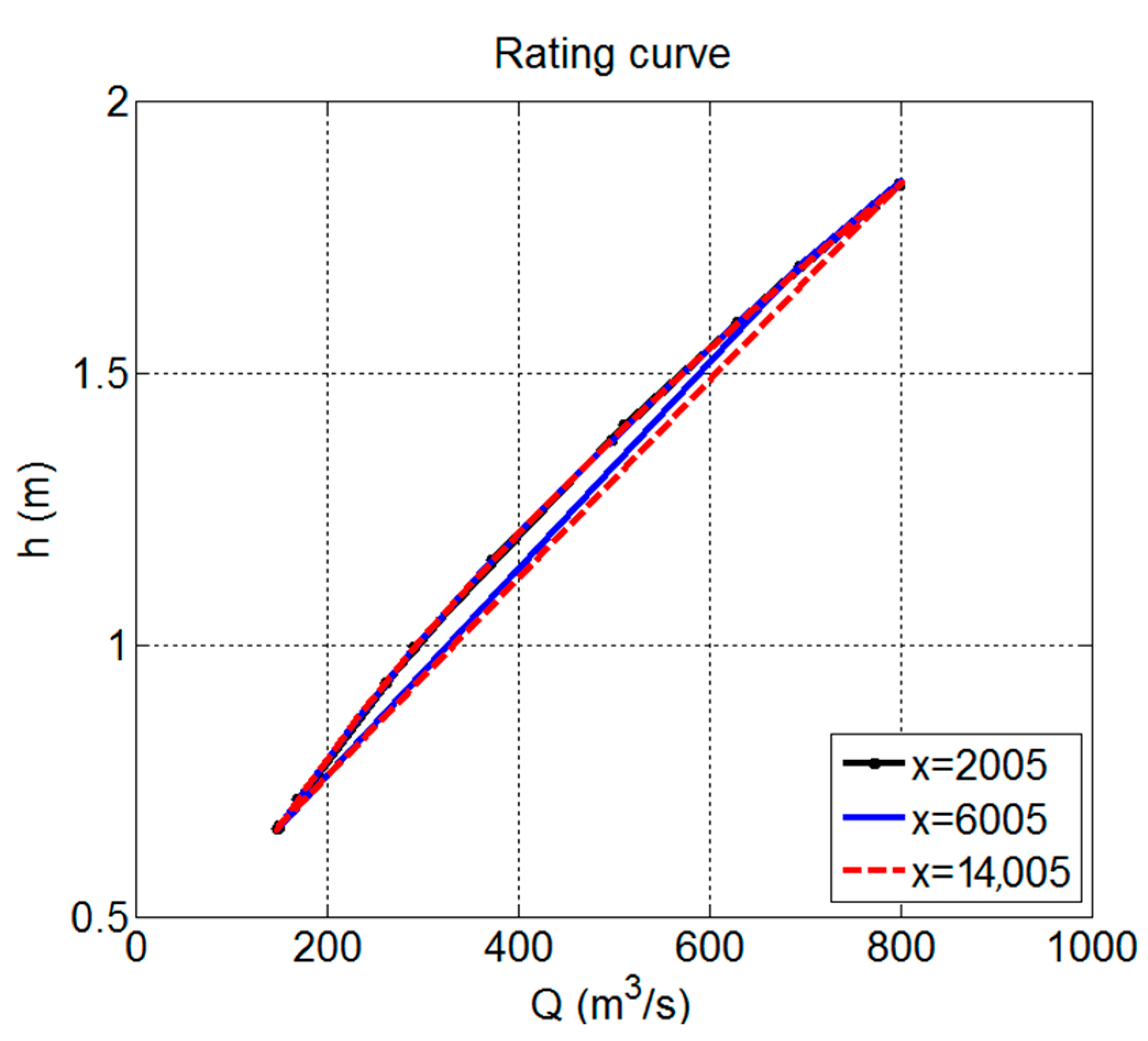
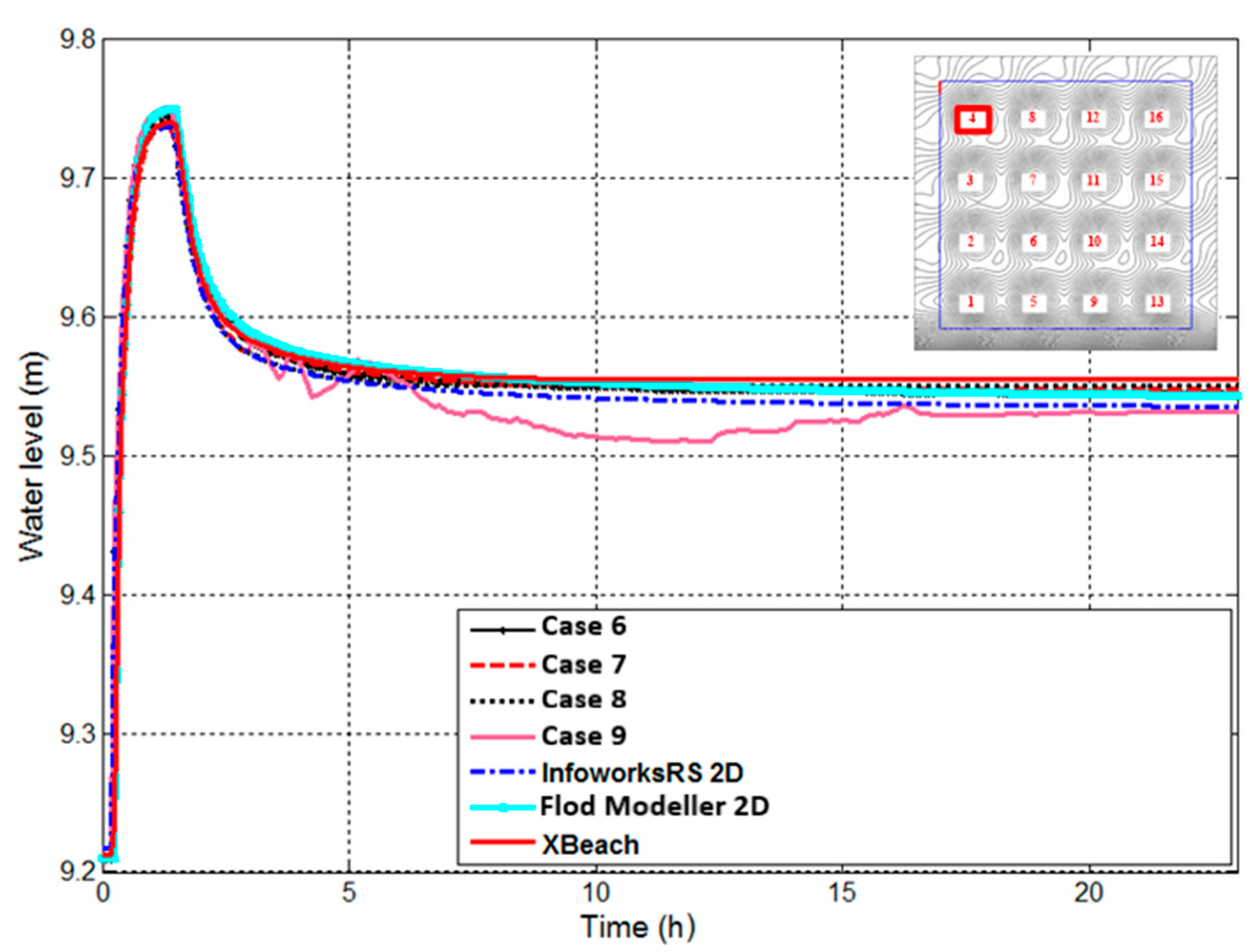
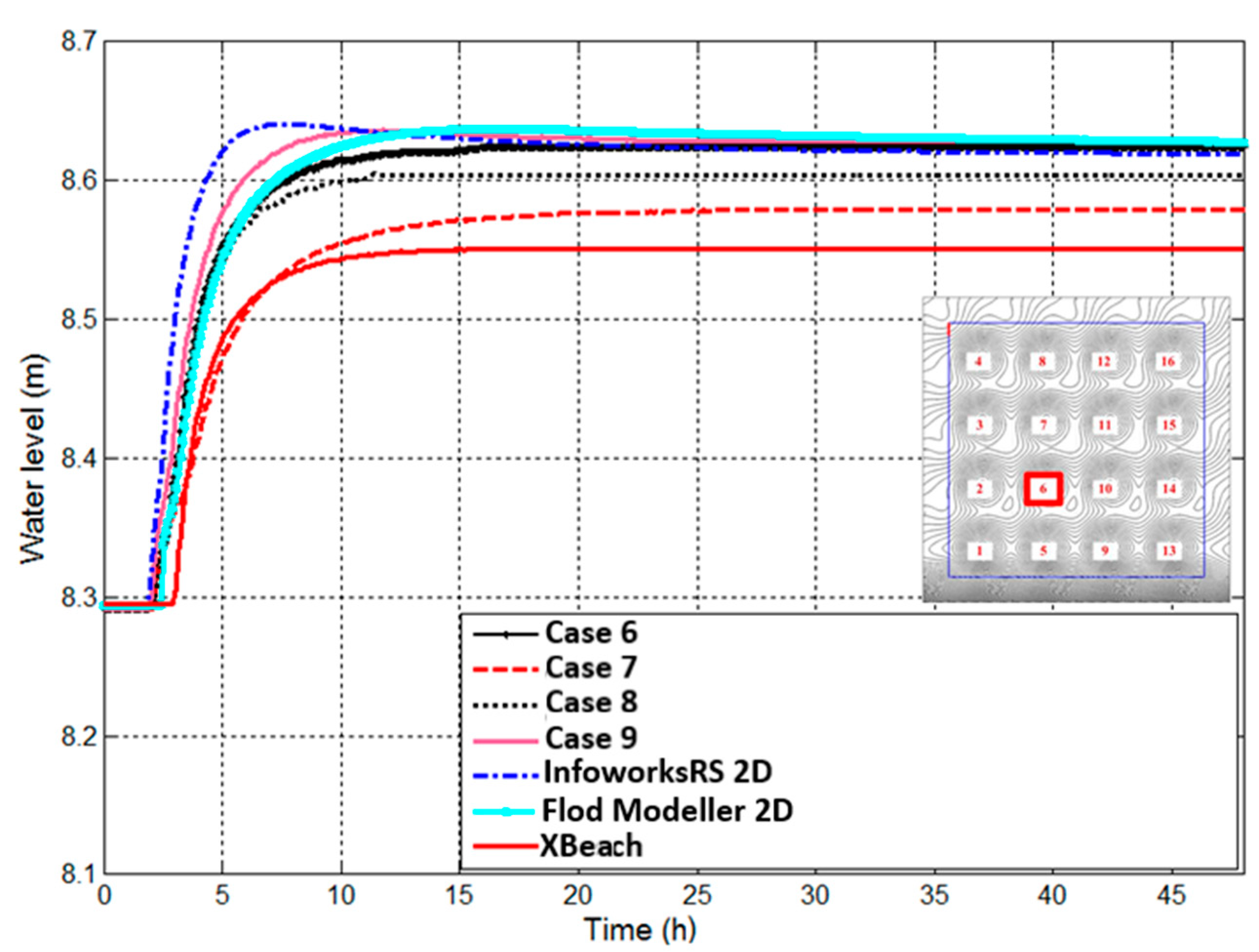
3.3.2. Filling of Floodplain Depressions
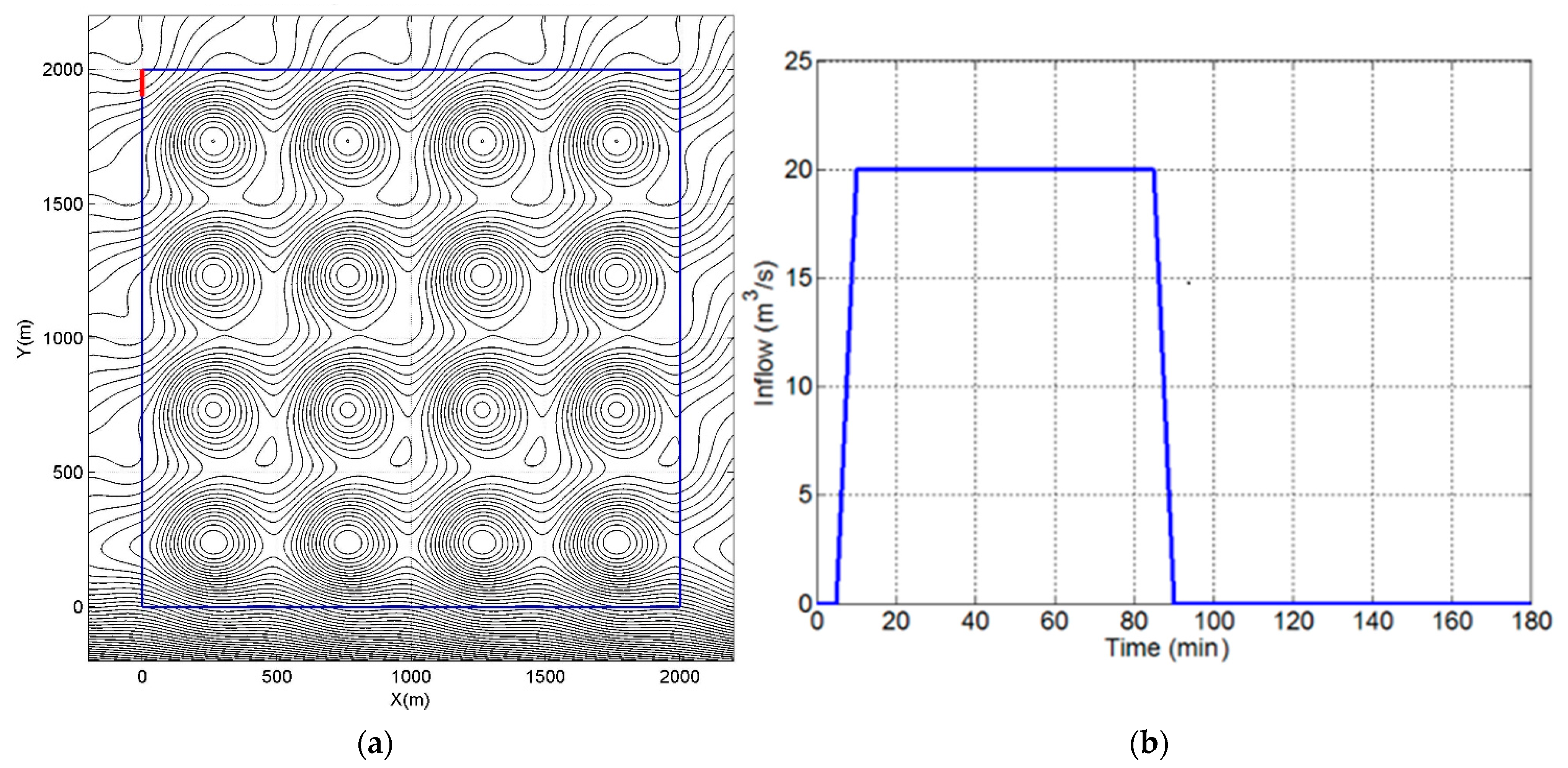
This test investigates the method capability to determine the final inundation extent and the water depth of low momentum flood over a complex geometry. It also assesses the ability to handle wetting and drying of a floodplain and to simulate disconnected water bodies. The test domain is a square area of 2000 × 2000 m
2 floodplain with 16 flattened egg-shape depressions of 0.5 m deep. The general slope of 1:1500 is applied from the north to south direction and the one of 1:3000 from the west to east direction, with a 2 m drop in elevation between the top left corner to the bottom right corner. The Digital elevation model (DEM) of this area is shown in
Figure 3a. The Manning coefficient for bed friction is 0.03.
The inflow boundary is applied along a 100 m line running south from the north-western corner of the test domain. The hydrograph applied on this boundary has a peak flow of 20 m
3/s and a time base of 85 min, as shown in
Figure 3b. Except for the inflow boundary, all other boundaries are closed boundaries. The total simulation time is 48 h, set to reach an inundation state over the whole domain. The water level in the middle center point of each depression is observed together with the final inundation extent.
Four cases were carried out to investigate the effect of having different inflow momentum and smaller resolution, as detailed in
Table 4.
Total inflow volume of the inflow hydrograph in
Figure 3 is 97,200 m
3 for the time base of 85 min.
5. Conclusions
The SPH approximation of the shallow water equations, SPH-SWEs, proved to have good results for river flow simulations. There are two different aspects to address in concluding remarks: limitation of the method to solve the posed problem and the limitations due to implementation.
Obtained results for the cases of water profiles in non-uniform flow and wave propagation are good, with a convergence to semi-analytical solution of approximate 1.4 × 10−3. These subcritical and supercritical flows were handled easily with no restrictions regarding bed complexity and steepness, which shows that the method can be used to solve such hydraulic problems. The momentum conservation property was verified, and the results were compared to other grid-based software results with an agreement of up to 0.5%. The overflow cases associated with low-momentum flow required high particle resolution to achieve better results.
Apart from the abovementioned advantages in using the SPH method of solution, some drawbacks are recognized, including the ones due to the implementation of the code. The existing approaches for closed boundary simulations cause some oscillatory behavior and decrease the method accuracy order. The closed boundary development needs to be extended to include an option for permeable close boundary for further coupling with sub-surface flow models. In terms of implementation, the open boundary simulation requires to associate velocities and water depth values to the open boundary particles. This requires the correct calculations of the velocities and water depths from the discharge hydrographs particularly when the open boundary is close to the area of interest. The effect of this is a loss in the inflow water volume especially when using coarse open boundary particle resolution.
The method requires a good definition of the friction term, which is very important, particularly in the region of very shallow water as it might overcome the gravitational force and causes particle to move opposite to the flow direction. This problem was noticed in cases with wave front advancing in an initially dry bed. Therefore, the determination of the minimum depth for friction is important for calculating the momentum for wave front particles. Furthermore, regarding the implementation, the distribution pattern used in the particle splitting procedure cannot be applied for particles close to the boundary as some of the daughter particles will be located outside of the domain. An adaptive particle splitting procedure that takes into consideration the particle locations when defining the daughter particles’ distribution pattern is welcomed.
The implementation of the SPH-SWEs allows for higher time step computation as compared to the SPH formulations for Navier–Stokes equations (SPH-NS), which might lead to less simulation computational time. Coupling of SPH-SWEs with other grid-based method can be done to utilize SPH-SWEs to solve the issue of wet-dry interfaces.
Finally, this research shows the SPH-SWEs method capabilities of handling hydraulic simulations while it opens up the possibility for the method to be used for both fluvial and coastal areas. SWE-SPHysics, as an open source code, gives an insight of how the method does work and provides a platform for researchers and users to further improve the method and add more functionalities to it.