1. Introduction
Removing excess surface water on the roadway (waterlogging) and restoring the natural drainage network are major challenges in the storm drainage design of roads and transportation facilities. Rain and road waterlogging can cause hazardous situations due to the reduction of both driving visibility and friction coefficients between vehicle wheels and the roadway [
1,
2,
3]. For this reason, most government administrations responsible for the design and management of roads and highways publish recommendations or design guidelines to provide safe passage of vehicles during such events (M.O.P.U. [
4] in Spain, Brown et al. [
5] in the USA, Dept. of Energy and Water Supply [
6] in Queensland, Australia, etc.).
The aforementioned guidelines for removing waterlogging on roads in different countries are fundamentally based on directing water from the roadway to lateral gutters. The design criteria of the gutters are generally based on limiting the spread of the flow using a simple uniform flow equation. Ultimately, the flow in the gutters is incorporated into underground drains by different types of inlets, for which the recommendations provide some basic guidelines regarding their location. These circulars in Spain, the USA, and Queensland present the different types of gutters that can be used, how they should be lined, and where they must be placed according to the slopes of the cuts and embankments of the roadway; all guidelines explicitly indicate that the hydraulic behavior for the design discharge should be checked under a uniform regime. Some requirements for flow conditions are suggested in the regulations. The Spanish guidelines recommend limitations for the average water velocity to avoid damages to the drainage elements (i.e., from 0.2–0.6 m/s in sandy terrains with no vegetation to 4.5–6 m/s for concrete-lined gutters). In Queensland, the recommendation is to limit the product of the water thickness and the average speed, that is, the specific discharge, to 0.6 m2/s. Finally, for highways and roads in the USA, the suggested design spread occupies at least the shoulder of the roadway plus one meter, and half the driving lane is recommended for local streets.
Each country adapts its recommendations to its particularities, which results in noticeable differences in the respective design guidelines. For example, in Spain, a return period of 25 years is considered, while in the USA and Queensland (Australia), depending on the road classification, a 10-year period is typically recommended. Additionally, Queensland provides roadway flow thickness and velocity limitations during minor and major storms for transverse and longitudinal flows. In addition, the Spanish guidelines discuss a particular procedure to divide the roadway into small basins, which allows the flow rate to be defined for each inlet. Thus, the set of inlets located at a low point must be capable of absorbing twice the sum of their own projected flow rate and the flow rate corresponding to thirty percent (30%) of the design discharge of up to three upstream inlets in each of the sloping sections that converge at the low point. On the other hand, the drainage design guidelines in the USA suggest some empirical relations, which allow the determination of the inlet efficiency depending on the inlet type and the road longitudinal slope.
A key aspect for the design of the drainage system is the inlet performance, that is, the ratio of captured discharge with respect to the discharge flowing on the road or street surface. Li et al. [
7] evaluated the efficiency of three common types of inlets used in urban streets in China by solving the two-dimensional shallow water equations (SWE) under different scenarios. Based on experimental results, Gómez and Russo [
8] and Russo et al. [
9] proposed a methodology to estimate the hydraulic efficiency of inlets depending upon the inlet and the road geometry as well as the hydraulics of the approaching flow. Later, the same authors [
8,
9] showed the influence of the hydraulic efficiency of clogging factors on grated inlets in an urban catchment in Barcelona. Similarly, Kim et al. [
10] estimated the flow intercepted by a grate inlet and determined the appropriate grate system design, proposing an equation to obtain the appropriate drainage grate size for different road conditions (longitudinal slope and transverse slope) and design capacity (5–30 years).
Based on the previous references, it is clear that the inlet spacing between road drainage elements is a key issue to minimize or better remove water from the roadway. Various authors have proposed different methodologies in this regard. Wong [
11] proposed a method based on the kinematic wave theory for a continuous grade road, applied to Singapore events; Nicklow and Hellman [
12], using a genetic algorithm, showed a decision-making mechanism for the cost-effective design of stormwater inlets in highway drainage.
The presence of a layer of water between the wheels of vehicles and the roadway can substantially reduce the grip of the wheels and cause the driver to lose control of the vehicle (aquaplaning or hydroplaning). Chesterton et al. [
13] performed an analysis of factors that contribute to hydroplaning, such as the environment, road geometry and pavement materials, pavement drainage, and vehicle, by comparing different methods to evaluate this phenomenon in a case study. In all cases, the proposed solutions always included changes to roadway drainage systems. Later, Burlacu et al. [
14] discussed several solutions to reduce water film thickness on the roadway depending on the vertical alignment slope, width, and roadway surface texture. Again, the discussed technical solutions consisted of improving the roadway drainage system. Finally, some recommendations are stated by national guidelines, such as in the USA [
5], which specifies that hydroplaning can occur at speeds over 89 km/h with a water thickness of 2 mm or less, and in Queensland [
15], which explicitly states that it is not possible to recommend definite design limits for water thickness, but partial hydroplaning may start at thicknesses of about 2.5 mm.
Additionally, some studies and recommendations on permeable pavements have recently appeared in several countries as an alternative or complementary solution to surface drainage [
16,
17,
18].
The present article presents a methodology based on numerical methods for the design of road drainage systems by solving the 2D shallow water equations (using the Iber model [
19]) and the drainage inlet efficiency assessment equations of Gómez and Russo [
8]. Specifically, the scope of this paper is:
To propose tools and criteria to analyze the hydraulic behavior of runoff on road surfaces in the presence of drainage elements.
To establish a methodology to determine the number, location, and performance of grate inlets and ensure appropriate drainage of roads.
To present an application of the proposed methodology in a case study.
2. Methodology
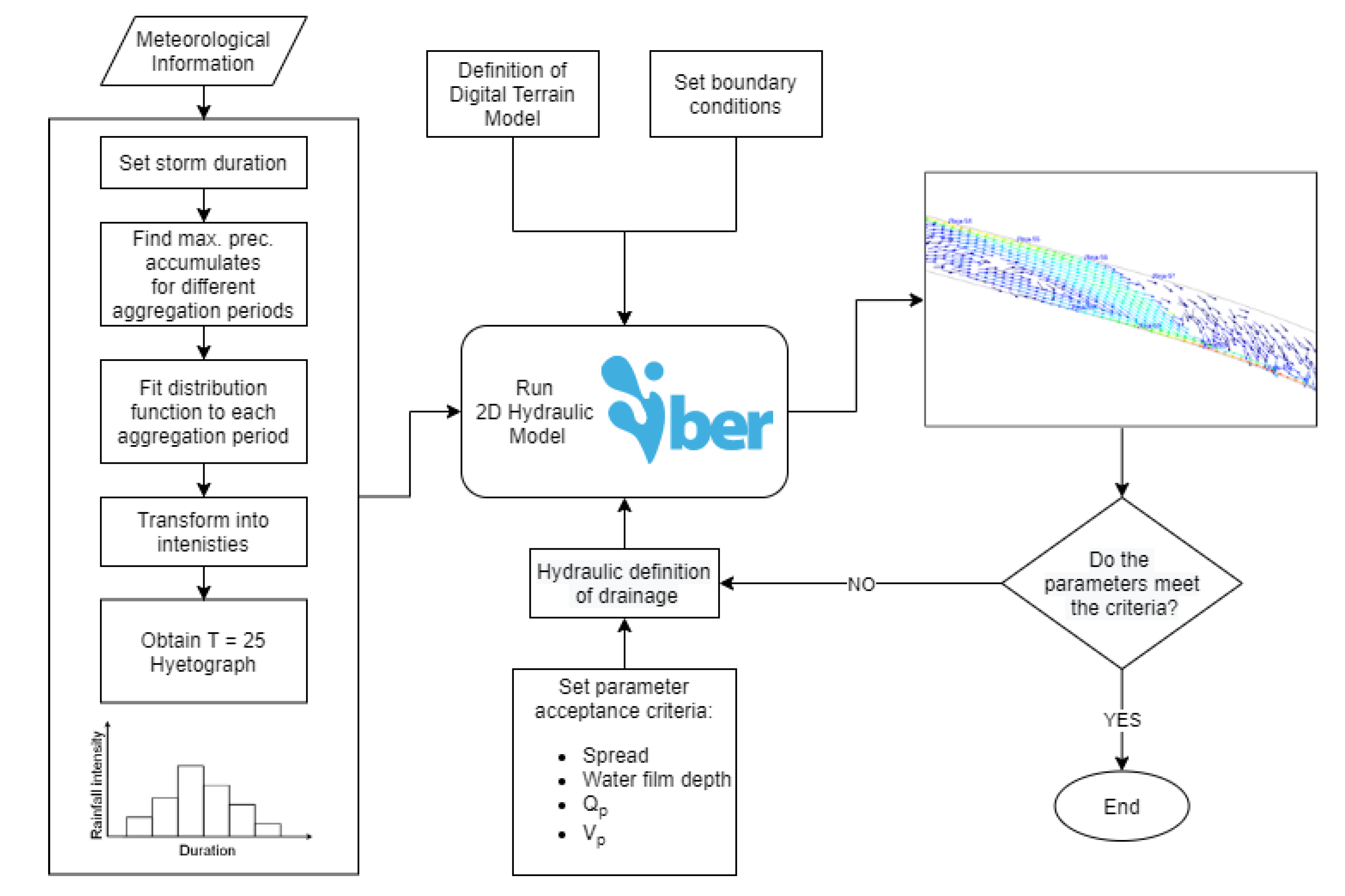
The methodology consisted of four steps: (1) obtaining the design hyetograph, (2) defining the road geometry as a digital terrain model, (3) setting parameter acceptance criteria, and (4) defining the hydraulic design of the drainage system by its implementation in the Iber model and analyzing simulation results. A workflow diagram of the methodology can be observed in
Figure 1.
2.1. Design Hyetograph
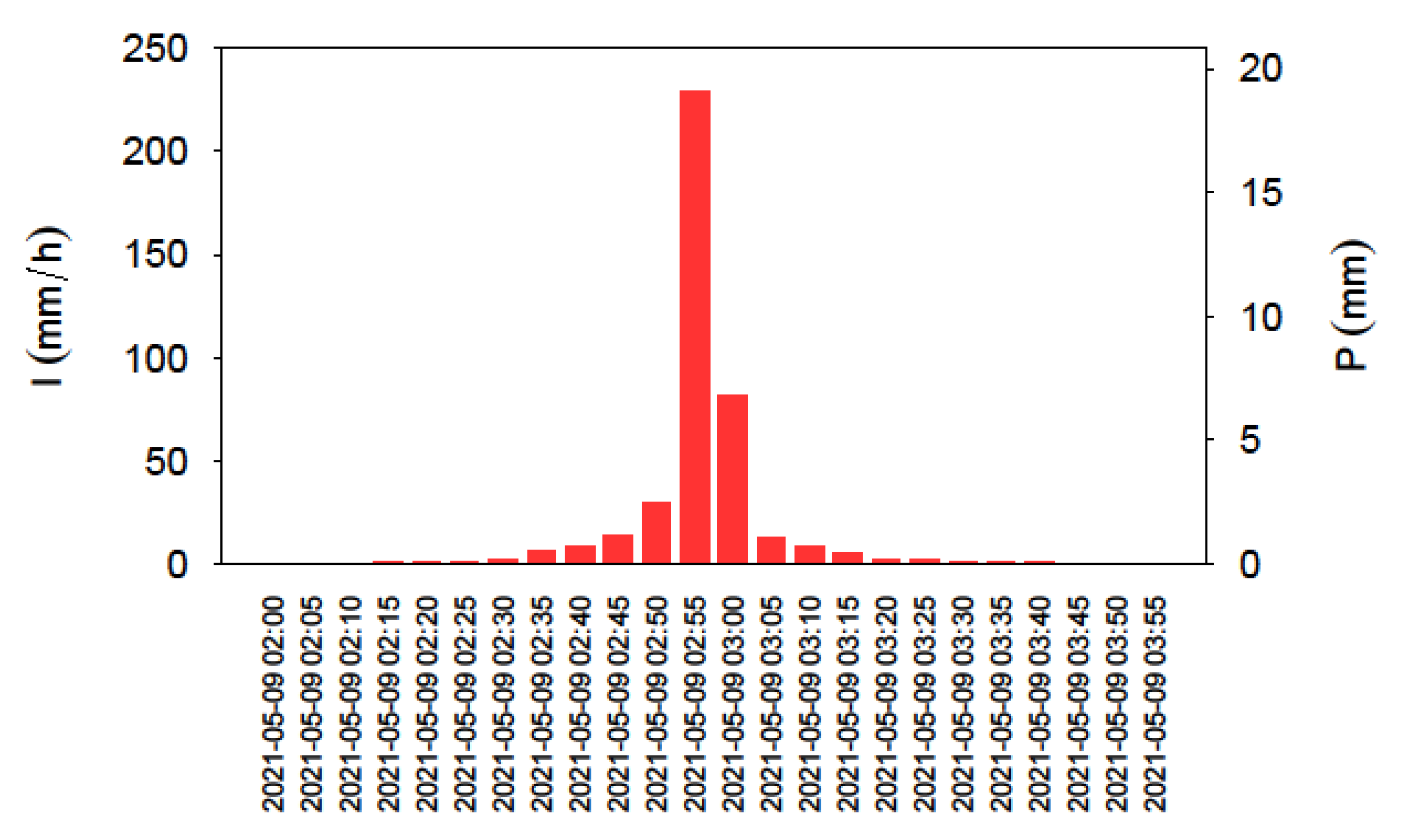
The storm hyetograph is critical in drainage design since it determines the peak flooding volume in a catchment and the corresponding drainage capacity demand for a given return period [
20]. Many approaches for defining design hyetographs can be found in the literature, such as the papers by Alfier et al. [
21] and Balbastre-Soldevilla et al. [
22].
In the present study, the design hyetograph was built from existing observations at a 5-min temporal resolution. First, considering the time of concentration and the rainfall statistics of the study area, the duration of the design storm was set to two hours. Second, maximum precipitation accumulates for different aggregation periods up to the storm duration were calculated from the observations. The values for each aggregation period were fitted to different distribution functions, and the best fit was obtained with the square root normal distribution (SQRT). Last, the T = 25-year quantiles for each aggregation period were calculated and converted into intensities to build the 25-year return period hyetograph. For the construction of the design hyetograph following the method of Balbastre-Soldevila et al. [
22], the Alternating Blocks Hyetograph Method [
23] was selected.
2.2. Digital Terrain Model
A two-dimensional hydraulic model for the simulation of free surface flow requires three-dimensional information of the study area. This can be achieved by providing an elevation in the previously defined mesh. The higher the accuracy of the representation of topography, the better the model will perform. Different altimetric sources of information at different resolutions can be found in the literature. Mainly, these sources are (1) vector models based on entities, essentially points and lines, defined by their coordinates [
24]; (2) raster models, in which each figure corresponds to the average value of elementary units of non-zero surface area that tessellate the terrain with a regular (matrix) distribution, without overlapping and with total coverage of the area represented [
25]; and (3) light detection and ranging (LiDAR) models, in which point clouds are digital lists of points with x, y, and z coordinates and one or more descriptive attributes, including a point identifier. For more details, see Rutzinger et al., [
26] and Zhao [
27].
Casas et al. [
28] compared the effects of the topographic data source and resolution on hydraulic modeling, concluding that LiDAR models presented the best results. These models can be applied when dealing with existing infrastructure in which a vectorial model is not available. However, in cases of new linear infrastructure in which vectorial models are available, as in our case study, LiDAR models will perform better since point elevations are perfectly defined for the entire model.
2.3. Parameter Acceptance Criteria
As discussed in the introduction, there are no common standardized criteria for drainage infrastructure design. Different approaches to limit excess surface water on roads can be found depending upon the design drainage standards of the country. However, there is a broad agreement among almost all standards to limit the values of four parameters: the generated storm peak flow, the total volume of water generated by the storm, and the water film thickness on the road and its spread.
The design criteria stated in the present paper are:
The generated storm peak and the total volume of water associated with the storm will be obtained for a 25-year period [
4].
The water spread and water film thickness are limited to 1.5 m and 0.4 mm, respectively. Both values are lower than those proposed in different works, as discussed in
Section 1.
As the case study is located in Spain, the aforementioned criteria are consistent with the recommendations of the Spanish standards. Nevertheless, the results presented in
Section 4 are suitable to be applied to a different combination of design criteria according to the regulations in different countries.
2.4. Iber Model
Iber is a freely distributed 2D numerical tool (
www.iberaula.com, accessed on 12 June 2021) initially developed for modeling hydrodynamic and sediment transport [
19,
24,
25,
26,
27,
28] that solves the SWEs on irregular geometries using the finite volume method (FVM). The tool has been continuously enhanced since it was first presented in 2010, and now includes a series of modules for different fluvial and hydrological processes, such as rainfall–runoff transformation [
29,
30,
31], water quality processes [
32,
33], large wood transport [
34], physical habitat suitability assessment [
35], the consideration of pressurized flow [
36,
37,
38,
39], and, more recently, non-Newtonian flows such as wood-laden flows [
40] and snow avalanches [
41,
42].
When applying Iber for the simulation of urban surface drainage problems, the source terms of the continuity equation must include rain intensity, infiltration, and the flow sinks due to the presence of drainage inlets toward the sewer system network [
43]; thus, the governing equations are:
with
where
is the flow thickness,
. and
. are the two velocity components on the horizontal directions of the unit discharge,
is the gravitational acceleration,
and
are the two bottom slope components, and
and
. are the two friction slope components, generally calculated with the Manning formula. For hydrological modeling (i.e., rainfall–runoff transformation)
. accounts for the effect of rainfall on overland flow [
44],
. accounts for the rate of distributed hydrological losses (infiltration, evapotranspiration, and interception) [
29], and
. accounts for the distributed losses of surface water due to its incorporation with the drainage system. Iber solves these 2D-SWEs using a conservative scheme based on the FVM on an unstructured mesh of triangles and/or quadrilaterals. For the convective fluxes, it uses an explicit first-order Godunov-type upwind scheme [
45], in particular, the Roe scheme [
46].
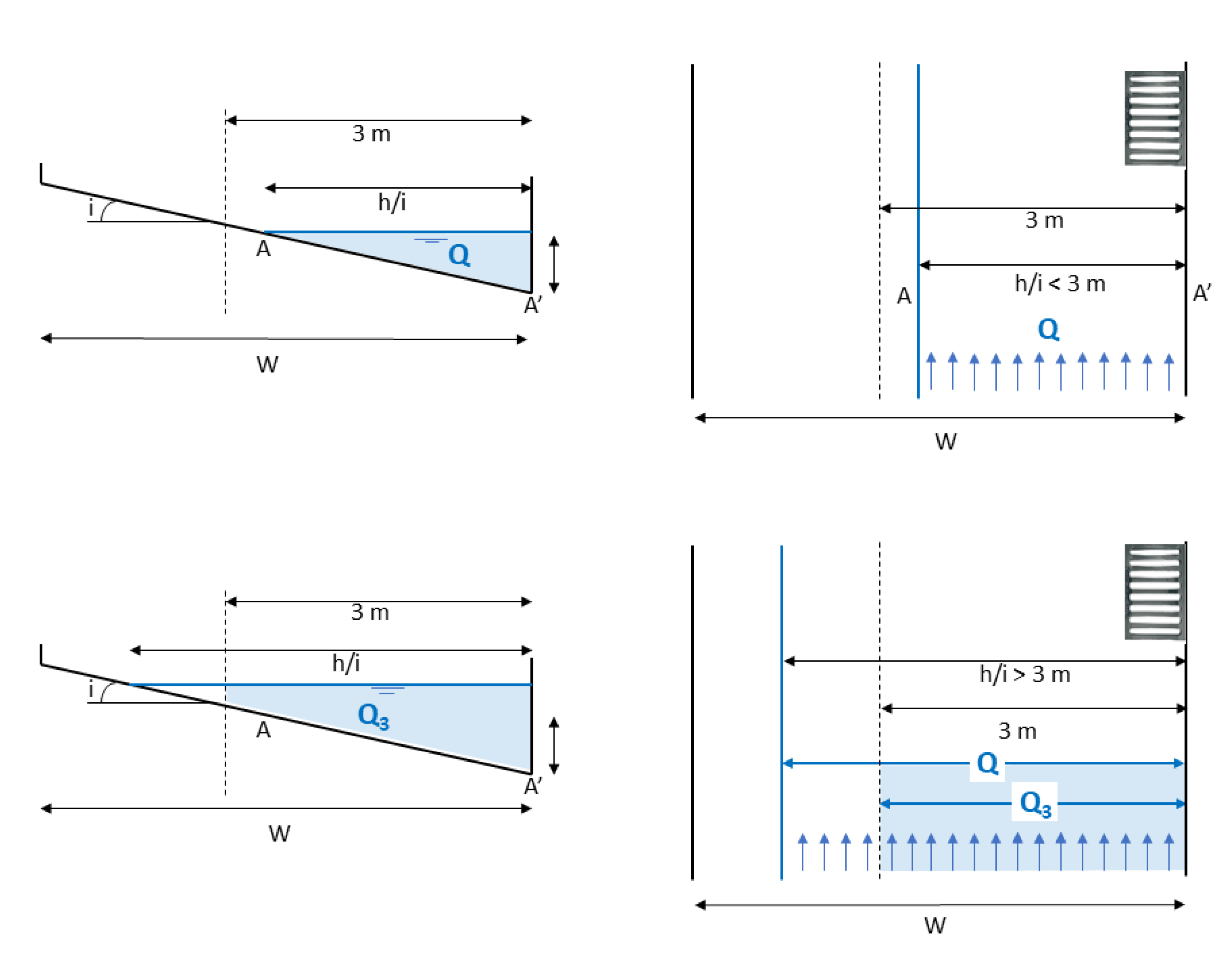
In the case of road drainage systems constituted by grate inlets,
. accounts for the discharge through inlets. The hydraulic capacity of a storm drainage inlet is a function of the grate type, gutter flow, and geometric road geometry. For the numerical modeling of road inlets, the classic methodology uses the hydraulic equations of weirs and orifices [
47]. More recent methodologies are based on the concept of inlet efficiency [
12]. With this approach, the efficiency of an inlet is defined as the ratio of the intercepted discharge by the inlet to the total discharge approaching the inlet:
where
E is the hydraulic inlet efficiency,
Qint is the intercepted discharge by the inlet (m
3/s), and
Q3 is the total discharge approaching the inlet along a 3-m bandwidth of the roadway (
Figure 2). The inlet efficiency can be estimated based on the knowledge of the grate characteristics (size, area, disposition, and number of holes) or the results of experimental laboratory tests [
48]. This UPC methodology [
48] proposes estimating the efficiency through a potential equation that relates the inlet efficiency with the flow thickness and the approximate rate flow through two characteristic parameters of the grate:
where
A and
B can be directly estimated with laboratory experience [
9] or an approximate equation [
49]. In the previous expressions,
. is the discharge through a bandwidth of 3 m because the authors used an experimental facility representing a 3 m wide street [
50]. For its inclusion in the formulation in the numerical model, the discharge
. in this last equation is estimated as [
43]:
where
. is the transversal slope of the road at the inlet point.
With this approach, the efficiency of each inlet, which varies over time in an unsteady surface flow with the approaching flow, can be calculated from Equations (4) and (5) at each computational time step. Thus, together with Equation (3), the value of the discharge intercepted by the grate inlet ( can be obtained using the known road geometry, grate characteristics, and approaching over-road flow characteristics.
2.5. Location of Grate Inlets: Sensitivity Analysis
This section presents the strategy used to set the location of the grate inlets so that the criteria established in
Section 2.3 are fulfilled. This strategy is based on a sensitivity analysis that assesses the configuration with the least number of grate inlets while satisfying the design criteria.
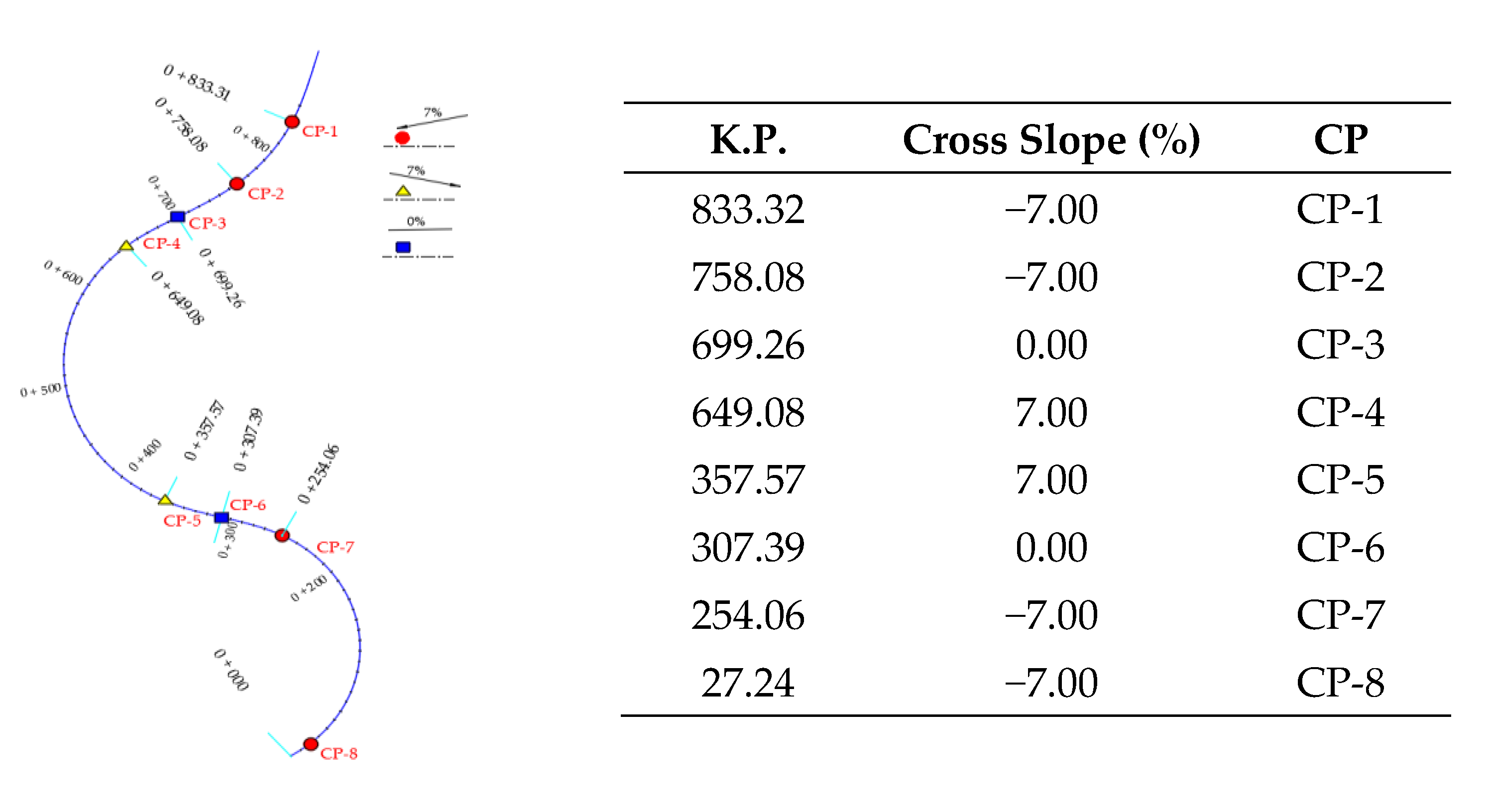
First, a set of critical points (hereafter referred to as control points) are identified. Their correct selection is critical for the implementation of the methodology since these are the locations where it will be verified that the criteria are met. Control points (CPs) must be located both at the beginning and at the end of any change in the road cross slope. The rationale behind this is that there is a change in the cross slope from these points onward, resulting in the formation of a flow across the road, which is precisely what it intends to prevent. Furthermore, additional control points may be placed in locations where the cross slope is zero as a consequence of the change of curvature. These control points are useful to characterize the potential flow across the road or the puddles formed by the stormwater.
Finally, grate inlets must be installed both at the beginning and the end of any change in the road cross slope. The rest of the grate inlets will be installed starting from these locations and in the upstream direction.
5. Discussion
The proposed method for designing the location of grate inlets for the drainage of a road allows total control of the hydraulic behavior at each location. For each location, it is possible to perform a detailed analysis of its hydraulic behavior and obtain characteristic variables, such as the evacuated flow through it at each instant and its performance, estimated as the ratio between the flow rate approaching the grate inlet and the flow rate collected by it. Based on this comprehensive information, it is possible to make decisions about the relevance of a certain spacing between scuppers, the possibility of removing some of them without compromising the global drainage system performance, and the need to introduce a transverse grate inlet across the entire width of the road if adequate flow values are not obtained using only longitudinal ones.
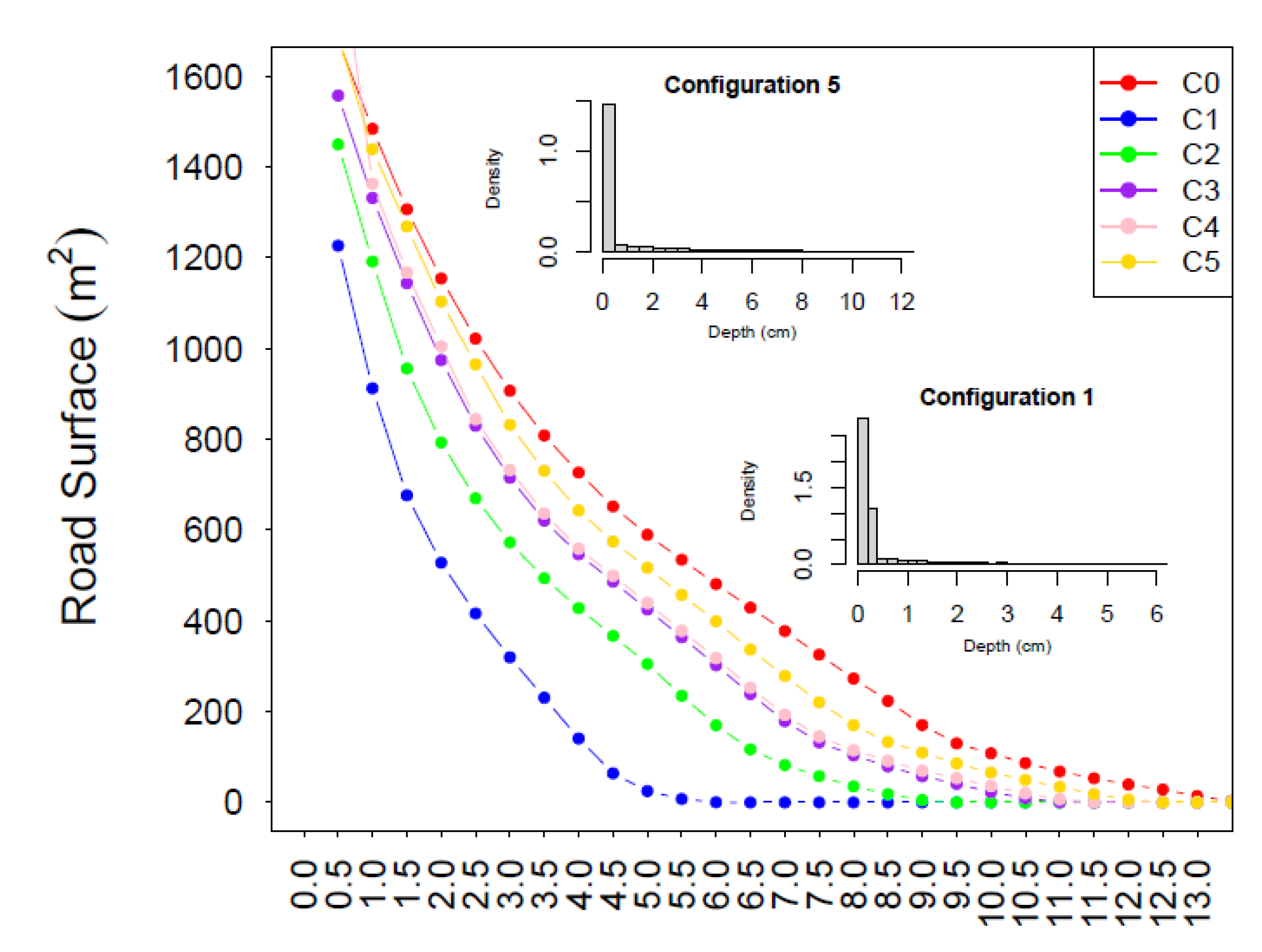
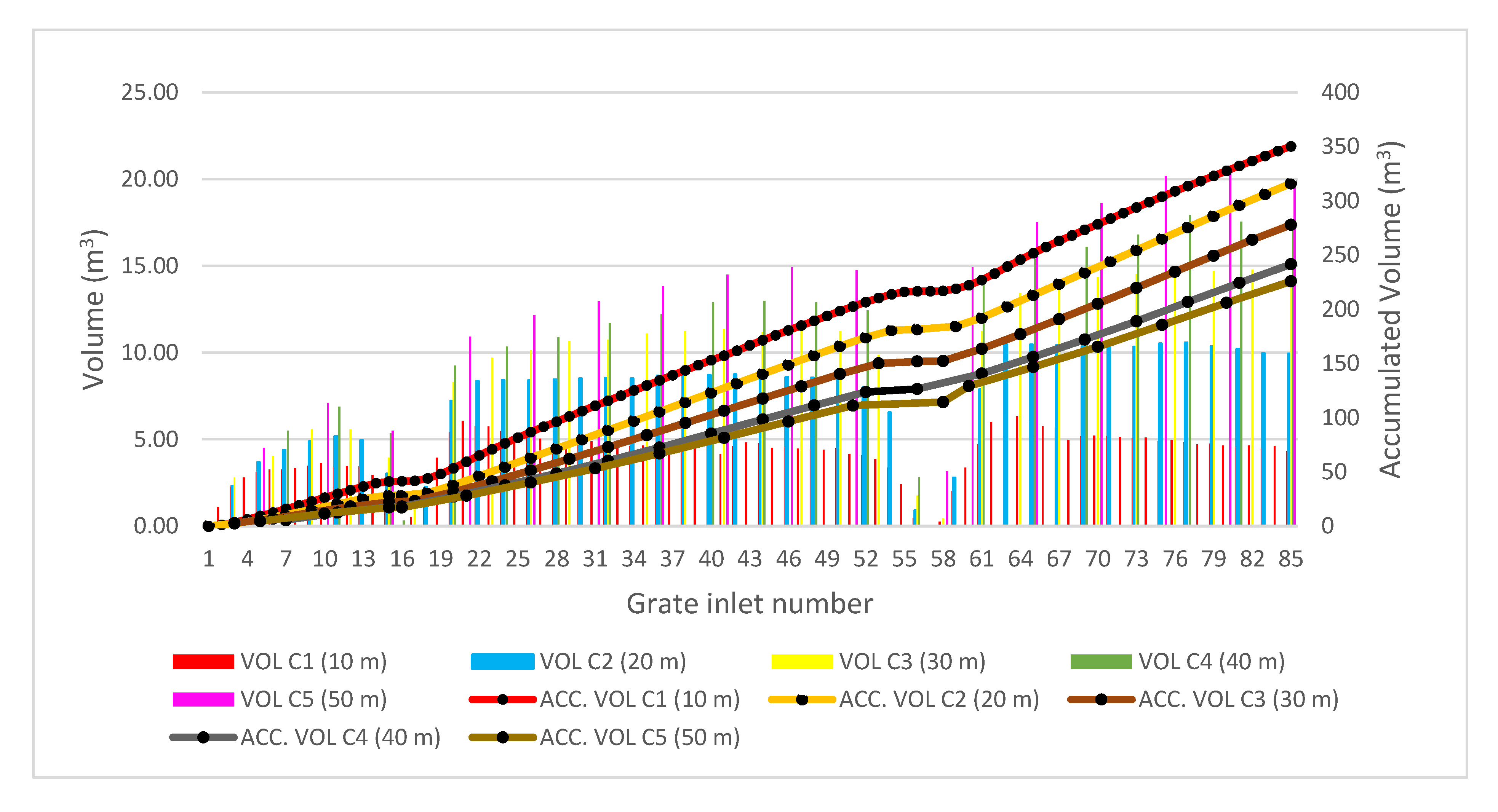
For the presented case study,
Figure 10 shows the volume captured by each scupper and the accumulated captured volume along the road depending on the spacing between them. It can be clearly seen that with smaller spacing (and thus a higher number of grate inlets), the accumulated captured volume is greater, but the captured volume for each grate inlet is smaller.
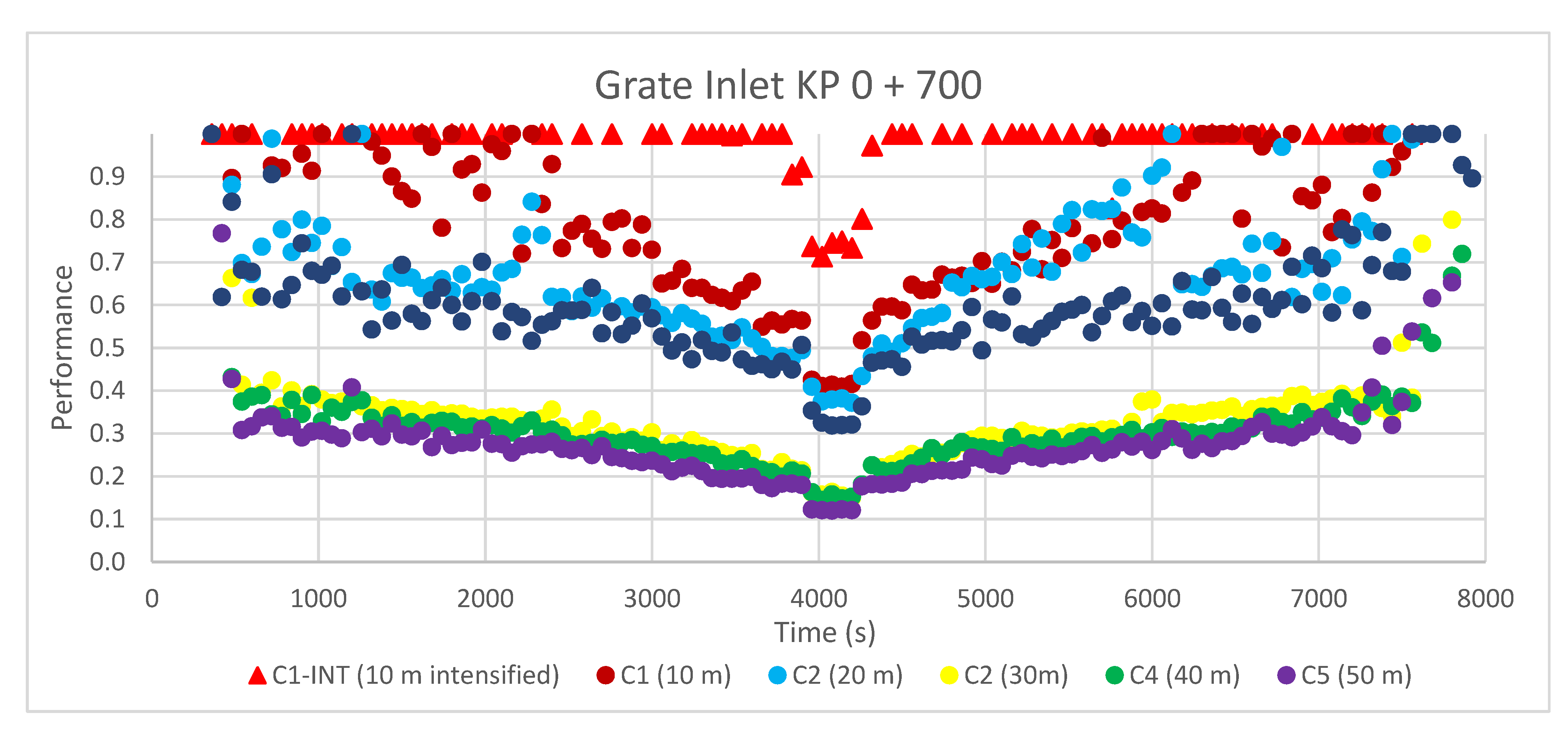
With the aim of analyzing the convenience of a particular inlet separation, the performance of grate inlets with distribution alternatives can be also analyzed by representing their hydraulic efficiency throughout the duration of the rainfall episode. This is shown in
Figure 11 for the inlet located at KP 0 + 700 (
Figure 6) and for different spacing distances between grates. A design with spacing C3 (30 m), C4 (40 m), and C5 (50 m) showed performances below 40%, with very small variations between configurations, which suggests that the upper efficiency limit for that particular road geometry was reached. By decreasing the distance between inlets, the efficiency of the inlet increases, which means that a greater portion of the discharge reaching them is captured. In this case, reasonably high values of efficiency were achieved with separations of C1 (10 m) and C2 (20 m), while in the case of C1_INT (10 m “intensified”), the efficiency was mostly equal to one. An efficiency of one for each inlet indicates that the entire flow approaching it is captured. This could be seen as a poor result in terms of the global efficiency of the drainage system; in other words, there are too many inlets, and a similar surface flow could be achieved with fewer inlets. In the presented inlet (KP 0 + 700), this would be the case for most of the rain episode, but not for the peak of the hyetograph, when the efficiency decreases to values of 0.7 and thus the proposed inlet distribution is justified.
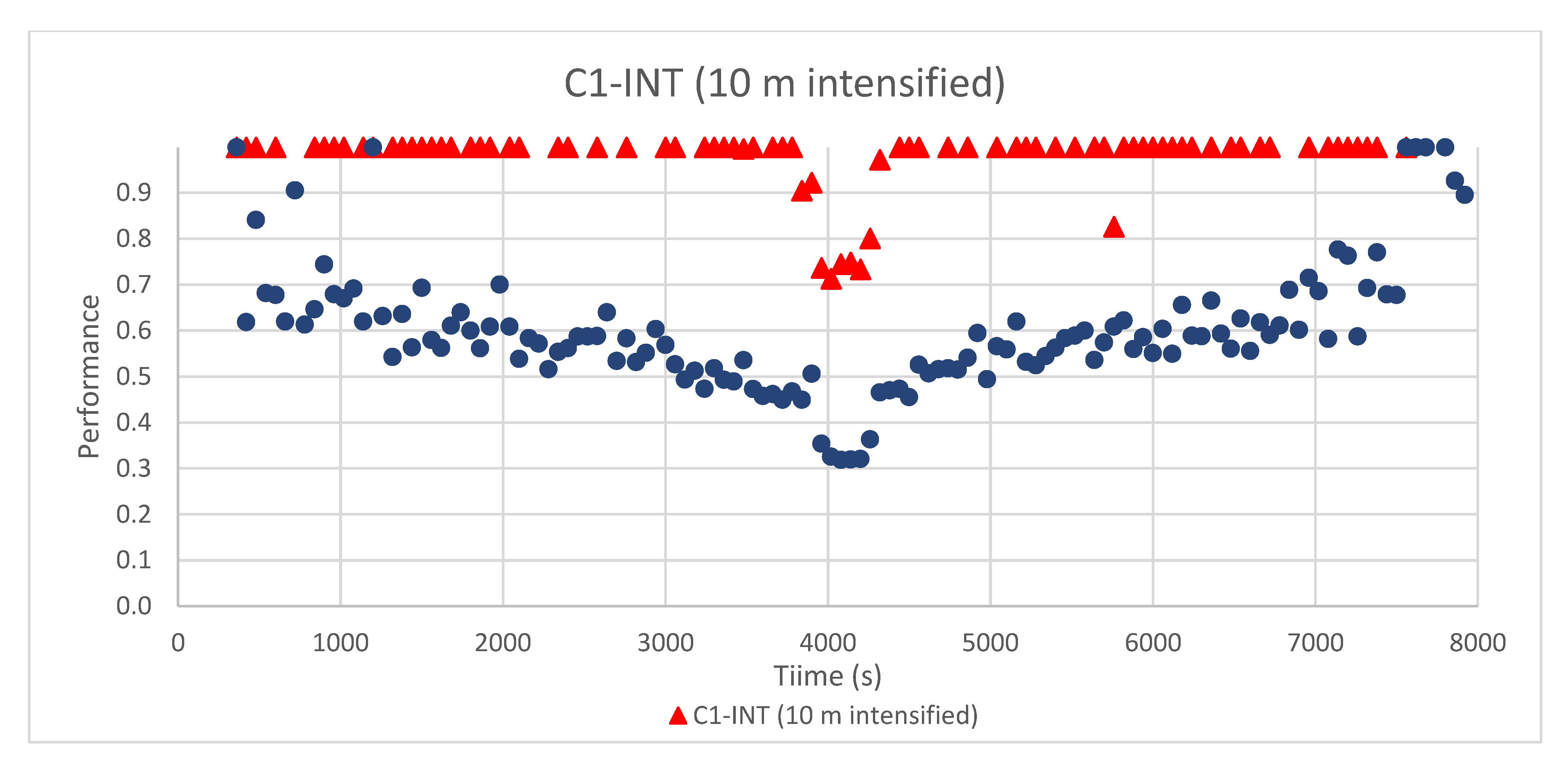
Figure 12 shows a comparison of the performance for inlets located at KP 0 + 700 and KP 0 + 270 (see
Figure 6) for a distance between inlets of C1_INT (10 m “intensified”). The inlet at KP 0 + 700 is located near the upstream end of the road. This means that the flow discharge reaching it is small and can be collected with high efficiency (1 for most of the simulation time). By contrast, the inlet at KP 0 + 270 receives a higher discharge and thus it is not able to capture all of it. Therefore, the efficiency graphs of
Figure 11 and
Figure 12 can be useful for fine-tuning the drainage design. A reasonable criterion would be a final drainage inlet distribution that achieves performances near or equal to one, but that with a slightly larger separation or rain intensity, the efficiency would drop to slightly lower than one, at least for the peak intensities. If the efficacy is still one with such an increase in separation or intensity, it means that the global design is not very efficient, as there are too many inlets.
The analysis presented in
Figure 10 opens the possibility for manually fine-tuning the inlet distribution or removing the most inefficient ones. In
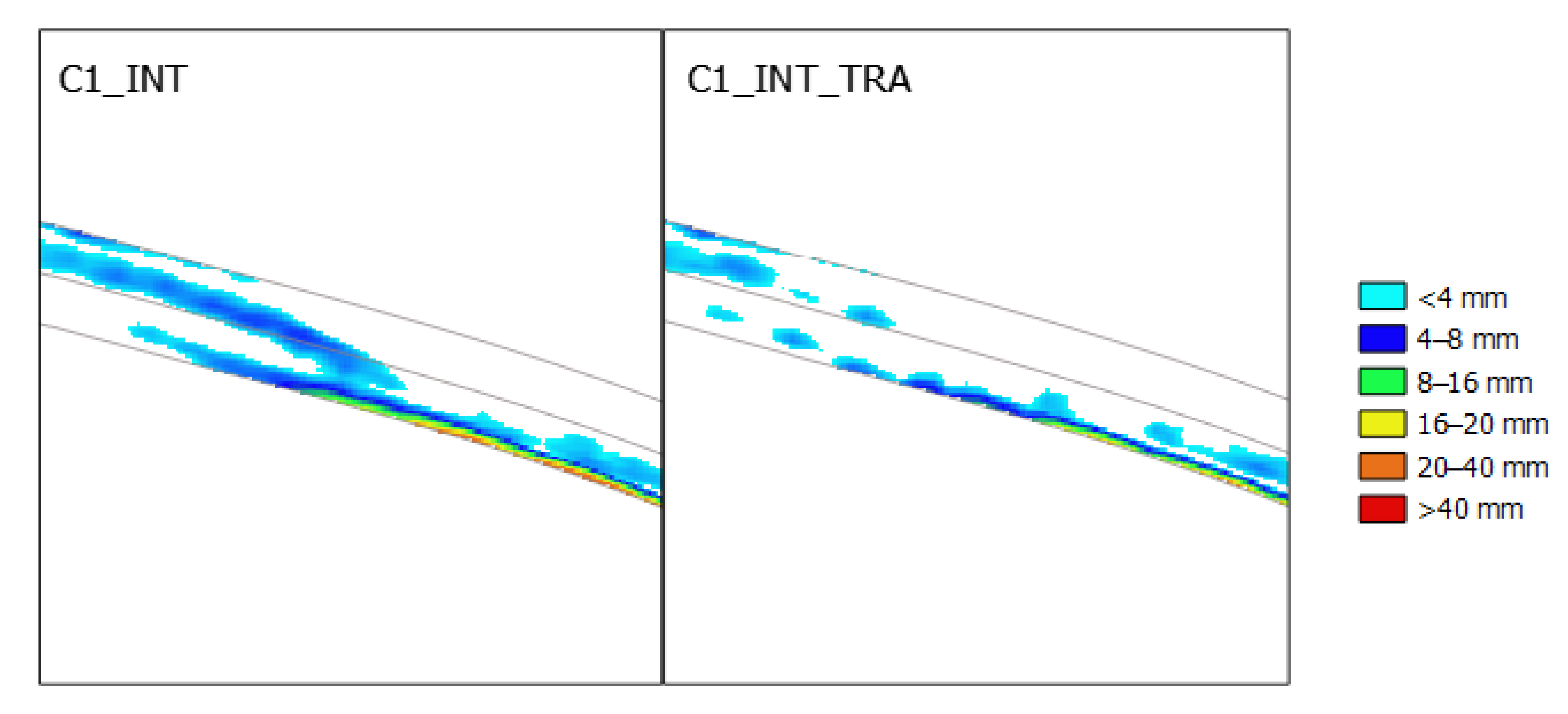
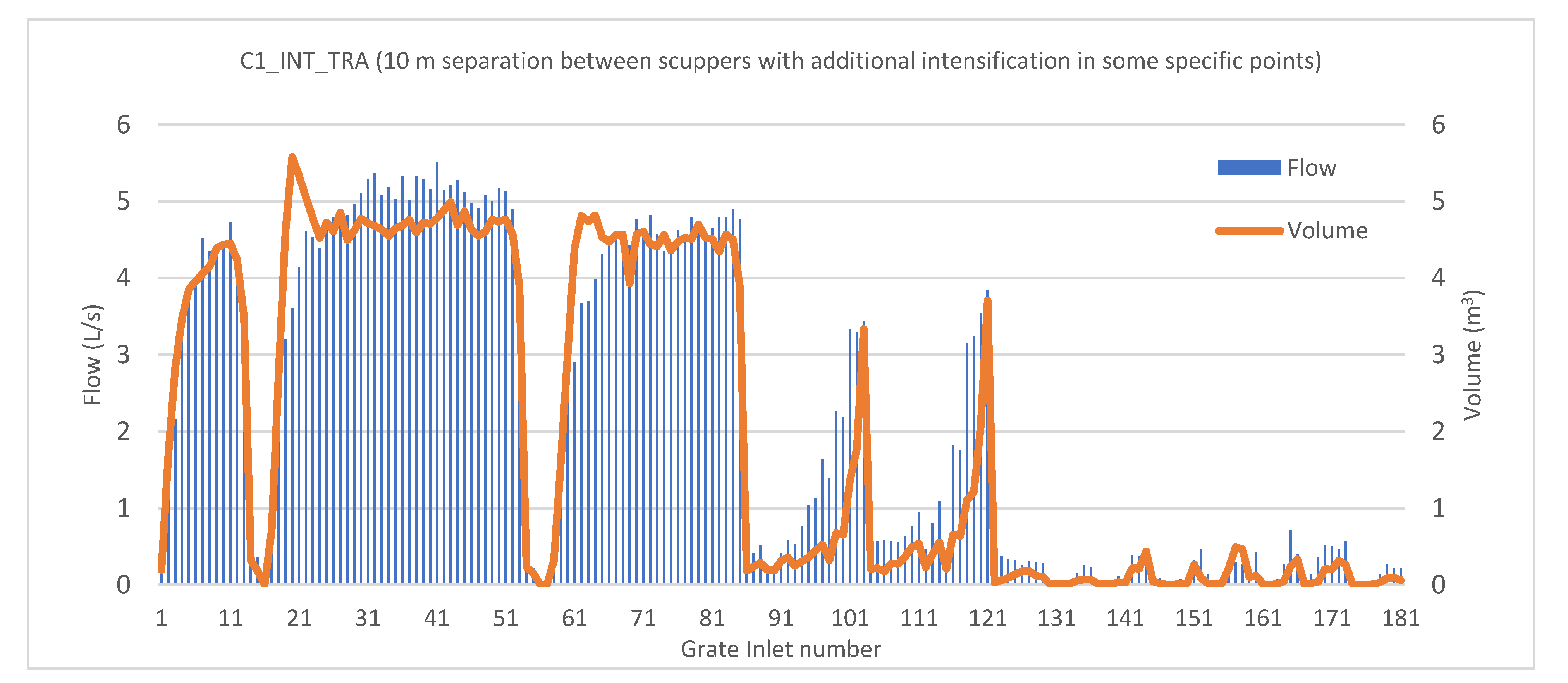
Figure 10, the flat regions of the accumulated volume curves at approximately inlet 16 and inlet 56 indicate that these inlets do not capture any flow, as there is little or no discharge approaching them. The same information can be presented for a particular case, for example, that of C1_INT_TRA, by representing the captured volume and discharge in every inlet, as shown in
Figure 13. In this figure, the flat areas in
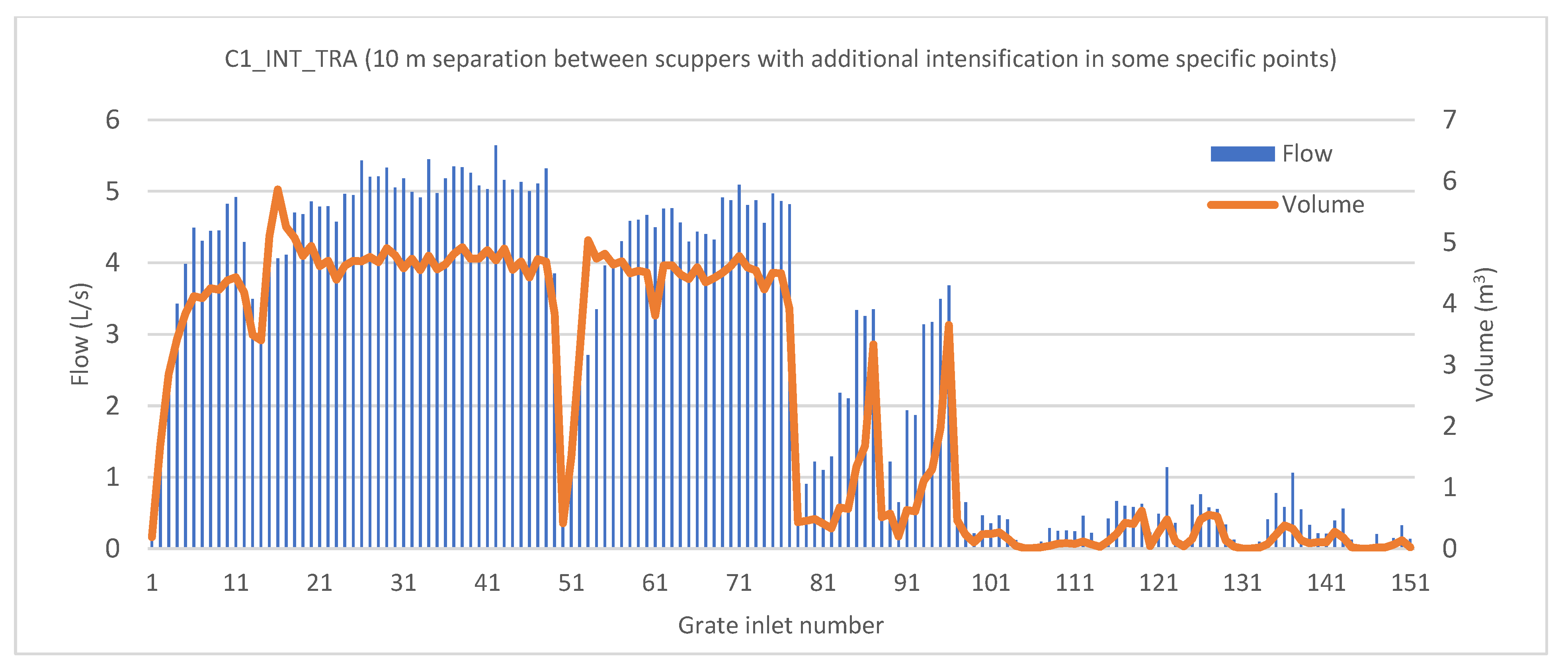
Figure 10 are now represented as “valleys”. Additionally, a large number of inlets with little captured discharge can be observed at the right end of the graph. All these elements could be removed from the design. With such criteria, removing the inlets with a maximum captured discharge of less than 0.1 L/s results in the suppression of 30 inlets; thus, the total number is reduced from 181 to 151. The consequences on the captured discharge and volume of the remaining inlets are shown in
Figure 14.
No substantial differences can be seen in
Figure 14 compared with
Figure 10, which indicates that the removed inlets were effectively unnecessary. In terms of final discharge and volume reaching the end of the road, the initial disposition C1_INT_TRA results in a maximum volume reaching this point of 362.5 m
3, with a maximum discharge of 5.5 L/s. After the suppression of 30 unrequired inlets, the maximum value increases slightly to 363.1 m
3/s, which represents a negligible increase of 0.17%; however, the maximum discharge increases to 5.6 L/s (1.8%), which justifies the removal of the selected inlets.
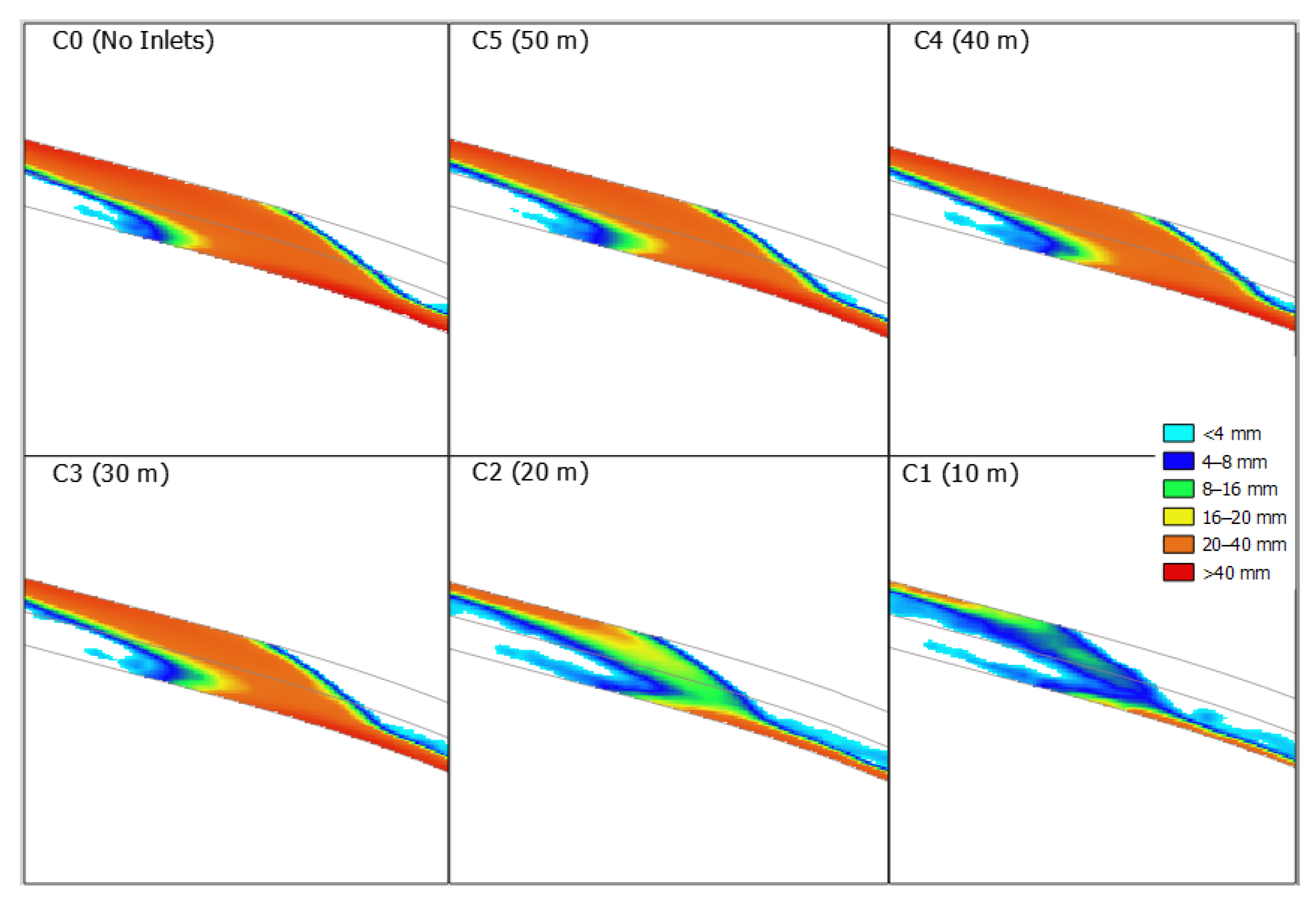
As already shown in
Figure 8 and
Figure 9, for a given inlet distribution and rainfall, the proposed method allows the prediction of hazardous scenarios likely to cause hydroplaning. The numerical results presented in
Figure 8 and
Figure 9 show a common situation in which the main water stream changes from one side of the road to the other as the road cant varies, similar to the images depicted in
Figure 15.