Development of a Multi-Methodological Approach to Support the Management of Water Supply Systems
Abstract
1. Introduction
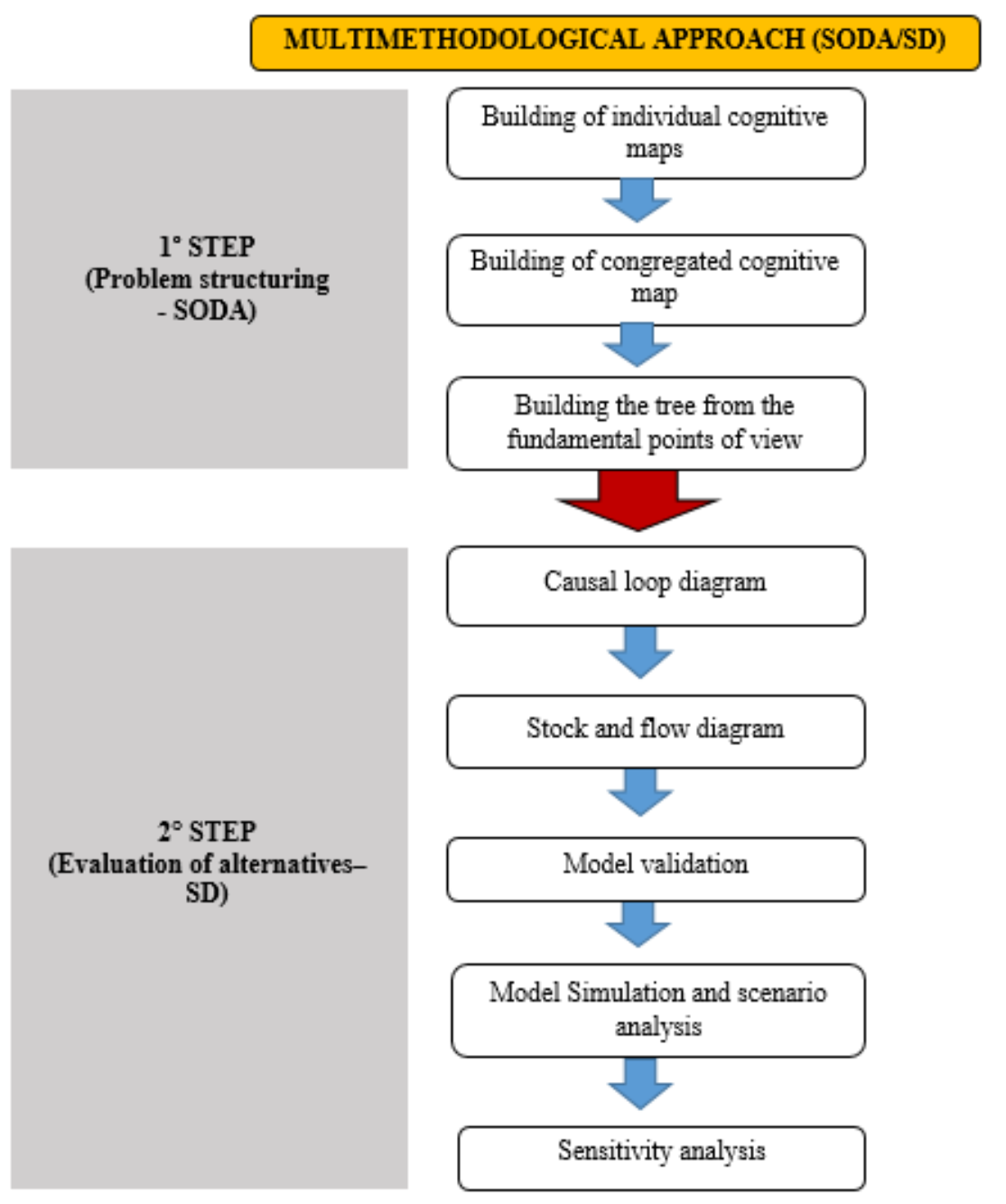
2. Approach
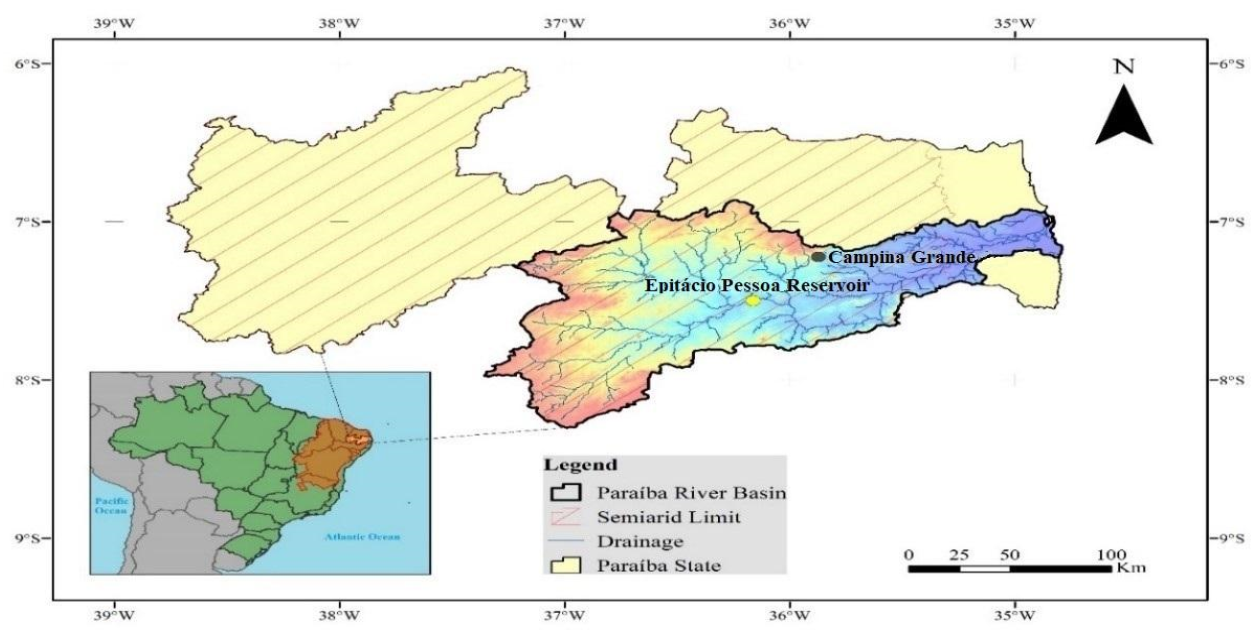
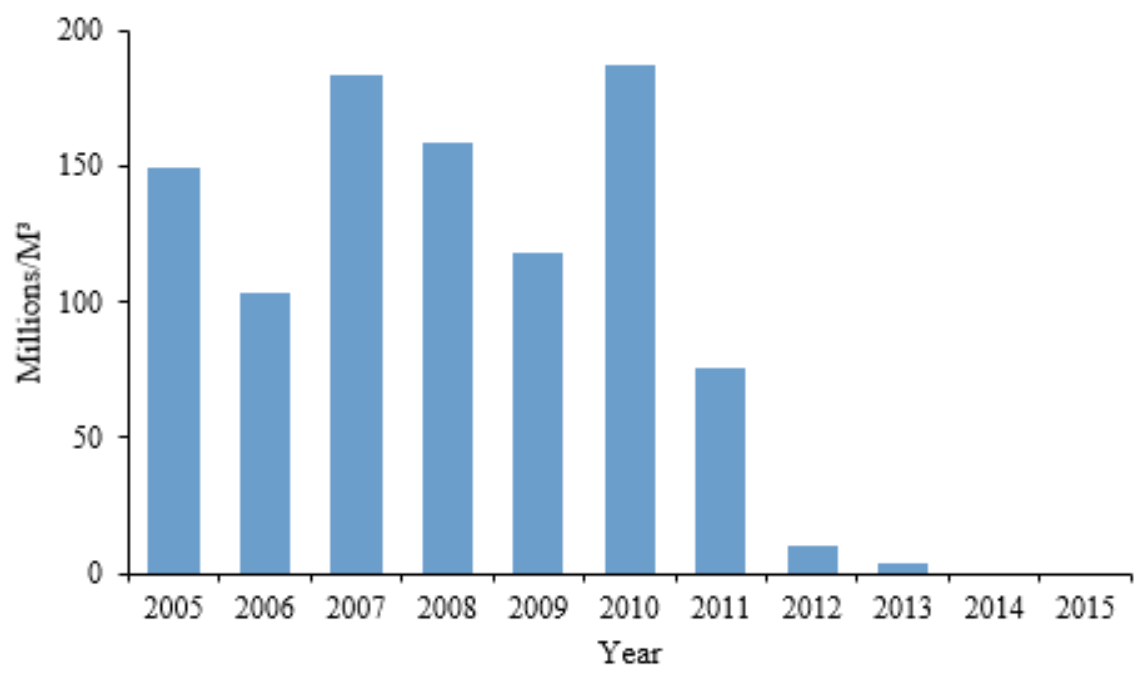
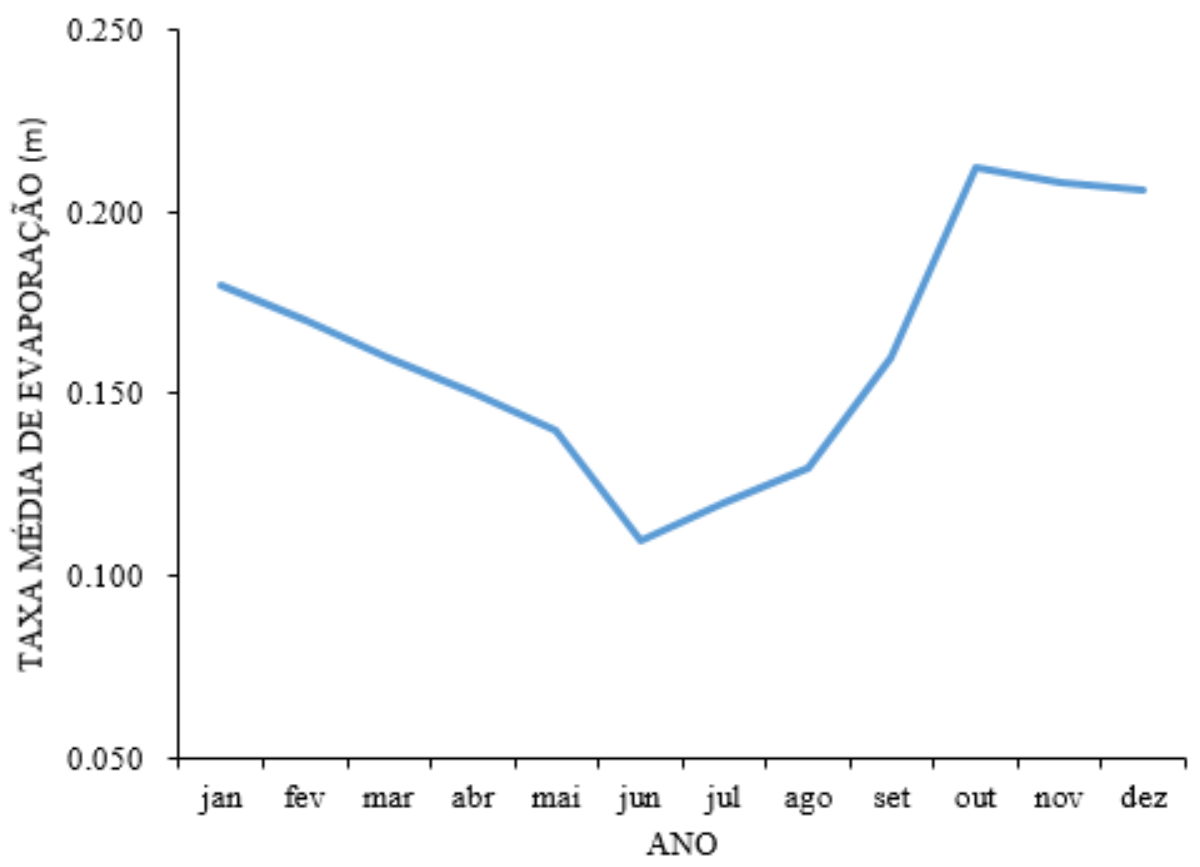
2.1. Case Study
2.2. System Dynamics
2.3. Proposal of the Multi-Methodological Approach SODA/SD: The Rationality
2.3.1. Step 1: Structuring the Problem
Building the Individual Cognitive Maps
Building the Congregated Cognitive Map
Construction of the Tree of Fundamental Viewpoints
2.3.2. Step 2: Application of System Dynamics for the Evaluation of Alternatives
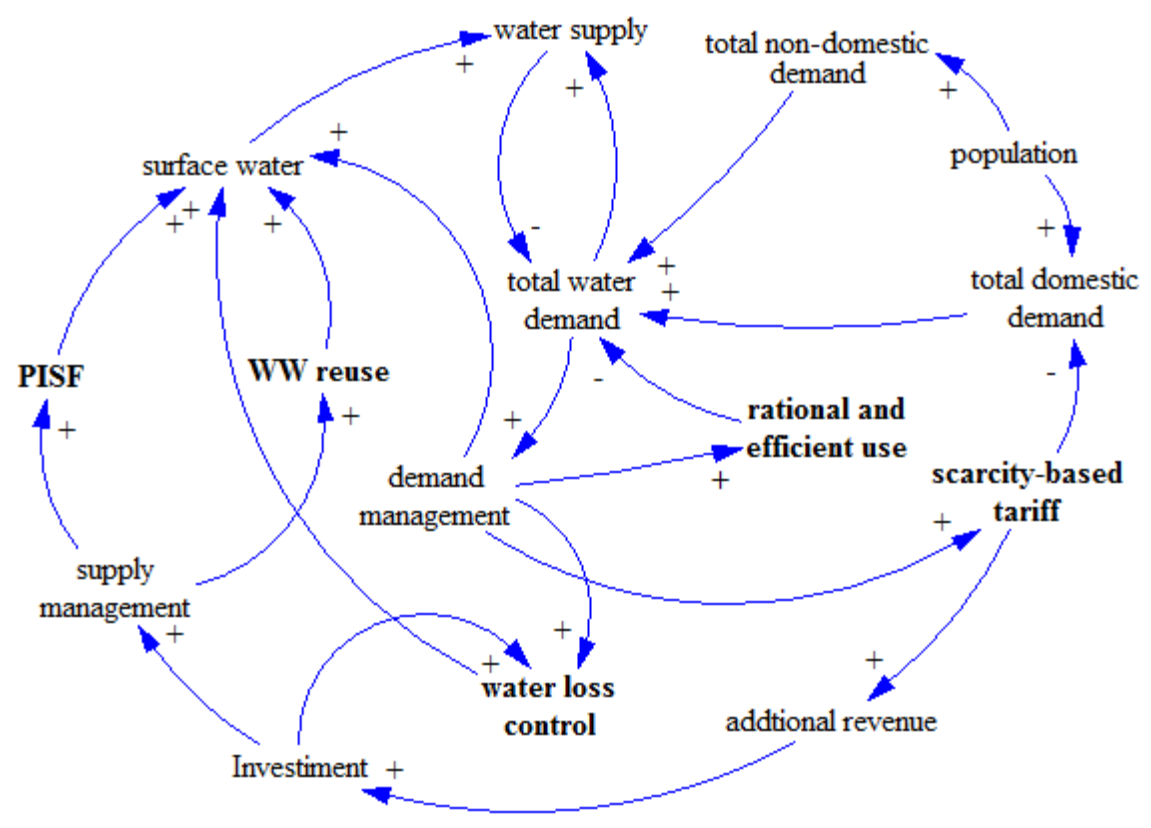
Construction of the Causal Loop Diagram
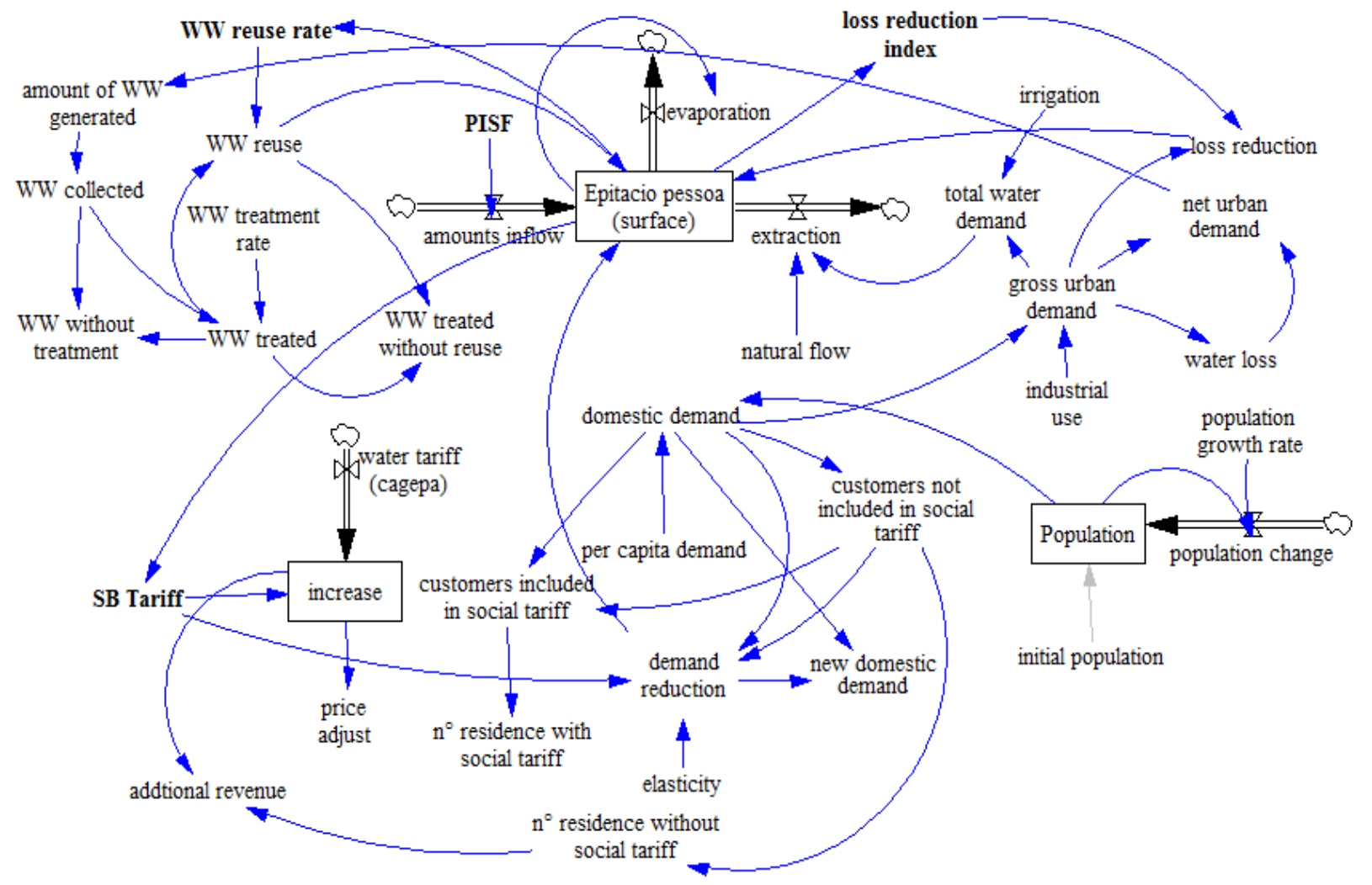
Building the Stock and Flow Diagrams
- Population sub-model
- Water supply sub-model
- Water demand sub-model
- Water tariff sub-model
- Returned water sub-model
Model Validation
Model Simulation and Scenario Analysis
Sensitivity Analysis
3. Results
3.1. Stage 1: Structuring the Problem
3.1.1. Construction of Cognitive Maps
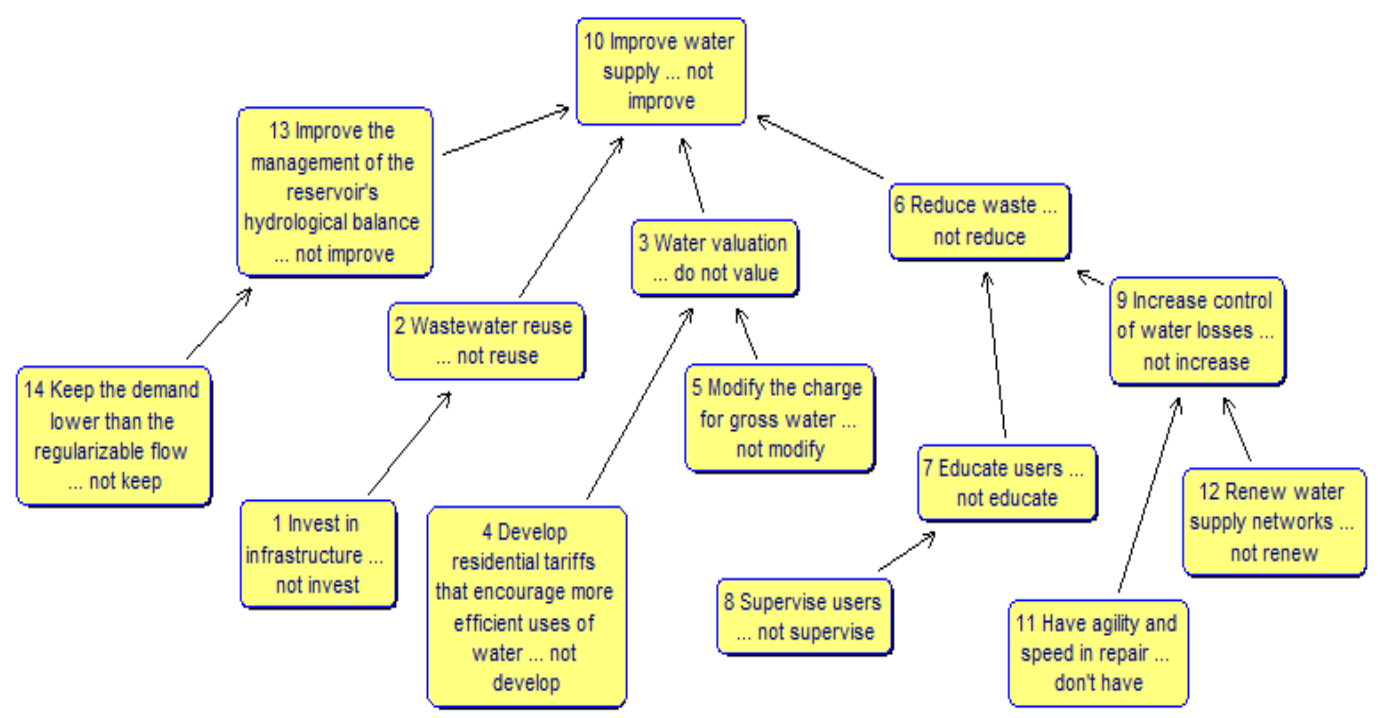
Step 1—Construction of the Individual Cognitive Maps
- (A)
- “improved management of the reservoir’s hydrological balance; reuse of wastewater; stimulating water charging through efficient tariffs; control of losses and environmental education for conscious use of water”;
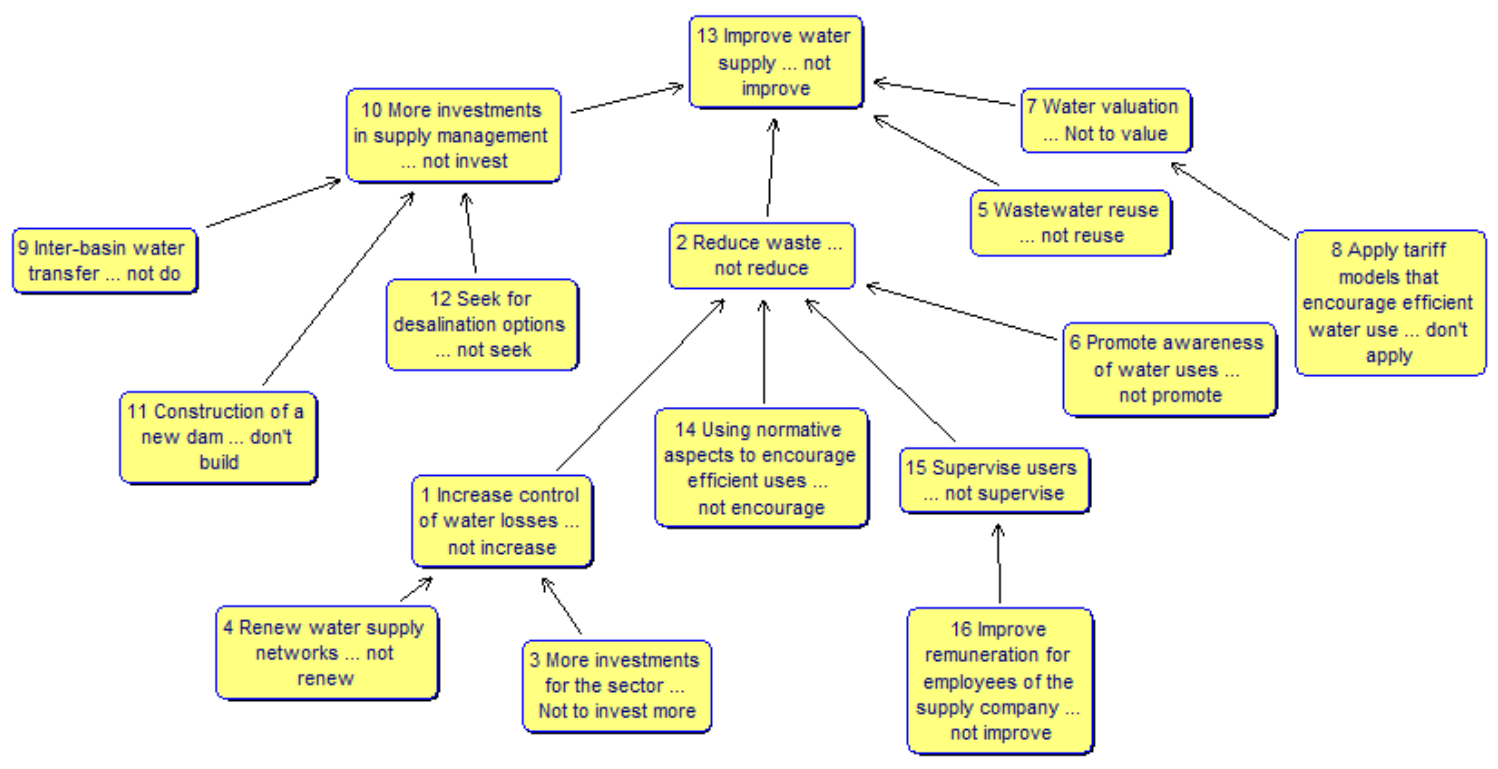
- (B)
- “inter-basin water transfer; desalination; loss control; wastewater reuse; efficient pricing models; construction of a new dam and environmental education for conscious water use”;
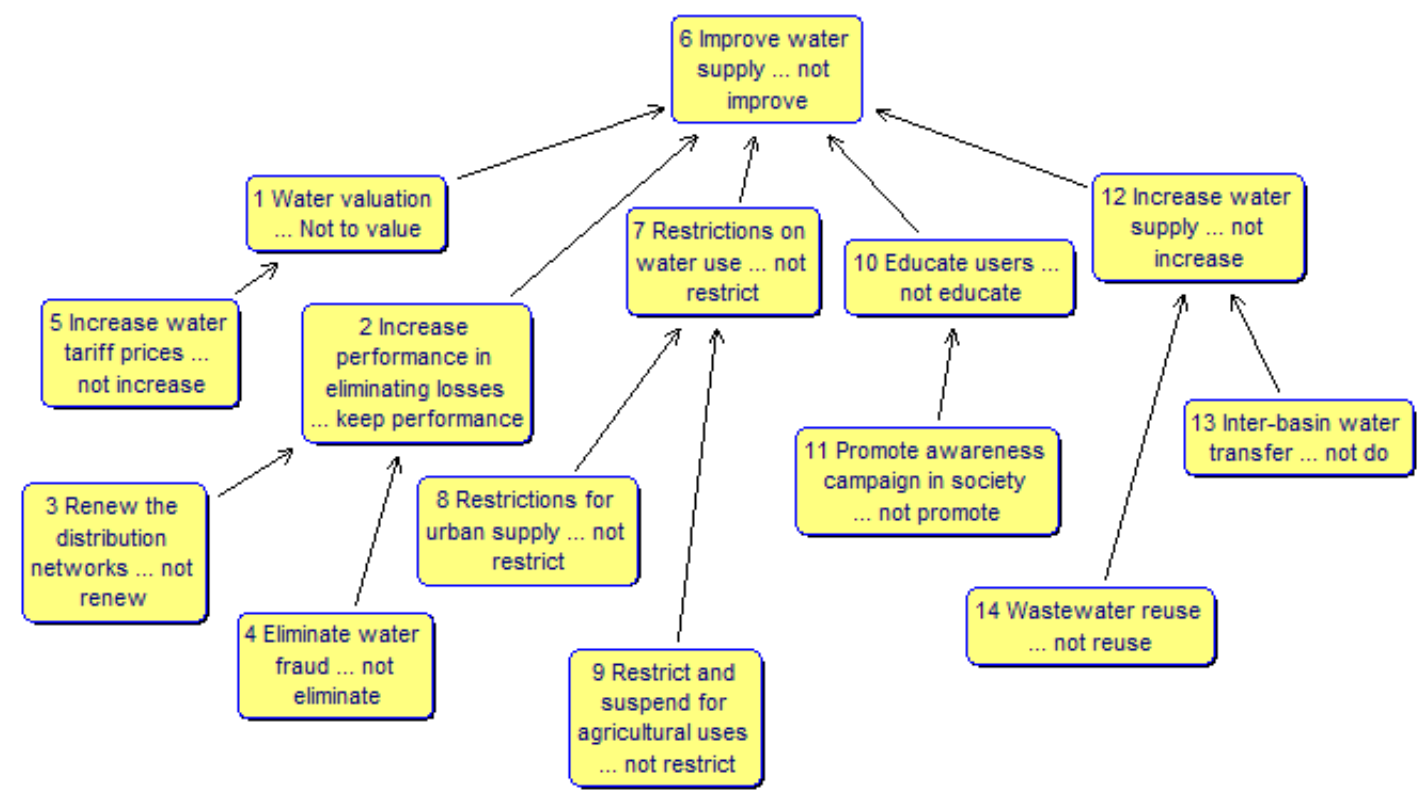
- (C)
- “ Expand the control of water losses; rationing water uses; raising water tariffs; conscious use of water resources; reuse of wastewater and transposition of water between river basins”;
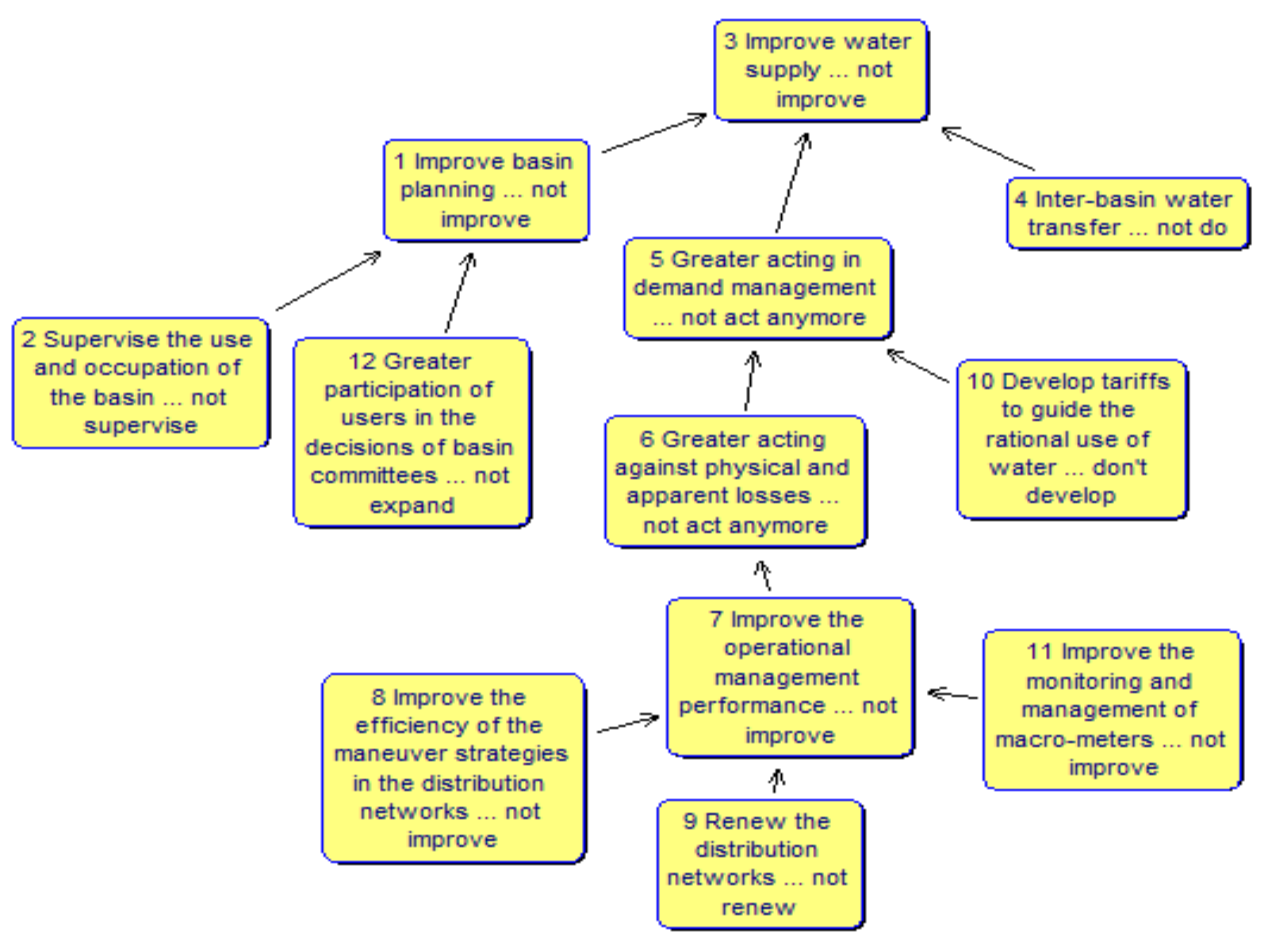
- (D)
- “improve watershed planning; greater action to control losses; develop tariffs that guide to rational water use and inter-basin water transfer”.
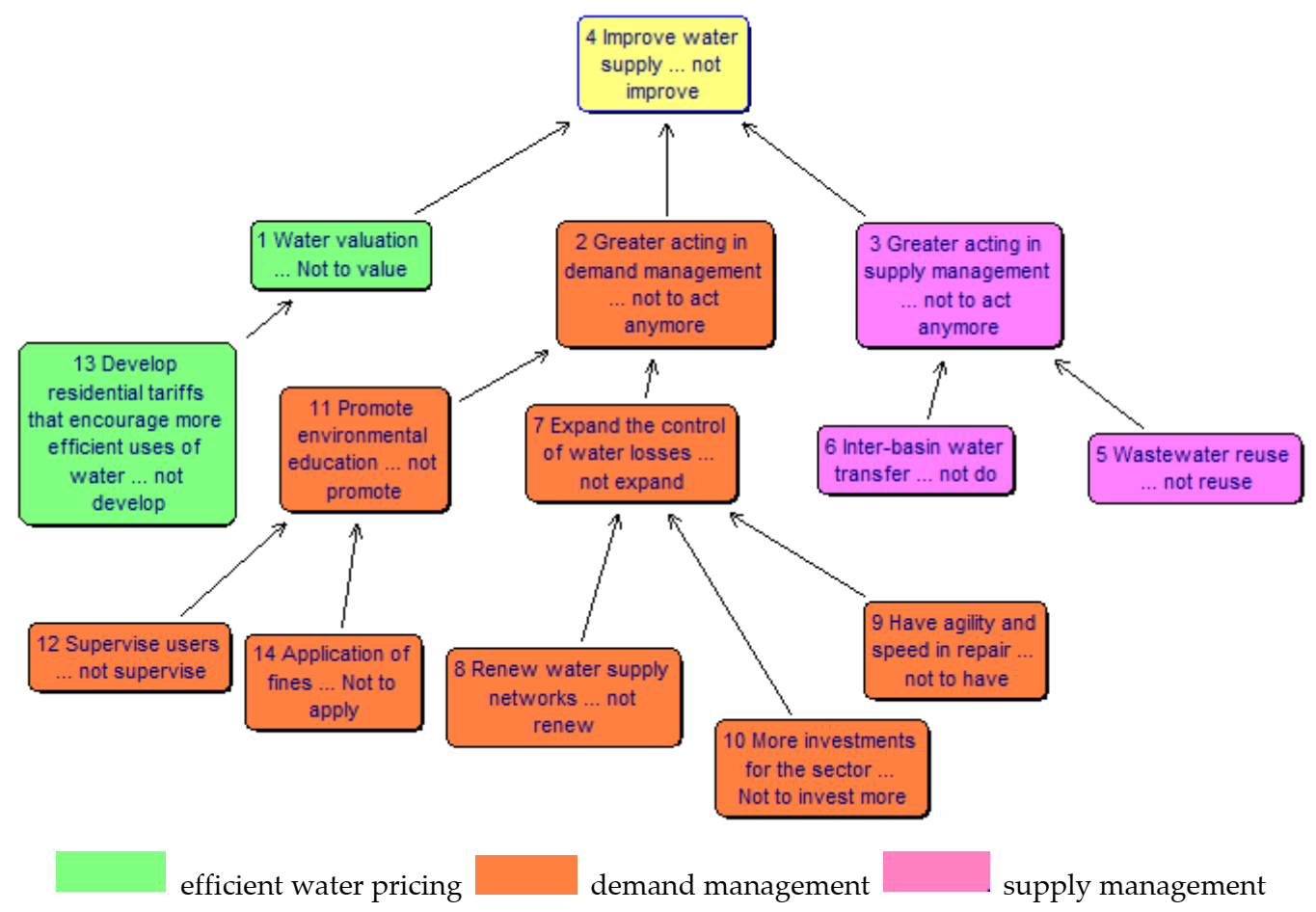
Step 2—Construction of the Congregated Cognitive Map
- Hierarchy of means-end concepts: Observing the congregated map, one can notice a relationship of influence between the concepts, where in the lower part of the map are located the “means” procedures, i.e., how it will achieve the objectives, and in the upper part are located the “ends” elements, which are the objectives;
- Concepts “heads” and “tails”: As can be seen, the map has only one concept “head”, represented by the number 4, located at the top of the map. This concept was proposed as a central objective that seeks to improve the water supply for the case studied. The “tails” concepts are congregated in the map and are represented by the following numbers: 13, 12, 11, 14, 7, 8, 6, 5, 10, and 9. These concepts “tails”, as described in the theoretical framework, are called means to reach the strategic and fundamental objectives of decision makers;
- Feedback loops: No feedback loop has been verified on the map;
- Clusters: The map shows the presence of three clusters, namely: efficient water pricing, demand management and supply management. The clusters are highlighted with different colours on the map (Figure 7).
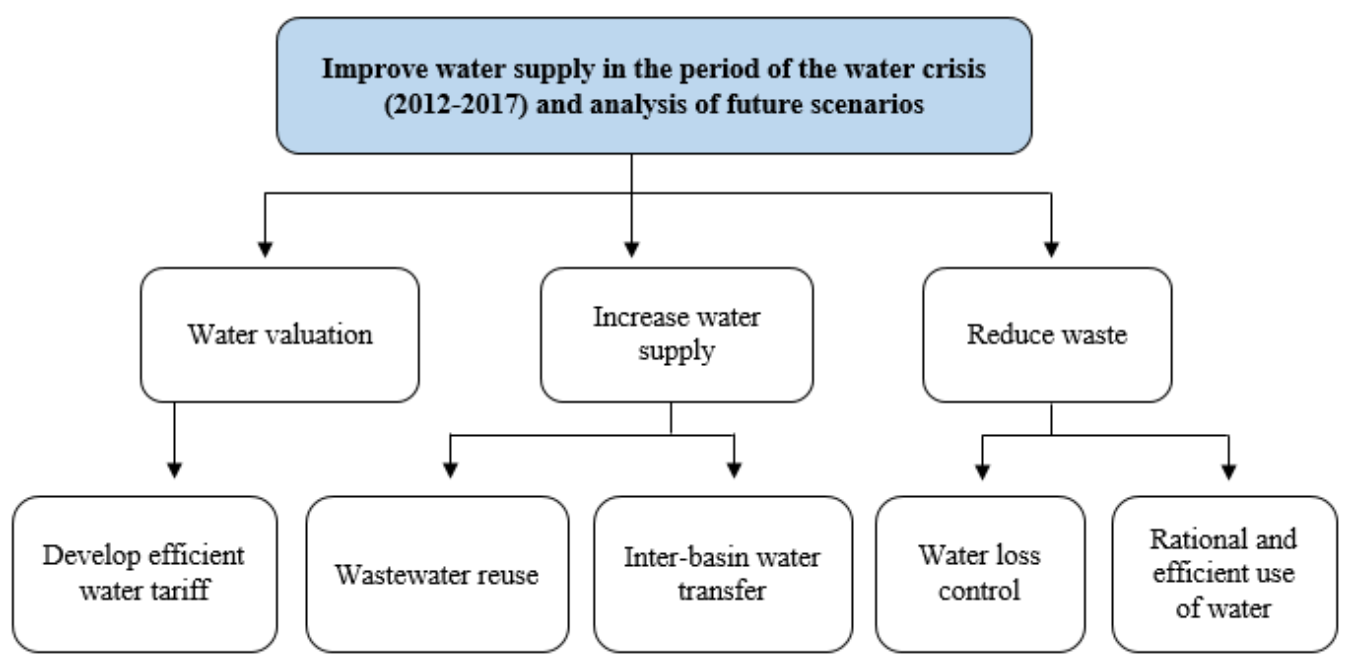
3.1.2. Construction of the Tree of Fundamental Viewpoints
3.2. Stage 2: Evaluation of Alternatives
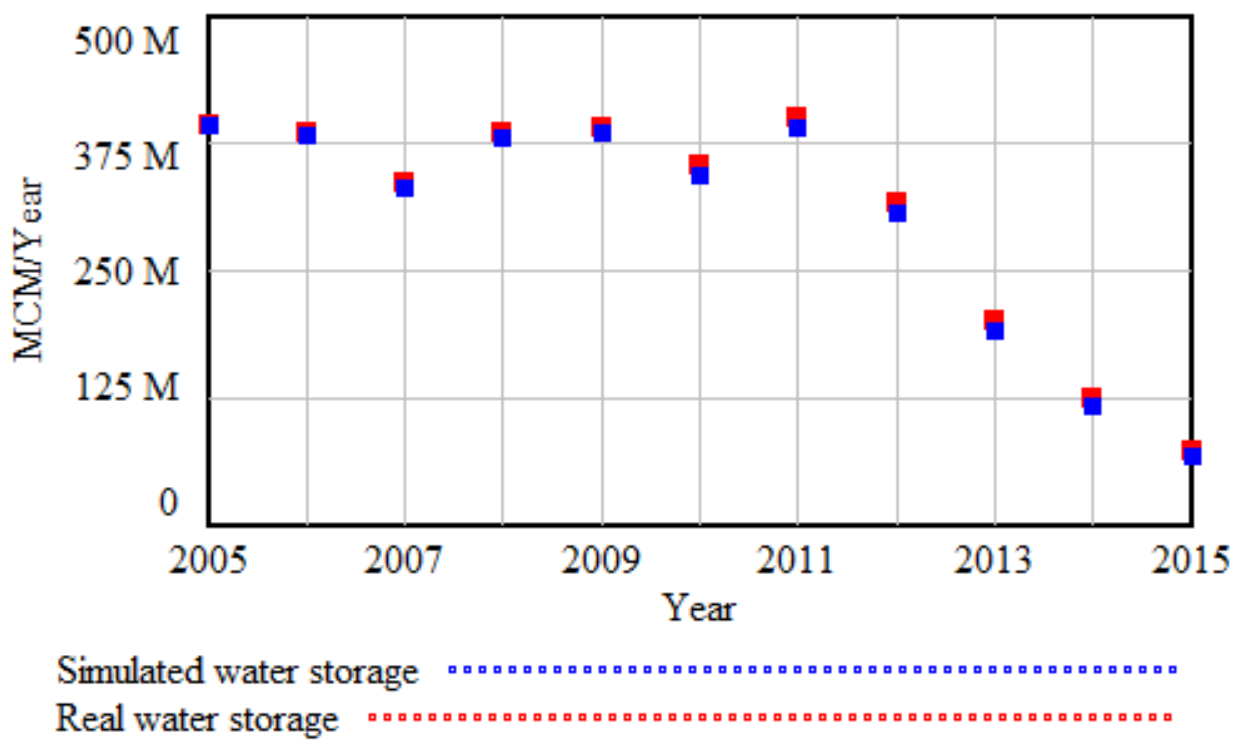
3.2.1. Model Validation
3.2.2. Model Simulation and Scenario Analysis
Simulation Results
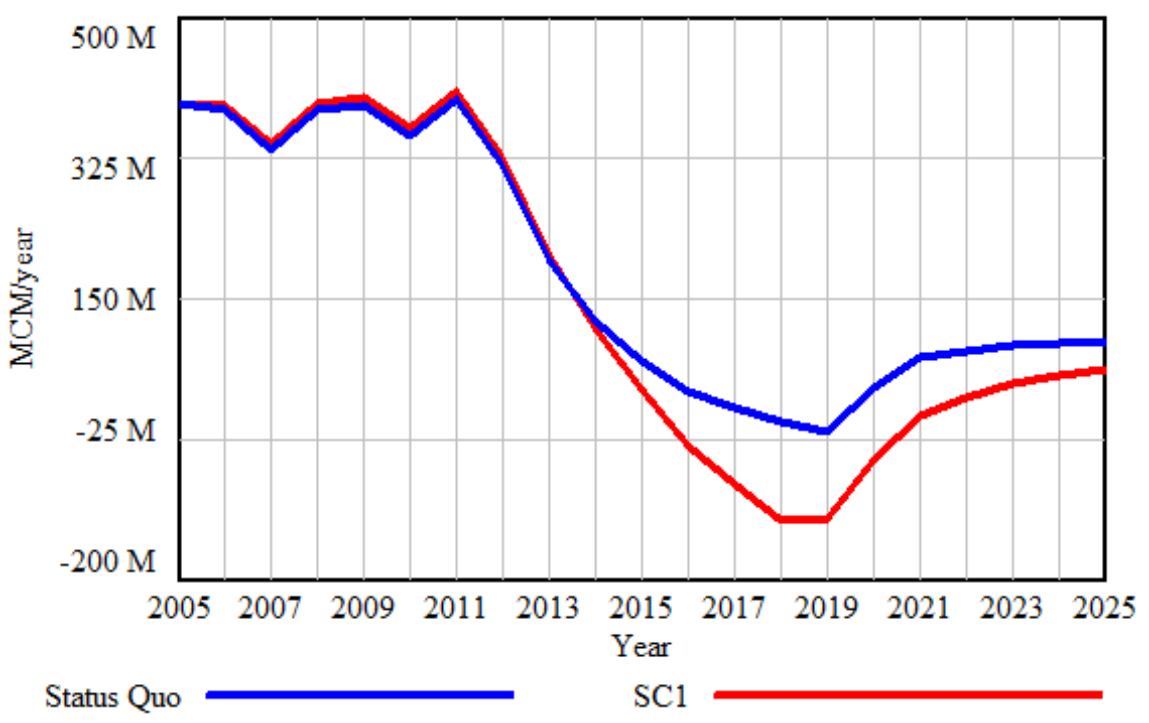
- Status Quo versus Scenario 1
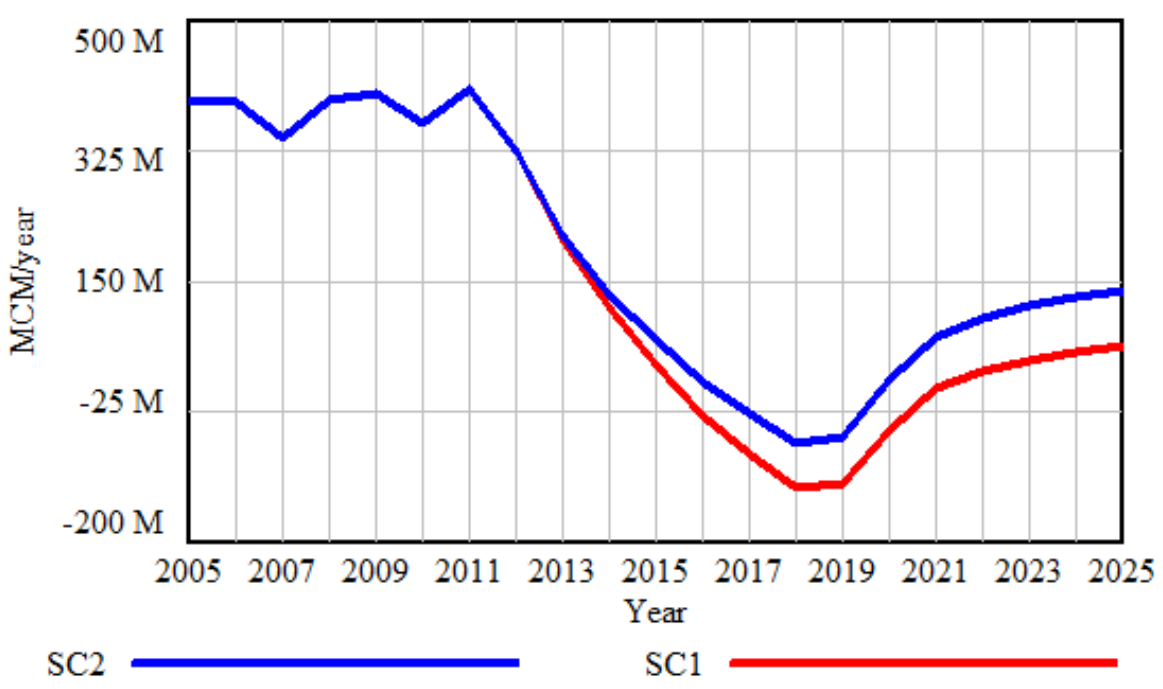
- Scenario 2 (Impacts of Scarcity-Based tariff on water conservation)
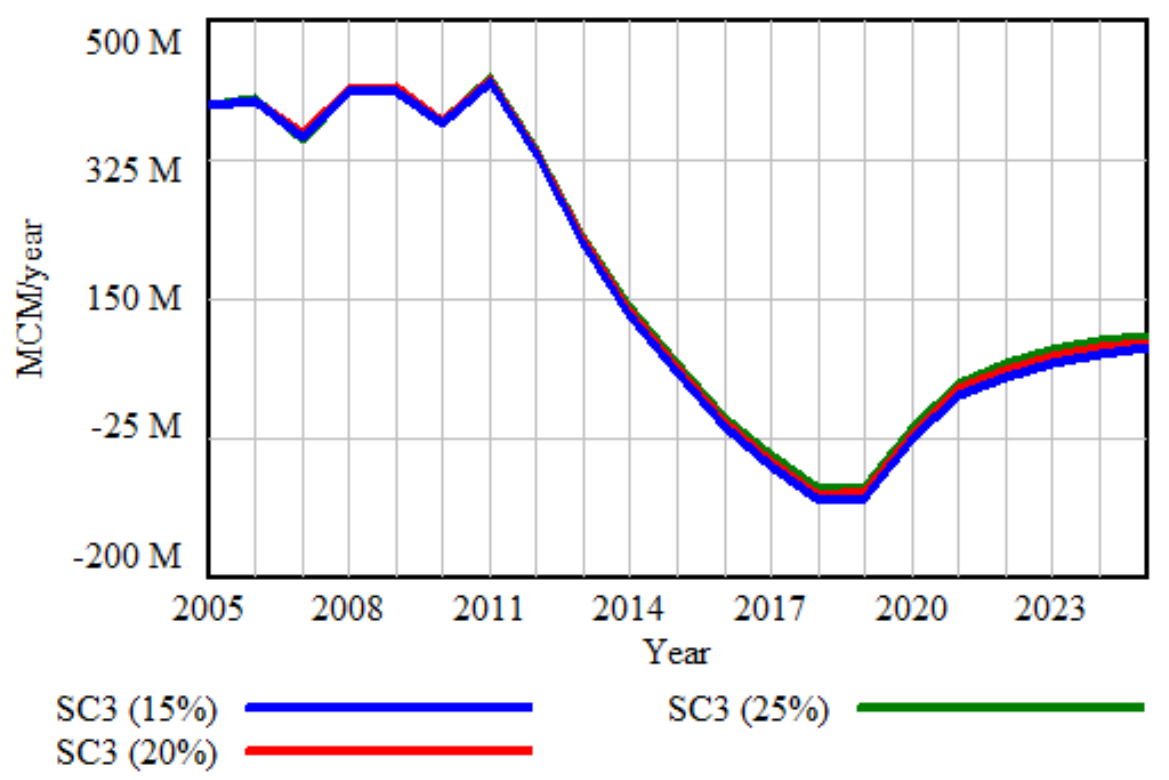
- Scenario 3 (Impacts of leakage control on water conservation)
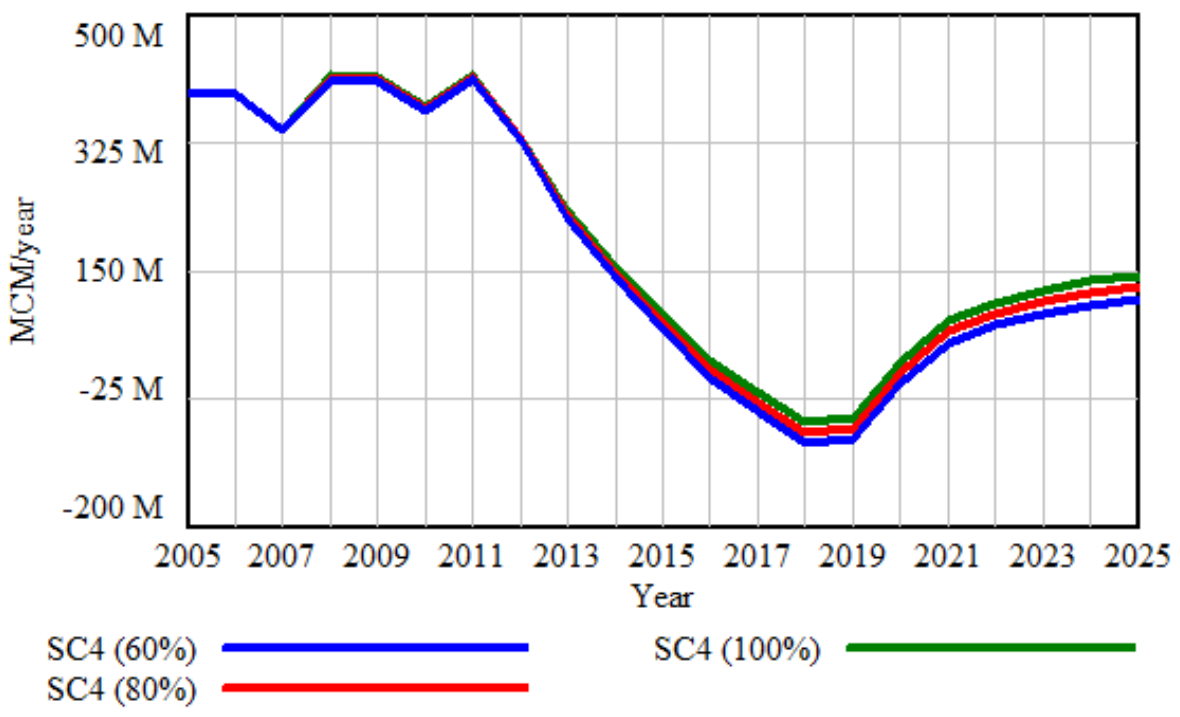
- Scenario 4 (Impacts of wastewater reuse on water supply)
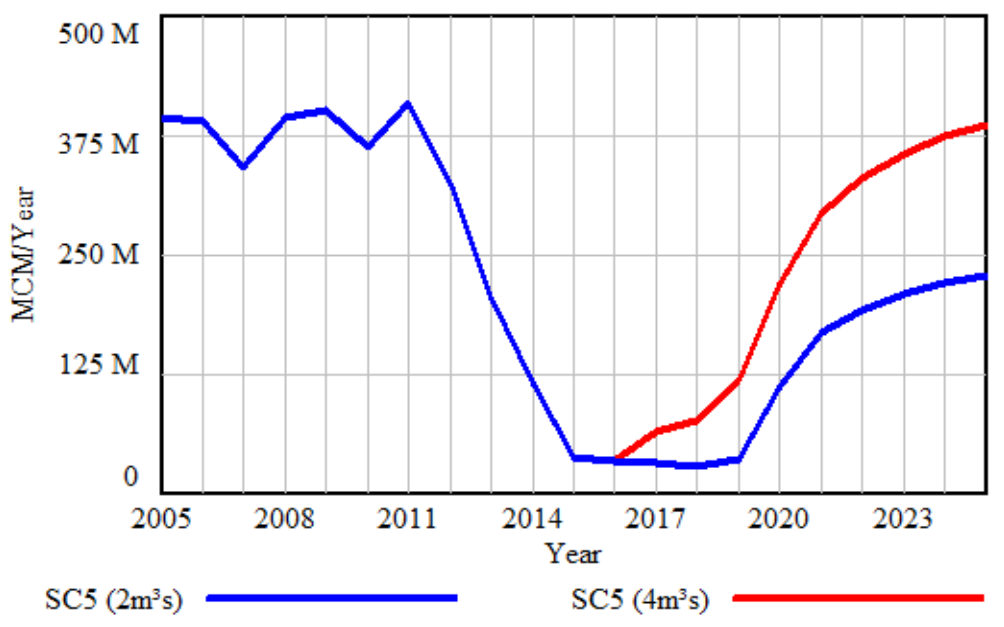
- Scenario 5 (Impacts of inter-basin water transfer on water supply)
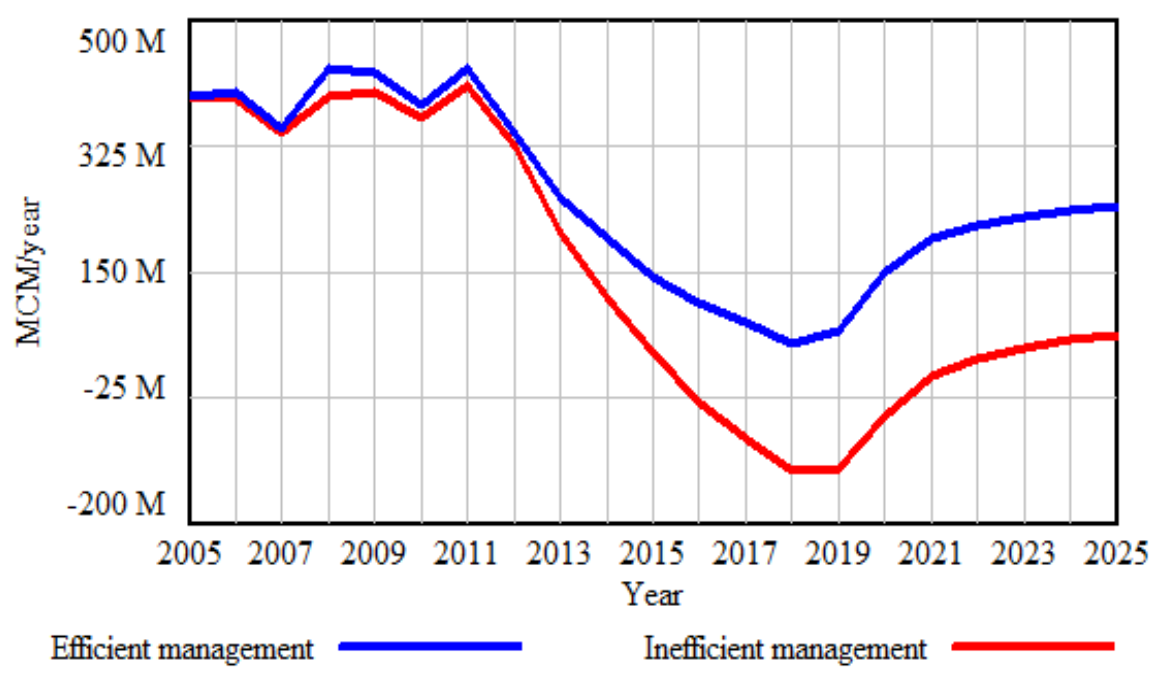
- Combining different scenarios
- -
- Efficient management: In which three types of management strategies were added, SBT, the reuse of wastewater for a scenario of 100% reuse and a control of losses with an index of 25%.
- -
- Inefficient management: No management strategy was taken into consideration.
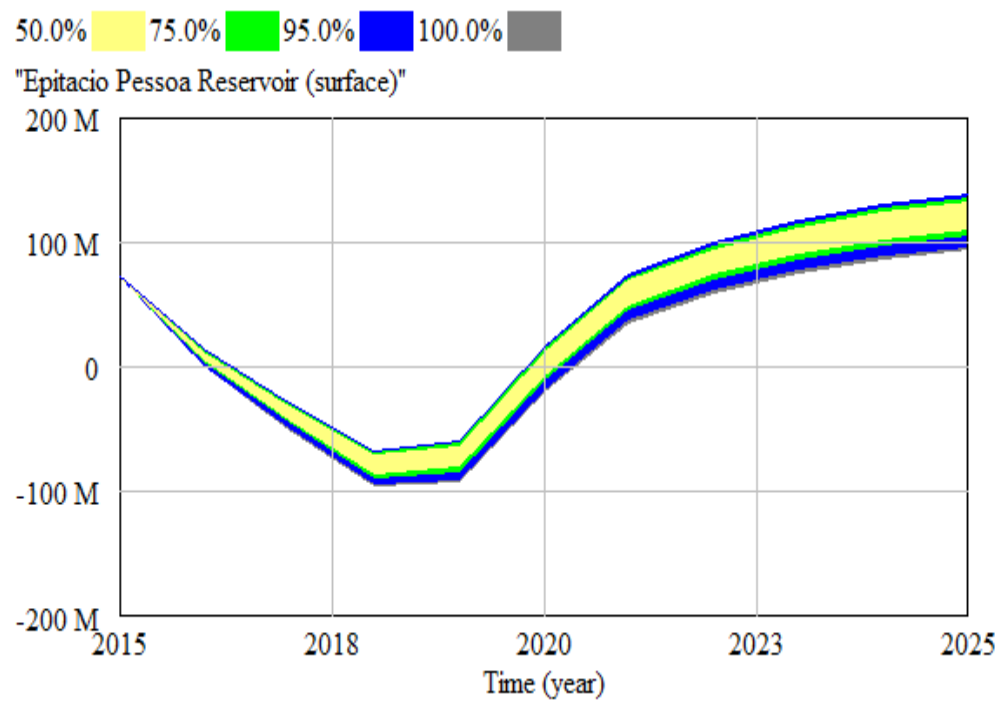
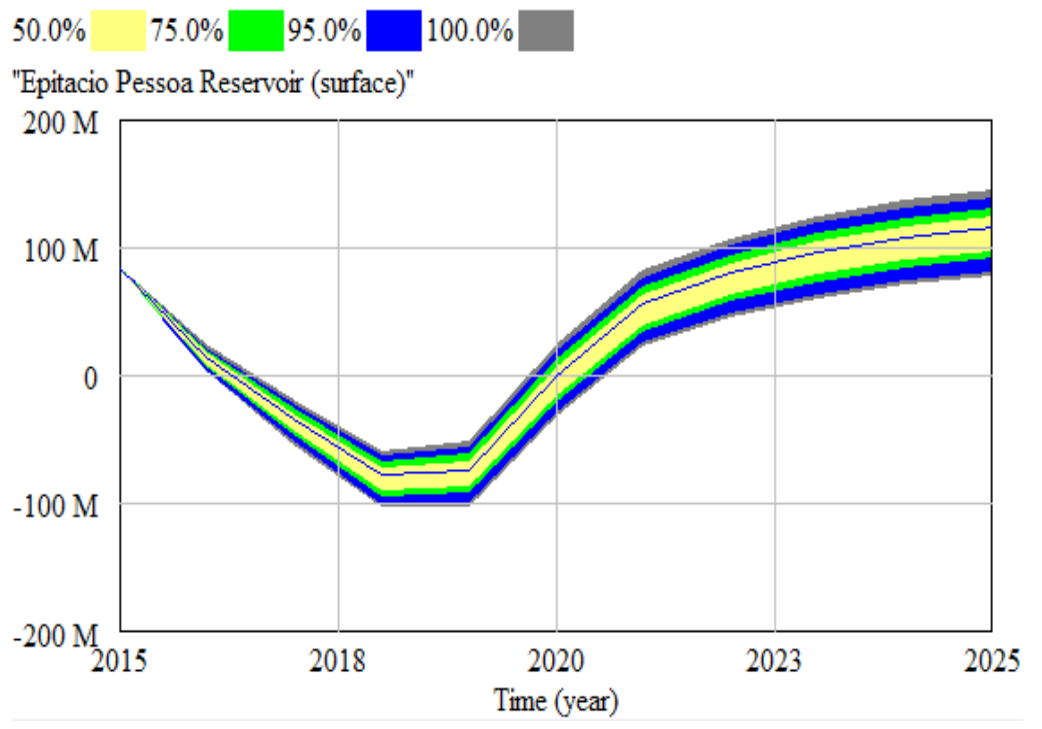
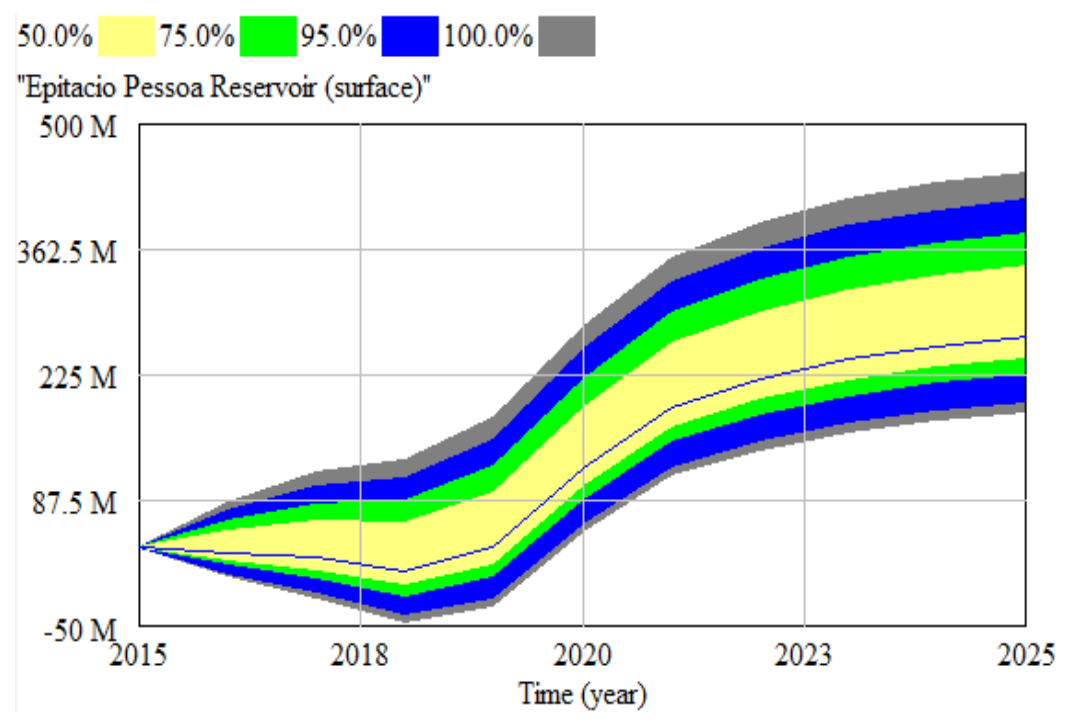
3.3. Uncertainty Simulation by Monte Carlo Simulation
4. Conclusions
- The elaboration of system dynamics models considering the SODA method in the problem identification and structuring phase can be an alternative for the construction of these system dynamics models, which are unable to provide a broad understanding of the problem considering its controversies and multiple decisions about the water management problem.
- The use of the insights generated from the interviews with the experts (construction of the cognitive maps of the SODA method) to assist the facilitator in the preparation of the causal and stock and flow models of the system dynamics, provided a greater understanding and ease when building these models.
- Another important contribution in this study was the development and application of a water tariff structure method, called here scarcity-based tariff (SBT), which encourages the rational use of water based on its availability in the reservoir, which in turn can increase revenue in times of low water stock levels and support investment in other water management strategies.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Individual Cognitive Maps
References
- United Nations. Available online: https://www.un.org/waterforlifedecade/sanitation.shtml (accessed on 21 January 2021).
- Balon, M.; Dehnad, F. Water crisis in arid and semi-arid regions: An international challenge. In Proceedings of the Symposium, Tehran, Iran, 12–13 September 2006. [Google Scholar]
- Araujo, W.C.; Esquerre, K.P.S.O.; Sahin, O. Building a System Dynamics Model to Support Water Management: A Case Study of the Semiarid Region in the Brazilian Northeast. Water 2019, 11, 2513. [Google Scholar] [CrossRef]
- Lucena, D.P.M.M. Simulations of the Implementation of Management Actions at Epitácio Pessoa and Their Impacts on the Water Crisis in Campina Grande-PB and Region. Master’s Thesis, Federal University Campina Grande, Campina Grande, Brazil, 2018. [Google Scholar]
- Grafton, R.Q.; Ward, M. Prices versus rationing: Marshallian surplus and mandatory water restrictions. Econ. Rec. 2008, 84, S57–S65. [Google Scholar] [CrossRef]
- Vairavamoorthy, K.; Gorantiwar, S.; Pathirana, A. Managing urban water supplies in developing countries e climate change and water scarcity scenarios. Phys. Chem. Earth 2008, 33, 330–339. [Google Scholar] [CrossRef]
- Grafton, R.Q.; Chu, L.; Kompas, T. Optimal water tariffs and supply augmentation for cost-of-service regulated water utilities. Util. Policy 2015, 34, 54–62. [Google Scholar] [CrossRef]
- Sahin, O.; Stewart, R.A.; Porter, G. Water security through scarcity pricing and reverse osmosis: A system dynamics approach. J. Clean. Prod. 2014, 88, 60–171. [Google Scholar] [CrossRef]
- Nassery, H.R.; Adinehvand, R.; Salavitabar, A.; Barati, R. Water management using system dynamics modeling in semi-arid regions. Civ. Eng. J. 2017, 3, 766–778. [Google Scholar] [CrossRef]
- Bao, C.; He, D. Scenario Modeling of Urbanization Development and Water Scarcity Based on System Dynamics: A Case Study of Beijing–Tianjin–Hebei Urban Agglomeration, China. Int. J. Environ. Res. Public Health 2019, 16, 3834. [Google Scholar] [CrossRef]
- Santos, L.D.; Schlindwein, S.L.; Fantini, A.C.; Belderrain, M.C.N. Uma adaptação do método de estrutução de Problemas Strategic Options Development and Analisys (SODA) para auxiliar a criação de Modelos de Dinâmica de Sistemas. In Proceedings of the 14º Congresso Brasileiro de Sistemas, Goiania, Brazil, 25–26 October 2018. [Google Scholar]
- Hipel, K.W.; Fang, L.; Cullmann, J.; Bristow, M. Conflict Resolution in Water Resources and Environmental Management; Springer: Cham, Switzerland, 2015; 463p. [Google Scholar]
- Andrade, A.L.O.; Morais, D.C. Study of methods for structuring problems related to Negotiation and Group Decision for Water Resources Management. In Proceedings of the XXIII Scientific Initiation Congress UFPE, Pernambuco, Brazil, 6–7 April 2015. [Google Scholar]
- Eden, C.; Jones, S.; Sims, D. Messing about Problems: An Informal Structured Approach to Their Identification and Management, 1st ed.; Pergamon Press: Oxford, UK, 1983; 121p. [Google Scholar]
- Morita, T. Uma Hierarquia De Soda-map Para Apoio à Dinâmica De Sistemas. In Proceedings of the XLIII Simpósio Brasileiro de Pesquisa Operacional, São Paulo, Brazil, 15–18 August 2011. [Google Scholar]
- Agência Nacional das Águas (ANA). Reservoir Monitoring System. Available online: http://sar.ana.gov.br/ (accessed on 14 December 2018).
- Instituto Brasileiro de Geografia E Estatística (IBGE). Population Estimation. Available online: https://www.ibge.gov.br/estatisticas/sociais/populacao.html (accessed on 22 January 2019).
- Vieira, Z.M.C.L. Metodologia De Análise De Conflitos Na Implementação De Medidas De Gestão Da Demanda De Água. Ph.D. Thesis, Universidade Federal de Campina Grande, Campina Grande, Brazil, 2008; 371p. [Google Scholar]
- Nunes, T.H.C.; Galvão, C.O.; Rego, J.C. Rule curve for seasonal increasing of water concessions in reservoirs with low regularized discharges. Braz. Water. Resour. J. 2016, 21, 493–501. [Google Scholar] [CrossRef][Green Version]
- Sistema Nacional de Informações sobre Saneamento (SNIS). Portal Eletrônico. Brasília. Available online: http://www.snis.gov.br (accessed on 9 January 2019).
- Rêgo, J.C.; Galvão, C.O.; Ribeiro, M.M.R.; Albuquerque, J.P.T.; Nunes, T.H.C. New considerations on the management of the water resources of the Epitácio Pessoa dam—The drought 2012–2014. In Proceedings of the XII Brazilian Symposium on Water Resources, Rio Grande do Norte, Brazil, 4–7 November 2014. [Google Scholar]
- Rêgo, J.C.; Galvão, C.O.; Ribeiro, M.M.R.; Albuquerque, J.P.T.; Nunes, T.H.C. The crisis of the large campina supply: Actions of the managers, users, public power, press and population. In Proceedings of the XXI Brazilian Symposium on Water Resources, Brasília, Brazil, 22–27 November 2015. [Google Scholar]
- Barisa, A.; Rosa, M. A system dynamics model for CO2 emission mitigation policy design in road transport sector. Energy Procedia 2018, 147, 419–427. [Google Scholar] [CrossRef]
- Fontoura, W.B.; Chaves, G.D.L.D.; Ribeiro, G.M. The Brazilian urban mobility policy: The impact in São Paulo transport system using system dynamics. Transp. Policy 2019, 73, 51–61. [Google Scholar] [CrossRef]
- Newell, B.; Siri, J. A role for low-order system dynamics models in urban health policy making. Environ. Int. 2016, 95, 93–97. [Google Scholar] [CrossRef]
- Hill, A.; Camacho, O.M. A system dynamics modelling approach to assess the impact of launching a new nicotine product on population health outcomes. Regul. Toxicol. Pharm. 2017, 86, 265–278. [Google Scholar] [CrossRef]
- Recio, A.; Linares, C.; Díaz, J. System dynamics for predicting the impact of traffic noise on cardiovascular mortality in Madrid. Environ. Res. 2018, 167, 499–505. [Google Scholar] [CrossRef]
- Rusiawan, W.; Tjiptoherijanto, P.; Suganda, E.; Darmajanti, L. System dynamics modeling for urban economic growth and CO2 emission: A case study of Jakarta, Indonesia. Procedia Environ. Sci. 2015, 28, 330–340. [Google Scholar] [CrossRef]
- Azis, R.; Blumberga, A.; Bazbauers, G. The role of forest biotechonomy industry in the macroeconomic development model of the national economy of Latvia: A system dynamics approach. Energy Procedia 2017, 128, 32–37. [Google Scholar] [CrossRef]
- Fang, W.; An, H.; Li, H.; Gao, X.; Sun, X.; Zhong, W. Accessing on the sustainability of urban ecological-economic systems by means of a coupled emergy and system dynamics model: A case study of Beijing. Energy Policy 2017, 100, 326–337. [Google Scholar] [CrossRef]
- Allington, G.R.H.; Li, W.; Brown, D.G. Urbanization and environmental policy effects on the future availability of grazing resources on the Mongolian Plateau: Modeling socio-environmental system dynamics. Environ. Sci. Policy 2017, 68, 35–46. [Google Scholar] [CrossRef]
- Wu, D.; Ning, S. Dynamic assessment of urban economy-environment-energy system using system dynamics model: A case study in beijing. Environ. Res. 2018, 164, 70–84. [Google Scholar] [CrossRef]
- Gottschamer, L.; Zhang, Q. The dynamics of political power: The socio-technical transition of California’s electricity system to renewable energy. Energy Res. Soc. Sci. 2020, 70, 101618. [Google Scholar] [CrossRef]
- Duran-Encalada, J.; Paucar-Caceres, A.; Bandala, E.; Wright, G. The impact of global climate change on water quantity and quality: A system dynamics approach to the US–Mexican transborder region. Eur. J. Oper. Res. 2016, 256, 567–581. [Google Scholar] [CrossRef]
- Wang, K.; Davies, E.G.; Liu, J. Integrated water resources management and modeling: A case study of Bow river basin. Can. J. Clean. Prod. 2019, 240, 118242. [Google Scholar] [CrossRef]
- Rubio-Martins, A.; Pulido-Velazquez, M.; Macian-Sorribes, H.; Garcia-Prats, A. System Dynamics Modeling for Supporting Drought-Oriented Management of the Jucar River System, Spain. Water 2020, 12, 1407. [Google Scholar] [CrossRef]
- Dai, S.S.; Li, L.H.; Xu, H.G.; Pan, X.L.; Li, X.M. A system dynamics approach for water resources policy analysis in arid land: A model for Manas River Basin. J. Arid Land. 2013, 5, 118–131. [Google Scholar] [CrossRef]
- Dawadi, S.; Ahmad, S. Evaluating the impact of demand-side management on water resources under changing climatic conditions and increasing population. J. Environ. Manag. 2013, 114, 261–275. [Google Scholar] [CrossRef] [PubMed]
- Sahin, O.; Siems, R.S.; Stewart, R.A.; Porter, M.G. Paradigm shift to enhanced water supply planning through augmented grids, scarcity pricing and adaptive factory water: A system dynamics approach. Environ. Model. Softw. 2016, 75, 348–361. [Google Scholar] [CrossRef]
- Park, S.; Sahleh, V.; Jung, S.Y. A System Dynamics Computer Model to Assess the Effects of Developing an Alternate Water Source on the Water Supply Systems Management. Procedia Eng. 2015, 119, 753–760. [Google Scholar] [CrossRef][Green Version]
- Huanhuan, Q.; Baoxiang, Z.; Fanhai, M. System dynamics modeling for sustainable water management of a coastal area in Shandong Province, China. J. Earth Sci. Eng. 2016, 4, 226–234. [Google Scholar] [CrossRef]
- Weil, T.; Lou, I.; Yang, Z.; Li, Y. A System dynamics urban water management model for Macau, China. J. Environ. Sci. 2016, 50, 117–126. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Zarghami, M. Should water supply for megacities depend on outside resources? A Monte-Carlo system dynamics simulation for Shiraz, Iran. Sustain. Cities Soc. 2019, 44, 163–170. [Google Scholar] [CrossRef]
- Tianhong, L.; Songnan, Y.; Mingxin, T. Simulation and optimization of water supply and demand balance in Shenzhen: A system dynamics approach. J. Clean. Prod. 2018, 207, 882–893. [Google Scholar] [CrossRef]
- Bakhshianlamouki, E.; Masia, S.; Karimi, P.; Van Der Zaag, P.; Susnik, J. A system dynamics model to quantify the impacts of restoration measures on the water-energy-food nexus in the Urmia lake Basin, Iran. Sci. Total Environ. 2020, 708, 134874. [Google Scholar] [CrossRef]
- Ravar, Z.; Zahraie, B.; Sharifinejad, A.; Gozini, H.; Jafari, S. System dynamics modeling for assessment of water-food-energy resources security and nexus in Gavkhuni basin in Iran. Ecol. Indic. 2020, 108, 105682. [Google Scholar] [CrossRef]
- Zarghami, M.; Akbariyeh, S. System dynamics modeling for complex urban water systems: Application to the city of Tabriz, Iran. Resour. Conserv. Recycl. 2012, 60, 99–106. [Google Scholar] [CrossRef]
- Companhia de Água E Esgoto da Paraiba (CAGEPA). Management and Sustainability Report–2018. Available online: http://www.cagepa.pb.gov.br/wp-content/uploads/2019/04/Relat%C3%B3rio_da_Administra%C3%A7%C3%A3o_e_de_Sustentabilidade_e_Balan%C3%A7o_2018.pdf (accessed on 18 April 2020).
- Del Grande, M.H.; Galvão, C.O.; Miranda, L.I.B.; Guerra, S.L.D. A percepção de usuários sobre os impactos do racionamento de água em suas rotinas domiciliares. Amb. Soc. 2016, 19, 163–182. [Google Scholar] [CrossRef]
- Santos, P.R.; Curo, R.S.G.; Balderrain, M.C.N. Aplicação do mapa cognitivo a um problema de decisão do setor aeroespacial de defesa do Brasil. J. Aeros. Technol. Manag. 2011, 3, 215–226. [Google Scholar] [CrossRef]
- Banxia. Decision Explorer Online Reference; Version 3.3; Banxia Software Limited: Kendal, UK, 2005. [Google Scholar]
- Tajra, S.M. Healthy Cities, Utopia and Complexity in Urban Planning: A Study of the Portuguese Network of Healthy Municipalities and Reflections for the Brazilian Scenario. Ph.D. Thesis, Universidade do Vale do Paraíba, São José dos Campos, Brazil, 2018. [Google Scholar]
- Ventana Systems. Vensim DSS, 7, 2nd ed.; Ventana Systems, Inc.: Harvard, MA, USA, 2018. [Google Scholar]
- Agência Nacional das Águas (ANA). Information Note nº 11/2017/COMAR/SER. 2017. Available online: https://www.ana.gov.br/regulacao/resolucoes-e-normativos/regras-especiais-de-uso-da-agua/marcos-regulatorios/nt_11_2017_comar_sre.pdf (accessed on 16 February 2019).
- Medeiros, P.C.; Ribeiro, M.M.R. Elasticidade de preço da demanda por água na bacia do rio Paraíba. In Proceedings of the VIII Simpósio de Recursos Hídricos do Nordeste, Gravatá, Pernambuco, Brazil, 17–20 October 2006. [Google Scholar]
- Bank of Northeast Brazil. Study of Water Demand in the Northeast and Update of the Cost-Efficiency Indexes of Sanitary Sewage Projects in the Northeast of Brazil; PBLM—Consulting Ltd.: Fortaleza, Brazil, 1997. [Google Scholar]
- Firouzabadi, M.A.K. A Note on Models’ Verification, Validation and Calibration. Int. J. Hum. 2012, 19, 15–32. [Google Scholar]
- Wagner, P.R.; Fahrni, R.; Klippel, M.; Frangi, A.; Sudret, B. Bayesian calibration and sensitivity analysis of heat transfer models for fire insulation panels. Eng. Struct. 2020, 205, 1–51. [Google Scholar] [CrossRef]
- Barlas, Y. Formal Aspects of model Validity and validation in system dynamics. Syst. Dynam. Rev. 1996, 12, 193–210. [Google Scholar] [CrossRef]
- Van der Voorn, T.; Pahl-Wostl, C.; Quist, J. Combining backcasting and adaptive management for climate adaptation in coastal regions: A methodology and a South African case study. J. Futures 2012, 4, 346–364. [Google Scholar] [CrossRef]
| Aspects | Values |
|---|---|
| Drainage area (km2) | 6727.69 |
| Minimum Temperature (°C) | 18–22 |
| Maximum Temperature (°C) | 28–31 |
| Precipitation (mm/year) | 600 |
| Rainfall concentration period (months) | 4 (February–May) |
| Evaporation (mm/year) | 2000–2500 |
| Scenarios | Scenario Description | Wastewater Reuse (No/Yes) | PISF (No/Yes) | |||
|---|---|---|---|---|---|---|
| Population Growth (%) | Water Use (L/P/D) | Loss Control (LC) (No/Yes) | SB Tariff (No/Yes) | |||
| Status Quo | 1.0% | Varying | No | No | No | No |
| SC1 | 1.0% | 222 | No | No | No | No |
| SC2 | 1.0% | 22 | No | Yes | No | No |
| SC3 | 1.0% | 222 | Yes | No | No | No |
| SC4 | 1.0% | 222 | No | No | Yes | No |
| SC5 | 1.0% | 222 | No | No | No | Yes |
| Parameters | Initial Value | Sensitivity Test Range |
|---|---|---|
| Loss control coefficient | 0.15 | [0.1, 0.3] |
| Scarcity-based tariff | 1 | (0, 3) |
| Rate of reuse of wastewater | 0.6 | [0.1, 1] |
| Population growth rate | 0.01 | [0.001, 0.04] |
| Domestic demand per capita | 48 | (40, 55) |
| Water transfer rate between basins | 2 | (1, 4) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Araujo, W.C.; Oliveira-Esquerre, K.P.; Sahin, O. Development of a Multi-Methodological Approach to Support the Management of Water Supply Systems. Water 2021, 13, 1655. https://doi.org/10.3390/w13121655
de Araujo WC, Oliveira-Esquerre KP, Sahin O. Development of a Multi-Methodological Approach to Support the Management of Water Supply Systems. Water. 2021; 13(12):1655. https://doi.org/10.3390/w13121655
Chicago/Turabian Stylede Araujo, Wanderbeg C., Karla P. Oliveira-Esquerre, and Oz Sahin. 2021. "Development of a Multi-Methodological Approach to Support the Management of Water Supply Systems" Water 13, no. 12: 1655. https://doi.org/10.3390/w13121655
APA Stylede Araujo, W. C., Oliveira-Esquerre, K. P., & Sahin, O. (2021). Development of a Multi-Methodological Approach to Support the Management of Water Supply Systems. Water, 13(12), 1655. https://doi.org/10.3390/w13121655







