CFD Modeling of a Stirred Anaerobic Digestion Tank for Evaluating Energy Consumption through Mixing
Abstract
1. Introduction
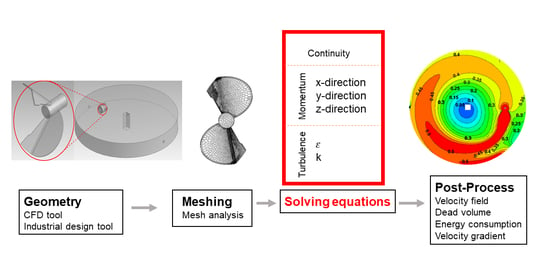
2. Materials and Methods
2.1. Geometry and Meshing
2.2. Assumptions
- Since the flow enters the digester for just 15 min during a six-hour period, the effect of the inlet and outlet flow is not significant.
- 2 m of the tank is filled by the feedstock.
- The shear-thinning non-Newtonian characteristics of the feedstock are considered.
- The density of the fluid is constant and calculated as 1001.7 kg/m3, based on [30].
- The effect of temperature is assumed as constant.
2.3. CFD Method
2.4. Equations
2.5. Physical Characteristics
2.6. Boundary and Zone Conditions
3. Results and Discussion
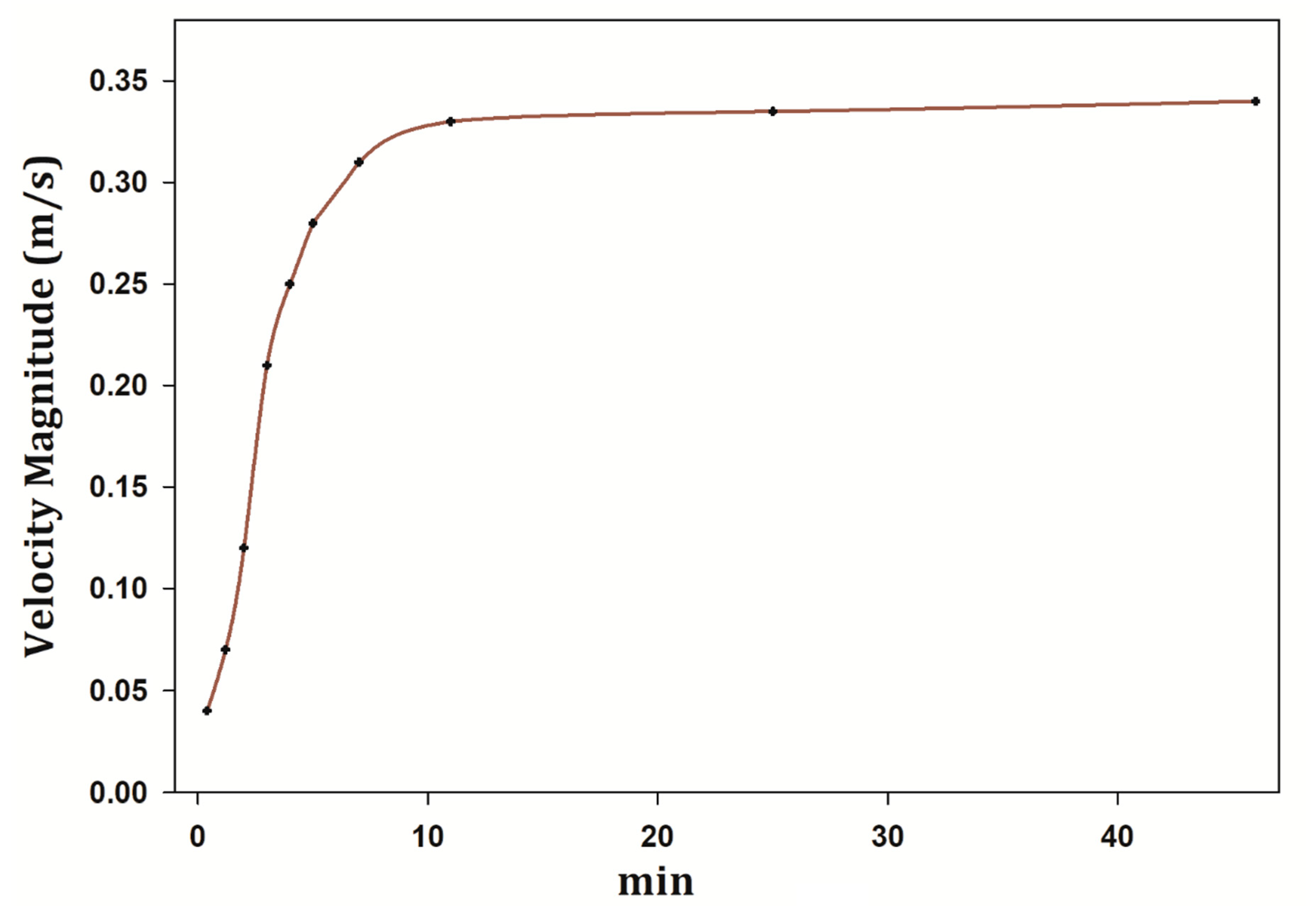
3.1. Validation
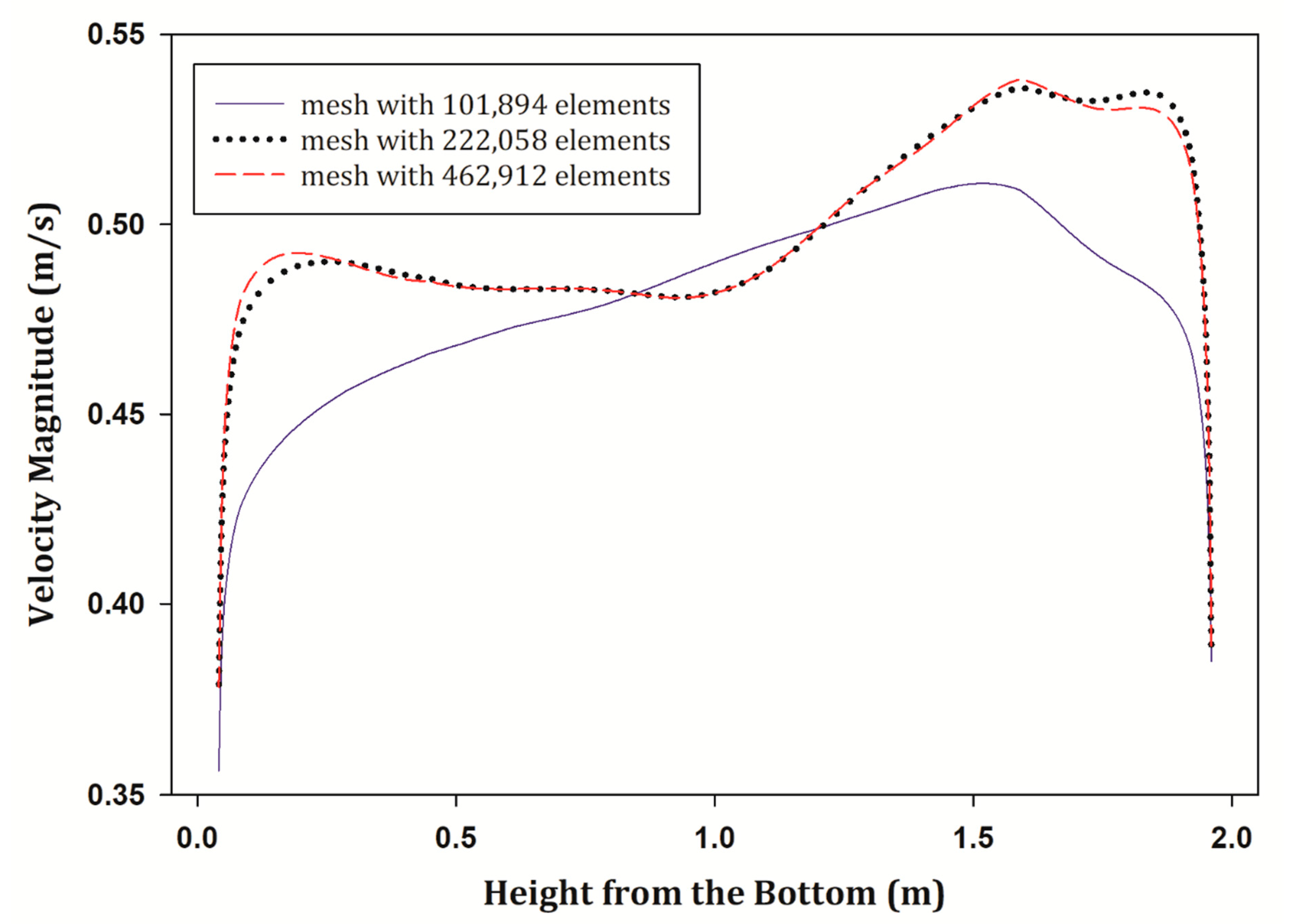
3.2. Grid Independence
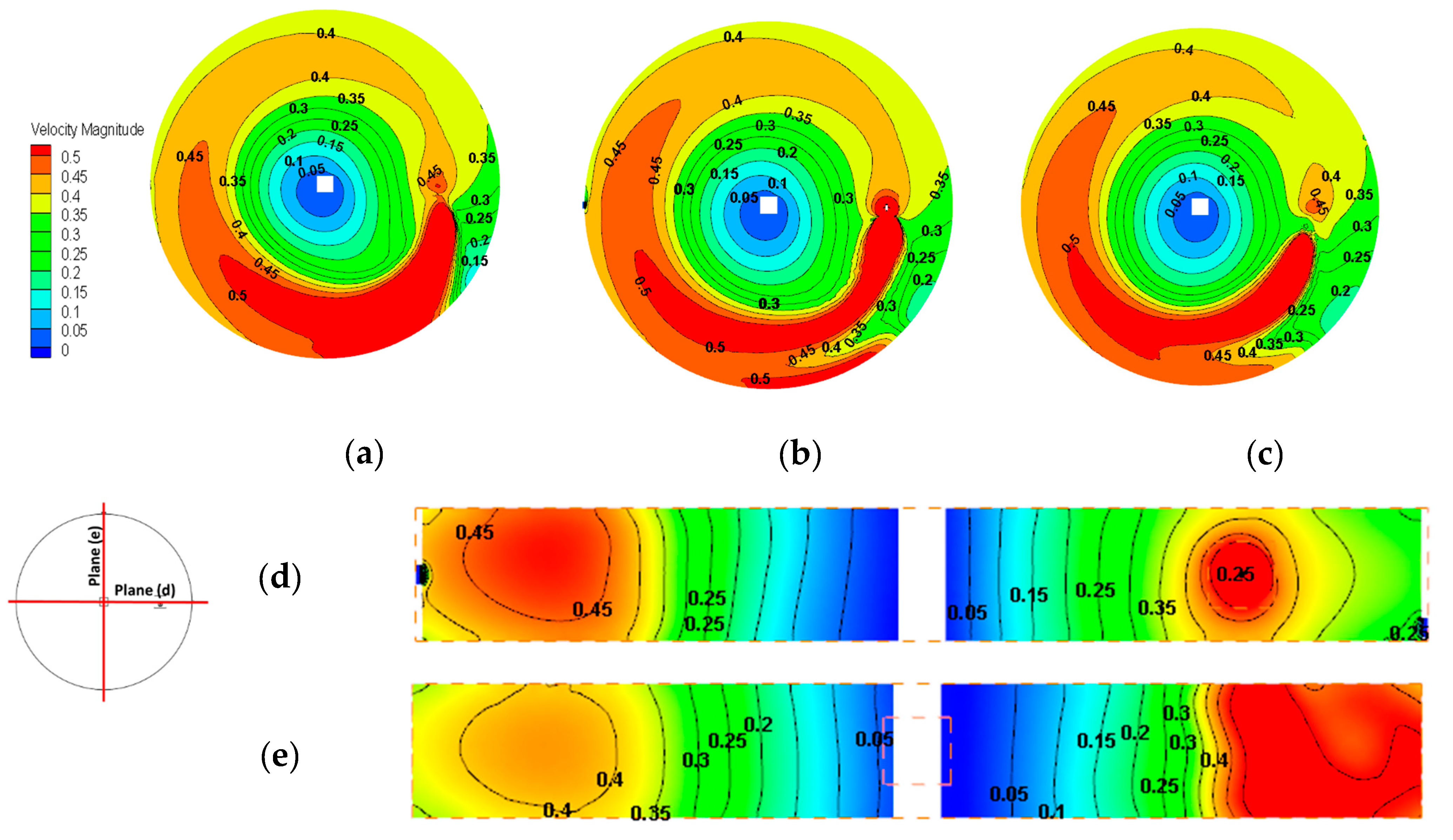
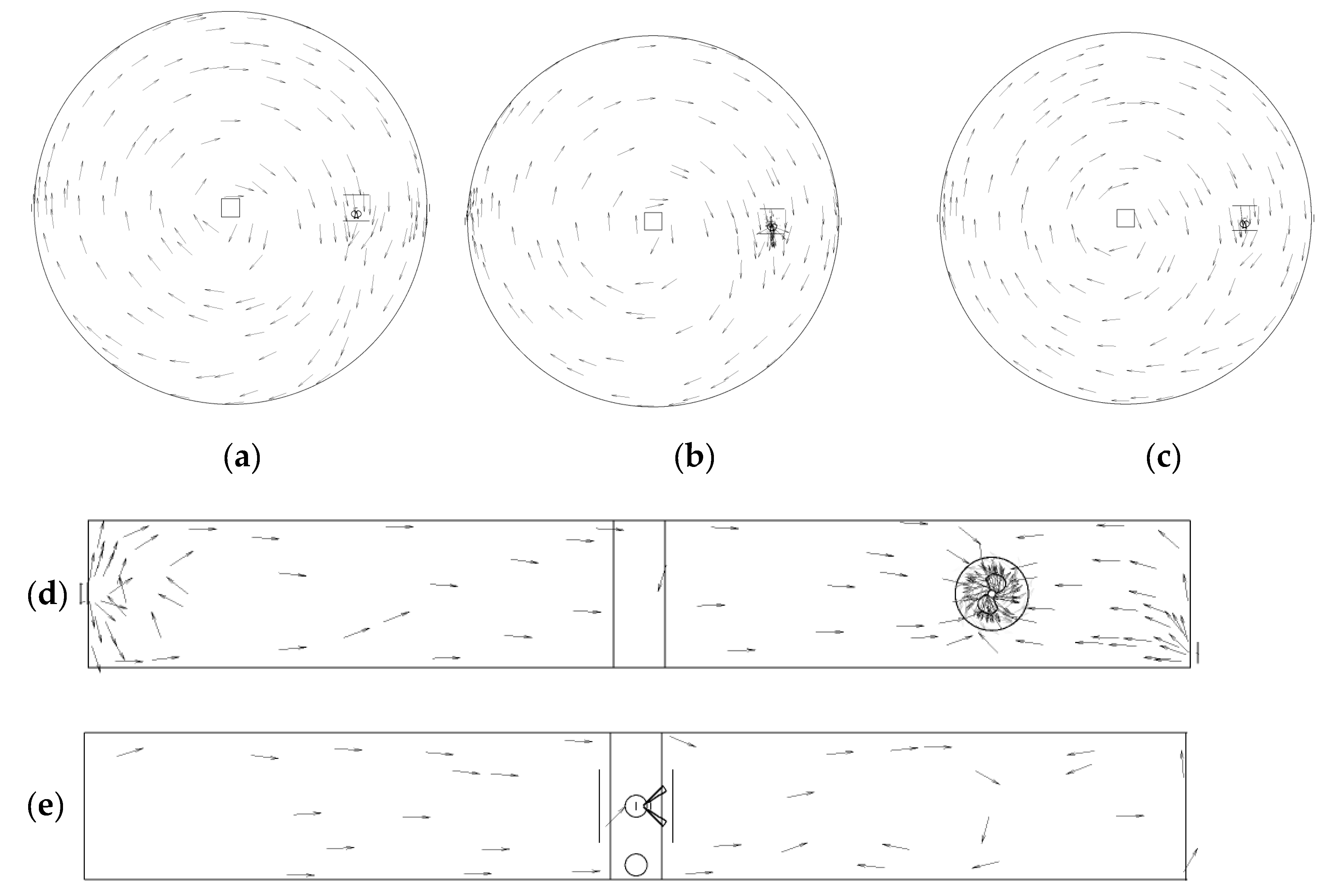
3.3. Contours and Vectors
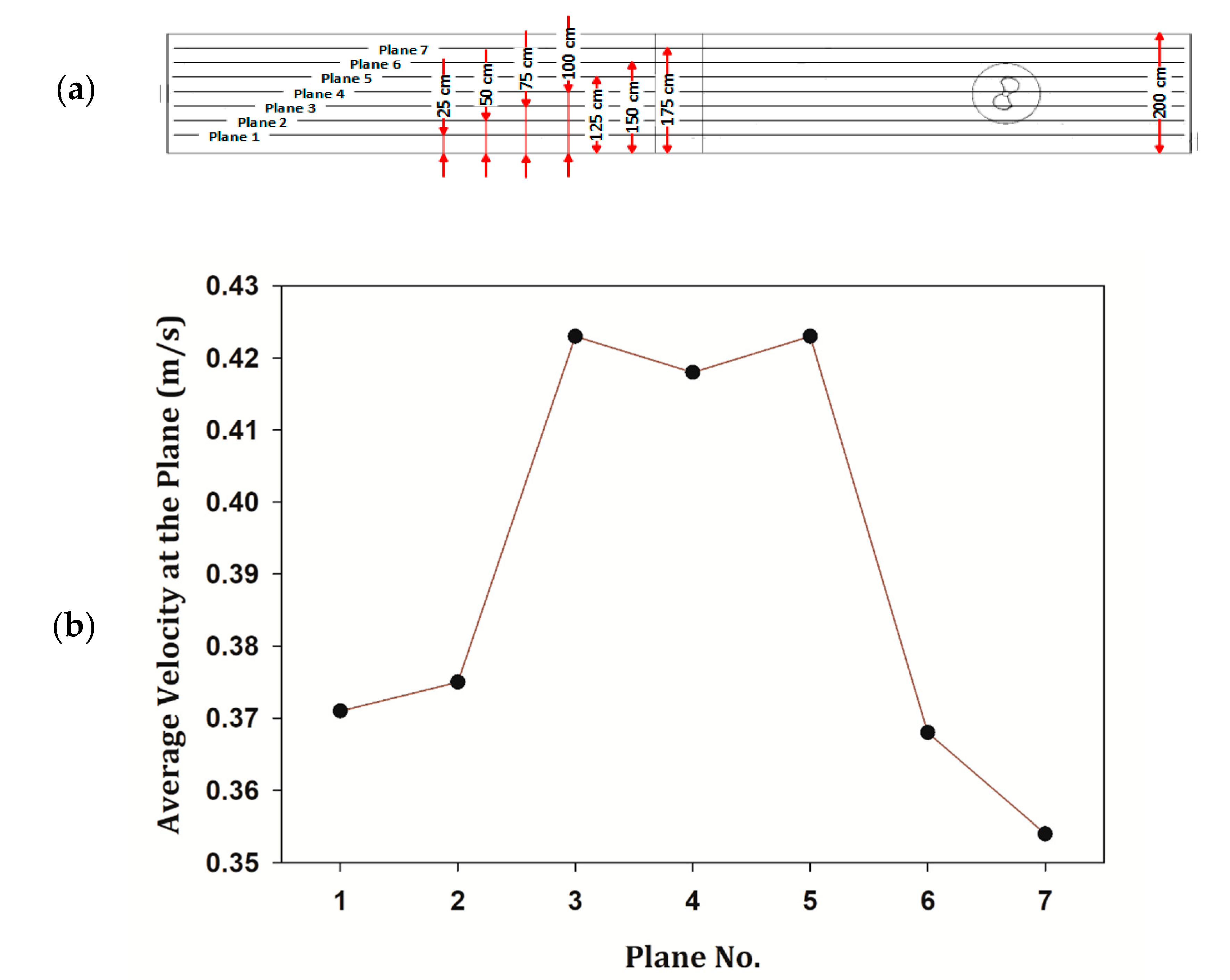
3.4. Data Analysis
4. Conclusions
- The dead zone was found near the central column and the walls of the digester because the applied mixer mostly affects the regions located at the same height and radial distance as the mixer.
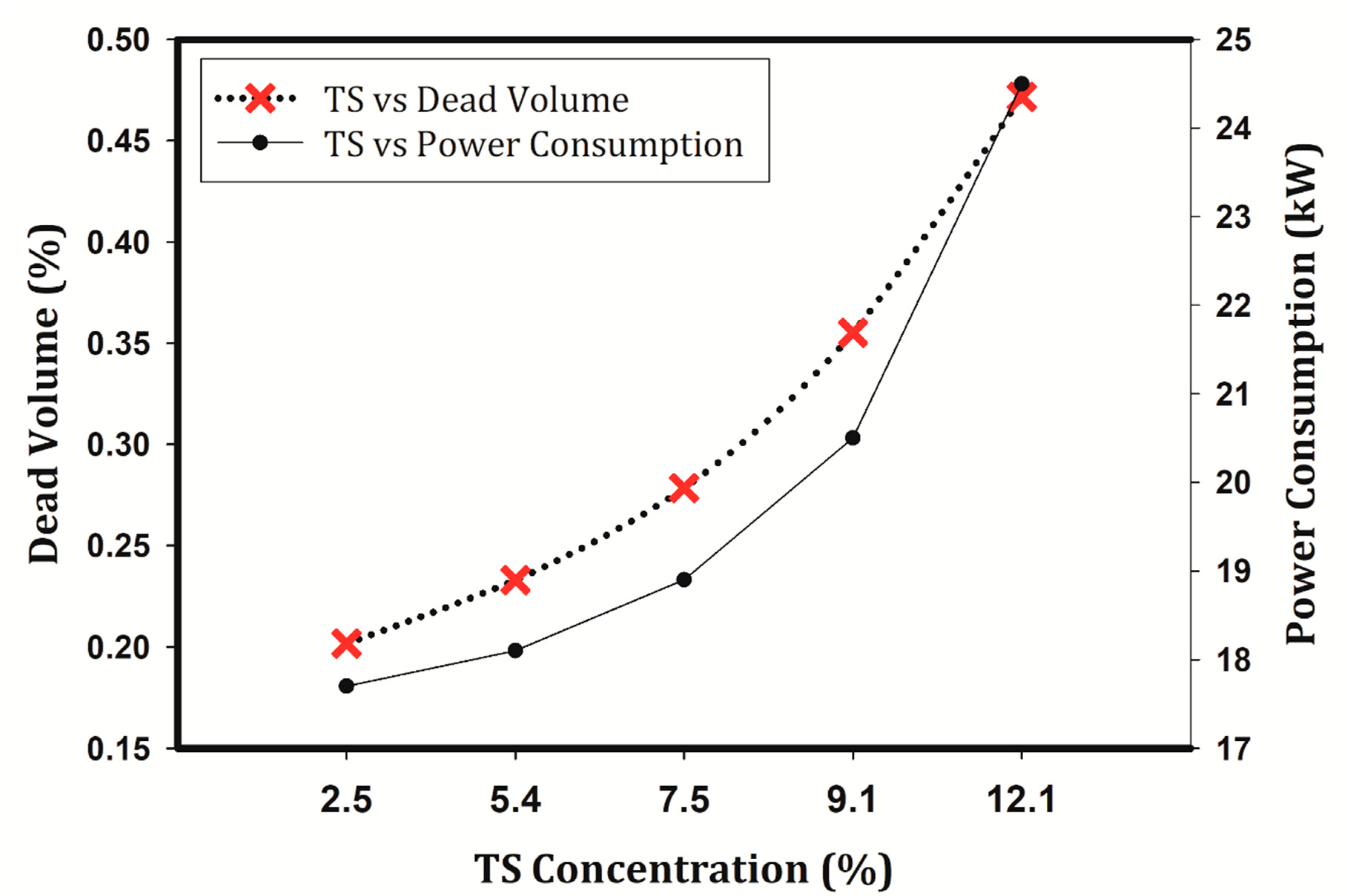
- Power consumption increases by increasing TS concentrations, especially at higher TS concentrations. Similarly, by increasing TS concentrations, the amount of dead volume increases considerably.
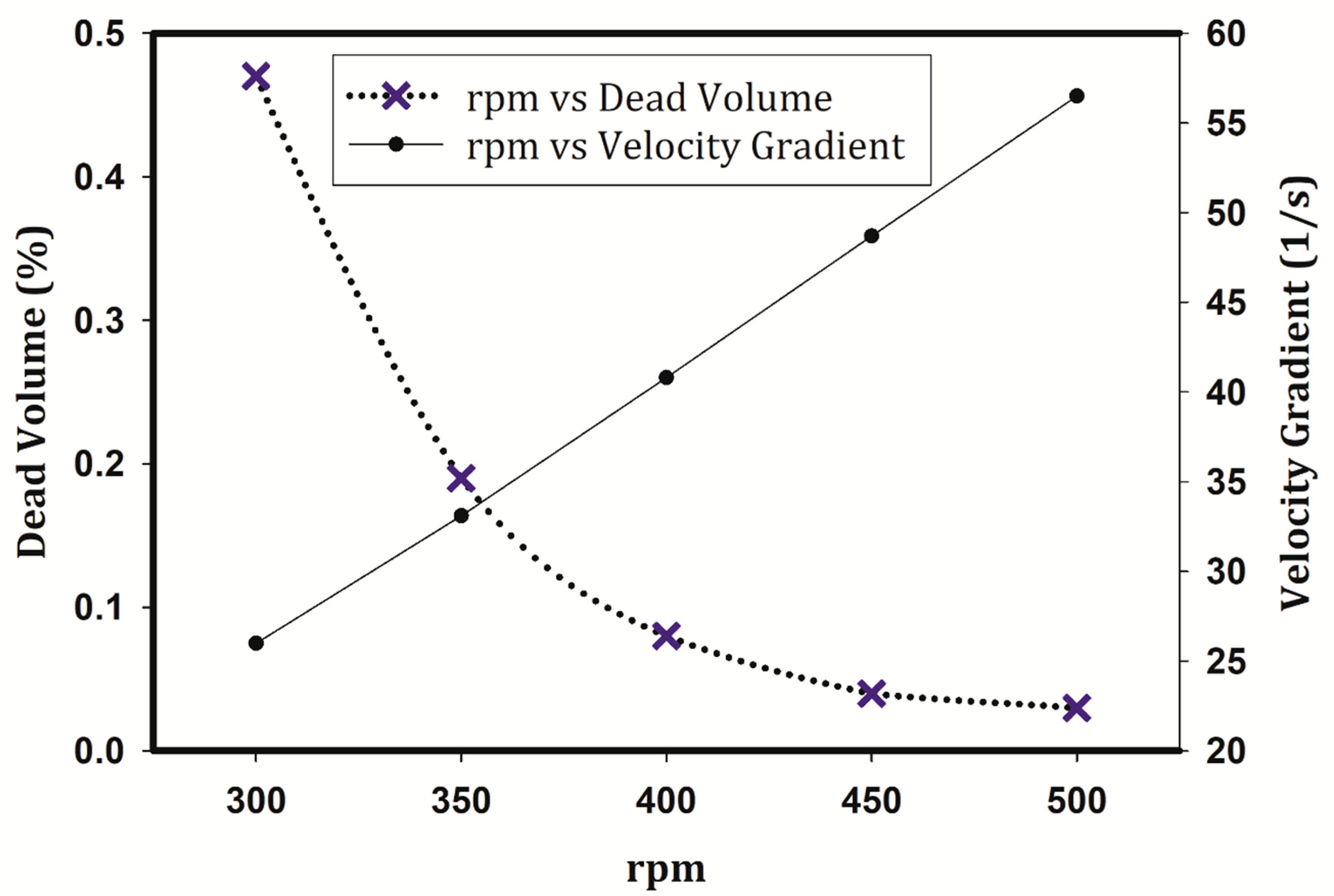
- There is not a huge change for dead volume once the mixer rotation speed increases to 400 rpm and higher, while the energy needed for mixing increases.
- It is not recommended to increase the mixer rotation speed to more than 300 rpm, since—besides the deteriorative effect of the higher velocity gradient—the energy consumption of the mixer increases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mitsch, W.J.; Bernal, B.; Nahlik, A.M.; Mander, Ü.; Zhang, L.; Anderson, C.J.; Jørgensen, S.E.; Brix, H. Wetlands, carbon, and climate change. Landsc. Ecol. 2013, 28, 583–597. [Google Scholar] [CrossRef]
- Bajpai, P. Anaerobic Technology in Pulp and Paper Industry; Springer: Singapore, 2017. [Google Scholar]
- Passos, F.; Ortega, V.; Donoso-Bravo, A. Thermochemical pretreatment and anaerobic digestion of dairy cow manure: Experimental and economic evaluation. Bioresour. Technol. 2017, 227, 239–246. [Google Scholar] [CrossRef] [PubMed]
- Sajjadi, B.; Raman, A.A.A.; Parthasarathy, R. Fluid dynamic analysis of non-Newtonian flow behavior of municipal sludge simulant in anaerobic digesters using submerged, recirculating jets. Chem. Eng. J. 2016, 298, 259–270. [Google Scholar] [CrossRef]
- Hamawand, I. Anaerobic digestion process and bio-energy in meat industry: A review and a potential. Renew. Sustain. Energy Rev. 2015, 44, 37–51. [Google Scholar] [CrossRef]
- Yang, L.; Kopsell, D.E.; Kottke, A.M.; Johnson, M.Q. Development of a cartridge design anaerobic digestion system for lignocellulosic biomass. Biosyst. Eng. 2017, 160, 134–139. [Google Scholar] [CrossRef]
- Melse, R.W.; Hol, J.M. Biofiltration of exhaust air from animal houses: Evaluation of removal efficiencies and practical experiences with biobeds at three field sites. Biosyst. Eng. 2017, 159, 59–69. [Google Scholar] [CrossRef]
- Guerci, M.; Knudsen, M.T.; Bava, L.; Zucali, M.; Schönbach, P.; Kristensen, T. Parameters affecting the environmental impact of a range of dairy farming systems in Denmark, Germany and Italy. J. Clean. Prod. 2013, 54, 133–141. [Google Scholar] [CrossRef]
- Turker, G.; Akyol, Ç.; Ince, O.; Aydin, S.; Ince, B. Operating conditions influence microbial community structures, elimination of the antibiotic resistance genes and metabolites during anaerobic digestion of cow manure in the presence of oxytetracycline. Ecotoxicol. Environ. Saf. 2018, 147, 349–356. [Google Scholar] [CrossRef]
- Fodor, Z.; Klemeš, J.J. Waste as alternative fuel–Minimising emissions and effluents by advanced design. Process Saf. Environ. Prot. 2012, 90, 263–284. [Google Scholar] [CrossRef]
- Coward, T.; Tribe, H.; Harvey, A.P. Opportunities for process intensification in the UK water industry: A review. J. Water Process Eng. 2018, 21, 116–126. [Google Scholar] [CrossRef]
- Rennie, T.J.; Baldé, H.; Gordon, R.J.; Smith, W.N.; VanderZaag, A.C. A 3-D model to predict the temperature of liquid manure within storage tanks. Biosysy. Eng. 2017, 163, 50–65. [Google Scholar] [CrossRef]
- Sindall, R.; Bridgeman, J.; Carliell-Marquet, C. Velocity gradient as a tool to characterise the link between mixing and biogas production in anaerobic waste digesters. Water Sci. Technol. 2013, 67, 2800–2806. [Google Scholar] [CrossRef] [PubMed]
- Low, S.C.; Eshtiaghi, N.; Slatter, P.; Baudez, J.-C.; Parthasarathy, R. Mixing characteristics of sludge simulant in a model anaerobic digester. Bioproc. Biosyst. Eng. 2016, 39, 473–483. [Google Scholar] [CrossRef] [PubMed]
- Wicklein, E.; Batstone, D.J.; Ducoste, J.; Laurent, J.; Griborio, A.; Wicks, J.; Saunders, S.; Samstag, R.; Potier, O.; Nopens, I. Good modelling practice in applying computational fluid dynamics for WWTP modelling. Water Sci. Tech. 2016, 73, 969–982. [Google Scholar] [CrossRef] [PubMed]
- ANSYS. Fluent 19.2 Theory Guide; ANSYS. Inc.: Canonsburg, PA, USA, 2018. [Google Scholar]
- Maluta, F.; Paglianti, A.; Montante, G. Modelling of biohydrogen production in stirred fermenters by Computational Fluid Dynamics. Process Saf. Environ. Protect. 2019, 125, 342–357. [Google Scholar] [CrossRef]
- Dapelo, D.; Bridgeman, J. A CFD strategy to retrofit an anaerobic digester to improve mixing performance in wastewater treatment. Water Sci. Technol. 2020, 81, 1646–1657. [Google Scholar] [CrossRef]
- Tobo, Y.M.; Rehman, U.; Bartacek, J.; Nopens, I. Partial integration of ADM1 into CFD: Understanding the impact of diffusion on anaerobic digestion mixing. Water Sci. Technol. 2020, 81, 1658–1667. [Google Scholar] [CrossRef]
- Zhang, Y.; Yu, G.; Yu, L.; Siddhu, M.A.H.; Gao, M.; Abdeltawab, A.A.; Al-Deyab, S.S.; Chen, X. Computational fluid dynamics study on mixing mode and power consumption in anaerobic mono-and co-digestion. Bioresour. Technol. 2016, 203, 166–172. [Google Scholar] [CrossRef]
- Bridgeman, J. Computational fluid dynamics modelling of sewage sludge mixing in an anaerobic digester. Adv. Eng. Softw. 2012, 44, 54–62. [Google Scholar] [CrossRef]
- Saini, A.K.; Paritosh, K.; Singh, A.K.; Vivekanand, V. CFD approach for pumped-recirculation mixing strategy in wastewater treatment: Minimizing power consumption, enhancing resource recovery in commercial anaerobic digester. J. Water Process Eng. 2020, 40, 101777. [Google Scholar] [CrossRef]
- Dapelo, D.; Alberini, F.; Bridgeman, J. Euler-Lagrange CFD modelling of unconfined gas mixing in anaerobic digestion. Water Res. 2015, 85, 497–511. [Google Scholar] [CrossRef] [PubMed]
- López-Jiménez, P.A.; Escudero-González, J.; Martínez, T.M.; Montañana, V.F.; Gualtieri, C. Application of CFD methods to an anaerobic digester: The case of Ontinyent WWTP, Valencia, Spain. J. Water Process Eng. 2015, 7, 131–140. [Google Scholar] [CrossRef]
- Meroney, R.N.; Sheker, R.E. CFD simulation of vertical linear motion mixing in anaerobic digester tanks. Water Environ. Res. 2014, 86, 816–827. [Google Scholar] [CrossRef] [PubMed]
- Meister, M.; Rezavand, M.; Ebner, C.; Pümpel, T.; Rauch, W. Mixing non-Newtonian flows in anaerobic digesters by impellers and pumped recirculation. Adv. Eng. Softw. 2018, 115, 194–203. [Google Scholar] [CrossRef]
- Low, S.C.; Eshtiaghi, N.; Shu, L.; Parthasarathy, R. Flow patterns in the mixing of sludge simulant with jet recirculation system. Process Saf. Environ. Protect. 2017, 112, 209–221. [Google Scholar] [CrossRef]
- Hernandez-Aguilar, E.; Alvarado-Lassman, A.; Osorio-Mirón, A.; Méndez-Contreras, J.M. Development of energy efficient mixing strategies in egg-shaped anaerobic reactors through 3D CFD simulation. J. Environ. Sci. Health A 2016, 51, 536–543. [Google Scholar] [CrossRef]
- EYS GmbH. Availabe online: https://www.eys-gmbh.de/ (accessed on 9 June 2021).
- Wu, B. CFD simulation of mixing in egg-shaped anaerobic digesters. Water Res. 2010, 44, 1507–1519. [Google Scholar] [CrossRef]
- Jamshidzadeh, M.; Kazemzadeh, A.; Ein-Mozaffari, F.; Lohi, A. Analysis of power consumption for gas dispersion in non-Newtonian fluids with a coaxial mixer: New correlations for Reynolds and power numbers. Chem. Eng. J. 2020, 401, 126002. [Google Scholar] [CrossRef]
- Li, J.; Deng, B.; Zhang, B.; Shen, X.; Kim, C.N. CFD simulation of an unbaffled stirred tank reactor driven by a magnetic rod: Assessment of turbulence models. Water Sci. Technol. 2015, 72, 1308–1318. [Google Scholar] [CrossRef]
- Gao, H.; Stenstrom, M. Evaluation of three turbulence models in predicting the steady state hydrodynamics of a secondary sedimentation tank. Water Res. 2018, 143, 445–456. [Google Scholar] [CrossRef]
- Orszag, S.A. Renormalisation group modelling and turbulence simulations. In Proceedings of the International Conference on Near Wall Turbulent Flows, Tempe, The Netherlands, 15–17 March 1993; pp. 1031–1046. [Google Scholar]
- Barrio, R.; Blanco, E.; Fernández, J.; Galdo, M. The use of computational fluid dynamics to estimate fluid residence time and flow hydrodynamics in open digesters of wastewater treatment plants: A case study. Desalination Water Treat. 2015, 53, 2613–2622. [Google Scholar] [CrossRef]
- White, F.M. Fluid Mechanics, 5th ed.; McGraw-Hill Book Company: Boston, MA, USA, 2003. [Google Scholar]
- Hurtado, F.; Kaiser, A.; Zamora, B. Fluid dynamic analysis of a continuous stirred tank reactor for technical optimization of wastewater digestion. Water Res. 2015, 71, 282–293. [Google Scholar] [CrossRef] [PubMed]
- Achkari-Begdouri, A.; Goodrich, P.R. Rheological properties of Moroccan dairy cattle manure. Bioresour. Technol. 1992, 40, 149–156. [Google Scholar] [CrossRef]
- Hoseini, S.; Najafi, G.; Ghobadian, B.; Akbarzadeh, A. Impeller shape-optimization of stirred-tank reactor: CFD and fluid structure interaction analyses. Chem. Eng. J. 2020, 413, 127497. [Google Scholar] [CrossRef]
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for estimation and reporting of uncertainty due to discretization in CFD applications. J. Fluid. Eng. T. ASME 2008, 130, 078001. [Google Scholar]
- Vesvikar, M.S.; Al-Dahhan, M. Flow pattern visualization in a mimic anaerobic digester using CFD. Biotechnol. Bioeng. 2005, 89, 719–732. [Google Scholar] [CrossRef]
- Zhang, D. Optimize Sedimentation Tank and Lab Flocculation Unit by CFD; Norwegian University of Life Sciences: As, Norway, 2014. [Google Scholar]
- Latha, K.; Velraj, R.; Shanmugam, P.; Sivanesan, S. Mixing strategies of high solids anaerobic co-digestion using food waste with sewage sludge for enhanced biogas production. J. Clean. Prod. 2019, 210, 388–400. [Google Scholar] [CrossRef]
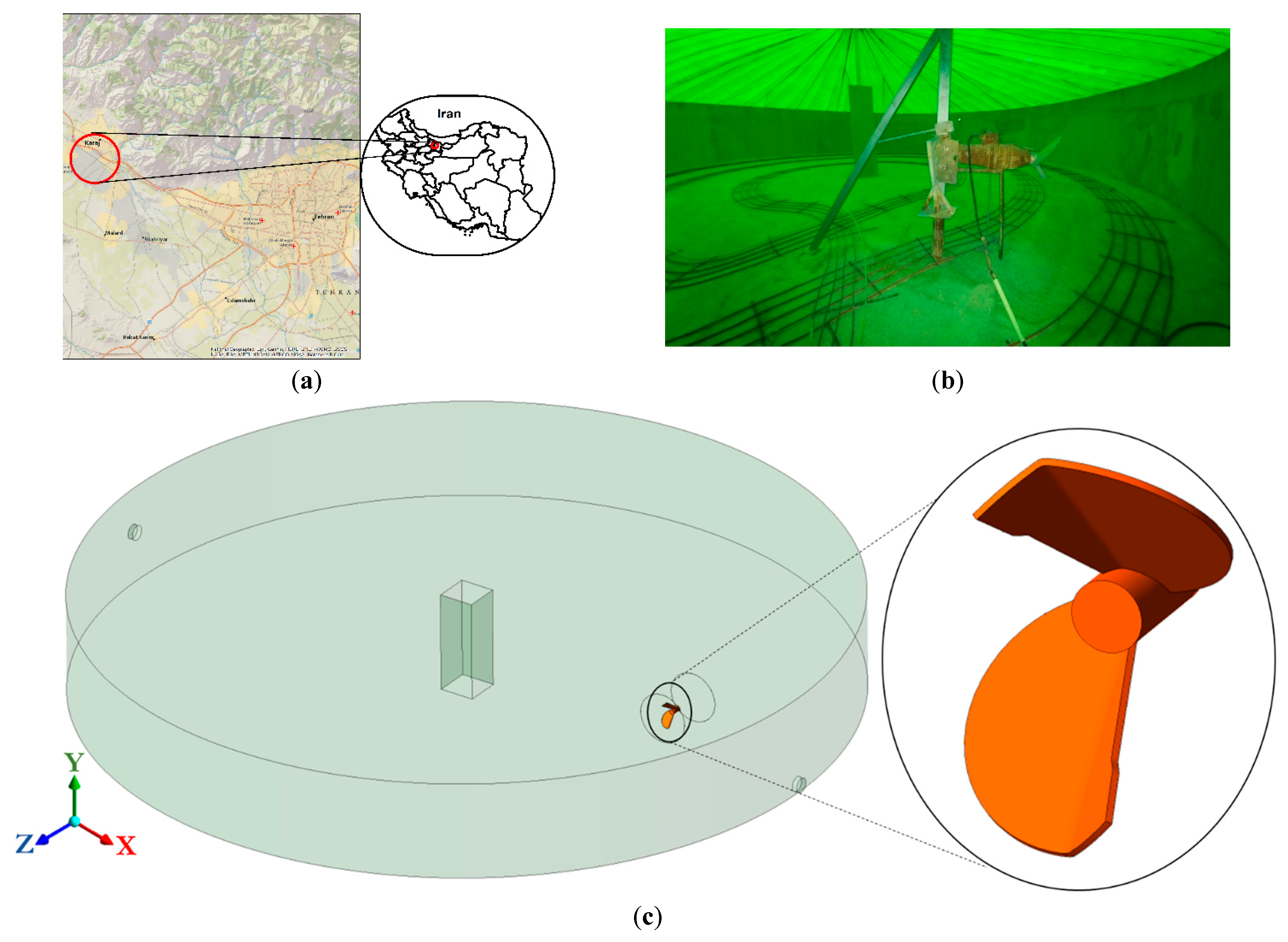
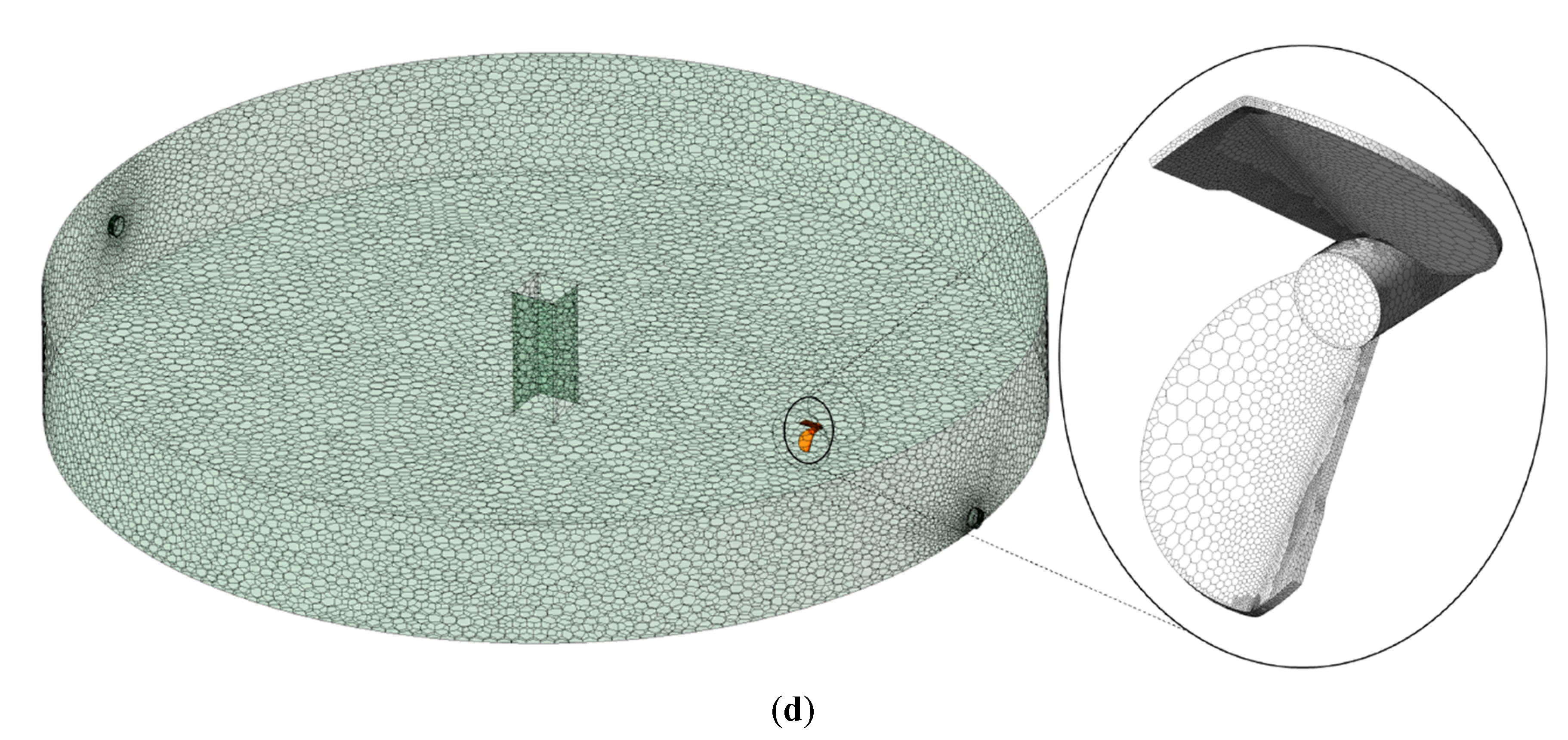

| 12.1 | 5.885 | 0.367 | 3–149 | 0.25 | 2.93 |
| Boundary | Type | Characteristic |
|---|---|---|
| Lateral walls | Wall | No-slip shear condition |
| Mixer impellers | ||
| Central column walls | ||
| Upper surface | ||
| Lower surface |
| Parameter | Unit | Value |
|---|---|---|
| φ1 | m/s | 0.4907 |
| φ2 | 0.4846 | |
| φ3 | 0.4839 | |
| | φ21| | m/s | 0.0061 |
| | φ32| | 0.0007 | |
| r21 | - | ≈1.3 |
| r32 | ≈1.3 | |
| p | - | 8.24 |
| e32 | % | 0.14 |
| Mixer Rotation Speed (rpm) | Power Consumption (kW) |
|---|---|
| 300 | 24.5 |
| 350 | 47.1 |
| 400 | 78.4 |
| 450 | 117.6 |
| 500 | 159.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dabiri, S.; Noorpoor, A.; Arfaee, M.; Kumar, P.; Rauch, W. CFD Modeling of a Stirred Anaerobic Digestion Tank for Evaluating Energy Consumption through Mixing. Water 2021, 13, 1629. https://doi.org/10.3390/w13121629
Dabiri S, Noorpoor A, Arfaee M, Kumar P, Rauch W. CFD Modeling of a Stirred Anaerobic Digestion Tank for Evaluating Energy Consumption through Mixing. Water. 2021; 13(12):1629. https://doi.org/10.3390/w13121629
Chicago/Turabian StyleDabiri, Soroush, Alireza Noorpoor, Maziar Arfaee, Prashant Kumar, and Wolfgang Rauch. 2021. "CFD Modeling of a Stirred Anaerobic Digestion Tank for Evaluating Energy Consumption through Mixing" Water 13, no. 12: 1629. https://doi.org/10.3390/w13121629
APA StyleDabiri, S., Noorpoor, A., Arfaee, M., Kumar, P., & Rauch, W. (2021). CFD Modeling of a Stirred Anaerobic Digestion Tank for Evaluating Energy Consumption through Mixing. Water, 13(12), 1629. https://doi.org/10.3390/w13121629