Influence of Substrate Material on Flow in Freezing Water Droplets—An Experimental Study
Abstract
1. Introduction
2. Materials and Methods
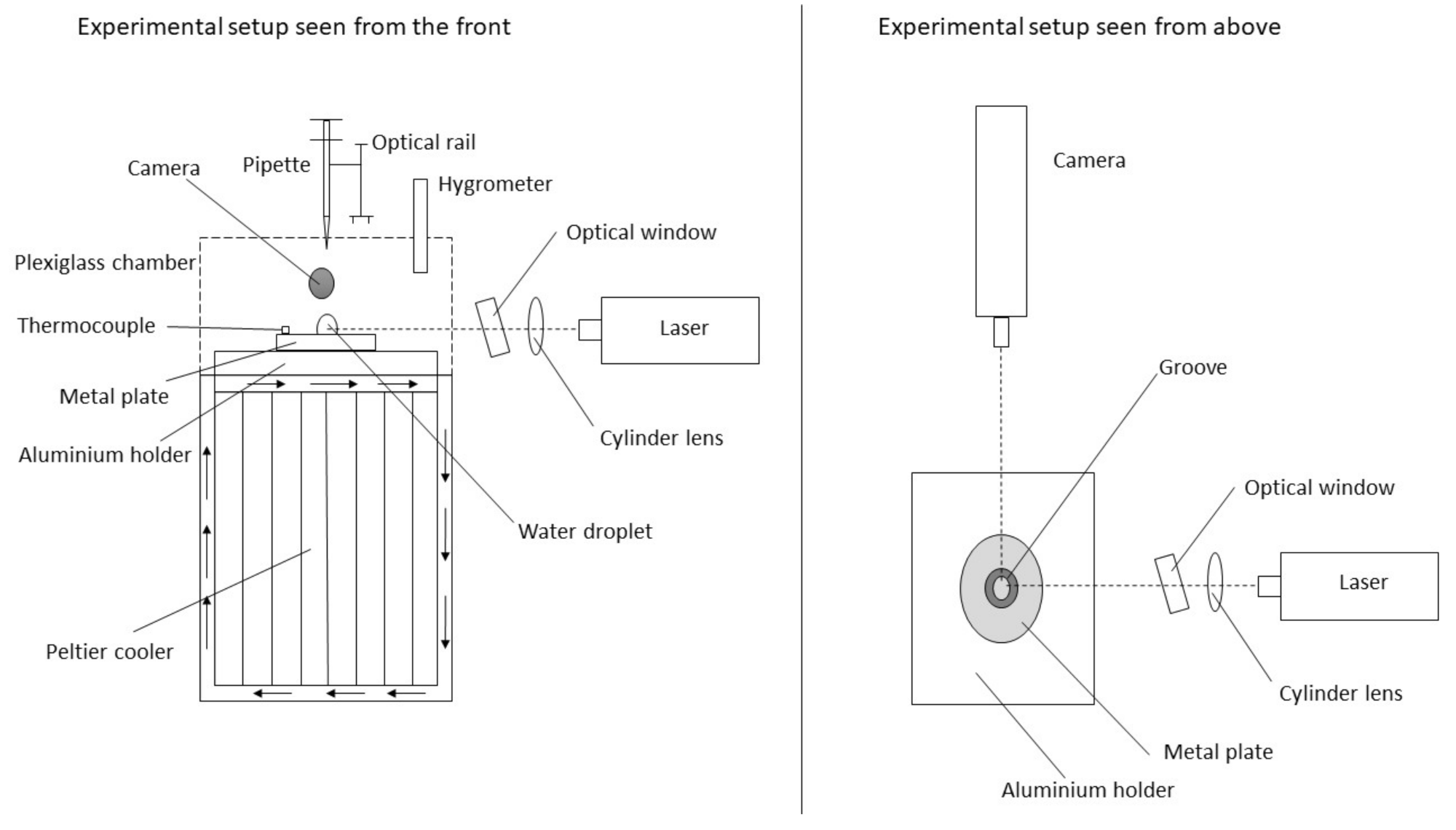
2.1. Experimental Setup
2.2. Experiment Procedure
- Fill the groove with DI water.
- Turn on the Peltier element to start the cooling of the plate.
- Remove the chamber and wipe the surface from all natural frost that has been formed from the moisture content of the air.
- Fill the pipette with the mix of DI water and particles and lower it into the chamber.
- Turn on the laser and start filming.
- Wait until the plate is at −8 °C.
- Release the droplet.
- When the singular tip can be observed and it is completely frozen, stop filming, turn off the laser and turn off the cooling of the plate.
- Wait until the droplets have melted and wipe all water off the plate and repeat.
2.3. Data and Uncertainty Analysis
3. Results and Discussion
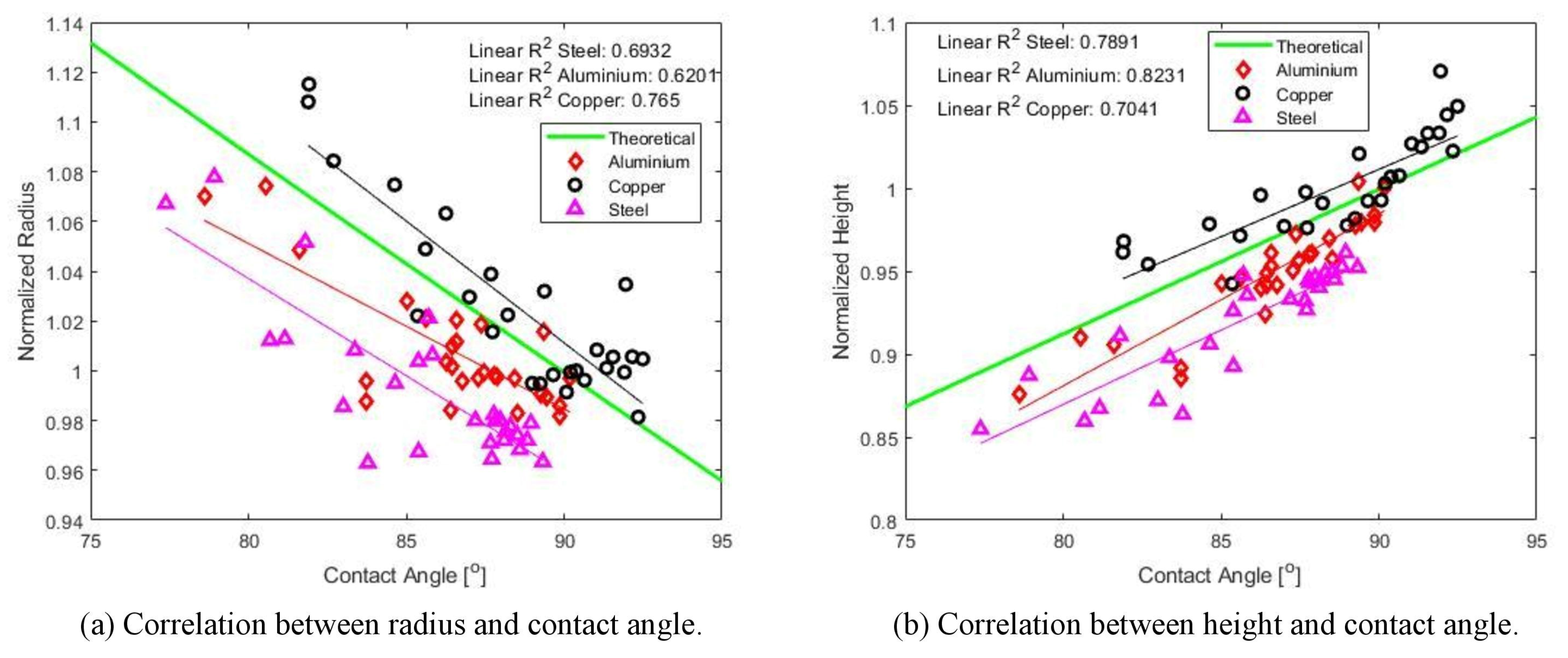
3.1. Droplet Radius and Contact Angle
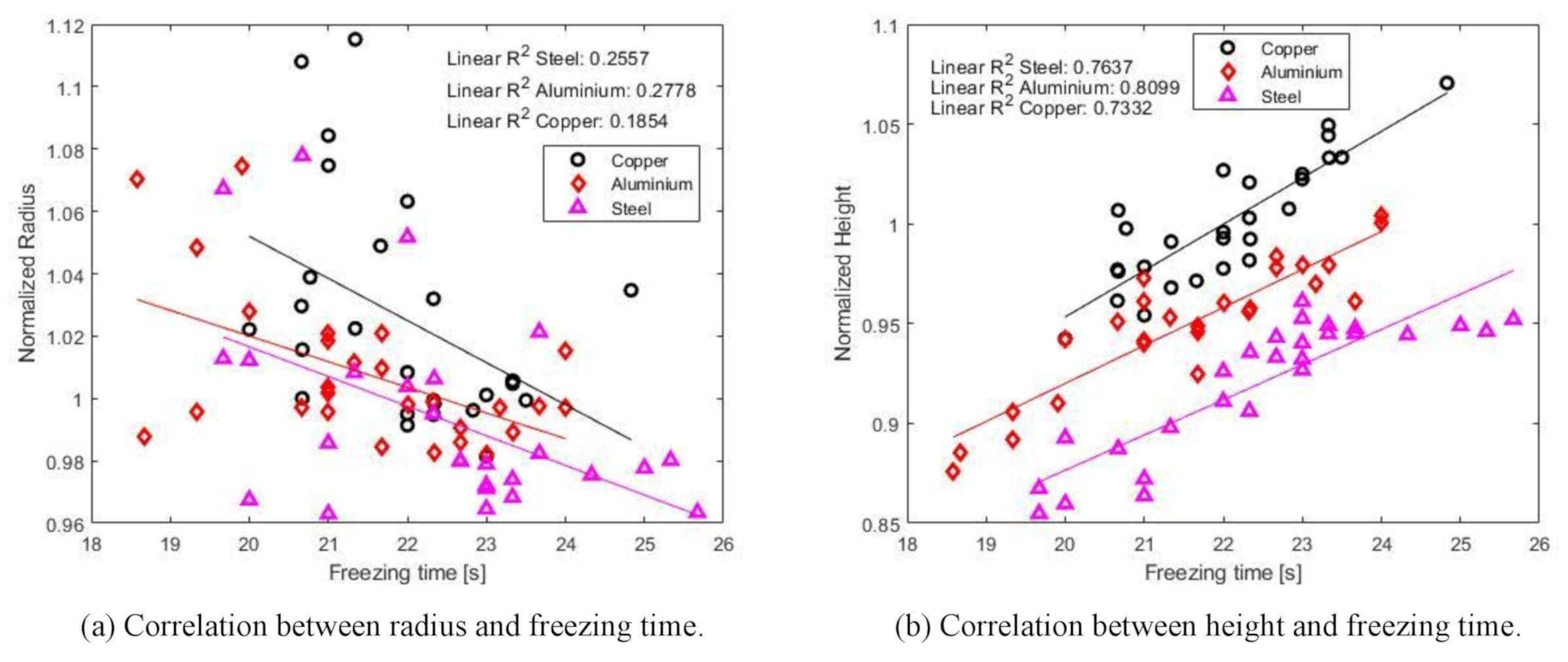
3.2. Freezing Time
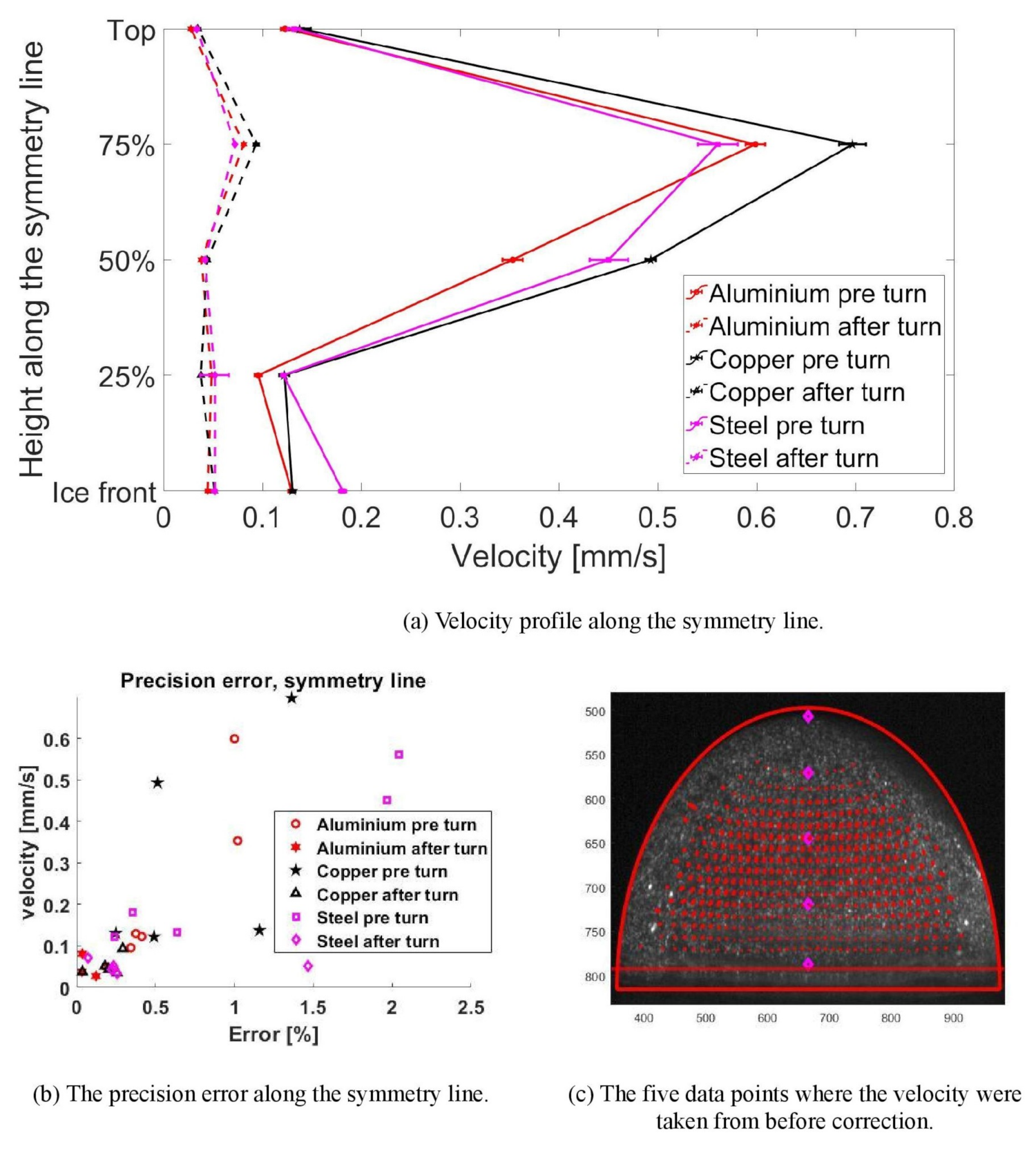
3.3. Velocity Profile
4. Conclusions
- From the experiments it can be concluded that the contact radius and angle of a droplets impact on a substrate can be controlled to a higher degree when using a groove filled with ice rather than impinging on a flat surface covered with a layer of natural frost. The repeatability study of 81 experiments showed to a rather high degree that, when introducing a groove in the plate, the contact radius could be predetermined with a standard deviation of 0.85%.
- The experimental results show that the freezing time is dependent on the contact angle and hence also the height of the droplet. A higher contact angle will increase the time of freezing. Dependence on contact radius is not as visible in this work since the contact radius between metal and droplet is rather constant due to the groove.
- The velocity profile was determined inside the droplet before and after the direction change for the three substrate materials. At the point where the velocity was highest (75% between the top and freezing front), copper had the highest velocity, followed by aluminium and then steel. The internal velocities thus follows the thermal conductivites with copper having the highest thermal conductivity and steel the lowest. This order only applies for the fastest point; both at the top and at a height of 50%, steel had a higher velocity than aluminium. The overall velocity difference between aluminium and steel is, however, rather small. Copper is 16.39% faster than aluminium, and aluminium is 5.78% faster than steel at the highest velocity. There is thus a difference in internal flow between the substrates, but the difference between aluminium and steel is not as distinct as for copper.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mengjie, S.; Chaobin, D.; Tomohira, H.; Eiji, H. Review of experimental data associated with the solidification characteristics of water droplets on a cold plate surface at the early frosting stage. Energy Build. 2020, 223, 110103. [Google Scholar]
- Liu, Z.; Zhang, X.; Wang, H.; Meng, S.; Cheng, S. Influences of surface hydrophilicity on frost formation on a vertical cold plate under natural convection conditions. Exp. Therm. Fluid Sci. 2007, 31, 789–794. [Google Scholar] [CrossRef]
- Jin, Z.; Dong, Q.; Jin, S.; Yang, Z. Visualization of the freezing and melting process of a small water droplet on a cold surface. In Proceedings of the International Conference on Fluid Dynamics and Thermodynamics Technologies (FDTT 2012), Singapore, 17–18 March 2012; Volume 33. [Google Scholar]
- Jung, S.; Tiwari, M.K.; Doan, N.V.; Poulikakos, D. Mechanism of supercooled droplet freezing on surfaces. Nat. Commun. 2012, 3, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Jin, Z.; Jin, S.; Yang, Z. Visualization of icing process of a water droplet impinging onto a frozen cold plate under free and forced convection. J. Vis. 2013, 16, 13–17. [Google Scholar] [CrossRef]
- Schremb, M.; Tropea, C. Solidification of supercooled water in the vicinity of a solid wall. Phys. Rev. E 2016, 94, 052804. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, X.; Min, J. Freezing and melting of a sessile water droplet on a horizontal cold plate. Exp. Therm. Fluid Sci. 2017, 88, 1–7. [Google Scholar] [CrossRef]
- Yao, Y.; Yang, R.; Li, C.; Tao, Z.; Zhang, H. Investigation of the freezing process of water droplets based on average and local initial ice fraction. Exp. Heat Transf. 2020, 33, 197–209. [Google Scholar] [CrossRef]
- Wang, J.; Liu, Z.; Gou, Y.; Zhang, X.; Cheng, S. Deformation of freezing water droplets on a cold copper surface. Sci. China Ser. E Technol. Sci. 2006, 49, 590–600. [Google Scholar] [CrossRef]
- Enríquez, O.R.; Marín, Á.G.; Winkels, K.G.; Snoeijer, J.H. Freezing singularities in water drops. Phys. Fluids 2012, 24, 091102. [Google Scholar] [CrossRef]
- Marin, A.G.; Enriquez, O.R.; Brunet, P.; Colinet, P.; Snoeijer, J.H. Universality of tip singularity formation in freezing water drops. Phys. Rev. Lett. 2014, 113, 054301. [Google Scholar] [CrossRef]
- Schetnikov, A.; Matiunin, V.; Chernov, V. Conical shape of frozen water droplets. Am. J. Phys. 2015, 83, 36–38. [Google Scholar] [CrossRef]
- Ismail, M.F.; Waghmare, P.R. Universality in freezing of an asymmetric drop. Appl. Phys. Lett. 2016, 109, 234105. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, H.; Yang, Z. Experimental investigation of the impact and freezing processes of a water droplet on an ice surface. Int. J. Heat Mass Transf. 2017, 109, 716–724. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, H.; Yang, Z. The impact and freezing processes of a water droplet on different cold cylindrical surfaces. Int. J. Heat Mass Transf. 2017, 113, 318–323. [Google Scholar] [CrossRef]
- Ju, J.; Jin, Z.; Zhang, H.; Yang, Z.; Zhang, J. The impact and freezing processes of a water droplet on different cold spherical surfaces. Exp. Therm. Fluid Sci. 2018, 96, 430–440. [Google Scholar] [CrossRef]
- Yao, Y.; Li, C.; Tao, Z.; Yang, R.; Zhang, H. Experimental and numerical study on the impact and freezing process of a water droplet on a cold surface. Appl. Therm. Eng. 2018, 137, 83–92. [Google Scholar] [CrossRef]
- Wang, L.; Kong, W.; Wang, F.; Liu, H. Effect of nucleation time on freezing morphology and type of a water droplet impacting onto cold substrate. Int. J. Heat Mass Transf. 2019, 130, 831–842. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, X.; Wu, X.; Min, J. Impacting-freezing dynamics of a supercooled water droplet on a cold surface: Rebound and adhesion. Int. J. Heat Mass Transf. 2020, 158, 119997. [Google Scholar] [CrossRef]
- Schultz, W.; Worster, M.; Anderson, D. Solidifying sessile water droplets. In Interactive Dynamics of Convection and Solidification; Springer: Berlin/Heidelberg, Germany, 2001; pp. 209–226. [Google Scholar]
- Hao, P.; Lv, C.; Zhang, X. Freezing of sessile water droplets on surfaces with various roughness and wettability. Appl. Phys. Lett. 2014, 104, 161609. [Google Scholar] [CrossRef]
- Yue, X.; Liu, W.; Wang, Y. Freezing and melting of sessile droplet on micro-and hierarchically-structured silicon surfaces. Appl. Therm. Eng. 2019, 161, 114185. [Google Scholar] [CrossRef]
- De Ruiter, R.; Colinet, P.; Brunet, P.; Snoeijer, J.H.; Gelderblom, H. Contact line arrest in solidifying spreading drops. Phys. Rev. Fluids 2017, 2, 043602. [Google Scholar] [CrossRef]
- Sun, M.; Kong, W.; Wang, F.; Liu, H. Impact freezing modes of supercooled droplets determined by both nucleation and icing evolution. Int. J. Heat Mass Transf. 2019, 142, 118431. [Google Scholar] [CrossRef]
- Stiti, M.; Castanet, G.; Labergue, A.; Lemoine, F. Icing of a droplet deposited onto a subcooled surface. Int. J. Heat Mass Transf. 2020, 159, 120116. [Google Scholar] [CrossRef]
- Huang, L.; Liu, Z.; Liu, Y.; Gou, Y.; Wang, L. Effect of contact angle on water droplet freezing process on a cold flat surface. Exp. Therm. Fluid Sci. 2012, 40, 74–80. [Google Scholar] [CrossRef]
- Kawanami, T.; Yamada, M.; Fukusako, S.; Kawai, H. Solidification characteristics of a droplet on a horizontal cooled wall. Heat Transf. Jpn. Res. 1997, 26, 469–483. [Google Scholar] [CrossRef]
- Karlsson, L.; Ljung, A.L.; Lundstrom, S. Influence of internal natural convection on water droplets freezing on cold surfaces. In Proceedings of the CONV-14: International Symposium on Convective Heat and Mass Transfer, Kusadasi, Turkey, 8–13 June 2014; Begel House Inc.: Danbury, CT, USA, 2014. [Google Scholar]
- Karlsson, L.; Ljung, A.L.; Lundström, T.S. Modelling the dynamics of the flow within freezing water droplets. Heat Mass Transf. 2018, 54, 3761–3769. [Google Scholar] [CrossRef]
- Karlsson, L.; Lycksam, H.; Ljung, A.L.; Gren, P.; Lundström, T.S. Experimental study of the internal flow in freezing water droplets on a cold surface. Exp. Fluids 2019, 60, 1–10. [Google Scholar] [CrossRef]
- Karlsson, L.; Ljung, A.L.; Lundström, T.S. Comparing Internal Flow in Freezing and Evaporating Water Droplets Using PIV. Water 2020, 12, 1489. [Google Scholar] [CrossRef]
- Nordling, C.; Österman, J. Physics Handbook for Science and Engineering; Studentlitteratur AB: Lund, Sweden, 2006. [Google Scholar]
- Kang, K.H.; Lee, S.J.; Lee, C.M.; Kang, I.S. Quantitative visualization of flow inside an evaporating droplet using the ray tracing method. Meas. Sci. Technol. 2004, 15, 1104. [Google Scholar] [CrossRef]
- Minor, G.; Oshkai, P.; Djilali, N. Optical distortion correction for liquid droplet visualization using the ray tracing method: Further considerations. Meas. Sci. Technol. 2007, 18, L23. [Google Scholar] [CrossRef]
- Coleman, H.; Steele, W. Experimentation, Validation, and Uncertainty Analysis for Engineers; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]

| Material | Thermal Conductivity [W m K ] |
|---|---|
| Copper | 400 |
| Aluminium | 238 |
| Steel | 45 |
| Ice | 2.1 |
| Pre Turn | Copper [%] | Aluminium [%] | Steel [%] | After Turn | Copper [%] | Aluminium [%] | Steel [%] |
|---|---|---|---|---|---|---|---|
| Top | 1.1586 | 0.4123 | 0.6355 | Top | 0.2568 | 0.1215 | 0.2567 |
| 75% | 1.3627 | 0.9999 | 2.0409 | 75% | 0.2917 | 0.0351 | 0.0706 |
| 50% | 0.4127 | 1.0202 | 1.9674 | 50% | 0.2026 | 0.0327 | 0.2223 |
| 25% | 0.4905 | 0.3430 | 0.2403 | 25% | 0.0358 | 0.1969 | 1.4643 |
| Ice front | 0.2478 | 0.3743 | 0.3556 | Ice front | 0.1785 | 0.2288 | 0.2339 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fagerström, E.; Ljung, A.-L.; Karlsson, L.; Lycksam, H. Influence of Substrate Material on Flow in Freezing Water Droplets—An Experimental Study. Water 2021, 13, 1628. https://doi.org/10.3390/w13121628
Fagerström E, Ljung A-L, Karlsson L, Lycksam H. Influence of Substrate Material on Flow in Freezing Water Droplets—An Experimental Study. Water. 2021; 13(12):1628. https://doi.org/10.3390/w13121628
Chicago/Turabian StyleFagerström, Erik, Anna-Lena Ljung, Linn Karlsson, and Henrik Lycksam. 2021. "Influence of Substrate Material on Flow in Freezing Water Droplets—An Experimental Study" Water 13, no. 12: 1628. https://doi.org/10.3390/w13121628
APA StyleFagerström, E., Ljung, A.-L., Karlsson, L., & Lycksam, H. (2021). Influence of Substrate Material on Flow in Freezing Water Droplets—An Experimental Study. Water, 13(12), 1628. https://doi.org/10.3390/w13121628







