Numerical Study of Discharge Adjustment Effects on Reservoir Morphodynamics and Flushing Efficiency: An Outlook for the Unazuki Reservoir, Japan
Abstract
1. Introduction
2. Case Study Description
2.1. Site Description
2.2. Field Observations and Data Arrangement
3. Numerical Model
4. Numerical Simulation
4.1. Model Setup and Calibration
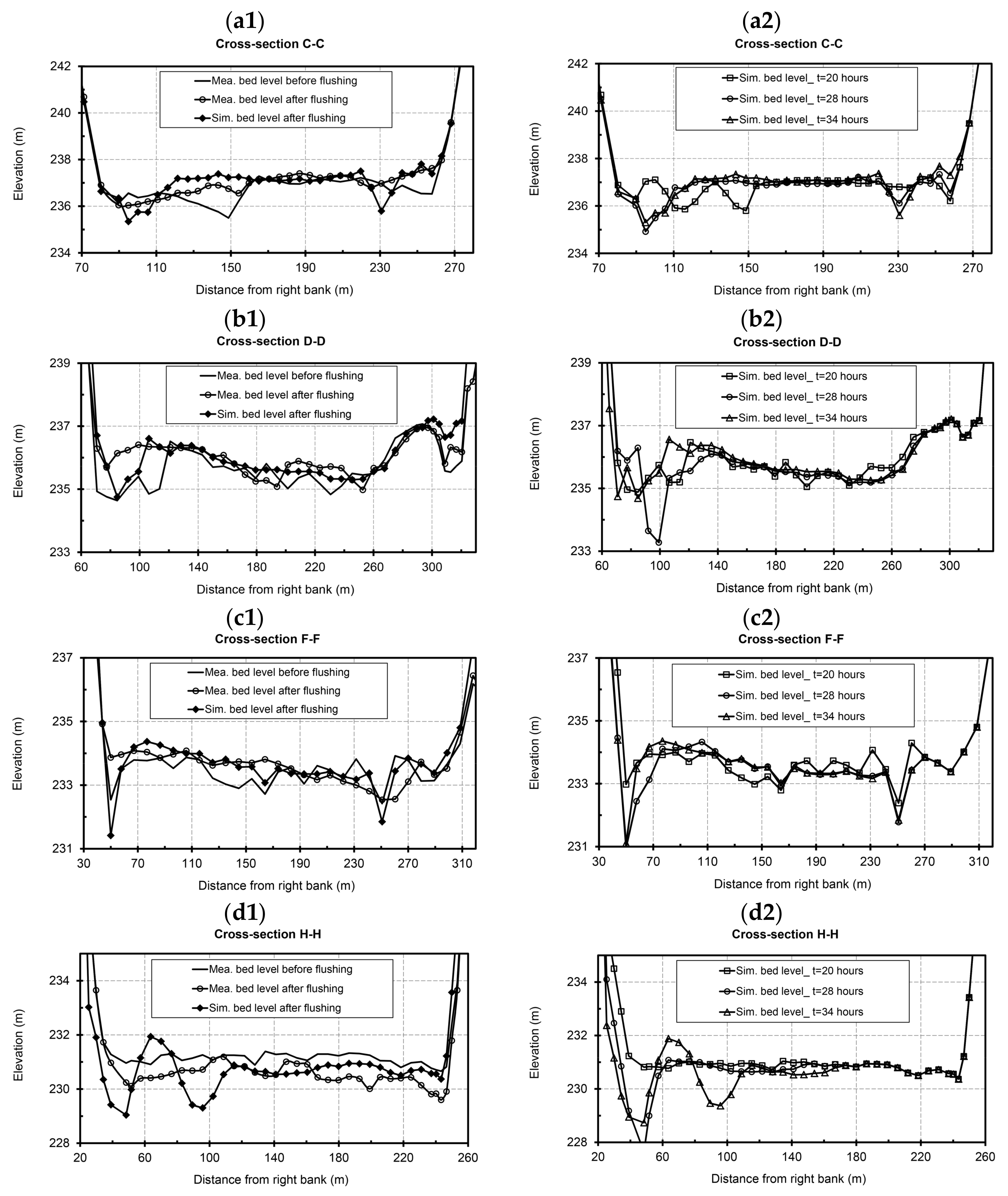
4.2. Evaluation of Morphological Bed Changes in the Reservoir Caused by the Flushing Operation
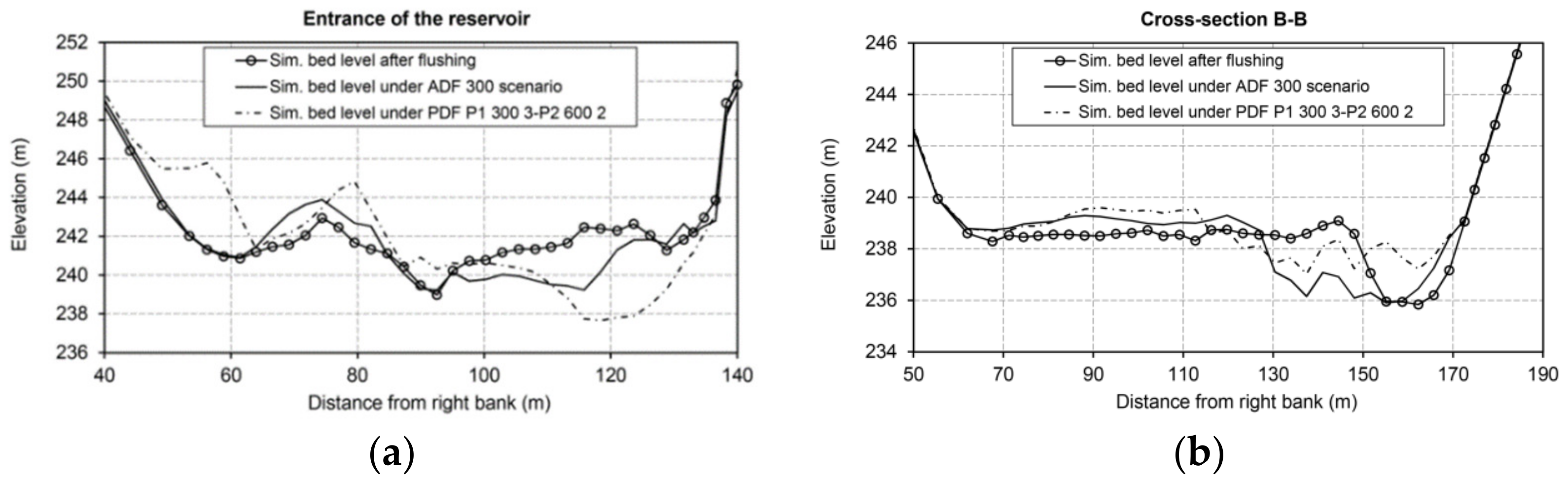
4.3. Discharge Adjustment Effect on Morphological Bed Changes and Flushing Efficiency
5. Conclusions
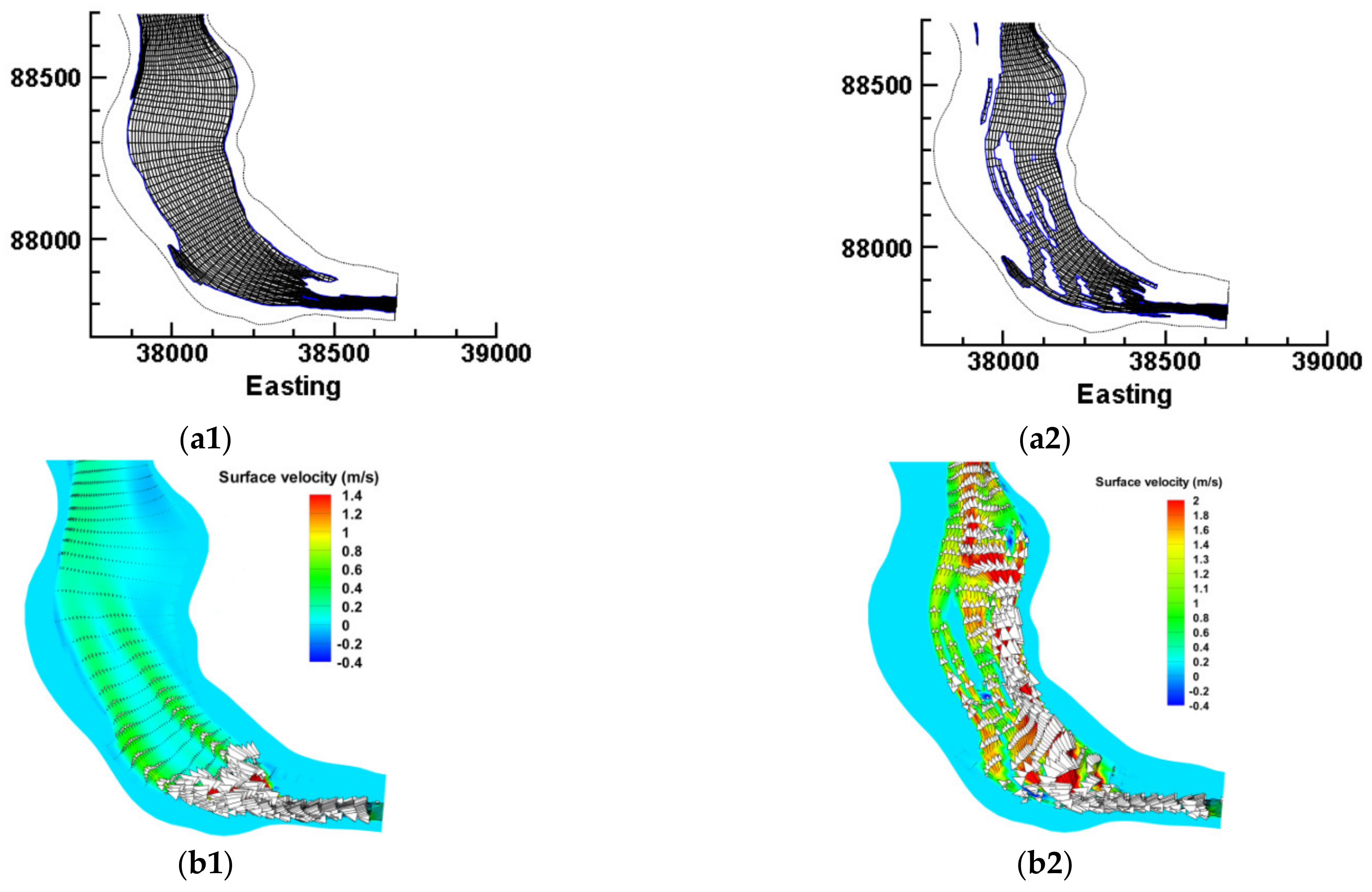
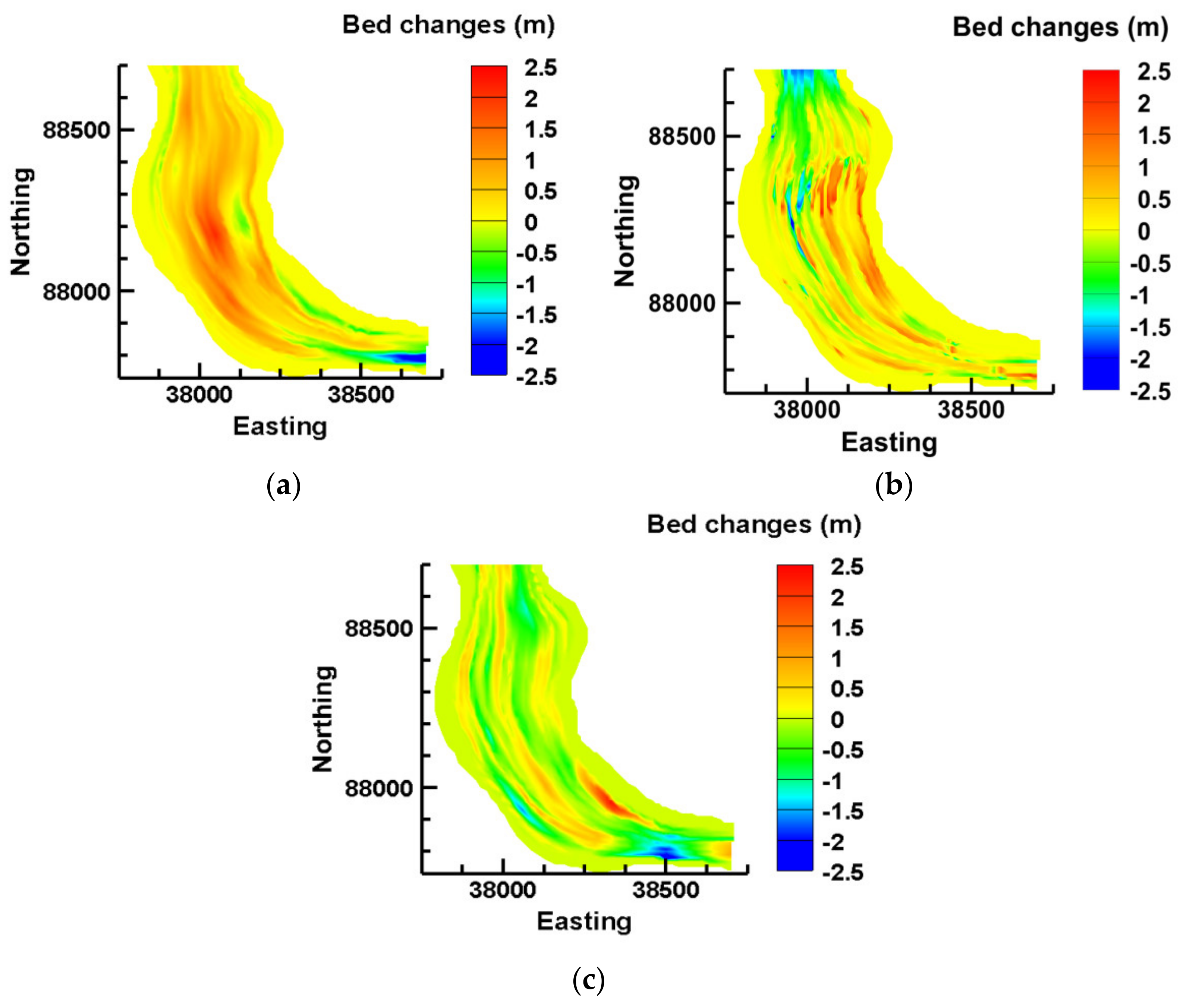
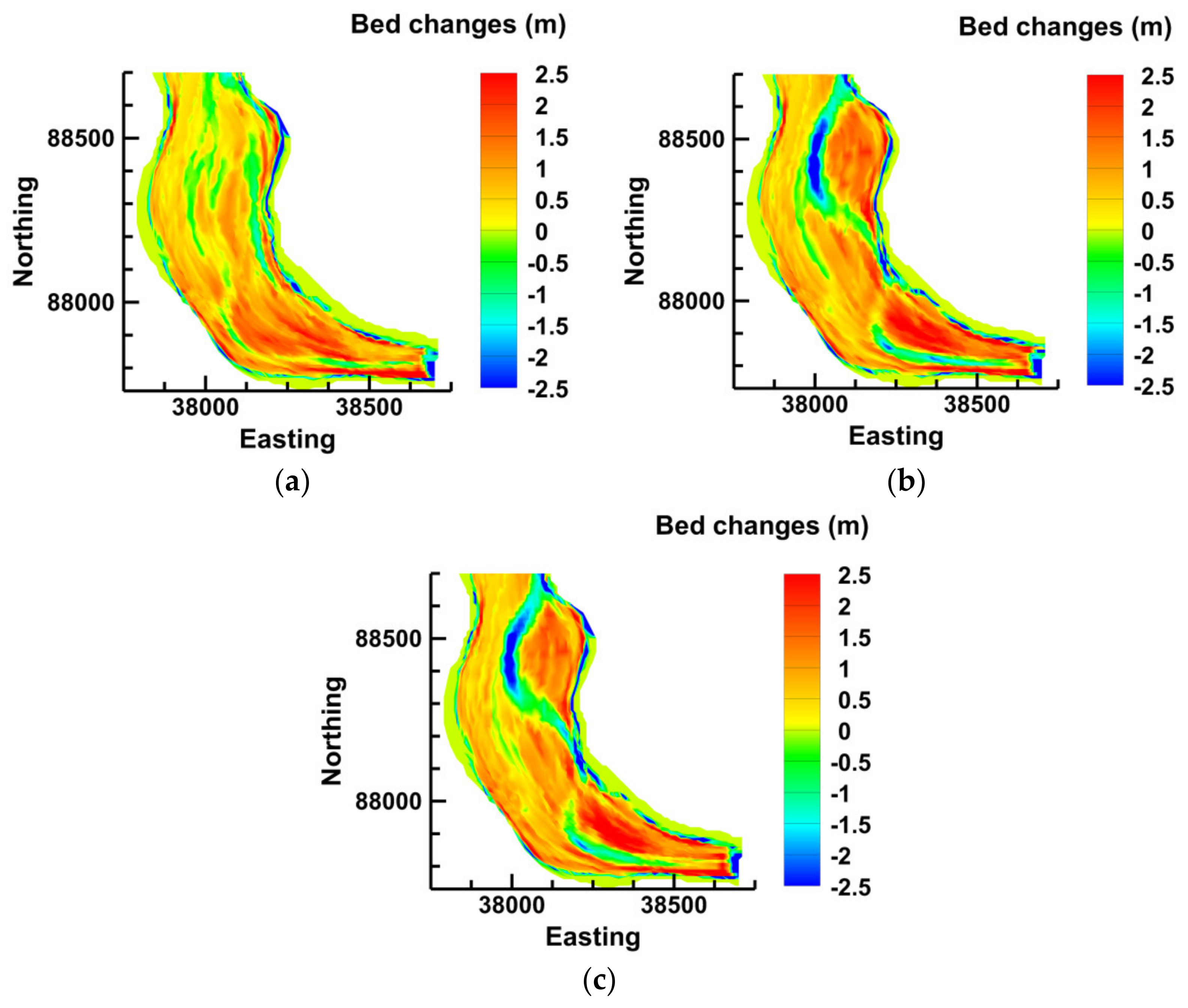
- In the study segment in the Unazuki Reservoir, a portion of the flushed sediment load released from the upstream Dashidaira Reservoir in addition to the flood-borne sediments will settle. Even a full water-level drawdown is not able to resuspend and scour these particles effectively, since sufficient driving force cannot be supplied by the ongoing regulations of operational flushing discharges. The study segment in the Unazuki Reservoir is wide, which contributes to developing shallow flow conditions, especially during the free-flow stage. Since there is no distinctive flushing channel to attract and stabilize the flow in this segment, flow deviation across the reservoir occurs during different stages of the flushing operation, which results in the development of a set of distributed scouring channels. The simulated surface flow velocity, bed changes of the reservoir and arrangement of the previously mentioned scouring channels were almost consistent with onsite observations and the aerial photograph taken soon after the flushing operation, which emphasizes the importance of picking onsite data before they are disturbed by the dynamic conditions of the reservoir. However, simulated bed changes showed some differences from bathymetric measurements conducted long after flushing. Thus, measurements of bed changes in the shortest possible time after completing the flushing operation can positively contribute to developing a more accurate model calibration. In this context, detecting the flushing flow directions by recording the entire operation in addition to measuring the real surface velocities can also be useful for a more accurate model calibration.
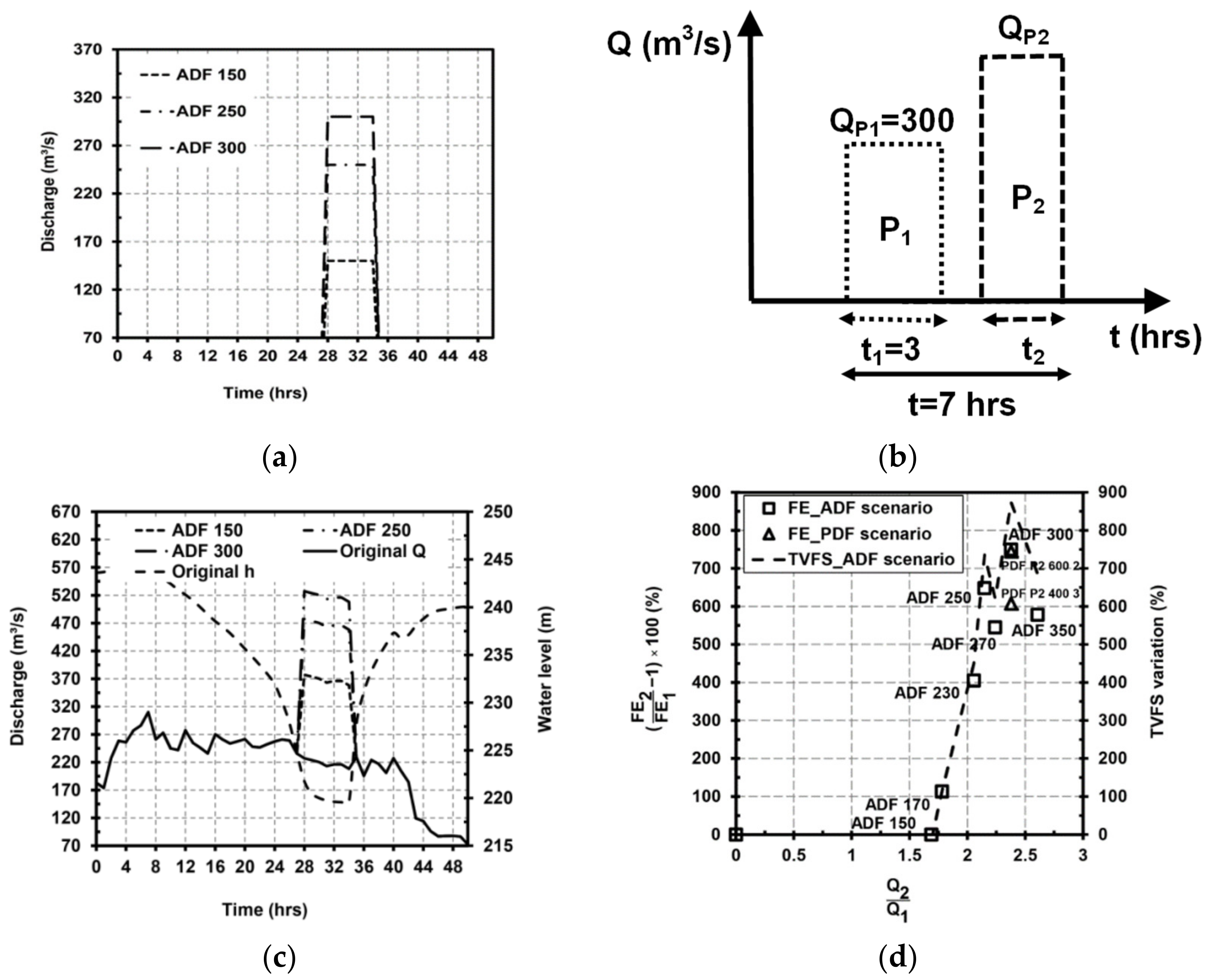
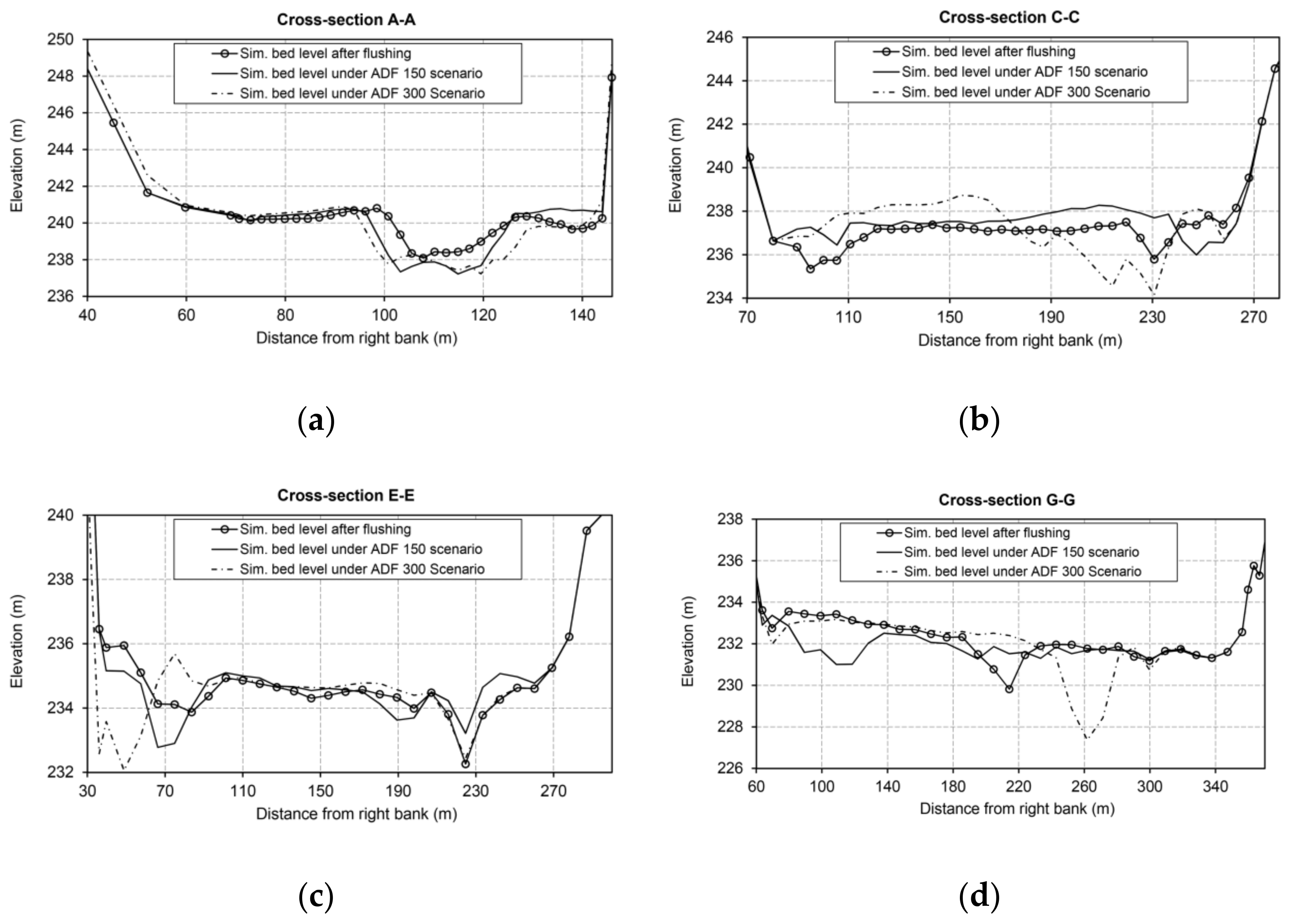
- If the average discharge during the free-flow condition increases by approximately 75% compared with the reference case, it can contribute to changing the dominant morphological process from deposition to erosion in the study segment of the reservoir, which is a valuable step forward to conducting the flushing operation in a more efficient manner. Subsequently, the total water volume used for flushing purposes increases by approximately 11% in the Unazuki Reservoir. If the single discharge pulse becomes larger under more intensive ADF scenarios (e.g., ADF 250 and ADF 300 scenarios), both TVFS and FE increase sharply due to excessive erosion, especially in the lower half of the study segment covered with finer sediments. In addition, the application of ADF scenarios with a high magnitude discharge pulse (e.g., ADF 300 scenario) can increase the erosion of coarser sediments from the upper half of the study segment, including the reservoir entrance area, and transport them further downstream, which is especially beneficial for remedying the excessive sedimentation within the study segment. Furthermore, this approach effectively contributes to fine sediment removal from the lower half of the study segment. In this context, the effect of providing a longer duration for the free-flow stage with higher magnitudes of discharge pulse can be considered to supply more driving forces aimed at eroding and flushing the coarse sediment sizes for further development of the current study. Outcomes show that discharge adjustment, in the form of two discharge pulses with a higher discharge pulse set in the second half of the free-flow stage, can potentially improve the erosion of coarser materials from the entrance area in the Unazuki Reservoir. Another notable effect would be on erosion of finer sediments located in the lower half of the study segment, similar to the ADF 300 scenario.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kondolf, G.M.; Gao, Y.; Annandale, G.W.; Morris, G.L.; Jiang, E.; Zhang, J.; Cao, Y.; Carling, P.; Fu, K.; Guo, Q. Sustainable sediment management in reservoirs and regulated rivers: Experiences from five continents. Earth’s Future 2014, 2, 256–280. [Google Scholar] [CrossRef]
- Morris, G.L.; Fan, J. Reservoir Sedimentation Handbook: Design and Management of Dams, Reservoirs and Watersheds for Sustainable Use; McGraw-Hill: New York, NY, USA, 1998. [Google Scholar]
- Shen, H.W. Flushing sediment through reservoirs. J. Hydraul. Res. 1999, 37, 743–757. [Google Scholar] [CrossRef]
- Sumi, T.; Kantoush, S.A. Integrated management of reservoir sediment routing by flushing, replenishing, and bypassing sediments in Japanese river basins. In Proceedings of the 8th International Symposium on Ecohydraulics, Seoul, Korea, 12–16 September 2010. [Google Scholar]
- Liu, J.; Minami, S.; Otsuki, H.; Liu, B.; Ashida, K. Prediction of concerted sediment flushing. J. Hydraul. Eng. 2004, 130, 1089–1096. [Google Scholar] [CrossRef]
- Esmaeili, T.; Sumi, T.; Kantoush, S.A.; Kubota, Y.; Haun, S.; Rüther, N. Three-dimensional numerical study of free-flow sediment flushing to increase the flushing efficiency: A case-study reservoir in Japan. Water 2017, 9, 900. [Google Scholar] [CrossRef]
- Fukuoka, S.; Uchida, T. Toward integrated multi-scale simulations of flow and sediment transport in rivers. J. Jpn. Soc. Civ. Eng. 2013, 69, II_1–II_10. [Google Scholar] [CrossRef]
- Olsen, N.R.B.; Haun, S. A numerical geotechnical model for computing soil slides at banks of water reservoirs. Geo-Engi. 2020, 11, 22. [Google Scholar] [CrossRef]
- Almeland, S.K.; Olsen, N.R.B.; Bråveit, K.; Aryal, P.R. Multiple solutions of the Navier-Stokes equations computing water flow in sand traps. Eng. App. Com. Fluid Mech. 2019, 13, 199–219. [Google Scholar] [CrossRef]
- Olsen, N.R.B.; Haun, S. Numerical modelling of bank failures during reservoir draw-down. In Proceedings of the River Flow 2018—9th International Conference on Fluvial Hydraulics, Lyon, France, 5–8 September 2018. [Google Scholar]
- Haun, S.; Kjærås, H.; Løvfall, S.; Olsen, N.R.B. Three-dimensional measurements and numerical modelling of suspended sediments in a hydropower reservoir. J. Hydrol. 2013, 479, 180–188. [Google Scholar] [CrossRef]
- Rüther, N.; Olsen, N.R.B. Modelling free-forming meander evolution in a laboratory channel using three-dimensional computational fluid dynamics. Geomorphology 2007, 89, 308–319. [Google Scholar] [CrossRef]
- Esmaeili, T.; Sumi, T.; Kantoush, S.A. Experimental and numerical study of flushing channel formation in shallow reservoirs. J. Jpn. Soc. Civ. Eng. 2014, 70, I_19–I_24. [Google Scholar] [CrossRef]
- Harb, G.; Haun, S.; Schneider, J.; Olsen, N.R.B. Numerical analysis of synthetic granulate deposition in a physical model study. Int. J. Sediment Res. 2014, 29, 110–117. [Google Scholar] [CrossRef]
- Haun, S.; Olsen, N.R.B. Three-dimensional numerical modelling of the flushing process of the Kali Gandaki hydropower reservoir. Lakes Reserv. 2012, 17, 25–33. [Google Scholar] [CrossRef]
- Saam, L.; Mouris, K.; Haun, S. Three-dimensional numerical modelling of reservoir flushing to obtain long-term sediment equilibrium. In Proceedings of the 38th IAHR World Congress, Panama City, Panama, 1–6 September 2019. [Google Scholar]
- Esmaeili, T.; Sumi, T.; Kantoush, S.A.; Kubota, Y. Free-Flow Sediment Flushing: Insights from Prototype-Scale Studies. J. Disaster Res. 2018, 13, 677–690. [Google Scholar] [CrossRef]
- Harb, G.; Dorfmann, C.; Schneider, J.; Badura, H. Numerical Analysis of Sediment Transport Processes during a Flushing Event of an Alpine Reservoir. In Proceedings of the 7th River Flow Conference, Lausanne, Switzerland, 2–5 September 2014. [Google Scholar]
- Hillebrand, G.; Klassen, I.; Olsen, N.R.B. 3D CFD modelling of velocities and sediment transport in the Iffezheim hydropower reservoir. Hydrol. Res. 2017, 48, 147–159. [Google Scholar] [CrossRef]
- Esmaeili, T.; Sumi, T.; Kantoush, S.A.; Kubota, Y.; Haun, S. Numerical study on flushing channel evolution, case study of Dashidaira reservoir, Kurobe river. J. Jpn. Soc. Civ. Eng. 2015, 71, I_115–I_120. [Google Scholar] [CrossRef]
- Haun, S.; Olsen, N.R.B. Three-dimensional numerical modelling of reservoir flushing in a prototype scale. Int. J. River Basin Manag. 2012, 10, 341–349. [Google Scholar] [CrossRef]
- Haun, S.; Dorfmann, C.; Harb, G.; Olsen, N.R.B. Numerical modelling of the reservoir flushing of the Bodendorf reservoir, Austria. In Proceedings of the 2nd IAHR European Congress, Munich, Germany, 27–29 June 2012. [Google Scholar]
- Kantoush, S.A.; Sumi, T.; Suzuki, T.; Murasaki, M. Impacts of sediment flushing on channel evolution and morphological processes: Case study of the Kurobe River, Japan. In Proceedings of the 5th River Flow Conference, Braunschweig, Germany, 8–10 June 2010. [Google Scholar]
- Minami, S.; Noguchi, K.; Otsuki, H.; Fukuri, H.; Shimahara, N.; Mizuta, J.; Takeuchi, M. Coordinated sediment flushing and effect verification of fine sediment discharge operation in Kurobe River. In Proceedings of the ICOLD Conference, Kyoto, Japan, 6–8 June 2012. [Google Scholar]
- Sumi, T. Evaluation of efficiency of reservoir sediment flushing in Kurobe River. In Proceedings of the 4th International Conference on Scour and Erosion, Tokyo, Japan, 5–7 November 2008. [Google Scholar]
- Olsen, N.R.B. A Three Dimensional Numerical Model for Simulation of Sediment Movement in Water Intakes with Multiblock Option; The Norwegian University of Science and Technology: Trondheim, Norway, 2014. [Google Scholar]
- Launder, B.E.; Spalding, D.B. Lectures in Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Patankar, S. Numerical Heat Transfer and Fluid Flow; Taylor & Francis: New York, NY, USA, 1980. [Google Scholar]
- Olsen, N.R.B. Numerical Modelling and Hydraulics; Department of Hydraulic and Environmental Engineering, The Norwegian University of Science and Technology: Trondheim, Norway, 2012. [Google Scholar]
- Olsen, N.R.B.; Haun, S. Free surface algorithms for 3-D numerical modeling of flushing. In Proceedings of the 5th River Flow Conference, Braunschweig, Germany, 8–10 June 2010. [Google Scholar]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Van Rijn, L.C. Sediment transport, part III: Bed forms and alluvial roughness. J. Hydraul. Eng. 1984, 110, 1733–1754. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment transport, part II: Suspended load Transport. J. Hydraul. Eng. 1984, 110, 1613–1641. [Google Scholar] [CrossRef]
- Van Rijn, L.C. Sediment transport, part I: Bed load transport. J. Hydraul. Eng. 1984, 110, 1431–1456. [Google Scholar] [CrossRef]
- Meyer-Peter, E.; Müller, R. Formulas for bed load transport. In Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research (IAHR), Stockholm, Sweden, 7–9 June 1948. [Google Scholar]
- Haun, S. Three-Dimensional Numerical Modelling of Sediment Transport during The Flushing of Hydropower Reservoirs. Ph.D. Thesis, The Norwegian University of Science and Technology, Trondheim, Norway, 2012. [Google Scholar]
- Brooks, H. Boundary shear stress in curved trapezoidal channels. J. Hydraul. Div. Am. Soc. Civ. Eng. 1963, 89, 327–333. [Google Scholar]
- Fischer-Antze, T.; Olsen, N.R.B.; Gutknecht, D. Three-dimensional CFD modeling of morphological bed changes in the Danube River. Water Resour. Res. 2008, 44, 44. [Google Scholar] [CrossRef]
- Kantoush, S.A.; Schleiss, A.J. Channel formation in large shallow reservoirs with different geometries during flushing. J. Environ. Technol. 2009, 30, 855–863. [Google Scholar] [CrossRef] [PubMed]
- Esmaeili, T.; Sumi, T.; Kantoush, S.A.; Haun, S.; Rüther, N. Three-dimensional numerical modelling of flow field in shallow reservoirs. Proc. Inst. Civ. Eng. Water Manag. 2016, 169, 229–244. [Google Scholar] [CrossRef]
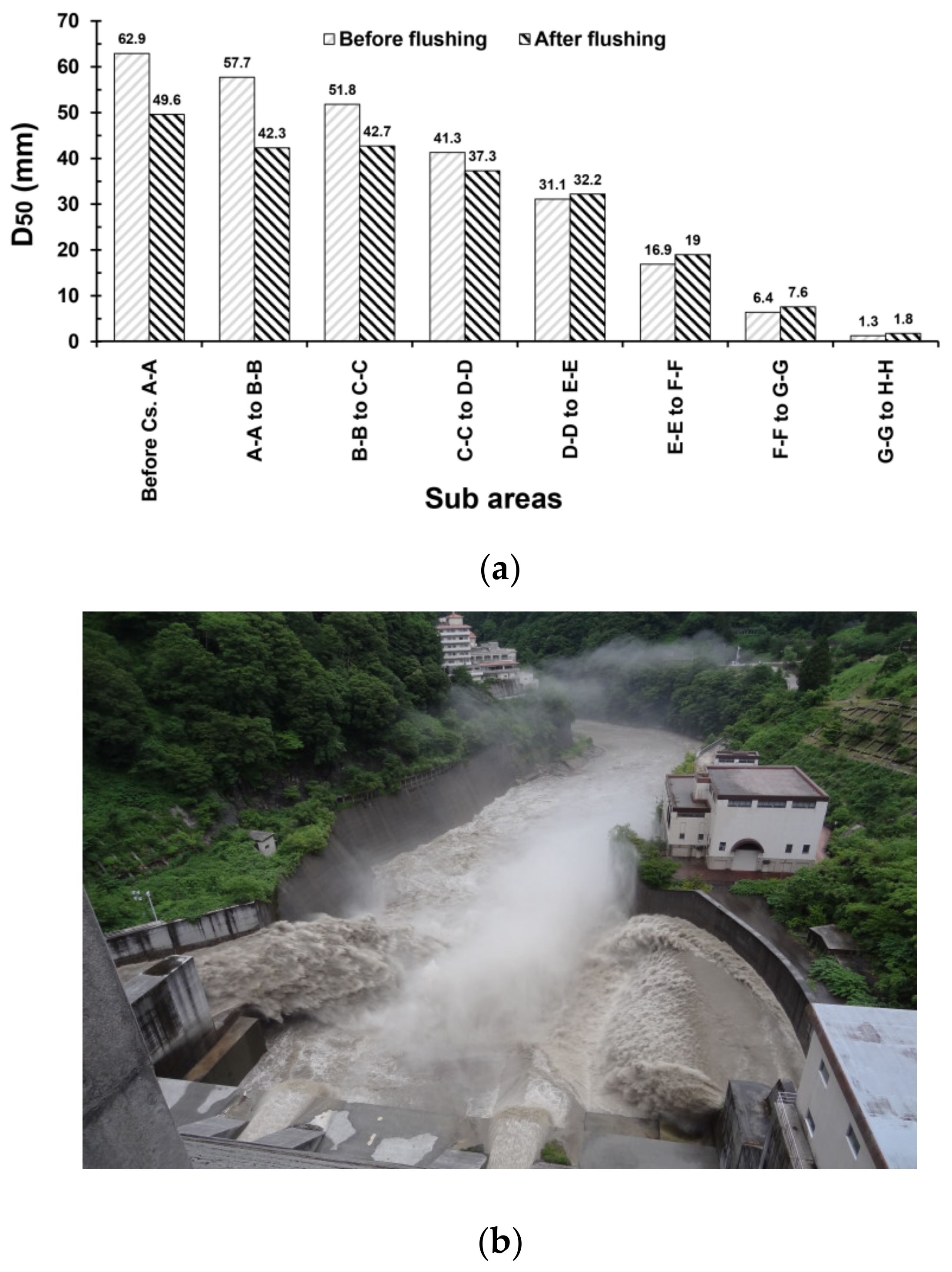
| Sediment Size (mm) | Cs. A-A (%) | Cs. B-B (%) | Cs. C-C (%) | Cs. D-D (%) | Cs. E-E (%) | Cs. F-F (%) | Cs. G-G (%) | Cs. H-H (%) |
|---|---|---|---|---|---|---|---|---|
| 118.3 | 73 | 63 | 53 | 53 | 40 | 10 | 1 | 0 |
| 37.4 | 16 | 21 | 26 | 26 | 36 | 38 | 21 | 1 |
| 11.8 | 8 | 10 | 9 | 9 | 10 | 20 | 23 | 5 |
| 3.7 | 1 | 1 | 3 | 3 | 8 | 12 | 22 | 16 |
| 1.2 | 0 | 0 | 0 | 0 | 0 | 4 | 10 | 29 |
| 0.37 | 2 | 5 | 9 | 9 | 6 | 16 | 23 | 49 |
| Area | Cross-Section | BCI (m) | TVFS (× 10−3 m3) | ||
|---|---|---|---|---|---|
| Measured | Simulated | Measured | Simulated | ||
| I | A–A | 0.04 | 0.14 | −24.49 | −20.89 |
| B–B | 0.13 | 0.04 | |||
| C–C | 0.24 | 0.27 | |||
| D–D | 0.32 | 0.39 | |||
| II | E–E | 0.25 | 0.14 | +4.60 | +13.67 |
| F–F | 0.14 | 0.13 | |||
| G–G | −0.06 | 0.11 | |||
| H–H | −0.58 | −0.46 | |||
| Scenario | ADF 150 | |||||||
|---|---|---|---|---|---|---|---|---|
| Segment | Before A-A | A-A to B-B | B-B to C-C | C-C to D-D | D-D to E-E | E-E to F-F | F-F to G-G | G-G to H-H |
| BCI (m) | −0.09 | 0.03 | 0.22 | 0.23 | 0.02 | 0 | −0.10 | −0.17 |
| Average D50 (mm) | 42 | 36.4 | 37.9 | 30.6 | 30.2 | 18.4 | 8.2 | 2.4 |
| TVFS (×10−3 m3) | −8.2 | |||||||
| Scenario | ADF 250 | |||||||
| Segment | Before A-A | A-A to B-B | B-B to C-C | C-C to D-D | D-D to E-E | E-E to F-F | F-F to G-G | G-G to H-H |
| BCI (m) | −0.48 | −0.15 | 0.07 | −0.05 | −0.23 | 0 | −0.11 | −0.19 |
| Average D50 (mm) | 38.7 | 42.7 | 43.7 | 41.6 | 32.3 | 19.5 | 9 | 2.4 |
| TVFS (×10−3 m3) | +45.8 | |||||||
| Scenario | ADF 270 | |||||||
| Segment | Before A-A | A-A to B-B | B-B to C-C | C-C to D-D | D-D to E-E | E-E to F-F | F-F to G-G | G-G to H-H |
| BCI (m) | −0.42 | −0.11 | 0.12 | −0.02 | −0.08 | 0.02 | −0.10 | −0.24 |
| Average D50 (mm) | 47 | 40.7 | 40.5 | 41.2 | 31.5 | 19.2 | 8.6 | 2.4 |
| TVFS (×10−3 m3) | +37.6 | |||||||
| Scenario | ADF 300 | |||||||
| Segment | Before A-A | A-A to B-B | B-B to C-C | C-C to D-D | D-D to E-E | E-E to F-F | F-F to G-G | G-G to H-H |
| BCI (m) | −0.30 | −0.14 | 0.06 | −0.05 | −0.24 | −0.06 | −0.15 | −0.29 |
| Average D50 (mm) | 41.7 | 40.7 | 41.6 | 42.9 | 32 | 19.8 | 9.1 | 2.5 |
| TVFS (×10−3 m3) | +55.8 | |||||||
| Scenario | PDF P1 300 3-P2 600 2 | |||||||
| Segment | Before A-A | A-A to B-B | B-B to C-C | C-C to D-D | D-D to E-E | E-E to F-F | F-F to G-G | G-G to H-H |
| BCI (m) | −0.55 | 0.10 | 0.23 | 0.05 | −0.13 | −0.06 | −0.33 | −0.29 |
| Average D50 (mm) | 41.7 | 40.7 | 38.9 | 38.2 | 32.8 | 18.9 | 8.8 | 2.8 |
| TVFS (×10−3 m3) | +55.4 | |||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Esmaeili, T.; Sumi, T.; Kantoush, S.A.; Kubota, Y.; Haun, S.; Rüther, N. Numerical Study of Discharge Adjustment Effects on Reservoir Morphodynamics and Flushing Efficiency: An Outlook for the Unazuki Reservoir, Japan. Water 2021, 13, 1624. https://doi.org/10.3390/w13121624
Esmaeili T, Sumi T, Kantoush SA, Kubota Y, Haun S, Rüther N. Numerical Study of Discharge Adjustment Effects on Reservoir Morphodynamics and Flushing Efficiency: An Outlook for the Unazuki Reservoir, Japan. Water. 2021; 13(12):1624. https://doi.org/10.3390/w13121624
Chicago/Turabian StyleEsmaeili, Taymaz, Tetsuya Sumi, Sameh A. Kantoush, Yoji Kubota, Stefan Haun, and Nils Rüther. 2021. "Numerical Study of Discharge Adjustment Effects on Reservoir Morphodynamics and Flushing Efficiency: An Outlook for the Unazuki Reservoir, Japan" Water 13, no. 12: 1624. https://doi.org/10.3390/w13121624
APA StyleEsmaeili, T., Sumi, T., Kantoush, S. A., Kubota, Y., Haun, S., & Rüther, N. (2021). Numerical Study of Discharge Adjustment Effects on Reservoir Morphodynamics and Flushing Efficiency: An Outlook for the Unazuki Reservoir, Japan. Water, 13(12), 1624. https://doi.org/10.3390/w13121624









