3-D Numerical Study of a Bottom Ramp Fish Passage Using Smoothed Particle Hydrodynamics

Abstract

Worldwide, the overwhelming number of man-made barriers in fluvial systems has been identified as one of the major causes of the reported staggering average declines of migratory fish. Fish passages have been shown to help mitigate such problems. Close-to-nature types of fish passages, such as bottom ramps, bypass channels, and fish ramps can be used to minimize the impact of artificial steep drops (e.g., weirs) on the migration of aquatic fauna, especially in cases of low-head barriers. This study focuses on the characterization of the flow pattern in a bottom ramp. A 3-D numerical model based on the meshless smoothed particle hydrodynamics (SPH) method was successfully validated and then employed for the simulation of turbulent free-surface flow in a straight channel with complex geometry. The effects of bed roughness, channel slope, and flow rate were quantified in terms of flow depth, velocity fields, and area‒velocity ratios. During the study, several new tools were developed, leading to new functionalities in pre-processing, solver, and post-processing which increase the applicability of DualSPHysics in the field of eco-hydraulics.

1. Introduction

Migratory freshwater fish populations are in continuous decline [1], indicating the unsuccessful attainment of the good ecological status goal set by the European Water Framework Directive. This mainly results from the overwhelming number of existing barriers in freshwater systems that hamper the bi-directional movement of fish [2]. As a mitigation measure, fish passages can be employed. These vary from more technical types (e.g., vertical slot fishways) to close-to-nature types (e.g., bottom ramps and slopes, bypass channels, and fish ramps) [3].

Fish passages, especially more technical ones with more uniform geometry, have been the subject of many studies. Guidelines on their design, operation, and applicability have been defined [4,5].

Physical hydraulic models of fish passages improved from scaled models with uniform geometry [6] to full-scale complex geometry models [7,8].

Moreover, numerical models that allow faster and cost-efficient characterization of flows have been developed, ranging from depth-averaged 2-D models [9,10,11,12] to fully 3-D models [13,14,15,16]. Recently, the smoothed particle hydrodynamics method (SPH) has been demonstrated to be a suitable tool for such investigations as it can accurately simulate turbulent free-surface flows and their interaction with solids with complex geometries [14,17].

The SPH method was initially developed for astrophysics [18], but it was later extended to multiple fields of application related to fluid dynamics [19,20,21]. DualSPHysics [22] is a fully 3-D numerical model based on the meshless SPH method. This open-source SPH solver is known for offering high performance on CPU and graphics processing unit (GPU) based computing systems as it is optimized for both architectures [23]. The initial focus for applications with DualSPHysics has been on wave generation [24,25] and its interaction with coastal structures with good results [26,27]. However, this code has then been applied successfully to hydraulic problems such as runoff on sloping terrain [28], dam safety [29], fish passage constructions [14,30], added mass and damping coefficient [31], and drag coefficient analysis in channels [32].

Especially relevant for the present investigation are studies where SPH models were applied in turbulent open channel flows over rough boundaries. In [33], the 2D Lagrangian form of the Navier‒Stokes equation was solved, in which a drag-based formulation was used on an effective roughness zone near the bed to account for the roughness effect of bed spheres, and an improved sub-particle-scale model was applied to account for the effect of turbulence. In [34], open-source code, SPHysics (i.e., the predecessor of Dual SPHysics), was used to simulate experimental shallow free surface turbulent flow over a rough bed made of uniformly sized spheres placed in a rectangular hexagonal pattern. The numerical model was modified with a turbulent closure based on the mixing length approach, and a drag force term was added into the momentum equation to account for the rough boundary. In [35], an improved boundary treatment was proposed to characterize bed roughness based on the ghost boundary particles. Finally, [36] brought SPH to a level that can be applied to simulate turbulent open channel flows over and within natural porous gravel beds. To achieve this, improvements were made with regards to turbulence modelling, open boundaries, and treatment of the rough interface boundary between the porous bed and the overlying free-flow.

The goal of the present work was to study the applicability of the SPH-based code DualSPHysics to provide fish passages design criteria, with the main focus on bottom ramps. The study was based on the idea of retrofitting a small weir located on the river Radušnica, Slovenia, into a bottom ramp. Improvements of the software were attained by introducing several new functionalities of DualSPHysics, which allowed quantification of turbulent 3-D shallow free-surface flow over a ramp. We expect that the results of this work will provide valuable information for the future development of close-to-nature fish passages and prove the applicability of DualSPHysics for eco-hydraulics studies.

The structure of the paper is as follows: Section 2 gives basic information on the study site and a brief overview of the SPH method and the DualSPHysics features; Section 3 presents validation cases; Section 4 describes the numerical setup and presents the main results of the present study; Section 5 includes conclusions and ideas for further work.

2. Materials and Methods

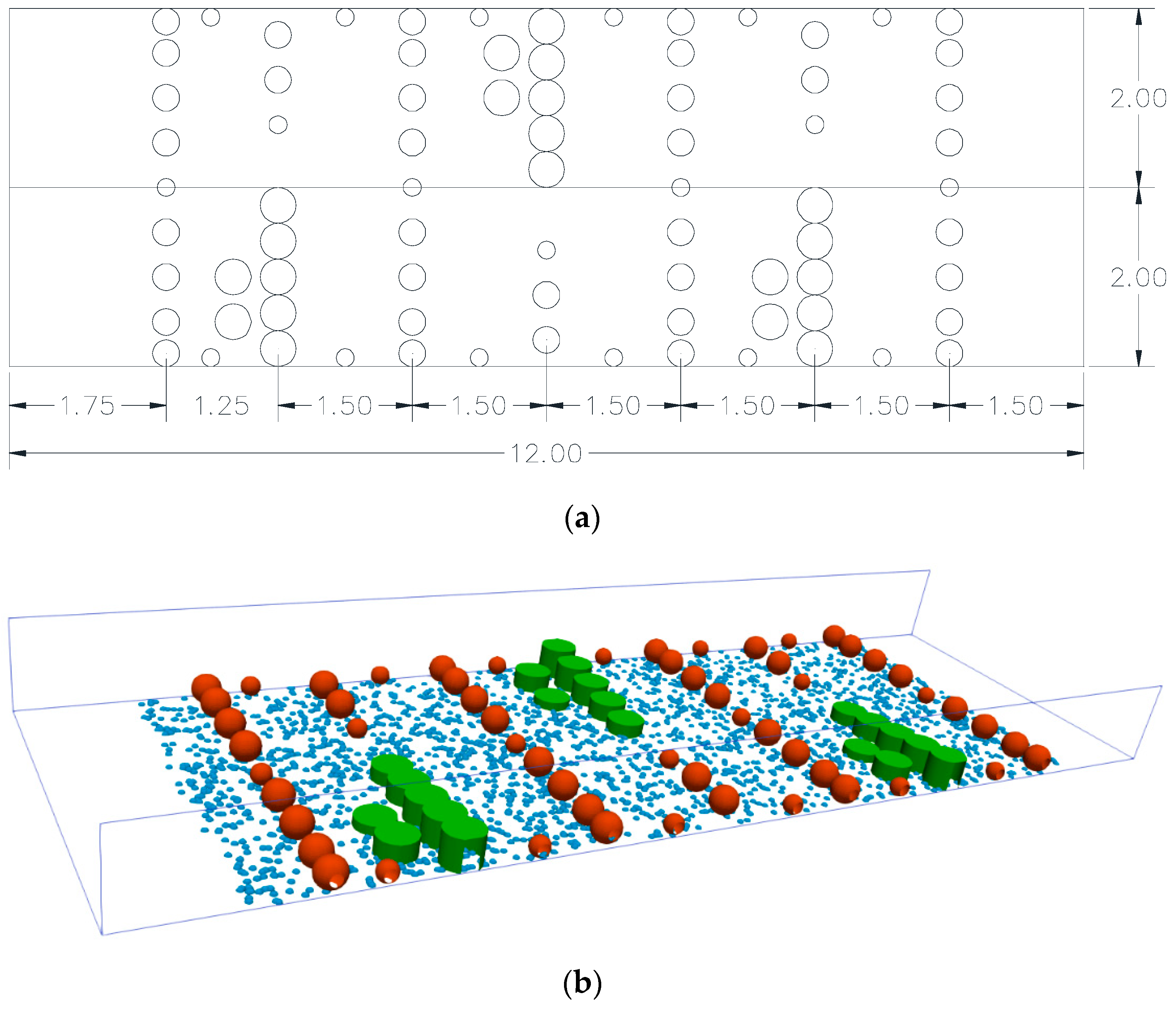
2.1. Study Site

This work focuses on a possible configuration of a bottom ramp that could be used to convert a steep drop of the existing weir at the Radušnica stream in Slovenia into a milder slope in order to restore fish migration as much as possible. The average slope of the observed stream is I = 1.5%.

The 1.3 m high concrete weir spans the entire 4 m width of the stream and is followed by several cascades with wooden sills (Figure 1). In this section, a series of ramps is proposed, with each ramp having a length of L = 10 m. Upstream, a gently meandering semi-natural channel with an average main section width of 2 m can be observed with a sequence of riffles and pools. The stones in the nearby natural reach of the stream have a diameter of up to 0.3 m.

No detailed hydrological data exist for the Radušnica stream; thus, some of the main parameters had to be estimated based on our field observations performed during low flow conditions. Average inflow velocity u = 0.5 m/s was calculated from the surface velocity that was measured upstream of the weir using wooden floats, employing the relation from our previous work on shallow flows [37]. Average water depth H = 0.1 m was also measured at the weir, leading to a discharge of approximately Q = 0.2 m³/s. It was estimated that typical and high flows would amount to approximately 0.4 and 0.6 m³/s, respectively. All the main input data for the model were measured. Channel width (B) water depth (H), and average velocity of the flow (u) were measured at the weir, average slope (I) of the stream was determined from existing geodetic data, while the shape, size, and distribution of substrate elements were measured upstream of the weir. Note that substrate elements in Figure 1 (i.e., rocks between sills, downstream of the weir) are larger than those present in the non-regulated sections of the stream.

2.2. SPH Method and DualSPHysics

This section gives a very short overview of SPH and relevant DualSPHysics characteristics. More details are given in [22].

2.2.1. Main Formulation of the SPH

SPH is a Lagrangian meshless method that discretizes a continuum using a set of material points, called particles. The discretized Navier–Stokes equations are integrated at the location of each particle, according to the physical properties of surrounding particles. The set of neighboring particles is determined by a distance-based function with an associated characteristic length, called smoothing length h. At each time step, new physical quantities are calculated for all particles, which then move according to these updated values. The effect the neighboring particles have on an individual particle is weighted depending on their distance from that particle, using a kernel function W and the smoothing length. The ratio h/dp = 2 is used in numerical simulations included in this study, where dp is the initial inter-particle distance. The governing equations in SPH are the continuity equation (expressing the conservation of mass) and the momentum equation (expressing the conservation of momentum).

The governing equations are Navier‒Stokes equations for a compressible fluid. The continuity equation in Lagrangian form can be written as:

$$\frac{d\rho }{dt}=-\rho \nabla \times v$$

(1)

where $d$ denotes the total or material derivative, $v$ is the velocity vector, and $\rho$ is density.

The momentum equation in Lagrangian form can be written as:

$$\frac{dv}{dt}=-\frac{1}{\rho }\nabla P+\mathsf{\Gamma }+f$$

(2)

where $P$ is pressure, $\mathsf{\Gamma }$ denotes the dissipation terms, and $f$ represents accelerations due to external forces, such as the gravity.

In the SPH formalism, the discrete form of the continuity equation at point a with position r_a reads [18]:

$$\frac{d\rho }{dt}={\rho }_a{\displaystyle \sum }_b\frac{m_b}{{\rho }_b}{v}_{ab}\times {\nabla }_a{W}_{ab}+D_a$$

(3)

where $W_{ab}=W\left(r_a-r_b,h\right)$ and ${\left(·\right)}_{ab}={\left(·\right)}_a-{\left(·\right)}_b$. The second term on the right is a numerical density diffusion term [38].

In the SPH formalism, the discrete form of momentum equation reads:

$$\frac{dv}{dt}=-{\displaystyle \sum }_b{m}_b\left(\frac{P_a+P_b}{{\rho }_a{\rho }_b}\right)\nabla W_{ab}+\langle {\mathsf{\Gamma }}_a\rangle ++f$$

(4)

where a symmetric SPH operator has been used that guarantees conservation of momentum [39] for the pressure term.

In the SPH formulation implemented in DualSPHysics, density and pressure are coupled by means of an equation of state allowing for weak compressibility of the fluid based on the numerical speed of sound [40]:

$$P=\frac{c_s^2{\rho }_0}{\gamma }\left[{\left(\frac{\rho }{{\rho }_0}\right)}^{\gamma }-1\right]$$

(5)

where $\gamma$ is the polytropic index (usually 7 for water, as is the case in the present study), ${\rho }_0$ is the reference density, and the numerical speed of sound is defined as $c_s=\sqrt{\partial P/\partial \rho }$. A numerical speed of sound $c_s$ is chosen based on a typical length scale and timescale of the domain which allows for much larger time steps within explicit time integration than would be possible with a physical speed of sound [40] with $c_s=10{\Vert v\Vert }_{max}$, where ${\Vert v\Vert }_{max}=\sqrt{g{h}_0}$ with $h_0$ the initial fluid height in the domain, a variation in density of up to about 1% generally occurs.

2.2.2. DualSPHysics

DualSPHysics is a 3-D SPH open-source code based on the weakly compressible formulation of SPH. It includes many features and below are only reported the ones that are more relevant to the present study, i.e., the viscosity model, turbulence treatment, density diffusion terms, and boundary conditions.

Modeling viscosity is achieved through an artificial diffusive term that is added to the momentum equation to reduce oscillations and stabilize the SPH scheme. Due to its simplicity, an artificial viscosity formulation is often used as a physical viscous dissipation term with an associated coefficient α. Based on scaled flume experiments, the default value of this coefficient in DualSPHysics is α = 0.01 [41].

The presence of an artificial viscosity term alone is not sufficient to model turbulent effects that commonly arise in river flow. To mitigate this issue, the large eddy simulation sub-particle scale model (SPS), as described by [42], using Favre averaging in a weakly compressible approach, is implemented in DualSPHysics. The SPS stress tensor $\tau$ is defined in Einstein notation over superscripts i, j and modelled via an eddy viscosity closure as:

$$\frac{{\tau }^{ij}}{\rho }=2{\nu }_{SPS}\left(S^{ij}-\frac{1}{3}{S}^{ii}{\delta }^{ij}\right)-\frac{2}{3}{C}_l{\mathsf{\Delta }}^2{\delta }_{ij}{\left|S^{ij}\right|}^2$$

(6)

Here, ${\nu }_{SPS}={\left[C_s\mathsf{\Delta }\right]}^2{\left|S^{ij}\right|}^2$, where $C_s=0.12$ is the Smagorinsky constant $C_l=0.0066$, $\mathsf{\Delta }$ is the particle spacing, and $\left|S^{ij}\right|=1/2{\left(2S^{ij}{S}^{ij}\right)}^{1/2}$, where $S^{ij}$ is an element of the SPS strain tensor.

The use of a density diffusion term in the SPH method is necessary to reduce the density fluctuations associated with this method that can be aggravated in long-term simulations. The density diffusion term proposed by [43] with coefficient 0.1 is used to perform the long simulations in this study.

Finally, boundary conditions for the riverbed and channel sides can be modeled in two ways. Dynamic boundary conditions (DBC) are represented by fixed particles with density computed from the continuity equation and pressure obtained from the equation of state [44]. When using DBC, an unphysical gap between the fluid and the solid boundaries appears, lowering the accuracy of the pressure prediction at the boundaries. To alleviate this, a second approach called modified dynamic boundary conditions (mDBC) has recently been added [30], with the density of boundary particles obtained from “ghost nodes” cleverly positioned within the fluid domain.

In the present investigation, several new features were added to DualSPHysics to increase its functionality. These improvements can be summarized as:

Pre-processing: randomly generated bed roughness elements; variables, conditionals, and lists to improve input XML files; clipping functions to manage complex geometries for mDBC normal;

Post-processing: flow depth (several options for several layers of fluid), vectors of velocity fields; area-velocity ratio.

Only the most interesting features are presented, including the generation of bed roughness, flow depth, vectors of velocity fields, and area-velocity ratio. These tools are described in more detail in the corresponding sub-sections within the results section.

3. Validation

The model was validated against the experiments by Kupferschmidt and Zhu [45], and the numerical study by Baki et al. [16].

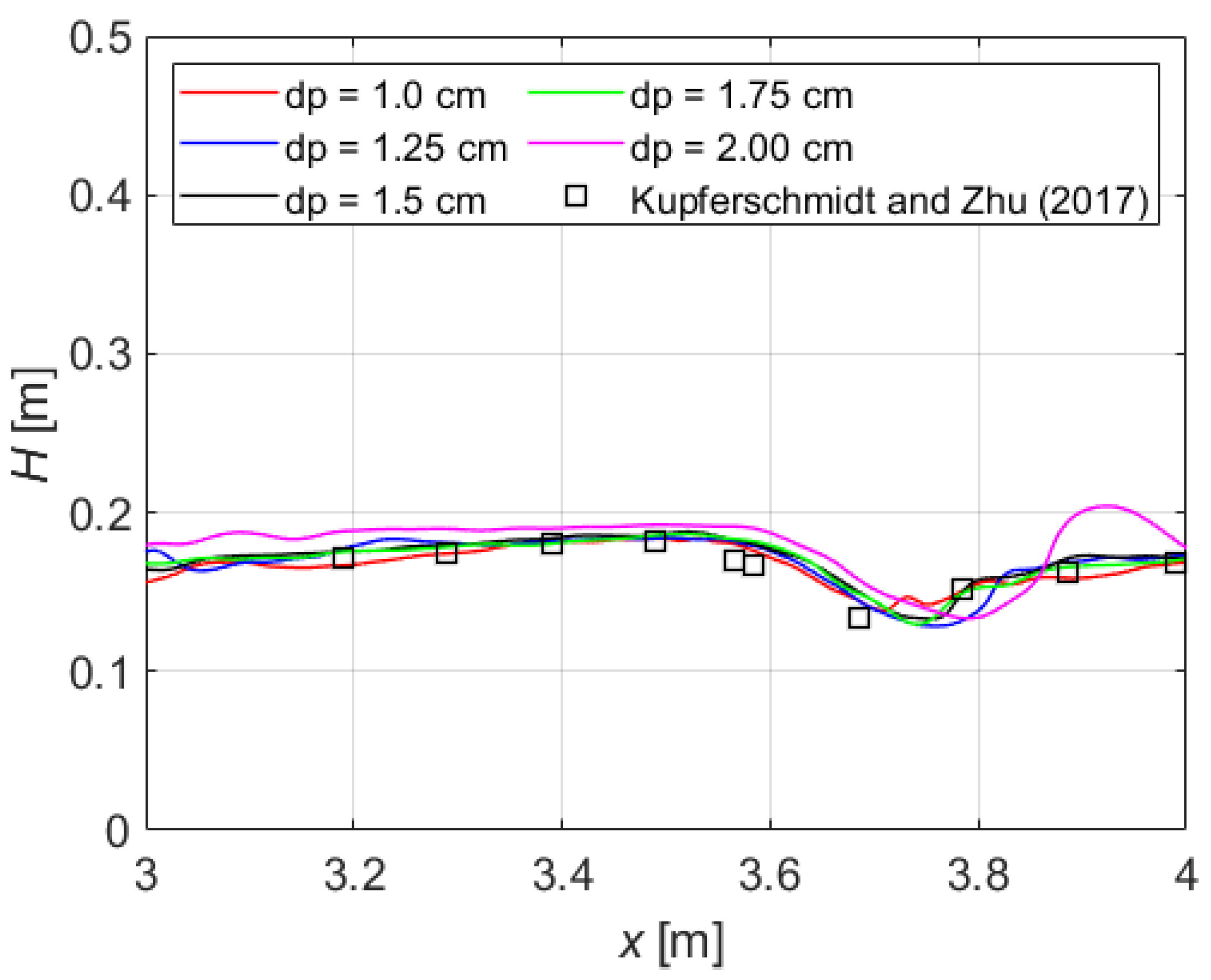
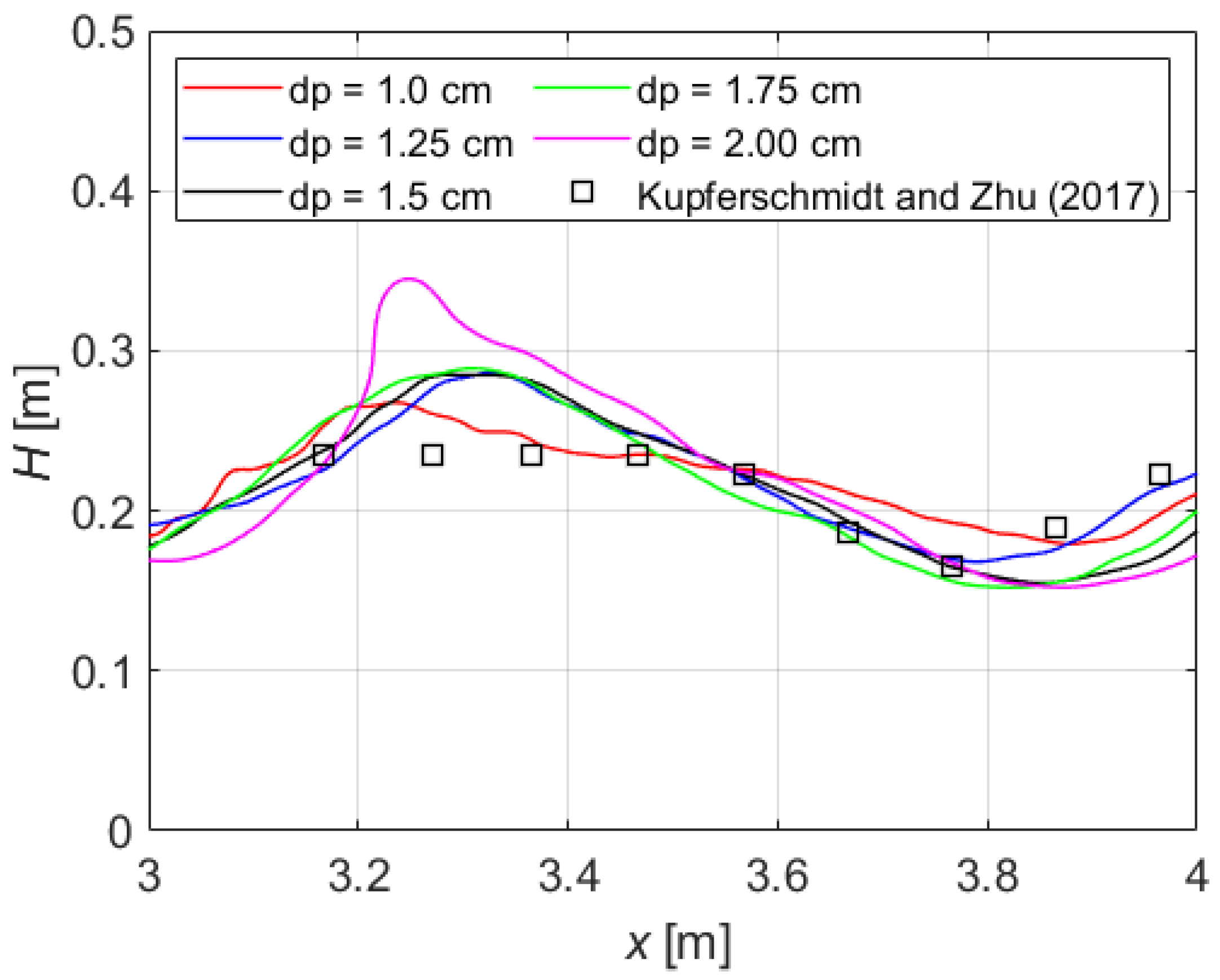
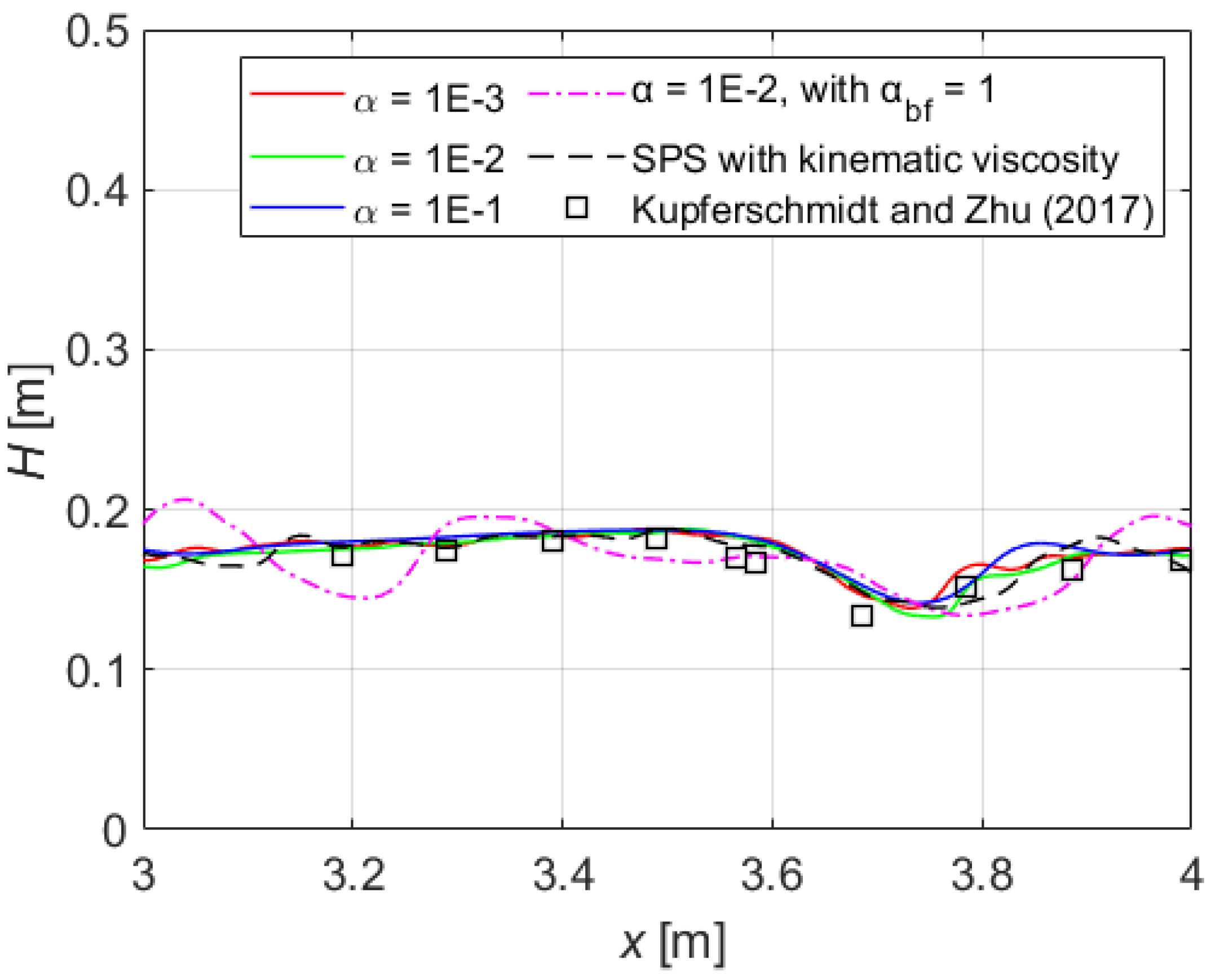
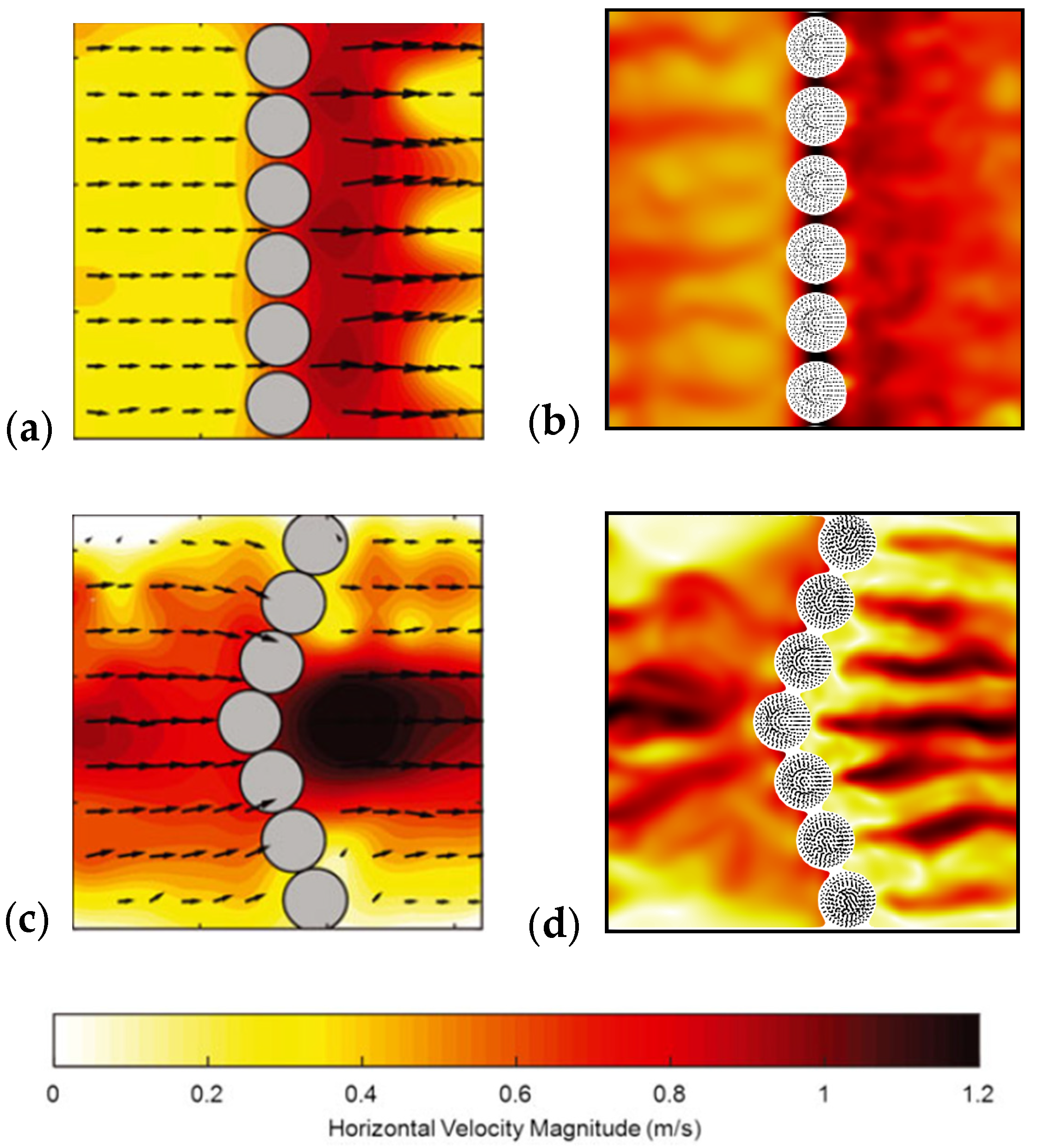
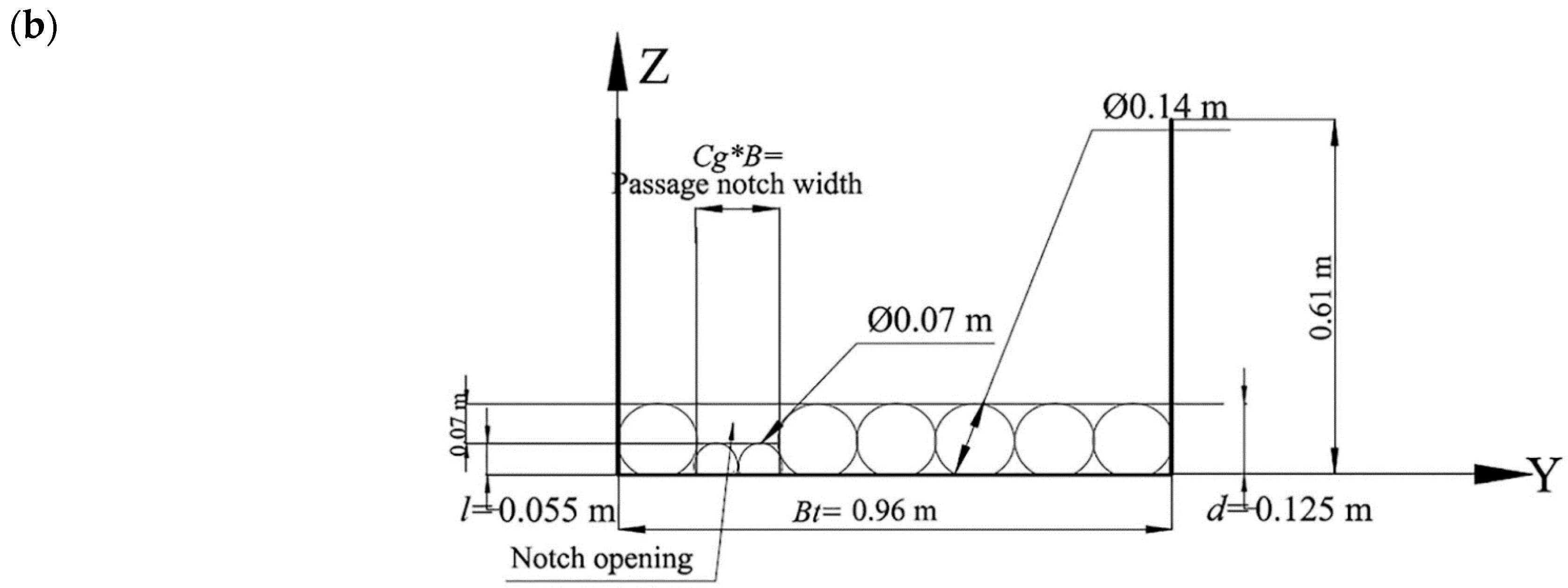
3.1. Validation against Experiments

In experiments by [45], physical models were used to study characteristics of water flow over various configurations of solid spheres in smooth rectangular channels. The spheres were partially embedded in the channel’s bottom, causing their effective height (i.e., size above the plane of the bed) to be smaller than the diameter. In the present study, the following two cases were simulated:

(1)

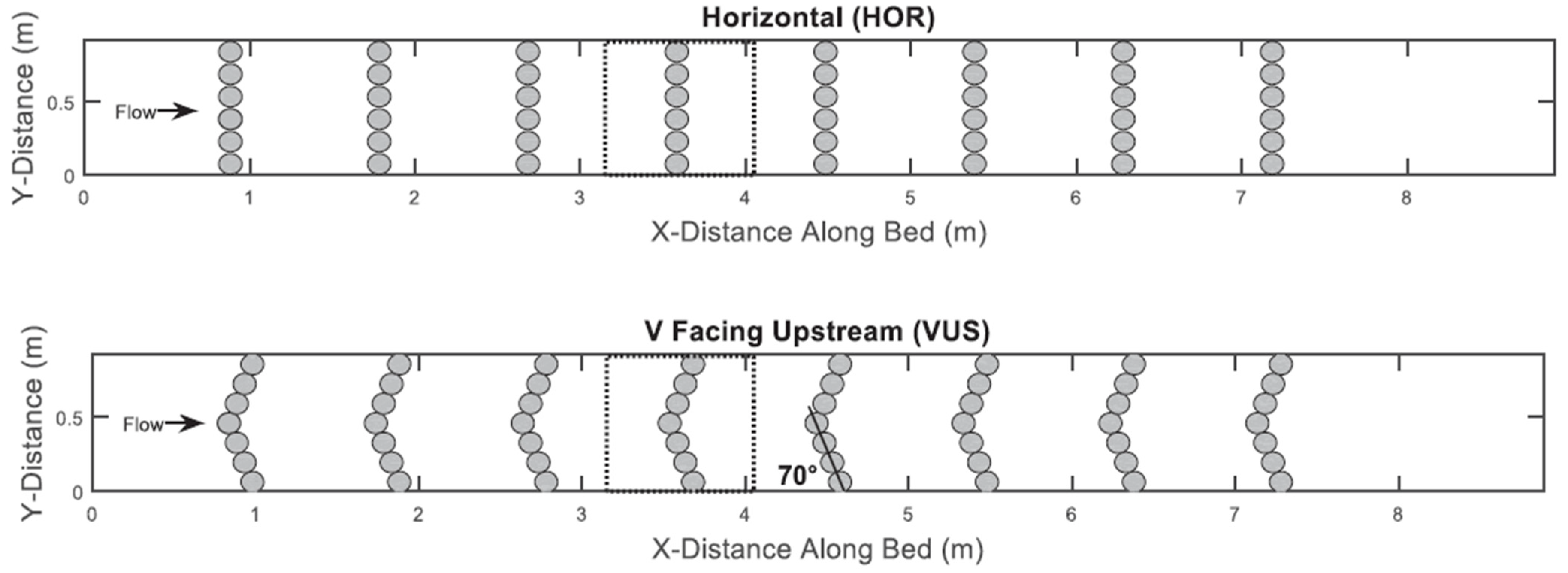
eight straight transverse lines, each including six equal spheres (having a diameter d = 0.14 m and effective height 0.125 m above the bed), with spheres located 0.01 m apart (i.e., the gap between the surfaces of two neighboring spheres, measured in the plane of the spheres’ centers), lines located 0.9 m apart, slope 3%, and discharge Q = 0.060 m³/s (denoted “HOR“ by the authors),

(2)

eight V-shaped formations, each including seven equal spheres (having a diameter d = 0.14 m and effective height 0.125 m above the bed), with V-formations located 0.9 m apart, slope 3%, and discharge Q = 0.120 m³/s (denoted “VUS“ by the authors).

Following the methodology in [45], the present study focused on water surface elevations and horizontal velocity magnitudes in the vicinity of the fourth line of spheres (Figure 2).

Several different parameters were analyzed, including the initial particle spacing dp (1, 1.25, 1.5, 1.75, 2 cm), the artificial viscosity coefficient α (0.001, 0.01, 0.025, 0.05, 0.1), the inclusion of the SPS turbulence model with a kinematic viscosity value of 10⁻⁶ m²s, and the effect of viscosity at the boundaries through the parameter denoted α_bf (the default value in this work being α_bf = 0). Comparisons are given in Figure 3, Figure 4 and Figure 5.

There is a good agreement between the numerical model and both experimental configurations, noted with the correlation coefficient R² = 0.88 and 0.81 for the HOR and VUS case, respectively.

Figure 5 shows the effect of various viscosity treatments. Results obtained using the observed values of α or the SPS turbulence model with a kinematic viscosity value of 10⁻⁶ m²s are very similar. Furthermore, employing a boundary viscosity coefficient different from zero resulted in a poorer agreement between the model and the experiment. Based on the above considerations, the following settings were used in all the subsequent simulations: dp = 1.5 cm, α = 0.01, and α_bf = 0.

Velocity magnitudes at the selected plane of the observed area are given in Figure 6. In the HOR case (Figure 6a,b), the measured average velocities increased from approximately 0.3 m/s upstream of the spheres to approximately 0.9 m/s downstream of the spheres (Figure 6a), while the model velocities increased from 0.5 to 1.0 m/s (Figure 6b). In the VUS case, measured average velocities in the main flow region increased from approximately 0.8 m/s upstream of the spheres to approximately 1.2 m/s downstream of the spheres (Figure 6c), while the model velocities increased from 0.9 to 1.2 m/s (Figure 6d). Note that figures only show the selected slice of the selected observation area and that sampling points in the physical model were spaced at 0.07 m intervals in the direction of flow and 0.10 m intervals across the width of the flume, while measurements were performed at correlation values of 40%. In contast, resolution of the SPH model was greater. In addition, Figure 6b,d show instantaneous velocity filed at the end of simulation, not average velocities. With this in mind, the model results show acceptable agreements for both HOR and VUS configurations.

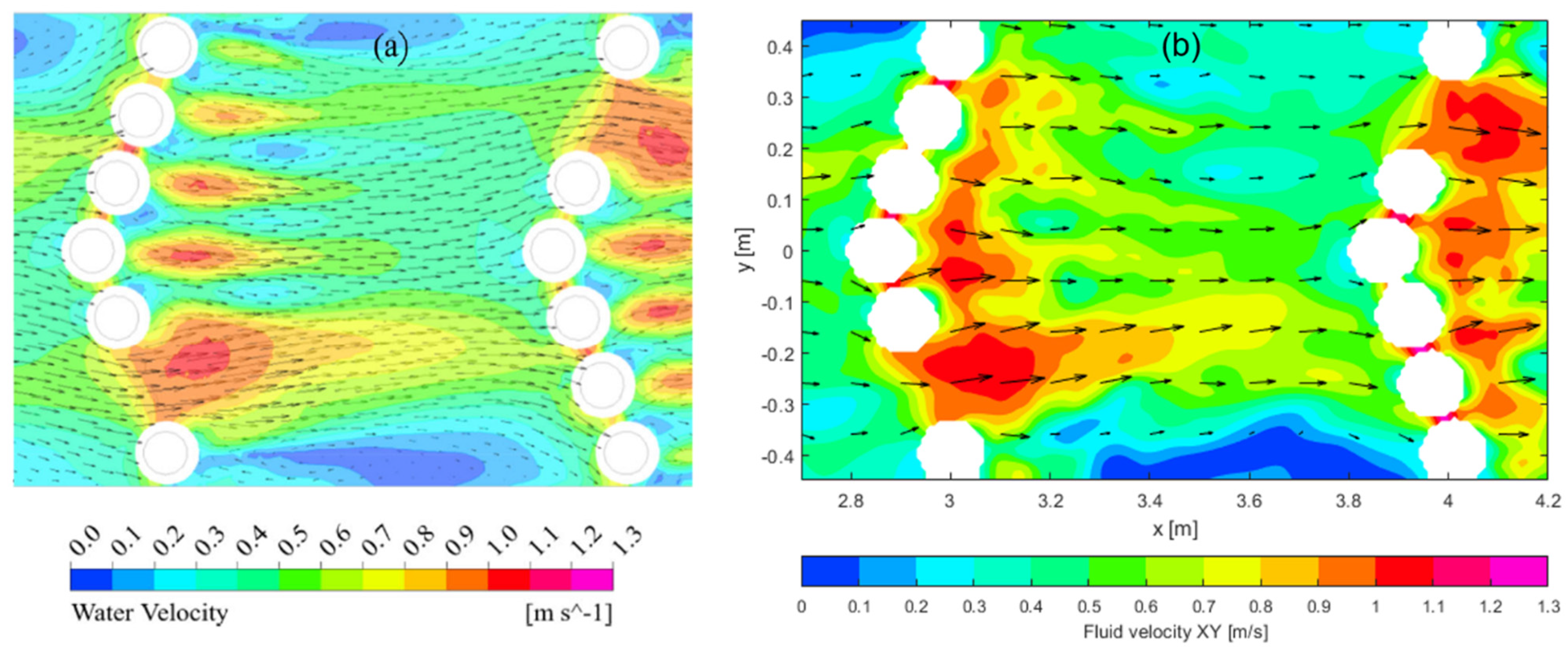
3.2. Validation against a Numerical Study

As a way of validating our model even further, some of the simulations by [16] were reproduced. We focused on the case with notches on alternating sides with flow Q = 0.060 m³/s, slope 3%, depth H = 0.17 m, denoted as “Configuration I—simulation A4” by the authors (Figure 7).

Figure 8 shows the velocity field at z = H/2 plane. In the reference study (Figure 8a), velocities in the main jet over the notch reached up to 1.1 m/s, with smaller jets flowing through the gaps between the spheres. There were two areas of low velocity (<0.1 m/s), larger at the right wall and smaller at the left wall. Velocity vectors in the observed pool were mostly horizontal, i.e., flow remained mostly longitudinal. In our model (Figure 8b), most of these characteristics were reproduced, except that there was a discrepancy in the velocities of the flow approaching the notches. In the reference study, these approach flow velocities were mostly around 0.4 to 0.6 m/s, while our model showed them to be 0.3 to 0.4 m/s. Note that the color schemes in Figure 8a,b are not completely identical and that the reference considered here is not an experimental study but rather another numerical simulation. Our model results are comparable to those presented in the reference study.

4. Results

4.1. Numerical Setup

In the present study, the model simulated a steady open channel turbulent flow with complex geometry. A 3-D model was applied to model a 12 m long and 4 m wide turbulent open channel flow representing a 10 m ramp with two additional 1 m sections to provide enough distance between both upstream and downstream boundaries and the observed area. Thus, the testing section included a reach from x = 1 to x = 11 m. The geometry of the model included a straight rectangular channel with various spheres (radius of 0.1 m and 0.15 m) and cylinders (radius 0.2 m, height 0.1 to 0.35 m) to mimic boulders and stones. The position of these elements was selected to create areas of different hydraulic characteristics (migration paths and resting zones) while maintaining a fairly uniform distribution of spheres and cylinders that provided a 2 m wide meandering main flow.

In addition, bed roughness elements consisting of 3000 randomly generated spheres with a radius of 0.03 m were employed to simulate pebbles (Figure 9).

Three different slopes of the ramp were simulated, I = 1.5, 3, and 5%, respectively. Each slope was modeled using a horizontal channel (i.e., I = 0 slope) with a correspondingly tilted gravity vector, following the methodology by [46]. For example, a constant slope of I = 1.5% was represented with a horizontal channel and the gravity vector components g_x = 0.147, g_y = 0, and g_z = −9.809 m/s². In majority of cases, the slope was set to I = 1.5% to equal the average slope of the observed stream, while I = 3% and I = 5% cases were simulated to make the comparisons.

Inflow and outflow were applied using open boundaries with buffers, described by [46]. At the inlet and outlet cross-sections, uniform velocity fields and constant water surface elevations were imposed. Three discharges were investigated, each with the same inlet velocity of u = 0.5 m/s, but with different flow depths: H₁ = 0.12 m (amounting to Q₁ = 0.24 m³/s), H₂ = 0.21 m (amounting to Q₂ = 0.42 m³/s), and H₃ = 0.30 m (amounting to Q₃ = 0.60 m³/s).

Modified dynamic boundary conditions (mDBC) were applied to simulate the interfaces between the fluid and solids. The default values of the main computational parameters were used. With the initial inter-particle distance set to dp = 1.5 cm, typical simulations included a total of 4.8 million particles and covered 30 s of physical time. With the initial velocity of the fluid equal to the value of the inflow velocity, these 30 s were enough to provide steady flow conditions. The convergence of various flow rates (calculated by the employment of a post-processing tool that determines the flow of fluid particles volumetrically) is shown in Figure 10. The different applied flowrates became constant after 30 s of simulation.

The number of particles ranged from a total of 3.6 million in the Q₁ case (of which 2.2 million were fluid particles) to 6.1 million in the Q₃ case (of which 4.7 million were fluid particles). Simulations were performed on a single GPU (GeForce GTX 1080 Ti).

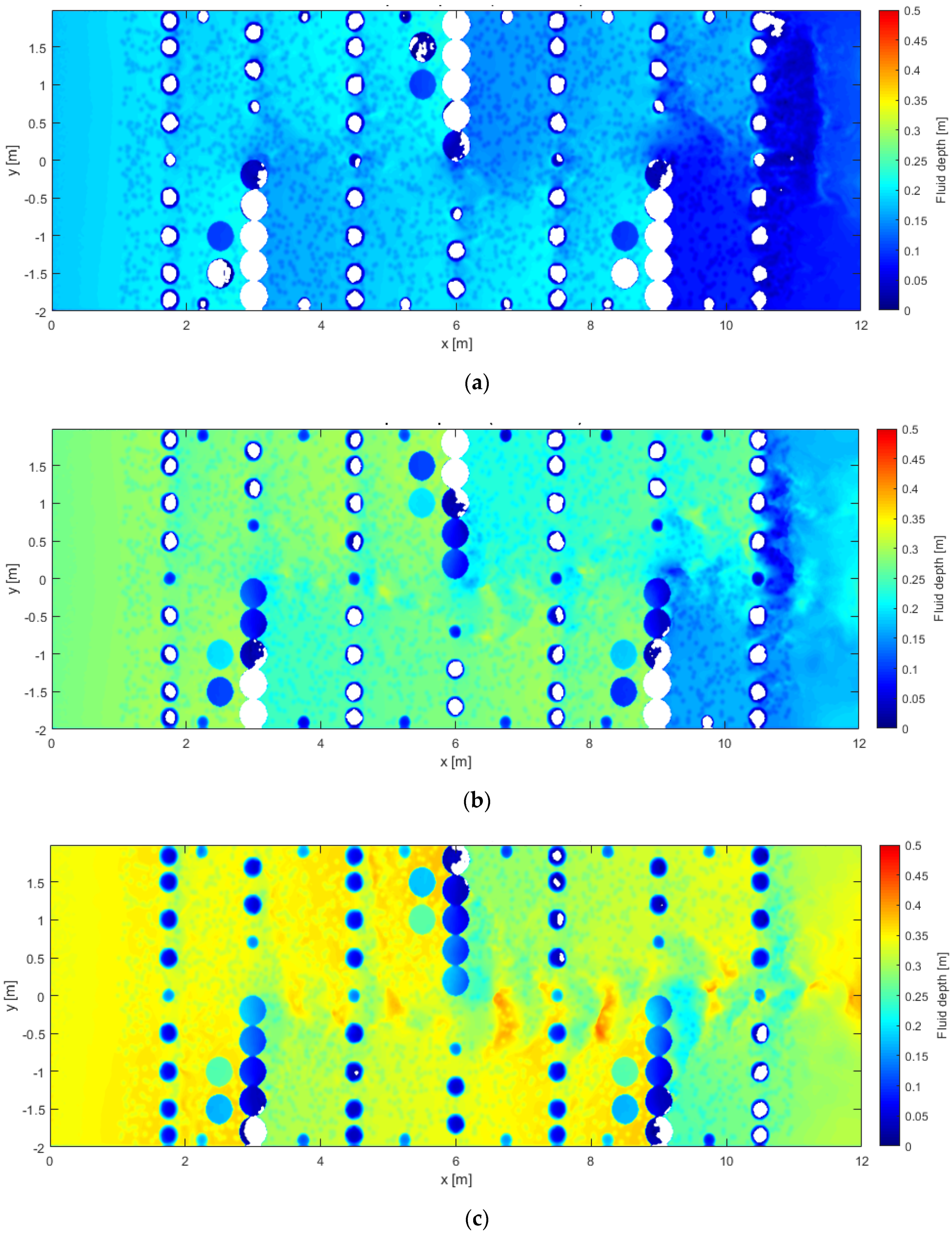
4.2. Depth Calculation Tool

The DualSPHysics solver and its post-processing tools are mainly focused on modelling the interaction between waves and fixed or floating structures in coastal and ocean engineering applications [24,25,26,29,47] where only the free-surface elevation of the fluid needs to be calculated and the depth is not required. However, obtaining the depth in hydraulic applications where the bottom has many irregularities is essential. The new post-processing tool allows the depth of the flow to be quantified in several different ways, i.e., as a fluid surface elevation, depth over the solid boundary, or height of the fluid between different solids at a given location. A SPH interpolation kernel is used to calculate the mass value at different heights from the surrounding fluid particles. These mass values allow the calculation of the position of the transition between fluid and fluid-free (or vice versa). The threshold value is half the mass of a fluid particle. In this way, the height of the water column is calculated, which may be divided into multiple sections due to the presence of obstacles. Herein, we present the flow depths that are determined from the height of a water column above the solid object at a given location, with this solid object representing either the channel bed, a roughness element, or a substrate element (Figure 11). Note that Figure 11 does not show water surface elevation above the z = 0 plane but rather the actual depth of the flow at a given location, with white areas representing dry areas.

Figure 11 shows that depth in the upstream part of the ramp increases due to the obstacles in that area. However, the average drop remains practically constant, as it amounts to 0.18 m − 0.12 m = 0.06 m in the Q₁ case, 0.27 m − 0.21 m = 0.06 m in the Q₂ case, and 0.35 m − 0.30 m = 0.05 m in the Q₃ case. Note that undulated surface (i.e., waves) of the main flow is visible in the Q₂ and Q₃ case (see arch-like shapes in the region x = 5 to 8 m, y = −0.75 to 0 m). The new depth tool can provide information on the depth of water flowing over the obstacles. These results can then be compared to the minimum water depth requirements of target fish species and thus contribute to the fish passage efficiency evaluation. However, to create a more close-to-nature ramp, substrate elements should be further repositioned to provide more diverse flow conditions.

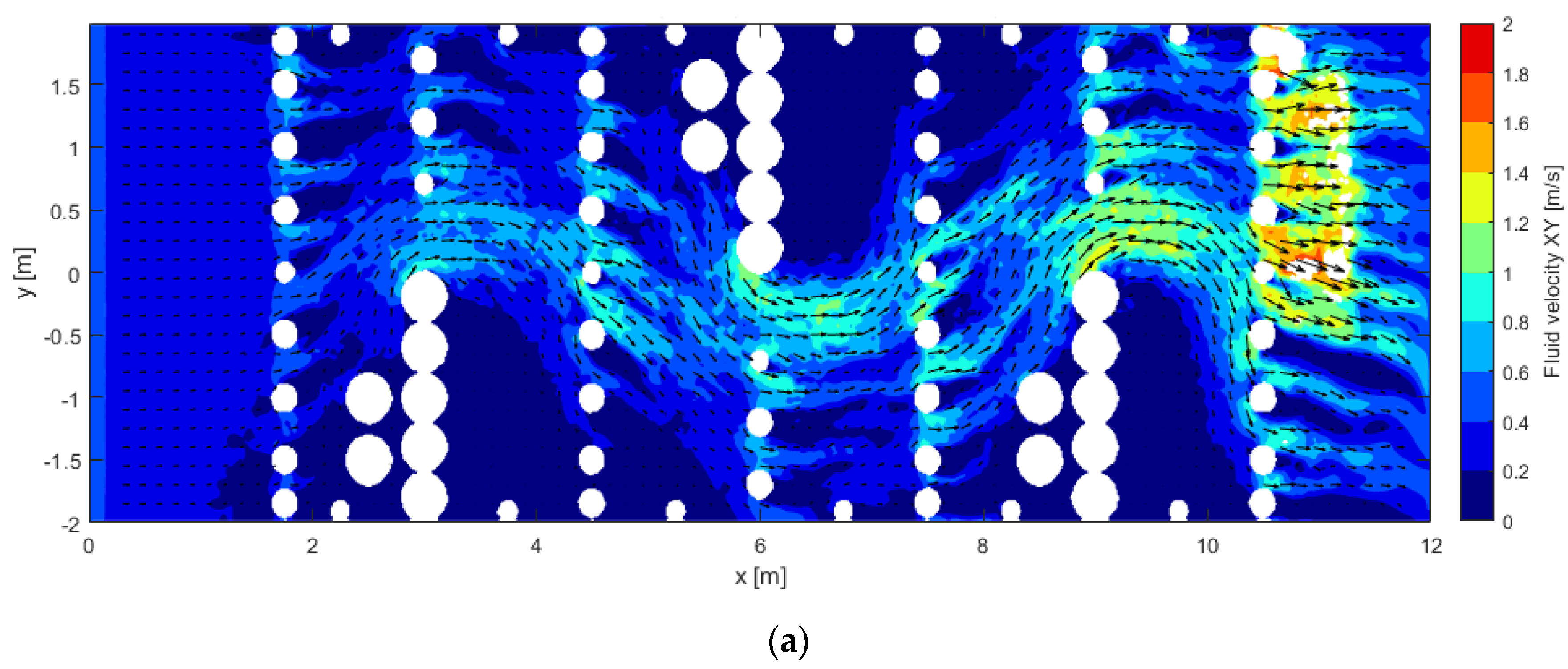
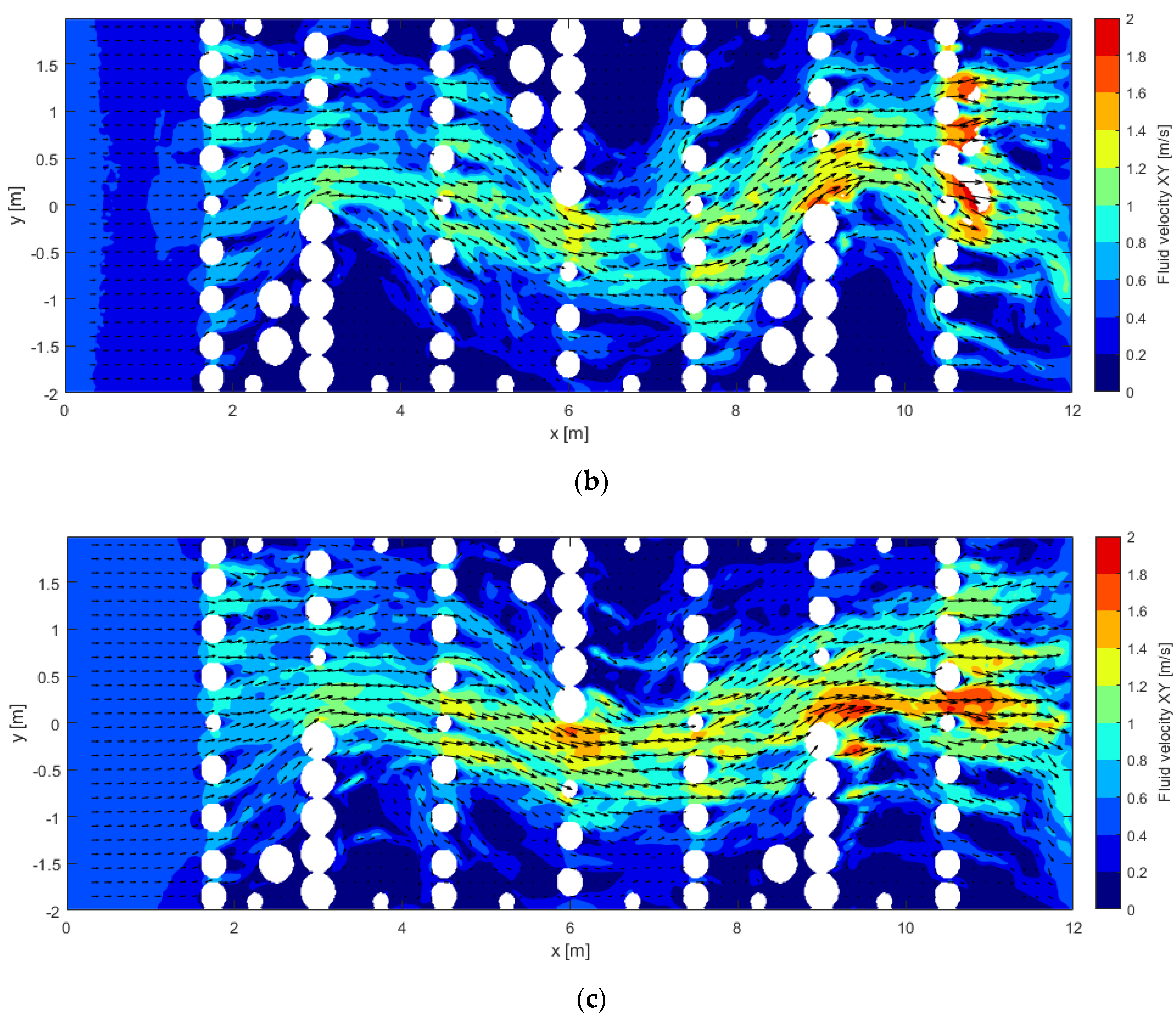
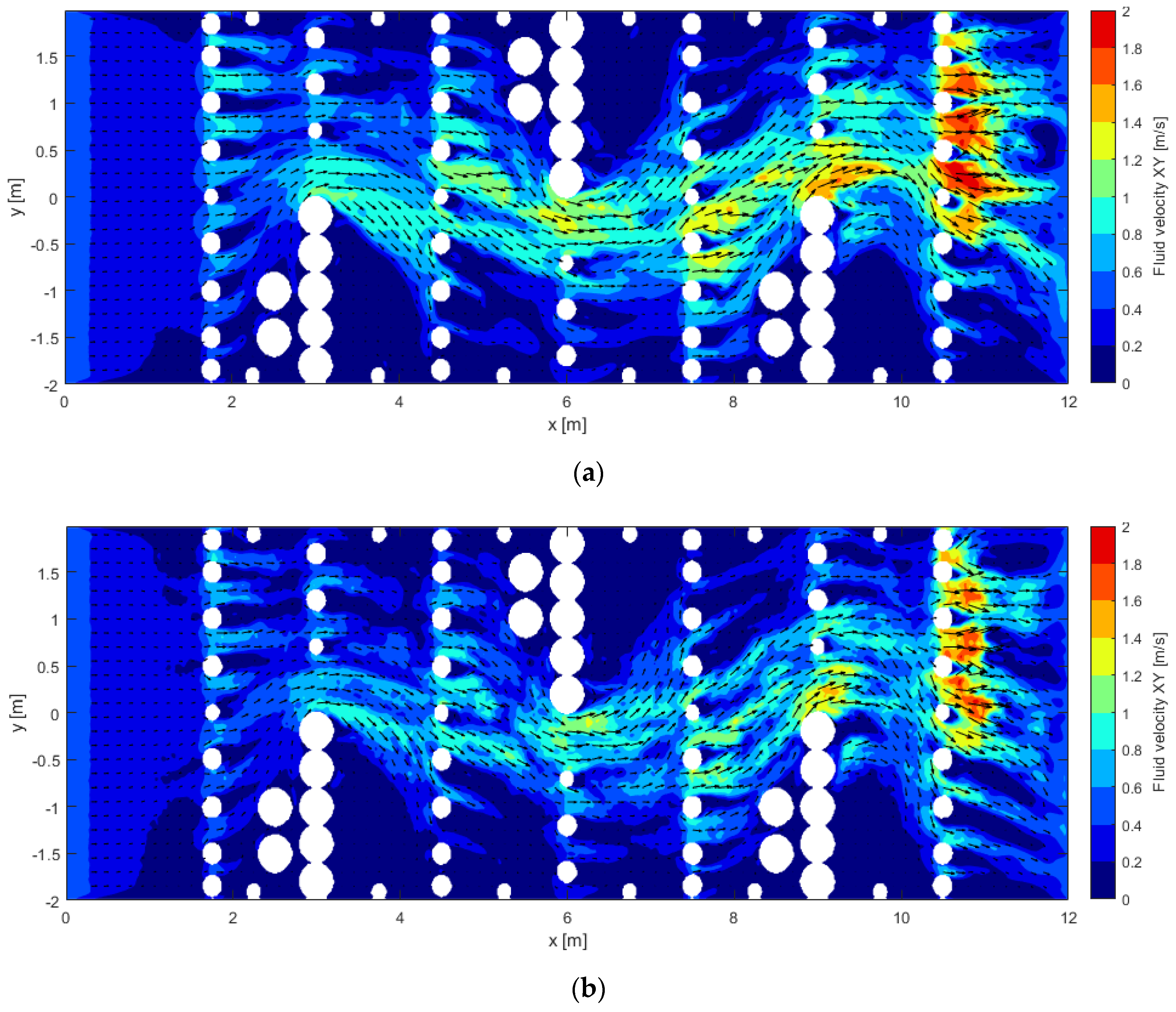
4.3. Velocity Field Tool

Characterization of the flow can be performed in different ways. Figure 12 shows longitudinal velocity u in different vertical cross-sections along the ramp. This figure shows that uniform inflow conditions (Figure 12a) change into significantly more diverse flow along the ramp, both in terms of velocities and depths.

Another method of flow characterization is the evaluation of velocity fields at selected planes above the channel bed. Results of the new velocity tool represent velocity vectors at the selected z = H/2 plane for all three discharges (Figure 13).

Figure 13 indicates the effect of the flow rate. It shows that the increase of flow rate from Q₁ to Q₃ results in higher maximum velocities (from 1.5 to 2 m/s), larger jets, and smaller areas of low velocities (u < 0.4 m/s). It can be expected that a less uniform distribution of obstacles would lead to a more diverse flow pattern.

Note that the present study does not attempt to address the turbulence in great detail and the resolution used in the simulations may not be enough to capture all the effects of turbulence around the smaller elements. The use of a more advanced turbulence model would be necessary to correctly model the effect of the small eddies that may appear on the bottom, but this issue is beyond the scope of the present work.

4.4. Bed Roughness Tool

The pre-processing tool (named GenCase) included in the DualSPHysics package is an advanced software that can generate hundreds of millions of particles in a few seconds [48] and was successfully used to create the initial condition of the simulation of a large wave impacting an oil platform with more than 10⁹ particles [49]. The input of GenCase is a XML (eXtensible Markup Language) file where geometry of boundaries, fluid areas, and other simulation parameters are defined. The basic boundary elements (e.g., boxes, spheres, cylinders…) are explicitly defined by indicating their position and dimensions, but more complex 3-D models can also be imported from format files STL, VTK, or PLY supported by design software such as Blender or AutoCAD. These options allow the creation of complex cases, but it is not easy to create non-regular cases closer to nature.

The pre-processing improvements implemented for this work allow the XML format to be used as a programming language with variables, conditionals, loops, and subroutines. This enhancement, in combination with the random functions supported by the new syntax of the XML input file, allows the creation of cases with high complexity and a certain degree of randomness more similar to nature.

In the presented results, this tool has been employed to produce 3000 small spheres (having radius r = 0.03 m) along the observed 10 m long reach. Each of these roughness spheres is embedded into the ramp bottom, so that only its upper half is above the z = 0 plane, while the lower half is removed from the model domain (by applying another new pre-processing option of clipping). The effect of such half-sphere bed roughness elements is shown in Figure 14.

Bed roughness elements decrease the velocities in the near-bottom region, thus providing favorable conditions for benthic species.

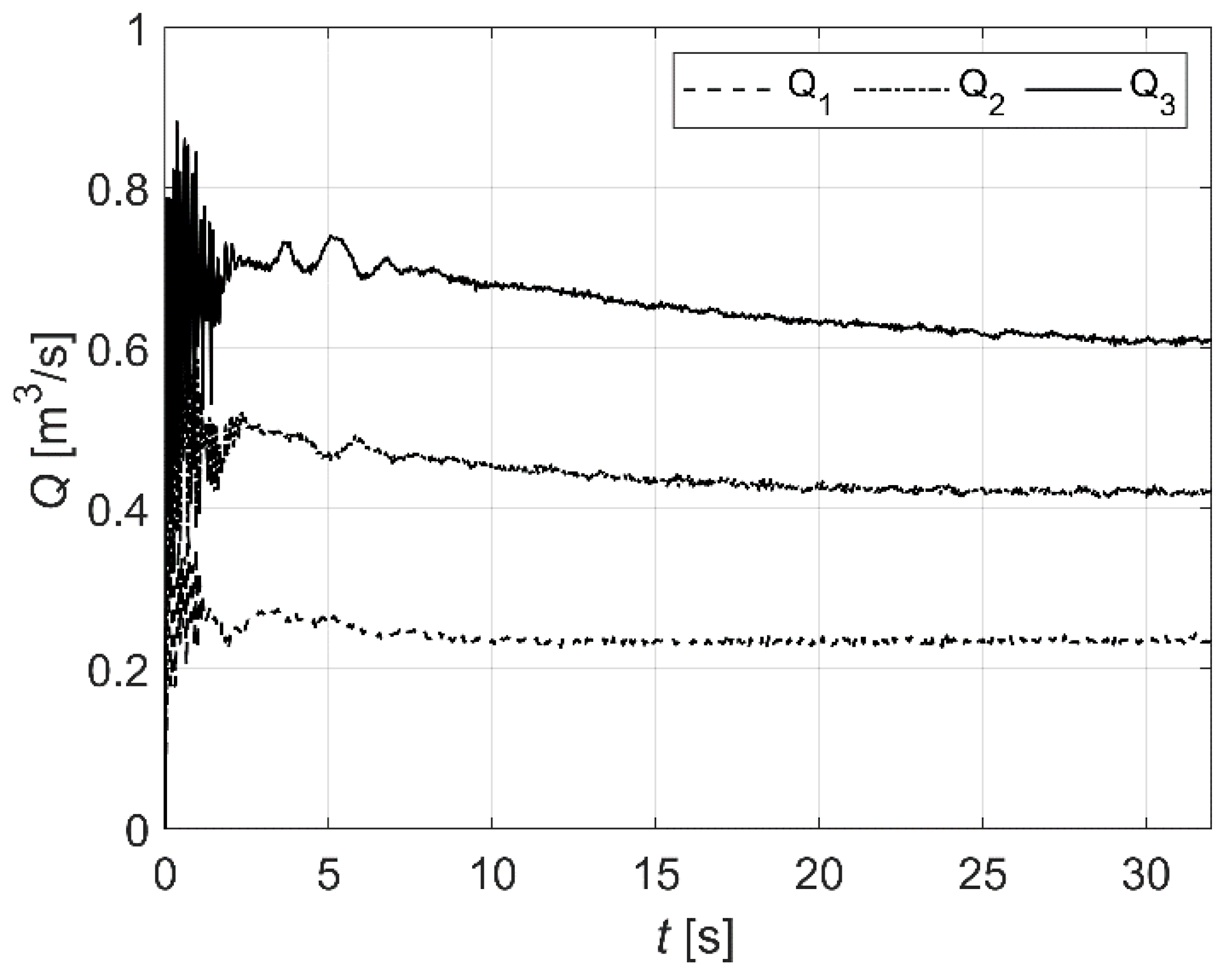
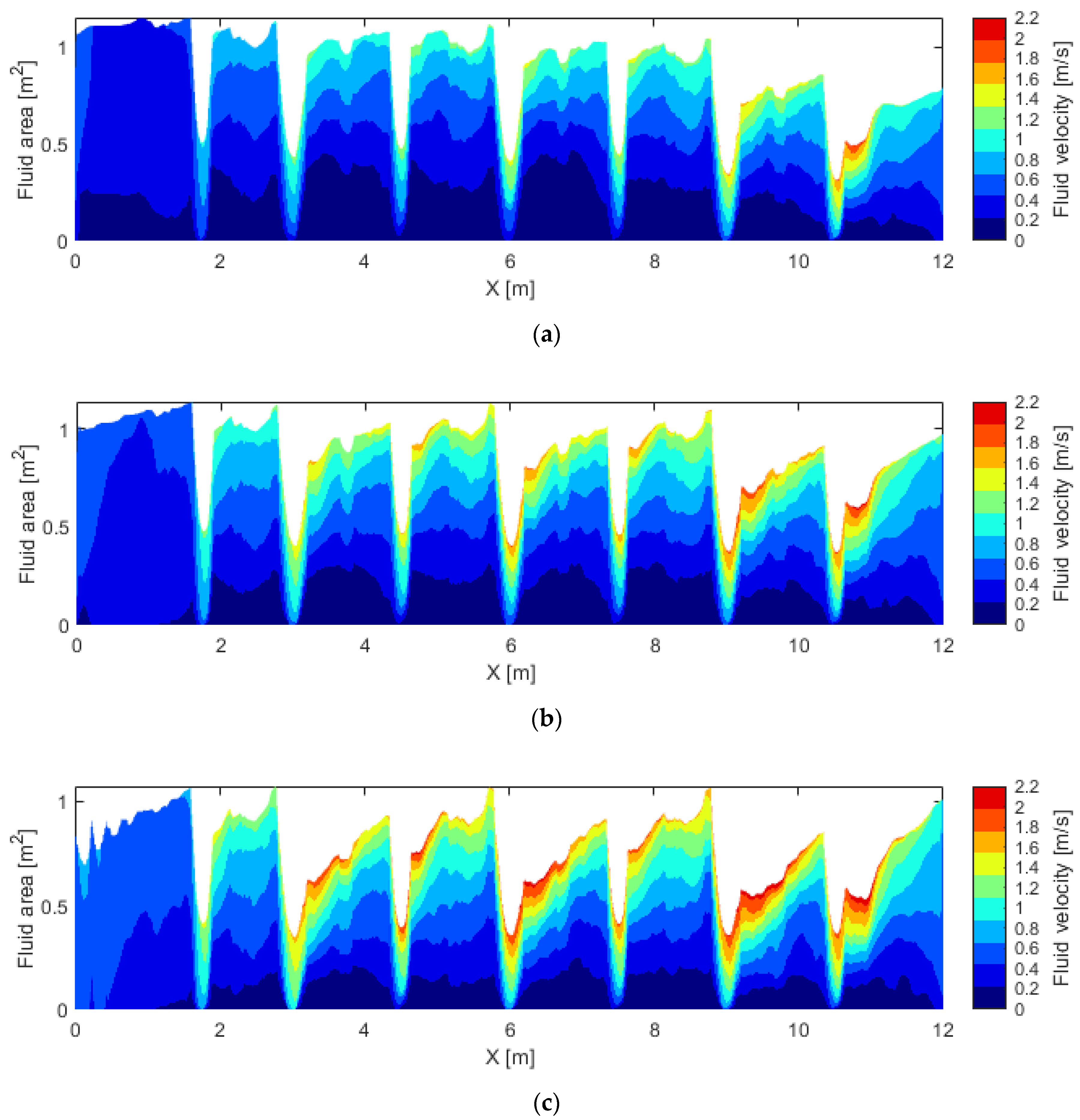
4.5. Area–Velocity Tool

The characterization of the flow can also be given as the area–velocity ratio between the cross-sectional area of the fluid at a certain location x along the channel and the velocities at the corresponding cross-section. The new area–velocity tool calculates how much of the cross-section area is occupied by a certain fluid velocity. This information is obtained with the procedure explained below. The cross-section for each x location is discretised in a regular grid of points with high resolution. Mass value at each point is computed via SPH interpolation using the mass of neighbouring fluid particles. The area represented by each point is considered fluid when the mass value reaches half the mass of a fluid particle. The same SPH interpolation is then applied to calculate the fluid velocity at the points that satisfied the above condition. In addition, the interpolated velocity is corrected when the kernel support is not complete (points close to the surface). Finally, the points considered fluid are sorted according to their velocity value. This allows the fluid areas of each cross-section to be grouped according to their velocity and to show what proportion reaches a given velocity. In the present study, this tool has been applied to investigate the effect of different slopes (Figure 15).

Figure 15 shows that area–velocity ratio corresponds to the geometry of the ramp and the resulting flow. Where there are sets of obstacles, i.e., spheres (at x = 1.75, 4.5, 7.5, 10.5 m) or cylinders (at x = 3, 6, and 9 m), the area of the fluid decreases (see white dents representing dry areas) and fluid velocity increases. In these locations, fluid area decreases from 0.5 m² at x = 1.75 m to 0.25 m² at x = 10.5 m in the Q₁ case and from 0.4 m² at x = 1.75 m to 0.3 m² at x = 10.5 m in the Q₃ case. Furthermore, in these locations, maximum fluid velocity increases from 0.8 m/s at x = 1.75 m to 1.6 m/s at x = 10.5 m for the Q₁ case and from 1.2 m/s at x = 1.75 m to 2.2 m/s at x = 10.5 m in the Q₃ case.

Figure 15 shows that steeper slopes result in higher velocities and locally smaller areas of the fluid. Moreover, straight lines of obstacles abruptly divide the flow into several sections. The area–velocity ratio in adjacent sections is similar, but it nevertheless varies along the length of the ramp.

5. Discussion

The design of an effective fish passage is a complex eco-hydraulics problem that requires the consideration of ecological and biomechanical requirements of the range of fish species present at the location. The conditions at the entrance of the fish passage should attract the fish to this area, whereas the conditions within the structure should facilitate fish passage with both minimum time delay and minimum required energy. To ensure this, the following aspects need to be taken into consideration: the different possible paths that different fish species and sizes can take during their migration along the fish pass, including the near-bottom region; the variety of flow directions, including the main region of longitudinal flow and areas of transverse flow; the frequency and size of resting areas; integration with natural upstream and downstream conditions, i.e., geometry resembling the natural conditions without abrupt transitions and with bed roughness and substrate elements similar to the ones at the actual site.

The new features of the presented SPH model provide a number of results that can be compared to the ecological capacities of the present fish, in addition to the flow velocity, which is often regarded as the only ecologically relevant result of such simulations.

6. Conclusions

The presented work shows the applicability of the SPH-based 3-D model in the field of eco-hydraulics. Successfully validated against experimental data and a similar numerical study, and with the employment of several new pre- and post-processing tools, the DualSPHysics model allowed a detailed characterization of a turbulent free-surface flow over a complex geometry bottom ramp in terms of flow depths, velocity fields, and area–velocity ratios.

The new tools allow detailed characterization of the flow, thus providing valuable information in eco-hydraulics simulations. The generation of bed roughness elements allows better prediction of specific flow conditions near the bottom. The new depth tool allows the estimation of fish passability based on the minimum water depth requirements. The new velocity field tool allows the quantification of magnitude and direction of the flow, potentially indicating backflow areas and resting zones. The new area‒velocity tool allows the quantification of the area‒velocity ratio at every location along the model and identifies potential bottleneck areas or high velocity regions.

The present study does not attempt to address the turbulence in great detail, and the resolution used here may not be enough to capture all the effects of turbulence around the smaller elements. This issue will be addressed in more detail in forthcoming studies.

Our further work will focus on the application of the presented improved functionalities of the model to design a close-to-nature ramp. The configuration of the presented ramp will be modified into a more non-uniform geometry and optimized to provide more diverse flow and thus better conditions for fish migration at Radušnica, Slovenia.